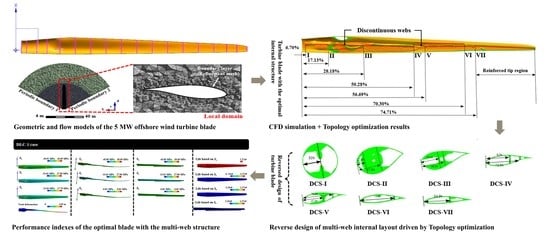
Topology Optimization-Driven Design for Offshore Composite Wind Turbine Blades
Abstract
1. Introduction
2. Analytical Preliminaries
2.1. Topology Optimization Method
2.2. CFD Model of Reference Composite Wind Turbine Blade
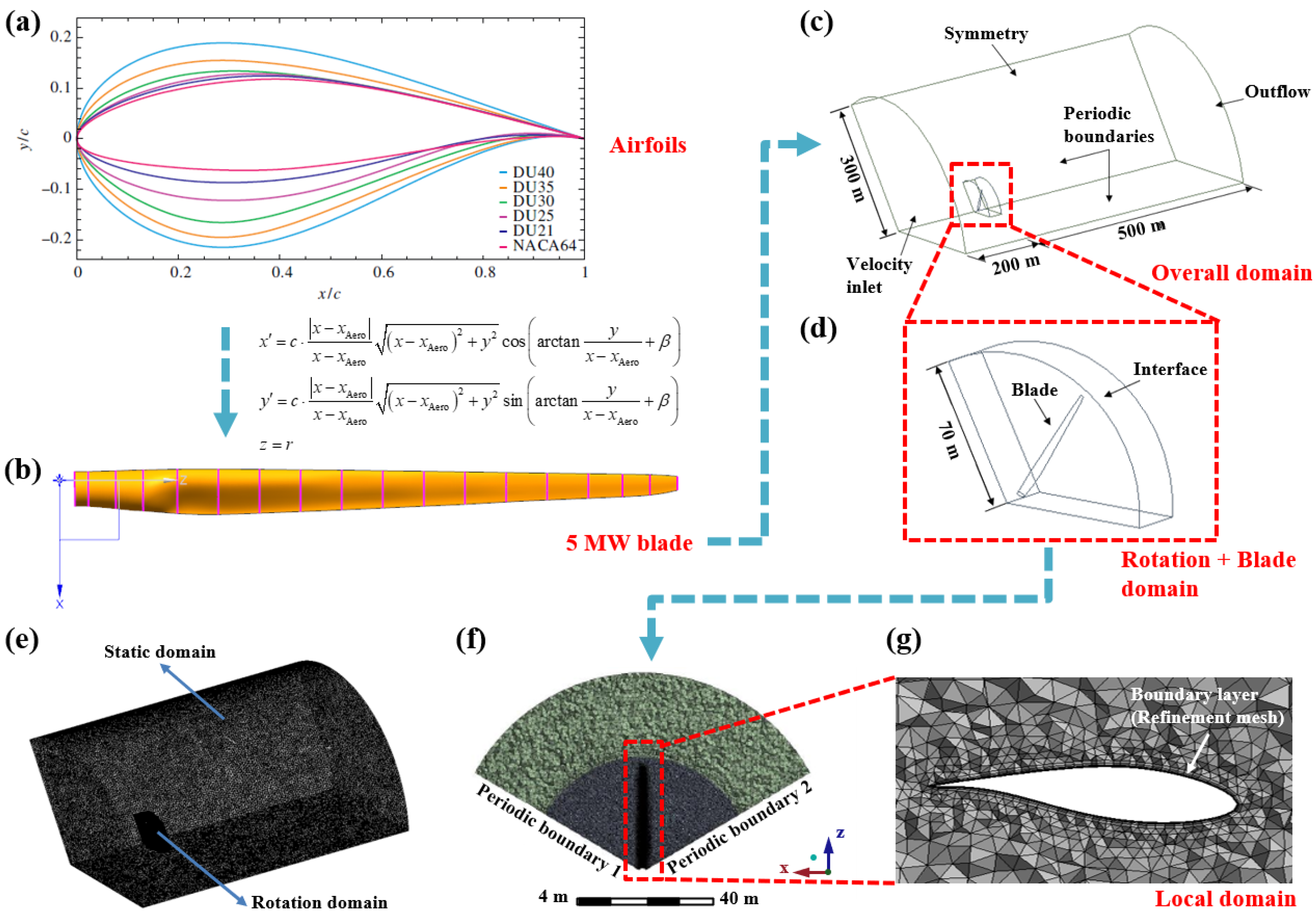
2.2.1. Control Equation, Geometric Model of Composite Wind Turbine Blade and Flow Field for CFD Simulation
2.2.2. Mesh Quality and Independence Verifications
2.2.3. Calculation Method for the CFD Simulation
2.3. Finite Element Model of Reference Composite Wind Turbine Blade
2.3.1. Mechanical Properties of Composite Materials of Wind Turbine Blades
2.3.2. Finite Element Model of Wind Turbine Blade
2.4. Design and Validation Cases of Wind Turbine Blade
- (1)
- DLC-1 (Worst working case)
- (2)
- DLC-2 (Cut-out wind speed working case)
- (3)
- DLC-3 (Shutdown working case)
3. Results
3.1. CFD Simulation of Wind Turbine Blade
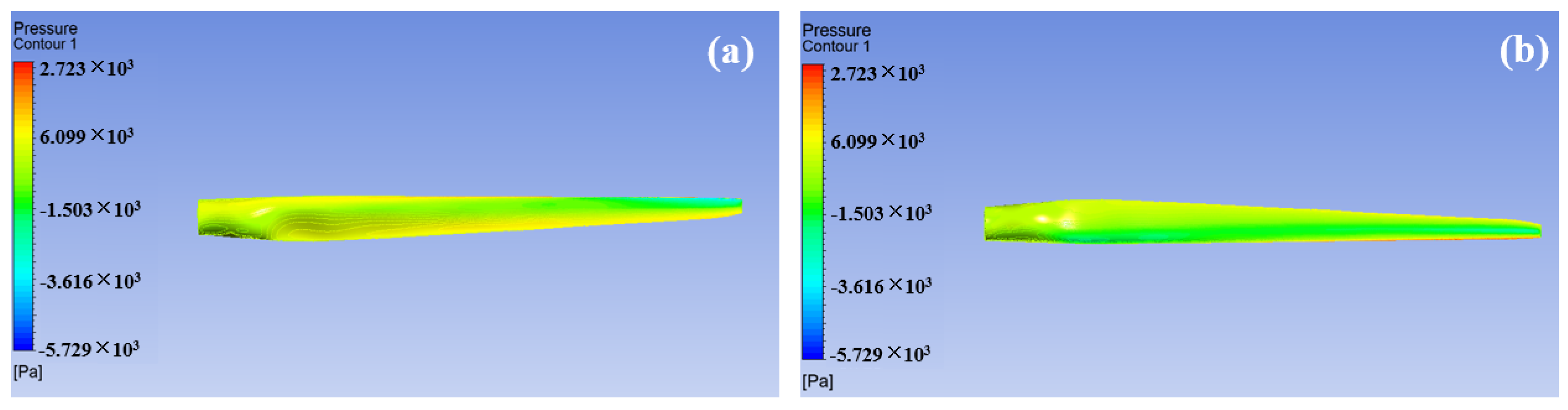
3.2. Structural Responses of Wind Pressure on the Surface of Wind Turbine Blade
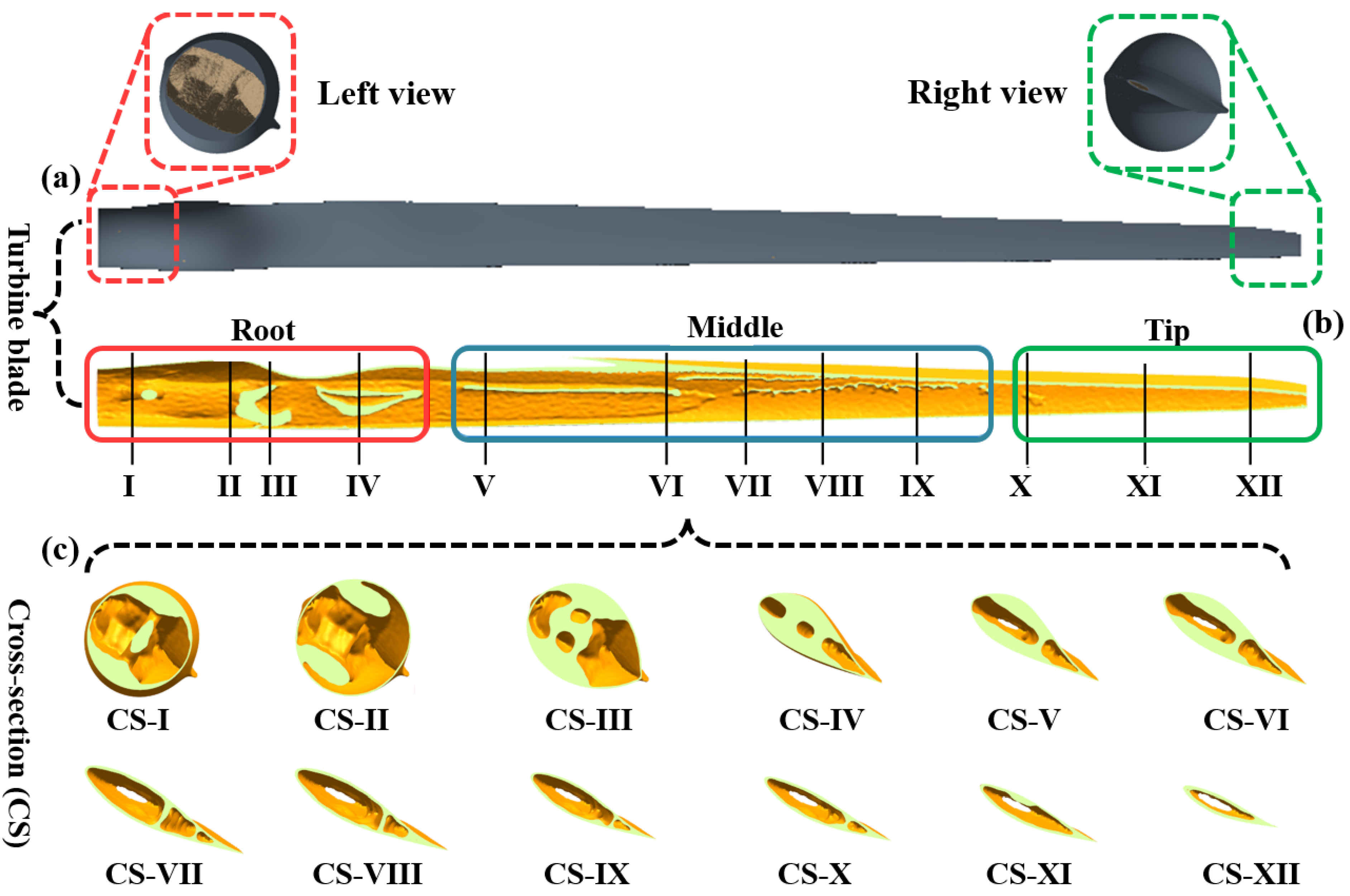
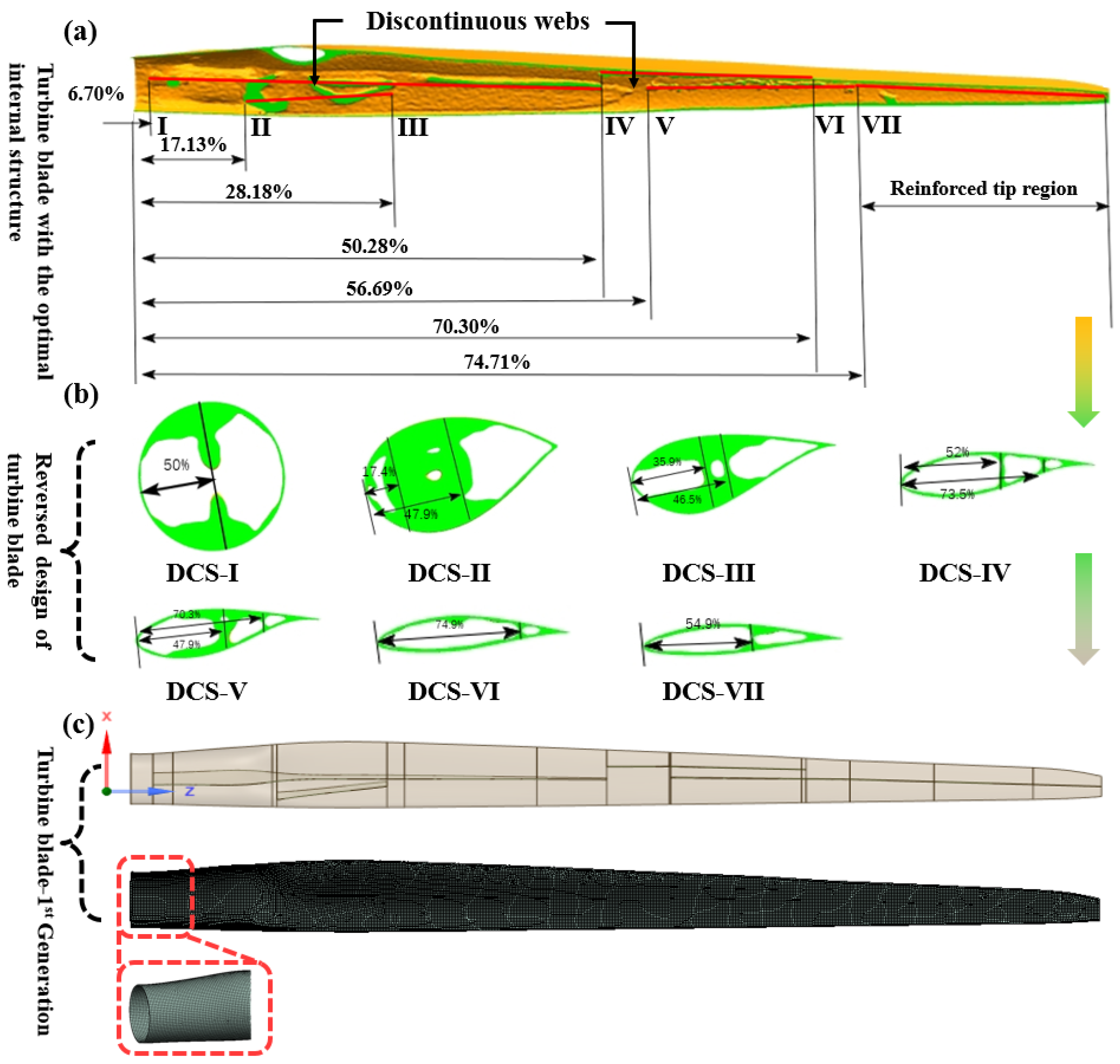
3.3. Topology Optimization Results of Internal Configuration of Wind Turbine Blade
3.4. Validation of Performance Indexes for the First Generation Wind Turbine Blade
4. Discussion
4.1. Comparison of Performance Indexes between the Novel and Reference Turbine Blades
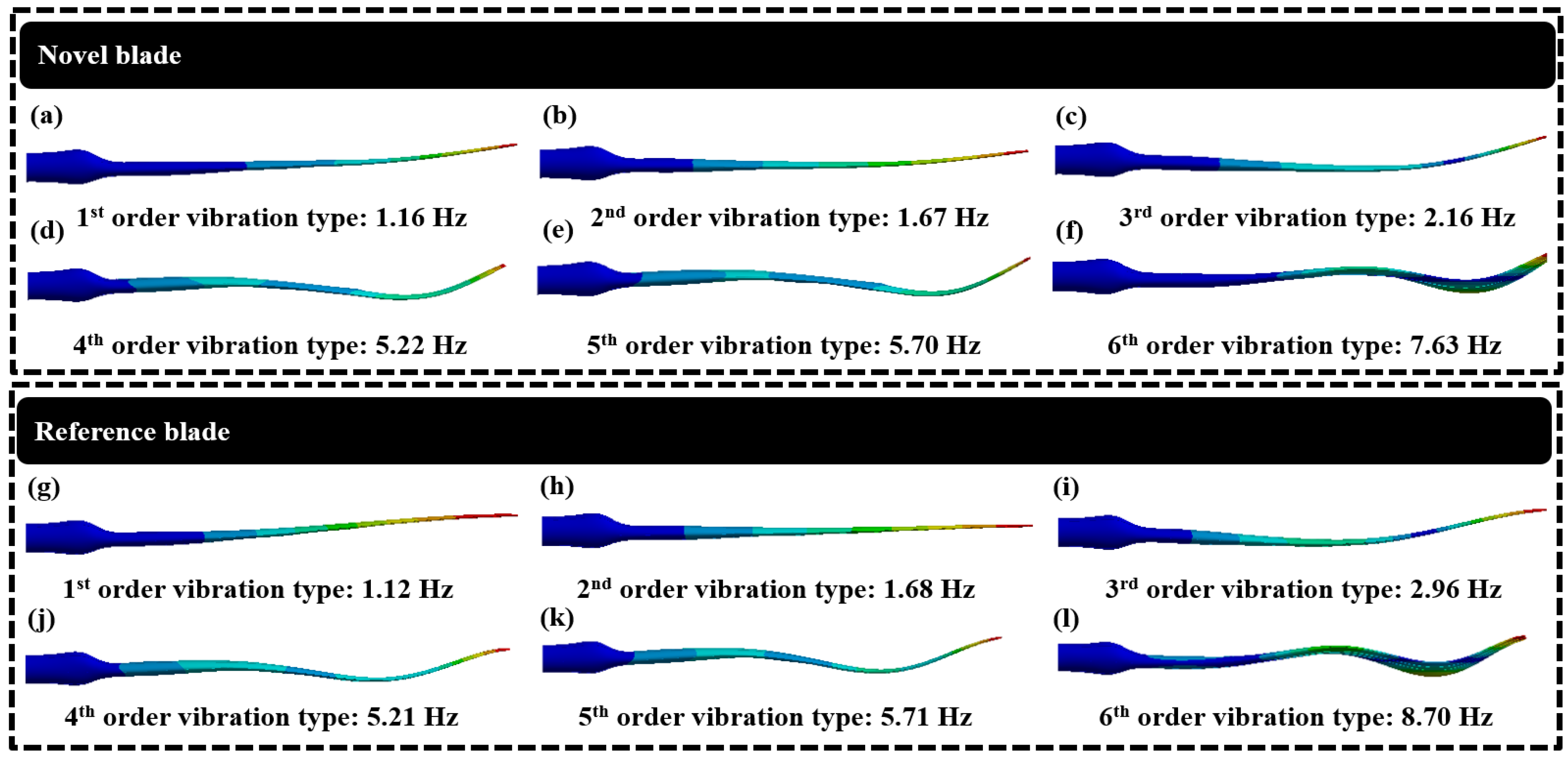
4.2. Modal Analysis of the Novel Wind Turbine Blade
4.3. Full Life Cycle Assessment of the Novel Wind Turbine Blade
5. Conclusions
- 1.
- The surface pressure was obtained based on the CFD simulation, and the two turbulence models, viz. k- SST and k-, were adopted. By comparing the output torques and power, the k- SST model was chosen to calculate the surface pressure distribution. Moreover, the simulation results obtained from the CFD were also validated in comparison with those calculated from the FAST.
- 2.
- The topology optimization model was established based on the full-scale internal structure of offshore wind turbine blade, considering stress, displacement and fatigue life constraints.
- 3.
- After the full-scale topology optimization, two multi-web layouts were theoretically obtained driven by the optimal topological configuration for the first time. By validation, the second generation optimal blade completely met all the requirements and the weight was reduced by 9.88% relative to the reference blade, which was a significant benefit in decreasing the cost of turbine blades.
- 4.
- Vibration modal and full life cycle of the novel blade were also evaluated. The first six vibration types of the novel blade were consistent with those of the reference blade, further indicating that the designed internal layout was reasonable. Moreover, the full life cycle of the novel blade is 21.9 years, theoretically verifying that the novel blade is able to service more than 20 years in the given sea domain.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oh, K.Y.; Nam, W.; Ryu, M.S.; Kim, J.Y.; Epureanu, B.I. A review of foundations of offshore wind energy convertors: Current status and future perspectives. Renew. Sustain. Energy Rev. 2018, 88, 16–36. [Google Scholar] [CrossRef]
- Liu, P.; Meng, F.R.; Barlow, C.Y. Wind turbine blade end-of-life options: An economic comparison. J. Clean. Prod. 2022, 180, 106202. [Google Scholar] [CrossRef]
- Mishnaevsky, L.; Johansen, N.F.; Fraisse, A.; Faster, S.; Jensen, T.; Bendixen, B. Technologies of Wind Turbine Blade Repair: Practical Comparison. Energies 2022, 15, 1767. [Google Scholar] [CrossRef]
- Dyrholm, M. GWEC|Global Wind Report; Global Wind Energy Council: Brussels, Belgium, 2021. [Google Scholar]
- Chou, J.S.; Chiu, C.K.; Huang, I.K.; Chi, K.N. Failure analysis of wind turbine blade under critical wind loads. Eng. Fail. Anal. 2013, 27, 99–118. [Google Scholar] [CrossRef]
- Liu, Y.; Hajj, M.; Bao, Y. Review of robot-based damage assessment for offshore wind turbines. Renew. Sustain. Energy Rev. 2022, 158, 112187. [Google Scholar] [CrossRef]
- Rafiee, R.; Hashemi, M.R. Failure analysis of a composite wind turbine blade at the adhesive joint of the trailing edge. Eng. Fail. Anal. 2021, 121, 105148. [Google Scholar] [CrossRef]
- Roh, C.; Ha, Y.J.; Ahn, H.J.; Kim, K.H. A Comparative Analysis of the Characteristics of Platform Motion of a Floating Offshore Wind Turbine Based on Pitch Controllers. Energies 2022, 15, 716. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Lian, J. Review of integrated installation technologies for offshore wind turbines: Current progress and future development trends. Energy Convers. Manag. 2022, 255, 115319. [Google Scholar] [CrossRef]
- Asim, T.; Islam, S.Z.; Hemmati, A.; Khalid, M.S. A Review of Recent Advancements in Offshore Wind Turbine Technology. Energies 2022, 15, 579. [Google Scholar] [CrossRef]
- Ibrahimbegovic, A. Flexible Blades Wind-Turbines: Giant Installations and System-of-Systems Approach to Optimizing Wind-Energy Farms. In CIGOS 2021, Emerging Technologies and Applications for Green Infrastructur; Springer: Berlin/Heidelberg, Germany, 2022; pp. 3–27. [Google Scholar]
- Zhu, J.; Cai, X.; Ma, D.; Zhang, J.; Ni, X. Improved structural design of wind turbine blade based on topology and size optimization. Int. J. Low-Carbon Technol. 2022, 17, 69–79. [Google Scholar] [CrossRef]
- Chen, J.; Kim, M.H. Review of Recent Offshore Wind Turbine Research and Optimization Methodologies in Their Design. J. Mar. Sci. Eng. 2021, 10, 28. [Google Scholar] [CrossRef]
- Naung, S.W.; Erfanian Nakhchi Toosi, M.; Rahmati, M. An Experimental and Numerical Study on the Aerodynamic Performance of Vibrating Wind Turbine Blade with Frequency-Domain Method. J. Appl. Comput. Mech. 2021, 7, 1737–1750. [Google Scholar]
- Naung, S.W.; Nakhchi, M.E.; Rahmati, M. High-fidelity CFD simulations of two wind turbines in arrays using nonlinear frequency domain solution method. Renew. Energy 2021, 174, 984–1005. [Google Scholar] [CrossRef]
- Nakhchi, M.E.; Naung, S.W.; Rahmati, M. High-resolution direct numerical simulations of flow structure and aerodynamic performance of wind turbine airfoil at wide range of Reynolds numbers. Energy 2021, 225, 120261. [Google Scholar] [CrossRef]
- Mamouri, A.R.; Khoshnevis, A.B.; Lakzian, E. Entropy generation analysis of S825, S822, and SD7062 offshore wind turbine airfoil geometries. Ocean Eng. 2019, 173, 700–715. [Google Scholar] [CrossRef]
- Mamouri, A.R.; Khoshnevis, A.B.; Lakzian, E. Experimental study of the effective parameters on the offshore wind turbine’s airfoil in pitching case. Ocean Eng. 2020, 198, 106955. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Q.; Shen, W.Z.; Pang, X.; Li, S.; Guo, X. Design, Structural optimization study of composite wind turbine blade. Mater. Des. 2013, 46, 247–255. [Google Scholar] [CrossRef]
- Ghiasi, H.; Fayazbakhsh, K.; Pasini, D.; Lessard, L. Optimum stacking sequence design of composite materials Part II: Variable stiffness design. Compos. Struct. 2010, 93, 1–13. [Google Scholar] [CrossRef]
- Zhang, Z.Y. Structural Design of Large Horizontal Axis Wind Turbine Blade Based on Fluid-Structural Interation. Ph.D. Thesis, Lanzhou University of Technology, Lanzhou, China, 2014. [Google Scholar]
- Liao, C.C.; Zhao, X.L.; Xu, J.Z. Blade layers optimization of wind turbines using FAST and improved PSO Algorithm. Renew. Energy 2012, 42, 227–233. [Google Scholar] [CrossRef]
- Song, J.; Zhang, Y.K.; Guo, X.; Hao, H.; Wen, W.D.; Cui, H.T. Topology and shape optimization of twin-web turbine disk. Struct. Multidiscip. Optim. 2022, 65, 1–20. [Google Scholar] [CrossRef]
- Rossow, M.P.; Taylor, J.E. A finite element method for the optimal design of variable thickness sheets. AIAA J. 1973, 11, 1566–1569. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Mlejnek, H.P.; Schirmacher, R. An engineer’s approach to optimal material distribution and shape finding. Comput. Methods Appl. Mech. Eng. 1993, 106, 1–26. [Google Scholar] [CrossRef]
- Joncas, S. Thermoplastic Composite Wind Turbine Blades: An Integrated Design Approach. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- Buckney, N.; Pirrera, A.; Green, S.D.; Weaver, P.M. Structural efficiency of a wind turbine blade. Thin-Walled Struct. 2013, 67, 144–154. [Google Scholar] [CrossRef]
- Yu, X. Optimal Design of Vertical Axis Wind Turbine Blade Structure with Honeycomb Core Layer Inside the Main Beam. Ph.D. Thesis, Tianjin University of Technology, Tianjin, China, 2021. [Google Scholar]
- Zhang, Y.Y.; Zheng, Y.J.; Chen, Y.Y.; Sun, M.M.; Tang, J.M. Structural topology optimization design of wind turbine blade. Shanxi Archit. 2017, 43, 203–204. [Google Scholar]
- Aage, N.; Andreassen, E.; Lazarov, B.S.; Sigmund, O. Giga-voxel computational morphogenesis for structural design. Nature 2017, 550, 84–86. [Google Scholar] [CrossRef]
- Zuo, W.; Saitou, K. Multi-material topology optimization using ordered SIMP interpolation. Struct. Multidiscip. Optim. 2017, 55, 477–491. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Lab: Golden, CO, USA, 2009.
- Mamouri, A.R.; Lakzian, E.; Khoshnevis, A.B. Entropy analysis of pitching airfoil for offshore wind turbines in the dynamic stall condition. Ocean Eng. 2019, 187, 106229. [Google Scholar] [CrossRef]
- Mahrooghi, A.; Lakzian, E. Optimization of Wells turbine performance using a hybrid artificial neural fuzzy inference system (ANFIS)—Genetic algorithm (GA). Ocean Eng. 2021, 226, 108861. [Google Scholar] [CrossRef]
- Davidson, A.A.; Salim, S.M. CFD Modelling of Rotating Annular Flow Using Wall y+, International MultiConference of Engineers and Computer Scientists. Trans. Eng. Technol. 2018, 1, 318–330. [Google Scholar]
- Manatbayev, R.; Baizhuma, Z.; Bolegenova, S. Numerical simulations on static Vertical Axis Wind Turbine blade icing. Renew. Energy 2021, 170, 997–1007. [Google Scholar] [CrossRef]
- Son, C.; Kim, T. Development of an icing simulation code for rotating wind turbines. J. Wind Eng. Ind. Aerodyn. 2020, 203, 104239. [Google Scholar] [CrossRef]
- Madsen, P.H.; Risø, D.J.R.N.L. Introduction to the IEC 61400-1 Standar; Technical Standard; Risø National Laboratory, Technical University of Denmark: Kongens Lyngby, Denmark, 2008. [Google Scholar]



| Mechanical Properties of Composites | Allowable Values of Composites | ||||||
|---|---|---|---|---|---|---|---|
| Items | Values | Items | Values | Items | Values | Items | Values |
| Ex | 4.5 × 104 MPa | µxz | 0.3 | TSx | 1.1 × 103 MPa | CSz | −120 MPa |
| Ey | 1.0 × 104 MPa | Gxy | 5.0 × 103 MPa | TSy | 35 MPa | GSxy | 80 MPa |
| Ez | 1.0 × 104 MPa | Gyz | 3.8 × 103 MPa | TSz | 35 MPa | GSyz | 46 MPa |
| µxy | 0.3 | Gxz | 5.0 × 103 MPa | CSx | −680 MPa | GSxz | 80 MPa |
| µyz | 0.4 | ρ | 2000 kg·m3 | CSy | −120 MPa | - | - |
| Load Case | Rotation Speed (RPM) | Pitch Angle (°) | Wind Speed (m/s) |
|---|---|---|---|
| DLC-1 (Design) | 12.1 | 0 | 13.8 |
| DLC-2 | 12.1 | 23.3 | 25 |
| DLC-3 | 0 | 89.3 | 37.5 |
| Wind Speed (m/s) | Pitch Angle (°) | Wind Turbine Torque | ||||
|---|---|---|---|---|---|---|
| FAST | k- SST | Error | k- | Error | ||
| 7 | 0 | 472.70 | 479.05 | 1.34% | 473.61 | 0.19% |
| 10 | 0 | 1017.03 | 976.36 | 4.00% | 976.36 | 4.00% |
| 11 | 0 | 1293.77 | 1238.20 | 4.30% | 1333.51 | 3.07% |
| 15 | 10.45 | 1393.37 | 1309.79 | 6.00% | 1289.05 | 7.49% |
| 20 | 17.47 | 1393.37 | 1302.96 | 6.49% | 1244.32 | 10.70% |
| 25 | 23.57 | 1393.37 | 1300.84 | 6.64% | 1237.86 | 11.16% |
| Wind Speed (m/s) | Pitch Angle (°) | Wind Turbine Power | ||||
|---|---|---|---|---|---|---|
| FAST | k- SST | Error | k- | Error | ||
| 7 | 0 | 419.20 | 424.86 | 1.35% | 420.03 | 0.2% |
| 10 | 0 | 1217.67 | 1168.75 | 4.02% | 1168.75 | 4.02% |
| 11 | 0 | 1611.07 | 1541.70 | 4.31% | 1660.39 | 3.06% |
| 15 | 10.45 | 1765.53 | 1659.65 | 6.00% | 1633.37 | 7.49% |
| 20 | 17.47 | 1765.57 | 1651.00 | 6.49% | 1576.69 | 10.70% |
| 25 | 23.57 | 1765.57 | 1648.30 | 6.64% | 1568.50 | 11.16% |
| Direction | Overall Stress of Blade | Localized Stress of Web | Min. Fatigue Life | Disp. of Tip | ||
|---|---|---|---|---|---|---|
| Max. TS | Max. CS | Max. TS | Max. CS | |||
| X | 45.56 MPa | 49.72 MPa | 39.16 MPa | 45.51 MPa | 1.27×109 | 4.38 m |
| Y | 27.49 MPa | 16.76 MPa | 27.49 MPa | 16.76 MPa | 6.45×108 | |
| Z | 17.66 MPa | 12.72 MPa | 27.49 MPa | 16.76 MPa | 8.97×107 | |
| Item | Overall Stress of Blade | Localized Stress of Web | Min. Fatigue Life | Disp. of Tip | ||
|---|---|---|---|---|---|---|
| Max. TS | Max. CS | Max. TS | Max. CS | |||
| First X | 45.56 MPa | 49.72 MPa | 39.16 MPa | 45.51 MPa | 1.27×109 | 4.38 m (first); 4.03 m (second); Δ = −7.99% |
| Second X | 45.77 MPa | 49.91 MPa | 36.69 MPa | 45.85 MPa | 1.27×109 | |
| Δ X | +0.46% | +0.38% | −6.31% | +0.75% | 0% | |
| First Y | 27.49 MPa | 16.76 MPa | 27.49 MPa | 16.76 MPa | 6.45×108 | |
| Second Y | 27.86 MPa | 13.61 MPa | 27.86 MPa | 13.61 MPa | 6.24×108 | |
| Δ Y | +1.35% | −18.79% | +1.35% | −18.79% | −3.26% | |
| First Z | 17.66 MPa | 12.72 MPa | 27.49 MPa | 16.76 MPa | 8.97×107 | |
| Second Z | 17.70 MPa | 12.84 MPa | 0.81 MPa | 0.81 MPa | 2.25×108 | |
| Δ Z | +0.23% | +0.94% | −97.05% | −95.17% | +150.84% | |
| Case | Direction | Overall Stress of Blade | Localized Stress of Web | Min. Fatigue Life | Disp. of Tip | ||
|---|---|---|---|---|---|---|---|
| Max. TS | Max. CS | Max. TS | Max. CS | ||||
| DLC-1 | X | 45.77 | 49.91 | 36.69 | 45.85 | 1.27e9 | 4.03 |
| Y | 27.86 | 13.61 | 27.86 | 13.61 | 6.24e8 | ||
| Z | 17.70 | 12.84 | 0.81 | 0.81 | 2.25e8 | ||
| DLC-2 | X | 24.83 | 28.53 | 24.16 | 27.98 | 1.27e9 | 1.18 |
| Y | 15.09 | 8.37 | 15.09 | 8.36 | 1.27e9 | ||
| Z | 9.70 | 7.06 | 0.50 | 0.51 | 5.98e8 | ||
| DLC-2 | X | 32.82 | 32.90 | 24.16 | 27.98 | 1.27e9 | 2.28 |
| Y | 8.53 | 17.71 | 15.09 | 8.36 | 1.27e9 | ||
| Z | 7.71 | 10.37 | 0.50 | 0.51 | 3.90e8 | ||
| Case | Dir. | Item | Overall Blade Stress | Localized Web Stress | Disp. of Tip | Overall Weight | ||
|---|---|---|---|---|---|---|---|---|
| Max. TS | Max. CS | Max. TS | Max. CS | |||||
| DLC-1 | X | Ref. blade | 32.70 | 30.60 | 14.30 | 16.00 | 3.42 (Ref.) 4.03 (New) Δ: 17.84% | 21,247 (Ref.); 19,148 (New) Δ: −9.88% |
| Nov. blade | 45.769 | 49.91 | 36.69 | 45.85 | ||||
| Δ | 39.97% | 63.10% | 156.57% | 186.56% | ||||
| Y | Ref. blade | 13.10 | 19.50 | 13.10 | 19.50 | |||
| Nov. blade | 27.86 | 13.61 | 27.86 | 13.61 | ||||
| Δ | 112.67% | −30.21% | 112.67% | −30.21% | ||||
| Z | Ref. blade | 19.30 | 13.60 | 0.15 | 0.18 | |||
| Nov. blade | 17.70 | 12.84 | 0.81 | 0.81 | ||||
| Δ | −8.29% | −5.59% | 440.00% | 350.00% | ||||
| DLC-2 | X | Ref. blade | 18.90 | 15.70 | 8.85 | 9.70 | 1.08 (Ref.) 1.18 (New) Δ: 9.26% | |
| Nov. blade | 24.83 | 28.53 | 24.16 | 27.98 | ||||
| Δ | 31.38% | 81.72% | 172.99% | 188.45% | ||||
| Y | Ref. blade | 7.15 | 10.40 | 7.15 | 10.40 | |||
| Nov. blade | 15.09 | 8.37 | 15.09 | 8.36 | ||||
| Δ | 111.05% | −19.52% | 111.05% | −19.62% | ||||
| Z | Ref. blade | 10.80 | 6.14 | 0.07 | 0.08 | |||
| Nov. blade | 9.70 | 7.06 | 0.50 | 0.51 | ||||
| Δ | −10.19% | 14.98% | 614.29% | 537.50% | ||||
| DLC-3 | X | Ref. blade | 23.80 | 25.50 | 6.08 | 5.61 | 1.94 (Ref.) 2.28 (New) Δ: 17.53% | |
| Nov. blade | 32.82 | 32.90 | 24.16 | 27.98 | ||||
| Δ | 37.90% | 29.02% | 297.37% | 398.75% | ||||
| Y | Ref. blade | 7.67 | 5.29 | 7.67 | 5.29 | |||
| Nov. blade | 8.53 | 17.71 | 15.09 | 8.36 | ||||
| Δ | 11.21% | 234.78% | 96.74% | 58.03% | ||||
| Z | Ref. blade | 9.96 | 7.42 | 0.09 | 0.09 | |||
| Nov. blade | 7.71 | 10.37 | 0.50 | 0.51 | ||||
| Δ | −22.59% | 39.76% | 455.56% | 466.67% | ||||
| Order | Frequency (Hz) | Order | Frequency (Hz) | ||
|---|---|---|---|---|---|
| Ref. Blade | Nov. Blade | Ref. Blade | Nov. Blade | ||
| 1 | 1.12 | 1.16 | 4 | 5.21 | 5.22 |
| 2 | 1.68 | 1.67 | 5 | 5.71 | 5.70 |
| 3 | 2.96 | 2.16 | 6 | 8.70 | 7.63 |
| Wind Speed (m/s) | Duration of Wind Speed (h) | Max. Stress (MPa) | Min. Stress (MPa) | Stress Range Weibull Distribution | Fatigue Limitation (MPa) | Fatigue Life | Fatigue Damage |
|---|---|---|---|---|---|---|---|
| 5 | 1526 | 12.84 | 3.85 | 0.210 | 40.4 | >2 × 108 | 0 |
| 7 | 1613 | 21.18 | 6.35 | 0.222 | 40.4 | >2 × 108 | 0 |
| 9 | 1425 | 42.43 | 12.73 | 0.197 | 40.4 | 1.70 × 108 | 1.16 × 10−9 |
| 11 | 1090 | 42.64 | 12.79 | 0.150 | 40.4 | 1.60 × 108 | 9.38 × 10−10 |
| 13 | 734 | 47.86 | 14.36 | 0.101 | 40.4 | 1.05 × 108 | 9.62 × 10−10 |
| 15 | 439 | 42.54 | 12.76 | 0.061 | 40.4 | 1.08 × 108 | 5.65 × 10−10 |
| 17 | 235 | 36.24 | 10.87 | 0.032 | 40.4 | >2 × 108 | 0 |
| 19 | 113 | 33.89 | 10.17 | 0.016 | 40.4 | >2 × 108 | 0 |
| 21 | 49 | 23.87 | 7.16 | 0.007 | 40.4 | >2 × 108 | 0 |
| 23 | 19 | 28.33 | 8.50 | 0.003 | 40.4 | >2 × 108 | 0 |
| 25 | 7 | 33.3 | 9.99 | 0.001 | 40.4 | >2 × 108 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Chen, J.; Wu, Y.; Li, L. Topology Optimization-Driven Design for Offshore Composite Wind Turbine Blades. J. Mar. Sci. Eng. 2022, 10, 1487. https://doi.org/10.3390/jmse10101487
Song J, Chen J, Wu Y, Li L. Topology Optimization-Driven Design for Offshore Composite Wind Turbine Blades. Journal of Marine Science and Engineering. 2022; 10(10):1487. https://doi.org/10.3390/jmse10101487
Chicago/Turabian StyleSong, Jian, Junying Chen, Yufei Wu, and Lixiao Li. 2022. "Topology Optimization-Driven Design for Offshore Composite Wind Turbine Blades" Journal of Marine Science and Engineering 10, no. 10: 1487. https://doi.org/10.3390/jmse10101487
APA StyleSong, J., Chen, J., Wu, Y., & Li, L. (2022). Topology Optimization-Driven Design for Offshore Composite Wind Turbine Blades. Journal of Marine Science and Engineering, 10(10), 1487. https://doi.org/10.3390/jmse10101487