Numerical Study of Flat Plate Impact on Water Using a Compressible CIP–IBM–Based Model
Abstract
:1. Introduction
2. Numerical Model
2.1. Governing Equations
2.2. Numerical Methods
2.2.1. CIP-Based Flow Solver
- (I)
- Advection term:
- (II)
- Diffusion term:
- (III)
- Pressure term:
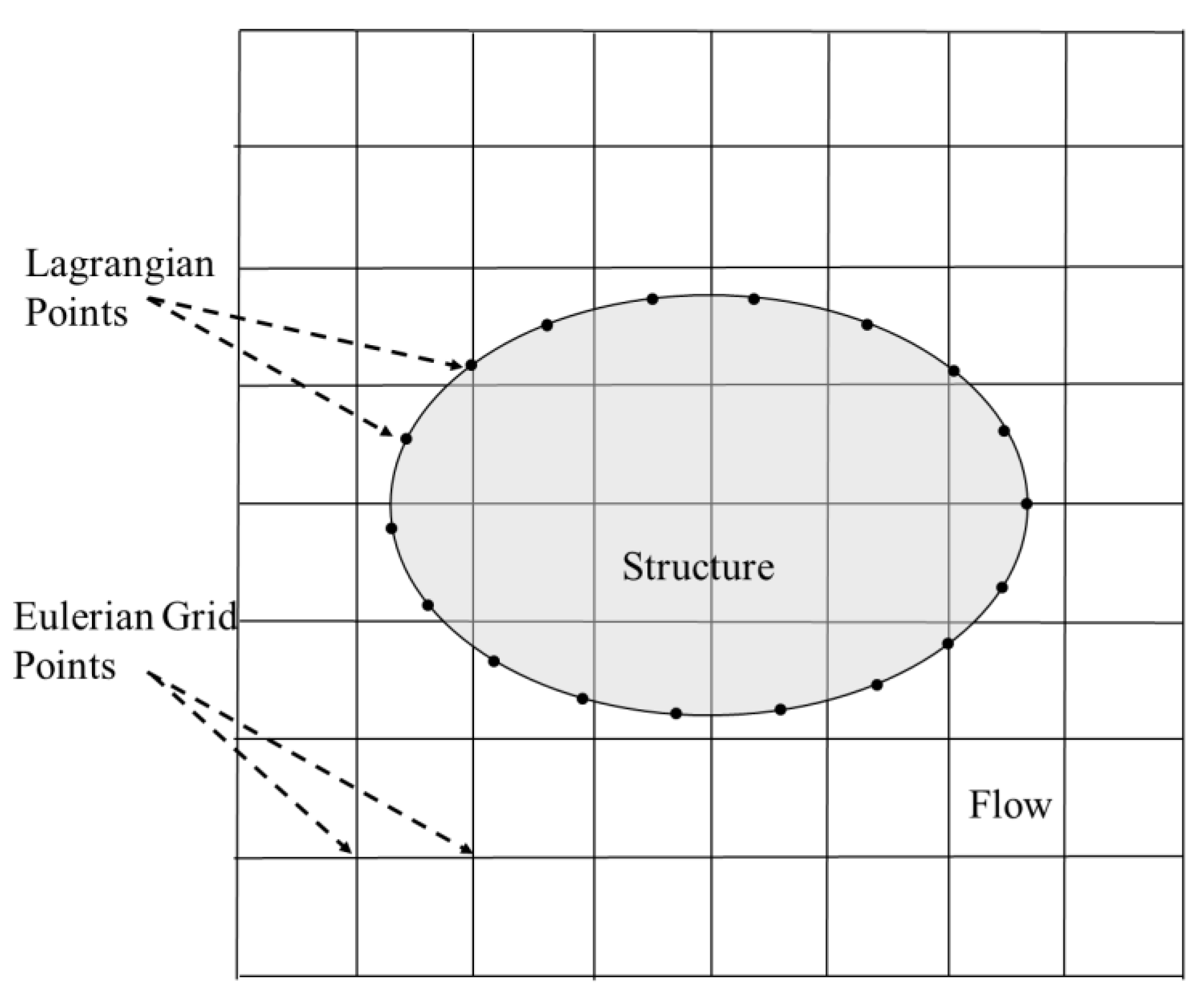
2.2.2. Implicit IBM Method
3. Solver Validation: 2D Flow Past a Stationary Cylinder
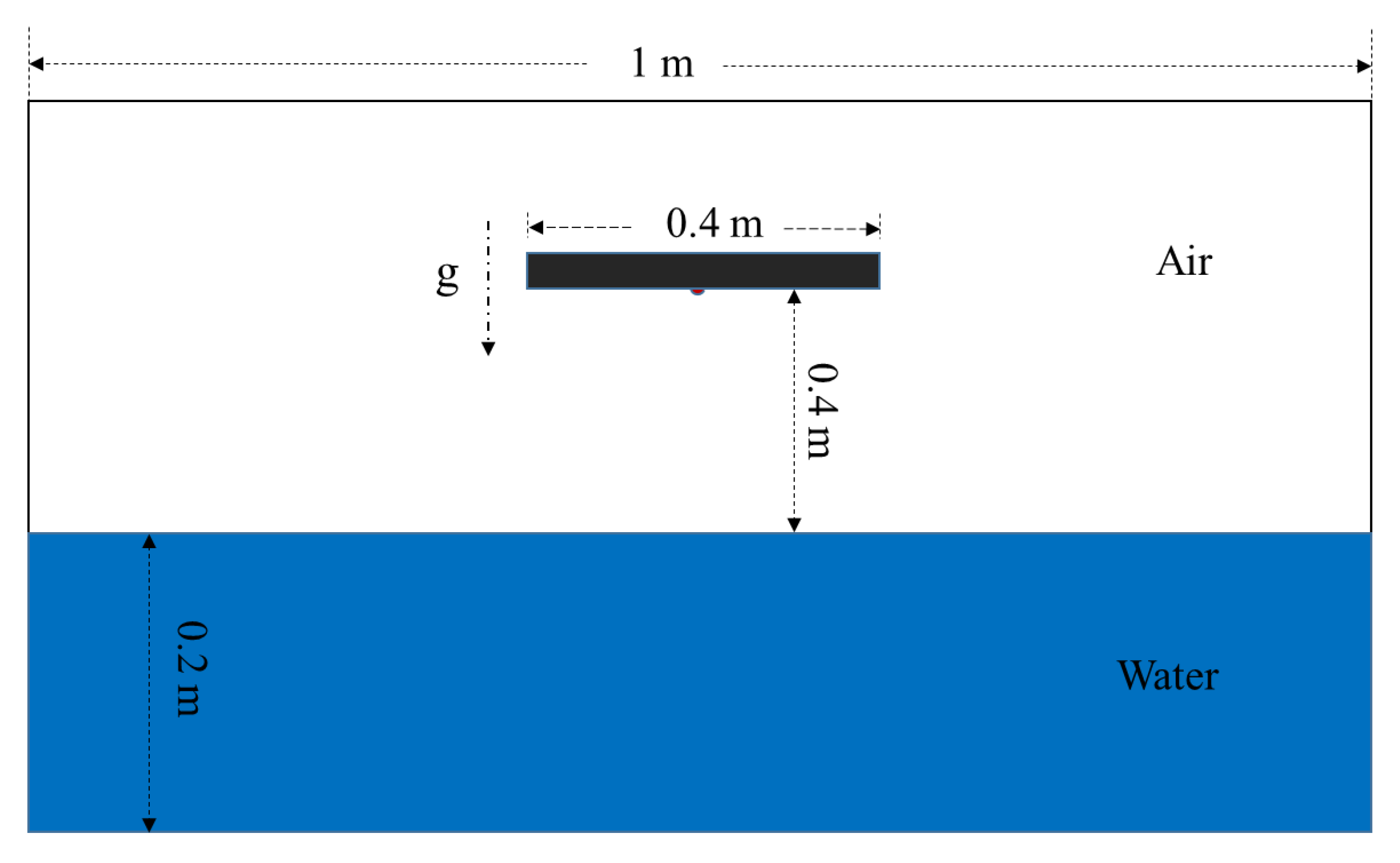
4. Simulation and Analysis of 2D Flat Plate Impact on Water
4.1. Equation of Body Motion
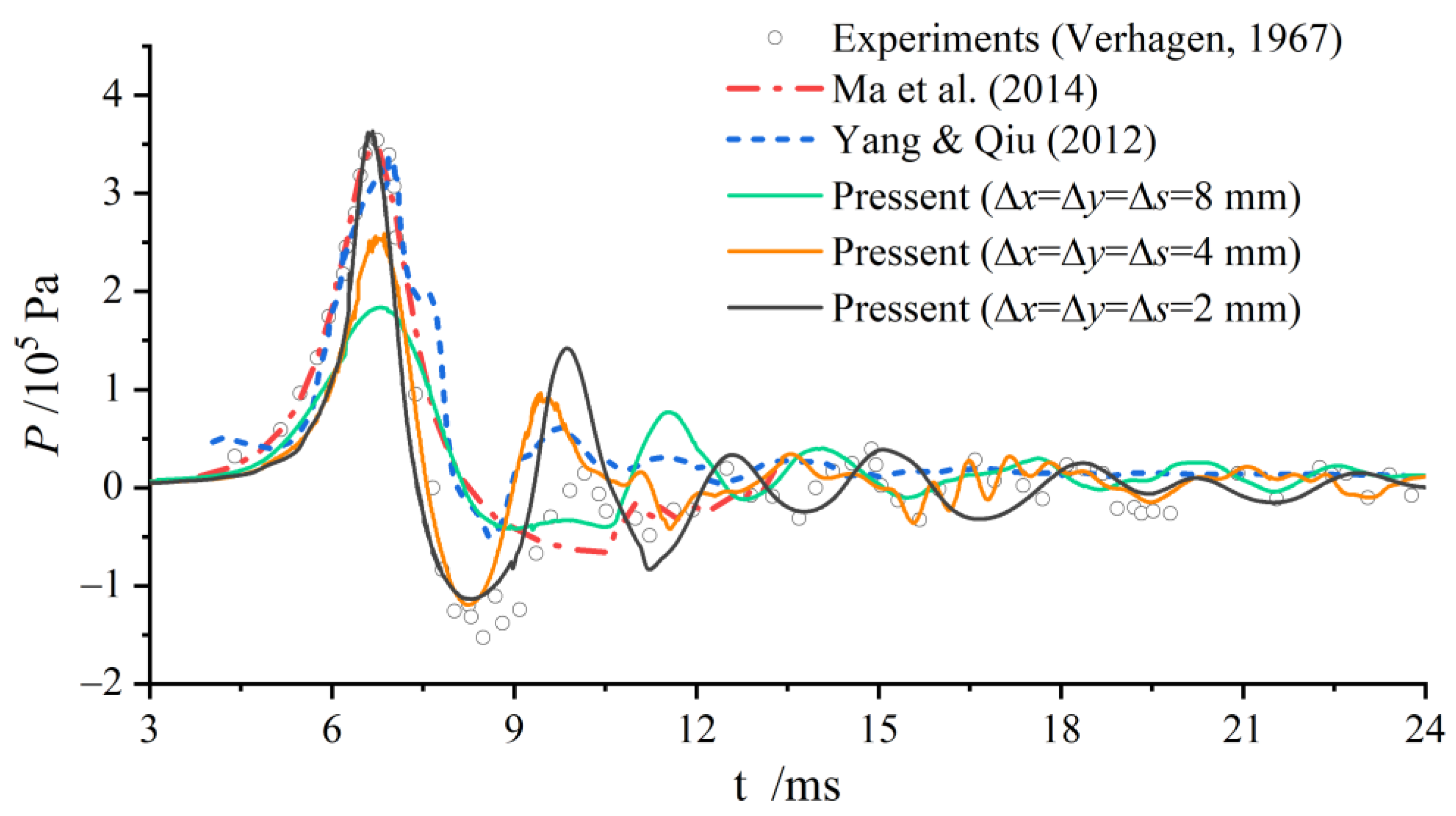
4.2. Description and Comparison
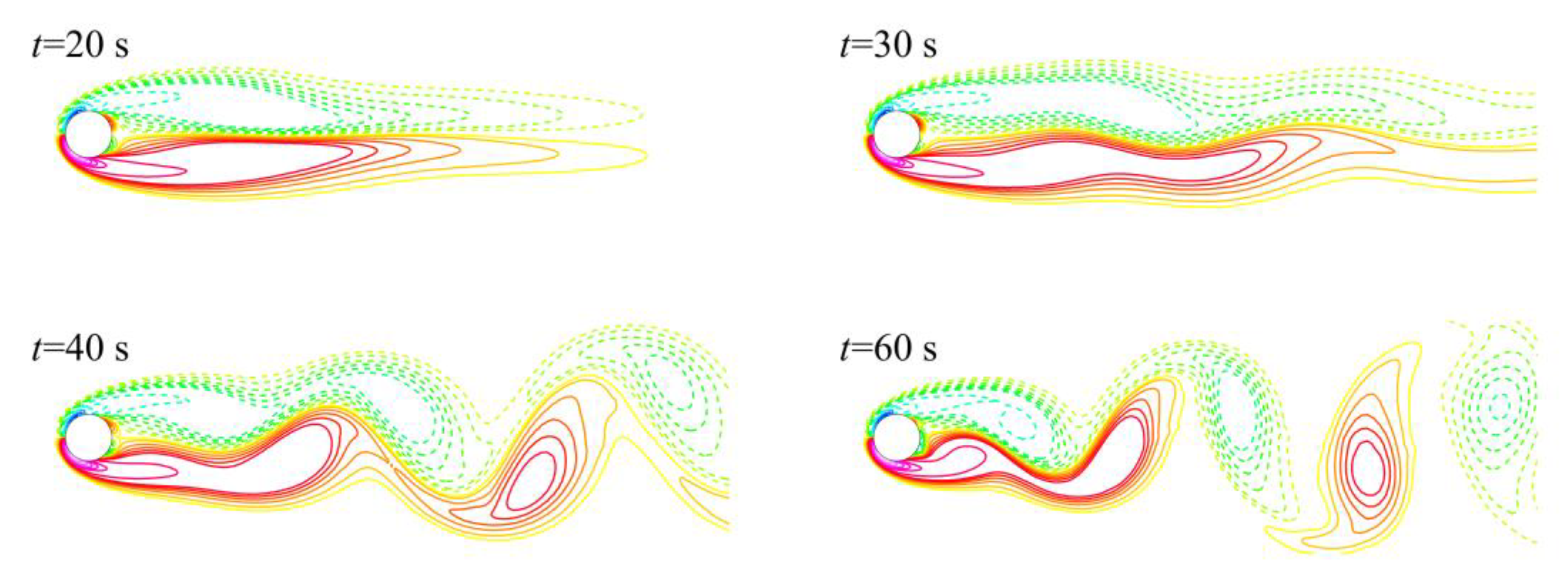
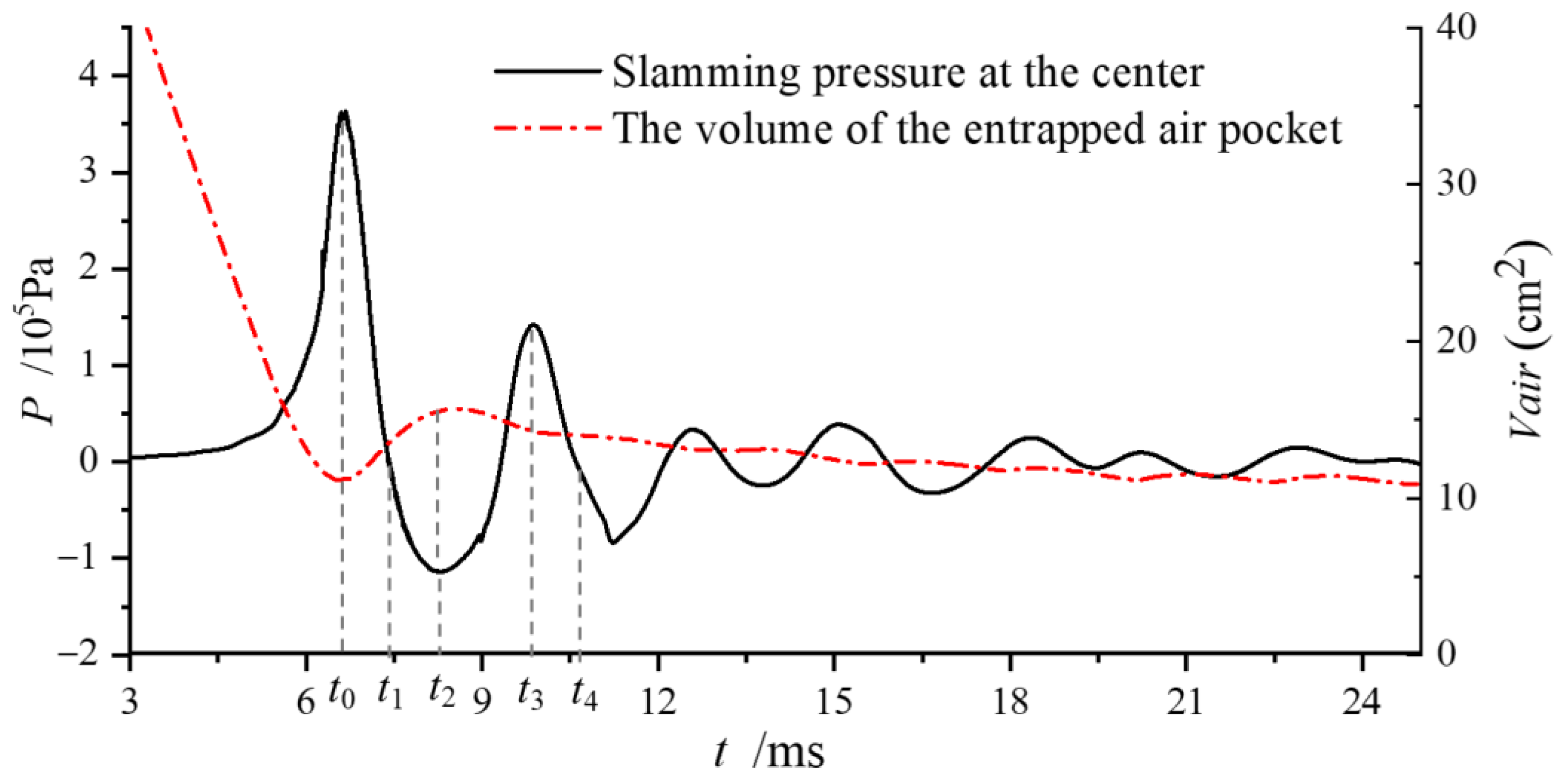
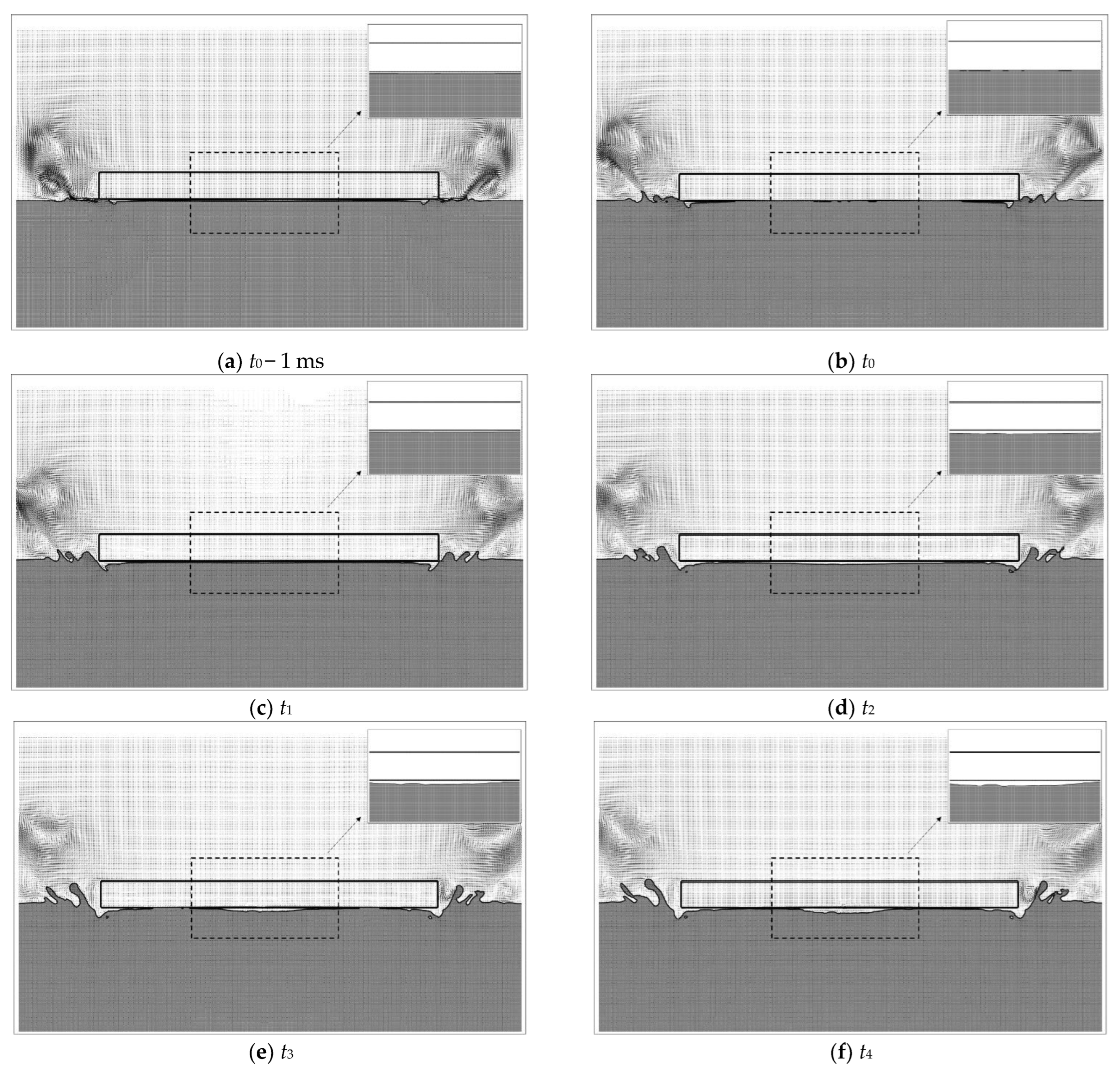
4.3. Evaluation of Water Surface and Air Cushion during Slamming
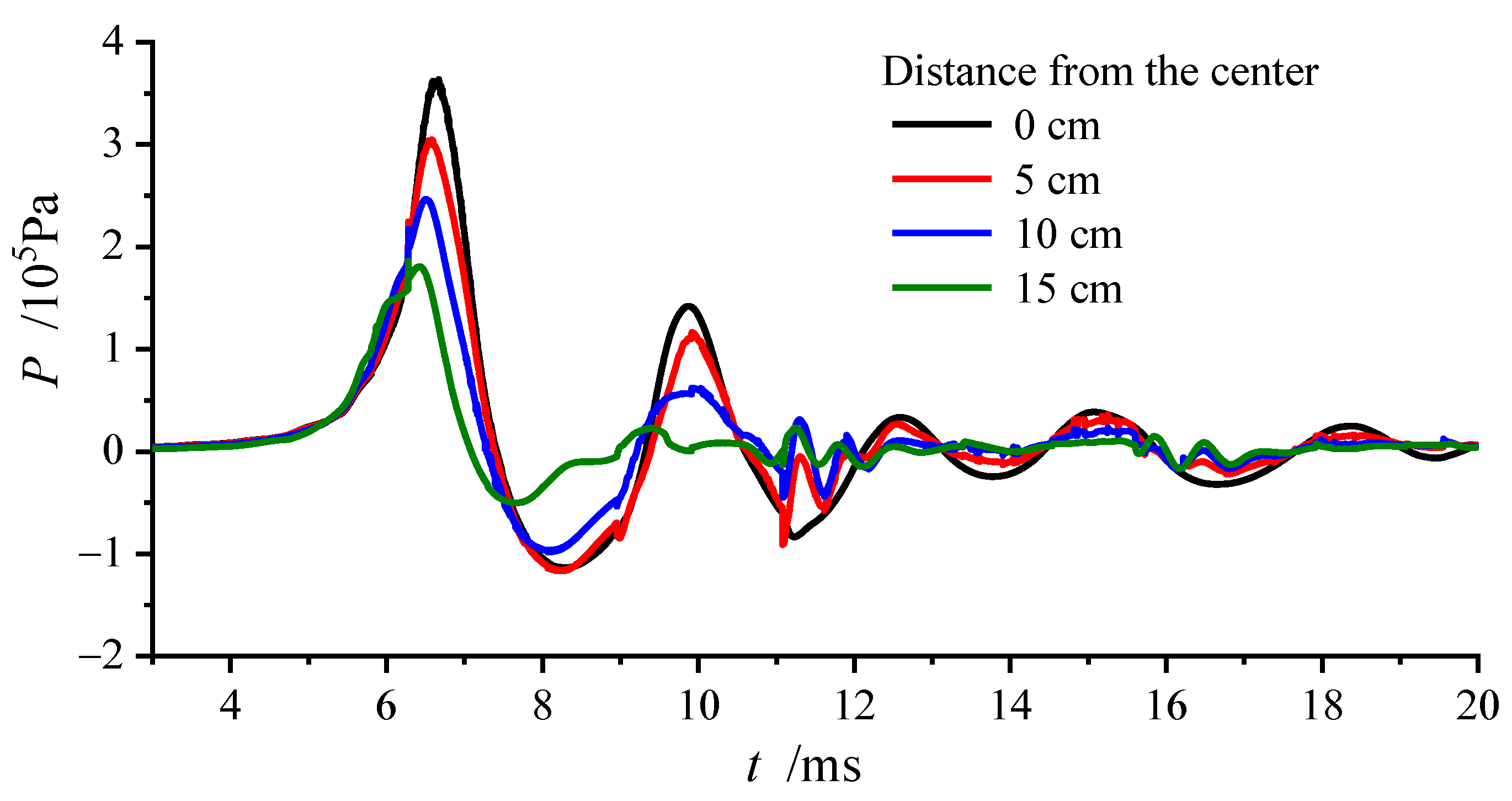
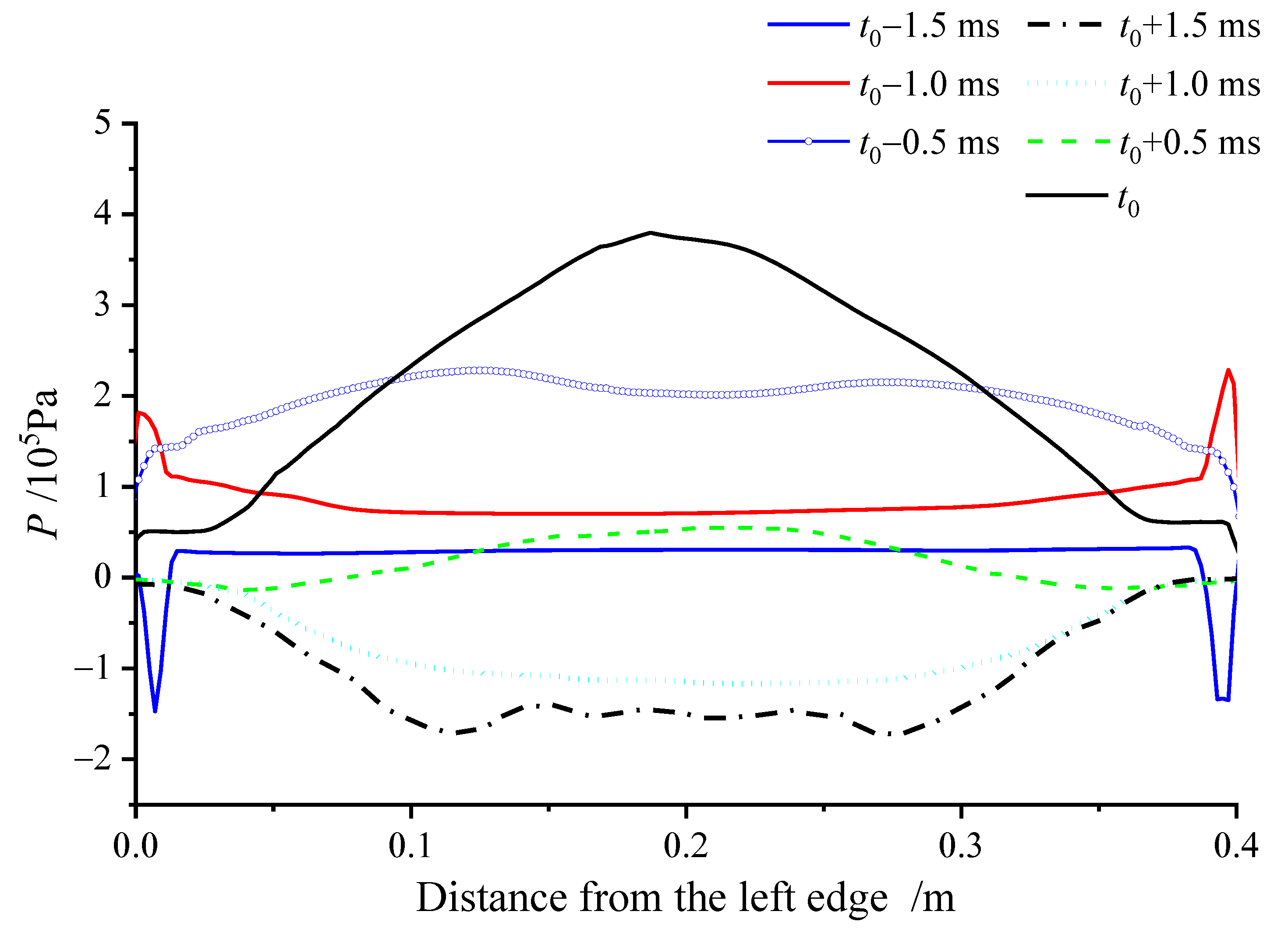
4.4. Distribution of the Slamming Pressure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chuang, S.L. Experiments on flat-bottom slamming. J. Ship Res. 1966, 10, 10–27. [Google Scholar] [CrossRef]
- Lewison, G.; Maclean, W.M. On the cushioning of water impact by entrapped air. J. Ship Res. 1968, 12, 116–130. [Google Scholar] [CrossRef]
- Verhagen, J.H.G. The impact of a flat plate on a water surface. J. Ship Res. 1967, 11, 211–223. [Google Scholar] [CrossRef]
- Chuang, S.L. Investigation of impact of rigid and elastic bodies with water. In Naval Ship Research and Development Center Report 3248; Defense Technical Information Center: Fort Belvoir, VA, USA, 1970. [Google Scholar]
- Huang, Z.Q.; Zhang, W.H. Experimental investigation on the reduction of flat-bottom body slamming. Huazhong Univ. Sci. Technol. 1986, 14, 725–730. (In Chinese) [Google Scholar]
- Lin, M.C.; Shieh, L.D. Simultaneous measurements of water impact on a two-dimensional body. Fluid Dyn. Res. 1997, 19, 125–148. [Google Scholar] [CrossRef]
- Kang, H.D.; Oh, S.H.; Kwon, S.H.; Chung, J.-Y.; Jung, K.H.; Jo, H.J. An experimental study of shallow water impact. In Proceedings of the 23rd International Workshop on Water Waves and Floating Bodys, Jeju, Korea, 13–16 April 2008. [Google Scholar]
- Oh, S.H.; Kown, S.H.; Chung, J.Y. A close look at air pocket evolution in flat impact. In Proceedings of the 24th International Workshop on Water Waves and Floating Bodys, Zelenogorsk, Russia, 19–20 April 2009. [Google Scholar]
- Mayer, H.C.; Krechetnikov, R. Flat plate impact on water. J. Fluid Mech. 2018, 850, 1066–1116. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.H.; Causon, D.M.; Qian, L.; Mingham, C.G.; Mai, T.; Greaves, D.; Raby, A. Pure and aerated water entry of a flat plate. Phys. Fluids 2016, 28, 016104. [Google Scholar] [CrossRef] [Green Version]
- Shin, H.; Seo, B.; Cho, S.R. Experimental investigation of slamming impact acted on flat bottom bodies and cumulative damage. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 294–306. [Google Scholar] [CrossRef]
- Mai, T.; Mai, C.; Raby, A.; Greaves, D. Aeration effects on water-structure impacts: Part 1. Drop plate impacts. Ocean Eng. 2019, 193, 106600. [Google Scholar] [CrossRef]
- Oumeraci, H.; Klammer, P.; Partenscky, H.W. Classification of breaking wave loads on vertical structures. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 381–397. [Google Scholar] [CrossRef]
- Lugni, C.; Brocchini, M.; Faltinsen, O.M. Wave impact loads: The role of the flip through. Physic Fluids 2006, 18, 1473–1486. [Google Scholar] [CrossRef]
- Bagnold, R. Interim report on wave-pressure research. J. Inst. Civ. Eng. 1939, 12, 201–226. [Google Scholar] [CrossRef]
- Takahashi, S.; Tanimoto, K.; Miyanaga, S. Uplift wave forces due to compression of enclosed air layer and their similitude law. Coast. Eng. J. 1985, 28, 191–206. [Google Scholar] [CrossRef]
- Cooker, M.J.; Peregrine, D.H. Computation of violent motion due to waves breaking against a wall. In Proceedings of the 22nd International Conference on Coastal Engineering, ASCE, Delft, The Netherlands, 29 January 1990; pp. 164–176. [Google Scholar]
- Kirkgoz, M.S. Impact pressure of breaking waves on vertical and sloping walls. Ocean Eng. 1991, 18, 45–59. [Google Scholar] [CrossRef]
- Topliss, M.E.; Cooker, M.J.; Peregrine, D.H. Pressure oscillations during wave impact on vertical walls. In Proceedings of the 23rd Coastal Engineering Conference, Venice, Italy, 4–9 October 1992; pp. 1639–1650. [Google Scholar]
- Hattori, M.; Arami, A.; Yui, T. Wave impact pressure on vertical walls under breaking waves of various types. Coast. Eng. 1994, 22, 79–114. [Google Scholar] [CrossRef]
- Walkden, M.J.; Wood, D.J.; Bruce, T.; Peregrine, D.H. Impulsive seaward loads induced by wave overtopping on caisson breakwaters. Coast. Eng. 2001, 42, 257–276. [Google Scholar] [CrossRef]
- Buccino, M.; Daliri, M.; Dentale, F.; Calabrese, M. CFD experiments on a low crested sloping top caisson breakwater. Part 2. Analysis of plume impact. Ocean Eng. 2019, 173, 345–357. [Google Scholar] [CrossRef]
- Liu, S.; Gatin, I.; Obhrai, C.; Ong, M.C.; Jasak, H. CFD simulations of violent breaking wave impacts on a vertical wall using a two-phase compressible solver. Coast. Eng. 2019, 154, 103564. [Google Scholar] [CrossRef]
- Gao, J.L.; Ma, X.Z.; Zang, J.; Dong, G.H.; Ma, X.J.; Zhu, Y.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, C.; Zhang, Q.; He, M.; Gao, X. Numerical Study on the Hydrodynamic Characteristics of a Double-Row Floating Breakwater Composed of a Pontoon and an Airbag. J. Mar. Sci. Eng. 2021, 9, 983. [Google Scholar] [CrossRef]
- Martin, M.B.; Pinon, G.; Reverllon, J.; Kimmoun, O. Computations of soliton impact onto a vertical wall: Comparing incompressible and compressible assumption with experimental validation. Coast. Eng. 2021, 170, 103817. [Google Scholar] [CrossRef]
- Gao, J.L.; Ma, X.Z.; Dong, G.H.; Chen, H.Z.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Ng, C.; Kot, S. Computations of water impact on a two-dimensional flat-bottomed body with a volume-of-fluid method. Ocean Eng. 1992, 19, 377–393. [Google Scholar] [CrossRef]
- Ma, Z.H.; Causon, D.M.; Qian, L.; Mingham, C.G.; Gu, H.B.; Martinez, P. A compressible multiphase flow model for violent aerated wave impact problems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 14, 351–360. [Google Scholar] [CrossRef]
- Aghaei, A.; Schimmels, S.; Schlurmann, T.; Hildebrandt, A. Numerical investigation of the effect of aeration and hydroelasticity on impact loading and structural response for elastic plates during water entry. Ocean Eng. 2020, 201, 107098. [Google Scholar] [CrossRef]
- Hu, X.-Z.; Liu, S.-J. Numerical simulation of calm water entry of flatted-bottom seafloor mining tool. J. Cent. South Univ. 2011, 18, 658–665. [Google Scholar] [CrossRef]
- Qu, Q.; Ji, G.; Liu, P.; Wu, X.; Agarwal, R.K. Numerical study of evolution of air pockets during water impact of a flat-bottom structure. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Yang, J.; Sun, Z.; Liang, S. The numerical investigation on the effects of support conditions and flanges during the water impact of a thin elastic plate. Ocean Eng. 2022, 253, 111284. [Google Scholar] [CrossRef]
- Yabe, T.; Xiao, F.; Utsumi, T. The constrained interpolation profile method for multiphase analysis. J. Comput. Phys. 2001, 169, 556–593. [Google Scholar] [CrossRef]
- Zhao, X.Z.; Hu, C.H. Numerical and experimental study on a 2-D floating body under extreme wave conditions. Appl. Ocean Res. 2012, 35, 1–13. [Google Scholar] [CrossRef]
- Hu, C.; Kashiwagi, M. A CIP-based method for numerical simulations of violent free-surface flows. J. Mar. Sci. Technol. 2004, 9, 143–157. [Google Scholar] [CrossRef]
- He, G.H. A new adaptive Cartesian-grid CIP method for computation of violent free-surface flows. Appl. Ocean Res. 2013, 43, 234–243. [Google Scholar] [CrossRef]
- Ji, Q.; Dong, S.; Luo, X.; Soares, C.G. Wave transformation over submerged breakwaters by the constrained interpolation profile method. Ocean Eng. 2017, 136, 294–303. [Google Scholar] [CrossRef]
- Wang, J.D.; He, G.H.; You, R.; Liu, P. Numerical study on interaction of a solitary wave with the submerged obstacle. Ocean Eng. 2018, 158, 1–14. [Google Scholar] [CrossRef]
- Yang, Q.Y.; Qiu, W. Numerical simulation of water impact for 2D and 3D bodies. Ocean Eng. 2012, 43, 82–89. [Google Scholar] [CrossRef]
- Sun, H.Y.; Sun, Z.C.; Liang, S.X.; Zhao, X.Z. Numerical study of air compressibility effects in breaking wave impacts using a CIP-based model. Ocean Eng. 2019, 174, 159–168. [Google Scholar] [CrossRef]
- Xiao, F.; Honma, Y.; Kono, T. A simple algebraic interface capturing scheme using hyperbolic tangent function. Int. J. Numer. Methods Fluids 2005, 48, 1023–1040. [Google Scholar] [CrossRef]
- Lai, M.-C.; Peskin, C. An immersed boundary method with formal second-order accuracy and reduced numerical viscosity. J. Comput. Phys. 2000, 160, 705–719. [Google Scholar] [CrossRef] [Green Version]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Shu, C. Implicit velocity correction-based immersed boundary-lattice Boltzmann method and its applications. J. Comput. Phys. 2009, 228, 1963–1979. [Google Scholar] [CrossRef]
- Tritton, D.J. Experiments on the flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 1959, 6, 547–567. [Google Scholar] [CrossRef]
- Coutanceau, M.; Bouard, R. Experimental determination of the main features of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow. J. Fluid Mech. 1977, 79, 231–256. [Google Scholar] [CrossRef]
- Ye, T.; Mittal, R.; Udaykumar, H.; Shyy, W. An Accurate Cartesian Grid Method for Viscous Incompressible Flows with Complex Immersed Boundaries. J. Comput. Phys. 1999, 156, 209–240. [Google Scholar] [CrossRef] [Green Version]
- Taira, K.; Colonius, T. The immersed boundary method: A projection approach. J. Comput. Phys. 2007, 225, 2118–2137. [Google Scholar] [CrossRef]
- Horng, T.; Hsieh, P.; Yang, S.; You, C. A simple direct-forcing immersed boundary projection method with prediction-correction for fluid-solid interaction problems. Comput. Fluids 2018, 176, 135–152. [Google Scholar] [CrossRef]
- Liu, C.; Zheng, X.; Sung, C.H. Preconditioned multigrid methods for unsteady incompressible flows. J. Comput. Phys. 1998, 139, 35–57. [Google Scholar] [CrossRef]
- Uhlmann, M. An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 2005, 209, 448–476. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.; Shao, X. A direct-forcing fictitious domain method for particulate flows. J. Comput. Phys. 2007, 227, 292–314. [Google Scholar] [CrossRef]
- Di, S.; Ge, W. Simulation of dynamic fluid-solid interactions with an improved direct-forcing immersed boundary method. Particuology 2015, 18, 22–34. [Google Scholar] [CrossRef]

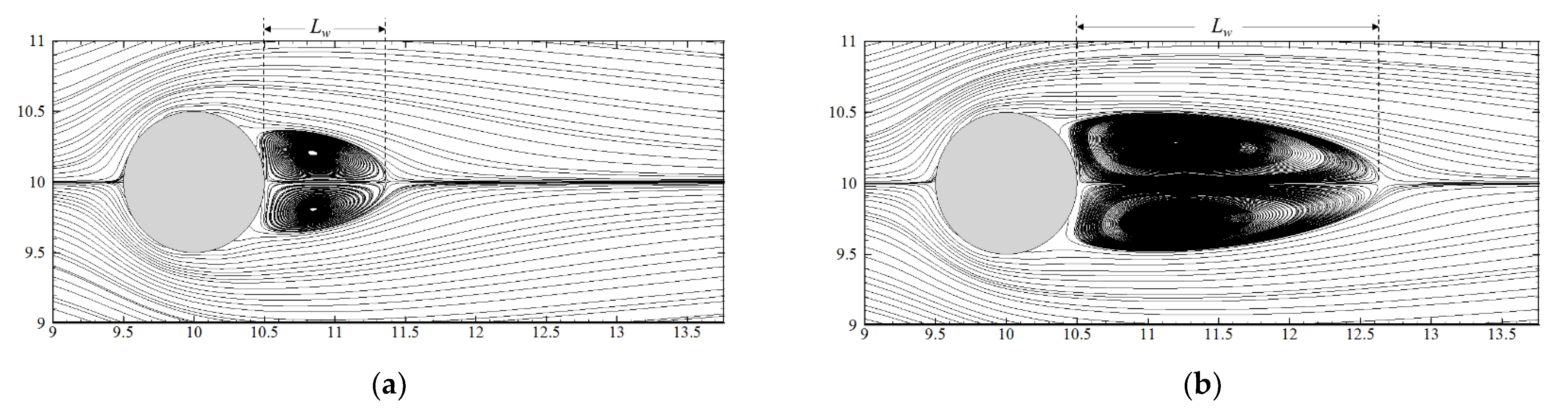

| Re = 20 | Re = 40 | |||
|---|---|---|---|---|
| Cd | Lw/D | Cd | Lw/D | |
| 2.20 | 0.99 | 1.65 | 2.37 | |
| 2.17 | 0.92 | 1.62 | 2.20 | |
| 2.14 | 0.89 | 1.60 | 2.14 | |
| Tritton (1959) [46] | 2.09 | - | 1.59 | - |
| Coutanceau and Bouard (1977) [47] | - | 0.93 | - | 2.13 |
| Ye et al. (1999) [48] | 2.03 | 0.92 | 1.52 | 2.27 |
| Taira and Colonius (2007) [49] | 2.06 | 0.94 | 1.54 | 2.30 |
| Horng et al. (2018) [50] | 2.10 | 0.93 | 1.56 | 2.18 |
| 1.433 | 0.012 | 0.312 | 0.161 | |
| 1.409 | 0.013 | 0.318 | 0.165 | |
| 1.395 | 0.013 | 0.322 | 0.167 | |
| Liu et al. (1998) [51] | 1.350 | 0.012 | 0.339 | 0.165 |
| Lai and Peskin (2000) [43] | 1.447 | - | 0.330 | 0.165 |
| Uhlmann (2005) [52] | 1.453 | 0.011 | 0.339 | 0.169 |
| Yu and Shao (2007) [53] | 1.394 | 0.009 | 0.316 | 0.174 |
| Di and Ge (2015) [54] | 1.385 | 0.009 | 0.344 | 0.168 |
| Horng et al. (2018) [50] | 1.40 | - | 0.36 | 0.170 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Ding, W.; Zhao, X.; Sun, Z. Numerical Study of Flat Plate Impact on Water Using a Compressible CIP–IBM–Based Model. J. Mar. Sci. Eng. 2022, 10, 1462. https://doi.org/10.3390/jmse10101462
Sun H, Ding W, Zhao X, Sun Z. Numerical Study of Flat Plate Impact on Water Using a Compressible CIP–IBM–Based Model. Journal of Marine Science and Engineering. 2022; 10(10):1462. https://doi.org/10.3390/jmse10101462
Chicago/Turabian StyleSun, Hongyue, Weiye Ding, Xizeng Zhao, and Zhaochen Sun. 2022. "Numerical Study of Flat Plate Impact on Water Using a Compressible CIP–IBM–Based Model" Journal of Marine Science and Engineering 10, no. 10: 1462. https://doi.org/10.3390/jmse10101462
APA StyleSun, H., Ding, W., Zhao, X., & Sun, Z. (2022). Numerical Study of Flat Plate Impact on Water Using a Compressible CIP–IBM–Based Model. Journal of Marine Science and Engineering, 10(10), 1462. https://doi.org/10.3390/jmse10101462