Study on the Wind and Wave Environmental Conditions of the Xisha Islands in the South China Sea
Abstract
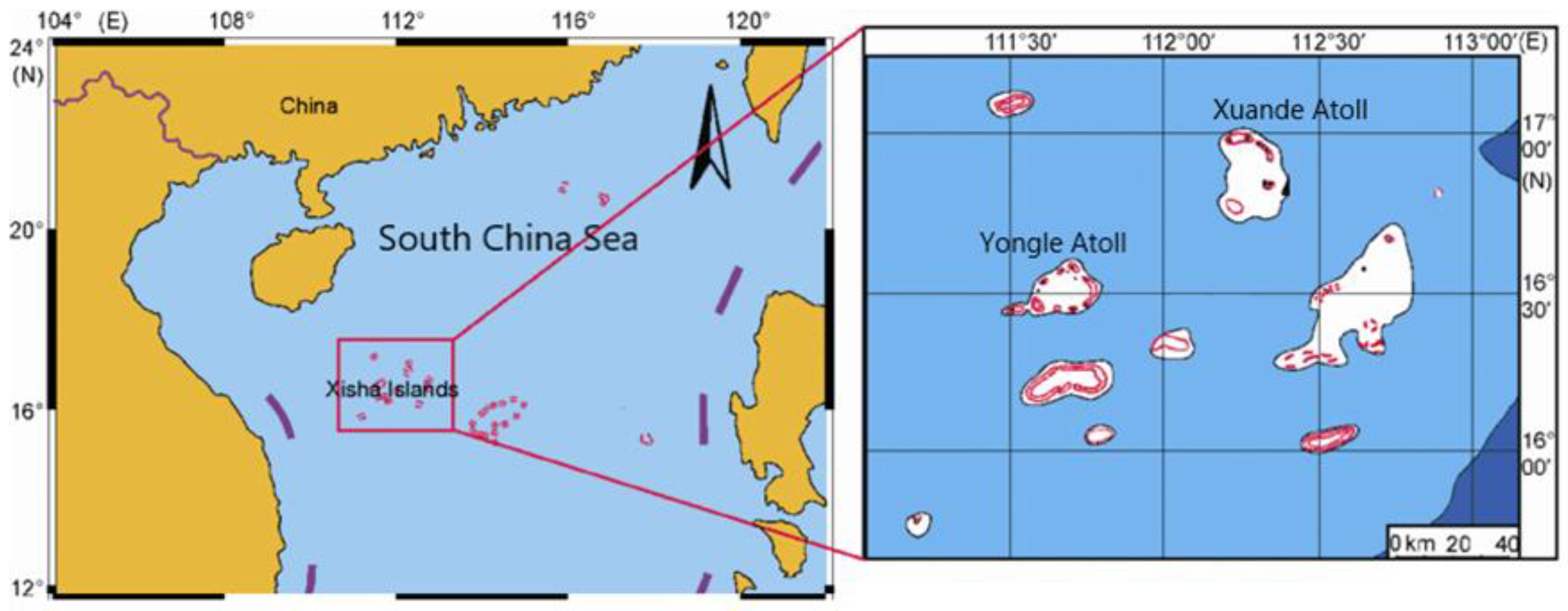
:1. Introduction
2. Data and Models
2.1. Wind Data
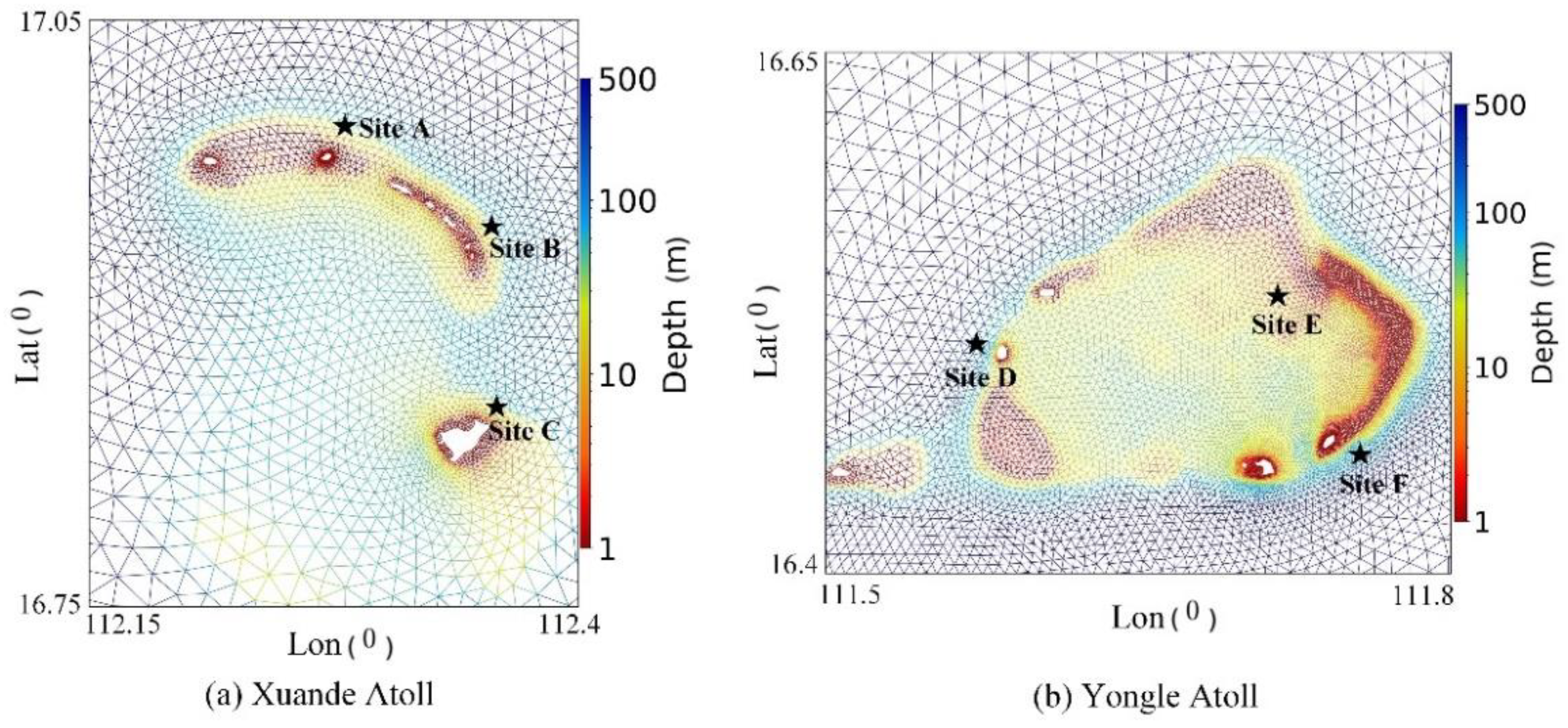
2.2. Unstructured Grid for Wave Modelling in the South China Sea
2.3. Validation of Hindcast Wave Characteristics
2.4. Extreme Value Analysis Methods
3. Wind and Wave Climate Analysis
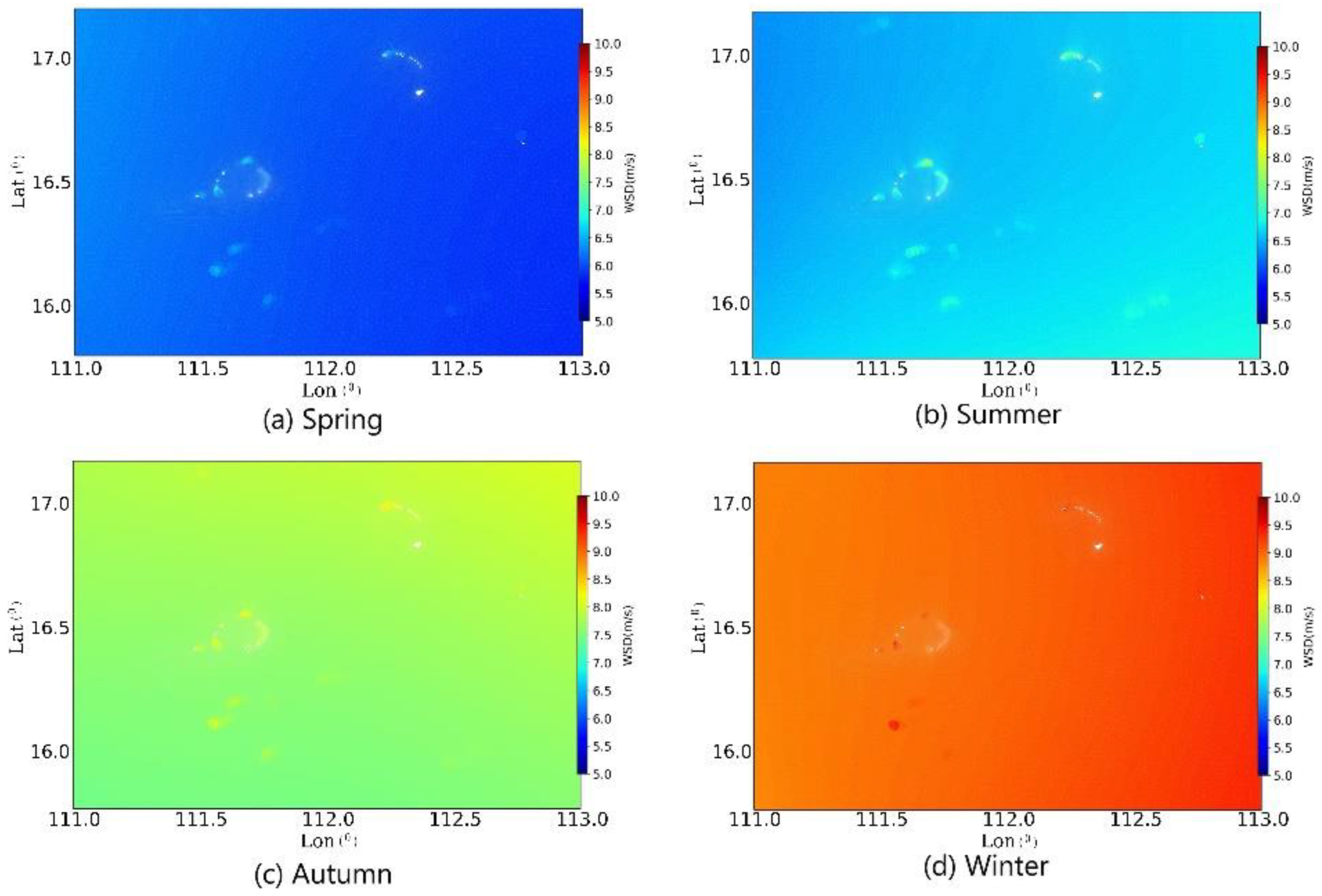
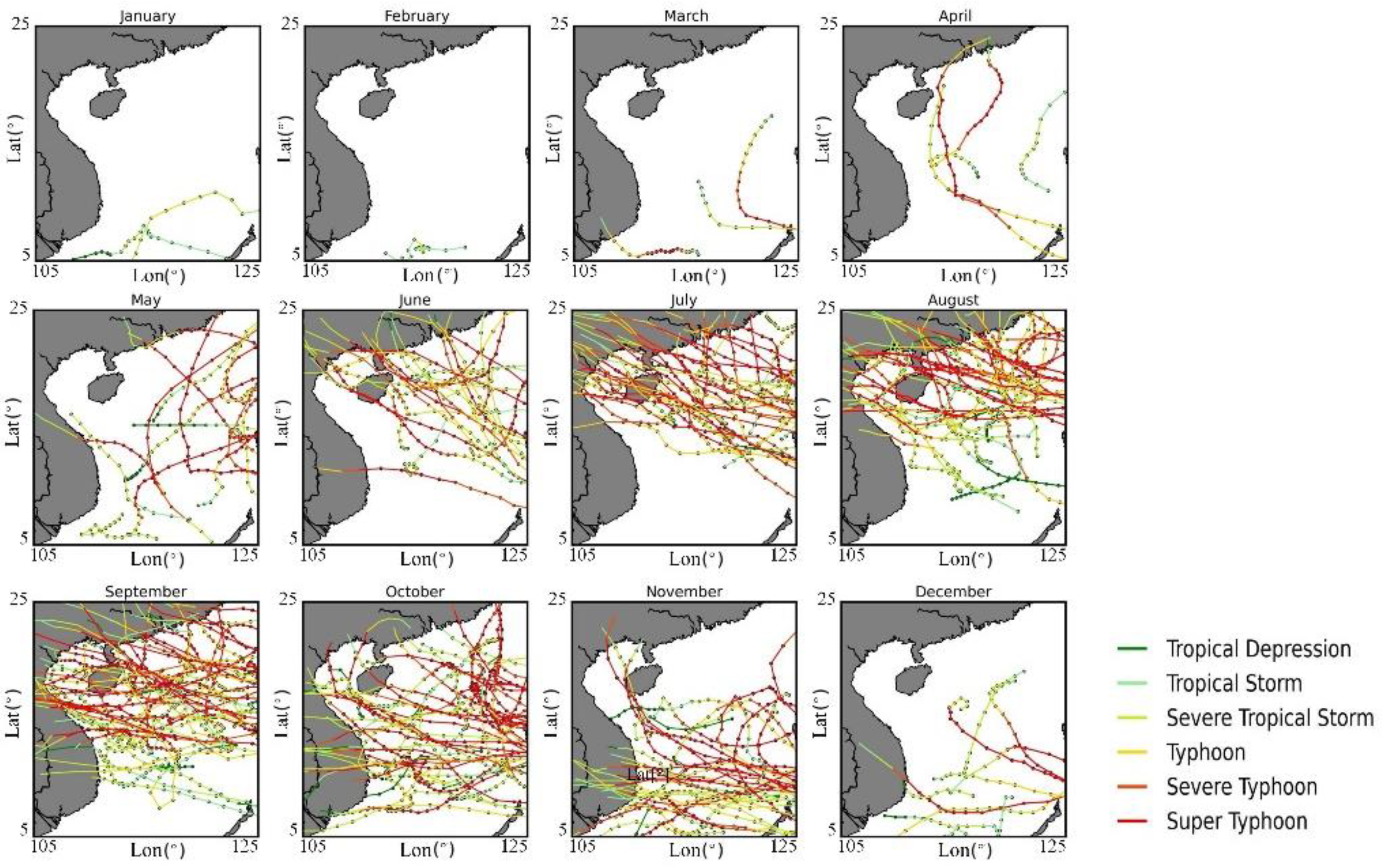
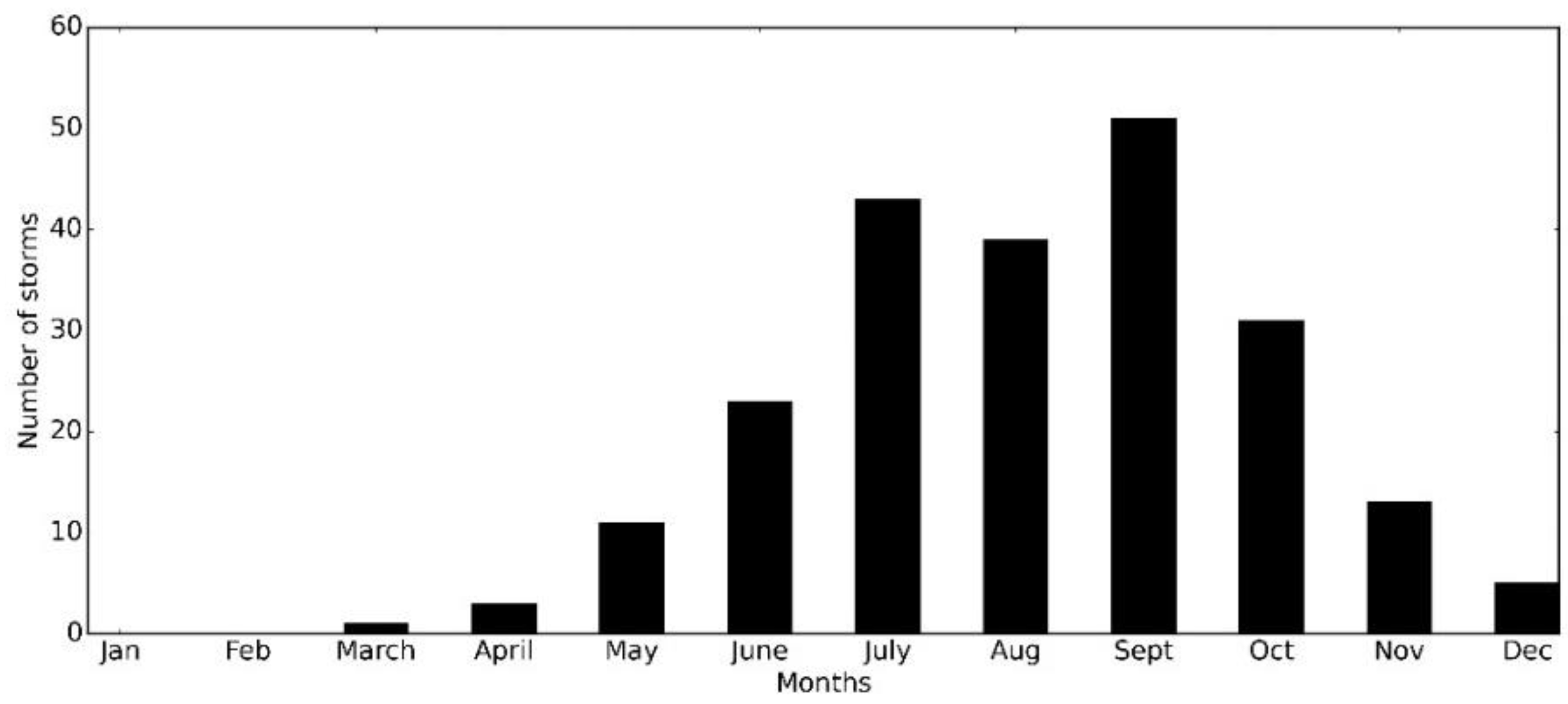
3.1. Spatio-Temporal Variations of Wind Characteristics
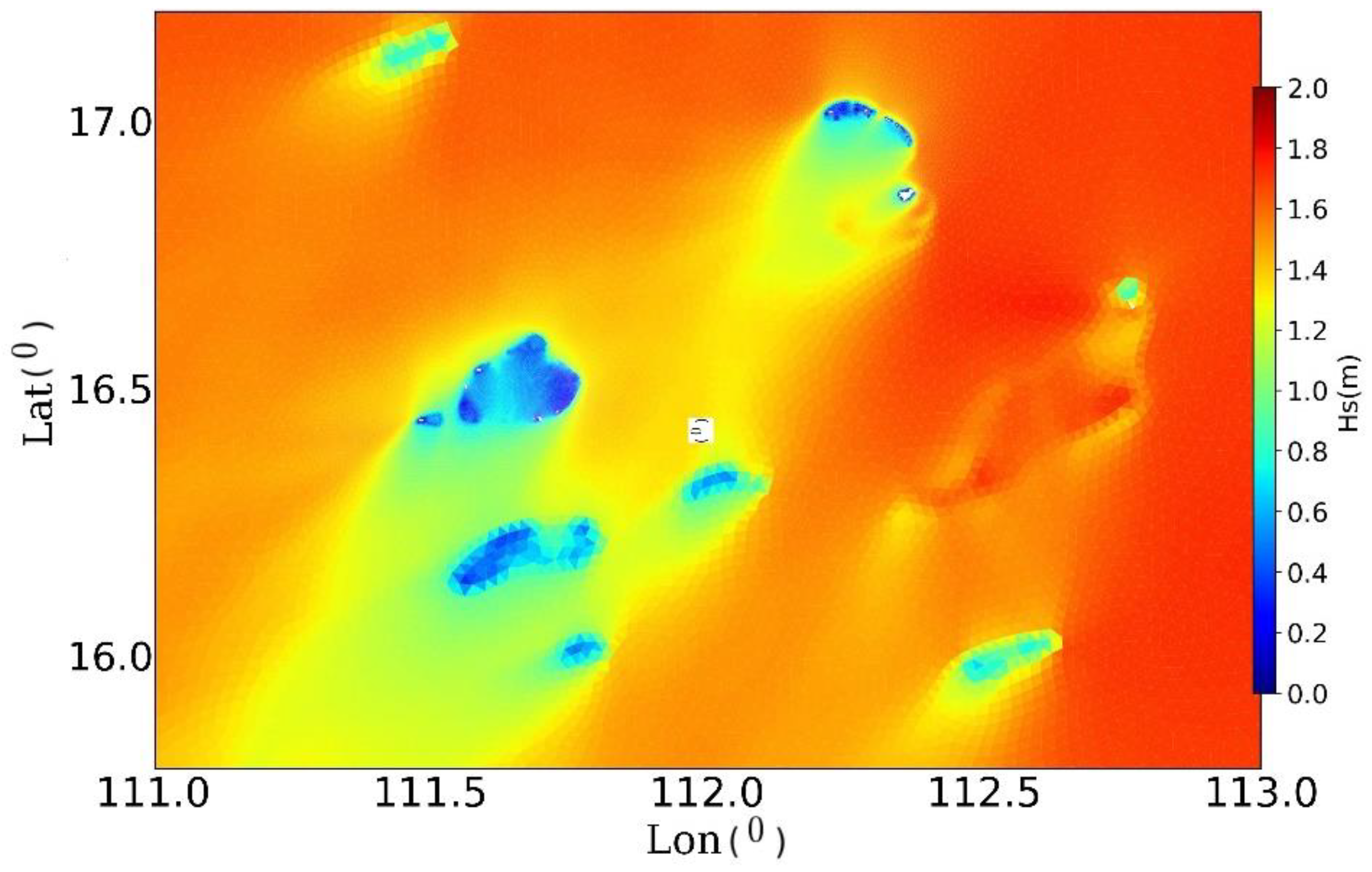
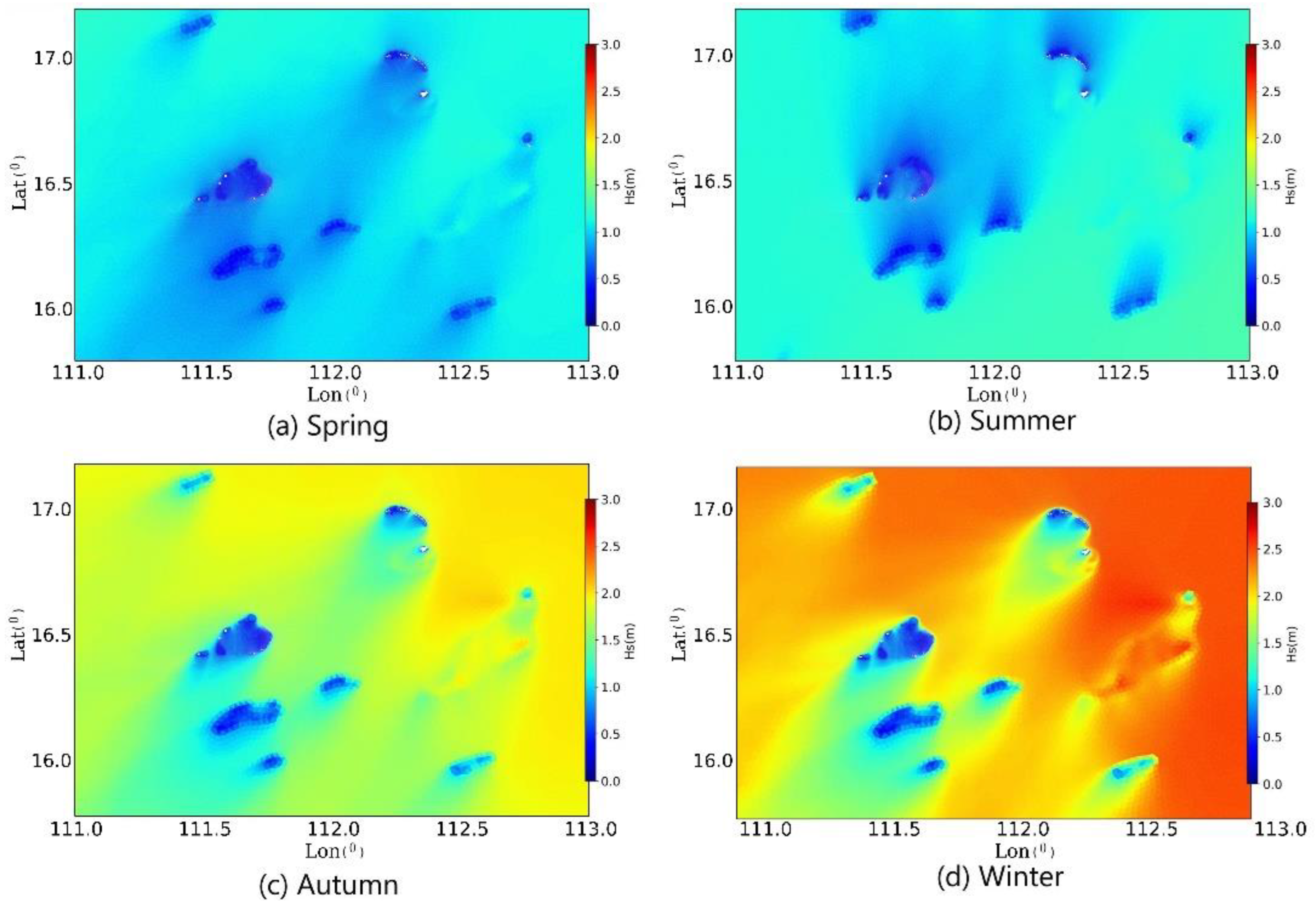
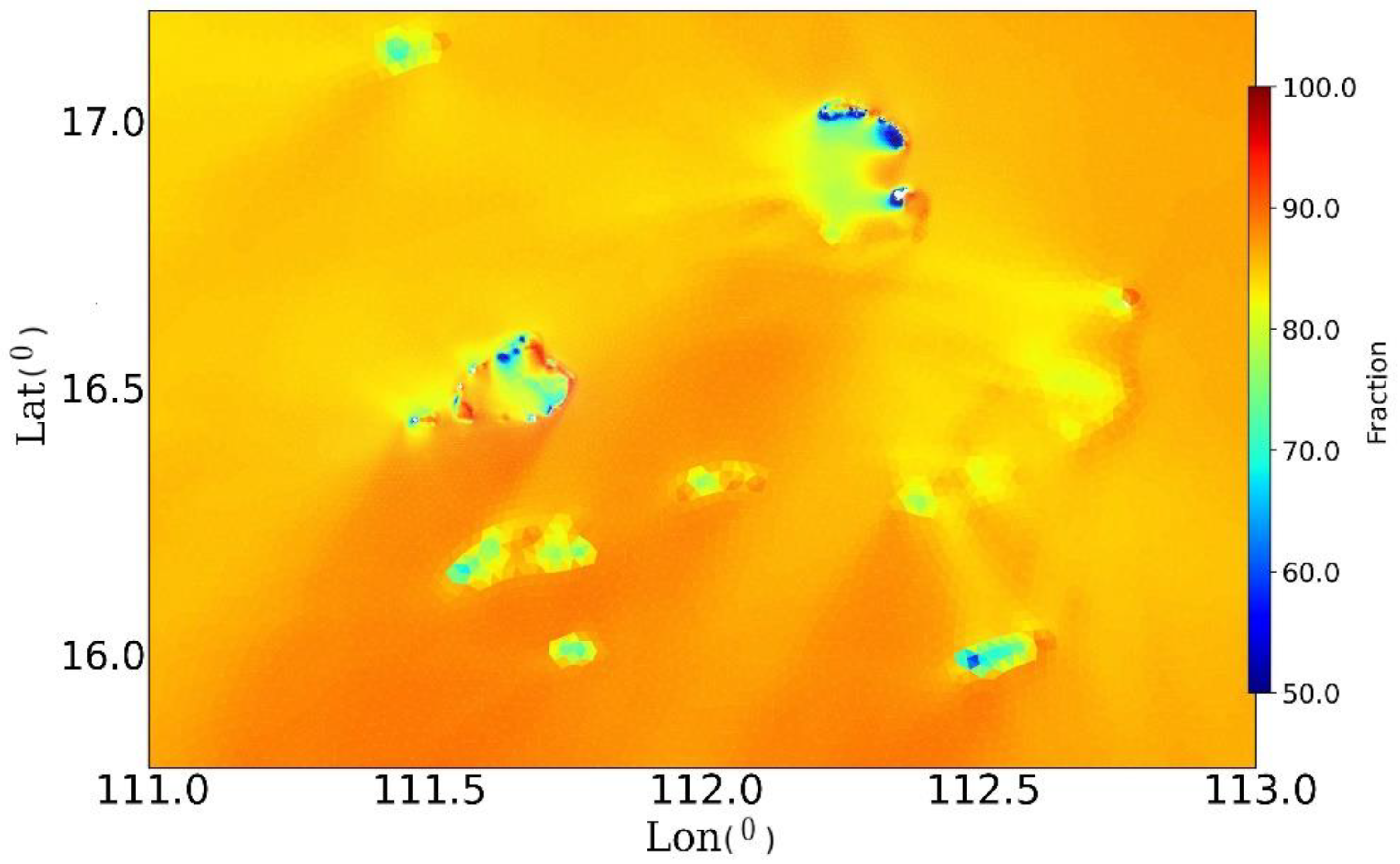
3.2. Spatio-Temporal Variations of Wave Characteristics
3.3. Long-Term Wind Characteristics
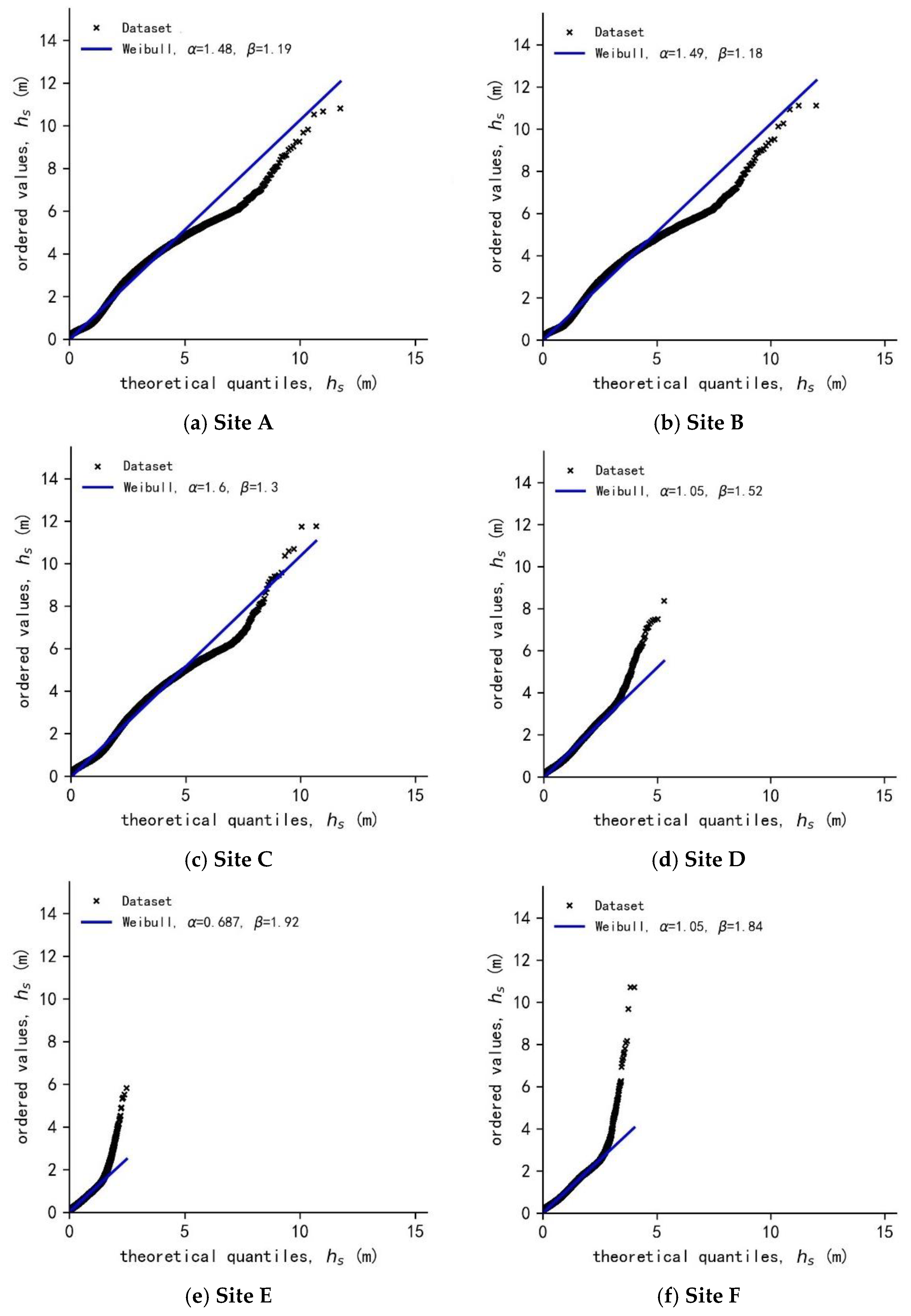
3.4. Long-Term Wave Characteristics
4. Extreme Wind and Wave Analysis
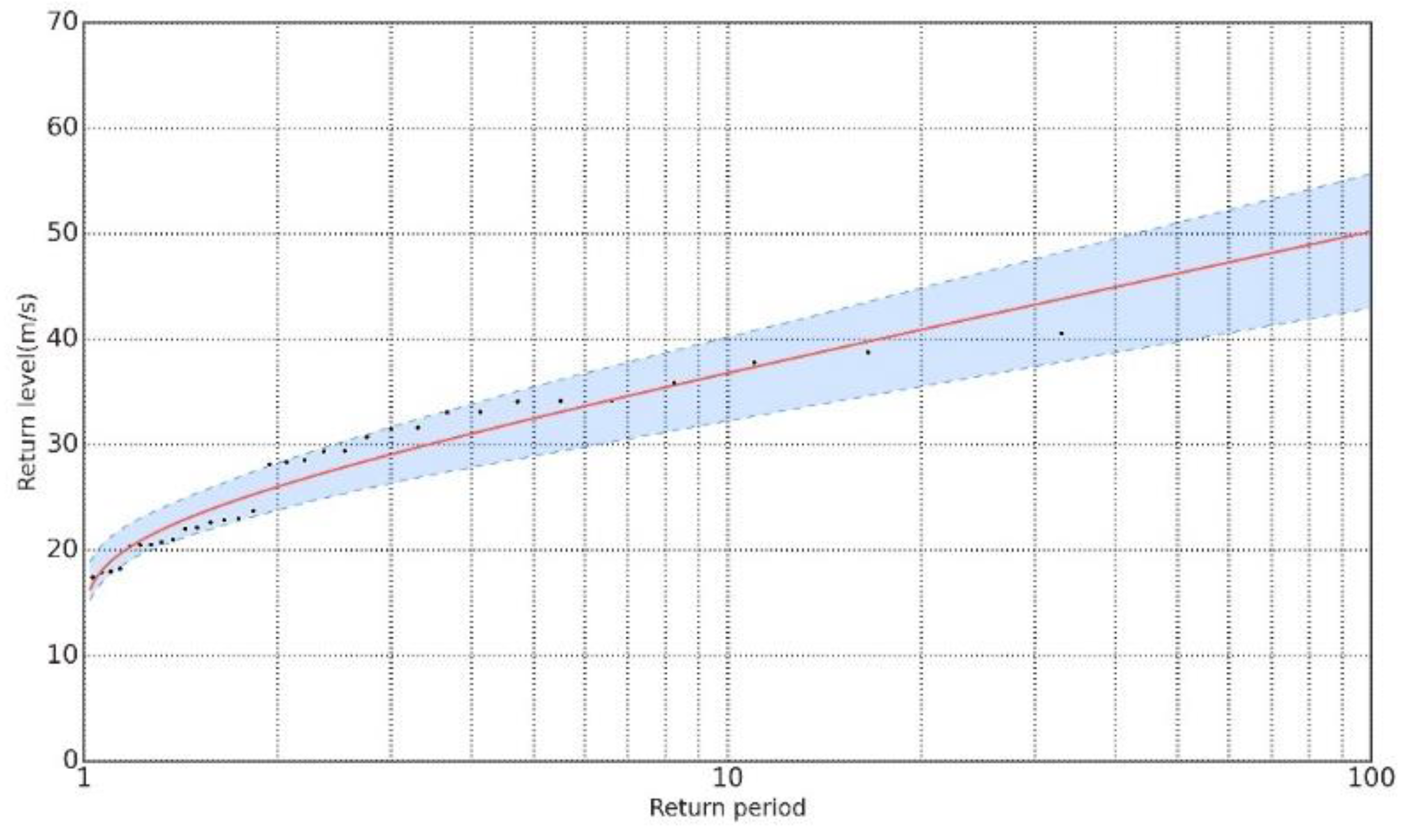
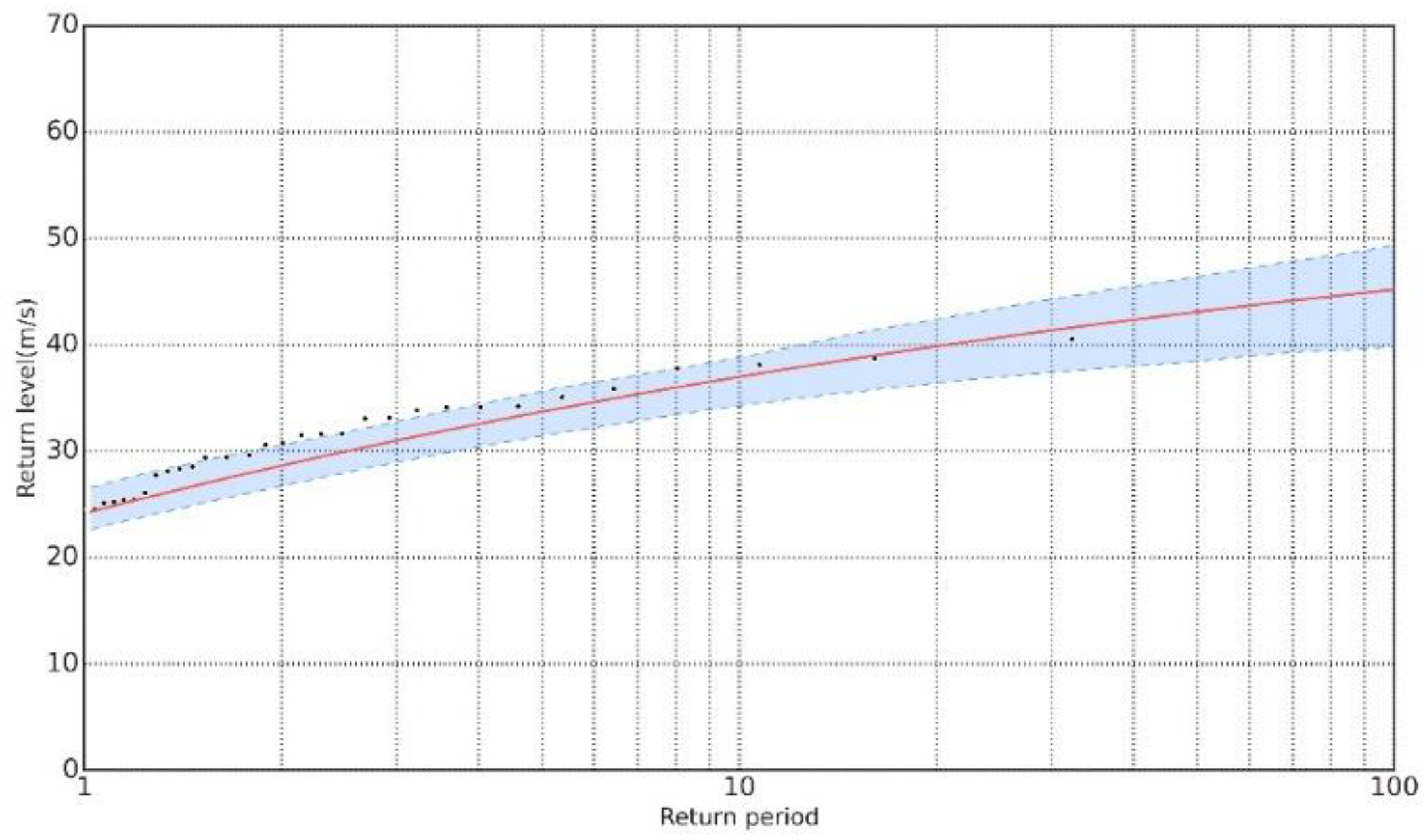
4.1. Extreme Value Analysis on Wind Speed
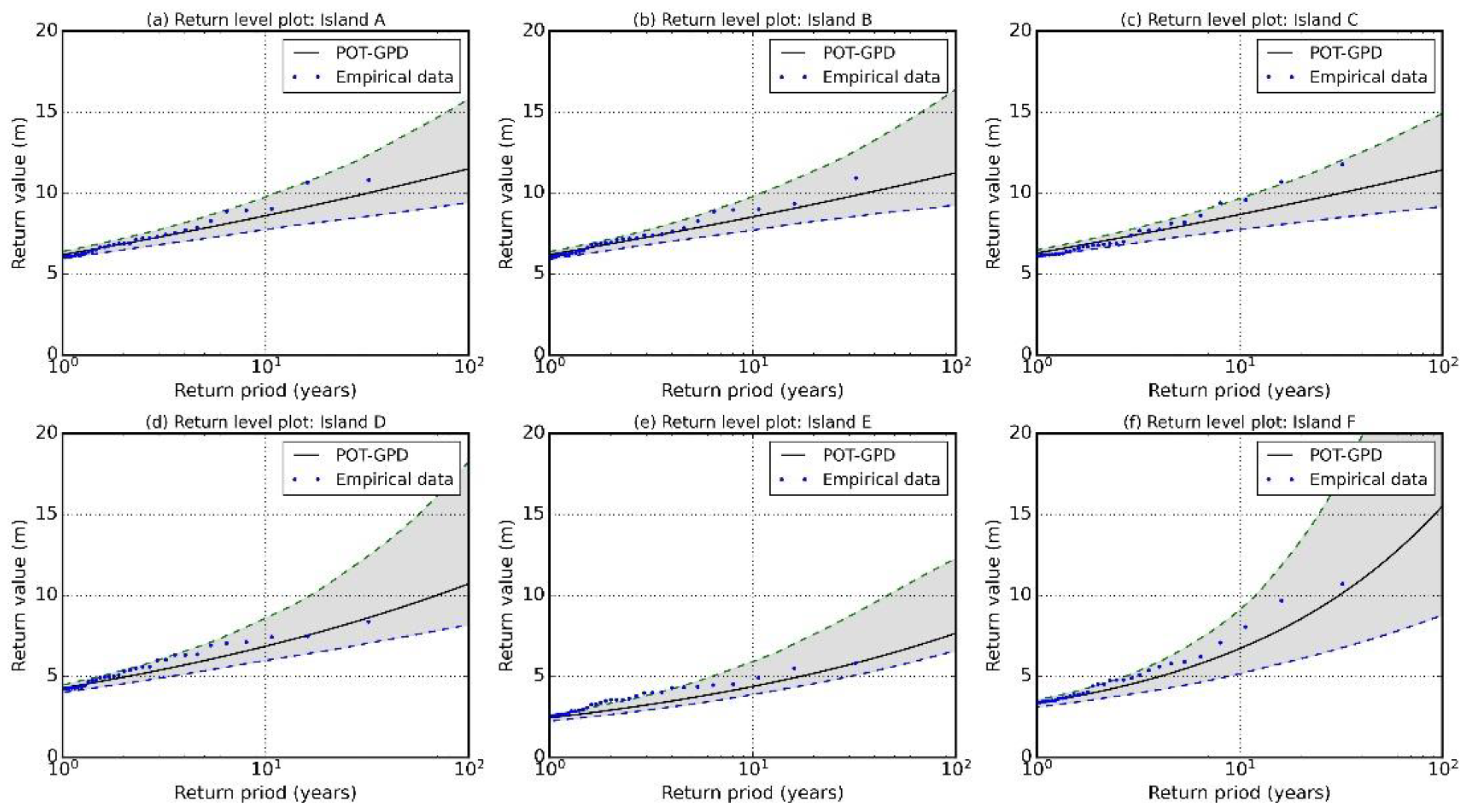
4.2. Extreme Value Analysis on Significant Wave Height
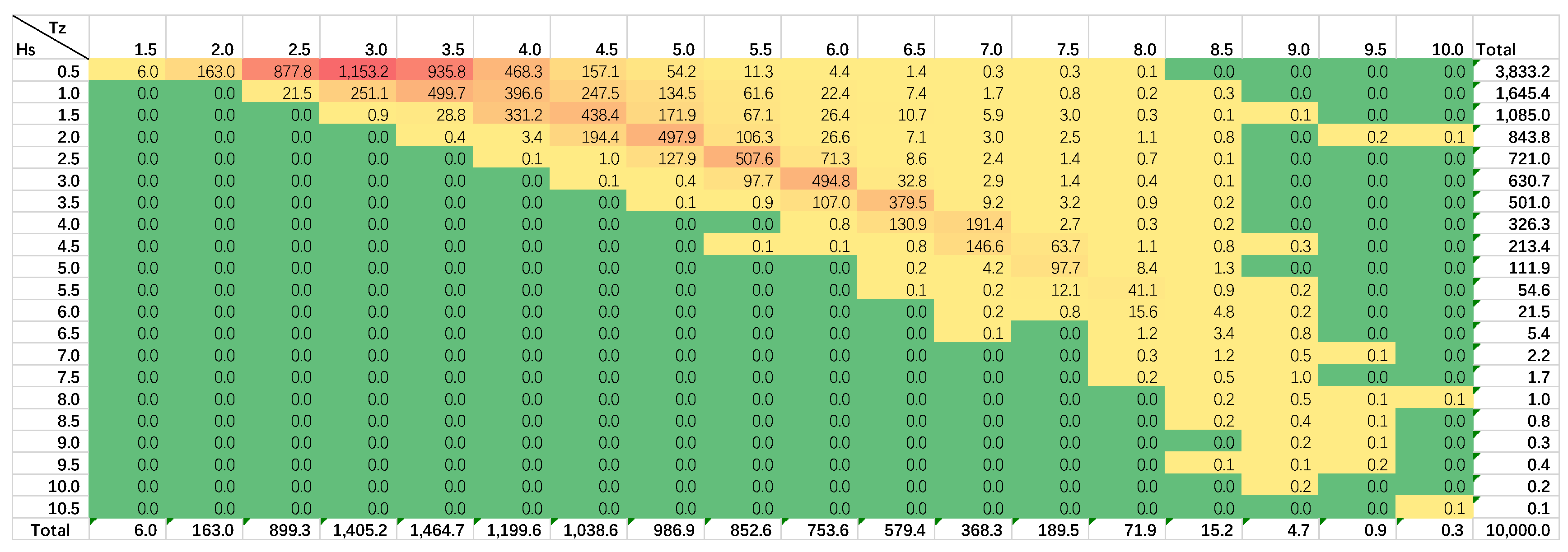
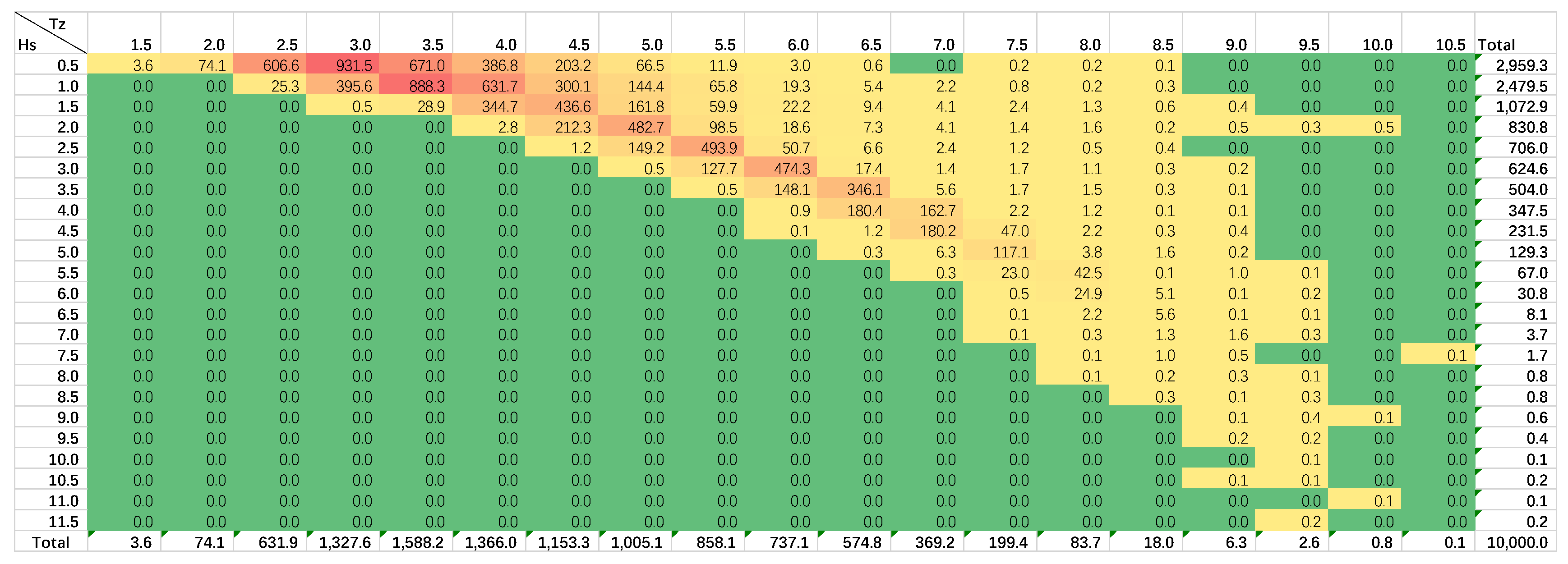
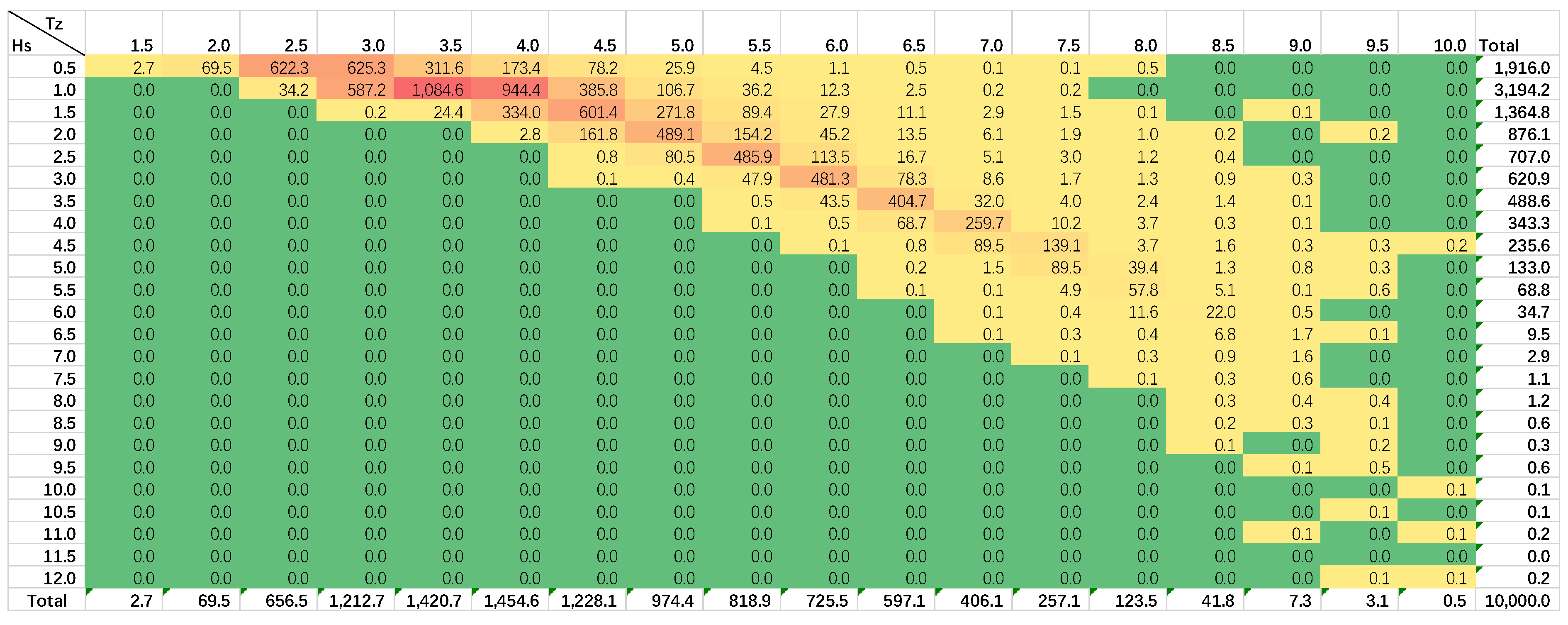
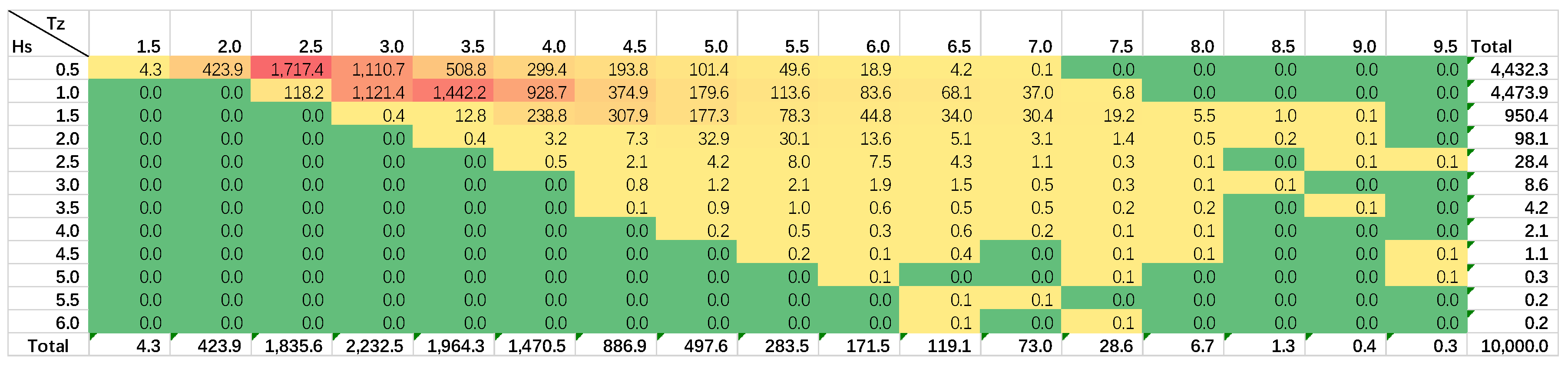
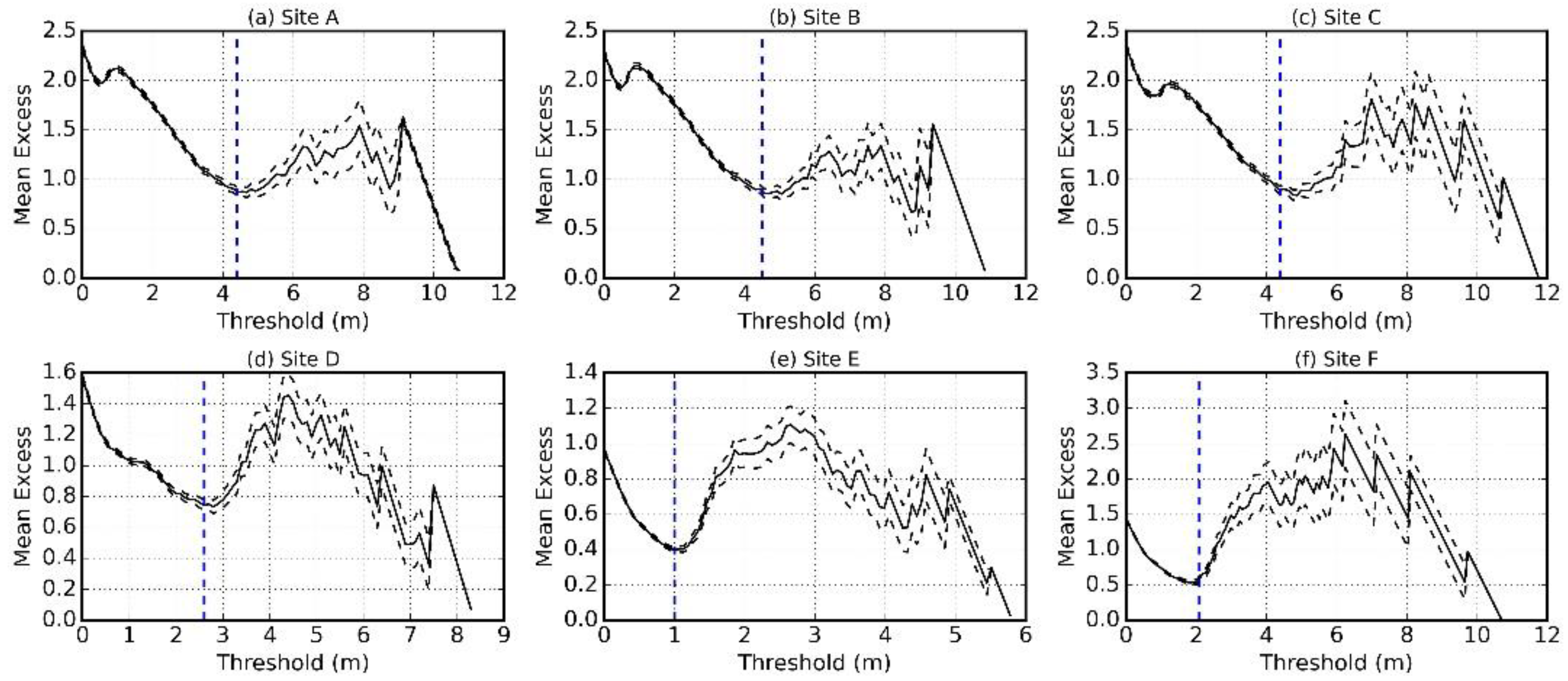
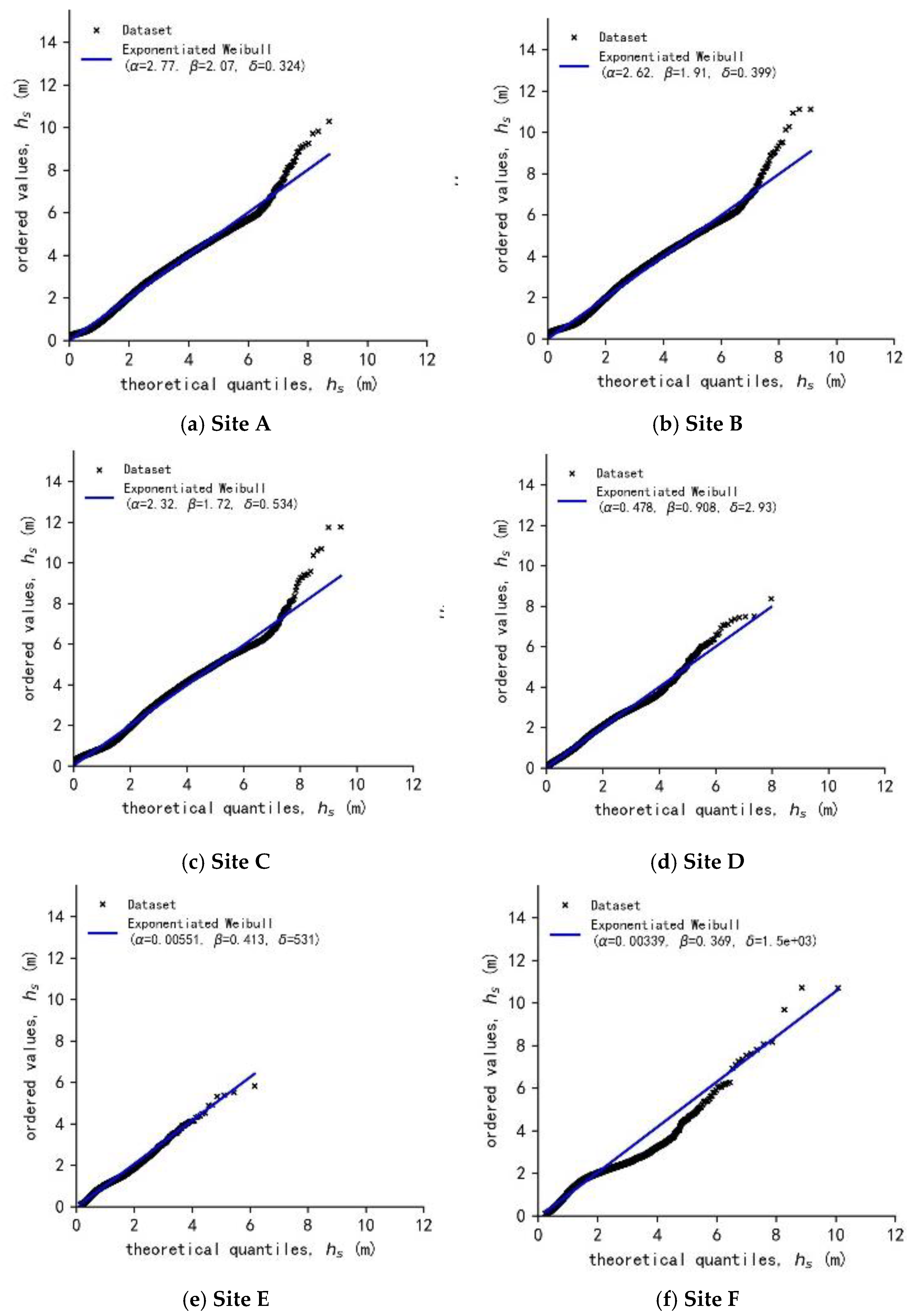
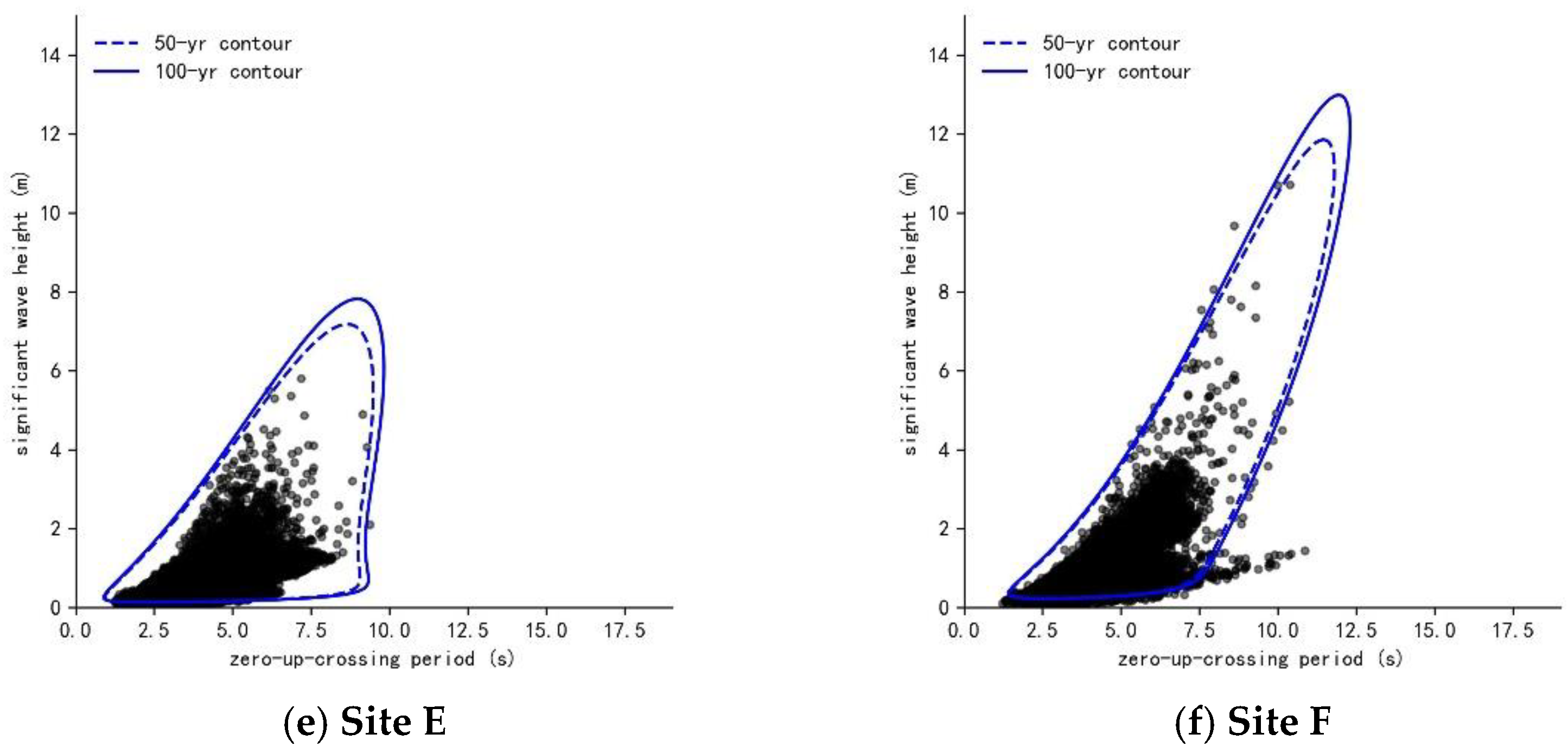
4.3. Extreme Sea-State Estimation at Selected Sites
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jonathan, P.; Ewans, K. Statistical modelling of extreme ocean environments for marine design: A review. Ocean Eng. 2013, 62, 91–109. [Google Scholar] [CrossRef]
- Shao, Z.; Liang, B.; Li, H.; Lee, D. Study of sampling methods for assessment of extreme significant wave heights in the South China Sea. Ocean Eng. 2018, 168, 173–184. [Google Scholar] [CrossRef]
- Chen, X.; Wang, K.; Zhang, Z.; Zeng, Y.; Zhang, Y.; O’Driscoll, K. An assessment of wind and wave climate as potential sources of renewable energy in the nearshore Shenzhen coastal zone of the South China Sea. Energy 2017, 134, 789–801. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Li, S.; Dong, S.; Wu, K.; Yu, H.; Wang, L.; Li, W. Extreme wave climate variability in South China Sea. Int. J. Appl. Earth Obs. 2018, 73, 586–594. [Google Scholar] [CrossRef]
- Wang, Z.; Duan, C.; Dong, S. Long-term wind and wave energy resource assessment in the South China sea based on 30-year hindcast data. Ocean Eng. 2018, 163, 58–75. [Google Scholar] [CrossRef]
- Zheng, C.; Li, C. Variation of the wave energy and significant wave height in the China Sea and adjacent waters. Renew. Sustain. Energy Rev. 2015, 43, 381–387. [Google Scholar] [CrossRef]
- Shao, Z.; Liang, B.; Li, H.; Li, P.; Lee, D. Extreme significant wave height of tropical cyclone waves in the South China Sea. Nat. Hazards Earth Syst. Sci. 2019, 19, 2067–2077. [Google Scholar] [CrossRef] [Green Version]
- Shamji, V.R.; Aboobacker, V.M.; Vineesh, T.C. Extreme value analysis of wave climate around Farasan Islands, southern Red Sea. Ocean Eng. 2020, 207, 107395. [Google Scholar] [CrossRef]
- Cieślikiewicz, W.; Paplińska-Swerpel, B. A 44-year hindcast of wind wave fields over the Baltic Sea. Coast. Eng. 2008, 55, 894–905. [Google Scholar] [CrossRef]
- Rusu, L. The wave and wind power potential in the western Black Sea. Renew. Energy 2019, 139, 1146–1158. [Google Scholar] [CrossRef]
- Bernardino, M.; Rusu, L.; Guedes Soares, C. Evaluation of extreme storm waves in the Black Sea. J. Oper. Oceanogr. 2020, 14, 114–128. [Google Scholar] [CrossRef]
- Sartini, L.; Besio, G.; Cassola, F. Spatio-temporal modelling of extreme wave heights in the Mediterranean Sea. Ocean Model. 2017, 117, 52–69. [Google Scholar] [CrossRef]
- Musić, S.; Nicković, S. 44-year wave hindcast for the Eastern Mediterranean. Coast. Eng. 2008, 55, 872–880. [Google Scholar] [CrossRef]
- Katalinić, M.; Parunov, J. Comprehensive Wind and Wave Statistics and Extreme Values for Design and Analysis of Marine Structures in the Adriatic Sea. J. Mar. Sci. Eng. 2021, 9, 522. [Google Scholar] [CrossRef]
- Divinsky, B.V.; Fomin, V.V.; Kosyan, R.D.; Ratner, Y.D. Extreme wind waves in the Black Sea. Oceanologia 2020, 62, 23–30. [Google Scholar] [CrossRef]
- Campos, R.M.; Alves, J.H.G.M.; Guedes Soares, C.; Guimaraes, L.G.; Parente, C.E. Extreme wind-wave modeling and analysis in the south Atlantic ocean. Ocean Model. 2018, 124, 75–93. [Google Scholar] [CrossRef]
- Moeini, M.H.; Etemad-Shahidi, A.; Chegini, V. Wave modeling and extreme value analysis off the northern coast of the Persian Gulf. Appl. Ocean Res. 2010, 32, 209–218. [Google Scholar] [CrossRef] [Green Version]
- Sartini, L.; Mentaschi, L.; Besio, G. Comparing different extreme wave analysis models for wave climate assessment along the Italian coast. Coast. Eng. 2015, 100, 37–47. [Google Scholar] [CrossRef]
- Cai, Z.W.; Chen, W.W.; Liu, X.L.; Sun, Z.; Ding, J. Characteristics of waves inside a lagoon of the south China sea. Ocean Eng. 2020, 208, 107404. [Google Scholar] [CrossRef]
- Cai, Z.W.; Chen, W.W.; Liu, X.L.; Sun, Z. Observations of Typhoon Waves in a Reef Lagoon of the South China Sea. J. Phys. Oceanogr. 2020, 50, 161–173. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, D.; Liu, X.; Zhang, H.; Cai, Z. Observation and simulation of wind waves near a typical reef lagoon in South China Sea. J. Hydrodyn. 2021, 33, 24–32. [Google Scholar] [CrossRef]
- Rusu, E.; Pilar, P.; Guedes Soares, C. Evaluation of the wave conditions in Madeira Archipelago with spectral models. Ocean Eng. 2008, 35, 1357–1371. [Google Scholar] [CrossRef]
- Li, N.; Cheung, K.F.; Stopa, J.E.; Hsiao, F.; Chen, Y.-L.; Vega, L.; Cross, P. Thirty-four years of Hawaii wave hindcast from downscaling of climate forecast system reanalysis. Ocean Model. 2016, 100, 78–95. [Google Scholar] [CrossRef] [Green Version]
- Smith, G.A.; Hemer, M.; Greenslade, D.; Trenham, C.; Zieger, S.; Durrant, T. Global wave hindcast with Australian and Pacific Island Focus: From past to present. Geosci. Data J. 2020, 8, 24–33. [Google Scholar] [CrossRef]
- Xiaolong, L.; Zhiwen, C.; Ze, S.; Wenwei, C.; Jun, Y.; Jun, D.; Yonglin, Y. Study on long-term distribution and short-term characteristics of the waves near islands and reefs in the SCS based on observation. Ocean Eng. 2020, 218, 108171. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; Volume 208. [Google Scholar]
- Ross, E.; Astrup, O.C.; Bitner-Gregersen, E.; Bunn, N.; Feld, G.; Gouldby, B.; Huseby, A.; Liu, Y.; Randell, D.; Vanem, E.; et al. On environmental contours for marine and coastal design. Ocean Eng. 2020, 195, 106194. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, H.; Xu, D.; Liu, X.; Ding, J. Assessment of wave power in the South China Sea based on 26-year high-resolution hindcast data. Energy 2020, 197, 117218. [Google Scholar] [CrossRef]
- Stopa, J.E.; Filipot, J.-F.; Li, N.; Cheung, K.F.; Chen, Y.-L.; Vega, L. Wave energy resources along the Hawaiian Island chain. Renew. Energy 2013, 55, 305–321. [Google Scholar] [CrossRef]
- Boccotti, P. Wave Mechanics and Wave Loads on Marine Structures; Butterworth Heinemann: London, UK, 2014. [Google Scholar]
- DNVGL. Environmental Conditions and Environmental Loads; Det Norske Veritas-Norway: Høvik, Norway, 2015. [Google Scholar]
- Winterstein, S.R.; Ude, T.C.; Bazurro, P. Ocean Environmental Contours for Structural Response Analysis and Experiment Design. In Proceedings of the 7th ASCE Probabilistic Mechanics Specialty Conference, Worcester, MA, USA, 7–9 August 1996. [Google Scholar]
- Huang, W.; Dong, S. Joint distribution of significant wave height and zero-up-crossing wave period using mixture copula method. Ocean Eng. 2021, 219, 108305. [Google Scholar] [CrossRef]
- Wrang, L.; Katsidoniotaki, E.; Nilsson, E.; Rutgersson, A.; Rydén, J.; Göteman, M. Comparative Analysis of Environmental Contour Approaches to Estimating Extreme Waves for Offshore Installations for the Baltic Sea and the North Sea. J. Mar. Sci. Eng. 2021, 9, 96. [Google Scholar] [CrossRef]
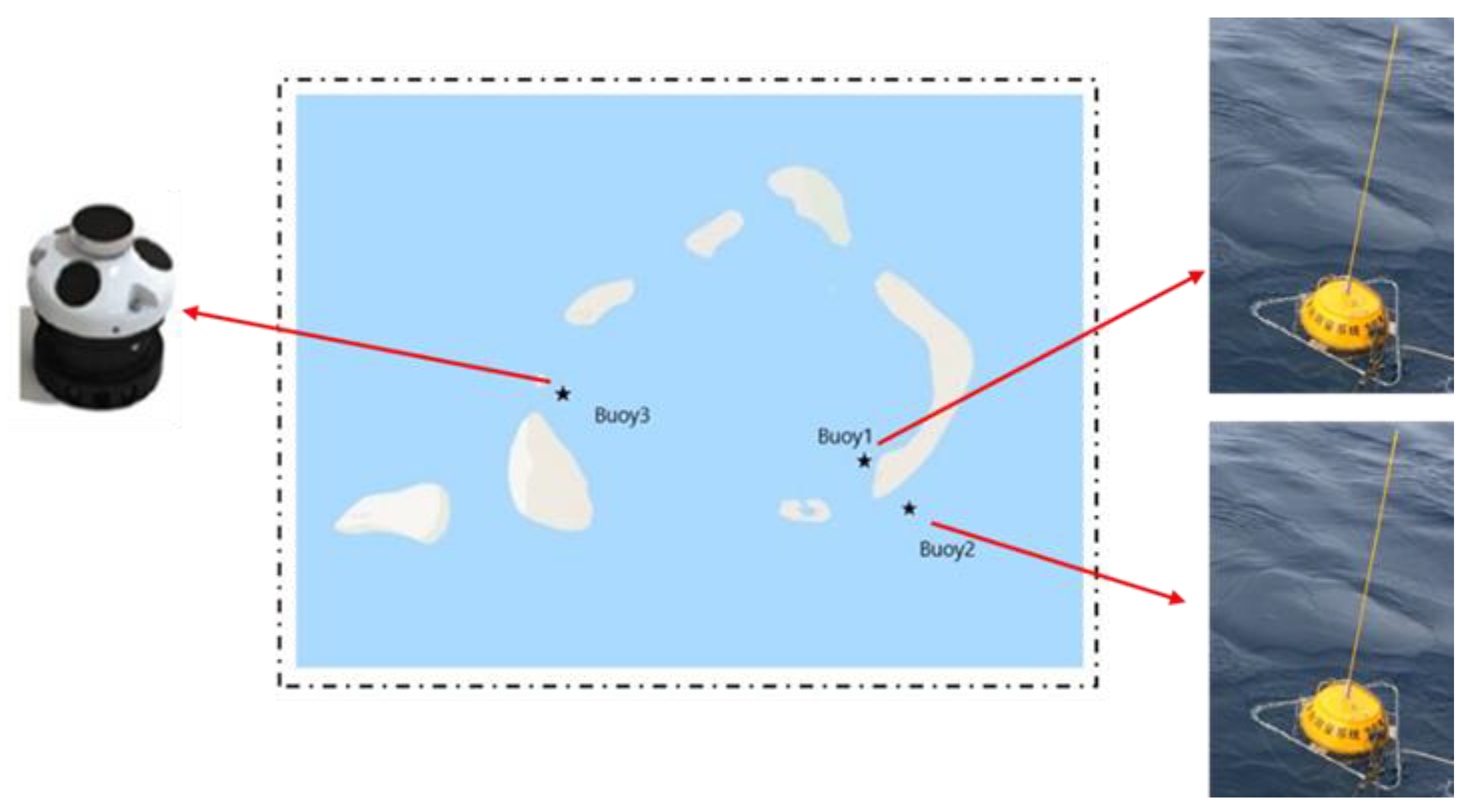
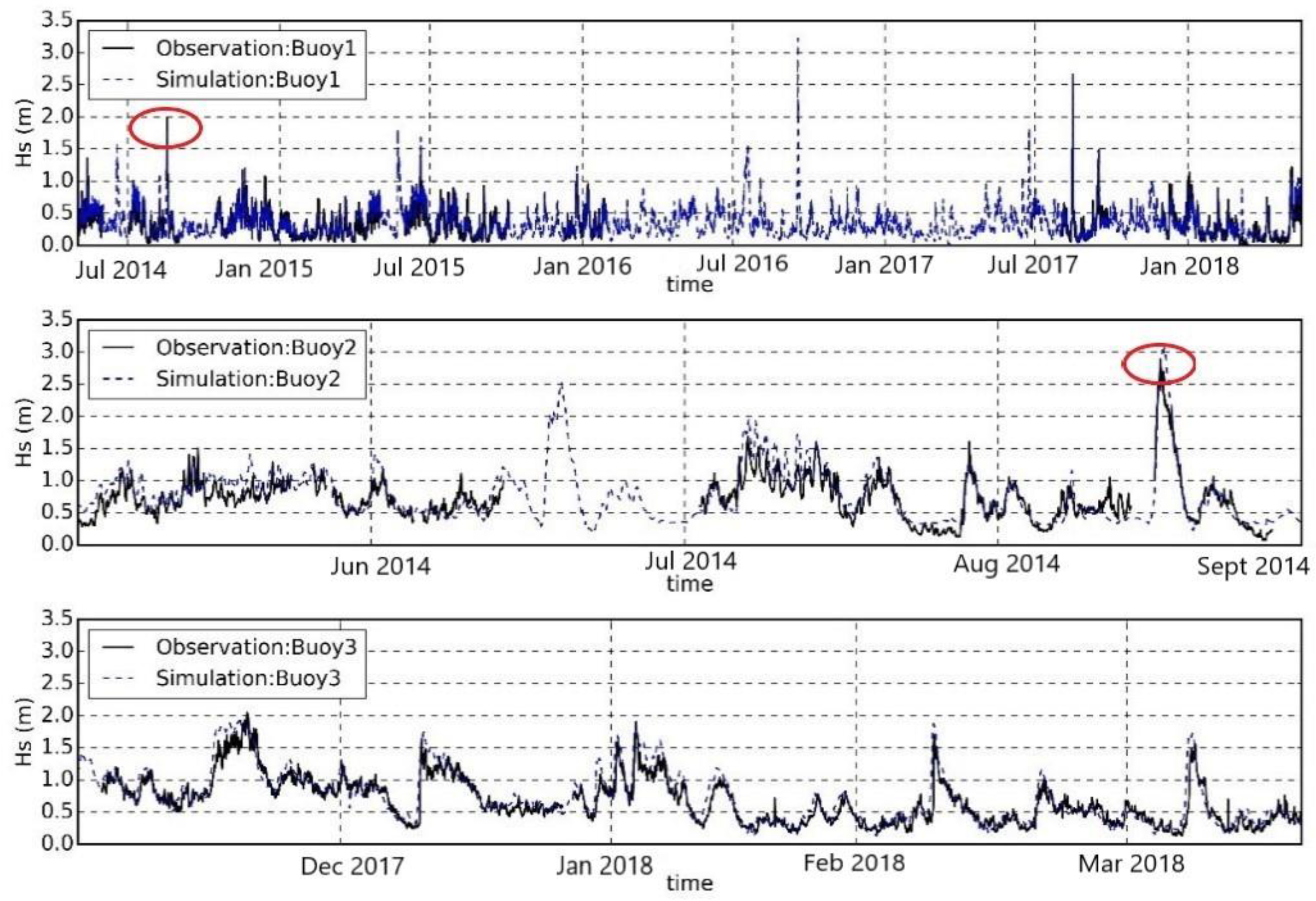









| Index | Number of Sea States | Correlation | Y–X Stdev (m) | Bias | Root Mean Square Error | Scatter Index |
|---|---|---|---|---|---|---|
| Buoy1 | 16,815 | 0.881 | 0.119 | 0.021 | 0.087 | 0.292 |
| Buoy2 | 2371 | 0.904 | 0.206 | 0.076 | 0.159 | 0.213 |
| Buoy3 | 3312 | 0.922 | 0.167 | 0.025 | 0.116 | 0.191 |
| Month | Frequency (%) | Maximum (m/s) | Mean(m/s) | Standard Deviation (m/s) | ||||
|---|---|---|---|---|---|---|---|---|
| Class < 3 | 3 < Class < 6 | 6 < Class < 7 | 7 < Class < 8 | 8 < Class | ||||
| U < 5.4 m/s | 5.5 m/s < U < 13.8 m/s | 13.9 m/s < U < 17.1 m/s | 17.2 m/s < U < 20.7 m/s | 20.8 m/s < U | ||||
| January | 14.54 | 78.47 | 5.27 | 1.72 | 0.00 | 20.76 | 8.78 | 3.07 |
| February | 27.21 | 69.71 | 3.04 | 0.04 | 0.00 | 18.26 | 7.54 | 3.01 |
| April | 34.79 | 63.89 | 1.28 | 0.04 | 0.00 | 17.85 | 6.66 | 2.58 |
| March | 44.84 | 54.58 | 0.54 | 0.04 | 0.00 | 34.13 | 5.93 | 2.29 |
| May | 49.15 | 50.45 | 0.18 | 0.22 | 0.00 | 28.22 | 5.67 | 2.42 |
| June | 28.24 | 70.74 | 0.48 | 0.35 | 0.19 | 37.80 | 6.84 | 2.65 |
| July | 35.44 | 63.07 | 0.98 | 0.37 | 0.14 | 33.07 | 6.51 | 2.87 |
| August | 43.42 | 55.12 | 1.01 | 0.20 | 0.25 | 31.6 | 6.16 | 3.04 |
| September | 56.59 | 40.86 | 1.46 | 0.67 | 0.42 | 40.57 | 5.51 | 3.29 |
| October | 26.97 | 68.44 | 3.11 | 0.92 | 0.56 | 38.11 | 7.76 | 3.55 |
| November | 13.32 | 75.93 | 9.26 | 1.07 | 0.42 | 38.76 | 9.56 | 3.56 |
| December | 7.33 | 76.61 | 14.08 | 1.88 | 0.10 | 35.88 | 10.49 | 3.33 |
| Total | 31.81 | 64.11 | 3.40 | 0.50 | 0.18 | 40.57 | 7.28 | 3.37 |
| Location | Water Depth (m) | |
|---|---|---|
| Xuande Atoll | Site A | 41.75 |
| Site B | 41.77 | |
| Site C | 44.25 | |
| Yongle Atoll | Site D | 52.45 |
| Site E | 29.91 | |
| Site F | 44.32 | |
| Xuande Atoll | Yongle Atoll | ||||||
|---|---|---|---|---|---|---|---|
| 100-Year Return Level (m) | Site A | Site B | Site C | Site D | Site E | Site F | |
| GEV | Lower Bound of 95% confidence intervals | 8.76 | 9.19 | 9.20 | 7.34 | 4.92 | 6.61 |
| Best fit | 13.10 | 13.69 | 14.14 | 10.87 | 6.77 | 12.78 | |
| Upper Bound of 95% confidence intervals | 21.99 | 23.16 | 24.88 | 17.96 | 9.43 | 25.01 | |
| POT-GPD | Lower Bound of 95% confidence intervals | 9.40 | 9.26 | 9.15 | 8.17 | 6.57 | 8.77 |
| Best fit | 11.49 | 11.23 | 11.42 | 10.70 | 7.65 | 15.52 | |
| Upper Bound of 95% confidence intervals | 15.80 | 16.39 | 14.90 | 18.24 | 12.26 | 33.41 | |
| Location | Weibull Distribution | Exponentiated Weibull Distribution | ||||
|---|---|---|---|---|---|---|
| α (Scale) | Β (Shape) | α (Scale) | β (Shape1) | δ (Shape2) | ||
| Xuande Atoll | Site A | 1.48 | 1.19 | 2.77 | 2.07 | 0.324 |
| Site B | 1.49 | 1.18 | 2.62 | 1.91 | 0.399 | |
| Site C | 1.6 | 1.3 | 2.32 | 1.72 | 0.534 | |
| Yongle Atoll | Site D | 1.05 | 1.52 | 0.478 | 0.908 | 2.93 |
| Site E | 0.687 | 1.92 | 0.00551 | 0.413 | 531 | |
| Site F | 1.05 | 1.84 | 0.00339 | 0.369 | 1500 | |
| Xuande Atoll | Yongle Atoll | ||||||
|---|---|---|---|---|---|---|---|
| Method | Parameter | Site A | Site B | Site C | Site D | Site E | Site F |
| Environmental Contour | Hs (m) | 13.29 | 13.58 | 11.95 | 9.25 | 7.82 | 12.98 |
| Tz (s) | 10.89 | 10.85 | 10.70 | 10.25 | 8.98 | 11.94 | |
| GEV | Hs (m) | 13.10 | 13.69 | 14.14 | 10.87 | 6.77 | 12.78 |
| POT-GPD | Hs (m) | 11.49 | 11.23 | 11.42 | 10.70 | 7.65 | 15.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Bian, M.; Ding, J.; Liu, J.; Zhang, H.; Xu, D. Study on the Wind and Wave Environmental Conditions of the Xisha Islands in the South China Sea. J. Mar. Sci. Eng. 2022, 10, 1459. https://doi.org/10.3390/jmse10101459
Sun Z, Bian M, Ding J, Liu J, Zhang H, Xu D. Study on the Wind and Wave Environmental Conditions of the Xisha Islands in the South China Sea. Journal of Marine Science and Engineering. 2022; 10(10):1459. https://doi.org/10.3390/jmse10101459
Chicago/Turabian StyleSun, Ze, Mengchun Bian, Jun Ding, Jiarui Liu, Haicheng Zhang, and Daolin Xu. 2022. "Study on the Wind and Wave Environmental Conditions of the Xisha Islands in the South China Sea" Journal of Marine Science and Engineering 10, no. 10: 1459. https://doi.org/10.3390/jmse10101459
APA StyleSun, Z., Bian, M., Ding, J., Liu, J., Zhang, H., & Xu, D. (2022). Study on the Wind and Wave Environmental Conditions of the Xisha Islands in the South China Sea. Journal of Marine Science and Engineering, 10(10), 1459. https://doi.org/10.3390/jmse10101459









