Influence of Stratification and Bottom Boundary Layer on the Classical Ekman Model
Abstract
:1. Introduction
- Numerically solve the equations of the classical Ekman model considering the turbulent viscosity coefficient as a function of depth and boundary conditions.
- Development of a layered profile for turbulent viscosity coefficient.
- Determine the deviation of the surface current of the modified Ekman model spiral.
- Determine the transport deviation for Ekman’s modified model.
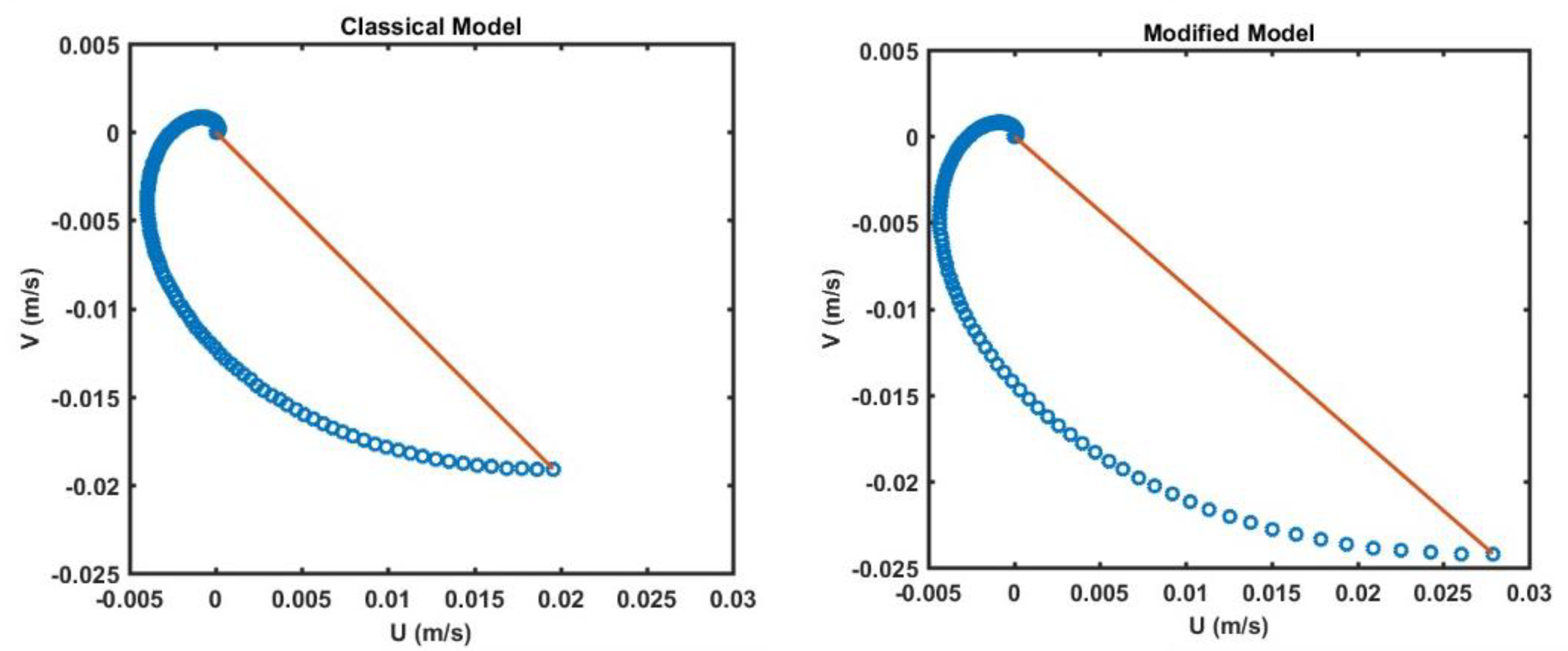
- Contrast the velocity profile for the classic and modified Ekman model.
2. Materials and Methods
2.1. Ekman Modified Model
2.2. Eddy Viscosity Coefficient
3. Results and Discussion
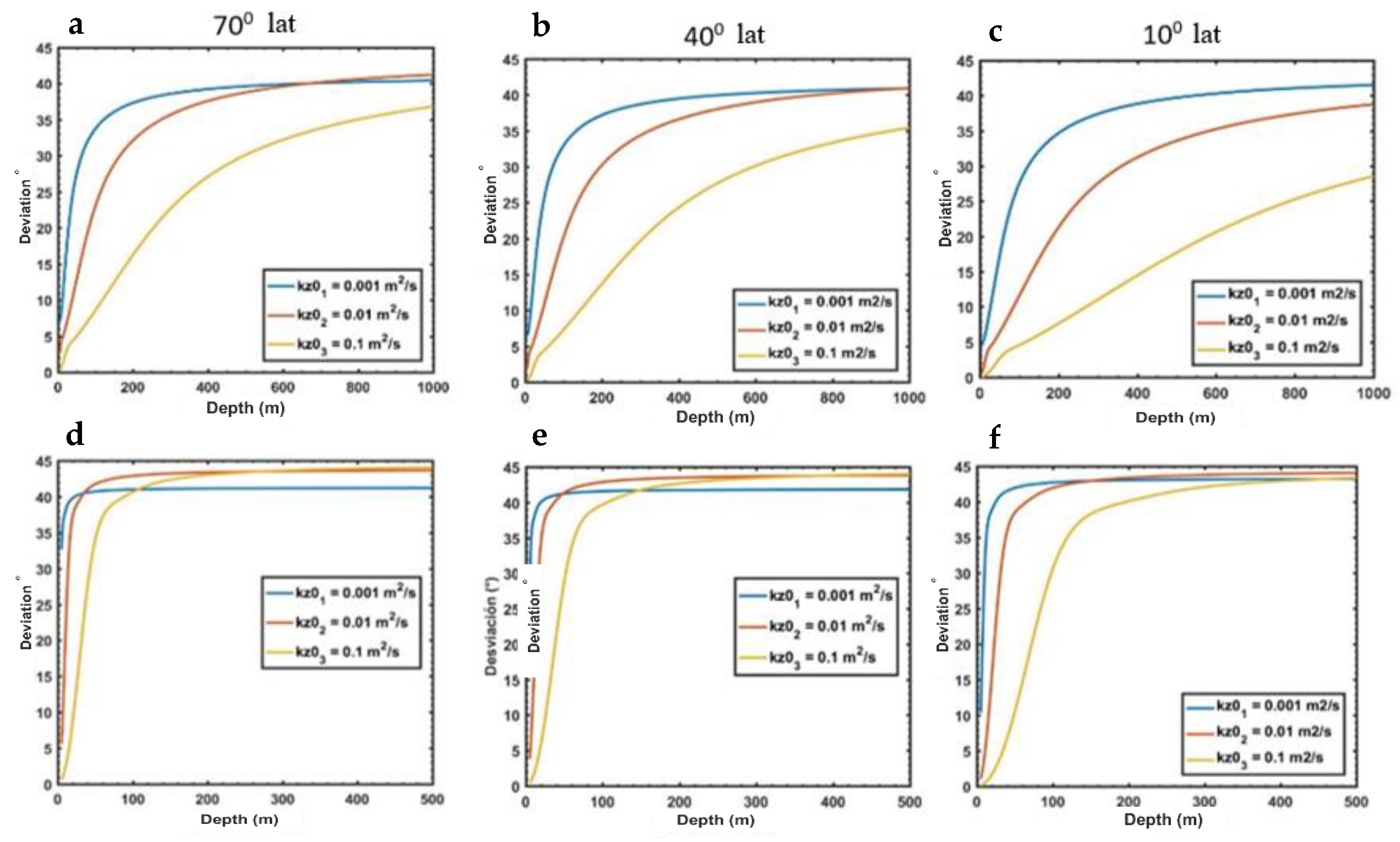
3.1. Superficial Ekman Current Deviation
3.2. Ekman Transport
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Lavergne, C.; Groeskamp, S.; Zika, J.; Johnson, H.L. The role of mixing in the large-scale ocean circulation. Ocean Mix. 2022, 3, 35–63. [Google Scholar]
- Ekman, V.W. On the Influence of the Earth’s Rotation on Ocean-Currents: With a Biography of the Author; Almqvist Wiksells boktr: Stockholm, Sweden, 1951. [Google Scholar]
- Wang, W.; Huang, R.X. Wind energy input to the Ekman layer. J. Phys. Oceanogr. 2004, 34, 1267–1275. [Google Scholar] [CrossRef]
- Dritschel, D.G.; Paldor, N.; Constantin, A. The Ekman spiral for piecewise-uniform viscosity. Ocean Sci. 2020, 16, 1089–1093. [Google Scholar] [CrossRef]
- Stewart, R.H. Introduction to Physical Oceanography; Robert, H., Ed.; Stewart: Louisville, KY, USA, 2008. [Google Scholar]
- Jacox, M.G.; Edwards, C.A.; Hazen, E.L.; Bograd, S.J. Coastal upwelling revisited: Ekman, Bakun, and improved upwelling indices for the U.S. West Coast. J. Geophys. Res. Ocean. 2018, 123, 7332–7350. [Google Scholar] [CrossRef]
- Alvarez, I.; Gomez-Gesteira, M.; DeCastro, M.; Lorenzo, M.N.; Crespo AJ, C.; Dias, J.M. Comparative analysis of upwelling influence between the western and northern coast of the Iberian Peninsula. Cont. Shelf Res. 2011, 31, 388–399. [Google Scholar] [CrossRef]
- Elkin, D.N.; Zatsepin, A.G.; Podymov, O.I.; Ostrovskii, A.G. Sinking of less dense water in the bottom Ekman layer formed by a coastal downwelling current over a sloping bottom. Oceanology 2017, 57, 478–484. [Google Scholar] [CrossRef]
- Austin, J.A.; Lentz, S.J. The inner shelf response to wind-driven upwelling and downwelling. J. Phys. Oceanogr. 2002, 32, 2171–2193. [Google Scholar] [CrossRef]
- Colling, A. Ocean Circulation (Vol. 3); Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
- DeWitt, P.W.; Leetmaa, A. A simple Ekman-type model for predicting thermocline displacement in the tropical Pacific. J. Phys. Oceanogr. 1978, 8, 811–817. [Google Scholar] [CrossRef]
- Woods, J.D.; Strass, V. The response of the upper ocean to solar heating II: The wind-driven current. Q. J. R. Meteorol. Soc. 1986, 112, 29–42. [Google Scholar]
- Zhang, Y.; Song, Z.; Wu, K.; Shi, Y. Influences of random surface waves on the estimates of wind energy input to the Ekman layer in the Antarctic circumpolar current region. J. Geophys. Res. Ocean. 2019, 124, 3393–3410. [Google Scholar] [CrossRef]
- Bryan, K.; Lewis, L.J. A water mass model of the world ocean. J. Geophys. Res. Ocean. 1979, 84, 2503–2517. [Google Scholar] [CrossRef]
- Ruiz, C.; Artal, O.; Pinilla, E.; Sepúlveda, H.H. Stratification and mixing in the Chilean Inland Sea using an operational model. Ocean Model. 2021, 158, 101750. [Google Scholar] [CrossRef]
- Li, G.; Cheng, L.; Zhu, J.; Trenberth, K.E.; Mann, M.E.; Abraham, J.P. Increasing ocean stratification over the past half-century. Nat. Clim. Chang. 2020, 10, 1116–1123. [Google Scholar] [CrossRef]
- Brown, J. Ocean Circulation: Prepared by an Open University Course Team; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Chen, W.; De Swart, H.E. Dynamic links between shape of the eddy viscosity profile and the vertical structure of tidal current amplitude in bays and estuaries. Ocean Dyn. 2016, 66, 299–312. [Google Scholar] [CrossRef]
- Yu, L.; O’Brien, J.J. Variational estimation of the wind stress drag coefficient and the oceanic eddy viscosity profile. J. Phys. Oceanogr. 1991, 21, 709–719. [Google Scholar] [CrossRef]
- Ianniello, J.P. Tidally Induced Residual Currents in Estuaries of Constant Breadth and Depth. J. Mar. Res. 1977, 35, 755–786. [Google Scholar]
- Cheng, P.; de Swart, H.E.; Valle-Levinson, A. Role of asymmetric tidal mixing in the subtidal dynamics of narrow estuaries. J. Geophys. Res. Ocean. 2013, 118, 2623–2639. [Google Scholar] [CrossRef] [Green Version]
- Caballero, R. Physics of the Atmosphere; IOP Publishing: Bristol, UK, 2014; Volume 150. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santander-Rodríguez, V.; Díez-Minguito, M.; Espinoza-Andaluz, M. Influence of Stratification and Bottom Boundary Layer on the Classical Ekman Model. J. Mar. Sci. Eng. 2022, 10, 1388. https://doi.org/10.3390/jmse10101388
Santander-Rodríguez V, Díez-Minguito M, Espinoza-Andaluz M. Influence of Stratification and Bottom Boundary Layer on the Classical Ekman Model. Journal of Marine Science and Engineering. 2022; 10(10):1388. https://doi.org/10.3390/jmse10101388
Chicago/Turabian StyleSantander-Rodríguez, Viviana, Manuel Díez-Minguito, and Mayken Espinoza-Andaluz. 2022. "Influence of Stratification and Bottom Boundary Layer on the Classical Ekman Model" Journal of Marine Science and Engineering 10, no. 10: 1388. https://doi.org/10.3390/jmse10101388
APA StyleSantander-Rodríguez, V., Díez-Minguito, M., & Espinoza-Andaluz, M. (2022). Influence of Stratification and Bottom Boundary Layer on the Classical Ekman Model. Journal of Marine Science and Engineering, 10(10), 1388. https://doi.org/10.3390/jmse10101388









