Adaptive Integral Sliding Mode Based Course Keeping Control of Unmanned Surface Vehicle
Abstract
:1. Introduction
- Waypoint control: In this strategy, Line of Sight (LOS) based approach is adopted to follow a certain waypoints, generated heuristically, in the required maritime environment.
- Path following control: In this strategy, a path generated through path planning algorithms is used as a reference, to be followed with no temporal constraints. Here, USV should converge and follow the desired path without any time constraints and simultaneously satisfies its assigned velocity profile.
- Trajectory tracking: In this strategy, temporal constraints are enforced upon the path generated using path planners. This is predominantly used with fully actuated marine vehicles reasoned with better maneuvering capabilities.
1.1. State of the Art
1.2. Major Contributions
- A number of simulation studies in the manuscript demonstrate that the proposed adaptive control approach can be reconfigured for various input trajectories and marine environmental disturbances, without requiring parametric adjustment.
- The cut-off frequency of the system response is an indication of the bound to be assigned to the disturbance derivative in the algorithm. This relationship is based on low-pass filtering properties associated with the second order adaptive linear dynamics generated at the sliding variable. As a result, frequencies over do not affect the sliding variable response. In practice, this feature offers some advantages when estimating the maximum value of the disturbance derivative is a challenging task.
- The proposed adaptive profile generates low/high gains based on the absolute error. As a result, the control input is not saturated when there is a large error (gain is small) and the response at steady state becomes fast disturbance compensation (gain is large).
- Based on the adaptive placement of two poles relating to a second order dynamical system with critical damping, we can generate an overdamped response that avoids the occurrence of considerable overshoots.
- By avoiding the need of the derivative of the fractional power terms with respect to time, the singularity problem associated with terminal sliding mode solutions can be avoided. Thus, the high sensitive performance around the equilibrium point generated by set value or fractional order functions can be reduced.
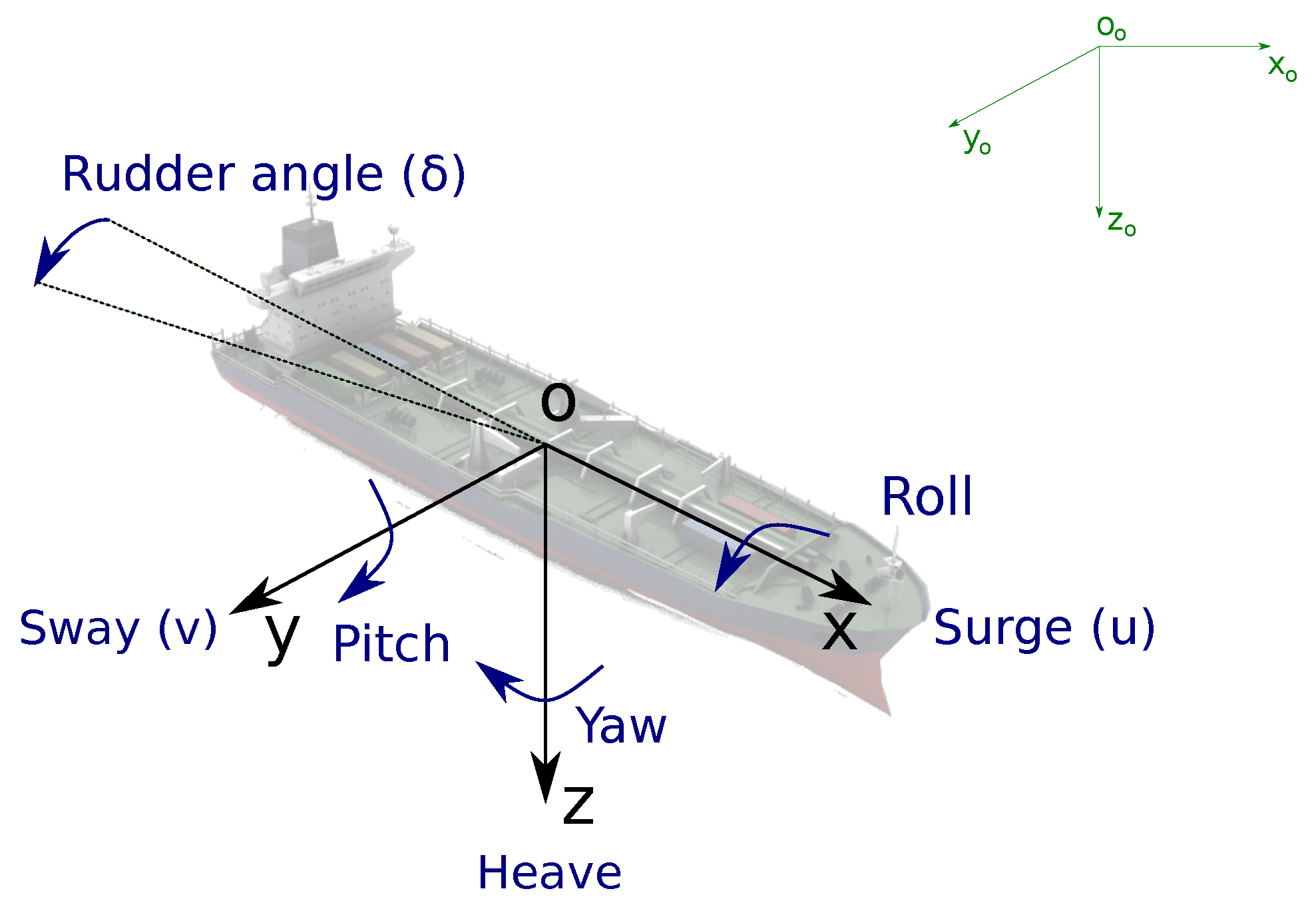
2. Problem Statement
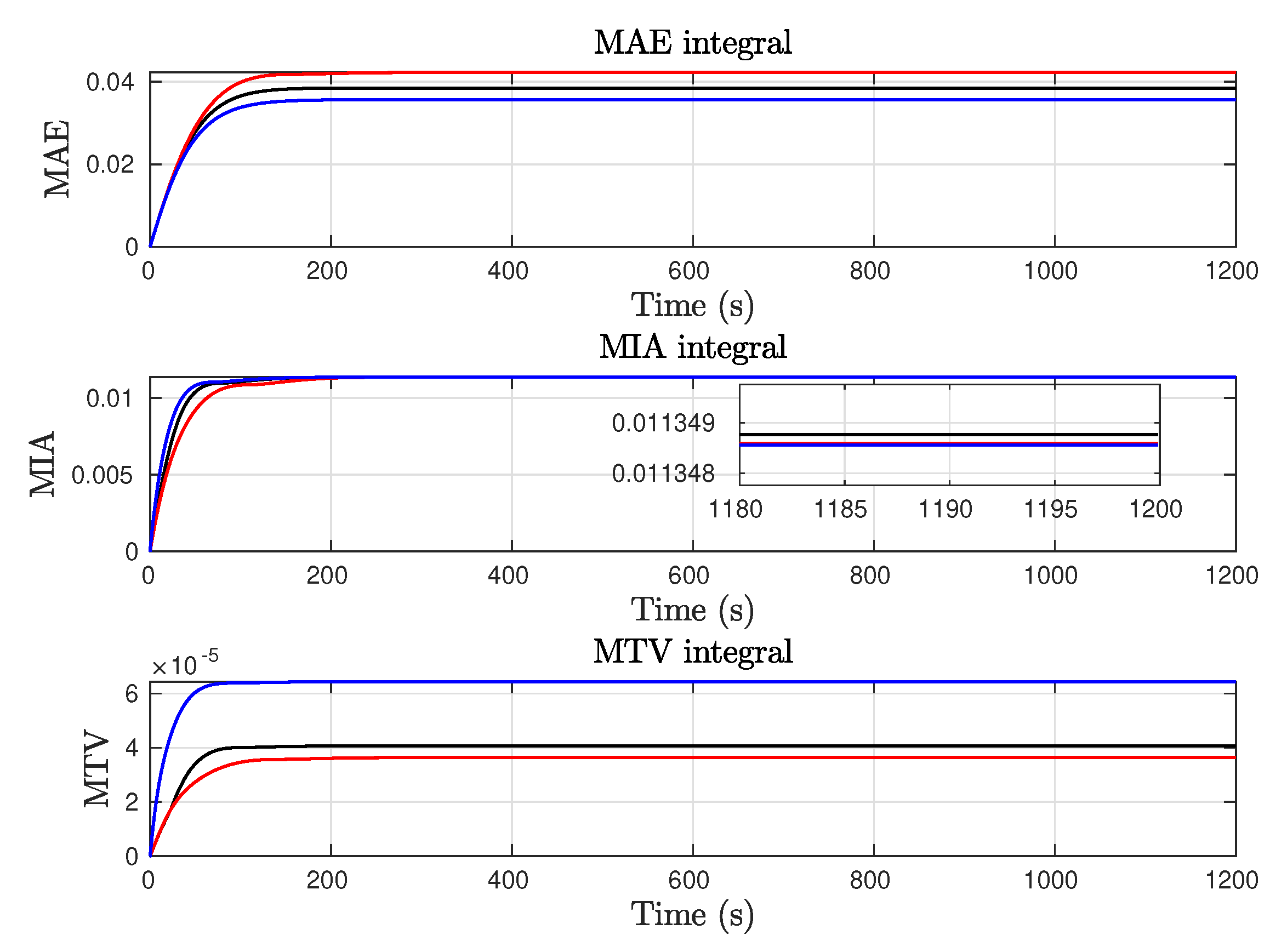
- The tests includes results without disturbances () and with disturbances ().
- The algorithm parameters are configured in the case of the step input reference without disturbances, such that all solutions provide the same value of the MIA index at the end of the test time.
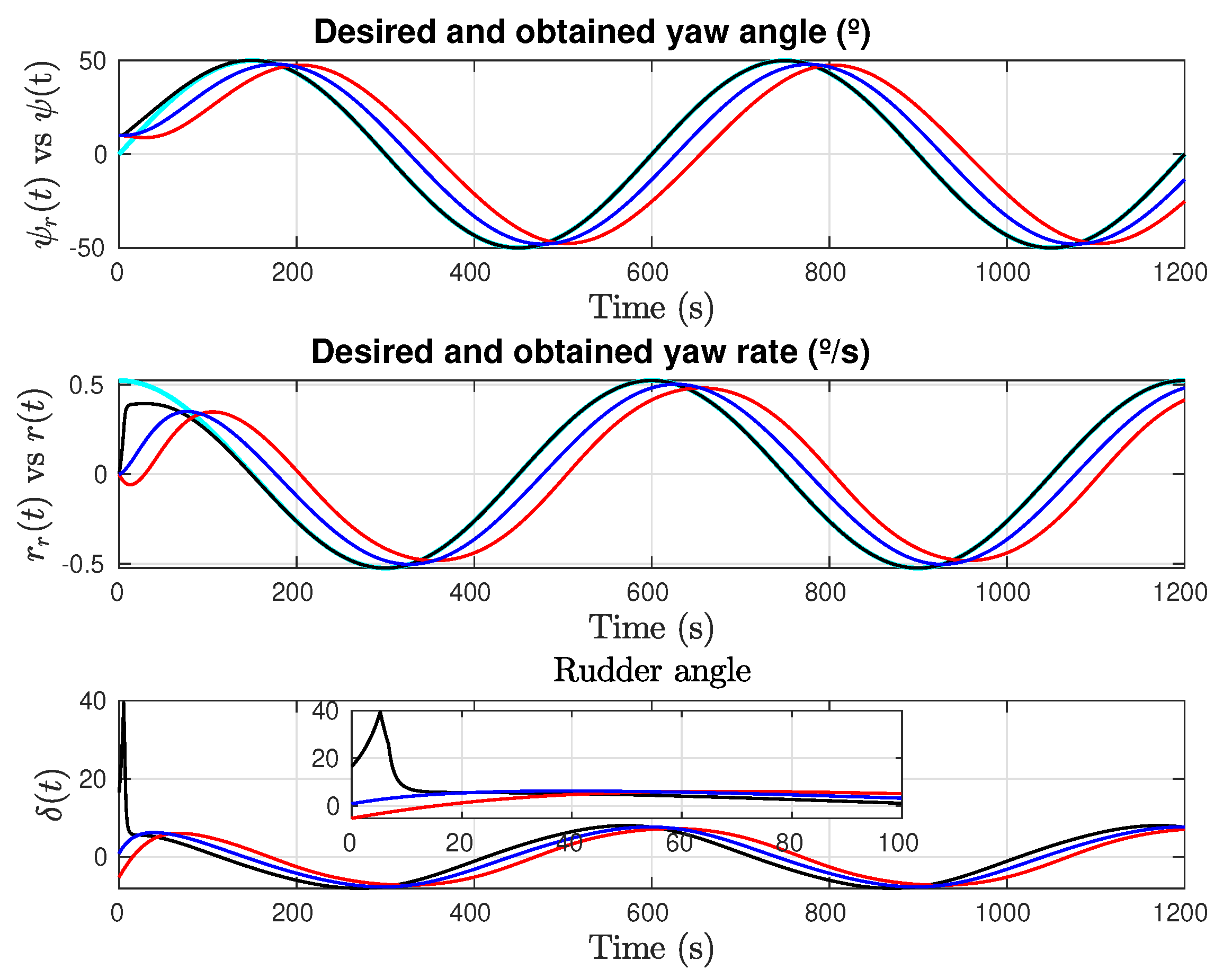
- After that, the algorithms parameters are fixed and tested in the case of step with disturbances and in the case of the sinusoidal input reference. In this way we check the robustness of the solutions with respect to its capacity of adaptation to different scenarios from a specific parameter configuration.
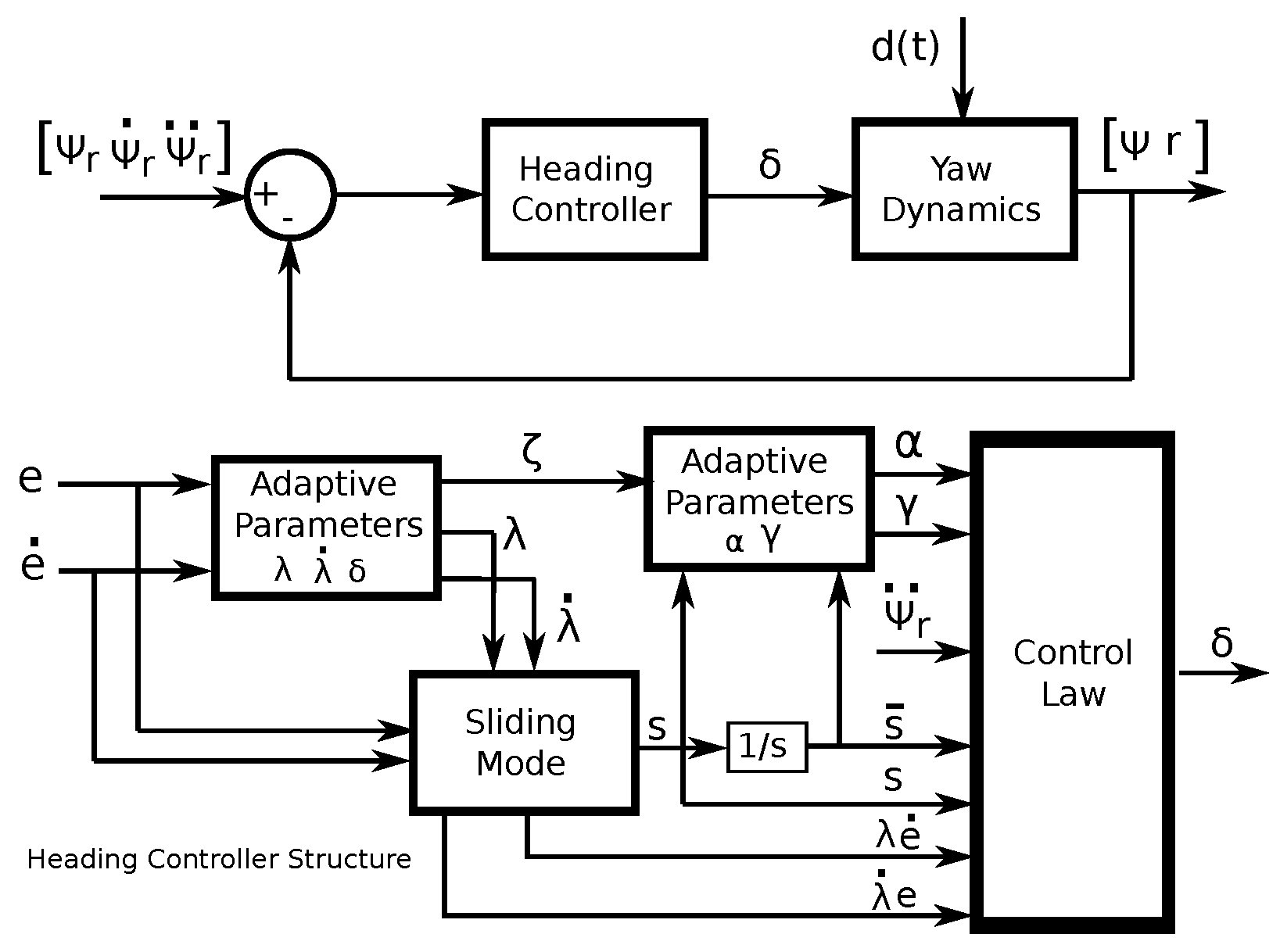
3. Adaptive Integral Sliding Mode Surface Control Design
- Case 1:Assuming the worst case scenario, that is, when , substitution of implies that the second order dynamics related to areLet’s define a sliding vector state asDynamics of are given bywithandLets’ defineand P a symmetric positive definite matrixwith determinantIt can be shown thatwhere Q is the identity matrix of size 2 × 2. Therefore, the selection of a Lyapunov candidate functionleads toLet’s defineThereforeApplying (51) and assumption 2 it is obtainedNote that , thus the closed set , which includes the origin, defined asis GUAS with exponential convergence (see [52]). The values of and determines the size of the stable closed set, so that this condition limits how the algorithm may be applied. Inside there are two possible cases
- −
- : implies that , that is, the dynamics is stable an converges to the origin, with a value of adjusted to keep this condition.
- −
- : implies that grows inside , that is, with an upper bound, or its value is stationary. According to (23) and (1), there exist an instant where the condition is met, which implies that grows, that is, condition is achieved. Therefore, grows only when it is needed to keep the sliding mode condition at steady state, which is related to the performance given by the value of .
- Case 2:Substitution of from (24) implies that the second order dynamics equation related to isApplying assumption 2 and condition implies thatwith . Accordingly, because of assumption 2, the characteristic polynomial of (54) is Hurwitz for all wherewith defined in (27). This implies that (34) is GUAS with respect to the closed set . Note that dynamics in (54) can be viewed as a second order linear dynamics with adaptive critical damping (exponential convergence related to the fastest response with no overshooting), being perturbed by the overestimation caused by the compensation of the unknown term. The roots of the perturbed solution of (54) are given byA condition of the following form can be used to avoid chattering (high frequency oscillations caused by a large imaginary value in the pole position as a result of overestimation) at the steady-state response.This provides an upper bound of the perturbation generated at the dynamics with respect to the solution with and . In order to estimate the correlation between the sampling time and the natural frequency (in ), we must verify that the frequency given by the Nyquist-Shannon sampling theorem (the maximum operating frequency for a system with sampling time ) does not create a change in sign in at the limit condition , that isApplying condition (58) an upper bound for as a function of , and the absolute value of is obtained asThis constraint provides a limit on the application of the method that employs the bound of the disturbance derivative, the sampling time and, taking into consideration relation (27), the required precision .Inside we have thatwhich geometrically entails:with defined in (32). Inside we have that
4. Numerical Simulations
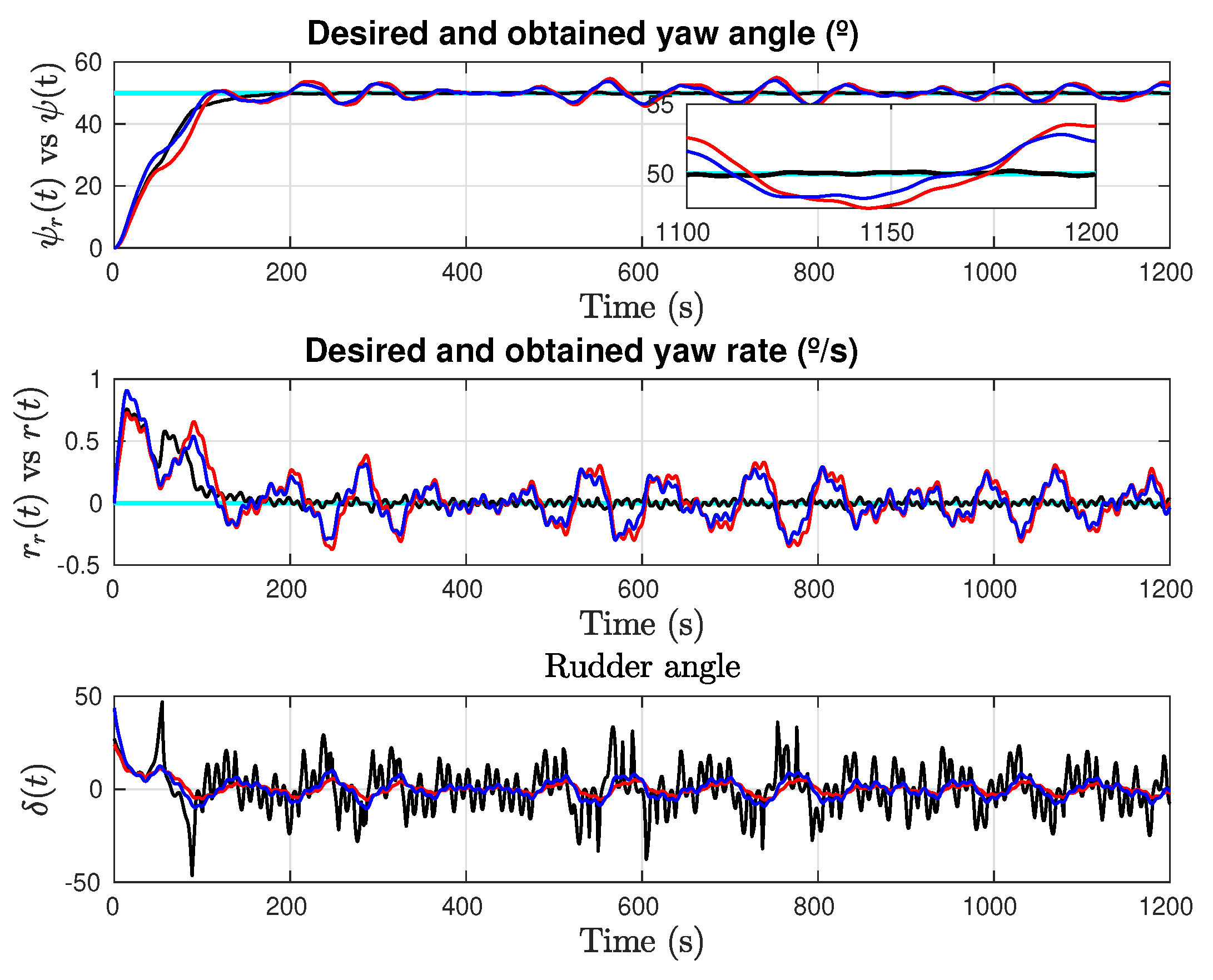
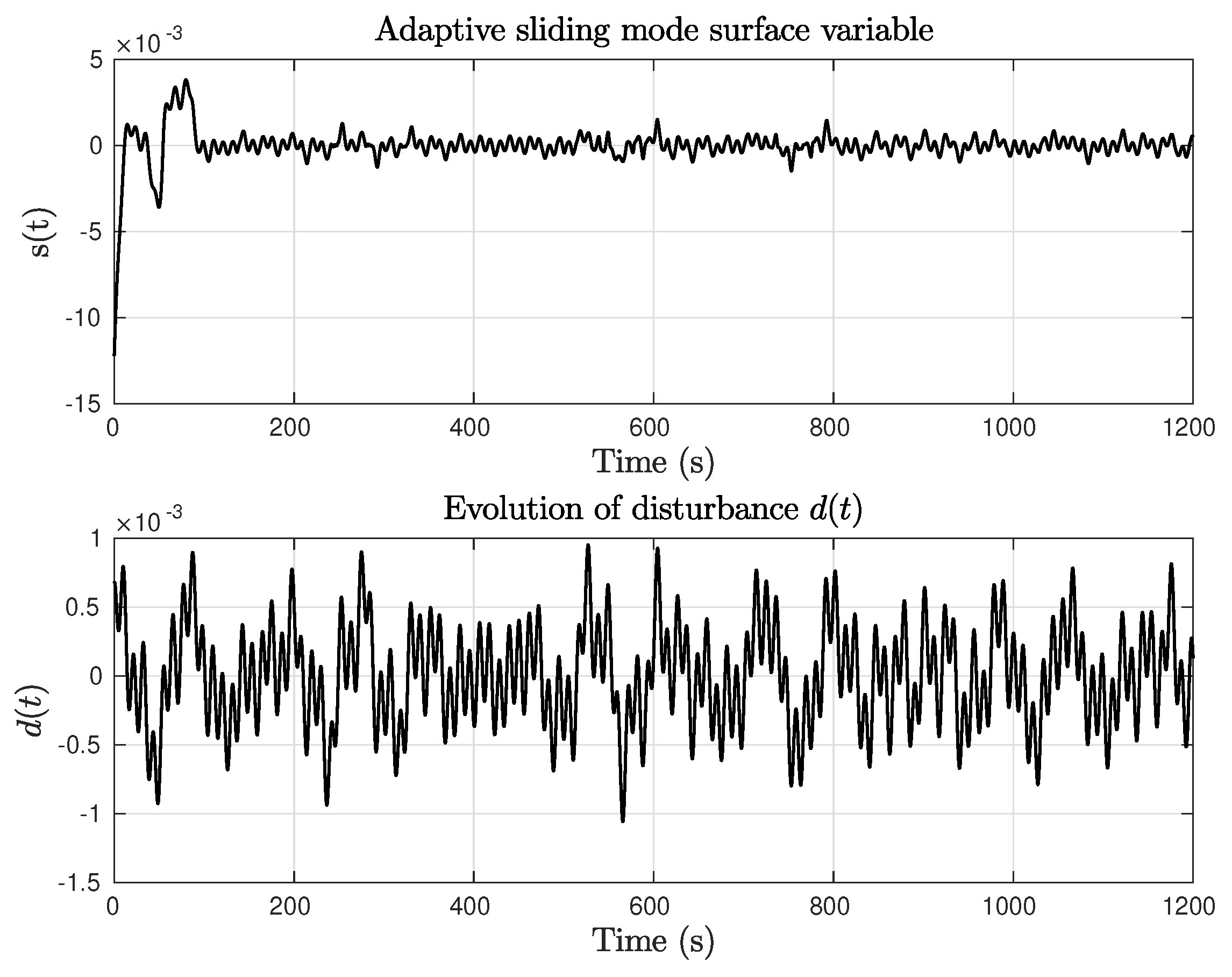
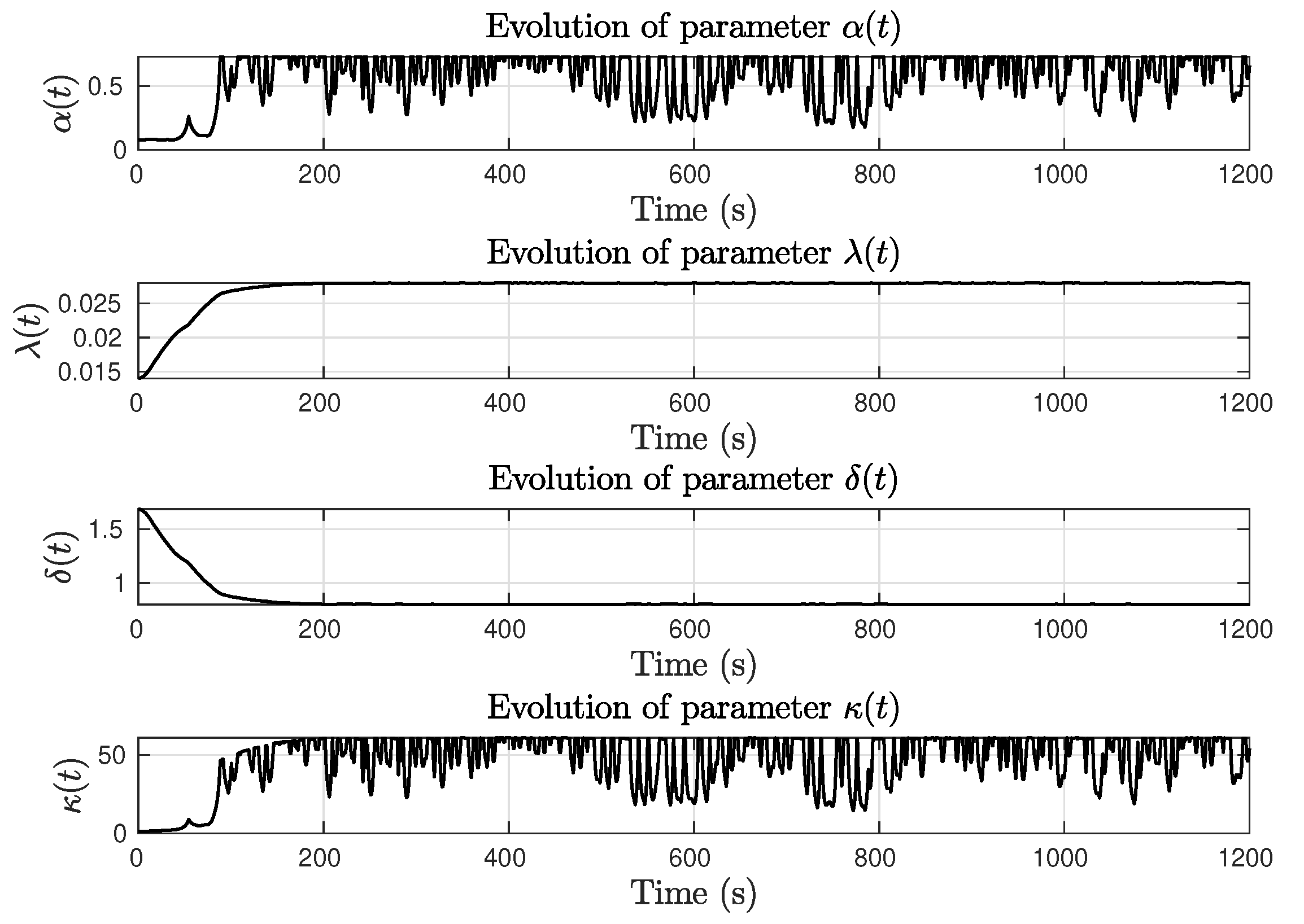
4.1. Constant Yaw Reference
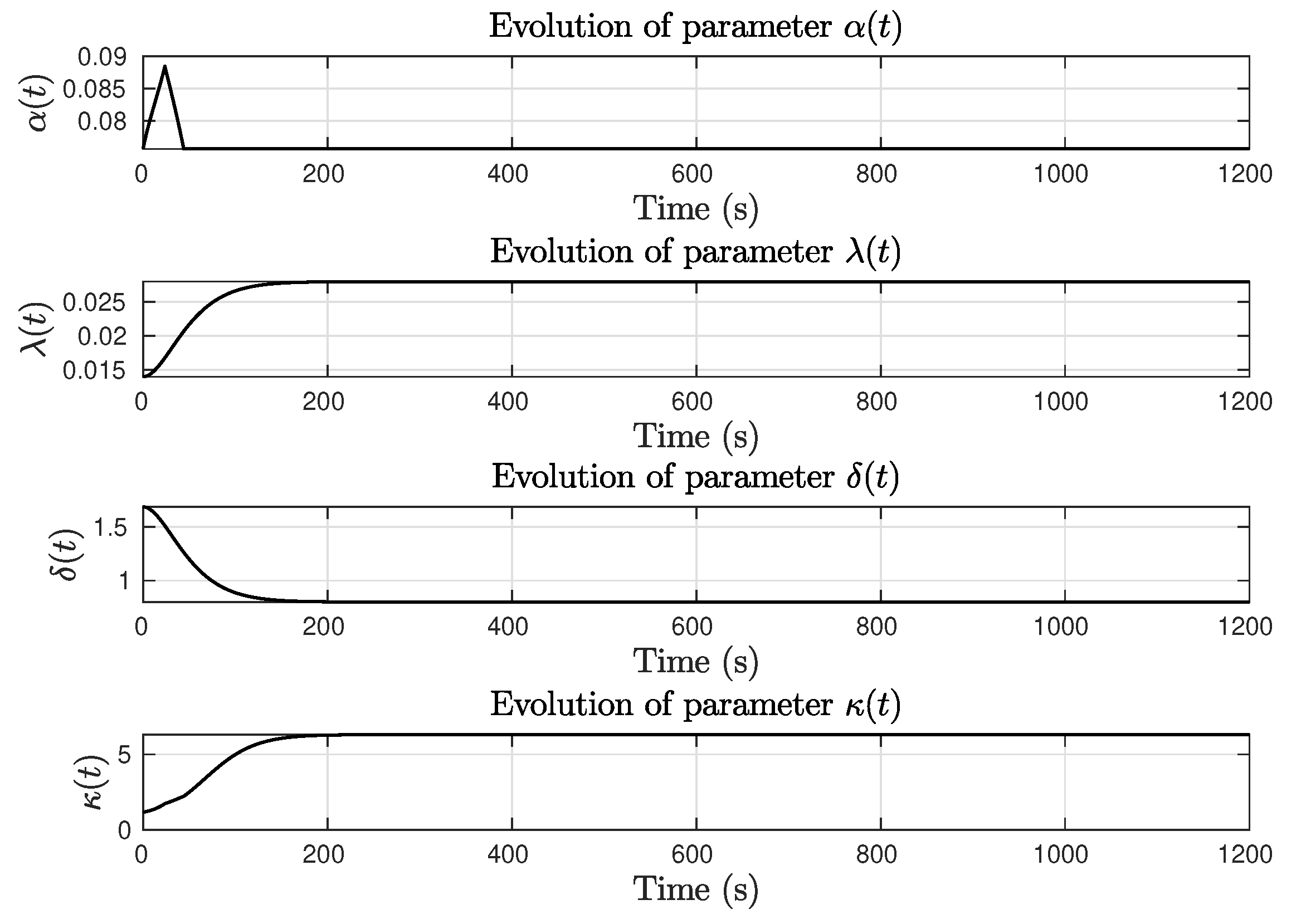
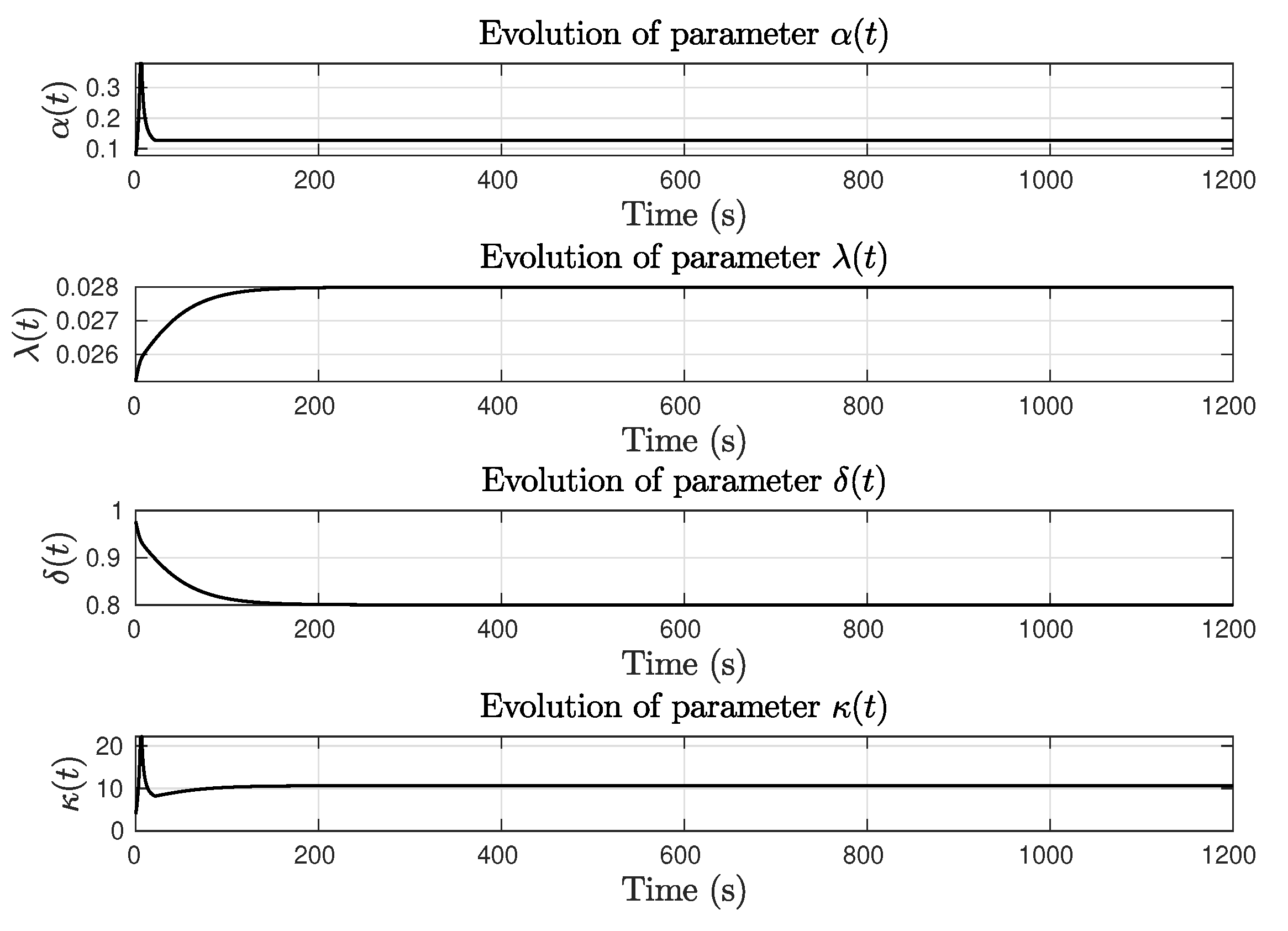
- Consider a settling time , a maximum desired yaw rate degrees per second and a required precision .
- The value of is obtained assuming an exponential convergence of the error from initial condition to desired precision with a desired settling timeThe values of and are selected as
- The value of is related to the initial conditions of the problem and the maximum desired yaw rate asand is calculated as
- The value of must be higher than in order to obtain a small value for . Due ti the low-pass filtering properties of (54), the value of can be further refined by estimating the cut-off frequency of the second order system related toTherefore is calculated as an adaptive gain that takes account of and the desired precision
- Simulations are used to set the values of and such that the value of the performance index MIA is equal to the value achieved with benchmark chosen controllers at the conclusion of the test period.This condition generates an adequate adaption of the value of that allows to obtain the desired power factor profile with respect to the absolute value of .
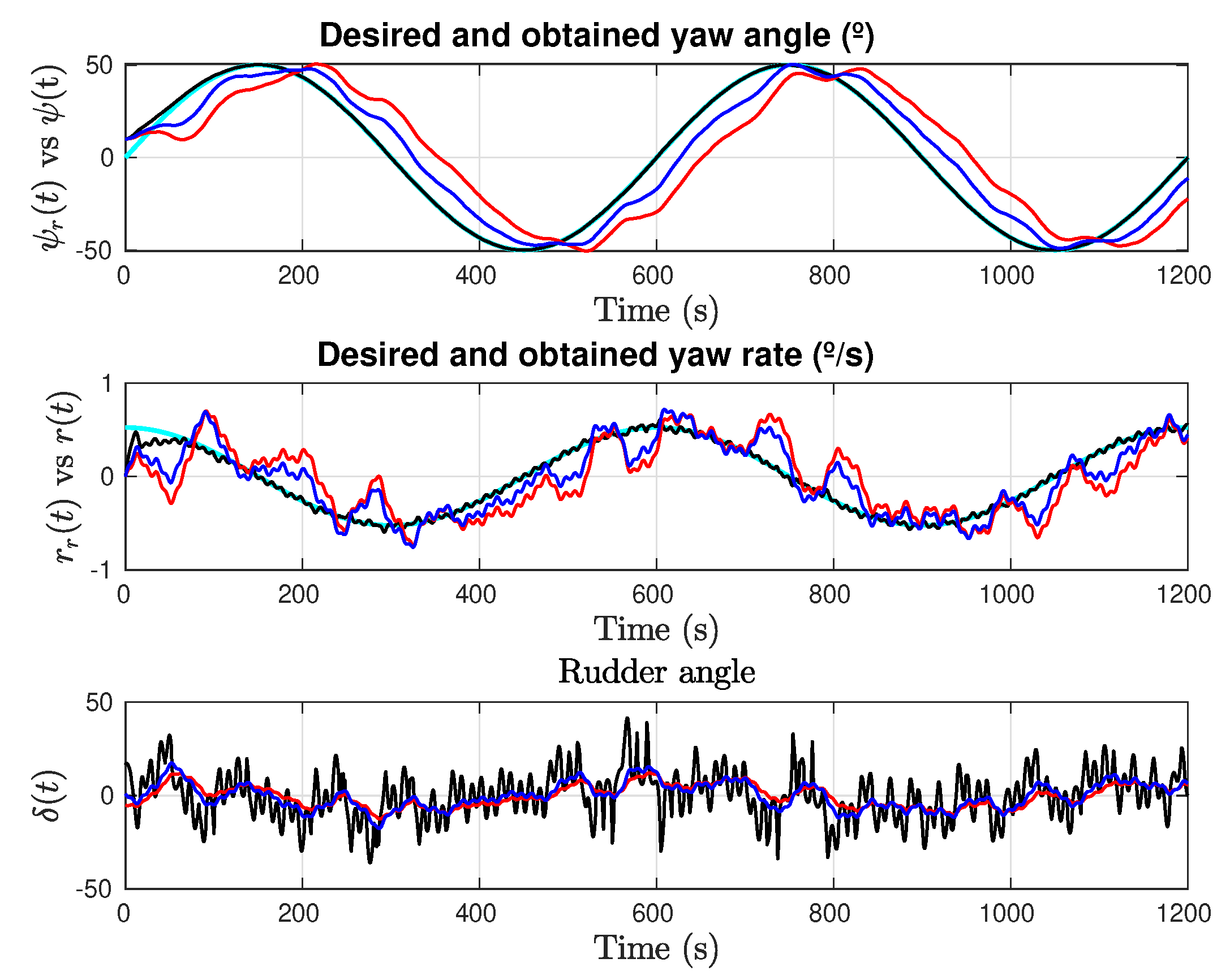
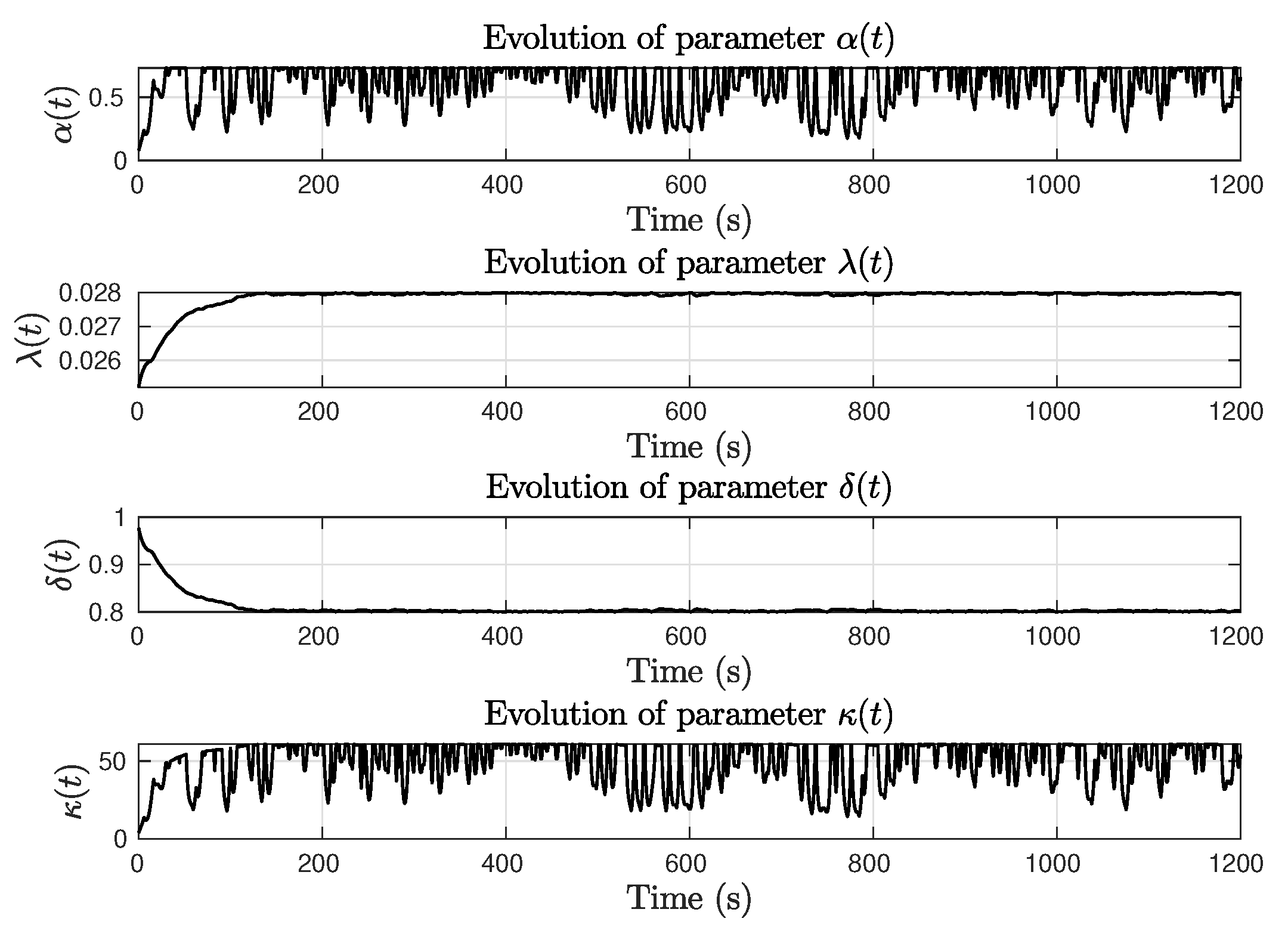
4.2. Sinusoidal Yaw Reference
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| USV | Unmanned Surface Vehicle |
| IMO | International Maritime Organisation |
| LOS | Line of Sight |
| SMC | Sliding Mode Control |
| AISM | Adaptive Integral Sliding Mode |
| GUAS | globally uniformly asymptotically stable |
| MAE | Mean Absolute Error |
| MIA | Mean Integral Absolute |
| MTV | Mean Total Variation |
References
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Do, K.D.; Pan, J. Control of Ships and Underwater Vehicles: Design for Underactuated and Nonlinear Marine Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Liu, Z. Ship adaptive course keeping control with nonlinear disturbance observer. IEEE Access 2017, 5, 17567–17575. [Google Scholar] [CrossRef]
- Ejaz, M.; Chen, M. Sliding mode control design of a ship steering autopilot with input saturation. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417703568. [Google Scholar] [CrossRef]
- Wan, L.; Su, Y.; Zhang, H.; Tang, Y.; Shi, B. Global fast terminal sliding mode control based on radial basis function neural network for course keeping of unmanned surface vehicle. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419829961. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, J.; Castañeda, H.; Gordillo, J.L. Design of an adaptive sliding mode control for a micro-AUV subject to water currents and parametric uncertainties. J. Mar. Sci. Eng. 2019, 7, 445. [Google Scholar] [CrossRef] [Green Version]
- Khaled, N.; Chalhoub, N.G. A self-tuning guidance and control system for marine surface vessels. Nonlinear Dyn. 2013, 73, 897–906. [Google Scholar] [CrossRef]
- Budak, G.; Beji, S. Controlled course-keeping simulations of a ship under external disturbances. Ocean. Eng. 2020, 218, 108126. [Google Scholar] [CrossRef]
- Zhang, X.-K.; Zhang, Q.; Ren, H.-X.; Yang, G.-P. Linear reduction of backstepping algorithm based on nonlinear decoration for ship course-keeping control system. Ocean. Eng. 2018, 147, 1–8. [Google Scholar] [CrossRef]
- Islam, M.M.; Siffat, S.A.; Ahmad, I.; Liaquat, M. Robust integral backstepping and terminal synergetic control of course keeping for ships. Ocean. Eng. 2021, 221, 108532. [Google Scholar] [CrossRef]
- Zhang, X.-K.; Han, X.; Guan, W.; Zhang, G.-Q. Improvement of integrator backstepping control for ships with concise robust control and nonlinear decoration. Ocean. Eng. 2019, 189, 106349. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, X. Nonlinear improved concise backstepping control of course keeping for ships. IEEE Access 2019, 7, 19258–19265. [Google Scholar] [CrossRef]
- Zheng, Z.; Sun, L. Path following control for marine surface vessel with uncertainties and input saturation. Neurocomputing 2016, 177, 158–167. [Google Scholar] [CrossRef]
- Zhang, X.-K.; Zhang, G.-Q. Design of ship course-keeping autopilot using a sine function-based nonlinear feedback technique. J. Navig. 2016, 69, 246–256. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Zhang, X.; Han, X. Nonlinear control algorithms for efficiency-improved course keeping of large tankers under heavy sea state conditions. Ocean. Eng. 2019, 189, 106371. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, X.-K.; Im, N.-K. Ship nonlinear-feedback course keeping algorithm based on MMG model driven by bipolar sigmoid function for berthing. Int. J. Nav. Archit. Ocean. Eng. 2017, 9, 525–536. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, X.-K.; Im, N.-K. Adaptive neural path-following control for underactuated ships in fields of marine practice. Ocean. Eng. 2015, 104, 558–567. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, T.; Liu, Z. Robust model predictive control for path-following of underactuated surface vessels with roll constraints. Ocean. Eng. 2017, 143, 125–132. [Google Scholar] [CrossRef]
- Sharma, S.K.; Sutton, R.; Motwani, A.; Annamalai, A. Non-linear control algorithms for an unmanned surface vehicle. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2014, 228, 146–155. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Li, J.; Jin, X.; Liu, C. Robust Adaptive Neural Control for Wing-Sail-Assisted Vehicle via the Multiport Event-Triggered Approach. IEEE Trans. Cybern. 2021, 1–13. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, X.; Zhu, H.; Li, Z. Course-keeping control for ships with nonlinear feedback and zero-order holder component. Ocean. Eng. 2020, 209, 107461. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Edwards, C.; Spurgeon, S. Sliding Mode Control: Theory And Applications; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Levant, A. Robust exact differentiation via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.K.; Patton, R.J. Sliding mode observers for fault detection and isolation. Automatica 2000, 36, 541–553. [Google Scholar] [CrossRef]
- Feng, Y.; Xinghuo, Y.; Zhihong, M. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Nersesov, S.G.; Ashrafiuon, H.; Ghorbanian, P. On estimation of the domain of attraction for sliding mode control of underactuated nonlinear systems. Int. J. Robust Nonlinear Control 2014, 24, 811–824. [Google Scholar] [CrossRef]
- Hao, Y.; Yi, J.; Zhao, D.; Qian, D. Robust control using incremental sliding mode for underactuated systems with mismatched uncertainties. In Proceedings of the American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 532–537. [Google Scholar]
- Liu, J.; Laghrouche, S.; Harmouche, M.; Wack, M. Adaptive-gain second-order sliding mode observer design for switching power converters. Control Eng. Pract. 2014, 30, 124–131. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Li, S.; Yu, X. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer. IEEE Trans. Ind. Electron. 2013, 60, 160–169. [Google Scholar] [CrossRef]
- Oliveira, T.R.; Cunha, J.P.V.; Hsu, L. Adaptive sliding mode control for disturbances with unknown bounds. In Proceedings of the 14th International Workshop on Variable Structure Systems (VSS), Nanjing, China, 1–4 June 2016; pp. 59–64. [Google Scholar]
- Hsu, L.; Oliveira, T.R.; Cunha, J.P.V.; Yan, L. Adaptive unit vector control of multivariable systems using monitoring functions. Int. J. Robust Nonlinear Control 2019, 29, 583–600. [Google Scholar] [CrossRef]
- Chen, M.; Wu, Q.; Cui, R. Terminal sliding mode tracking control for a class of SISO uncertain nonlinear systems. ISA Trans. 2013, 52, 198–206. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.D.; Yi, J.Q. Structure design of two types of sliding-mode controllers for a class of under-actuated mechanical systems. IET Control Theory Appl. 2007, 1, 163–172. [Google Scholar] [CrossRef]
- Thanh, H.L.N.N.; Mung, N.X.; Nguyen, N.P.; Phuong, N.T. Perturbation observer-based robust control using a multiple sliding surfaces for nonlinear systems with influences of matched and unmatched uncertainties. Mathematics 2020, 8, 1371. [Google Scholar] [CrossRef]
- Alattas, K.A.; Mobayen, S.; Din, S.U.; Asad, J.H.; Fekih, A.; Assawinchaichote, W.; Vu, M.T. Design of a non-singular adaptive integral-type finite time tracking control for nonlinear systems with external disturbances. IEEE Access 2021, 9, 102091–102103. [Google Scholar] [CrossRef]
- Li, Y.-X.; Yang, G.-H. Adaptive integral sliding mode control fault tolerant control for a class of uncertain nonlinear systems. IET Control Theory Appl. 2018, 12, 1864–1872. [Google Scholar] [CrossRef]
- Liu, D.; Yang, G.-H. Prescribed performance model-free adaptive integral sliding mode control for discrete-time nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 2222–2230. [Google Scholar] [CrossRef]
- Edwards, C.; Shtessel, Y.B. Adaptive continuous higher order sliding mode control. Automatica 2016, 65, 183–190. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Han, F.; Yu, X. Chattering free full-order sliding-mode control. Automatica 2014, 50, 1310–1314. [Google Scholar] [CrossRef]
- Bandyopadhyay, B.; Deepak, F.; Kim, K. Sliding Mode Control Using Novel Sliding Surfaces; Springer: Berlin/Heidelberg, Germany, 2009; Volume 392. [Google Scholar]
- González, J.A.; Barreiro, A.; Dormido, S.; Banos, A. Nonlinear adaptive sliding mode control with fast non-overshooting responses and chattering avoidance. J. Frankl. Inst. 2017, 354, 2788–2815. [Google Scholar] [CrossRef]
- González, J.A.; Barreiro, A.; Dormido, S. A practical approach to adaptive sliding mode control. Int. J. Control 2019, 17, 2452–2461. [Google Scholar] [CrossRef]
- Polyakov, A. Generalized Homogeneity in Systems and Control; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Mojallizadeh, M.R.; Brogliato, B.; Acary, V. Time-discretizations of differentiators: Design of implicit algorithms and comparative analysis. Int. J. Robust Nonlinear Control 2021, 31, 7679–7723. [Google Scholar] [CrossRef]
- Witkowska, A.; Śmierzchalski, R. Designing a ship course controller by applying the adaptive backstepping method. Int. J. Appl. Math. Comput. Sci. 2012, 22, 985–997. [Google Scholar] [CrossRef]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D. Path Planning of an Autonomous Surface Vehicle Based on Artificial Potential Fields in a Real Time Marine Environment; Cardiff University Press: Cardiff, UK, 2017. [Google Scholar]
- Polvara, R.; Sharma, S.; Wan, J.; Manning, A.; Sutton, R. Obstacle avoidance approaches for autonomous navigation of unmanned surface vehicles. J. Navig. 2018, 71, 241–256. [Google Scholar] [CrossRef] [Green Version]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D. Optimal path planning of an unmanned surface vehicle in a real-time marine environment using a dijkstra algorithm. In Marine Navigation; CRC Press: Boca Raton, FL, USA, 2017; pp. 241–256, 399–402. [Google Scholar]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. A constrained A* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents. Ocean. Eng. 2018, 169, 187–201. [Google Scholar] [CrossRef] [Green Version]
- Panteley, E.; Loria, A. On global uniform asymptotic stability of nonlinear time-varying systems in cascade. Syst. Control Lett. 1998, 33, 131–138. [Google Scholar] [CrossRef]
- Khalil, H.K.; Grizzle, J.W. Nonlinear Systems; Prentice Hall: Hoboken, NJ, USA, 1996. [Google Scholar]


| Parameter | Value |
|---|---|
| K | 0.21 |
| T | 107.76 |
| 13.17 | |
| 16,323.46 |
| Parameter | Value |
|---|---|
| 0.0017 | |
| 0.6000 |
| Parameter | Value |
|---|---|
| 0.090 | |
| 1.891 | |
| 28.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Prieto, J.A.; Pérez-Collazo, C.; Singh, Y. Adaptive Integral Sliding Mode Based Course Keeping Control of Unmanned Surface Vehicle. J. Mar. Sci. Eng. 2022, 10, 68. https://doi.org/10.3390/jmse10010068
González-Prieto JA, Pérez-Collazo C, Singh Y. Adaptive Integral Sliding Mode Based Course Keeping Control of Unmanned Surface Vehicle. Journal of Marine Science and Engineering. 2022; 10(1):68. https://doi.org/10.3390/jmse10010068
Chicago/Turabian StyleGonzález-Prieto, José Antonio, Carlos Pérez-Collazo, and Yogang Singh. 2022. "Adaptive Integral Sliding Mode Based Course Keeping Control of Unmanned Surface Vehicle" Journal of Marine Science and Engineering 10, no. 1: 68. https://doi.org/10.3390/jmse10010068
APA StyleGonzález-Prieto, J. A., Pérez-Collazo, C., & Singh, Y. (2022). Adaptive Integral Sliding Mode Based Course Keeping Control of Unmanned Surface Vehicle. Journal of Marine Science and Engineering, 10(1), 68. https://doi.org/10.3390/jmse10010068








