Reproductive Biology of Wild Blueberry (Vaccinium angustifolium Aiton)
Abstract
1. Introduction
2. Materials and Methods
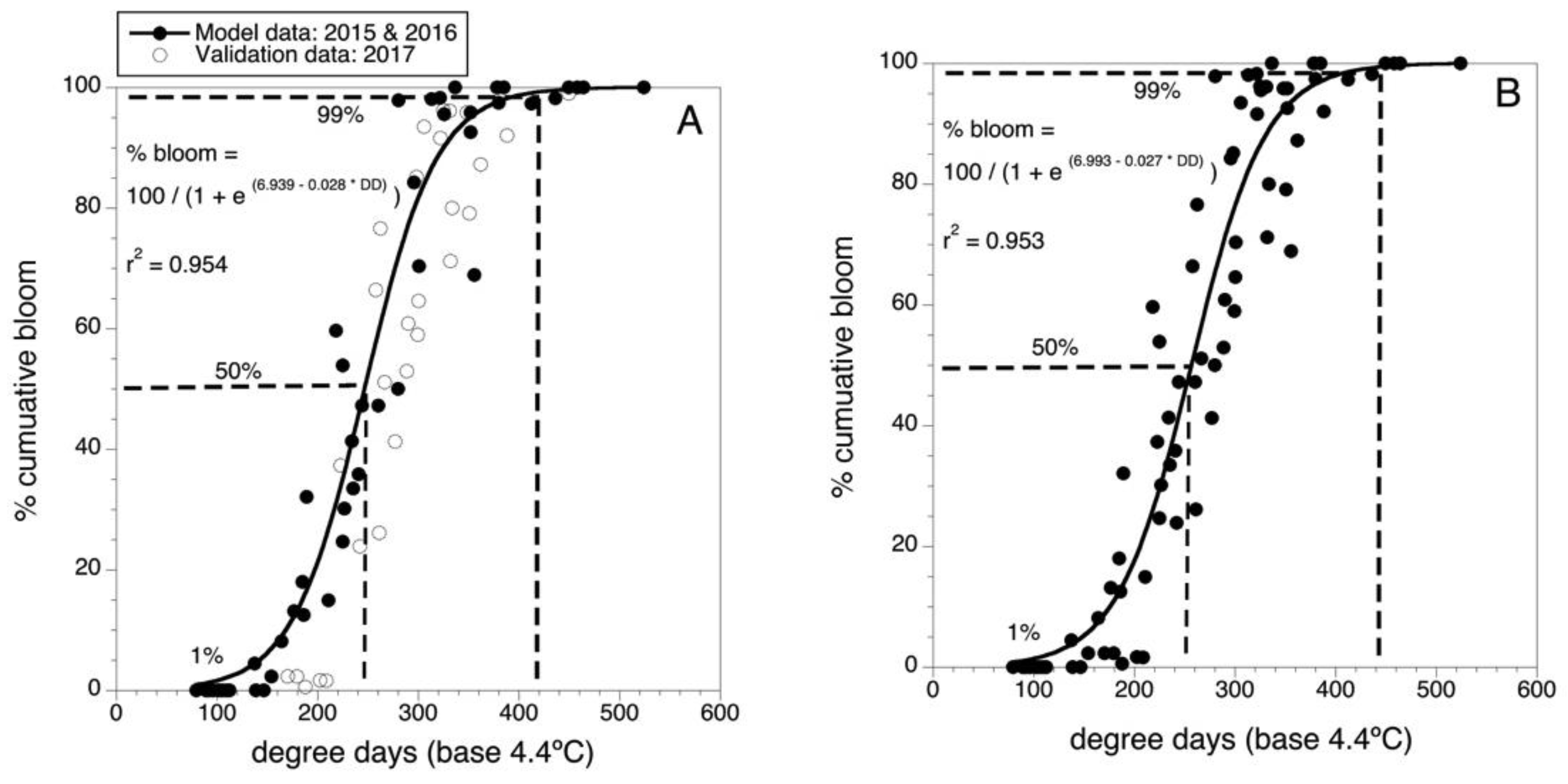
2.1. Phenology of Bloom
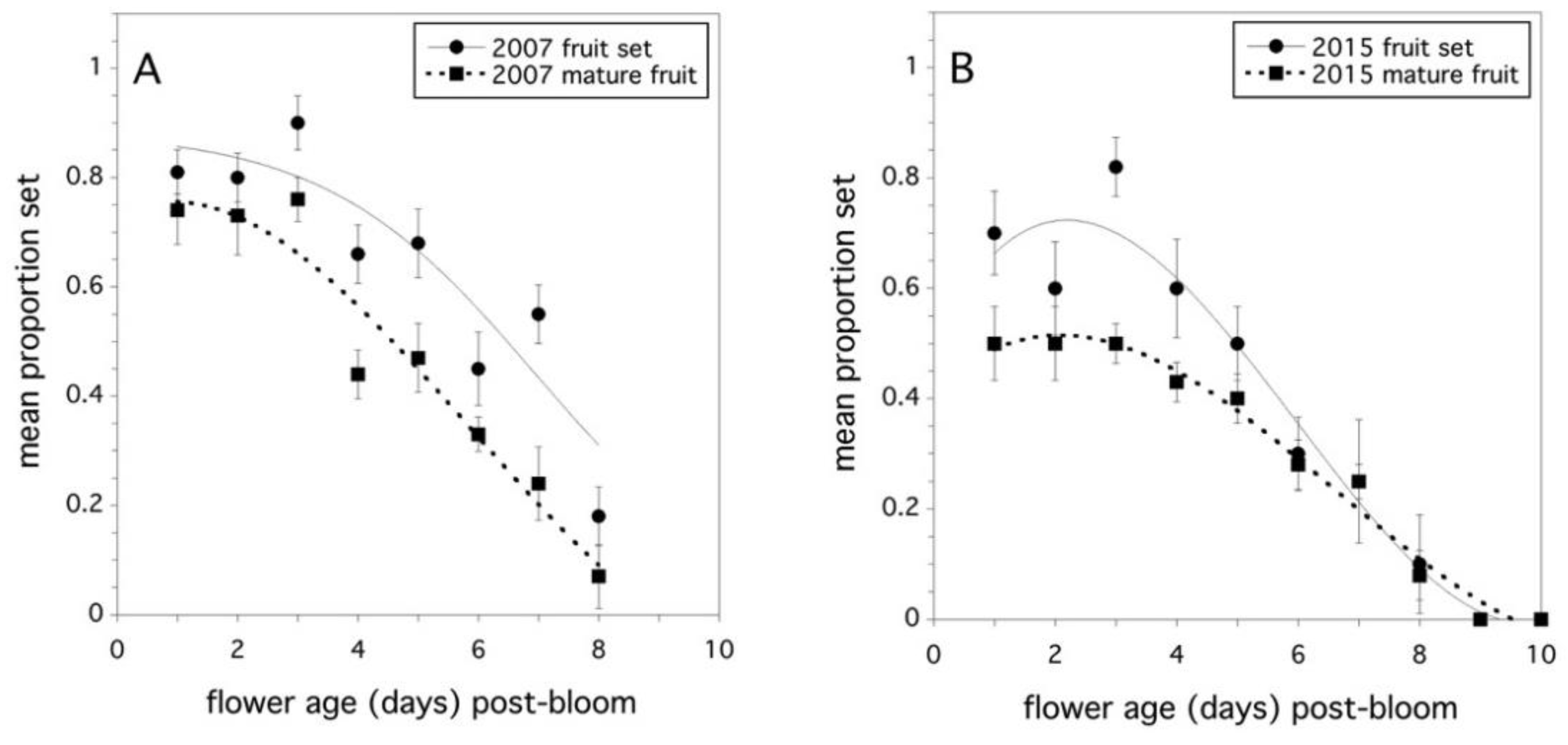
2.2. Stigma Longevity and Fruit Set
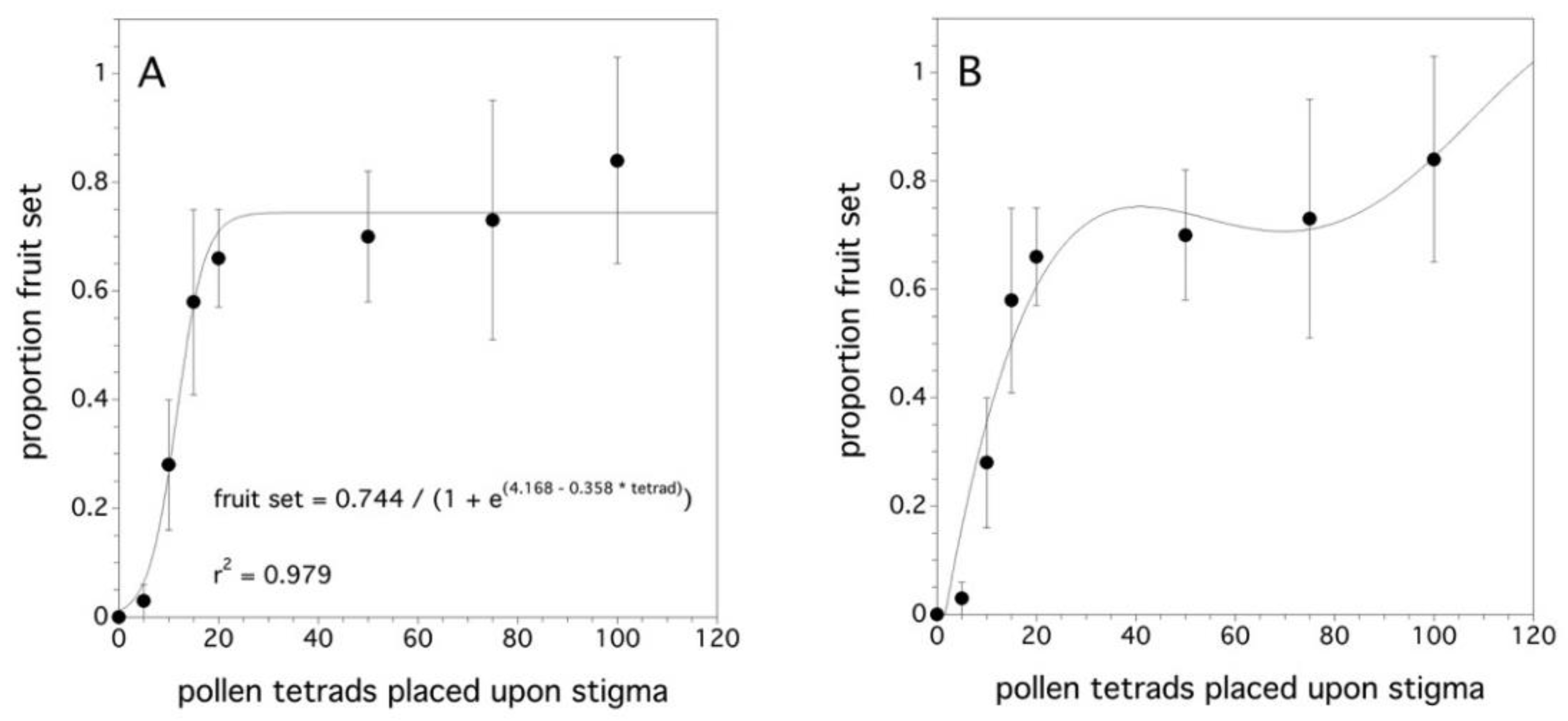
2.3. Fruit Set as a Function of Pollen Tetrad Quantity
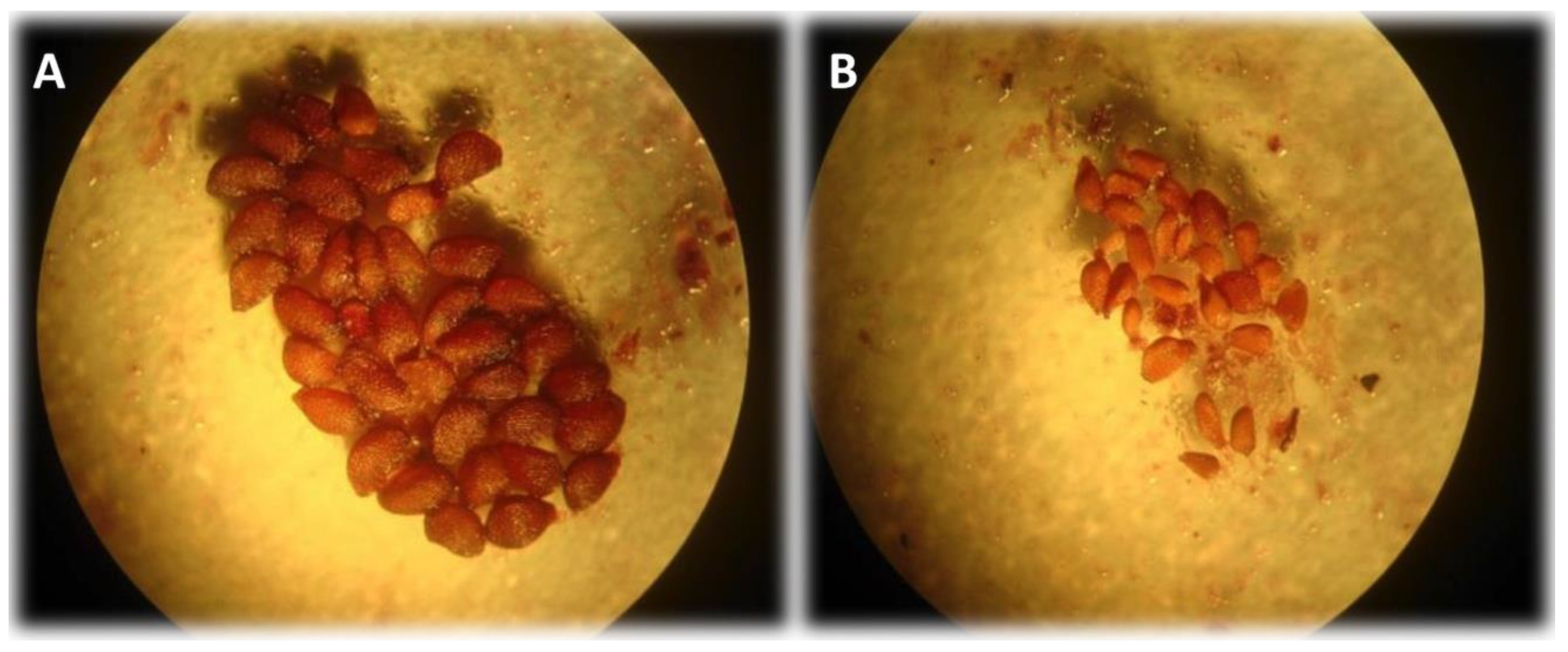
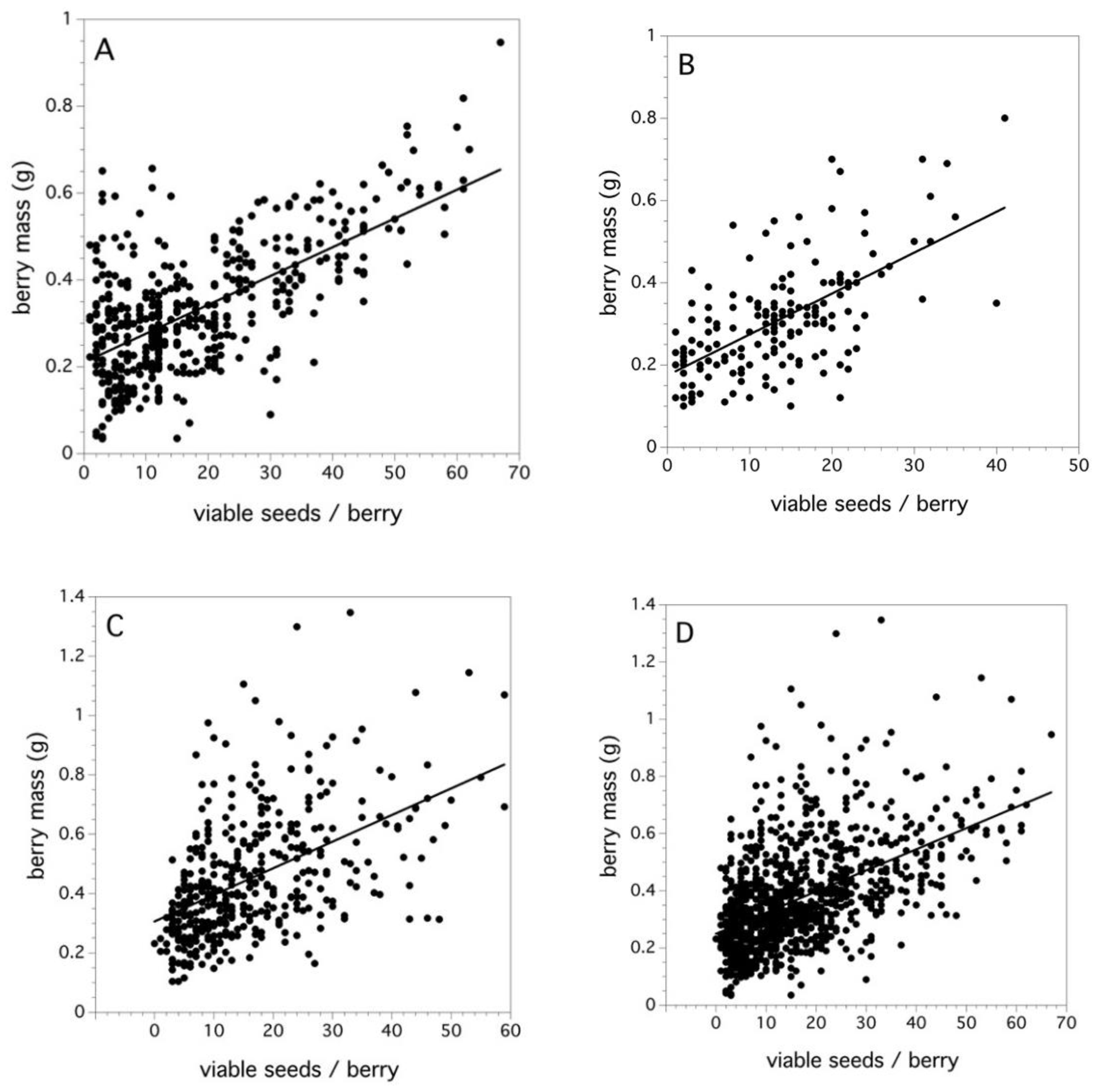
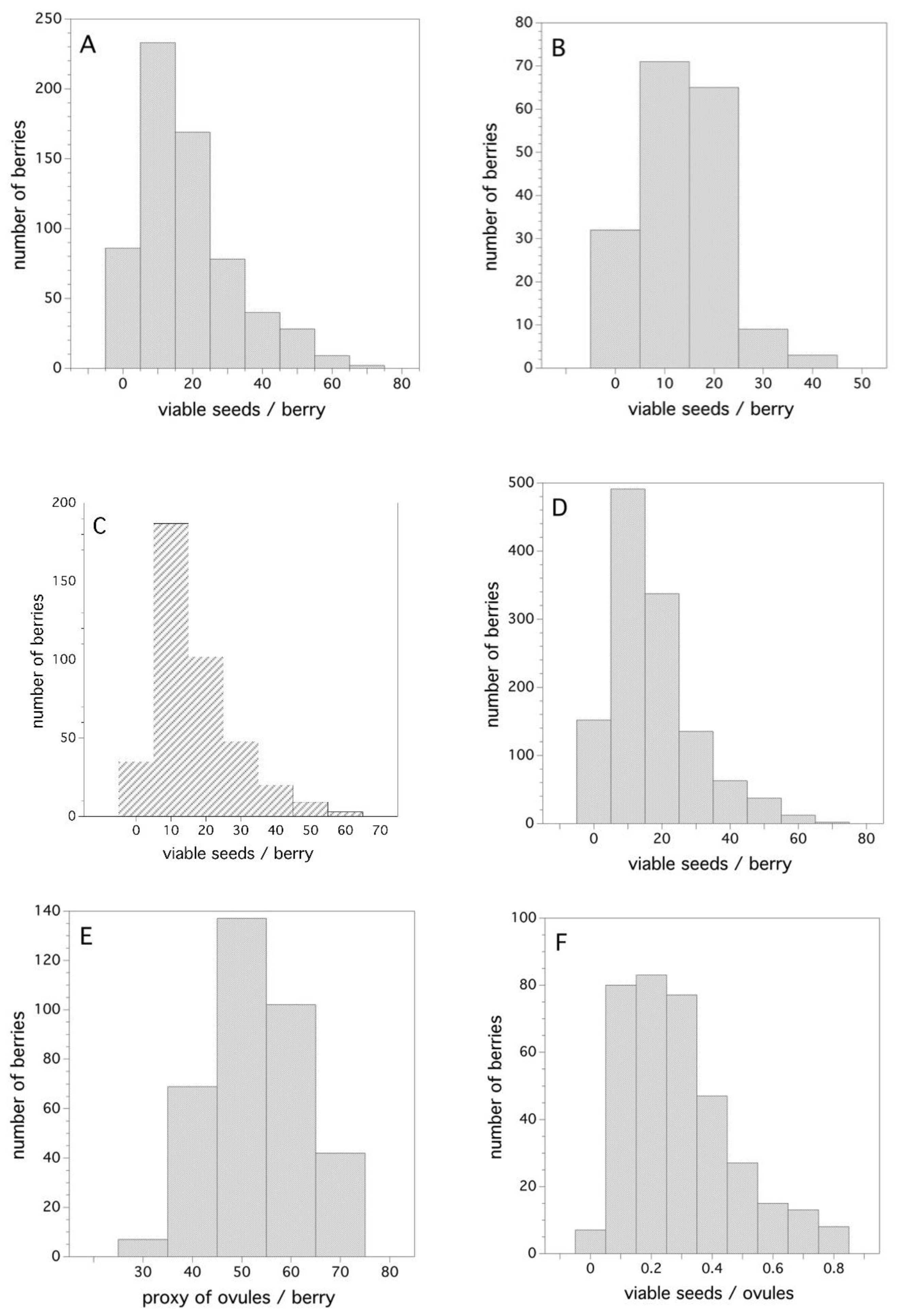
2.4. Fruit Set and Seed Development in Fruit
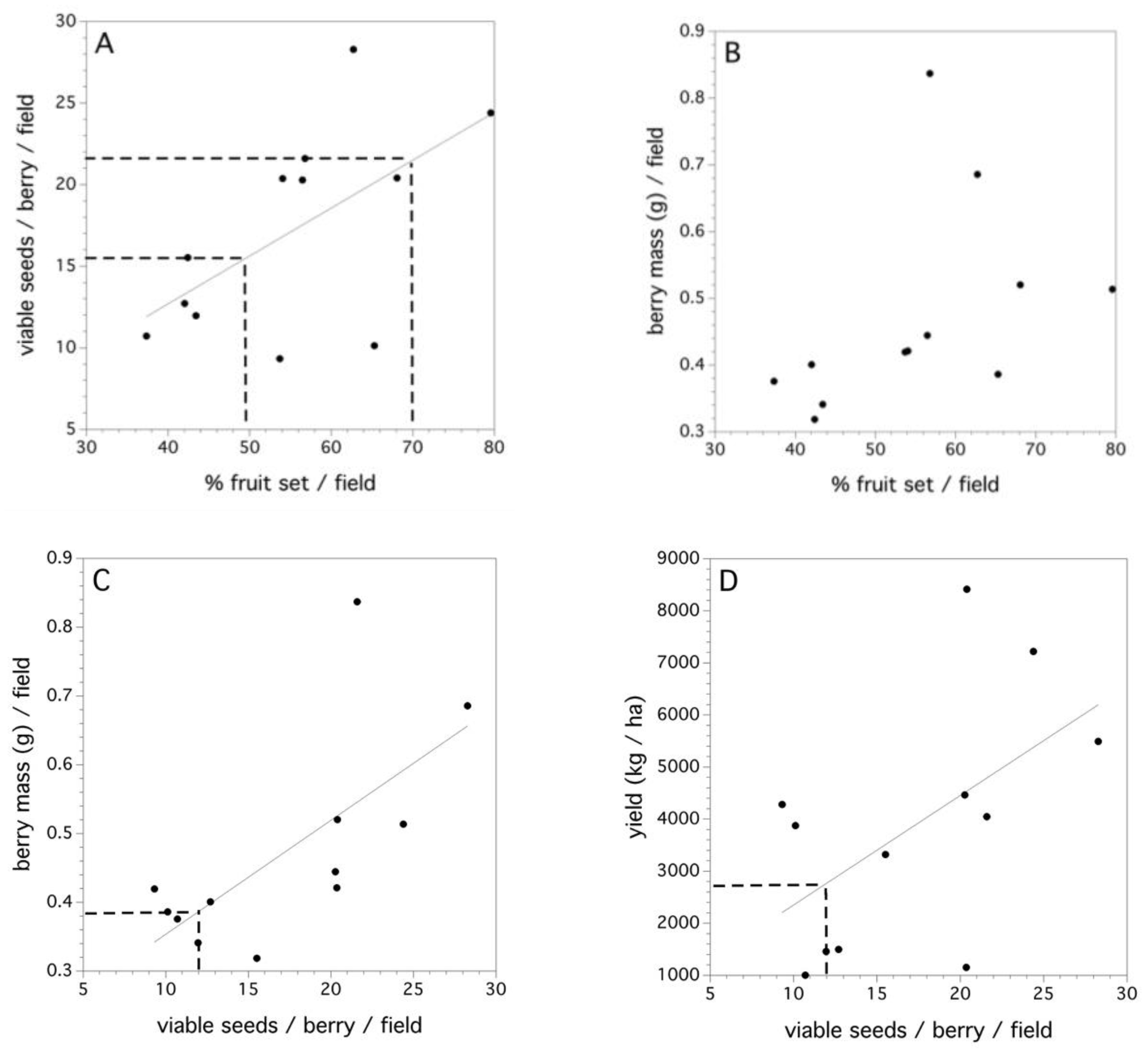
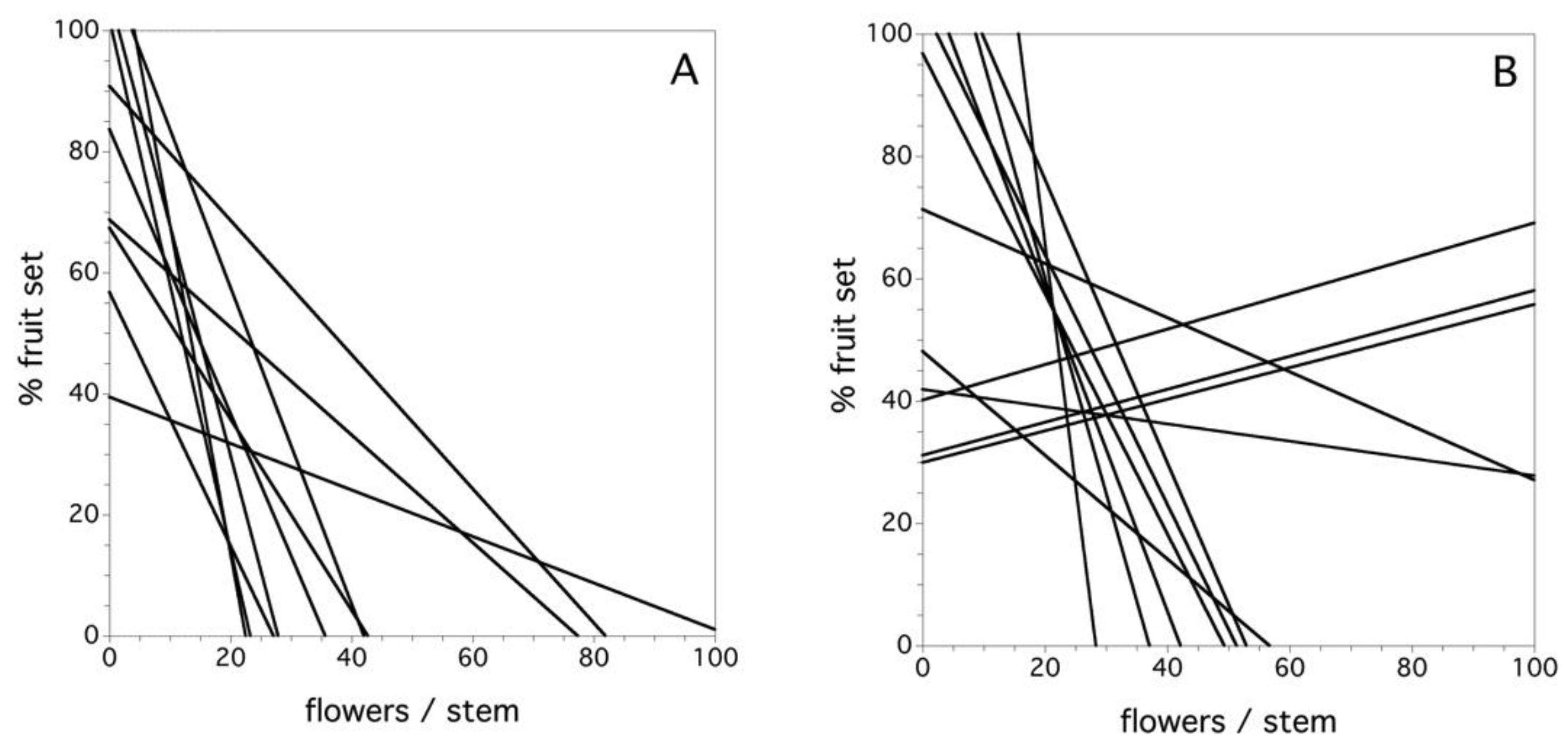
2.5. Decomposition of Total Variance in the Fruit Set
3. Results
3.1. Phenology of Bloom
3.2. Stigma Longevity and Fruit Set
3.3. Fruit Set as a Function of Pollen Tetrad Quantity
3.4. Fruit Set and Seed Development in Fruit
3.5. Decomposition of the Total Variance in the Fruit Set
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rowland, L.J.; Drummond, F.A.; Graham, J.; Alkharouf, N.; Buck, E.J.; Hancock, J.F.; Bassil, N.V.; Finn, C.E.; Olmstead, J.W. Generating genomic tools for blueberry improvement. Int. J. Fruit Sci. 2012, 12, 276–287. [Google Scholar] [CrossRef]
- Aalders, L.E.; Hall, I.V.; Brydon, A.C. Yield of native clones of lowbush blueberry under cultivation. Fruit Var. J. 1978, 32, 64–67. [Google Scholar]
- Drummond, F.A.; Smagula, J.; Annis, S.; Yarborough, D. Organic Wild Blueberry Production. Univ. Maine Agric. For. Exp. Stn. Tech. Bull. 2009, 852, 43. [Google Scholar]
- Yarborough, D.E. Wild Blueberry Culture in Maine. Wild Blueberry Fact Sheet. No. 220, Bulletin No. 2088. 2009. Available online: https://extension.umaine.edu/blueberries/factsheets/production/wild-blueberry-culture-in-maine/ (accessed on 6 March 2019).
- Jones, M.S.; Vanhanen, H.; Peltola, R.; Drummond, F.A. A global review of arthropod-mediated ecosystem-services in Vaccinium berry agroecosystems. Terr. Arthro. Rev. 2014, 7, 41–78. [Google Scholar] [CrossRef]
- Strik, B.C.; Yarborough, D.E. Blueberry production trends in North America, 1992 to 2003, and predictions for growth. HortTechnology 2005, 15, 91–398. [Google Scholar] [CrossRef]
- Asare, E.; Hoshide, A.K.; Drummond, F.A.; Chen, X.; Criner, G.K. Economic risk of bee pollination in Maine wild blueberry, Vaccinium angustifolium Aiton. J. Econ. Entomol. 2017, 110, 1980–1992. [Google Scholar] [CrossRef]
- Yarborough, D.; Drummond, F.A.; Annis, S.; D’Appollonio, J. Maine wild blueberry systems analysis. Acta Hort. 2017, 1180, 151–160. [Google Scholar] [CrossRef]
- Bushmann, S.; Drummond, F.A. Abundance and diversity of wild bees (Hymenoptera: Apoidea) found in lowbush blueberry growing regions of Downeast Maine. Environ. Entomol. 2015, 43, 1–15. [Google Scholar] [CrossRef]
- Cutler, C.G.; Reeh, K.W.; Sproule, J.M.; Ramanaidu, K. Berry unexpected: Nocturnal pollination of lowbush blueberry. Can. J. Plant Sci. 2012, 92, 707–711. [Google Scholar] [CrossRef]
- Drummond, F.A.; (University of Maine, Orono, ME, USA). Personal communication, 2019.
- Dicenta, F.; Ortega, E.; Canovas, J.A.; Egea, J. Self-pollination vs. cross-pollination in almond: Pollen tube growth, fruit set and fruit characteristics. Plant Breeding 2002, 121, 163–167. [Google Scholar] [CrossRef]
- Scorza, R.; Bassi, D.; Liverani, A. Genetic interactions of pillar (columnar), compact, and dwarf peach tree genotypes. J. Am. Soc. Hort. Sci. 2002, 127, 254–261. [Google Scholar] [CrossRef]
- Frankel, R.; Galun, E. Pollination Mechanisms, Reproduction and Plant Breeding; Springer Science & Business Media: Berlin, Germany, 2012; Volume 2, 284p. [Google Scholar]
- Ramírez, F.; Davenport, T.L. Apple pollination: A review. Sci. Hort. 2013, 162, 188–203. [Google Scholar] [CrossRef]
- Hepler, P.R.; Yarborough, D.E. Natural variability in yield of lowbush blueberries. J. Am. Soc. Hort. Sci. 1991, 26, 245–246. [Google Scholar] [CrossRef]
- Bell, D.J.; Rowland, L.J.; Smagula, J.; Drummond, F.A. Recent advances in the biology and genetics of lowbush blueberry. Maine Agric. For. Exp. Stn. Tech. Bull. 2009, 203, 36. [Google Scholar]
- Bell, D.J.; Rowland, L.J.; Stommel, J.; Drummond, F.A. Yield variation among clones of lowbush blueberry as a function of kinship and self-compatibility. J. Hort Sci. 2010, 135, 1–12. [Google Scholar]
- Bajcz, A.; Hiebeler, D.; Drummond, F.A. Grid-Set-Match, an agent-based simulation model, predicts fruit set for the Maine lowbush blueberry (Vaccinium angustifolium) agroecosystem. Ecol. Model. 2017, 361, 80–94. [Google Scholar] [CrossRef]
- Qu, H.; Drummond, F.A. Simulation-based modeling of wild blueberry pollination. Electr. Comp. Agric. 2018, 144, 94–101. [Google Scholar] [CrossRef]
- Boulanger, L.W.; Wood, G.W.; Osgood, E.A.; Dirks, C.O. TB26: Native Bees Associated with the Low-Bush Blueberry in Maine and Eastern Canada. Maine Life Sci. Tech. Bull. 1967, 26, 23. [Google Scholar]
- Drummond, F.A.; Dibble, A.C.; Stubbs, C.; Bushmann, S.; Ascher, J.; Ryan, J. A natural history of change in native bees associated with lowbush blueberry in Maine. Northeast. Nat. 2017, 24, 49–68. [Google Scholar] [CrossRef]
- Javorek, S.K.; Mackenzie, K.E.; Vander Kloet, S.P. Comparative pollination effectiveness among bees (Hymenoptera: Apoidea) on lowbush blueberry (Ericaceae: Vaccinium angustifolium). Ann. Entomol. Soc. Am. 2002, 95, 345–351. [Google Scholar] [CrossRef]
- Drummond, F.A. Behavior of bees associated with the wild blueberry agro-ecosystem in the USA. Inter. J. Entomol. Nematol. 2016, 2, 27–41. [Google Scholar]
- Wood, G.W. The influence of honeybee pollination on fruit set of the lowbush blueberry. Can. J. Plant Sci. 1961, 41, 332–335. [Google Scholar] [CrossRef]
- Aras, P.; De Oliveira, D.; Savoie, L. Effect of a honey bee (Hymenoptera: Apidae) gradient on the pollination and yield of lowbush blueberry. J. Econ. Entomol. 1996, 89, 1080–1083. [Google Scholar] [CrossRef]
- Eaton, L.J.; Murray, J.E. Relationships of pollinator numbers in blueberry fields to fruit development and yields. Acta Hort. 1996, 446, 181–188. [Google Scholar] [CrossRef]
- Drummond, F.A.; Stubbs, C.S. Potential for management of the blueberry bee, Osmia atriventris Cresson. Acta Hort. 1997, 446, 77–86. [Google Scholar] [CrossRef]
- Stubbs, C.S.; Drummond, F.A. Pollination of wild lowbush blueberry, Vaccinium angustifolium by the alfalfa leafcutting bee, Megachile rotundata. Acta Hort. 1997, 446, 189–196. [Google Scholar] [CrossRef]
- Stubbs, C.S.; Drummond, F.A. Management of the alfalfa leafcutter bee, Megachile rotundata (Hymenoptera: Megachilidae), for pollination of wild lowbush blueberry. J. Kan. Ent. Soc. 1997, 70, 81–93. [Google Scholar]
- Stubbs, C.S.; Drummond, F.A.; Yarborough, D. How to Manage Alfalfa Leafcutting Bees for Wild Blueberry Pollination. Wild Blueberry Fact Sheet. No. 300, Bulletin No. 2413. 1997. Available online: https://extension.umaine.edu/blueberries/factsheets/bees/300-how-to-manage-alfalfa-leafcutting-bees-for-wild-blueberry-production/ (accessed on 6 March 2019).
- Stubbs, C.S.; Drummond, F.A.; Allard, S.L. Bee conservation and increasing Osmia spp. in Maine wild blueberry fields. Northeast. Nat. 1997, 4, 133–144. [Google Scholar] [CrossRef]
- Stubbs, C.S.; Drummond, F.A.; Yarborough, D. Field Conservation Management of Native Leafcutting and Mason Osmia Bees. Wild Blueberry Fact Sheet. No. 301, Bulletin No. 2420. 2000. Available online: https://extension.umaine.edu/blueberries/factsheets/bees/301-field-conservation-management-of-native-leafcutting-and-mason-osmia-bees/ (accessed on 6 March 2019).
- Stubbs, C.S.; Drummond, F.A. Bombus impatiens (Hymenoptera: Apidae): An alternative to Apis mellifera (Hymenoptera: Apidae) for lowbush blueberry pollination. J. Econ. Entomol. 2001, 94, 609–616. [Google Scholar] [CrossRef] [PubMed]
- Stubbs, C.S.; Drummond, F.A.; Osgood, E.A. Osmia ribifloris biedermannii and Megachile rotundata (Hymenoptera: Megachilidae) introduced into the lowbush blueberry agroecosystem in Maine. J. Kansas Ent. Soc. 1994, 67, 173–185. [Google Scholar]
- Stubbs, C.; Drummond, F.A. Blueberry and cranberry (Vaccinium spp.) pollination: A comparison of managed and native bee foraging behavior. Acta Hort. 1997, 437, 341–343. [Google Scholar] [CrossRef]
- Stubbs, C.S.; Drummond, F.A. Pollination of lowbush blueberry by Anthophora pallipes villosula and Bombus impatiens (Hymenoptera: Anthophoridae and Apidae). J. Kan. Entomol. Soc. 2000, 72, 330–333. [Google Scholar]
- Stubbs, C.S.; Drummond, F.A.; Yarborough, D. Commercial Bumble Bee, Bombus impatiens, Management for Lowbush Blueberry. Wild Blueberry Fact Sheet. No. 302, Bulletin No. 2421. 2001. Available online: https://extension.umaine.edu/blueberries/factsheets/bees/302-commercial-bumble-bee-bombus-impatiens-management-for-wild-blueberry-pollination/ (accessed on 6 March 2019).
- Desjardins, È.C.; De Oliveira, D. Commercial bumble bee, Bombus impatiens (Hymenoptera: Apidae) as a pollinator in lowbush blueberry (Ericale: Ericaceae) fields. J. Econ. Entomol. 2006, 99, 443–449. [Google Scholar] [CrossRef]
- Eaton, L.J.; Nams, V.O. Honey bee stocking numbers and wild blueberry production in Nova Scotia. Can. J. Plant Sci. 2012, 92, 1305–1310. [Google Scholar] [CrossRef]
- Drummond, F.A. Commercial bumblebee pollination of lowbush blueberry. Int. J. Fruit Sci. 2012, 12, 54–64. [Google Scholar] [CrossRef]
- Venturini, E.M.; Drummond, F.A.; Ballman, E. Native Andrena response to burning in the wild blueberry agroecosystem. J. Kan. Entomol. Soc. 2017, 90, 131–145. [Google Scholar] [CrossRef]
- Drummond, F.; Collum, K.; Hanes, S.; Wilson, M.; Skinner, J.; Collins, J. A Pollination Toolbox for Wild Blueberry Growers. In Proceedings of the NABREW Conference 2014, Atlantic City, NJ, USA, 24 June 2014; Available online: http://dx.doi.org/doi:10.7282/T3NZ8980 (accessed on 6 March 2019).
- Kevan, P.G. Forest application of the insecticide Fenitrothion and its effect on wild bee pollinators (Hymenoptera: Apoidea) of lowbush blueberries (Vaccinium spp.) in Southern New Brunswick. Can. Biol. Conserv. 1975, 7, 301–309. [Google Scholar] [CrossRef]
- Stubbs, C.S.; Drummond, F.A. Asana, impact on alfalfa leafcutting bees and other pollinators. Arthro. Manag. Tests 1998, 23, 52. [Google Scholar] [CrossRef]
- Drummond, F.A.; Stubbs, C.S. Wild Bee Conservation for Wild Blueberry Fields. Wild Blueberry Fact Sheet. No. 630, Bulletin No. 2111. 2003. Available online: https://extension.umaine.edu/blueberries/factsheets/bees/630-wild-bee-conservation-for-wild-blueberry-fields/ (accessed on 6 March 2019).
- Bushmann, S.L.; Drummond, F.A.; Beers, L.A.; Groden, E. Wild bumblebee (Bombus) diversity and Nosema (Microsporidia: Nosematidae) infection levels associated with lowbush blueberry (Vaccinium angustifolium) production and commercial bumblebee pollinators. Psyche 2012, 429398. [Google Scholar] [CrossRef]
- Venturini, E.M.; Berg-Stack, L.; Dibble, A.; Drummond, F.A.; Hoshide, A. Enhancing Native Bees for Wild Lowbush Blueberry Crop Pollination: Bee Pasture. Wild Blueberry Fact Sheet. 2015. Available online: http://umaine.edu/blueberries/files/2010/05/2015-Bee-Pasture-Fact-Sheet.pdf (accessed on 6 March 2019).
- Venturini, E.M.; Drummond, F.A.; Hoshide, A.K.; Dibble, A.C.; Stack, L.B. Pollination reservoirs in Maine lowbush blueberry. J. Econ. Entomol. 2017, 110, 333–346. [Google Scholar] [PubMed]
- Cote, J.; Yarborough, D.E.; Drummond, F.A.; Collins, J.A. Maine Wild Blueberry Pesticide Chart–1 of 3. 2018. Available online: http://umaine.edu/blueberries/files/2010/05/2013-ME-Wild-BB-Pesticide-Chart-Insecticides.pdf (accessed on 6 March 2019).
- Dibble, A.C.; Leach, M.; Drummond, F.A. Pollinator habitat: Demonstration gardens at two sites in Maine, a cooperative project between the landfill industry and wild blueberry growers. J. Exten. Rural Devel. 2018, 10, 89–98. [Google Scholar] [CrossRef]
- Venturini, E.M.; Drummond, F.A.; Hoshide, A.K. Organic establishment of pollination reservoirs in the lowbush blueberry (Ericales: Ericaceae) agroecosystem. Open Agric. 2018, 3, 393–403. [Google Scholar] [CrossRef]
- Calderwood, L.; Drummond, F.A. Bees–IPM Tactics to Reduce Pesticide Exposure to Honey and Native Bees. Wild Blueberry Fact Sheet. No. 2009. 2009. Available online: https://extension.umaine.edu/blueberries/factsheets/bees/2009-ipm-tactics-to-reduce-pesticide-exposure-to-honey-and-native-bees/ (accessed on 6 March 2019).
- Stubbs, C.S.; Jacobson, H.A.; Osgood, E.A.; Drummond, F.A. Alternative forage plants for native (wild) bees associated with lowbush blueberry, Vaccinium spp., in Maine. Maine Agric. For. Exp. Stn. Tech. Bull. 1992, 148, 54. [Google Scholar]
- Drummond, F.A.; Stubbs, C.S. Sampling bee populations in lowbush blueberry in Maine. Proc. VI Int. Symp. on Vaccinium Cult. Acta Hort. 1997, 446, 101–108. [Google Scholar] [CrossRef]
- Drummond, F.A.; Ballman, E.; Collins, J. Are They Weeds or a Life Force? Or Sustainability on the Edge. Spire Maine J. Cons. Sustain. 2017. Available online: https://umaine.edu/spire/2017/05/04/drummond-et-al/ (accessed on 6 March 2019).
- Groff, S.C.; Loftin, C.S.; Drummond, F.A.; Bushmann, S.; McGill, B. Spatial prediction of lowbush blueberry native bee pollinators in Maine, USA. Environ. Model. Soft. 2016, 79, 1–9. [Google Scholar] [CrossRef]
- Du Clos, B.; Loftin, C.; Drummond, F.A. BeeMapper tool Quick reference Guide. 2017. Available online: https://umaine.edu/beemapper/wp-content/uploads/sites /353/2017/07/ BeeMapper-Quick-Guide-for-Web.pdf (accessed on 6 March 2019).
- Drummond, F.A.; Yarborough, D. Growing season effects on wild blueberry (Vaccinium angustifolium) in Maine and implications for management. Acta Hort. 2014, 1017, 101–108. [Google Scholar] [CrossRef]
- Bajcz, A.W.; Drummond, F.A. Flower power: Floral and resource manipulations reveal the consequences of reproductive effort in lowbush blueberry (Vaccinium angustifolium). Ecol. Evol. 2017, 7, 1–15. [Google Scholar] [CrossRef]
- Bajcz, A.W.; Drummond, F.A. Bearing fruit: Flower removal reveals the trade-offs associated with high reproductive effort for lowbush blueberry. Oecologia 2017, 185, 13–26. [Google Scholar] [CrossRef] [PubMed]
- Aalders, L.E.; Hall, I.V. Pollen incompatibility and fruit set in lowbush blueberries. Can. J. Gen. Cytol. 1961, 3, 300–307. [Google Scholar] [CrossRef]
- Wood, G.W. Self-fertility in the lowbush blueberry. Can. J. Plant Sci. 1968, 48, 431–433. [Google Scholar] [CrossRef]
- Hokanson, K.; Hancock, J. Early-acting inbreeding depression in three species of Vaccinium (Ericaceae). Sex. Plant Repro. 2000, 13, 145–150. [Google Scholar] [CrossRef]
- Bell, D.J.; Rowland, L.J.; Zhang, D.; Drummond, F.A. Spatial genetic structure of lowbush blueberry, Vaccinium angustifolium, in four fields in Maine. Botany 2009, 87, 932–946. [Google Scholar] [CrossRef]
- Bell, D.J.; Rowland, L.J.; Drummond, F.A. Fine-scale spatial genetic structure associated with Vaccinium angustifolium Aiton (Ericaceae). Int. J. Bot. 2012, 2, 72–82. [Google Scholar]
- Myra, M.; MacKenzie, K.; Vander Kloet, S.P. Investigation of a possible sexual function specialization in the lowbush blueberry (Vaccinium angustifolium Ait. Ericaceae). Small Fruits Rev. 2004, 3, 313–324. [Google Scholar] [CrossRef]
- Bell, D.J.; Drummond, F.A.; Rowland, J.L. Evidence of functional gender polymorphisms in a population of the hermaphroditic lowbush blueberry (Vaccinium angustifolium Ait.). Botany 2012, 90, 393–399. [Google Scholar] [CrossRef]
- Bell, D.J.; Rowland, L.J.; Drummond, F.A. Does pollen neighborhood affect berry yield in lowbush blueberry (Vaccinium angustifolium Ait.)? Int. J. Fruit Sci. 2012, 12, 65–74. [Google Scholar] [CrossRef]
- Rowland, L.J.; Ogden, E.L.; Bell, D.J.; Drummond, F.A. Pollen-mediated gene flow in managed fields of lowbush blueberry. 2019; Manuscript in preparation. [Google Scholar]
- White, S.N.; Boyd, N.S.; van Acker, R.C. Growing degree-day models for predicting lowbush blueberry (Vaccinium angustifolium Ait.) ramet emergence, tip dieback, and flowering in Nova Scotia, Canada. HortScience 2012, 47, 1014–1021. [Google Scholar] [CrossRef]
- Collins, J.A.; Drummond, F.A. Fertilizer and fungicides: Effects on wild blueberry growth, insect attack, and disease incidence. Proc. NABREW 2019, 1–24. Available online: https://digitalcommons.library.umaine.edu/cgi/viewcontent.cgi?article=1014&context=nabrew2018 (accessed on 6 March 2019).
- Kanzow, C.; Yamashita, N.; Fukushima, M. Levenberg-Marquardt methods with strong local convergence properties for solving nonlinear equations with convex constraints. JCAM 2004, 172, 375–397. [Google Scholar] [CrossRef]
- Cook, R.D.; Weisberg, S. Residuals and Influence in Regression; Chapman and Hall: New York, NY, USA, 1982; 230p, ISBN 0-412-24280-0. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Durbin, J.; Watson, G.S. Testing for serial correlation in least squares regression III. Biometrika 1971, 58, 1–19. [Google Scholar] [CrossRef]
- SAS Institute. JMP® Version 14; SAS Institute Inc.: Cary, NC, USA, 2017; pp. 1989–2007. [Google Scholar]
- Dafni, A.; Maués, M.M. A rapid and simple procedure to determine stigma receptivity. Sex. Plant. Repro. 1998, 11, 177–180. [Google Scholar] [CrossRef]
- Galen, C.; Plowright, R.C. Testing the accuracy of using peroxidase activity to indicate stigma receptivity. Can. J. Bot. 1987, 65, 107–111. [Google Scholar] [CrossRef]
- Egea, J.; Burgos, L.; Garcia, J.E.; Egea, L. Stigma receptivity and style performance in several apricot cultivars. J. Am. Soc. Hort. Sci. 1991, 66, 19–25. [Google Scholar] [CrossRef]
- González, M.V.; Coque, M.; Herrero, M. Stigmatic receptivity limits the effective pollination period in kiwifruit. J. Am. Hort. Sci. 1995, 120, 199–202. [Google Scholar] [CrossRef]
- Yi, W.; Law, S.E.; Mccoy, D.; Wetzstein, H.Y. Stigma development and receptivity in almond (Prunus dulcis). Ann. Bot. 2005, 97, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Sanzol, J.; Rallo, P.; Herrero, M. Asynchronous development of stigmatic receptivity in the pear (Pyrus communis; Rosaceae) flower. Am. J. Bot. 2003, 90, 78–84. [Google Scholar] [CrossRef] [PubMed]
- Batra, L.R.; Batra, S.W. Floral mimicry induced by mummy-berry fungus exploits host’s pollinators as vectors. Science 1985, 228, 1011–1013. [Google Scholar] [CrossRef] [PubMed]
- Ehlenfeldt, M.K.; Stretch, A.W.; Brewster, V. Genetic and morphological factors influence mummy berry blight resistance in highbush blueberry cultivars. HortScience 1996, 31, 252–254. [Google Scholar] [CrossRef]
- Luckwill, L.C. Studies of fruit development in relation to plant hormones: I. Hormone production by the developing apple seed in relation to fruit drop. J. Am. Soc. Hort. Sci. 1953, 28, 14–24. [Google Scholar] [CrossRef]
- Xie, R.J.; Deng, L.; Jing, L.; He, S.L.; Ma, Y.T.; Yi, S.L.; Zheng, Y.Q.; Zheng, L. Recent advances in molecular events of fruit abscission. Biol. Planta 2013, 57, 201–209. [Google Scholar] [CrossRef]
- Racskó, J.; Leite, G.B.; Petri, J.L.; Zhongfu, S.; Wang, Y.; Szabó, Z.; Soltész, M.; Nyéki, J. Fruit drop: The role of inner agents and environmental factors in the drop of flowers and fruits. Inter. J. Am. Soc. Hort. Sci. 2007, 13, 13–23. [Google Scholar]
- Cane, J.H. Pollen viability and pollen tube attrition in cranberry (Vaccinium macrocarpon Aiton). Proc. IXth Inter. Symp. Vaccinium Cult. Acta Hort. 2009, 810, 563–566. [Google Scholar] [CrossRef]
- Cane, J.H.; Schiffhauer, D. Dose-response relationships between pollination and fruiting refine pollinator comparisons for cranberry (Vaccinium macrocarpon [Ericaceae]). Am. J. Bot. 2003, 90, 1425–1432. [Google Scholar] [CrossRef]
- Brown, A.O.; McNeil, J.N. Fruit production in cranberry (Ericaceae: Vaccinium macrocarpon): A bet-hedging strategy to optimize reproductive effort. Am. J. Bot. 2006, 93, 910–916. [Google Scholar] [CrossRef]
- Baumann, T.E.; Eaton, G.W. Competition among berries on the cranberry upright. J. Am. Soc. Hort. Sci. 1986, 111, 869–872. [Google Scholar]
- Benoit, G.R.; Grant, W.J.; Ismail, A.A.; Yarborough, D.E. Effect of soil moisture and fertilizer on the potential and actual yield of lowbush blueberries. Can. J. Plant Sci. 1984, 64, 683–689. [Google Scholar] [CrossRef]
- Snow, A.A. Pollination intensity and potential seed set in Passiflora vitifolia. Oecologia 1982, 55, 231–237. [Google Scholar] [CrossRef]
- Galen, C. Regulation of seed-set in Polemonium viscosum: Floral scents, pollination, and resources. Ecology 1985, 66, 792–797. [Google Scholar] [CrossRef]
- Delaplane, K.S.; Mayer, D.R.; Mayer, D.F. Crop Pollination by Bees; Cabi Publishing: London, UK, 2000; 344p. [Google Scholar]
- Silander, J.A.; Primack, R.B. Pollination intensity and seed set in the evening primrose (Oenothera fruticosa). Am. Mid. Nat. 1978, 100, 213–216. [Google Scholar] [CrossRef]
- Morandin, L.A.; Winston, M.L. Wild bee abundance and seed production in conventional, organic, and genetically modified canola. Ecol. Appl. 2005, 15, 871–881. [Google Scholar] [CrossRef]
- Hanes, S.P.; Collum, K.; Hoshide, A.K.; Drummond, F.A.; Asare, E. Grower perceptions of native pollinators and pollination strategies in the lowbush blueberry industry. Renew. Agric. Food Sys. 2013, 28, 1–8. [Google Scholar] [CrossRef]
- Stevens, T.; Hoshide, A.K.; Drummond, F. Willingness to pay for native pollination of blueberries: A conjoint analysis. Int. J. Agric. Mark. 2015, 2, 68–77. [Google Scholar]
- Hanes, S.; Collum, K.; Hoshide, A.; Drummond, F. Assessing wild pollinators in conventional agriculture: A case study from Maine, USA’s blueberry industry. Hum. Ecol. Rev. 2018, 24, 97–113. [Google Scholar] [CrossRef]
- Hoshide, A.K.; Drummond, F.A.; Stevens, T.H.; Venturini, E.M.; Hanes, S.P.; Sylvia, M.M.; Loftin, C.S.; Yarborough, D.E.; Averill, A.L. What is the value of wild bee pollination for wild blueberries and cranberries and who values it? Environments 2018, 5, 98. [Google Scholar] [CrossRef]
| Study | Source of Variation | Variance | % of Total Variance |
|---|---|---|---|
| 1966–1971 * | year | 271.9 | 11.2 |
| clone | 144.0 | 5.9 | |
| section | 96.2 | 4.0 | |
| stem | 1911.0 | 78.9 | |
| total | 2423.1 | 100.0 | |
| 2011–2015 | year | 29.4 | 3.5 |
| field | 170.5 | 20.2 | |
| clone | 96.8 | 11.4 | |
| stem | 549.4 | 64.9 | |
| total | 846.1 | 100.0 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drummond, F. Reproductive Biology of Wild Blueberry (Vaccinium angustifolium Aiton). Agriculture 2019, 9, 69. https://doi.org/10.3390/agriculture9040069
Drummond F. Reproductive Biology of Wild Blueberry (Vaccinium angustifolium Aiton). Agriculture. 2019; 9(4):69. https://doi.org/10.3390/agriculture9040069
Chicago/Turabian StyleDrummond, Frank. 2019. "Reproductive Biology of Wild Blueberry (Vaccinium angustifolium Aiton)" Agriculture 9, no. 4: 69. https://doi.org/10.3390/agriculture9040069
APA StyleDrummond, F. (2019). Reproductive Biology of Wild Blueberry (Vaccinium angustifolium Aiton). Agriculture, 9(4), 69. https://doi.org/10.3390/agriculture9040069





