Combination of Fuzzy Logic and Analytical Hierarchy Process Techniques to Assess Potassium Saturation Percentage of Some Calcareous Soils (Case Study: Fars Province, Southern Iran)
Abstract
:1. Introduction
2. Materials and Methods
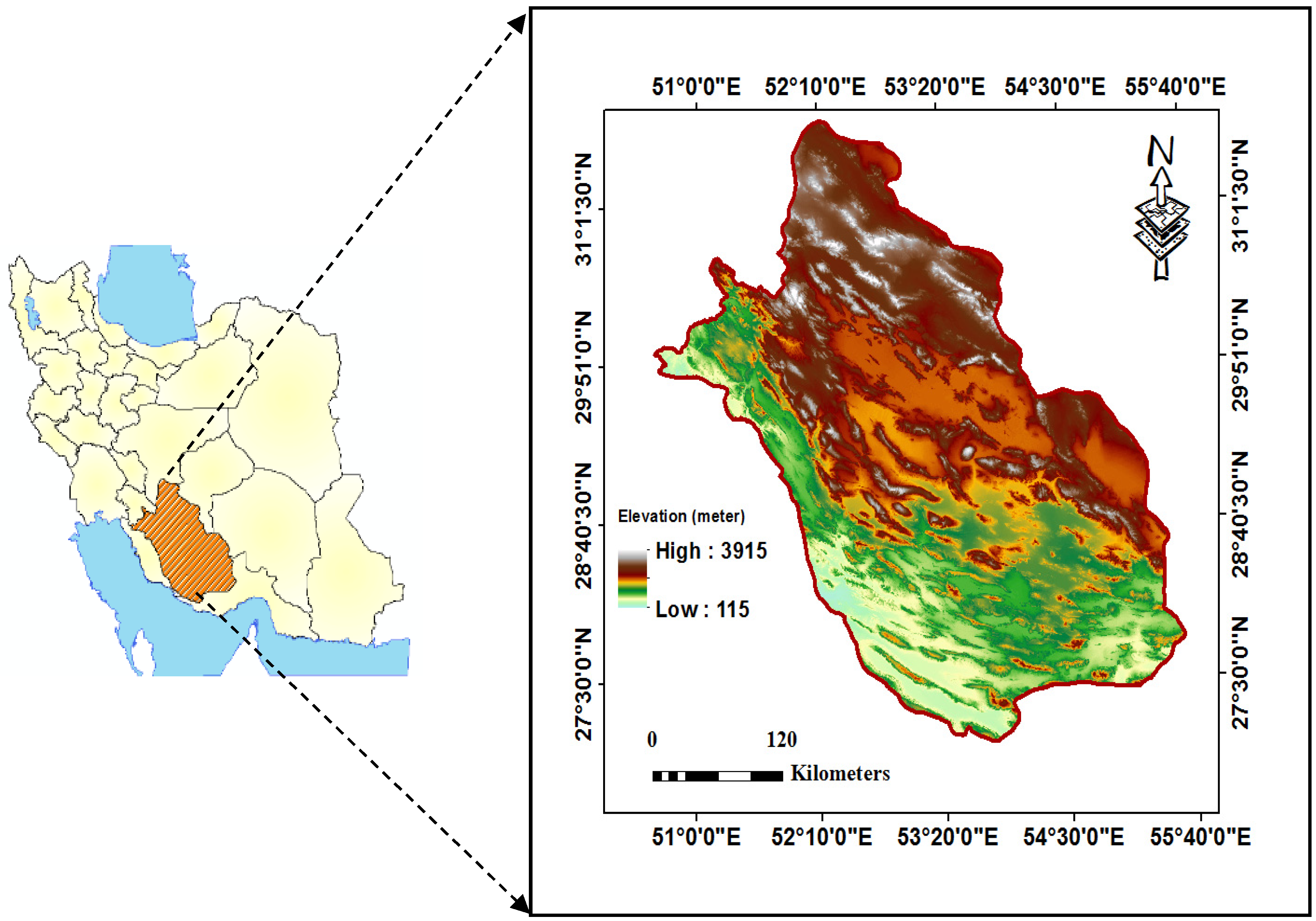
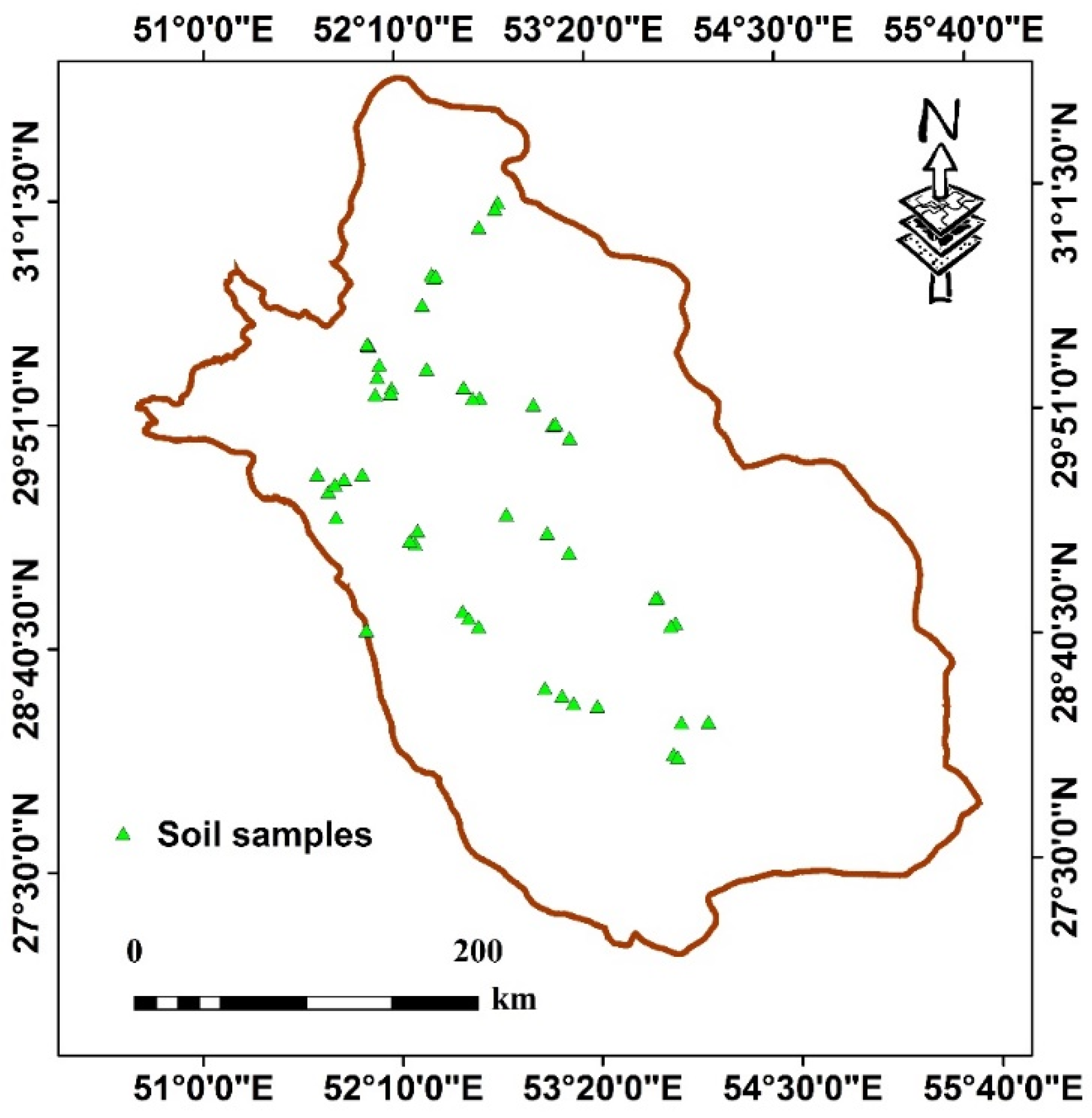
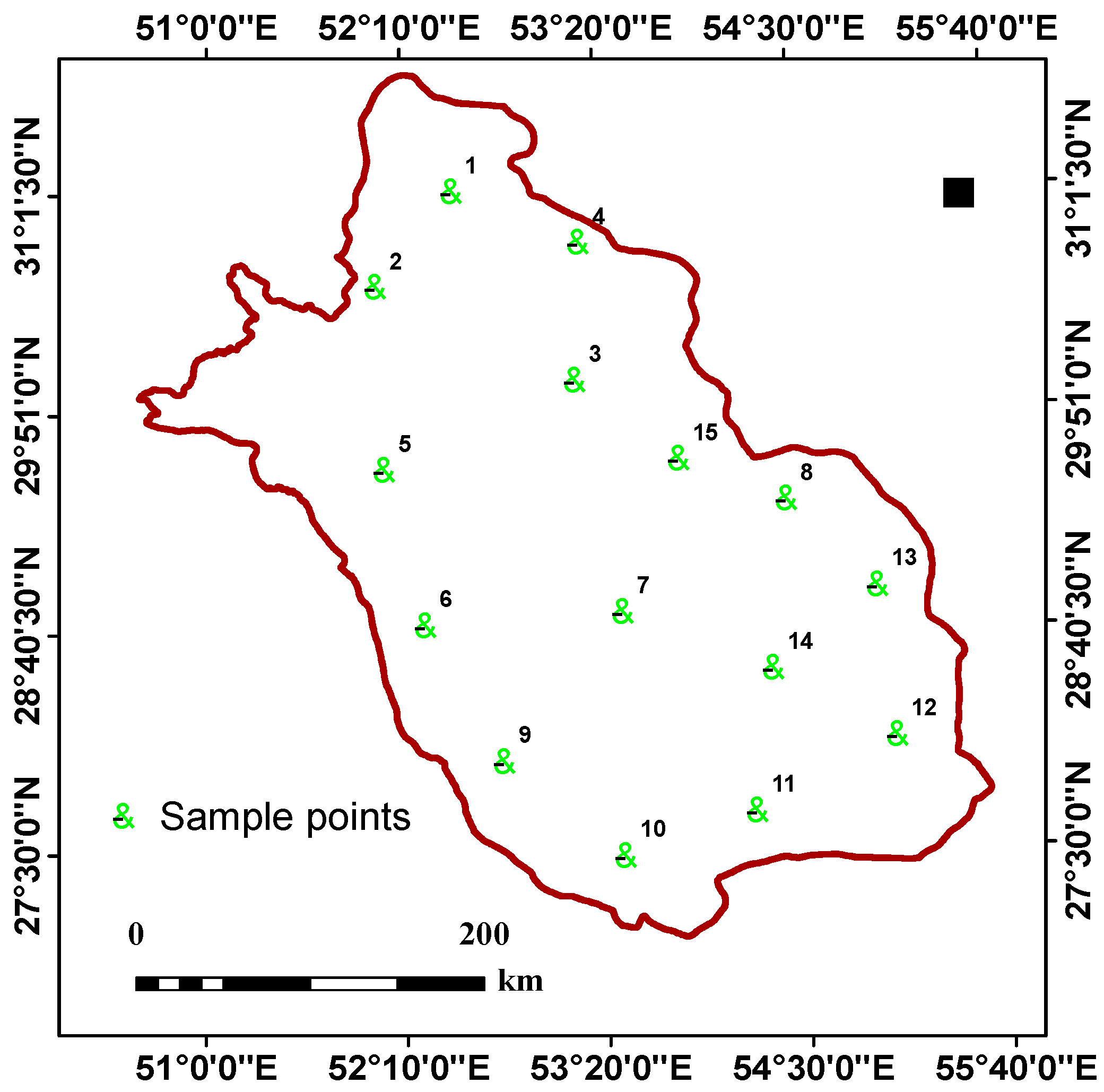
2.1. Study Area and Data Set
2.2. Methods
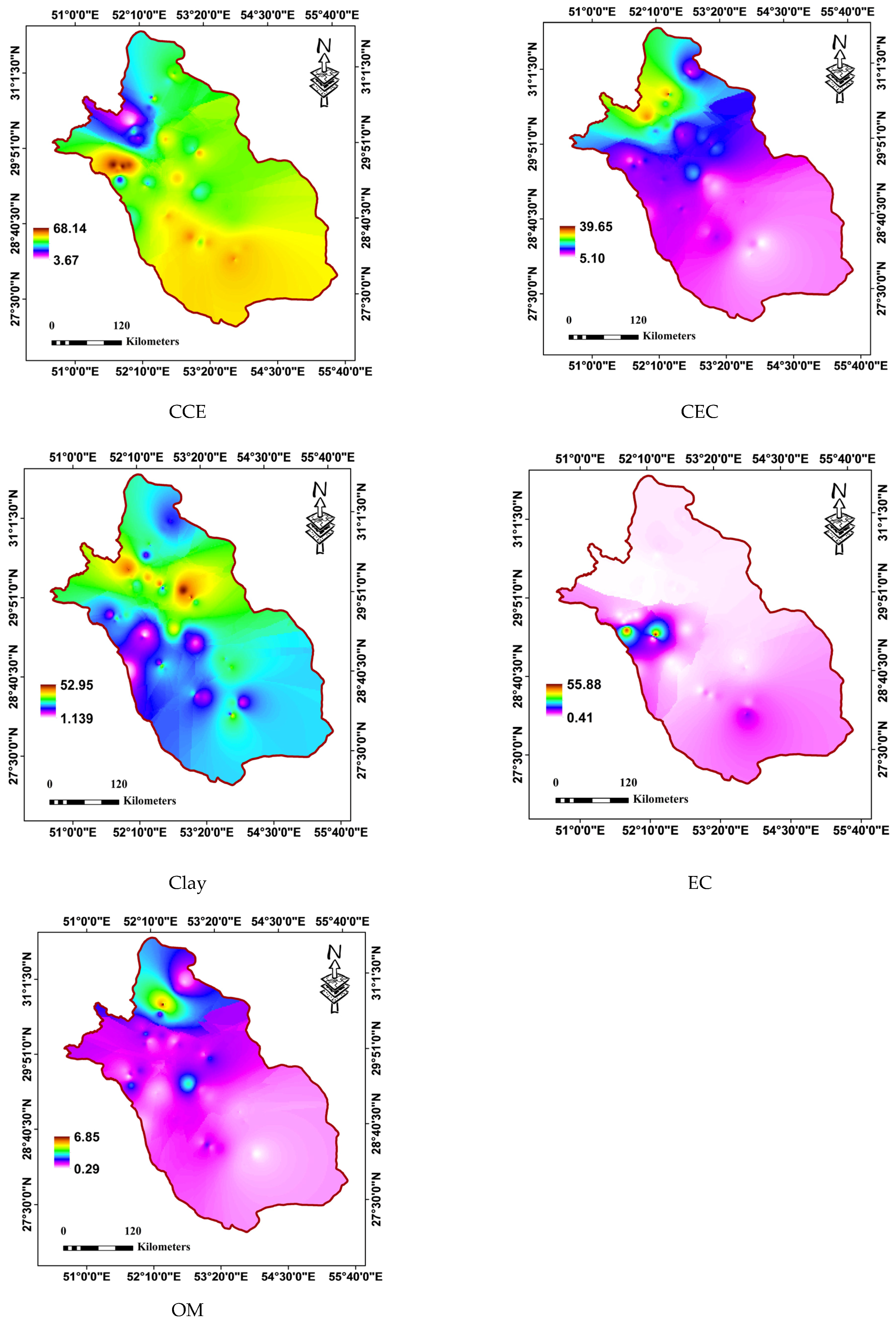
2.2.1. Kriging Interpolation
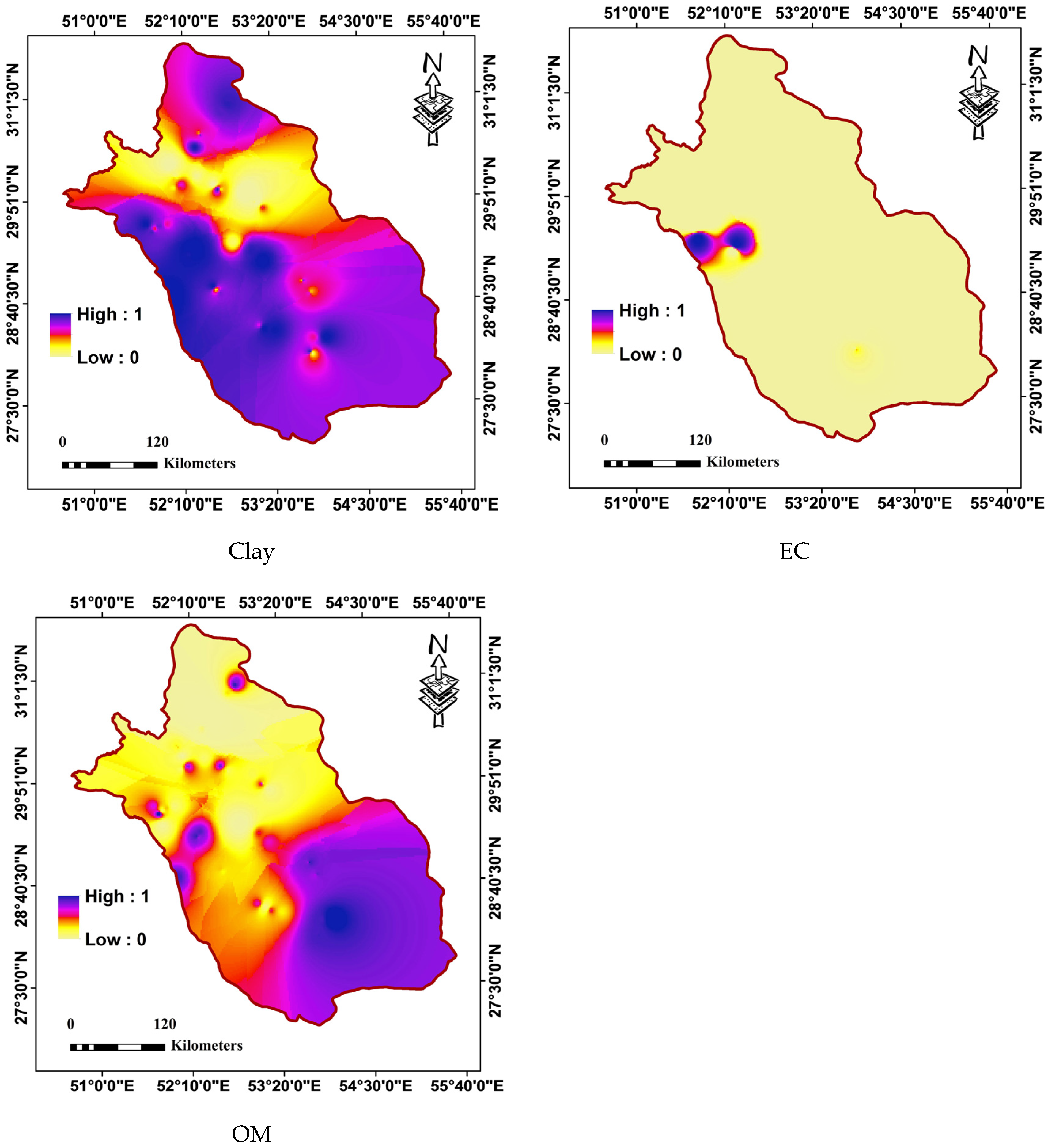
2.2.2. Fuzzy Classification
2.2.3. The Analytical Hierarchy Process Method
2.2.4. Combination of Fuzzy and AHP methods
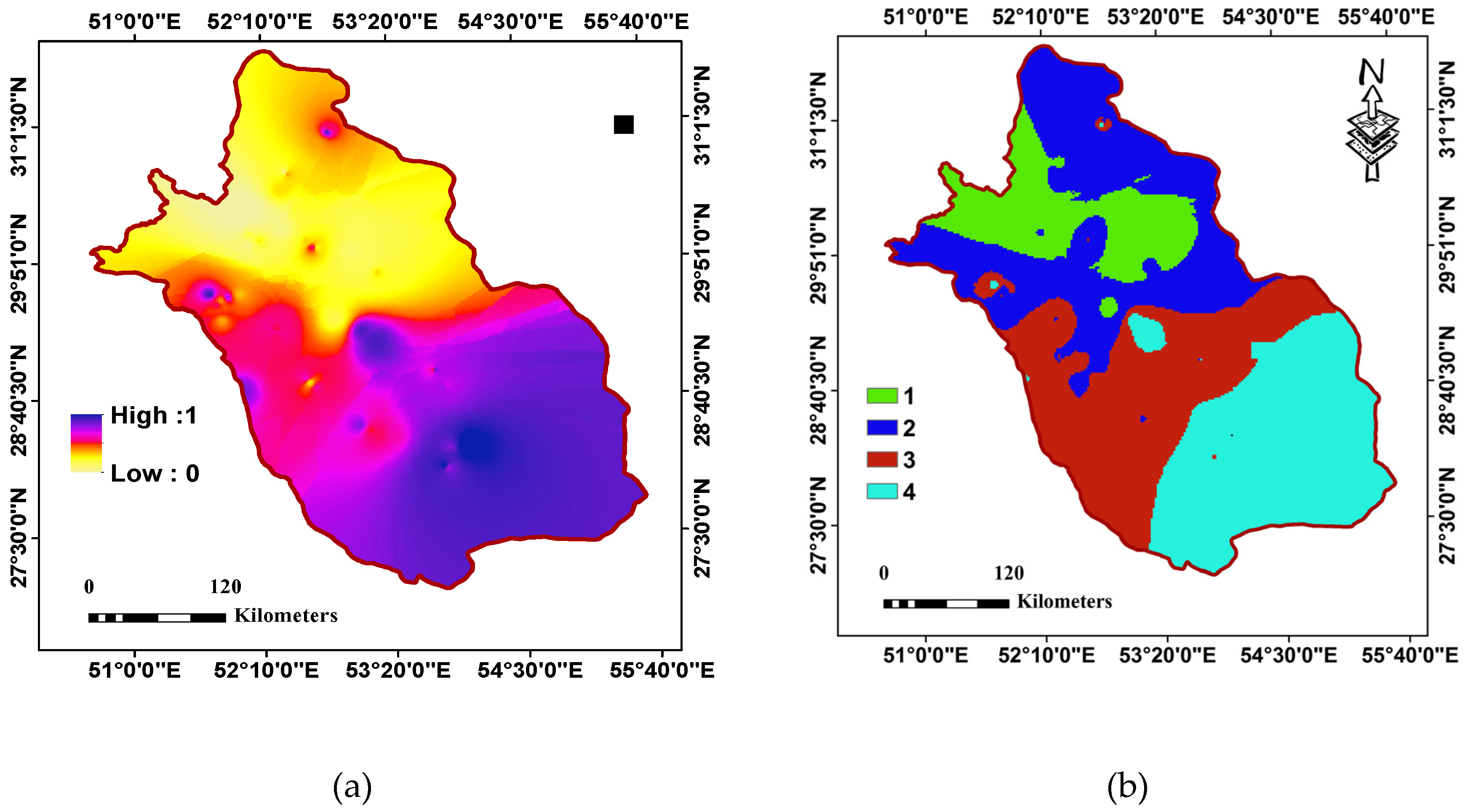
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Najafi-Ghiri, M.; Abtahi, A.; Owliaie, H.; Hashemi, S.S.; Koohkan, H. Factors Affecting Potassium Pools Distribution in Calcareous Soils of Southern Iran. Arid Land Res. Manag. 2011, 25, 313–327. [Google Scholar] [CrossRef]
- Sharpley, A.N. Reaction of fertilizer potassium in soils of differing mineralogy. Soil Sci. 1990, 149, 44–51. [Google Scholar] [CrossRef]
- Al-Zubaidi, A.; Yanni, S.; Bashour, I. Potassium status in some Lebanese soils. Leban. Sci. J. 2008, 9, 81–97. [Google Scholar]
- Pagel, H.; Insa, I. Veranderung wichtiger Grossern des K–Haushaltes in Mangroveboden Guineas unter dem Einfluss der Nutzung. Trans. Int. Congr. Soil Sci. 1974, 4, 349–357. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resources Allocation; McGraw: New York, NY, USA, 1980. [Google Scholar]
- Bello-Dambatta, A.; Farmani, R.; Javadi, A.A.; Evans, B. The Analytical Hierarchy Process for contaminated land management. Adv. Eng. Inform. 2009, 23, 433–441. [Google Scholar] [CrossRef]
- Giri, S.; Nejadhashemi, A.P. Application of analytical hierarchy process for effective selection of agricultural best management practices. J. Environ. Manag. 2014, 132, 165–177. [Google Scholar] [CrossRef] [PubMed]
- Rahaman, S.A.; Ajeez, S.A.; Aruchamy, S.; Jegankumar, R. Prioritization of Sub Watershed Based on Morphometric Characteristics Using Fuzzy Analytical Hierarchy Process and Geographical Information System—A Study of Kallar Watershed, Tamil Nadu. Aquat. Procedia 2015, 4, 1322–1330. [Google Scholar] [CrossRef]
- Ahamed, T.N.; Rao, K.G.; Murthy, J. GIS-based fuzzy membership model for crop-land suitability analysis. Agric. Syst. 2000, 63, 75–95. [Google Scholar] [CrossRef]
- Cengiz, T.; Akbulak, C. Application of analytical hierarchy process and geographic information systems in land-use suitability evaluation: A case study of Dümrek village (Çanakkale, Turkey). Int. J. Sustain. Dev. World Ecol. 2009, 16, 286–294. [Google Scholar] [CrossRef]
- Rowell, D.L. Soil Science: Methods and Applications; Longman Group Limited, Longman Scientific & Technical: Essex, UK, 1994. [Google Scholar]
- USSL Staff. Diagnosis and Improvement of Saline and Alkali Soils; United States Department of Agriculture: Washington, DC, USA, 1954.
- Nelson, D.W.; Sommers, L.E.; Sparks, D.; Page, A.; Helmke, P.; Loeppert, R.; Soltanpour, P.; Tabatabai, M.; Johnston, C.; Sumner, M. Total carbon, organic carbon, and organic matter. In Methods of Soil Analysis; Science Society of America: Madison, WI, USA, 1996. [Google Scholar]
- Chapman, H.D. Cation-exchange capacity. In Methods of Soil Analysis; Clemson University: Clemson, SC, USA, 1965. [Google Scholar]
- Pratt, P.P. Chemical and Microbiological Properties (methodsofsoilanb). In Methods of Soil Analysis; Clemson University: Clemson, SC, USA, 1965; pp. 1022–1030. [Google Scholar]
- Goovaerts, P. Geostatistics in soil science: State-of-the-art and perspectives. Geoderma 1999, 89, 1–45. [Google Scholar] [CrossRef]
- McBratney, A.B.; Odeh, I.O. Application of fuzzy sets in soil science: Fuzzy logic, fuzzy measurements and fuzzy decisions. Geoderma 1997, 77, 85–113. [Google Scholar] [CrossRef]
- Braimoh, A.K.; Vlek, P.L.; Stein, A. Land evaluation for maize based on fuzzy set and interpolation. Environ. Manag. 2004, 33, 226–238. [Google Scholar]
- Hamzeh, S.; Mokarram, M.; Alavipanah, S.K. Combination of fuzzy and AHP methods to assess land suitability for barley: Case Study of semi arid lands in the southwest of Iran. Desert 2014, 19, 173–181. [Google Scholar]
- Mokarram, M.; Rangzan, K.; Moezzi, A.; Baninemeh, J. Land suitability evaluation for wheat cultivation by fuzzy theory approach as compared with parametric method. ISPRS 2010, 38, 140–145. [Google Scholar]
- Burrough, P. Fuzzy mathematical methods for soil survey and land evaluation. J. Soil Sci. 1989, 40, 477–492. [Google Scholar] [CrossRef]
- Najafi Ghiri, M. Study of Morphological and Mineralogical Properties and Potassium Status of Soils of Fars Province. Ph.D. Thesis, Department of Soil Science, Shiraz University, Shiraz, Iran, 2010; p. 222. [Google Scholar]
- Nabiollahy, K.; Khormali, F.; Bazargan, K.; Ayoubi, S. Forms of K as a function of clay mineralogy and soil development. Clay Miner. 2006, 41, 739–749. [Google Scholar] [CrossRef]
- Al-Zubaidi, A. Potassium status in Iraqi soils. In Proceedings of the Regional Workshop: Potassium and Water Management in West Asia and North Africa; Johnston, A.E., Ed.; International Potash Institute: Horgen, Switzerland, 2003; pp. 129–142. [Google Scholar]
- Havlin, J.; Beaton, J.; Tisdale, S.; Nelson, W. Soil Fertility and Fertilizers; Pretince Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Soil Survey Staff. Soil Taxonomy: A Basic System of Soil Classification for Making and Interpreting Soil Survey; U.S. Government Printing Office: Washington, DC, USA, 1999.
- Soil Survey Staff. Keys to Soil Taxonomy; Natural Resources Conservation Service: Washington, DC, USA, 2006.
- Soil Survey Staff. Soil Survey Manual; USDA: Washington, DC, USA, 1993.
- Ayoubi, Sh.; Jalalian, A. Land Evaluation (Agriculture and Natural Resources); Sanati Isfahan University Press: Isfahan, Iran, 2006. [Google Scholar]
- Najafi-Ghiri, M.; Abtahi, A. Factors affecting potassium fixation in calcareous soils of southern Iran. Arch. Agron. Soil Sci. 2012, 58, 335–352. [Google Scholar] [CrossRef]
- Bijanzadeh, E.; Mokarram, M. The use of fuzzy-AHP methods to assess fertility classes for wheat and its relationship with soil salinity: East of Shiraz, Iran: A case study. Aust. J. Crop Sci. 2013, 7, 1699–1706. [Google Scholar]

| Soil Properties | Clay % | Sand % | Silt % | CCE % | CEC Cmol(+)kg−1 | EC dSm−1 | OM % |
|---|---|---|---|---|---|---|---|
| Maximum | 53 | 81 | 89 | 69 | 56 | 57.1 | 21.0 |
| Minimum | 1 | 1 | 12 | 3 | 5 | 0.2 | 0.1 |
| Average | 25 | 27 | 48 | 41 | 15 | 4.2 | 3.1 |
| SD | 13.57 | 17.31 | 12.24 | 16.65 | 9.00 | 10.19 | 3.02 |
| Factor | Kriging | IDW | Spline | |||
|---|---|---|---|---|---|---|
| Gaussian | Circular | Spherical | Exponential | |||
| Clay, % | 1.28 | 1.10 | 1.21 | 1.31 | 1.11 | 1.12 |
| Sand, % | 3.20 | 3.17 | 3.71 | 3.21 | 4.10 | 4.20 |
| Silt, % | 3.10 | 2.98 | 3.40 | 3.53 | 3.21 | 3.10 |
| CCE, % | 3.33 | 3.24 | 3.41 | 3.54 | 3.28 | 3.81 |
| CEC, Cmol(+)kg−1 | 4.10 | 3.56 | 3.81 | 4.10 | 5.20 | 4.90 |
| EC, dSm−1 | 3.30 | 2.94 | 3.10 | 3.20 | 2.98 | 3.00 |
| OM, % | 1.36 | 1.04 | 1.28 | 1.31 | 1.25 | 1.91 |
| Factor | Low | Moderate | High | Very High |
|---|---|---|---|---|
| Clay, % | <18 | 18–35 | 35-60 | >60 |
| CCE, % | <2 | 2–15 | 15-40 | >40 |
| CEC, Cmol(+)kg−1 | <8 | 8–16 | 16-32 | >32 |
| EC, dSm−1 | <4 | 4–8 | 8-16 | >16 |
| OM, % | <1 | 1–5 | 5-10 | >10 |
| Factors | CEC | Clay | CCE | OM | EC | Weight |
|---|---|---|---|---|---|---|
| CEC | 1 | 2 | 3 | 4 | 5 | 0.42 |
| Clay | 1/2 | 1 | 2 | 3 | 4 | 0.26 |
| CCE | 1/3 | 1/2 | 1 | 2 | 3 | 0.16 |
| OM | 1/4 | 1/3 | 1/2 | 1 | 2 | 0.10 |
| EC | 1/5 | 1/4 | 1/3 | 1/2 | 1 | 0.06 |
| Class | Area (%) | Area (km2) |
|---|---|---|
| Very low | 14.05 | 17,477 |
| Low | 28.98 | 36,067 |
| Moderate | 27.48 | 34,198 |
| High | 29.49 | 36,700 |
| Total | 100 | 124,442 |
| Sample Point | CCE, % | CEC, cmol(+)kg−1 | Clay, % | EC, dS m−1 | OM, % | KSP, % | Class |
|---|---|---|---|---|---|---|---|
| 1 | 36.22 | 20.36 | 22.01 | 20.36 | 2.39 | 1 to 3 | 2 |
| 2 | 39.67 | 18.13 | 24.70 | 18.13 | 2.22 | 1 to 3 | 2 |
| 3 | 20.70 | 29.68 | 35.13 | 29.68 | 2.75 | <1 | 1 |
| 4 | 40.99 | 14.87 | 42.51 | 14.87 | 1.44 | <1 | 1 |
| 5 | 43.21 | 12.16 | 31.25 | 12.16 | 1.31 | 1 to 3 | 2 |
| 6 | 55.74 | 13.53 | 22.42 | 13.53 | 1.46 | 1 to 3 | 2 |
| 7 | 43.63 | 9.97 | 27.59 | 9.97 | 0.90 | 3 to 5 | 3 |
| 8 | 47.56 | 8.35 | 22.79 | 8.35 | 0.76 | >5 | 4 |
| 9 | 45.23 | 9.24 | 22.86 | 9.24 | 0.87 | 3 to 5 | 3 |
| 10 | 45.47 | 11.21 | 16.30 | 11.21 | 1.15 | 3 to 5 | 3 |
| 11 | 50.28 | 7.70 | 21.73 | 7.70 | 0.66 | >5 | 4 |
| 12 | 50.44 | 8.06 | 22.61 | 8.06 | 0.74 | >5 | 4 |
| 13 | 51.67 | 9.91 | 18.66 | 9.91 | 1.13 | 3 to 5 | 3 |
| 14 | 52.27 | 7.52 | 23.07 | 7.52 | 0.70 | >5 | 4 |
| 15 | 51.90 | 8.30 | 22.19 | 8.30 | 0.84 | >5 | 4 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mokarram, M.; Najafi-Ghiri, M. Combination of Fuzzy Logic and Analytical Hierarchy Process Techniques to Assess Potassium Saturation Percentage of Some Calcareous Soils (Case Study: Fars Province, Southern Iran). Agriculture 2016, 6, 59. https://doi.org/10.3390/agriculture6040059
Mokarram M, Najafi-Ghiri M. Combination of Fuzzy Logic and Analytical Hierarchy Process Techniques to Assess Potassium Saturation Percentage of Some Calcareous Soils (Case Study: Fars Province, Southern Iran). Agriculture. 2016; 6(4):59. https://doi.org/10.3390/agriculture6040059
Chicago/Turabian StyleMokarram, Marzieh, and Mahdi Najafi-Ghiri. 2016. "Combination of Fuzzy Logic and Analytical Hierarchy Process Techniques to Assess Potassium Saturation Percentage of Some Calcareous Soils (Case Study: Fars Province, Southern Iran)" Agriculture 6, no. 4: 59. https://doi.org/10.3390/agriculture6040059
APA StyleMokarram, M., & Najafi-Ghiri, M. (2016). Combination of Fuzzy Logic and Analytical Hierarchy Process Techniques to Assess Potassium Saturation Percentage of Some Calcareous Soils (Case Study: Fars Province, Southern Iran). Agriculture, 6(4), 59. https://doi.org/10.3390/agriculture6040059





