Path Planning for Agricultural UAVs Based on Deep Reinforcement Learning and Energy Consumption Constraints

Abstract

Traditional pesticide application methods pose systemic threats to sustainable agriculture due to inefficient spraying practices and ecological contamination. Although agricultural drones demonstrate potential to address these challenges, they face critical limitations in energy-constrained complete coverage path planning for field operations. This study proposes a novel BiLG-D3QN algorithm by integrating deep reinforcement learning with Bi-LSTM and Bi-GRU architectures, specifically designed to optimize segmented coverage path planning under payload-dependent energy consumption constraints. The methodology encompasses four components: payload-energy consumption modeling, soybean cultivation area identification using Google Earth Engine-derived spatial distribution data, raster map construction, and enhanced segmented coverage path planning implementation. Through simulation experiments, the BiLG-D3QN algorithm demonstrated superior coverage efficiency, outperforming DDQN by 13.45%, D3QN by 12.27%, Dueling DQN by 14.62%, A-Star by 15.59%, and PPO by 22.15%. Additionally, the algorithm achieved an average redundancy rate of only 2.45%, which is significantly lower than that of DDQN (18.89%), D3QN (17.59%), Dueling DQN (17.59%), A-Star (21.54%), and PPO (25.12%). These results highlight the notable advantages of the BiLG-D3QN algorithm in addressing the challenges of pesticide spraying tasks in agricultural UAV applications.

1. Introduction

Conventional pesticide application methodologies have been identified as systemic barriers to sustainable agricultural development due to inherent precision deficiencies that induce active ingredient dissipation and ecological contamination risks [1,2,3,4]. Agricultural UAV technologies, leveraging precision spraying mechanisms and three-dimensional operational capabilities, demonstrate significant potential to enhance agrochemical utilization efficiency while minimizing phytotoxicity, thereby offering a technological pathway to address these persistent challenges. However, the realization of fully autonomous operations in complex agricultural landscapes remains constrained by a critical research gap: the development of intelligent path-planning algorithms capable of synergistic optimization under concurrent constraints of coverage efficiency and energy consumption. This technological bottleneck, which necessitates sophisticated adaptation to heterogeneous terrain morphology and dynamic payload-energy relationships, fundamentally governs the translational progression of agricultural UAV systems from localized technical solutions to scalable field implementations [5,6,7,8,9].

Against this backdrop, deep reinforcement learning (DRL) offers a viable solution for further optimizing these challenges [10]. As a technology integrating the perceptual capabilities of deep learning with the decision-making strengths of reinforcement learning, it enables real-time formulation and optimization of action plans in unknown environments using limited prior knowledge [11,12,13,14,15,16,17]. Compared to traditional path-planning algorithms, DRL demonstrates enhanced flexibility and efficiency in complex scenarios, allowing UAVs to optimize flight paths according to mission requirements while effectively avoiding obstacles. Consequently, the application of DRL is poised to elevate the operational efficiency and intelligence of agricultural UAVs, providing robust technical support for modern agricultural development [18].

In recent years, Zhang et al. proposed an improved A-Star algorithm, referred to as RFA-Star, to address the path planning challenges of UAVs in environments with high obstacle density [19]. By incorporating a spatial topological relationship model and a feature-point-based search mechanism, the algorithm demonstrated enhanced efficiency and stability in terms of computation time and path quality. He et al. proposed a hybrid algorithm for UAV path planning in complex environments, which integrates an improved A* algorithm with the Dynamic Window Approach through a dual-layer optimization framework [20]. By optimizing node expansion strategies, dynamically adjusting the weights of the heuristic function, and extracting key path nodes, the proposed method achieved significant improvements in both path search efficiency and trajectory smoothness. Yao et al. proposed a memory-enhanced dueling deep Q-network (ME-dueling DQN) for path planning of unmanned helicopters in battlefield environments [21], which demonstrated certain improvements in algorithm convergence speed and learning efficiency. Xing et al. developed a DRL-based method for complete coverage path planning of unmanned surface vehicles (USVs) in complex aquatic environments [22]. By preprocessing grid maps and optimizing action selection mechanisms, this approach enhanced path planning efficiency and reduced path redundancy. Zhu et al. integrated the Hexagonal Area Search (HAS) algorithm with DRL to address overlapping coverage issues in unknown environments, proposing the HAS-DQN algorithm [23]. Wang et al. introduced a novel re-DQN algorithm for complete coverage path planning in kiwifruit harvesting robots [24]. By employing a path quality evaluation function and an experience replay mechanism, the value of the entire path is updated, thereby enabling more effective propagation of reward information.

The A* algorithm has received considerable attention in traditional pathfinding approaches. However, its performance remains constrained by heavy reliance on heuristic functions, making it difficult to balance accuracy and computational efficiency in complex scenarios. In deep reinforcement learning applications, basic algorithms such as DQN, DDQN, and Dueling DQN are predominantly employed. The conventional DQN architecture suffers from systematic overestimation of Q-values due to its reliance on a single network for both value estimation and action selection. Although DDQN mitigates this issue through decoupled network structures, it demonstrates poor convergence performance in environments characterized by substantial action-value disparities or sparse rewards. The Dueling DQN architecture enhances learning efficiency through value-advantage decomposition but faces two principal challenges: the identifiability problem inherent in network structure design and increased architectural complexity.

There are certain limitations in current CPP research at the technical level, and several theoretical aspects also remain underdeveloped and in need of further refinement. Existing studies predominantly focus on coverage efficiency optimization and redundant path avoidance mechanisms, whereas systematic integration of energy consumption models for unmanned aerial vehicles (UAVs) has not been achieved within current analytical frameworks. Particularly for UAVs widely deployed in agricultural applications, operational efficacy is constrained by the inherent payload-endurance paradox. Given the physical limitations of battery energy density and carrying capacity, such UAV platforms necessitate periodic return mechanisms for battery replenishment during large-scale field operations, thereby generating path optimization challenges under energy constraints.

This fundamental challenge revolves around achieving complete area coverage through multi-phase trajectory planning while minimizing path redundancy around replenishment nodes under finite endurance conditions. Current algorithms exhibit notable theoretical deficiencies in coupling dynamic energy management with spatial segmentation optimization, directly compromising operational effectiveness in complex farmland environments. The present study therefore aims to develop a novel CPP methodology that concurrently optimizes coverage efficiency and minimizes path repetition in segmented agricultural missions with payload-dependent energy consumption considerations.

The principal contributions of this study are threefold:

• To address the D3QN algorithm’s limitations in capturing temporal dependencies within task map states, a novel BiLG-D3QN algorithm is proposed through integration of DRL with Bi-LSTM and Bi-GRU architectures. The enhanced temporal information processing capability is validated through comparative simulated experiments, demonstrating a 19.7% improvement in sequential pattern recognition accuracy.
• A spectral band-based task mapping framework is developed to enhance algorithmic learning precision and applicability. This framework incorporates remote sensing data acquired via Google Earth Engine (GEE) with grid-based modeling techniques to simulate practical agricultural UAV operational environments.
• An energy consumption constraint model is established and implemented to address payload-dependent segmented path planning requirements. This model systematically integrates battery drain characteristics with dynamic payload variations during agricultural missions.

The manuscript is organized as follows:

Section 2 details the task mapping methodology, energy consumption modeling framework, and the proposed enhanced BiLG-D3QN algorithm architecture. Section 3 presents the experimental design, comparative performance evaluation metrics, and critical analysis of empirical results. Section 4 concludes with substantive findings and proposes future research directions for adaptive agricultural robotics.

2. Materials and Methods

2.1. Designed Planning Area Description

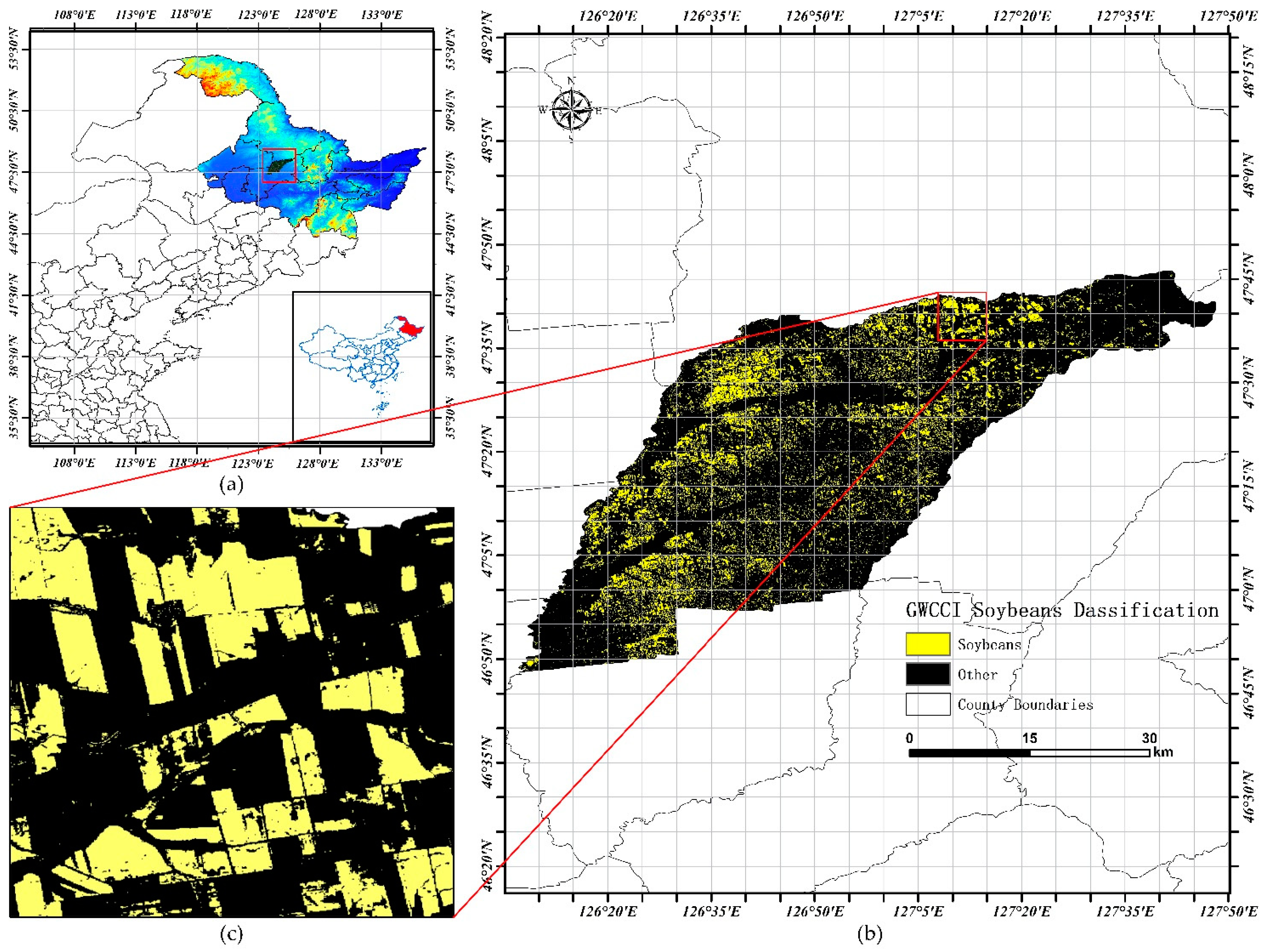
Soybean (Glycine max), as a globally strategic oilseed crop, exhibits spatiotemporal dynamics in cultivation patterns that directly influence regional agricultural economic stability and food supply chain resilience. Empirical evidence suggests that contemporary large-scale cultivation systems demonstrate homogenization of agricultural practices, with persistent monoculture patterns inducing soil microbial community dysbiosis and enrichment of soil-borne pathogens. These biophysical perturbations consequently manifest as diminished stress tolerance and yield instability in continuous cropping systems. This study therefore strategically selects soybean cultivation zones for task mapping framework development.

Complementing this approach, Chen et al. (2023) developed the Greenness and Water Content Composite Index (GWCCI), a novel spectral metric for soybean mapping using multispectral satellite imagery [25]. This methodology demonstrates exceptional classification accuracy and cross-regional robustness across diverse climatic regimes and agri-landscape configurations, particularly when integrated with GEE cloud computing capabilities.

The study area encompasses Hailun City (46°58′ N–47°52′ N, 126°14′ E–127°45′ E) in Heilongjiang Province, China, situated within the central mollisol zone of the Songnen Plain. This strategic black soil region spans 3105 km² of arable land (approximately 4.65 million acres), exhibiting a stepped topographic gradient descending northeast-to-southwest through successive geomorphological units: low hills, elevated plains, river terraces, and alluvial floodplains [26,27,28]. Accelerated by agricultural restructuring initiatives over the past decade, soybean cultivation now occupies >65% of total cropland (Figure 1), establishing this region as an exemplary model for intensive legume production systems in temperate agroecozones.

The methodological framework employed Sentinel-2 satellite imagery (10 m spatial resolution) acquired through the GEE platform, focusing on Hailun City during the 2021 growing season. Cloud-contaminated pixels were systematically removed using the QA60 bitmask algorithm, generating monthly cloud-free composites. Spectral bands critical for vegetation analysis—Near-Infrared (NIR: Band 8), Red (Band 4), and Short-Wave Infrared (SWIR: Band 11)—were extracted for subsequent processing. Following the methodology established by Chen, the Greenness and Water Content Composite Index (GWCCI) was calculated through the band combination formula presented in Equation (1), enabling precise soybean cultivation area delineation within the study region.

$$GWCCI={\displaystyle \frac{{\rho }_{NIR}-{\rho }_{RED}}{{\rho }_{NIR}+{\rho }_{RED}}}\ast {\rho }_{SWIR}$$

(1)

Following the acquisition of the GWCCI index map, the threshold method was employed to classify the index values, partitioning the map into soybean cultivation areas (task regions) and non-soybean areas (non-task regions). These classified regions were subsequently converted into a computer-processable raster map, as illustrated in Figure 2.

2.2. Environmental Constraints on UAV Energy Consumption Based on Payload Characteristics

During pesticide spraying operations, the UAV’s payload is progressively diminished as chemicals are continuously consumed, resulting in dynamically adjusted power consumption characteristics. To mathematically characterize this energy expenditure, a linear energy consumption model grounded in a black-box approach is proposed to quantify mission-specific power usage, as formalized in Equation (2).

$$P_{ij}=C_{move}+{K\ast C}_{load}+e$$

(2)

In the formulated model, $P_{ij}$ denotes the energy expenditure during transit from node i to j, where $C_{move}$ represents the base energy expenditure during unloaded flight. The variable m corresponds to the time-variant payload mass, which progressively decreases throughout mission execution. The payload power coefficient $K$ quantifies the additional power demand per unit mass, while $e$ serves as an empirical correction factor accounting for unmodeled energy consumption sources, including aerodynamic drag and avionics overhead.

The battery state-of-charge update mechanism is governed by Equation (3), $B_t$ denotes the battery charge level at time step t, while $B_{t-1}$ represents the battery charge level at time step t − 1.

$$B_t=B_{t-1}-P_{ij}$$

(3)

The dynamic return decision protocol for UAVs is mathematically formalized in Equation (4), where L denotes the distance scaling coefficient, (x, y) represent current positional coordinates, and ($x_{station}{,y}_{station}$) indicate charging station locations. $\left(x_{next},y_{next}\right)$ represent the position of the UAV after the action is performed. Autonomous battery replenishment is triggered when the residual charge level equals or falls below the energy threshold required for station navigation, at which point the UAV is systematically redirected to the designated charging coordinates. If this condition is not met, the energy consumed during the current movement is subtracted from the remaining battery level, and the UAV proceeds to the next position accordingly.

$$\left\{\begin{array}{c} B_t=100 \mathrm{and} Uav\left(x_{station},y_{station}\right), if B_t\le L\sqrt{{\left(x-x_{station}\right)}^2+{\left(y-y_{station}\right)}^2}\\ B_t=B_{t-1}-P_{ij} \mathrm{and} Uav\left(x_{next},y_{next}\right), other\hfill \end{array}\right.$$

(4)

2.3. State Space

In this study, the state space is used to represent relevant features of the task environment and serves as input information for the model. Within the grid-based task map, each grid cell represents an environmental state. Specifically, each element ${Env}_{\left(x,y\right)}$ in the state space denotes the environmental state at position (x, y) on the map, with a numerical value assigned to describe its specific status. For example, the grid value may indicate whether the location belongs to a task area, non-task area, or covered task area (as shown in

Table 1. Map state corresponding to different values.

Value (${\mathit{E}\mathit{n}\mathit{v}}_{\left(\mathit{x},\mathit{y}\right)}$)	Description
0	Covered task area
1	Task area
2	Current position of UAV
3	Non-task area
4	Charging pile

).

The state space representation is mathematically formalized in Equation (5).

$$S_t=\left[{env}_{\left(\mathrm{1,1}\right),}{env}_{\left(\mathrm{1,2}\right),}\cdots {env}_{\left(x,y\right),}\right]$$

(5)

2.4. Action Space and Action Selection Strategy

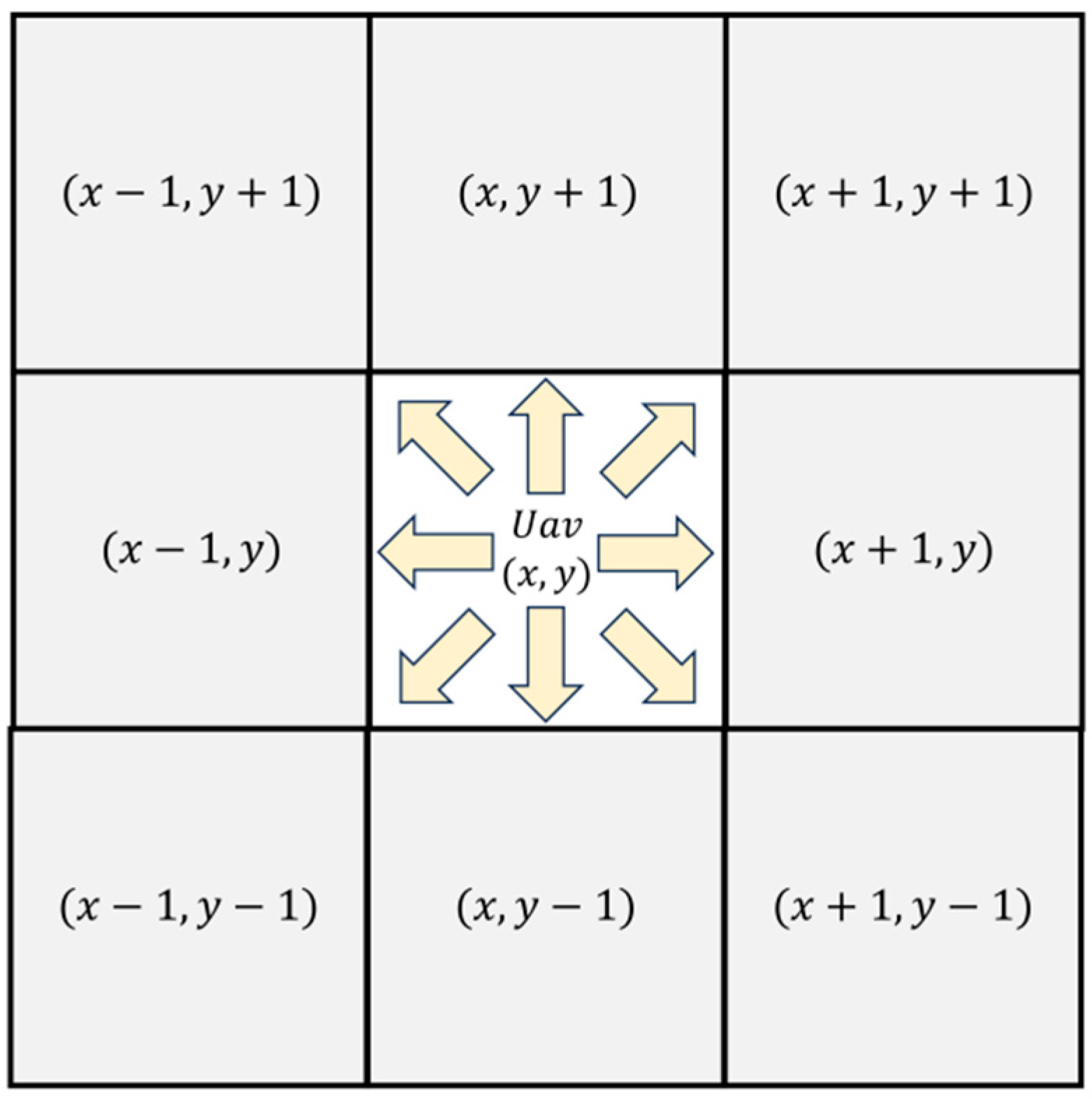
The action space is designed to characterize the set of feasible maneuvers available to UAVs during path planning operations. While continuous action spaces theoretically permit infinite directional variations through angular rotations and velocity modulations, empirical evaluations reveal that excessive action options lead to computational inefficiencies and degraded path optimization performance. This necessitates systematic action space parameterization, where the dimensionality and operational boundaries are strategically constrained to balance planning effectiveness with computational tractability.

The UAV’s motion repertoire was explicitly defined as eight discrete actions (Figure 3), incorporating angular directional actions at 45° increments to enhance exploration capability in complex map geometries. This design enhancement effectively mitigates motion space-induced planning constraints while maintaining computational efficiency through controlled action dimensionality.

An ε-greedy policy was implemented as the action selection mechanism to optimize the exploitation-exploration trade-off, where exploitation denotes selecting actions with maximum expected Q-values from known states, while exploration facilitates environmental knowledge acquisition through stochastic action sampling. The policy’s mathematical formulation follows, as specified in Equation (6).

$$Action=\left\{\begin{array}{cc}argmaxQ\left(s,a\right),\hfill & \mathrm{if} \mathrm{RN} > \epsilon \\ randomaction,\hfill & Otherwise\end{array}\right.$$

(6)

In this formulation, $\mathrm{RN}$ denotes a random number generated within the [0, 1] interval at each timestep, while $\epsilon$ serves as the parameter governing the exploitation-exploration trade-off. When $\mathrm{RN}$ exceeds $\epsilon$, the action corresponding to the maximum Q-value is selected; otherwise, a random action is chosen from the action space for exploratory purposes.

However, empirical observations reveal critical limitations in employing fixed $\epsilon$ values throughout training: Excessively low $\epsilon$ values induce premature reliance on current Q-value estimations, leading to entrapment in local optima during early training phases. Conversely, overly high $\epsilon$ settings generate substantial non-productive exploration, resulting in computational resource wastage, decelerated convergence rates, and diminished training efficiency.

Therefore, in this study, a linear decay approach is employed to dynamically adjust the value of $\epsilon$. This adjustment allows the model to prioritize exploration in the early stages while gradually shifting its focus toward exploitation in later stages, thereby accelerating convergence, improving training efficiency, and enhancing adaptability, as expressed in Equation (7). Here, ${\epsilon }_{min}$ represents the minimum exploration probability, ${\epsilon }_{max}$ denotes the maximum exploration probability, $Decay rate$ defines the rate at which the exploration probability decreases, and $currunt episode$ refers to the present training stage.

$$\epsilon ={\epsilon }_{min}+\left({\epsilon }_{max}-{\epsilon }_{min}\right)\times e^{-Decay rate \times currunt episode}$$

(7)

2.5. Enhanced DQN Algorithm

2.5.1. Basic Theory

The Deep Q-Network (DQN) algorithm addresses decision-making in discrete action spaces by integrating deep learning with reinforcement learning, where neural networks are employed to approximate the Q-value function. Training stability is enhanced through mechanisms such as experience replay and target networks [29]. However, the algorithm’s reliance on a single neural network for Q-value approximation introduces estimation biases that may systematically overvalue specific actions. These errors propagate and magnify throughout the training cycle, as formalized in the Q-value update rule (Equation (8)).

$$Q^{\prime \left(s,a\right)}\leftarrow Q\left(s,a\right)+\alpha \left[r+\gamma {max}_{a^{\prime }}Q\left(s^{\prime },a^{\prime }\right)-Q\left(s,a\right)\right]$$

(8)

The Double Deep Q-Network (DDQN) algorithm addresses this limitation by modifying the target value computation protocol. Two architecturally identical neural networks are systematically decoupled [30]; an evaluation network selects the action corresponding to the maximum Q-value, while the target network calculates the target value using the chosen action a, as formalized in Equation (9). Here, r denotes the immediate reward, γ represents the discount factor, and ${\mathrm{argmax}}_{a}Q\left(s_{t+1},a;\theta \right)$ determines the optimal action based on the subsequent state $s_{t+1}$.

$$y=r+\gamma Q\left(s_{t+1},{\mathrm{argmax}}_{a}Q\left(s_{t+1},a;\theta \right)\right)$$

(9)

To mitigate Q-value overestimation, the Dueling DQN algorithm introduces architectural modifications by decoupling the Q-value into two distinct components: state value and action advantage. These parallel network branches are computationally aggregated to derive the final Q-value [31], as formalized in Equation (10), where $V\left(s_t\right)$ represents the state-specific value function and $A\left(s_t,a_t\right)$ denotes the advantage metric for each action under state $s_t$.

$$Q\left(s_t,a_t\right)=V\left(s_t\right)+A\left(s_t,a_t\right)-{\displaystyle \frac{1}{\left|A\right|}}\sum _{a^{\prime }}A\left(s_t,a^{\prime }\right)$$

(10)

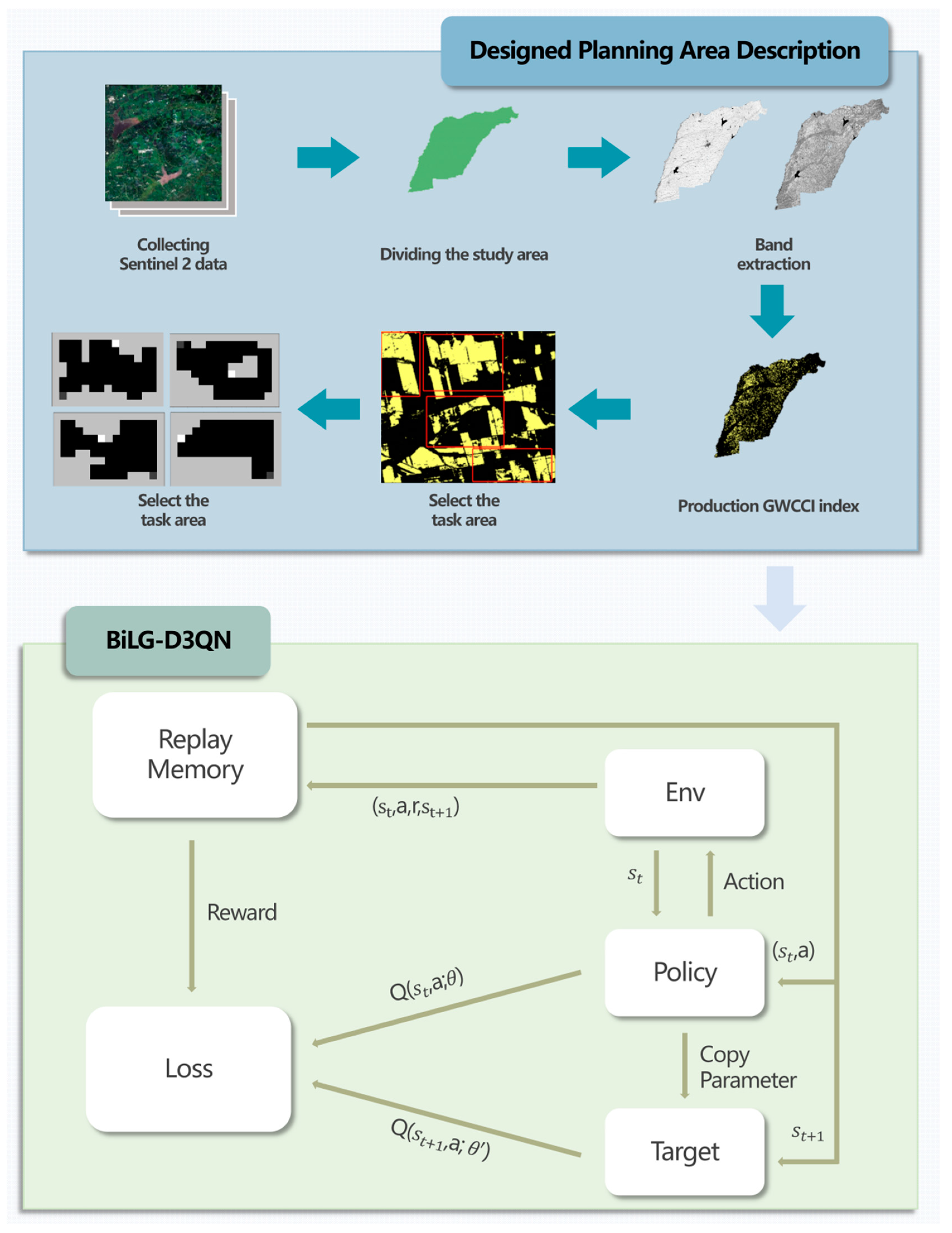
2.5.2. BiLG-D3QN

To further mitigate Q-value overestimation during training, the Double Dueling Deep Q-Network (D3QN) was developed through the integration of dueling architecture with the DDQN framework [32]. This hybrid configuration employs an evaluation network to identify optimal actions and a target network for precise value estimation, effectively decoupling action selection from value calculation.

However, in practical CPP scenarios involving sequential decision-making processes where each action influences subsequent path selections, the D3QN architecture exhibits inherent limitations. Although current state-action pairs are rigorously evaluated, the algorithm insufficiently incorporates historical decision impacts, as its Q-value computation predominantly focuses on instantaneous state-action relationships rather than temporal dependencies.

To address this limitation, the BiLG-D3QN algorithm is proposed by integrating Bi-LSTM and Bi-GRU networks into the D3QN architecture, as illustrated in Figure 4. This enhanced framework employs temporal modeling to extract comprehensive contextual features, thereby strengthening the model’s capacity to capture action-state dependencies across sequential decisions.

Both Bi-LSTM and Bi-GRU are variants of recurrent neural networks (RNNs). The Bi-LSTM layer consists of two independent LSTM chains operating in forward and backward directions. Each LSTM unit incorporates three control gates: the input gate, forget gate, and output gate (as shown in Figure 4a). The forget gate, activated by a sigmoid function, determines the extent to which past memory is retained. The input gate regulates the influence of current input on memory updates, while the output gate controls the contribution of the memory cell to the output at each time step. This structure enables the LSTM to effectively capture long-term dependencies, particularly excelling at identifying long-range patterns within sequences.

In contrast, the GRU layer employs a simplified gating mechanism. The update gate dynamically fuses past states with current inputs, while the reset gate controls the degree to which historical information is forgotten (as shown in Figure 4b). Owing to this design, GRUs require approximately 33% fewer parameters than LSTMs, significantly improving computational efficiency while maintaining strong temporal modeling capability. GRUs are more responsive to short-term variations or rapid fluctuations in sequences.

Both structures are employed in a bidirectional configuration. This heterogeneous dual-stream architecture allows the BiLG layer to simultaneously capture long-range state transition patterns through the LSTM branch and quickly react to local state shifts via the GRU branch. Such a design facilitates the extraction of global relationships. Furthermore, the combination of both architectures helps mitigate the risk of overfitting—particularly beneficial in scenarios with complex or noisy data—thereby enhancing the model’s robustness. The output of the BiLG layer is formulated as shown in Equation (11).

$$\left\{\begin{array}{c}{f}_t^{\mathrm{BiLSTM}}=\left[\begin{array}{c}\overrightarrow{\mathrm{LSTM}}\left(S_t\right),\overleftarrow{\mathrm{LSTM}}\left(S_t\right)\end{array}\right]\hfill \\ h_t^{\mathrm{BiGRU}}=\left[\overrightarrow{\mathrm{GRU}}\left(f_t^{\mathrm{BiLSTM}}\right),\overleftarrow{\mathrm{GRU}}\left(f_t^{\mathrm{BiLSTM}}\right)\right]\hfill \end{array}\right.$$

(11)

The Q-value update mechanism is mathematically formalized in Equation (12).

$$Q^{\prime \left(s,a\right)}\leftarrow Q\left(s,a\right)+\alpha ·\delta$$

(12)

The updated temporal difference (TD) error $\delta$ is formalized in Equation (13), where $Q\left(s,a;\theta \right)$ denotes the Q-value from the evaluation network with parameters $\theta$, while $\left(s^{\prime },a^{\prime };{\theta }^{-}\right)$ represents the target network’s Q-value computed using periodically synchronized parameters $\theta$. The calculation incorporates the action advantage function A, state value function $V$, immediate reward r, discount factor γ, and learning rate α, which collectively govern the credit assignment mechanism for future reward attenuation and parameter update magnitude.

$$\delta =y-Q\left(s,a;\theta \right)$$

(13)

The target Q-value update is mathematically formalized in Equation (14).

$$y=r+\gamma (V(s^{\prime };{\theta }^{-})+(A(s^{\prime },{\mathrm{argmax}}_{a}Q(s^{\prime },a^{\prime };\theta );{\theta }^{-})-\frac{1}{\left|\mathcal{A}\right|}\underset{a^{\prime }}{\Sigma }A(s^{\prime },a^{\prime };{\theta }^{-})\left)\right)$$

(14)

The optimization process employs the Smooth L1 Loss function to compute prediction–target discrepancies, whereby network parameters are iteratively refined through backpropagation. As formalized in Equation (15), this mechanism enables UAV to progressively learn reward-maximizing actions in given states through extensive training iterations, with policy updates being governed by the differential between evaluated Q-values and temporal difference targets.

$$L\left(y,\widehat{y}\right)=\left\{\begin{array}{cc}0.5{\left(Q\left(s,a;\theta \right)-y\right)}^2& \mathrm{if}\left|Q\left(s,a;\theta \right)-y\right|<1\\ \left|Q\left(s,a;\theta \right)-y\right|-0.5& \mathrm{otherwise}\end{array}\right.$$

(15)

2.6. Reward

DRL exclusively utilizes feedback from agent-environment interactions for policy optimization. Therefore, the efficacy and precision of the algorithm are fundamentally determined by an effective reward mechanism that explicitly encodes task-specific operational requirements. Given the spatiotemporal constraints of CPP tasks and the characteristics of payload energy consumption models, a novel reward formulation is proposed to simultaneously optimize traversal step minimization, path redundancy reduction, and complete area coverage, as mathematically defined in Equation (16).

$$r_t=\left\{\begin{array}{c}{r}_{Nontask}, Non-taskarea\hfill \\ r_{overlay}, Task area coverage\hfill \\ r_{step}, Maximum remaining score/Maximumnumber of steps\hfill \\ r_{accomplish}, Complete the coverage task\hfill \end{array}\right.$$

(16)

The $r_{Nontask}$ reward component imposes substantial penalties when the UAV is positioned in non-target areas (coded as numerical 4), which triggers immediate episode termination. This constraint mechanism is mathematically formalized in Equation (17), where the penalty magnitude is strategically calibrated to exceed cumulative step rewards, thereby enforcing strict adherence to operational boundaries through inverse reinforcement learning principles.

$$r_{Nontask}=-5 \mathit{and} End the current episode, if Uav\left(x,y\right)=4$$

(17)

The $r_{overlay}$ reward mechanism is structured into dual components based on spatial coverage states. When the UAV visits an unvisited task zone (encoded as 1), a compound positive reward is granted, comprising a base reward F and a coverage incentive proportional to ${\displaystyle \frac{C_{initial}-C_{current}}{C_{initial}}}$, where $C_{initial}$ denotes the cardinality of initially uncovered task areas and $C_{current}$ represents the instantaneous count of remaining uncovered regions. Conversely, traversal through previously covered areas (encoded as 0) incurs a demotion penalty scaled by the redundancy mitigation factor $\rho$, as mathematically formalized in Equation (18). This differential reward architecture explicitly incentivizes maximal primary coverage while disincentivizing path redundancy through adaptive credit assignment.

$$r_{overlay}=\left\{\begin{array}{cc}F+\phi e^{{\displaystyle \frac{C_{initial}-C_{current}}{C_{initial}}}}& \mathrm{if} Uav\left(x,y\right)=1\\ -\rho F\hfill & \mathrm{if} Uav\left(x,y\right)=0\end{array}\right.$$

(18)

$r_{step}$ represents the penalty associated with both the maximum step limit and the UAV’s consecutive unsuccessful attempts to score. Specifically, S denotes the current step count, while $S_{max}$ refers to the maximum step threshold. Similarly, N represents the number of consecutive unsuccessful steps, and $N_{max}$ indicates the maximum allowable unsuccessful steps. A penalty is imposed, and the current episode is terminated whenever either the step count or the number of consecutive unsuccessful steps reaches the predefined threshold.

$$r_{step}=\left\{\begin{array}{cc}M \mathit{and} End the current episode& \mathrm{if} S\ge S_{max}\\ M \mathit{and} End the current episode& \mathrm{if} N\ge N_{max}\end{array}\right.$$

(19)

3. Results

In this section, simulation experiments for UAV path planning were conducted using the GWCCI index-based task map for soybean cultivation area extraction constructed in the preceding section, combined with the proposed BiLG-D3QN algorithm. Experimental results were systematically analyzed, whereby the effectiveness of the proposed algorithm was validated.

3.1. Experimental Setup

Table 2. Experimental hyperparameter setting table.

Parameter	Value
$E_{max}$	60,000
$\gamma$	0.95
$B$	128
$M$	60,000
learning rate	1 × 10−4
${ϵ}_{max}$	0.8
${ϵ}_{min}$	0.1
Decay rate	5000
$n$	20
$N_{actions}$	8
Optimizer	Adam

presents the hyperparameter configurations for the BL-DQN algorithm. The maximum episode ($E_{max}$ = 60,000) provides sufficient training iterations for policy maturation, while the discount rate ($\gamma$ = 0.95) emphasizes mid-term reward acquisition in agricultural path planning scenarios. A batch size of 128 enables efficient gradient estimation while maintaining memory constraints. The experience replay buffer capacity ($M$ = 60,000) preserves temporal diversity in state transitions, crucial for breaking data correlations in sequential decision-making. The learning rate (1 × 10⁻⁴) and Adam optimizer configuration ensure stable gradient descent in high-dimensional action spaces. The ε-greedy strategy (${ϵ}_{max}$ = 0.8 to ${ϵ}_{min}$ = 0.1 over 5000 decay steps) initially promotes environmental exploration before transitioning to exploitation dominance. Delayed network updates (n = 20) and 8-directional action space design specifically address the kinematic constraints of agricultural UAVs.

3.2. Experimental Results

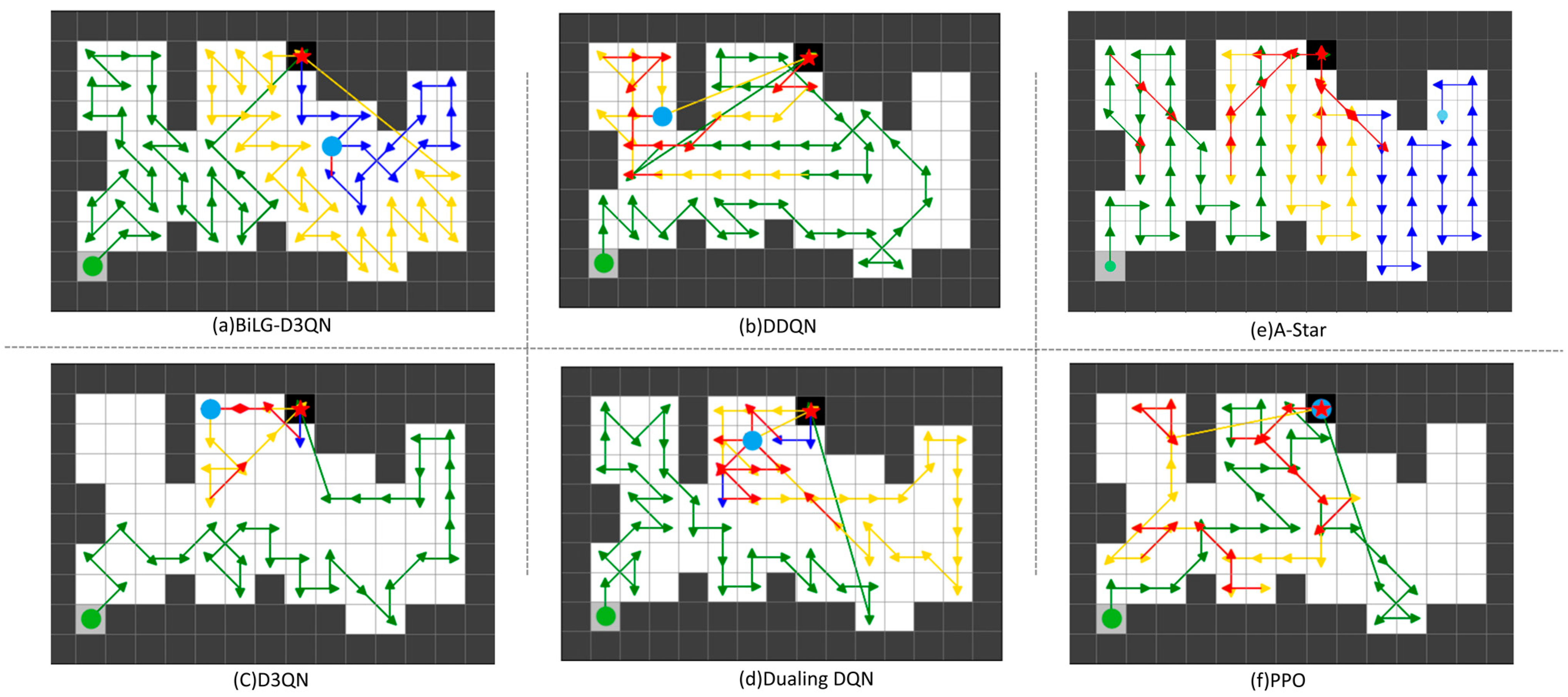
Within the task map framework, the comparative efficacy of the proposed BiLG-D3QN algorithm was rigorously validated against three baseline methods: DDQN, Dueling DQN, and D3QN. Controlled experiments were conducted across four distinct 15 × 10 simulated environments derived from task map configurations. All algorithms underwent standardized training procedures involving 60,000 episodes, with subsequent performance evaluations quantifying operational metrics across multiple validation cycles.

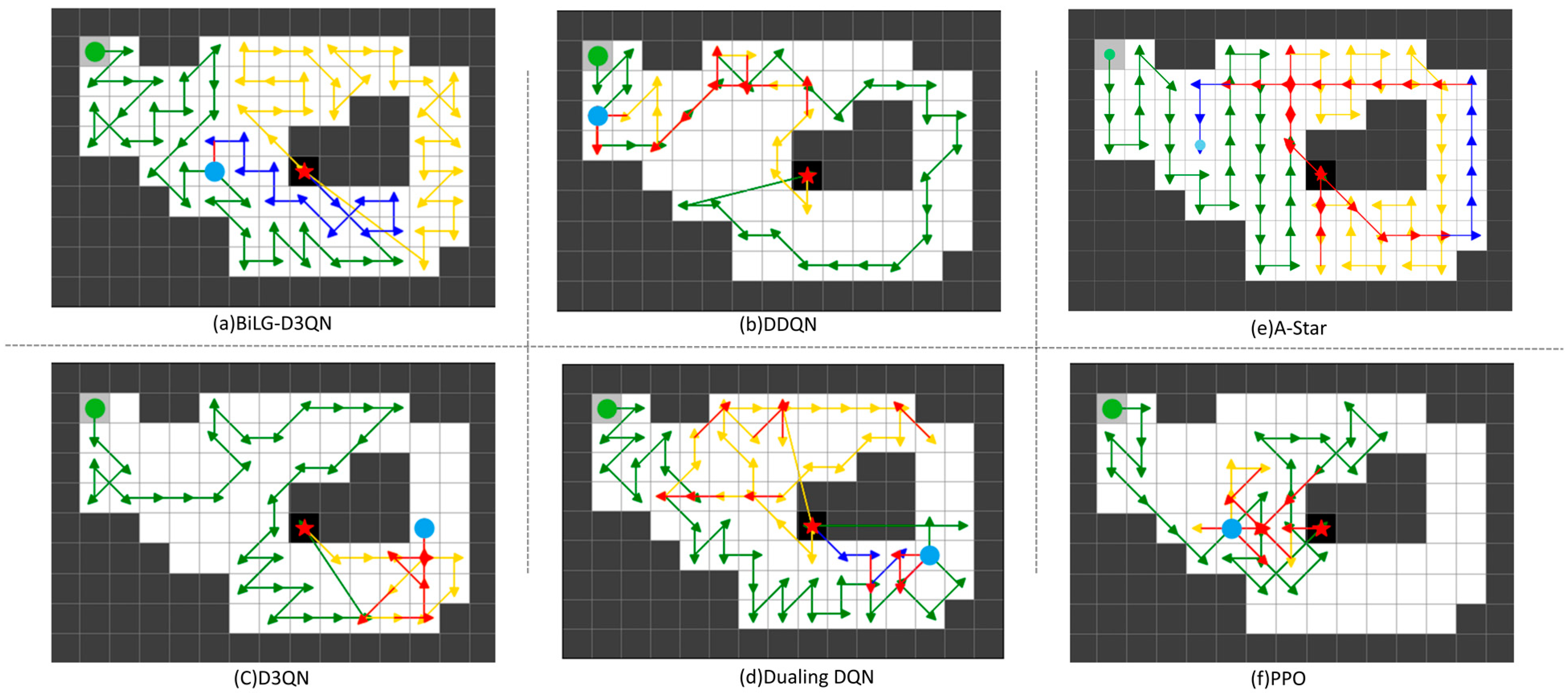
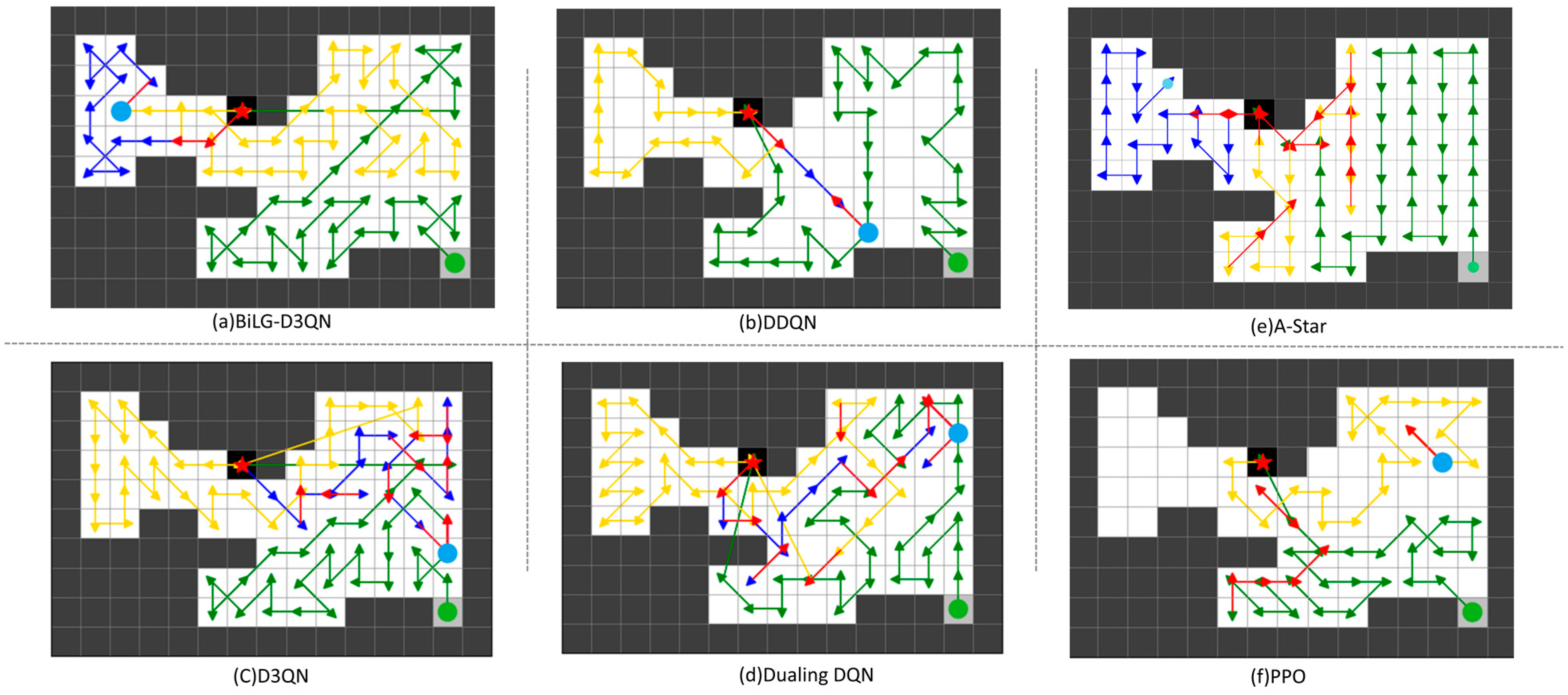
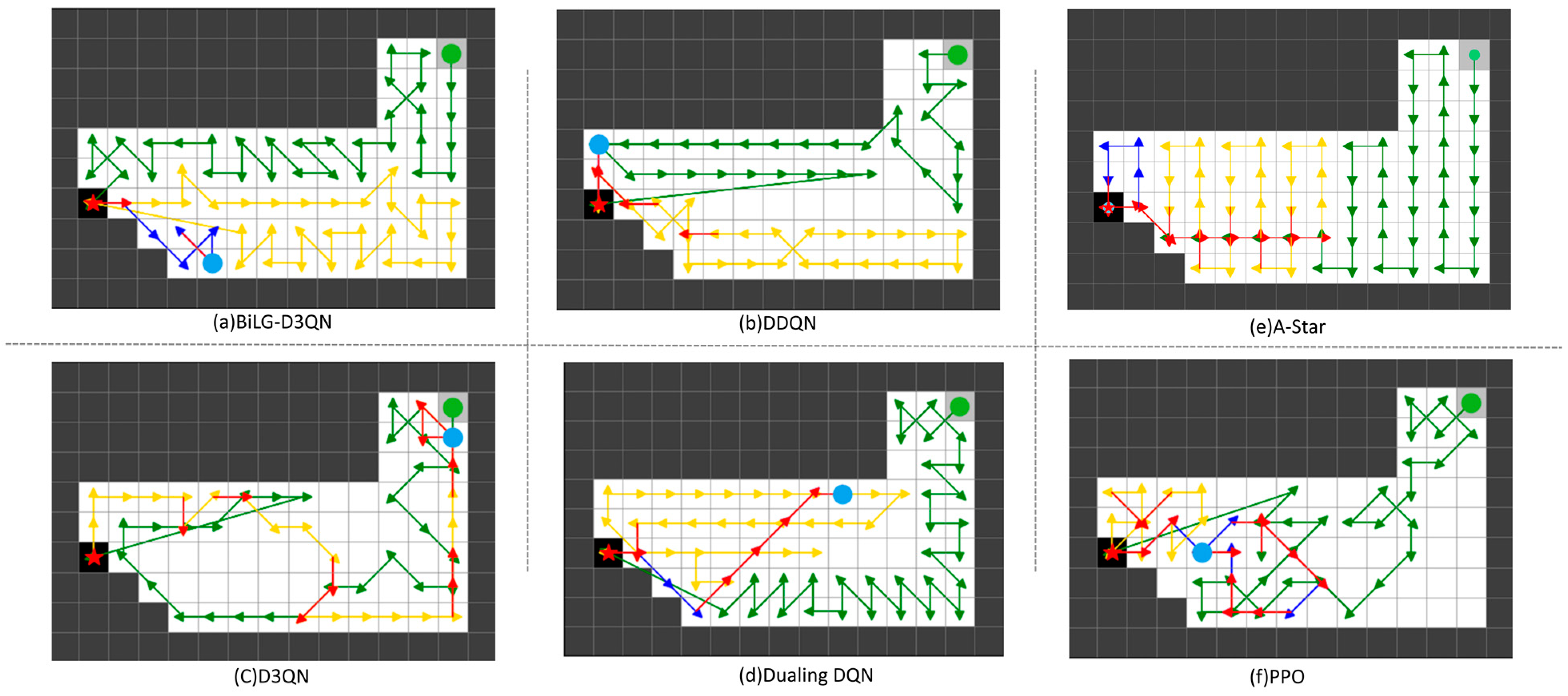
The path planning results are shown in Figure 5, Figure 6, Figure 7 and Figure 8. The UAV’s starting point is marked with a green circle on the map, the current position is indicated by a blue circle, and the replenishment point is represented by a red pentagram. To highlight the phased planning effect, three distinct colored lines are used to annotate the trajectory segments, with specific meanings detailed in

Table 3. Description of experimental paths.

Color	Description
Green	Initial Route
Yellow	Second Supply Route
Blue	Third Supply Route
Red	Repeating Route

.

From the analysis in Figure 5, Figure 6, Figure 7 and Figure 8, the BiLG-D3QN algorithm demonstrates superior performance in segmented path coverage tasks. Throughout the experiment, the UAV returned to the replenishment point only twice for battery replacement, with minor path redundancy occurring solely at the end of the third path-planning phase.

Under the same episode settings, the other three algorithms failed to complete the coverage task. As shown in Figure 5, Figure 6, Figure 7 and Figure 8, although most UAVs completed two replenishment cycles, these algorithms exhibited critical flaws: ineffective learning of temporal dependencies, lack of holistic planning awareness, and insufficient attention to map details. These deficiencies led to significant coverage gaps and irrational path planning during the initial stages. Consequently, in later phases, the UAVs generated extensive redundant paths to compensate for incomplete coverage, yet ultimately failed to accomplish the task.

Although the A-Star algorithm successfully completes the task, its approach of decomposing the coverage mission into multiple sub-tasks leads to fragmented path segments and a significant amount of redundant traversal. On the other hand, PPO, as an on-policy model, does not utilize historical experience and relies exclusively on data generated from the most recent policy. This results in low sample efficiency, a tendency to converge to local optima, and insufficient exploration of the state space, ultimately leading to suboptimal task performance.

To ensure an accurate evaluation of each algorithm’s performance, three evaluation metrics were employed to assess the outcomes of the simulation experiments. A detailed comparison of the results is presented in

Table 4. Experimental data statistics.

Map	Algorithms	Step	${\mathit{A}\mathit{r}\mathit{e}\mathit{a}}_{\mathit{r}\mathit{e}\mathit{p}\mathit{e}\mathit{a}\mathit{t}}$	${\mathit{A}\mathit{r}\mathit{e}\mathit{a}}_{\mathit{c}\mathit{o}\mathit{v}\mathit{e}\mathit{r}}$	Repeat (%)	Coverage Efficiency	Number of Supplies
Map1	BiLG-D3QN	77	1	76	1.32%	0.987	2
	DDQN	69	11	58	18.97%	0.8406	2
	D3QN	47	7	40	17.5%	0.8511	2
	DualingDQN	72	13	59	22.03%	0.8194	2
	A-Star	94	17	76	22.37%	0.8085	2
	PPO	59	14	45	31.11%	0.7627	1
Map2	BiLG-D3QN	74	1	73	1.37%	0.9865	2
	DDQN	54	14	40	35%	0.7407	1
	D3QN	62	6	56	10.71%	0.9032	2
	DualingDQN	71	14	57	24.56%	0.8028	2
	A-Star	81	18	73	24.66%	0.9012	2
	PPO	41	8	33	24.24%	0.8049	1
Map3	BiLG-D3QN	74	3	71	4.23%	0.95.95	2
	DDQN	56	7	49	14.29%	0.875	2
	D3QN	83	13	70	18.57%	0.8434	2
	DualingDQN	81	15	66	22.73%	0.8148	2
	A-Star	85	14	71	19.72%	0.8353	2
	PPO	54	7	47	14.89%	0.8704	1
Map4	BiLG-D3QN	69	2	67	2.99%	0.971	2
	DDQN	60	6	54	11.11%	0.9	2
	D3QN	57	11	46	23.91	0.807	1
	DualingDQN	69	8	61	13.11	0.8841	2
	A-Star	80	13	67	19.4%	83.75%	2
	PPO	56	13	43	30.23%	76.79%	2

.

(a)

Path length: UAV’s movement steps.

(b)

Coverage efficiency: ratio of effectively covered area to total target region area, as shown in Equation (20).

$$E={\displaystyle \frac{{Area}_{cover}}{Step}}\times 100\%$$

(20)

(c)

Redundancy rate: ratio of repeatedly visited areas to total covered regions in the planned path, as formalized in Equation (21)

$$R_{repeat}={\displaystyle \frac{{Area}_{repeat}}{{Area}_{cover}}}\times 100\%$$

(21)

3.3. Experimental Analysis

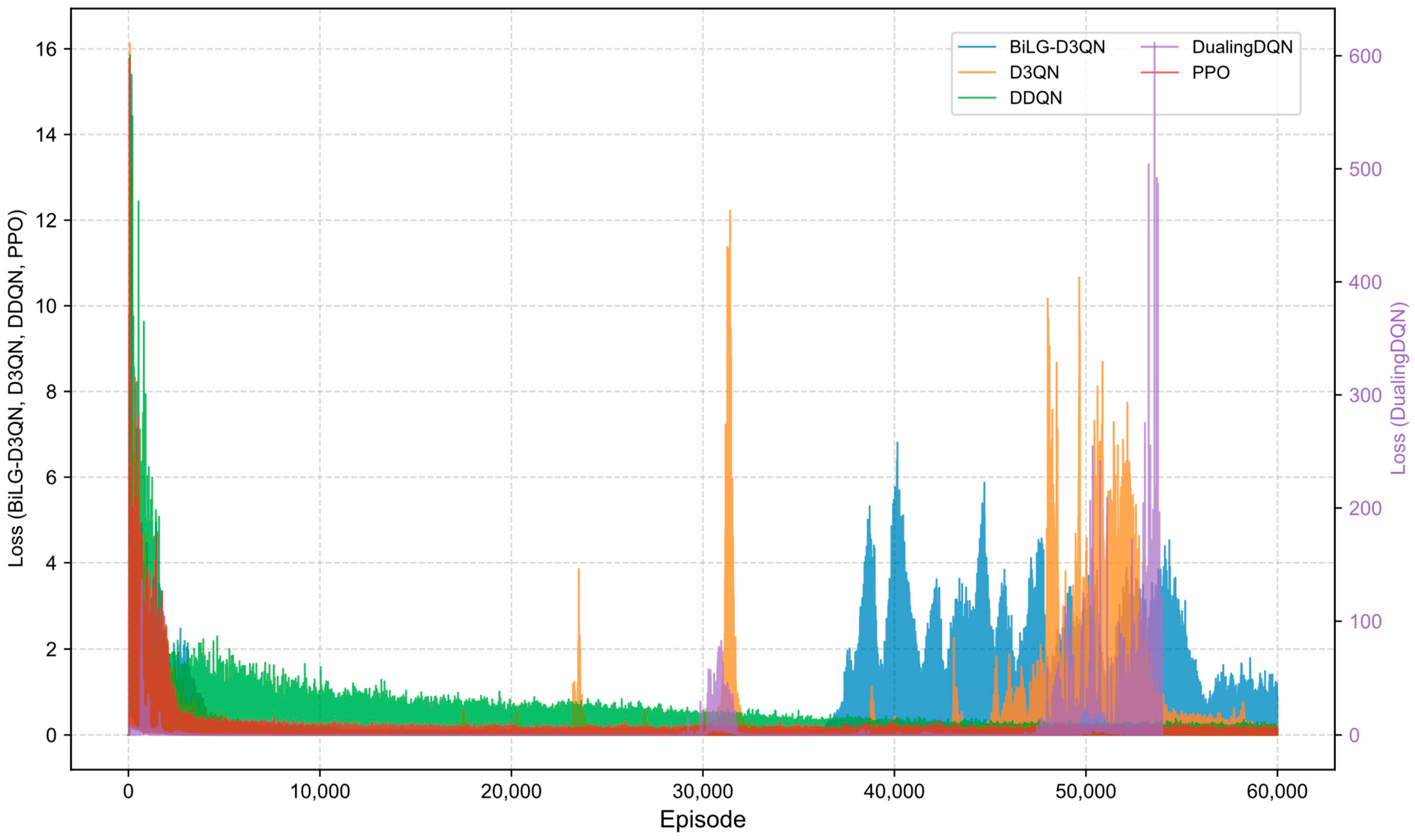
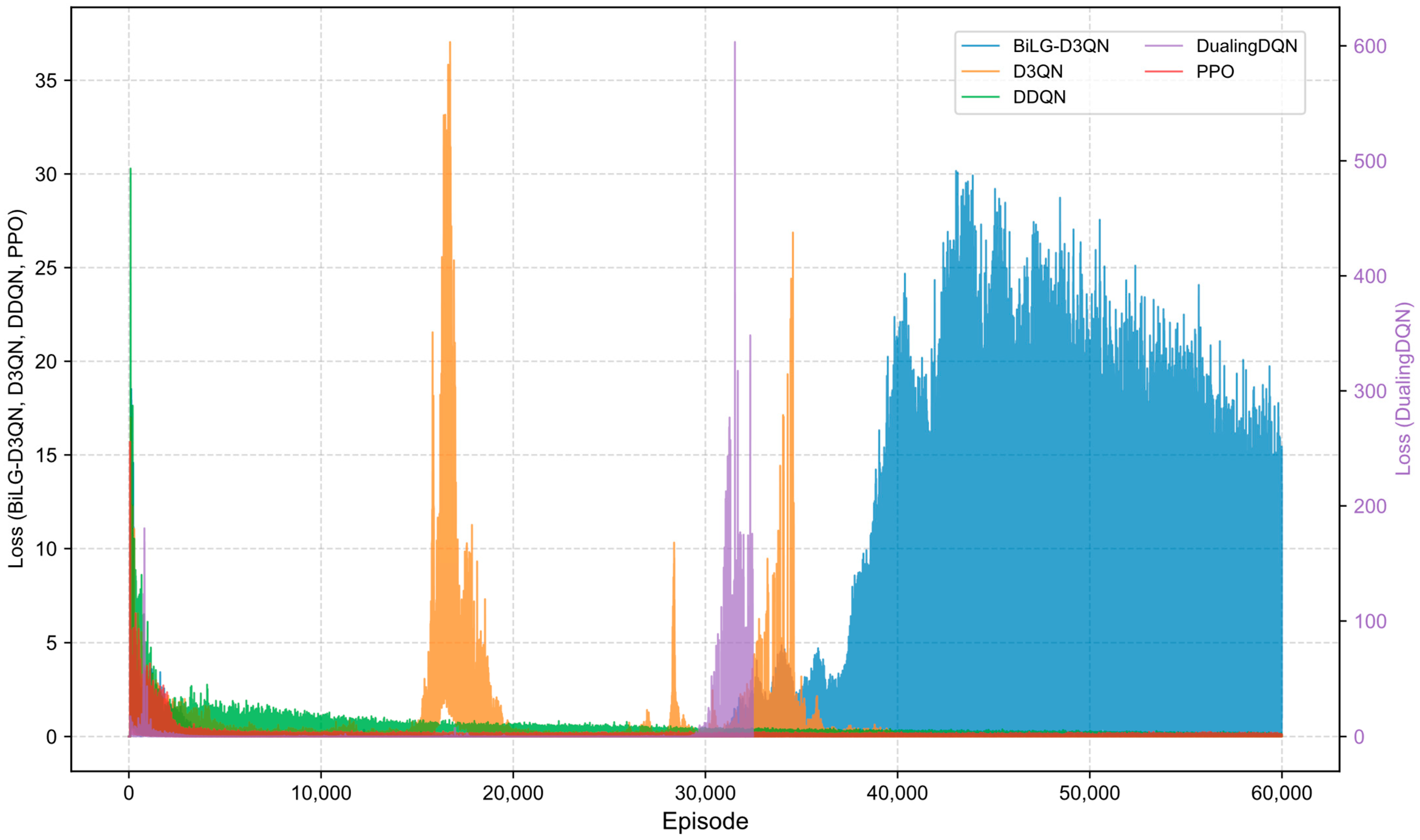
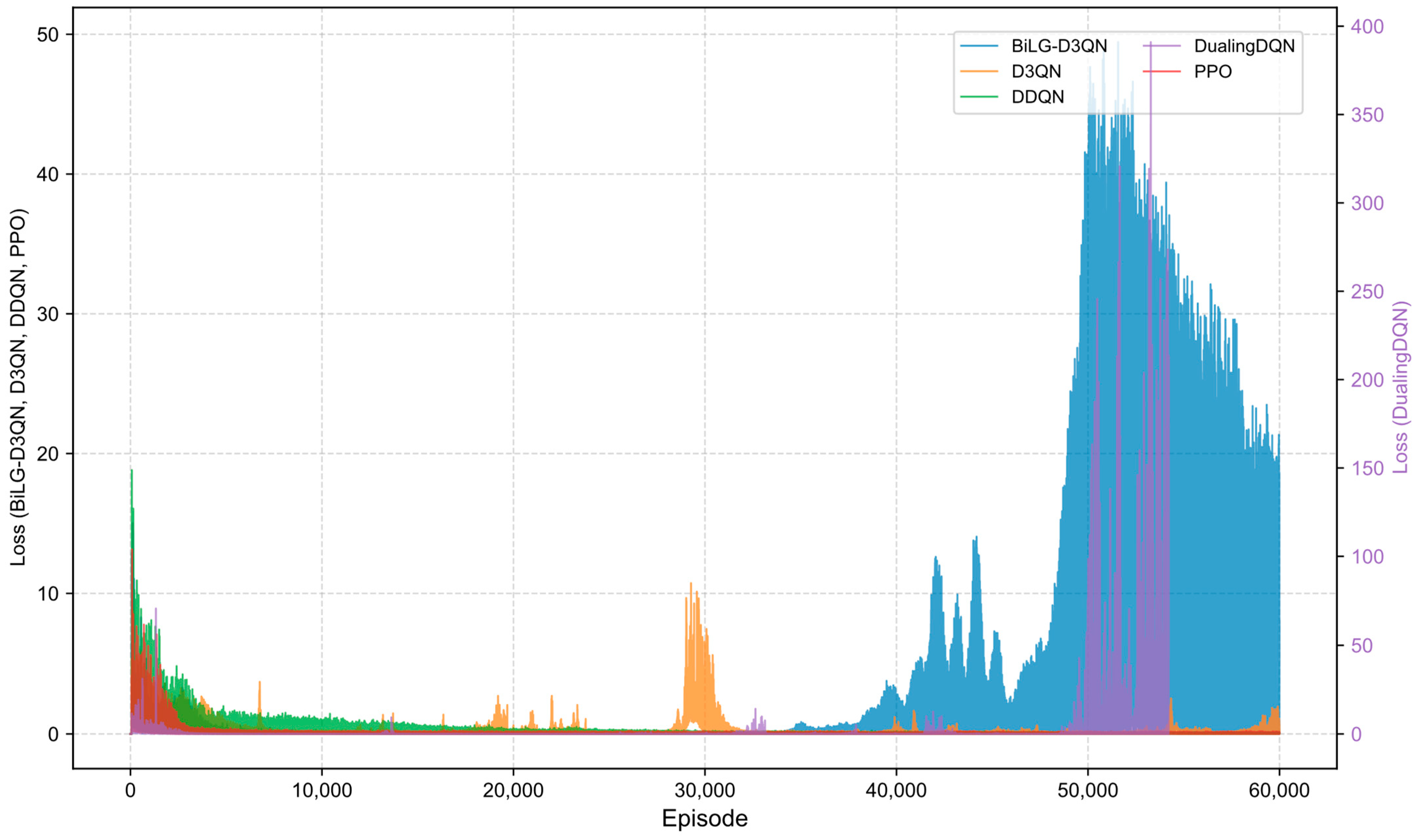
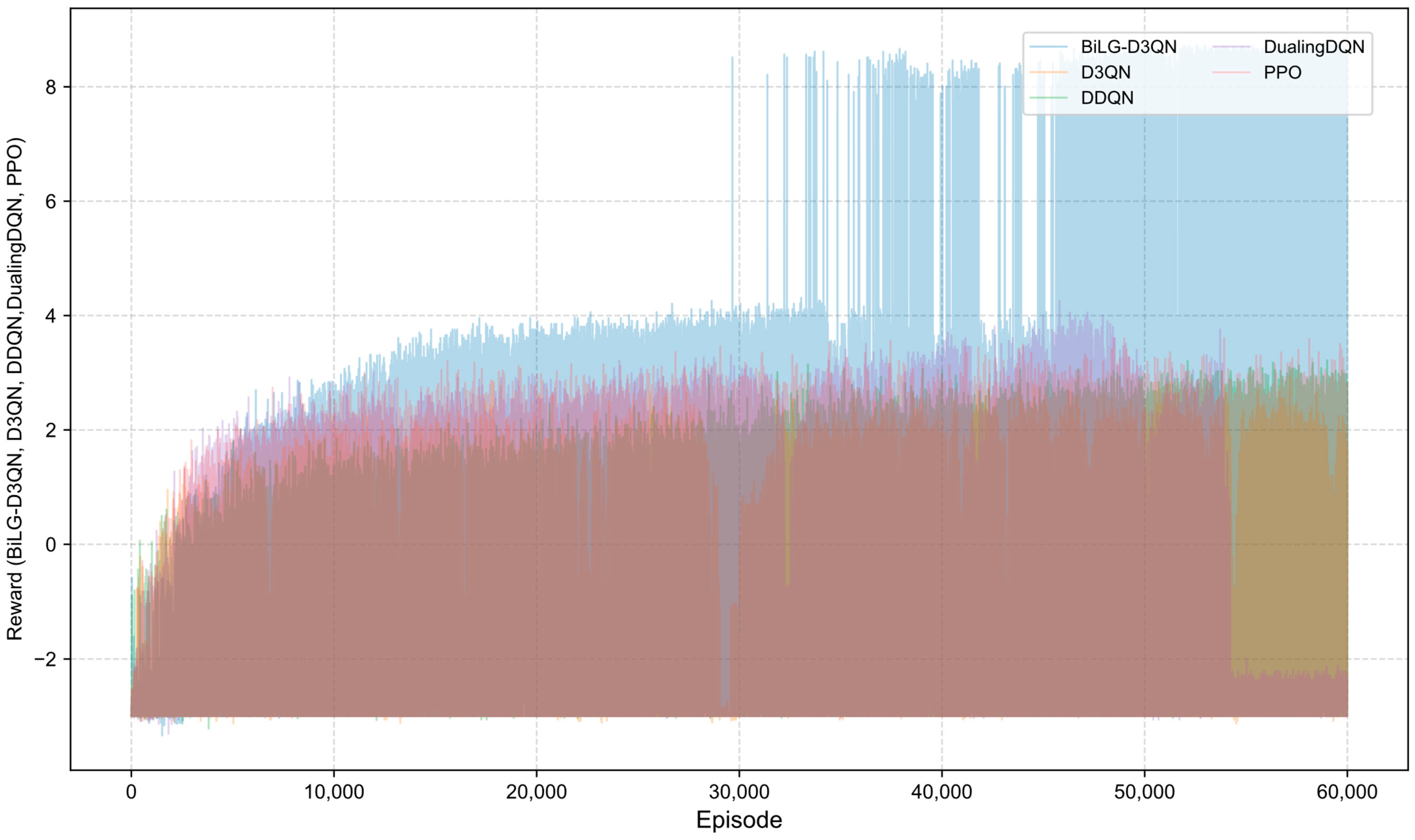
Figure 9, Figure 10, Figure 11 and Figure 12 illustrate the training loss trajectories across evaluated algorithms. The BiLG-D3QN architecture exhibited elevated initial loss values followed by rapid decay, indicating efficient early-phase learning. Stabilization occurred at approximately 10,000 episodes, with training completion achieved by 35,000 episodes, though minor post-convergence fluctuations emerged due to mild overfitting tendencies.

The D3QN baseline demonstrated comparable initial loss magnitudes that escalated into pronounced oscillations during mid-training phases due to ineffective capture of critical state-action relationships. While the DDQN implementation displayed accelerated loss reduction during preliminary phases—stabilizing within 5000 episodes—its consistent low-magnitude oscillations throughout training indicated reliable policy acquisition in most states. However, this configuration proved inadequate for modeling long-range temporal dependencies, preventing full convergence. The Dueling DQN framework exhibited catastrophic divergence due to systematic Q-value overestimation within its policy network architecture, precipitating premature training termination through gradient explosion mechanisms. The PPO algorithm, being an on-policy method, requires data generated by the most recent policy, resulting in lower sample efficiency. This limitation often leads to entrapment in local optima and insufficient exploration of the state space. Although the reward curve appears smooth, the actual performance of the model is suboptimal.

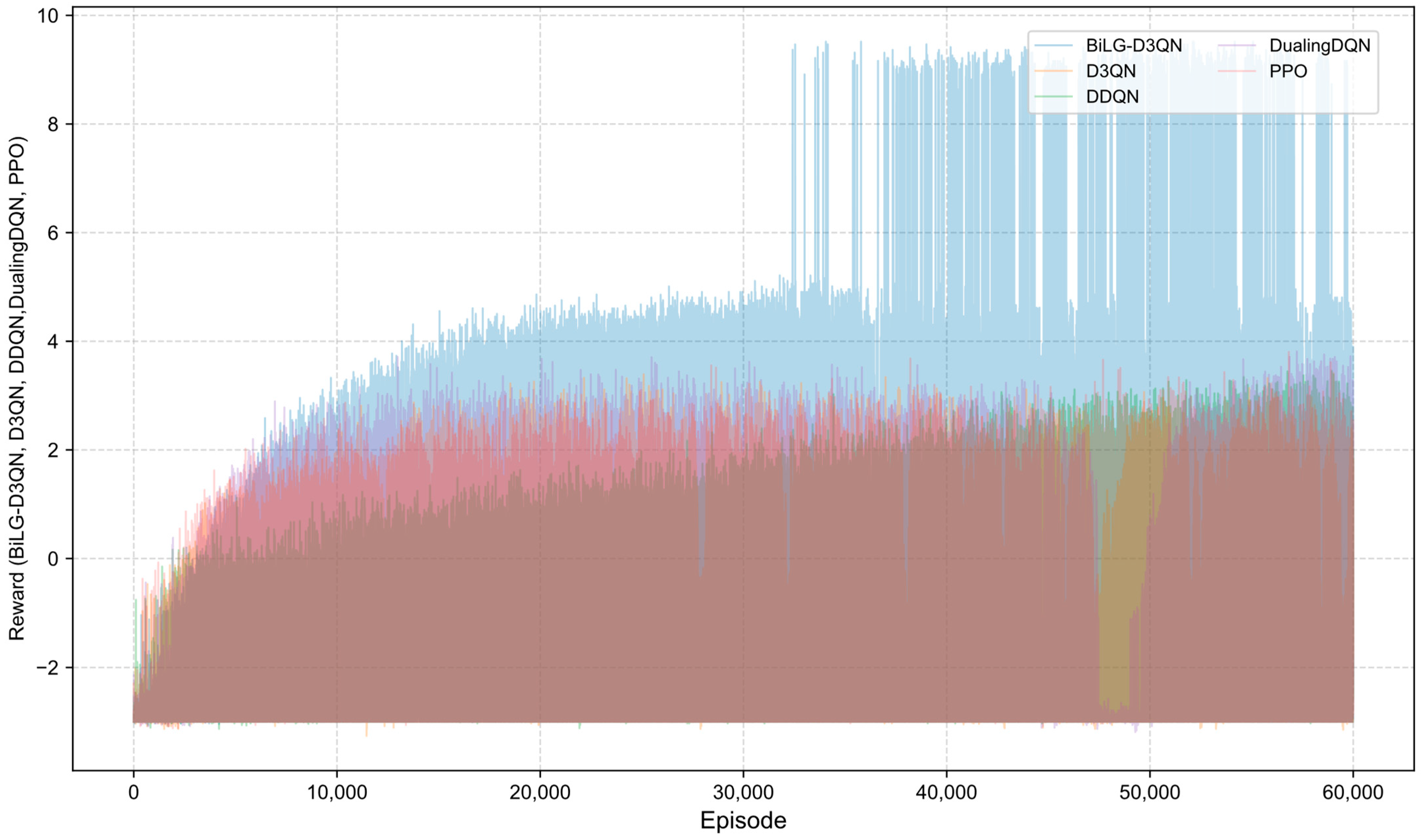
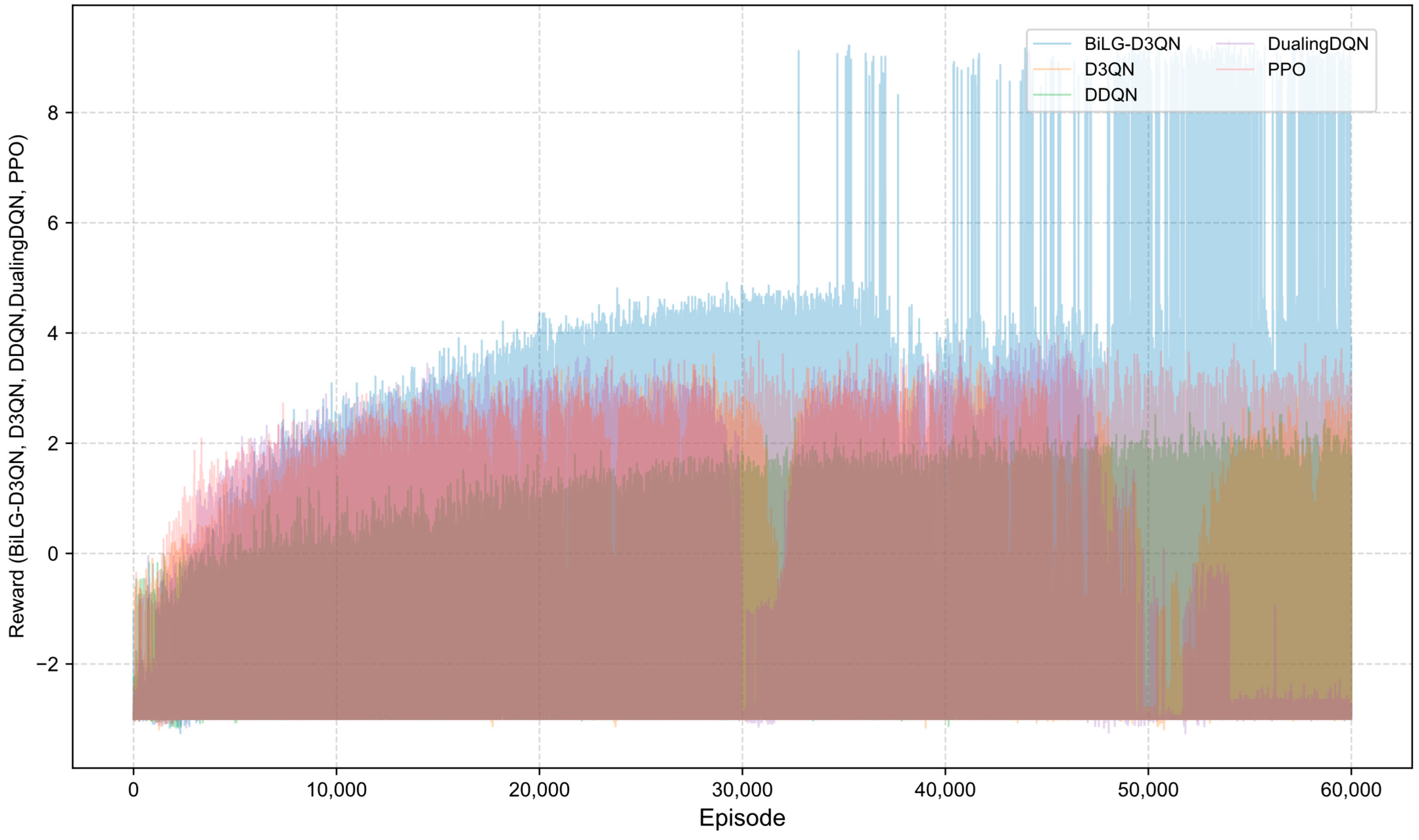
A comparative analysis of algorithmic reward profiles is presented in Figure 13, Figure 14, Figure 15 and Figure 16. The BiLG-D3QN algorithm demonstrates progressive reward escalation throughout training, with stabilized growth observed after approximately 10,000 episodes and mission completion achieved at 34,000 episodes. This trajectory indicates the algorithm’s successful acquisition of effective policies and its enhanced capacity to model temporal dependencies.

In contrast, the four baseline models exhibit suboptimal performance due to inherent limitations: (1) structural instability during state processing, (2) inadequate relational feature extraction, (3) systemic overestimation of Q-values, and (4) gradient explosion phenomena. These compounded deficiencies prevent convergence toward optimal policy solutions.

4. Conclusions

A novel BiLG-D3QN algorithm was developed through the integration of DRL techniques with bidirectional long short-term memory (Bi-LSTM) and gated recurrent unit (Bi-GRU) architectures, specifically addressing energy-constrained complete coverage path planning for agricultural field operations. The methodological framework encompassed four critical components: (1) UAV energy consumption modeling, (2) soybean cultivation area identification using GEE-derived spatial distribution data, (3) raster map construction, and (4) enhanced CPP algorithm implementation. Simulation results demonstrate that the BiLG-D3QN algorithm performs exceptionally well in addressing the segmented complete coverage path planning (CPP) problem under load-aware energy consumption constraints. Specifically, the BiLG-D3QN algorithm achieved a coverage efficiency improvement of 13.45% over DDQN, 12.27% over D3QN, 14.62% over Dueling DQN, 15.59% over the A-Star algorithm, and 22.15% over PPO. Moreover, the algorithm attained an average revisit rate of only 2.45%, which is significantly lower than that of DDQN (18.89%), D3QN (17.59%), Dueling DQN (17.59%), A-Star (21.54%), and PPO (25.12%). observed in comparative methods. These metrics validate the algorithm’s enhanced temporal information fusion capability, which substantially improves operational efficiency and intelligent decision-making in agricultural UAV path planning, thereby advancing precision agriculture and sustainable agricultural mechanization.

Shortcomings and future research directions:

• Multi-UAV collaborative planning:

While the current study focuses on single-UAV operations, future work will investigate coordinated multi-UAV segmented path planning to optimize workload distribution and mission completion efficiency. This extension is critical for addressing large-scale agricultural operations and aligns with emerging trends in swarm robotics.

2.

Multi-objective task integration:

The algorithm’s performance in complex agricultural environments requiring simultaneous execution of heterogeneous tasks (e.g., spraying, monitoring, and sampling) will be systematically evaluated. Key challenges include minimizing inter-task interference while maintaining individual task efficiency through adaptive priority scheduling mechanisms.

3.

Field validation:

In future work, experimental validation of the proposed algorithm in real-world scenarios is planned. This validation will be conducted in two stages. In the first stage, the algorithm will be deployed on a lightweight UAV using a Raspberry Pi development board for testing in an indoor simulation environment. In the second stage, the algorithm will be integrated into a plant protection UAV for field testing under real conditions to further assess its efficiency, safety, and effectiveness.