Calibration of Parameters for Leaf-Stem-Cutting Model of Tuber Mustard (Brassica juncea L.) Based on Discrete Element Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Measurement of the Physical Parameters
2.2. Measurement of Intrinsic Parameters
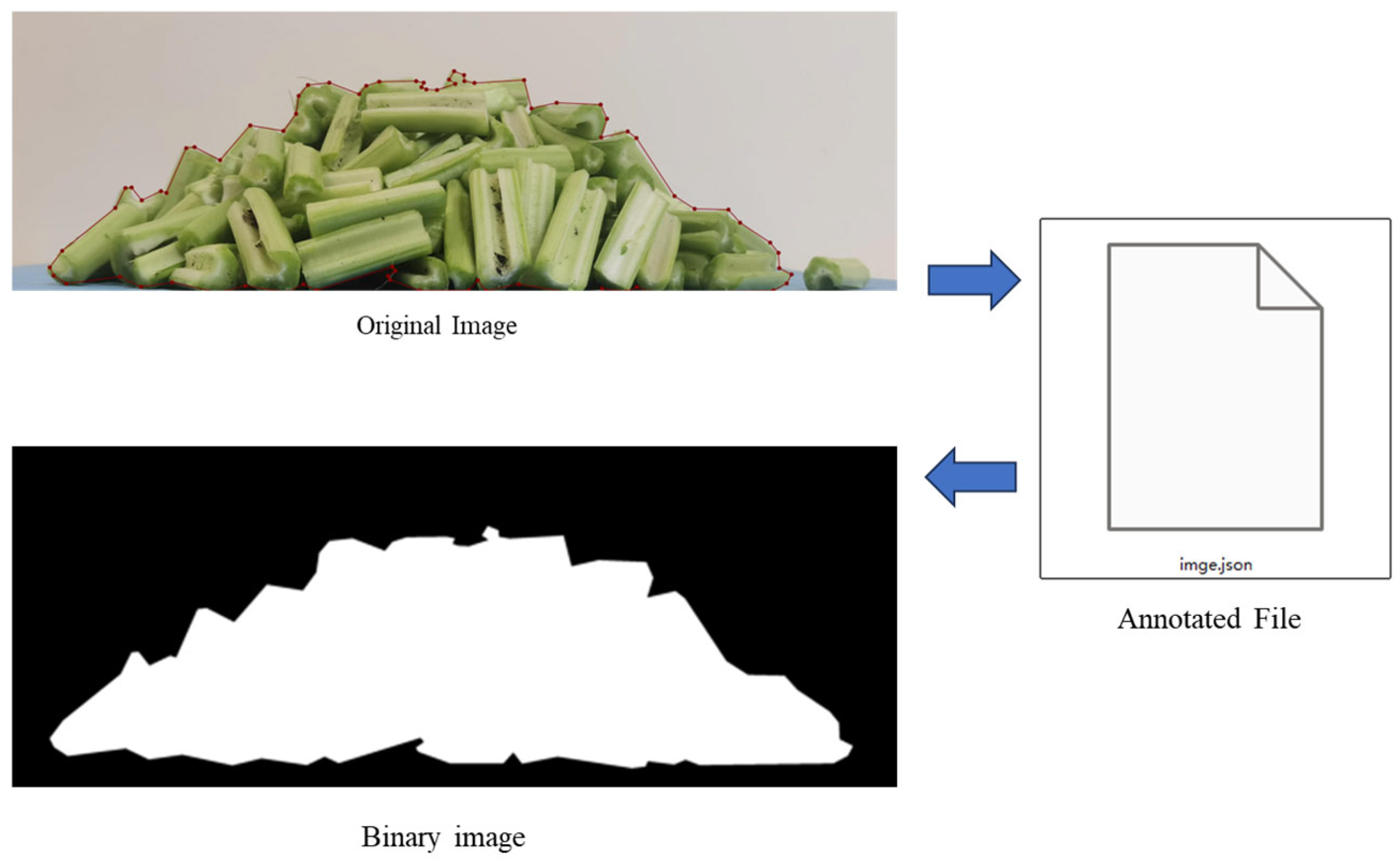
2.3. The Measurement of the Stacking Angle
2.4. Discrete Element Simulation Modeling
2.4.1. Simulation Modeling of Stacking Angle
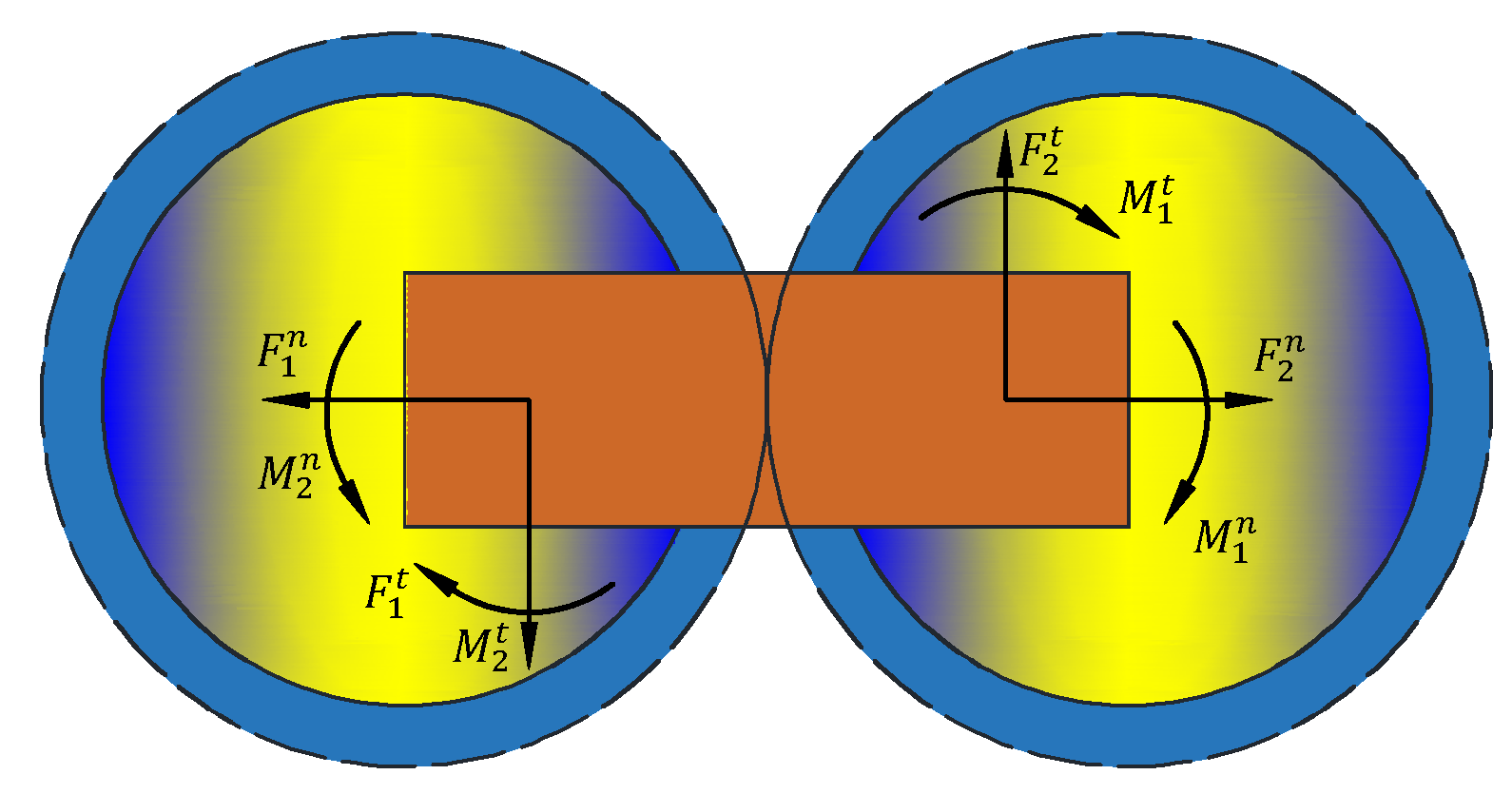
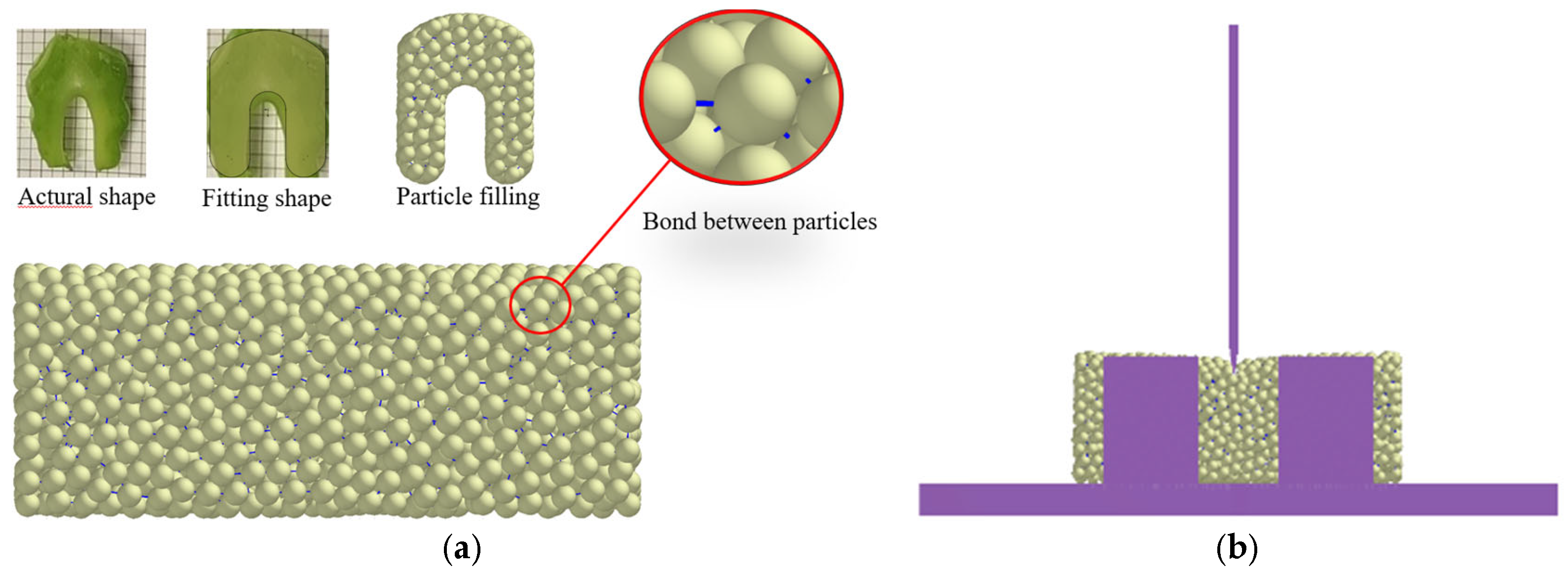
2.4.2. Bonding of Leaf Stem Simulation Model
2.5. Calibration Test of Contact Parameters in Discrete Element Model
2.5.1. Two-Level Factorial Tests
2.5.2. Steepest Climbing Test
2.5.3. Central Composite Design Test
2.6. Calibration and Correction of Bonding Parameters
3. Results and Discussion
3.1. Analysis of Contact Parameter Calibration Test Results
3.1.1. Results of Two-Level Factorial Tests
3.1.2. Results of Steepest Climbing Test
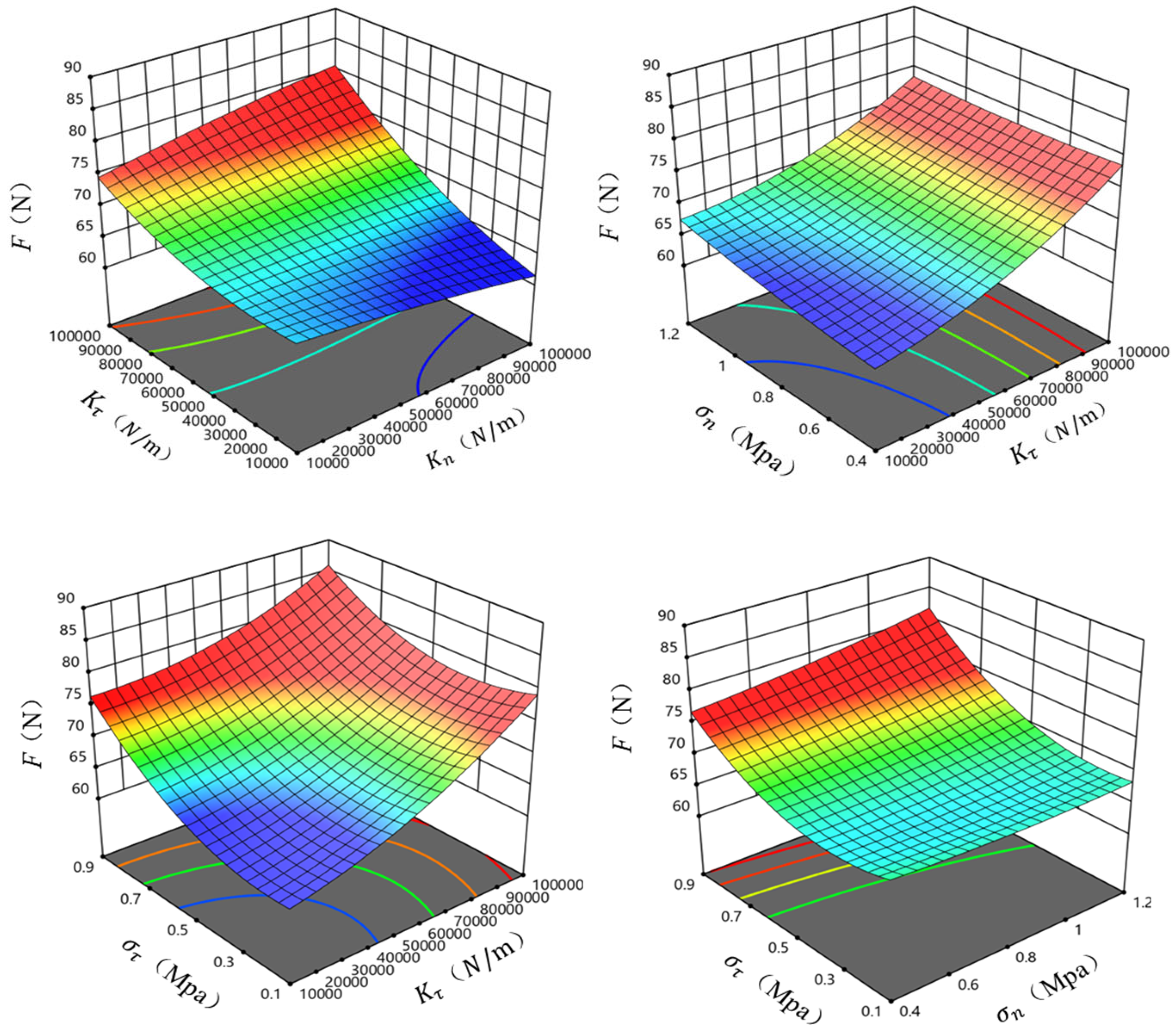
3.1.3. Results of Central Composite Test
3.2. Calculation and Correction of Bonding Parameters
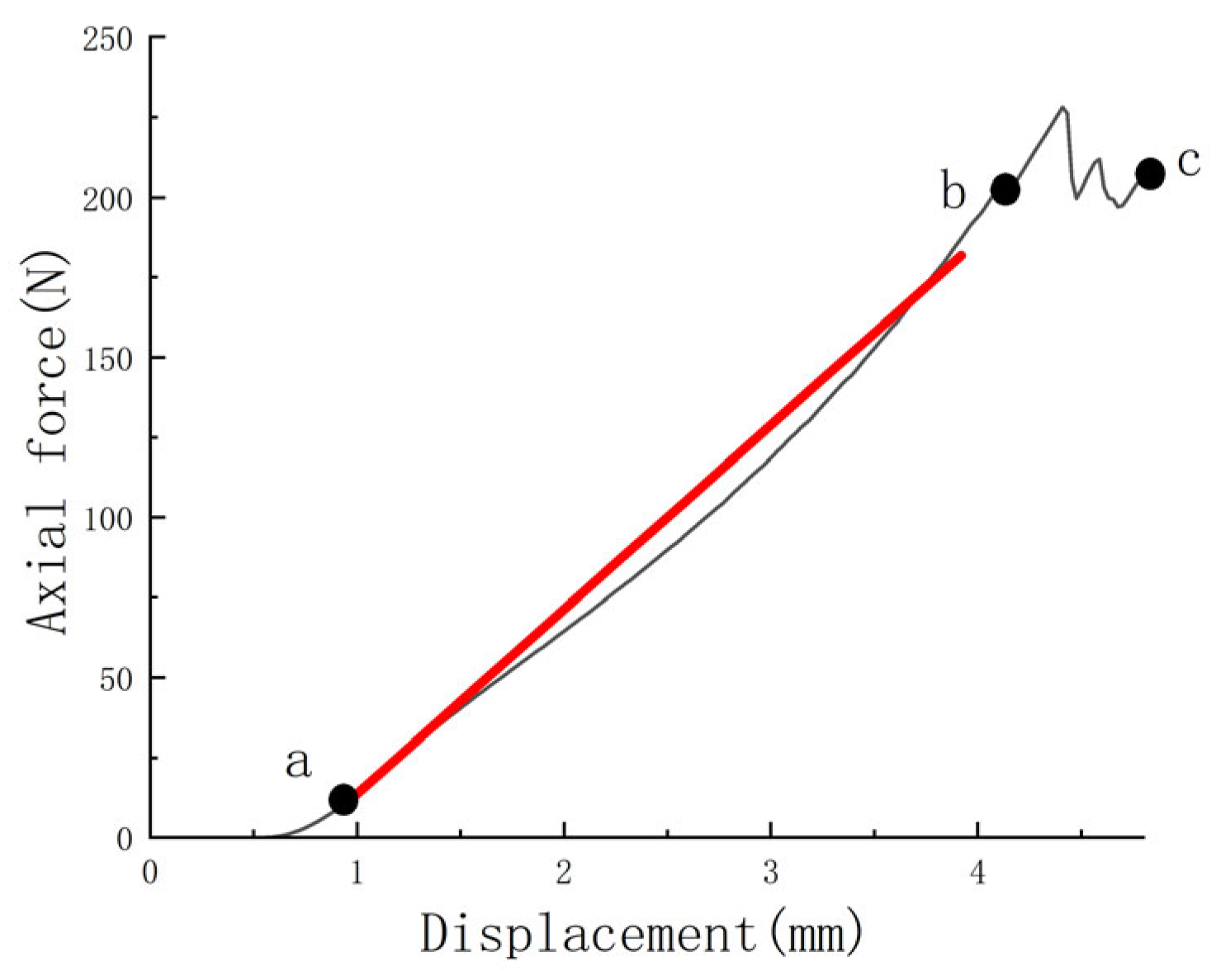
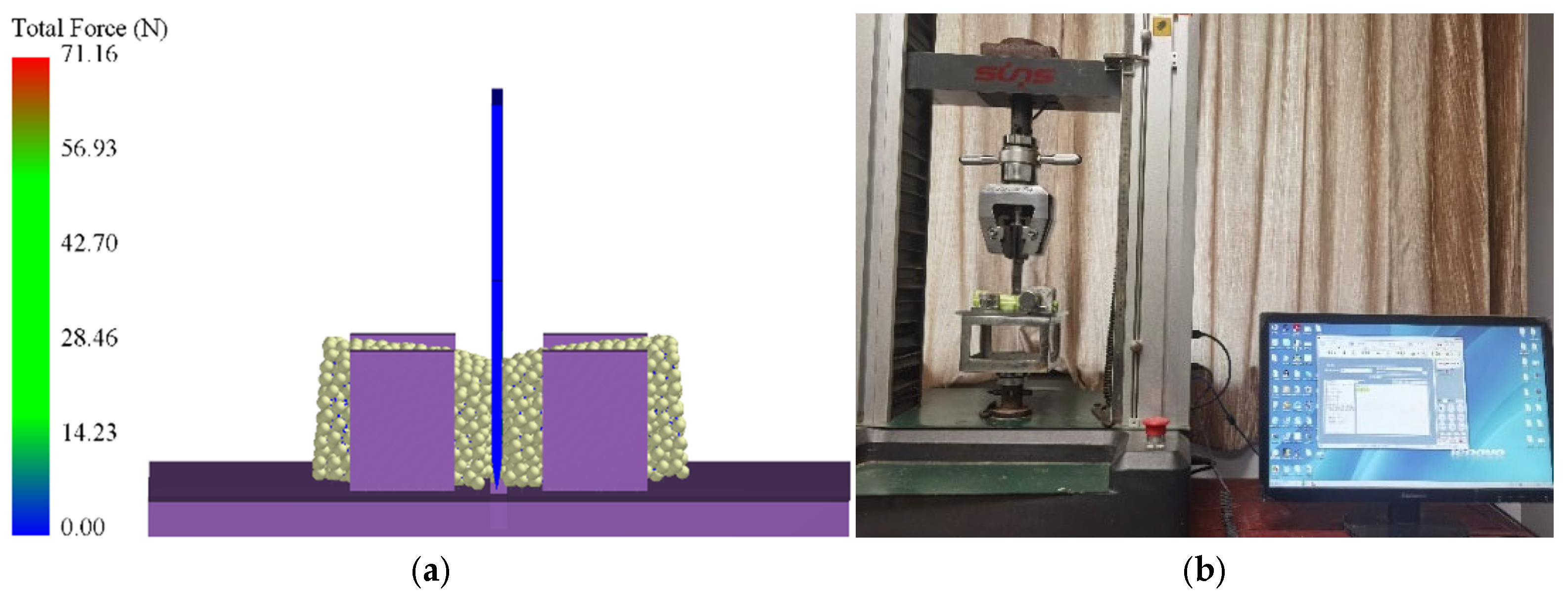
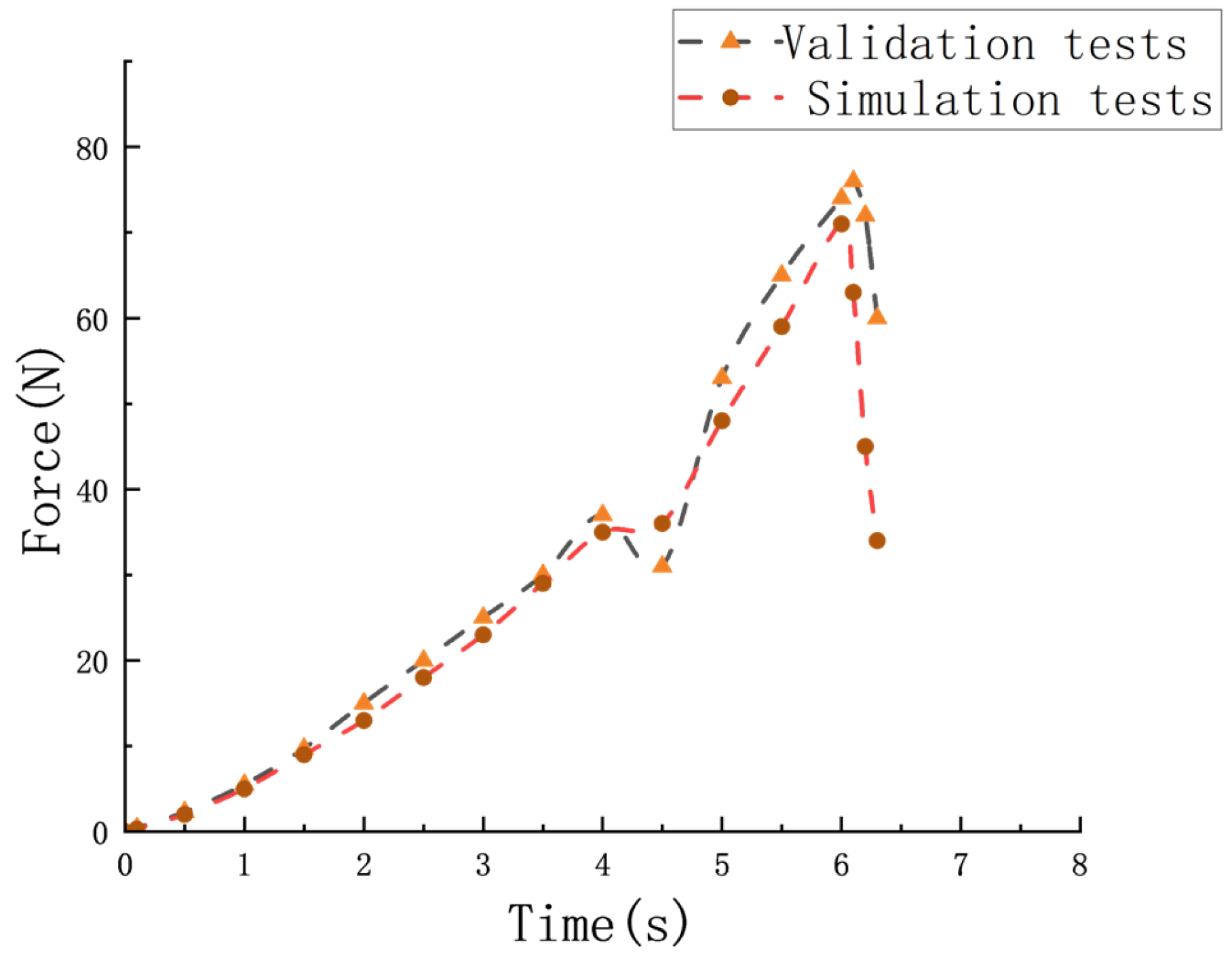
3.3. Model Validation
3.4. Discussion
- (1)
- Among the contact parameters, such as collision recovery coefficient, static friction coefficient, and dynamic friction coefficient, that can be measured by the experiments, the parameters used in this study are ranges based on similar studies. The accuracy of the calibration value can be measured by testing first to reduce the range of the calibration parameters.
- (2)
- The leaf stem, in reality, consists of multiple components, including the epidermis, surface layers, phloem, xylem, and other parts. For a more accurate bonding model, it is important to consider that the parameters of these different parts vary. However, in this study, the test focused solely on the maximum cutting force, without considering the influence of these anatomical differences. As a result, the actual shear behavior may differ from the results obtained in the simulation.
4. Conclusions
- (1)
- The contact and bonding parameters for the discrete element model of tuber mustard leaf stems were successfully calibrated. The collision recovery, static friction, and rolling friction coefficients between the leaf stems were determined as 0.45, 0.457, and 0.167, respectively. For interactions between leaf stems and steel, these values were 0.45, 0.55, and 0.175, respectively. The bonding parameters, including normal stiffness ( N/m), tangential stiffness ( N/m), and critical stresses ( MPa, = 0.34 MPa), were optimized using the Hertz–Mindlin with bonding model.
- (2)
- The calibrated model was validated through simulation and physical shear tests, showing a relative error of less than 5% in the maximum shear force. This confirms the model’s accuracy and reliability for simulating the cutting process of tuber mustard leaf stems.
- (3)
- This study provides essential parameter references for the design and optimization of tuber mustard harvesting equipment, making the cutting process of leaf stems more visually interpretable. Future research should focus on incorporating the anatomical structure of stems and expanding the range of contact parameters to further enhance the model’s precision and applicability.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, J. Research on the Design and Optimization of the Cabbage Head Cutting Device. Master’s Thesis, Southwest University, Chongqing, China, 2019. [Google Scholar]
- Yu, G.; Zheng, H.; Xue, X.; Yang, H. Research Status and Prospect of Mustard Harvesting Equipment. J. Chin. Agric. Mach. Chem. 2021, 42, 17–20. [Google Scholar] [CrossRef]
- Ye, J. Design and Experimental Study of Mustard Harvesting Machine for Hilly Areas in Fuling District. Master’s Thesis, Zhejiang Agriculture and Forestry University, Hangzhou, China, 2023. [Google Scholar]
- Xiang, W.; Sun, Y.; Liu, F.; Li, M.; Xie, S.; Ke, C.; Huang, Y. Development of a Shrinking Stem Sliding Cutter for Cabbage Head. Trans. Chin. Soc. Agric. Eng. 2023, 39, 266–275. [Google Scholar]
- Wang, T.; Lou, T.; Fei, Y.; Liu, G.; Zhang, J. Key Technologies for Mechanized Harvesting of Mustard in Hilly Areas. J. Chin. Agric. Mach. Chem. 2023, 44, 11–16. [Google Scholar] [CrossRef]
- Wang, L.; Ye, J.; Yang, S.; Liu, L.; Chen, J. Design and Experiment of Pulling and Conveying Mechanism for Mustard Harvesting Machine. J. Agric. Mech. Res. 2018, 40, 138–141+246. [Google Scholar] [CrossRef]
- Xue, X.; Zheng, H.; Ye, Y.; Yu, G.; Wu, M.; Ren, N. Design and Experiment of Fixed Knife Sliding Cutter for Mustard Harvesting Machine. J. Chin. Agric. Mach. Chem. 2023, 44, 48–55. [Google Scholar] [CrossRef]
- Jin, Y.; Xiao, H.; Song, Z.; Jiang, Q.; Zhang, J.; Yang, G. Design and Experiment of Hand-Pushed Self-Propelled Cabbage Head Harvester. J. Chin. Agric. Mach. Chem. 2020, 41, 45–50. [Google Scholar] [CrossRef]
- Zheng, H.; Xue, X.; Yu, G. Cutting Mechanical Characteristics of Mustard Shortened Stems. Zhejiang Agric. Sci. 2021, 33, 1939–1945. [Google Scholar]
- Zeng, Z.; Ma, X.; Cao, X.; Li, Z.; Wang, X. Application Status and Prospect of Discrete Element Method in Agricultural Engineering. J. Agric. Mech. 2021, 52, 1–20. [Google Scholar]
- Li, N.; Liu, L.; Xu, P.; Li, J.; Jiang, H.; Wang, W. Simulation and Experiment of Soapberry Seed Separation Based on Discrete Element Method. J. Chin. Agric. Mach. Chem. 2023, 44, 163–169. [Google Scholar] [CrossRef]
- Luo, Q.; Huang, X.; Wu, J.; Mou, X.; Xu, Y.; Li, S.; Ma, G.; Wan, F.; Peng, L. Simulation Analysis and Parameter Optimization of Seed-Flesh Separation Process of Seed Melon Crushing and Seed Extraction Separator Based on DEM. Agriculture 2024, 14, 1008. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, X.; Yu, Y. Modeling Method of Corn Kernel Based on Discrete Element Method and Its Experimental Study. Agriculture 2024, 14, 2195. [Google Scholar] [CrossRef]
- Wang, X.; Tian, H.; Xiao, Z.; Zhao, K.; Li, D.; Wang, D. Numerical Simulation and Experimental Study of Corn Straw Grinding Process Based on Computational Fluid Dynamics–Discrete Element Method. Agriculture 2024, 14, 325. [Google Scholar] [CrossRef]
- Hosseinpour-Zarnaq, M.; Minaei, S.; Bazyar, P. Determination of the Mechanical Properties of Parsley Stems Related to the Design of Processing Machines. Chem. Proc. 2022, 10, 16. [Google Scholar] [CrossRef]
- Ma, Y.; Song, C.; Xuan, C.; Wang, H.; Yang, S.; Wu, P. Simulation Parameter Calibration of Alfalfa Straw Compression Using Discrete Element Method. Trans. Chin. Soc. Agric. Eng. 2020, 36, 22–30. [Google Scholar]
- Hu, Y.; Xiang, W.; Duan, Y.; Yan, B.; Ma, L.; Liu, J.; Lyu, J. Calibration of Ramie Stalk Contact Parameters Based on the Discrete Element Method. Agriculture 2023, 13, 1070. [Google Scholar] [CrossRef]
- Zhao, Y.; Tang, Z.; Chen, S. Loading Model and Mechanical Properties of Mature Broccoli (Brassica oleracea L. Var. Italica Plenck) Stems at Harvest. Agriculture 2022, 12, 1519. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, H.; Xue, H.; Ni, C.; Wang, C. Discrete Element Parameter Calibration and Testing of Ginseng Stems. J. Agric. Mech. 2023, 54, 61–70+91. [Google Scholar]
- Zhang, G.; Chen, L.; Liu, H.; Dong, Z.; Zhang, Q.; Zhou, Y. Discrete Element Simulation Parameter Calibration and Testing for Water Chestnut. Trans. Chin. Soc. Agric. Eng. 2022, 38, 41–50. [Google Scholar]
- Xie, W.; Peng, L.; Jiang, P.; Meng, D.; Wang, X. Establishment and Optimization of Dual-Layer Bonding Discrete Element Model for Oilseed Rape Stem at Harvest. J. Agric. Mech. 2023, 54, 112–120. [Google Scholar]
- Zhang, X.; Hu, X.; Liu, J.; Yang, Y.; Li, Y. Discrete Element Simulation Bonding Model Parameter Calibration and Testing of Banana Stems. J. Agric. Mech. 2023, 54, 121–130. [Google Scholar]
- GB/T 5262-2008; Measuring Methods for Agricultural Machinery Testing Conditions—General Rules. Standardization Administration of China: Beijing, China, 2008.
- Fan, J.; Li, Y.; Wang, B.; Gu, F.; Wu, F.; Yang, H.; Yu, Z.; Hu, Z. An Experimental Study of Axial Poisson’s Ratio and Axial Young’s Modulus Determination of Potato Stems Using Image Processing. Agriculture 2022, 12, 1026. [Google Scholar] [CrossRef]
- Zhang, F.; Song, X.; Zhang, X.; Zhang, F.; Wei, W.; Dai, F. Mechanical Characteristics and Simulation of Corn Straw Crushing Process. Trans. Chin. Soc. Agric. Eng. 2019, 35, 58–65. [Google Scholar]
- Hu, S. Design and Experimental Study of Water Celery Stalk Cutting Test Platform. Master’s Thesis, Yangzhou University, Yangzhou, China, 2024. [Google Scholar]
- Zhang, H. Design and Experiment of Small-Row Mustard Planting Device Based on Mechanical-Crop-Soil Coupling Model. Master’s Thesis, Shandong Agricultural University, Tai’an, China, 2024. [Google Scholar]
- Zhang, T.; Li, Y.; Song, S.; Pang, Y.; Shao, W.; Tang, X. Design and Experiment of Cabbage Head Harvester Based on Flexible Clamping. J. Agric. Mech. 2020, 51, 162–169+190. [Google Scholar]
- Liao, Y.; Liao, Q.; Tian, B.; Shu, C.; Wang, J.; Ma, A. Experimental Study on Mechanical Properties of Reeds at the Bottom of the Stem During Harvest. Trans. Chin. Soc. Agric. Eng. 2007, 124–129. [Google Scholar]
- Chen, K.; Yin, X.; Ma, W.; Jin, C.; Liao, Y. Contact Parameter Calibration for Discrete Element Potato Minituber Seed Simulation. Agriculture 2024, 14, 2298. [Google Scholar] [CrossRef]
- Luo, W.; Chen, X.; Qin, M.; Guo, K.; Ling, J.; Gu, F.; Hu, Z. Design and Experiment of Uniform Seed Device for Wide-Width Seeder of Wheat after Rice Stubble. Agriculture 2023, 13, 2173. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, X.; Wu, S.; Chen, C.; Wang, J.; Yuan, S.; Chen, B.; Li, P.; Xu, R. Numerical simulation of particle motion at cucumber straw grinding process based on EDEM. Int. J. Agric. Biol. Eng. 2020, 13, 227–235. [Google Scholar]
- Shi, Y.; Xin, S.; Wang, X.; Hu, Z.; Newman, D.; Ding, W. Numerical simulation and field tests of minimum-tillage planter with straw smashing and strip laying based on EDEM software. Comput. Electron. Agric. 2019, 166, 105021. [Google Scholar]



| Parameters | Maximum | Minimum | Average Value | Standard Deviation |
|---|---|---|---|---|
| Plant height (mm) | 617 | 535 | 565 | 31.19 |
| Density (g/cm3) | 0.98 | 0.87 | 0.929 | 0.03 |
| Moisture content (%) | 81.83 | 77.91 | 79.72 | 1.19 |
| Type | Shape | Discrete Element Model | Proportion |
|---|---|---|---|
| a |  |  | 0.12 |
| b |  |  | 0.53 |
| c |  |  | 0.27 |
| d |  |  | 0.08 |
| Discrete Element Parameter | Value | Remarks |
|---|---|---|
| Poisson’s ratio, | 0.41 | Measured value |
| Shear modulus, /Mpa | 1.6 | Measured value |
| Density, | 0.929 | Measured value |
| Coefficient of restitution between leaf stems, A | 0.2–0.7 | Reference range of variables |
| Coefficient of static friction between leaf stems, B | 0.3–0.8 | Reference range of variables |
| Coefficient of rolling friction between leaf stems, C | 0.05–0.3 | Reference range of variables |
| Coefficient of restitution between leaf stems and steel, D | 0.2–0.7 | Reference range of variables |
| Coefficient of static friction between leaf stems and steel, E | 0.3–0.8 | Reference range of variables |
| Coefficient of rolling friction between leaf stems and steel, F | 0.05–0.3 | Reference range of variables |
| No. | A | B | C | D | E | F | Stacking Angle |
|---|---|---|---|---|---|---|---|
| 1 | 0.7 | 0.3 | 0.3 | 0.2 | 0.8 | 0.05 | 36.36 |
| 2 | 0.2 | 0.3 | 0.3 | 0.7 | 0.3 | 0.05 | 33.29 |
| 3 | 0.7 | 0.3 | 0.05 | 0.2 | 0.3 | 0.3 | 25.57 |
| 4 | 0.2 | 0.3 | 0.05 | 0.7 | 0.8 | 0.3 | 29.32 |
| 5 | 0.2 | 0.3 | 0.3 | 0.7 | 0.3 | 0.05 | 33.09 |
| 6 | 0.2 | 0.8 | 0.05 | 0.2 | 0.8 | 0.05 | 36.26 |
| 7 | 0.7 | 0.8 | 0.05 | 0.7 | 0.3 | 0.05 | 27.37 |
| 8 | 0.7 | 0.8 | 0.3 | 0.7 | 0.8 | 0.3 | 45.56 |
| 9 | 0.7 | 0.3 | 0.3 | 0.2 | 0.8 | 0.05 | 33.67 |
| 10 | 0.7 | 0.8 | 0.05 | 0.7 | 0.3 | 0.05 | 25.58 |
| 11 | 0.2 | 0.8 | 0.05 | 0.2 | 0.8 | 0.05 | 30.26 |
| 12 | 0.7 | 0.3 | 0.05 | 0.2 | 0.3 | 0.3 | 26.33 |
| 13 | 0.7 | 0.8 | 0.3 | 0.7 | 0.8 | 0.3 | 42.52 |
| 14 | 0.2 | 0.3 | 0.05 | 0.7 | 0.8 | 0.3 | 29.54 |
| 15 | 0.2 | 0.8 | 0.3 | 0.2 | 0.3 | 0.3 | 42.52 |
| 16 | 0.2 | 0.8 | 0.3 | 0.2 | 0.3 | 0.3 | 41.93 |
| Parameter | Effect | Mean Square Sum | Contribution | Significance Ranking |
|---|---|---|---|---|
| A | −1.01 | 10.97 | 1.66 | 5 |
| B | 7.18 | 125.61 | 18.99 | 2 |
| C | 12.60 | 387.20 | 58.54 | 1 |
| D | −1.06 | 2.75 | 0.42 | 6 |
| E | 4.45 | 48.34 | 7.31 | 3 |
| F | 4.39 | 46.96 | 7.10 | 4 |
| No. | B | C | Stacking Angle (°) | Relative Error (%) |
|---|---|---|---|---|
| 1 | 0.3 | 0.05 | 28.31 | 14.11 |
| 2 | 0.4 | 0.1 | 30.27 | 8.16 |
| 3 | 0.5 | 0.15 | 33.17 | 0.6 |
| 4 | 0.6 | 0.2 | 35.62 | 8.07 |
| 5 | 0.7 | 0.25 | 38.31 | 16.23 |
| 6 | 0.8 | 0.3 | 40.96 | 24.3 |
| Code | Coefficient of Static Friction (B) | Coefficient of Rolling Friction (C) |
|---|---|---|
| −1.414 | 0.36 | 0.08 |
| −1 | 0.4 | 0.1 |
| 0 | 0.5 | 0.15 |
| 1 | 0.6 | 0.2 |
| 1.414 | 0.64 | 0.22 |
| No. | Coefficient of Static Friction B | Rolling Friction Factor C | Stacking Angle (°) | Relative Error (%) |
|---|---|---|---|---|
| 1 | 0.6 | 0.1 | 34.25 | 3.91 |
| 2 | 0.64 | 0.15 | 35.62 | 8.07 |
| 3 | 0.4 | 0.2 | 32.35 | 1.85 |
| 4 | 0.5 | 0.15 | 32.76 | 0.61 |
| 5 | 0.5 | 0.15 | 33.27 | 0.94 |
| 6 | 0.4 | 0.1 | 31.79 | 3.55 |
| 7 | 0.5 | 0.08 | 31.96 | 3.03 |
| 8 | 0.6 | 0.2 | 34.76 | 5.46 |
| 9 | 0.5 | 0.15 | 33.45 | 1.49 |
| 10 | 0.5 | 0.22 | 33.62 | 2 |
| 11 | 0.36 | 0.15 | 32.26 | 2.12 |
| 12 | 0.5 | 0.15 | 33.27 | 0.94 |
| 13 | 0.5 | 0.15 | 32.89 | 0.21 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 14.48 | 5 | 2.90 | 36.59 | <0.0001 ** |
| B | 11.57 | 1 | 11.57 | 146.25 | <0.0001 ** |
| C | 1.46 | 1 | 1.46 | 18.45 | 0.0036 ** |
| BC | 0.0006 | 1 | 0.0006 | 0.0079 | 0.9317 |
| B2 | 1.04 | 1 | 1.04 | 13.14 | 0.0085 ** |
| C2 | 0.2469 | 1 | 0.2469 | 3.12 | 0.1207 * |
| Residual | 0.5289 | 7 | 0.0756 | ||
| Lack of fit | 0.3624 | 3 | 0.1208 | 2.90 | 0.1650 |
| Pure error | 0.1665 | 4 | 0.0416 | ||
| Cor total | 15.06 | 12 |
| No. | Normal Stiffness Kn | Tangential Stiffness Kτ | Normal Critical Stress σn | Tangential Critical Stress στ | Maximum Shear Force Ft |
|---|---|---|---|---|---|
| 1 | 55,000 (0) | 100,000 (1) | 1.2 (1) | 0.5 (0) | 78.3 |
| 2 | 55,000 (0) | 10,000 (−1) | 0.4 (−1) | 0.5 (0) | 63.6 |
| 3 | 10,000 (−1) | 55,000 (0) | 0.4 (−1) | 0.5 (0) | 67.3 |
| 4 | 55,000 (0) | 55,000 (0) | 0.8 (0) | 0.5 (0) | 69.8 |
| 5 | 55,000 (0) | 55,000 (0) | 0.4 (−1) | 0.9 (1) | 77.2 |
| 6 | 10,000 (−1) | 10,000 (−1) | 0.8 (0) | 0.5 (0) | 66.6 |
| 7 | 10,000 (−1) | 55,000 (0) | 0.8 (0) | 0.1 (−1) | 68.2 |
| 8 | 55,000 (0) | 100,000 (1) | 0.8 (0) | 0.1 (−1) | 79.9 |
| 9 | 55,000 (0) | 55,000 (0) | 0.8 (0) | 0.5 (0) | 68.2 |
| 10 | 100,000 (1) | 55,000 (0) | 0.4 (−1) | 0.5 (0) | 68.3 |
| 11 | 55,000 (0) | 100,000 (1) | 0.4 (−1) | 0.5 (0) | 78.5 |
| 12 | 10,000 (−1) | 55,000 (0) | 0.8 (0) | 0.9 (1) | 78.7 |
| 13 | 55,000 (0) | 55,000 (0) | 1.2 (1) | 0.1 (−1) | 67.9 |
| 14 | 100,000 (1) | 55,000 (0) | 0.8 (0) | 0.9 (1) | 78.9 |
| 15 | 55,000 (0) | 10,000 (−1) | 0.8 (0) | 0.9 (1) | 75.6 |
| 16 | 100,000 (1) | 55,000 (0) | 0.8 (0) | 0.1 (−1) | 67.1 |
| 17 | 55,000 (0) | 10,000 (−1) | 1.2 (1) | 0.5 (0) | 68.2 |
| 18 | 55,000 (0) | 100,000 (1) | 0.8 (0) | 0.9 (1) | 85.2 |
| 19 | 55,000 (0) | 55,000 (0) | 1.2 (1) | 0.9 (1) | 82.1 |
| 20 | 55,000 (0) | 55,000 (0) | 0.8 (0) | 0.5 (0) | 69.6 |
| 21 | 10,000 (−1) | 55,000 (0) | 1.2 (1) | 0.5 (0) | 69.5 |
| 22 | 100,000 (1) | 10,000 (−1) | 0.8 (0) | 0.5 (0) | 61.1 |
| 23 | 55,000 (0) | 55,000 (0) | 0.8 (0) | 0.5 (0) | 69.1 |
| 24 | 55,000 (0) | 55,000 (0) | 0.8 (0) | 0.5 (0) | 68.2 |
| 25 | 10,000 (−1) | 100,000 (1) | 0.8 (0) | 0.5 (0) | 74.9 |
| 26 | 55,000 (0) | 55,000 (0) | 0.4 (−1) | 0.1 (−1) | 68.3 |
| 27 | 100,000 (1) | 100,000 (1) | 0.8 (0) | 0.5 (0) | 81.1 |
| 28 | 55,000 (0) | 10,000 (−1) | 0.8 (0) | 0.1 (−1) | 62.3 |
| 29 | 100,000 (1) | 55,000 (0) | 1.2 (1) | 0.5 (0) | 70.6 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 1123.47 | 14 | 80.25 | 135.9 | <0.0001 ** |
| 0.3008 | 1 | 0.3008 | 0.5094 | 0.4871 | |
| 540.02 | 1 | 540.02 | 914.5 | <0.0001 ** | |
| 14.96 | 1 | 14.96 | 25.34 | 0.0002 ** | |
| 341.33 | 1 | 341.33 | 578.03 | <0.0001 ** | |
| 34.22 | 1 | 34.22 | 57.95 | <0.0001 ** | |
| 0.0025 | 1 | 0.0025 | 0.0042 | 0.949 | |
| 0.4225 | 1 | 0.4225 | 0.7155 | 0.4119 | |
| 5.76 | 1 | 5.76 | 9.75 | 0.0075 ** | |
| 16 | 1 | 16 | 27.1 | 0.0001 ** | |
| 7.02 | 1 | 7.02 | 11.89 | 0.0039 ** | |
| 2 | 1.19 | 1 | 1.19 | 2.01 | 0.1784 |
| 2 | 38.86 | 1 | 38.86 | 65.8 | <0.0001 ** |
| 2 | 1.69 | 1 | 1.69 | 2.86 | 0.1131 |
| 2 | 129.03 | 1 | 129.03 | 218.5 | <0.0001 ** |
| Residual | 8.27 | 14 | 0.5905 | ||
| Lack of fit | 5.98 | 10 | 0.5979 | 1.05 | 0.5283 |
| Error | 2.29 | 4 | 0.572 | ||
| Total | 1131.74 | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, M.; Shen, H.; Luo, W.; Ling, J.; Wang, B.; Gu, F.; Song, S.; Pan, L.; Hu, Z. Calibration of Parameters for Leaf-Stem-Cutting Model of Tuber Mustard (Brassica juncea L.) Based on Discrete Element Method. Agriculture 2025, 15, 773. https://doi.org/10.3390/agriculture15070773
Gu M, Shen H, Luo W, Ling J, Wang B, Gu F, Song S, Pan L, Hu Z. Calibration of Parameters for Leaf-Stem-Cutting Model of Tuber Mustard (Brassica juncea L.) Based on Discrete Element Method. Agriculture. 2025; 15(7):773. https://doi.org/10.3390/agriculture15070773
Chicago/Turabian StyleGu, Man, Haiyang Shen, Weiwen Luo, Jie Ling, Bokai Wang, Fengwei Gu, Shumin Song, Liang Pan, and Zhichao Hu. 2025. "Calibration of Parameters for Leaf-Stem-Cutting Model of Tuber Mustard (Brassica juncea L.) Based on Discrete Element Method" Agriculture 15, no. 7: 773. https://doi.org/10.3390/agriculture15070773
APA StyleGu, M., Shen, H., Luo, W., Ling, J., Wang, B., Gu, F., Song, S., Pan, L., & Hu, Z. (2025). Calibration of Parameters for Leaf-Stem-Cutting Model of Tuber Mustard (Brassica juncea L.) Based on Discrete Element Method. Agriculture, 15(7), 773. https://doi.org/10.3390/agriculture15070773







