Analyzing the Risk of Short-Term Losses in Free-Range Egg Production Using Commercial Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
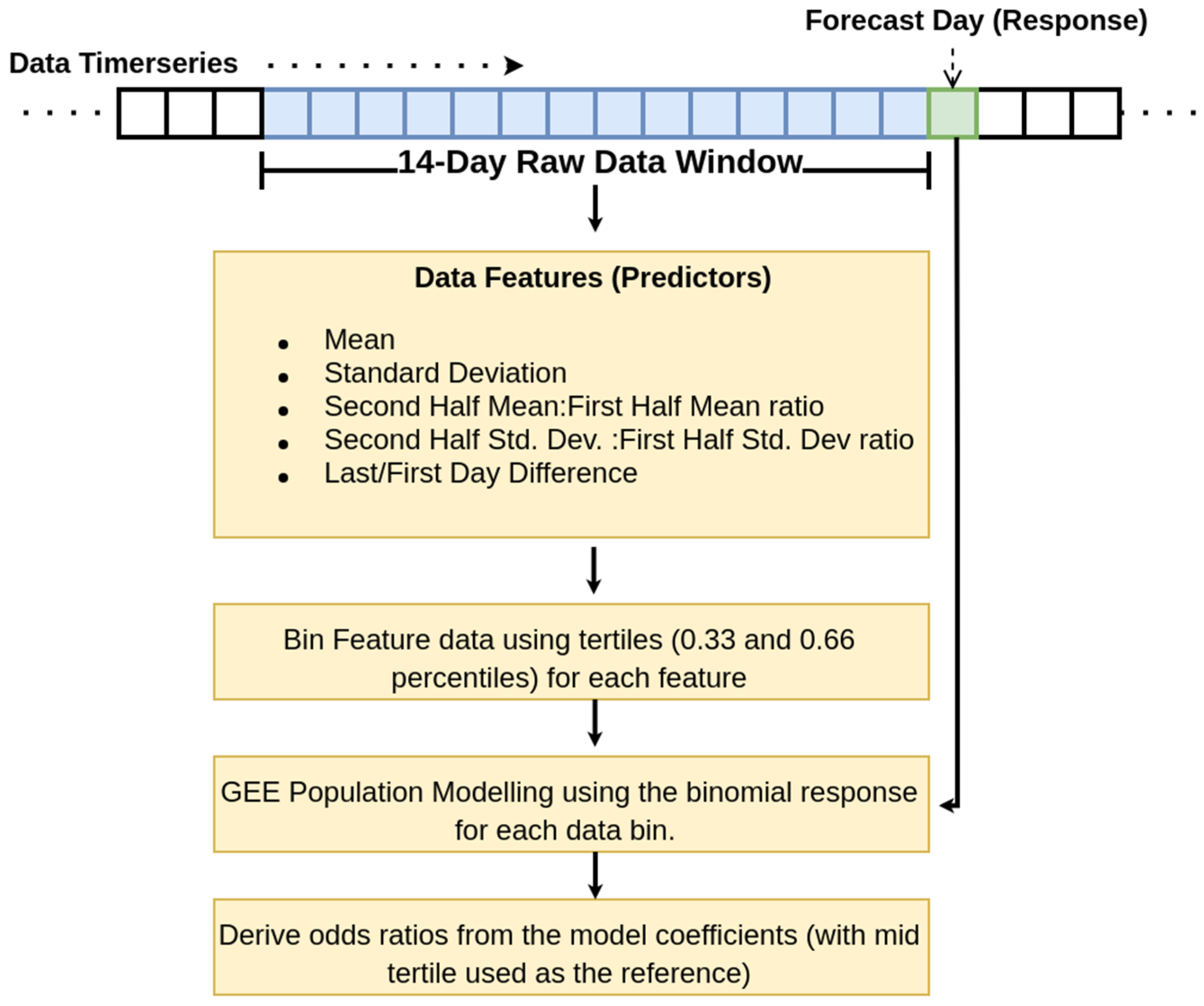
2.2. Feature Dataset
- Mean;
- Standard deviation;
- The ratio of the mean calculated across the second half of the window to the mean calculated across the first half of the window is denoted as SH mean/FH mean ratio. This feature provided a reliable indication of the trend of the raw feature;
- The ratio of the standard deviation calculated across the second half of the window to the standard deviation across the first half of the window is denoted as the SH Std. Dev/FH Std. Dev. This feature provided an indication of the variation in data features across the window;
- The difference between the first and last day of the 14-day window is denoted as the last day–first day difference. This provides a more sensitive indication of production trends over time, compared to the SH mean/FH mean ratio.
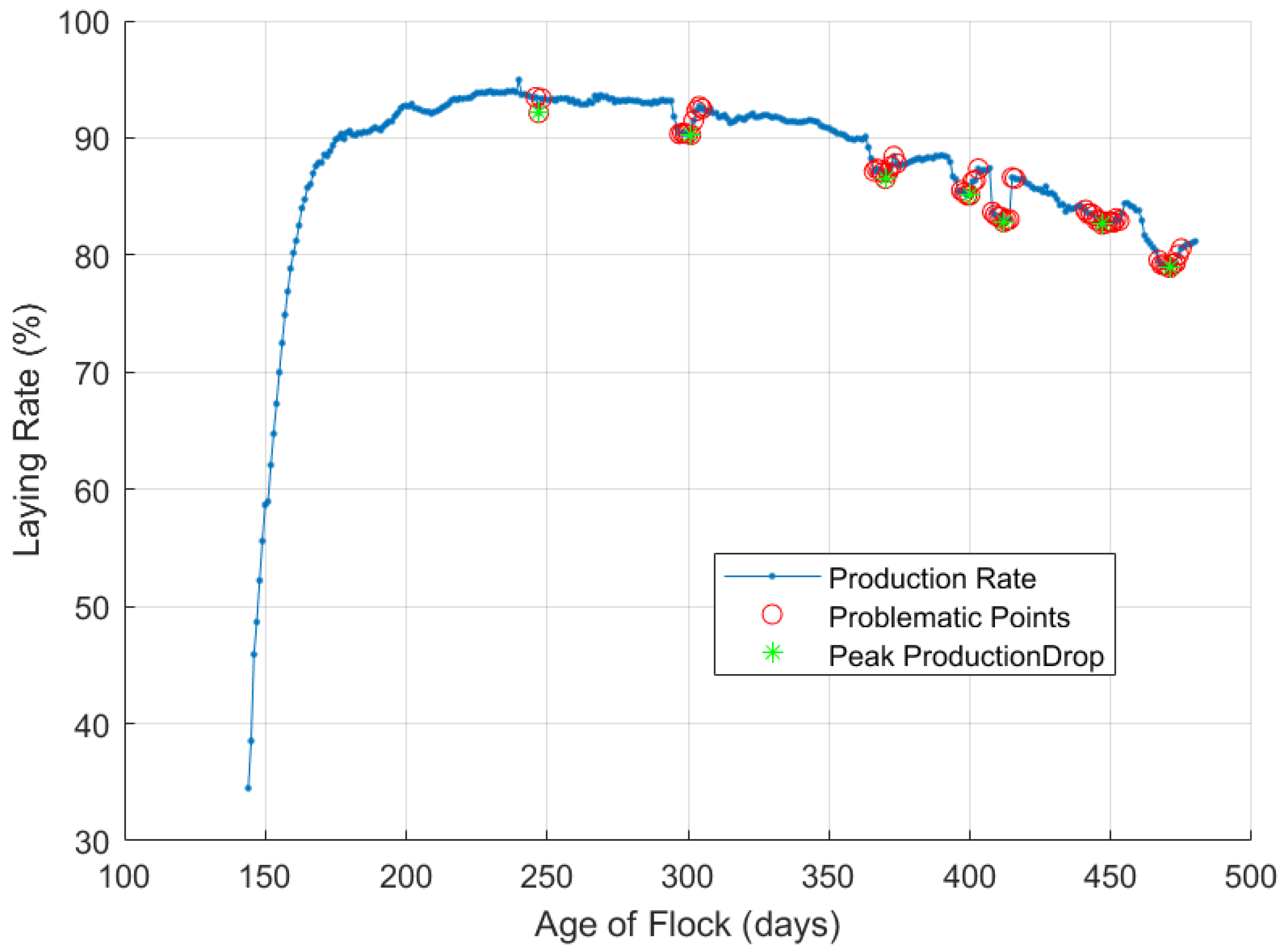
2.3. Detection of Short-Term Production Losses
- The prominence of a drop measured how much the peak stood out due to its intrinsic height and its location relative to the surrounding data points. The prominence was measured by taking the distance halfway between the mean of all values in the window and the lowest point in the window. The value for this parameter was set to 2.5 based on numerical inspection of the resulting flagged data points within each production curve using a prominence range of [0.5–3.0]. Through the numerical inspection, it was identified that values for the prominence of <2.5 resulted in the detection of relatively minor fluctuations in the laying rate that were not consistent with fluctuations in the laying resulting from production issues. Conversely, prominence values > 2.5 failed to detect many of the major fluctuations that were consistent with production issues. The prominence value of 2.5 was applied across the production curves of all flocks under study to ensure a consistent detection of production drops.
- The duration was defined by the minimum number of data points that comprised the sudden drop in the laying rate. The value was set to 3 days—where a reduction in egg production with a duration shorter than this was excluded to account for the common day-to-day variations in daily egg collection procedures. This threshold prevents variations such as single-day fluctuations that would typically indicate a collection issue (counting error, equipment failures, etc.) from being detected as a production fluctuation.
2.4. Generalized Estimating Equations
2.5. Odds Ratio Representation
3. Results
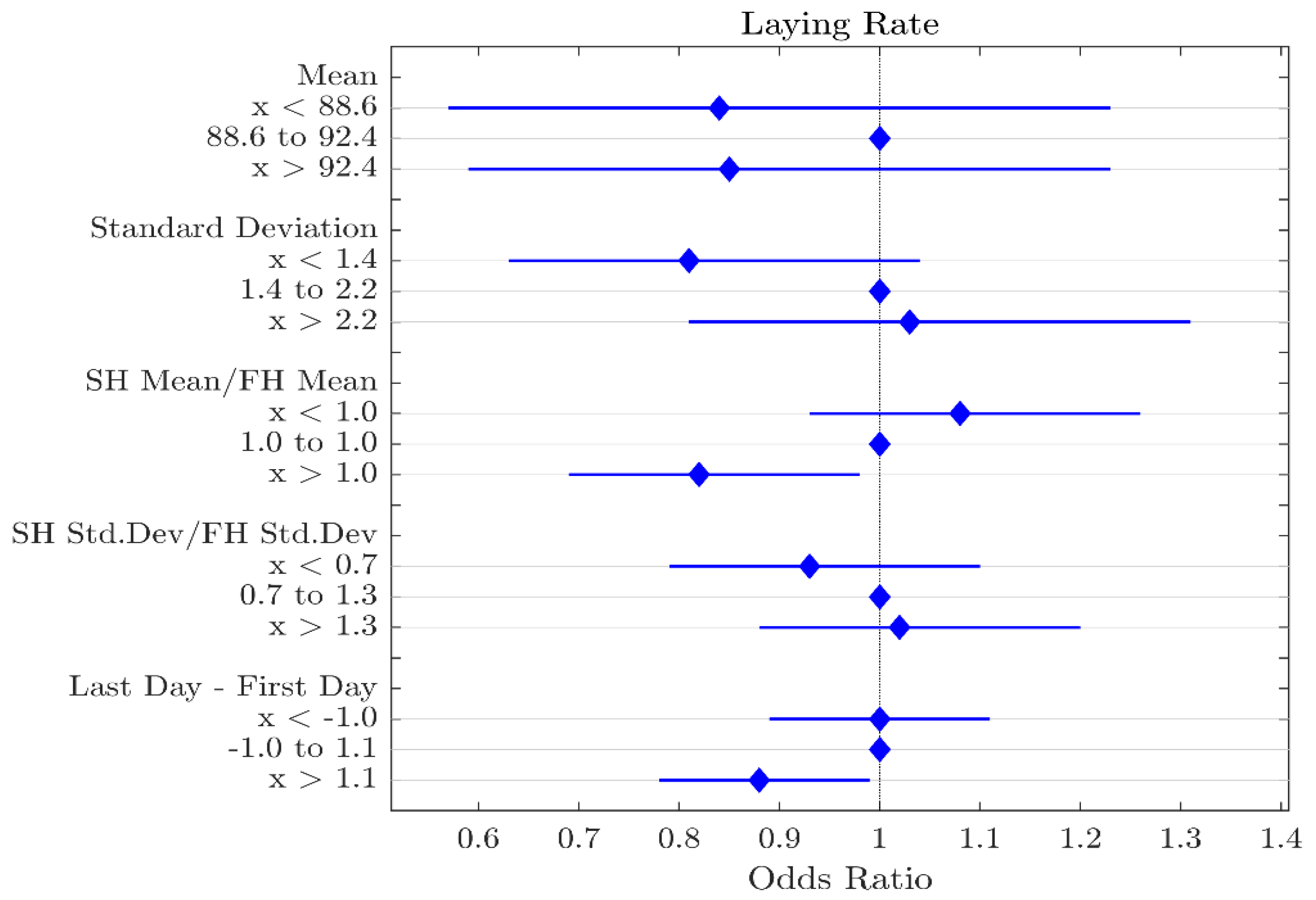
3.1. Production Variable Features
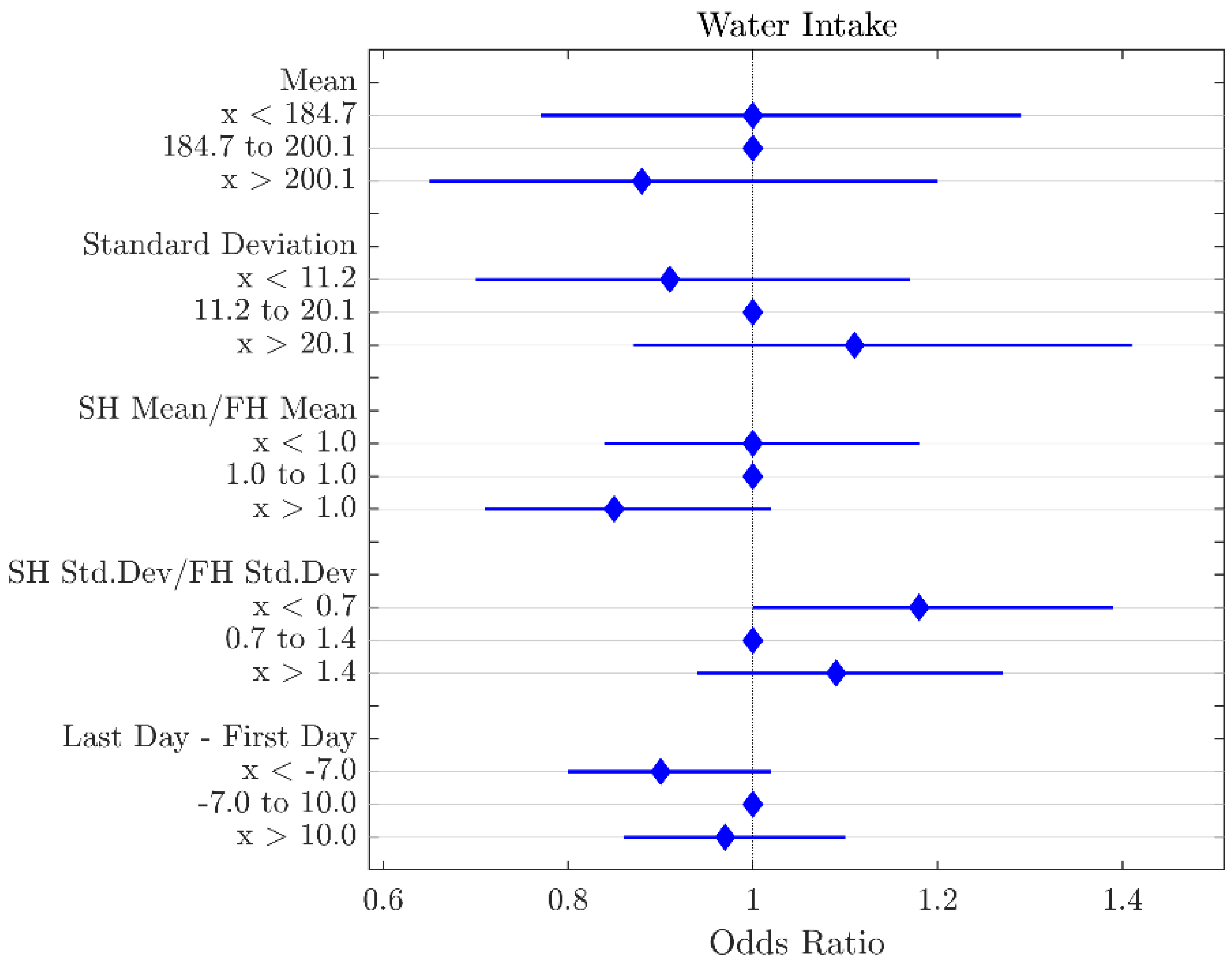
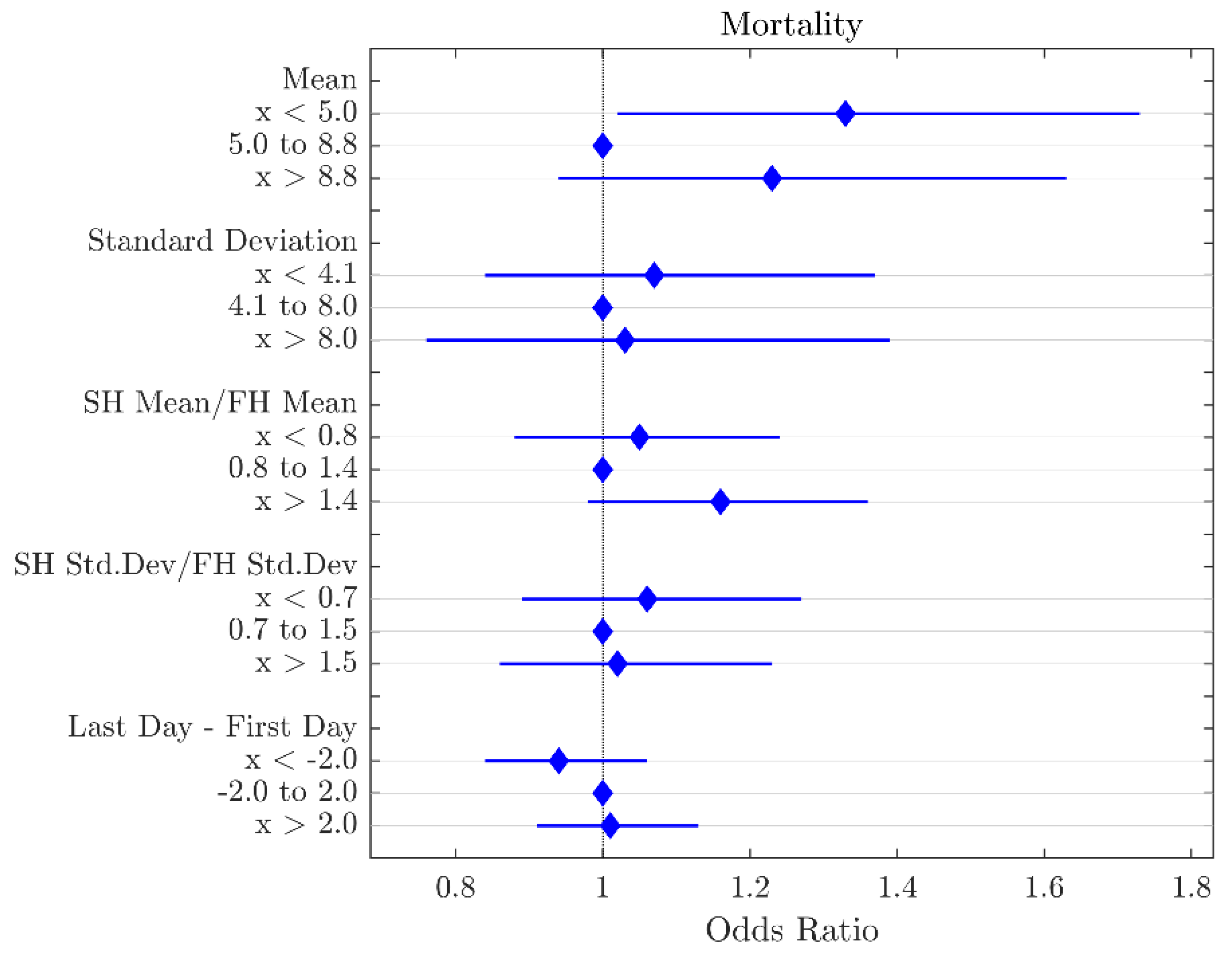
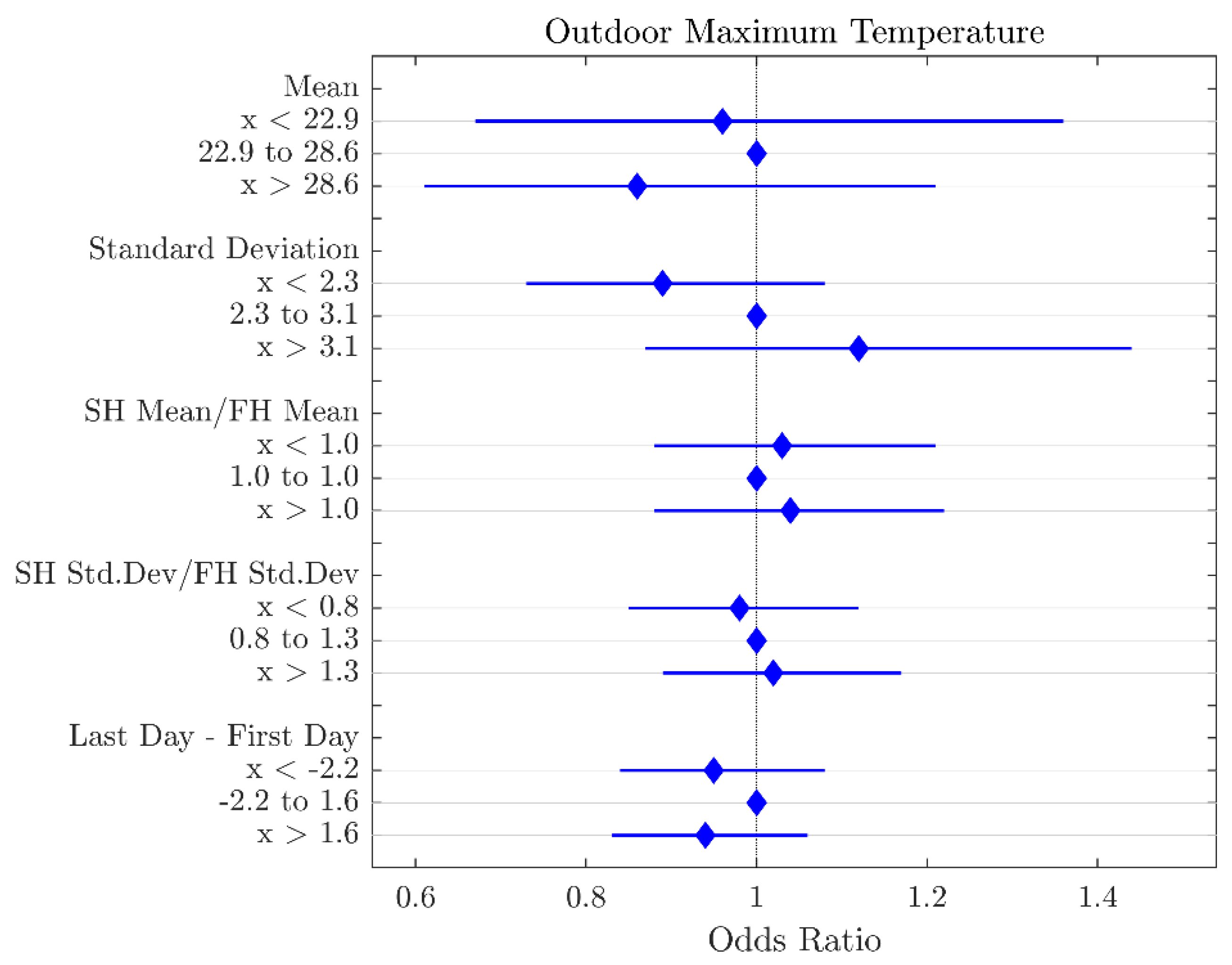
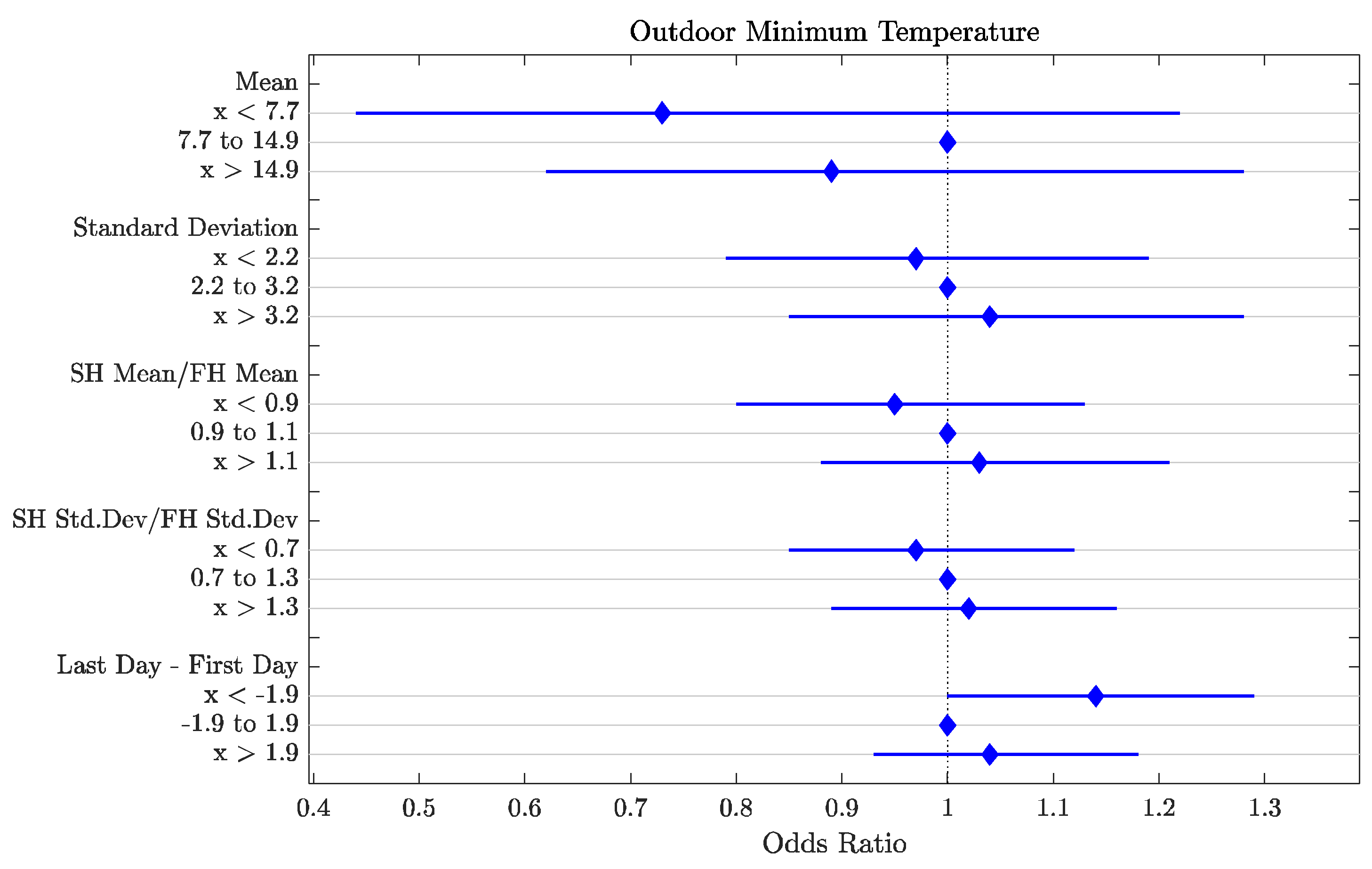
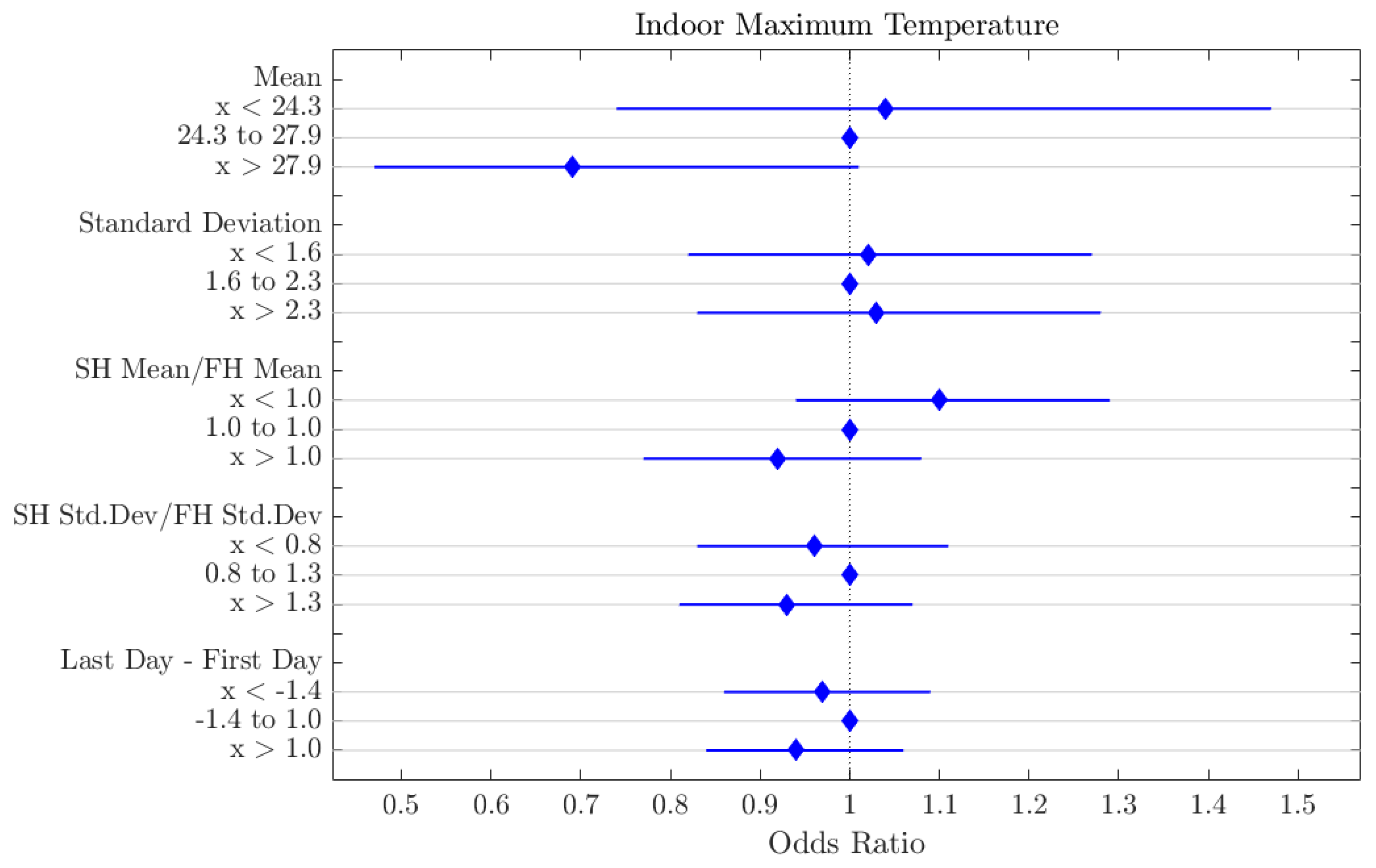
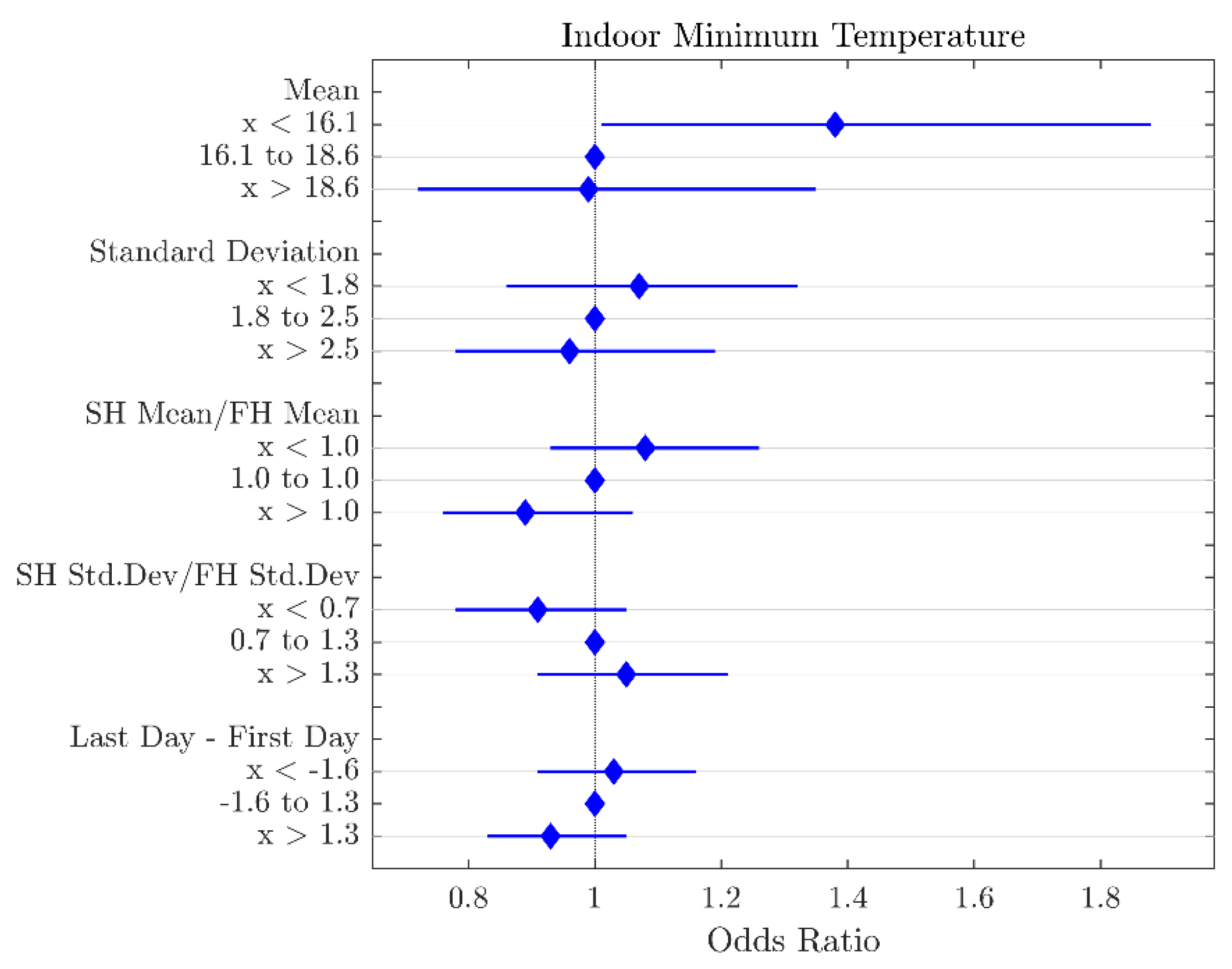
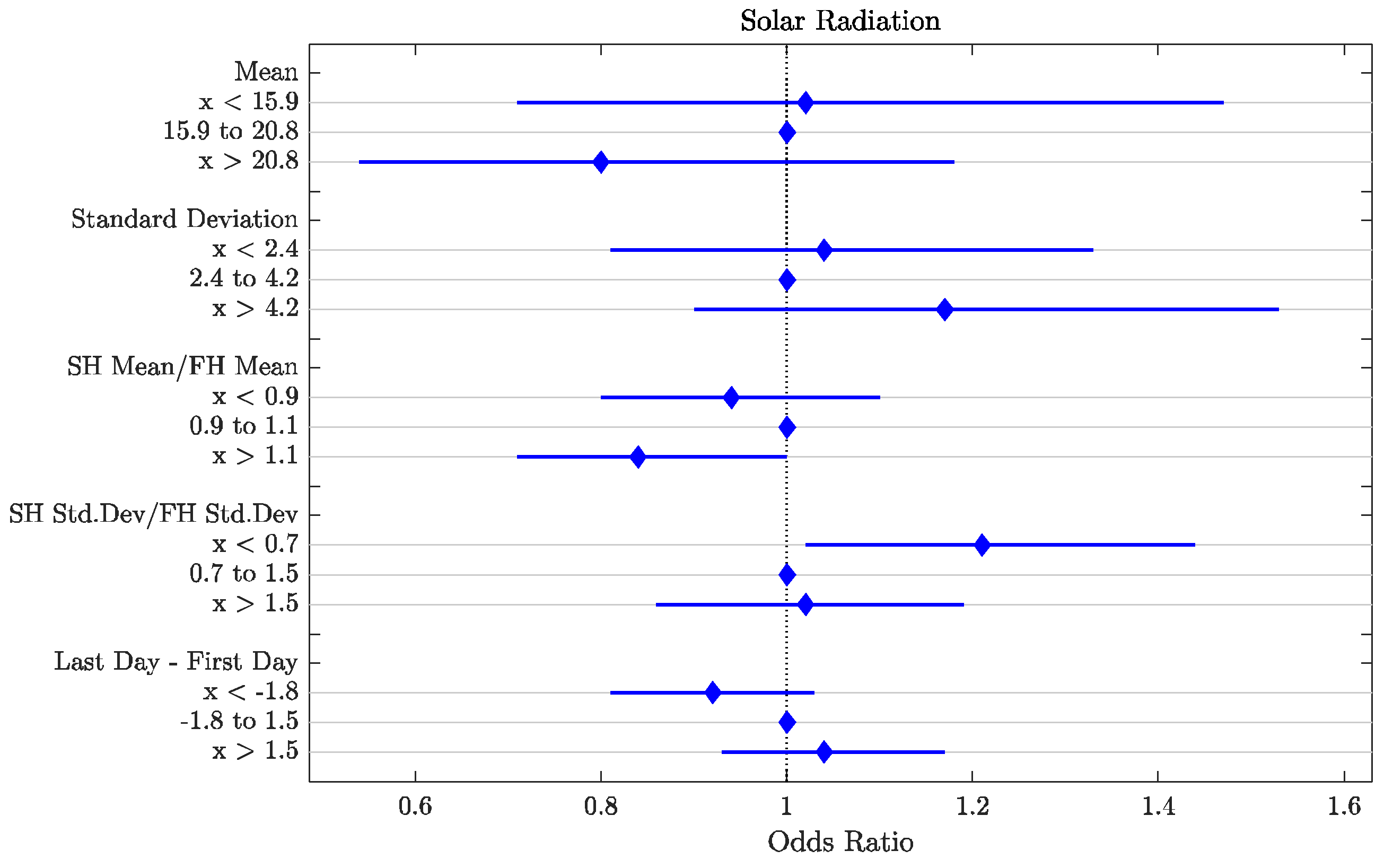
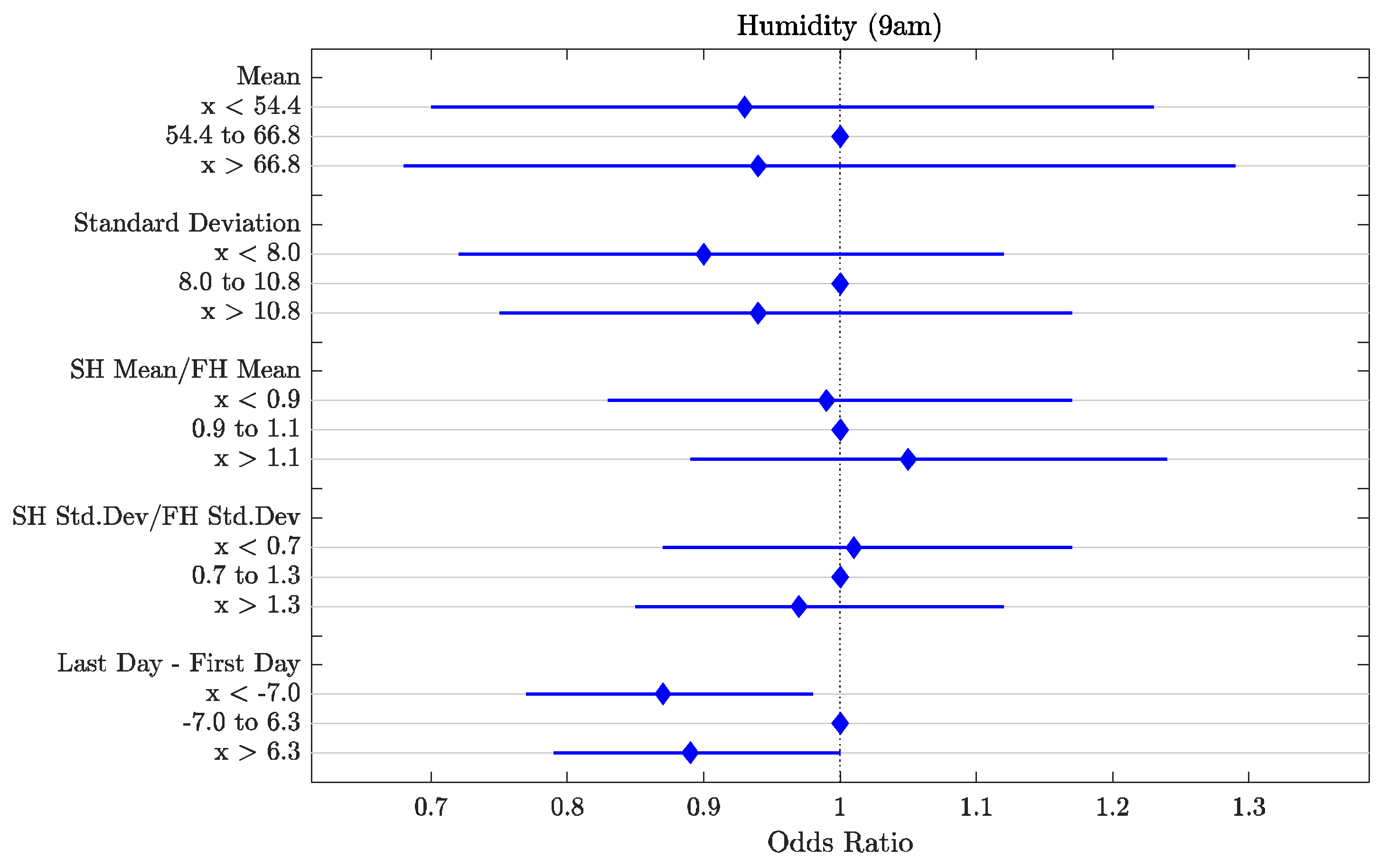
3.2. Environmental Variable Features
4. Discussion
4.1. Production Parameters
4.2. Environmental Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bray, H.J.; Ankeny, R.A. Happy Chickens Lay Tastier Eggs: Motivations for Buying Free-range Eggs in Australia. Anthrozoös 2017, 30, 213–226. [Google Scholar] [CrossRef]
- Pettersson, I.C.; Weeks, C.A.; Wilson, L.R.M.; Nicol, C.J. Consumer perceptions of free-range laying hen welfare. Br. Food J. 2016, 118, 1999–2013. [Google Scholar] [CrossRef]
- AustralianEggs. Annual Report 2024. 2024. Available online: https://www.australianeggs.org.au/who-we-are/annual-reports (accessed on 26 March 2025).
- Nicol, C.J.; Potzsch, C.; Lewis, K.; Green, L.E. Matched concurrent case-control study of risk factors for feather pecking in hens on free-range commercial farms in the UK. Br. Poult. Sci. 2003, 44, 515–523. [Google Scholar] [CrossRef]
- Koch, G.; Elbers, A.R.W. Outdoor ranging of poultry: A major risk factor for the introduction and development of High-Pathogenicity Avian Influenza. Wagen. J. Life Sci. 2021, 54, 179–194. [Google Scholar] [CrossRef]
- Bestman, M.; Bikker-Ouwejan, J. Predation in Organic and Free-Range Egg Production. Animals 2020, 10, 177. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, Y.K.; Lee, S.D.; Lee, K.W. Impact of relative humidity on the laying performance, egg quality, and physiological stress responses of laying hens exposed to high ambient temperature. J. Therm. Biol. 2022, 103, 103167. [Google Scholar] [CrossRef]
- Abdelqader, A.; Irshaid, R.; Al-Fataftah, A.R. Effects of dietary probiotic inclusion on performance, eggshell quality, cecal microflora composition, and tibia traits of laying hens in the late phase of production. Trop. Anim. Health Prod. 2013, 45, 1017–1024. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Yan, T.; Wang, X.; Kuang, S.; Xiao, Y.; Lu, W.; Bi, D. Probiotic mixture ameliorates heat stress of laying hens by enhancing intestinal barrier function and improving gut microbiota. Ital. J. Anim. Sci. 2016, 16, 292–300. [Google Scholar] [CrossRef]
- Nagle, T.A.; Glatz, P.C. Free range hens use the range more when the outdoor environment is enriched. Asian-Australas. J. Anim. Sci. 2012, 25, 584–591. [Google Scholar] [CrossRef]
- AustralianEggs. Available online: https://www.australianeggs.org.au/farming/egg-quality-standards (accessed on 11 September 2024).
- Zhai, Z.; Zhang, J.; Chai, X.; Kong, F.; Wu, J.; Zhang, J.; Han, S. A laying hen breeding environment monitoring system based on internet of things. IOP Conf. Ser. Earth Environ. Sci. 2019, 371, 032039. [Google Scholar]
- BigDutchman. NATURA® Step and Step XL Aviary Systems; BigDutchman: Holland, MI, USA, 2023; Available online: https://www.bigdutchmanusa.com/wp-content/uploads/2023/04/NATURA%C2%AE-Step-and-Step-XL_Eng.pdf (accessed on 24 March 2025).
- FarmMark. Aviary PRO11; FarmMark: Queensland, Australia, 2023. [Google Scholar]
- Morales, I.R.; Cebrián, D.R.; Blanco, E.F.; Sierra, A.P. Early warning in egg production curves from commercial hens: A SVM approach. Comput. Electron. Agric. 2016, 121, 169–179. [Google Scholar] [CrossRef]
- Gonzalez-Mora, A.F.; Rousseau, A.N.; Larios, A.D.; Godbout, S.; Fournel, S. Assessing environmental control strategies in cage-free aviary housing systems: Egg production analysis and Random Forest modeling. Comput. Electron. Agric. 2022, 196, 106854. [Google Scholar] [CrossRef]
- Omomule, T.G.; Ajayi, O.O.; Orogun, A.O. Fuzzy prediction and pattern analysis of poultry egg production. Comput. Electron. Agric. 2020, 171, 105301. [Google Scholar] [CrossRef]
- Fossum, O.; Jansson, D.S.; Etterlin, P.E.; Vagsholm, I. Causes of mortality in laying hens in different housing systems in 2001 to 2004. Acta Vet. Scand. 2009, 51, 3. [Google Scholar] [CrossRef] [PubMed]
- Sherwin, C.M.; Richards, G.J.; Nicol, C.J. Comparison of the welfare of layer hens in 4 housing systems in the UK. Br. Poult. Sci. 2010, 51, 488–499. [Google Scholar] [CrossRef]
- Bryden, W.L.; Li, X.; Ruhnke, I.; Zhang, D.; Shini, S. Nutrition, feeding and laying hen welfare. Anim. Prod. Sci. 2021, 61, 893–914. [Google Scholar] [CrossRef]
- PoultryHub. Nutrient Requirements of Egg Laying Chickens. 2024. Available online: https://www.poultryhub.org/all-about-poultry/nutrition/nutrient-requirements-of-egg-laying-chickens (accessed on 14 August 2024).
- Howard, B.R. Water balance of the hen during egg formation. Poult. Sci. 1975, 54, 1046–1053. [Google Scholar] [CrossRef]
- Wasti, S.; Sah, N.; Mishra, B. Impact of Heat Stress on Poultry Health and Performances, and Potential Mitigation Strategies. Animals 2020, 10, 1266. [Google Scholar] [CrossRef]
- Donkoh, A. Ambient temperature: A factor affecting performance and physiological response of broiler chickens. Int. J. Biometeorol. 1989, 33, 259–265. [Google Scholar] [CrossRef]
- Reece, F.; Deaton, J. Use of evaporative cooling for broiler chicken production in areas of high relative humidity. Poult. Sci. 1971, 50, 100–104. [Google Scholar] [CrossRef]
- Kim, H.R.; Ryu, C.; Lee, S.D.; Cho, J.H.; Kang, H. Effects of Heat Stress on the Laying Performance, Egg Quality, and Physiological Response of Laying Hens. Animals 2024, 14, 1076. [Google Scholar] [CrossRef] [PubMed]
- Sampaio, F.B.G.; Passerino, A.S.; Kozicki, L.E.; Weber, S.; Teixeira, V.N.; Pereira, J.F.S.; Segui, M.S. Effect of temperature, air humidity, and rainfall on the reproductive season of Rhea americana (Linaeus, 1758) at latitude 25°S. Der Zoologische Garten 2015, 84, 127–134. [Google Scholar] [CrossRef]
- Rana, M.S.; Lee, C.; Lea, J.M.; Campbell, D.L.M. Relationship between sunlight and range use of commercial free-range hens in Australia. PLoS ONE 2022, 17, e0268854. [Google Scholar] [CrossRef]
- Pyrzak, R.; Snapir, N.; Goodman, G.; Perek, M. The effect of light wavelength on the production and quality of eggs of the domestic hen. Theriogenology 1987, 28, 947–960. [Google Scholar] [CrossRef]
- Hardin, J.W.; Hilbe, J.M. Generalized Estimating Equations; Chapman and Hall/CRC: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Cummins, C.; Welch, M.; Inkster, B.; Cupples, B.; Weaving, D.; Jones, B.; King, D.; Murphy, A. Modelling the relationships between volume, intensity and injury-risk in professional rugby league players. J. Sci. Med. Sport 2019, 22, 653–660. [Google Scholar] [CrossRef] [PubMed]
- Jaspers, A.; Kuyvenhoven, J.P.; Staes, F.; Frencken, W.G.P.; Helsen, W.F.; Brink, M.S. Examination of the external and internal load indicators’ association with overuse injuries in professional soccer players. J. Sci. Med. Sport 2018, 21, 579–585. [Google Scholar] [CrossRef]
- Ratcliffe, S.J.; Shults, J. GEEQBOX: A MATLAB toolbox for generalized estimating equations and quasi-least squares. J. Stat. Softw. 2008, 25, 1–14. [Google Scholar] [CrossRef]
- The MathWorks, Inc. MATLAB, version 9.6.0.1114505 (R2019a); The MathWorks, Inc.: Natick, MA, USA, 2019. [Google Scholar]
- Bland, J.M.; Altman, D.G. The odds ratio. BMJ 2000, 320, 1468. [Google Scholar] [CrossRef]
- Petek, M.; Alpay, F.; Gezen, S.S.; Çibik, R. Effects of Housing System and Age on Early Stage Egg Production and Quality in Commercial Laying Hens. Kafkas Univ. Vet. Fak. Derg. 2009, 15, 57–62. [Google Scholar]
- Li, Y.; Ito, T.; Nishibori, M.; Yamamoto, S. Effects of environmental temperature on heat production associated with food intake and on abdominal temperature in laying hens. Br. Poult. Sci. 1992, 33, 113–122. [Google Scholar] [CrossRef]
- Grimes, T.; Reece, R. Spotty liver disease–an emerging disease in free-range egg layers in Australia. In Proceedings of the Sixtieth Western Poultry Disease Conference, Sacramento, CA, USA, 20–23 March 2011. [Google Scholar]
- Crawshaw, T. A review of the novel thermophilic Campylobacter, Campylobacter hepaticus, a pathogen of poultry. Transbound Emerg. Dis. 2019, 66, 1481–1492. [Google Scholar] [CrossRef] [PubMed]
- Li, G.M.; Liu, L.P.; Yin, B.; Liu, Y.Y.; Dong, W.W.; Gong, S.; Zhang, J.; Tan, J.H. Heat stress decreases egg production of laying hens by inducing apoptosis of follicular cells via activating the FasL/Fas and TNF-alpha systems. Poult. Sci. 2020, 99, 6084–6093. [Google Scholar] [CrossRef]
- Wu, X.; Zheng, B.; Mei, Z.; Yu, C.; Song, Z.; Sheng, Z.; Gong, Y. Key parameters of physiological responses to acute heat stress in two commercial layers determined by Fisher discriminant analyses. J. Therm. Biol. 2023, 117, 103694. [Google Scholar] [CrossRef]
- Kim, D.H.; Song, J.Y.; Park, J.; Kwon, B.Y.; Lee, K.W. The Effect of Low Temperature on Laying Performance and Physiological Stress Responses in Laying Hens. Animals 2023, 13, 3824. [Google Scholar] [CrossRef] [PubMed]
- Paura, L.; Arhipova, I.; Jankovska, L.; Bumanis, N.; Vitols, G.; Adjutovs, M. Evaluation and association of laying hen performance, environmental conditions and gas concentrations in barn housing system. Ital. J. Anim. Sci. 2022, 21, 694–701. [Google Scholar] [CrossRef]
- de Oliveira, E.M.; de Oliveira, L.Q.M.; do Nascimento Mós, J.V.; Teixeira, B.E.; Nascimento, S.T.; dos Santos, V.M. Solar radiation limits the use of paddocks by laying hens raised in the free-range system. Trop. Anim. Health Prod. 2022, 54, 181. [Google Scholar] [CrossRef]
- Yahav, S.; Shinder, D.; Razpakovski, V.; Rusal, M.; Bar, A. Lack of response of laying hens to relative humidity at high ambient temperature. Br. Poult. Sci. 2000, 41, 660–663. [Google Scholar] [CrossRef]



| Parameter | Unit | Summary of Justification | Reference |
|---|---|---|---|
| Laying rate | % | Indicates productivity | [15] |
| Mortality rate | % | Indicates disease incidence or management problems | [18,19] |
| Feed intake/hen/day | g | Influences the nutrient intake and egg production | [20,21] |
| Water intake/hen/day | mL | Needed for metabolic processes and egg production | [22] |
| Indoor minimum/maximum temperature | °C | Affects egg production and hen health | [23,24] |
| Relative humidity 9 a.m./3 p.m. | % | Influences hen performance | [7,25] |
| Outdoor minimum/maximum temperature | °C | Affects egg production | [26] |
| Precipitation | mm/day | Influences egg production and weight | [27] |
| Solar radiation | MJ/m2/day | Influences egg production and range use | [28,29] |
| Variable | Feature | Group | Odds Ratio | p-Value |
|---|---|---|---|---|
| Laying Rate (%) | SH:FH Mean Ratio | x > 1.0 | 0.82 | 0.03 |
| Laying Rate (%) | Last Day–First Day | x > 1.1 | 0.88 | 0.03 |
| Feed Intake (g) | SH:FH Mean Ratio | x > 1.0 | 0.81 | 0.01 |
| Feed Intake (g) | Mean | x < 113 | 1.28 | 0.00 |
| Water Intake (mL) | SH Std. Dev.:SH Std. Dev. Ratio | x< 0.7 | 1.18 | 0.04 |
| Mortality (%) | Mean | x < 5.0 | 1.32 | 0.04 |
| Variable | Feature | Group | Odds Ratios | p-Value |
|---|---|---|---|---|
| Outdoor Minimum Temperature (%) | Last Day–First Day | x < −1.9 | 1.14 | 0.02 |
| Indoor Minimum Temperature (%) | Mean | x < 16.1 | 1.38 | 0.04 |
| Solar Radiation (MJ/m2/day) | SH:FH Mean Ratio | x > 1.1 | 0.84 | 0.04 |
| Solar Radiation (MJ/m2/day) | SH Std. Dev.:SH Std. Dev. Ratio | x < 0.7 | 1.21 | 0.03 |
| Precipitation (mm/day) | Std. Deviation | x < 0.5 | 0.64 | 0.04 |
| Humidity (9 a.m.) (%) | Last Day–First Day | x < −0.7 | 0.87 | 0.02 |
| Humidity (9 a.m.) (%) | Last Day–First Day | x > 0.63 | 0.89 | 0.04 |
| Humidity (3 p.m.) (%) | SH:FH Mean Ratio | x < 0.9 | 0.77 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adejola, Y.A.; Sibanda, T.Z.; Ruhnke, I.; Boshoff, J.; Pokhrel, S.; Welch, M. Analyzing the Risk of Short-Term Losses in Free-Range Egg Production Using Commercial Data. Agriculture 2025, 15, 743. https://doi.org/10.3390/agriculture15070743
Adejola YA, Sibanda TZ, Ruhnke I, Boshoff J, Pokhrel S, Welch M. Analyzing the Risk of Short-Term Losses in Free-Range Egg Production Using Commercial Data. Agriculture. 2025; 15(7):743. https://doi.org/10.3390/agriculture15070743
Chicago/Turabian StyleAdejola, Yusuf Adewale, Terence Zimazile Sibanda, Isabelle Ruhnke, Johan Boshoff, Saluna Pokhrel, and Mitchell Welch. 2025. "Analyzing the Risk of Short-Term Losses in Free-Range Egg Production Using Commercial Data" Agriculture 15, no. 7: 743. https://doi.org/10.3390/agriculture15070743
APA StyleAdejola, Y. A., Sibanda, T. Z., Ruhnke, I., Boshoff, J., Pokhrel, S., & Welch, M. (2025). Analyzing the Risk of Short-Term Losses in Free-Range Egg Production Using Commercial Data. Agriculture, 15(7), 743. https://doi.org/10.3390/agriculture15070743







