Study on Predicting Blueberry Hardness from Images for Adjusting Mechanical Gripper Force
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Field
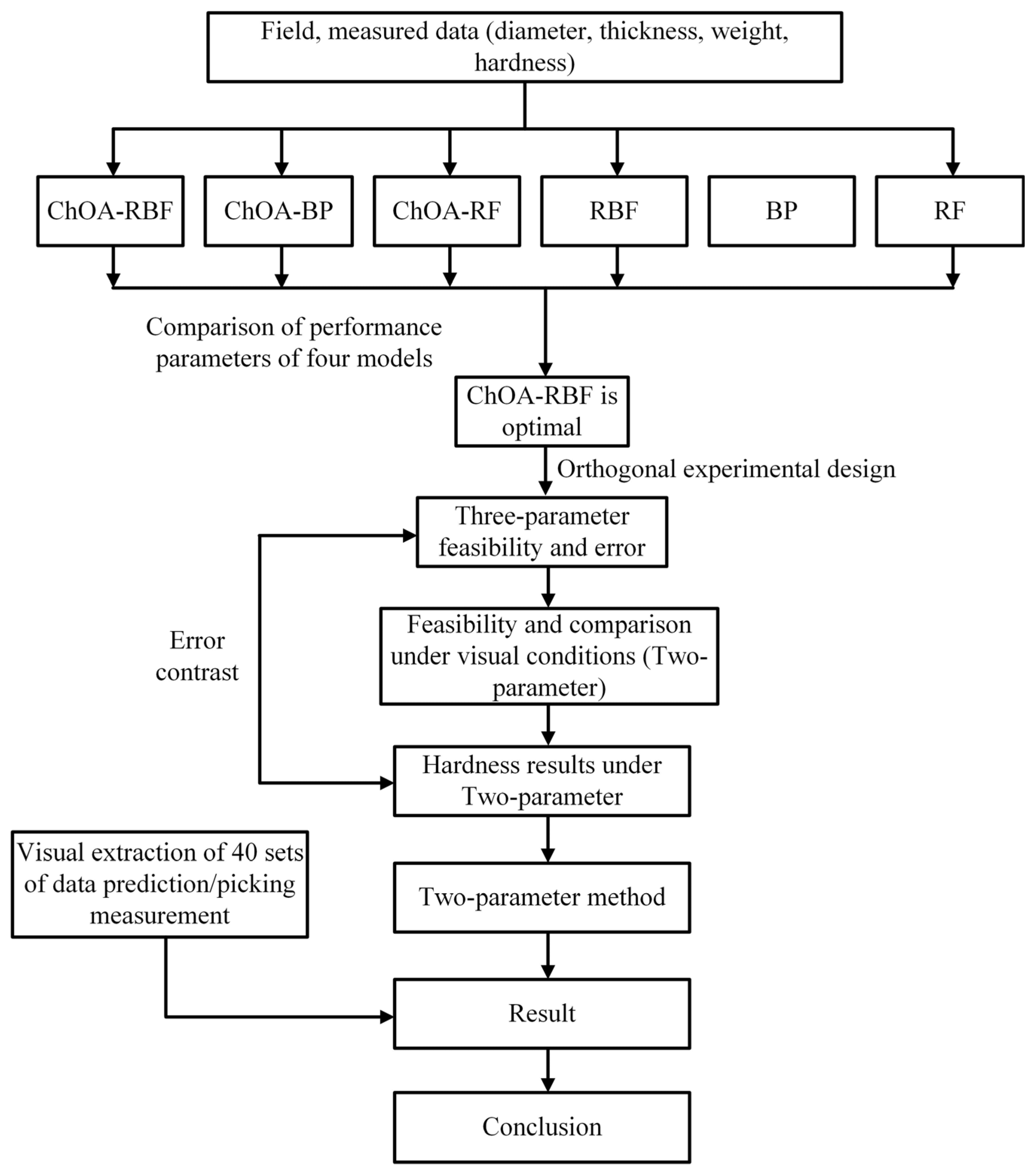
2.2. Design Plan
2.2.1. Analysis of Method Rationality
2.2.2. Research Process
2.3. Analytical Methods
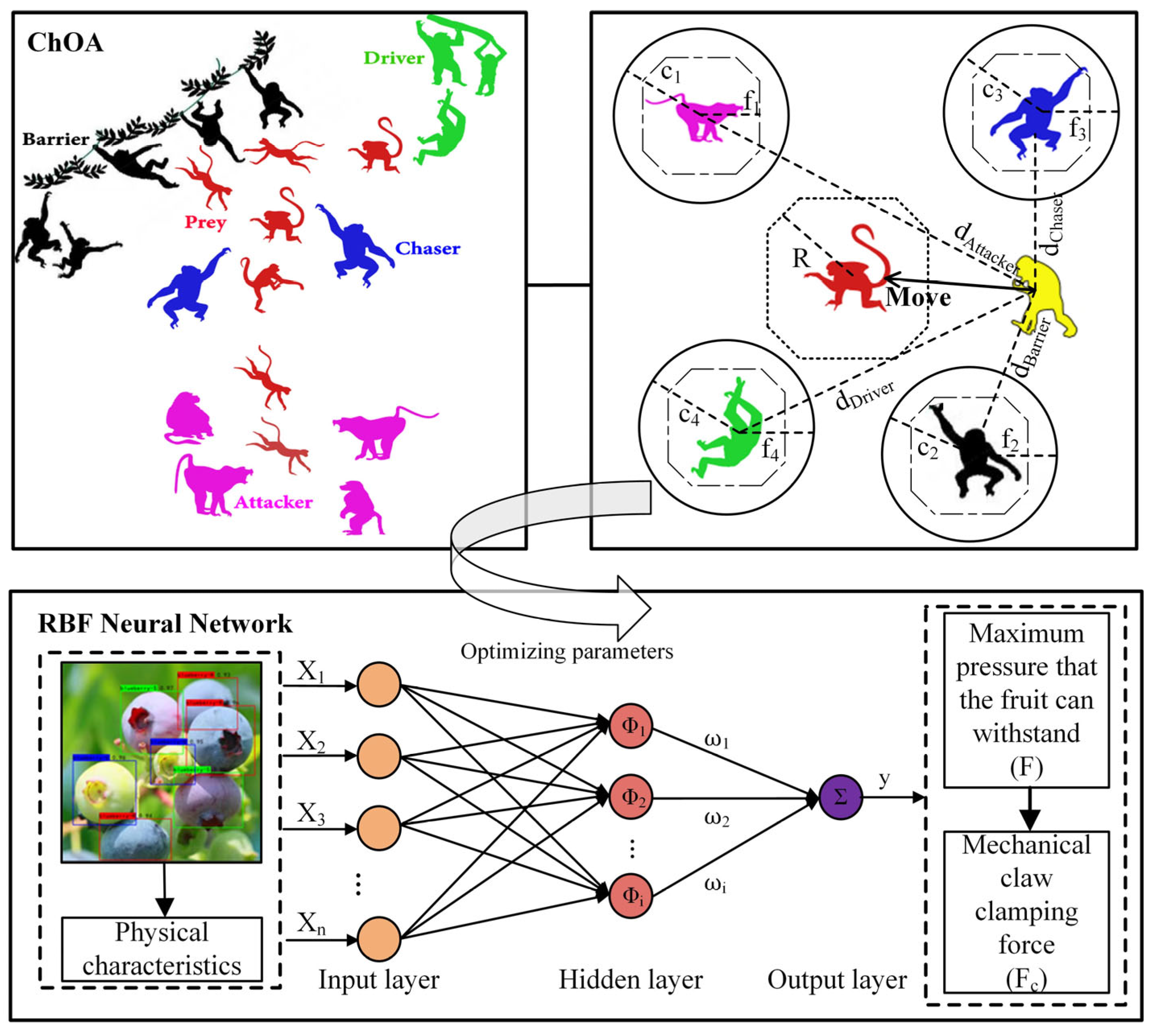
2.3.1. Prediction Model
- 1.
- Driving and Chasing the Prey
- 2.
- Attack
- 3.
- Social Motivation
- 4.
- RBF Prediction Model
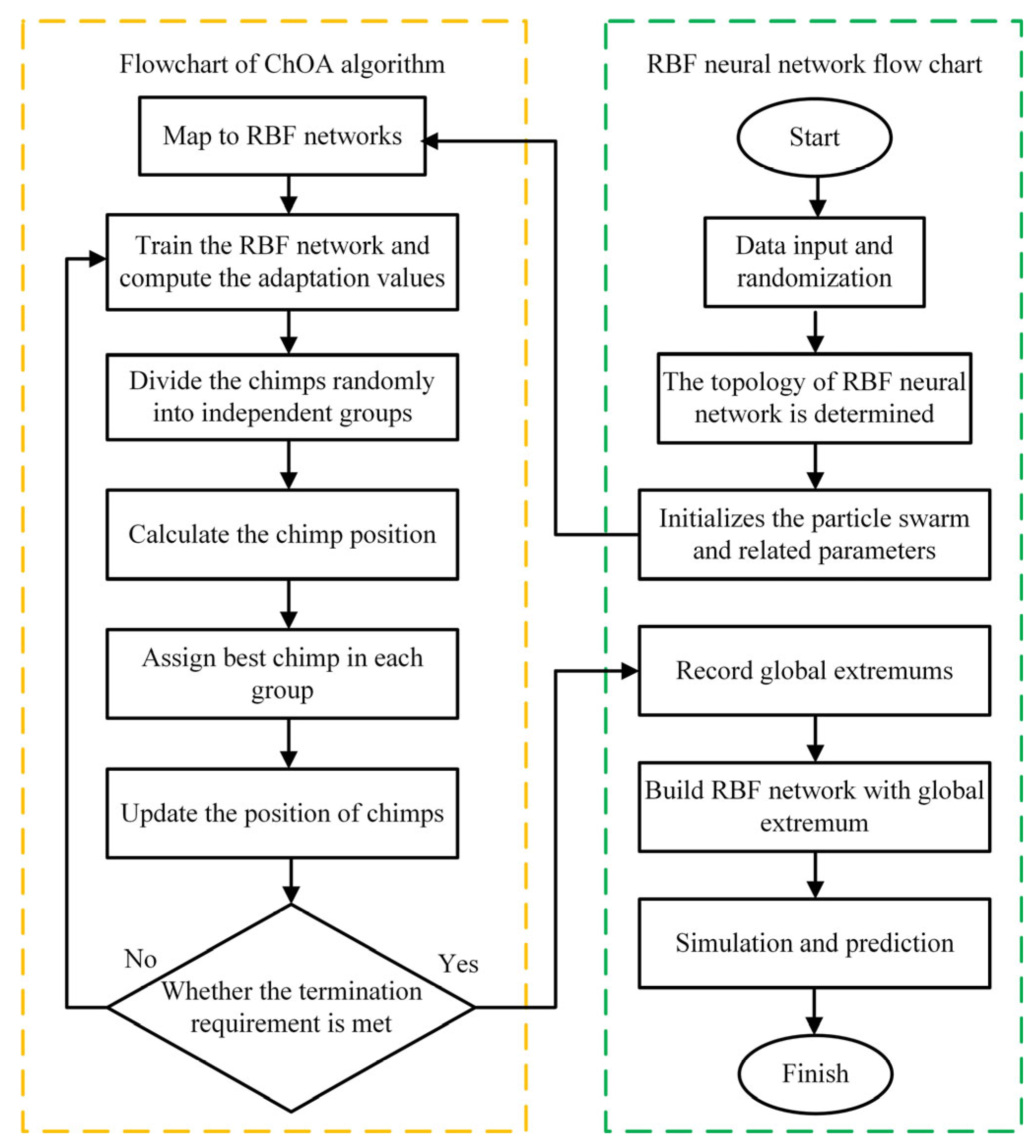
2.3.2. Algorithm Flow
2.3.3. Model Construction and Evaluation
2.3.4. Modeling the Relationship Between Fruit Hardness and Mechanical Gripper Force
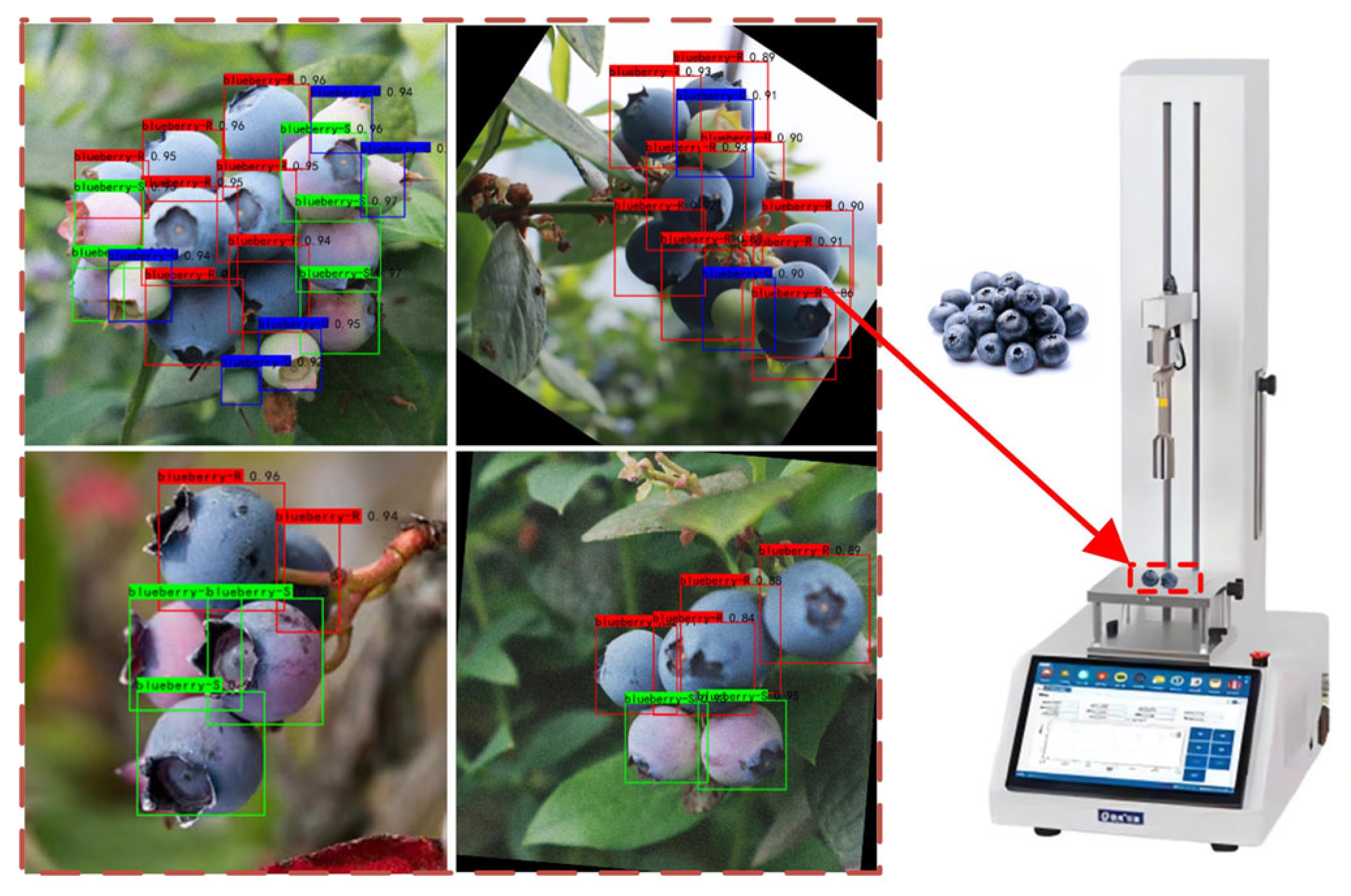
2.4. Visual Recognition and Experimental Design
3. Results and Discussion
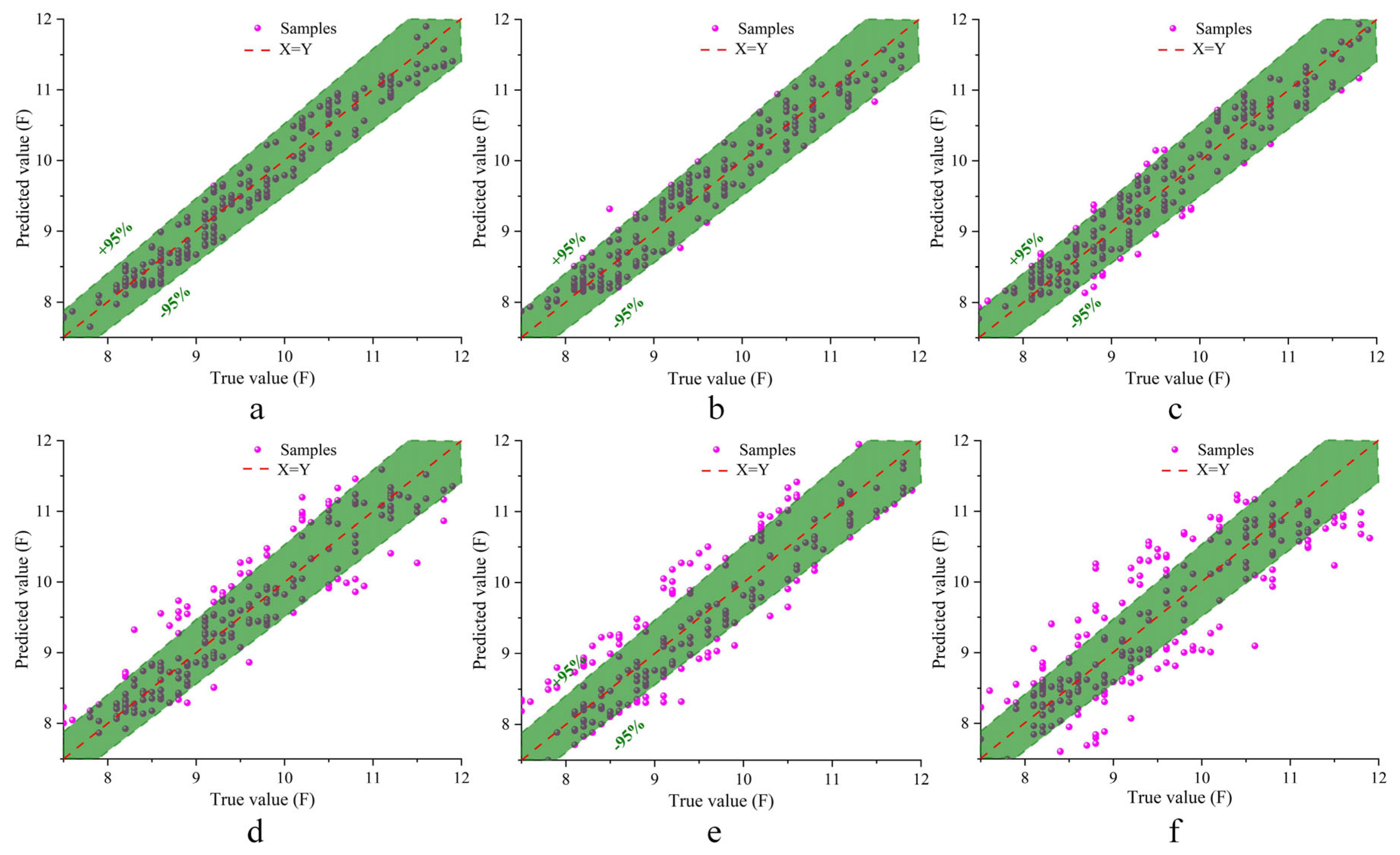
3.1. Model Prediction Results
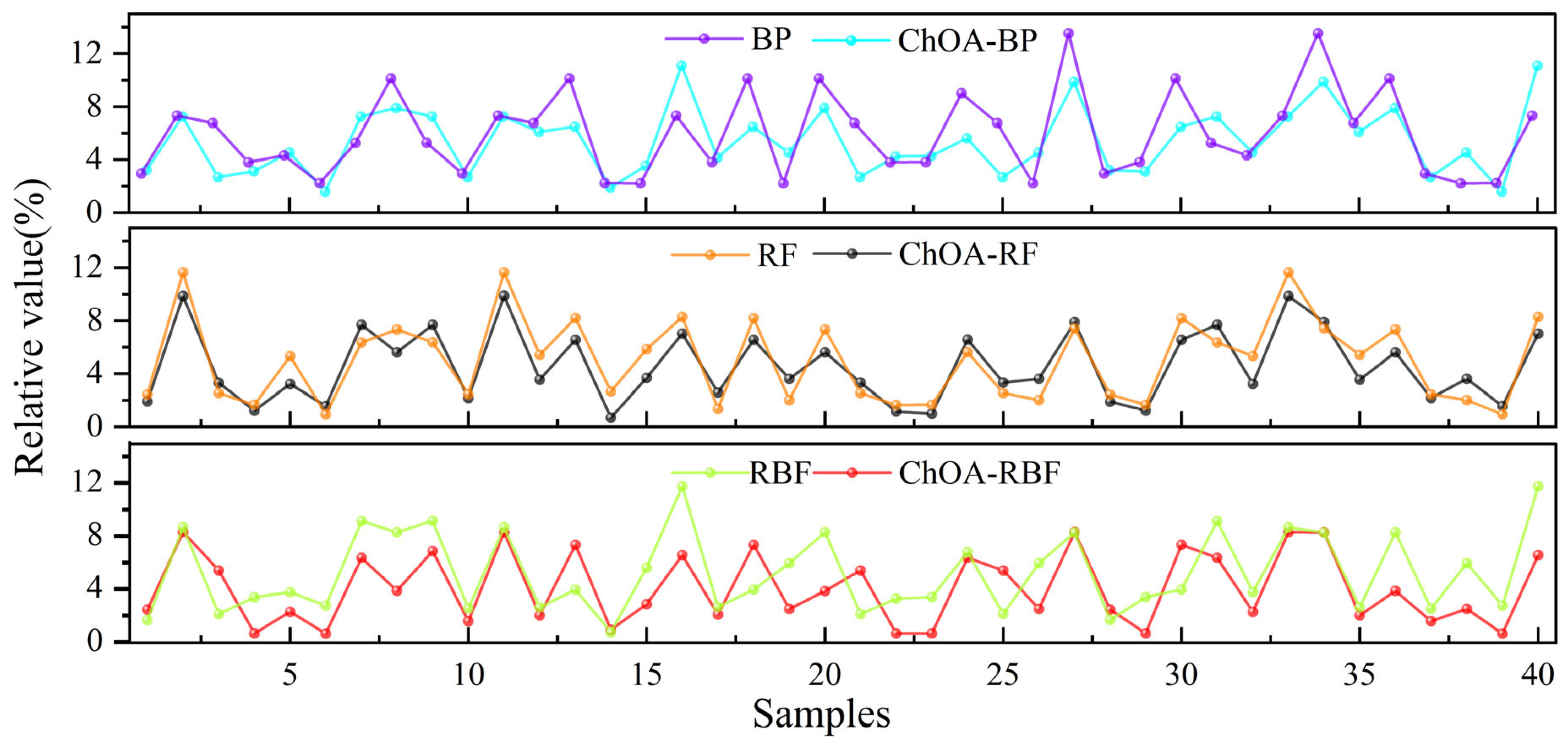
3.1.1. Results and Analysis
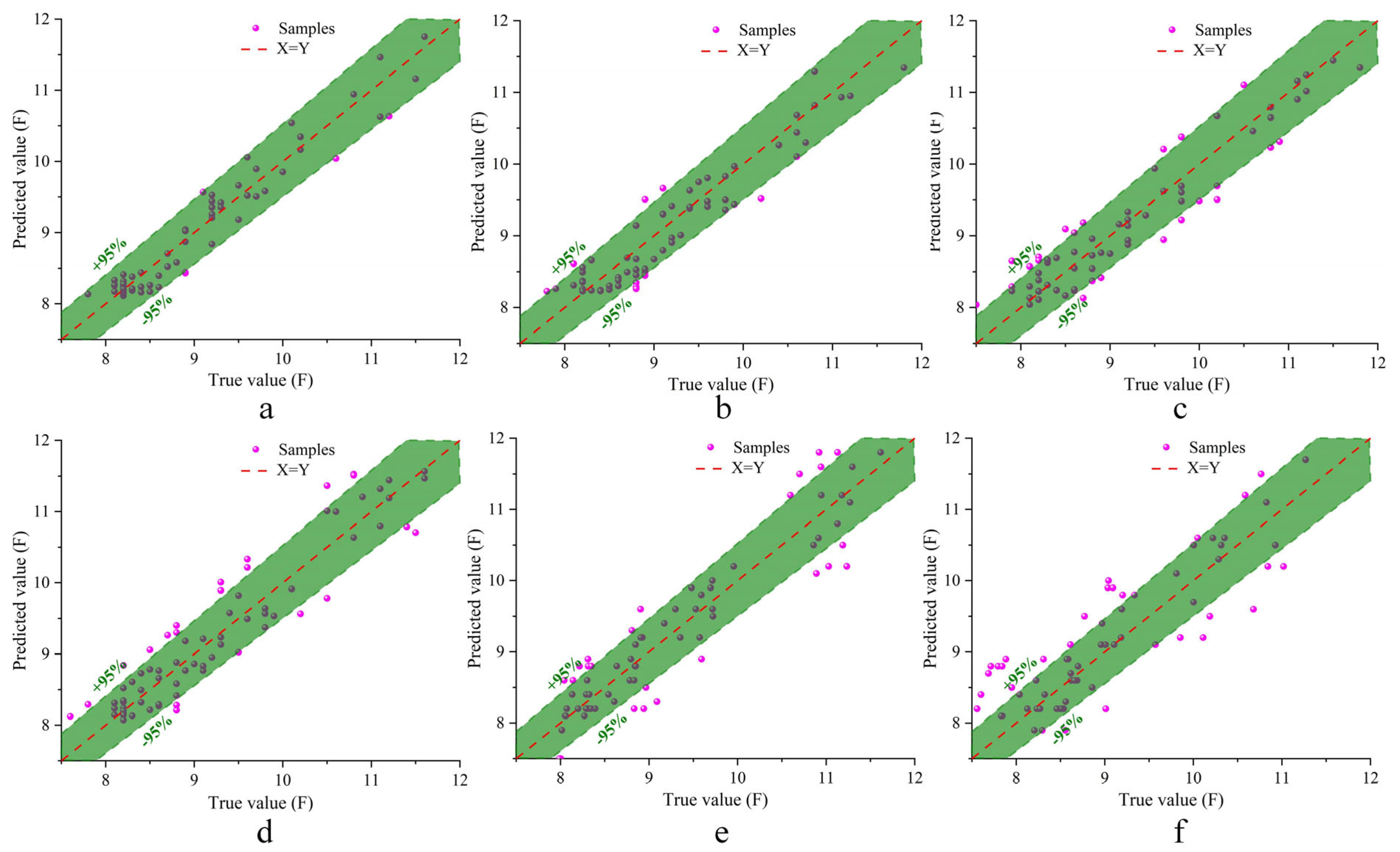
3.1.2. Orthogonal Test Validation
3.2. Two-Parameter Method
3.2.1. Design Principles
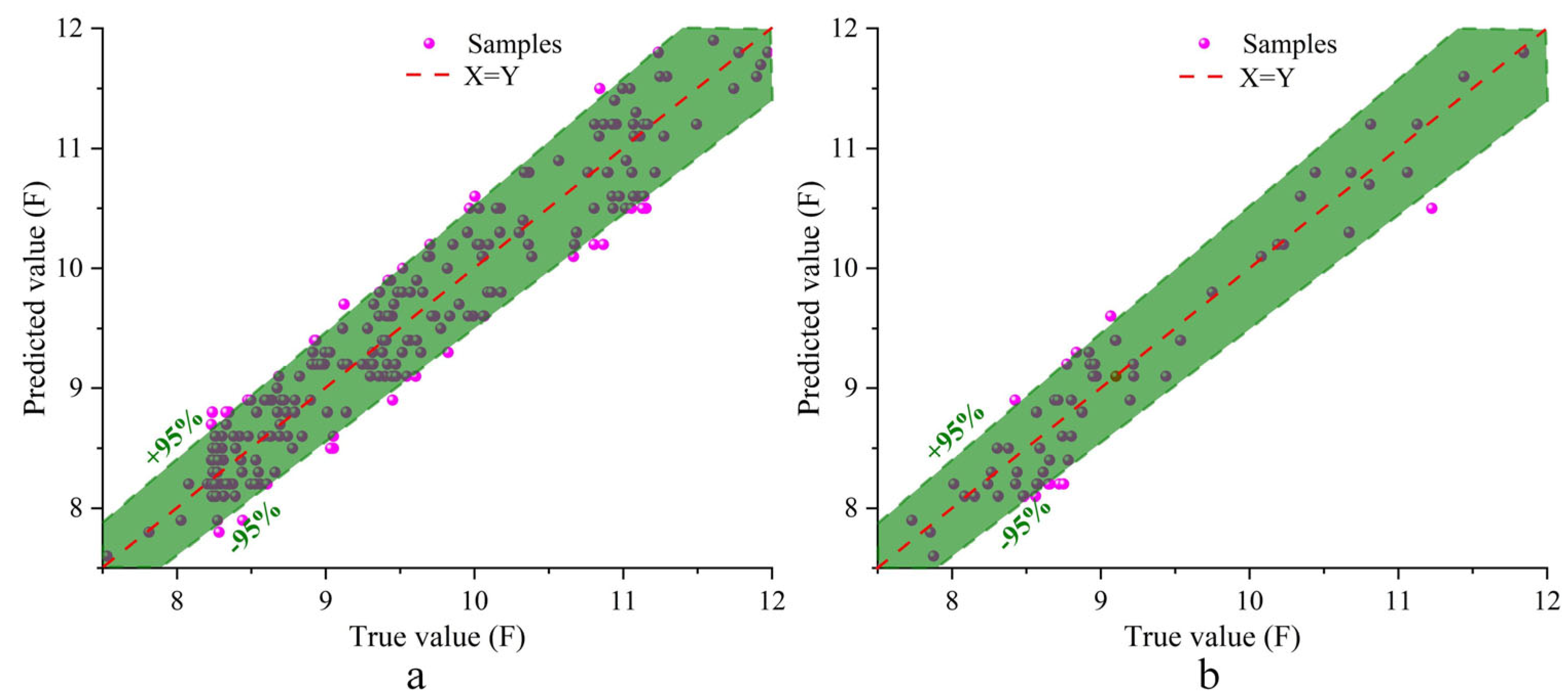
3.2.2. Prediction Results and Validation
3.3. Model Recognition and Application
4. Discussion
5. Conclusions
- 1.
- A New Approach for Predicting Fruit Hardness: A novel method is proposed to directly extract the fruit’s pressure resistance from the blueberry image, identifying the correlation between fruit color and hardness. By predicting the hardness, the gripping force of the mechanical claw can be adjusted. Calculations and experiments demonstrate that this design is feasible and can improve harvesting efficiency while preventing fruit damage.
- 2.
- Mapping Physical Properties to Hardness Using the ChOA-RBF Model: The ChOA-RBF model is applied to establish the mapping relationship between physical properties and hardness, compared with RBF, BP, and RF models from different angles. Evaluation metrics and error plots indicate that the ChOA-RBF model has significant advantages in fruit hardness prediction. Orthogonal experiments confirm that the maximum error of this model does not exceed 5%.
- 3.
- Two-Parameter Method as a Practical Solution: Considering the limitations of the visual recognition device and practical operational applications, a two-parameter method is proposed as an alternative. Though the R2 value and some parameters slightly decrease, the actual prediction error remains under 8%. Furthermore, the method results in faster execution speed and higher harvesting efficiency in practical applications.
- 4.
- By comparing the model recognition results with the actual test results, it was found that there is some discrepancy, which is caused by slight errors in the parameters extracted by the recognition device. However, the final result shows that the maximum relative error is less than 8%, with an average relative error of 3.91%, which is acceptable within the error range considering the safety factor of 1.3.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Silva, S.; Costa, E.M.; Veiga, M.; Morais, R.M.; Calhau, C.; Pintado, M. Health promoting properties of blueberries: A review. Crit. Rev. Food Sci. Nutr. 2020, 60, 181–200. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Zang, H.; Guo, X.; Li, S.; Xin, X.; Li, Y. A systematic study on composition and antioxidant of 6 varieties of highbush blueberries by 3 soil matrixes in China. Food Chem. 2025, 472, 142974. [Google Scholar] [CrossRef]
- DeVetter, L.W.; Yang, W.Q.; Takeda, F.; Chen, J. Harvesting Blueberries: A Guide to Machine Pick Blueberries for Fresh Market; Washington State University: Spokane, WA, USA, 2022. [Google Scholar] [CrossRef]
- Takeda, F.; Yang, W.Q.; Li, C.; Freivalds, A.; Sung, K.; Xu, R.; Hu, B.; Williamson, J.; Sargent, S. Applying New Technologies to Transform Blueberry Harvesting. Agronomy 2017, 7, 33. [Google Scholar] [CrossRef]
- Cappai, F.; Amadeu, R.R.; Benevenuto, J.; Cullen, R.; Garcia, A.; Grossman, A.; Ferrao, L.F.V.; Munoz, P. High-Resolution Linkage Map and QTL Analyses of Fruit Firmness in Autotetraploid Blueberry. Front. Plant Sci. 2020, 11, 562171. [Google Scholar] [CrossRef]
- Arak, M.; Soots, K.; Starast, M.; Olt, J. Mechanical properties of blueberry stems. Res. Agric. Eng. 2018, 64, 202–208. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, L.; Zhao, J.; Hang, X.; Zhou, H. Effective excitation conditions for the intense motion of the ginkgo seed-stem system during mechanical vibration harvesting. Biosyst. Eng. 2022, 215, 239–248. [Google Scholar] [CrossRef]
- Freitas Grupioni, C.M.; Santos, F.L.; Velloso, N.S.; Magalhães Valente, D.S.; Assis de Carvalho Pinto, F. Macaw palm supply chain: Evaluation of a semi-mechanized fruit harvesting system. Ind. Crops Prod. 2020, 151, 112444. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, H.; Zhang, Y.; Zhang, Q.; Chen, H.; Xu, X.; Wang, G. “Is this blueberry ripe?”: A blueberry ripeness detection algorithm for use on picking robots. Front. Plant Sci. 2023, 14, 1198650. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, D.; Guo, X.; Yang, H. Lightweight Algorithm for Apple Detection Based on an Improved YOLOv5 Model. Plants 2023, 12, 3032. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, K.; Zhai, S.; Zhang, D.; Liu, L.; Zhao, J.; Long, Y.; Cui, Y. Design of an Apple-Picking End Effector. J. Mech. Eng./Stroj. Vestn. 2018, 64, 216. [Google Scholar] [CrossRef]
- Zhou, Q.; Gao, R.; Ma, Z.; Cao, G.; Chen, J. Research on system integration and control methods of an apple-picking robot in unstructured environment. Ind. Robot. Int. J. Robot. Res. Appl. 2024, 51, 369–379. [Google Scholar] [CrossRef]
- Bu, L.; Chen, C.; Hu, G.; Sugirbay, A.; Sun, H.; Chen, J. Design and evaluation of a robotic apple harvester using optimized picking patterns. Comput. Electron. Agric. 2022, 198, 107092. [Google Scholar] [CrossRef]
- Hu, M.-H.; Dong, Q.-L.; Liu, B.-L.; Opara, U.L.; Chen, L. Estimating blueberry mechanical properties based on random frog selected hyperspectral data. Postharvest Biol. Technol. 2015, 106, 1–10. [Google Scholar] [CrossRef]
- Oh, H.; Stapleton, L.; Giongo, L.; Johanningsmeier, S.; Mollinari, M.; Mainland, C.M.; Perkins-Veazie, P.; Iorizzo, M. Prediction of blueberry sensory texture attributes by integrating multiple instrumental measurements. Postharvest Biol. Technol. 2024, 218, 113160. [Google Scholar] [CrossRef]
- Yang, W.; Ma, X.; Hu, W.; Tang, P. Lightweight Blueberry Fruit Recognition Based on Multi-Scale and Attention Fusion NCBAM. Agronomy 2022, 12, 2354. [Google Scholar] [CrossRef]
- Montanaro, G.; Dichio, B.; Xiloyannis, C.; Lang, A. Fruit transpiration in kiwifruit: Environmental drivers and predictive model. AoB Plants 2012, 2012, pls036. [Google Scholar] [CrossRef]
- Zhai, Y.; Liang, Z.; Xu, S.; Huang, C.; Zhou, X.; Li, M.; Huang, Y. Machine learning based blueberry detection method by CIE-YOLOv5. Proc. SPIE 2024, 13105, 131051U. [Google Scholar] [CrossRef]
- Gai, R.; Liu, Y.; Xu, G. TL-YOLOv8: A Blueberry Fruit Detection Algorithm Based on Improved YOLOv8 and Transfer Learning. IEEE Access 2024, 12, 86378–86390. [Google Scholar] [CrossRef]
- Xu, H.; Li, Q.; Chen, J. Highlight Removal from A Single Grayscale Image Using Attentive GAN. Appl. Artif. Intell. 2022, 36, 1988441. [Google Scholar] [CrossRef]
- Zhuang, J.; Chen, W.; Guo, B.; Yan, Y. Infrared Weak Target Detection in Dual Images and Dual Areas. Remote Sens. 2024, 16, 3608. [Google Scholar] [CrossRef]
- Gholipoor, M.; Nadali, F. Fruit yield prediction of pepper using artificial neural network. Sci. Hortic. 2019, 250, 249–253. [Google Scholar] [CrossRef]
- Aherwadi, N.; Mittal, U.; Singla, J.; Jhanjhi, N.Z.; Yassine, A.; Hossain, M.S. Prediction of Fruit Maturity, Quality, and Its Life Using Deep Learning Algorithms. Electronics 2022, 11, 4100. [Google Scholar] [CrossRef]
- Qiao, J.; Guo, M.; Wu, Y.; Gao, J.; Yue, Z. Research on Strawberry Cold Chain Transportation Quality Perception Method Based on BP Neural Network. Appl. Sci. 2022, 12, 8872. [Google Scholar] [CrossRef]
- Lin, H.; Song, X.; Dai, F.; Zhang, F.; Xie, Q.; Chen, H. Research on Machine Learning Models for Maize Hardness Prediction Based on Indentation Test. Agriculture 2024, 14, 224. [Google Scholar] [CrossRef]
- Rocha, H.; Dias, J.M. Early prediction of durum wheat yield in Spain using radial basis functions interpolation models based on agroclimatic data. Comput. Electron. Agric. 2019, 157, 427–435. [Google Scholar] [CrossRef]
- Chen, H.; Liang, Y.; Huang, H.; Huang, Q.; Gu, W.; Liang, H. Live Pig-Weight Learning and Prediction Method Based on a Multilayer RBF Network. Agriculture 2023, 13, 253. [Google Scholar] [CrossRef]
- Li, J.; Cheng, J.-H.; Shi, J.-Y.; Huang, F. Brief Introduction of Back Propagation (BP) Neural Network Algorithm and Its Improvement. In Advances in Computer Science and Information Engineering; Springer: Berlin/Heidelberg, Germany, 2012; pp. 553–558. [Google Scholar] [CrossRef]
- Pang, A.; Chang, M.W.; Chen, Y. Evaluation of Random Forests (RF) for Regional and Local-Scale Wheat Yield Prediction in Southeast Australia. Sensors 2022, 22, 717. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Lu, L.; Ding, J.; Zhang, F.; He, B. Estimating Fractional Vegetation Cover of Row Crops from High Spatial Resolution Image. Remote Sens. 2021, 13, 3874. [Google Scholar] [CrossRef]
- Cai, J.; Ding, S.; Zhang, Q.; Liu, R.; Zeng, D.; Zhou, L. Broken ice circumferential crack estimation via image techniques. Ocean. Eng. 2022, 259, 111735. [Google Scholar] [CrossRef]
- Ma, X.; Ding, J.; Wang, T.; Lu, L.; Sun, H.; Zhang, F.; Cheng, X.; Nurmemet, I. A Pixel Dichotomy Coupled Linear Kernel-Driven Model for Estimating Fractional Vegetation Cover in Arid Areas From High-Spatial-Resolution Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Li, W.; Yin, H.; Li, Y.; Liu, X.; Liu, J.; Wang, H. Research on the Jet Distance Enhancement Device for Blueberry Harvesting Robots Based on the Dual-Ring Model. Agriculture 2024, 14, 1563. [Google Scholar] [CrossRef]
- Rivera, S.; Giongo, L.; Cappai, F.; Kerckhoffs, H.; Sofkova-Bobcheva, S.; Hutchins, D.; East, A. Blueberry firmness-A review of the textural and mechanical properties used in quality evaluations. Postharvest Biol. Technol. 2022, 192, 112016. [Google Scholar] [CrossRef]
- Rivera, S.; Hort, J.; Sofkova-Bobcheva, S.; Kerckhoffs, H.; Hutchins, D.; East, A. Instrumental mechanical parameters related to hand-feel touch firmness of blueberries. Postharvest Biol. Technol. 2023, 205, 112530. [Google Scholar] [CrossRef]
- Ban, S.; Tian, M.; Hu, D.; Xu, M.; Yuan, T.; Zheng, X.; Li, L.; Wei, S. Evaluation and Early Detection of Downy Mildew of Lettuce Using Hyperspectral Imagery. Agriculture 2025, 15, 444. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Daoud, M.S.; Shehab, M.; Abualigah, L.; Alshinwan, M.; Elaziz, M.A.; Shambour, M.K.Y.; Oliva, D.; Alia, M.A.; Zitar, R.A. Recent Advances of Chimp Optimization Algorithm: Variants and Applications. J. Bionic Eng. 2023, 20, 2840–2862. [Google Scholar] [CrossRef]
- Strumiłło, P.; Kamiński, W. Radial Basis Function Neural Networks: Theory and Applications. Neural Netw. Soft Comput. 2003, 19, 107–119. [Google Scholar] [CrossRef]
- Wang, Z.; Yin, H.; Li, W.; Li, Y.; Liu, J. Research on the Design Method of Blueberry Automatic Harvesting Clamp Force Based on Neural Networks. Appl. Eng. Agric. 2024, 40, 327–338. [Google Scholar] [CrossRef]




| Models | Evaluation Index | |||||||
|---|---|---|---|---|---|---|---|---|
| Training Set | Testing Set | |||||||
| RMSE | MAE | MBE | R2 | RMSE | MAE | MBE | R2 | |
| ChOA-RBF | 0.5963 | 0.4124 | 0.0184 | 0.8313 | 0.5490 | 0.4123 | −0.0120 | 0.7910 |
| ChOA-BP | 0.7238 | 0.5114 | 0.0487 | 0.6992 | 0.7206 | 0.4931 | 0.0651 | 0.6233 |
| ChOA-RF | 0.6223 | 0.4729 | 0.0201 | 0.7952 | 0.5573 | 0.5211 | −0.0146 | 0.7655 |
| RBF | 0.7117 | 0.4908 | −0.0283 | 0.7175 | 0.6709 | 0.5501 | −0.0153 | 0.5845 |
| BP | 0.7504 | 0.5963 | −0.0624 | 0.6693 | 0.8135 | 0.6384 | 0.0565 | 0.5778 |
| RF | 0.7265 | 0.5287 | 0.0517 | 0.6776 | 0.7637 | 0.4826 | 0.0634 | 0.7134 |
| No. | Diameter (mm) | Thickness (mm) | Weight (g) | Predicted Data (N) | Actual Data (N) | Absolute Error (N) | Relative Error (%) |
|---|---|---|---|---|---|---|---|
| 1 | 13.07 | 8.02 | 1.21 | 8.35 | 8.44 | −0.09 | −1.02 |
| 2 | 13.19 | 9.45 | 1.25 | 8.89 | 8.81 | 0.08 | 0.89 |
| 3 | 13.31 | 9.56 | 1.28 | 8.37 | 8.28 | 0.09 | 1.03 |
| 4 | 13.54 | 9.56 | 1.31 | 8.76 | 8.63 | 0.13 | 1.47 |
| 5 | 14.52 | 11.02 | 1.58 | 9.00 | 8.94 | 0.06 | 0.68 |
| 6 | 14.19 | 9.56 | 1.72 | 8.67 | 8.62 | 0.05 | 0.62 |
| 7 | 14.77 | 10.24 | 1.91 | 8.81 | 8.78 | 0.03 | 0.33 |
| 8 | 15.25 | 9.57 | 1.95 | 9.18 | 9.16 | 0.02 | 0.27 |
| 9 | 15.28 | 10.19 | 1.98 | 9.78 | 9.61 | 0.17 | 1.76 |
| 10 | 16.46 | 10.17 | 2.15 | 9.52 | 9.73 | −0.21 | −2.19 |
| 11 | 16.65 | 12.01 | 2.25 | 10.06 | 9.84 | 0.22 | 2.23 |
| 12 | 16.81 | 11.73 | 2.24 | 10.52 | 10.19 | 0.33 | 3.21 |
| 13 | 17.74 | 10.74 | 2.76 | 10.17 | 10.08 | 0.09 | 0.85 |
| 14 | 18.03 | 11.15 | 3.17 | 10.48 | 10.51 | −0.03 | −0.27 |
| 15 | 18.65 | 12.10 | 3.24 | 9.76 | 9.63 | 0.13 | 1.35 |
| 16 | 19.05 | 13.14 | 3.83 | 9.87 | 9.87 | 0 | 0 |
| 17 | 19.97 | 12.24 | 3.19 | 9.73 | 9.63 | 0.1 | 1.03 |
| 18 | 20.07 | 13.43 | 3.90 | 9.53 | 9.39 | 0.14 | 1.47 |
| 19 | 20.36 | 12.61 | 3.57 | 10.35 | 10.24 | 0.11 | 1.03 |
| 20 | 20.38 | 12.19 | 3.61 | 12.07 | 11.64 | 0.43 | 3.68 |
| 21 | 21.10 | 11.19 | 3.92 | 11.07 | 11.26 | −0.19 | −1.69 |
| 22 | 21.36 | 12.78 | 4.23 | 11.52 | 11.83 | −0.31 | −2.62 |
| 23 | 21.44 | 12.71 | 3.98 | 11.43 | 11.24 | 0.19 | 1.66 |
| 24 | 22.96 | 14.73 | 4.34 | 12.45 | 12.17 | 0.28 | 2.34 |
| 25 | 23.01 | 14.01 | 4.21 | 11.89 | 11.73 | 0.16 | 1.38 |
| 26 | 23.89 | 14.83 | 4.88 | 11.71 | 11.62 | 0.09 | 0.75 |
| 27 | 24.77 | 14.16 | 5.46 | 12.95 | 12.51 | 0.44 | 3.54 |
| Methods | Evaluation Index | |||||||
|---|---|---|---|---|---|---|---|---|
| Training Set | Testing Set | |||||||
| RMSE | MAE | MBE | R2 | RMSE | MAE | MBE | R2 | |
| Three-parameter | 0.5963 | 0.4124 | 0.0184 | 0.8313 | 0.5490 | 0.4123 | 0.0565 | 0.7910 |
| Two-parameter | 0.7013 | 0.5138 | 0.0194 | 0.7076 | 0.6328 | 0.5261 | 0.0571 | 0.6534 |
| No. | Diameter (mm) | Thickness (mm) | Actual Result (N) | Predicted Value (N) | Error (N) | Relative Error (%) |
|---|---|---|---|---|---|---|
| 1 | 15.27 | 10.73 | 9.40 | 8.72 | 0.68 | 7.23 |
| 2 | 22.68 | 12.24 | 11.54 | 11.13 | 0.41 | 3.55 |
| 3 | 15.61 | 13.16 | 10.63 | 10.93 | 0.30 | 2.82 |
| 4 | 19.32 | 14.13 | 9.31 | 9.21 | 0.10 | 1.07 |
| 5 | 14.26 | 9.39 | 8.48 | 8.62 | 0.14 | 1.66 |
| 6 | 18.84 | 14.91 | 10.23 | 10.45 | 0.22 | 2.15 |
| 7 | 13.71 | 9.58 | 8.51 | 8.32 | 0.19 | 1.98 |
| 8 | 13.15 | 12.38 | 9.98 | 10.50 | 0.52 | 5.21 |
| 9 | 15.28 | 12.96 | 9.81 | 10.12 | 0.31 | 3.16 |
| 10 | 16.67 | 12.41 | 8.80 | 8.18 | 0.62 | 7.05 |
| 11 | 19.38 | 12.13 | 10.82 | 10.58 | 0.24 | 2.22 |
| 12 | 18.52 | 12.69 | 11.23 | 10.96 | 0.27 | 2.40 |
| 13 | 15.13 | 10.37 | 10.01 | 10.73 | 0.72 | 7.19 |
| 14 | 18.14 | 13.31 | 10.53 | 9.92 | 0.61 | 5.79 |
| 15 | 19.53 | 14.44 | 11.40 | 10.82 | 0.58 | 5.09 |
| 16 | 13.41 | 9.36 | 8.25 | 8.43 | 0.18 | 2.18 |
| 17 | 15.31 | 9.91 | 9.36 | 8.74 | 0.62 | 6.62 |
| 18 | 16.65 | 11.92 | 8.80 | 9.18 | 0.38 | 4.32 |
| 19 | 13.59 | 10.97 | 9.01 | 9.32 | 0.31 | 3.44 |
| 20 | 18.25 | 12.14 | 10.08 | 9.87 | 0.21 | 1.73 |
| 21 | 13.95 | 9.69 | 8.20 | 8.61 | 0.41 | 5.00 |
| 22 | 14.71 | 11.04 | 12.25 | 11.65 | 0.60 | 4.90 |
| 23 | 14.25 | 12.15 | 10.32 | 9.91 | 0.41 | 3.97 |
| 24 | 18.73 | 11.9 | 8.54 | 8.53 | 0.01 | 0.12 |
| 25 | 17.79 | 12.49 | 9.90 | 10.39 | 0.49 | 4.95 |
| 26 | 15.31 | 9.96 | 8.71 | 9.24 | 0.53 | 6.08 |
| 27 | 15.38 | 11.87 | 9.17 | 9.08 | 0.09 | 0.98 |
| 28 | 17.54 | 11.86 | 12.20 | 11.36 | 0.84 | 6.89 |
| 29 | 20.65 | 13.92 | 11.86 | 11.45 | 0.59 | 4.97 |
| 30 | 13.18 | 10.33 | 7.86 | 8.12 | 0.26 | 3.31 |
| 31 | 12.91 | 10.10 | 8.82 | 8.17 | 0.65 | 7.37 |
| 32 | 15.83 | 12.48 | 9.44 | 9.91 | 0.47 | 4.98 |
| 33 | 17.38 | 12.77 | 9.32 | 9.81 | 0.49 | 5.26 |
| 34 | 12.83 | 9.60 | 8.20 | 8.16 | 0.04 | 0.49 |
| 35 | 16.74 | 10.89 | 10.14 | 9.87 | 0.27 | 2.66 |
| 36 | 15.24 | 12.15 | 8.43 | 8.91 | 0.48 | 5.69 |
| 37 | 22.76 | 14.43 | 12.26 | 11.66 | 0.60 | 4.89 |
| 38 | 22.59 | 14.46 | 11.99 | 11.57 | 0.42 | 3.50 |
| 39 | 13.01 | 9.86 | 8.21 | 8.22 | 0.01 | 0.12 |
| 40 | 18.24 | 13.15 | 10.58 | 10.97 | 0.39 | 3.69 |
| AVG | 16.54 | 11.86 | 9.81 | 9.76 | 0.39 | 3.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, H.; Li, W.; Wang, H.; Li, Y.; Liu, J.; Li, B. Study on Predicting Blueberry Hardness from Images for Adjusting Mechanical Gripper Force. Agriculture 2025, 15, 603. https://doi.org/10.3390/agriculture15060603
Yin H, Li W, Wang H, Li Y, Liu J, Li B. Study on Predicting Blueberry Hardness from Images for Adjusting Mechanical Gripper Force. Agriculture. 2025; 15(6):603. https://doi.org/10.3390/agriculture15060603
Chicago/Turabian StyleYin, Hao, Wenxin Li, Han Wang, Yuhuan Li, Jiang Liu, and Baogang Li. 2025. "Study on Predicting Blueberry Hardness from Images for Adjusting Mechanical Gripper Force" Agriculture 15, no. 6: 603. https://doi.org/10.3390/agriculture15060603
APA StyleYin, H., Li, W., Wang, H., Li, Y., Liu, J., & Li, B. (2025). Study on Predicting Blueberry Hardness from Images for Adjusting Mechanical Gripper Force. Agriculture, 15(6), 603. https://doi.org/10.3390/agriculture15060603






