Development of an Improved Jellyfish Search (JS) Algorithm for Solving the Optimal Path Problem of Multi-Robot Collaborative Multi-Tasking in Complex Vertical Farms

Abstract

This paper proposes an improved Jellyfish Search algorithm, namely TLDW-JS, for solving the problem of optimal path planning of multi-robot collaboration in the multi-tasking of complex vertical farming environments. Vertical farming is an efficient way to solve the global food problem, but how to deploy agricultural robots in the environment constitutes a great challenge, which involves energy consumption and task efficiency. The most important improvements introduced by the proposed TLDW-JS algorithm are as follows: the Tent Chaos used to generate a high-quality, diversified initial population, Lévy flight used in the improved JS to strengthen global exploration, and finally, the nonlinear dynamically weighted adjustment with logistic functions to balance exploration and exploitation. A Vertical Farming System Multi-Robot Collaborative Trajectory Planning (VFSMRCTP) model has been developed in accordance with the environmental constraints specific to vertical farms, the task constraints, and the constraints between agricultural robots. The VFSMRCTP model is solved using the TLDW-JS algorithm and a number of comparison algorithms in order to analyze the algorithm’s performance. Comparative experiments demonstrate that TLDW-JS outperforms classic optimization algorithms such as the Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Dung Beetle Optimization (DBO), achieving superior path length optimization, reduced energy consumption, and improved convergence speed. The results indicate that TLDW-JS achieved a 34.3% reduction in average path length, obtained one of the top three optimal solutions in 74% of cases, and reached convergence within an average of 55.9 iterations. These results validate the efficiency of TLDW-JS in enhancing energy optimization and demonstrate its potential for enabling automated systems in vertical farming.

1. Introduction

Rapid urbanization, coupled with disruptions in food supply chains during the COVID-19 pandemic, has intensified food security challenges in metropolitan areas [1]. In response, vertical farming (Figure 1) has emerged as a promising solution, offering a sustainable method of food production in space-constrained urban environments. By utilizing multi-layered structures and controlled-environment agriculture, vertical farming can optimize year-round crop production. However, this approach faces challenges such as high energy consumption, which can impact its economic feasibility and broader adoption [2,3].

A key component of vertical farms’ automation involves the deployment of multiple agricultural robots to perform tasks such as planting, monitoring, harvesting, and transporting produce. In many scenarios, these tasks require collaboration among different robot types or platforms; for instance, a transport robot may deliver crop trays to a fixed position, whereupon a harvesting robot takes over. However, inefficient path planning, especially when multiple robots are simultaneously performing different but interdependent tasks, can significantly amplify total energy use. Even minor suboptimal routes, repeated daily by multiple robots, accumulate into substantial resource wastage. Therefore, minimizing the path length of these collaborative robots represents a practical and high-impact strategy to reduce overall power consumption, thus improving the economic return of vertical farms [5,6,7].

Many researchers have focused on collaborative path planning for agricultural robots. Wang et al. (2023) proposed a joint optimization method for task allocation and path planning, which improved operational efficiency while reducing robot waiting time and operational costs [8]. Guo et al. (2024) introduced a GA-based collaborative evolutionary algorithm for task allocation and scheduling, effectively reducing idle time for robots in smart farms and enhancing their collaboration capabilities [9]. Kiani et al. (2022) developed Ex-GWO and O-GWO for robot path planning in farmland terrain, successfully reducing path costs by 55.56% [10]. Jo and Son (2024) extended the traditional multi-agent path finding (MAPF) approach, which allows for much shorter path costs for agricultural robots [11].

Most existing studies primarily focus on small-scale robots and tasks in two-dimensional farm environments, without sufficient research on the three-dimensional structure, limited space, and dense obstacles present in vertical farms. This study establishes a corresponding model based on the specific characteristics of vertical farms. The model includes large-scale tasks (10–50) and multiple robots (4–10) and simulates large-sized maps and narrow passageways, providing a more realistic representation of vertical farm operations.

Another major challenge in multi-robot collaborative path planning for vertical farms is the significant computational load caused by the increasing number of robots and tasks. To address this, this study adopts a hierarchical scheduling method to reduce computational overhead. A centralized architecture is used for overall task allocation, while distributed scheduling is employed when collaborative robots reach task points, allowing them to share environmental information in real time.

Additionally, vertical farms involve multiple types of tasks and continuously changing environmental conditions. If the system lacks real-time performance, it can lead to delayed scheduling, path conflicts, resource wastage, or even task failure. To address these real-time challenges, this study implements a multi-threading mechanism and priority-based scheduling strategy to ensure that urgent tasks are prioritized, improving system responsiveness and operational efficiency.

This paper aims to improve the energy efficiency and productivity of vertical farming systems by focusing on multi-robot collaborative multi-task trajectory planning. Therefore, this research has three tasks:

• To formulate a Vertical Farming System Multi-Robot Collaborative Trajectory Planning (VFSMRCTP) model, which represents a real vertical farm as a mathematical model, enabling the use of objective and constraint functions that can be interpreted by computers.
• To develop a novel TLDW-JS algorithm for solving the optimal path planning problem for multi-robot collaboration in vertical farms.
• To evaluate the performance of the TLDW-JS algorithm by comparing it with existing benchmark algorithms.

In the remainder of this paper, Section 2 details the VFSMRCTP model and describes the environmental constraints of vertical farms, task sequences, and cooperative requirements among multiple robots. And introduces the TLDW-JS algorithm, highlighting its key improvements over the basic JS. Section 3 presents and visualizes all experimental results. Section 4 discusses the results and limitations of this study. Finally, Section 5 provides the conclusions and outlines future work. And the research structure is shown in Figure 2.

2. Materials and Methods

2.1. Build VFSMRCTP Model

2.1.1. Problem Statement

The problem of vertical farm multi-robot collaborative multi-task trajectory planning is described as follows: In this paper, it is demonstrated that single-function agricultural robots are unable to perform certain complex agricultural tasks that arise in vertical farms. Consequently, these tasks must be completed using multi-function agricultural robots or multiple single-function agricultural robots. The purchase price of multi-function agricultural robots is high, they consume more energy, and they are not straightforward to maintain. It is therefore more economically beneficial for vertical farms to utilize multiple agricultural robots with different functions to complete complex tasks.

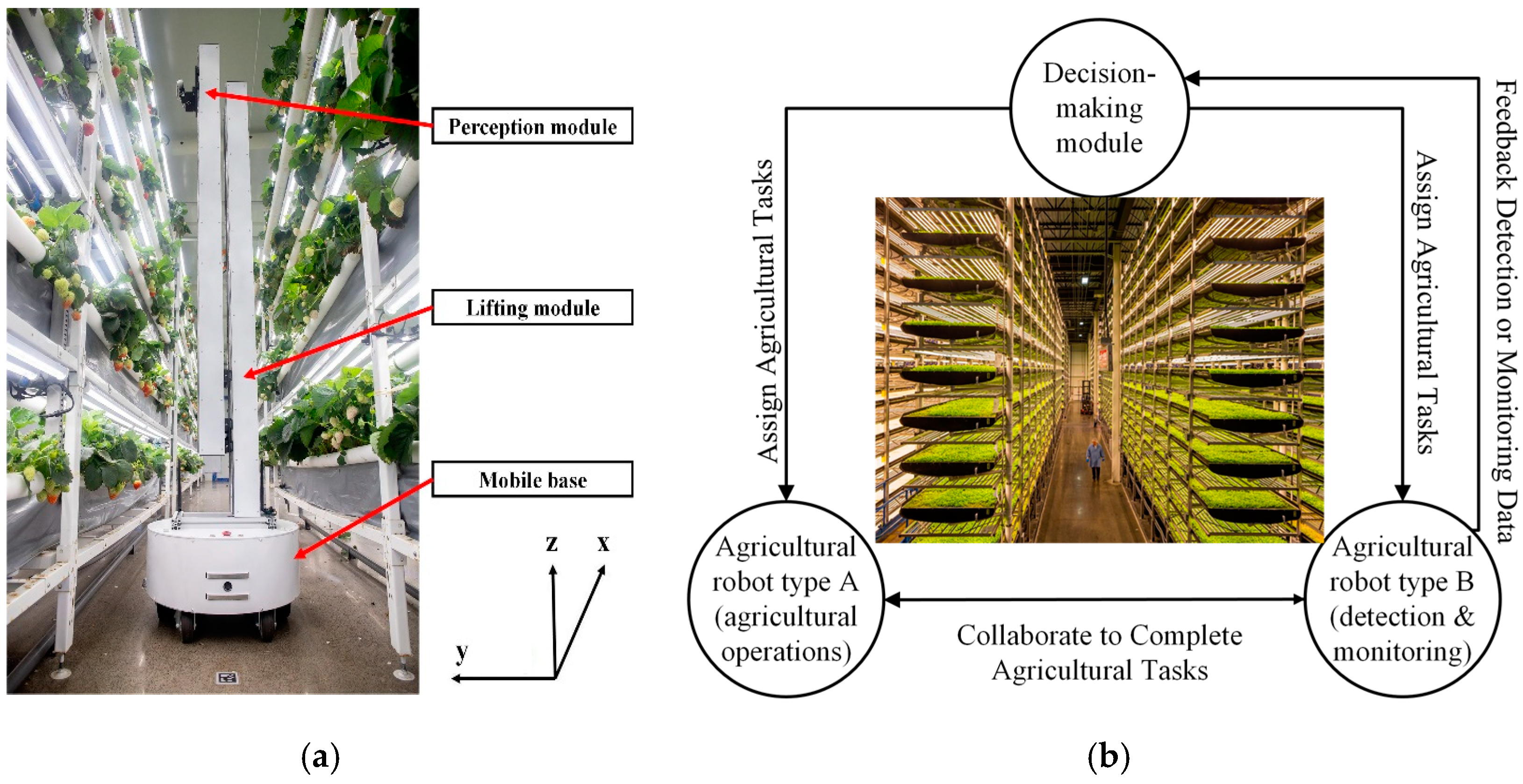
Figure 3a illustrates the functions of agricultural robots. In this study, A-type and B-type robots cooperatively performed tasks, each requiring two robots. For instance, in planting and transplanting, one robot grasped the seedling while the other prepared the planting hole and secured it. For crop monitoring and maintenance, one robot scanned plants using a camera or sensors, while the other performed localized actions like fertilization, pruning, or disease treatment. Similarly, one robot measured soil or hydroponic solution parameters, while the other adjusted nutrient levels to support plant growth. The VFSMRCTP schematic is shown in Figure 3b.

In vertical farming, agricultural robots handle tasks of varying complexity and priority, from simple operations like planting to advanced functions such as crop health monitoring and nutrient adjustment. The VFSMRCTP model classifies tasks into three priority levels (

Table 1. Heterogeneous task characteristics.

Task Type	Complexity Level	Priority	Number of Tasks
Crop planting and transplanting	Low	Low	3
Nutrient adjustment	Medium	High	2
Pest and disease detection and sampling	Medium	Medium	5

), assigning higher weights to more critical tasks. When using the TLDW-JS algorithm for collaborative path planning, the algorithm resolves path conflicts and execution sequences by prioritizing tasks with higher weights, ensuring essential operations receive adequate resources.

Agricultural robots used various end effectors to execute tasks, but efficient movement in vertical farms was challenging due to multi-level planting racks and confined spaces. Given the frequency and interdependence of tasks like transplanting and crop maintenance, a collaborative path planning approach was essential, especially for coordinating two specialized robots arriving at the same location. Without effective coordination, unnecessary detours and idle times increase travel distance and energy costs, reducing farm efficiency. Therefore, developing a suitable algorithm for collaborative path planning is crucial, with the primary goal of minimizing total traveled distance to reduce the overall energy consumption.

When constructing the VFSMRCTP model, the following assumptions are made in order to reduce the complexity of the model and maintain its relevance to reality:

• All agri-robots move horizontally and vertically within the vertical farm structure.
• Agri-robots start and stop instantly, regardless of inertial dynamics.
• Agri-robots have sufficient energy reserves to complete their tasks.
• Agri-robots have an accurate positioning system.
• Agri-robots communicate with the system instantaneously and without error.
• Agri-robots move at a constant speed.
• Agri-robots of the same type have the same work capacity.
• Tasks must be carried out by two agri-robots working together.

2.1.2. Symbol Definitions

The symbols were defined as follows:

$D_{am}$ and $D_{bm}$ represent the total distance traveled by type a and type b robots to complete the task, respectively.

$m_a$ is the number of tasks for the a-type robot.

$U_a$ represents the set of task sequences of the a-type robot.

${\mathcal{U}}_{am}$ represents the m-th task of a robot, $m=\mathrm{1,2},...a$.

$R$ represents the set of charging tasks.

$R_a$ represents the set of path nodes of the charging tasks.

$r_{am}$ represents the driving path node corresponding to the m-th charging task of each robot, $m=\mathrm{1,2},\dots ,m_a$.

$V_a$ represents the set of path nodes of the a-type robot.

$v_{a}m$ presents the driving path node corresponding to the m-th task of each robot, $m=\mathrm{1,2},...a$.

$W_a$ represents the set of traveling time windows of the a-type robot.

$w_{am}$ represents the time to reach each node in the traveling path, corresponding to the m-th task of each robot, $m=$ 1, 2…$a$.

$N$ represents the set of charging stations, $n=\mathrm{1,2},nϵN$.

$s_m$ and $e_m$ represent the start and end points of task m, respectively.

$T_a$ represents the traveling time of each robot.

$T{E}_a$ represents the time taken for each robot to complete all the sequences of tasks.

$T_{am}^n$ represents the time taken to arrive at charging station n after completing task m or the travel time from charging station n to the start point of task m.

$T_{e_m}^a$ and $T_{s_m}^a$ represent the time at which charging starts and ends after completing task m, respectively.

$j$,$k$ represents the nodes in the path network, $V$ is the set of nodes, and $j,kϵV$.

$x_{ajkt}$ represents that when robot $a$ starts traveling from $j$ to $k$ at time $t,$ it has a value of 1; otherwise, the value is 0.

$P_a$ and $P_b$ represent the positions of robot type a and robot type b, respectively.

$S$ represents the collaborative task location point.

2.1.3. Model Objective and Constraint Functions

The objective function (F) is

$$F=min{\displaystyle \sum _{a\in A,b\in B}\left(D_{am}+D_{bm}\right)}$$

(1)

Equation (1) defines the objective function of this study, which aims to minimize the total travel distance of all agricultural robots, similar to the approach used by Sun et al. [13]. Here, D represents the set of path lengths for each robot from its starting point through task completion, with an optional return to the initial location. Minimizing the total distance ${\displaystyle \sum D}$ effectively reduces the energy consumption, as travel distance is a key factor in power usage.

This study involves two types of agricultural robots, A-type and B-type, both subject to basic constraints. Using the A-type robot as an example, Tao, Liu, and Guo [14,15,16] applied similar constraint functions in their research. Equation (2) defines the task sequence, Equation (3) represents the travel path, and Equation (4) sets the travel time window. Equation (5) establishes the relationship between tasks and task sets, while Equations (6) and (7) calculate the total travel time during task execution. Equation (8) sums all execution times, and Equations (9)–(11) ensure that the robot passes through only one point at a time. Since A-type and B-type robots collaborate, they must satisfy the cooperative constraint in Equation (12). Let S be the task point, and P_a and P_b be the end points of A-type and B-type robots’ paths, respectively. When P_a and P_b coincide at S, both robots have reached the task location and can perform the task together. If not, coordination is low, and the optimal path is recalculated through iteration.

The constraint functions are

$$U_a={\displaystyle \sum _{m=1}^{m_a}{u}_{am}},a\in A$$

(2)

$$V_a={\displaystyle \sum _{m=1}^{m_a}{\nu }_{am}},a\in A$$

(3)

$$W_a={\displaystyle \sum _{m=1}^{m_a}{w}_{am}},a\in A$$

(4)

$$R_a={\displaystyle \sum _{m=1}^{m_a}{r}_{am}},a\in A$$

(5)

$$T_a={\displaystyle \sum _{j\in V_a}{\displaystyle \sum _{k\in V_a}{\displaystyle \sum _{a\in A}{t}_{jk}^a}}}{x}_{ajkd}+{\displaystyle \sum _{m\in R}{\displaystyle \sum _{a\in A}{\displaystyle \sum _{n\in N}\left(T_{am}^n+T_{a{m}^{\prime }}^n\right)}}}$$

(6)

$$T{E}_a=T_a+{\displaystyle \sum _{m\in U_a}{\displaystyle \sum _{a\in A}^s{w}_m^a}}\left(T_{e_m}^a-T_{s_m}^a\right),a\in A$$

(7)

$$T=maxT{E}_a,a\in A$$

(8)

$${\displaystyle \sum _{j\in V}{\displaystyle \sum _{k\in V}{x}_{ajjk}}}=1,\forall a\in A$$

(9)

$${\displaystyle \sum _{a\in A}{\displaystyle \sum _{k\in V}{x}_{ajkt}}}=1,\forall j\in V$$

(10)

$${\displaystyle \sum _{a\in A}{\displaystyle \sum _{j\in V}{x}_{ajkt}}}=1,\forall k\in V$$

(11)

The collaborative constraint function (Sync) is

$$Sync(P_a,P_b,S)=\left\{\begin{array}{cc}\mathrm{true},& \mathrm{if}\hspace{0.33em}{P}_a(s)=P_b(s)\hspace{0.33em}\mathrm{for}\hspace{0.33em}\mathrm{all}\hspace{0.33em}s\in S\\ \mathrm{false},& \mathrm{otherwise}\end{array}\right.$$

(12)

2.2. Propose TLDW-JS Algorithm

2.2.1. Overview of TLDW-JS Algorithm

To clearly illustrate the improved Jellyfish Search (TLDW-JS) algorithm, a detailed flowchart is presented (as shown in Figure 4). The population is initialized using the Tent chaotic map, after which fitness evaluation is conducted. A dynamic weight parameter is calculated using a nonlinear adjustment based on the logistic function. The jellyfish positions are then updated based on the time control factor Ar, balancing active motion and passive drifting. Finally, Lévy flight is applied to avoid local optima, and the optimal solution is returned after reaching the maximum iteration.

2.2.2. Optimization Algorithm Selection

Collaborative path optimization is used in fields like transportation, logistics, robotics, military defense, and smart farming. While algorithms such as PSO, GA, DBO, and JS are commonly used, they often face issues with local optima, poor global performance, and limited robustness. Chou and Truong introduced the bio-inspired JS algorithm [17], which this study aims to improve by enhancing its ability to escape local optima, achieve global optima, and balance exploration and exploitation, while improving robustness and stability. JS is promising due to its adaptability and strong exploration capabilities.

Several studies have worked to improve the JS algorithm for path optimization. For example, Meng et al. proposed the ESE-MSJS algorithm, improving accuracy, feasibility, and stability in multi-UAV path planning [18]. Utama et al. developed the hybrid jellyfish (HJF) algorithm to address the fuel consumption vehicle routing problem, successfully reducing fuel usage [19].

2.2.3. Basic JS Algorithm

The artificial Jellyfish Search (JS) algorithm mimics the foraging behavior of jellyfish, which involves three main movement types: following currents, active movements, and passive movements within a colony. Jellyfish regulate their movements through a control mechanism that includes a regulatory function $C(t)$ and a constant $C_0=0.5$, enabling them to switch between different behaviors. They navigate the ocean in search of food, being naturally drawn to areas with higher food concentrations, where the optimal location is determined by the food ratio. By replicating these behaviors, the JS algorithm effectively balances global and local search, enhancing optimization efficiency [17].

$$C(t)=|(2\cdot rand(0,1)-1)\cdot (1-{\displaystyle \frac{t}{T}})|$$

(13)

where in Equation (13), t is the current number of iterations, and T is the total number of iterations.

When $C\left(t\right)>C_0$, the jellyfish will move with the current. The direction of the current’s motion is determined by the best position of the jellyfish in the current population, and the average position of all jellyfish together, which can be calculated by Equation (14).

$$v_{trend}=X_g(t)-\lambda \cdot rand(0,1)\cdot X_m(t)$$

(14)

$$X_m(t)={\displaystyle \frac{1}{N_p}}{\displaystyle \sum _{i=1}^{N_p}{X}_i}(t)$$

(15)

where in Equations (14) and (15), $X_g(t)$ represents the current best position of the jellyfish, $X_m(t)$ denotes the average position of the entire jellyfish population, and $N_p$ refers to the total number of jellyfish individuals. $\lambda$ is the distribution factor, set to a constant value of $3$.

The positions of the jellyfish are updated according to Equation (16).

$$X_i(t+1)=X_i(t)+rand(0,1)\cdot v_{trend}$$

(16)

When $C\left(t\right)\le C_0$ and $1-C\left(t\right)<rand\left(0,1\right)$, the jellyfish enters the active motion phase. In this phase, information is exchanged between the jellyfish to generate the direction of motion $v_{step}$, as shown in Equation (17), which allows the jellyfish to update its position.

$$v_{step}=\left\{\begin{array}{cc}{X}_i(t)-X_j(t),& if\hspace{0.17em}{X}_i(t)\hspace{0.33em}\mathrm{inferior}\hspace{0.33em}\mathrm{to}\hspace{0.33em}{X}_j(t)\\ X_j(t)-X_i(t),& otherwise\end{array}\right.$$

(17)

$$X_i(t+1)=X_i(t)+rand(0,1)\cdot v_{step}$$

(18)

where $X_j(t)$ represents the randomly selected position of jellyfish j. It can be observed that jellyfish i tends to move towards the position of jellyfish j when its current location has access to a poorer food source compared to jellyfish j. Conversely, jellyfish i will move away from jellyfish j if its position offers a better food source.

When $C\left(t\right)\le C_0$ and $1-C\left(t\right)\ge rand\left(0,1\right)$, the jellyfish will move passively within the colony, searching for a food source by moving around its current position. The updated position of the jellyfish is described in Equation (19).

$$X_i(t+1)=X_i(t)+rand(0,1)\cdot \delta \cdot (ub-lb)$$

(19)

where in Equation (19), the coefficient of motion is denoted by $\delta =0.1$, while $ub\hspace{0.17em},\hspace{0.17em}lb$ represent the upper and lower bounds, respectively, of the search space where the jellyfish is situated [20,21,22].

2.2.4. Population Initialization Based on Tent Chaos Factor

Multi-robot collaborative multi-tasking path optimization in complex environments, such as vertical farms, is challenged by the JS algorithm’s sensitivity to initial population quality. The basic JS algorithm relies on random initialization, often leading to poor population diversity and unstable quality, which reduces convergence efficiency. To address this, population initialization should incorporate a Tent Chaos factor, which enhances population diversity, improves search space coverage, and lowers the risk of premature convergence to local minima [23,24]. Several studies have demonstrated the effectiveness of the Tent Chaos factor in path optimization [23,25].

Chaotic systems have a relatively high degree of randomness. This gives the initial population a significant advantage over the conventional initialized population $X_1$. And then, the improved algorithm can be combined with the Tent Mapping to obtain the initialized population $X_2$ [26]. The resulting mapping is specified by the following Equation (20):

$$X_{i,j}=\left\{\begin{array}{l}{X}_{i,j}/m,0\le X_{i,j}<m\hfill \\ \left(1-X_{i,j}\right)/(1-m),m\le X_{i,j}\le 1\hfill \end{array}\right.$$

(20)

where in Equation (20), $i$ refers to the population size, $i=\mathrm{1,2},...,p$. $j$ specifically refers to the chaos number, $j=\mathrm{1,2},...,p$. $m$ refers to the chaos parameter, $m\in \left[\mathrm{0,2}\right]$, and in general take 0.5.

$$x_{i,j}=l_j+\left[X_{i,j}\hspace{0.33em}\left(u_j-l_j\right)\right]$$

(21)

where in Equation (21), $[l_j,u_j]$ refers to the search interval of $x_{i,j}$.

2.2.5. Jellyfish Population Renewal Based on Lévy Flights Strategy

Premature convergence and local optima present significant challenges in multi-robot collaborative multi-tasking path optimization, particularly in complex environments like vertical farms. To mitigate these issues, Lévy flight is an effective strategy. Characterized by long jumps interspersed with shorter steps, Lévy flight enables broader search space exploration, enhancing the algorithm’s ability to escape local optima and increasing the likelihood of reaching the global optimum. Additionally, it strengthens the JS algorithm by balancing exploration and exploitation, mimicking efficient natural search behaviors, and improving overall search efficiency [27]. Various studies have applied Lévy flight to enhance path optimization algorithms [28,29].

During the global search phase of the Lévy flight Jellyfish Search (L-JS) algorithm, jellyfish individuals executed large jumps and random steps via the Lévy flight strategy, enhancing global optimization. In this study, integrating Lévy flight into the search phase allows for more effective global searches and improved convergence performance [30]. Equation (22) is as follows:

$$X_i^t={\displaystyle \frac{X_1+X_2+X_3}{3}},X_i^{t+1}=X_i^t+L\cdot (X_{best}^t-X_i^t)$$

(22)

where in Equation (22), $X_i^t$ represent the solutions at generation $t$, $X_i^{t+1}$ represent the solutions at generation $t+1$. $X_{best}^t$ is the globally optimal solution at generation $t$. $L$ is the Lévy step size, and $L$ is calculated as the following Equation (23).

$$L~{\displaystyle \frac{\lambda \Gamma (\lambda )\sin (\pi \lambda /2)}{\pi }}\cdot {\displaystyle \frac{1}{s^{1+\lambda }}}$$

(23)

where in Equation (23), $\lambda =3/2$. $\Gamma (\lambda )$ is the standard gamma function. $s$ is the length of each move step, and calculated as Equation (24):

$$s={\displaystyle \frac{U}{|V{|}^{1/\lambda }}}$$

(24)

where in Equation (24), $U~N(0,{\sigma }^2)$ obeys a Gaussian distribution with mean zero and standard deviation ${\delta }^2$, and $V~N(0,1)$ obeys a standard Gaussian distribution.

2.2.6. Nonlinear Dynamic Weight Adjustment Based on Logistic Function

Multi-robot collaborative multi-tasking path optimization in complex environments, such as vertical farms, requires a balance between exploration and exploitation in JS algorithms. To achieve this, nonlinear inertia weights with logistic functions are employed to dynamically regulate exploration and exploitation. This approach ensures smooth parameter adjustments, enhancing the JS algorithm’s overall performance [31]. Logistic functions have been used in various optimization algorithms to improve path planning efficiency [32,33].

In Equation (25), in the initial stage of the algorithm (when iterations are small), the logistic function is in the negative interval, causing the weight to be close to its maximum. This favors global exploration. In the intermediate stage (with medium iterations), the weight decreases, balancing global exploration and local exploitation. In the later stages (with high iterations), the weight becomes smaller, reducing the search step and promoting fine local exploitation.

In Equation (25), the weight’s maximum is $w_{\max }=0.9$, the minimum is $w_{\min }=0.4$, and b controls the rate of change, set to 0.5. $iter$ is the current number of iterations. $Max\_iter$ is the maximum number of iterations.

$$w=w_{\max }+(w_{\min }-w_{\max })\cdot {\displaystyle \frac{1}{1+\exp (-10\cdot b\cdot (\frac{2\cdot iter}{Max\_ite\mathrm{r}}-1))}}$$

(25)

The new jellyfish updated Equation (26) is obtained by putting the nonlinear dynamic weights w based on the logistic function into the jellyfish updated Equation (16).

$$X_i(t+1)=X_i(t)+w\cdot rand(0,1)\cdot v_{trend}$$

(26)

2.2.7. Comparative Analysis and Innovation of TLDW-JS

The TLDW-JS algorithm is proposed as a means of solving multi-robot collaborative multi-task path planning in complex vertical farming. This is achieved by fusing the Tent Chaos strategy, Levy flight strategy, and nonlinear dynamic weight adjustment based on logistic function into the basic JS algorithm. The overall logic and key steps of the algorithm are shown in pseudocode (Algorithm 1).

Algorithm 1 Tent chaos L’evy flight Dynamic Weight Jellyfish Search (TLDW- JS)

1: Input: Problem instance P, parameters (population size, max iterations, etc.) 2: Output: Optimal solution to P 3: Initialize the population of jellyfish using Tent chaos mapping 4: for each jellyfish in the population do 5:        Calculate fitness based on the objective function 6: end for 7: while iteration < max iterations do 8:        Calculate the dynamic weight w based on the current iteration 9:        Update the positions of jellyfish using w 10:      Calculate the time control factor Ar 11:      if |Ar| ≥ 0.5 then 12:              Update position following the ocean current 13:      else 14:             if random value ≤ 1 − Ar then 15:                       Determine direction and update position (active motion) 16:             else 17:                       Move jellyfish around itself (passive motion) 18:             end if 19:      end if 20:      for each jellyfish in the population do 21:             Check if jellyfish is within the boundaries 22:             Recalculate fitness if position is updated 23:      end for 24:      Update the position of jellyfish using L’evy flight 25:      if max number of iterations reached then 26:             break the loop 27:      end if 28: end while 29: Return the best solution

2.3. Simulation Experiment Settings

To validate the effectiveness of the TLDW-JS algorithm for the VFSMRCTP model, improvement strategies were added incrementally to the basic JS algorithm to assess their contributions. The TLDW-JS algorithm was then tested against classical optimization algorithms under the same model conditions, involving 3 A-type and 3 B-type robots (totaling 6 agricultural robots) performing 10 tasks with varying priorities. The algorithms were run for a maximum of 100 iterations as the stopping criterion.

The performance of TLDW-JS was compared with widely used algorithms, including GA, PSO, DBO, and JS. GA and PSO are well-established algorithms, while DBO is a newer bio-inspired method based on dung beetle foraging behavior. JS, the base algorithm for TLDW-JS, was included to evaluate the effectiveness of the proposed improvements. These algorithms represent different optimization strategies, providing a comprehensive comparison. The results show that TLDW-JS enhances JS and outperforms key optimization methods, demonstrating its efficiency and applicability in collaborative trajectory planning for vertical farm robots. The experiments were conducted on an Intel i7-11800H processor (Intel Corporation, Santa Clara, CA, USA) with MATLAB (version R2023b, MathWorks, Natick, MA, USA) and Microsoft Excel (version 2021, Microsoft Corporation, Redmond, WA, USA) used for simulations. Each experiment was repeated 50 times, with average convergence curves generated to illustrate convergence speed and stability, providing valuable insights into the global search capabilities of each algorithm. The algorithm parameters were set as shown in

Table 2. Algorithm parameter settings.

Algorithm	Parameters
GA	n = 20 p1 = 0.8 lb = 0	Max_iteration = 100 p2 = 0.3 ub = 1
PSO	n = 20 w = 0.4 v = randn(size(x)) lb = 0	Max_iteration = 100 c1 = 1.2 c2 = 1.2 ub = 1
DBO	n = 20 p = 0.2 lb = 0	Max_iteration = 100 ub = 1
JS, TLDW-JS	n = 20 dim = 1 Max_iteration = 100	lb = 0 ub = 1

.

3. Results

3.1. Ablation Study Results of Various Strategies

3.1.1. Chaos Factor Tent Population Initialization Effectiveness

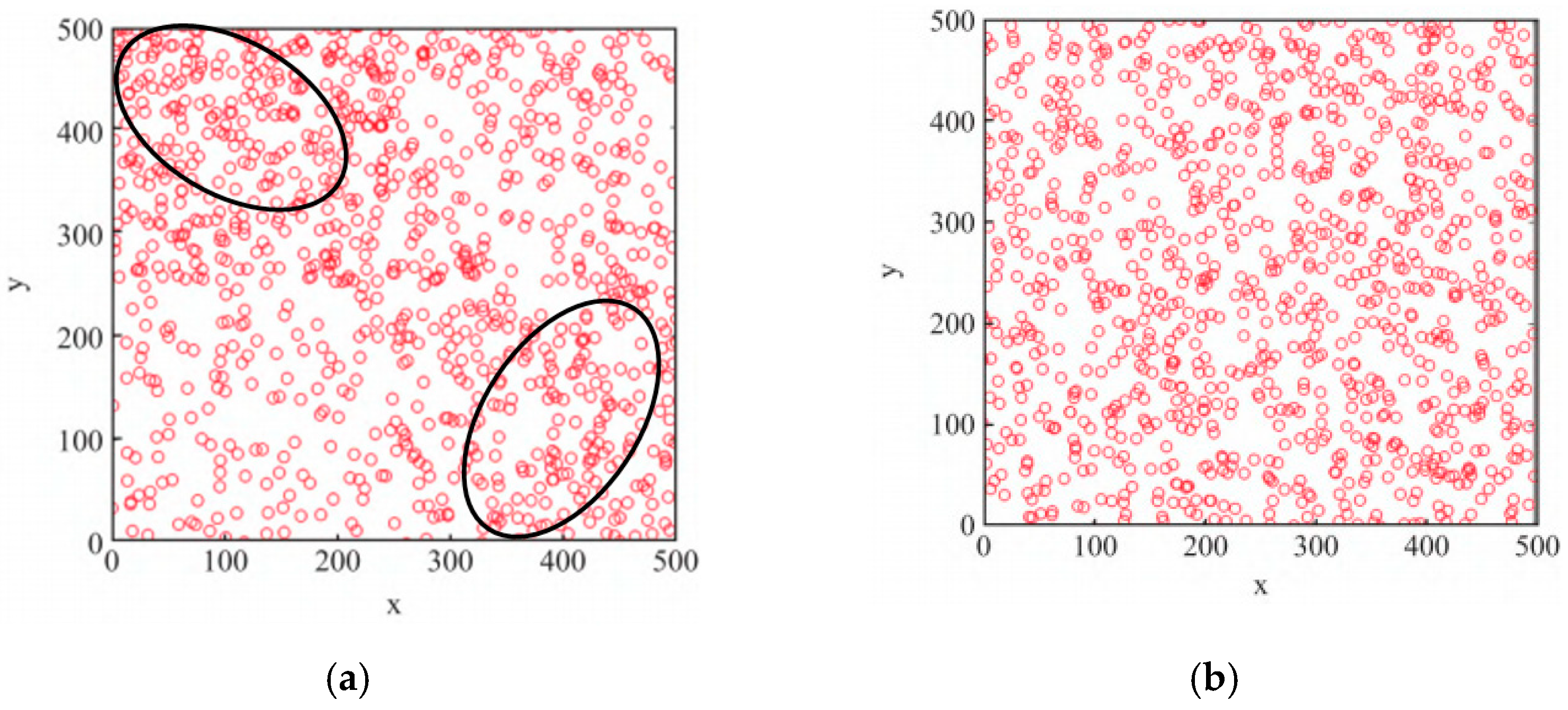
Figure 5a shows the distribution of the randomly initialized population in the JS algorithm, where clustering occurs, leading to an uneven distribution. In contrast, Figure 5b illustrates the population generated using Tent Chaos mapping, which is more uniformly distributed. A uniform initialization mitigates quality fluctuations, improving algorithm stability. This addresses a key limitation of JS, which depends on a high-quality initial population for optimal performance.

3.1.2. Effectiveness of Population Renewal Based on Lévy Flights

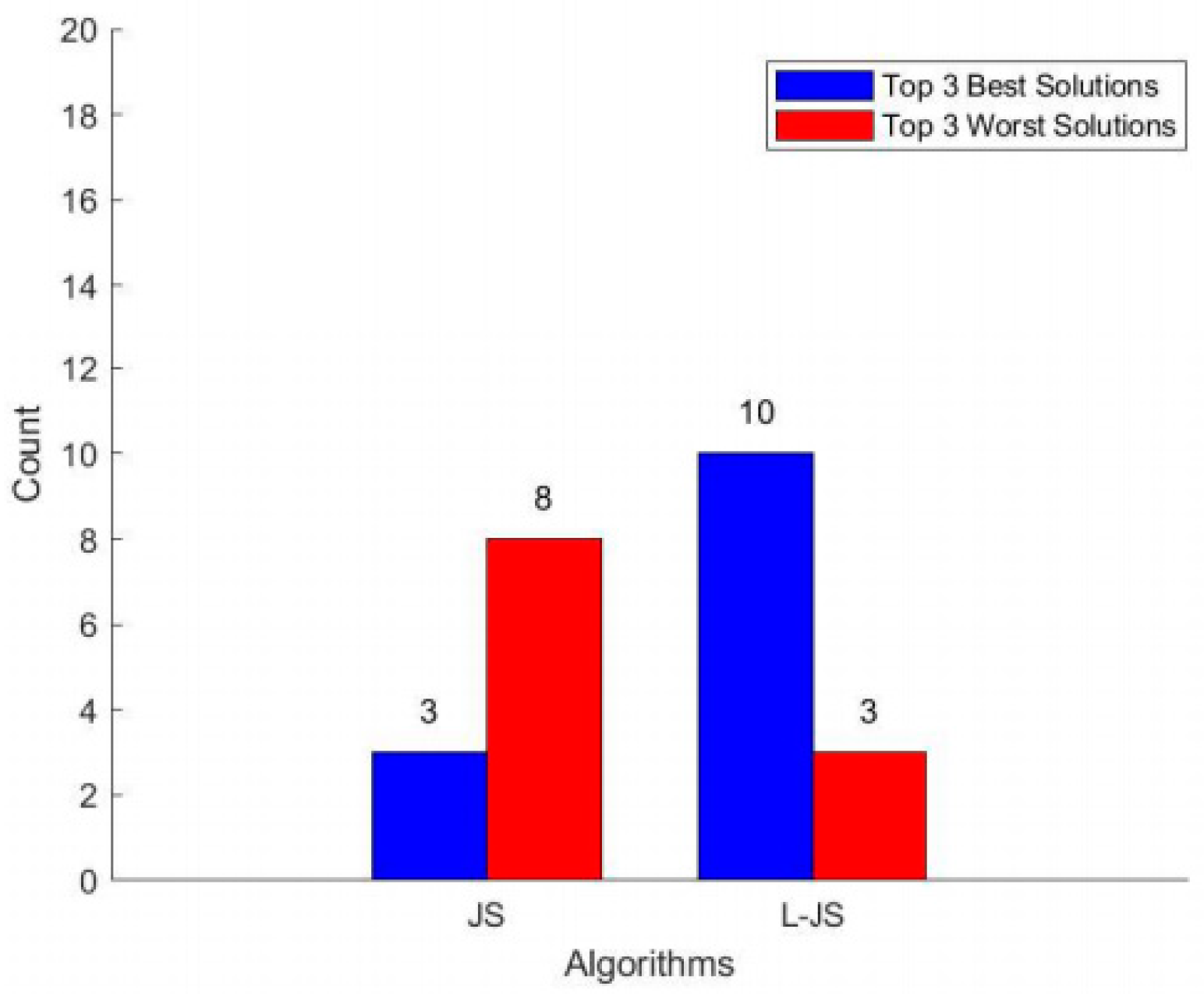
Figure 6 shows that the JS algorithm produces fewer best solutions and more worst solutions than the L-JS algorithm, demonstrating L-JS’s superior ability to escape local optima. Figure 7 presents the average path length over iterations, where the JS algorithm gradually decreases and stabilizes, while L-JS converges faster with a steeper decline in path length, consistently maintaining a lower average. These results confirm that L-JS outperforms JS in trajectory optimization, highlighting the effectiveness of Lévy flight in improving global search and avoiding local optima.

3.1.3. Effectiveness of Nonlinear Dynamic Weight Adjustment Based on Logistic Function

Figure 8 shows that in the JS algorithm’s path lengths range from approximately 690 to 750 m, with a median slightly above 730 m. The large interquartile range indicates high variability in performance. In contrast, the DW-JS algorithm produces path lengths within a narrower range of 700 to 740 m, with a median around 720 m. The smaller interquartile range suggests reduced variability, leading to more consistent and shorter path lengths. This highlights DW-JS’s improved stability and efficiency in path planning compared to JS.

3.2. TLDW-JS Algorithm Performance Analysis

3.2.1. Energy Consumption Comparison of Different Algorithms

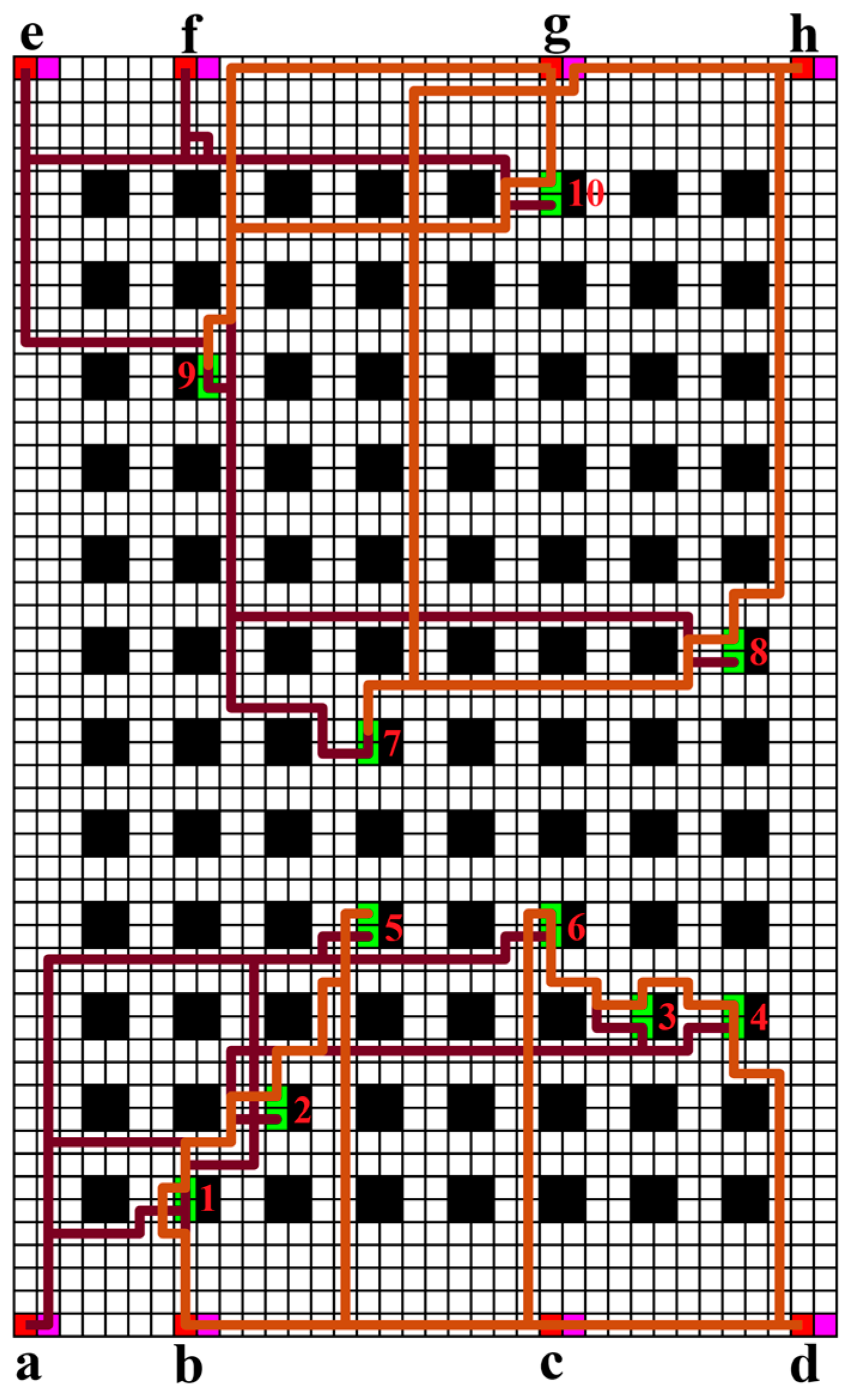
Figure 9 presents the optimized paths generated by the TLDW-JS algorithm for multi-robot trajectory planning on a vertical farm. The grid map represents the farm layout, with black and white cells indicating different areas. The colored paths show the optimized trajectories, balancing task allocation and minimizing travel distance. The algorithm ensures efficient task coverage, obstacle avoidance, and progressive task completion within the farm. The movement sequence of each robot is ac-1-2-5-ac, bd-4-3-6-bd, eg-9-10-eg, and fh-8-7-fh.

Table 3. Path length metrics (max, min, average, std dev) for different algorithms.

Algorithm	Min (m)	Max (m)	Average (m)	Std Dev
GA	702	826	734.8	17.2
PSO	692	826	736.5	21.2
JS	692	826	732.9	20.8
DBO	692	826	717.8	22.4
TLDW-JS	692	826	707.2	15.7

compares optimization algorithms for the VFSMRCTP model. TLDW-JS excels in agricultural robot path planning, with the shortest average path length (707.2 m) and lowest standard deviation (15.7), demonstrating efficiency and consistency. GA performs poorly with a longer path length (734.8 m). PSO achieves the shortest individual path (692 m) but shows high variability. JS outperforms GA and PSO but is still less effective than TLDW-JS. DBO matches the shortest path length but lacks the stability and balanced exploration–exploitation of TLDW-JS

From Table 3, the unoptimized path length is 1076 m, and with TLDW-JS, it is reduced to 707.2 m, representing a 34.3% improvement according to Equation (27).

$$S=\left({\displaystyle \frac{L_{original}-L_{optimized}}{L_{original}}}\right)\times 100\%$$

(27)

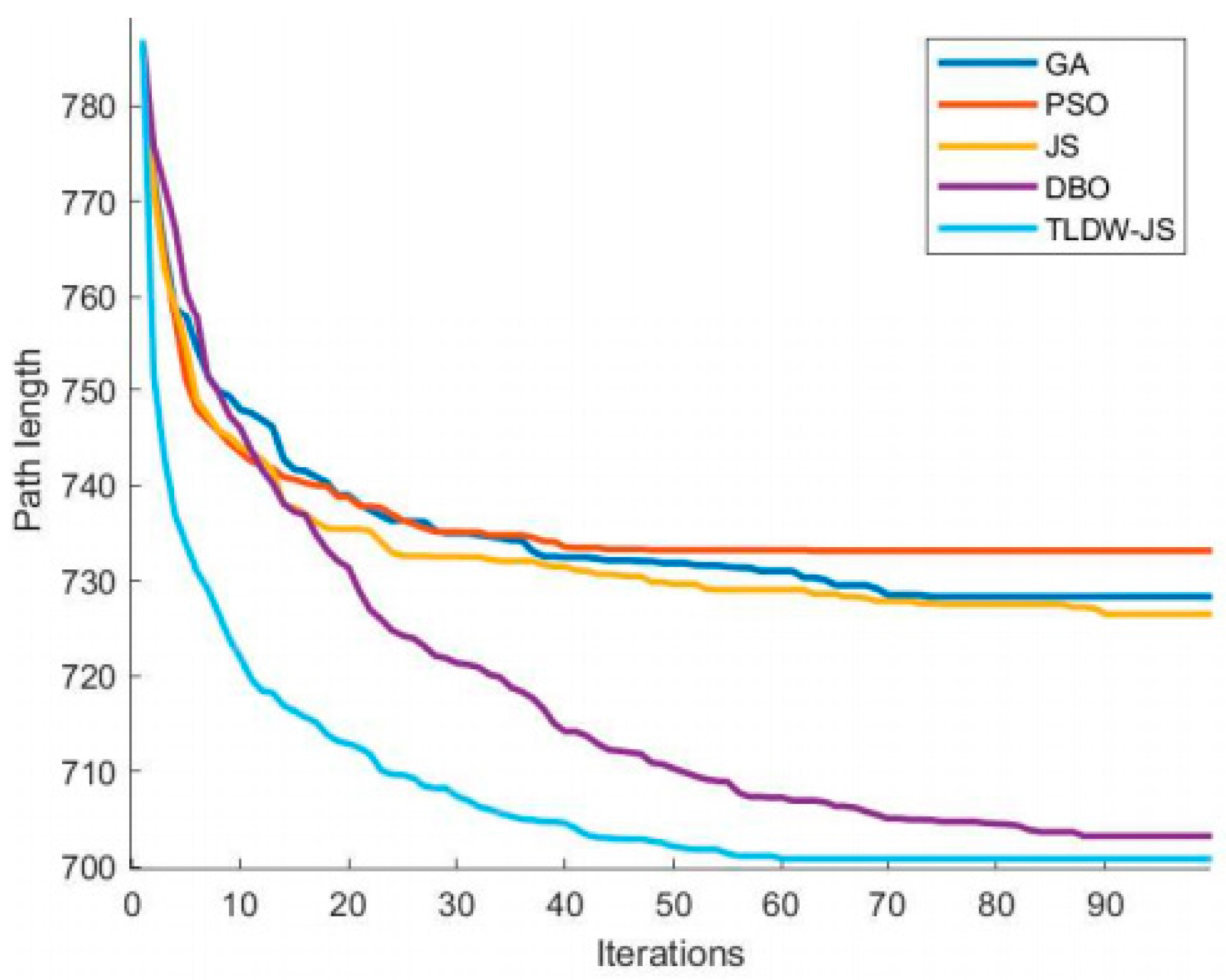
Figure 10 presents the average convergence curves of five algorithms over 100 iterations. GA converges after 30 iterations, with a final path length of 730 m, while PSO stabilizes after 20 iterations, slightly above 730 m. JS converges more slowly, reaching 735 m, whereas DBO shows a steeper initial decline, converging at 720 m, indicating better performance. TLDW-JS outperforms all algorithms, achieving the fastest convergence and the shortest final path length (710 m).

TLDW-JS’s rapid early convergence highlights the effectiveness of its improved strategy in the initial optimization phase. DBO ranks second in speed, while PSO and GA perform similarly but slower. JS exhibits the slowest convergence with significant fluctuations. The superior performance of TLDW-JS confirms its strong global search capability and ability to find the optimal solution efficiently.

3.2.2. Convergence Efficiency Comparison of Different Algorithms

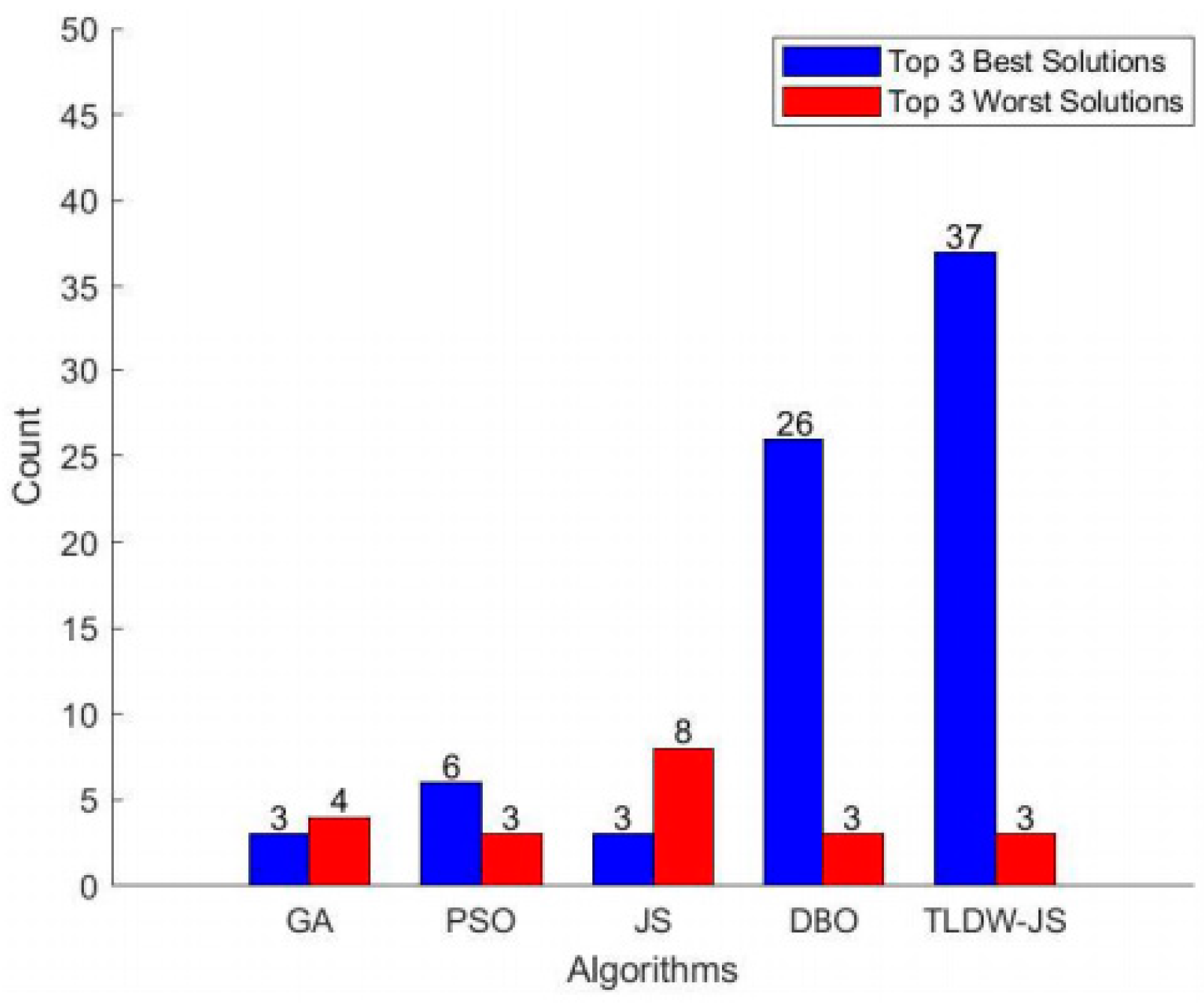
Figure 11 compares the top three and worst three solutions across five algorithms. TLDW-JS leads with 37 top optimal solutions, outpacing DBO (26) and PSO (6). GA and JS only achieved three optimal solutions each, with JS also recording the most suboptimal results (eight occurrences). TLDW-JS, DBO, and PSO had greater stability, each producing just three suboptimal solutions, highlighting TLDW-JS’s superior convergence and robustness.

Table 4. Convergence iteration metrics for different algorithms.

Algorithm	Min Convergence Iteration	Max Convergence Iteration	Average Convergence Iteration	Average Iteration Times (s)
GA	3	97	44.7	1.1
PSO	3	43	19.3	0.9
JS	2	72	31.3	1.3
DBO	13	88	55.9	0.9
TLDW-JS	9	62	42.6	3.2

shows iteration counts for five algorithms applied to the VFSMRCTP model. JS converges the fastest with two iterations, followed by GA and PSO, requiring three iterations. DBO and TLDW-JS take more iterations, with minimum counts of 13 and 9, respectively. GA shows the highest variability, reaching up to 97 iterations, while PSO is more stable with a maximum of 43 iterations. PSO also has the fastest average convergence speed (19.3 iterations), while TLDW-JS averages 42.6 iterations. In terms of average iteration time, PSO and DBO have the lowest times (0.9 s per iteration), while TLDW-JS takes 3.2 s due to its more complex approach.

In summary, while GA and JS require fewer iterations than TLDW-JS, Figure 10 and Figure 11 show that their rapid convergence often leads to local optima, with significantly fewer top three optimal solutions, indicating lower convergence efficiency. TLDW-JS has a moderate average convergence rate but achieves top three optimal solutions in about 50% of cases, demonstrating a high probability of reaching the global optimum. Additionally, it converges to shorter path lengths. Despite requiring more iterations and having higher computational costs, TLDW-JS achieves the highest convergence efficiency, offering superior accuracy and stability in approximating the global optimal solution.

3.2.3. Stability and Scalability Comparison of Different Algorithms

Figure 12 shows a box plot comparing the stability of various algorithms through IQR and median path length. TLDW-JS has the narrowest IQR and lowest median, indicating superior stability and path optimization. DBO shows good stability but performs worse than TLDW-JS. PSO has more variability with a wider IQR, while GA and JS show noticeable outliers, reflecting significant fluctuations and lower stability

Table 5. Experimental results of varying task numbers.

Number of Tasks	Algorithm	Mean Path Length (m)	Mean Convergence Iteration
10	GA	734.8	44.7
10	TLDW-JS	707.2	42.5
10	DBO	717.8	55.9
10	PSO	736.5	19.3
10	JS	732.9	31.2
20	GA	1054.3	46.3
20	TLDW-JS	962.5	43.9
20	DBO	988.4	63.5
20	PSO	1102.8	35.8
20	JS	1012.5	37.9
30	GA	1590.2	62.5
30	TLDW-JS	1388.2	45.1
30	DBO	1420.0	66.5
30	PSO	1450.6	48.8
30	JS	1456.5	52.8
40	GA	2856.9	78.5
40	TLDW-JS	2034.6	52.8
40	DBO	3072.6	82.5
40	PSO	3244.1	62.2
40	JS	2734.3	71.2
50	GA	6328.2	83.5
50	TLDW-JS	4628.5	53.2
50	DBO	5825.8	80.2
50	PSO	6128.6	60.5
50	JS	5878.5	80.6

compares different algorithms (GA, TLDW-JS, DBO, PSO, and JS) based on mean path length and convergence iterations as task numbers increase from 10 to 50. TLDW-JS consistently outperforms others, achieving the shortest mean path lengths and competitive convergence iterations. For example, with 50 tasks, TLDW-JS reaches a mean path length of 4628.5 m, significantly shorter than GA (6328.2 m) and DBO (5825.8 m), while maintaining a lower mean convergence iteration (53.2 iterations). This highlights TLDW-JS’s efficiency in handling path planning with increasing task complexity.

Figure 13a shows the variation in average convergence iterations for each algorithm with different task numbers. GA steadily increases, peaking at 50 tasks, while TLDW-JS maintains the lowest iterations, demonstrating superior convergence and stability. DBO performs well with fewer tasks but increases sharply as task numbers grow. PSO starts with the fewest iterations but becomes unstable with more tasks, while JS shows significant increases, indicating poor stability. Figure 13b compares the convergence performance, where TLDW-JS remains the most stable and efficient, with minimal iteration growth despite rising task complexity, showcasing its scalability in multi-tasking environments.

Table 6. Experimental results of varying agri-robot numbers.

Number of Agri-Robots	Algorithm	Average Path Length	Average Convergence Iteration
4	GA	502.1	52.6
4	TFDW-JS	464.4	47.2
4	DBO	474.6	64.6
4	PSO	474.5	42.7
4	JS	466.7	50.3
6	GA	552.4	47.2
6	TFDW-JS	522.4	44.5
6	DBO	548.3	57.3
6	PSO	538.4	30.5
6	JS	554.5	40.5
8	GA	734.8	44.7
8	TFDW-JS	707.2	42.5
8	DBO	717.8	55.9
8	PSO	736.5	19.3
8	JS	732.9	31.2
10	GA	640.5	35.6
10	TFDW-JS	630.8	32.4
10	DBO	644.2	40.5
10	PSO	642.6	26.7
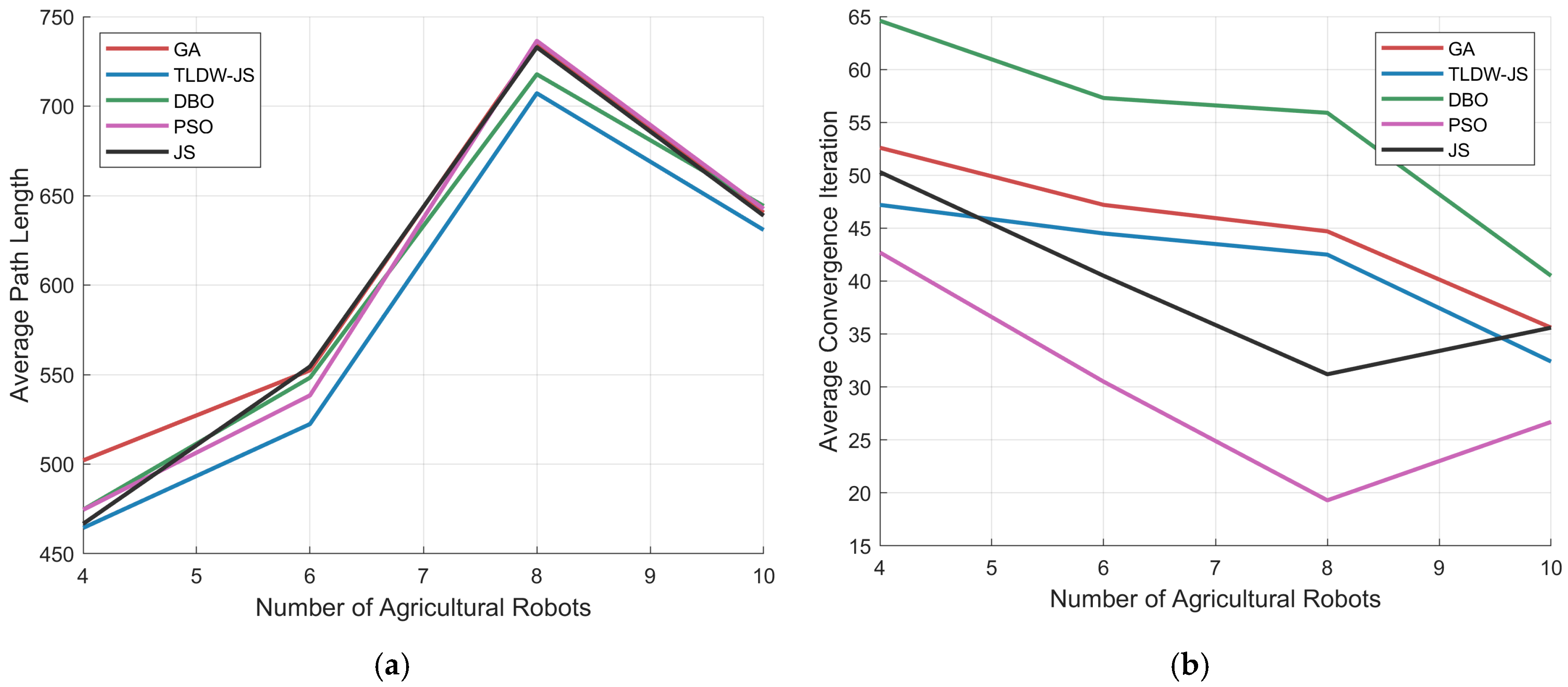
10	JS	638.8	35.6

compares trajectory planning algorithms (GA, TLDW-JS, DBO, PSO, and JS) with varying numbers of agricultural robots (four, six, eight, and ten). Path lengths generally increase with more robots, but TLDW-JS consistently achieves the shortest lengths, especially with four robots (464.4) and six robots (522.4). PSO converges fastest, requiring only 30.5 iterations for six robots and 19.3 for eight robots. TLDW-JS also shows efficient convergence, with 47.2, 44.5, and 42.5 iterations for four, six, and eight robots, respectively, balancing path optimization and convergence speed effectively.

Figure 14a,b show that as the number of robots increases, the path length grows for all algorithms. TLDW-JS consistently achieves the shortest paths, outperforming others, while PSO and GA show higher path lengths, especially for eight and ten robots. PSO converges the fastest, requiring only 19.3 iterations for eight robots, while TLDW-JS maintains efficient convergence with 42.5 iterations. DBO has the slowest convergence (57.3–64.6 iterations). Overall, TLDW-JS balances path optimization and convergence efficiency, whereas PSO, despite its speed, results in longer paths with more robots.

4. Discussion

The TLDW-JS algorithm developed in this study advances multi-robot collaborative trajectory planning for vertical farms. By incorporating multiple strategies such as Tent Chaos initialization, Lévy flight-based population updates, and nonlinear dynamic weight adjustment via a logistic function, the algorithm enhances the basic JS algorithm to address the unique challenges of vertical farming. These improvements overcome the key limitations of traditional optimization techniques, enabling better adaptation to the complex vertical farming environment.

Vertical farming, as an emerging sustainable agricultural solution, faces unique challenges when deploying multi-robot systems. These farms typically operate in space-constrained, multi-layered environments where robots must navigate between layers to perform tasks such as planting, monitoring, and harvesting. These tasks require collaboration between robots, making path planning more complex. Additionally, energy consumption is a key issue, as excessive use can compromise the economic viability of vertical farms. Given the complexity of the environment and interdependencies between robots, an optimization algorithm that ensures both accuracy and efficiency in path planning is essential.

The simulation results confirm TLDW-JS’s superior performance in multi-robot collaborative trajectory planning for vertical farms. Compared with traditional algorithms like GA, PSO, and DBO, TLDW-JS demonstrated several advantages (

Table 7. Performance comparison of TLDW-JS and traditional algorithms.

Algorithm	Average Path Length (m)	Path Length Reduction (%)	Optimal Top Three Solutions (%)	Average Iterations to Converge
GA	734.8	31.7	12	44.7
PSO	736.5	31.6	24	19.3
DBO	717.8	33.2	52	55.9
JS	732.9	31.9	6	31.3
TLDW-JS	707.2	34.3	74	42.6

). Specifically, TLDW-JS (707.2 m) outperformed GA (734.8 m) and PSO (736.5 m) in optimized path length, reducing the average path length by 34.3%. In terms of convergence consistency, TLDW-JS achieved the optimal top three solutions 74% of the time, far surpassing GA (6%) and PSO (12%). This indicates its ability to explore the solution space more effectively and avoid the local minimum.

Though DBO reduced the average path length by 33.2%, it required 31.2% more iterations than TLDW-JS (55.9 iterations), and TLDW-JS also found 29.7% more optimal solutions than DBO. Moreover, compared to the original JS algorithm, TLDW-JS demonstrated better path length, solution consistency, and stability.

In vertical farming, task interdependencies and the need for robot collaboration make path optimization more challenging. GA struggles with dynamic coordination between robots and tends to become trapped in local optima, particularly in complex environments like vertical farms. PSO, while effective in simpler problems, is also limited by local optima in multi-robot collaborative tasks. DBO excels at finding global optima but struggles with slow convergence and precision, which compromises its suitability for coordinating multiple robots in dynamic environments.

TLDW-JS outperforms other algorithms due to its unique design and adaptability to vertical farming scenarios. The Lévy flight mechanism enhances the global search capability, allowing the algorithm to avoid local optima and better handle multi-modal problems. This is crucial in vertical farms, where global optimization and coordination across multiple tasks are necessary. Additionally, Tent Chaos initialization ensures a more uniform and diverse initial population distribution, reducing exploration issues that are common with random initialization methods. The nonlinear dynamic weight adjustment mechanism balances exploration and exploitation throughout the optimization process, improving convergence speed and solution refinement, which is critical for multi-robot collaboration in complex environments.

Despite its advantages, TLDW-JS has computational cost limitations. The introduction of mechanisms like Lévy flight, Tent Chaos initialization, and dynamic weight adjustment significantly improves search efficiency and solution quality but increases computational complexity. Specifically, Lévy flight adds to the computational burden during each iteration, particularly in large-scale applications. The algorithm’s computational load increases with the number of tasks and robots, and its time complexity may become a bottleneck in practical applications. Additionally, the dynamic weight adjustment mechanism introduces further computational demands, which could impact real-time performance, especially in large-scale systems with higher hardware requirements. Thus, while TLDW-JS offers considerable performance improvements, balancing its optimization capabilities with computational costs remains a challenge for practical implementation.

5. Conclusions

This paper presents three main contributions to the field of multi-robot collaborative trajectory planning in vertical farming. First, this study formulated the Vertical Farming System Multi-Robot Collaborative Trajectory Planning (VFSMRCTP) model, which captures the complexities of a real vertical farm in a mathematical form that can be interpreted by computers. Second, this study developed the TLDW-JS algorithm, a novel approach for solving the optimal path planning problem for multi-robot collaboration in vertical farms. Finally, this study evaluated the performance of TLDW-JS through a comparison with benchmark algorithms.

Simulation results demonstrate that TLDW-JS outperforms traditional algorithms (GA, PSO, DBO, and JS) in key performance metrics. TLDW-JS reduced the average path length by 34.3%, achieved the optimal top three solutions 74% of the time, and required an average of 55.9 iterations to converge. These findings confirm the effectiveness of TLDW-JS in optimizing energy efficiency and supporting the feasibility of automated systems in vertical farming.

Future research could refine multi-objective optimization, enhance energy modeling, and improve VFSMRCTP’s robustness. Testing TLDW-JS in dynamic environments would aid real-world deployment. Beyond agriculture, its applications extend to manufacturing, logistics, and automation, optimizing efficiency and adaptability, and investigating the real-time performance of the TLDW-JS algorithm, particularly in dynamic environments with changing tasks and robot interactions, to assess its applicability in live vertical farming operations. Additionally, this study will be extended from simulations to real-world vertical farming environments, with physical experiments conducted to further validate and optimize the proposed methods.