Research on the Prediction Model and Formation Law of Drying Cracks of Paddy Based on Multi-Physical Field Coupling
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Material
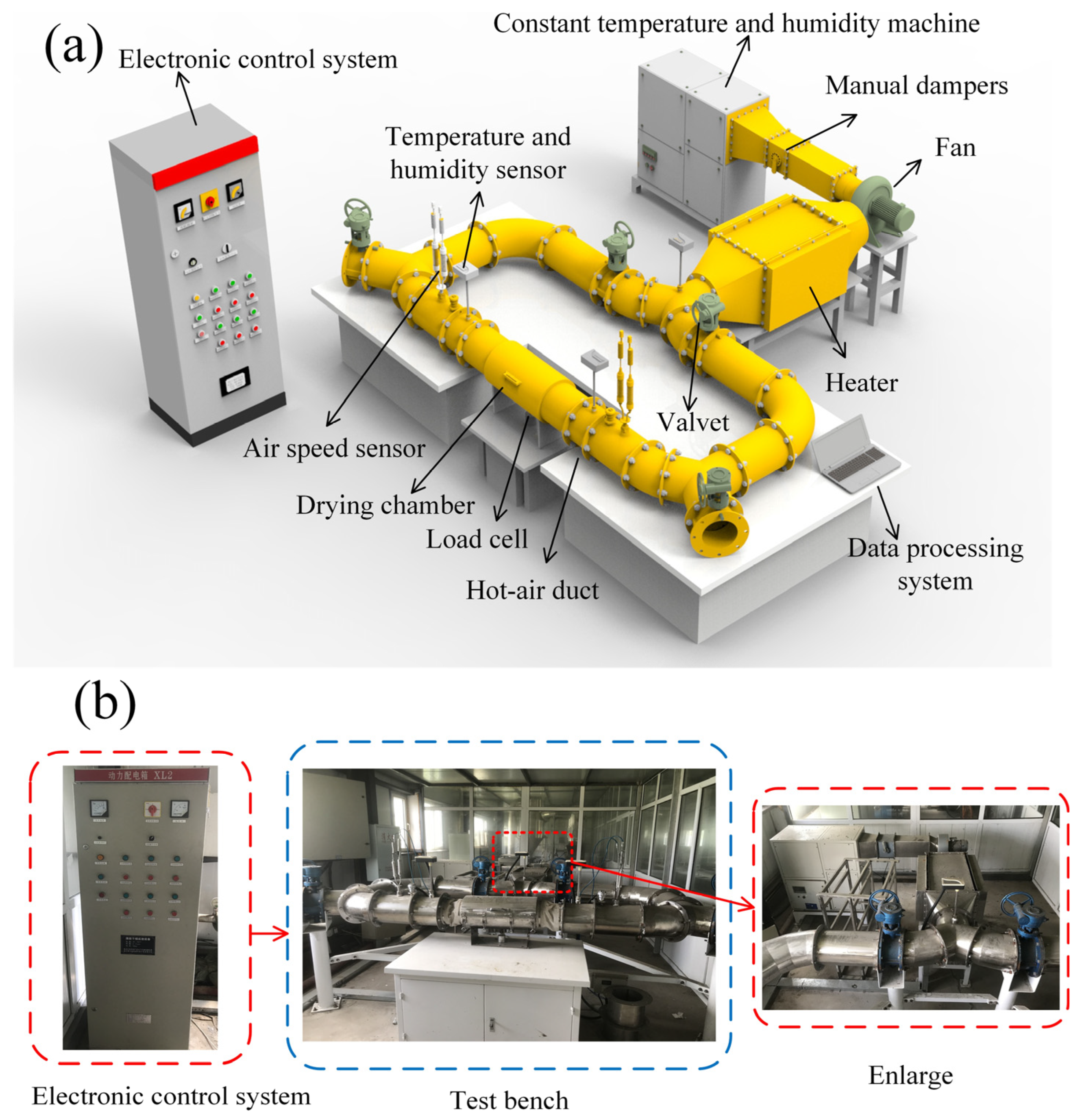
2.2. Experimental Devices and Processes
2.3. Drying Parameters
2.4. Three-Point Bending Test
2.5. Cracking Statistics
2.6. Numerical Simulation of Drying
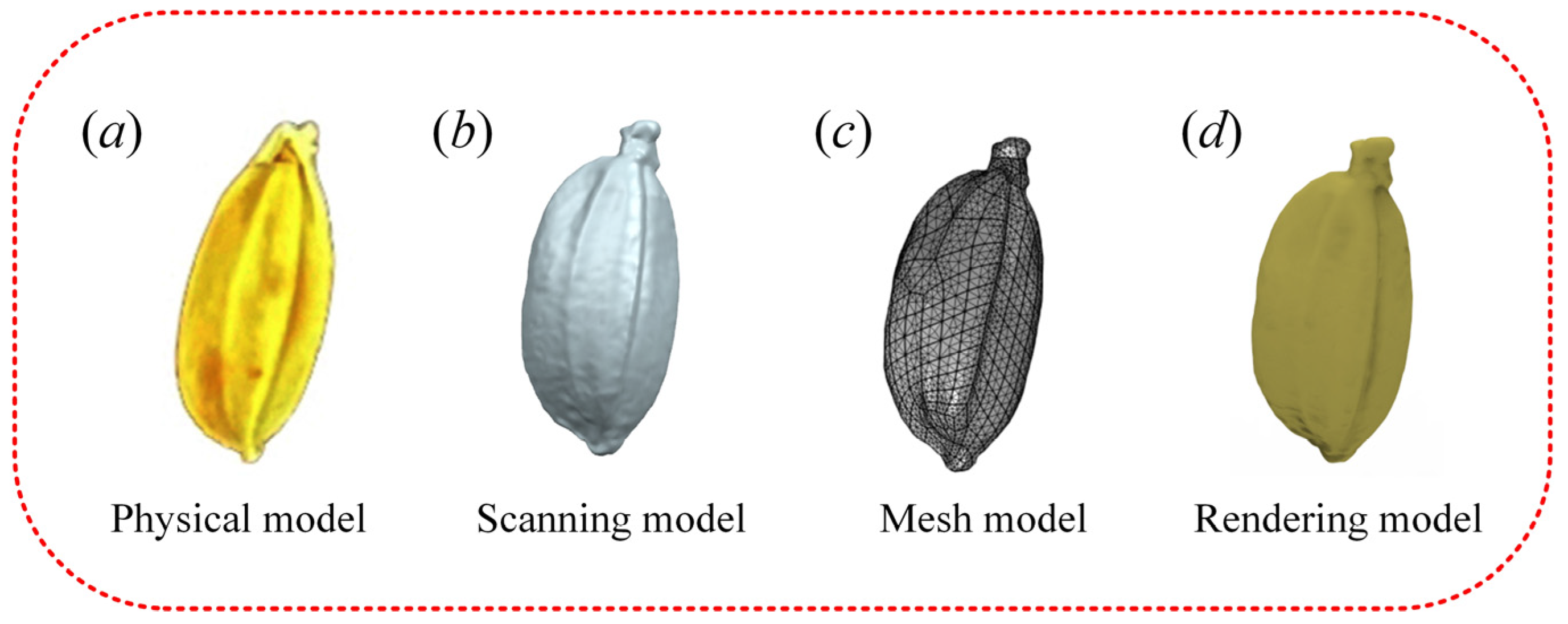
2.6.1. Geometric Modeling of Paddy
2.6.2. Assumptions of the Model
2.6.3. Heat Transfer Equation
2.6.4. Mass Transfer Equation
2.6.5. Stress Modeling
2.6.6. Model Solving
3. Results and Discussion
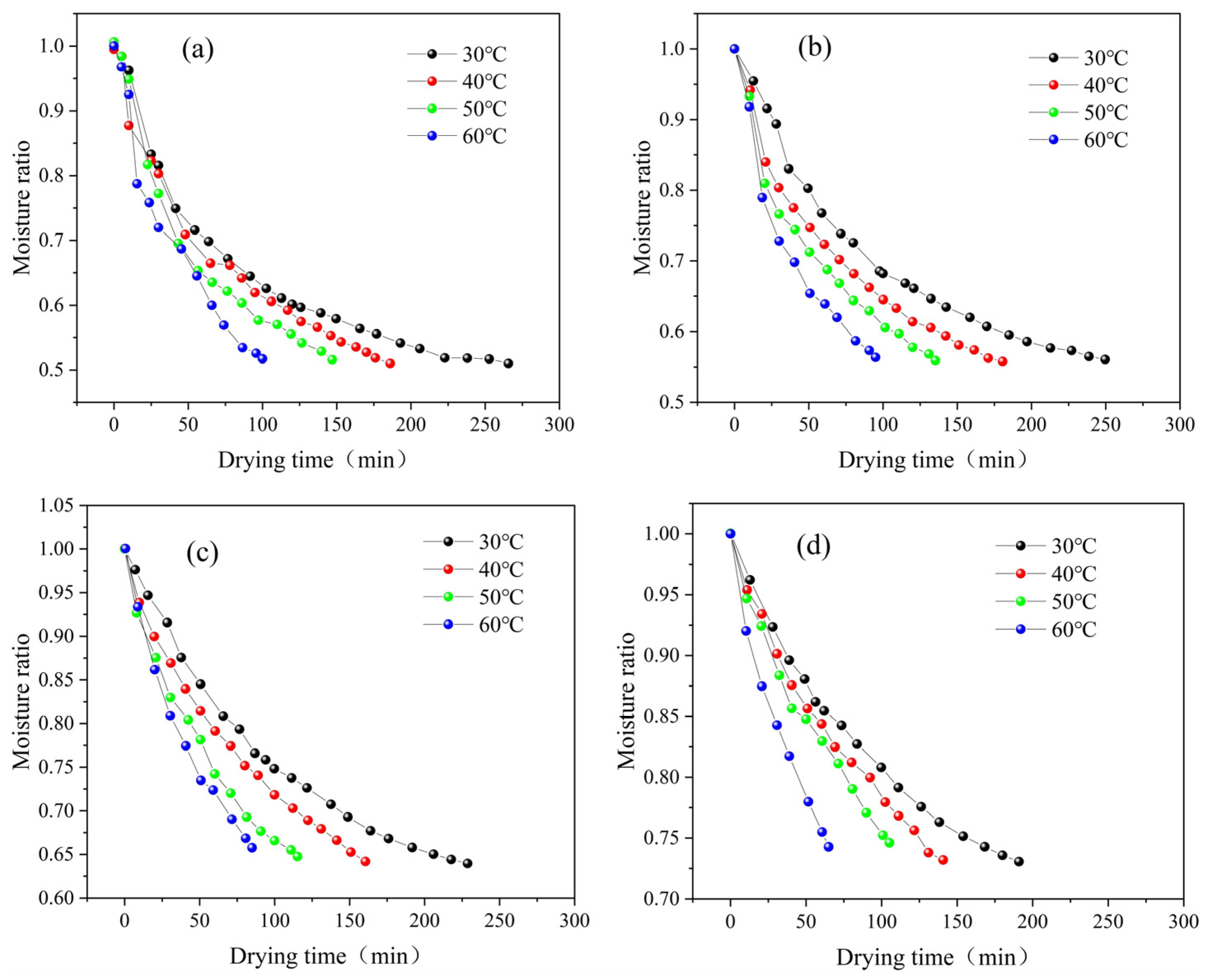
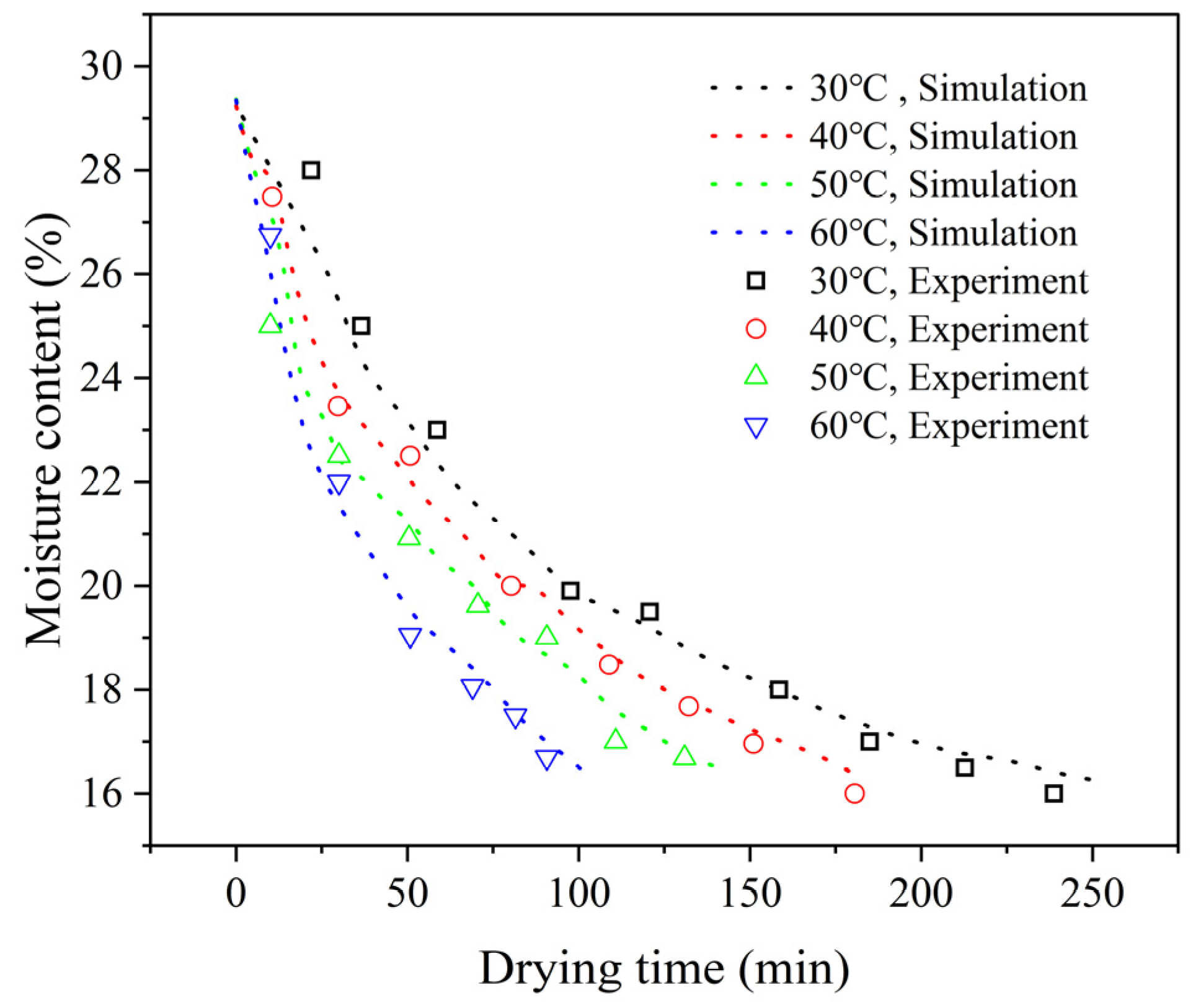
3.1. Drying Characteristics of Paddy Under Drying Conditions at 30, 40, 50 and 60 °C
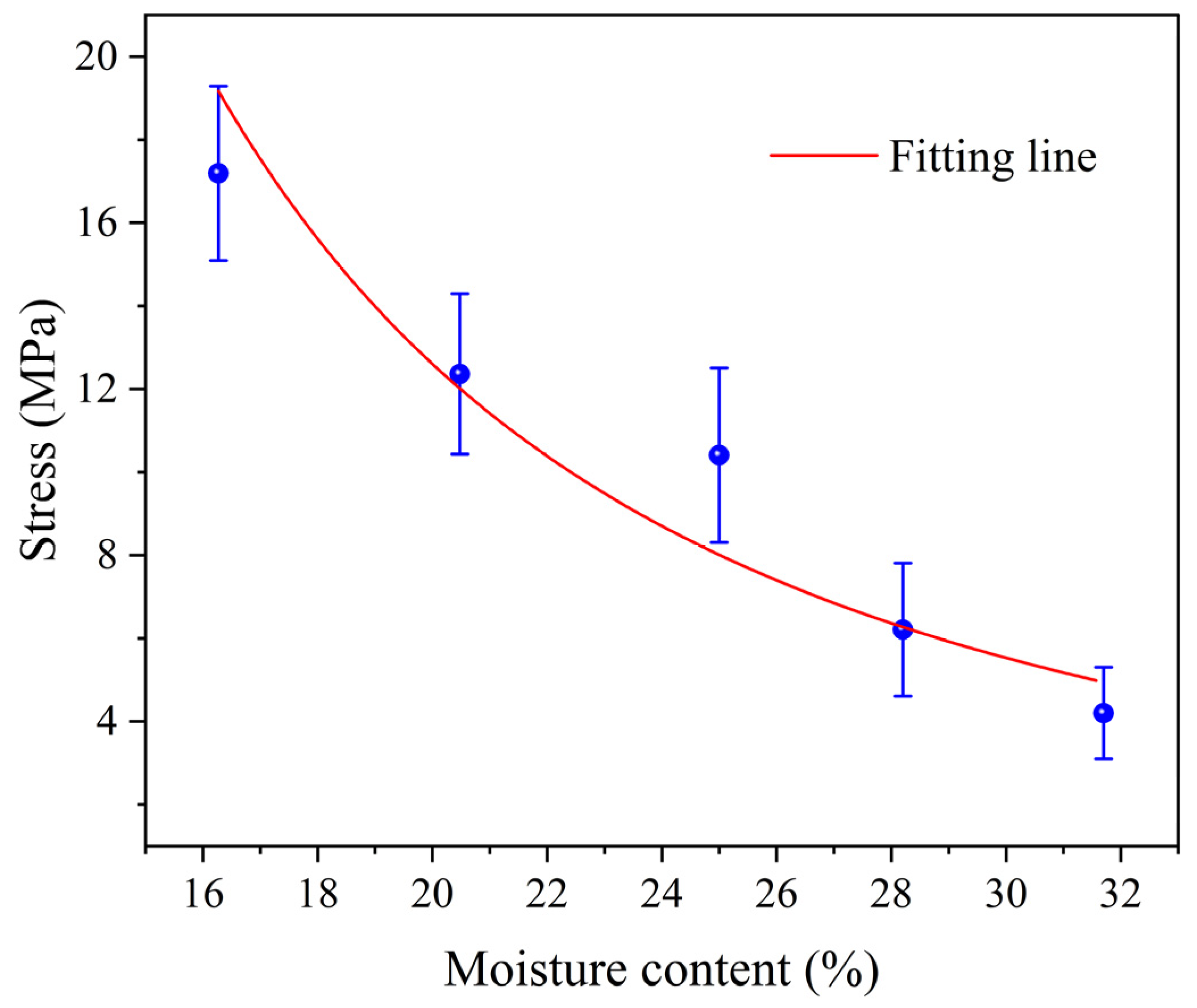
3.2. Statistical Analysis of the Percentage of Drying Cracks During Paddy Drying
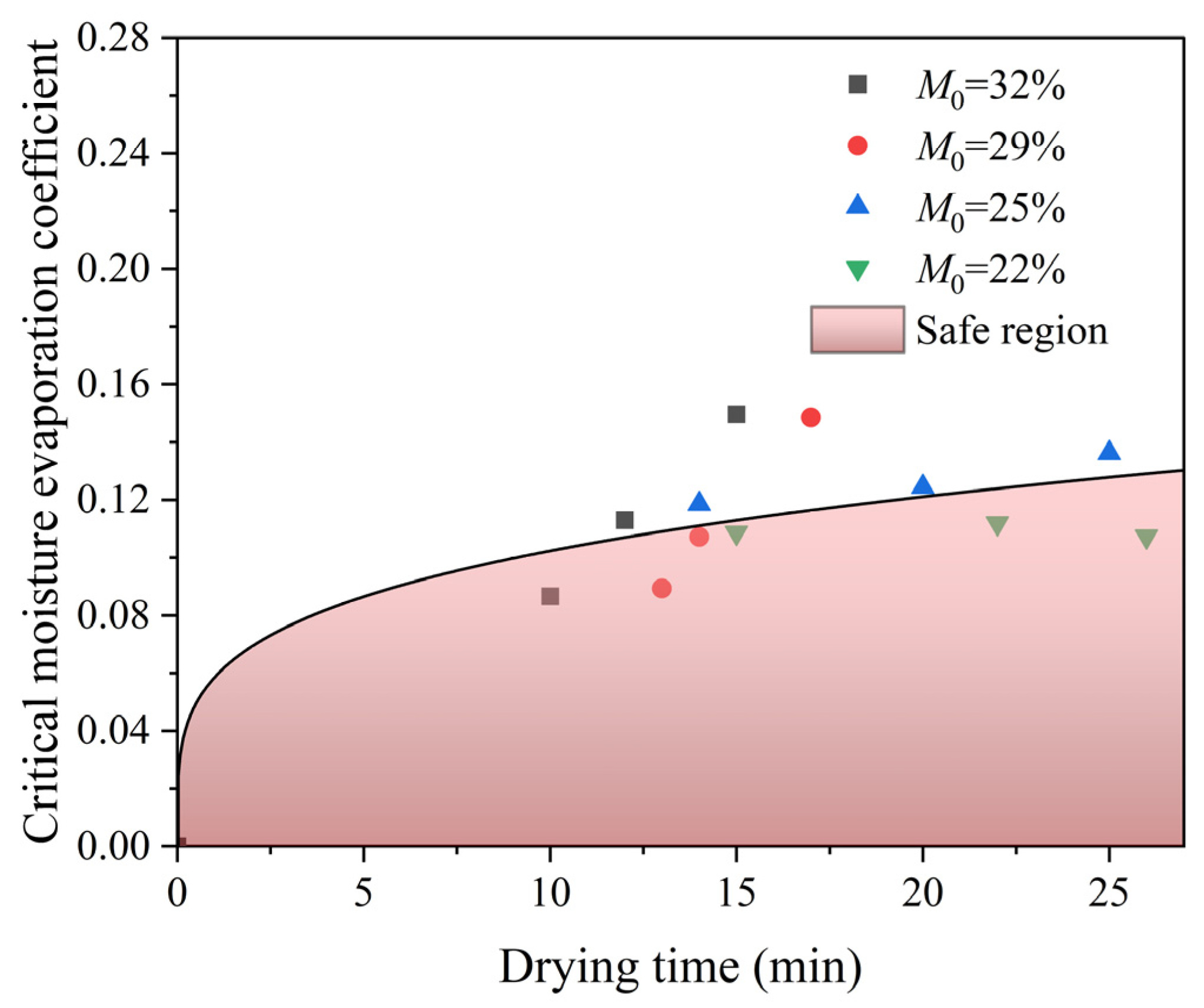
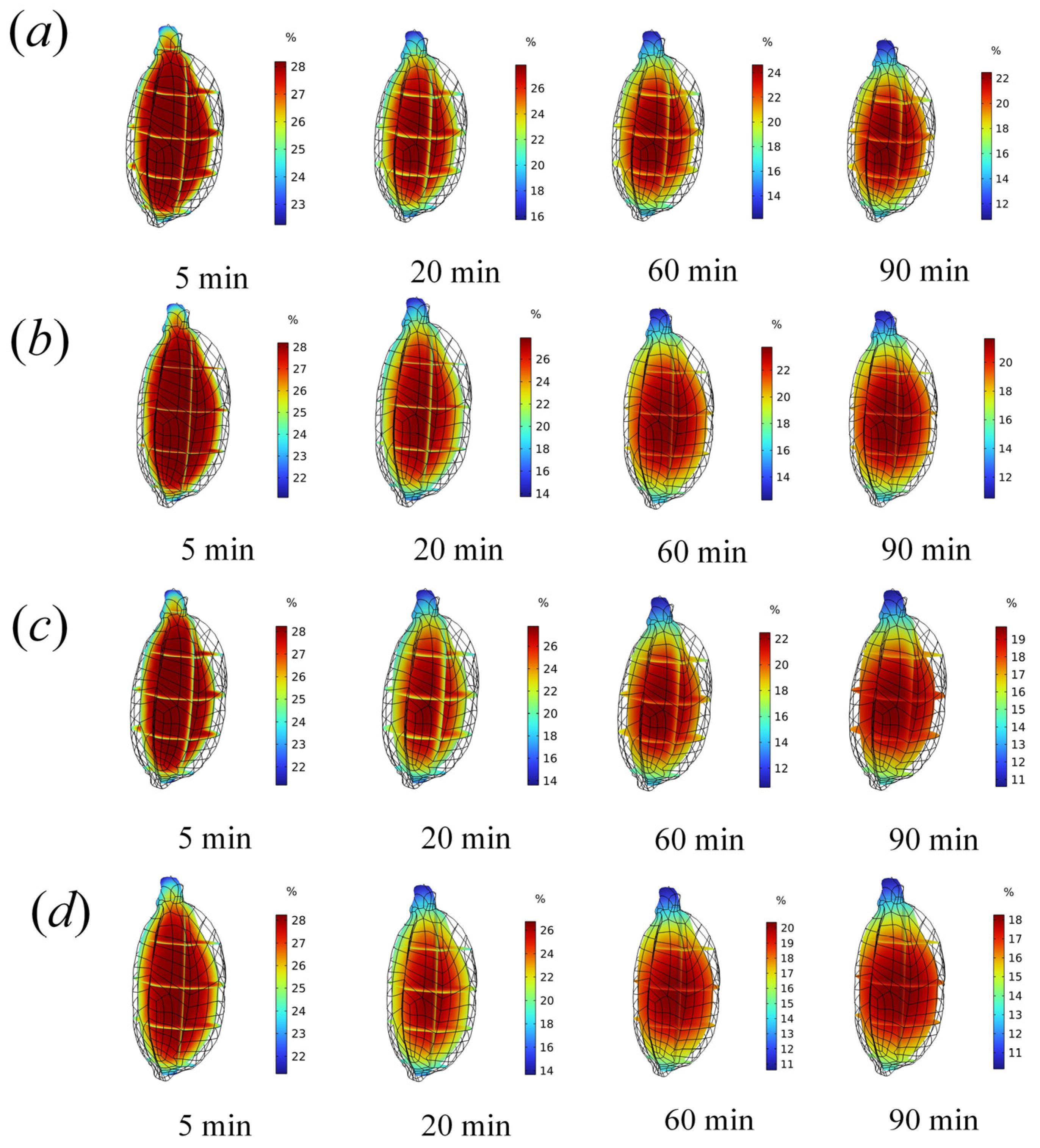
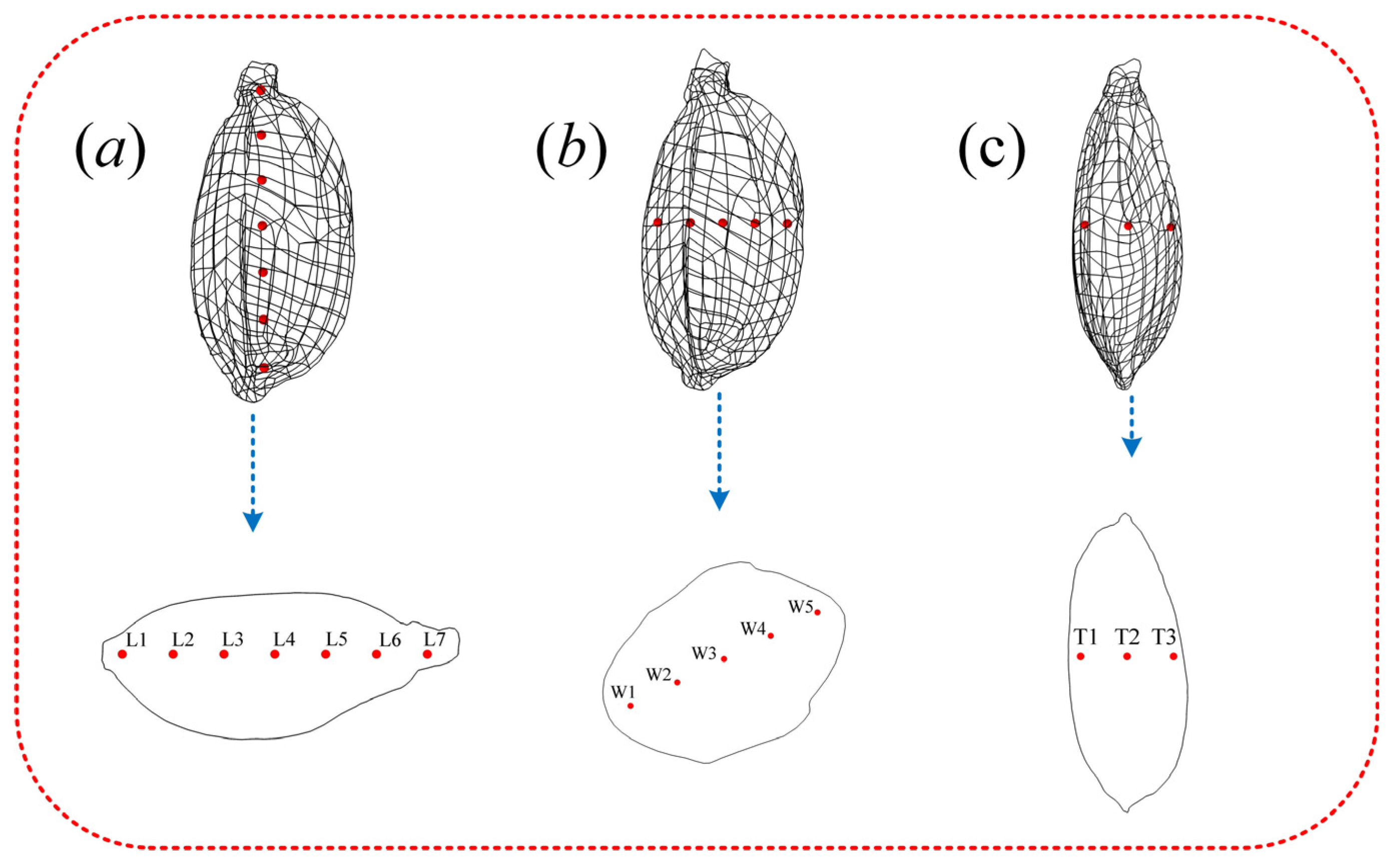
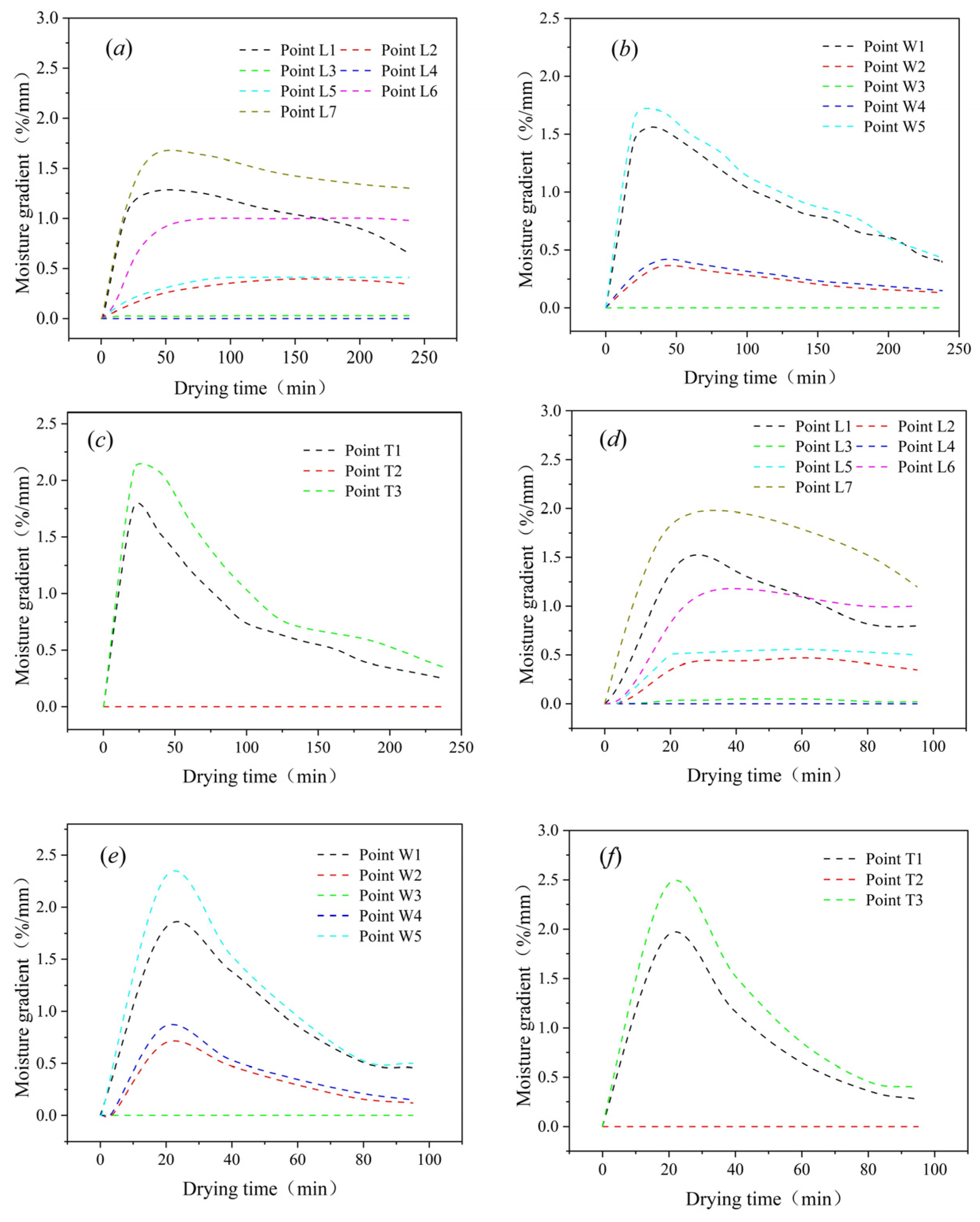
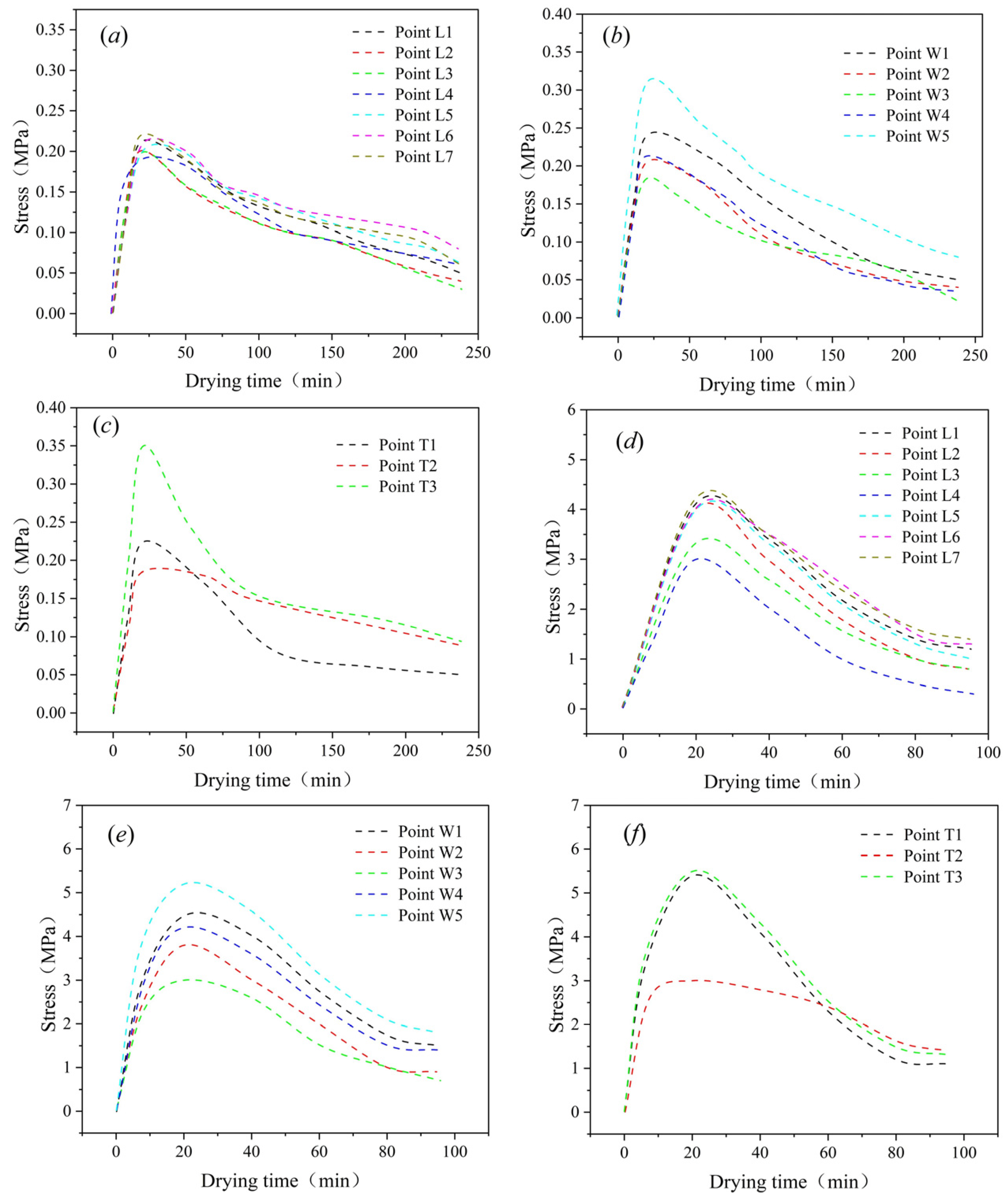
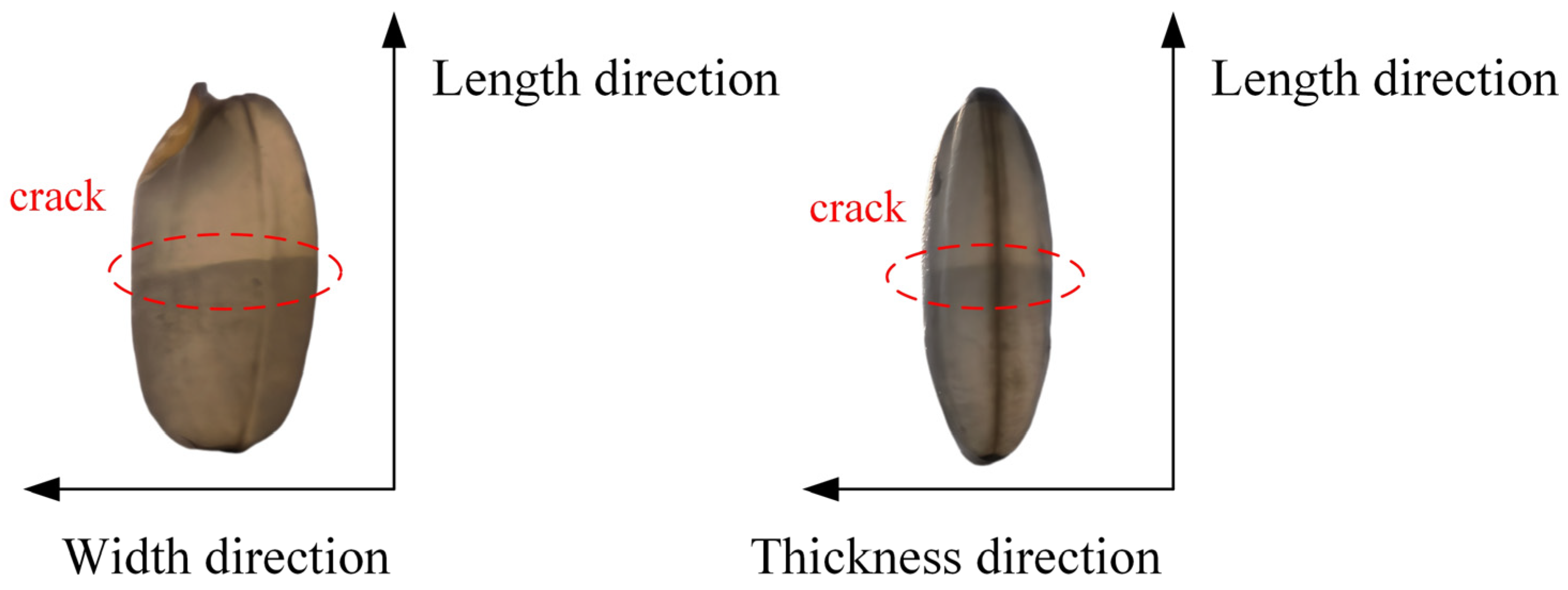
3.3. Regional Division of Drying Crack Formation in Paddy
3.4. Analysis of Crack Formation Mechanism
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Mahmood, N.; Liu, Y.; Zheng, X.; Munir, Z.; Pandiselvam, R.; Zhang, Y.; Ali Saleemi, M.; Yves, H.; Sufyan, M.; Lei, D. Influences of emerging drying technologies on rice quality. Food Res. Int. 2024, 184, 114264. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Che, G.; Wan, L.; Wang, X.; Tang, H. Combination of LF-NMR and BP-ANN to monitor the moisture content of rice during hot-air drying. J. Food Process Eng. 2022, 45, e14102. [Google Scholar] [CrossRef]
- Wang, C.; Pei, Y.; Mu, Z.; Fan, L.; Kong, J.; Tian, G.; Miao, S.; Meng, X.; Qiu, H. Simulation analysis of 3-D airflow and temperature uniformity of paddy in a laboratory drying oven. Foods 2024, 13, 3466. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Fang, Z.; Li, C.; Li, C. Deep-learning-based model predictive control of an industrial-Scale multistate counter-flow paddy drying process. Foods 2023, 13, 43. [Google Scholar] [CrossRef]
- Qiu, Z.; Wu, F.; Hu, H.; Guo, J.; Wu, C.; Wang, P.; Ling, J.; Cui, Y.; Ye, J.; Fang, G.; et al. Deciphering the microbiological mechanisms underlying the impact of different storage conditions on rice grain quality. Foods 2024, 13, 266. [Google Scholar] [CrossRef]
- Shen, L.; Zhu, Y.; Wang, L.; Liu, C.; Liu, C.; Zheng, X. Improvement of cooking quality of germinated brown rice attributed to the fissures caused by microwave drying. J. Food Sci. Technol. 2019, 56, 2737–2749. [Google Scholar] [CrossRef]
- Chokphoemphun, S.; Hongkong, S.; Chokphoemphun, S. Artificial neural network for drying behavior prediction of paddy in developed chamber fluidized–bed dryer. Comput. Electron. Agric. 2024, 220, 108888. [Google Scholar] [CrossRef]
- Wang, H.; Che, G.; Wan, L.; Tang, H. Effects of drying approaches combined with variable temperature and tempering on the physicochemical quality of rice. Dry. Technol. 2022, 41, 1199–1213. [Google Scholar] [CrossRef]
- Mahmood, N.; Liu, Y.; Munir, Z.; Zhang, Y.; Niazi, B. Effects of hot air assisted radio frequency drying on heating uniformity, drying characteristics and quality of paddy. LWT-Food Sci. Technol. 2022, 158, 113131. [Google Scholar] [CrossRef]
- Chitsuthipakorn, K.; Thanapornpoonpong, S. Effect of large-Sscale paddy rice drying process using hot air combined with radio frequency heating on milling and cooking qualities of milled rice. Foods 2022, 11, 519. [Google Scholar] [CrossRef]
- Ying, T.; Spang, E. Paddy drying technologies: A review of existing literature on energy consumption. Processes 2024, 12, 532. [Google Scholar] [CrossRef]
- Zhang, P.; Li, B.; Hu, Z.; Zhang, Q.; Zhu, Y.; Hao, W. Effects of ultrasonic and microwave treatment on color, quality and drying characteristics of rice. J. Cereal Sci. 2024, 116, 103856. [Google Scholar] [CrossRef]
- Mondal, M.H.T.; Sarker, M.S.H. Comprehensive energy analysis and environmental sustainability of industrial grain drying. Renew. Sustain. Energy Rev. 2024, 199, 114442. [Google Scholar] [CrossRef]
- Wang, H.; Che, G.; Wan, L.; Chen, Z.; Sun, W.; Tang, H. Effect of variable temperature levels on drying characteristics and quality indices of rice in continuous drying and multi-stage intermittent drying. J. Food Process Eng. 2023, 46, e14356. [Google Scholar] [CrossRef]
- Wang, H.; Che, G.; Wan, L. Analysis of the diffusion characteristics and activation energy of rice drying using low-field nuclear magnetic resonance. J. Food Process Eng. 2021, 44, e13870. [Google Scholar] [CrossRef]
- Liu, H.; He, Y.; Tang, T.; Zhai, M. Cracking prediction of germinated brown rice based on intragranular drying kinetics. Powder Technol. 2022, 406, 117587. [Google Scholar] [CrossRef]
- Ghasemi, A.; Sadeghi, M.; Mireei, S.A. Multi-stage intermittent drying of rough rice in terms of tempering and stress cracking indices and moisture gradients interpretation. Dry. Technol. 2017, 36, 109–117. [Google Scholar] [CrossRef]
- Chayjan, R.A.; Ghasemi, A.; Sadeghi, M. Stress fissuring and process duration during rough rice convective drying affected by continuous and stepwise changes in air temperature. Dry. Technol. 2018, 37, 198–207. [Google Scholar] [CrossRef]
- Chungcharoen, T.; Prachayawarakorn, S.; Soponronnarit, S.; Tungtrakul, P. Effect of drying temperature on drying characteristics and quality of germinated rices prepared from paddy and brown rice. Dry. Technol. 2012, 30, 1844–1853. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Zhang, Y.; Chen, H.; Sun, J.; He, L. A stochastic analysis of glass crack initiation under thermal loading. Appl. Therm. Eng. 2014, 67, 447–457. [Google Scholar] [CrossRef]
- Chen, Z.; Wassgren, C.; Ambrose, R. Measured damage resistance of corn and wheat kernels to compression, friction, and repeated impacts. Powder Technol. 2021, 380, 638–648. [Google Scholar] [CrossRef]
- Dong, R.; Lu, Z.; Liu, Z.; Nishiyama, Y.; Cao, W. Moisture distribution in a rice kernel during tempering drying. J. Food Eng. 2009, 91, 126–132. [Google Scholar] [CrossRef]
- Pruengam, P.; Soponronnarit, S.; Prachayawarakorn, S.; Devahastin, S. Evolution of mechanical properties of parboiled brown rice kernels during impinging stream drying. Dry. Technol. 2016, 34, 1843–1853. [Google Scholar] [CrossRef]
- Cnossen, A.G.; Jiménez, M.J.; Siebenmorgen, T.J. Rice fissuring response to high drying and tempering temperatures. J. Food Eng. 2003, 59, 61–69. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, H.; Li, F. A study on drying models and internal stresses of the rice kernel during infrared drying. Dry. Technol. 2017, 35, 680–688. [Google Scholar] [CrossRef]
- Wang, H.; Che, G.; Wan, L.; Liu, M.; Sun, W. Experimental study on drying characteristics of rice by low-field nuclear magnetic resonance. J. Food Process Eng. 2021, 44, e13705. [Google Scholar] [CrossRef]
- Shen, L.; Gao, M.; Zhu, Y.; Liu, C.; Wang, L.; Kamruzzaman, M.; Liu, C.; Zheng, X. Microwave drying of germinated brown rice: Correlation of drying characteristics with the final quality. Innov. Food Sci. Emerg. Technol. 2021, 70, 102673. [Google Scholar] [CrossRef]
- Xiao, H.; Pang, C.; Wang, L.; Bai, J.; Yang, W.; Gao, Z. Drying kinetics and quality of Monukka seedless grapes dried in an air-impingement jet dryer. Biosyst. Eng. 2010, 105, 233–240. [Google Scholar] [CrossRef]
- Li, X.; Yang, K.; Wang, Y.; Du, X. Study on heat and moisture transfer of nonspherical rice during hot-air drying in thin-layer grain pile. J. Food Process Eng. 2024, 47, e14597. [Google Scholar] [CrossRef]
- Rattanamechaiskul, C.; Junka, N.; Prachayawarakorn, S.; Soponronnarit, S. Modeling the improved textural properties of purple waxy rice dried through fluidization. Dry. Technol. 2017, 36, 1061–1075. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, J.; Wang, S.; Wu, Z. Investigation of glass transition behavior in a rice kernel drying process by mathematical modeling. Dry. Technol. 2019, 38, 1092–1105. [Google Scholar] [CrossRef]
- Law, M.C.; Chang, J.S.L.; Chan, Y.S.; Pui, D.Y.; You, K.Y. Experimental characterization and modeling of microwave heating of oil palm kernels, mesocarps, and empty fruit bunches. Dry. Technol. 2018, 37, 69–91. [Google Scholar] [CrossRef]
- Srisang, N.; Soponronnarit, S.; Thuwapanichayanan, R.; Prachayawarakorn, S. Modeling heat and mass transfer–induced stresses in germinated brown rice kernels during fluidized bed drying. Dry. Technol. 2015, 34, 619–634. [Google Scholar] [CrossRef]
- Le, K.H.; Tran, T.T.H.; Kharaghani, A.; Tsotsas, E. Experimental benchmarking of diffusion and reduced models for convective drying of single rice grains. Dry. Technol. 2019, 38, 200–210. [Google Scholar] [CrossRef]
- Kumar, C.; Karim, M.; Joardder, M. Intermittent drying of food products: A critical review. J. Food Eng. 2014, 121, 48–57. [Google Scholar] [CrossRef]
- Li, M.; Chen, Y.; Wang, X.; Cheng, S.; Liu, F.; Huang, L. Determination of drying kinetics and quality changes of Panax quinquefolium L. dried in hot-blast air. LWT-Food Sci. Technol. 2019, 116, 108563. [Google Scholar] [CrossRef]
- Li, L.; Zhang, M.; Yang, P. Suitability of LF-NMR to analysis water state and predict dielectric properties of Chinese yam during microwave vacuum drying. LWT-Food Sci. Technol. 2019, 105, 257–264. [Google Scholar] [CrossRef]
- Dalbhagat, C.G.; Mishra, H.N. Effect of the drying process on the color change, fissure development, and morphology of fortified rice kernels. J. Food Process Eng. 2021, 44, e13719. [Google Scholar] [CrossRef]
- GB/T 21015-2023; Drying Technical Specifications for Paddy. Standards of China: Beijing, China, 2023.
- Nosrati, M.; Zare, D.; Nassiri, S.M.; Chen, G.; Jafari, A. Experimental and numerical study of intermittent drying of rough rice in a combined FIR-dryer. Dry. Technol. 2021, 40, 1967–1979. [Google Scholar] [CrossRef]
- Nasrnia, E.; Sadeghi, M.; Raeisi Isa-Abadi, A.; Mireei, S.A. A novel simulation model to analyze rice intermittent drying considering glass transition concept. J. Food Eng. 2024, 364, 111819. [Google Scholar] [CrossRef]
- Odek, Z.R.; Siebenmorgen, T.J.; Saxena, A. Fissuring kinetics of rough rice during the drying process. Appl. Eng. Agric. 2020, 36, 639–645. [Google Scholar] [CrossRef]
- Apinyavisit, K.; Nathakaranakule, A.; Mittal, G.S.; Soponronnarit, S. Heat and mass transfer properties of longan shrinking from a spherical to an irregular shape during drying. Biosyst. Eng. 2018, 169, 11–21. [Google Scholar] [CrossRef]


| M0 (%) | Drying Temperature (°C) | a | b | c | d | Coefficient of Determination | Mean Relative Percentage Error (%) |
|---|---|---|---|---|---|---|---|
| 32 | 30 | −26.98 | 0.001 | 27.68 | 0.032 | 0.86 | 10.68 |
| 40 | −5.69 | 0.002 | 6.51 | 0.033 | 0.92 | 8.53 | |
| 50 | 0.007 | 0.04 | 1.44 | 0.106 | 0.94 | 7.86 | |
| 60 | 0.001 | 0.14 | 0.82 | 0.28 | 0.97 | 5.44 | |
| 29 | 30 | −0.001 | 0.038 | 0.22 | 0.006 | 0.92 | 10.24 |
| 40 | −69.65 | 0.001 | 70.31 | 0.11 | 0.87 | 11.42 | |
| 50 | −8.96 | 0.003 | 9.89 | 0.16 | 0.97 | 7.54 | |
| 60 | −0.18 | 0.0403 | 0.55 | 0.35 | 0.99 | 4.7 | |
| 25 | 30 | −9.86 | 0.001 | 9.91 | 0.017 | 0.93 | 10.25 |
| 40 | −53.36 | 0.0017 | 54.13 | 0.115 | 0.86 | 11.16 | |
| 50 | 338.46 | 0.0016 | −337.81 | −0.46 | 0.96 | 8.7 | |
| 60 | −14.63 | 0.008 | 15.59 | 0.45 | 0.95 | 9.73 | |
| 22 | 30 | −8.99 | 0.0018 | 9.02 | 0.025 | 0.87 | 10.32 |
| 40 | −113.2 | 0.001 | 113.8 | 0.17 | 0.85 | 9.7 | |
| 50 | −1.99 | 0.011 | 2.55 | 0.15 | 0.98 | 7.04 | |
| 60 | −32.12 | 0.008 | 32.84 | 0.69 | 0.98 | 5.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, Z.; Che, G.; Wan, L.; Chen, Z. Research on the Prediction Model and Formation Law of Drying Cracks of Paddy Based on Multi-Physical Field Coupling. Agriculture 2025, 15, 383. https://doi.org/10.3390/agriculture15040383
Wang H, Wang Z, Che G, Wan L, Chen Z. Research on the Prediction Model and Formation Law of Drying Cracks of Paddy Based on Multi-Physical Field Coupling. Agriculture. 2025; 15(4):383. https://doi.org/10.3390/agriculture15040383
Chicago/Turabian StyleWang, Hongchao, Ziyu Wang, Gang Che, Lin Wan, and Zhengfa Chen. 2025. "Research on the Prediction Model and Formation Law of Drying Cracks of Paddy Based on Multi-Physical Field Coupling" Agriculture 15, no. 4: 383. https://doi.org/10.3390/agriculture15040383
APA StyleWang, H., Wang, Z., Che, G., Wan, L., & Chen, Z. (2025). Research on the Prediction Model and Formation Law of Drying Cracks of Paddy Based on Multi-Physical Field Coupling. Agriculture, 15(4), 383. https://doi.org/10.3390/agriculture15040383





