Data-Driven Management of Mountain Meadows in Central Spanish Pyrenees: Enhancing Productivity and Quality via Random Forests Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Simulation and Statistical Analysis
3. Results
3.1. Cutting Date Delay
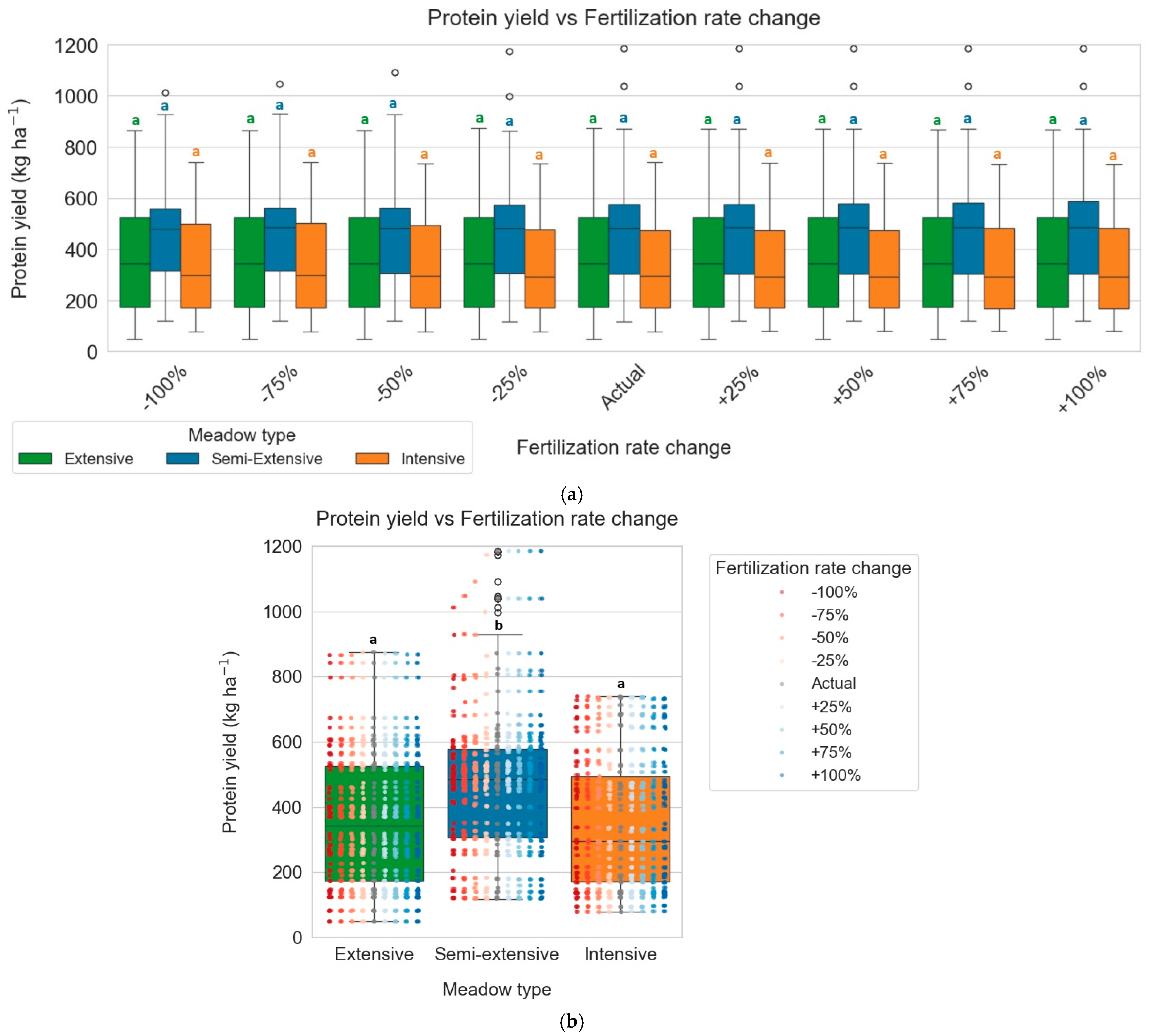
3.2. Fertilization Change
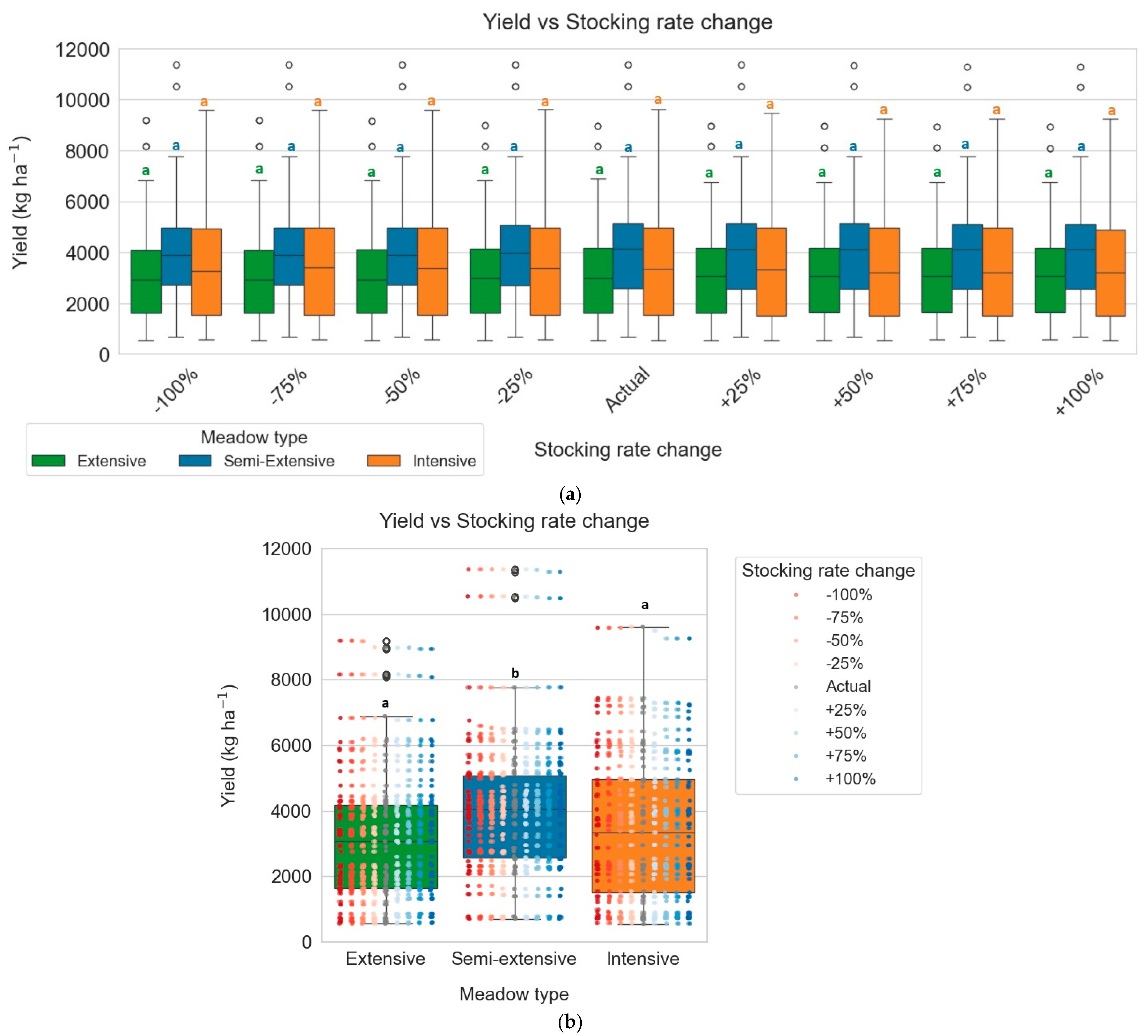
3.3. Stocking Rate Change
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reiné, R.; Barrantes, O.; Chocarro, C.; Juárez-Escario, A.; Broca, A.; Maestro, M.; Ferrer, C. Pyrenean Meadows in Natura 2000 Network: Grass Production and Plant Biodiversity Conservation. Span. J. Agric. Res. 2014, 12, 61–77. [Google Scholar] [CrossRef]
- Chocarro, C.; Reiné, R.J. El cultivo de los prados en el Pirineo. In Pastos del Pirineo; Consejo Superior de Investigaciones Científicas (CSIC): Chamartín, Madrid, 2008; pp. 141–158. ISBN 978-84-00-08614-5. [Google Scholar]
- Jones, J.A.; Hutchinson, R.; Moldenke, A.; Pfeiffer, V.; Helderop, E.; Thomas, E.; Griffin, J.; Reinholtz, A. Landscape Patterns and Diversity of Meadow Plants and Flower-Visitors in a Mountain Landscape. Landsc. Ecol. 2019, 34, 997–1014. [Google Scholar] [CrossRef]
- Michaud, A.; Plantureux, S.; Baumont, R.; Delaby, L. Grasslands, a Source of Richness and Support for Innovation for More Sustainable and Acceptable Ruminant Livestock Farming. INRA Prod. Anim. 2020, 33, 153–171. [Google Scholar] [CrossRef]
- Ascaso, J.; Reiné, R.; Barrantes, O. Evolution of Hay Meadows between 1956, 1986, and 2016 and Its Relation to the Characteristics and Location of the Parcels in the Valley of the River Esera (Pyrenees, Spain). Agronomy 2020, 10, 329. [Google Scholar] [CrossRef]
- Andales, A.A.; Derner, J.D.; Ahuja, L.R.; Hart, R.H. Strategic and Tactical Prediction of Forage Production in Northern Mixed-Grass Prairie. Rangel. Ecol. Manag. 2006, 59, 576–584. [Google Scholar] [CrossRef]
- Pavlů, V.; Hejcman, M.; Pavlů, L.; Gaisler, J.; Nežerková, P. Effect of Continuous Grazing on Forage Quality, Quantity and Animal Performance. Agric. Ecosyst. Environ. 2006, 113, 349–355. [Google Scholar] [CrossRef]
- Ascaso, J.; Reiné, R. Temporal Variations in the Production—Quality and Optimal Cutting Date of Hay Meadows in the Central Pyrenees (Spain). Agronomy 2022, 12, 918. [Google Scholar] [CrossRef]
- Gabrovska-Evstatieva, K.; Evstatiev, B. Overview of Methods and Technologies Used for Smart Management of Pastures and Meadows. AIP Conf. Proc. 2022, 2570, 040011. [Google Scholar] [CrossRef]
- Álvarez, J.; Afif, E.; Díaz, T.E.; García, L.; Oliveira, J.A. Effects of Management Practices on Soil Properties and Plant Nutrition in Hay Meadows in Picos de Europa. Environments 2021, 8, 38. [Google Scholar] [CrossRef]
- Bagcilar, S.H.; Reed, C.C.; Poulson, S.R.; Verburg, P.S.J.; Sullivan, B.W. Does Montane Meadow Restoration Influence the Mineral Association and Stability of Soil Carbon? Biogeochemistry 2024, 167, 1089–1105. [Google Scholar] [CrossRef]
- Boob, M.; Truckses, B.; Seither, M.; Elsäßer, M.; Thumm, U.; Lewandowski, I. Management Effects on Botanical Composition of Species-Rich Meadows within the Natura 2000 Network. Biodivers. Conserv. 2019, 28, 729–750. [Google Scholar] [CrossRef]
- Duffkova, R.; Kvívtek, T. Effect of Cutting Regime on Soil Physical Properties of Wet Thistle Meadows. Soil Water Res. 2009, 4, 104–115. [Google Scholar] [CrossRef]
- Bathgate, A.; Revell, C.; Kingwell, R. Identifying the Value of Pasture Improvement Using Wholefarm Modelling. Agric. Syst. 2009, 102, 48–57. [Google Scholar] [CrossRef]
- Ben Touhami, H.; Lardy, R.; Barra, V.; Bellocchi, G. Screening Parameters in the Pasture Simulation Model Using the Morris Method. Ecol. Model. 2013, 266, 42–57. [Google Scholar] [CrossRef]
- Kasperczyk, M. Mountain meadow yielding depending on meteorological conditions. Acta Agroph. 2004, 3, 263–269. [Google Scholar]
- Fu, L.; Bo, T.; Du, G.; Zheng, X. Modeling the Responses of Grassland Vegetation Coverage to Grazing Disturbance in an Alpine Meadow. Ecol. Model. 2012, 247, 221–232. [Google Scholar] [CrossRef]
- Fer, I.; Kelly, R.; Moorcroft, P.R.; Richardson, A.D.; Cowdery, E.M.; Dietze, M.C. Linking Big Models to Big Data: Efficient Ecosystem Model Calibration through Bayesian Model Emulation. Biogeosciences 2018, 15, 5801–5830. [Google Scholar] [CrossRef]
- Reyana, A.; Kautish, S.; Karthik, P.M.S.; Al-Baltah, I.A.; Jasser, M.B.; Mohamed, A.W. Accelerating Crop Yield: Multisensor Data Fusion and Machine Learning for Agriculture Text Classification. IEEE Access 2023, 11, 20795–20805. [Google Scholar] [CrossRef]
- Bala, A. Machine Learning Approaches for Crop Yield Prediction-Review. Int. J. Comput. Eng. Technol. 2020, 11, 23–27. [Google Scholar]
- Bogireddy, S.R.; Murari, H. Enhancing Crop Yield Prediction through Random Forest Classifier: A Comprehensive Approach. In Proceedings of the 2024 5th International Conference on Smart Electronics and Communication (ICOSEC), Trichy, India, 18–20 September 2024; pp. 1663–1668. [Google Scholar]
- Sahu, S.; Chawla, M.; Khare, N. An Efficient Analysis of Crop Yield Prediction Using Hadoop Framework Based on Random Forest Approach. In Proceedings of the 2017 International Conference on Computing, Communication and Automation (ICCCA), Greater Noida, India, 5–6 May 2017; pp. 53–57. [Google Scholar]
- Elavarasan, D.; Vincent, P.M.D.R. A Reinforced Random Forest Model for Enhanced Crop Yield Prediction by Integrating Agrarian Parameters. J. Ambient Intell. Hum. Comput. 2021, 12, 10009–10022. [Google Scholar] [CrossRef]
- Vogeler, I.; Kluß, C.; Peters, T.; Taube, F. How Much Complexity Is Required for Modelling Grassland Production at Regional Scales? Land 2023, 12, 327. [Google Scholar] [CrossRef]
- Jarne, A.; Usón, A.; Reiné, R. Predictive Production Models for Mountain Meadows: A Review. Agronomy 2024, 14, 830. [Google Scholar] [CrossRef]
- Ash, A.; Hunt, L.; McDonald, C.; Scanlan, J.; Bell, L.; Cowley, R.; Watson, I.; McIvor, J.; MacLeod, N. Boosting the Productivity and Profitability of Northern Australian Beef Enterprises: Exploring Innovation Options Using Simulation Modelling and Systems Analysis. Agric. Syst. 2015, 139, 50–65. [Google Scholar] [CrossRef]
- Barrett, P.D.; Laidlaw, A.S.; Mayne, C.S. Development of a European Herbage Growth Model (the EU Grazemore Project). In Land Use Systems in Grassland Dominated Regions. Proceedings of the 20th General Meeting of the European Grassland Federation, Luzern, Switzerland, 21–24 June 2004; Grassland Science in Europe; vdf Hochschulverlag AG an der ETH Zurich: Zurich, Switzerland, 2004; Volume 9, Available online: https://www.cabidigitallibrary.org/journal/ab (accessed on 23 November 2025).
- Ben Touhami, H.; Bellocchi, G. Bayesian Calibration of the Pasture Simulation Model (PaSim) to Simulate European Grasslands under Water Stress. Ecol. Inform. 2015, 30, 356–364. [Google Scholar] [CrossRef]
- Janišová, M.; Bojko, I.; Ivașcu, C.M.; Iuga, A.; Biro, A.-S.; Magnes, M. Grazing Hay Meadows: History, Distribution, and Ecological Context. Appl. Veg. Sci. 2023, 26, e12723. [Google Scholar] [CrossRef]
- Jarne, A.; Usón, A.; Reiné, R. Assessing the Impact of Environmental and Management Variables on Mountain Meadow Yield and Feed Quality Using a Random Forest Model. Plants 2025, 14, 2150. [Google Scholar] [CrossRef] [PubMed]
- Van Soest, P.J.; Robertson, J.B.; Lewis, B.A. Methods for Dietary Fiber, Neutral Detergent Fiber, and Nonstarch Polysaccharides in Relation to Animal Nutrition. J. Dairy Sci. 1991, 74, 3583–3597. [Google Scholar] [CrossRef]
- Linn, J.G.; Martin, N.P. Forage Quality Tests and Interpretation (Revised 1989); University of Minnesota: Minneapolis, MN, USA, 1989. [Google Scholar]
- Ivanova, N. Global Overview of the Application of the Braun-Blanquet Approach in Research. Forests 2024, 15, 937. [Google Scholar] [CrossRef]
- Daly, A.J.; Baetens, J.M.; Baets, B.D.; Daly, A.J.; Baetens, J.M.; Baets, B.D. Ecological Diversity: Measuring the Unmeasurable. Mathematics 2018, 6, 119. [Google Scholar] [CrossRef]
- JupyterLab Documentation—JupyterLab v.4.5.0a0 Documentation. Available online: https://jupyterlab.readthedocs.io/en/latest/ (accessed on 25 May 2025).
- Scikit-Learn: Machine Learning in Python—Scikit-Learn v.1.6.1 Documentation. Available online: https://scikit-learn.org/stable/ (accessed on 25 May 2025).
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 2623–2631. [Google Scholar]
- Botero-Valencia, J.; García-Pineda, V.; Valencia-Arias, A.; Valencia, J.; Reyes-Vera, E.; Mejia-Herrera, M.; Hernández-García, R. Machine Learning in Sustainable Agriculture: Systematic Review and Research Perspectives. Agriculture 2025, 15, 377. [Google Scholar] [CrossRef]
- Pugh, N.A.; Young, A.; Ojha, M.; Emendack, Y.; Sanchez, J.; Xin, Z.; Puppala, N. Yield Prediction in a Peanut Breeding Program Using Remote Sensing Data and Machine Learning Algorithms. Front. Plant Sci. 2024, 15, 1339864. [Google Scholar] [CrossRef]
- Sheskin, D.J. Handbook of Parametric and Nonparametric Statistical Procedures, 3rd ed.; Chapman and Hall/CRC: New York, NY, USA, 2003; ISBN 978-0-429-18616-5. [Google Scholar]
- Baltosser, W.H. Biostatistical Analysis, 3rd ed. Ecology 1996, 77, 2266–2268. [Google Scholar] [CrossRef]
- Sokal, R.R.; Rohlf, F.J. Biometry: The Principles and Practice of Statistics in Biological Research; W.H. Freeman and Co.: New York, NY, USA, 1995; ISBN 978-0-7167-2411-7. [Google Scholar]
- Tan, J.; Jiang, L.; Wei, Y.; Yao, N.; Zhao, G.; Yu, Q.; Tan, J.; Jiang, L.; Wei, Y.; Yao, N.; et al. Optimized Random Forest Framework for Integrating Cultivar, Environmental, and Phenological Interactions in Crop Yield Prediction. Agronomy 2025, 15, 2273. [Google Scholar] [CrossRef]
- Cosenza, D.N.; Korhonen, L.; Maltamo, M.; Packalen, P.; Strunk, J.L.; Næsset, E.; Gobakken, T.; Soares, P.; Tomé, M. Comparison of Linear Regression, k-Nearest Neighbour and Random Forest Methods in Airborne Laser-Scanning-Based Prediction of Growing Stock. Forestry 2021, 94, 311–323. [Google Scholar] [CrossRef]
- Reiné, R.; Ascaso, J.; Barrantes, O. Nutritional Quality of Plant Species in Pyrenean Hay Meadows of High Diversity. Agronomy 2020, 10, 883. [Google Scholar] [CrossRef]
- Schellberg, J.; Möseler, B.M.; Kühbauch, W.; Rademacher, I. Long-Term Effects of Fertilizer on Soil Nutrient Concentration, Yield, Forage Quality and Floristic Composition of a Hay Meadow in the Eifel Mountains, Germany. Grass Forage Sci. 1999, 54, 195–207. [Google Scholar] [CrossRef]
- Isbell, F.; Craven, D.; Connolly, J.; Loreau, M.; Schmid, B.; Beierkuhnlein, C.; Bezemer, T.M.; Bonin, C.; Bruelheide, H.; De Luca, E.; et al. Biodiversity Increases the Resistance of Ecosystem Productivity to Climate Extremes. Nature 2015, 526, 574–577. [Google Scholar] [CrossRef] [PubMed]
- Van Oijen, M.; Bellocchi, G.; Höglind, M. Effects of Climate Change on Grassland Biodiversity and Productivity: The Need for a Diversity of Models. Agronomy 2018, 8, 14. [Google Scholar] [CrossRef]
- Dolezal, J.; Lanta, V.; Mudrak, O.; Leps, J. Seasonality Promotes Grassland Diversity: Interactions with Mowing, Fertilization and Removal of Dominant Species. J. Ecol. 2019, 107, 203–215. [Google Scholar] [CrossRef]
- Radkowski, A.; Radkowska, I.; Godyn, D. Effects of Fertilization with an Amino Acid Preparation on the Dry Matter Yield and Chemical Composition of Meadow Plants. J. Elem. 2018, 23, 947–958. [Google Scholar] [CrossRef]
- Rodríguez, A.; Canals, R.M.; Sebastià, M.-T. Positive Effects of Legumes on Soil Organic Carbon Stocks Disappear at High Legume Proportions Across Natural Grasslands in the Pyrenees. Ecosystems 2022, 25, 960–975. [Google Scholar] [CrossRef]
- Comakli, B.; Mentese, O.; Koc, A. Nitrogen Fertilizing and Pre-Anthesis Cutting Stage Improve Dry Matter Production, Protein Content and Botanical Composition in Meadows. Acta Agric. Scand. Sect. B—Soil Plant Sci. 2005, 55, 125–130. [Google Scholar] [CrossRef]
- Graux, A.-I.; Resmond, R.; Casellas, E.; Delaby, L.; Faverdin, P.; Le Bas, C.; Ripoche, D.; Ruget, F.; Thérond, O.; Vertès, F.; et al. High-Resolution Assessment of French Grassland Dry Matter and Nitrogen Yields. Eur. J. Agron. 2020, 112, 125952. [Google Scholar] [CrossRef]
- Liu, H.; Gong, Y.; Li, Y.; Liu, S.; Yu, Z.; Zhao, R. Does Grazing Exclusion Enhance Grassland Restoration? Evidence from Northern China. Ecol. Indic. 2023, 149, 110166. [Google Scholar] [CrossRef]
- Wezel, A.; Stöckli, S.; Tasser, E.; Nitsch, H.; Vincent, A. Good Pastures, Good Meadows: Mountain Farmers’ Assessment, Perceptions on Ecosystem Services, and Proposals for Biodiversity Management. Sustainability 2021, 13, 5609. [Google Scholar] [CrossRef]
- Simon, S.M.; Glaum, P.; Valdovinos, F.S. Interpreting Random Forest Analysis of Ecological Models to Move from Prediction to Explanation. Sci. Rep. 2023, 13, 3881. [Google Scholar] [CrossRef]
- Evans, J.S.; Murphy, M.A.; Holden, Z.A.; Cushman, S.A. Modeling Species Distribution and Change Using Random Forest. In Predictive Species and Habitat Modeling in Landscape Ecology: Concepts and Applications; Drew, C.A., Wiersma, Y.F., Huettmann, F., Eds.; Springer: New York, NY, USA, 2011; pp. 139–159. ISBN 978-1-4419-7390-0. [Google Scholar]
- Chavent, M.; Lacaille, J.; Mourer, A.; Olteanu, M. Handling Correlations in Random Forests: Which Impacts on Variable Importance and Model Interpretability? In Proceedings of the ESANN 2021—European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Virtual, 6–8 October 2021; pp. 569–574. [Google Scholar]









| Intensive Meadow | Semi-Extensive Meadow | Extensive Meadow | |
|---|---|---|---|
| Altitude (m) | 602–890 | 902–1290 | 1100–1612 |
| GPS Range (approx.) | 42.60–42.70 N; 0.10–0.25 E | 42.55–42.75 N; 0.15–0.35 E | 42.50–42.80 N; 0.20–0.40 E |
| Slope (%) | 9.63 ± 4.13 | 18.6 ± 4.99 | 16.1 ± 5.35 |
| Soil type (WRB) | Haplic Regosol | Haplic Phaeozem | Haplic Phaeozem |
| Clay (%) | 30.47 ± 4.87 | 23.62 ± 4.26 | 16.29 ± 5.04 |
| Sand (%) | 21.01 ± 7.92 | 40.50 ± 9.49 | 51.61 ± 9.88 |
| pH | 7.71 ± 0.3 | 6.94 ± 0.29 | 6.82 ± 0.41 |
| Electric conductivity (dS/m) | 0.23 ± 0.05 | 0.28 ± 0.06 | 0.21 ± 0.06 |
| Organic matter (%) | 3.78 ± 2.12 | 9.93 ± 3.58 | 9.25 ± 3.18 |
| Fertilization type | Compound NPK (5-15-15) + urea (46% N) | Composted cattle manure/cattle slurry | Composted cattle manure/None |
| Fertilization frequency | Yearly | Yearly | Rarely |
| Nitrogen kg ha−1 | 66.22 ± 37.77 | 214.71 ± 136.05 | 6.17 ± 10.69 |
| Phosphorus kg ha−1 | 47.04 ± 15.06 | 305.09 ± 280.11 | 10.06 ± 11.55 |
| Potassium kg ha−1 | 69.32 ± 35.29 | 140.14 ± 145.10 | 11.57 ± 20.05 |
| Livestock load LU ha−1 year−1 | 0.59 ± 0.10 | 0.35 ± 0.33 | 0.20 ± 0.10 |
| Shannon Index | 1.82 ± 0.15 | 2.81 ± 0.31 | 3.23 ± 0.14 |
| Legume cover (%) | 26.25 ± 21.99 | 24.3 ± 5.95 | 23.3 ± 5.33 |
| Dominant species | Dactylis glomerata | Arrhenatherum elatius | Festuca rubra |
| Phenological stage of dominant species at cutting | Flowering | Flowering | Flowering |
| Cutting date | May-15 ± 16 days | Jun-5 ± 21 days | Jun-13 ± 20 days |
| Model | Yield | RFV | Protein Yield |
|---|---|---|---|
| N estimators | 158 | 198 | 206 |
| Max depth | 14 | 27 | 16 |
| Min samples split | 5 | 5 | 5 |
| Min samples leaf | 1 | 1 | 1 |
| Random state | 42 | 42 | 42 |
| R2 | 0.79 | 0.72 | 0.73 |
| RMSE | 963.62 | 13.86 | 115.34 |
| Extensive | Semi Extensive | Intensive | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Cutting Date | Yield | RFV | Protein Yield | Yield | RFV | Protein Yield | Yield | RFV | Protein Yield |
| −30 | −655.74 | 13.95 | −21.31 | −797.26 | 13.08 | −61.47 | −753.05 | 9.86 | −63.66 |
| −25 | −489.07 | 11.94 | −13.3 | −675.38 | 11.44 | −36.11 | −642.41 | 9.43 | −45.46 |
| −20 | −372.95 | 10.63 | −3.7 | −578.49 | 11.17 | −10.88 | −482.57 | 7.47 | −21.04 |
| −15 | −271.75 | 6.99 | 5.22 | −436.85 | 8.63 | 1.81 | −388.91 | 6.52 | −11.61 |
| −10 | −185.54 | 4.71 | 5.28 | −163.49 | 6.66 | 13.95 | −333.32 | 5.53 | −6.66 |
| −5 | −186.13 | 2.12 | −2.11 | −54.98 | 3.05 | 16.36 | −142.25 | 3.48 | 3.02 |
| Actual | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 216.52 | −4.36 | 13.21 | 117.72 | −5.21 | −10.77 | 178.58 | −0.67 | −1.23 |
| 10 | 234.12 | −6.62 | 6.74 | 213.98 | −7.19 | −9.52 | 411.13 | −2.97 | 2.86 |
| 15 | 319.13 | −8.04 | 6.09 | 251.54 | −9.97 | −8.42 | 524.83 | −6.2 | 5.46 |
| 20 | 332.49 | −12.01 | −4.06 | 261.89 | −12.64 | −13.92 | 566.76 | −7.82 | 8.17 |
| 25 | 465.38 | −14.73 | 1.5 | 297 | −15.02 | −12.3 | 736.04 | −10.51 | 11.2 |
| 30 | 599.8 | −15.92 | 5.32 | 340.5 | −15.52 | −12.4 | 747.55 | −12.38 | 10.08 |
| Extensive | Semi Extensive | Intensive | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Fertilization Rate | Yield | RFV | Protein Yield | Yield | RFV | Protein Yield | Yield | RFV | Protein Yield |
| −100% | −41.84 | −0.02 | −0.74 | −387.96 | 1.32 | −12.7 | −197.03 | −0.15 | 0.64 |
| −75% | −41.78 | 0.01 | −0.54 | −273.98 | 1.25 | −10.13 | −199.02 | −0.09 | 1.09 |
| −50% | −42.58 | 0.05 | −0.47 | −215.5 | 1.19 | −8.24 | −96.27 | −0.35 | 1.16 |
| −25% | 1.36 | 0.08 | −0.06 | −28.57 | 1.27 | −1.54 | −18.49 | −0.18 | 0.08 |
| Actual | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| +25% | 9.76 | 0.02 | 0.32 | 6.09 | −0.8 | 2 | −4.61 | 0.33 | −0.66 |
| +50% | 9.74 | 0.02 | 0.36 | 24.76 | −1.3 | 2.07 | −3.46 | 0.35 | −0.85 |
| +75% | 9.32 | 0.06 | 0.28 | 27.66 | −1.64 | 3.11 | 7.81 | 0.4 | −0.77 |
| +100% | 20.93 | 0.06 | 0.28 | 61.28 | −1.63 | 3.34 | 113.34 | 0.43 | 0.62 |
| Extensive | Semi Extensive | Intensive | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Fertilization Rate | Yield | RFV | Protein Yield | Yield | RFV | Protein Yield | Yield | RFV | Protein Yield |
| −100% | −30.04 | −0.56 | −14.88 | −69.79 | −3.1 | −37.88 | −29.37 | −2.31 | −26.3 |
| −75% | −30.04 | −0.56 | −14.88 | −50.53 | −2.48 | −30.76 | −14.2 | −1.12 | −10.09 |
| −50% | −20.58 | −0.38 | −7.08 | −53.05 | −2.44 | −29.75 | 4.97 | −1 | 1.16 |
| −25% | −9.56 | 0.14 | −0.79 | −37.57 | −2.03 | −23.55 | 7.67 | −1.02 | 0.34 |
| Actual | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| +25% | 37.14 | 0.24 | 11.48 | −2 | 0.23 | −0.66 | −14.49 | 1.78 | 0 |
| +50% | 54.18 | 0.56 | 17.26 | 12.49 | 0.41 | 5.61 | −60.65 | 4.99 | −1.3 |
| +75% | 61.7 | 0.58 | 17.65 | 10.67 | 0.39 | 5.7 | −65.08 | 5.66 | −1.87 |
| +100% | 60.41 | 0.77 | 17.16 | 12.5 | 0.38 | 5.84 | −73.85 | 6.04 | −2.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jarne, A.; Usón, A.; Reiné, R. Data-Driven Management of Mountain Meadows in Central Spanish Pyrenees: Enhancing Productivity and Quality via Random Forests Models. Agriculture 2025, 15, 2440. https://doi.org/10.3390/agriculture15232440
Jarne A, Usón A, Reiné R. Data-Driven Management of Mountain Meadows in Central Spanish Pyrenees: Enhancing Productivity and Quality via Random Forests Models. Agriculture. 2025; 15(23):2440. https://doi.org/10.3390/agriculture15232440
Chicago/Turabian StyleJarne, Adrián, Asunción Usón, and Ramón Reiné. 2025. "Data-Driven Management of Mountain Meadows in Central Spanish Pyrenees: Enhancing Productivity and Quality via Random Forests Models" Agriculture 15, no. 23: 2440. https://doi.org/10.3390/agriculture15232440
APA StyleJarne, A., Usón, A., & Reiné, R. (2025). Data-Driven Management of Mountain Meadows in Central Spanish Pyrenees: Enhancing Productivity and Quality via Random Forests Models. Agriculture, 15(23), 2440. https://doi.org/10.3390/agriculture15232440






