Temporal and Spatial Dynamics of Groundwater Drought Based on GRACE Satellite and Its Relationship with Agricultural Drought
Abstract
1. Introduction
2. Materials and Methods
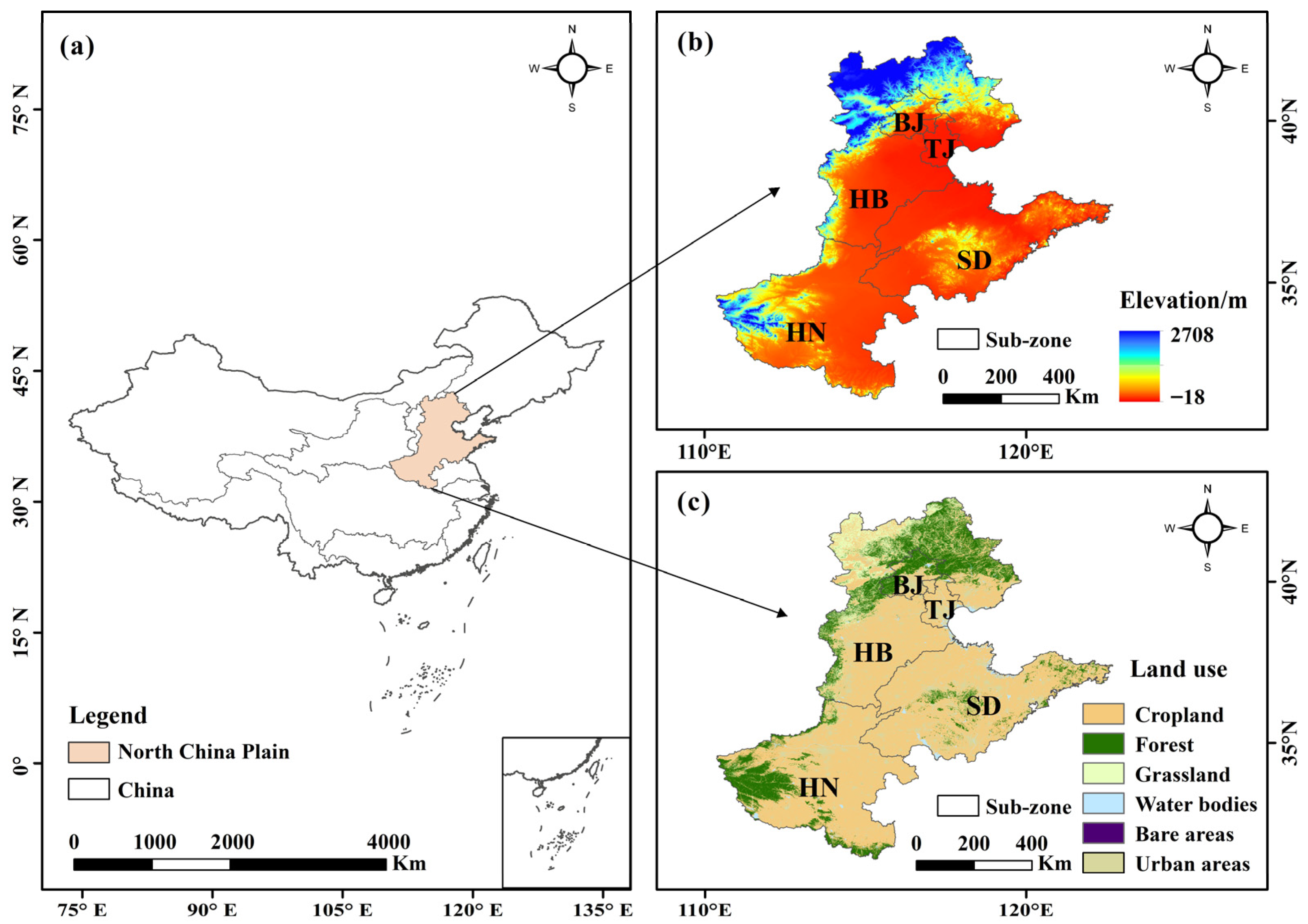
2.1. The Research Area
2.2. Dataset
2.2.1. GRACE Satellite
2.2.2. GLDAS Land Surface Process Model
2.2.3. Digital Elevation Model
2.3. Methodology
2.3.1. Construction Principle of Groundwater and Agricultural Drought Index
2.3.2. Bayesian Estimator of Abrupt Seasonal and Trend Change (BEAST)
2.3.3. Spatial Mann–Kendall Trend Test Method (SMK)
2.3.4. Wavelet Coherence Analysis
3. Results
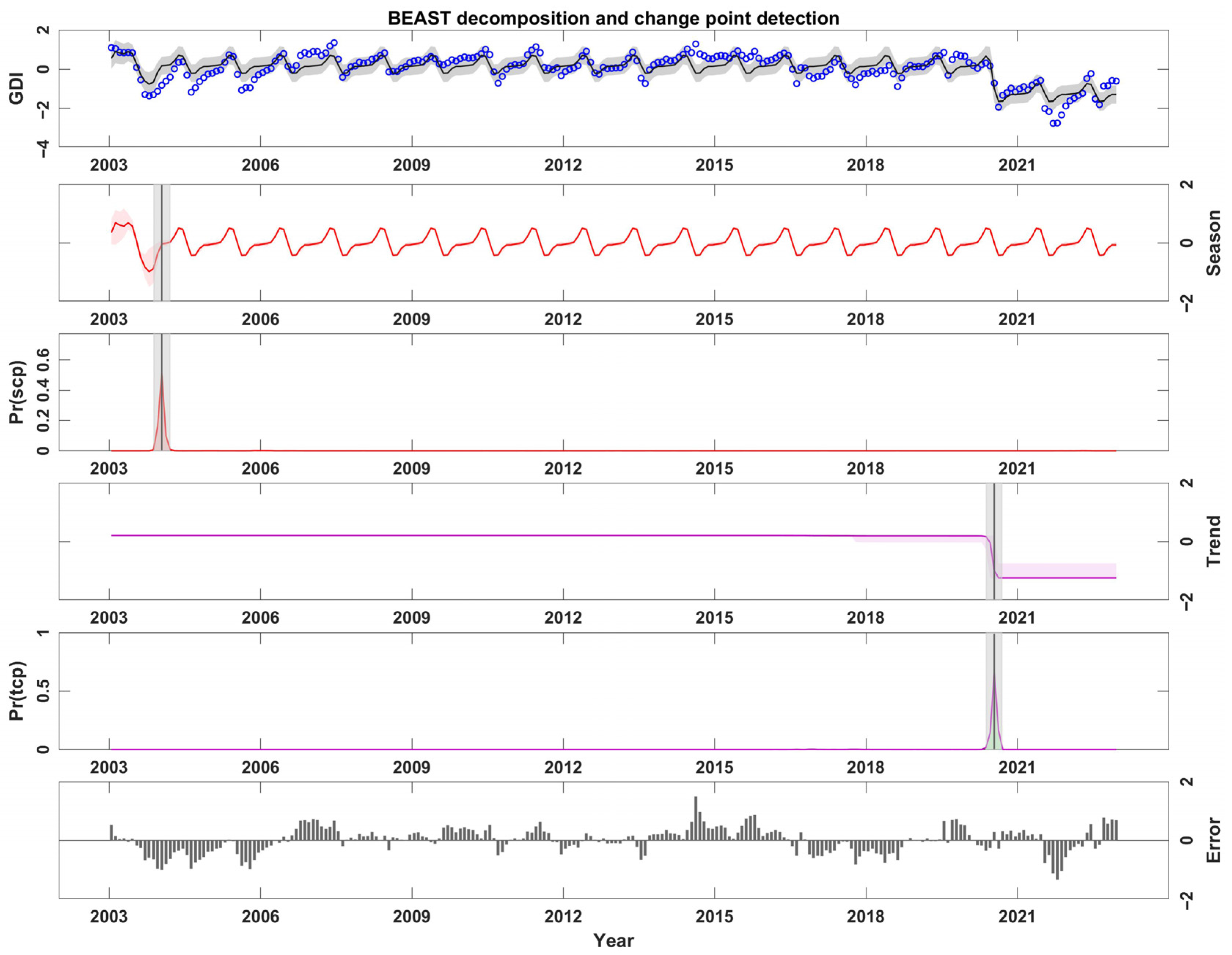
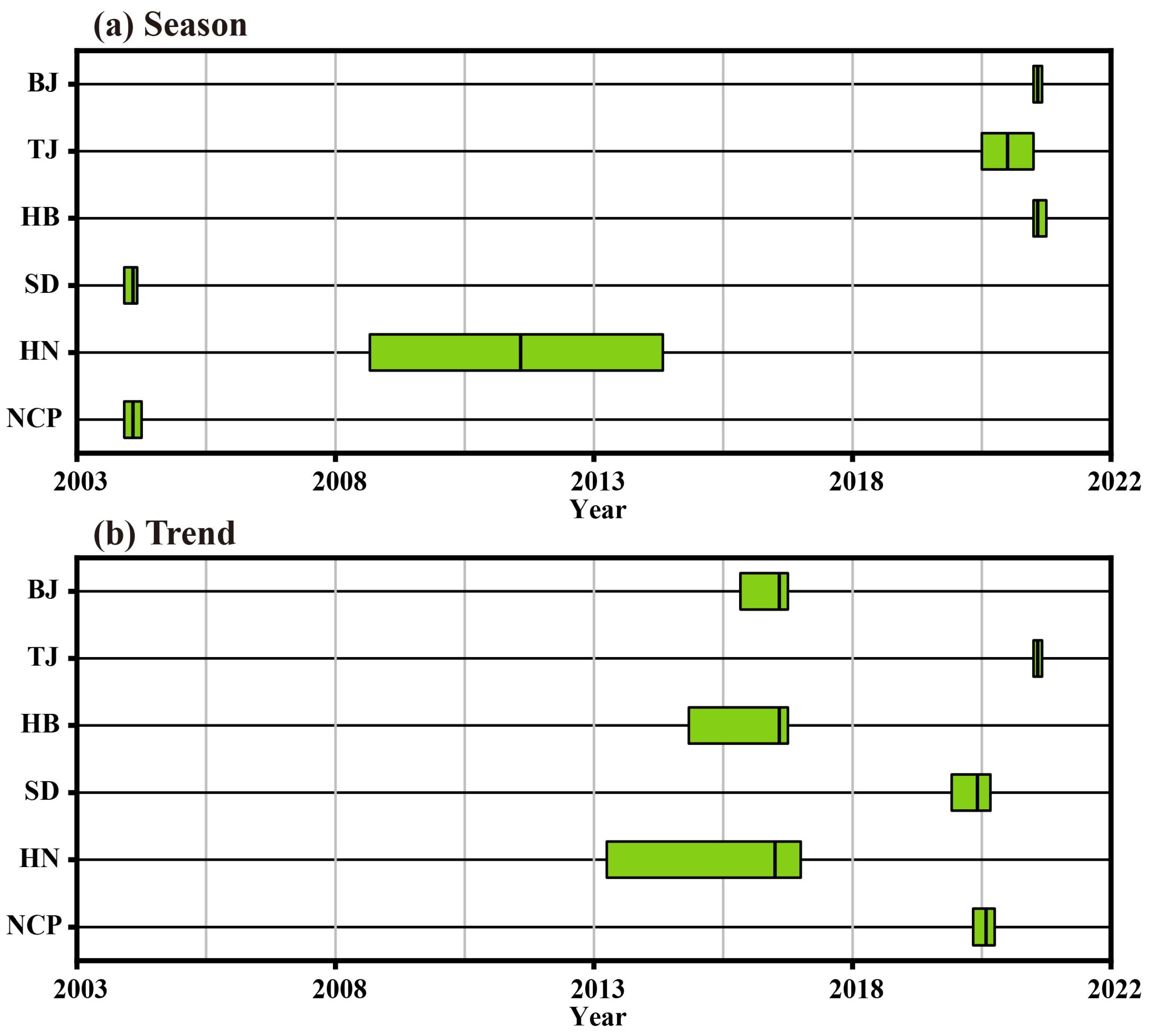
3.1. Time Series Decomposition of Groundwater Drought Based on Bayesian Algorithm
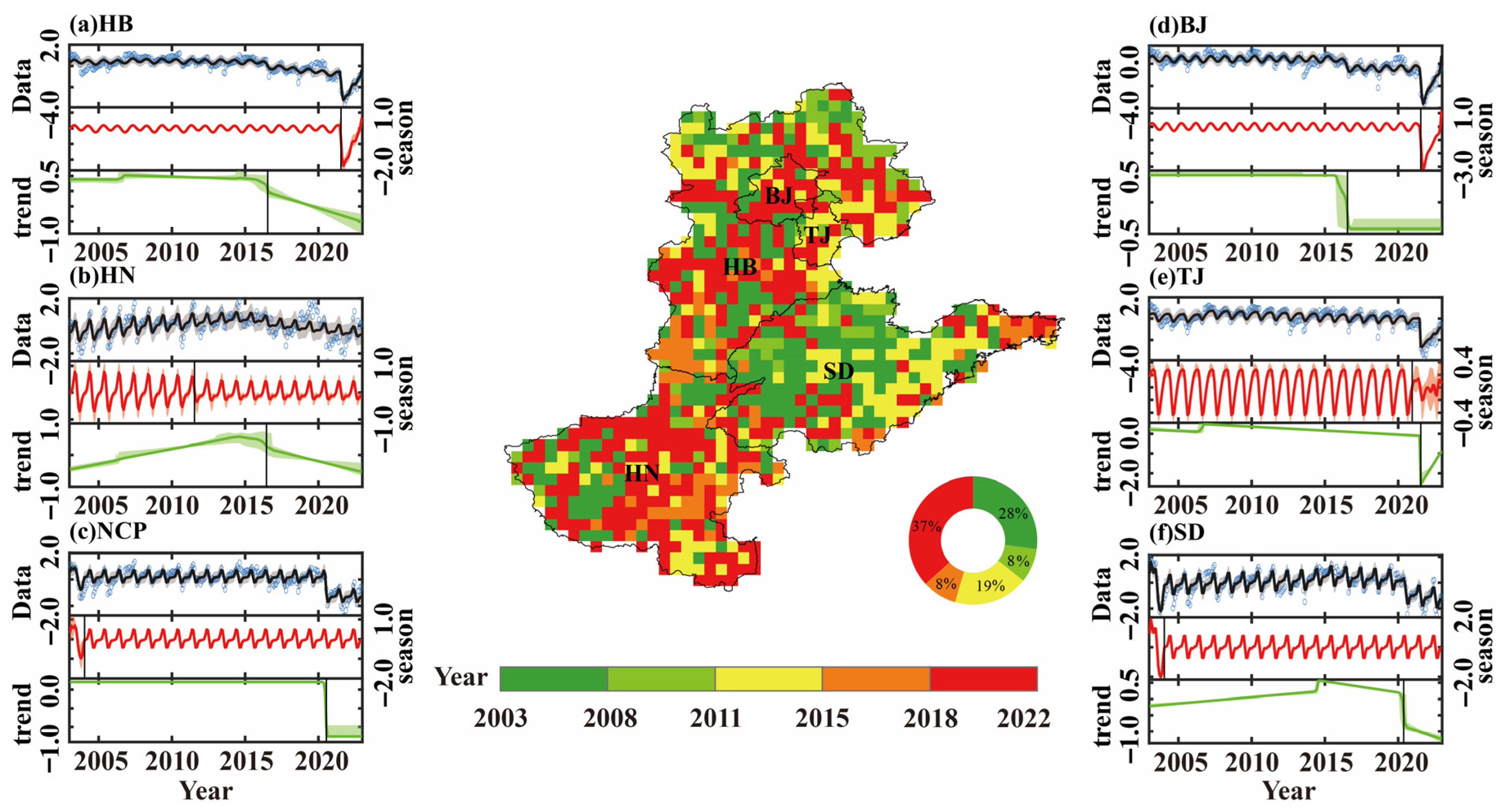
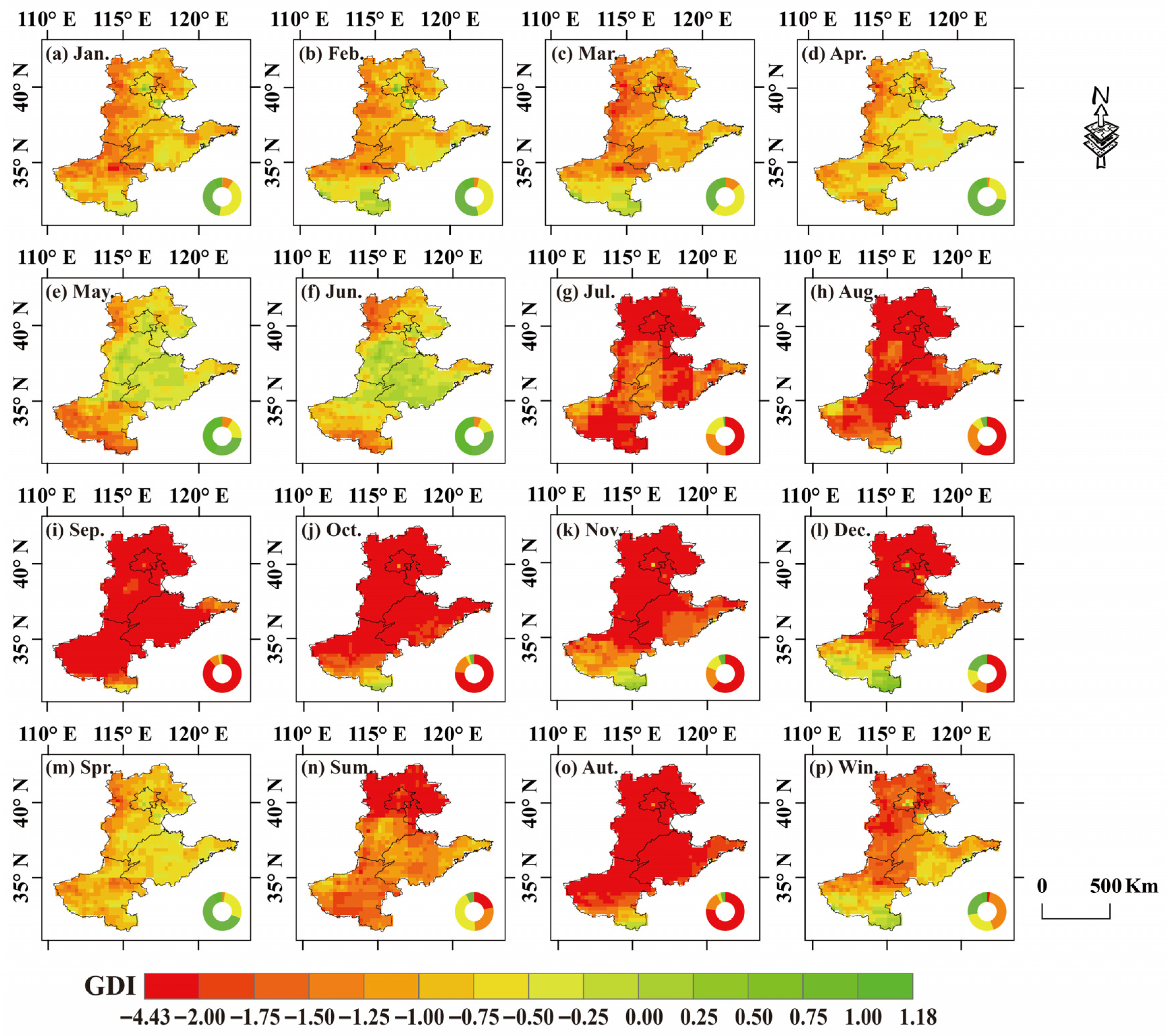
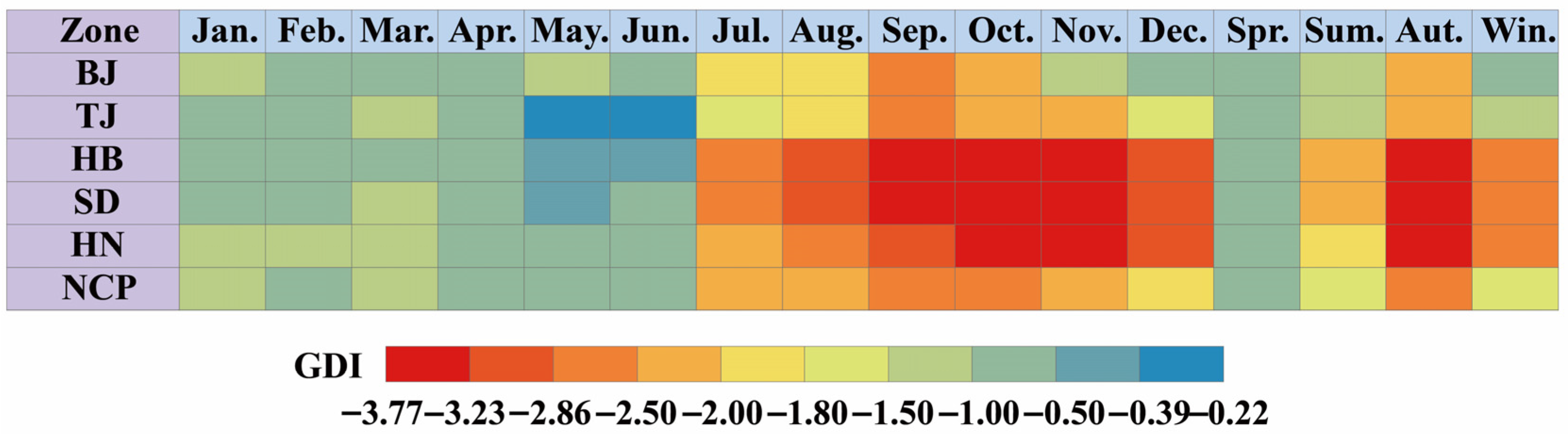
3.2. Spatial Distribution Characteristics of Groundwater Drought
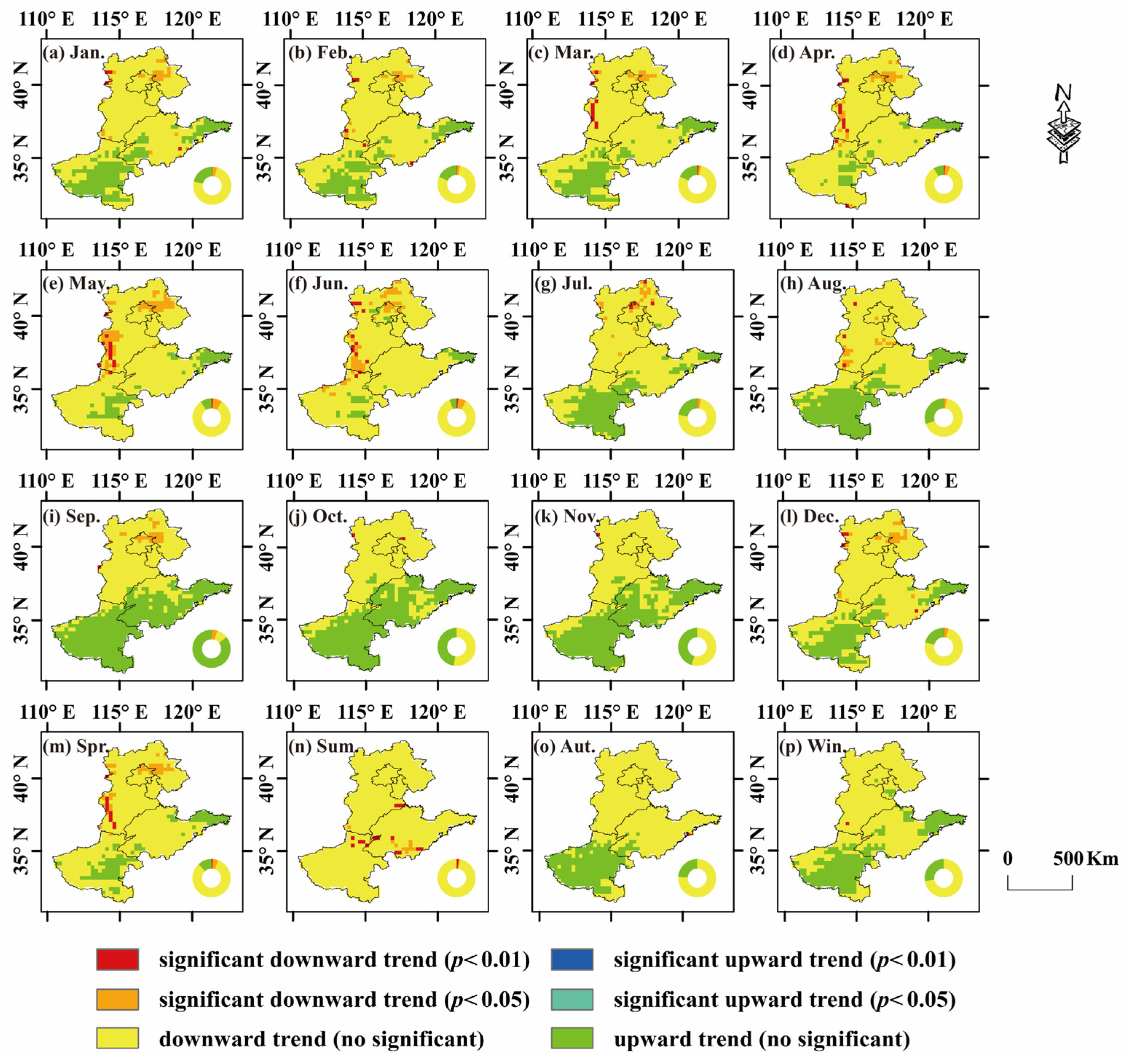
3.3. Gridded Trend Feature Identification
3.4. The Relationships Between Climate Factors and Groundwater Drought
3.5. The Propagation Time from Groundwater Drought to Agricultural Drought
4. Discussion
4.1. Advantages and Uncertainties
4.2. Future Prospects
5. Conclusions
- (1)
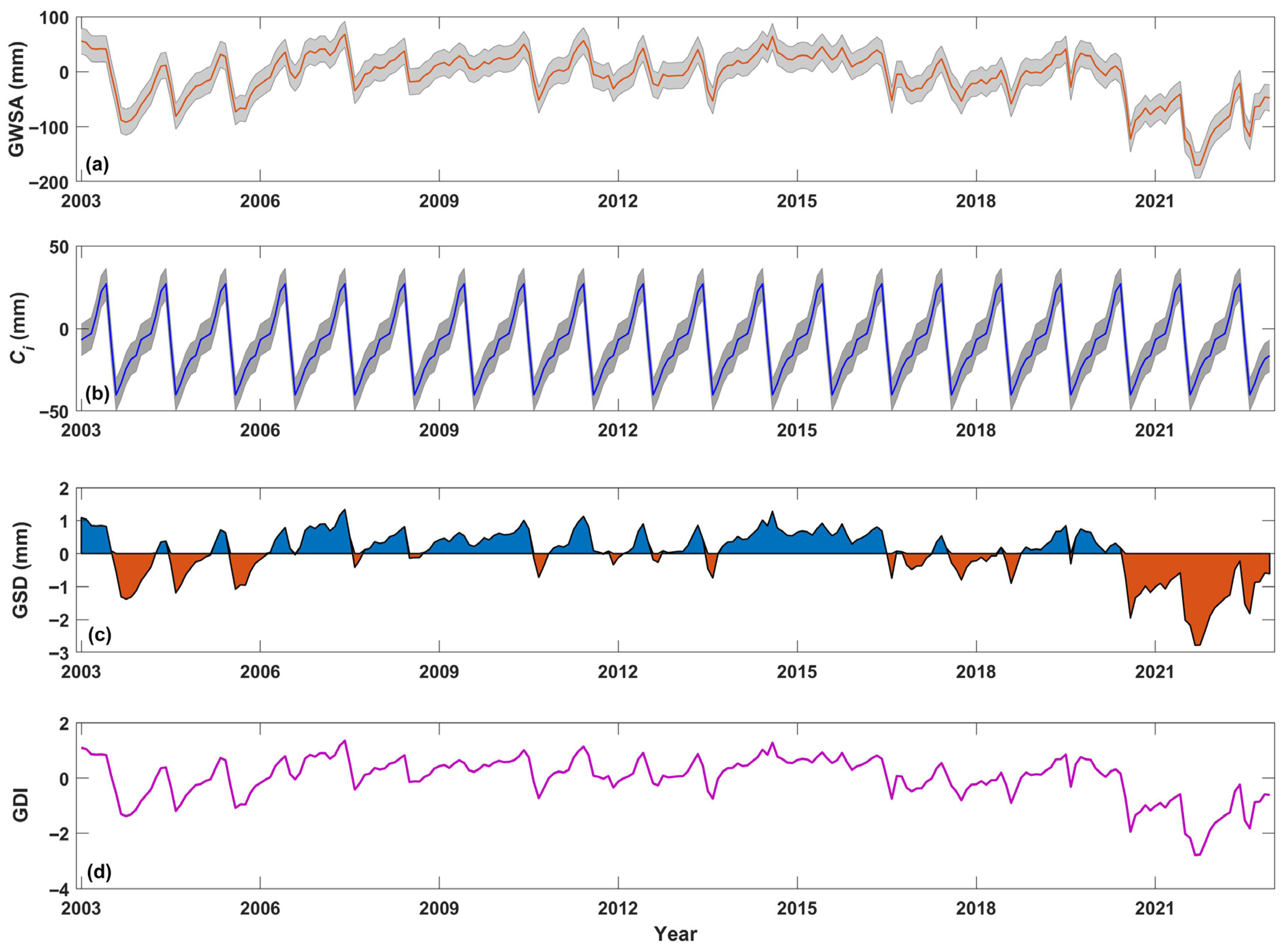
- From 2003 to 2022, the most severe groundwater drought in the NCP occurred in September 2021 (GDI = −1.59). The linear trend rate of GDI was −0.035/10a, indicating a gradually intensifying trend in groundwater drought. The seasonal abrupt change point (probability 79.15%) and the trend abrupt change point (probability 99.83%) of groundwater drought occurred in January 2004 (confidence interval: November 2003 to March 2004) and July 2020 (confidence interval: April 2020 to September 2020), respectively.
- (2)
- On an annual scale, the most severe groundwater drought occurred in 2021 (GDI = −1.59). In that year, the monthly average GDI across the NCP ranged between −0.58 and −2.78, with particularly severe groundwater drought conditions observed in July (GDI = −2.02), August (GDI = −2.17), September (GDI = −2.78), and October (GDI = −2.77). On a seasonal scale, the minimum (−2.63) and maximum (−0.86) GDI values occurred in autumn (drought-affected area: 98.60%) and spring (drought-affected area: 91.81%), respectively.
- (3)
- Complex nonlinear relationships exist between groundwater drought and climatic factors (SM, AH, AT, ET, PC, and ST) in the NCP from 2003 to 2022. Specifically, based on partial wavelet coherence, the optimal single-variable explanatory factor for groundwater drought was SM (PASC = 19.13%).
- (4)
- The maximum correlation coefficient between GDI and SVWI ranged from –0.18 to 0.98, with a mean of 0.52, indicating a generally significant positive correlation. Across sub-regions, areas where groundwater drought significantly influenced agricultural drought were mainly located in the eastern parts of BJ, TJ, HB, and the western part of SD. In the BJ, TJ, and HB regions, propagation times were primarily concentrated within 1–5 months, with mean lags of 2.87, 3.20, and 2.92 months, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wada, Y. Modeling groundwater depletion at regional and global scales: Present state and future prospects. Surv. Geophys. 2015, 55, 229–261. [Google Scholar]
- Song, X.H.; Chen, H.; Chen, T.; Qin, Z.H.; Chen, S.; Yang, N.; Deng, S.L. GRACE-based groundwater drought in the Indochina Peninsula during 1979–2020: Changing properties and possible teleconnection mechanisms. Sci. Total Environ. 2023, 908, 168423. [Google Scholar] [CrossRef]
- Nigatu, Z.M.; You, W.; Melesse, A.M. Drought Dynamics in the Nile River Basin: Meteorological, Agricultural, and Groundwater Drought Propagation. Remote Sens. 2024, 16, 919. [Google Scholar] [CrossRef]
- Christelis, V.; Mansour, M.; Jackson, C.R. Characterisation of Groundwater Drought Using Distributed Modelling, Standardised Indices, and Principal Component Analysis. Water Resour. Manag. 2025, 39, 4227–4241. [Google Scholar] [CrossRef]
- Thomas, B.F.; Famiglietti, J.S.; Landerer, F.W.; Wiese, D.N.; Molotch, N.P.; Argus, D.F. GRACE Groundwater Drought Index: Evaluation of California Central Valley groundwater drought. Remote Sens. Environ. 2017, 198, 384–392. [Google Scholar] [CrossRef]
- Han, Z.M.; Huang, S.Z.; Zhao, J.; Leng, G.Y.; Huang, Q.; Zhang, H.B.; Li, Z. Long-chain propagation pathways from meteorological to hydrological, agricultural and groundwater drought and their dynamics in China. J. Hydrol. 2023, 625, 130131. [Google Scholar] [CrossRef]
- Liu, Q.P.; Zhang, X.; Xu, Y.; Li, C.; Zhang, X.; Wang, X.F. Characteristics of groundwater drought and its correlation with meteorological and agricultural drought over the North China Plain based on GRACE. Ecol. Indic. 2024, 161, 111925. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Kumar, S.; Beaudoing, H.K.; Getirana, A.; Zaitchik, B.F.; de Goncalves, L.G.; Cossetin, C.; Bhanja, S.; Mukherjee, A.; et al. Global GRACE Data Assimilation for Groundwater and Drought Monitoring: Advances and Challenges. Water Resour. Res. 2019, 55, 7564–7586. [Google Scholar] [CrossRef]
- Pham, Q.B.; Kumar, M.; Di Nunno, F.; Elbeltagi, A.; Granata, F.; Islam, A.M.T.; Talukdar, S.; Nguyen, X.C.; Ahmed, A.N.; Al Anh, D.T. Groundwater level prediction using machine learning algorithms in a drought-prone area. Neural Comput. Appl. 2022, 34, 10751–10773. [Google Scholar] [CrossRef]
- Geng, G.P.; Zhang, B.; Gu, Q.; He, Z.X.; Zheng, R.L. Drought propagation characteristics across China: Time, probability, and threshold. J. Hydrol. 2024, 631, 130805. [Google Scholar] [CrossRef]
- Xiao, D.P.; Shen, Y.J.; Qi, Y.Q.; Moiwo, J.P.; Min, L.L.; Zhang, Y.C.; Guo, Y.; Pei, H.W. Impact of alternative cropping systems on groundwater use and grain yields in the North China Plain Region. Agric. Syst. 2017, 153, 109–117. [Google Scholar] [CrossRef]
- Kang, S.; Eltahir, E.A.B. North China Plain threatened by deadly heatwaves due to climate change and irrigation. Nat. Commun. 2018, 9, 2894. [Google Scholar] [CrossRef]
- Du, J.; Laghari, Y.; Wei, Y.C.; Wu, L.Y.; He, A.L.; Liu, G.Y.; Yang, H.H.; Guo, Z.Y.; Leghari, S.J. Groundwater Depletion and Degradation in the North China Plain: Challenges and Mitigation Options. Water 2024, 16, 354. [Google Scholar] [CrossRef]
- Dai, M.; Zhou, H.; Ma, W.J.; Tang, L.; Xu, S.Y.; Luo, Z.C. Tracking shallow and deep groundwater storage changes in North China Plain with improved fusion method and hybrid spectral analysis approach. J. Hydrol. 2024, 633, 131001. [Google Scholar] [CrossRef]
- Tian, J.Z.; Chen, Y.; Wang, S.; Chen, X.L.; Cheng, H.B.; Tian, X.L.; Wang, X.; Tan, K. Spatiotemporal monitoring of water storage in the North China Plain from 2002 to 2022 based on an improved GRACE downscaling method. J. Hydrol. Reg. Stud. 2025, 59, 102370. [Google Scholar] [CrossRef]
- Zhao, A.; Xiang, K.; Zhang, A.; Zhang, X. Spatial-temporal evolution of meteorological and groundwater droughts and their relationship in the North China Plain. J. Hydrol. 2022, 610, 127903. [Google Scholar] [CrossRef]
- Huang, J.; Cao, L.; Wang, L.; Liu, L.; Yu, B.; Han, L. Identification and spatiotemporal migration analysis of groundwater drought events in the North China Plain. Atmosphere 2023, 14, 961. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef]
- Do, S.K.; Akhtar, F.; Goffin, B.; Aryal, A.; Tran, T.N.D.; Lipscomb, M.; Lakshmi, V. Assessing terrestrial water storage variations in Afghanistan using GRACE and FLDAS-Central Asia data. J. Hydrol. Reg. Stud. 2024, 55, 101906. [Google Scholar] [CrossRef]
- Duan, A.; Zhong, Y.L.; Xu, G.D.; Yang, K.J.; Tian, B.M.; Wu, Y.L.; Bai, H.B.; Hu, E. Quantifying the 2022 extreme drought in the Yangtze River Basin using GRACE-FO. J. Hydrol. 2024, 630, 130680. [Google Scholar] [CrossRef]
- Carlson, G.; Werth, S.; Shirzaei, M. A novel hybrid GNSS, GRACE, and InSAR joint inversion approach to constrain water loss during a record-setting drought in California. Remote Sens. Environ. 2024, 311, 114303. [Google Scholar] [CrossRef]
- Yang, F.; Forootan, E.; Liu, S.H.; Schumacher, M. A Monte Carlo Propagation of the Full Variance-Covariance of GRACE-Like Level-2 Data with Applications in Hydrological Data Assimilation and Sea-Level Budget Studies. Water Resour. Res. 2024, 60, e2023WR036764. [Google Scholar] [CrossRef]
- Feng, W.; Shum, C.K.; Zhong, M.; Pan, Y. Groundwater Storage Changes in China from Satellite Gravity: An Overview. Remote Sens. 2018, 10, 674. [Google Scholar] [CrossRef]
- Wu, T.T.; Zheng, W.; Yin, W.J.; Zhang, H.W. Spatiotemporal Characteristics of Drought and Driving Factors Based on the GRACE-Derived Total Storage Deficit Index: A Case Study in Southwest China. Remote Sens. 2020, 13, 79. [Google Scholar] [CrossRef]
- Yin, W.J.; Yang, S.; Hu, L.T.; Tian, S.Y.; Wang, X.L.; Zhao, R.X.; Li, P.J. Improving understanding of spatiotemporal water storage changes over China based on multiple datasets. J. Hydrol. 2022, 612, 128098. [Google Scholar] [CrossRef]
- Shen, Y.F.; Zheng, W.; Zhu, H.Z.; Yin, W.J.; Xu, A.G.; Pan, F.; Wang, Q.; Zhao, Y.L. Inverted Algorithm of Groundwater Storage Anomalies by Combining the GNSS, GRACE/GRACE-FO, and GLDAS: A Case Study in the North China Plain. Remote Sens. 2022, 14, 5683. [Google Scholar] [CrossRef]
- Su, K.; Zheng, W.; Yin, W.J.; Hu, L.T.; Shen, Y.F. Improving the Accuracy of Groundwater Storage Estimates Based on Groundwater Weighted Fusion Model. Remote Sens. 2022, 14, 202. [Google Scholar] [CrossRef]
- Qu, W.; Zhang, P.F.; Chen, P.N.; Li, J.Y.; Gao, Y. Spatiotemporal Variations and Sustainability Characteristics of Groundwater Storage in North China from 2002 to 2022 Revealed by GRACE/GRACE Follow-On and Multiple Hydrologic Data. Remote Sens. 2024, 16, 1176. [Google Scholar] [CrossRef]
- Gerdener, H.; Kusche, J.; Schulze, K.; Döll, P.; Klos, A. The global land water storage data set release 2 (GLWS2.0) derived via assimilating GRACE and GRACE-FO data into a global hydrological model. J. Geod. 2023, 97, 73. [Google Scholar] [CrossRef]
- Al-Abadi, A.M.; Hassan, A.A.; Al-Moosawi, N.M.; Handhal, A.M.; Alzahrani, H.; Jabbar, F.K.; Anderson, N.L. Drought susceptibility mapping in Iraq using GRACE/GRACE-FO, GLDAS, and machine learning algorithms. Phys. Chem. Earth 2024, 134, 103583. [Google Scholar] [CrossRef]
- Wu, B.; Wang, J.; Li, F.; Zhu, D.; Pan, J.; He, J.; Wang, W. Spatiotemporal variation characteristics and the possible causes of groundwater storage based on GRACE in the Huai River Basin, China. Nat. Hazards 2025, 121, 18435–18452. [Google Scholar] [CrossRef]
- Cui, L.; Zhong, L.; Meng, J.; An, J.; Zhang, C.; Li, Y. Spatiotemporal Evolution Features of the 2022 Compound Hot and Drought Event over the Yangtze River Basin. Remote Sens. 2024, 16, 1367. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, R.; Ma, M.; Bu, Q. Identifying Groundwater Droughts and Its Recovery Based on Long-Term Groundwater Storage Simulation in Catchments Across Poyang Lake Basin. Hydrol. Process. 2025, 39, 70248. [Google Scholar] [CrossRef]
- Li, Z.; Huang, S.; Zhou, S.; Leng, G.; Liu, D.; Huang, Q.; Wang, H.; Han, Z.; Liang, H. Clarifying the Propagation Dynamics from Meteorological to Hydrological Drought Induced by Climate Change and Direct Human Activities. J. Hydrometeorol. 2021, 22, 2359–2378. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Zhang, Y.Q.; Tian, J.; Tang, Z.X.; Wang, L.H.; Yang, X.N. Understanding the propagation of meteorological drought to groundwater drought: A case study of the North China Plain. Water 2024, 16, 501. [Google Scholar] [CrossRef]
- Liu, M.Y.; Geng, D.; Wu, L.; Min, L.L.; Wang, S.Q.; Shen, Y.J. The impact of agricultural land use change on water and nitrate fluxes in the deep vadose zone, the North China Plain. J. Hydrol. Reg. Stud. 2025, 62, 102914. [Google Scholar] [CrossRef]
- Wang, F.; Lai, H.X.; Men, R.Y.; Wang, Z.P.; Li, Y.B.; Qu, Y.P.; Feng, K.; Guo, W.X.; Jiang, Y.Z. Dynamic Variations of Agricultural Drought and Its Response to Meteorological Drought: A Drought Event-Based Perspective. J. Geophys. Res. Atmos. 2024, 129, e2024JD041044. [Google Scholar] [CrossRef]
- Wang, C.Y.; Liu, M.H.; Han, Y.P.; Chen, S.; Zhang, F.F.; Qiu, R.J.; Wu, D.F.; Zhang, G.C.; Wang, F.Q.; Liu, J.G. Assessing the impacts of irrigation and soil types on the water balance and groundwater depletion in an irrigation district of the North China Plain based on a coupled SWAT-MODFLOW model. Agric. Water Manag. 2025, 321, 109890. [Google Scholar] [CrossRef]
- Schumacher, M.; Forootan, E.; van Dijk, A.; Schmied, H.; Crosbie, R.; Kusche, J.; Döll, P. Improving drought simulations within the Murray-Darling Basin by combined calibration/assimilation of GRACE data into the WaterGAP Global Hydrology Model. Remote Sens. Environ. 2018, 204, 212–228. [Google Scholar] [CrossRef]
- Kashani, A.; Safavi, H.R. Assessing groundwater drought in Iran using GRACE data and machine learning. Sci. Rep. 2025, 15, 14671. [Google Scholar] [CrossRef]
- Yin, Y.; Guo, B.; Zhong, Y.; Deng, H.; Chang, L. Can GRACE and CMIP6 historical data identify groundwater drought in North China Plain? Theor. Appl. Climatol. 2023, 152, 1203–1219. [Google Scholar] [CrossRef]
- Liu, M.; Pei, H.; Shen, Y. Evaluating dynamics of GRACE groundwater and its drought potential in Taihang Mountain Region, China. J. Hydrol. 2022, 612, 128156. [Google Scholar] [CrossRef]
- Aon, S.; Nandi, S.; Sen, S.; Biswas, S. GRACE based groundwater drought evaluation of Ganga Basin and analysis of drought propagation using wavelet based quantitative approach. Sci. Total Environ. 2024, 951, 175666. [Google Scholar] [CrossRef]
- Mo, X.; Wu, J.; Wang, Q.; Zhou, H. Variations in water storage in China over recent decades from GRACE observations and GLDAS. Nat. Hazards Earth Syst. Sci. 2016, 16, 469–482. [Google Scholar] [CrossRef]
- Wu, Q.; Si, B.; He, H.; Wu, P. Determining Regional-Scale Groundwater Recharge with GRACE and GLDAS. Remote Sens. 2019, 11, 154. [Google Scholar] [CrossRef]
- Moghim, S. Assessment of Water Storage Changes Using GRACE and GLDAS. Water Resour. Manag. 2020, 34, 685–697. [Google Scholar] [CrossRef]
- Gu, Z.; Gu, L.; Yin, J.; Fang, W.; Xiong, L.; Guo, J.; Zeng, Z.; Xia, J. Impact of atmospheric circulations on droughts and drought propagation over China. Sci. China Earth Sci. 2024, 67, 2633–2648. [Google Scholar] [CrossRef]
- Guth, P.L.; Van Niekerk, A.; Grohmann, C.H.; Muller, J.P.; Hawker, L.; Florinsky, I.V.; Gesch, D.; Reuter, H.I.; Herrera-Cruz, V.; Riazanoff, S.; et al. Digital Elevation Models: Terminology and Definitions. Remote Sens. 2021, 13, 3581. [Google Scholar] [CrossRef]
- Ahmad, M.H.; Abubakar, A.; Ishak, M.Y.; Danhassan, S.S.; Zhang, J.H.; Alatalo, J.M. Modeling the influence of daily temperature and precipitation extreme indices on vegetation dynamics in Katsina State using statistical downscaling model (SDM). Ecol. Indic. 2023, 155, 110979. [Google Scholar] [CrossRef]
- Lidberg, W.; Nilsson, M.; Lundmark, T.; Ågren, A.M. Evaluating preprocessing methods of digital elevation models for hydrological modelling. Hydrol. Process. 2017, 31, 4660–4668. [Google Scholar] [CrossRef]
- Jiang, T.; Su, X.; Zhang, G.; Zhang, T.; Wu, H. Estimating propagation probability from meteorological to ecological droughts using a hybrid machine learning copula method. Hydrol. Earth Syst. Sci. 2023, 27, 559–576. [Google Scholar] [CrossRef]
- Jiang, T.; Su, X.; Qu, Y.; Singh, V.; Zhang, T.; Chu, J.; Hu, X. Determining the response of ecological drought to meteorological and groundwater droughts in Northwest China using a spatio-temporal matching method. J. Hydrol. 2024, 633, 130753. [Google Scholar] [CrossRef]
- Cai, Y.T.; Liu, S.T.; Lin, H. Monitoring the vegetation dynamics in the Dongting lake wetland from 2000 to 2019 using the BEAST algorithm based on dense Landsat time series. Appl. Sci. 2020, 10, 4209. [Google Scholar] [CrossRef]
- Zhao, K.G.; Wulder, M.A.; Hu, T.X.; Bright, R.; Wu, Q.; Qin, H.; Li, Y.; Toman, E.; Mallick, B.; Zhang, X.; et al. Detecting change-point, trend, and seasonality in satellite time series data to track abrupt changes and nonlinear dynamics: A Bayesian ensemble algorithm. Remote Sens. Environ. 2019, 232, 111181. [Google Scholar] [CrossRef]
- White, J.H.R.; Walsh, J.E.; Thoman, R.L., Jr. Using Bayesian statistics to detect trends in Alaskan precipitation. Int. J. Climatol. 2021, 41, 2045–2059. [Google Scholar] [CrossRef]
- Arra, A.; Keskin, M.; Şişman, E. Trend analysis of hydro-meteorological variables using Mann-Kendall and Sen’s Slope with Standardization (SSS): Case study of the Kızılırmak catchment, Türkiye. Phys. Chem. Earth 2025, 141, 104115. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Leng, G.; Huang, Q. Integrated index for drought assessment based on variable fuzzy set theory: A case study in the Yellow River basin, China. J. Hydrol. 2015, 527, 608–618. [Google Scholar] [CrossRef]
- Wang, F.; Lai, H.; Li, Y.; Feng, K.; Zhang, Z.; Tian, Q.; Zhu, X.; Yang, H. Dynamic variation of meteorological drought and its relationships with agricultural drought across China. Agric. Water Manag. 2022, 261, 107301. [Google Scholar] [CrossRef]
- Hudgins, L.; Friehe, C.A.; Mayer, M.E. Wavelet transforms and atmospheric turbulence. Phys. Rev. Lett. 1993, 71, 3279–3282. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Tan, X.; Chen, X.; Lin, K. Dynamic changes of the dryness/wetness characteristics in the largest river basin of South China and their possible climate driving factors. Atmos. Res. 2020, 232, 104685. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Biswas, A.; Gharabaghi, B.; Hu, W. A multiscale and multivariate analysis of precipitation and streamflow variability in relation to ENSO, NAO and PDO. J. Hydrol. 2019, 574, 288–307. [Google Scholar] [CrossRef]
- Fang, Q.X.; Ma, L.; Green, T.R.; Yu, Q.; Wang, T.D.; Ahuja, L.R. Water resources and water use efficiency in the North China Plain: Current status and agronomic management options. Agric. Water Manag. 2010, 97, 1102–1116. [Google Scholar] [CrossRef]
- Qin, H.; Cao, G.; Kristensen, M.; Refsgaard, J.; Rasmussen, M.; He, X.; Liu, J.; Shu, Y.; Zheng, C. Integrated hydrological modeling of the North China Plain and implications for sustainable water management. Hydrol. Earth Syst. Sci. 2013, 17, 3759–3778. [Google Scholar] [CrossRef]
- Xu, Y.; Gong, H.; Chen, B.; Zhang, Q.; Li, Z. Long-term and seasonal variation in groundwater storage in the North China Plain based on GRACE. Int. J. Appl. Earth Obs. 2021, 104, 102560. [Google Scholar] [CrossRef]
- Zhu, C.; Li, W. Comparison of GRACE/GRACE-FO Spherical Harmonic Coefficient and Mascon Products in Explaining the Influence of South-to-North Water Transfer Project on Water Reserves in the North China Plain. Water 2023, 15, 2343. [Google Scholar] [CrossRef]
- Boergens, E.; Kvas, A.; Eicker, A.; Dobslaw, H.; Schawohl, L.; Dahle, C.; Murböck, M.; Flechtner, F. Uncertainties of GRACE-Based Terrestrial Water Storage Anomalies for Arbitrary Averaging Regions. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022081. [Google Scholar] [CrossRef]
- Wang, F.; Lai, H.; Li, Y.; Feng, K.; Zhang, Z.; Tian, Q.; Zhu, X.; Yang, H. Identifying the status of groundwater drought from a GRACE mascon model perspective across China during 2003–2018. Agric. Water Manag. 2022, 260, 107251. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Felfelani, F.; Wada, Y.; Longuevergne, L.; Pokhrel, Y.N. Natural and human-induced terrestrial water storage change: A global analysis using hydrological models and GRACE. J. Hydrol. 2017, 553, 105–118. [Google Scholar] [CrossRef]
- Long, D.; Yang, Y.T.; Wada, Y.; Hong, Y.; Liang, W.; Chen, Y.N.; Yong, B.; Hou, A.Z.; Wei, J.F.; Chen, L. Deriving scaling factors using a global hydrological model to restore GRACE total water storage changes for China’s Yangtze River Basin. Remote Sens. Environ. 2015, 168, 177–193. [Google Scholar] [CrossRef]
- Sun, Z.L.; Zhu, X.F.; Pan, Y.Z.; Zhang, J.S.; Liu, X.F. Drought evaluation using the GRACE terrestrial water storage deficit over the Yangtze River Basin, China. Sci. Total Environ. 2018, 634, 727–738. [Google Scholar] [CrossRef] [PubMed]
- Zavareh, M.; Mahjouri, N.; Rahimzadegan, M.; Rahimpour, M. A drought index based on groundwater quantity and quality: Application of multivariate copula analysis. J. Clean. Prod. 2023, 417, 137959. [Google Scholar] [CrossRef]
- Han, S.; Sauber, J.; Broerse, T.; Pollitz, F.; Okal, E.; Jeon, T.; Seo, K.; Stanaway, R. GRACE and GRACE Follow-On Gravity Observations of Intermediate-Depth Earthquakes Contrasted with Those of Shallow Events. J. Geophys. Res. Solid Earth 2024, 129, e2023JB028362. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, C.; Jing, Y.; Ru, Q.; Yan, F.; Zhang, Y. GRACE/GRACE-FO Satellite Assessment of Sown Area Expansion Impacts on Groundwater Sustainability in Jilin Province. Sustainability 2025, 17, 7731. [Google Scholar] [CrossRef]
- Haile, M.; Li, F.; Ai, Z.; Chen, G.; Leng, P. Spatiotemporal characteristics and driving factors of groundwater drought in Nile River Basin (NRB). Catena 2025, 257, 109194. [Google Scholar] [CrossRef]
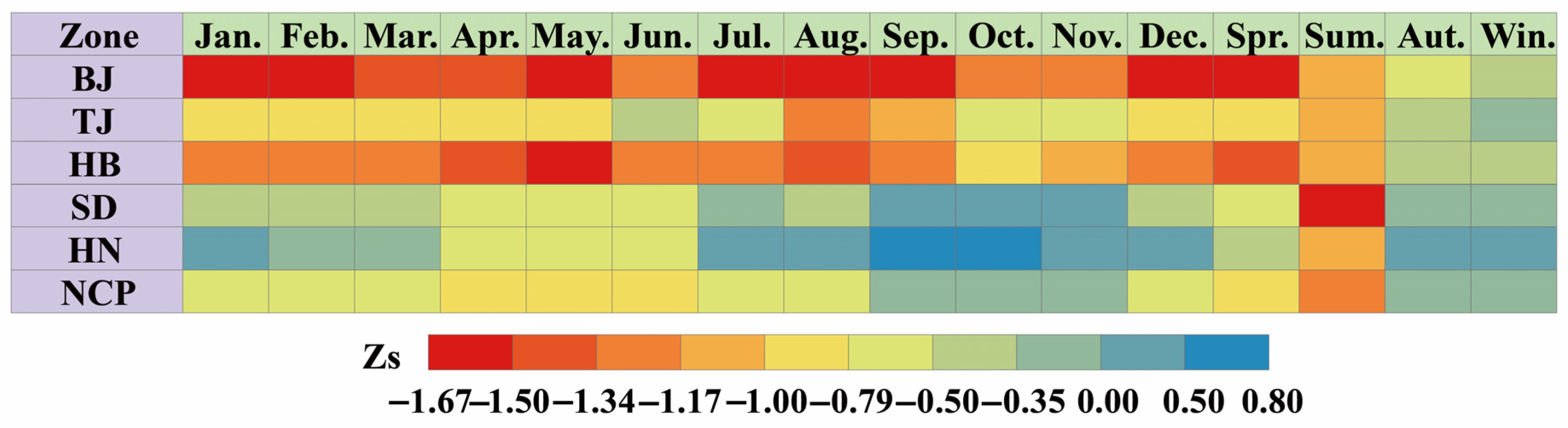
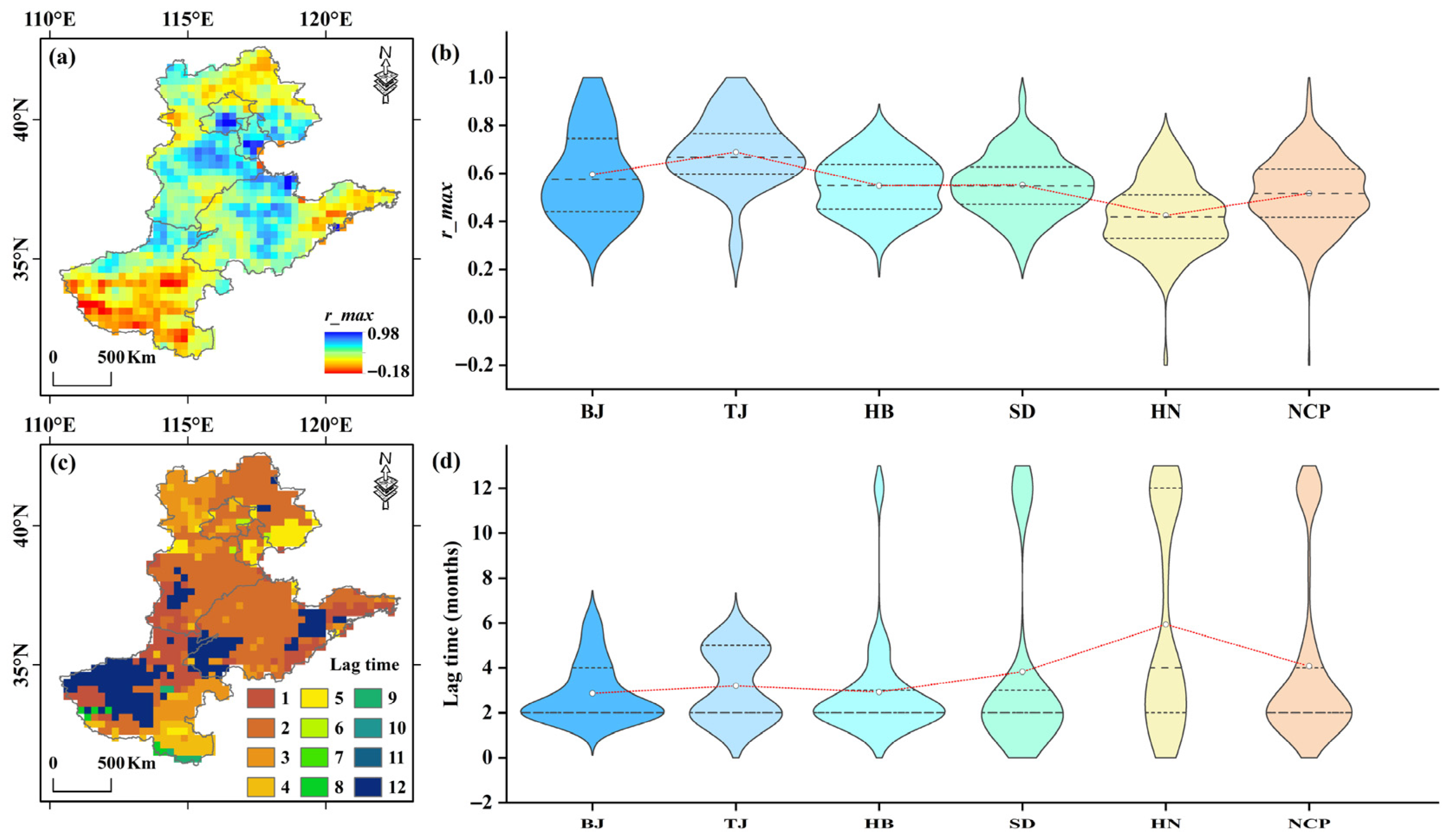
| Metric | Scale | SM | AH | AT | ET | PC | ST |
|---|---|---|---|---|---|---|---|
| PASC (%) | Small | 35.19 | 7.76 | 5.10 | 5.24 | 3.42 | 4.34 |
| Medium | 15.33 | 4.48 | 1.91 | 3.61 | 0.95 | 2.47 | |
| Large | 1.81 | 17.33 | 0.01 | 0.98 | 0.93 | 0.96 | |
| Total | 19.13 | 8.56 | 2.59 | 3.49 | 1.86 | 2.66 | |
| AWC | Small | 0.94 | 0.92 | 0.93 | 0.93 | 0.93 | 0.93 |
| Medium | 0.90 | 0.90 | 0.90 | 0.90 | 0.88 | 0.91 | |
| Large | 0.87 | 0.92 | 0.91 | 0.90 | 0.86 | 0.88 | |
| Total | 0.93 | 0.92 | 0.92 | 0.91 | 0.91 | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, W.; Wang, F.; Du, M.; Guo, J.; Li, Z.; Li, N.; Li, R.; Men, R.; Lai, H.; Xu, Q.; et al. Temporal and Spatial Dynamics of Groundwater Drought Based on GRACE Satellite and Its Relationship with Agricultural Drought. Agriculture 2025, 15, 2431. https://doi.org/10.3390/agriculture15232431
Luo W, Wang F, Du M, Guo J, Li Z, Li N, Li R, Men R, Lai H, Xu Q, et al. Temporal and Spatial Dynamics of Groundwater Drought Based on GRACE Satellite and Its Relationship with Agricultural Drought. Agriculture. 2025; 15(23):2431. https://doi.org/10.3390/agriculture15232431
Chicago/Turabian StyleLuo, Weiran, Fei Wang, Mengting Du, Jianzhong Guo, Ziwei Li, Ning Li, Rong Li, Ruyi Men, Hexin Lai, Qian Xu, and et al. 2025. "Temporal and Spatial Dynamics of Groundwater Drought Based on GRACE Satellite and Its Relationship with Agricultural Drought" Agriculture 15, no. 23: 2431. https://doi.org/10.3390/agriculture15232431
APA StyleLuo, W., Wang, F., Du, M., Guo, J., Li, Z., Li, N., Li, R., Men, R., Lai, H., Xu, Q., Feng, K., Li, Y., Huang, S., & Tian, Q. (2025). Temporal and Spatial Dynamics of Groundwater Drought Based on GRACE Satellite and Its Relationship with Agricultural Drought. Agriculture, 15(23), 2431. https://doi.org/10.3390/agriculture15232431





