Study on Lag Law of Irrigation Return Flow Based on Unit Hydrograph and Hydrus
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Design Framework
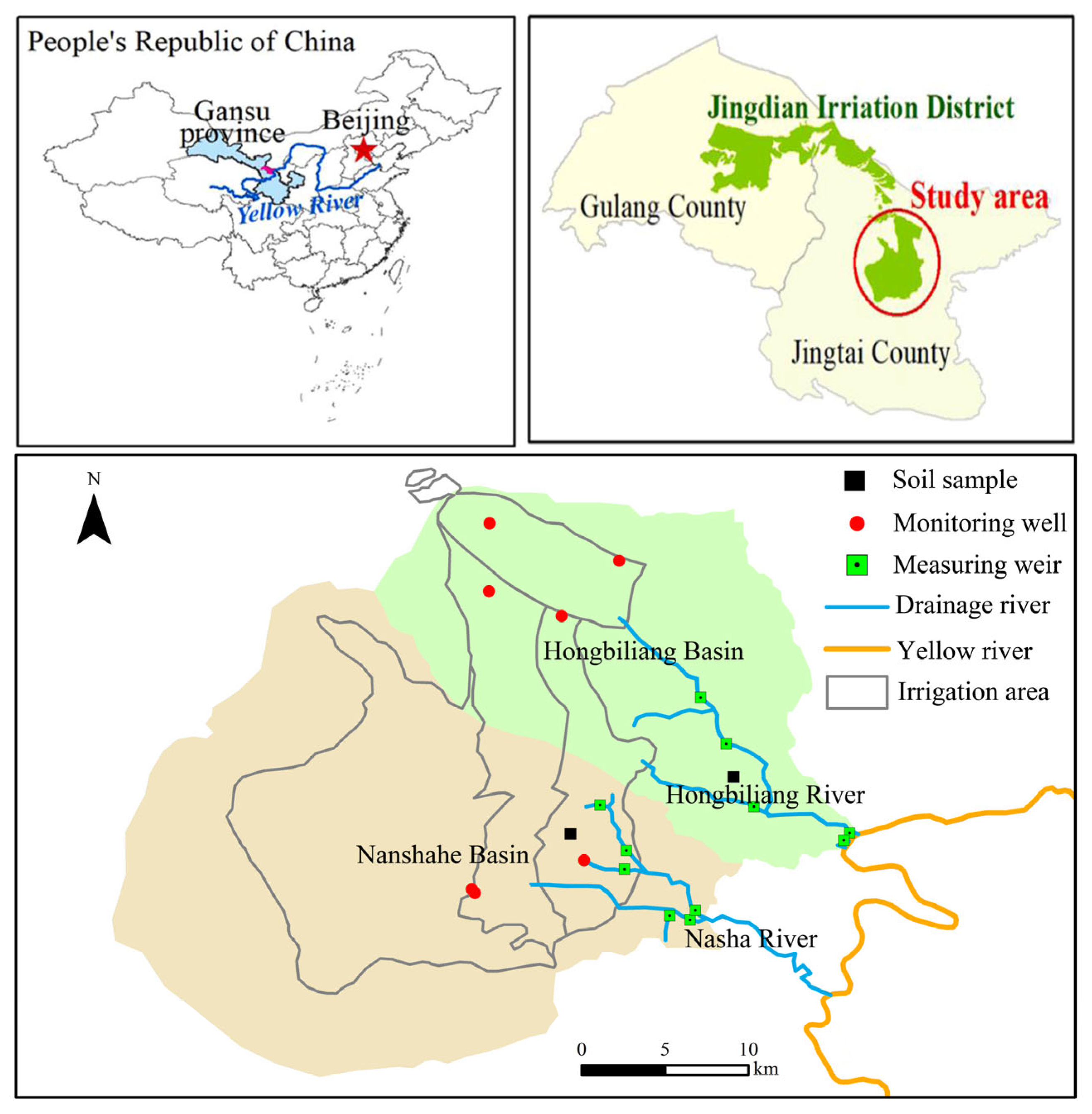
2.2. Analysis of the Study Area
2.2.1. Overview of the Study Area
2.2.2. Data Sources
2.2.3. Calculation of Irrigation Return Flow
- First step: Calculate the field runoff volume and deep percolation volume in different time periods using SCS model [40].
- Second step: Based on the calculation results of deep percolation volume, use the unit hydrograph and the principles of proportion and superposition to calculate the groundwater return flow volume in different time periods.
- Third step: The sum of the field runoff volume and groundwater return flow volume is the total irrigation return flow volume.
2.2.4. Principle of the Unit Hydrograph
2.3. Numerical Simulation of Irrigation Return Flow Based on Hydrus
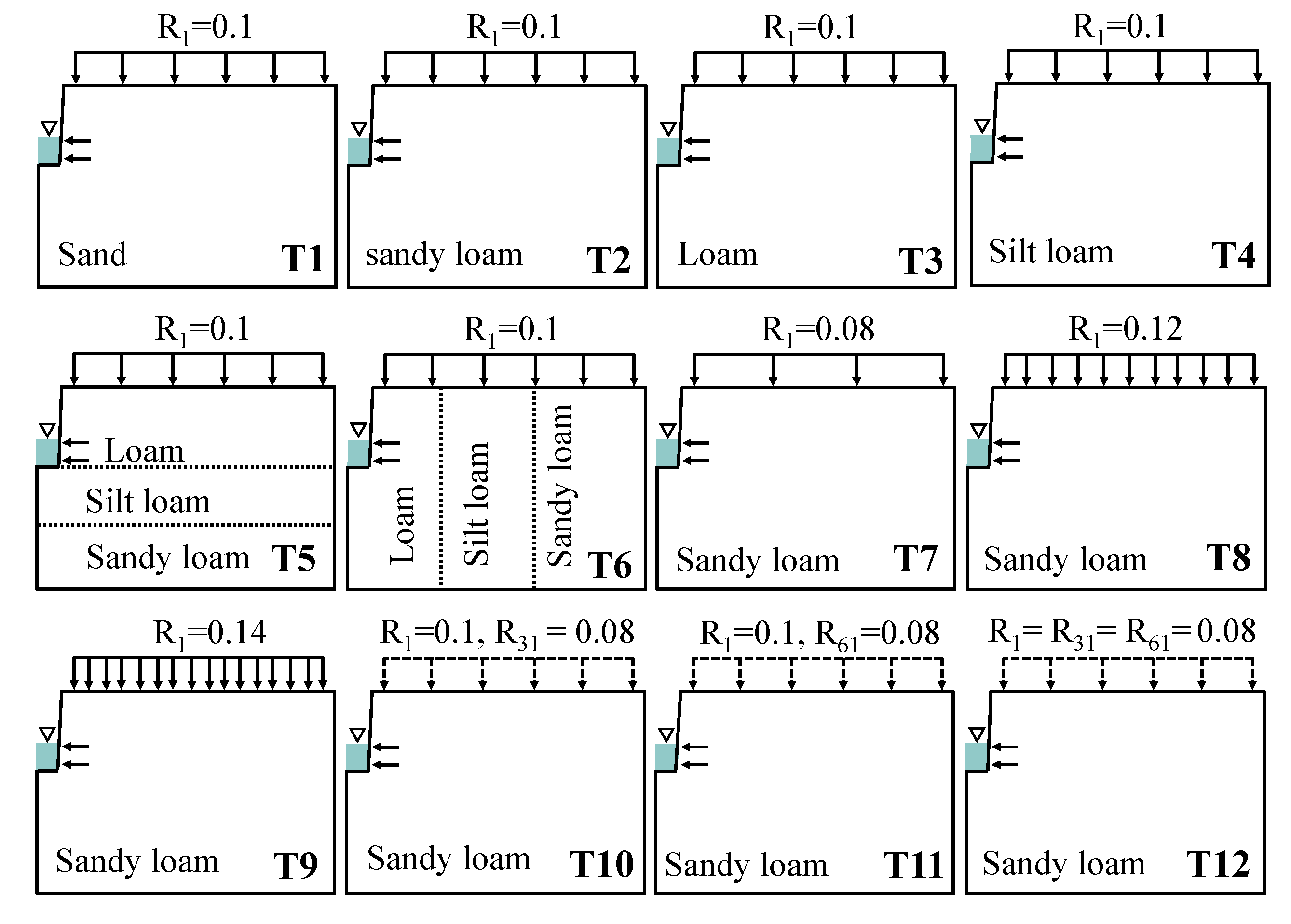
2.3.1. Model Establishment
- Constant flow boundary
- 2.
- Constant head boundary
- 3.
- Free seepage boundary
2.3.2. Simulation Schemes
3. Results
3.1. Lag Law of Irrigation Return Flow in the Study Area
3.1.1. Lag Law of Groundwater Level
3.1.2. Lag Law of Irrigation Return Flow
- An angle of 0° (→) signifies that the two are in phase, with no lag relationship.
- An angle of 90° (↓) indicates a lag relationship of 1/4 cycle between the two.
- An angle of 180° (←) denotes that the two are in opposite phases, with a lag relationship of 1/2 cycle.
- An angle of 270° (↑) suggests a lag relationship of 3/4 cycle between the two.
- For the resonance period of 1–2 months, the phase angle is approximately 45°, indicating that return flow lags behind precipitation by 1/8 of a cycle, with a lag time of about 0.1–0.3 months.
- For the resonance period of 5–6 months, the phase angle is approximately 0°, showing no significant lag.
- For the resonance period of 2–4 months, the phase angle is approximately 180°, indicating that return flow lags behind precipitation by 1/2 of a cycle, with a lag time of about 1–2 months.
- The resonance period of 8.5–11 months exhibits the strongest energy, with a phase angle of approximately 75°, indicating that return flow lags behind precipitation by 5/24 of a cycle, resulting in a lag time of about 1.8–2.3 months.
- For the 2–3 month resonance period, the phase angle is approximately 45°, indicating that return flow lags behind irrigation by 1/8 of a cycle, corresponding to a lag time of about 0.3–0.4 months.
- In the 6.5–7 month resonance period, the phase angle is approximately 75°, suggesting that return flow lags behind precipitation by approximately 1.4–1.5 months.
- The 9–11 month resonance period exhibits the strongest energy, with a phase angle of about 70°, indicating that return flow lags behind irrigation by 7/36 of a cycle, resulting in a lag time of approximately 1.8–2.1 months.
- For the resonance period of 3 to 6 months, the phase angle is approximately 30°, indicating that the return flow lags behind precipitation by one-twelfth of a cycle, corresponding to a lag time of about 0.3 to 0.5 months.
- The resonance period of 9 to 11 months exhibits the highest energy, with a phase angle of approximately 165°, indicating that the return flow lags behind precipitation by eleven twenty-fourths of a cycle, resulting in a lag time of about 4.1 to 5.0 months.
- For a resonance period of 4–7 months, the phase angle is approximately 150°, indicating that the return flow lags behind irrigation by 5/12 of a cycle, corresponding to a lag time of about 1.7–2.9 months.
- For a resonance period of 6–7 months, the phase angle is approximately 145°, signifying that the return flow lags behind precipitation by approximately 2.4–2.8 months.
- The resonance period of 9–11 months exhibits the strongest energy, with a phase angle of about 160°, indicating that the return flow lags behind irrigation by 4/9 of a cycle, resulting in a lag time of approximately 4–4.9 months.
- For the Hongbiliang Basin, the lag times of return flow relative to precipitation and irrigation range from 0 to 2.3 months, with lag times in the high-energy intervals consistently around 2 months.
- In the Nanshahe Basin, the lag times of return flow in relation to precipitation and irrigation vary from 0 to 5 months, with lag times in the high-energy intervals generally between 4 and 5 months.
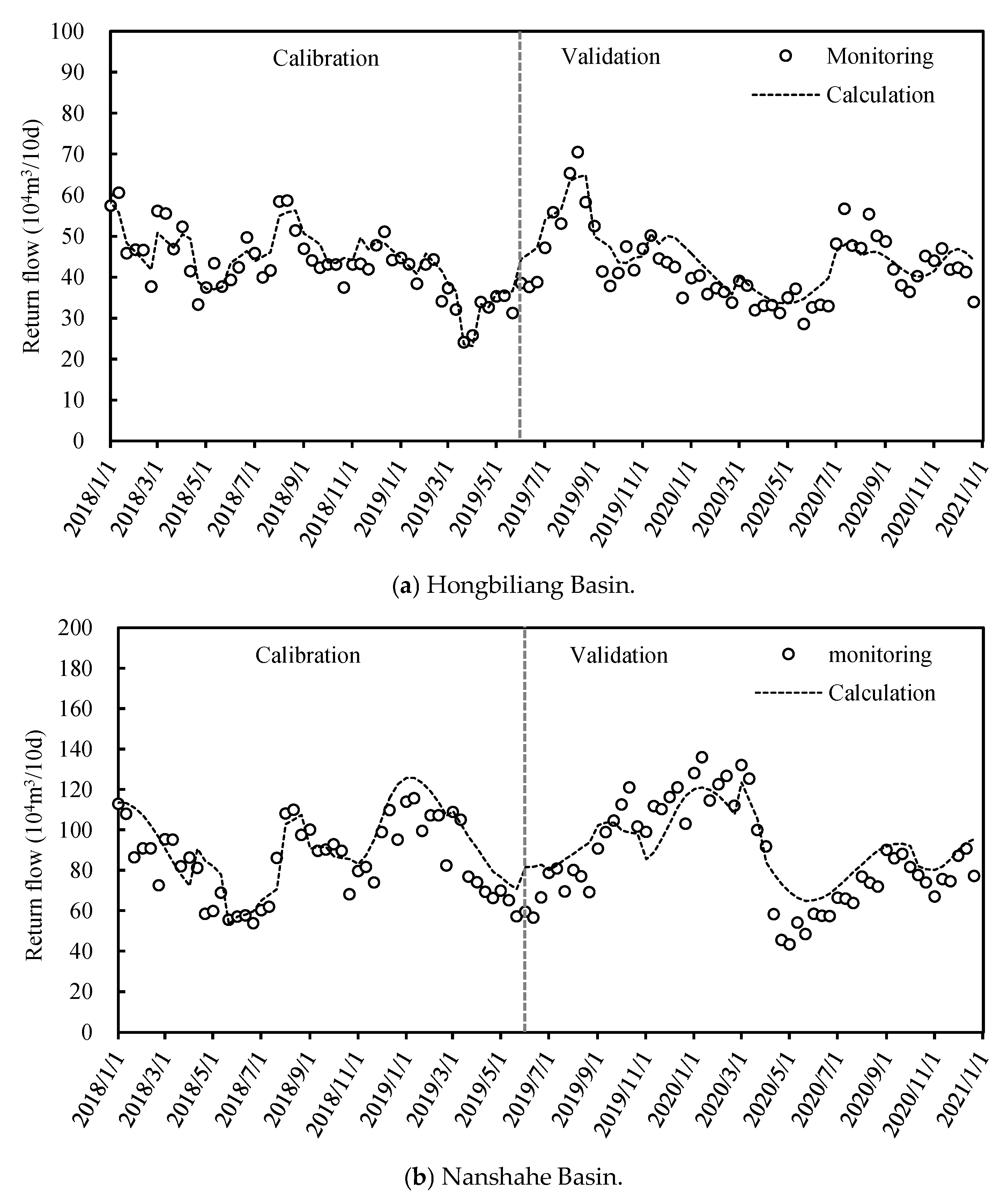
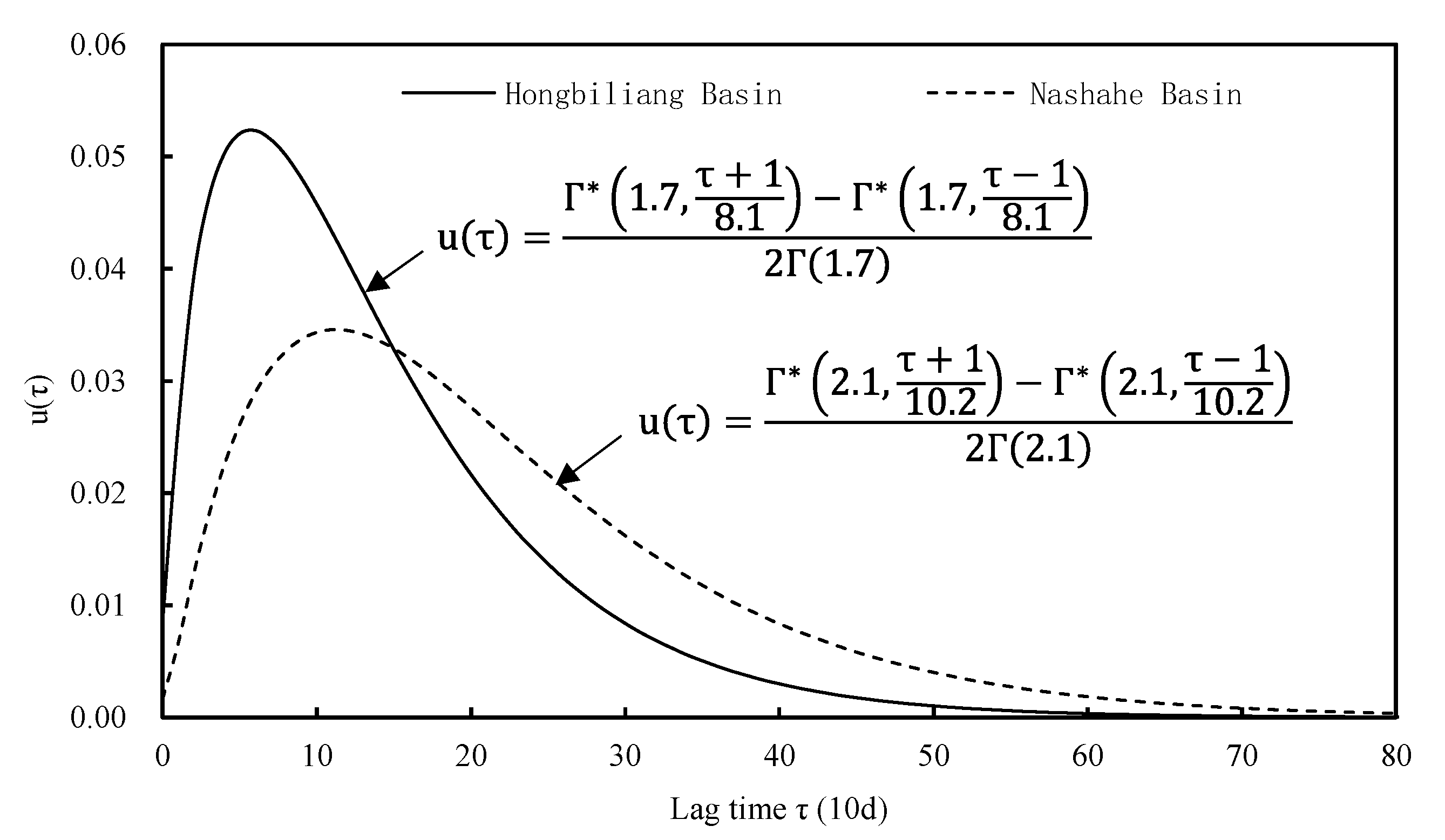
3.1.3. Calibration of Unit Hydrograph Parameters for Irrigation Return Flow
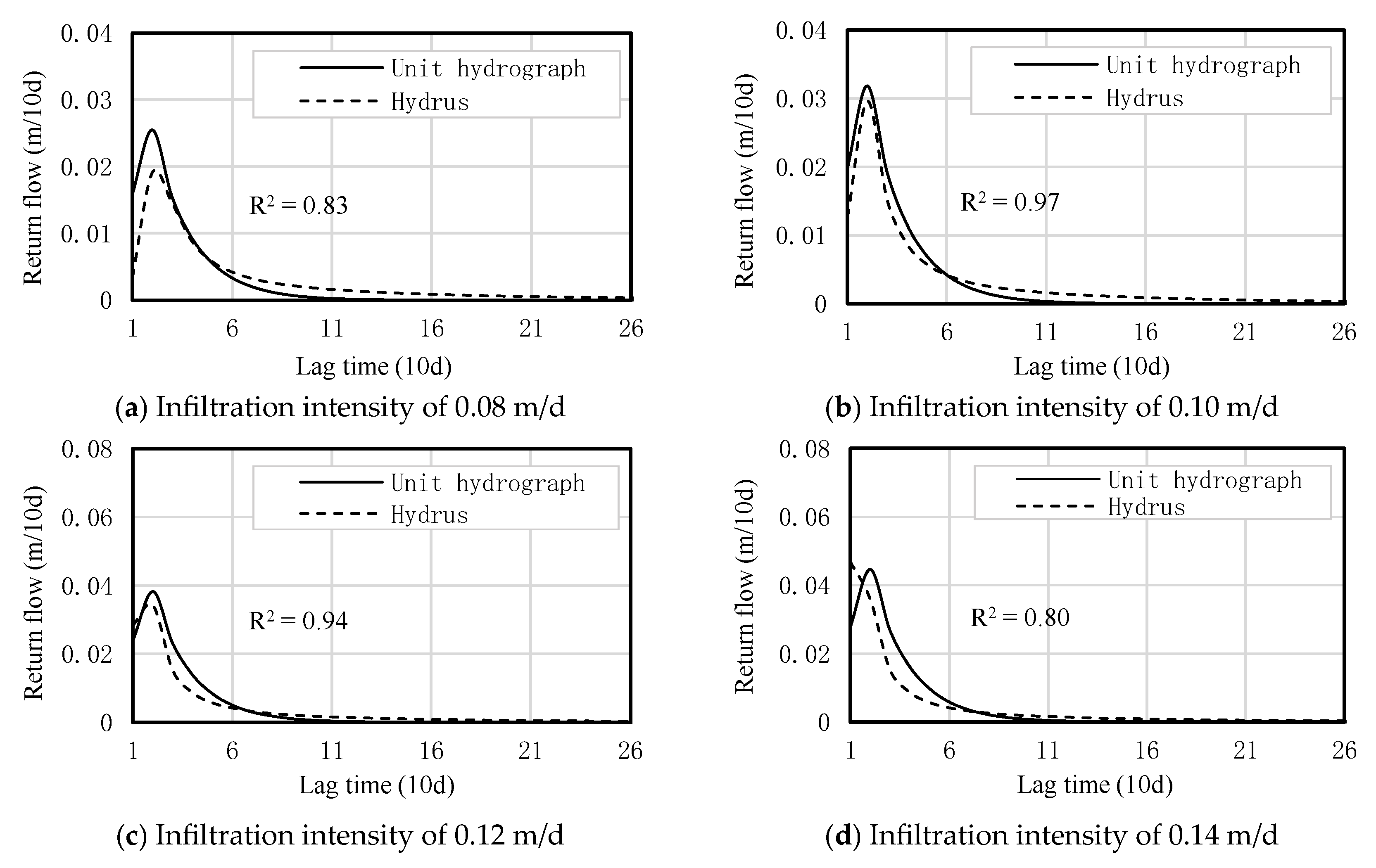
- For the Hongbiliang Basin, the variation trends of the predicted and monitored return flow volumes are consistent. The coefficient of determination (R2) for both the calibration and validation periods exceeds 0.72, while the mean relative error (MRE) during these periods is below 9.2%, indicating a strong fitting performance.
- For the Nanshahe Basin, the variation trends of the predicted and monitored return flow volumes are similarly consistent. The coefficient of determination (R2) for both the calibration and validation periods exceeds 0.74, and the mean relative error (MRE) during these periods is below 11.6%, also indicating a strong fitting performance.
- The unit hydrograph of the Hongbiliang Basin exhibits a “slender and tall” shape, demonstrating an increasing trend from 0 to 60 days (0 to 6 ten-day periods), followed by a gradual decrease after 60 days (6 ten-day periods).
- In contrast, the unit hydrograph of the Nanshahe Basin displays a “short and broad” shape, showing a gradual increase from 0 to 110 days (0 to 11 ten-day periods), and subsequently decreasing after 110 days (11 ten-day periods).
3.2. Analysis of Influencing Factors on Unit Hydrograph Parameters Based on Hydrus
3.2.1. Hydrodynamic Process of Irrigation Return Flow
- Hydrodynamic Analysis
- 2.
- Analysis of Water Velocity
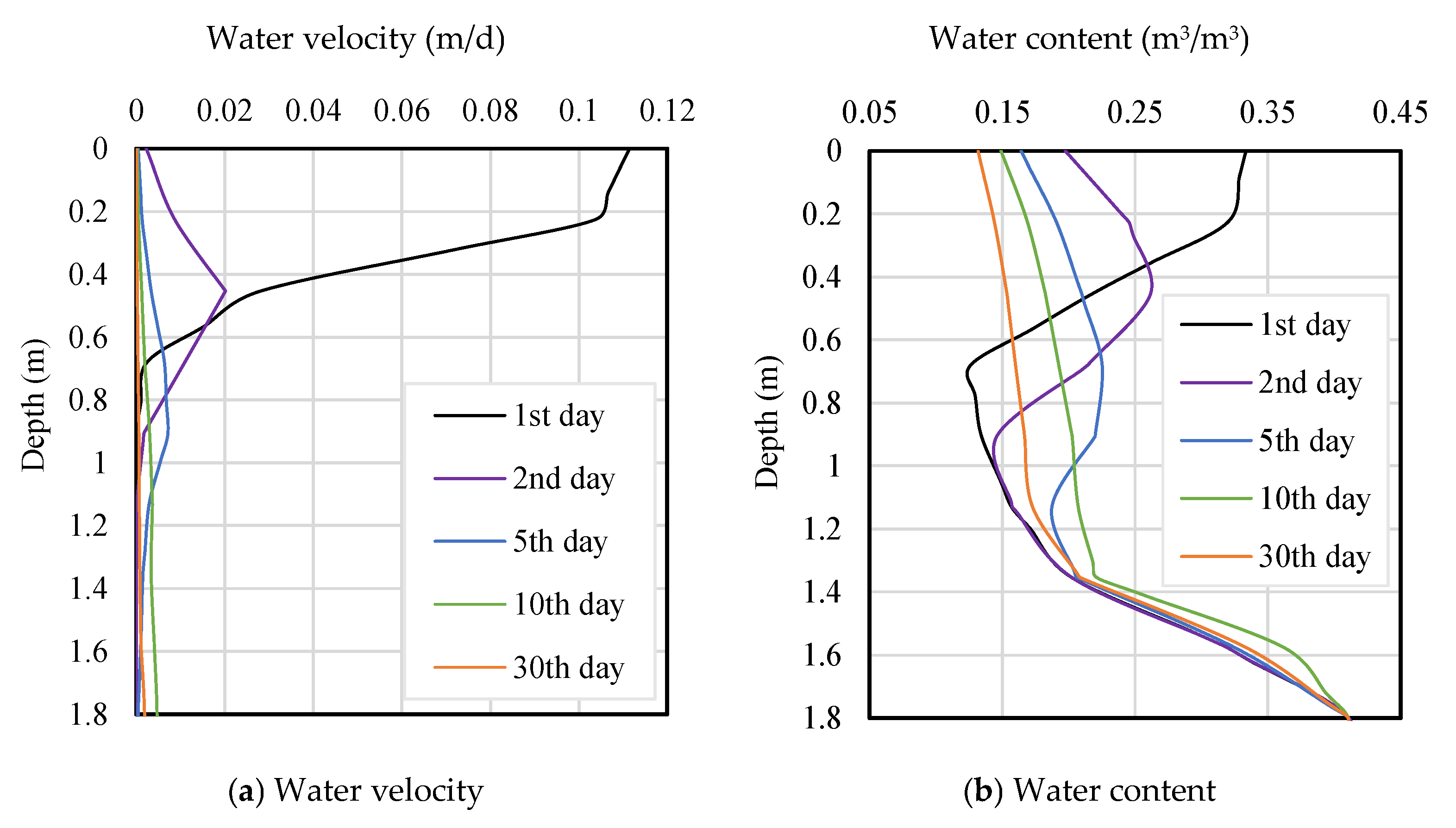
- Horizontal Distribution of Flow Velocity: The groundwater flow velocity exhibits significant variation along the horizontal direction; specifically, it increases as one approaches the channel. This phenomenon occurs because, under a constant flow rate, a smaller cross-sectional area results in a higher flow velocity. The wetted perimeter of the channel is considerably smaller than the width of the flow cross-section within the saturated zone, which contributes to the elevated groundwater flow velocity near the channel.
- Temporal Variation in Flow Velocity: Between Day 1 and Day 10, the flow velocity in Section 2 steadily increased. This increase is attributed to the recharge of groundwater by soil water, which causes a gradual rise in the groundwater level. On the side adjacent to the channel, groundwater drainage is unobstructed, leading to a lower groundwater level; conversely, on the side further from the channel, the water level is higher. As the groundwater level continues to rise, the horizontal hydraulic gradient also increases, resulting in an associated rise in flow velocity. From Day 10 to Day 30, the volume of groundwater recharge diminishes, resulting in a gradual decline in the water level and a corresponding decrease in the horizontal hydraulic gradient—thus, the groundwater flow velocity decreases accordingly.
- Soil Water Infiltration Stage: Water primarily moves vertically downward, with the rate of movement gradually decreasing.
- Groundwater Recharge Stage: In the unsaturated zone (vadose zone), the rate of water movement decreases gradually, while groundwater flow velocity in the saturated zone increases. The groundwater recharge rate initially rises before subsequently declining.
- Channel Drainage Stage: Groundwater flow predominantly occurs in a horizontal direction. Both the groundwater flow velocity and the channel drainage rate exhibit a trend of first increasing and then decreasing.
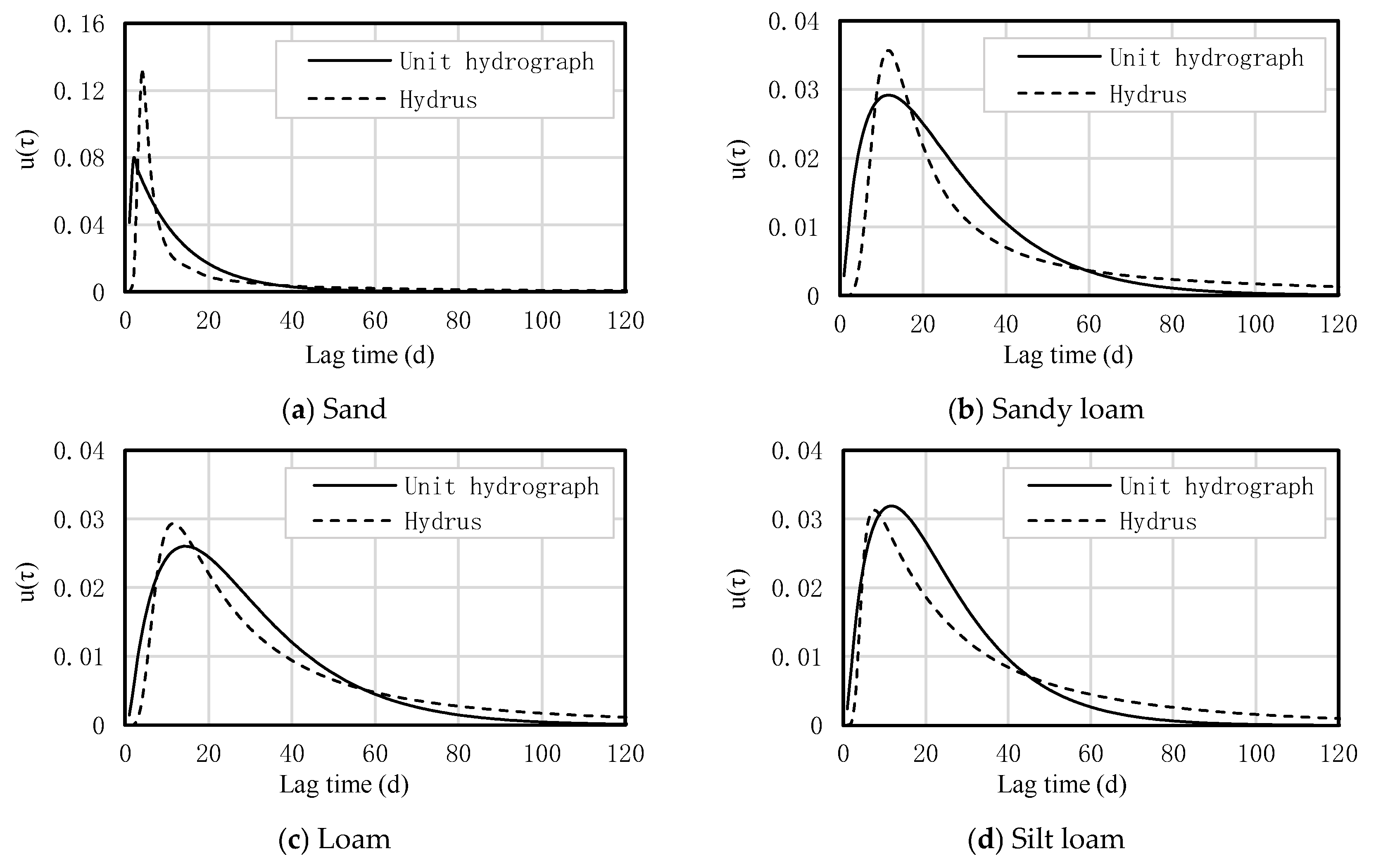
3.2.2. Influence of Soil Properties on the Unit Hydrograph
- Influence of Soil Texture on the Unit Hydrograph
- 2.
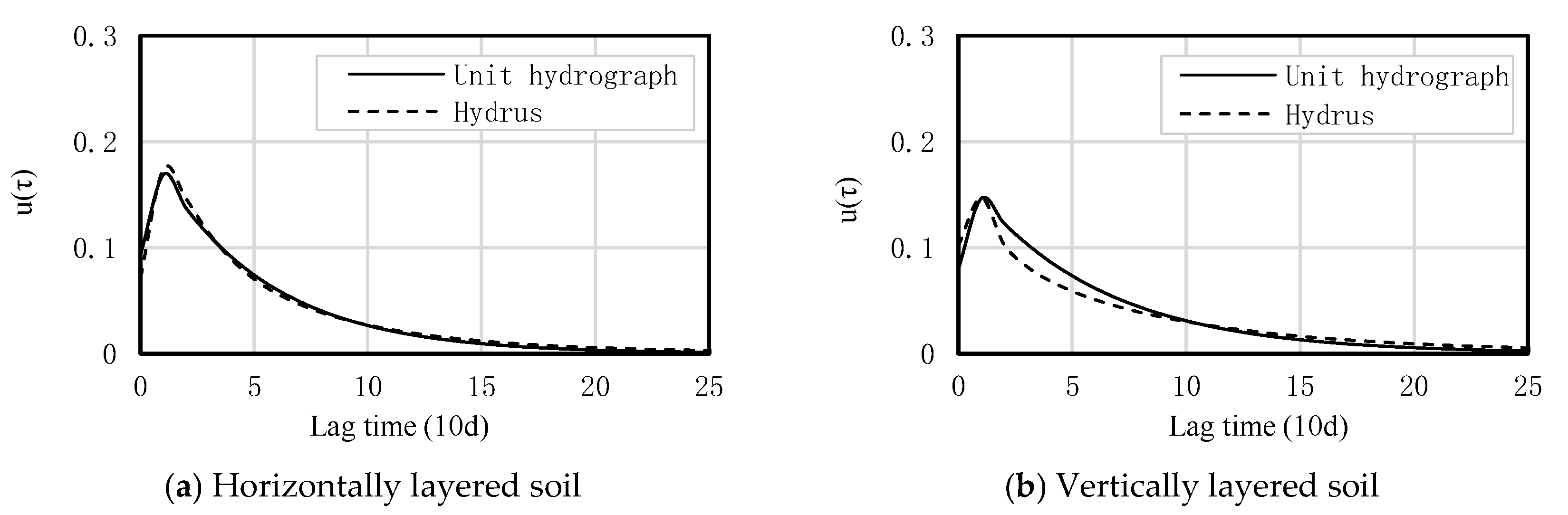
- Influence of Soil Heterogeneity on the Unit Hydrograph
3.2.3. Applicability Analysis of Proportionality and Superposition Principles
- Applicability Analysis of the Proportionality Principle
- 2.
- Applicability Analysis of the Superposition Principle
4. Discussions
4.1. Interpretation of Lag Differences in Study Area
4.2. Applicability and Influencing Factors of Unit Hydrograph
4.3. Research Value and Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Liu, X.; Zhang, T.; Du, X.; Zhao, Y.; Luo, J.; Qiu, W.; Wu, S.; Liu, H. Nitrogen and gray water footprints of various cropping systems in irrigation districts: A case from Ningxia, China. Water 2025, 17, 717. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, P. A simulation-based optimization model for control of soil salinization in the Hetao Irrigation District, Northwest China. Sustainability 2023, 15, 4467. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, H.; Wang, Z.; Shang, G.; Huang, Y.; Li, H. Analysis of the evolution pattern and driving mechanism of lakes in the Northern Ningxia Yellow Diversion Irrigation Area. Water 2022, 14, 3658. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, C.; Yang, Z.; Fan, X. Ecological security of desert–oasis areas in the Yellow River Basin, China. Land 2023, 12, 2080. [Google Scholar] [CrossRef]
- Li, C.; Feng, H.; Luo, X.; Li, Y.; Wang, N.; Wu, W.; Zhang, T.; Dong, Q.; Siddique, K.H.M. Limited irrigation and fertilization in sand-layered soil increases nitrogen use efficiency and economic benefits under film mulched ridge-furrow irrigation in arid areas. Agric. Water Manag. 2022, 262, 107406. [Google Scholar] [CrossRef]
- He, K.; Zhang, Q.; Ai, Z.; Xu, N.; Qiao, Y.; Tian, C.; Leng, P.; Cheng, H.; Chen, G.; Li, F. Characteristics and influence factors of soil water and salt movement in the Yellow River Irrigation District. Agronomy 2024, 14, 92. [Google Scholar] [CrossRef]
- Tulip, S.S.; Siddik, M.S.; Islam, M.N.; Rahman, A.; Haghighi, A.T.; Mustafa, S.M.T. The impact of irrigation return flow on seasonal groundwater recharge in northwestern Bangladesh. Agric. Water Manag. 2022, 266, 107593. [Google Scholar] [CrossRef]
- Caschetto, M.; Sacchi, E.; Pinti, D.L.; Riparbelli, C.; Bruno, S.; Zanotti, C.; Bonomi, T.; Rotiroti, M. Surface-water-irrigation return flow dominates groundwater recharge, groundwater age and nitrate dynamics in an alluvial basin aquifer. Water Res. 2025, 285, 124040. [Google Scholar] [CrossRef]
- Abdi, D.E.; Owen, J.S.; Brindley, J.C.; Birnbaum, A.; Cregg, B.M.; Fernandez, R.T. Irrigation return flow and nutrient movement mitigation by irrigation method for container plant production. Irrig. Sci. 2021, 39, 567–585. [Google Scholar] [CrossRef]
- Park, Y.; Kim, Y.; Park, S.-K.; Shin, W.-J.; Lee, K.-S. Water quality impacts of irrigation return flow on stream and groundwater in an intensive agricultural watershed. Sci. Total Environ. 2018, 630, 859–868. [Google Scholar] [CrossRef]
- Jie, F.; Fei, L.; Peng, Y.; Li, S.; Ge, Y. Optimal allocation of water resources in irrigation areas considering irrigation return flow and uncertainty. Appl. Sci. 2025, 15, 2380. [Google Scholar] [CrossRef]
- Lee, K.-S.; Park, Y.; Shin, W.-J. Hydrograph separation for a small agricultural watershed: The role of irrigation return flow. J. Hydrol. 2021, 593, 125831. [Google Scholar] [CrossRef]
- Ketchum, D.; Hoylman, Z.H.; Huntington, J.; Brinkerhoff, D.; Jencso, K.G. Irrigation intensification impacts sustainability of streamflow in the Western United States. Commun. Earth Environ. 2023, 4, 479. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, J.; Duan, L. Simulation of irrigation-induced groundwater recharge in an arid area of China. Hydrogeol. J. 2021, 29, 525–540. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, Y.; Han, S.; Yang, Y.; Ai, Z.; Wang, J.; Ma, F. Identifying changes in irrigation return flow with gradually intensified water-saving technology using HYDRUS for regional water resources management. Agric. Water Manag. 2017, 194, 33–47. [Google Scholar] [CrossRef]
- Mohan, S.; Vijayalakshmi, D.P. Prediction of irrigation return flows through a hierarchical modeling approach. Agric. Water Manag. 2009, 96, 233–246. [Google Scholar] [CrossRef]
- Eluwa, C.; Francois, B.; Bernstein, A.; Brown, C. Exploring the implications of modeling choices on prediction of irrigation water savings. Water Resour. Res. 2023, 59, e2021WR031618. [Google Scholar] [CrossRef]
- Chien, C.P.; Fang, W.T. Modeling irrigation return flow for the return flow reuse system in paddy fields. Paddy Water Environ. 2012, 10, 187–196. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, V.; Saini, R.K.; Pant, N.; Singh, R.; Singh, A.; Kumar, S.; Singh, S.; Yadav, B.K.; Krishan, G.; et al. Floodplains landforms, clay deposition and irrigation return flow govern arsenic occurrence, prevalence and mobilization: A geochemical and isotopic study of the mid-Gangetic floodplains. Environ. Res. 2021, 201, 111516. [Google Scholar] [CrossRef]
- Veettil, A.V.; Green, T.R.; Kipka, H.; Arabi, M.; Lighthart, N.; Mankin, K.; Clary, J. Fully distributed versus semi-distributed process simulation of a highly managed watershed with mixed land use and irrigation return flow. Environ. Model. Softw. 2021, 140, 105000. [Google Scholar] [CrossRef]
- Chatrabhuj; Meshram, K.; Mishra, U.; Omar, P.J. Integration of remote sensing data and GIS technologies in river management system. Discov. Geosci. 2024, 2, 67. [Google Scholar] [CrossRef]
- Attar, H.K.; Noory, H.; Ebrahimian, H.; Liaghat, A.-M. Efficiency and productivity of irrigation water based on water balance considering quality of return flows. Agric. Water Manag. 2020, 231, 106025. [Google Scholar] [CrossRef]
- Liu, W.; Fu, Q.; Meng, J.; Li, T.; Cheng, K. Simulation and analysis of return flow at the field scale in the northern rice irrigation area of China. Agric. Water Manag. 2019, 224, 105735. [Google Scholar] [CrossRef]
- Li, D. Quantifying water use and groundwater recharge under flood irrigation in an arid oasis of northwestern China. Agric. Water Manag. 2020, 240, 106326. [Google Scholar] [CrossRef]
- Kattan, Z. Estimation of evaporation and irrigation return flow in arid zones using stable isotope ratios and chloride mass-balance analysis: Case of the Euphrates River, Syria. J. Arid Environ. 2008, 72, 730–747. [Google Scholar] [CrossRef]
- Séraphin, P.; Vallet-Coulomb, C.; Gonçalvès, J. Partitioning groundwater recharge between rainfall infiltration and irrigation return flow using stable isotopes: The Crau aquifer. J. Hydrol. 2016, 542, 241–253. [Google Scholar] [CrossRef]
- Ansari, M.A.; Noble, J.; Kumar, U.S.; Deodhar, A.; Akhtar, N.; Singh, P.; Raj, R. Assessing the groundwater recharge processes in intensively irrigated regions: An approach combining isotope hydrology and machine learning. Geosci. Front. 2025, 16, 102105. [Google Scholar] [CrossRef]
- Kang, T.; Shin, Y.; Shin, M.; Lee, D.; Lim, K.J.; Kim, J. Evaluation of the effect of agricultural return flow on water quality, water quantity and aquatic ecology in downstream rivers. Water 2024, 16, 1604. [Google Scholar] [CrossRef]
- Han, J.; Lee, S.; Kim, J. Quantifying stream return flow of agricultural water using SWAT-MODFLOW-PADDY model in Korean paddy fields. Agronomy 2024, 14, 2440. [Google Scholar] [CrossRef]
- Rujner, H.; Leonhardt, G.; Marsalek, J.; Viklander, M. High-resolution modelling of the grass swale response to runoff inflows with Mike SHE. J. Hydrol. 2018, 562, 411–422. [Google Scholar] [CrossRef]
- Long, S.A.; Cook, A.M.; Fennema, R.; Tachiev, G.I.; Villamizar, V.; Kotun, K.; Miralles-Wilhelm, F. Analysis of bridge construction as a restoration technique for Everglades National Park, FL, USA, using hydrological numerical modeling. J. Hydraul. Eng. 2016, 142, 05015005. [Google Scholar] [CrossRef]
- Naghedifar, S.M.; Ziaei, A.N.; Ansari, H. Simulation of irrigation return flow from a Triticale farm under sprinkler and furrow irrigation systems using experimental data: A case study in arid region. Agric. Water Manag. 2018, 210, 185–197. [Google Scholar] [CrossRef]
- Stewart, R.D.; Lee, J.G.; Shuster, W.D.; Darner, R.A. Modelling hydrological response to a fully-monitored urban bioretention cell. Hydrol. Process. 2017, 31, 4626–4638. [Google Scholar] [CrossRef]
- Pérez-Blanco, C.D.; Essenfelder, A.H.; Gutiérrez-Martín, C. A tale of two rivers: Integrated hydro-economic modeling for the evaluation of trading opportunities and return flow externalities in inter-basin agricultural water markets. J. Hydrol. 2020, 584, 124676. [Google Scholar] [CrossRef]
- Jie, F.; Fei, L.; Li, S.; Hao, K.; Liu, L.; Li, J.; Liu, N. Quantitative effects of vadose zone thickness on delayed recharge of groundwater for an irrigation district in an arid area of Northwest China. J. Hydrol. Reg. Stud. 2022, 40, 101022. [Google Scholar] [CrossRef]
- Jafari, H.; Raeisi, E.; Zare, M.; Haghighi, A.A.K. Time series analysis of irrigation return flow in a semi-arid agricultural region, Iran. Arch. Agron. Soil Sci. 2011, 58, 673–689. [Google Scholar] [CrossRef]
- Khalaj, M.; Kholghi, M.; Saghafian, B.; Bazrafshan, J. Impact of climate variation and human activities on groundwater quality in northwest of Iran. J. Water Supply Res. Technol. 2019, 68, 121–135. [Google Scholar] [CrossRef]
- Tu, Q.; Li, H.; Wang, X. Multi-criteria evaluation of small-scale sprinkler irrigation systems using grey relational analysis. Water Resour. Manag. 2014, 28, 4665–4684. [Google Scholar] [CrossRef]
- Wu, D.; Cui, Y.; Luo, Y. Irrigation efficiency and water-saving potential considering reuse of return flow. Agric. Water Manag. 2019, 221, 519–527. [Google Scholar] [CrossRef]
- Jie, F. Study on the Lag and Uncertainty of Return Flow in a Large Yellow River Irrigation District. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2023. (In Chinese). [Google Scholar]
- Nash, J.E. The Form of the Instantaneous Unit Hydrograph. In Proceedings of the International Association of Scientific Hydrology (IAHS) General Assembly, Toronto, ON, Canada, 3–14 September 1957; pp. 114–121. [Google Scholar]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
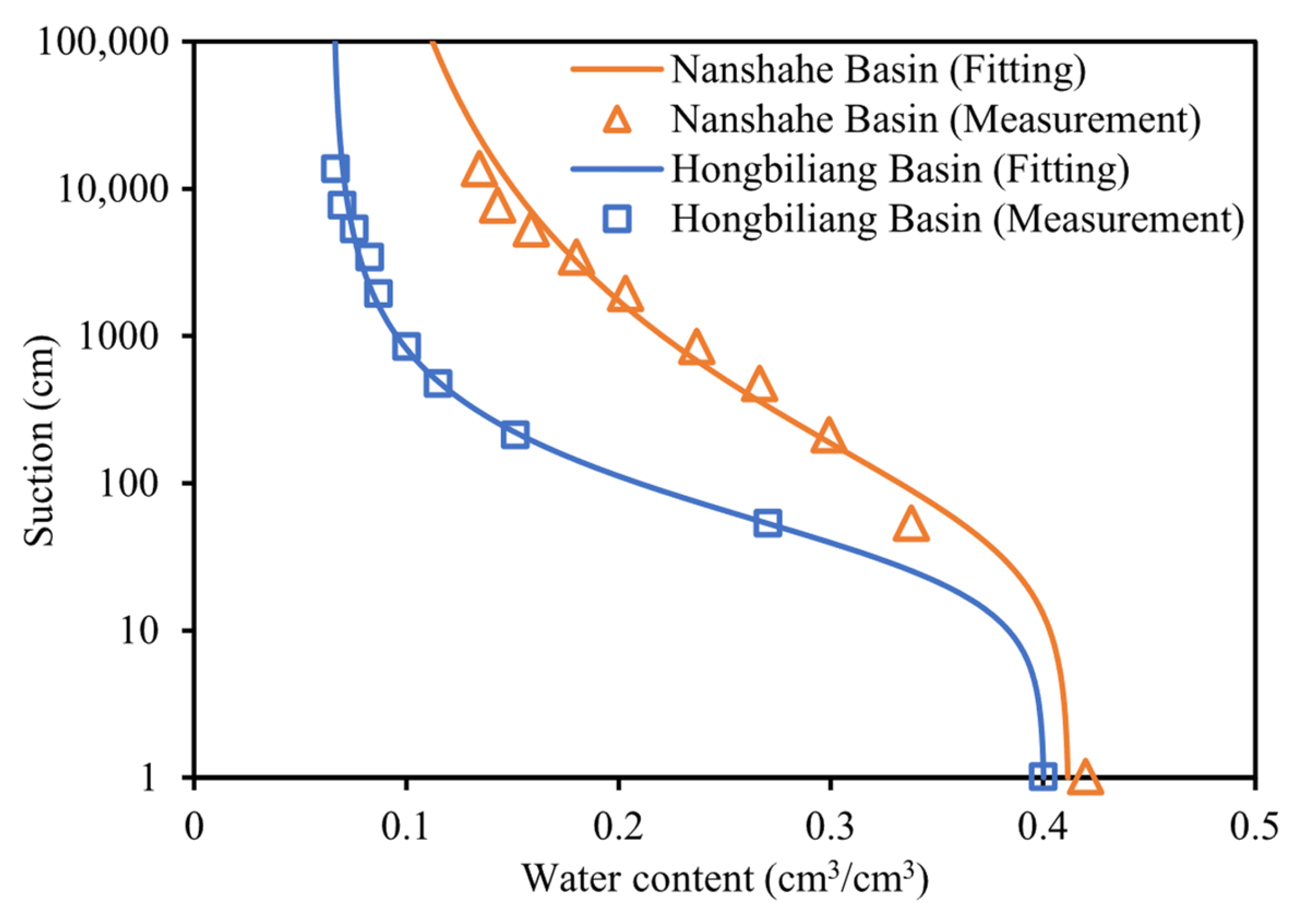














| River Basin | Soil Texture | Bulk Density (g/cm3) | Saturated Water Content (cm3/cm3) | Field Capacity (cm3/cm3) | Saturated Hydraulic Conductivity (cm/min) |
|---|---|---|---|---|---|
| Nanshahe Basin | Silt Loam | 1.44 | 0.42 | 0.28 | 0.004 |
| Hongbiliang Basin | Sandy Loam | 1.53 | 0.40 | 0.25 | 0.049 |
| Basin | Influencing Factor | Significant Interval of Lag Time (Months) | High-Energy Interval of Lag Time (Months) |
|---|---|---|---|
| Hongbiliang Basin | Precipitation | [0.1, 0.3], [1, 2], [1.8~2.3] | [1.8~2.3] |
| Irrigation | [0.3, 0.4], [1.4, 1.5], [1.8~2.1] | [1.8~2.1] | |
| Nanshahe Basin | Precipitation | [0.3, 0.5], [4.1~5.0] | [4.1~5.0] |
| Irrigation | [1.7, 2.9], [2.4, 2.8], [4~4.9] | [4~4.9] |
| Basin | n | k | Calibration | Validation |
|---|---|---|---|---|
| Hongbiliang Basin | 1.7 | 8.1 | R2 = 0.77 MRE = 7.3% | R2 = 0.72 MSE = 9.2% |
| Nanshahe Basin | 2.7 | 10.2 | R2 = 0.74 MRE = 10.3% | R2 = 0.79 MRE = 11.6% |
| Time Scale | Soil Texture | n | k | RSS | R2 |
|---|---|---|---|---|---|
| Daily Scale | Sand | 1.00 | 11.60 | 0.017 | 0.67 |
| Sandy Loam | 1.75 | 14.20 | 0.002 | 0.87 | |
| Loam | 1.92 | 14.62 | 0.001 | 0.95 | |
| Silt Loam | 1.87 | 12.18 | 0.001 | 0.95 | |
| Ten-Day Scale | Sand | 1.00 | 0.41 | 0.140 | 0.68 |
| Sandy Loam | 1.00 | 1.97 | 0.010 | 0.97 | |
| Loam | 1.10 | 2.26 | 0.002 | 0.99 | |
| Silt Loam | 1.00 | 2.97 | 0.005 | 0.96 |
| Heterogeneity Type | Soil Texture | n | k | RSS | R2 |
|---|---|---|---|---|---|
| Horizontally Layered Soil | Loam, Silt Loam, Sand | 1.00 | 4.86 | 0.001 | 0.99 |
| Vertically Layered Soil | Loam, Silt Loam, Sand | 1.00 | 5.78 | 0.002 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jie, F.; Peng, Y.; Fei, L. Study on Lag Law of Irrigation Return Flow Based on Unit Hydrograph and Hydrus. Agriculture 2025, 15, 2387. https://doi.org/10.3390/agriculture15222387
Jie F, Peng Y, Fei L. Study on Lag Law of Irrigation Return Flow Based on Unit Hydrograph and Hydrus. Agriculture. 2025; 15(22):2387. https://doi.org/10.3390/agriculture15222387
Chicago/Turabian StyleJie, Feilong, Youliang Peng, and Liangjun Fei. 2025. "Study on Lag Law of Irrigation Return Flow Based on Unit Hydrograph and Hydrus" Agriculture 15, no. 22: 2387. https://doi.org/10.3390/agriculture15222387
APA StyleJie, F., Peng, Y., & Fei, L. (2025). Study on Lag Law of Irrigation Return Flow Based on Unit Hydrograph and Hydrus. Agriculture, 15(22), 2387. https://doi.org/10.3390/agriculture15222387





