Wear Calculation Method of Tripping Mechanism of Knotter Based on Rigid–Flexible Coupling Dynamic Model
Abstract
1. Introduction
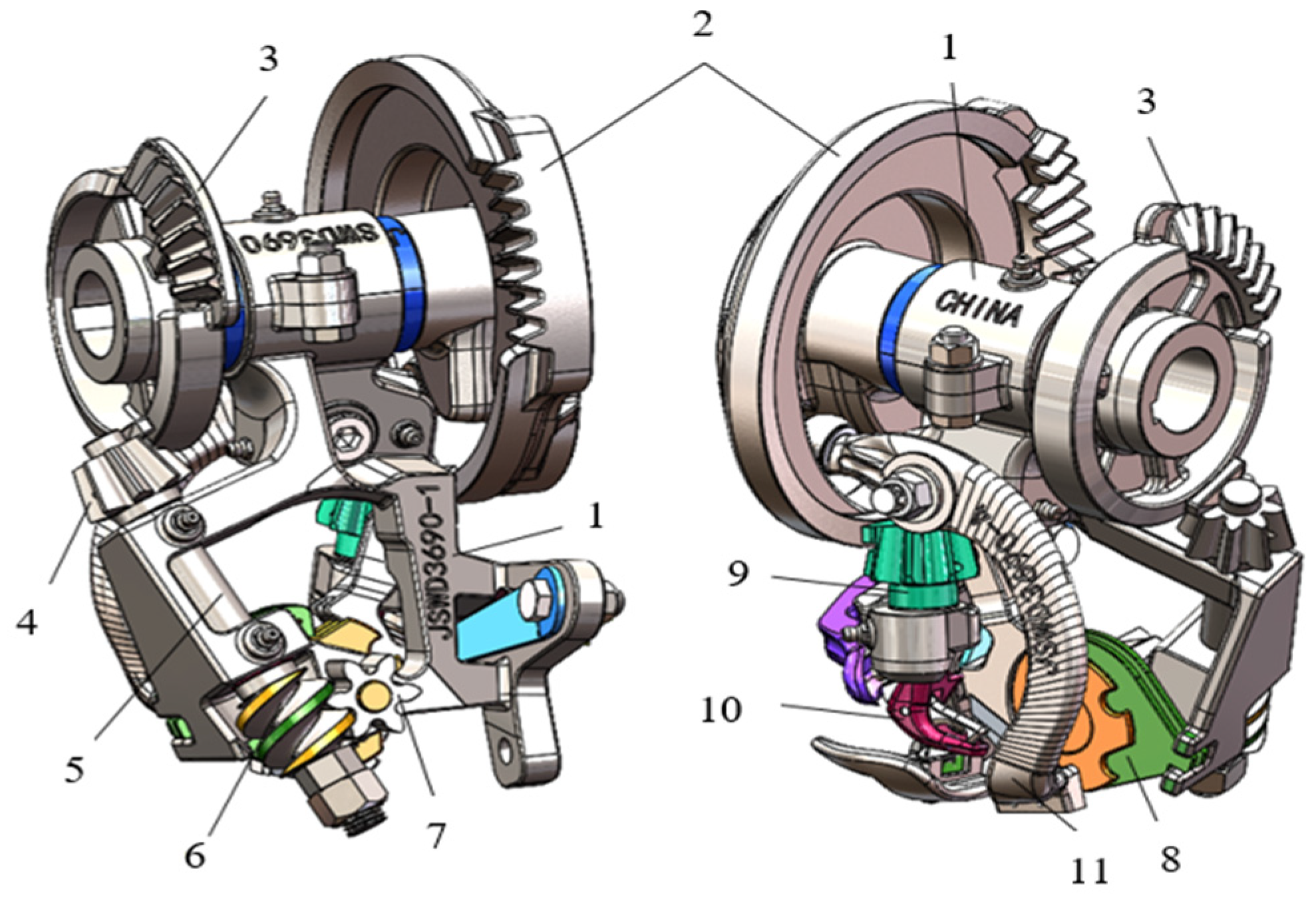
2. Design of the Tripping Mechanism Based on the Principle of Elastic Deformation
3. Simulation of the Tripping Mechanism Based on Rigid–Flexible Coupling Dynamic Model
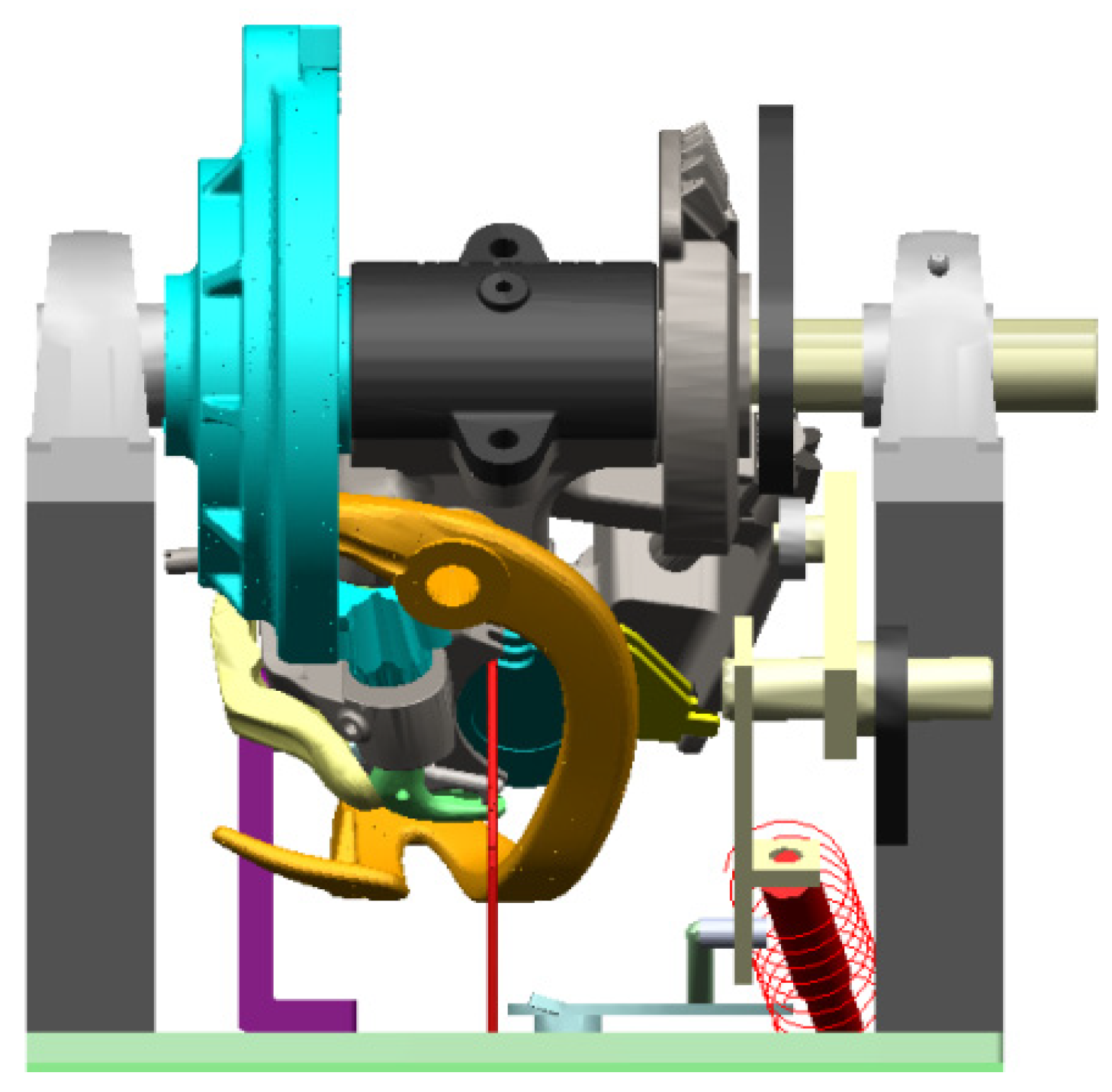
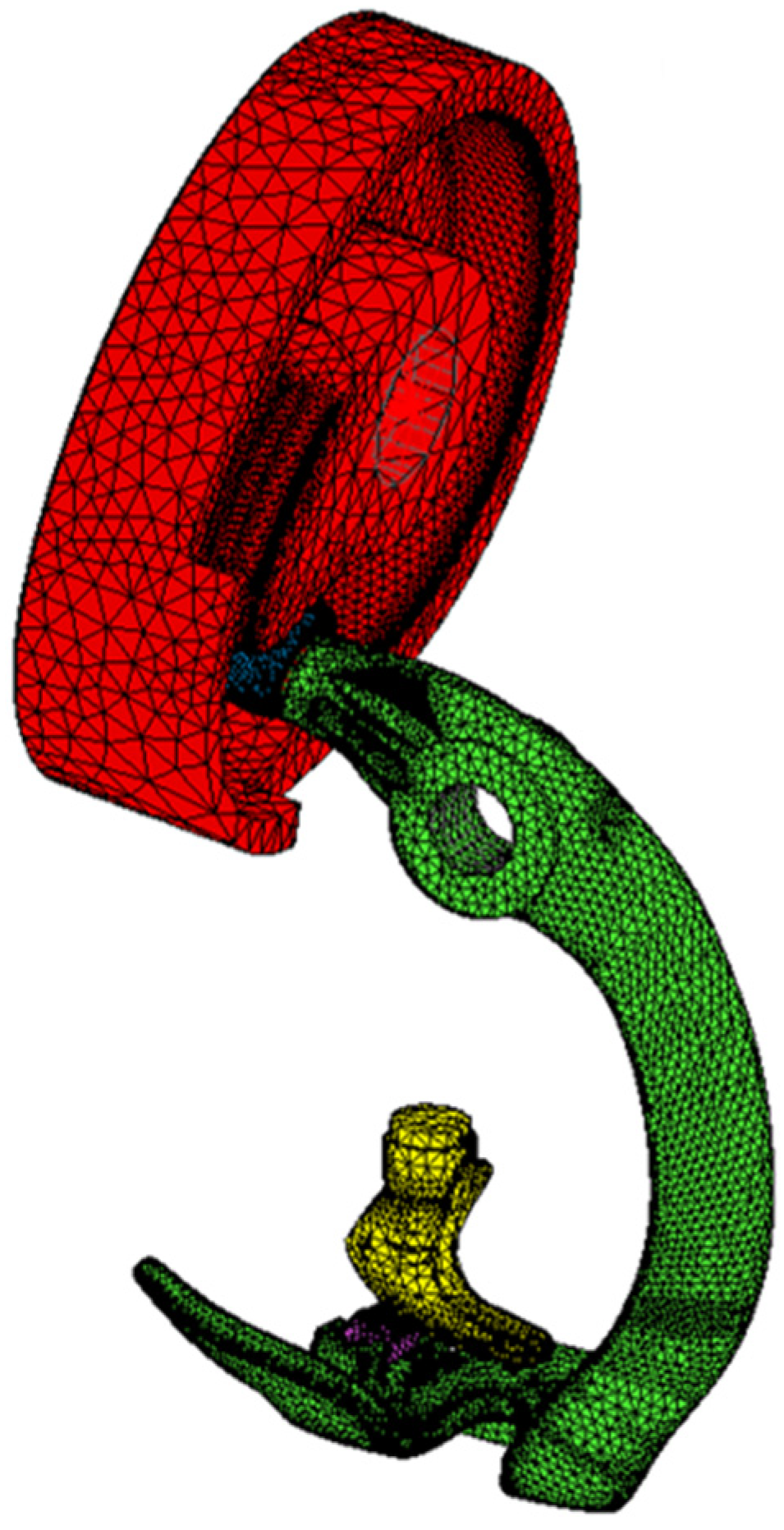
3.1. Pre-Processing of Finite Element Model of the Tripping Mechanism Parts
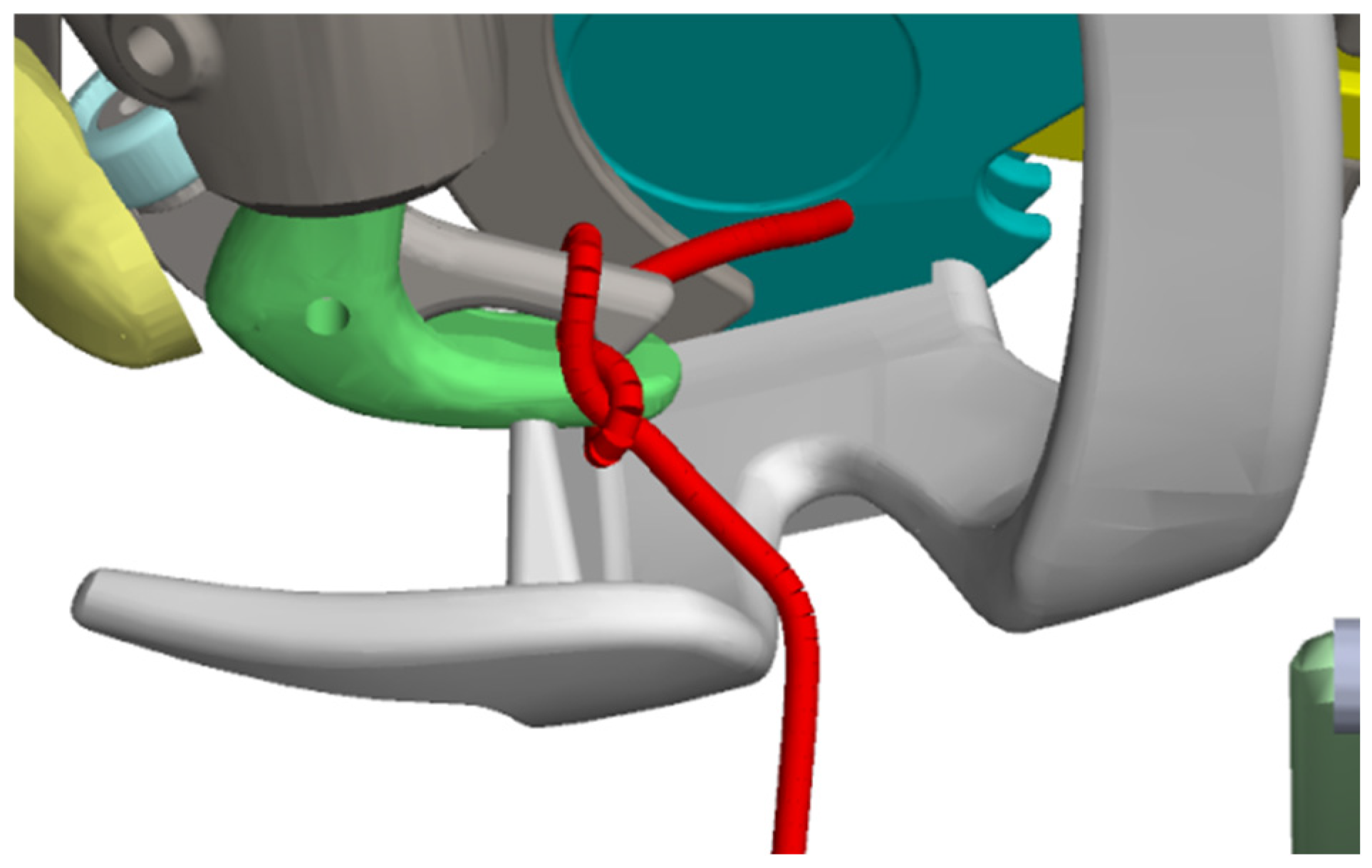
3.2. Construction of Rigid–Flexible Dynamic Model of the Tripping Mechanism
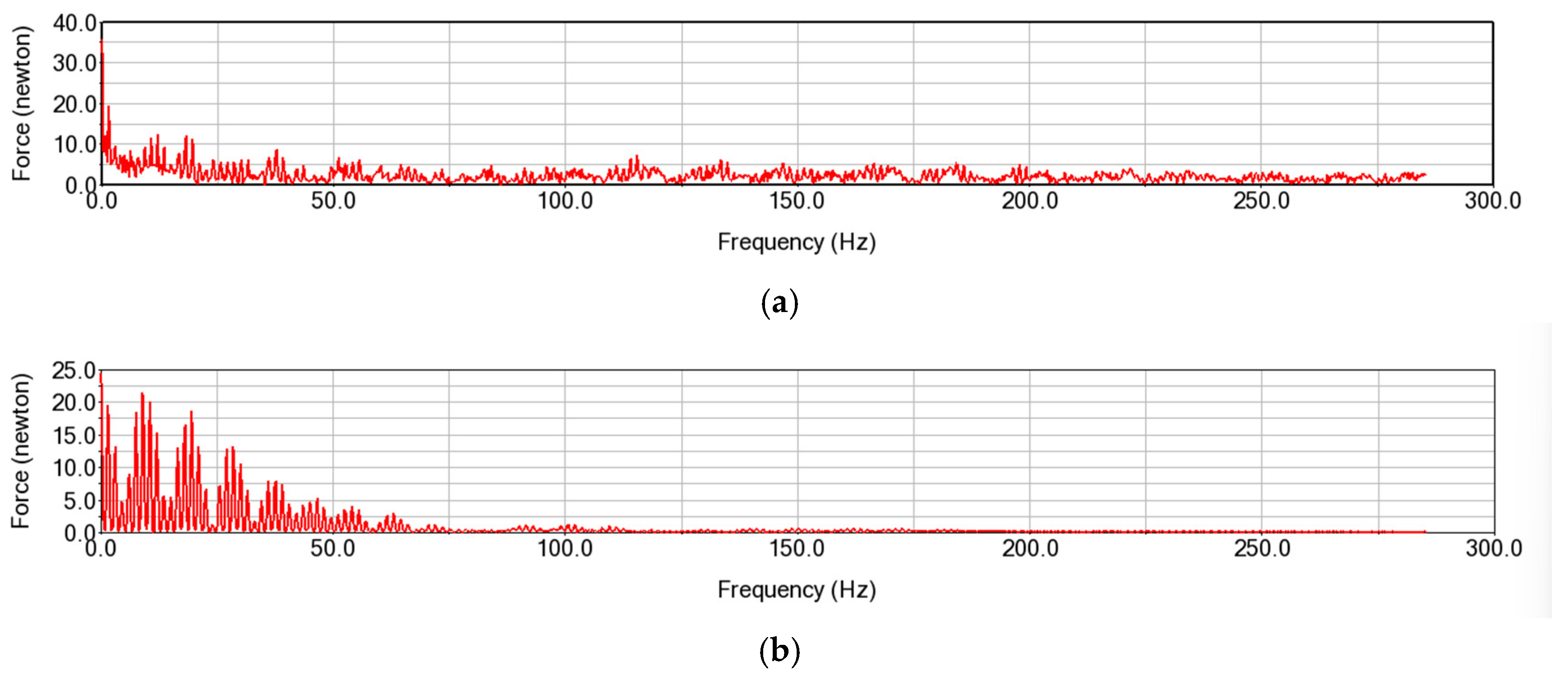
3.3. Solution of Rigid–Flexible Coupling Dynamic Model
4. Wear Calculation and Prediction of Tripping Mechanism
4.1. Constitutive Model of Wear
4.2. Construction of Finite Element Wear Model
4.2.1. Establishment of Model
4.2.2. Setting of Boundary Conditions and Contact
4.2.3. Setting of Driving and Analysis Working Conditions
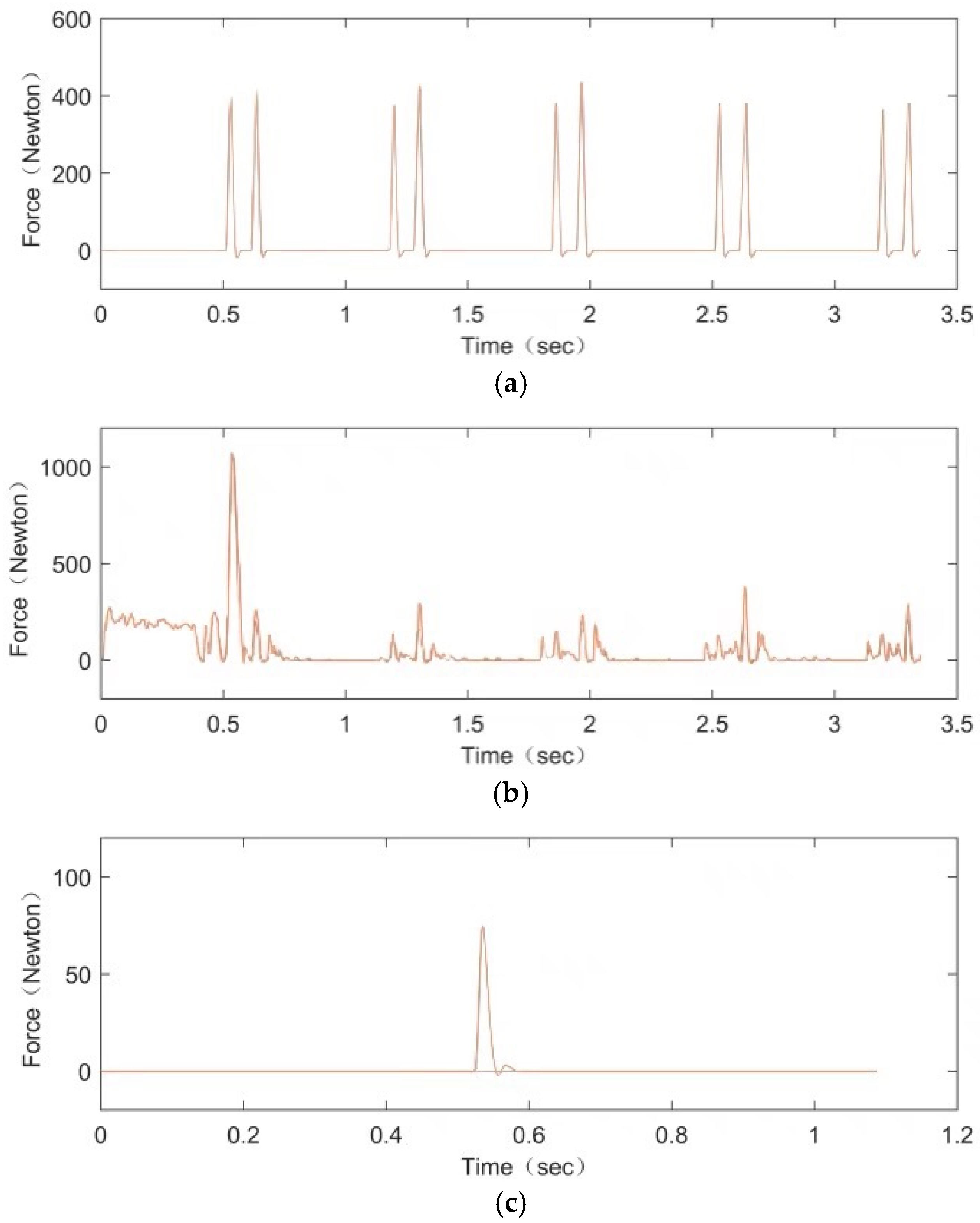
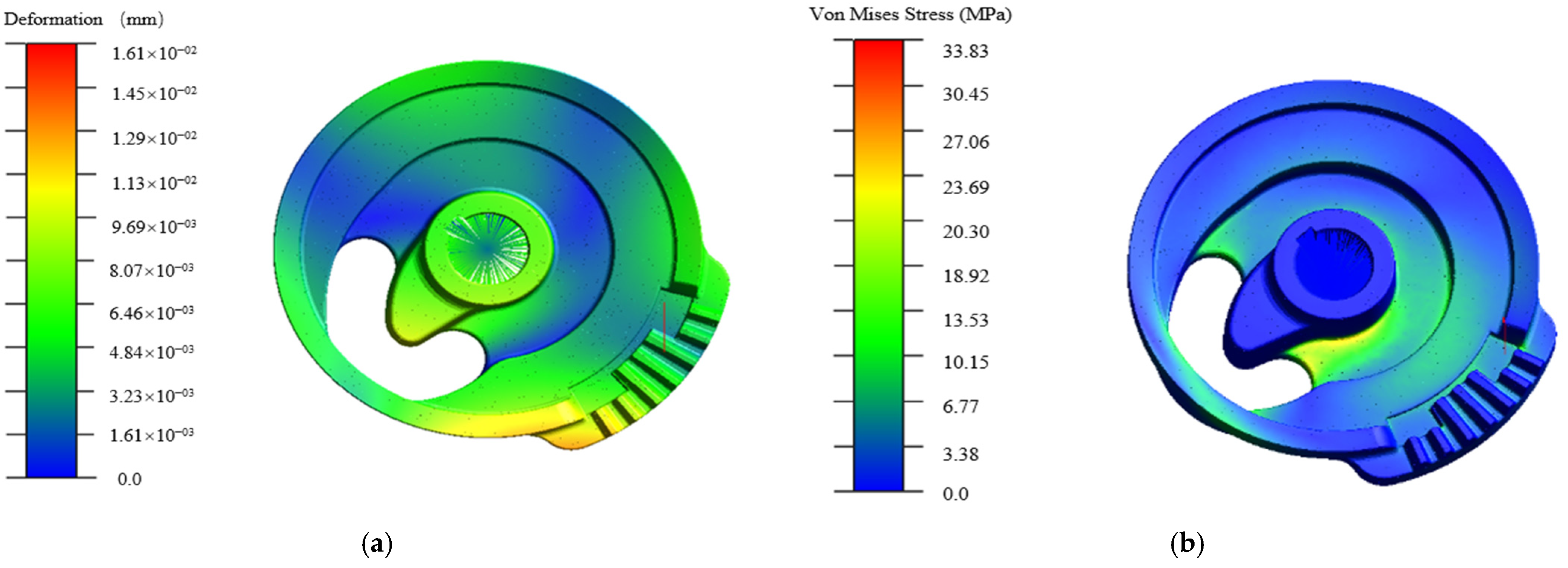
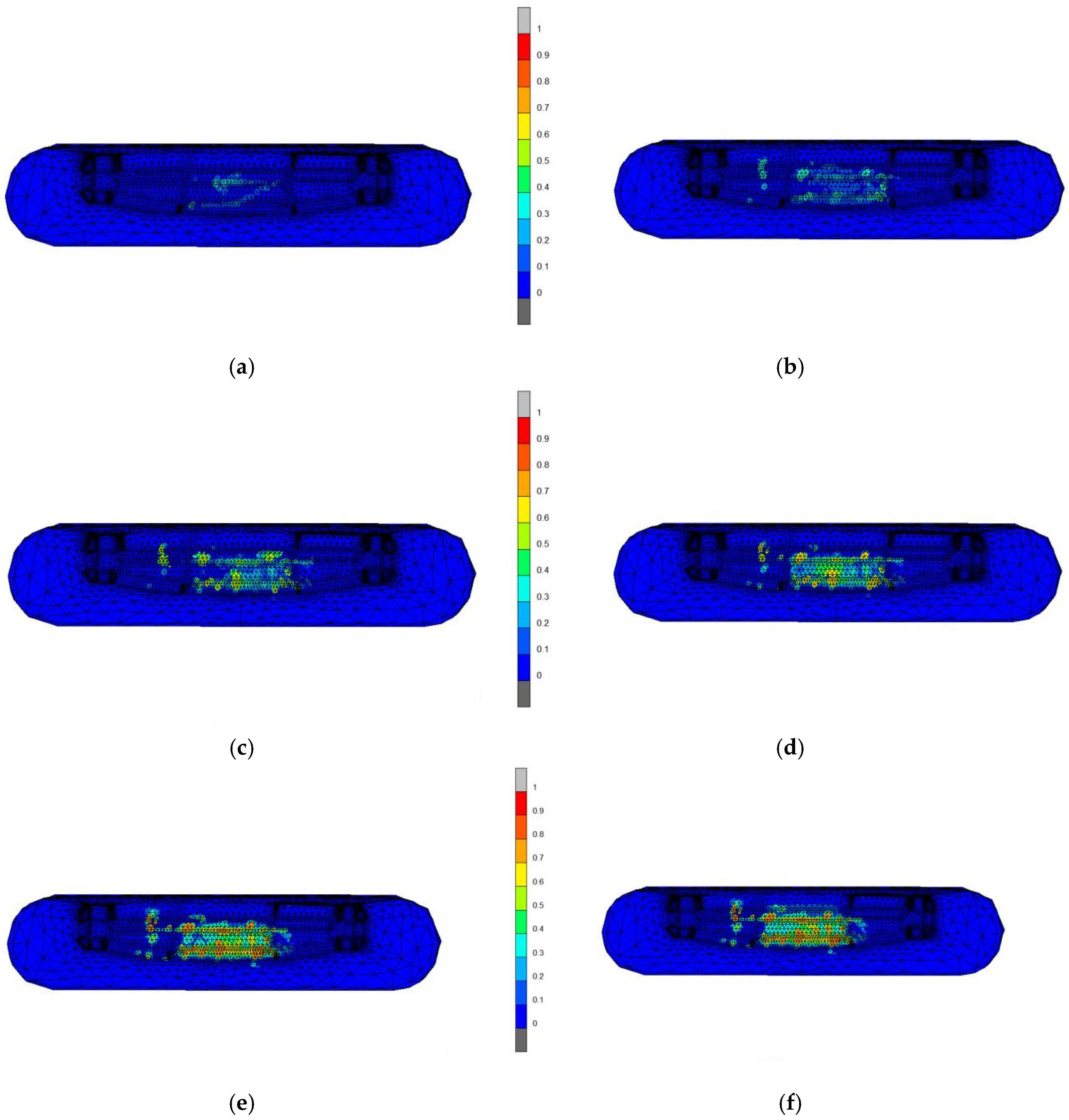
4.3. Simulation Results and Analysis
5. Wear Model Verification of Tripping Mechanism
5.1. Test Materials and Test Equipment
5.2. Wear Measurement and Result Analysis of the Tripping Mechanism
5.3. Suggestions on Heat Treatment Process for Wear Resistance of Parts
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, D.; Li, M.; Li, Y.; Qi, J.; Liu, K.; Cong, X.; Tian, X. Detection of ground straw coverage under conservation tillage based on deep learning. Comput. Electron. Agric. 2020, 172, 105369. [Google Scholar] [CrossRef]
- Yin, J.; Chen, Z.; Lv, S.; Wu, H.; Gao, Y.; Wu, L. Design and fatigue life analysis of the rope-clamping drive mechanism in a knotter. Agriculture 2024, 14, 1254. [Google Scholar] [CrossRef]
- Zhao, Z.; Huang, H.; Yin, J.; Yang, S.X. Dynamic analysis and reliability design of round baler feeding device for rice straw harvest. Biosyst. Eng. 2018, 174, 10–19. [Google Scholar] [CrossRef]
- Tang, Z.; Li, Y.; Cheng, C. Development of multi-functional combine harvester with grain harvesting and straw baling. Span. J. Agric. Res. 2017, 15, e0202. [Google Scholar] [CrossRef]
- Li, H.; He, J.; Li, H.; Wang, Q.; Cao, Q.; Lu, W. Spatial parameters of knotters of square balers. Trans. Chin. Soc. Agric. Mach. 2013, 44, 99–105. [Google Scholar]
- Xiong, Y.; Li, H.; Chen, L.; Zhan, S.; Wei, W.; Han, L. Analysis and modification of interaction between wiper mechanism and billhook mechanism for knotter. Transactions of the Chinese Society for Agricultural Machinery. Trans. Chin. Soc. Agric. Mach. 2016, 47, 44–50. [Google Scholar]
- Li, H.; Xiong, Y.; Chen, J.; Zhang, S.; Li, X.; Han, L. Wear research and improved design of D-knotter wiper mechanism. Trans. Chin. Soc. Agric. Mach. 2015, 46, 118–124. [Google Scholar]
- Lv, S.; Chen, Y.; Yin, J.; Zhou, M.; Chen, Z. Anti-wear design of the knot-tripping mechanism and knot-tying test for the knotter. Lubricants 2023, 11, 475. [Google Scholar] [CrossRef]
- Chen, S.; Ding, H.; Tang, Z.; Hao, S.; Zhao, Y. Influence of rice straw forming factors on ring die wear and improved wear prediction model during briquetting. Biosyst. Eng. 2022, 214, 122–137. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, Y.; Tang, Z.; Ding, H.; Su, Z.; Ding, Z. Structural model of straw briquetting machine with vertical ring die and optimization of briquetting performance. Agriculture 2022, 12, 736. [Google Scholar] [CrossRef]
- Bose, K.K.; Ramkumar, P. Finite element method based sliding wear prediction of steel-on-steel contacts using extrapolation techniques. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 1446–1463. [Google Scholar] [CrossRef]
- Wang, S.; Yang, X.; Li, X.; Chai, C.; Wang, G.; Wang, X. Simulation and experimental study on wear of u-shaped rings of power connection fittings under strong wind environment. Materials 2021, 14, 735. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, T.; Utsunomiya, T.; Gotoh, K.; Sato, I. Quantitative wear estimation for mooring chain of floating structures and its validation. J. Jpn. Soc. Nav. Arch. Ocean Eng. 2019, 30, 131–141. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, M.; Yuan, Q.; Li, Z.; Xu, R.; Kang, C.; Xiao, J. Research on the parameters design of inner lock for the aircraft landing gear retract actuator. Mach. Des. Manuf. Eng. 2016, 45, 74–79. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, R.; Nie, H. A numerical study on the friction and wear predictions of finger lock chuck in landing gear. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 231, 109–123. [Google Scholar] [CrossRef]
- Li, D.; Wang, Z.; Liang, Z.; Zhu, F.; Xu, T.; Cui, X.; Zhao, P. Analyzing rice grain collision behavior and monitoring mathematical model development for grain loss sensors. Agriculture 2022, 12, 839. [Google Scholar] [CrossRef]
- Wang, W.; Lv, X.; Yi, Z. Parameter optimization of reciprocating cutter for chinese little greens based on finite element simulation and experiment. Agriculture 2022, 12, 2131. [Google Scholar] [CrossRef]
- Huang, J.; Tan, L.; Tian, K.; Zhang, B.; Ji, A.; Liu, H.; Shen, C. Formation mechanism for the laying angle of hemp harvester based on ANSYS-ADAMS. Int. J. Agric. Biol. Eng. 2023, 16, 109–115. [Google Scholar] [CrossRef]
- Yin, J.; Gao, Q.; Chen, Y. Virtual knotting method of knotter based on rigid-flexible contact dynamics. Trans. Chin. Soc. Agric. Mach. 2016, 47, 85–92. [Google Scholar]
- Gao, Q. Research on Design Method of Knotter Based on Rigid-Flexible Contact Dynamics and Knotting Test. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2016. [Google Scholar]
- Jiang, R.; Zhang, M.; Cai, J. Analysis on axial stiffness characteristics of a laminated rubber-metal spring. Mach. Des. Manuf. Eng. 2016, 45, 87–90. [Google Scholar] [CrossRef]
- Hu, Z.; Liang, K.; Wang, E.; Liu, X.; Jia, F. Numerical investigation on fretting wear in steel wires by introducing system stiffness and dissipated friction energy. Adv. Eng. Softw. 2025, 209, 103999. [Google Scholar] [CrossRef]
- Hutchings, I.; Shipway, P. Tribology: Friction and Wear of Engineering Materials, 2nd ed.; Elsevier Ltd.: Oxford, UK, 2017. [Google Scholar]
- Chintha, A.R. Metallurgical aspects of steels designed to resist abrasion, and impact-abrasion wear. Mater. Sci. Technol. 2019, 35, 1133–1148. [Google Scholar] [CrossRef]








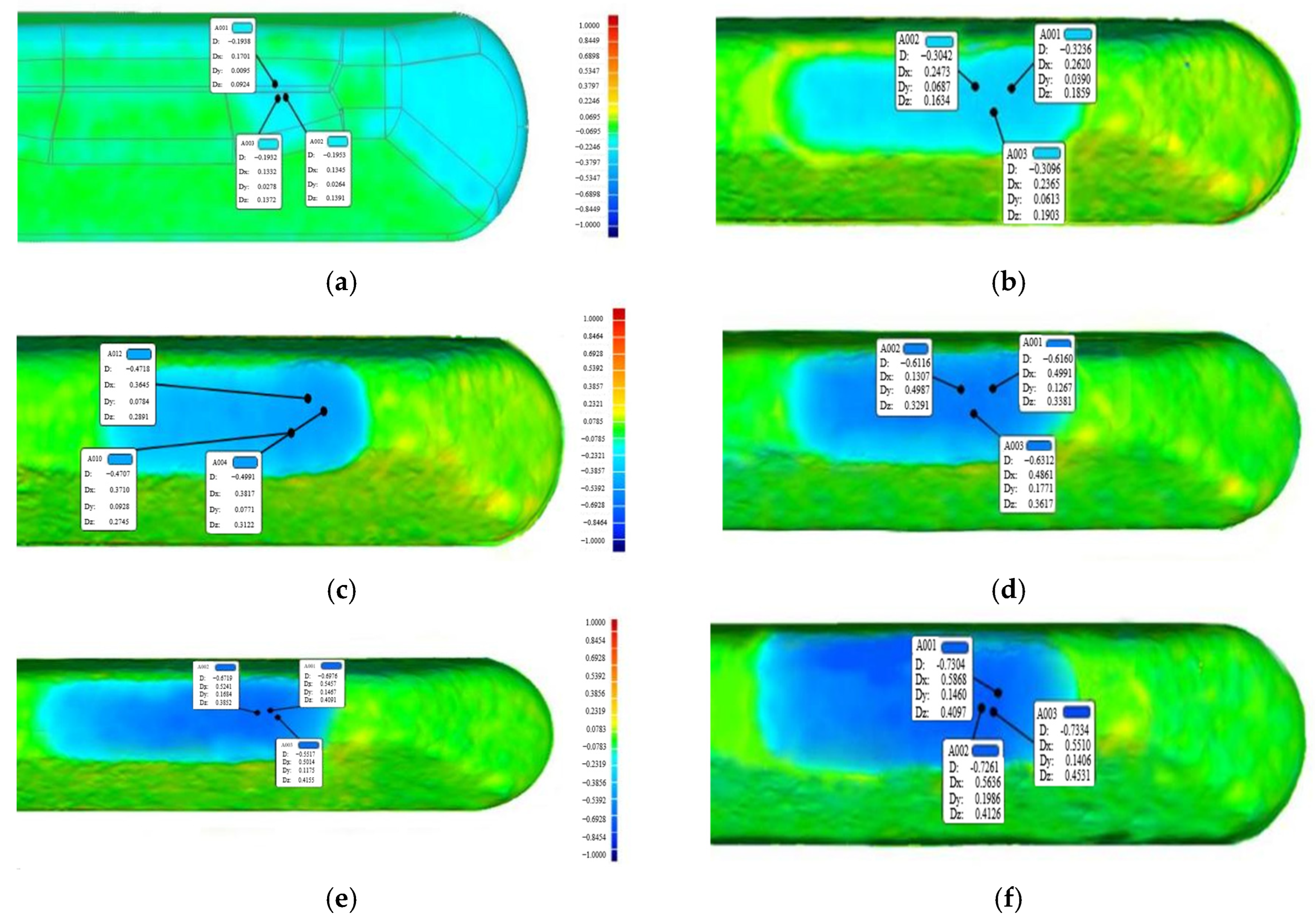
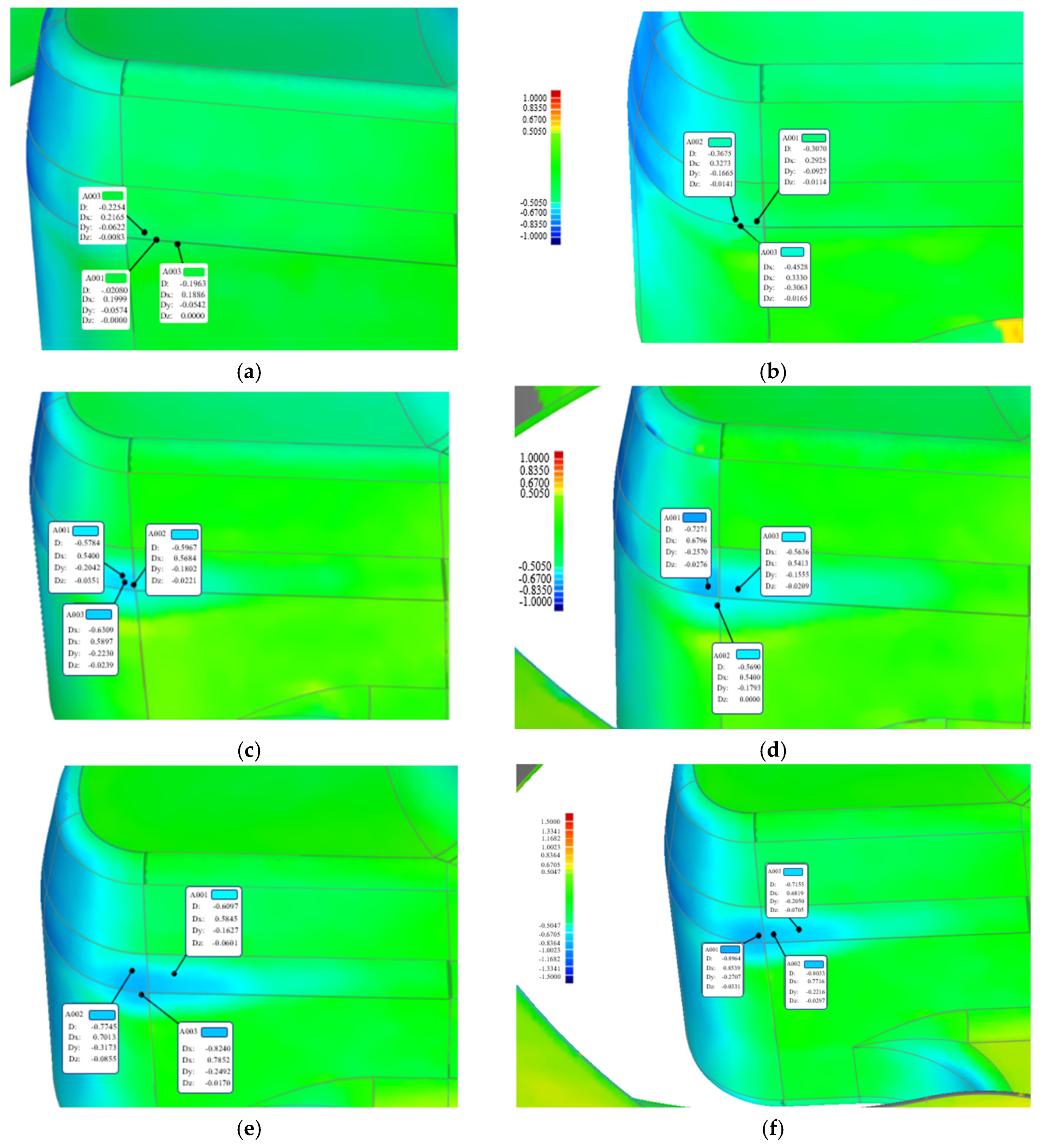

| Component | Material | Elastic Modulus (Mpa) | Poisson’s Ratio | Density (kg/m3) |
|---|---|---|---|---|
| Knife arm, large fluted disc, knotter jaw | ZG40CrMo | 210,000 | 0.3 | 7850 |
| Tripping block | 40Cr | 210,000 | 0.3 | 7850 |
| Ball roller | 304 | 193,000 | 0.29 | 7930 |
| Trips | Tripping Block (mm) | Grooved Cam (mm) |
|---|---|---|
| 1000 | 0.2123 | 0.2496 |
| 2000 | 0.3594 | 0.5039 |
| 3000 | 0.5321 | 0.6802 |
| 4000 | 0.6534 | 0.7945 |
| 5000 | 0.7323 | 0.8650 |
| 6000 | 0.7471 | 0.9123 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, J.; Gao, Y.; Guo, R.; Lv, S.; Zhou, M.; Yu, D. Wear Calculation Method of Tripping Mechanism of Knotter Based on Rigid–Flexible Coupling Dynamic Model. Agriculture 2025, 15, 2229. https://doi.org/10.3390/agriculture15212229
Yin J, Gao Y, Guo R, Lv S, Zhou M, Yu D. Wear Calculation Method of Tripping Mechanism of Knotter Based on Rigid–Flexible Coupling Dynamic Model. Agriculture. 2025; 15(21):2229. https://doi.org/10.3390/agriculture15212229
Chicago/Turabian StyleYin, Jianjun, Yansu Gao, Ruipeng Guo, Shiyu Lv, Maile Zhou, and Deng Yu. 2025. "Wear Calculation Method of Tripping Mechanism of Knotter Based on Rigid–Flexible Coupling Dynamic Model" Agriculture 15, no. 21: 2229. https://doi.org/10.3390/agriculture15212229
APA StyleYin, J., Gao, Y., Guo, R., Lv, S., Zhou, M., & Yu, D. (2025). Wear Calculation Method of Tripping Mechanism of Knotter Based on Rigid–Flexible Coupling Dynamic Model. Agriculture, 15(21), 2229. https://doi.org/10.3390/agriculture15212229






