Fusion of LSTM-Based Vertical-Gradient Prediction and 3D Kriging for Greenhouse Temperature Field Reconstruction
Abstract
1. Introduction
2. Data Acquisition and Feature Engineering
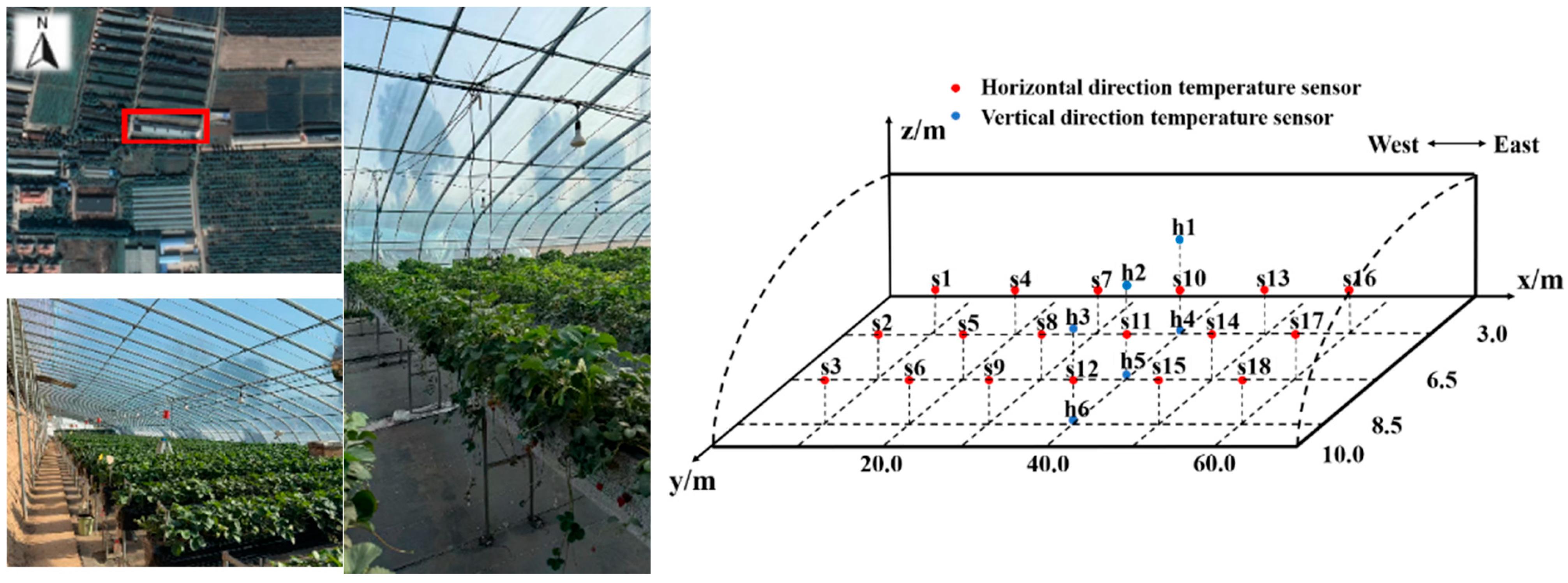
2.1. Overview of the Experimental Greenhouse
2.2. Data Preprocessing and Feature Variable Construction
2.2.1. Missing Value Handling and Outlier Correction
2.2.2. Feature Selection and Lagged Variable Design
2.2.3. Data Normalization
3. Model Construction and Forecasting Methods
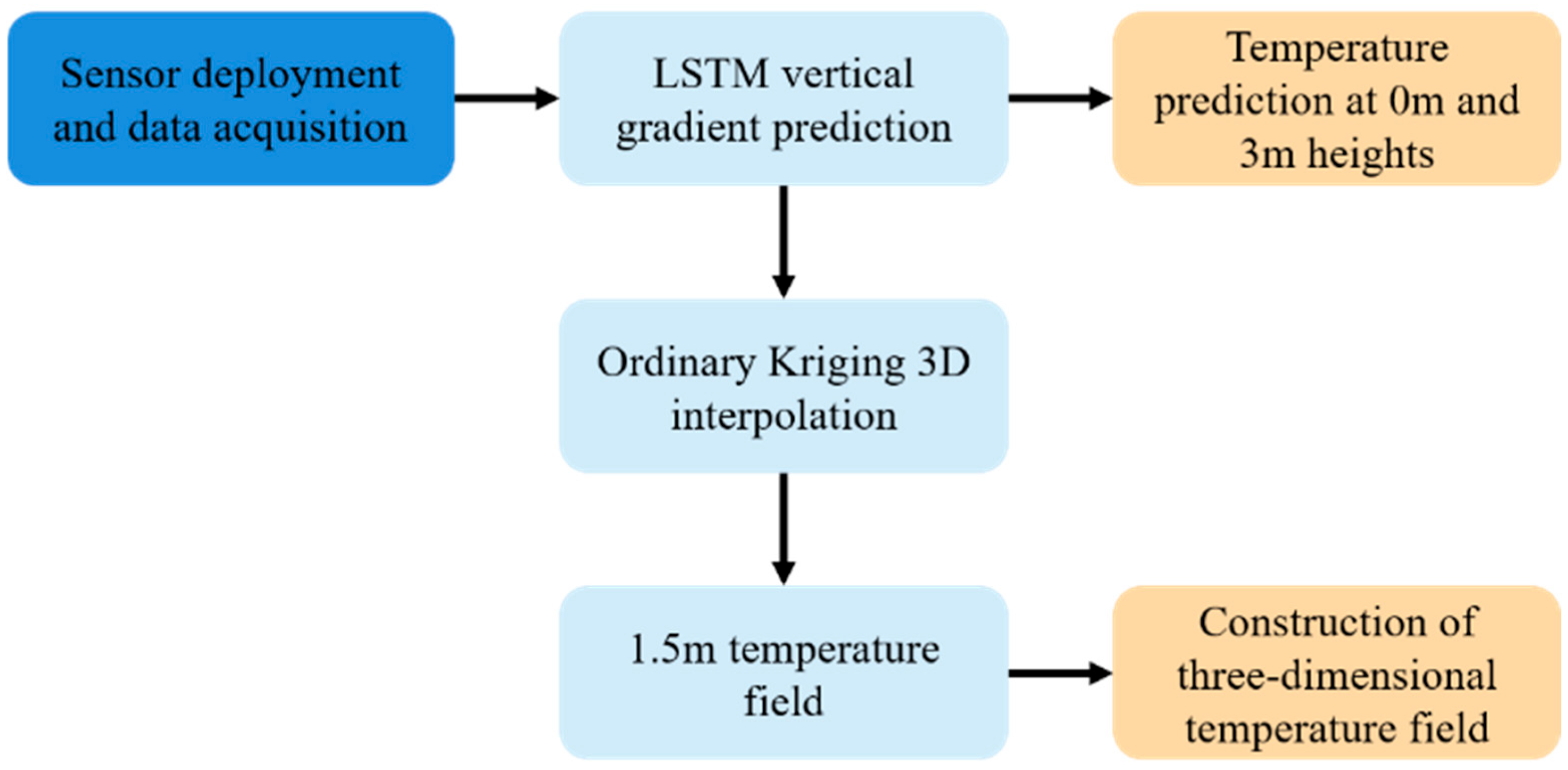
3.1. Construction of a Vertical-Gradient Model Based on Deep Learning
3.2. Implementation Details and Model Evaluation
3.3. Three-Dimensional Temperature Modeling in Greenhouse Spaces
3.3.1. Three-Dimensional Ordinary Kriging Spatial Interpolation Method
3.3.2. Construction of a Three-Dimensional Temperature Field Model
4. Experimental Results and Analysis
4.1. Deep Learning Algorithm Model Selection
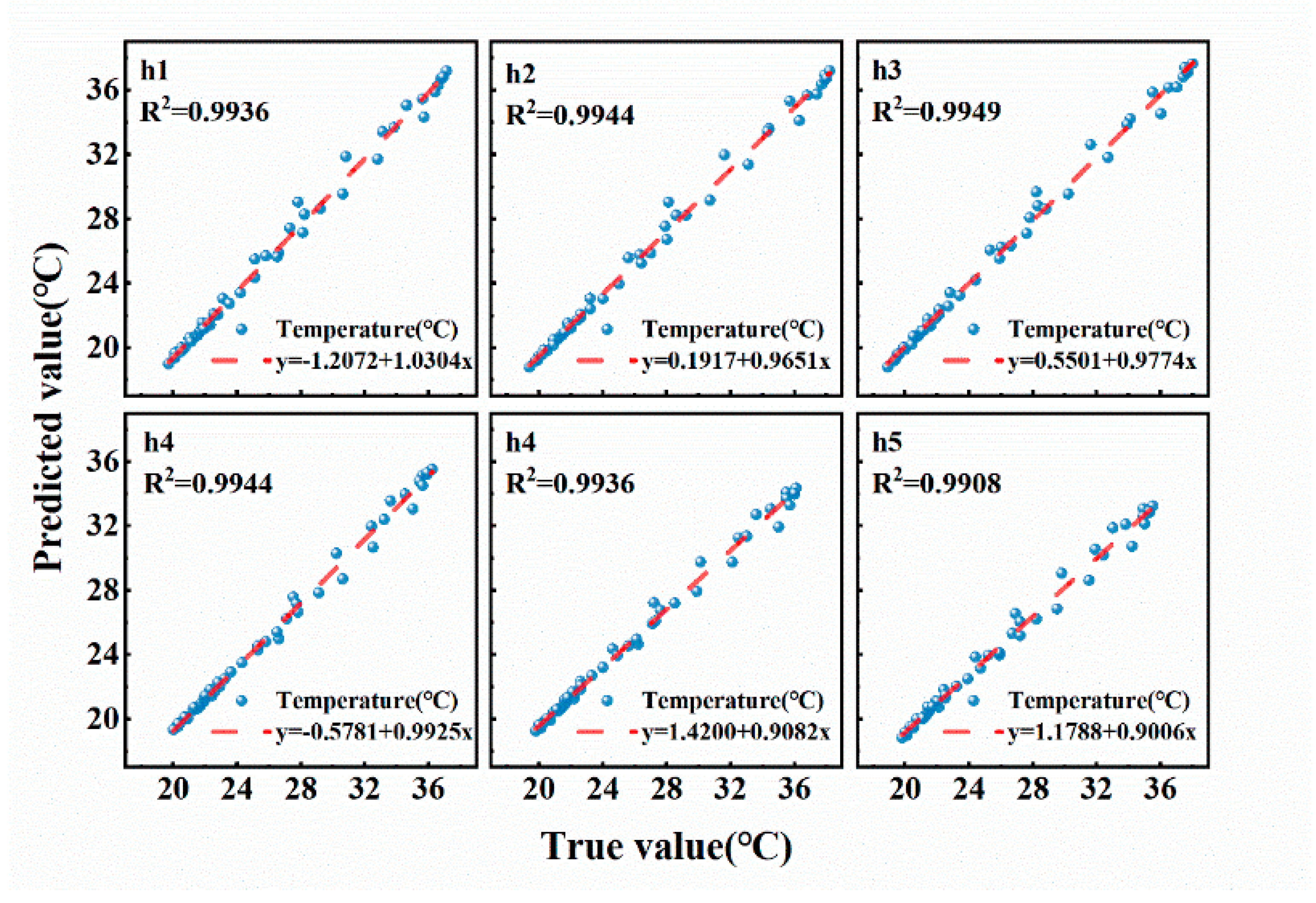
4.2. Evaluation Based on the LSTM Vertical-Gradient Model
4.3. Validation of Vertical Extrapolation and LSTM–Kriging Integration
- (1)
- Trend-only (LSTM)—direct extrapolation using the LSTM-predicted vertical gradient;
- (2)
- Kriging-only (3D OK)—purely spatial interpolation based on the remaining observed heights; and
- (3)
- Trend + Residual Kriging—a combination of LSTM trend and kriged residuals.
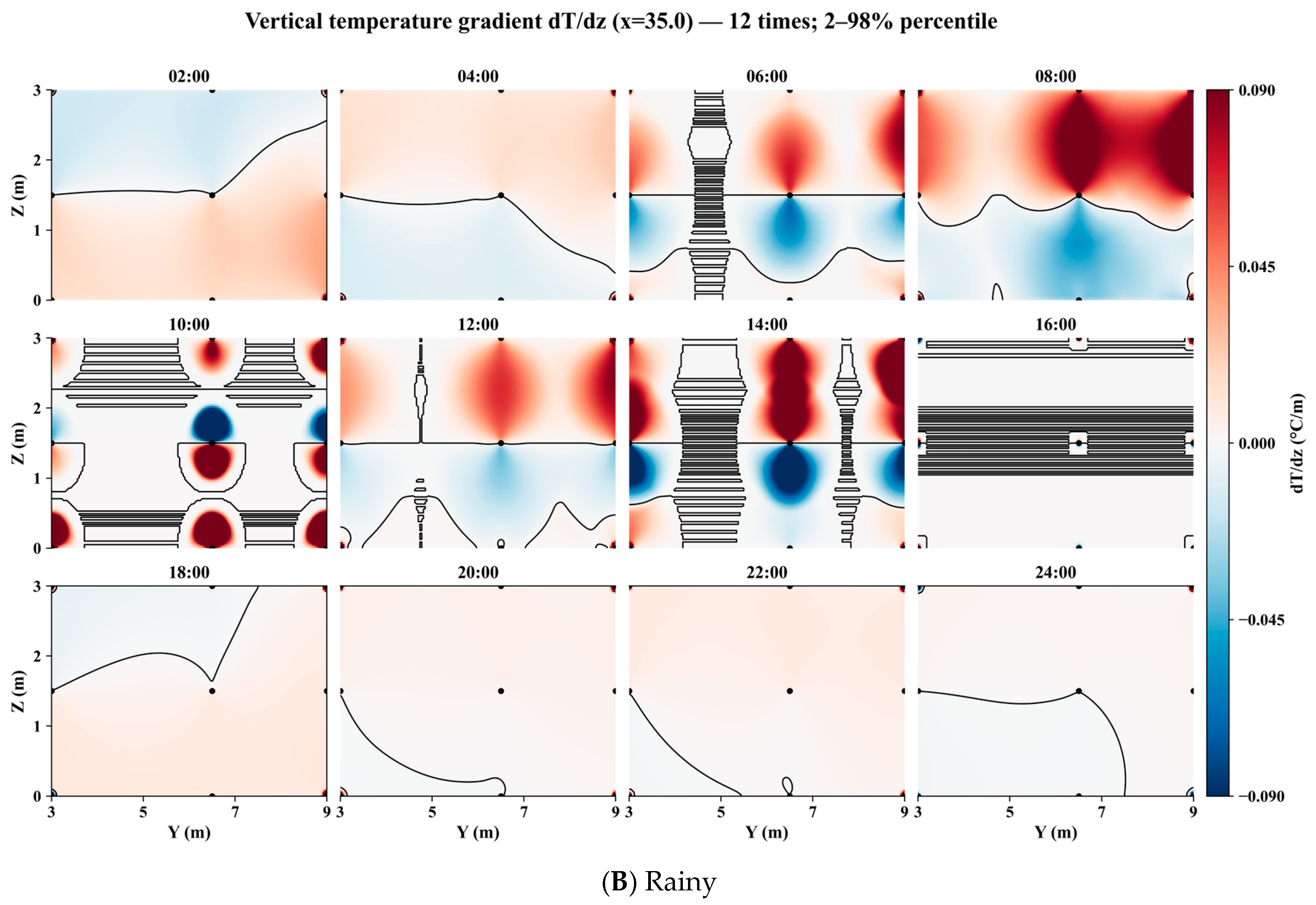
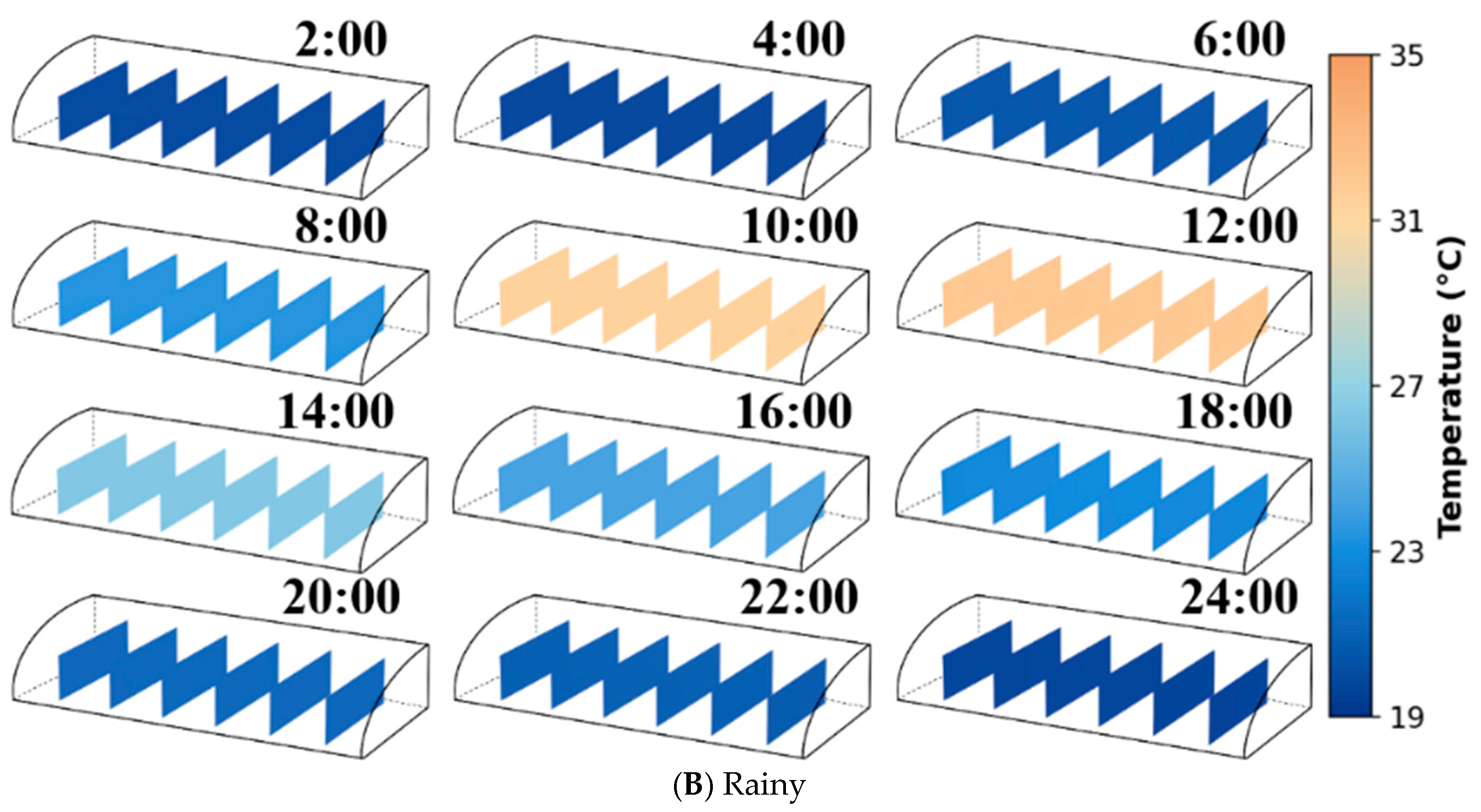
4.4. Analysis of Model Applicability Under Different Weather Conditions
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Singh, K.A.P.; Goutam, P.K.; Xaxa, S.; Nasima, S.P.; Panotra, N.; Rajesh, G. The role of greenhouse technology in streamlining crop production. J. Exp. Agric. Int. 2024, 46, 776–798. [Google Scholar] [CrossRef]
- Xiao, Y.; Gong, J.; Wang, Y.; Wang, C. Intelligent agricultural greenhouse control system based on internet of things and machine learning. In Proceedings of the 2025 International Conference on Machine Learning and Neural Networks, Suzhou, China, 18–20 April 2025; pp. 292–300. [Google Scholar]
- Boersma, S.; Cheng, X. A Bayesian Neural ODE for a Lettuce Greenhouse. In Proceedings of the 2024 IEEE Conference on Control Technology and Applications (CCTA), Newcastle upon Tyne, UK, 21–23 August 2024; pp. 782–786. [Google Scholar]
- Boulard, T.; Wang, S. Greenhouse crop transpiration simulation from external climate conditions. Agric. For. Meteorol. 2000, 100, 25–34. [Google Scholar] [CrossRef]
- Körner, O.S.G.V.; Van Straten, G. Decision support for dynamic greenhouse climate control strategies. Comput. Electron. Agric. 2008, 60, 18–30. [Google Scholar] [CrossRef]
- Tong, G.; Christopher, D.M.; Li, B. Numerical modelling of temperature variations in a Chinese solar greenhouse. Comput. Electron. Agric. 2009, 68, 129–139. [Google Scholar] [CrossRef]
- Abou-Mehdi-Hassani, F.; Zaguia, A.; Ait Bouh, H.; Mkhida, A. Systematic literature review of smart greenhouse monitoring. SN Comput. Sci. 2025, 6, 95. [Google Scholar] [CrossRef]
- Săcăleanu, D.-I.; Matache, M.-G.; Roșu, Ș.-G.; Florea, B.-C.; Manciu, I.-P.; Perișoară, L.-A. IoT-enhanced decision support system for real-time greenhouse microclimate monitoring and control. Technologies 2024, 12, 230. [Google Scholar] [CrossRef]
- Bhujel, A.; Basak, J.K.; Khan, F.; Arulmozhi, E.; Jaihuni, M.; Sihalath, T.; Lee, D.; Park, J. Sensor systems for greenhouse microclimate monitoring and control: A review. J. Biosyst. Eng. 2020, 45, 341–361. [Google Scholar] [CrossRef]
- Cheng, X.; Li, D.; Shao, L.; Ren, Z. A virtual sensor simulation system of a flower greenhouse coupled with a new temperature microclimate model using three-dimensional CFD. Comput. Electron. Agric. 2021, 181, 105934. [Google Scholar] [CrossRef]
- Cai, H.; Liang, Z.; Lyu, Y.; Qin, Y. Numerical Simulation Analysis of Large-Scale Three-Dimensional Planting Greenhouse Based on Orthogonal Test Method. J. Appl. Math. Phys. 2025, 13, 914–932. [Google Scholar] [CrossRef]
- Fatnassi, H.; Bournet, P.E.; Boulard, T.; Roy, J.C.; Molina-Aiz, F.D.; Zaaboul, R. Use of computational fluid dynamic tools to model the coupling of plant canopy activity and climate in greenhouses and closed plant growth systems: A review. Biosyst. Eng. 2023, 230, 388–408. [Google Scholar] [CrossRef]
- Rezvani, S.M.E.D.; Shamshiri, R.R.; Hameed, I.A.; Abyane, H.Z.; Godarzi, M.; Momeni, D.; Balasundram, S.K. Greenhouse crop simulation models and microclimate control systems, a review. In Next-Generation Greenhouses for Food Security; IntechOpen: London, UK, 2021. [Google Scholar]
- Li, X.; Zhang, L.; Wang, X.; Liang, B. Forecasting greenhouse air and soil temperatures: A multi-step time series approach employing attention-based LSTM network. Comput. Electron. Agric. 2024, 217, 108602. [Google Scholar] [CrossRef]
- Liu, Y.; Li, D.; Wan, S.; Wang, F.; Dou, W.; Xu, X.; Qi, L. A long short-term memory-based model for greenhouse climate prediction. Int. J. Intell. Syst. 2022, 37, 135–151. [Google Scholar] [CrossRef]
- Arnaud, S.E.; Calisti, M.; Polydoros, A. Data-Driven Greenhouse Climate Regulation in Lettuce Cultivation Using BiLSTM and GRU Predictive Control. arXiv 2025, arXiv:2507.21669. [Google Scholar]
- Jung, D.H.; Kim, H.S.; Jhin, C.; Kim, H.J.; Park, S.H. Time-serial analysis of deep neural network models for prediction of climatic conditions inside a greenhouse. Comput. Electron. Agric. 2020, 173, 105402. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Feng, G.; Zhang, L.; Ai, F.; Zhang, Y.; Hou, Y. An improved temporal fusion transformers model for predicting supply air temperature in high-speed railway carriages. Entropy 2022, 24, 1111. [Google Scholar] [CrossRef]
- Seri, E.; Petitta, M.; Cornaro, C. Sustainable Greenhouse Management: A Comparative Analysis of Recurrent and Graph Neural Networks. arXiv 2025, arXiv:2502.17371. [Google Scholar] [CrossRef]
- Yin, H.; Wang, K.; Zeng, J.; Pang, Z. CFD Analysis and Optimization of a Plastic Greenhouse with a Semi-Open Roof in a Tropical Area. Agronomy 2024, 14, 876. [Google Scholar] [CrossRef]
- Guo, Z.; Feng, L. Multi-step prediction of greenhouse temperature and humidity based on temporal position attention LSTM. Stoch. Environ. Res. Risk Assess. 2024, 38, 4907–4934. [Google Scholar] [CrossRef]
- Shasteen, K.C.; Kacira, M. Predictive modeling and computer vision-based decision support to optimize resource use in vertical farms. Sustainability 2023, 15, 7812. [Google Scholar] [CrossRef]
- Panda, M.; Khilar, P.M. Distributed self fault diagnosis algorithm for large scale wireless sensor networks using modified three sigma edit test. Ad Hoc Netw. 2015, 25, 170–184. [Google Scholar] [CrossRef]
- Blu, T.; Thévenaz, P.; Unser, M. Linear interpolation revitalized. IEEE Trans. Image Process. 2004, 13, 710–719. [Google Scholar] [CrossRef] [PubMed]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Bhanja, S.; Das, A. Impact of data normalization on deep neural network for time series forecasting. arXiv 2018, arXiv:1812.05519. [Google Scholar]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Xia, H.; Liu, Y.; Gong, Y.; Ren, N.; Jin, J. Comparative study on greenhouse three-dimensional temperature field construction methods based on spatial interpolation. J. Chin. Agric. Mech. 2025, 46, 176–182. [Google Scholar] [CrossRef]
- Gharghory, S.M. Deep network based on long short-term memory for time series prediction of microclimate data inside the greenhouse. Int. J. Comput. Intell. Appl. 2020, 19, 2050013. [Google Scholar] [CrossRef]
- Esparza-Gómez, J.M.; Guerrero-Osuna, H.A.; Ornelas-Vargas, G.; Luque-Vega, L.F. RNN-LSTM Applied in a Temperature Prediction Model for Greenhouses. Res. Comput. Sci. 2021, 150, 31–41. [Google Scholar]
- Guillén, M.A.; Llanes, A.; Imbernón, B.; Martínez-España, R.; Bueno-Crespo, A.; Cano, J.C.; Cecilia, J.M. Performance evaluation of edge-computing platforms for the prediction of low temperatures in agriculture using deep learning. J. Supercomput. 2021, 77, 818–840. [Google Scholar] [CrossRef]
- Balendonck, J.; Os, E.V.; Schoor, R.V.D.; Tuijl, B.V.; Keizer, L.C.P. Monitoring spatial and temporal distribution of temperature and relative humidity in greenhouses based on wireless sensor technology. In Proceedings of the International Conference on Agricultural Engineering, Clermont-Ferrand, France, 6–8 September 2010. [Google Scholar]
- Wang, Y.; Yuan, F.; Cammarano, D.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Integrating machine learning with spatial analysis for enhanced soil interpolation: Balancing accuracy and visualization. Smart Agric. Technol. 2025, 11, 101032. [Google Scholar] [CrossRef]
- Shi, J.; Wang, H.; Wang, J. Cfd simulation study on the cooling characteristics of shading and natural ventilation in greenhouse of a botanical garden in shanghai. Sustainability 2023, 15, 3056. [Google Scholar] [CrossRef]
- Hua, Y.; Zhao, X.; Sun, W.; Sun, Q. Satellite-Based Reconstruction of Atmospheric CO2 Concentration over China Using a Hybrid CNN and Spatiotemporal Kriging Model. Remote Sens. 2024, 16, 2433. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.; Gräler, B. Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef] [PubMed]



| Category | Representative Studies | Advantages | Limitations |
|---|---|---|---|
| Sensor-based monitoring | IoT deployments and WSN reviews [7,8]; sensor-system review [9] | Provide real-time, in situ high-fidelity measurements; capture local microclimate and transient events; enable closed-loop control | High installation and maintenance costs for dense coverage; sparse networks miss 3D continuity of temperature field; sensors require calibration and can drift |
| Numerical simulation (CFD) | CFD ventilation/microclimate studies and method reviews [12,21] | Resolve three-dimensional airflow and heat-transfer processes; test ventilation/roof/vent configurations and canopy effects; useful for design and what-if analyses | High computational cost; results sensitive to mesh, turbulence model and boundary conditions; requires experimental data for calibration/validation |
| Statistical/data-driven modeling | Multi-step and attention/LSTM forecasting, hybrid ML studies [12,22] | Efficient for short-term forecasting and real-time applications; can learn complex nonlinear relations and act as surrogates for control; lower computational cost than full CFD | Often trained on limited sensor locations (spatial extrapolation challenges); may not explicitly represent physical processes or 3D spatial structure; generalization depends on training-data representativeness |
| Temperature Sensor | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coordinates | s1 | s2 | s3 | s4 | s5 | s6 | s7 | s8 | s9 | s10 | s11 | s12 | s13 | s14 | s15 | s16 | s17 | s18 |
| x | 5 | 5 | 5 | 15 | 15 | 15 | 25 | 25 | 25 | 35 | 35 | 35 | 45 | 45 | 45 | 55 | 55 | 55 |
| y | 3 | 6.5 | 9 | 3 | 6.5 | 9 | 3 | 6.5 | 9 | 3 | 6.5 | 9 | 3 | 6.5 | 9 | 3 | 6.5 | 9 |
| z | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| Temperature Sensor | ||||||
|---|---|---|---|---|---|---|
| Coordinates | h1 | h2 | h3 | h4 | h5 | h6 |
| x | 35 | 35 | 35 | 35 | 35 | 35 |
| y | 3 | 6.5 | 9 | 3 | 6.5 | 9 |
| z | 3 | 3 | 3 | 0 | 0 | 0 |
| Temperature Point | h1 | h2 | h3 | h4 | h5 | h6 |
|---|---|---|---|---|---|---|
| s10 | 0.9973 *** | 0.9941 *** | 0.9937 *** | 0.9867 *** | 0.9817 *** | 0.9758 *** |
| s11 | 0.9977 *** | 0.9973 *** | 0.9981 *** | 0.9846 *** | 0.9829 *** | 0.9788 *** |
| s12 | 09960 *** | 0.9965 *** | 0.9977 *** | 0.9828 *** | 0.9820 *** | 0.9772 *** |
| Variogram Model | RMSE (°C) | MAE (°C) | R2 | n_Valid |
|---|---|---|---|---|
| Spherical | 0.76353 | 0.50312 | 0.96655 | 648 |
| Exponential | 0.76135 | 0.50153 | 0.96674 | 648 |
| Gaussian | 0.76658 | 0.50317 | 0.96628 | 648 |
| Model | R2 | RMSE (°C) | MAE (°C) | Training Time (Min) | Stability (σRMSE) |
|---|---|---|---|---|---|
| LSTM | (0.9796, 0.9852) | (0.5827, 0.6761) | (0.4230, 0.4657) | 0.54 | 0.2929 |
| GRU | (0.9771, 0.9844) | (0.5962, 0.7140) | (0.4018, 0.4651) | 0.69 | 0.3599 |
| Transformer | (0.9811, 0.9849) | (0.5835, 0.7109) | (0.3826, 0.4479) | 0.64 | 0.5022 |
| TFT | (0.9813, 0.9847) | (0.5866, 0.7093) | (0.3886, 0.4570) | 0.72 | 0.3568 |
| Method | N | RMSE (°C) | MAE (°C) | Bias (°C) |
|---|---|---|---|---|
| Trend-only (LSTM) | 216 | 3.5948 | 2.9367 | −0.2939 |
| Kriging-only (3D-OK) | 216 | 0.47966 | 0.29367 | −0.1660 |
| Trend + Residual Kriging | 216 | 0.45558 | 0.33987 | −0.03148 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Liu, X.; Zhao, X.; Gao, Z.; Li, Y.; He, X.; Fan, X.; Li, L.; Zhang, W. Fusion of LSTM-Based Vertical-Gradient Prediction and 3D Kriging for Greenhouse Temperature Field Reconstruction. Agriculture 2025, 15, 2222. https://doi.org/10.3390/agriculture15212222
Zhang Z, Liu X, Zhao X, Gao Z, Li Y, He X, Fan X, Li L, Zhang W. Fusion of LSTM-Based Vertical-Gradient Prediction and 3D Kriging for Greenhouse Temperature Field Reconstruction. Agriculture. 2025; 15(21):2222. https://doi.org/10.3390/agriculture15212222
Chicago/Turabian StyleZhang, Zhimin, Xifeng Liu, Xiaona Zhao, Zihao Gao, Yaoyu Li, Xiongwei He, Xinping Fan, Lingzhi Li, and Wuping Zhang. 2025. "Fusion of LSTM-Based Vertical-Gradient Prediction and 3D Kriging for Greenhouse Temperature Field Reconstruction" Agriculture 15, no. 21: 2222. https://doi.org/10.3390/agriculture15212222
APA StyleZhang, Z., Liu, X., Zhao, X., Gao, Z., Li, Y., He, X., Fan, X., Li, L., & Zhang, W. (2025). Fusion of LSTM-Based Vertical-Gradient Prediction and 3D Kriging for Greenhouse Temperature Field Reconstruction. Agriculture, 15(21), 2222. https://doi.org/10.3390/agriculture15212222





