Canonical Analysis of the Impact of Climate Predictors on Sugarcane Yield in the Eastern Region of Pernambuco, Brazil
Abstract
1. Introduction
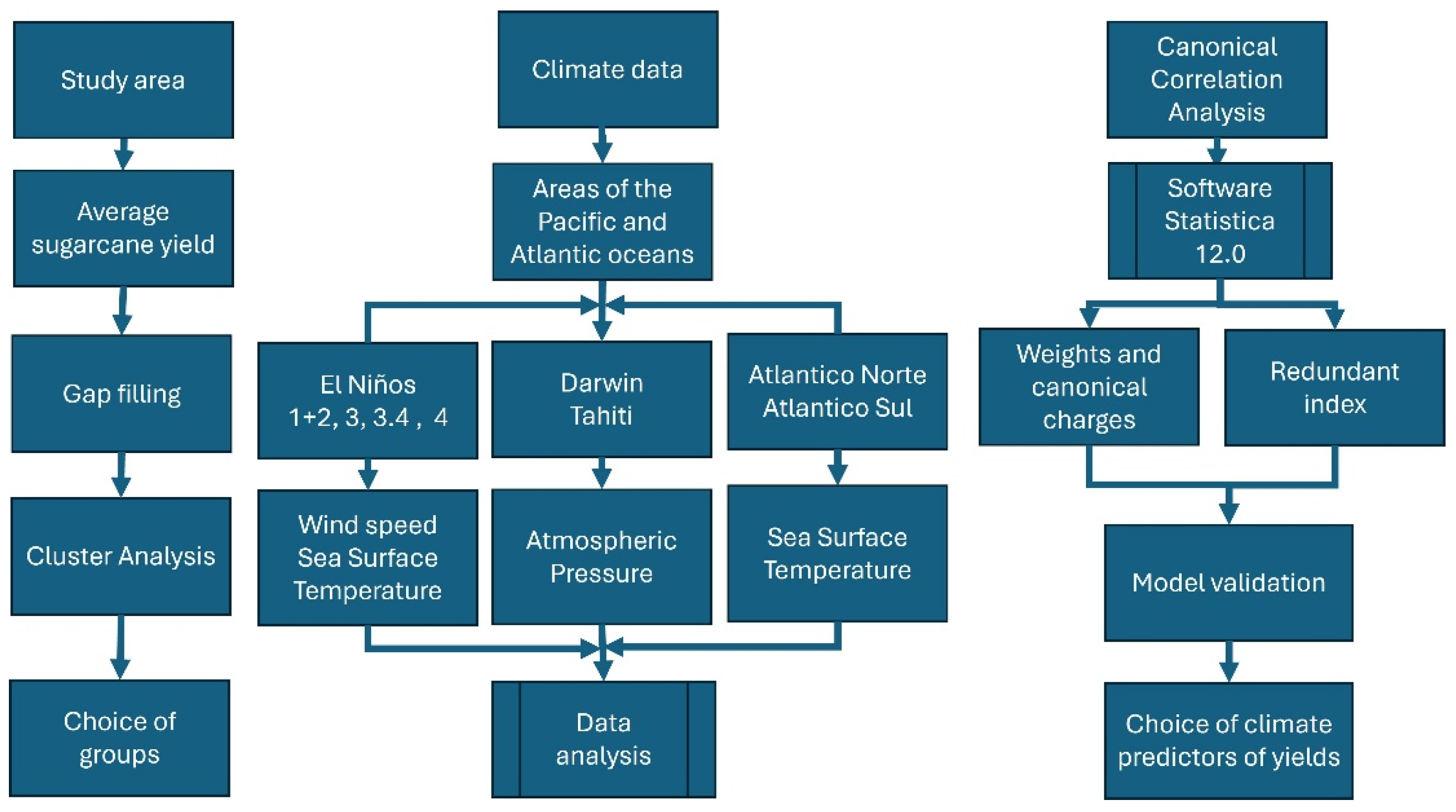
2. Material and Methods
2.1. Study Area and Data
| Slope | Floor | Floodplain | Tableland | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Manual | Mechanized | |||||||||||||||||||
| Varieties | A | B | C | D | A | B | C | D | A | B | C | D | A | B | C | D | A | B | C | D |
| RB 72-454 | X | X | X | X | X | X | X | X | X | X | ||||||||||
| RB 73-2577 | X | X | X | X | X | X | X | X | ||||||||||||
| RB 75-126 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | ||||||
| RB 76-3710 | X | X | X | X | X | X | X | X | X | X | X | X | ||||||||
| RB 81-3804 | X | X | X | X | X | X | X | |||||||||||||
| RB 83-102 | X | X | X | X | ||||||||||||||||
| SP 70-1143 | X | X | X | X | X | X | ||||||||||||||
| SP 71-6949 | X | X | X | X | X | X | X | |||||||||||||
| SP 77-5181 | X | X | ||||||||||||||||||
| SP 78-4764 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | ||||||
| SP 79-1011 | X | X | X | X | X | X | X | X | X | X | X | |||||||||
| B 8008 | X | X | X | |||||||||||||||||
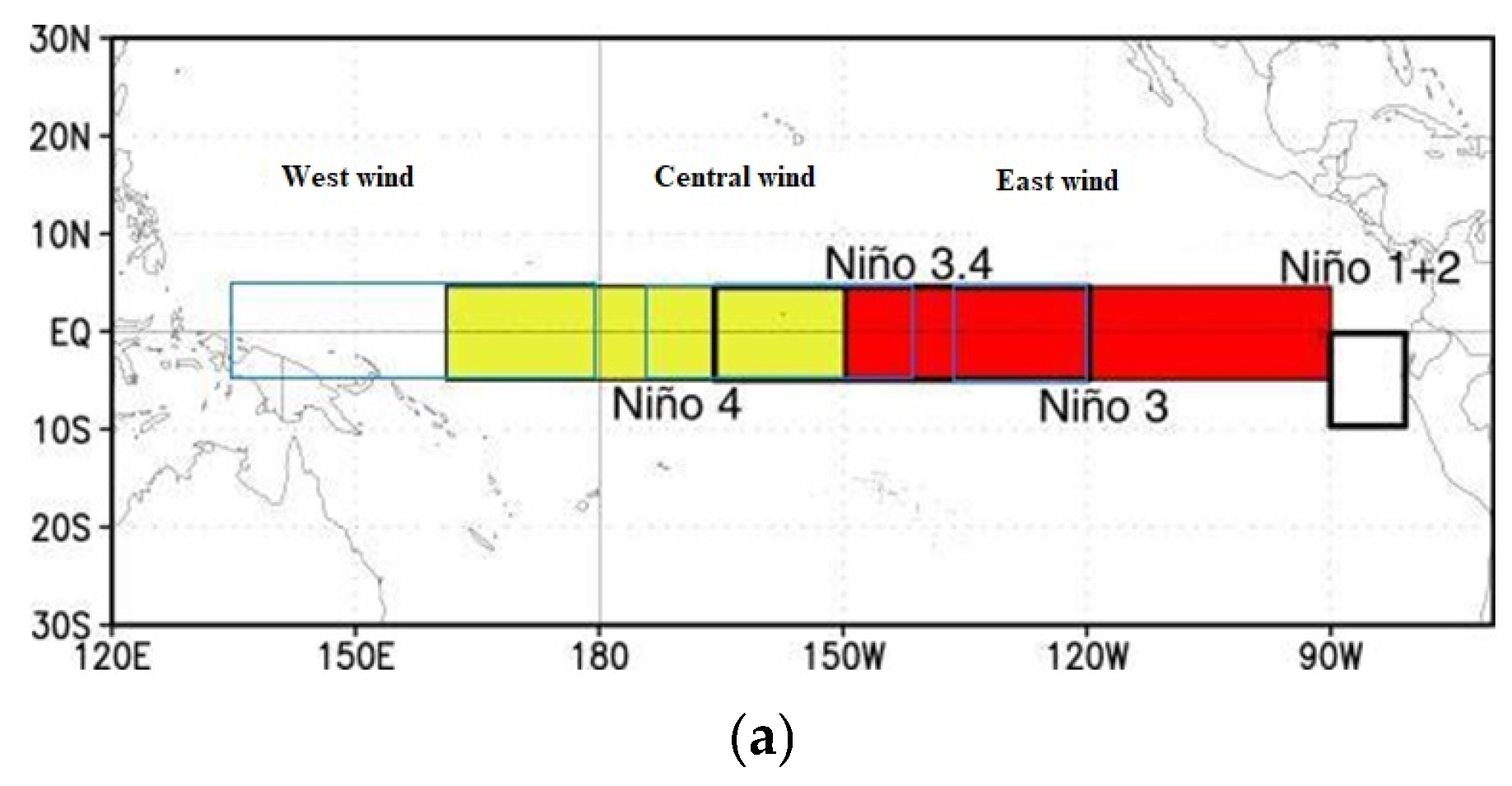
2.2. Climate Data
2.3. Ward’s Method for Hierarchical Clustering
2.4. Linear Correlations
2.5. Canonical Variable and Canonical Correlation
2.6. Interpretation of Canonical Statistical Variables
3. Results
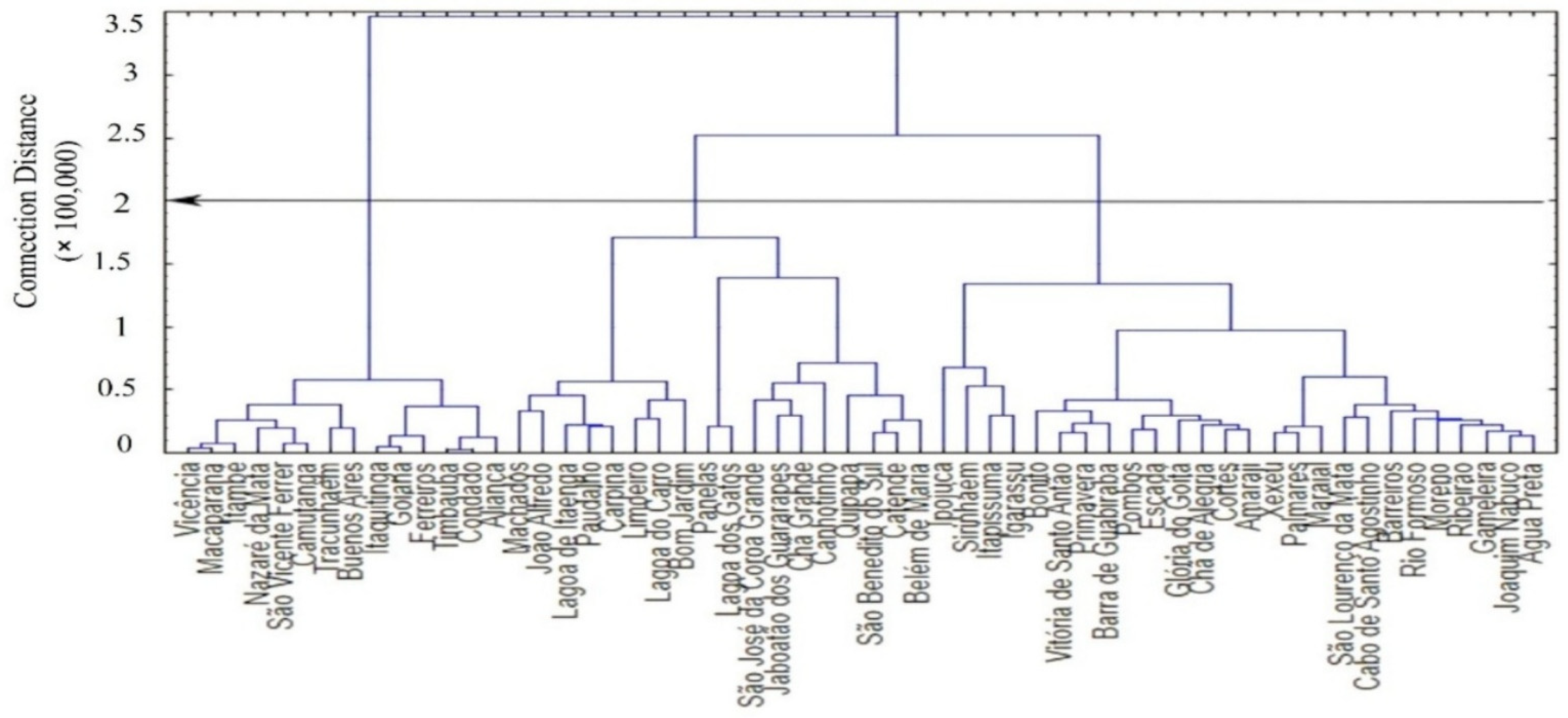
3.1. Cluster Analysis
3.2. Analysis Linear Correlations Three Months Before Sugarcane Yield
3.3. Statistical and Practical Significance Analysis of the 3-Month Delay in Sugarcane Yields
3.4. Redundancy Analysis of Independent Variables for Three Months Delay in Sugarcane Yield
3.5. Canonical Weights of the Three Canonical Functions
3.6. Structural Canonical Loadings for the Three Canonical Functions
3.7. Canonical Cross-Loadings for the Three Canonical Functions
3.8. Validation and Diagnosis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Compre Rural. Cana de Açúcar Movimenta Maismovimenta mais de R$ 100 Bi Por Ano Nobi por ano no Brasil. 2022. Available online: https://www.comprerural.com/cana-de-acucar-movimenta-mais-de-r-100-bi-por-ano-no-brasil/ (accessed on 13 May 2025).
- CONAB—Companhia Nacional de Abastecimento. CANA-DE-AÇÚCAR. Acompanhamento Da Safra Brasileira De Cana-De-Açúcar. Brasília. Safra 2019/20. Quarto Levantamento. CONAB: Brasília, Brazil, 2020; Volume 6, pp. 1–58. Available online: https://www.conab.gov.br/info-agro/safras/cana/boletim-da-safra-de-cana-de-acucar/item/download/31590_6cfbbc41aa04783c69113c50fa499cba (accessed on 24 February 2024).
- NovaBio. Atual Safra de Cana-De-Açúcar Deve Crescer 3,5% em Pernambuco. 2024. Available online: https://novabio.org/atual-safra-de-cana-de-acucar-deve-crescer-35-em-pernambuco/ (accessed on 24 February 2024).
- Melo, P.J.D.; Lúcio, A.D.C.; Torres, E.M.J.; Lopes, S.J.; Lambrecht, D.M.; Diel, M.I. Association technological and agronomic traits sugarcane for the quantitative and qualitative production of brown sugar. Rev. Bras. Ciênc. Agrár. 2023, 18, e2980. [Google Scholar] [CrossRef]
- Machado, S. Why Is Burning of Sugarcane Fields Still Allowed in the Country Despite the Fires? 2024. Available online: https://www.bbc.com/portuguese/articles/cjdk41z41zno (accessed on 13 May 2025).
- Almeida, A.C.S.; Souza, J.L.; Teodoro, I.; Barbosa, G.V.S.; Moura Filho, G.; Ferreira Júnior, R.A. Desenvolvimento vegetativo e produção de variedades de cana-de-açúcar em relação à disponibilidade hídrica e unidades térmicas. Ciência Agrotec. 2008, 32, 1441–1448. [Google Scholar] [CrossRef]
- Luchiari, A., Jr.; Ramos, N.P. Impacts. 2022. Available online: https://www.embrapa.br/agencia-de-informacao-tecnologica/cultivos/cana/pre-producao/meio-ambiente/impactos#:~:text=Os%20preju%C3%ADzos%20s%C3%A3o:%20perda%20de.consumidores%20e%20dos%20pr%C3%B3prios%20agricultores (accessed on 23 January 2025).
- Da Silva, V.D.P.; Oliveira, S.D.D.; Dos Santos, C.A.; Silva, M.T. Risco climático da cana-de-açúcar cultivada na região nordeste do Brasil. Rev. Bras. De Eng. Agrícola E Ambient 2013, 17, 180–189. [Google Scholar] [CrossRef][Green Version]
- IPCC—Intergovernmental Panel on Climate Change. Climate Change 2021: The Physical Science Basis. Summary for Policy Makers Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Available online: https://www.ipcc.ch/report/sixth-assessment-report-cycle/ (accessed on 24 September 2022).[Green Version]
- IPCC—Intergovernmental Panel on Climate Change. Climate Change 2007: The Physical Science Basis. Summary for Policy Makers Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. 2007. Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/ar4-wg1-frontmatter-1.pdf (accessed on 22 May 2025).[Green Version]
- de Carvalho, A.L.; Menezes, R.S.C.; Nóbrega, R.S.; Pinto, A.d.S.; Ometto, J.P.H.B.; von Randow, C.; Giarolla, A. Impact of climate changes on potential sugarcane yield in Pernambuco. Northeast. Reg. Brazil. Renew. Energy 2015, 78, 26–34. [Google Scholar] [CrossRef]
- Moura, G.B.A.; Brito, J.I.B.; Sousa, F.A.S.; Cavalcanti, E.P.; Silva, J.L.B.; Nascimento, C.R.; Lopes, P.M.O. Identificação de Preditores Para as Chuvas do Setor Leste do Nordeste do Brasil Utilizando Análise de Correlação Canônica. Rev. Bras. Geog. Fís. 2020, 13, 1463. [Google Scholar] [CrossRef]
- Lambert, Z.V.; Durand, R.M. Some Precautions in Using Canonical Analysis. J. Mark. Res. 1975, 12, 468–475. [Google Scholar] [CrossRef]
- Trugilho, P.F.; Lima, J.T.; Mori, F.A. Correlação canônica das características químicas e físicas da madeira de clones de Eucalyptus grandis e Eucalyptus saligna. Rev. Cer. 2003, 9, 66–80. [Google Scholar]
- Mingoti, S.A. Análise De Dados Através De Métodos De Estatística Multivariada: Uma Abordagem Aplicada; UFMG: Belo Horizonte, Brazil, 2005; 297p. [Google Scholar]
- Rossi, D.A.; da Silva Menezes, B.R.; Daher, R.E.F.; de Amaral Gravina, G.; de Lima, R.N.; da Silva Ledo, F.J.E.; Gottardo, R.D.; Campostrini, E.; de Souza, C.A.L.M. Canonical correlations in elephant grass for energy purposes. Afr. J. Biot. 2014, 13, 3666–3671. [Google Scholar]
- L’Heureux, M.L.; Tippett, M.K.; Barnston, A.G. Characterizing ENSO coupled variability and its impact on North American seasonal precipitation and temperature. J. Clim. 2015, 28, 4231–4245. [Google Scholar] [CrossRef]
- Rana, S.; Renwick, J.; McGregor, J.; Singh, A. Seasonal prediction of winter precipitation anomalies over Central Southwest Asia: A canonical correlation analysis approach. J. Clim. 2018, 31, 727–741. [Google Scholar] [CrossRef]
- Nobre, D.A.C.; dos Santos Silva, F.C.; Guimarães, J.F.R.; de Resende, J.C.F.; Macedo, W.R. Análise de Trilha e Correlação Canônica nos Componentes do Desempenho de Girassol. J. Eng. Exac. Scie. 2018, 4, 364–369. [Google Scholar] [CrossRef]
- Masri, M.I.; Shaban, S.A.; El-Hennawy, H.H.; El–Taib, A.B.A.; Abu-El-lail, F.F.B. Phenotypic and genotypic correlations and path coefficient analysis in sugarcane at first clonal selection stage. Egypt. J. Plant Breed. 2015, 19, 297–321. [Google Scholar] [CrossRef]
- Barbosa, R.P.; Neto, F.A.; Gravina, M.L.; Gravina, G.A.; Portela, M.G.; Bezerra, A.A. Seleção antecipada de cana-de-açúcar usando análise de trilha. Genet. Mol. Res. 2017, 16, e16019038. [Google Scholar]
- Ali, A.; Khan, S.A.; Tahir, M.; Farid, A.; Khan, A.; Khan, S.M.; Ali, N. Evaluation of various sugarcane genotypes for association of quality characters with cane yield. Adv. Crop Sci. Technol. 2018, 6, e1000371. [Google Scholar] [CrossRef]
- Ali, A.; Khan, S.A.; Tahir, M.; Farid, A.; Khan, A.; Khan, S.M.; Ali, N. Clonal selection strategy in sugarcane (Saccharum officinarumL.) based on the association of quality traits and cane yield. J. Anim. E Plant Sci. 2019, 29, 889–893. [Google Scholar]
- Forootan, E.; Khandu; Awange, J.L.; Schumacher, M.; Anyah, R.O.; Van Dijk, A.I.J.M.; Kusche, J. Quantifying the impacts of ENSO and IOD on rain gauge and remotely sensed precipitation products over Australia. Remote Sens. Environ. 2016, 172, 50–66. [Google Scholar] [CrossRef]
- Luciano, A.C.S.; Picoli, M.C.A.; Duft, D.G.; Rocha, J.V.; Leal, M.R.L.; Maire, G.L. Empirical model for forecasting sugarcane yield on a local scale brazil using Landsat imagery and random forest algorithm. Comput. Electron. Agric. 2022, 184, e106063. [Google Scholar] [CrossRef]
- Castro Manrique, D.R.; Lopes, P.M.O.; Nascimento, C.R.; Ribeiro, E.P.; Silva, A.S.d. Phenological Monitoring of Irrigated Sugarcane Using Google Earth Engine, Time Series, and TIMESAT in the Brazilian Semi-Arid. AgriEngineering 2024, 6, 3799–3822. [Google Scholar] [CrossRef]
- Mbhamali, T.; Jury, M. Climate-sensitivity of sugarcane yield in the southeastern Africa lowlands. Int. J. Biometeorol. 2021, 41, 4187–4200. [Google Scholar] [CrossRef]
- Verma, A.K.; Garg, P.K.; Prasad, K.S.H.; Dadhwal, V.K. Variety-specific sugarcane yield simulations and climate change impacts on sugarcane yield using DSSAT-CSM-CANEGRO model. Agric. Water Manag. 2023, 275, 108034. [Google Scholar] [CrossRef]
- Legendre, B.L. Ripening of Sugarcane: Effects of Sunlight, Temperature, and Rainfall1. Crop Sci. 1975, 15, 349–352. [Google Scholar] [CrossRef]
- Araujo, R.; Júnior, J.; Casaroli, D.; Pêgo Evangelista, A. Variation in the sugar yield in response to drying-off of sugarcane before harvest and the occurrence of low air temperatures. Bragantia 2016, 75, 118–127. [Google Scholar] [CrossRef]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; de Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef] [PubMed]
- Nóbrega, R.S.; Vital, L.A.d.B. Paisagens Entre Espaços Urbanos Distintos Como Elemento Para Analise Microclimática; Estudos multidisciplinares: Abordagem holística; Ribeiro, E.P., Lima, M.S.d.R., Eds.; UFPE: Recife, Brazil, 2014. [Google Scholar]
- APAC—Agência Pernambucana de Águas e Clima. 1º de Abril—Início da Quadra Chuvosa Do Leste de Pernambuco. 2025. Available online: https://www.apac.pe.gov.br/noticias/23-noticias/meteorologia/632-1-de-abril-inicio-da-quadra-chuvosa-do-leste-de-pernambuco (accessed on 23 May 2025).
- Google, Map Data. 2015. Available online: https://www.google.at/permissions/geoguidelines/attr-guide.html (accessed on 7 July 2025).
- IBGE—Instituto Brasileiro de Geografia e Estatística—Municipal Agricultural Production (PAM) Between 1990 and 2019. 2020. Available online: https://sidra.ibge.gov.br/Tabela/1612 (accessed on 26 May 2025).
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- CONAB—Companhia Nacional de Abastecimento. Acompanhamento Da Safra Brasileira De Cana-De-Açúcar. CONAB: Brasília, Brazil, 2025; Volume 9. Available online: https://www.conab.gov.br/info-agro/safras/cana/ (accessed on 25 June 2025).
- MaisAgro. Broca-Da-Cana: 3 Descobertas Que Estão Transformando O Manejo. 2024. Available online: https://maisagro.syngenta.com.br/inovacoes-e-tendencias/broca-da-cana-3-descobertas-que-estao-transformando-o-manejo/ (accessed on 5 August 2025).
- Melo, L.D.; Oliveira, F.D.; Bastos, G.Q.; Anunciação Filho, C.D.; Reis, O.D. Agroindustrial performance of sugar cane cultivars in the coastal-forest zone of Pernambuco. Ciência E Agrotecnologia 2009, 33, 684–691. [Google Scholar] [CrossRef]
- Albuquerque, A.P.d.C.; Bastos, G.Q.; Dutra Filho, J.d.A.; Souto, L.S.; Maracajá, P.B.; Simões Neto, D.E. Selection of sugarcane cultivars to the North Forest Zone of Pernambuco III: Final crop. Rev. Verde De Agroecol. E Desenvolv. Sustentável 2016, 11, 39–43. [Google Scholar]
- Simões Neto Neto, D.E. Variedades de cana–de–açúcar no estado de Pernambuco contribuição do melhoramento clássico da RIDESA–UFRPE. Anais da Academia Pernambucana de Ciência Agronômica. Recife 2008, 5, 125–146. [Google Scholar]
- Rosseto, R.; Santiago, A.D. Cana. Portal Embrapa. 2022. Available online: https://www.embrapa.br/agencia-de-informacao-tecnologica/cultivos/cana/producao/manejo/plantio (accessed on 8 August 2025).
- IPA—Instituto Agronomiaco de Pernamco. Cana-de-Açúcar. Folhetos Explicativos. 2025. Available online: http://www.ipa.br/resp20.php (accessed on 8 August 2025).
- Moura, A.D.; Shukla, J. On the dynamics of droughts in northeast Brazil: Observations. theory and numerical experiments with a general circulation model. J. Atm. Scie. 1981, 38, 2653–2675. [Google Scholar] [CrossRef]
- Servain, J. Simple Climatic Indices for the Tropical Atlantic Ocean and some applications. J. Geophys. Res. 1991, 96, 137–146. [Google Scholar] [CrossRef]
- Trenberth, K.E. The Definition of El Niño. Bull. Amer. Meteor. Soc. 1997, 78, 2771–2777. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Stepaniak, D.P. Indices of El Niño evolution. J. Climate. 2001, 14, 1697–1701. [Google Scholar] [CrossRef]
- NOAA—National Oceanic and Atmospheric Administration. 2025. Available online: https://www.cpc.ncep.noaa.gov/ (accessed on 23 May 2025).
- Enfield, D.B.; Mestas, A.M.; Mayer, D.A.; Cid-Serrano, L. How ubiquitous is the dipole relationship in tropical Atlantic sea surface temperatures. J. Geogr. Res.-Oceans 1999, 104, 7841–7848. [Google Scholar] [CrossRef]
- Abril-Salcedo, D.S.; Melo-Velandia, L.F.; Parra-Amado, D. Impactos de los fenómenos climáticos sobre el precio de los alimentos en Colombia Impacts of weather anomalies on food prices in Colombia. Ens. Sobre Política Econ. 2016, 34, 146–158. [Google Scholar]
- Schlanger, V.; Heres, J. Condições Meteorológicas: A Oscilação Do Sul E O El Nino. Environmental Science Published for Every Round the Earth. Hngarian Meteorological Service. 2006. Available online: https://klimat.czn.uj.edu.pl/enid/2__Principais_sistemas_de_vento/-_El_Ni_o___SOI_4z1.html (accessed on 7 July 2025).
- Ultsch, A.; Lötsch, J. Euclidean distance-optimized data transformation for cluster analysis in biomedical data (EDOtrans). BMC Bioinform. 2022, 23, 233. [Google Scholar] [CrossRef] [PubMed]
- Ward, J.R.; Joe, H. Hierarchical grouping to optimize an objective function. J. Amer. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Hotelling, H. The most predictable criterion. J. Educ. Psychol. 1935, 26, 139–142. [Google Scholar] [CrossRef]
- Anderson, T.W. An Introduction to Multivariate Statistical Analysis, 2nd ed.; John Wiley: Hoboken, NJ, USA, 1984; pp. 439–449. [Google Scholar]
- Anderson, T.W. An Introduction to Multivariate Statistical Analysis, 3rd ed.; John Wiley: Hoboken, NJ, USA, 2003; pp. 459–469. [Google Scholar]
- STATSOFT. Statistica (Data Analysis Software System). Version 12. 2023. Available online: https://statistica.software.informer.com/12.0/ (accessed on 7 May 2025).
- Pearson, E.S.; Hartley, H.O. Biometrika Table for Statisticians. Table 8. Cambridge University Press: Cambridge, UK, 1966; Volume 1, pp. 137–138. Available online: https://www.datageeks.com.br/wp-content/uploads/2024/05/tabela-qui-quadrado.jpg (accessed on 4 July 2025).
- de Melo, C.G.B.; Rolim, M.M.; Cavalcanti, R.Q.; da Silva, M.V.; Candeias, A.L.B.; Lopes, P.M.O.; Ortiz, P.F.S.; de Lima, R.P. RGB Composition Obtained by a UAV in the Monitoring of Sugarcane Row Gaps Using the Biophysical Index. Agriengineering 2025, 7, 17. [Google Scholar] [CrossRef]
- Jardim, A.M.d.R.F.; Silva, M.V.d.; Silva, A.R.; Santos, A.d.; Pandorfi, H.; Oliveira-Júnior, J.F.d.; De Lima, J.L.M.P.; Souza, L.S.B.d.; Araújo Júnior, G.d.N.; Lopes, P.M.O.; et al. Spatiotemporal climatic analysis in Pernambuco State, Northeast Brazil. J. Atmos. Sol.-Terr. Phys. 2021, 223, 105733. [Google Scholar] [CrossRef]
- Bezerra, A.C.; Silva, J.L.B.d.; Moura, G.B.d.A.; Lopes, P.M.O.; Nascimento, C.R.; Ribeiro, E.P.; Galvíncio, J.D.; Silva, M.V.d. Dynamics of land cover and land use in Pernambuco (Brazil): Spatio-temporal variability and temporal trends of biophysical parameters. Remote Sens. Appl.-Soc. Environ. 2022, 25, 100677. [Google Scholar] [CrossRef]
- Bordonal, R.D.O.; Carvalho, J.L.N.; Lal, R.; de Figueiredo, E.B.; de Oliveira, B.G.; La Scala, N. Sustainability of sugarcane production in Brazil. A review. Agron. Sustain. Dev. 2018, 38, 13. [Google Scholar] [CrossRef]
- Du, C.; Kulay, L.; Cavalett, O.; Dias, L.; Freire, F. Life cycle assessment addressing health effects of particulate matter of mechanical versus manual sugarcane harvesting in Brazil. Int. J. Life Cycle Assess. 2018, 23, 787–799. [Google Scholar] [CrossRef]
- Silva, M.J.; Neves, L.O.; Correa, M.H.F.; de Souza, C.H.W. Quality indexes and performance in mechanized harvesting of sugarcane at a burnt cane and green cane. Sugar Tech. 2021, 23, 499–507. [Google Scholar] [CrossRef]
- Afifi, A.; Clark, V.A. Computer-Aided Multivariate Analysis, 3rd ed.; Chapman and Hall: London, UK, 1996; p. 505. [Google Scholar]
- Mazouz, R.; Assani, A.A.; Rodríguez, M.A. Application of redundancy analysis to hydroclimatology: A case study of spring heavy floods in southern Québec (Canada). J. Hydrol. 2013, 496, 187–194. [Google Scholar] [CrossRef]
- Protásio, T.d.P.; TonoliII, G.H.D.; JúniorIII, M.G.; Bufalino, L.; Couto, A.M.; Trugilho, P.F. Correlações canônicas entre as características químicas e energéticas de resíduos lignocelulósicos. Cerne 2012, 18, 433–439. [Google Scholar] [CrossRef]
- Hair Junior, J.F.; Anderson, R.E.; Tatham, R.L.; Black, W.C. Análise Multivariada de Dados; Bookman: Porto Alegre, Brazil, 2005; 593p. [Google Scholar]
- Barnett, T.P.; Preisendorfer, R. Origins and levels of monthly and seasonal forecast skill for United States surface air temperatures determined by canonical correlation analysis. Mon. Weather. Rev. 1987, 115, 1825–1850. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, L.-X.; Ai, J.; Zhang, Z.-F.; Deng, J.; Zhang, Y.-B. Climate Variations in the Low-Latitude Plateau Contribute to Different Sugarcane (Saccharum spp.) Yields and Sugar Contents in China. Plants 2023, 12, 2712. [Google Scholar] [CrossRef]
- lack-Prain, S.; Shi, L.; Zhu, P.; da Rocha, H.R.; Cabral, O.; Hu, S.; Williams, M. The impact of climate change and climate extremes on sugarcane production. GCB Bioenergy 2021, 13, 408–424. [Google Scholar] [CrossRef]
- Marin, F.R.; Lopes-Assad, M.L.; Assad, E.D.; Vian, C.E.; Santos, M.C. Sugarcane crop efficiency in two growing seasons in São Paulo State, Brazil. Pesqui. Agropecu. Bras. 2008, 43, 1449–1455. [Google Scholar] [CrossRef]
- NOVACANA. Climas Diferentes Na Zona Canavieira de Pernambuco Afetam Produção. 2021. Available online: https://www.novacana.com/noticias/climas-diferentes-zona-canavieira-pernambuco-afetam-producao-150321 (accessed on 1 August 2025).
- Wildt, A.R.; Lambert, Z.V.; Durand, R.M. Applying the Jackknife Statistic in Testing and Interpreting Canonical Weights, Loadings, and Cross-Loadings. J. Mark. Res. 1982, 19, 99–107. [Google Scholar] [CrossRef]
- Ribeiro, M.D.d.S.B. Basic Wood Density of Eucalyptus spp. Forest Plantations: Associations with Site AND Plantation Variables and Estimates with Artificial Neural Networks. Ph.D. Thesis, Unesp, São Paulo, Brazil, 2018. Available online: https://repositorio.unesp.br/server/api/core/bitstreams/db46edc3-122e-47af-a20b-812f69d8986c/content (accessed on 26 June 2025).
- Fischer, G.R.; Diniz, G.B.; Marques, J.R.Q. Previsão do número de dias de chuva para a metade sul do Rio Grande do Sul utilizando a temperatura da superfície do mar (TSM). Ver. Bras. Met. 2008, 23, 146–151. [Google Scholar] [CrossRef]
- Stockdale, T.N.; Alves, O.; Boer, G.; Deque, M.; Ding, Y.; Kumar, A.; Kumar, K.; Landman, W.; Mason, S.; Nobre, P.; et al. Understanding and predicting seasonal-to-interannual climate variability-the producer perspective. Procedia Environ. Sci. 2010, 1, 55–80. [Google Scholar] [CrossRef]
- Oliveira, N.L.; Marcuzzo, F.F.N. Correlação da temperatura na parte sul do oceano Atlântico com o NDC em Mato Grosso. GEOgrap 2013, 18, 183–206. [Google Scholar] [CrossRef]
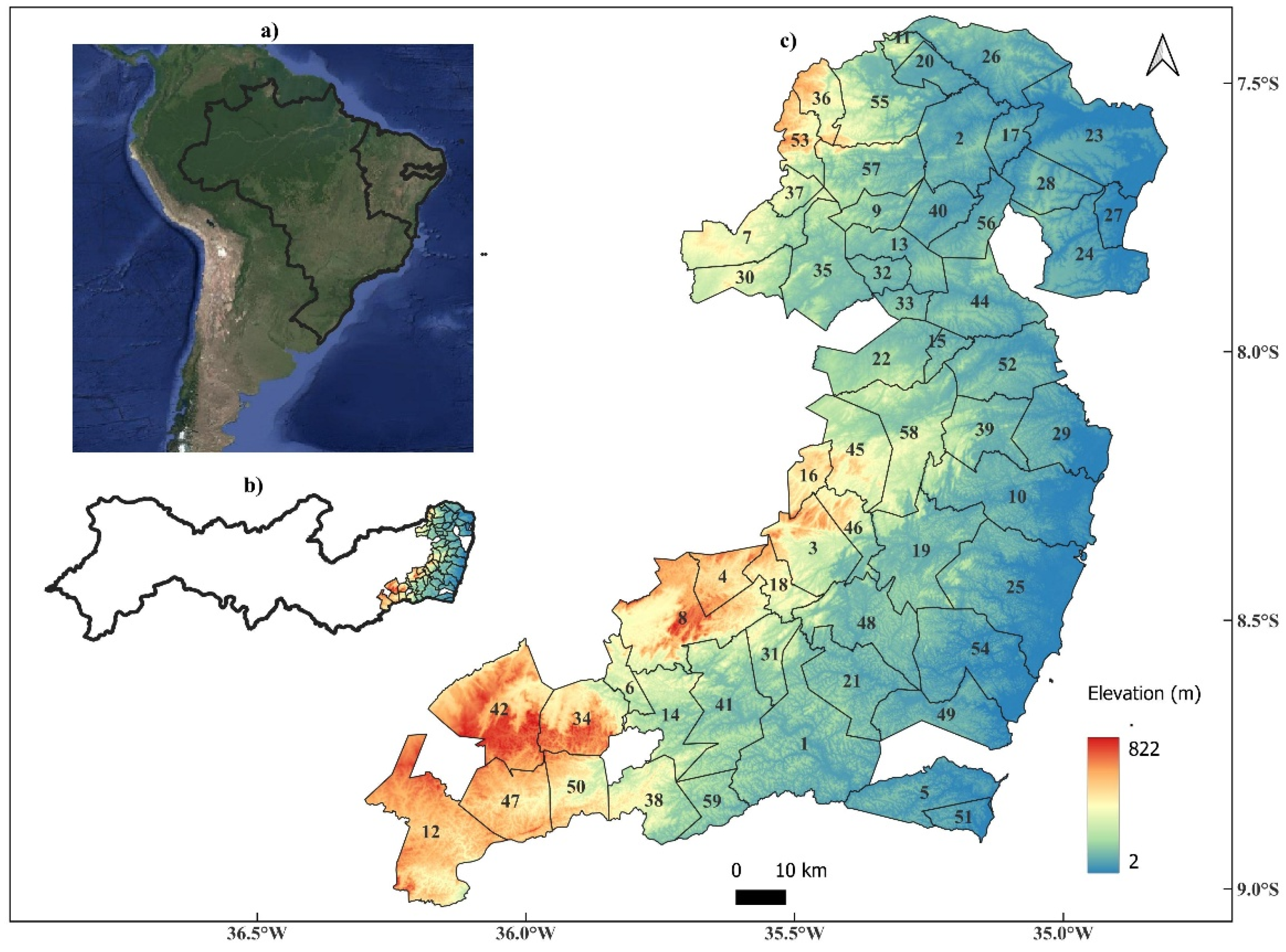


| ID | Locations | ϕ (°) | λ (°) | ID | Locations | ϕ (°) | λ (°) | ID | Locations | ϕ (°) | λ (°) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Água Preta | −8.74 | −35.53 | 21 | Gameleira | −8.62 | −35.38 | 41 | Palmares | −8.67 | −35.61 |
| 2 | Aliança | −7.64 | −35.17 | 22 | Glória do Goitá | −8.02 | −35.33 | 42 | Panelas | −8.64 | −36.03 |
| 3 | Amaraji | −8.41 | −35.46 | 23 | Goiana | −7.61 | −34.90 | 43 | Paudalho | −7.91 | −35.16 |
| 4 | Barra Guabiraba | −8.45 | −35.62 | 24 | Igarassu | −7.84 | −34.95 | 44 | Pombos | −8.20 | −35.38 |
| 5 | Barreiros | −8.81 | −35.24 | 25 | Ipojuca | −8.44 | −35.06 | 45 | Primavera | −8.32 | −35.39 |
| 6 | Belém de Maria | −8.61 | −35.82 | 26 | Itambé | −7.45 | −35.13 | 46 | Quipapá | −8.85 | −36.03 |
| 7 | Bom Jardim | −7.81 | −35.63 | 27 | Itapissuma | −7.74 | −34.89 | 47 | Ribeirão | −8.51 | −35.37 |
| 8 | Bonito | −8.50 | −35.74 | 28 | Itaquitinga | −7.69 | −35.04 | 48 | Rio Formoso | −8.69 | −35.17 |
| 9 | Buenos Aires | −7.75 | −35.35 | 29 | Jaboatão dos Guararapes | −8.16 | −35.01 | 49 | São Benedito do Sul | −8.81 | −35.91 |
| 10 | Cabo S. Agostinho | −8.23 | −35.20 | 30 | João Alfredo | −7.86 | −35.55 | 50 | São José da Coroa Grande | −8.87 | −35.17 |
| 11 | Camutanga | −7.43 | −35.29 | 31 | Joaquim Nabuco | −8.55 | −35.55 | 51 | São Lourenço da Mata | −8.04 | −35.12 |
| 12 | Canhotinho | −8.92 | −36.14 | 32 | Lagoa do Carro | −7.85 | −35.33 | 52 | São Vicente Férrer | −7.62 | −35.48 |
| 13 | Carpina | −7.83 | −35.26 | 33 | Lagoa de Itaenga | −7.91 | −35.29 | 53 | Sirinhaém | −8.55 | −35.16 |
| 14 | Catende | −8.66 | −35.72 | 34 | Lagoa dos Gatos | −8.68 | −35.91 | 54 | Timbaúba | −7.56 | −35.36 |
| 15 | Chã de Alegria | −7.99 | −35.21 | 35 | Limoeiro | −7.88 | −35.46 | 55 | Tracunhaém | −7.77 | −35.15 |
| 16 | Chã Grande | −8.24 | −35.48 | 36 | Macaparana | −7.50 | −35.46 | 56 | Vicência | −7.65 | −35.35 |
| 17 | Condado | −7.611 | −35.11 | 37 | Machados | −7.71 | −35.50 | 57 | Vitória de Santo Antão | −8.15 | −35.28 |
| 18 | Cortês | −8.45 | −35.52 | 38 | Maraial | −8.84 | −35.73 | 58 | Xexéu | −8.83 | −35.65 |
| 19 | Escada | −8.37 | −35.28 | 39 | Moreno | −8.15 | −35.14 | ||||
| 20 | Ferreiros | −7.47 | −35.25 | 40 | Nazaré da Mata | −7.75 | −35.25 |
| Static Parameters | G1 | G2 | G3 |
|---|---|---|---|
| Mean | 52,033.45 tons/ha | 43,184.862 tons/ha | 49,293.44 tons/ha |
| Standard Error | 1234.80 tons/ha | 1031.22 tons/ha | 675.09 tons/ha |
| Median | 53,335.86 tons/ha | 43,122.036 tons/ha | 49,444.39 tons/ha |
| Standard Deviation | 6763.28 tons/ha | 5648.26 tons/ha | 3697.66 tons/ha |
| Sample Variation | 45,741,896.8 tons/ha | 31,902,266.02 tons/ha | 13,672,688.35 tons/ha |
| Kurtosis | 3.85 | 0.596 | 4.23 |
| Asymmetry | −1.64 | −0.96 | −1.34 |
| Interval | 32,372.80 tons/ha | 20,911.76 tons/ha | 20,240.74 tons/ha |
| Minimum | 28,571.43 tons/ha | 29,264.71 tons/ha | 36,283.22 tons/ha |
| Maximum | 60,944.23 tons/ha | 50,176.47 tons/ha | 56,523.96 tons/ha |
| Sum | 1,561,003.52 tons/ha | 1,295,545.81 tons/ha | 1,478,803.23 tons/ha |
| Sample number | 30 | 30 | 30 |
| Groups | Municipalities (id) |
|---|---|
| G1 | Aliança (2), Buenos Aires (9), Camutanga (11), Condado (17), Ferreiros (20), Goiana (23), Itambé (26), Itaquitinga (28), Macaparana (36), Nazaré da Mata (40), São Vicente Férrer (53), Timbaúba (55), Tracunhaém (56), Vicência (57). |
| G2 | Belém de Maria (6), Bom Jardim (7), Canhotinho (12), Carpina (13), Chã Grande (16), Jaboatão dos Guararapes (29), João Alfredo (30), Lagoa do Carro (32), Lagoa de Itaenga (33), Lagoa dos Gatos (34), Limoeiro (35), Machados (37), Panelas (42), Paudalho (44), Quipapá (47), São Benedito do Sul (50), São José da Coroa Grande (51). |
| G3 | Água Preta (1), Amaraji (3), Barra de Guabiraba (4), Barreiros (5), Bonito (8), Cabo de Santo Agostinho (10), Catende (14), Chã de Alegria (15), Cortês (18), Escada (19), Gameleira (21), Glória do Goitá (22), Igarassu (24), Ipojuca (25), Itapissuma (27), Joaquim Nabuco (31), Maraial (38), Moreno (39), Palmares (41), Pombos (45), Primavera (46), Ribeirão (48), Rio Formoso (49), São Lourenço da Mata (52), Sirinhaém (54), Vitória de Santo Antão (58), Xexéu (59). |
| Groups (G) and Variables | Mean | SD | G1 | G2 | G3 | sstSA | sstNA | Darwin | Tahiti | EN1+2 | EN3 | EN4 | WC | WE | WW |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | 52,033 ton/ha | 6763 ton/ha | 1.0 | 0.5 | 0.3 | 0.3 | 0.2 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.01 | −0.3 | 0.2 |
| G2 | 43,185 ton/ha | 5648 ton/ha | 1.0 | 0.8 | 0.3 | 0.4 | −0.1 | 0.1 | −0.2 | 0.1 | 0.2 | 0.2 | 0.1 | 0.1 | |
| G3 | 49,293 ton/ha | 3698 ton/ha | 1.0 | 0.3 | 0.2 | 0.1 | 0.2 | −0.1 | 0.1 | 0.1 | 0.1 | 0.0 | −0.1 | ||
| sstSA (°C) | 24.8 °C | 0.3 °C | 1.0 | 0.3 | 0.2 | −0.2 | 0.6 | 0.5 | 0.2 | −0.2 | −0.4 | 0.1 | |||
| sstNA (°C) | 26.9 °C | 0.3 °C | 1.0 | −0.2 | 0.1 | −0.1 | −0.1 | −0.1 | 0.2 | 0.0 | 0.4 | ||||
| Darwin (hPa) | 1007.5 hPa | 0.9 hPa | 1.00 | −0.7 | 0.7 | 0.8 | 0.8 | −0.9 | −0.6 | −0.8 | |||||
| Tahiti (hPa) | 1011.3 hPa | 0.9 hPa | 1.0 | −0.6 | −0.7 | −0.8 | 0.9 | 0.5 | 0.7 | ||||||
| EN1+2 (°C) | 23.0 °C | 1.1 °C | 1.0 | 0.9 | 0.6 | −0.8 | −0.9 | −0.4 | |||||||
| EN3 (°C) | 25.3 °C | 1.2 °C | 1.0 | 0.8 | −0.8 | −0.9 | −0.5 | ||||||||
| EN4 (°C) | 28.5 °C | 0.8 °C | 1.0 | −0.7 | −0.6 | −0.7 | |||||||||
| WC (m/s) | 8.4 m/s | 2.5 m/s | 1.0 | 0.7 | 0.7 | ||||||||||
| WE (m/s) | 9.1 m/s | 1.3 m/s | 1.0 | 0.3 | |||||||||||
| WW(m/s) | 1.4 m/s | 2.2 m/s | 1.0 |
| Canonical Function | R | R2 | χ2 | df | p | Wilks’ Lambda |
|---|---|---|---|---|---|---|
| 1 | 0.82 | 0.67 | 44.18 | 27 | 0.02 | 0.14 |
| 2 | 0.62 | 0.38 | 19.37 | 16 | 0.25 | 0.42 |
| 3 | 0.56 | 0.32 | 8.62 | 7 | 0.28 | 0.68 |
| Variables | Canonical Loading | Canonical Loading Squared | Average Loadings Squared | Canonical R2 | Redundancy Index |
|---|---|---|---|---|---|
| Groups of Dependent Variables | |||||
| G1 | 0.668 | 0.446 | 0.297 | ||
| G2 | 0.949 | 0.901 | 0.599 | ||
| G3 | 0.886 | 0.785 | 0.522 | ||
| Sum of Square canonical loadings | 2.131 | 0.710 | 0.665 | 0.473 * | |
| Independent Climate Variables | |||||
| sstSA | 0.427 | 0.182 | 0.121 | ||
| sstNA | 0.303 | 0.083 | 0.061 | ||
| Darwin | 0.035 | 0.001 | 0.001 | ||
| Tahiti | 0.222 | 0.034 | 0.033 | ||
| EN1+2 | −0.088 | 0.004 | 0.005 | ||
| EN3 | 0.096 | 0.012 | 0.006 | ||
| WC | 0.184 | 0.027 | 0.023 | ||
| WE | −0.074 | 0.019 | 0.004 | ||
| WW | 0.057 | 0.012 | 0.002 | ||
| Sum of Square canonical loadings | 0.449 | 0.041 | 0.002 | 0.028 * | |
| Standardized Variance of the Dependent Variables Explained by | |||||
|---|---|---|---|---|---|
| Their Own Canonical Variate (Shared Variance) | The Opposite Canonical Variate (Redundancy) | ||||
| Canonical Function | Percentage | Cumulative Percentage | Canonical R2 | Percentage | Cumulative Percentage |
| 1 | 0.6554 | 0.6554 | 0.6655 | 0.4362 | 0.4362 |
| 2 | 0.1635 | 0.8189 | 0.3787 | 0.0619 | 0.4981 |
| 3 | 0.1811 | 1.000 | 0.3191 | 0.0578 | 0.5559 |
| Standardized Variance of the Independent Variables Explained by | |||||
| Their Own Canonical Variate (Shared Variance) | The Opposite Canonical Variate (Redundancy) | ||||
| Canonical Function | Percentage | Cumulative Percentage | Canonical R2 | Percentage | Cumulative Percentage |
| 1 | 0.0191 | 0.0191 | 0.6655 | 0.0127 | 0.0127 |
| 2 | 0.1201 | 0.1392 | 0.3787 | 0.0455 | 0.0582 |
| 3 | 0.0401 | 0.1794 | 0.3191 | 0.0128 | 0.0710 |
| Standardized Canonical Coefficients | Function 1 | Function 2 | Function 3 |
|---|---|---|---|
| Groups of Dependent Variables | Canonical Weights | Canonical Weights | Canonical Weights |
| G1 | 0.2544 | 1.0412 | −0.5457 |
| G2 | 0.4859 | −1.5050 | −0.8432 |
| G3 | 0.4166 | 0.8277 | 1.3147 |
| Independent Climate Variables | |||
| sstSA | 0.8243 | 0.3287 | 0.4054 |
| sstNA | −0.0465 | −0.3847 | 0.2834 |
| Darwin | 0.9806 | 1.0991 | −0.5930 |
| Tahiti | 0.5113 | 0.5564 | 1.3655 |
| EN1+2 | −2.3312 | −0.2823 | 0.5105 |
| EN3 | 1.0140 | −0.9627 | 0.2567 |
| WC | 0.6518 | −1.2415 | −1.9951 |
| WE | −0.9910 | −0.5345 | 1.6829 |
| WW | −0.1420 | 1.2590 | −0.5408 |
| Function 1 | Function 2 | Function 3 | ||||
|---|---|---|---|---|---|---|
| Groups of Dependent Variables | Canonical loadings | CV (%) | Canonical loadings | CV (%) | Canonical loadings | CV (%) |
| G1 | 0.6676 | 20.92 | 0.5161 | 75.49 | −0.5365 | 55.78 |
| G2 | 0.9490 | 42.26 | −0.2929 | 24.31 | −0.1164 | 2.63 |
| G3 | 0.8858 | 36.82 | 0.0264 | 0.20 | 0.4633 | 41.60 |
| Independent Climate Variables | ||||||
| sstSA | 0.4267 | 47.40 | 0.2682 | 7.30 | 0.1892 | 13.57 |
| sstNA | 0.3033 | 23.95 | −0.0810 | 0.67 | −0.0837 | 2.66 |
| Darwin | 0.0347 | 0.31 | 0.2515 | 6.42 | 0.1696 | 10.91 |
| Tahiti | 0.2222 | 12.85 | 0.0628 | 0.40 | 0.1708 | 11.06 |
| EN1+2 | −0.0875 | 1.99 | 0.4824 | 23.61 | 0.0643 | 1.57 |
| EN3 | 0.0964 | 2.42 | 0.3179 | 10.25 | 0.0001 | 0.00 |
| WC | 0.1840 | 8.81 | −0.3654 | 13.54 | −0.1199 | 5.45 |
| WE | −0.0735 | 1.41 | −0.5776 | 33.84 | 0.2234 | 18.92 |
| WW | 0.0570 | 0.85 | 0.1980 | 3.98 | −0.3075 | 35.86 |
| Function 1 | Function 2 | Function 3 | ||||
|---|---|---|---|---|---|---|
| Groups of Dependent Variables | Canonical Cross-Loadings | CV (%) | Canonical Cross-Loadings | CV (%) | Canonical Cross-Loadings | CV (%) |
| G1 | 0.5447 | 20.93 | 0.3176 | 75.50 | −0.3031 | 55.79 |
| G2 | 0.7742 | 42.26 | −0.1802 | 24.30 | −0.0657 | 2.62 |
| G3 | 0.7226 | 36.82 | 0.0162 | 0.20 | 0.2617 | 41.59 |
| Independent Climate Variables | ||||||
| sstSA | 0.3481 | 47.40 | 0.1650 | 7.87 | 0.1069 | 15.71 |
| sstNA | 0.2474 | 23.94 | −0.0498 | 0.72 | −0.0473 | 3.08 |
| Darwin | 0.0283 | 0.31 | 0.1548 | 6.92 | 0.0958 | 12.62 |
| Tahiti | 0.1813 | 12.86 | 0.0387 | 0.43 | 0.0965 | 12.80 |
| EN1+2 | −0.0714 | 1.99 | 0.2969 | 25.47 | 0.0363 | 1.81 |
| EN3 | 0.0786 | 2.42 | 0.1957 | 11.06 | 0.0000 | 0.00 |
| WC | 0.1501 | 8.81 | −0.2248 | 14.60 | −0.0677 | 6.30 |
| WE | −0.0600 | 1.41 | −0.3555 | 36.51 | 0.1262 | 21.90 |
| WW | 0.0465 | 0.85 | 0.1218 | 4.29 | −0.1737 | 41.49 |
| Result After Deletion of | ||||
|---|---|---|---|---|
| Complete variate | sstNA | WC | EN3 | |
| Canonical correlation (R) | 0.82 | 0.82 | 0.81 | 0.79 |
| Canonical root (R2) | 0.67 | 0.67 | 0.65 | 0.63 |
| Dependent variate | ||||
| G1 | 0.67 | 0.68 | 0.65 | 0.73 |
| G2 | 0.95 | 0.95 | 0.91 | 0.91 |
| G3 | 0.89 | 0.88 | 0.92 | 0.87 |
| Shared variance | 0.66 | 0.66 | 0.63 | 0.67 |
| Redundancy index | 0.47 | 0.47 | 0.46 | 0.44 |
| Independent variate | ||||
| Canonical Loadings | ||||
| sstSA | 0.43 | 0.43 | 0.46 | 0.46 |
| sstNA | 0.30 | - | 0.29 | 0.30 |
| Darwin | 0.04 | 0.04 | 0.06 | 0.06 |
| Tahiti | 0.22 | 0.22 | 0.24 | 0.23 |
| EN12 | −0.09 | −0.08 | −0.06 | −0.05 |
| EN3 | 0.10 | 0.10 | 0.11 | - |
| WC | 0.18 | −0.18 | - | 0.16 |
| WE | −0.07 | −0.08 | −0.09 | −0.13 |
| WW | 0.06 | 0.06 | 0.05 | 0.08 |
| Shared variance | 0.02 | 0.02 | 0.01 | 0.02 |
| Redundancy | 0.03 | 0.02 | 0.03 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, R.R.d.; Moura, G.B.d.A.; Lopes, P.M.O.; Nascimento, C.R.; Giongo, P.R. Canonical Analysis of the Impact of Climate Predictors on Sugarcane Yield in the Eastern Region of Pernambuco, Brazil. Agriculture 2025, 15, 2162. https://doi.org/10.3390/agriculture15202162
Silva RRd, Moura GBdA, Lopes PMO, Nascimento CR, Giongo PR. Canonical Analysis of the Impact of Climate Predictors on Sugarcane Yield in the Eastern Region of Pernambuco, Brazil. Agriculture. 2025; 15(20):2162. https://doi.org/10.3390/agriculture15202162
Chicago/Turabian StyleSilva, Rodrigo Rogério da, Geber Barbosa de Albuquerque Moura, Pabrício Marcos Oliveira Lopes, Cristina Rodrigues Nascimento, and Pedro Rogério Giongo. 2025. "Canonical Analysis of the Impact of Climate Predictors on Sugarcane Yield in the Eastern Region of Pernambuco, Brazil" Agriculture 15, no. 20: 2162. https://doi.org/10.3390/agriculture15202162
APA StyleSilva, R. R. d., Moura, G. B. d. A., Lopes, P. M. O., Nascimento, C. R., & Giongo, P. R. (2025). Canonical Analysis of the Impact of Climate Predictors on Sugarcane Yield in the Eastern Region of Pernambuco, Brazil. Agriculture, 15(20), 2162. https://doi.org/10.3390/agriculture15202162







