Non-Invasive Inversion and Characteristic Analysis of Soil Moisture in 0–300 cm Agricultural Soil Layers
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Study Area
2.2. Data Collection and Preprocessing
2.2.1. Soil Data Collection and Processing
2.2.2. Meteorological Data Acquisition
2.3. Multi-Model Construction and Systematic Performance Evaluation
2.4. Model Interpretability Mechanism Analysis
3. Results
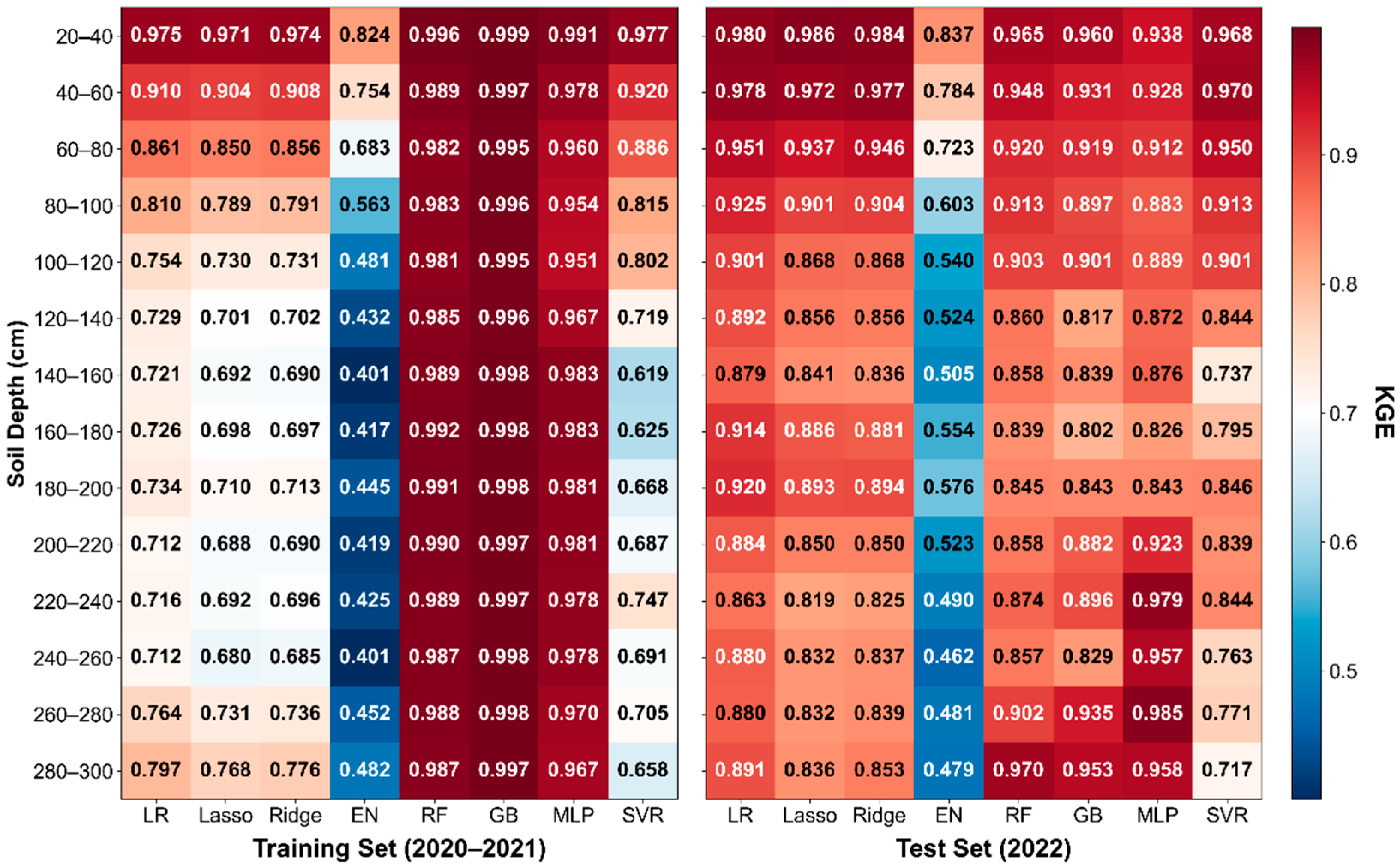
3.1. Model Construction and Evaluation
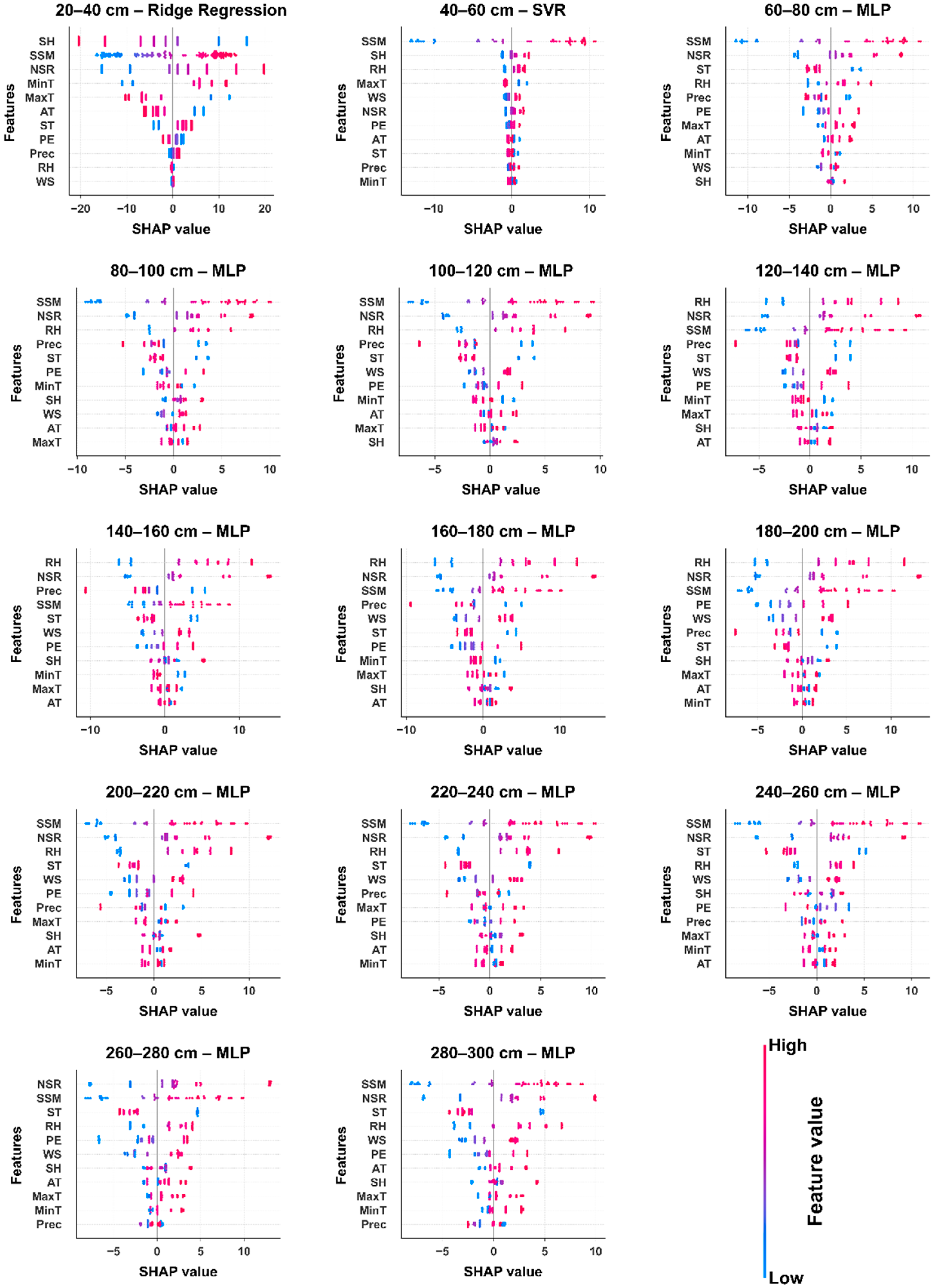
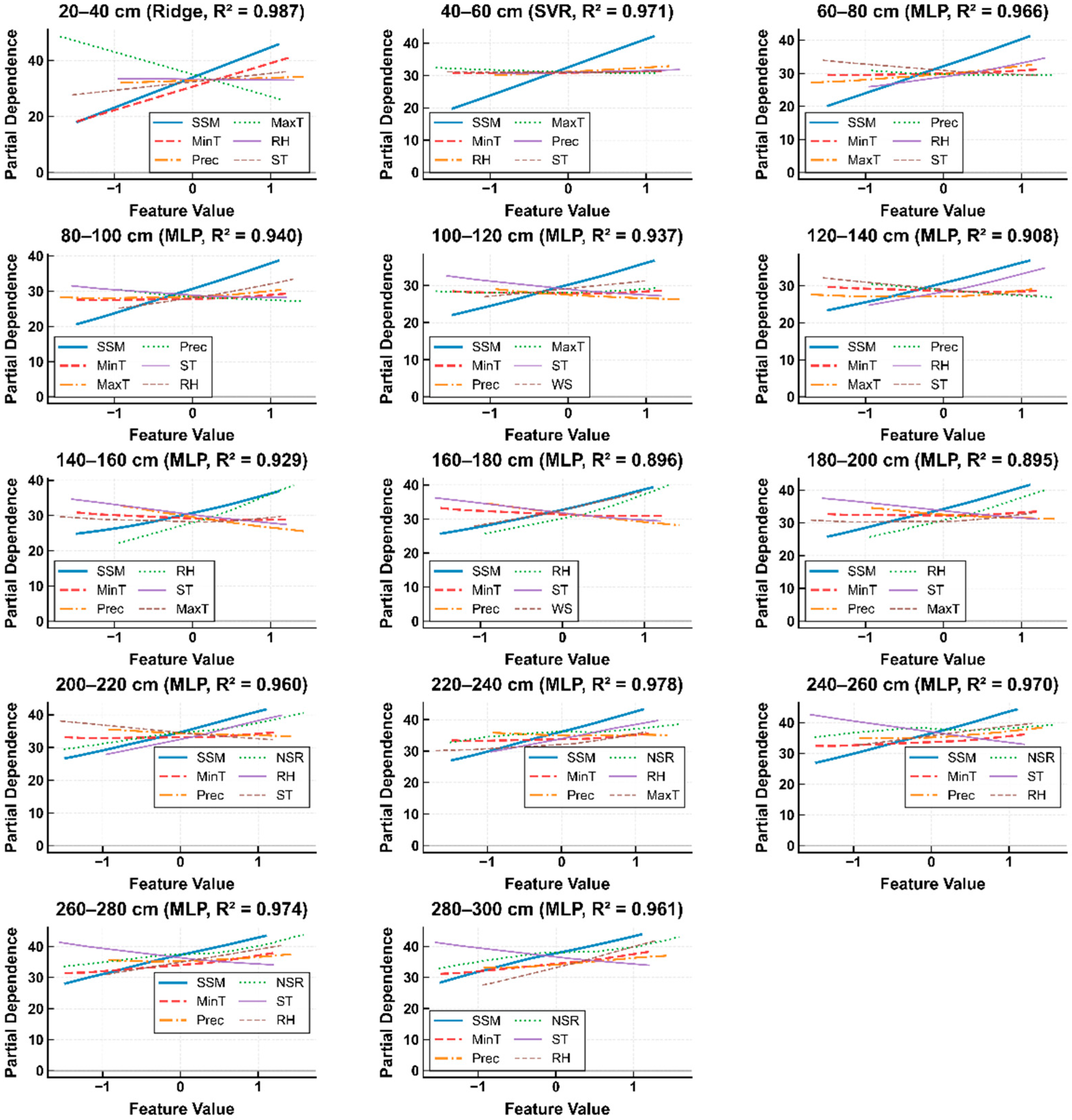
3.2. Model Interpretability and Variable Action Mechanism Revelation
4. Discussion
5. Conclusions
- (1)
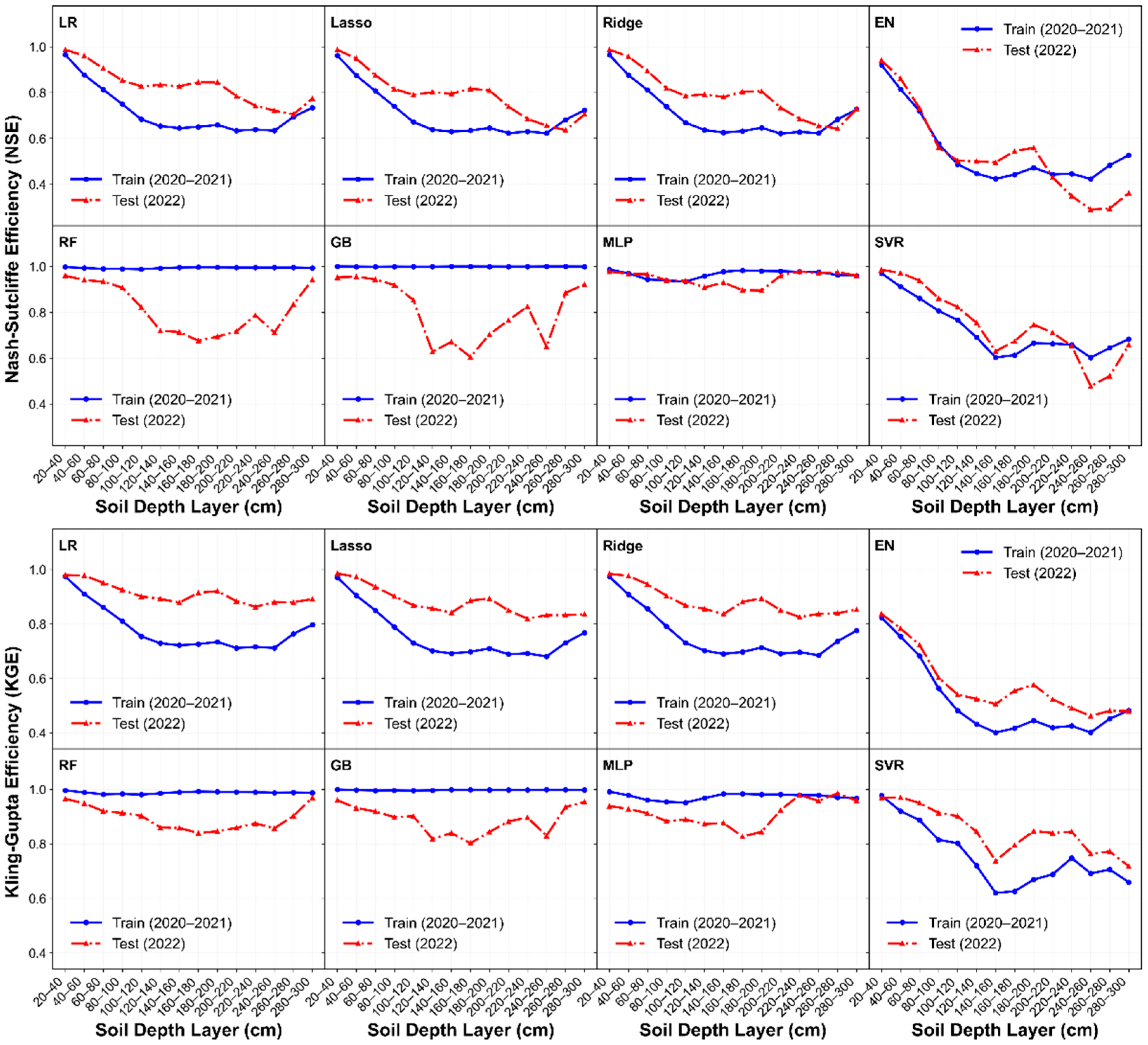
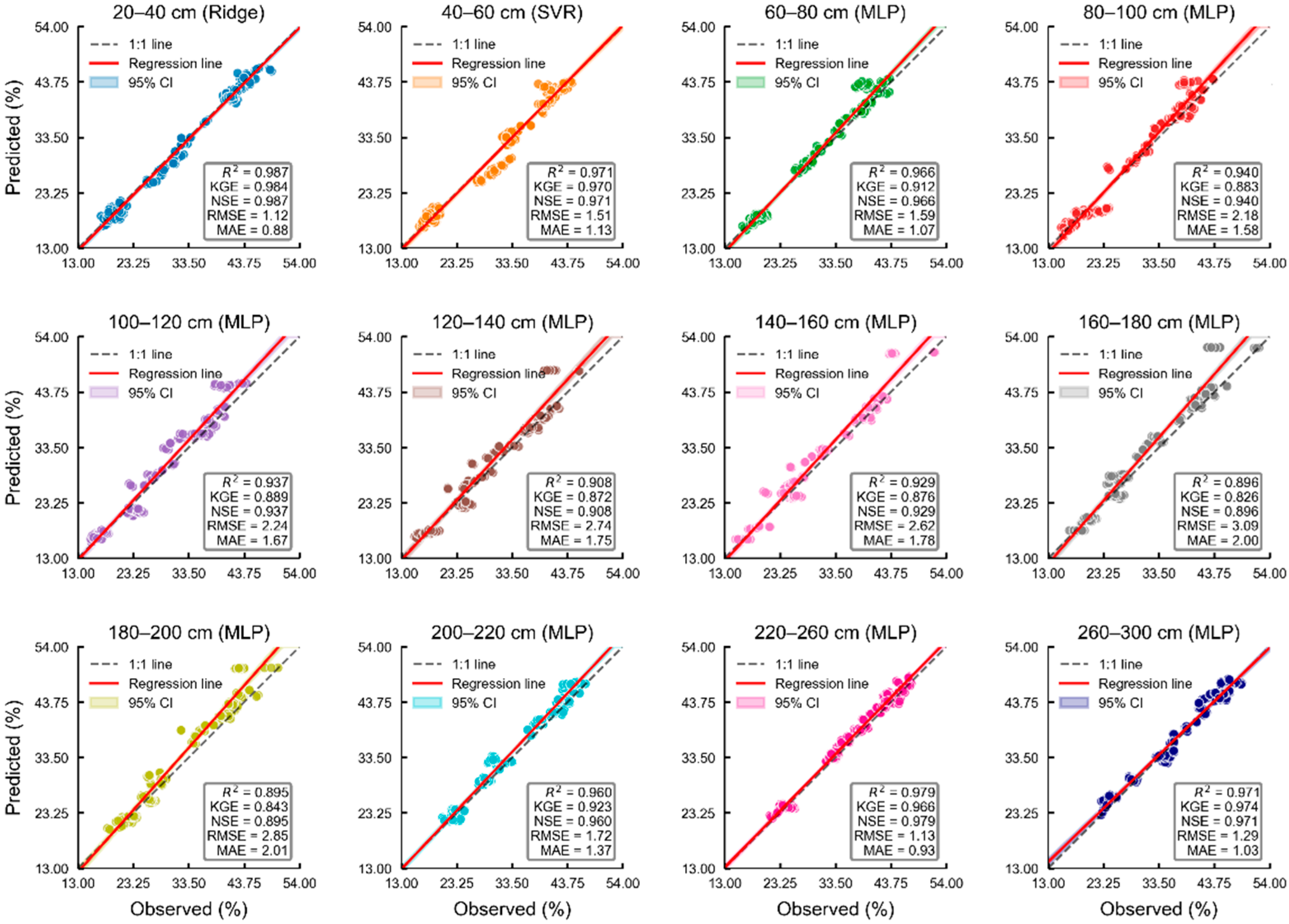
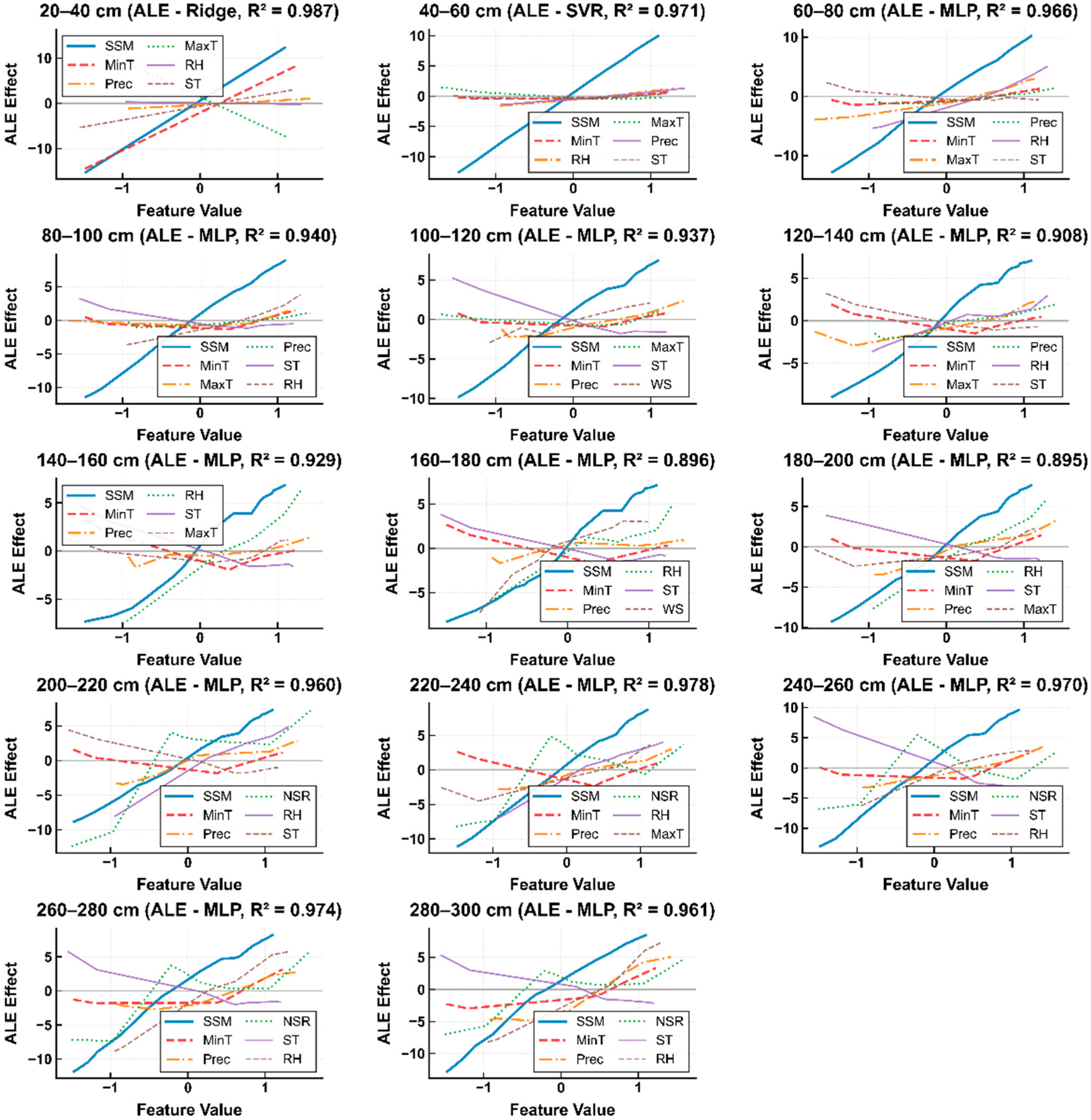
- Machine learning models demonstrated excellent temporal generalization capability in deep soil moisture prediction. Non-linear models achieved R2 of 0.895–0.987 on the 2022 test set across the full profile, making them significantly superior to traditional linear algorithms. Multi-layer perceptron dominated middle and deep layers (60–300 cm), while Ridge Regression performed optimally in 20–40 cm shallow layers (R2 = 0.987), and support vector regression excelled at 40–60 cm (R2 = 0.971).
- (2)
- Surface soil moisture served as the core variable for deep prediction, with the highest SHAP values and strongest contributions across all depth layers. Minimum temperature appeared as a major negative influence factor at all depths, with most significant negative contributions in shallow layers (20–140 cm). Precipitation served as an important positive driving factor in shallow layers (20–100 cm), with its influence gradually weakening with increasing depth. Relative humidity and net solar radiation showed enhanced importance in middle and deep layers (100–300 cm).
- (3)
- PDP analysis showed surface moisture exhibited positive linear responses at all depths, with influence intensity progressively strengthening from shallow to deep layers. Minimum temperature maintained consistent negative regulation, while maximum temperature displayed positive upward responses in shallow layers. Precipitation showed gentle positive responses in shallow layers, relative humidity presented relatively stable trends in middle layers (100–200 cm), and net solar radiation exhibited moderate positive slopes in deep layers (200–300 cm).
- (4)
- ALE analysis eliminated feature correlation biases, confirming surface moisture ALEs increased from 8–10 units in shallow layers to 12–18 units in deep layers, validating the “surface-to-deep information transmission amplification” mechanism. Minimum temperature exhibited consistent negative linear effects. Relative humidity at 160–180 cm and 180–200 cm transition zones showed significant positive responses, revealing the high sensitivity of these depth zones as moisture transition layers to atmospheric humidity conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SSM | Surface Soil Moisture |
| AT | Average Temperature |
| MaxT | Maximum Temperature |
| MinT | Minimum Temperature |
| Prec | Precipitation |
| ST | Surface Temperature |
| RH | Relative Humidity |
| WS | Wind Speed |
| NSR | Net Solar Radiation |
| SH | Sunshine Hours |
| PE | Potential Evaporation |
References
- Wu, F.; Yang, B.; Guo, S.; Huang, W.; Lei, Y.; Xiong, S.; Han, Y.; Wang, Z.; Feng, L.; Li, X.; et al. Adopting different cotton cropping systems may regulate the spatiotemporal variation in soil moisture and affect the growth, WUE and yield of cotton. Ind. Crops Prod. 2022, 186, 115259. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Xiao, J.; Ma, M. Evapotranspiration components and water use efficiency from desert to alpine ecosystems in drylands. Agric. For. Meteorol. 2021, 298, 108283. [Google Scholar] [CrossRef]
- Miro, M.E.; Groves, D.; Tincher, B.; Syme, J.; Tanverakul, S.; Catt, D. Adaptive water management in the face of uncertainty: Integrating machine learning, groundwater modeling and robust decision making. Clim. Risk Manag. 2021, 34, 100383. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Cai, X.; Huo, Z.; Zhang, C. Simulation-optimization based real-time irrigation scheduling: A human-machine interactive method enhanced by data assimilation. Agric. Water Manag. 2023, 276, 108059. [Google Scholar] [CrossRef]
- Yu, Y.; Yu, R.; Chen, X.; Yu, G.; Gan, M.; Disse, M. Agricultural water allocation strategies along the oasis of Tarim River in Northwest China. Agric. Water Manag. 2017, 187, 24–36. [Google Scholar] [CrossRef]
- Chaney, N.W.; Roundy, J.K.; Herrera-Estrada, J.E.; Wood, E.F. High-resolution modeling of the spatial heterogeneity of soil moisture: Applications in network design. Water Resour. Res. 2015, 51, 619–638. [Google Scholar] [CrossRef]
- Li, X.; Liu, F.; Ma, C.; Kristofer, L.; Bogena, H.; Mancilla, G.; Vereecken, H.; Franssen, H.J.H. Land data assimilation: Harmonizing theory and data in land surface process studies. Rev. Geophys. 2024, 62, e2022RG000801. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, X.; Funk, T.; Schumann, A.W.; Khosla, R.; Sudduth, K.A.; Drummond, S.T. A critical review for real-time continuous soil monitoring: Advantages, challenges, and perspectives. Environ. Sci. Technol. 2022, 56, 13546–13564. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, G.; Li, L.; Yang, Y.; Li, S.; Gao, Z.; Wang, J.; Sun, B.; Li, Z. A monitoring method for agricultural soil moisture using wireless sensors and the Biswas model. Agriculture 2025, 15, 344. [Google Scholar] [CrossRef]
- Kornelsen, K.C.; Coulibaly, P. Root-zone soil moisture estimation using data-driven methods. Water Resour. Res. 2014, 50, 2946–2962. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, Y.; Fan, B.; Guo, J.; Ju, Q.; Wei, C.; Zheng, H. Preferential flow influences the temporal stability of soil moisture in a headwater catchment. Geoderma 2023, 437, 116590. [Google Scholar] [CrossRef]
- Song, Y.; Mei, W.; Li, M.; Wang, L.; Sun, L.; Zhang, Y.; Liu, J.; Zhang, C. Soil water content and RubisCO activity control the carbon storage in soil under different land uses in Sanjiang Plain, China. Catena 2024, 243, 108211. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y. Spatial-temporal variability pattern of multi-depth soil moisture jointly driven by climatic and human factors in China. J. Hydrol. 2023, 619, 129313. [Google Scholar] [CrossRef]
- Togneri, R.; Dos Santos, D.F.; Camponogara, G.; Nagassaki, T.K.; Ferreira, A.S.; Nagasaki, G.K.; Marin, F.R. Soil moisture forecast for smart irrigation: The primetime for machine learning. Expert Syst. Appl. 2022, 207, 117653. [Google Scholar] [CrossRef]
- Yang, J.J.; Cai, H.J.; Wang, S.H.; Xie, H.X. Study on the relationship between shallow and deep soil moisture in Yangling area. Agric. Res. Arid Areas 2010, 3, 53–57. (In Chinese) [Google Scholar]
- Jia, S.; Cui, M.; Chen, L.; Sun, Y.; Wang, Y.; Li, C.; Feng, L.; Zhao, Q.; Zhang, H. Soybean water monitoring and water demand prediction in arid region based on UAV multispectral data. Agronomy 2024, 15, 88. [Google Scholar] [CrossRef]
- Li, Y.; Qu, T.; Wang, Y.; Zhao, Q.; Jia, S.; Yin, Z.; Guo, Z.; Wang, G.; Li, F.; Zhang, W. UAV-Based Remote Sensing to Evaluate Daily Water Demand Characteristics of Maize: A Case Study from Yuci Lifang Organic Dry Farming Experimental Base in Jinzhong City, China. Agronomy 2024, 14, 729. [Google Scholar] [CrossRef]
- Diaz-Gonzalez, F.A.; Vuelvas, J.; Correa, C.A.; Vallejo, V.E.; Patino, D. Machine learning and remote sensing techniques applied to estimate soil indicators—Review. Ecol. Indic. 2022, 135, 108517. [Google Scholar] [CrossRef]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
- Jamei, M.; Ali, M.; Karbasi, M.; Shahid, S.; Yaseen, Z.M. A high dimensional features-based cascaded forward neural network coupled with MVMD and Boruta-GBDT for multi-step ahead forecasting of surface soil moisture. Eng. Appl. Artif. Intell. 2023, 120, 105895. [Google Scholar] [CrossRef]
- Sungmin, O.; Orth, R. Global soil moisture data derived through machine learning trained with in-situ measurements. Sci. Data 2021, 8, 170. [Google Scholar] [CrossRef]
- Bakht, M.P.; Mohd, M.N.H.; Ibrahim, B.S.K.K.; Khan, N.; Sheikh, U.U.; Rahman, A.A.-H.A. Advanced automated machine learning framework for photovoltaic power output prediction using environmental parameters and SHAP interpretability. Results Eng. 2025, 25, 103838. [Google Scholar] [CrossRef]
- Nohara, Y.; Matsumoto, K.; Soejima, H.; Nakashima, N. Explanation of machine learning models using shapley additive explanation and application for real data in hospital. Comput. Methods Programs Biomed. 2022, 214, 106584. [Google Scholar] [CrossRef]
- Mitra, U.; Sarkar, P.; Mondal, J.; Shome, S.; Saha, A.; Halder, U. Enhancing interpretability in diabetics prediction: A comparative study of SHAP, LIME and permutation feature importance. In Proceedings of the 2025 AI-Driven Smart Healthcare for Society 5.0, Kolkata, India, 14–15 February 2025; IEEE: Piscataway, NJ, USA, 2025. [Google Scholar]
- Zhang, C.; Chen, Y.; Wei, Y.; Guo, Y.; Li, Y.; Sun, S.; Li, C. Unraveling the threshold and interaction effects of environmental variables on soil organic carbon mapping in plateau watershed. Geoderma 2024, 450, 117032. [Google Scholar] [CrossRef]
- Apley, D.W.; Zhu, J. Visualizing the effects of predictor variables in black box supervised learning models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2020, 82, 1059–1086. [Google Scholar] [CrossRef]
- Zhao, Q.; Hastie, T. Causal interpretations of black-box models. J. Bus. Econ. Stat. 2021, 39, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Reynolds, S.G. The gravimetric method of soil moisture determination Part III An examination of factors influencing soil moisture variability. J. Hydrol. 1970, 11, 288–300. [Google Scholar] [CrossRef]
- Zhang, Q.; Min, L.; Wang, Y.; Feng, H.; Chen, S.; Niu, Y.; Zhang, Q. Accuracies of soil moisture sensors in typical soils in the Hebei Plain. Chin. J. Eco-Agric. 2023, 31, 1851–1859. [Google Scholar]
- Eltarabily, M.G.; Mohamed, A.Z.; Begna, S.; Elshishiney, H.; Linquist, B.A. Simulated soil water distribution patterns and water use of Alfalfa under different subsurface drip irrigation depths. Agric. Water Manag. 2024, 293, 108693. [Google Scholar] [CrossRef]
- Feddes, R.A.; Hoff, H.; Bruen, M.; Dawson, T.; De Rosnay, P.; Dirmeyer, P.; Jackson, R.B.; Kabat, P.; Kleidon, A.; Lilly, A.; et al. Modeling root water uptake in hydrological and climate models. Bull. Am. Meteorol. Soc. 2001, 82, 2797–2809. [Google Scholar] [CrossRef]

| Depth Layer (cm) | Bulk Density (g/cm3) |
|---|---|
| 0–20 | 1.35 |
| 20–40 | 1.42 |
| 40–60 | 1.5 |
| 60–80 | 1.54 |
| 80–100 | 1.56 |
| 100–120 | 1.58 |
| 120–140 | 1.6 |
| 140–160 | 1.62 |
| 160–180 | 1.64 |
| 180–200 | 1.66 |
| 200–220 | 1.67 |
| 220–240 | 1.68 |
| 240–260 | 1.69 |
| 260–280 | 1.7 |
| 280–300 | 1.71 |
| Model | Parameter Settings |
|---|---|
| RandomForest | Number of trees = 100 Random state = 42 Max depth = 15 |
| LinearRegression | Default parameters |
| MLPRegressor | Hidden layer structure = (64, 32) Maximum iterations = 1000 Random state = 42 |
| Ridge | Regularization coefficient (α) = 0.1 |
| GradientBoosting | Number of trees = 200 Learning rate = 0.1 Maximum depth = 5 Random state = 42 |
| ElasticNet | Regularization coefficient (α) = 0.5 L1 ratio = 0.7 Maximum iterations = 10,000 |
| Lasso | Regularization coefficient (α) = 0.01 Maximum iterations = 10,000 |
| SVR | Kernel function = RBF C = 100 γ = 0.01 ε = 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, S.; Li, Y.; Cao, B.; Cheng, Y.; Mashori, A.S.; Bai, Z.; Cui, M.; Zhang, Z.; Deng, L.; Zhang, W. Non-Invasive Inversion and Characteristic Analysis of Soil Moisture in 0–300 cm Agricultural Soil Layers. Agriculture 2025, 15, 2143. https://doi.org/10.3390/agriculture15202143
Jia S, Li Y, Cao B, Cheng Y, Mashori AS, Bai Z, Cui M, Zhang Z, Deng L, Zhang W. Non-Invasive Inversion and Characteristic Analysis of Soil Moisture in 0–300 cm Agricultural Soil Layers. Agriculture. 2025; 15(20):2143. https://doi.org/10.3390/agriculture15202143
Chicago/Turabian StyleJia, Shujie, Yaoyu Li, Boxin Cao, Yuwei Cheng, Abdul Sattar Mashori, Zheyu Bai, Mingyi Cui, Zhimin Zhang, Linqiang Deng, and Wuping Zhang. 2025. "Non-Invasive Inversion and Characteristic Analysis of Soil Moisture in 0–300 cm Agricultural Soil Layers" Agriculture 15, no. 20: 2143. https://doi.org/10.3390/agriculture15202143
APA StyleJia, S., Li, Y., Cao, B., Cheng, Y., Mashori, A. S., Bai, Z., Cui, M., Zhang, Z., Deng, L., & Zhang, W. (2025). Non-Invasive Inversion and Characteristic Analysis of Soil Moisture in 0–300 cm Agricultural Soil Layers. Agriculture, 15(20), 2143. https://doi.org/10.3390/agriculture15202143







