Parameter Identification of Soil Material Model for Soil Compaction Under Tire Loading: Laboratory vs. In-Situ Cone Penetrometer Test Data

Abstract

Accurate numerical simulations of soil-tire interactions are essential for optimizing agricultural machinery to minimize soil compaction and enhance crop yield. This study developed and compared two approaches for identifying and validating parameters of a LS-Dyna soil model. The laboratory-based approach derives parameters from triaxial, consolidation, and cone penetrometer tests (CPT), while the optimization-based method refines them using in-situ CPT data via LS-OPT to better capture field variability. Simulations employing Multi-Material Arbitrary Lagrangian–Eulerian (MM-ALE), Smoothed Particle Hydrodynamics (SPH), and Hybrid-SPH methods demonstrate that Hybrid-SPH achieves the optimal balance of accuracy (2% error post-optimization) and efficiency (14-h runtime vs. 22 h for SPH). Optimized parameters improve soil–tire interaction predictions, including net traction and tire sinkage across slip ratios from −10% to 30% (e.g., sinkage of 12.5 mm vs. 11.1 mm experimental at 30% slip, with overall mean-absolute percentage error (MAPE) reduced to 3.5% for sinkage and 4.2% for traction) and rut profiles, outperforming lab-derived values. This framework highlights the value of field-calibrated optimization for sustainable agriculture, offering a cost-effective alternative to field trials for designing low-compaction equipment and reducing yield losses from soil degradation. While sandy loam soil at 0.4% moisture content was used in this study, future extensions to different soil types with varied moisture are recommended.

1. Introduction

Soil compaction, a critical factor in sustainable agriculture, can significantly reduce crop yield, and accurate numerical simulations are essential for predicting and mitigating compaction caused by heavy agricultural machinery. This has been a key area of research, as demonstrated by recent studies that focus on the numerical simulation of soil–tire interactions and the effect of tire parameters on soil compaction [1,2]. The reliability of such a simulation hinges on the accuracy of the soil constitutive material model and the numerical methods employed [3]. However, modeling soil behavior is complex due to its non-linear, plastic, time-dependent, and anisotropic properties, which are further influenced by environmental factors like moisture content [4].

In recent years, several soil constitutive models have been developed to capture these complex behaviors, ranging from simple elastic-plastic models like Mohr–Coulomb (MC) and Drucker–Prager (DP) to more advanced models like the Cap Plasticity (CP) model, which accounts for strain hardening in the cap region of the yield surface [5]. Parameter identification for these models has traditionally relied on laboratory tests, such as triaxial compression, hydrostatic compression, and oedometer tests, where parameters like cohesion, friction angle, and moduli are directly fitted from stress-strain data [3,4,6]. For instance, a comprehensive study on sandy loam soil [6] was performed in Abaqus software (2022HF2) (Dassault Systemes, Vélizy-Villacoublay, France), selecting a CP material model and identifying/validating parameters using experimental data from triaxial, consolidation, and cone penetrometer tests (CPT). That study compared the performance of mesh-based (Coupled Eulerian–Lagrangian, CEL) and meshless (Smoothed Particle Hydrodynamics, SPH) methods, finding that SPH better captured the granular nature of soil, achieving a 2% error in CPT simulations compared to CEL’s 20% error.

Despite these advances, the current state of parameter identification methods reveals significant limitations. Lab-based approaches, while foundational, are often expensive, time-consuming, and may not fully represent in situ soil conditions due to sample disturbance, scale effects, and environmental variability [3,7,8]. Inverse methods, such as optimization algorithms (e.g., least-squares fitting or genetic algorithms integrated with tools like LS-OPT [9,10,11,12]), have emerged to refine parameters by minimizing discrepancies between simulations and experimental data. However, just a few applications were published in the identification of soil parameters, and lack integration with field-specific tests like CPT for direct in situ calibration [3,6]. In addition, few studies have explored various non-Lagrangian approaches (e.g., meshless methods) developed recently in robust platforms like LS-Dyna 2025 R16 (ANSYS, Canonsburg, PA, USA) [13], which excels in non-linear finite element field.

To address these gaps, this study compares a (1) direct derivation for parameter identification in the MAT_005 soil model from lab tests (triaxial and consolidation) to (2) an innovative optimization-based refinement using in-situ CPT data to capture field realism better, reducing reliance on costly lab procedures [13]. In addition, soil behavior under wheel loads is simulated and compared using three LS-Dyna computational approaches (MM-ALE, SPH, and Hybrid-SPH), with Hybrid-SPH offering the best balance of accuracy (errors reduced to 2–5%) and efficiency (14-h runtime vs. 22 h for SPH). By bridging lab and field data through optimization, this work enhances innovation in sustainable farming simulations, providing a cost-effective alternative to field trials for designing low-compaction machinery.

The paper is organized as follows: Section 2 outlines the materials and methods, detailing the agricultural relevance of soil parameters, laboratory-based parameter identification (via triaxial, consolidation, and CPT tests, with numerical CPT setups using MM-ALE, SPH, and Hybrid-SPH), optimization-based in situ parameter identification, and a case study on soil-tire compaction using Hybrid FEM-SPH, building on methodologies established in [6]. Section 3 discusses results, including lab-derived parameters, triaxial and CPT simulation outcomes compared to findings in [6], optimization results, sensitivity analysis, soil–tire interaction findings, and limitations. Section 4 concludes with key findings, agricultural implications, and future research directions.

2. Materials and Methods

Material models that include stress-strain constitutive equations describe the underloading soil’s behavior. Currently, in Ls-Dyna, a few material models are available for analyzing soil under loadings, including the geologic cap model [14,15], hysteretic soil [15], and the FHWA (Federal Highway Administration) soil model [16]. These models consider pressure hardening, strain hardening, and strain rate dependency of soil material, but not all are suitable for new modeling approach elements, such as ALE and SPH [15]. Therefore, in this study, the material soil and foam (MAT_005 in LS-Dyna [15]), a robust and straightforward linearly elastic perfectly plastic model [17] based on isotropic plasticity [7], was used with a focus on simulating soil compaction under wheel loads to support agricultural engineering applications. Limitations of this model include the absence of strain hardening and softening features, but it is compatible with all Lagrangian, ALE, and SPH elements. The methodology aims to enable accurate numerical simulations that reduce the reliance on costly and time-consuming field tests, which can cost USD 5000–10,000 per trial [18], for designing low-compaction agricultural machinery and addressing soil compaction, a critical factor in sustainable farming. Two complementary approaches are employed (Figure 1). The sandy loam soil at 0.4% moisture content is used as an example. The process begins with extracting experimental data from triaxial and consolidation tests [6] and estimating parameters for MAT_005 (Figure 1a).

Numerical simulations of the triaxial test are then performed to verify the model parameters using the Lagrangian meshing method. Subsequently, CPT simulations involving extensive mesh deformation are carried out using advanced meshing techniques such as MM-ALE, SPH, and Hybrid-SPH to validate the parameters against experimental data. The second approach focuses on parameter identification directly from in situ CPT test data (Figure 1b). This approach uses an optimization-based method to determine the model parameters using FE simulation with a Hybrid FEM-SPH model. Finally, the material models with optimized parameters are used in CPT simulations using different soil modelling approaches. They were applied in a practical agricultural case study to simulate soil compaction under tractor wheel loads, demonstrating their utility in replacing field trials.

2.1. Agricultural Relevance of the Soil Parameters

Key soil parameters for the MAT_005 model (

Table 1. Agricultural relevance of parameters for sandy loam soil.

Parameter	Description	Agricultural Impact
c	Cohesion	Reduces compaction depth
φ	Friction Angle	Influences the load-bearing capacity
G	Shear Modulus	Affects traction and compaction extent
K	Bulk Modulus	Govern compaction depth under wheels
ε, P	Volumetric-Strain, Pressure	Impacts density increases under compressive loads

), critical for modeling soil compaction under wheel loads, are determined through experimental tests and optimized via simulations to enhance machinery performance and soil health. Cohesion (c) governs soil shear strength, influencing resistance to compaction. The compaction depth is reduced by enhancing soil cohesion, critical for minimizing soil damage under wheel loads [3]. Friction Angle (φ) affects load-bearing capacity, impacting the soil’s ability to support heavy machinery without excessive compaction [3]. Shear Modulus $\left(G\right)$ controls soil stiffness under shear, influencing tire traction and compaction extent. Higher G increases resistance to deformation but may increase compaction under heavy loads [2]. Bulk Modulus $\left(K\right)$ dictates soil compressibility directly affecting compaction depth and bulk density increase under wheel loads. Lower K reduces compaction depth by up to 15% [1]. Volumetric Strain Hardening (ε, P) is derived from consolidation tests this reflects soil response to compressive loads, modulating density increase under wheel-induced compaction [19]. Finally, it is important to note that the shear strength parameters of soil are strongly influenced by its water content. Cohesion $\left(c\right)$ typically exhibits a non-monotonic trend with increasing moisture—initially rising as water promotes capillary bonding and apparent cohesion, then decreasing beyond the optimum water content due to elevated pore pressures and loss of matric suction [20,21,22]. Conversely, the internal friction angle (φ) generally decreases with increasing water content, reflecting the reduction in interparticle friction as lubrication and water film thickness increase between soil grains [23,24]. Consequently, at lower moisture levels—such as around 0.4% in the present study, both $c$ and $\phi$ are relatively elevated, resulting in greater soil resistance to compaction compared with wetter states, where cohesion and friction are weakened. Similar moisture-dependent behaviors have been widely reported for sandy loam and clayey soils under varying compaction degrees and drying–wetting cycles [22].

These parameters are derived and validated through the two approaches below and applied in a case study (Section 2.4) to simulate soil compaction under wheel loads, ensuring practical value for agricultural engineering.

2.2. Lab Testing Approach: Parameter Identification

Triaxial and consolidation tests were conducted on sandy loam soil (73% sand, 27% silt, 0% clay) from the Norfolk region of Virginia, USA, at a moisture content of 0.4%, consistent with the experimental setup described in [6]. The soil was classified as Silty Loam (SL) per the USDA soil classification triangle [14]. The soil’s natural moisture content is 0.4%, and its maximum dry density is 1923 kg/m³.

2.2.1. Triaxial Test

To determine the shear strength parameters of sandy loam soil for use in LS-DYNA simulations with the MAT_005 model, experimental data from unconsolidated-undrained (UU) triaxial tests were utilized [6]. UU triaxial tests are often preferred for studying the shear strength of unsaturated soils due to their cost and time effectiveness [15]. A cylindrical soil specimen was prepared at specified compaction and moisture levels. The specimen was subjected to predetermined confining pressures, followed by a deviator (shearing) load applied vertically at a strain rate of 12.5%/min (Figure 2). The 12.5%/min strain rate was chosen to approximate the soil deformation rate under typical agricultural wheel loading, corresponding to fast but quasi-static compaction during tire passage. Previous studies have shown that this rate captures soil strength parameters without introducing significant rate-dependent effects, making it representative of machinery-induced loading conditions [15,19,25,26]. The tests were performed per ASTM D2850 [27] using Loadtrac 2 testing equipment (Geocomp Inc., Atlanta, GA, USA). These tests provide critical parameters such as cohesion (c) and friction angle (φ), which are derived by plotting Mohr circles based on the test results [16].

The stress–strain data defined the MAT_005 model’s parameters, ensuring consistency with the experimental conditions [6]. These parameters were further verified through numerical simulations of the triaxial test. The numerical simulation of the triaxial test was performed using the Lagrangian method in LS-DYNA software (LSTC, Livermore, CA, USA) [13]. To replicate the experimental triaxial test conditions, a complete three-dimensional cylindrical soil specimen with a radius of 50 mm and a height of 220 mm is modeled (Figure 3). The Lagrangian meshing approach is adopted since the triaxial test involves small to moderate deformations, where large deformation processes are not dominant, making this method suitable for accurately capturing material behavior [7]. Following LS-DYNA best practices, the model is discretized using a structured mesh of 8-node solid elements (hexahedral elements), with sufficient refinement to ensure numerical accuracy and computational efficiency [13]. The bottom boundary of the specimen is fixed in the vertical direction $(u_z=0)$ to prevent rigid body motion, the lateral and bottom surfaces are subjected to a confining pressure of 5 psi to simulate the isotropic consolidation phase, consistent with established soil modeling techniques [8,28].

The simulation is conducted in two stages, consistent with standard triaxial test procedures. In the first stage, the confining pressure of 5 psi is applied uniformly to the bottom and lateral surfaces of the cylindrical specimen. In the second stage, a downward axial velocity $(-u_z)$ corresponding to a strain rate of 12.5%/min is imposed on the top surface until an axial strain of 15% is reached. The axial stress–strain response is computed throughout the simulation, and the numerical results are compared with both the experimental data and the results from the Critical State Plasticity (CP) model, as reported in [6]

2.2.2. Consolidation Test

One-dimensional consolidation tests were utilized to study the compressibility of sandy loam soil and obtain pressure–volumetric strain data for the MAT_005 model in LS-DYNA. These tests are essential for defining the hardening behavior of elastic-plastic constitutive material models (Figure 4). Cylindrical soil specimens were prepared and enclosed in a metal ring, then subjected to incremental static loads as per ASTM D2435 [29] using Loadtrac 3 testing equipment (Geocomp Inc., Atlanta, GA, USA) [6].

The parameters for the MAT_005 model in LS-DYNA were derived using a systematic procedure adapted from the Cap Plasticity (CP) model parameters [6], which consists of the following steps (Figure 5):

(1) Obtained Principal Stresses from Triaxial Test Results: Unconsolidated-undrained triaxial test data at confining pressures of 5 psi [6] were used to determine the principal stresses (${\sigma }_1, {\sigma }_2, {\sigma }_3$) for the sandy loam soil at 0.4% moisture content.

(2) Draw Mohr Circles and Fit Tangent Line to All Circles: Mohr circles were constructed for each confining pressure using the principal stresses. A best-fit straight line was drawn as the tangent to all Mohr circles, representing the Mohr–Coulomb failure envelope.

(3) Obtain Cohesion ($c$) as Y-Intercept and Friction Angle ($\varnothing$) as Slope: From the Mohr–Coulomb failure envelope, the y-intercept provided the cohesion ($c=0.023 \mathrm{M}\mathrm{P}\mathrm{a}$), and the slope gave the friction angle ($\varnothing = {59.5}^{°}$) consistent with the values reported by [6] for 0.4% moisture content.

(4) Calculate $A_0, A_1, A_2$ for MAT_005 via Yield Function Comparison: The MAT_005 model in LS-DYNA employs a Drucker–Prager yield function to describe the plastic behavior of soil [14], so on the yield surface:

$$J_2= A_0+A_1 P+ A_2{P}^2$$

(1)

where $J_2$ is the second invariant of the stress deviator, $p$ is the hydrostatic pressure (positive in compression), and $A_0,$ $A_1$ and $A_2$ are yield function constants. These constants were derived by mapping the Mohr–Coulomb failure envelope, obtained from triaxial test data to the Drucker–Prager yield surface using the analytical algorithm by [30]. The derivation leverages the relationship between principal stresses $({\sigma }_1, {\sigma }_2)$ from unconsolidated–undrained (UU) triaxial tests and the Mohr–Coulomb shear strength parameters.

Mathematical Derivation:

The Mohr–Coulomb failure criterion defines the shear strength of soil as $\tau =c+\sigma \tan \phi$ where $\tau$ is the shear stress, $\sigma$ is the normal stress, $c$ is cohesion, and $\phi$ is the internal friction angle. In a triaxial compression test, the principal stresses are ${\sigma }_1$ (vertical, major) ${\sigma }_3$ (horizontal, confining, minor), with ${\sigma }_2={\sigma }_3$. At failure, the shear and normal stresses on the failure plane are related to the principal stresses by [31]:

$$\tau = {\displaystyle \frac{{\sigma }_1- {\sigma }_2}{2}} \cos \phi$$

(2)

$$\sigma =\left({\displaystyle \frac{{\sigma }_1+{\sigma }_3}{2}}-{\displaystyle \frac{{\sigma }_1-{\sigma }_3}{2}}\right)\sin \phi$$

(3)

The hydrostatic pressure $p$ is defined as:

$$p= {\displaystyle \frac{1}{3}} ({\sigma }_1+2{\sigma }_3)$$

(4)

The Mohr–Coulomb failure envelope can be expressed in terms of principal stresses using the classic relationship for triaxial compression [1]:

$${\sigma }_3= {\sigma }_1{\tan \left( {45}^{°}- {\displaystyle \frac{\phi }{2}}\right)}^2 -2c\tan \left( {45}^{°}- {\displaystyle \frac{\phi }{2}}\right)$$

(5)

Rearrange to express the stress difference:

$${\sigma }_1- {\sigma }_3= {\sigma }_1-\left[ {\sigma }_1 {\tan \left( {45}^{°}-{\displaystyle \frac{\phi }{2}}\right)}^2-2c\tan ({45}^{°}- {\displaystyle \frac{\phi }{2}}\right)]$$

(6)

$${\sigma }_1-{\sigma }_3={\sigma }_1\left[ 1-{\tan \left( {45}^{°}-{\displaystyle \frac{\phi }{2}}\right)}^2\right]+2c\tan \left( {45}^{°}-{\displaystyle \frac{\phi }{2}}\right)$$

(7)

Define intermediate variables:

$$C=1-{\tan \left( {45}^{°}-{\displaystyle \frac{\phi }{2}}\right)}^2$$

(8)

$$D=2c\tan \left( {45}^{°}-{\displaystyle \frac{\phi }{2}}\right)$$

(9)

Thus:

$${\sigma }_1- {\sigma }_3=C{\sigma }_1+D$$

(10)

express $p$ in terms of ${\sigma }_1$:

$$p= {\displaystyle \frac{1}{3}}{\sigma }_1+ {\displaystyle \frac{2}{3}}{\sigma }_3$$

(11)

Substitute ${\sigma }_3= {\sigma }_1{\tan \left( {45}^{°}- {\displaystyle \frac{\phi }{2}}\right)}^2 -2c\tan \left( {45}^{°}- {\displaystyle \frac{\phi }{2}}\right)$:

$$p= {\displaystyle \frac{1}{3}}{\sigma }_1+{\displaystyle \frac{2}{3}} [{\sigma }_1{\left( {45}^{°}-{\displaystyle \frac{\phi }{2}}\right)}^2-2c\tan \left( {45}^{°}-{\displaystyle \frac{\phi }{2}}\right)]$$

(12)

$$p= {\sigma }_1 \left[{\displaystyle \frac{1}{3}}+{\displaystyle \frac{2}{3}} {\tan \left( {45}^{°}-{\displaystyle \frac{\phi }{2}}\right)}^2\right]-{\displaystyle \frac{4}{3}} c\tan \left( {45}^{°}-{\displaystyle \frac{\phi }{2}}\right)$$

(13)

Define:

$$A= {\displaystyle \frac{1}{3}}+{\displaystyle \frac{2}{3}} {\tan \left( {45}^{°}- {\displaystyle \frac{\phi }{2}}\right)}^2$$

(14)

$$B={\displaystyle \frac{4}{3}}c\tan \left( {45}^{°}-{\displaystyle \frac{\phi }{2}}\right)$$

(15)

$$p=A{\sigma }_{1 }-B$$

(16)

Solve for ${\sigma }_1$:

$${\sigma }_1={\displaystyle \frac{p+B}{A}}$$

(17)

Substitute into the stress difference equation:

$${\sigma }_1-{\sigma }_3=C\left({\displaystyle \frac{p+B}{A}}\right)+D= {\displaystyle \frac{C}{A^p}}+ {\displaystyle \frac{CB}{A}}+D$$

(18)

Define:

$$\alpha = {\displaystyle \frac{C}{A}}$$

(19)

$$\beta ={\displaystyle \frac{CB}{A}}+D$$

(20)

$${\sigma }_1-{\sigma }_3=\alpha p+\beta$$

(21)

In triaxial compression, the second invariant $J_2$ is related to the stress difference [32]:

$$J_2= {\displaystyle \frac{1}{3}} {({\sigma }_1-{\sigma }_3)}^2$$

(22)

$$J_2={\displaystyle \frac{1}{3}} {(\alpha p+\beta )}^2$$

(23)

Expand:

$${(\alpha p+\beta )}^2= {\alpha }^2{p}^2+2\alpha \beta p+ {\beta }^2$$

(24)

$$J_2={\displaystyle \frac{1}{3}}{\alpha }^2{p}^2+{\displaystyle \frac{2}{3}}\alpha \beta p+{\displaystyle \frac{1}{3}}{\beta }^2$$

(25)

Comparing Equations (1) and (25) we get:

$$A_0= {\displaystyle \frac{1}{3}}{\beta }^2$$

(26)

$$A_1={\displaystyle \frac{2}{3}}\alpha \beta$$

(27)

$$A_2={\displaystyle \frac{1}{3}}{\alpha }^2$$

(28)

(5) Define Stress vs. Volumetric Strain for Hardening from Consolidation Test Results: The consolidation test results provided the stress vs. volumetric plastic strain data, which defines the hardening behavior of MAT_005. This data was adapted from the cap hardening curve of the CP model [6].

2.2.3. Cone Penetrometer Test (CPT)

Cone penetrometer tests (CPTs) were employed (1) to characterize the in-situ behavior of sandy loam soil, providing data to validate the LS-DYNA simulations using the MAT_005 model (parameter identification: lab testing approach), and (2) to be used in the parameter identification using FE simulation-based optimization (approach 2). The CPTs [6] were conducted using an HS-4210 digital static cone penetrometer instrument (Humboldt, Elgin, IL, USA), a 30-degree cone with a base diameter of 0.5 in. (Figure 6). The device recorded the cone resistance force required to penetrate the ground. Soil samples were prepared and compacted to match the conditions of the triaxial and consolidation tests (Figure 6). The penetration was performed at a rate of 20 mm/s to a depth of 150 mm, and the maximum resistance experienced by the cone was recorded.

2.2.4. Numerical Setup of CPT Simulations

CPT simulations were performed using three numerical methods in LS-DYNA (version 16.0 solver ls-dyna_mpp_s_R16_0_0_x64): Multi-Material Arbitrary Lagrangian–Eulerian (MM-ALE), Smoothed Particle Hydrodynamics (SPH), and Hybrid-SPH. The cone penetrometer geometry was modeled as a rigid body with dimensions consistent with [6] and a penetration rate of 20 mm/s was applied to a depth of 150 mm. The soil was modeled using the MAT_005 material model with identified parameters. The setups for each method are detailed below, with key parameters summarized in Table 2, Table 3 and Table 4. The mesh characteristics used in parameter identification were derived from mesh convergence studies (Appendix A).

The Multi-Material Arbitrary Lagrangian–Eulerian (MM-ALE) Setup: The MM-ALE method modeled the soil as a multi-material Eulerian domain to capture large deformations during cone penetration [33,34]. The framework used a Lagrangian mesh for the cone penetrometer and an Eulerian mesh for the soil and air (defined with MAT_140_VACUUM) [35]. Soil and air domains used ELFORM = 11 (1-point ALE multi-material element) for multi-phase interactions [33]. A fine mesh (Figure 7a) ensured accurate soil-cone interaction [36]. Contact was modeled with CONSTRAIN_LAGRANGE_IN _SOLID (CTYPE = 4, DIREC = 2), active in compression, with optimized penalty stiffness (negative PFAC) and coupling forces extracted from DBFSI files, aligning with [37]. Fixed lateral and bottom boundaries (Figure 7b) prevented spurious deformations, per [38]. The setup parameters are in Table 2.

Table 2. Setup parameters for MM-ALE CPT simulation.

Parameter	Value	Source
Soil Domain Size (mm)	100 × 100 × 220	Domain study (Appendix A)
Vacuum Domain Size (mm)	100 × 100 × 30	Domain study (Appendix A)
Number of Elements	300,000	Convergency study (Appendix A)
Coefficient of Friction	0.3	[19]
Cone Penetration Velocity (mm/s)	20	[39]

Table 2. Setup parameters for MM-ALE CPT simulation.

Parameter	Value	Source
Soil Domain Size (mm)	100 × 100 × 220	Domain study (Appendix A)
Vacuum Domain Size (mm)	100 × 100 × 30	Domain study (Appendix A)
Number of Elements	300,000	Convergency study (Appendix A)
Coefficient of Friction	0.3	[19]
Cone Penetration Velocity (mm/s)	20	[39]

Table 3. Setup parameters for SPH CPT simulation.

Parameter	Value	Source
Soil Domain Size (mm)	140 × 140 × 220	Domain study (Appendix A)
Encasement Material	Steel	Domain study (Appendix A)
Encasement Thickness (mm)	5	Domain study (Appendix A)
Number of SPH Particles	350,000	Convergency study (Appendix A)
Coefficient of Friction	0.3	[19]
Cone Penetration Velocity (mm/s)	20	[39]

Table 3. Setup parameters for SPH CPT simulation.

Parameter	Value	Source
Soil Domain Size (mm)	140 × 140 × 220	Domain study (Appendix A)
Encasement Material	Steel	Domain study (Appendix A)
Encasement Thickness (mm)	5	Domain study (Appendix A)
Number of SPH Particles	350,000	Convergency study (Appendix A)
Coefficient of Friction	0.3	[19]
Cone Penetration Velocity (mm/s)	20	[39]

Table 4. Setup parameters for Hybrid-SPH CPT simulation.

Parameter	Value	Source
SPH Soil Domain Size (mm)	70 × 70 × 220	Domain study (Appendix A)
Lagrangian Domain Size (mm)	140 × 140 × 240	Domain study (Appendix A)
Number of SPH Particles	350,000	Convergency study (Appendix A)
Solid Elements	33,000	Convergency study (Appendix A)
Coefficient of Friction	0.3	[19]
Cone Penetration Velocity (mm/s)	20	[39]

Table 4. Setup parameters for Hybrid-SPH CPT simulation.

Parameter	Value	Source
SPH Soil Domain Size (mm)	70 × 70 × 220	Domain study (Appendix A)
Lagrangian Domain Size (mm)	140 × 140 × 240	Domain study (Appendix A)
Number of SPH Particles	350,000	Convergency study (Appendix A)
Solid Elements	33,000	Convergency study (Appendix A)
Coefficient of Friction	0.3	[19]
Cone Penetration Velocity (mm/s)	20	[39]

SPH Setup: The Smoothed Particle Hydrodynamics (SPH) method was used to model soil granular behavior and large deformations during cone penetration, as validated by [33]. The soil domain, encased in a rigid steel modeled with solid elements, used CONTACT_AUTOMATIC_NODE_TO_SURFACE in LS-DYNA for robust soil-encasement and soil-cone interactions, following [40]. The cone penetrometer was a rigid body with solid elements. The soil was discretized with 350,000 SPH particles (uniform radius, Figure 8a) for high-resolution deformation capture. For stability, fixed boundary conditions, adapted from [41], were applied to the encasement (Figure 8b). Table 3 summarizes the setup parameters (domain size, encasement thickness, friction, penetration velocity).

Hybrid-SPH Setup: The Hybrid-SPH method integrates SPH particles with Lagrangian elements to balance computational efficiency and accuracy in modeling soil behavior during cone penetration, as inspired by [33]. The outer soil domain was modeled with Lagrangian solid elements (geometry per Table 3), while the inner region (60 mm × 60 mm × 220 mm) was replaced with 350,000 SPH particles (Figure 9a). The SPH and Lagrangian regions were coupled using CONTACT_AUTOMATIC_NODE_TO_SURFACE_TIE in LS-DYNA for robust interaction, following [40]. The combined soil domain interacted with a rigid cone penetrometer (solid elements) via CONTACT_AUTOMATIC_NODE_TO_SURFACE. Boundary conditions fixed the lateral and bottom surfaces of the domain (Figure 9b), aligning with [41] for stability. Table 4 summarizes setup parameters, including domain sizes, SPH particle count, friction coefficient, and penetration velocity.

2.3. Optimization Approach: Parameter Identification

An optimization study was conducted using LS-OPT (Ansys, Canonsburg, PA, USA) to calibrate soil model parameters against in situ CPT data [18]. The goal was to minimize the deviation of the simulated vertical force on the cone penetrometer from the experimental cone resistance force vs. penetration depth corridor, ensuring the simulated force remains within the experimental bounds. The soil was modeled using a Hybrid-Lagrangian-SPH approach, which effectively managed large deformations [6]. The cone penetrometer was modeled with a Lagrangian approach and assigned an initial velocity corresponding to a drop height of 150 mm.

2.3.1. Design Variables and Fixed Parameters

The design variables in this study include the cohesion ($c$), friction angle ($\phi$), shear modulus ($G$), and bulk modulus for loading (K), with variable ranges derived from laboratory test data and literature for sandy loam, consistent with cohesive soil parameters from [32] (

Table 5. Design variables used for sensitivity study (units: mm-s-tone).

Design Variable	Description	Initial Value	Lower Bound	Upper Bound	Source
$\mathit{G}$	Shear modulus of the soil	3.23	3.0	6.00	[32]
$\mathit{K}$	Bulk modulus of the soil	8.17	7.00	15.00	[42]
$\mathit{c}$	Cohesion	0.0213	0.018	0.03	[43]
$\mathit{\phi }$	Friction angle	${42.5}^{°}$	${42.0}^{°}$	${71.4}^{°}$	[44]

). The yield function constants $A_0, A_1, and A_2$ are then computed as dependent variables using expressions derived using the values of c and $\phi$ (Equations (26)–(28)). These ranges were estimated by varying c and $\phi$ within their defined limits, and the dependent variables are dynamically updated in the LS-DYNA simulation as ϕ and c change during optimization.

2.3.2. Optimization Methodology

A Latin Hypercube Sampling (LHS) Design of Experiments (DOE) scheme was employed to generate 43 sampling points, selected based on a LS-Opt guideline of approximately 10–11 samples per design variable (here, four variables: cohesion, friction angle, shear modulus, bulk modulus) to ensure sufficient coverage for an accurate elliptical metamodel while minimizing computational expense [32,42,43,44]. LS-DYNA simulations were conducted corresponding to a maximum penetration depth of 150 mm

The composite objective function quantifies the deviation of the simulated vertical force from a target corridor of 150–200 N, derived from the mean range (± standard deviation) of multiple in situ CPT tests on sandy loam soil (0.4% moisture) as reported in [6], starting from a penetration depth of 50 mm to 150 mm in 5 mm increments, and is expressed as:

$$err=\sum {( CTP\_fotrce(d)-175)}^2$$

No additional constraints are imposed, providing flexibility to align the simulated force within the specified corridor. A final Cone Penetration Test (CPT) simulation was performed in LS-DYNA using the optimized soil model parameters (variables $c$, $\phi$, $G$,$K$ and dependent variables $A_0, A_1, A_2$) to check the calibrated model against the experimental force corridor.

2.4. Case Study: Soil Compaction Simulation Using Hybrid FEM-SPH

This section describes the rigid tire geometry discretization, model preparation, and numerical setup used to simulate agricultural soil compaction under wheel loading with the identified MAT_005 parameters. The simulations focus on a 3 kN normal load with slip ratios ranging from −10% to 30% to enable a comprehensive comparison with the experimental results for soil-tire interaction.

2.4.1. Tire Geometry and FE Discretization

The geometry and FE model of the non-pneumatic tire used in this study were prepared in three steps. First, the tire was scanned with an 3D Einstar handheld scanner to capture tread lugs and shoulder details. The reconstructed geometry was cleaned (hole filling, smoothing only on non-critical surfaces) and rebuilt into a watertight solid in Altair HyperMesh. Finally, the tire model was discretized (

Table 6. Tire geometry and FE discretization.

Parameter	Dimensions (mm)
Tire diameter	720
Tire width	254
Lug height	37
Lug width	45
Number of Lugs	22
Hex mesh size	10
Total elements	50,632

) with hexahedral elements and exported for use in LS-DYNA where it was modeled as rigid to reduce computational time and focus on soil response.

2.4.2. Numerical Simulation Setup

To investigate the soil compaction under the tire of agricultural machinery, the soil was modeled using a Hybrid FEM–SPH soil approach, which captures large deformation beneath the tire while keeping the far field efficient. The tire acts as a rigid body with prescribed translation and rotation to realize the target slip ratio [45]. For both soil material parameter sets (lab-based and optimized), each simulation follows the same three-stage procedure for the normal load and various slip ratios. First, gravity is applied to the soil domain to establish in-situ stresses and allow settlement. Second, the prescribed normal load is ramped onto the rigid tire, and contact is stabilized. Third, longitudinal translation $V_y$ and rotation $\omega$ are imposed simultaneously to realize the target driving slip $s$ using $\omega = {\displaystyle \frac{v_y}{R(1-s)}}$.

All model settings used in these steps—including soil domain size, contact friction, $V_{\mathrm{y}}$, s, applied normal load, and the resulting ω are summarized in

Table 7. Setup parameters for Soil-Rigid Tire Interaction Simulation.

Parameter	Value	Source
SPH Soil Domain Size (mm)	2220 × 320 × 200	Domain study (Appendix A)
Lagrangian Domain Size (mm)	2200 × 750 × 240	Domain study (Appendix A)
Number of SPH Particles	500,000	Convergency study (Appendix A)
Solid Elements	300,000	Convergency study (Appendix A)
Applied Longitudinal Velocity, ${\mathit{V}}_{\mathit{y}}$	138 mm/s	[45]
Friction coefficient soil-tire	0.23	[45]
Target slip ratios (driving)	−10% to 30%	[45]
Applied normal load on the tire	3 kN	[45]

. The boundary condition and domain discretization are also shown (Figure 10). The contact area, normal and shear contact forces, net traction, and tire sinkage history plots are extracted from the numerical simulations.

The simulation evaluates key performance indicators in tire–soil interaction, including net traction, tire sinkage, stress distribution, and plastic strain, with a focus on comparing the predictive accuracy of lab-tested soil parameters (Soil-A) and optimized parameters (Soil-B) under a 3 kN normal load across slip ratios from −10% to 30%. Traction represents the contribution of the motion resistance force governed by soil shear strength and the friction force at the tire–soil interface. For the driving mode (positive slip ratio), friction contributes positively to net traction, while its sensitivity to slip ratio remains moderate. Motion resistance increases with shear strain until reaching peak soil strength, after which it stabilizes, influencing the net traction trend.

3. Results and Discussion

3.1. Lab Testing Approach: Identified Parameters and Simulation Results

This section presents the results of the laboratory-based approach for identifying and verifying the parameters of the MAT_005 model in LS-DYNA, tailored for sandy loam soil at 0.4% moisture content. Subsequent numerical simulations of triaxial and cone CPT tests verify these parameters [6].

3.1.1. Identified Parameters of Soil Constitutive Material Model

Following the methodology outlined previously (Figure 5), the parameters for the MAT_005 model in LS-DYNA were derived from triaxial and consolidation tests (the laboratory testing approach) (Table 8). The hardening behavior, defined by volumetric strain (ε1, ε2, …) and corresponding pressures (P1, P2, …), were obtained from the consolidation test data (Figure 10). These parameters provide a robust foundation for the MAT_005 model to simulate the elastic-plastic response of sandy loam soil in triaxial and cone penetrometer test (CPT) simulations, as discussed in subsequent sections. The parameters effectively capture the soil’s mechanical behavior, although the model’s limitations, such as the lack of strain softening, may influence its performance in specific failure scenarios.

Table 8. Identified parameters for MAT_005 at 0.4% moisture content (units mm-s-tone).

Parameter	Description	Value	Source
ρ	Mass density	1845.3 × 10−9	Triaxial Test
G	Shear Modulus	4.23	Calculated from $E$ and $\mu$
K	Bulk modulus	9.17	Calculated from $E$ and $\mu$
A0	Yield function constant	0.0003566	Triaxial Test
A1	Yield function constant	0.05279	Triaxial Test
A2	Yield function constant	1.905	Triaxial Test
PC	Pressure cutoff for tensile fracture (<0)	−0.0328	Adapted from Cap Hardening
VCR	Volumetric crushing option	0.0 (on)
REF	Use reference geometry to initialize pressure	0.0 (off)	Triaxial Test
ε1 …	Volumetric strain values	See Figure 11	Triaxial Test
P1 …	Pressure corresponding to volumetric strain	See Figure 11	Triaxial Test

Table 8. Identified parameters for MAT_005 at 0.4% moisture content (units mm-s-tone).

Parameter	Description	Value	Source
ρ	Mass density	1845.3 × 10−9	Triaxial Test
G	Shear Modulus	4.23	Calculated from $E$ and $\mu$
K	Bulk modulus	9.17	Calculated from $E$ and $\mu$
A0	Yield function constant	0.0003566	Triaxial Test
A1	Yield function constant	0.05279	Triaxial Test
A2	Yield function constant	1.905	Triaxial Test
PC	Pressure cutoff for tensile fracture (<0)	−0.0328	Adapted from Cap Hardening
VCR	Volumetric crushing option	0.0 (on)
REF	Use reference geometry to initialize pressure	0.0 (off)	Triaxial Test
ε1 …	Volumetric strain values	See Figure 11	Triaxial Test
P1 …	Pressure corresponding to volumetric strain	See Figure 11	Triaxial Test

Figure 11. Consolidation compression test data for Sandy Loam [6].

Figure 11. Consolidation compression test data for Sandy Loam [6].

3.1.2. Triaxial Test Simulation Results

The triaxial test simulations were performed to verify the identified parameters of the MAT_005 model at a confining pressure of 5 psi, matching the experimental conditions reported [6]. The deviator stress versus axial strain plot (Figure 12) indicates that the MAT_005 model captures the brittle failure behavior observed in the experimental results, consistent with the CP model’s performance in our previous study in Abaqus [6]. However, the MAT_005 model underpredicts the peak deviator stress by approximately 6% compared to the experimental mean, with experimental data showing a standard deviation of 0.038, Cap-Plasticity [6] at 0.050680432, and MAT_005 at 0.052323652, and overall simulation errors ranging from 0–6%. This underprediction is attributed to the simplified yield function in MAT_005, which lacks strain-hardening and softening mechanisms, unlike the CP model that better captures complex behavior in the cap region [5,6]. Despite this, the overall stress–strain trend aligns well with the experimental data, confirming the reliability of the identified parameters for simulating triaxial test conditions in LS-Dyna.

3.1.3. Initial CPT Simulation Results (with Experimental Data)

The cone resistance force as a function of penetration depth, obtained from CPT simulations using the MM—ALE, SPH, and Hybrid—SPH numerical methods with the MAT_005 model, was compared against experimental data and CP model results from a previous study [6] results. The results reveal distinct performance differences among the methods. The MM—ALE results of the MAT_005 model are compared with the results of another meshed method (CEL) [6], which used the CP model (Figure 13a). The slightly better performance of MM—ALE (15% error) over CEL (20% error) may be attributed to differences in contact formulations and mesh handling between LS—DYNA and Abaqus. The Hybrid-SPH method provided the best balance of accuracy and computational efficiency. The cone resistance force versus penetration depth obtained with the SPH method and the MAT_005 model (this study) was compared with the SPH results with the CP model [6] (Figure 13b). Both meshless models predict cone resistance forces within the experimental corridor, with the MAT_005 model achieving a 5% error and the CP model a 2% error, as reported by [6]. The close agreement suggests that the MAT_005 model, when paired with the SPH method, effectively captures the granular behavior of sandy loam soil during penetration.

Finally, the cone resistance force across all three numerical methods (MM—ALE, SPH, and Hybrid—SPH) in LS-Dyna was compared with the experimental force corridor (Figure 13c). The meshless methods (SPH and Hybrid—SPH) predict forces within the experimental corridor, with 5% and 4% errors, respectively. In contrast, the meshed techniques, such as the MM—ALE method, predict the resistance force with a 15% error. This discrepancy is likely due to MM—ALE’s mesh-based nature, which struggles to capture localized granular behavior compared to the meshless SPH methods.

The stress and strain distributions during the CPT simulations provide insight into the soil’s behavior under penetration. The contour plot of the equivalent elastic-plastic strain for the MM—ALE (Figure 14a), SPH (Figure 14b), and Hybrid—SPH (Figure 14c) methods is presented (Figure 14). The SPH and Hybrid-SPH methods exhibit more localized plastic strain around the cone tip, consistent with the granular nature of sandy loam soil, as noted by [6]. In contrast, the MM—ALE method shows a more diffuse distribution of strain, which aligns with its tendency to overpredict cone resistance force due to less accurate modeling of localized deformation. The contour plot of the stress in the Z-direction (S33) for the three methods was also presented (Figure 15). The SPH (Figure 15b) and Hybrid-SPH (Figure 15c) methods predict a more concentrated stress bulb beneath the cone tip than the MM-ALE (Figure 15a) method, indicating better soil compaction and contact area representation at the cone–soil interface.

3.2. Optimization Approach: Identified Parameters and Sensitivity Analysis

3.2.1. Optimization Results

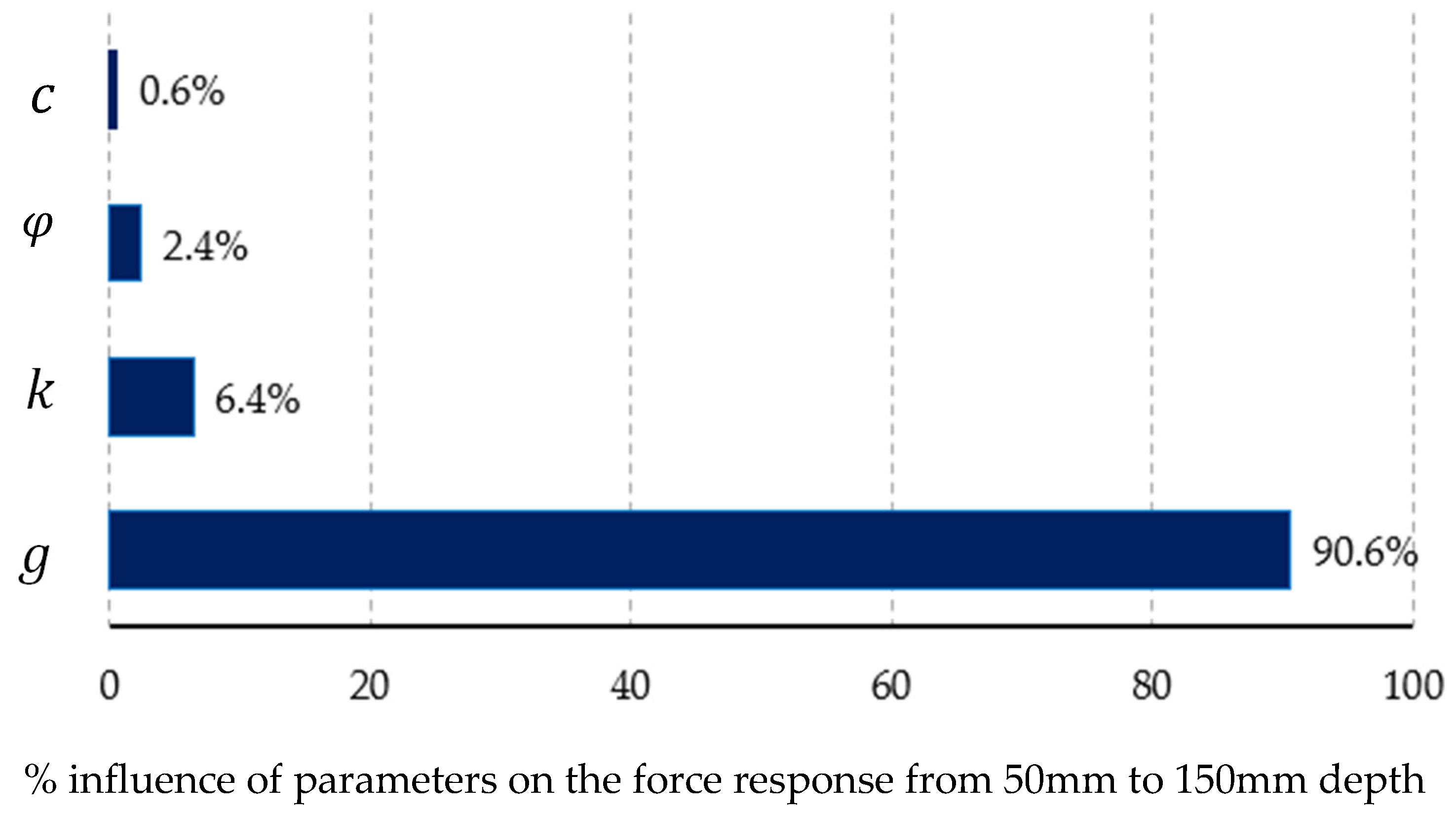
The sensitivity analysis (Figure 16) revealed that the shear modulus (G) was the most influential parameter on the composite output (force—penetration response described in Section 2.2.2), contributing 90.6% to the variation in the cone resistance force. This was followed by bulk modulus (K) with 6.4% influence, the angle of friction parameter ($\phi$) with 2.4%, and cohesion (c) with a minimal impact of 0.6%.

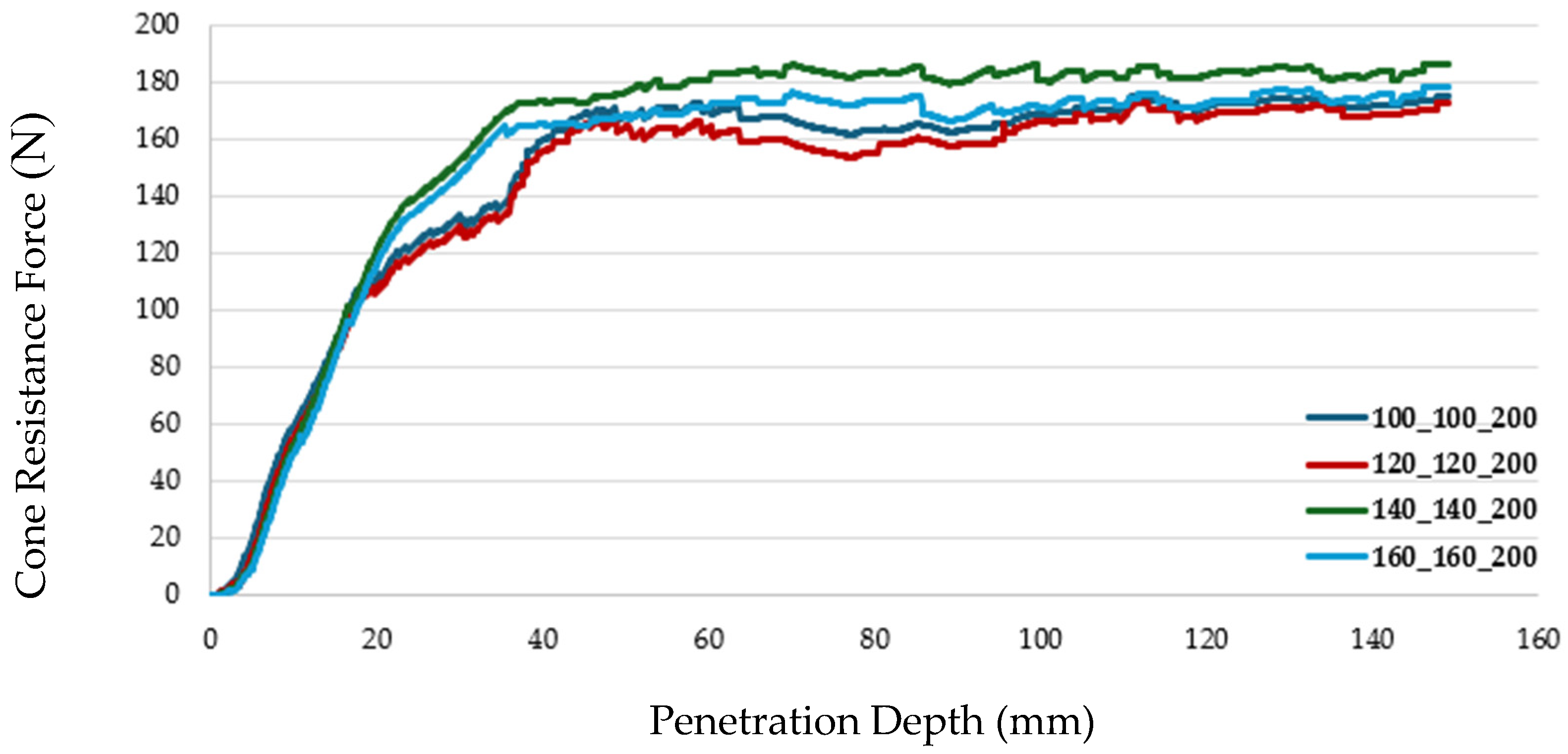
The optimized parameters (

Table 9. Optimized parameters vs. experimental parameters for MAT_005 at 0.4% moisture.

Parameter	Description	Approach 2	Approach 1	Diff. (%)
G	Shear Modulus	4.283	4.231	+1.2
K	Bulk modulus	9.167	9.173	−0.065
$\mathit{\phi }$	Friction angle	${54.73}^{°}$	${59.5}^{°}$	−8
$\mathit{c}$	Cohesion	0.02006	0.023	−12.8
${\mathit{A}}_{\mathbf{0}}$	Yield function constant	0.000356	0.0003566	−0.2
${\mathit{A}}_{\mathbf{1}}$	Yield function constant	0.05276	0.05279	−0.1
${\mathit{A}}_{\mathbf{2}}$	Yield function constant	1.678	1.905	−11.916

) included a 0.057% increment in A₁, a 0.168% reduction in A₀, a 1.229% increase in G, and a 0.065% reduction in K. Additionally, φ was reduced by 8.017%, c by 12.8%, and A₂ by 11.916%. These parameter adjustments significantly improved the model’s ability to capture the peak cone resistance force, enhancing the agreement between the finite element simulation and the experimental force corridor across the 150 mm penetration depth. As a result, the FEM—SPH simulation error decreased from 5% to 2%, as detailed in Section 3.2. The optimization results demonstrated a significantly improved fit to the experimental force corridor, with the optimized cone resistance force consistently lying within the corridor across the 150 mm penetration depth. These results validated the sensitivity analysis for sandy loam soil at 0.4% moisture content, accurately reflecting in situ behavior, particularly for granular soils where localized effects drive penetration resistance (Section 3.1.3) The optimized soil parameters, also listed in the table below, will be used for the final part of the paper’s objective, involving a comprehensive CPT simulation employing MM—ALE, SPH, and Hybrid FEM—SPH methods to compare their performance and ensure high-fidelity representation of the soil behavior.

3.2.2. Final CPT Simulation Results with Optimized Parameters

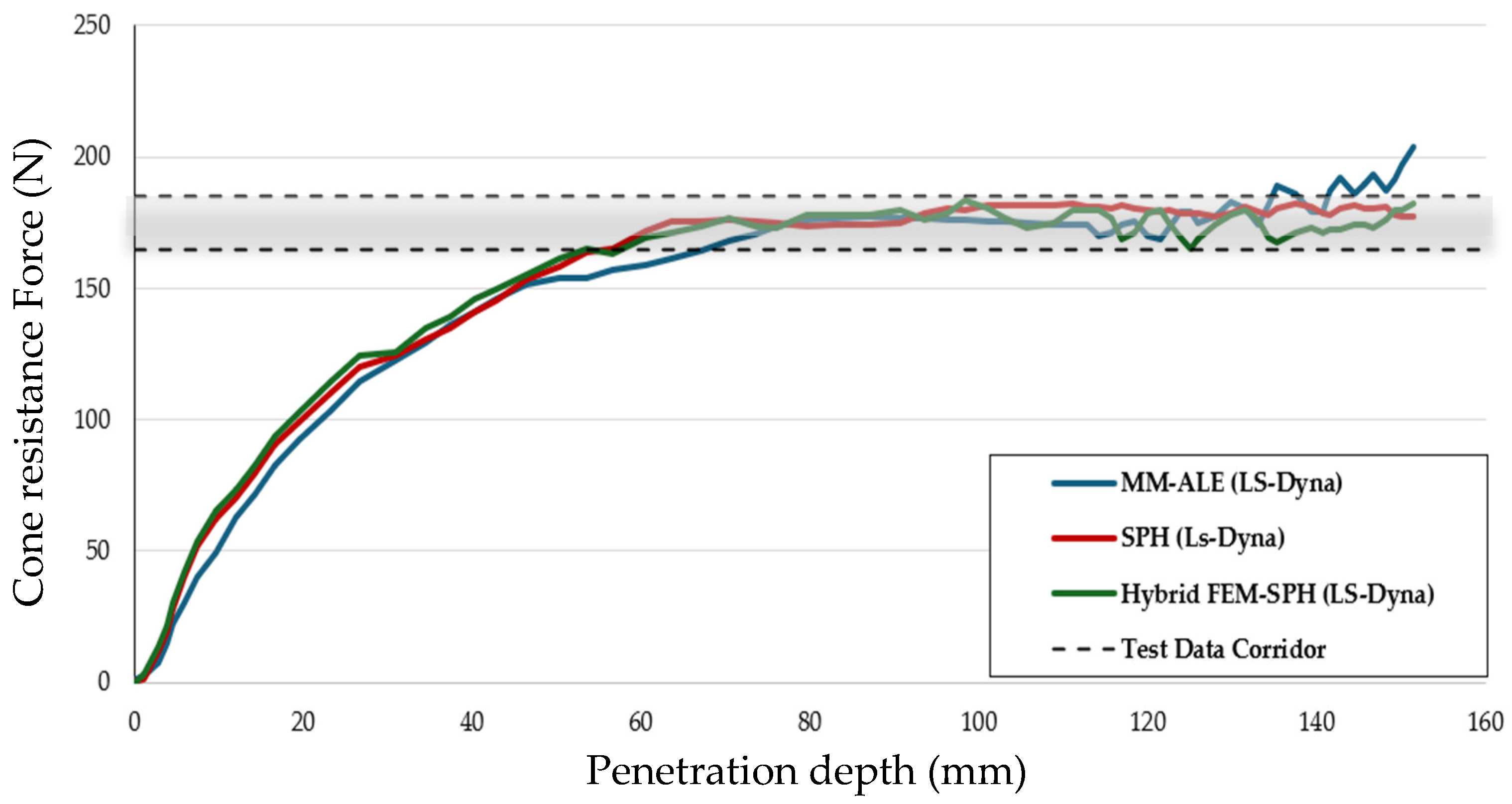
Final CPT simulations were conducted with the optimized MAT_005 parameters using MM—ALE, SPH, and Hybrid FEM—SPH methods. Force penetration curves for all three methods using optimized parameters align with the experimental corridor across the 150 mm penetration depth (Figure 17). The Hybrid FEM—SPH method achieved the highest accuracy, with an error of only 2% compared to the experimental corridor, significantly improving from the initial 4% error as shown in (Figure 18). This result was expected because this method was used in the optimization process. The SPH method followed with a 3% error, improved from the initial 5% error, aligning closely with the CP model [6], which achieved a 2–3% error range [3]. The MM—ALE method showed an error of 8%, a notable improvement from the initial 15% error (Section 3.1.3), yet it still underperformed compared to the CEL method (20% error) and lagged the SPH-based approaches due to their mesh-based limitations in modeling localized deformations, as discussed in Section 3.1.3.

To further highlight the impact of parameter optimization, the percentage errors of the cone resistance force for the initial and optimized simulations across all three methods were compared (Figure 18) alongside the experimental average error range. Comparing the initial and optimized parameter simulations, the optimization process significantly enhanced accuracy across all methods. The MM—ALE method’s error decreased from 15% to 8%, the SPH method’s error reduced from 5% to 3%, and the Hybrid FEM—SPH method’s error improved from 4% to 2%. The optimized curves for SPH and Hybrid FEM—SPH now lie almost entirely within the experimental corridor (Figure 18), showing a tighter fit than the initial simulations, where the curves occasionally deviated at higher penetration depths (beyond 100 mm). The MM—ALE method, while improved, still tends to overpredict the force, especially at deeper penetration depths, consistent with its initial behavior but with a reduced magnitude of error. The experimental average error, ranging between 2% and 3%, serves as a benchmark, confirming that the optimized Hybrid FEM—SPH and SPH methods now match or exceed this accuracy level. This visual comparison underscores the effectiveness of the optimization process in refining the MAT_005 model parameters, particularly for the meshless methods, which now exhibit errors within or below the experimental benchmark.

These results validate the proposed methodology and highlight the potential of LS-DYNA for high-fidelity soil–tire/tool interaction simulations in agricultural applications. The findings align with previous observations. on the advantages of meshless methods, especially the Hybrid FEM-SPH approach, which showed a good balance of precision and computational efficiency, making it a promising method for future studies.

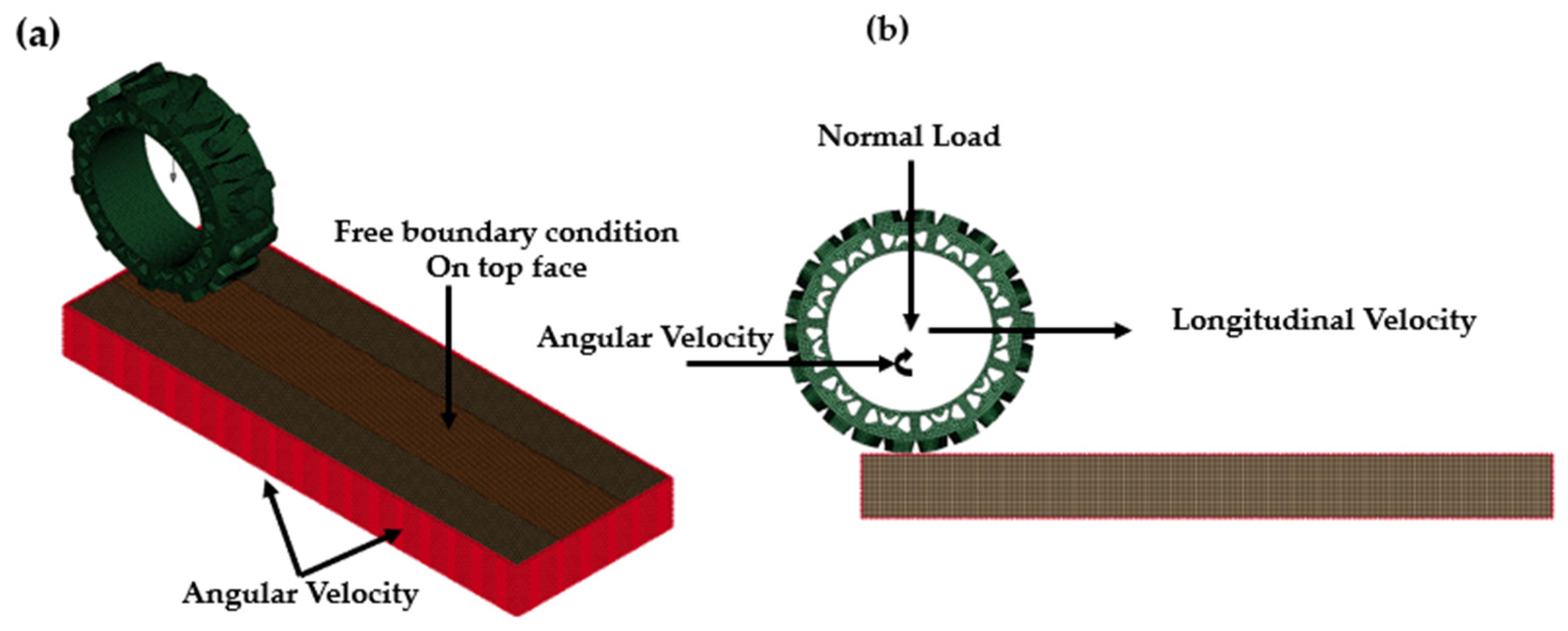
3.2.3. Soil-Tire Interaction Simulation Results

The traction response of the tire–soil system across slip ratios from −10% to 30% is shown in Figure 19. The experimental data demonstrate traction increasing from −600 N at −10% slip to approximately 800 N at 30% slip. Soil-A consistently underpredicts traction, reaching 800 N at 30% slip, while Soil-B closely follows the experimental curve, predicting ~724 N at the same slip level.

Quantitative error analysis highlights the advantage of Soil-B over Soil-A. Across the full slip range, Soil-A exhibited a root-mean-square deviation (RMSE) of 60 N and a MAPE of 10%, while Soil-B achieved significantly lower errors, with an RMSE of 20 N and a MAPE of 4.2% relative to experimental values.

This reduction in error demonstrates that the optimized Soil-B parameters better capture the nonlinear traction–slip behavior and prevent underestimation of drawbar pull, particularly at higher slip ratios. Accurate traction prediction is critical for agricultural applications, as it directly affects fuel efficiency, soil disturbance, and the development of optimized tire designs for sustainable field operations [46].

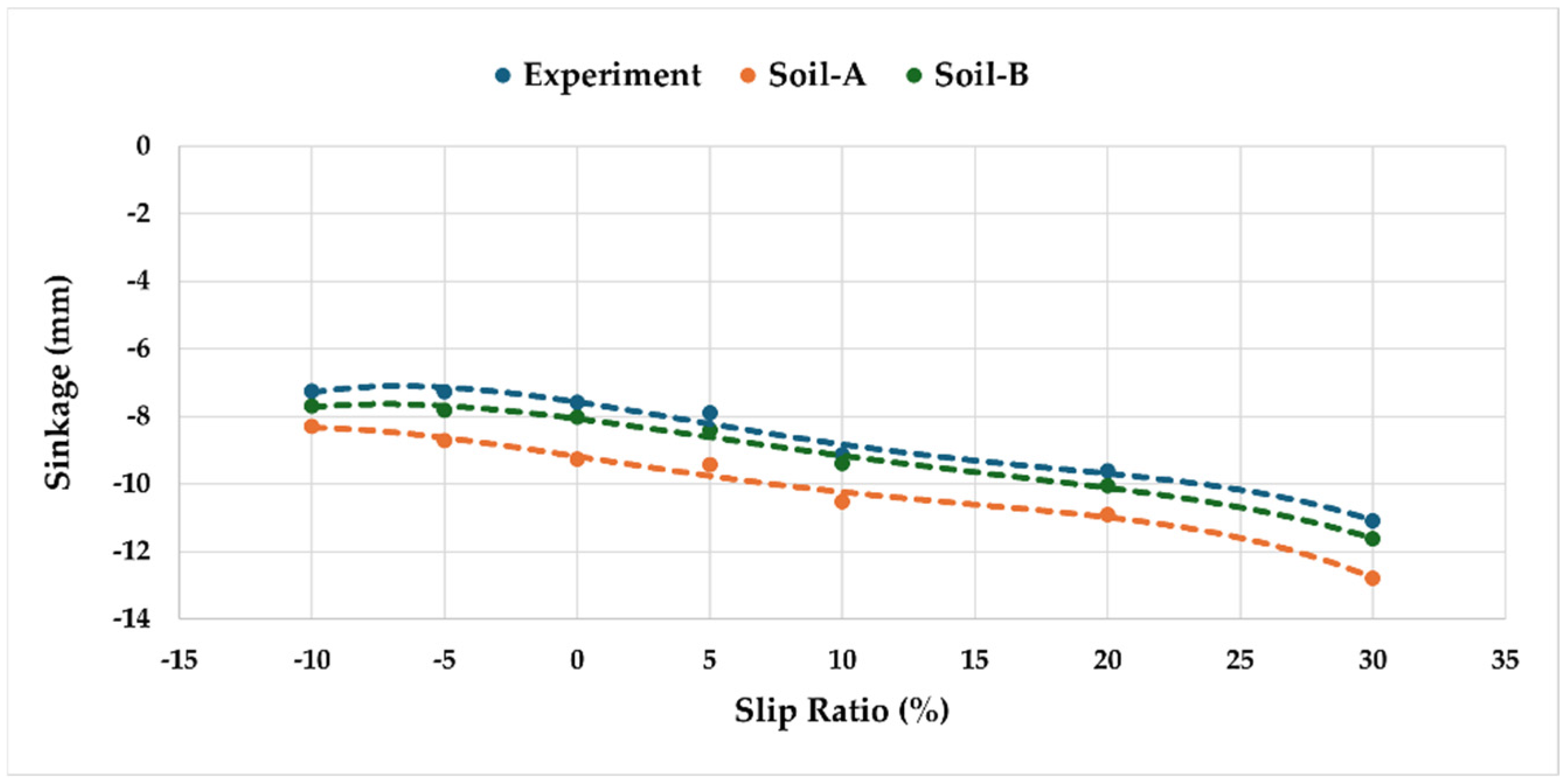
The tire sinkage response across slip ratios from −10% to 30% is shown in Figure 20. All three datasets Experiment, Soil-A, and Soil-B—capture the initial compaction phase followed by progressive rut deepening as slip increases. The experimental results indicate sinkage increasing from −7.5 mm at −10% slip to −12.5 mm at 30% slip. Soil-A consistently underestimates sinkage, predicting a final depth of −13.5 mm, while Soil-B provides a closer match with −12.5 mm at 30% slip.

Error analysis further confirms the improved accuracy of the optimized Soil-B parameters. Across the slip ratio range, Soil-A exhibited an RMSE of 0.9 mm and a MAPE of 10%, whereas Soil-B achieved substantially lower errors, with an RMSE of 0.3 mm and a MAPE of 3.5% relative to experimental data.

The improved predictive performance of Soil-B demonstrates its capability to capture soil deformation trends more reliably under operational loading. This is critical in agricultural applications, as excessive rut depth directly correlates with soil compaction, reduced porosity, impaired water infiltration, and potential yield losses of 20–50% depending on soil type and severity [17,38]. By more accurately representing soil deformation, Soil-B supports better evaluation of field traffic impacts and enables tire design and load management strategies that protect long-term soil productivity.

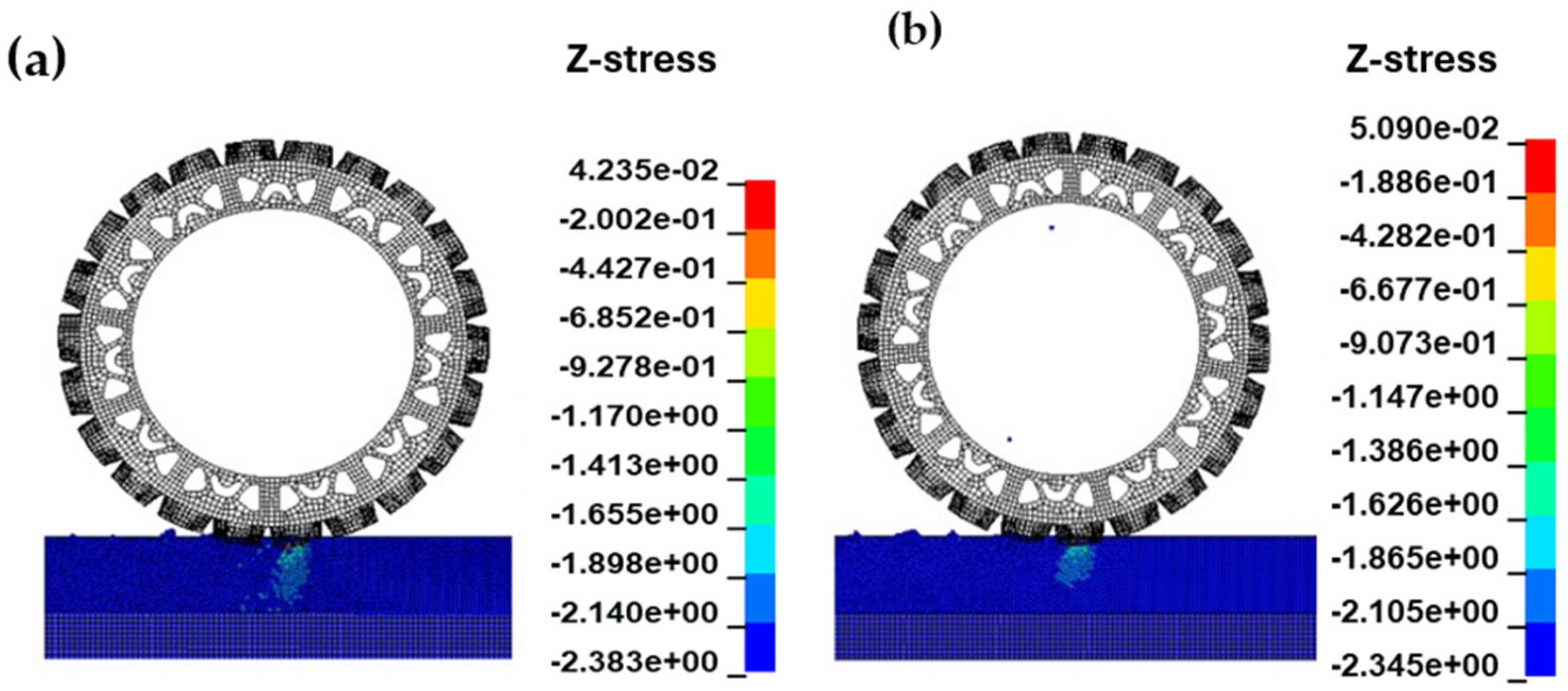
The comparison of normal stress (Figure 21), shear stress (Figure 22), effective plastic strain (Figure 23), and rut profiles (Figure 24) for the lab-tested soil parameters (Soil-A) and optimized parameters (Soil-B) under a 3 kN normal load and 0% slip ratio, benchmarked against experimental 3D-scanned rut profiles [45]. In the standard stress contour plots (Figure 21), both Soil-A and Soil-B captured the stress bulb formation beneath the tire—a key indicator of soil compaction and load transfer in off-road agricultural applications [46,47] but Soil-B produced a distribution and magnitude that more closely matched experimental observations, particularly in the uniformity and depth of the stress bulb. The shear stress plots (Figure 22) further revealed that Soil-B’s contours aligned more closely with the experimentally observed slip plane, with a more realistic distribution of tensile stresses in front of the tire and compressive stress behind it, improving the prediction of traction efficiency and energy loss during field operations [48]. In the effective plastic strain plots (Figure 23), Soil-B better reproduced the depth and lateral spread of permanent deformation zones, closely matching the experimental rut shapes, which is vital for assessing cumulative soil compaction effects that can reduce porosity and crop yield [49,50]. Finally, the rut profile comparison (Figure 24) confirmed that Soil-B more accurately replicated rut depth, width, and lug imprint geometry, while Soil-A underestimated both deformation depth and the lateral soil displacement around the rut. Overall, across all four figure sets, the improved agreement of Soil-B with experimental data highlights the advantage of optimized parameters in predicting soil response, making them more reliable for evaluating tire performance and developing strategies to mitigate harmful compaction in agricultural operations.

3.2.4. Comparative Analysis and Limitations

This study adopts two complementary methodologies for identifying the material parameters of sandy loam soil at 0.4% moisture content in the MAT_005 model for LS-DYNA: a conventional laboratory testing approach and a computational optimization-based approach. As Section 2.2 and Section 3.1 outlined, the laboratory approach relied on triaxial and consolidation tests to determine key parameters such as cohesion, friction angle, shear modulus, bulk modulus, and volumetric strain–pressure relationships. These experimentally derived values provided a solid baseline for initial simulations, capturing fundamental soil mechanical behavior under controlled conditions [6]. However, despite their physical reliability, laboratory-derived parameters exhibited limitations when applied directly to complex in situ conditions. The initial Cone Penetrometer Test (CPT) simulations (Section 3.1.3) showed higher prediction errors 15% for MM-ALE, 5% for SPH, and 4% for Hybrid FEM–SPH, indicating that laboratory data alone may not fully capture site-specific variability, boundary effects, and the natural heterogeneity of agricultural soils, as similarly reported in agriculture studies on soil compaction variability [1].

The optimization-based approach using LS-OPT (Section 2.3 and Section 3.2) was introduced to address these shortcomings by calibrating the MAT_005 parameters directly against in situ CPT data. This inverse analysis method allowed targeted adjustment of model parameters to match field-measured penetration resistance within a defined corridor, significantly improving predictive accuracy for real-world conditions. Sensitivity analysis identified the shear modulus as the dominant contributor to the force–penetration response, followed by bulk modulus, friction angle, and cohesion. The optimization process produced measurable improvements in CPT simulation accuracy: Hybrid FEM–SPH achieved the lowest error at 2%, SPH followed closely at 3%, and MM-ALE improved to 8%—a notable gain over its pre-optimization performance but still limited by mesh-based representation of granular flow. These findings reinforce earlier conclusions in meshless soil modeling research [1,46] that SPH-based methods excel in replicating localized deformation and stress transmission in granular media.

A closer examination of stress and strain distributions (Figure 13 and Figure 14) highlighted key differences in the numerical approaches. SPH and Hybrid FEM–SPH methods accurately localized plastic strain and stress concentration beneath the cone tip, consistent with observed granular soil mechanics and in line with results reported by and agriculture-focused soil compaction studies [26,47]. In contrast, MM-ALE produced more diffuse stress and strain patterns, which may explain its tendency to overpredict cone resistance at deeper penetrations. These results underscore the importance of selecting numerical methods that align with the physical characteristics of the target soil and the scale of deformation being modeled.

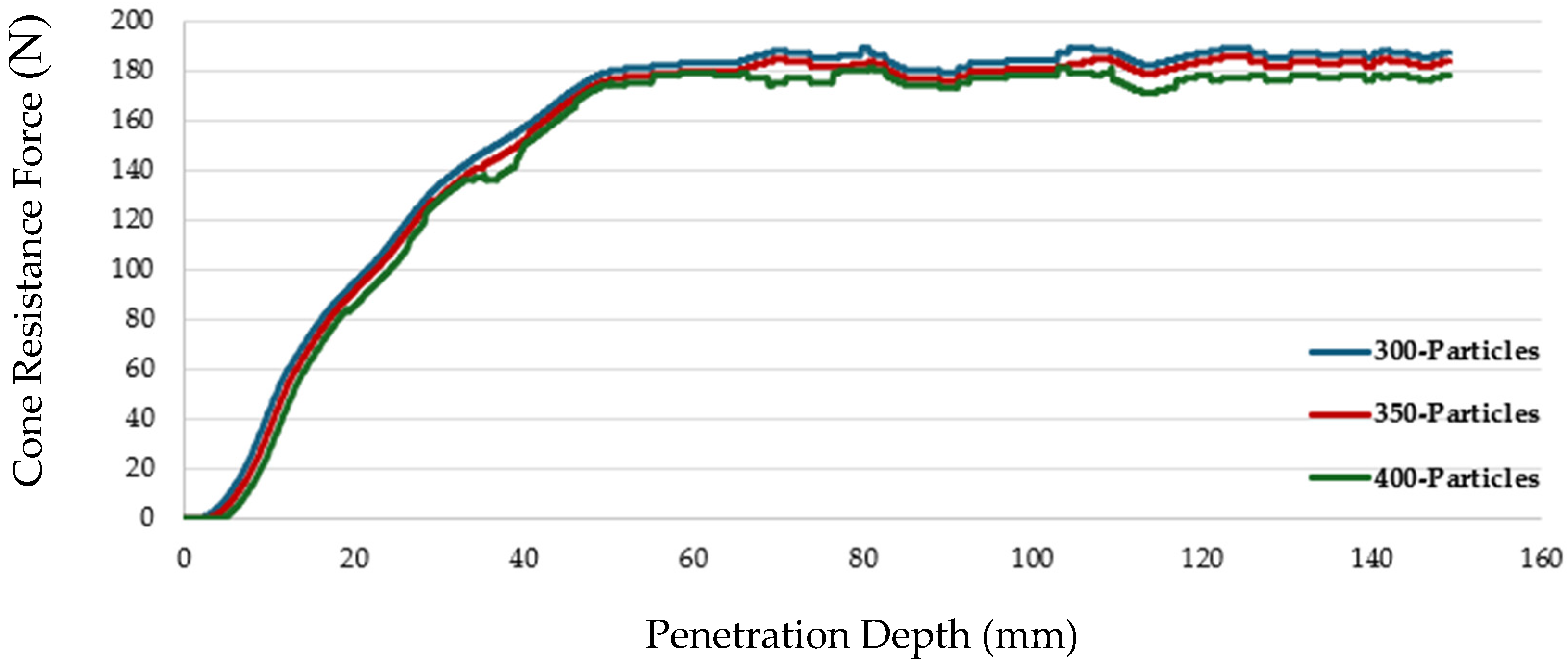
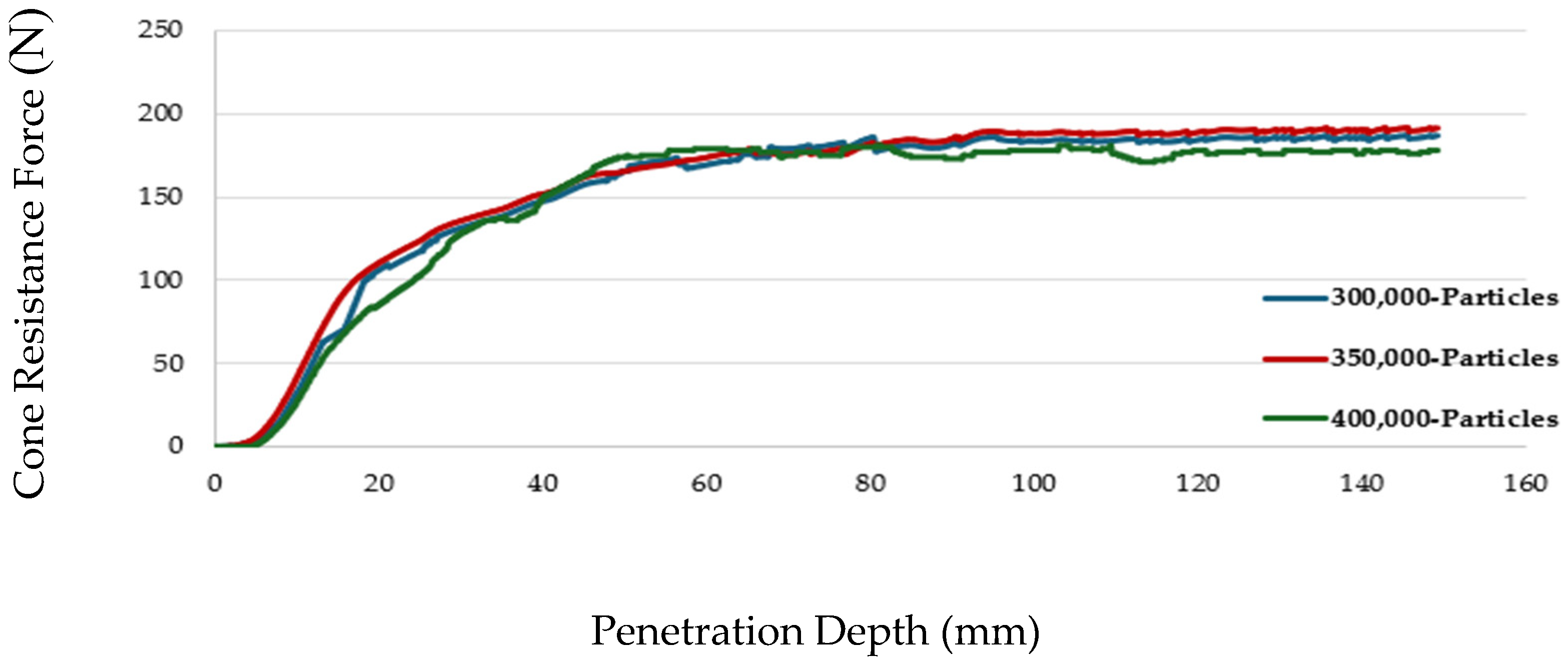
For large soil deformations, the Coupled Eulerian–Lagrangian (CEL) method [6] typically offers higher computational efficiency (e.g., shorter runtimes due to reduced computational volume) but struggles with granular behavior, yielding 20% errors in CPT simulations. In contrast, SPH in LS-Dyna provides superior accuracy (2–5% error) for granular soils but is computationally intensive (e.g., 22 h and high memory for 350,000 particles in our CPT simulation). The Multi-Material Arbitrary Lagrangian–Eulerian (MM-ALE) method takes less computational time (e.g., 16 h with 300,000 elements), while Hybrid-SPH balances accuracy and efficiency, completing simulations by combining SPH and Lagrangian elements [9] (e.g., in 14 h in our CPT simulation).

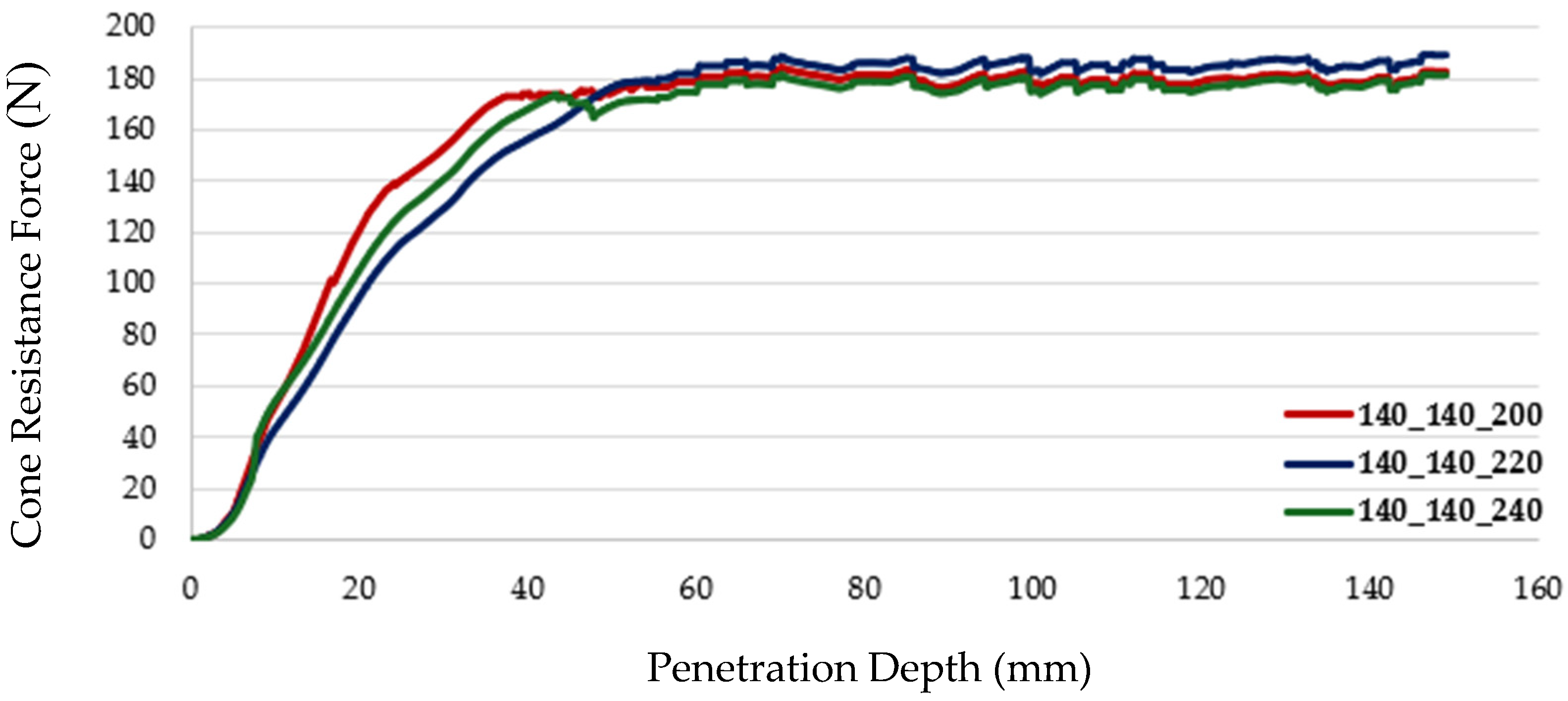
While validated for sandy loam, the methodology’s applicability to other soil types, such as clay (higher cohesion, lower permeability) or silt (intermediate granularity), warrants consideration. In clays, parameter identification may be more sensitive to moisture due to pronounced pore pressure effects, potentially increasing optimization iterations and errors (e.g., 5–10% higher than sandy loam) without strain softening. The Hybrid-SPH method could excel in capturing mixed granular-cohesive behavior for silts, but field CPT data calibration would need adjustment for texture-specific yield surfaces [3,5]. Future studies should test these adaptations to broaden the model’s utility across soil textures.

The benefits of optimized parameters extended beyond penetration simulations to the soil–tire interaction case study (Section 3.2.3). Under identical loading and slip conditions, optimized parameters (Soil-B) consistently produced results closer to experimental benchmarks than lab-based parameters (Soil-A). Notably, Soil-B predicted tire sinkage at 13.8 mm—within 0.6 mm of measured 13.2 mm, while Soil-A underestimated at 12 mm. Similar improvements were seen in net traction prediction, stress bulb formation, shear band development, and rut geometry reproduction, reflecting a better alignment with experimental 3D rut profiles. These enhancements are consistent with findings from [46,48] that accurate soil–tire interaction models are critical for evaluating field traffic impacts, optimizing wheel load management, and mitigating soil compaction in precision agriculture.

Despite these improvements, the MAT_005 model retains inherent limitations. Its simplified elastic–perfectly plastic yield surface lacks strain hardening and softening mechanisms, limiting its ability to model progressive failure and post-peak softening in real soils under cyclic or repeated loading. This is evident in the triaxial simulations (Section 3.1.2), where peak deviator stress was slightly underpredicted compared to both experimental data and the Cap Plasticity (CP) model results [26]. The study’s focus on a single moisture content (0.4%) restricts its applicability across the full range of moisture conditions encountered in agricultural soils. As demonstrated in [5,6], soil compaction response can vary significantly with moisture content, texture, and structure, necessitating broader experimental coverage. Furthermore, the available CPT dataset was limited to peak cone resistance values without continuous force–depth profiles, constraining detailed validation of simulation curves.

Overall, the optimized MAT_005 model combined with SPH and Hybrid FEM–SPH methods demonstrated predictive capabilities comparable to the CP model for granular soils while maintaining compatibility with LS-DYNA’s advanced numerical frameworks. These results validate the integration between field-calibrated parameter identification and meshless methods for accurate, computationally efficient modeling of soil compaction under agricultural traffic. Future research should aim to integrate strain softening into the MAT_005 formulation, extend the methodology to other soil types (including cohesive clays and partially frozen soils), explore moisture-dependent parameterization, and employ high-resolution CPT equipment for capturing continuous penetration resistance profiles. Such developments would expand the applicability of this workflow in precision agriculture, enabling improved design of low-compaction machinery and more sustainable soil management practices [46,47].

4. Conclusions

In this study two methodologies for identifying parameters of the MAT_005 soil model in LS-Dyna, focusing on soil-tire interaction simulations for agricultural applications, were developed and compared. The soil was represented by sandy loam soil (0.4% moisture content), but these methodologies could be applied to other soils as well. The laboratory-based approach, using triaxial and consolidation tests from [6], provided a robust baseline but showed limitations in capturing in-situ soil variability, with initial CPT simulation errors of 15% (MM-ALE), 5% (SPH), and 4% (Hybrid-SPH). The optimization-based approach, leveraging in-situ CPT data with optimization algorithms, significantly improved accuracy, reducing errors to 2% for Hybrid FEM-SPH and 3% for SPH, outperforming lab-based results and matching or exceeding the Cap Plasticity model’s performance (2–3% error) [6]. In addition, optimization approach avoids expensive and time-consuming soil lab tests. Sensitivity analysis identified shear modulus as the dominant parameter (90.6% influence), guiding precise calibration.

In soil-tire interaction simulations, optimized parameters (Soil-B) predicted net traction (~724 N vs. approximately 678 N experimental at 30% slip) and tire sinkage (12.5 mm vs. 11.1 mm experimental at 30% slip) with higher fidelity, closely matching experimental rut profiles and stress distributions. The Hybrid FEM-SPH method balanced accuracy and computational efficiency (14 h runtime vs. 22 h for SPH), making it ideal for high-fidelity soil modeling. Quantitative error analysis across the full slip range from −10% to 30% showed Soil-A with an RMSE of 60 N and 0.9 mm, and a MAPE of 9.1% and 9.0% for traction and sinkage, respectively, while Soil-B achieved significantly lower errors with an RMSE of 20 N and 0.33 mm, and a MAPE of 4.2% and 3.5% for traction and sinkage, respectively.

For practical implementation in agricultural machinery design, follow these steps: (1) conduct in situ CPT tests to capture seasonal moisture variations and establish force corridors; (2) calibrate MAT_005 parameters quarterly using the optimization approach, prioritizing shear modulus and validating against CPT data; (3) simulate wheel loads with Hybrid-SPH to evaluate compaction, iterating tire parameters (e.g., pressure, tread) for low-impact designs, reducing field trial needs. This workflow promotes sustainable practices. Despite limitations (e.g., lack of strain softening) in soil material model (MAT_005) and focus on a single moisture content, the approach demonstrates practical value for sustainable soil management. Future work should incorporate strain softening, explore varied soil types and moisture levels, and use high-resolution CPT data for broader applicability in precision agriculture.