Research on the Operational Parameters and Performance of Key Components of an Industrial Hemp Harvester and Drier
Abstract
1. Introduction
2. Materials and Methods
2.1. Study on the Mechanical Properties of Industrial Hemp Stems
2.1.1. Experimental Materials and Instruments
2.1.2. Moisture Content Determination
2.1.3. Shear Mechanical Property Testing Study
2.2. Analysis and Simulation of Key Component Operational Parameters of the Harvesting Platform for Industrial Hemp Swathers
2.2.1. Overall Machine Structure and Working Principle
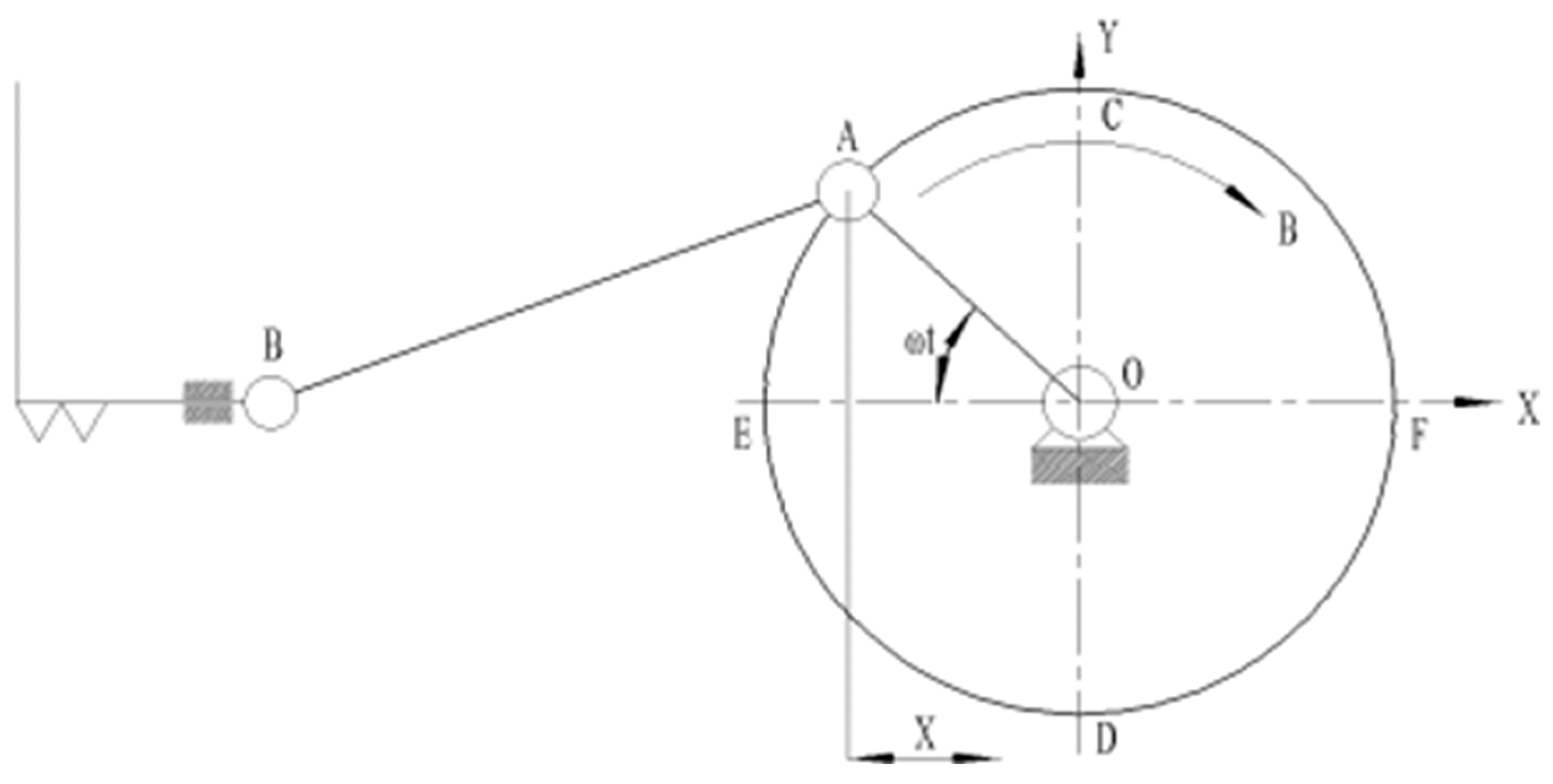
2.2.2. Analysis of the Operating Parameters of the Cutting Components
- (1)
- Analysis of the cutter movement
- (2)
- Cutter Cutting Diagram
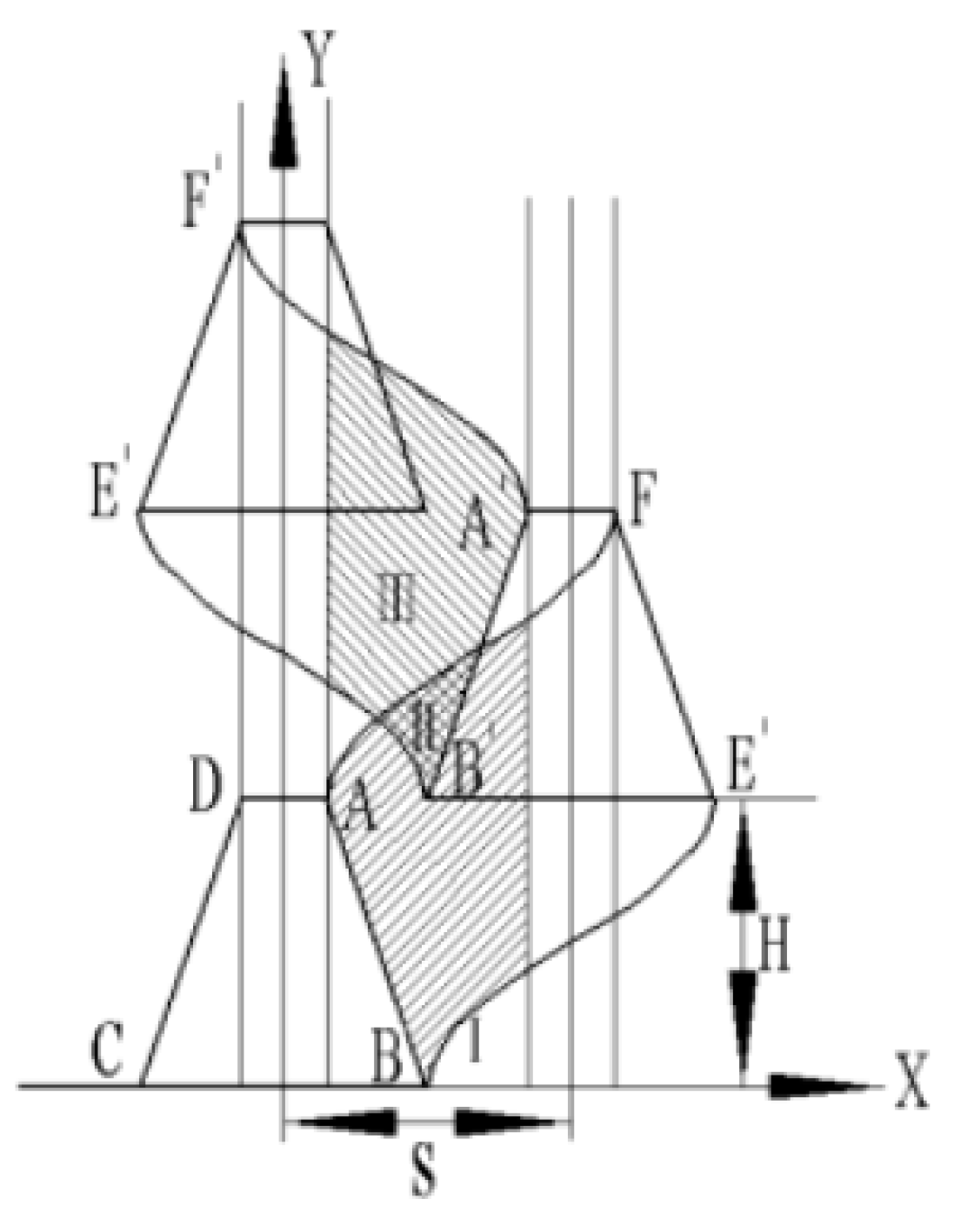
- (3)
- Theoretical Analysis of Cutting Speed
- (4)
- Cutting Speed Diagram
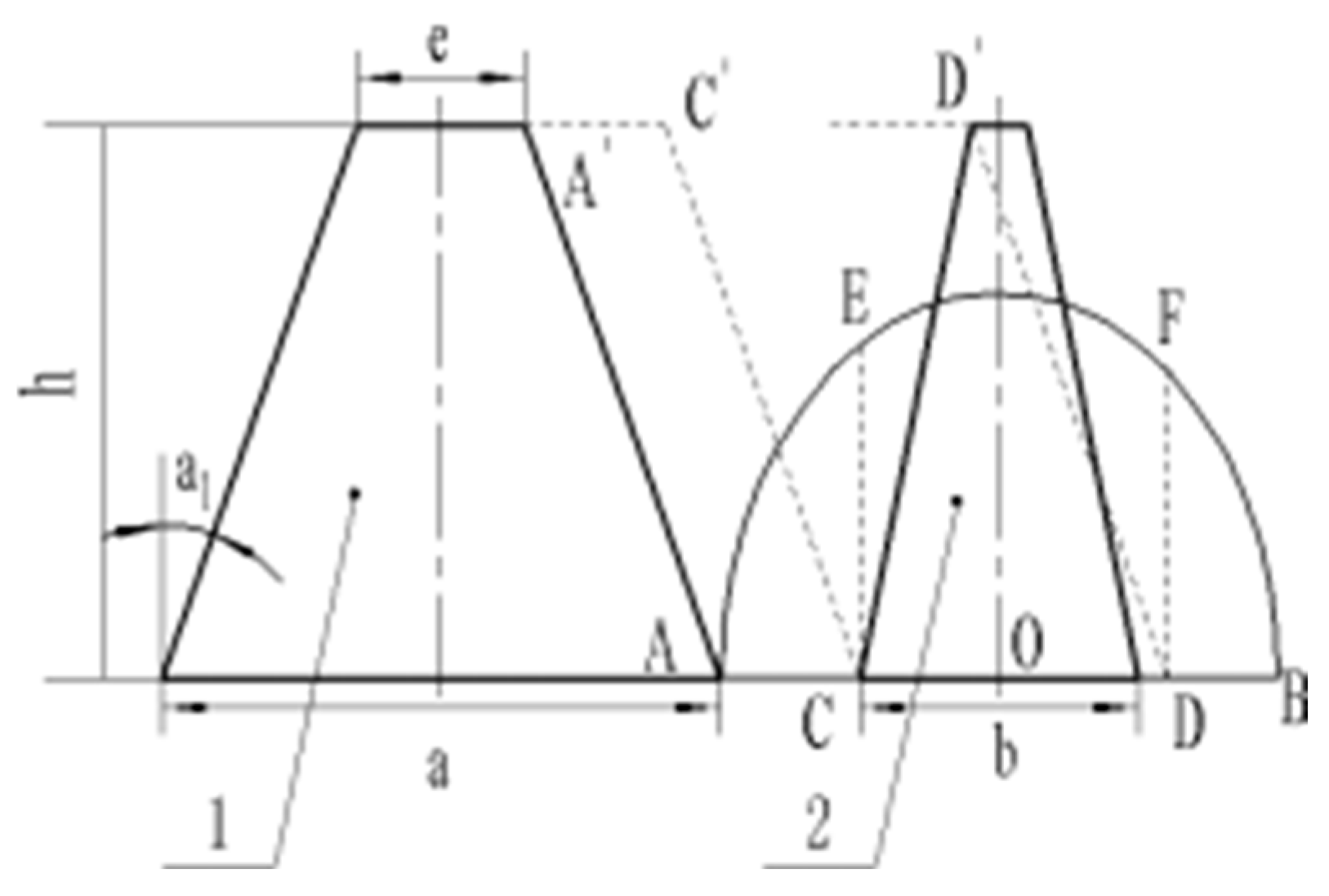
2.3. Analysis of Conveying Component Operating Parameters
2.3.1. Conditions for No Clogging During Plant Conveying
2.3.2. Analysis of Plant Falling Process
2.3.3. Final Conveyor Speed Analysis
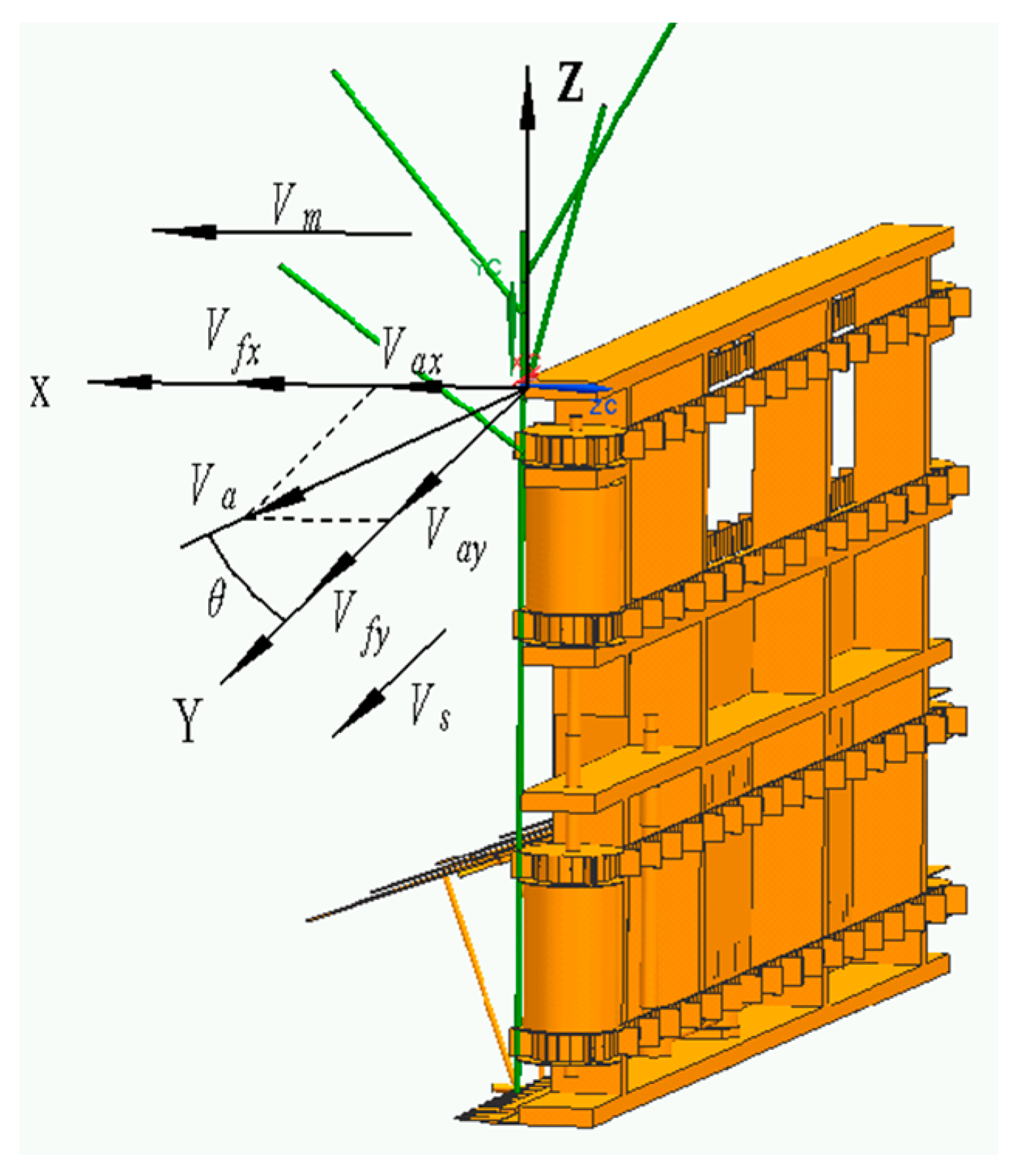
2.4. Simulation Analysis of the Cutting Platform of the Industrial Hemp Harvester
2.4.1. Overall Machine Modeling
2.4.2. Simulation Analysis of the Industrial Hemp Plant Cutting Process
2.4.3. Simulation Analysis of the Hemp Plant Transportation Process
- (1)
- Conveyor Motion Simulation and Analysis
- (2)
- Determine the range of actual operating parameters.
3. Results
3.1. Results and Analysis of Multi-Factor Orthogonal Experiment
3.2. Validation Test of Operating Parameters for the Industrial Hemp Harvester’s Cutter Bar
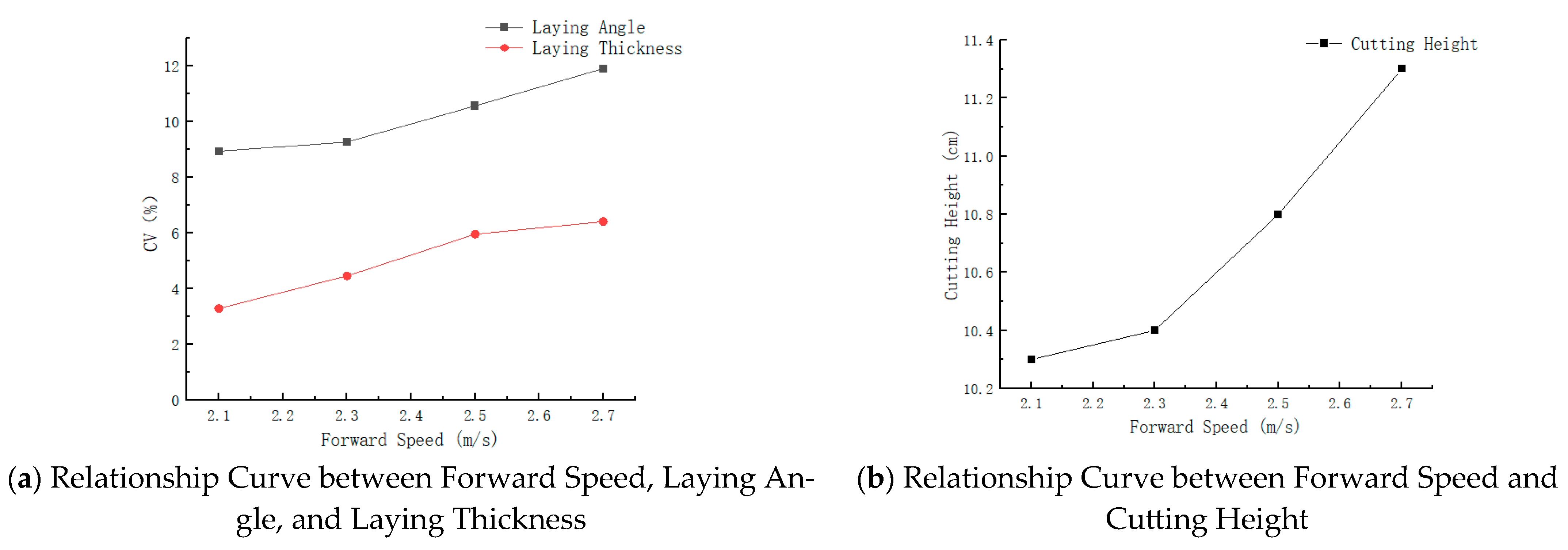
3.2.1. Single-Factor Experiment on Forward Speed
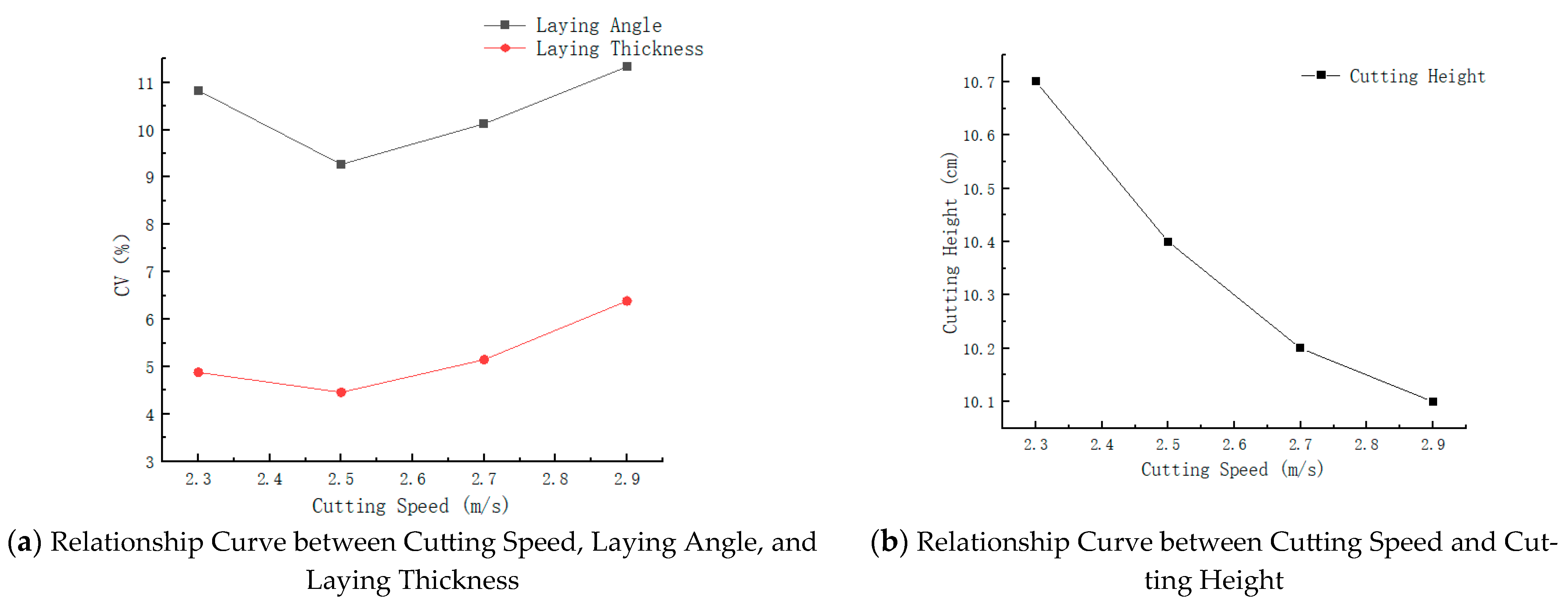
3.2.2. Single-Factor Experiment on Cutting Speed
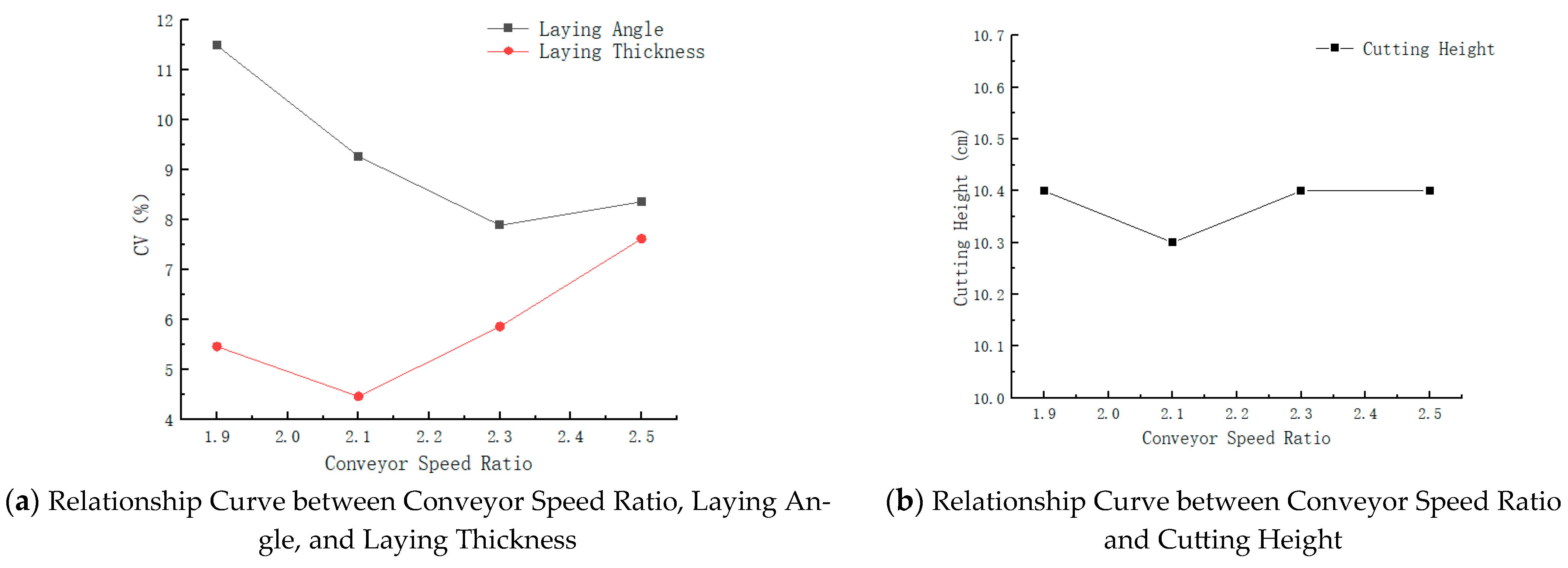
3.2.3. Single-Factor Experiment on Conveyor Speed Ratio
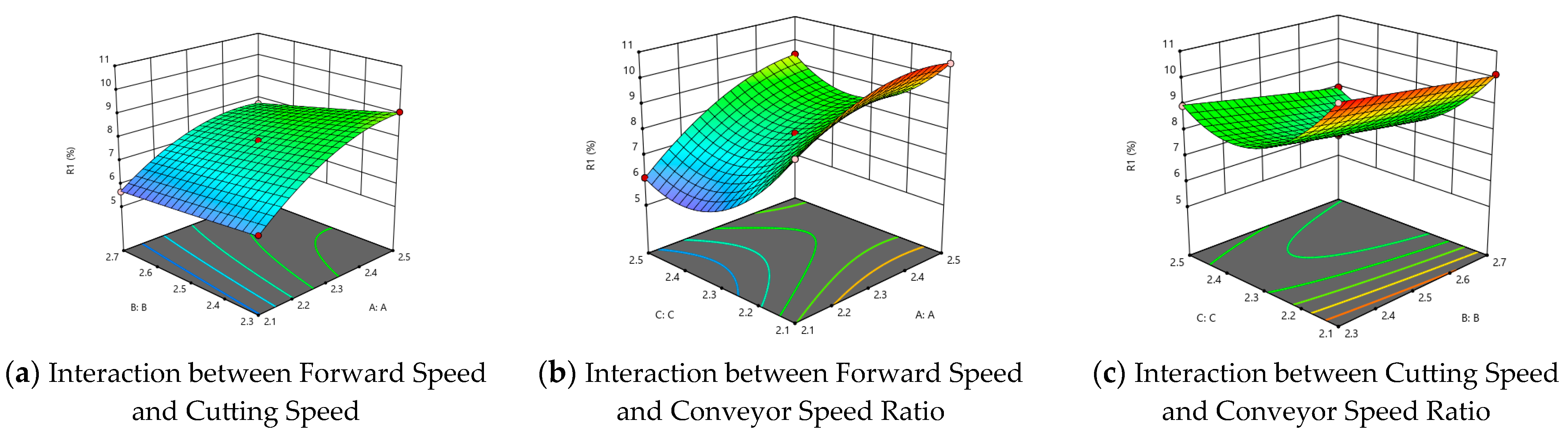
3.2.4. Multi-Factor Experiment
- (1)
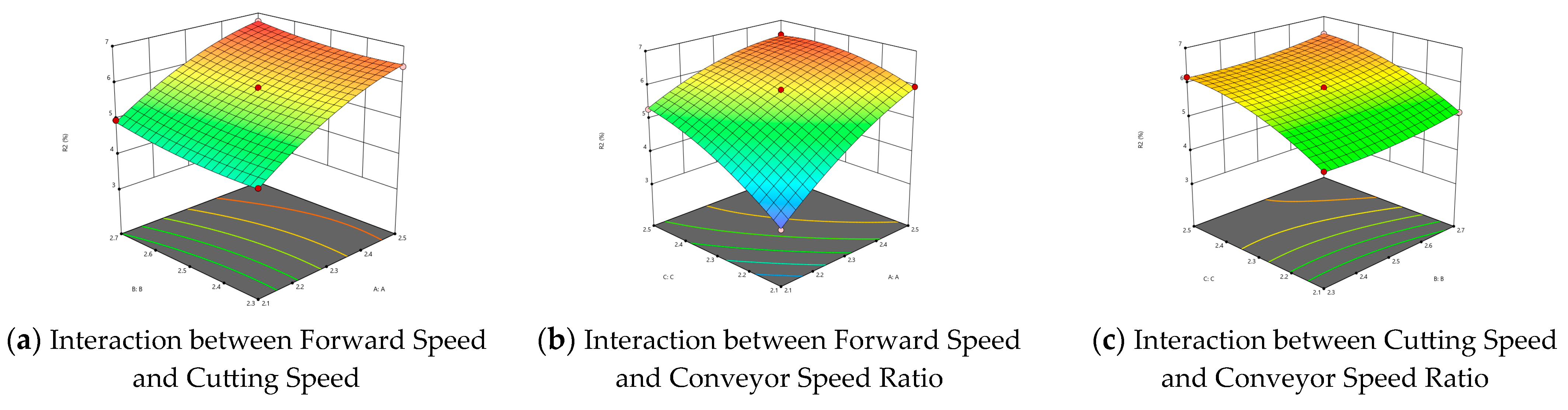
- Influencing Factors and Analysis of the Coefficient of Variation for Laying Angle
- (2)
- Factors Influencing the Coefficient of Variation of Laying Thickness and Analysis
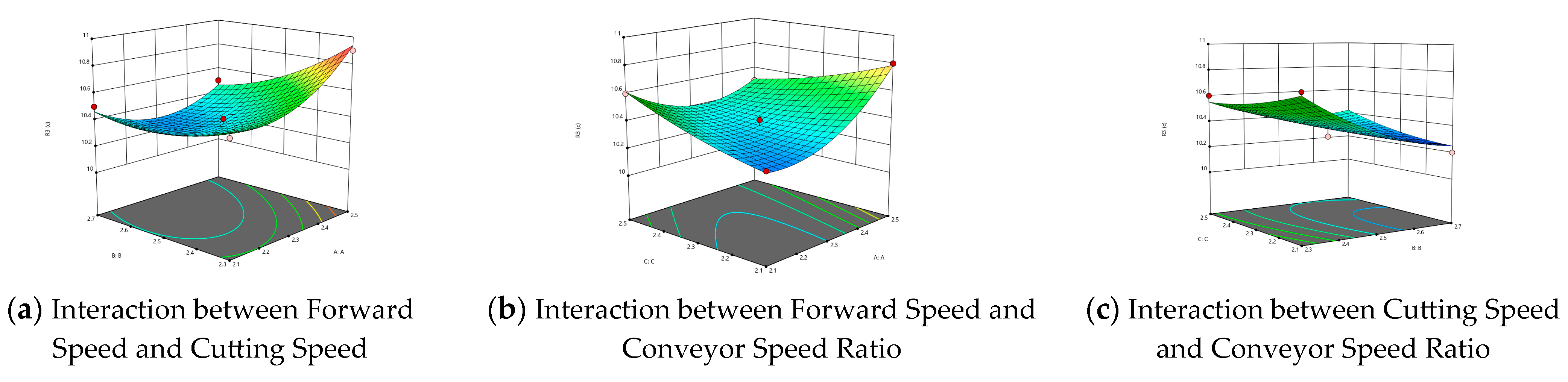
- (3)
- Factors Affecting Cutting Height and Analysis
- (4)
- Optimal Parameter Combination and Validation of Each Indicator
4. Discussion
5. Conclusions
- (1)
- The linear relationship between shear speed, stalk moisture content, stalk diameter, shear force, and shear strength was derived by measuring fiber hemp plant samples. The results show that the shear speed has the most significant effect on stalk shear energy consumption, followed by shear time, stalk moisture content, and shear force, with all factors being highly significant. The shear speed has the most significant effect on stalk shear force, followed by stalk diameter and stalk moisture content, all of which are also highly significant.
- (2)
- Through the analysis and simulation of the operational parameters of key components of the industrial hemp harvesting machine’s cutting platform, the range values for cutting speed, forward speed, and conveyor speed that match both practical operations and theoretical calculations were determined, as follows: the cutting speed range is 1.9~3.7 m/s; the conveyor speed ratio range is 1.9–2.5; and the optimal cutting speed is 2.5 m/s.
- (3)
- Field trials of the fiber hemp harvesting machine revealed the optimal operational parameters as follows: forward speed 2.1 m/s, cutting speed 2.5 m/s, and conveyor speed ratio 2.2; with these parameters, the variation coefficient of the laying angle was 6.88%, the variation coefficient of the laying thickness was 4.11%, and the cutting height was 10.4 cm. The overlap rate was 8.4%, with no missed cutting.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Q.; Zhang, X.; Li, Q.; Wang, S.; Xie, L. Progress on Cultivating Cannabis under Different Cultivation Condiotons. Northeast Agric. Sci. 2020, 45, 45–49. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, G.; Song, X.; Zhang, L.; Fang, Y.; Zheng, N.; Wu, G.; Song, X.; Chen, J. Advantages and Countermeasures of the Development of the Hemp Industry in Heilongjiang Province. Heilongjiang Agric. Sci. 2018, 1, 125–128. [Google Scholar]
- Xiang, W.; Ma, L.; Liu, J.; Yan, B.; Duan, Y.; Lv, J. Research Progress on Primary Technology and Equipment of Industrial Hemp. Chin. J. Agric. Mech. Chem. 2022, 43, 96–103. [Google Scholar] [CrossRef]
- Si, S. Design and Optimization of the Conveying and Baling Device for Ramie Cutting and Baling Machine; Chinese Academy of Agricultural Sciences: Beijing, China, 2023. [Google Scholar] [CrossRef]
- Liu, L.-J.; Lao, C.-Y.; Zhang, N. The effect of new continuous harvest technology of ramie on fiber yield and quality. Ind. Crops Prod. 2013, 44, 677–683. [Google Scholar] [CrossRef]
- Zhou, Y. Design and Experimental Research of Hemp Plate Cutter; Chinese Academy of Agricultural Sciences: Beijing, China, 2017. [Google Scholar]
- Tan, L.T.; Yu, C.M.; Chen, P.; Wang, Y.Z.; Chen, J.K.; Wen, L.; Xiong, H.P. Research Status and Prospective Development of Bast Fiber Crops for Multi-purpose. Plant Fiber Sci. China 2012, 34, 94–99. [Google Scholar]
- Wang, B.; Hu, J.; Liu, C. Current Situation and Development Countermeasures of Hemp Industry in Heilongjiang Province. South. Agric. Mach. 2021, 52, 50–52. [Google Scholar]
- Khan, M.R.; Chen, Y.; Laguë, C.; Landry, H.; Peng, Q.; Zhong, W. Compressive properties of Hemp (Cannabis sativa L.) stalks. Biosyst. Eng. 2010, 106, 315–323. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, J.; Gratton, J.-L. Engineering perspectives of the hemp plant, harvesting and processing. J. Ind. Hemp 2004, 9, 23–39. [Google Scholar] [CrossRef]
- Zheng, W. Design of Sweet Potato Vine Recycling Machine and Study on Cutting Mechanism; Shandong Agricultural University: Tai’an, China, 2019. [Google Scholar] [CrossRef]
- Khan, M.M.R.; Chen, Y.; Laguë, C.; Landry, H.; Peng, Q.; Zhong, W. Hemp (Cannabis sativa L.) decortications using the drop weight method. Appl. Eng. Agric. 2013, 29, 79–87. [Google Scholar] [CrossRef]
- Deyholos, M.K.; Potter, S. Engineering bast fiber feedstocks for use in composite materials. Biocatal. Agric. Biotechnol. 2014, 3, 53–57. [Google Scholar] [CrossRef]
- Xiang, W.; Ma, L.; Liu, J.J.; Yan, B.; Duan, Y.P.; Hu, Y.; Lyu, J.N. Review on Technology and Equipment of Mechanization for Industrial Hemp in China. China Hemp Sci. 2021, 43, 320–332. [Google Scholar]
- Mu, S.L.; Chen, C.L.; Zhang, B.; Luo, X.Y.; Li, X.W. Current Situation and Existing Problem of Bast Fiber Harvester in China. China Agric. Mach. 2010, 3, 11–14. [Google Scholar]
- Tang, B.; Li, X.-W.; Yuan, J.-N.; Zhang, B.; Huang, J. Analysis of technology and development for hemp micro-harvesting machinery. J. Chin. Agric. Mech. 2018, 39, 17–21. [Google Scholar]
- Huang, J.-C.; Li, X.-W.; Zhang, B.; Tian, K.-P.; Shen, C.; Wang, J.-G. Research on the 4LMZ160 crawler ramie combine harvester. J. Agric. Mech. Res. 2015, 9, 155–158. [Google Scholar]
- Lv, J.-N.; Ma, L.; Liu, J.-J.; Long, C.-H.; Zhou, W. The investigation on the development of industrial hemp and its harvesting machinery of Heilongjiang province. Plant Fiber Sci. China 2017, 39, 94–102. [Google Scholar]
- Cao, Y.; Yao, C. Development and use of the 4GS-2880 hemp harvesting machine. Agric. Mach. Technol. Promot. 2015, 5, 44–45. [Google Scholar]
- Zhu, H.; Zhang, Z.; Yu, G. Development and Test of the Hemp Swather. Agric. Eng. 2018, 8, 95–98. [Google Scholar]
- Gong, Y.; Cao, H.; Wang, Z.; Zhang, X. Research and design of the 4GL-285 hemp harvesting machine. Agric. Mach. Usage Maint. 2020, 7, 11–12. [Google Scholar] [CrossRef]
- Marrot, L.; Lefeuvre, A.; Pontoire, B.; Bourmaud, A.; Baley, C. Analysis of the hemp fiber mechanical properties and their scattering. Ind. Crops Prod. 2013, 51, 317–327. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Du, G.; Wu, Z.; Meng, Y. Variation in physical and mechanical properties of hemp stalk fibers along height of stem. Ind. Crops Prod. 2013, 42, 344–348. [Google Scholar] [CrossRef]
- Beaugrand, J.; Nottez, M.; Konnerth, J.; Bourmaud, A. Multi-scale analysis of the structure and mechanical performance of woody hemp core and the dependence on the sampling location. Ind. Crops Prod. 2014, 60, 193–204. [Google Scholar] [CrossRef]
- Guo, Y.; Deng, Y.; Hu, S.; Lai, Q.; Liu, M.; Deng, J.; Li, C. Experimental Study on the Shear Mechanical Properties of Fibrous Roots of Polygonatum. J. Jiangxi Agric. Univ. 2024, 1–16. Available online: http://kns.cnki.net/kcms/detail/36.1028.S.20241129.1755.019.html. (accessed on 28 December 2024).
- Chinese Academy of Agricultural Mechanization Sciences. Agricultural Machinery Design Handbook; China Agricultural Science and Technology Press: Beijing, China, 2007. [Google Scholar]
- Jing, F. The Experimental Study About The Structural and Motion Parameters of The Maize Straw Transverse Transporter of The Corn Harvester. Henan Univ. Sci. Technol. 2011, 32, 1–5. [Google Scholar]
- Liu, Y. Design and Experiment of Key Components of the Sunflower Combine Harvester’s Reaper Chain-Type Cutter Bar; Huazhong Agricultural University: Wuhan, China, 2021. [Google Scholar] [CrossRef]
- Qu, T.J. Design and Experiment of Low-Damage Cutting Platform for Soybean Harvester; Sichuan Agricultural University: Yaan, China, 2021. [Google Scholar] [CrossRef]
- Liu, D.; Xiao, H.; Jin, Y.; Yang, G. Finite Element Analysis of Stalk Cutting of Chinese Little Greens Based on ANSYS and Verification Test. China Agric. Sci. Technol. Bull. 2018, 20, 85–93. [Google Scholar] [CrossRef]
- Li, K. Study on Design and Parameter Optimization of The Harvesting Device for Industrialized Shanghaiqing; Southwest University: Chongqing, China, 2020. [Google Scholar] [CrossRef]
- Liu, Y.C. Simulation and Experimental Study of Corn Straw Crimping Based on Discrete Element Method; Gansu Agricultural University: Lanzhou, China, 2023. [Google Scholar]
- Wang, T. Design and Experimental Study of a Wild Chrysanthemum Stem Cutter; Northwest A&F University: Xianyang, China, 2023. [Google Scholar]



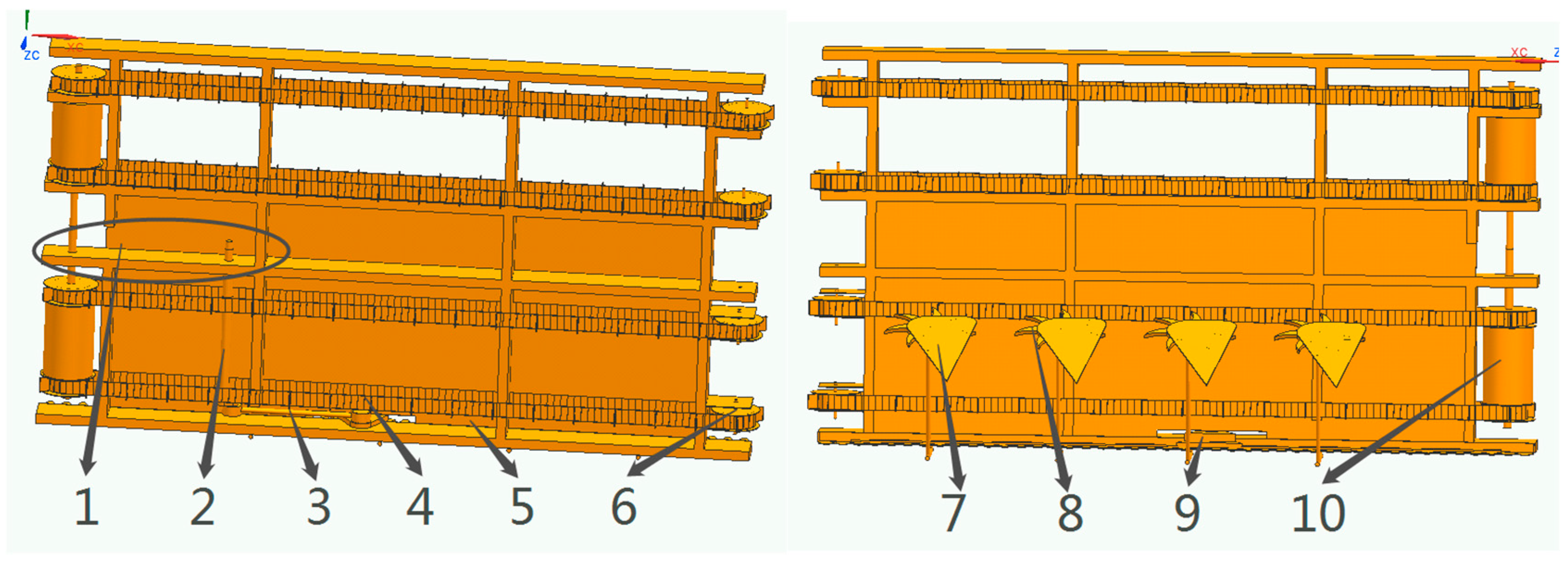
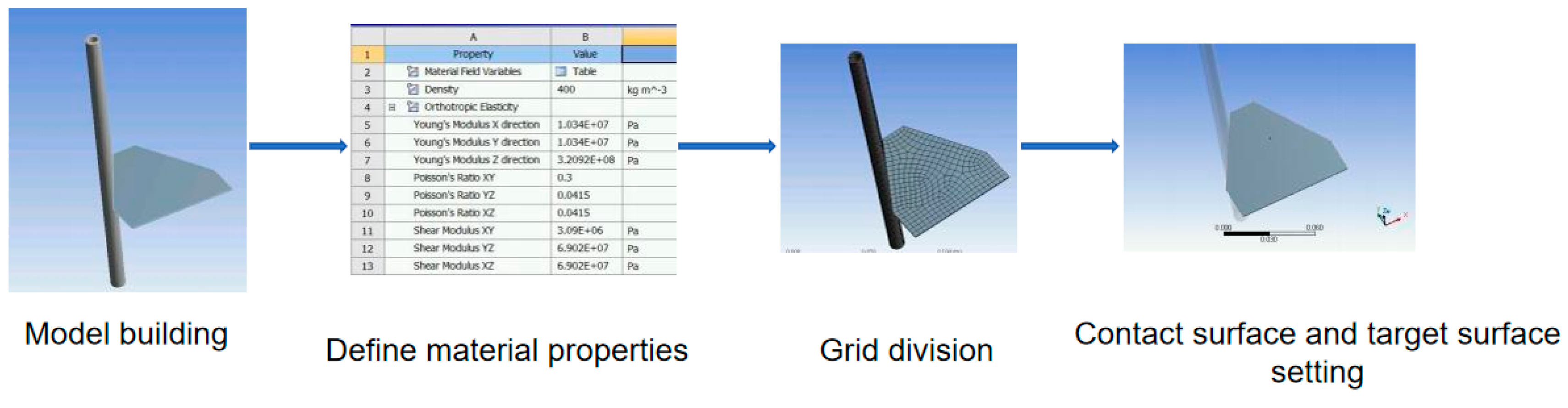
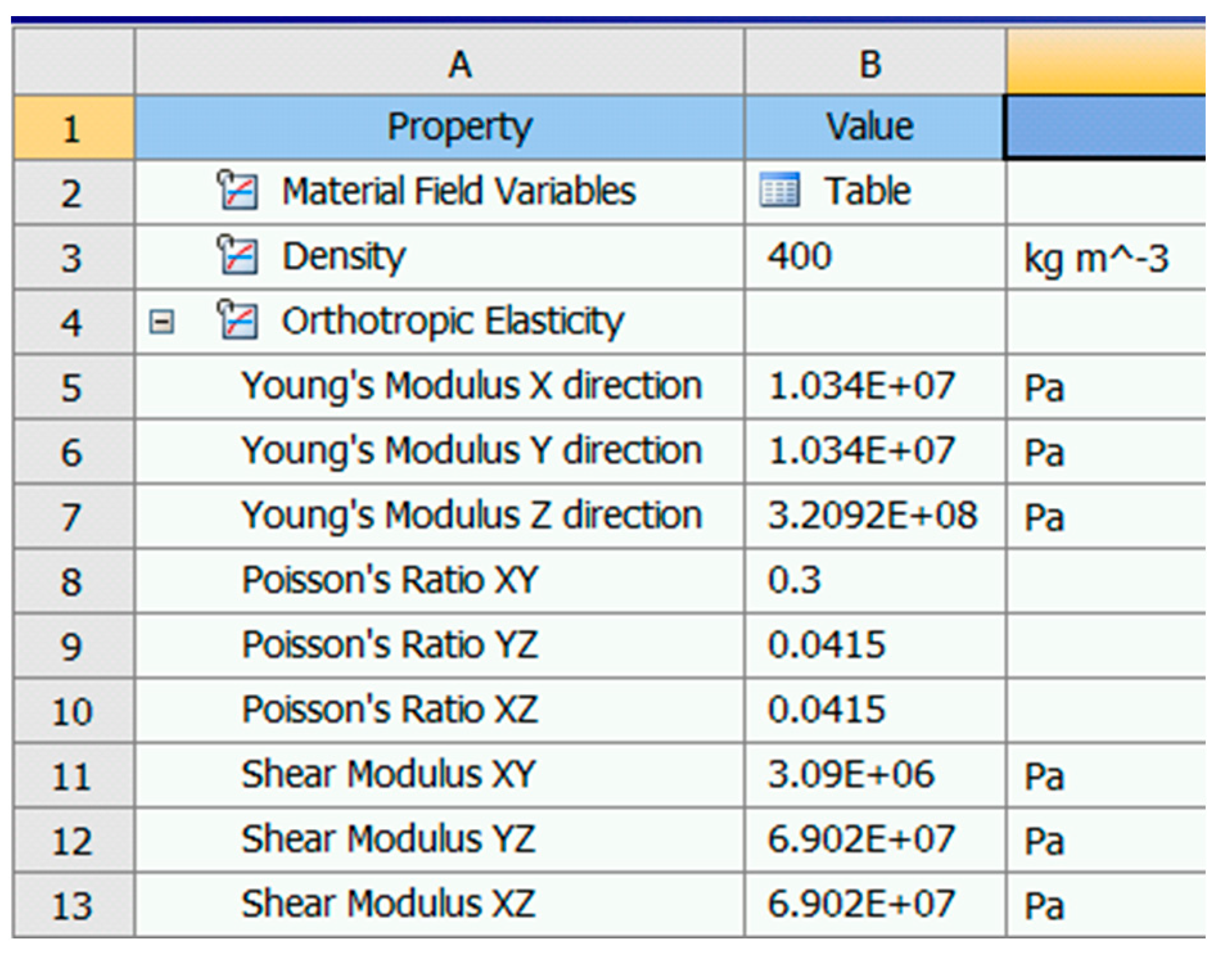






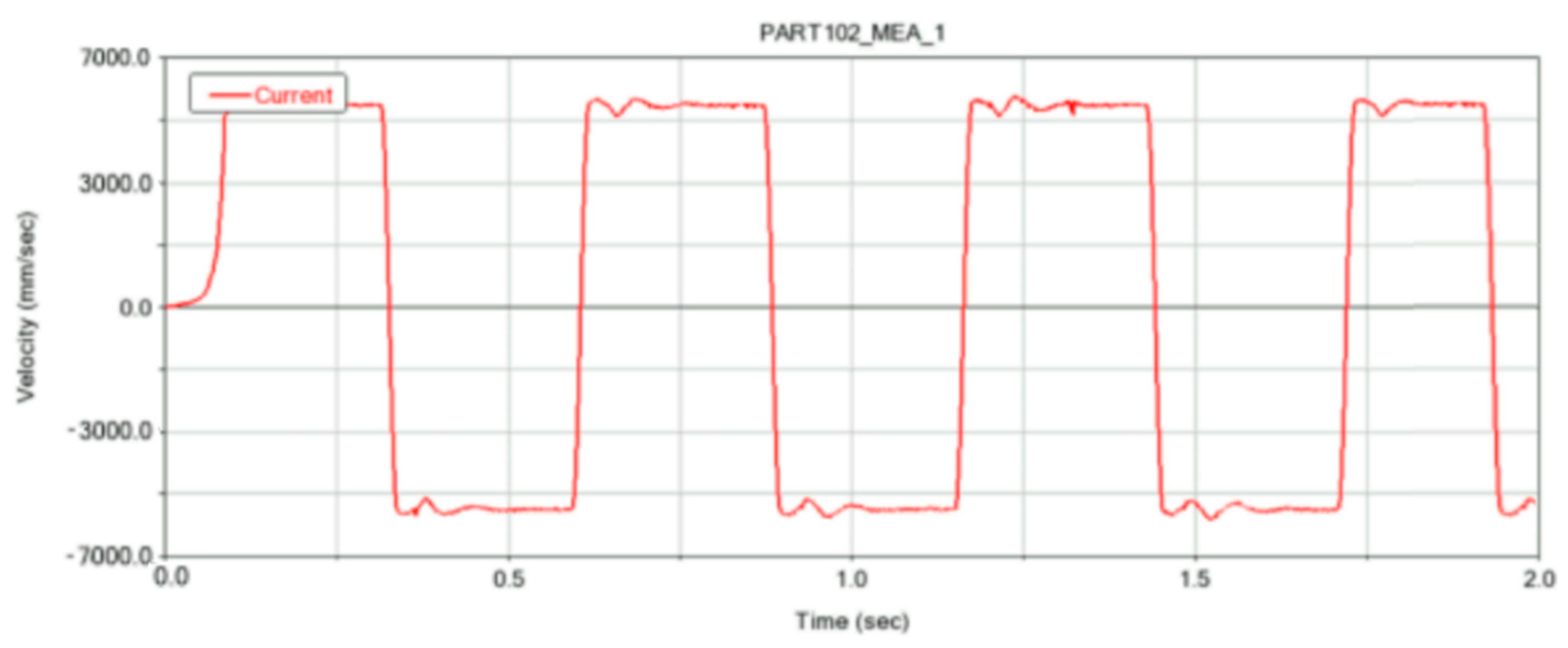

| Shear Speed (mm/s) | Stem Diameter (mm) | Stem Moisture Content (%) | Shear Force (N) | Energy (J) | Time (s) |
|---|---|---|---|---|---|
| 5 | 10 | 35.86 | 100.5 | 1.01 | 2.35 |
| 10 | 37.53 | 106.2 | 1.06 | 2.47 | |
| 10 | 39.20 | 109 | 1.09 | 2.65 | |
| 10 | 40.87 | 116.8 | 1.17 | 2.76 | |
| 10 | 42.54 | 122.2 | 1.22 | 2.88 | |
| 8 | 35.86 | 91.2 | 0.73 | 1.86 | |
| 8 | 37.53 | 95.1 | 0.76 | 1.98 | |
| 8 | 39.20 | 100.7 | 0.81 | 2.13 | |
| 8 | 40.87 | 103.9 | 0.83 | 2.27 | |
| 8 | 42.54 | 109.5 | 0.88 | 2.41 | |
| 5 | 35.86 | 84.5 | 0.42 | 1.17 | |
| 5 | 37.53 | 88.1 | 0.44 | 1.29 | |
| 5 | 39.20 | 90.1 | 0.45 | 1.44 | |
| 5 | 40.87 | 95.9 | 0.48 | 1.59 | |
| 5 | 42.54 | 101.1 | 0.51 | 1.78 | |
| 7 | 10 | 35.86 | 96.3 | 0.96 | 1.65 |
| 10 | 37.53 | 100.9 | 1.01 | 1.79 | |
| 10 | 39.2 | 106 | 1.06 | 1.94 | |
| 10 | 40.87 | 111.9 | 1.12 | 2.21 | |
| 10 | 42.54 | 118.1 | 1.18 | 2.57 | |
| 8 | 35.86 | 84.1 | 0.67 | 1.33 | |
| 8 | 37.53 | 87.3 | 0.70 | 1.58 | |
| 8 | 39.2 | 91.5 | 0.73 | 1.71 | |
| 8 | 40.87 | 95.4 | 0.76 | 1.83 | |
| 8 | 42.54 | 100.3 | 0.80 | 1.98 | |
| 5 | 35.86 | 74.5 | 0.37 | 1.13 | |
| 5 | 37.53 | 79.5 | 0.40 | 0.86 | |
| 5 | 39.2 | 81.3 | 0.41 | 0.94 | |
| 5 | 40.87 | 86 | 0.43 | 1.14 | |
| 5 | 42.54 | 92.3 | 0.46 | 1.39 | |
| 9 | 10 | 35.86 | 87.7 | 0.88 | 1.35 |
| 10 | 37.53 | 92.9 | 0.93 | 1.47 | |
| 10 | 39.2 | 96.5 | 0.97 | 1.65 | |
| 10 | 40.87 | 101.8 | 1.02 | 1.77 | |
| 10 | 42.54 | 110.4 | 1.10 | 1.96 | |
| 8 | 35.86 | 76.5 | 0.61 | 0.94 | |
| 8 | 37.53 | 80 | 0.64 | 1.08 | |
| 8 | 39.2 | 94.1 | 0.75 | 1.21 | |
| 8 | 40.87 | 95.4 | 0.76 | 1.46 | |
| 8 | 42.54 | 98.52 | 0.79 | 1.51 | |
| 5 | 35.86 | 66.6 | 0.33 | 0.66 | |
| 5 | 37.53 | 71.9 | 0.36 | 0.74 | |
| 5 | 39.2 | 75 | 0.38 | 0.86 | |
| 5 | 40.87 | 79.1 | 0.40 | 0.91 | |
| 5 | 42.54 | 85 | 0.43 | 1.04 | |
| 11 | 10 | 35.86 | 79.1 | 0.79 | 0.95 |
| 10 | 37.53 | 84.9 | 0.85 | 1.07 | |
| 10 | 39.2 | 91.4 | 0.91 | 1.16 | |
| 10 | 40.87 | 96.7 | 0.97 | 1.28 | |
| 10 | 42.54 | 101.3 | 1.01 | 1.43 | |
| 8 | 35.86 | 68.7 | 0.55 | 0.85 | |
| 8 | 37.53 | 79.73 | 0.64 | 0.96 | |
| 8 | 39.2 | 78.3 | 0.63 | 1.11 | |
| 8 | 40.87 | 83.3 | 0.67 | 1.32 | |
| 8 | 42.54 | 88 | 0.70 | 1.45 | |
| 5 | 35.86 | 57.5 | 0.29 | 0.51 | |
| 5 | 37.53 | 65.1 | 0.33 | 0.67 | |
| 5 | 39.2 | 68.9 | 0.34 | 0.78 | |
| 5 | 40.87 | 76 | 0.38 | 0.84 | |
| 5 | 42.54 | 77.8 | 0.39 | 0.97 | |
| 13 | 10 | 35.86 | 68.8 | 0.69 | 0.81 |
| 10 | 37.53 | 72.5 | 0.73 | 0.92 | |
| 10 | 39.2 | 78.3 | 0.78 | 1.01 | |
| 10 | 40.87 | 82 | 0.82 | 1.17 | |
| 10 | 42.54 | 86.8 | 0.87 | 1.35 | |
| 8 | 35.86 | 63.3 | 0.51 | 0.69 | |
| 8 | 37.53 | 67 | 0.54 | 0.74 | |
| 8 | 39.2 | 69.6 | 0.56 | 0.85 | |
| 8 | 40.87 | 74 | 0.59 | 0.96 | |
| 8 | 42.54 | 79.5 | 0.64 | 1.10 | |
| 5 | 35.86 | 50.37 | 0.25 | 0.45 | |
| 5 | 37.53 | 66 | 0.33 | 0.51 | |
| 5 | 39.2 | 66.6 | 0.33 | 0.67 | |
| 5 | 40.87 | 69.9 | 0.35 | 0.79 | |
| 5 | 42.54 | 80.45 | 0.40 | 0.92 |
| Name of Kinematic Pairs | Application Location | Number of Applications |
|---|---|---|
| Revolute joint | Transmission shaft and frame | 1 |
| Crank and connecting rod | 1 | |
| Connecting rod and moving blade | 1 | |
| Driving shaft and frame | 1 | |
| Translational joint | Driven shaft and frame | 1 |
| Every two adjacent segments of the conveyor belt | 1 | |
| Moving blade and fixed blade | 218 | |
| Prismatic joint | Frame and ground | 1 |
| Transmission shaft and crank | 1 | |
| Fixed knife and frame | 1 |
| Experiment Number | Forward Speed (m/s) | Power Output Shaft Speed (r/min) | Cutting Speed (m/s) | Conveyor Speed Ratio |
|---|---|---|---|---|
| 1 | 1.5 | 900 | 1.7 | 2.4 |
| 2 | 1.7 | 1100 | 1.9 | 2.4 |
| 3 | 1.9 | 1200 | 2.1 | 2.2 |
| 4 | 2.1 | 1300 | 2.3 | 2.3 |
| 5 | 2.3 | 1400 | 2.5 | 2.3 |
| 6 | 2.5 | 1500 | 2.7 | 2.3 |
| 7 | 2.7 | 1600 | 2.9 | 2.3 |
| 8 | 2.9 | 1700 | 3.1 | 2.3 |
| 9 | 3.1 | 1800 | 3.3 | 2.4 |
| 10 | 3.3 | 1900 | 3.5 | 2.3 |
| 11 | 3.5 | 2000 | 3.7 | 2.4 |
| Unstandardized Coefficients | Standardized Coefficients | T-Value | Significance | ||
|---|---|---|---|---|---|
| B | Standard Error | Beta | |||
| Constant | 0.046 | 0.094 | 0.488 | 0.62701 | |
| Shear Force | 0.021 | 0.001 | 1.209 | 17.569 | 0.00016 |
| Shear Speed | 0.760 | 0.031 | 0.829 | 24.397 | 0.00036 |
| Shear Time | 0.192 | 0.029 | 0.430 | 6.646 | 0.00028 |
| Stem Moisture Content | −0.054 | 0.003 | −0.493 | −17.747 | 0.00024 |
| Experiment Number | Forward Speed (m/s) | Number of Teeth on the Large Sprocket | Laying Angle C.V1 (%) | Laying Thickness C.V2 (%) | Cutting Height (cm) |
|---|---|---|---|---|---|
| 1 | 2.1 | 30 | 8.94 | 3.29 | 10.3 |
| 2 | 2.3 | 27 | 9.27 | 4.46 | 10.4 |
| 3 | 2.5 | 25 | 10.57 | 5.96 | 10.8 |
| 4 | 2.7 | 23 | 11.91 | 6.41 | 11.3 |
| Experiment Number | Cutting Speed (m/s) | Number of Teeth on the Large Sprocket | Laying Angle C.V1 (%) | Laying Thickness C.V2 (%) | Cutting Height (cm) |
|---|---|---|---|---|---|
| 1 | 2.3 | 24 | 10.83 | 4.88 | 10.7 |
| 2 | 2.5 | 27 | 9.27 | 4.46 | 10.4 |
| 3 | 2.7 | 29 | 10.13 | 5.15 | 10.2 |
| 4 | 2.9 | 32 | 11.33 | 6.39 | 10.1 |
| Experiment Number | Conveyor Speed Ratio | Number of Teeth on the Large Sprocket | Laying Angle C.V1 (%) | Laying Thickness C.V2 (%) | Cutting Height (cm) |
|---|---|---|---|---|---|
| 1 | 1.9 | 30 | 11.49 | 5.46 | 10.4 |
| 2 | 2.1 | 27 | 9.27 | 4.46 | 10.3 |
| 3 | 2.3 | 25 | 7.89 | 5.86 | 10.4 |
| 4 | 2.5 | 22 | 8.36 | 7.62 | 10.4 |
| Forward Speed (m/s) | Cutting Speed (m/s) | Conveyor Speed Ratio | Laying Angle C.V1 (%) | Laying Thickness C.V2 (%) | Stubble Height (cm) |
|---|---|---|---|---|---|
| 2.10 | 2.56 | 2.20 | 6.91 | 4.14 | 10.3 |
| Laying Angle C.V1 (%) | Laying Thickness C.V2 (%) | Stubble Height (cm) | |
|---|---|---|---|
| Optimal model value | 6.92 | 4.14 | 10.3 |
| Field actual value | 6.88 | 4.11 | 10.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, C.; Liu, C.; Wang, B.; Shi, H.; Sun, H.; Li, Y.; Hu, J. Research on the Operational Parameters and Performance of Key Components of an Industrial Hemp Harvester and Drier. Agriculture 2025, 15, 141. https://doi.org/10.3390/agriculture15020141
Feng C, Liu C, Wang B, Shi H, Sun H, Li Y, Hu J. Research on the Operational Parameters and Performance of Key Components of an Industrial Hemp Harvester and Drier. Agriculture. 2025; 15(2):141. https://doi.org/10.3390/agriculture15020141
Chicago/Turabian StyleFeng, Chao, Changxi Liu, Bosheng Wang, Hang Shi, Hao Sun, Yufei Li, and Jun Hu. 2025. "Research on the Operational Parameters and Performance of Key Components of an Industrial Hemp Harvester and Drier" Agriculture 15, no. 2: 141. https://doi.org/10.3390/agriculture15020141
APA StyleFeng, C., Liu, C., Wang, B., Shi, H., Sun, H., Li, Y., & Hu, J. (2025). Research on the Operational Parameters and Performance of Key Components of an Industrial Hemp Harvester and Drier. Agriculture, 15(2), 141. https://doi.org/10.3390/agriculture15020141







