Intelligent 3D Potato Cutting Simulation System Based on Multi-View Images and Point Cloud Fusion
Abstract
1. Introduction
2. Materials and Methods
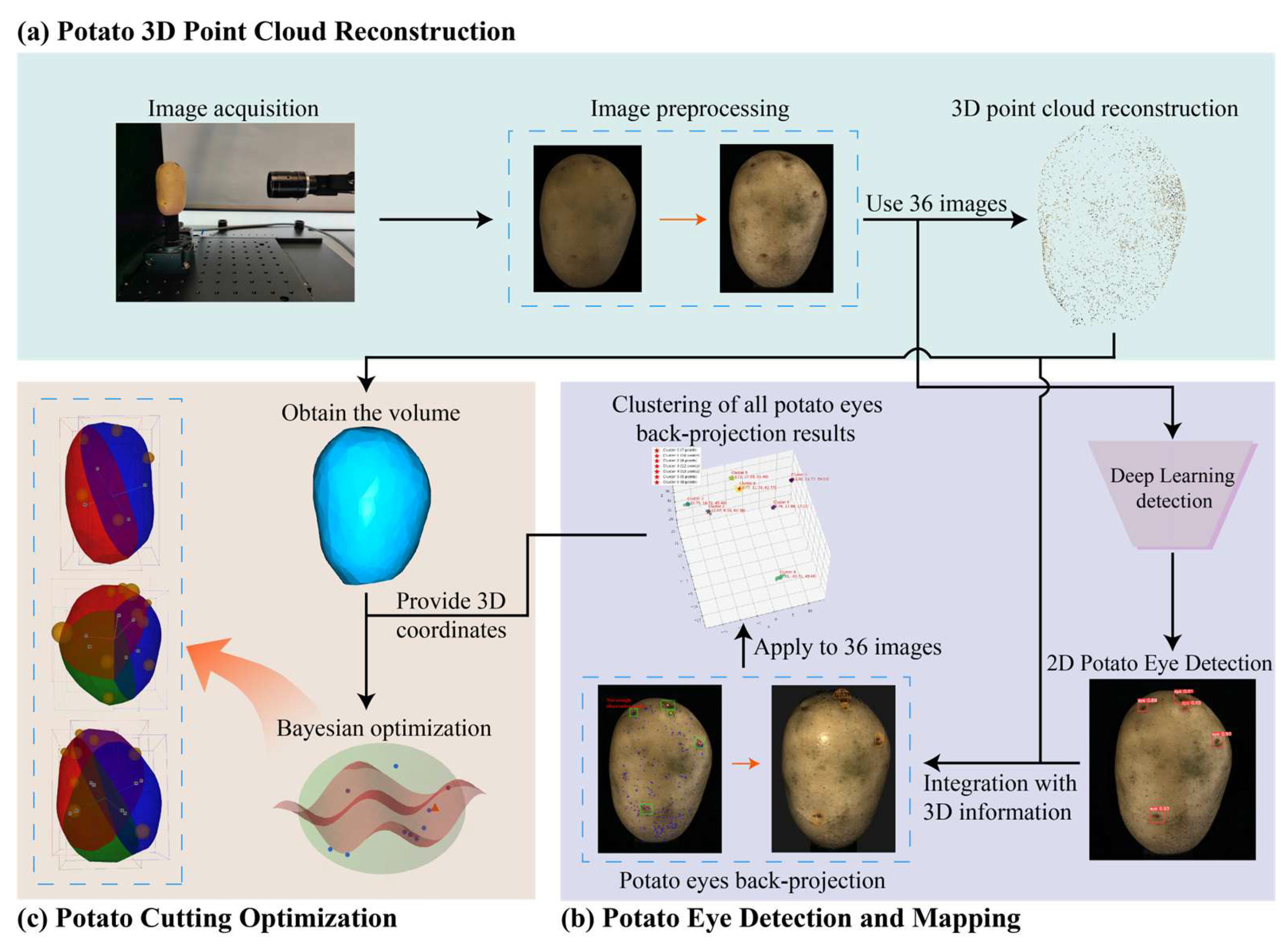
2.1. System Architecture
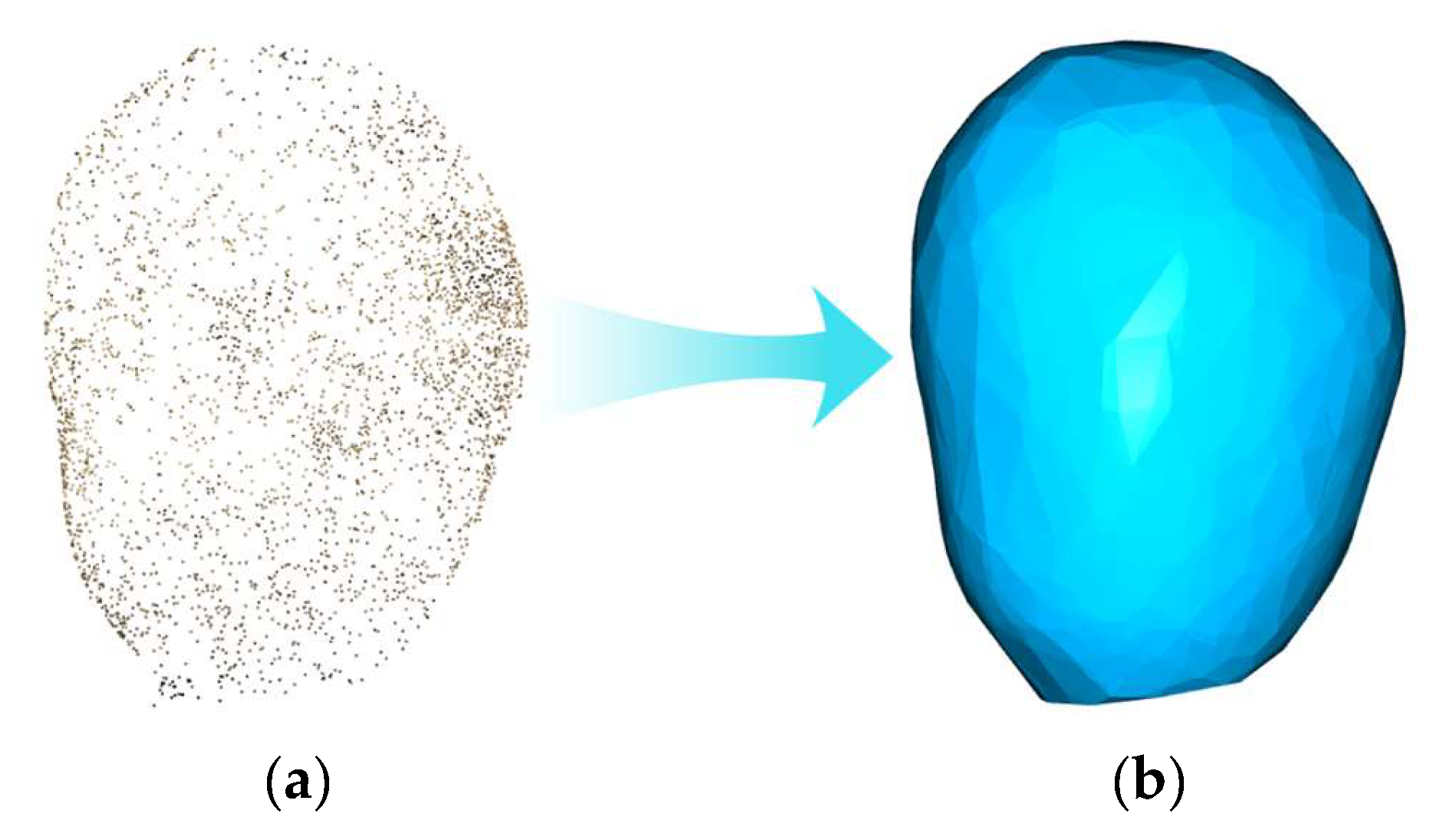
2.2. Potato 3D Point Cloud Reconstruction
2.3. Potato Eye Detection and Mapping
2.3.1. 2D-to-3D Back-Projection Method
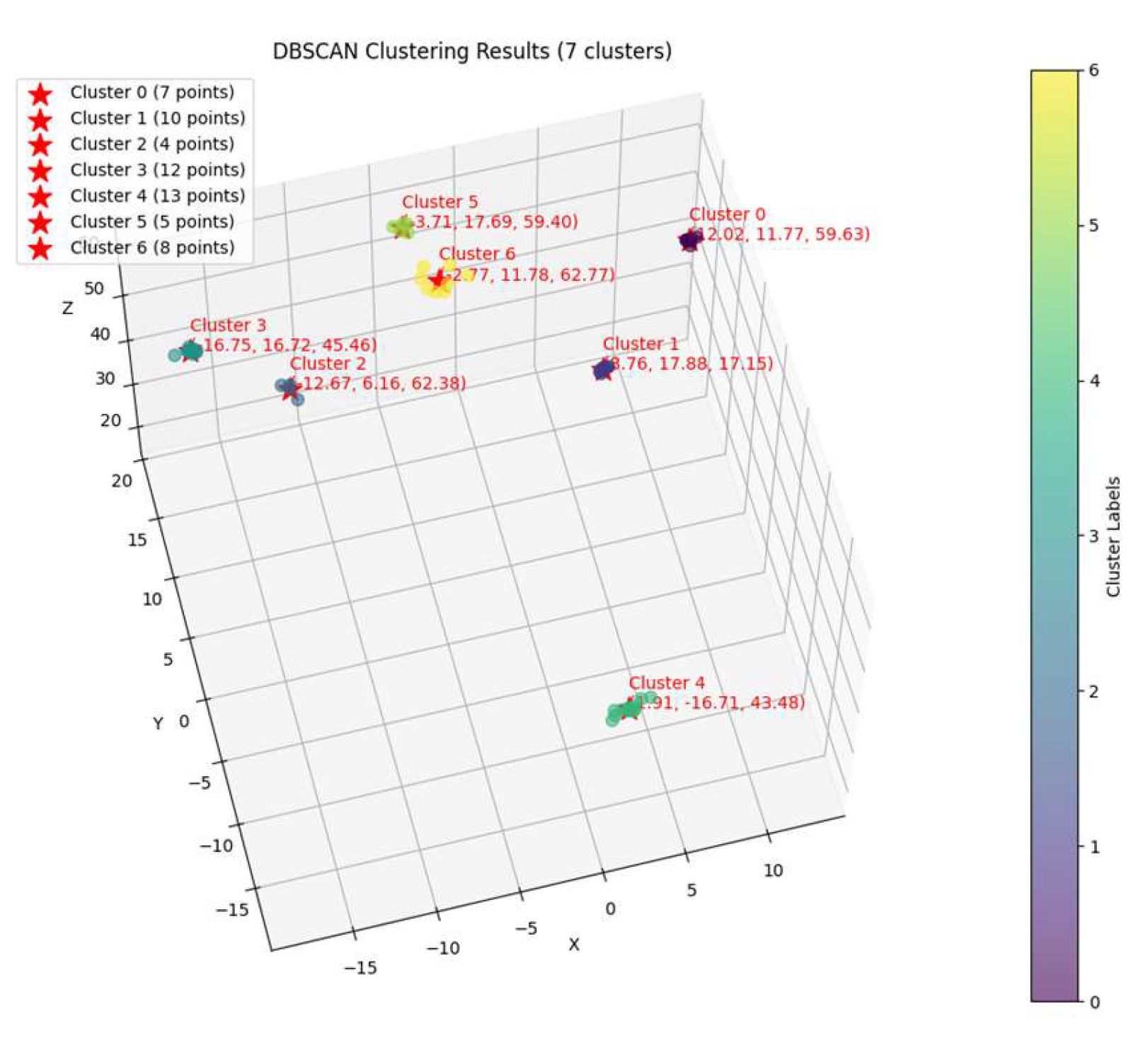
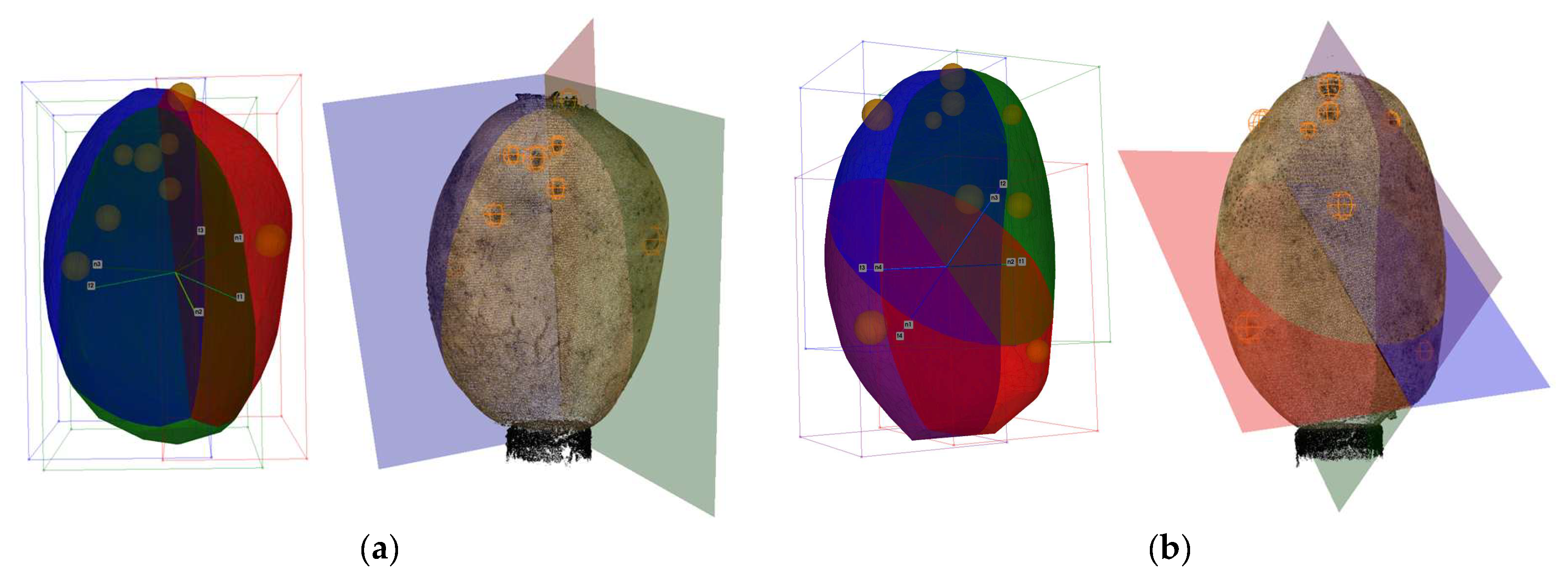
2.3.2. Multi-View Clustering
2.4. Potato Cutting Optimization
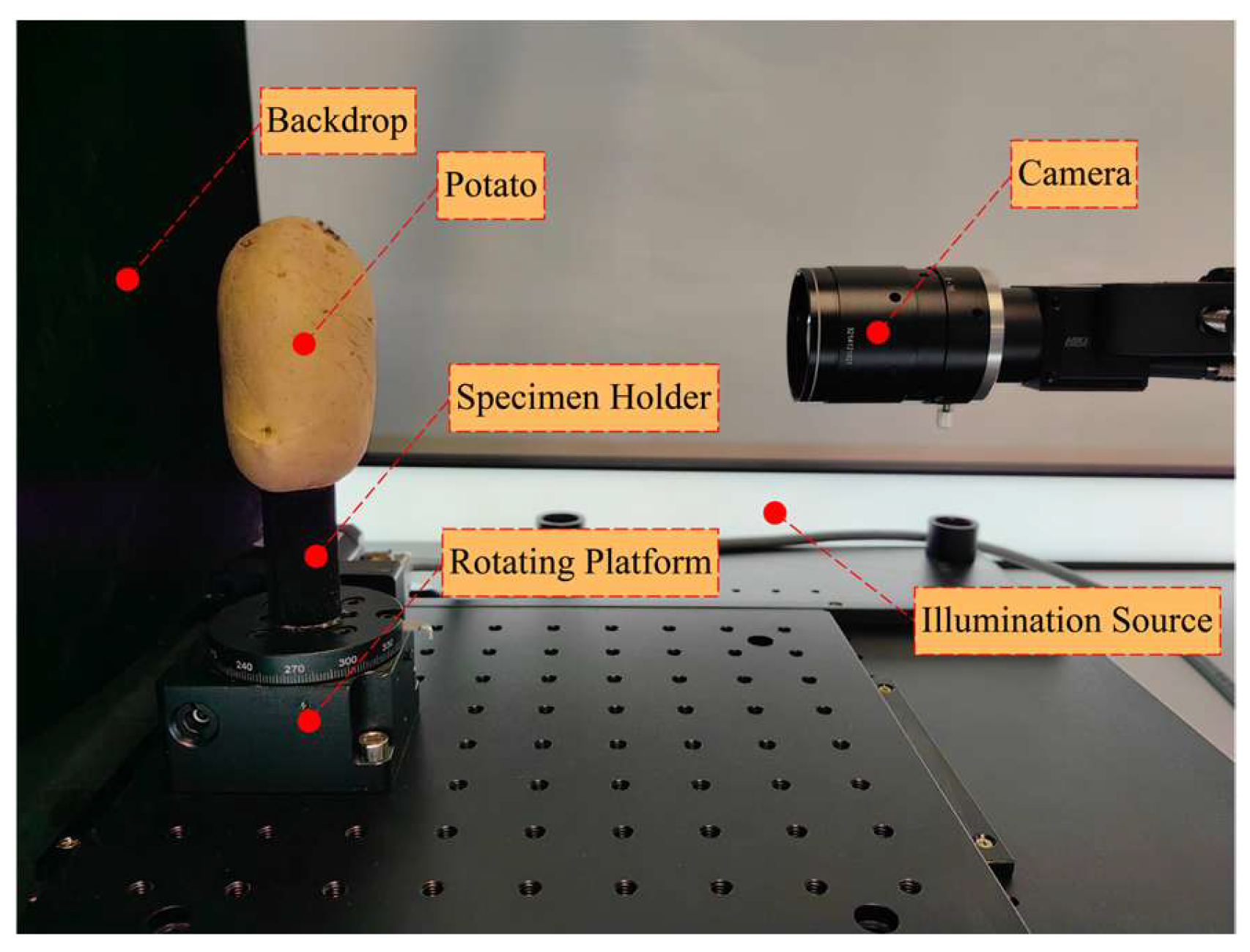
2.5. Experimental Setup
3. Results and Discussion
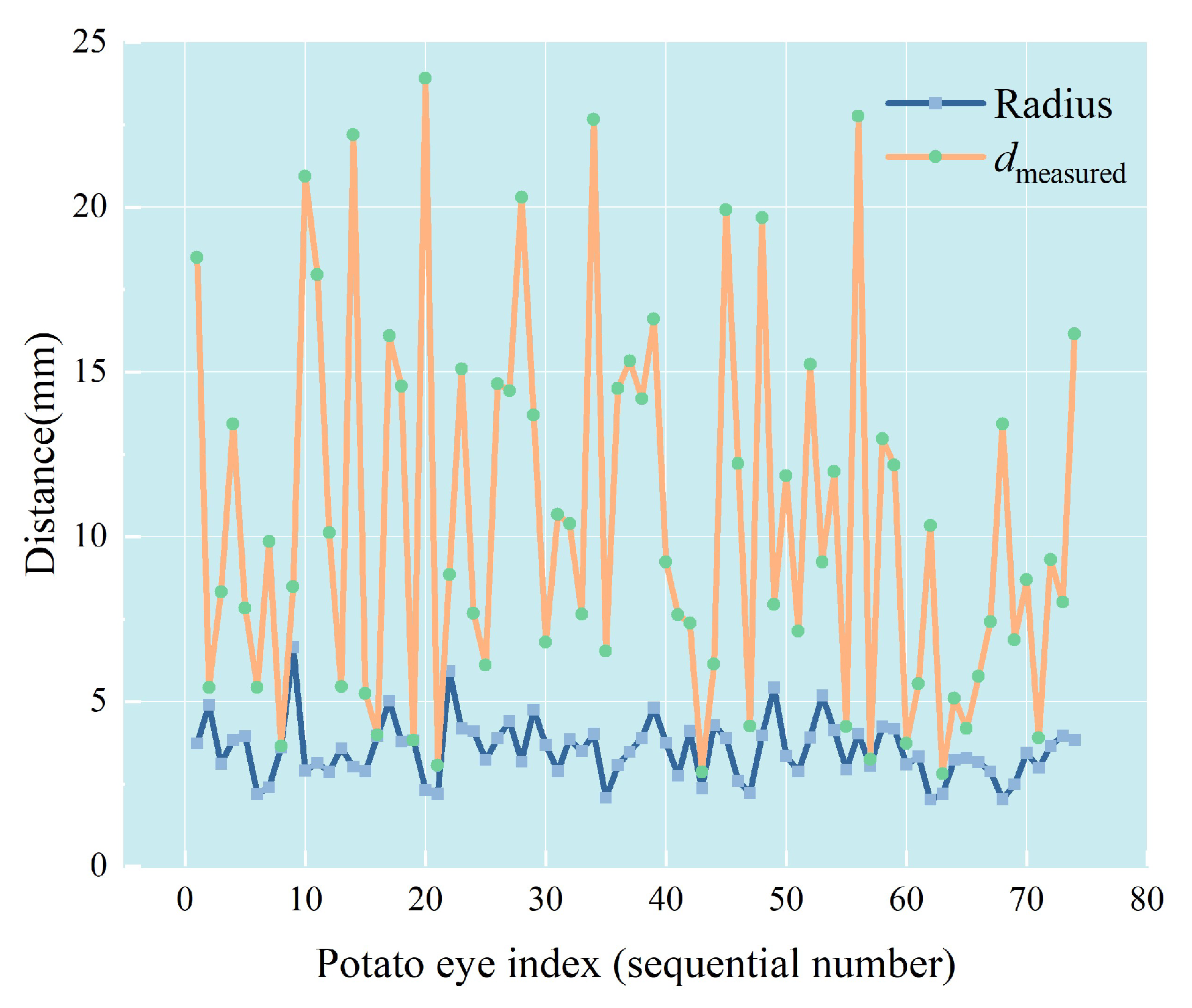
3.1. Potato Eye Detection and Mapping Results
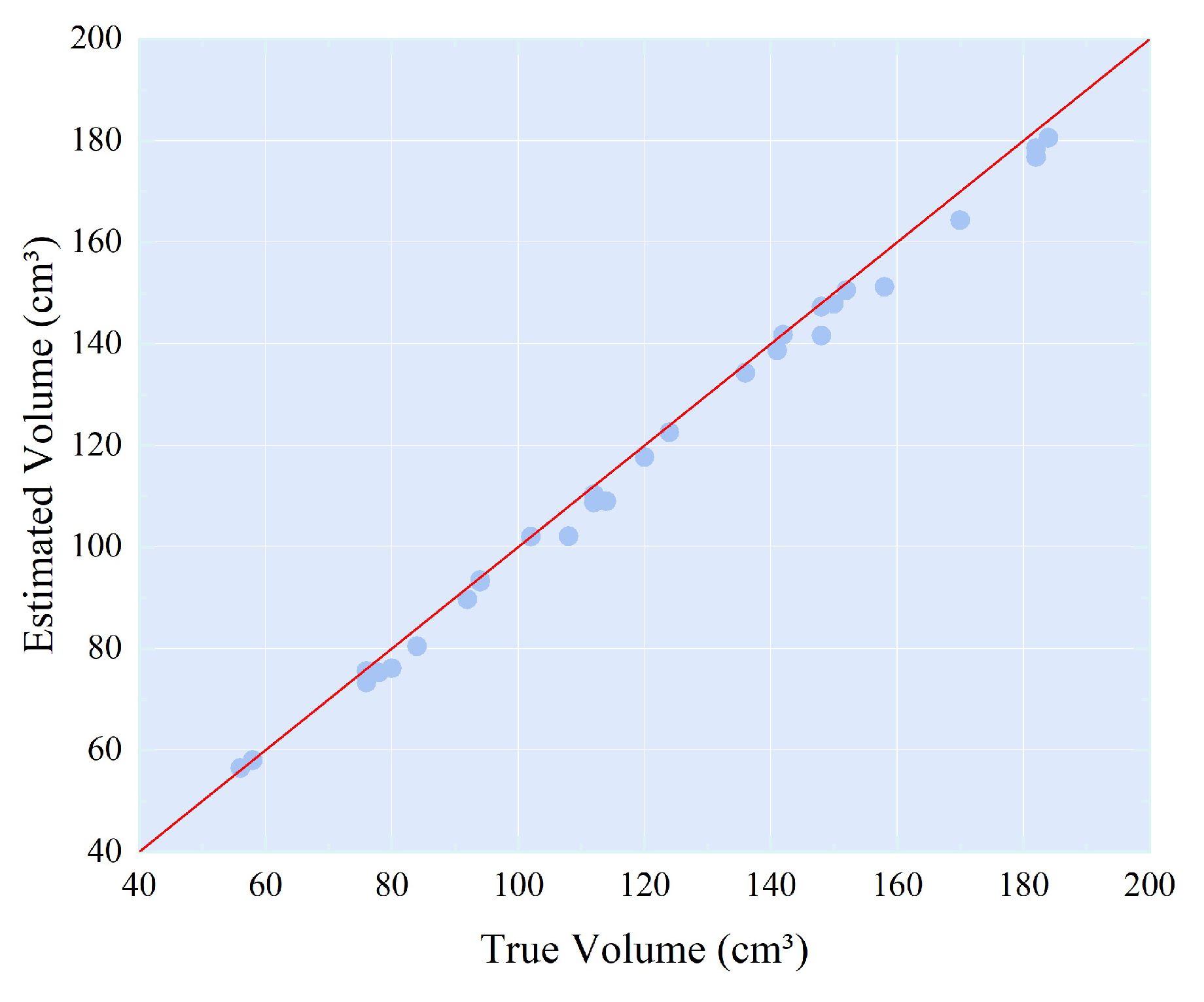
3.2. Volume Estimation Results
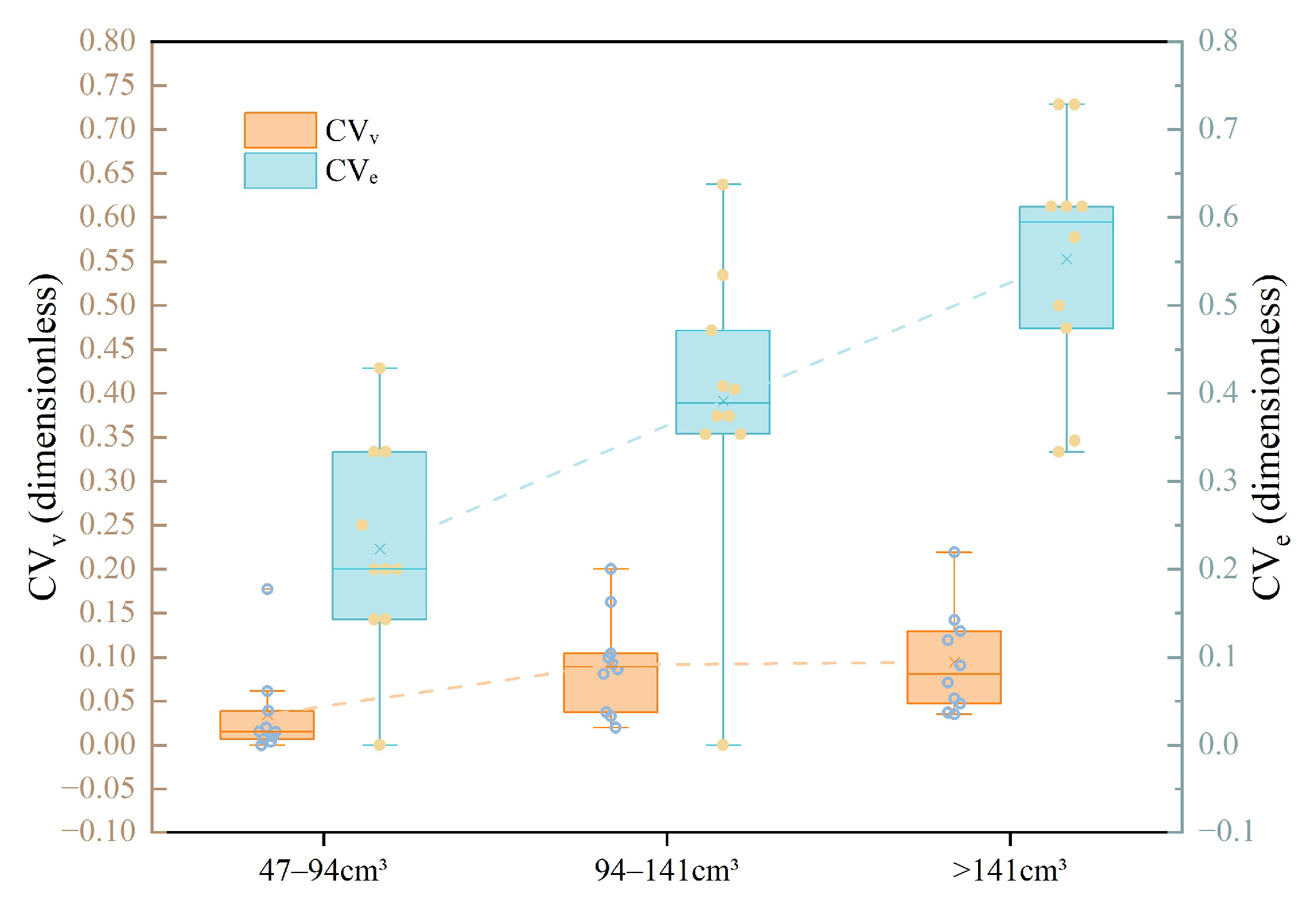
3.3. Cutting Optimization Results
3.4. Comprehensive Performance Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SfM | Structure from Motion |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| CVᵥ | Volume coefficient of variation |
| CVₑ | Potato eye count coefficient of variation |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| TP | True Positives |
| FN | False Negatives |
| FP | False Positives |
References
- Johnson, C.M.; Auat Cheein, F. Machinery for Potato Harvesting: A State-of-the-Art Review. Front. Plant Sci. 2023, 14, 1156734. [Google Scholar] [CrossRef]
- Food and Agriculture Organization Corporate Statistical (FAOSTAT). Crops and Livestock Products—Global Potato Production and Harvested Area Data (2012–2022). Available online: https://www.fao.org/faostat/en/#data/QCL (accessed on 22 August 2025).
- Huang, J.; Yi, F.; Cui, Y.; Wang, X.; Jin, C.; Cheein, F.A. Design and Implementation of a Seed Potato Cutting Robot Using Deep Learning and Delta Robotic System with Accuracy and Speed for Automated Processing of Agricultural Products. Comput. Electron. Agric. 2025, 237, 110716. [Google Scholar] [CrossRef]
- Lü, J.Q.; Yang, X.H.; Li, Z.H.; Li, J.C.; Liu, Z.Y. Design and Test of Seed Potato Cutting Device with Vertical and Horizontal Knife Group. Trans. Chin. Soc. Agric. Mach. 2020, 51, 89–97. [Google Scholar] [CrossRef]
- Barbosa Júnior, M.R.; Moreira, B.R.D.A.; Carreira, V.D.S.; Brito Filho, A.L.D.; Trentin, C.; Souza, F.L.P.D.; Tedesco, D.; Setiyono, T.; Flores, J.P.; Ampatzidis, Y.; et al. Precision Agriculture in the United States: A Comprehensive Meta-Review Inspiring Further Research, Innovation, and Adoption. Comput. Electron. Agric. 2024, 221, 108993. [Google Scholar] [CrossRef]
- Tian, H.; Wang, T.; Liu, Y.; Qiao, X.; Li, Y. Computer Vision Technology in Agricultural Automation—A Review. Inf. Process. Agric. 2020, 7, 1–19. [Google Scholar] [CrossRef]
- Yu, S.; Liu, X.; Tan, Q.; Wang, Z.; Zhang, B. Sensors, Systems and Algorithms of 3D Reconstruction for Smart Agriculture and Precision Farming: A Review. Comput. Electron. Agric. 2024, 224, 109229. [Google Scholar] [CrossRef]
- Masoudi, M.; Golzarian, M.R.; Lawson, S.S.; Rahimi, M.; Islam, S.M.S.; Khodabakhshian, R. Improving 3D Reconstruction for Accurate Measurement of Appearance Characteristics in Shiny Fruits Using Post-Harvest Particle Film: A Case Study on Tomatoes. Comput. Electron. Agric. 2024, 224, 109141. [Google Scholar] [CrossRef]
- Gené-Mola, J.; Sanz-Cortiella, R.; Rosell-Polo, J.R.; Escolà, A.; Gregorio, E. In-Field Apple Size Estimation Using Photogrammetry-Derived 3D Point Clouds: Comparison of 4 Different Methods Considering Fruit Occlusions. Comput. Electron. Agric. 2021, 188, 106343. [Google Scholar] [CrossRef]
- Vázquez-Arellano, M.; Reiser, D.; Paraforos, D.S.; Garrido-Izard, M.; Burce, M.E.C.; Griepentrog, H.W. 3-D Reconstruction of Maize Plants Using a Time-of-Flight Camera. Comput. Electron. Agric. 2018, 145, 235–247. [Google Scholar] [CrossRef]
- Ghahremani, M.; Williams, K.; Corke, F.; Tiddeman, B.; Liu, Y.; Wang, X.; Doonan, J.H. Direct and Accurate Feature Extraction from 3D Point Clouds of Plants Using RANSAC. Comput. Electron. Agric. 2021, 187, 106240. [Google Scholar] [CrossRef]
- Chen, C.; Li, J.; Liu, B.; Huang, B.; Yang, J.; Xue, L. A Robust Vision System for Measuring and Positioning Green Asparagus Based on YOLO-Seg and 3D Point Cloud Data. Comput. Electron. Agric. 2025, 230, 109937. [Google Scholar] [CrossRef]
- George, R.; Thuseethan, S.; Ragel, R.G.; Mahendrakumaran, K.; Nimishan, S.; Wimalasooriya, C.; Alazab, M. Past, Present and Future of Deep Plant Leaf Disease Recognition: A Survey. Comput. Electron. Agric. 2025, 234, 110128. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.; Chun, C.; Wen, Y.; Xu, G. Multi-Scale Feature Adaptive Fusion Model for Real-Time Detection in Complex Citrus Orchard Environments. Comput. Electron. Agric. 2024, 219, 108836. [Google Scholar] [CrossRef]
- Mirhaji, H.; Soleymani, M.; Asakereh, A.; Mehdizadeh, S.A. Fruit Detection and Load Estimation of an Orange Orchard Using the YOLO Models through Simple Approaches in Different Imaging and Illumination Conditions. Comput. Electron. Agric. 2021, 191, 106533. [Google Scholar] [CrossRef]
- Li, Y.H.; Li, T.H.; Niu, Z.R.; Wu, Y.Q.; Zhang, Z.L.; Hou, J.L. Potato Bud Eyes Recognition Based on Three-Dimensional Geometric Features of Color Saturation. Trans. Chin. Soc. Agric. Eng. 2018, 34, 158–164. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, X.; Huang, M.; Wang, X.; Zhu, Q. Multispectral Image Based Germination Detection of Potato by Using Supervised Multiple Threshold Segmentation Model and Canny Edge Detector. Comput. Electron. Agric. 2021, 182, 106041. [Google Scholar] [CrossRef]
- Xi, R.; Hou, J.; Lou, W. Potato Bud Detection with Improved Faster R-CNN. Trans. ASABE 2020, 63, 557–569. [Google Scholar] [CrossRef]
- Huang, J.; Wang, X.; Jin, C.; Cheein, F.A.; Yang, X. Estimation of the Orientation of Potatoes and Detection Bud Eye Position Using Potato Orientation Detection You Only Look Once with Fast and Accurate Features for the Movement Strategy of Intelligent Cutting Robots. Eng. Appl. Artif. Intell. 2025, 142, 109923. [Google Scholar] [CrossRef]
- Zhao, W.S.; Feng, Q.; Sun, B.G.; Sun, W. Optimization and Cutting Decision of Potato Seed Based on Visual Detection. For. Mach. Woodwork. Equip. 2024, 52, 76–82. [Google Scholar] [CrossRef]
- Wu, Y.; La, X.; Zhao, X.; Liu, F.; Yan, J. Design and Performance Testing of Seed Potato Cutting Machine with Posture Adjustment. Agriculture 2025, 15, 732. [Google Scholar] [CrossRef]
- Kalaitzakis, M.; Cain, B.; Carroll, S.; Ambrosi, A.; Whitehead, C.; Vitzilaios, N. Fiducial Markers for Pose Estimation: Overview, Applications and Experimental Comparison of the ARTag, AprilTag, ArUco and STag Markers. J. Intell. Robot. Syst. 2021, 101, 71. [Google Scholar] [CrossRef]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. EPnP: An Accurate O(n) Solution to the PnP Problem. Int. J. Comput. Vis. 2009, 81, 155–166. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD’96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Meng, L.; Wang, S.; Wang, C.; Wang, X.; Wang, W. Design of Potato Seed Cutter System on PLC and MCGS. J. Agric. Mech. Res. 2022, 44, 95–101. [Google Scholar] [CrossRef]
- Frazier, P.I. A Tutorial on Bayesian Optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar] [CrossRef]
- Gan, W.; Ji, Z.; Liang, Y. Acquisition Functions in Bayesian Optimization. In Proceedings of the 2021 2nd International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE), Zhuhai, China, 24–26 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 129–135. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Furuuchi, S.; Yamada, S. Verifying the Effect of Initial Sample Size in Bayesian Optimization. Total Qual. Sci. 2024, 10, 8–19. [Google Scholar] [CrossRef]






| Number of Observation Pixels | Average Distance (Pixels) | Recall |
|---|---|---|
| 1 | 22.29 | 94.2% |
| 2 | 20.87 | 94.1% |
| 3 | 19.36 | 94.1% |
| 4 | 22.26 | 92.7% |
| 5 | 23.28 | 89.9% |
| 6 | 23.5 | 86.4% |
| 7 | 26.83 | 82.6% |
| Number of Observation Pixels | Average Distance (Pixels) |
|---|---|
| 1 | 10.27 |
| 2 | 12.82 |
| 3 | 15.23 |
| 4 | 17.41 |
| 5 | 19.35 |
| 6 | 21.18 |
| 7 | 22.67 |
| Sample ID | Estimated Volume (cm3) | True Volume (cm3) | Absolute Percentage Error | Detected Potato Eyes | True Potato Eyes | True Positives (TP) | False Negatives (FN) | False Positives (FP) | Precision | Recall |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 80.5 | 84 | 4.17% | 7 | 7 | 7 | 0 | 0 | 100% | 100% |
| 2 | 75.33 | 78 | 3.42% | 6 | 7 | 6 | 1 | 0 | 100% | 86% |
| 3 | 122.59 | 124 | 1.14% | 10 | 10 | 10 | 0 | 0 | 100% | 100% |
| 4 | 73.33 | 76 | 3.51% | 6 | 7 | 6 | 1 | 0 | 100% | 86% |
| 5 | 110.18 | 112 | 1.62% | 6 | 7 | 6 | 1 | 0 | 100% | 86% |
| 6 | 89.68 | 92 | 2.52% | 7 | 7 | 7 | 0 | 0 | 100% | 100% |
| 7 | 76.12 | 80 | 4.85% | 6 | 6 | 6 | 0 | 0 | 100% | 100% |
| 8 | 102.04 | 102 | 0.04% | 10 | 10 | 10 | 0 | 0 | 100% | 100% |
| 9 | 57.97 | 58 | 0.05% | 7 | 8 | 7 | 1 | 0 | 100% | 88% |
| 10 | 75.58 | 76 | 0.55% | 5 | 5 | 5 | 0 | 0 | 100% | 100% |
| 11 | 93.12 | 94 | 0.94% | 5 | 8 | 5 | 3 | 0 | 100% | 63% |
| 12 | 56.43 | 56 | 0.77% | 5 | 5 | 5 | 0 | 0 | 100% | 100% |
| 13 | 147.81 | 150 | 1.46% | 7 | 6 | 6 | 0 | 1 | 86% | 100% |
| 14 | 102.15 | 108 | 5.42% | 9 | 10 | 9 | 1 | 0 | 100% | 90% |
| 15 | 108.68 | 112 | 2.96% | 7 | 7 | 7 | 0 | 0 | 100% | 100% |
| 16 | 134.3 | 136 | 1.25% | 8 | 9 | 8 | 1 | 0 | 100% | 89% |
| 17 | 150.6 | 152 | 0.92% | 8 | 8 | 8 | 0 | 0 | 100% | 100% |
| 18 | 93.49 | 94 | 0.54% | 7 | 7 | 7 | 0 | 0 | 100% | 100% |
| 19 | 138.68 | 141 | 1.65% | 7 | 8 | 7 | 1 | 0 | 100% | 88% |
| 20 | 108.97 | 114 | 4.41% | 8 | 7 | 7 | 0 | 1 | 88% | 100% |
| 21 | 110.37 | 112 | 1.46% | 8 | 8 | 8 | 0 | 0 | 100% | 100% |
| 22 | 117.7 | 120 | 1.92% | 3 | 5 | 3 | 2 | 0 | 100% | 60% |
| 23 | 176.79 | 182 | 2.86% | 8 | 8 | 8 | 0 | 0 | 100% | 100% |
| 24 | 164.36 | 170 | 3.32% | 9 | 8 | 8 | 0 | 1 | 89% | 100% |
| 25 | 180.57 | 184 | 1.86% | 8 | 8 | 8 | 0 | 0 | 100% | 100% |
| 26 | 141.74 | 142 | 0.18% | 9 | 9 | 9 | 0 | 0 | 100% | 100% |
| 27 | 151.18 | 158 | 4.32% | 5 | 6 | 5 | 1 | 0 | 100% | 83% |
| 28 | 178.55 | 182 | 1.90% | 8 | 8 | 8 | 0 | 0 | 100% | 100% |
| 29 | 141.56 | 148 | 4.35% | 6 | 6 | 6 | 0 | 0 | 100% | 100% |
| 30 | 147.27 | 148 | 0.49% | 9 | 9 | 9 | 0 | 0 | 100% | 100% |
| Mean | 116.92 | 119.5 | 2.16% | -- | -- | -- | -- | -- | 98% | 94% |
| Volume Range/cm3 | Sample Count | MAE | MAPE |
|---|---|---|---|
| 47–94 | 10 | 1.731 | 2.13% |
| 94–141 | 10 | 2.542 | 2.19% |
| >141 | 10 | 3.557 | 2.17% |
| Overall | 30 | 2.61 | 2.16% |
| Volume Range/cm3 | Number of Pieces | Mean CVᵥ | Mean CVₑ | Potato Eye Protection Rate |
|---|---|---|---|---|
| 47–94 | 2 | 0.0347 | 0.2230 | 100% |
| 94–141 | 3 | 0.0914 | 0.3911 | 100% |
| >141 | 4 | 0.0943 | 0.5525 | 100% |
| Overall | -- | 0.0735 | 0.3889 | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.; Chen, C.; Liu, F.; Xie, S. Intelligent 3D Potato Cutting Simulation System Based on Multi-View Images and Point Cloud Fusion. Agriculture 2025, 15, 2088. https://doi.org/10.3390/agriculture15192088
Xu R, Chen C, Liu F, Xie S. Intelligent 3D Potato Cutting Simulation System Based on Multi-View Images and Point Cloud Fusion. Agriculture. 2025; 15(19):2088. https://doi.org/10.3390/agriculture15192088
Chicago/Turabian StyleXu, Ruize, Chen Chen, Fanyi Liu, and Shouyong Xie. 2025. "Intelligent 3D Potato Cutting Simulation System Based on Multi-View Images and Point Cloud Fusion" Agriculture 15, no. 19: 2088. https://doi.org/10.3390/agriculture15192088
APA StyleXu, R., Chen, C., Liu, F., & Xie, S. (2025). Intelligent 3D Potato Cutting Simulation System Based on Multi-View Images and Point Cloud Fusion. Agriculture, 15(19), 2088. https://doi.org/10.3390/agriculture15192088





