Abstract
Making effective decisions about scaling up on-farm irrigation practices to the district level requires a comprehensive assessment of irrigation management at the farm level. In this context, a bucket-type water mass balance model was developed, calibrated, and validated over five irrigation seasons on a 121-hectare rice farm located in the lower Ter River valley (north-east Spain), to assess the water use efficiency and the impact of different irrigation practices on water savings. The model was implemented considering the spatial variability of the soils within the farm. It showed a satisfactory performance in both the calibration (2020, 2021, 2022) and validation (2023, 2024) cropping seasons, with NSE values greater than 0.50, PBIAS lower than ±20%, and RSR lower than 0.70. After model validation, the simulation of alternative water management practices revealed that the 10-day fixed-turn irrigation reduced irrigation water use by 30% compared to the traditional water management, although it may negatively impact rice yield. Simulations of an early irrigation cut-off at the end of the season and dry seeding with delayed flooding accounted for 17% and 15% irrigation water savings, respectively. The implementation of the no-runoff practice only accounted for a 6% reduction in water use. The water-saving potential of the simulated strategies was mainly driven by shortening the flooded period of rice paddies, thus demonstrating that managing the ponding water level is critical to diminishing water use in rice irrigation.
1. Introduction
Mediterranean rice agroecosystems, although representing a small fraction of the total worldwide rice production, are regionally significant for food production and for the provision of ecological services such as carbon sequestration [1], biodiversity preservation [2], and groundwater recharge [3,4]. Furthermore, rice production in the Mediterranean region contributes to the attainment of strategic policy goals in several countries, notably through the reinforcement of food system localization, adherence to high quality standards, fulfilment of local consumer preferences, and the creation of added economic value. However, the increasing frequency and severity of hydrological droughts in these regions due to climate change is placing additional pressure on these systems, where adequate water management is critical for their sustainability.
In recent decades, new water management strategies to produce rice using less water have been tested around the globe, mainly in Asian countries and the United States of America [5,6,7,8,9]. Nevertheless, to ensure proper implementation, an assessment must also be carried out in other regions, considering the specific rice varieties and crop management practices that can guarantee the environmental sustainability and economic viability of the rice farms [10].
Arouna et al. [11] and Mallareddy et al. [12] provided a comprehensive review of a wide range of water-saving technologies applied worldwide in irrigated rice production. Some studies assessing water-saving irrigation methods in Mediterranean rice cropping areas [13,14,15] show that dry seeding and delayed flooding (DFL) and alternate wetting and drying (AWD) are the most economically sustainable and promising irrigation methods to be considered as alternatives to traditional irrigation in this region, which is wet seeding and continuous flooding (WFL). As a matter of fact, DFL has shown 14–36% reductions in irrigation water use when compared to WFL in other areas within the Mediterranean basin [4,14]. Nevertheless, in other studies performed around the world no water savings have been reported [7,16]. Although such results are relevant, it should be noticed that the impact of these and other water-saving techniques is rarely assessed at farm and district levels, where the complex interactions between irrigation, groundwater recharge, runoff water, and groundwater reuse could affect the overall irrigation efficiency [17,18].
Calculating water mass balances in agricultural areas is fundamental to assess irrigation management strategies and to support water management decisions [19,20]. While water mass balances are commonly applied at field scale, where most experiments regarding new irrigation techniques and technologies are carried out, they become more complex when upscaling from a single field to groups of fields, farms, or irrigation districts that share irrigation distribution and drainage networks. Although district-level assessments are vital for regional water resource planning and governance, the hydrological outcomes are ultimately influenced by on-farm management decisions and practices. Adopting a farm-scale modelling approach provides a more accurate representation of site-specific management practices, water deliveries, soil properties, and hydrological responses. This level of detail is particularly relevant in paddy rice systems, where management heterogeneity can significantly impact irrigation demand and return flows. Furthermore, farm-level results can facilitate a more effective dialogue between irrigators and water authorities, improving transparency and enabling adaptive water governance—that is, a flexible and data-driven approach in managing water resources in response to the specific conditions of each farm.
Conceptual bucket water balance models are a practical and robust tool for assessing and making decisions about water management. Unlike physically based models, which simulate hydrological processes in greater detail, the bucket approach offers a computationally efficient and easy to calibrate alternative to simulate irrigation requirements in paddy fields. This is because the bucket approach is conceptually simple, requires limited input data, and lends itself to integration with operational monitoring frameworks, enabling their use for real-time applications and decision-making at the farm level. These models can be flexible enough to account for the spatial variability in features such as soil properties and irrigation management practices. The bucket approach implementation involves clustering irrigation fields with similar hydrological characteristics into larger hydrological response units (HRUs) for which the hydrological balance is then calculated. Knowledge of the topological relationships between the HRUs enables analysis of water distribution in an irrigation farm or district, and, in an additional step, the transport and accumulation of substances such as salts and nitrogen. This makes these models useful for evaluating the environmental impacts associated with water management [21,22].
This study aims to develop, calibrate, and validate a bucket mass balance model to evaluate the effect of different water-saving rice irrigation methods at farm-scale. Although a recent study has proved the bucket methodology effective at the district-scale [18], this work expands its application to the farm level. This is particularly relevant in the study area, where persistent hydrological droughts [23] combined with strong competition for water resources, highlight the urgent need for efficient water management strategies.
This paper is structured in four main sections: introduction, materials and methods, results and discussion, and conclusions. Section 2 first provides a general description of the study farm. This is followed by a detailed description of the model and its parametrization, calibration, and validation criteria, thereby ensuring its replicability in other study areas. Finally, the alternative water management practices that were modelled and the indicators used for their evaluation are described. Section 3 begins by presenting the model conceptualization and parametrization results, followed by a goodness-of-fit evaluation, and it ends by discussing the results from the simulated water management scenarios, using both numerical and graphical data. Finally, Section 4 highlights the most relevant results of this work, as well as their impact on irrigation water management.
2. Materials and Methods
2.1. Experimental Farm
The experimental farm, which includes 121 hectares of rice, is located in the lower valley of the Ter River in Girona, Spain. This area, known as ‘Baix Ter’, covers approximately 1000 hectares of rice. The farm’s geographical coordinates are 42°00′57.8″ N, 3°09′26.0″ E (Figure 1). The soils are classified as Aquic Xerofluvents [24], and the soil texture of the first 30 cm varies spatially from loam to silty clay loam. Experimental data was retrieved during five cropping seasons (2020–2024) both at farm-scale and in two representative fields of the farm.
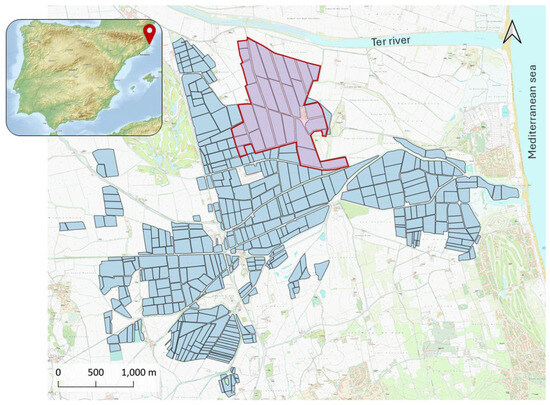
Figure 1.
The experimental farm location (red area) within the Baix Ter rice irrigation district (blue area). Each polygon represents a rice field.
The study area has a Mediterranean climate, with an average annual rainfall of 399 mm between 2020 and 2024, concentrated in spring and autumn. The mean annual reference evapotranspiration (ETo) was 2.53 mm day−1 during the same period, with the highest values recorded in July (mean of 4.85 mm day−1). In the rice agroecosystem, the traditional irrigation practice is WFL (water seeding and continuous flooding) combined with a continuous or punctual runoff of the fields and irrigation until harvest. However, over the past decade, other irrigation strategies have been introduced due to water management constraints in the region.
Irrigation water was taken from the Ter River by the Irrigation Consortium and was delivered to the farm in 7 to 14 days shifts over three consecutive days, following a rotational calendar. Additionally, the water deliveries from the Irrigation Consortium were supplemented by discharges lifted by an Archimedes screw located at the farm’s main water inlet. The average electrical conductivity of the irrigation water was 0.67 ± 0.10 dS m−1, with a sodium adsorption ratio of 1.11 ± 0.38. According to the guidelines of Ayers and Westcot [25], the observed values are considered adequate for rice irrigation. The farm had its own water distribution network, consisting of ramified parabolic section channels made of reinforced concrete, with a maximum discharge capacity of 0.40 m3 s−1. On average, the fields of the farm had one irrigation inlet and one drainage outlet per hectare. All inlets were regulated using gate valves with an inner diameter of 150 mm, and all outlets were using butterfly valves with an inner diameter of 160 mm. However, the outlets were not used in the experimental farm during the period 2020–2024 because the no-runoff strategy was applied.
One month before sowing, all the farm’s fields were annually levelled to a 0% slope using a dual grade laser (GL722, Spectra Precision, Dayton, OH, USA), achieving an accuracy of ±1.59 mm. Sowing took place from May to early June, and harvesting took place from mid-October to mid-November. The irrigation strategy adopted was DFL (dry seeding and delayed flooding), except for a 1.2-hectare field during the 2020–2022 period, where WFL was implemented. Irrigation management involved maintaining the fields flooded with a variable ponding water table throughout the season, except for during pesticide treatments (herbicide or fungicide applications) and for approximately 30 days before harvest (early cut-off).
2.2. Model Description
A bucket mass balance approach was set up to calculate the daily water balance of the study farm. To achieve this, a topological diagram was developed to represent the water flow directions within the farm. This diagram showed how the irrigated fields were connected through the irrigation distribution and drainage networks (see Section 3.1). Spatial soil variability was considered by assigning a soil category to the fields with similar hydraulic characteristics. Information was collected from the 1:25000 soil map of the area [26], from a 1:5000 specific soil study carried out in the farm and involving 22 soil pits and 12 auger drillings, and from textural analyses executed in 2018 within the upper 30 cm of the 28 fields of the farm. Two soil categories were identified within the farm. Consequently, fields sharing the same irrigation network ramification, draining to the same drainage ditch, and belonging to the same soil category were clustered into the same hydrological response unit (HRU).
The daily water balance (Equation (1)) was calculated in each HRU considering the lower part of the root system and the top of the ponding water level as boundaries of the control volume.
where V is the water storage (mm); I is the irrigation (mm); P is the precipitation (mm); ETc is the crop evapotranspiration (mm); R is the water runoff (mm); DP is the percolation (mm); i is the day for which the water balance is computed; and j is the HRU.
The water storage term of the water balance was defined as:
where Vθ is the soil water storage (mm) and Vh is the ponding water depth (mm).
The water balance was calculated from one day before rice sowing until the harvest in order to quantify the daily values of the water balance terms for the entire farm.
The model was driven by a management input, defined as the target ponding water depth (Vhtarget), representing the desired ponding water level to be maintained in the paddy fields above the soil surface. This variable reflected an active decision in rice irrigation management and was the system’s main control variable. At each time step, the irrigation depth for each unit was calculated as the amount of water needed to restore the water storage to the target value from the current state:
where Vθsat is the soil water depth at saturation (mm).
When the application of Equation (3) resulted in a value exceeding the unit’s maximum daily hydrant supply capacity, this limit was considered.
Daily precipitation (P) was one of the model’s inputs. For water balance calculations, only precipitation events occurring between one day before sowing and the harvesting date of each HRU were considered. Consequently, different seasonal precipitation values were obtained among the HRUs depending on their sowing dates, leading to P also being treated as a model output.
ETc was assumed to be equal to potential evapotranspiration and was calculated using reference evapotranspiration (ETo) and single crop coefficients (Kc), as suggested by Allen et al. [27]:
Water runoff was calculated for each unit using a corrected version of the Torricelli principle that incorporates a coefficient to account for energy losses under real operating conditions:
where c is the valve coefficient (dimensionless); x is the drainage valve opening fraction (0 ≤ xi ≤ 1); and 8640 is a unit conversion factor.
Vertical percolation was calculated by linking the model with Hydrus-1D [28]. Specifically, different soil matric potentials were simulated in Hydrus under unsaturated and saturated conditions. Then, the vertical water infiltration in the bottom boundary of the control volume was retrieved, and linear regressions with V were obtained. A more detailed description of this process is provided in Section 2.4.2.
where a is the slope of the linear regression (day−1); and b is the interception parameter of the linear regression (mm). Their values are different under unsaturated () and saturated () conditions.
In the water balance equation, the variables I, R, and DP were dependent on V (Equations (3), (4), (6), and (7)), while V itself depended on I, R, and DP, as well as of P and ETc (Equation (1)). To address the co-dependency of these variables computationally, an iterative approach was employed. This involved updating V continuously until achieving a complete closure of the water balance. These iterations were computed using the modified Newton–Raphson numerical method, in which the V value in each subsequent iteration was calculated as follows:
where k is referring to the iteration number, α is the damping factor, and F(V) is referring to the water balance equation obtained from Equation (1):
Since Vi−1,j,k, Pi,j,k, and ETci,j,k in Equation (10) were constants, the F(V) derivative was computed as:
A flowchart of the modelling process, as well as the illustration of the model inputs, parameters, and outputs is shown in Figure 2.
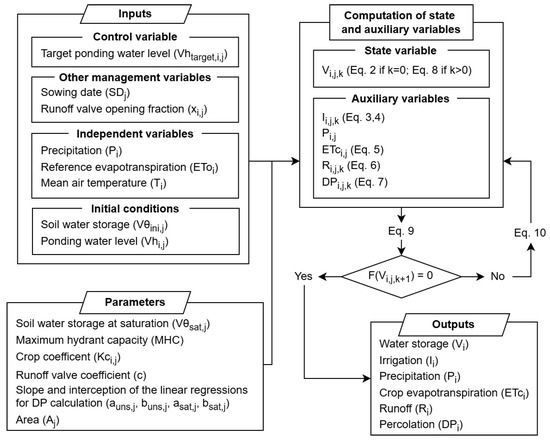
Figure 2.
Flowchart of the modelling and the Newton–Raphson iteration processes.
2.3. Model Parametrization
The model was parametrized using data collected at both farm and field spatial scales during the 2020, 2021, and 2022 cropping seasons. To achieve this, two 1.2-hectare fields, each representative of a soil category, were selected for further monitoring. This approach was implemented to improve the accuracy and representativeness of the water balance estimates under contrasting percolation conditions. As a result, field 1 was representative of soil category I, and field 2 was representative of soil category II.
Soil water content at saturation for each soil category was determined using the maximum values recorded by Drill and Drop probes (Sentek, Stepney, Australia) having a declared accuracy of 0.03%. These probes were installed in the two monitored fields, which were subjected to prolonged soil saturation conditions due to the irrigation practice.
The maximum hydrant capacity was set according to the maximum values recorded by the flow meters installed in the two monitored fields. The technical specifications of these instruments are reported in Section 2.4.2.
Single crop coefficients (Kc) were set according to Pereira et al. [29] recommendations. These values varied with the rice development stage (initial, development, midseason, and final) and the irrigation practice of each HRU (WFL, DFL, irrigation until harvest, and early cut-off). The duration of each stage was parametrized by adjusting the Kc curve to the temporal evolution of the rice canopy cover. To achieve this, the crop canopy cover was measured on a weekly basis by taking four images at 2 m above the soil surface at solar noon for each date and field. These images were then processed using the Canopeo App [30], which allowed the quantification of the percentage of the soil surface that was covered by the rice leaves. Finally, the mean value of canopy cover value for each date and field was considered and graphically represented as function of the accumulated growing degree days (GDD). The duration of the development stages was expressed in accumulated GDD instead of natural days to allow for a more accurate ETc calculation.
Finally, the runoff valve coefficient was parametrized according to the valve’s technical specifications, which provided information regarding its discharge coefficient.
2.4. Calibration and Validation of the Model
The model was calibrated using data collected at farm and field scales during the 2020, 2021, and 2022 cropping seasons, and it was then validated using data from the 2023 and 2024 seasons. Calibration and validation involved assessing the goodness-of-fit between simulated and observed irrigation data at both the farm and field levels using the metrics described in Section 2.4.3.
Observed irrigation data at the farm scale were provided by NivuFlow 750 (NIVUS, Eppingen, Germany) volumetric water meters, with a declared accuracy of ±1%. Irrigation discharges at field scale were measured using the ultrasonic flow meter CZ Octave US DN150 (Contazara, Zaragoza, Spain) in field 1 and the tangential turbine meter CZ TJ125 (Contazara, Zaragoza, Spain) in field 2, both with a declared accuracy of ±1%.
2.4.1. Input Data
The daily target ponding water level for model calibration and validation purposes was set according to experimental measurements carried out in the monitored fields. Specifically, water level above ground surface was measured in the two fields using the radar transmitter Sitrans LR100 (Siemens, Munich, Germany), with an accuracy of ±0.005 m. After the first flooding event in DFL, these registers were averaged between the two fields for each time step of the water balance, and these values were used in all the HRUs of the farm.
The sowing dates and the daily drainage valve opening fraction of each HRU were set according to the farmer’s operations.
Daily values of precipitation, reference evapotranspiration, and mean air temperature were obtained from the nearest agro-climatic meteorological station belonging to the network of automatic meteorological stations of the Catalan Meteorological Service [31].
The initial soil water storage and ponding water level of each year and soil category was set according to the registers provided by the multilevel Drill and Drop probes and by the radar transmitters Sitrans LR100 in the two monitored fields of the farm.
2.4.2. Model Calibration
The calibration process consisted of adjusting the slope and interception parameters of the DP equation (Equations (7) and (8)) for each soil category until a satisfactory agreement between the simulated and the observed irrigation was achieved at both spatial scales. To this end, the bucket-model was linked with the percolation outputs obtained from Hydrus-1D under steady-state conditions.
Firstly, sand, silt, and clay mineral fractions and bulk density within the upper 30 cm (model boundary) were quantified in both monitored fields. Bulk density was characterized as the mean value of three undisturbed soil samples collected at two different layers (0–20 and 20–30 cm depth) to account for the possible higher density and lower permeability of the compacted bottom layer, which would be the result of the puddling operations in rice fields. Then, the van Genuchten [32] and Mualem [33] parameters of each layer were estimated from these soil properties using the Rosetta pedotransfer functions [34] (Table 1).

Table 1.
Soil hydraulic properties for the two monitored fields in Hydrus-1D based on the van Genuchten–Mualem model.
The van Genuchten–Mualem soil hydraulic properties allowed the simulation of DP in Hydrus-1D under unsaturated (−40, −30, −20, −10, and −5 kPa of soil matric potential) and saturated (0, 5, 10, 15, and 20 cm of ponding water depth) conditions. Then, the water infiltration below the control volume in Hydrus-1D was graphically represented as function of these simulation conditions, which were expressed as water storage within the control volume (Vj). Afterwards, the DP linear equations were adjusted for each soil category.
Finally, irrigation in the two fields and in the whole farm was simulated using the bucket mass balance model. If the goodness-of-fit of the irrigation output at both spatial scales was not satisfactory, a calibration of the soils hydraulic conductivity (Ks) of the compacted layer was performed and new parameters of the DP equations were obtained. In this context, Ks was considered as an adjustment parameter, considering the combined effect of the soil texture, structure, and other non-controlled variables such as the existence of contour drains at the perimeter of the fields, which increase vertical percolation below the control volume due to higher subsurface fluxes flowing to the drainage ditches. Consequently, in the context of this conceptually based model, Ks should not be treated as an inherent parameter derived from soil texture, but rather as an effective and functional parameter. A scheme of the calibration process is shown in Figure 3.
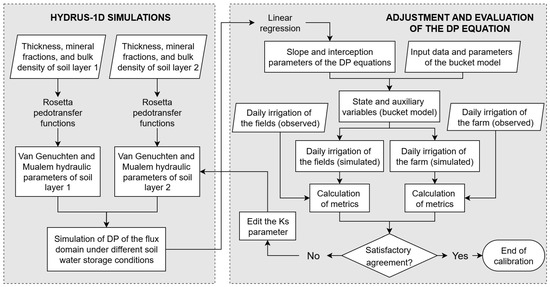
Figure 3.
The flowchart illustrates the calibration procedure for the slope and interception parameters of the percolation functions. This process was carried out for the two soil categories within the farm.
2.4.3. Model Performance
The goodness-of-fit of the model was evaluated using statistics and graphical data representation.
The selected statistics were the Nash–Sutcliffe efficiency index (NSE) [35], the percent bias (PBIAS, expressed in %) [36], the coefficient of determination (R2), the root mean square error (RMSE, expressed in m3 day−1), and the RMSE-observation standard deviation ratio (RSR) [37].
where Oi are the observed values; Pi are the simulated values; is the mean of the observed values; is the mean of predicted values; and n is the number of predicted or observed values.
A 5-day moving average filter was applied to the daily data to reduce the impact of short-term variability and better capture the overall system dynamics. This approach is commonly used to improve model performance and interpretability, especially when working with simplified models and noisy input data [37,38].
The interpretation of the statistical indicators was based on the work of Moriasi et al. [37,39], who reported that a satisfactory model performance is achieved when NSE > 0.5, PBIAS < ±25%, R2 > 0.60, and RSR ≤ 0.70.
2.5. Scenarios of Alternative Water Management Practices
Once the model had been calibrated and validated, five water management scenarios (A, B, C, D, and E) were simulated for the study period (2020–2024). These scenarios were defined according to actual water management strategies that the rice farmers and the Irrigation Consortium were implementing in the area. Scenarios A and B were designed to reflect the traditional irrigation practices in the area, that is, all the HRUs were managed by adopting WFL, there was continuous ponding water level and drainage valves were opened to drain the fields prior to pesticide treatments. Additionally, scenario A assumed that the ponding water level was maintained in the field until harvest, whereas scenario B modelled the situation of closing the irrigation water inlets approximately one month before harvest, during the crop maturation stages (early cut-off).
Scenario C simulated water distribution within the farm under the assumption that WFL and early cut-off were implemented and that the drainage valves were closed throughout the entire irrigation period (no-runoff); thus, the water use reduction associated with the closure of the runoff valves could be evaluated.
Scenario D simulated water distribution if all fields were DFL managed, alongside the no-runoff and early cut-off practices. As in the previous scenarios, a continuous ponding water table was considered during the irrigation period.
Finally, scenario E simulated the effect of the fixed-turn irrigation, whereby water would be delivered to the HRUs for three consecutive days in ten-days shifts, following the Irrigation Consortium’s rotational calendar. The other inputs of this scenario were equal to those of scenario D; thus, DFL, no-runoff and early cut-off practices were implemented in all units.
A summary of the water management practices simulated in each scenario is provided in Table 2.

Table 2.
Combination of the water management practices that were simulated in each scenario.
In the scenario simulations, the daily target ponding water level was set based on rice phenological stages and the International Rice Research Institute recommendations [40]: 3 cm during the initial stage, 5 cm during the development stage, and 10 cm from the midseason stage to the end of irrigation. Sowing dates were scheduled according to a standard calendar reflecting the farmers’ usual practice during the study period (2020–2024) and taking into account the maximum flow capacity of the irrigation network. The daily drainage valve opening fraction for each HRU was set according to the purpose of each scenario. Finally, the data on initial soil water storage, initial ponding water level, daily values of precipitation, reference evapotranspiration, and mean air temperature were the same as those used during the model calibration and validation phases.
2.6. Water Management Indicators
Irrigation performance of the simulated scenarios was assessed using four indicators: Relative Irrigation Supply (RIS), Relative Water Supply (RWS), Irrigation Consumptive Use Coefficient (ICUC), and Deep Percolation Fraction (DPF). All of them were computed from the seasonal model outputs. The indicators were calculated as follows:
where I is irrigation (mm), P is precipitation (mm), ETc is potential crop evapotranspiration (mm), DP is percolation (mm), and is the water storage variation (mm).
3. Results and Discussion
3.1. Model Development
3.1.1. Conceptualization of the System
The topological diagram representing the major irrigation and drainage water flows in the study farm, while also considering the spatial soil variability, is presented in Figure 4. As shown, the conceptualization of the system resulted in clustering the 28 fields of the farm into 15 units. Soil I was assigned to units 3, 5, 7, 9, 12, 13, 14, and 15, and soil II was assigned to the other units.
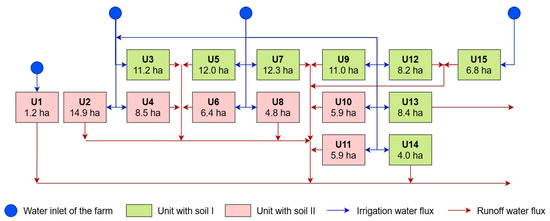
Figure 4.
Topological diagram conceptualizing HRUs and their interconnections.
3.1.2. Model Parameters
The model parameters that resulted from the data collection in 2020, 2021, and 2022 are shown in Table 3.

Table 3.
Quantification of the model parameters.
3.2. Model Calibration and Validation
The model was calibrated and validated by comparing the irrigation discharges measured in the two monitored fields and at the farm level during the 2020–2024 irrigation seasons. Table 4 shows the calibrated linear regression parameters of the functions linking DP with V for each soil category, which were obtained using Hydrus-1D with a flux domain of 30 cm (the maximum rooting depth). Table 5 shows the performance indices calculated for the calibration and validation periods.

Table 4.
Calibrated parameters for the linear functions linking DP and V for the two soil categories on the farm (Equation (7)). The coefficient of determination (R2) of the linear regressions is shown, as well as the V value for which the equations are valid.

Table 5.
Model performance statistics for five-day moving averages in the 2020–2024 irrigation seasons.
During the calibration and validation periods, the NSE produced values greater than 0.5 for all years and spatial scales (Table 5). PBIAS was lower than ±10% in all cases except in 2023, when it accounted for −19.5% at the farm scale. R2 was greater than 0.60 in all cases except for field I in 2020, for which it was 0.54. The RMSE results oscillated between 6.6 and 11.7 mm day−1 at the field scale, and between 2.6 and 4.0 mm day−1 at the farm scale. The RSR index was below 0.70 in all cases, indicating that the RMSE values can be considered as low. Similar model goodness-of-fit was observed in the calibration and validation periods, although slightly better NSE values were obtained in the validation period in Field 1. This situation might be the result of a higher variability of the experimental data during the calibration period in this field, thus slightly reducing the goodness-of-fit of the model during the calibration years in comparison to the validation period. Overall, the results of the computed statistics indicated a satisfactory model performance for the five-day moving averages of the daily data.
A graphical representation of the observed and simulated irrigation discharges (Figure 5) enabled periods of significant discrepancy to be identified, as well as their impact on the accumulated discharges at the end of the season. Generally, the simulated values corresponded well with the observed discharges, as demonstrated by the model evaluation indexes (Table 5).
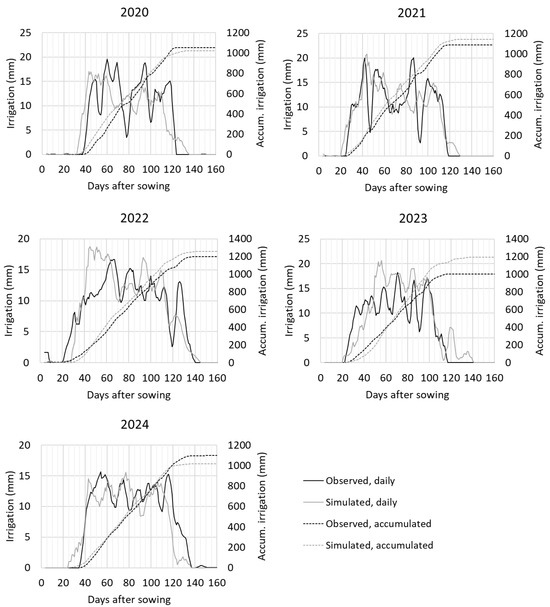
Figure 5.
Five-day moving average pattern of observed and simulated irrigation discharges on the study farm throughout the irrigation seasons 2020–2022 (calibration) and 2023–2024 (validation). Both daily and accumulated data are presented.
Additionally, the goodness-of-fit of the observed and simulated irrigation was also satisfactory when considering the seasonal data instead of the daily values. In fact, considering both the field and the farm spatial scales (Figure 6) resulted in an NSE of 0.98, a PBIAS of 0.9%, an R2 of 0.99, an RMSE of 92.8 mm season−1, representing just 7% of the seasonal inputs, and an RSR of 0.15.
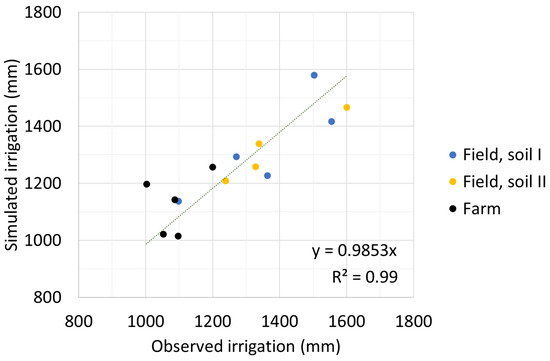
Figure 6.
Observed vs. simulated irrigation discharges at field and farm scales during the 2020–2024 cropping seasons.
3.3. Simulation of Alternative Water Management Scenarios
3.3.1. Water Mass Balance Results
The seasonal results of the alternative water management scenarios described in Section 2.6 are presented in Table 6. Specifically, it shows the averages and standard deviations of the irrigation seasons 2020–2024.

Table 6.
Simulated water balance terms for the two soil categories and the whole farm considering the five water management scenarios in the period 2020–2025. Averages and standard deviations for the period 2020–2024 are shown.
The irrigation water use resulting from the scenario analysis was approximately between 1200 and 3100 mm. These values varied depending on the scenario and soil category but were consistent with those reported by other authors in the Mediterranean region [4,14,18,41,42]. Additionally, the model showed that soil I always resulted in lower irrigation requirements than soil II; however, in scenario E, these differences were less important than in the other cases. The lower irrigation requirements in soil I were consistent with its lower percolation fluxes and demonstrate the importance of percolation in determining the necessary irrigation requirements to restore the ponding water level. Furthermore, given the recurrent hydrological droughts in the region, these results suggest that if a reduction in the rice cropping area is necessary, farm decision-makers should prioritize irrigating soil I over soil II to maximize water productivity.
During the 2020–2024 cropping seasons, precipitation averaged 181 mm, accounting for 6–12% of total water inputs at the farm level. These differences were due to the variable contribution of irrigation to total water inputs depending on the scenario. Crop evapotranspiration also differed slightly depending on the irrigation practice. In scenario E, it was 89 mm lower than in scenario A due to the combination of DFL and early cut-off. This reduction was due to a 19% decrease in the initial Kc and a 24% decrease in the final Kc when DFL and an early cut-off were implemented, respectively, compared to traditional irrigation [29], which could result in a reduction in rice yield. Finally, the small differences in P and ETc between the two soil categories within each scenario were not due to the distinction in soil, but to the different sowing dates of the HRUs within each soil category.
When implemented, punctual runoff only represented around 4% of the total water input (scenarios A and B). This value was much lower than in other paddy areas. For instance, Playán et al. [41] found that runoff accounted for 18% of the total water input in a group of rice paddies covering 5.31 hectares in Aragón (Spain), and Cuadrado-Alarcón et al. [18] quantified a 62% runoff at the district scale in the Guadalquivir marches of Spain. However, it should be noted that in these studies, continuous rather than punctual runoff was implemented, thus increasing the seasonal runoff outputs.
Percolation accounted for the highest water output in all scenarios. Its behaviour followed the same trend as the irrigation term, showing high variability among scenarios. In the current model, percolation was driven by the water storage term, i.e., soil water storage plus ponding water level. This approach aligns with previous published works that concluded that when paddies are flooded, DP is strongly influenced by the ponding water height as well as by other factors such as soil hydraulic conductivity of the most-impeding layer and aquifer depth [42,43,44,45,46].
3.3.2. Water Savings of the Irrigation Practices
The comparison of the seasonal irrigation among scenarios indicated their water-saving potential in the context of the study farm (Table 6). The graphical representation of the temporal evolution of the water balance components (Figure 7) enabled the results to be analyzed in more detail.
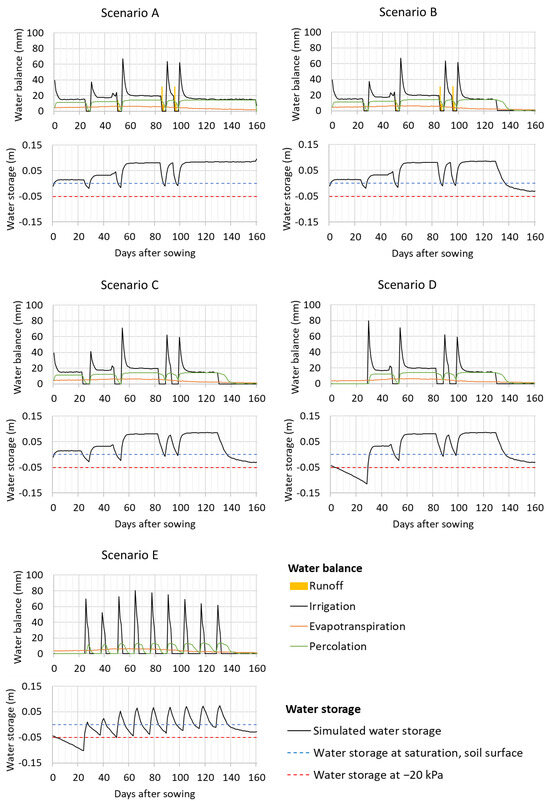
Figure 7.
Temporal evolution of the water balance components and the ponding water level in the five simulated scenarios. The mean values for the HRUs and the five simulated cropping seasons (2020–2024) are presented.
The early cut-off and the DFL water management practices resulted in water savings of 17% and 15%, respectively (Table 6). These water savings were calculated by comparing irrigation in scenarios A and B for the early cut-off, and in scenarios C and D for the DFL. The similar water-saving potential of these two practices can be explained by the fact that they both consist of eliminating irrigation for approximately one month, thereby shortening the rice crop’s irrigation season and reducing ETc. These values are consistent with previous findings at plot and field scales [4], although the literature does report some discrepancy in the reduction in water use when implementing DFL. For instance, Linquist et al. [7] monitored 14.6–45.7-hectare commercial fields in California over three years and found no difference in water use between WFL and DFL, averaging 1839 mm. However, in this region, one, two, or even three flush irrigations were typically carried out during the initial dry period to ensure adequate soil moisture for early rice development, likely due to the lack of precipitation during this period. These flush irrigations might have eclipsed the potential water use reduction in DFL if precipitation had occurred. Conversely, Cesari de Maria et al. [14] registered a 26% and 16% reduction in total water use in 2012 and 2013, respectively, when implementing DFL in experimental fields. Gilardi et al. [17] calculated a 19% reduction in irrigation water use when simulating this strategy in a 1000-hectare district. Leaving aside the case reported by Linquist et al. [7], the results from the current work are consistent with those reported in other studies in a Mediterranean climate.
There were no meaningful precipitation events in the first month of the season in 2021 and 2022, with an average of 2.5 mm day−1 during the first 30 days after sowing. Consequently, water storage decreased significantly during this period when DFL was implemented (scenarios D and E). This probably led to crop water stress, which can occur when the soil matric potential in the root zone is below −20 kPa [47]. As shown in Figure 7, the water storage during the dry period in DFL, based on the average value of the five simulated years, was significantly below −20 kPa. According to this criterion, the DFL strategy may have impacted the final rice yield. The low water storage during the initial cropping period also resulted in a higher water discharge requirement for the first flooding event compared to WFL. As observed in 2020, 2023, and 2024, precipitation events during the initial crop development stage mitigated the sharp decrease in water storage during the non-flooded period in DFL, thereby reducing the high irrigation discharge requirements for the first flooding event. Additionally, according to the results of Gilardi et al. [17], DFL probably delayed the typical rise in the groundwater table level during the first month of the cropping season. A similar observation can be made for the early cut-off practice, which may shorten the period during which the groundwater table is at its shallowest value, usually associated with rice irrigation.
The irrigation discharges in scenarios B and C showed that the no-runoff strategy led to an average reduction in irrigation of 6% during the study period compared to punctual runoff (Table 6). This suggests that rice fields can be drained for short periods and on ad hoc basis without having a significant impact on seasonal irrigation discharges. However, if the runoff valves had been opened throughout the irrigation season, the water-saving potential of the no-runoff practice at the study farm might have been greater. This detail is important because continuous runoff is a common practice in other rice-growing areas to allow higher water recirculation among fields and to improve salt leaching. This leads to higher water use, as reported by Facchi et al. [42] and by Cuadrado-Alarcón et al. [18].
The 10-day fixed-turn irrigation practice resulted in the greatest irrigation water savings, accounting for an average of 30%, compared to continuous flooding (Table 6). The significant water-saving potential of the fixed turn on the study farm was due to the variable and shallower simulated ponding water level compared to continuous flooding (Figure 7). Maintaining a continuous ponding water level throughout the rice cropping cycle is essential for minimizing water stress and promoting optimal crop development. Consequently, it would be essential to evaluate the effects of the fixed-turn irrigation approach on both crop evolution and final yield within the study area to guarantee the farm’s economic sustainability. As shown in Figure 7, the −20 kPa threshold was reached or nearly reached on multiple occasions in scenario E, indicating that combining DFL with 10-day fixed-turn irrigation could reduce yield.
The 30% reduction in irrigation water usage achieved through fixed-turn was significant, but relatively low compared to the findings of Cesari de Maria et al. [48], who observed a 58% water use reduction when implementing an irrigation event every 10 days in experimental fields with sandy soils. Conversely, Gilardi et al. [17] modelled a 32% reduction in irrigation use when implementing 8-day fixed-turn irrigation combined with DFL at a district scale characterized by loamy to sandy–loamy soils. Specifically, their study considered an initial 10-day flooding period during the tillering phase, followed by an irrigation event of 120 mm every eight days, according to a rotational calendar. In the current study, the combination of DFL and fixed-turn irrigation resulted in a 40% reduction in water use, which is greater than that reported by Gilardi et al. [17] due to the longer intervals between irrigation events. However, the fixed-turn irrigation required higher irrigation discharges at each event, which usually were greater than 70 mm day−1, since the water storage before each irrigation was far below target values (Figure 7). While such discharges were also necessary in the continuous irrigation scenarios to flood the fields after phytosanitary treatments, fixed-turn increased the frequency of these events. These results emphasize the critical need of ensuring an adequate water flow during each irrigation event when implementing this practice.
The fixed-turn irrigation practice also resulted in a 40% decrease in the DP term of the water balance (Table 6). While this reduction is favourable for improving water use efficiency at field and farm scales, it may impact the overall recharge of the shallow aquifer of the area. Consequently, the overall improvement on irrigation water use efficiency at the district or watershed scales may be relevant, but lower than expected [48].
3.3.3. Irrigation Performance Indexes
The irrigation performance indexes computed for all the simulated scenarios are reported in Table 7.

Table 7.
Irrigation performance indexes for the five irrigation management scenarios at the farm level. Average values ± standard deviation for the 2020–2024 irrigation seasons are presented.
According to RIS, RWS, and ICUC, traditional irrigation (scenario A) resulted in the lowest efficiencies. In this scenario, water inputs were approximately four times higher than the consumptive water uses. Implementing the early cut-off, no-runoff, and DFL practices improved these indexes. Nevertheless, even in the most efficient scenario (E), the total amount of water entering the system more than doubled the consumptive water uses (RWS index), indicating relatively low water use efficiency in rice irrigation. However, these values were similar to those reported in other rice-growing areas [14,17,18].
The DPF quantified the fraction of all water inputs that left the system through percolation and contributed to groundwater recharge. In all scenarios, percolation represented the highest water output, accounting for 0.68 in scenarios A, B, C, and D (average value over the five years and the four scenarios), and 0.55 in scenario E. Similar DPF results across the five scenarios emphasized the relationship between irrigation and percolation, since both were functions of the water storage. Specifically, when the absolute value of one of these two terms was reduced, the other followed the same pattern, thus resulting in similar DPF values. In fact, DPF only decreased when irrigation was low enough to increase the proportion of precipitation in the total water inputs, as reflected in scenario E.
4. Conclusions
A daily water mass balance model was successfully developed, calibrated and validated using a five year irrigation discharge data series in a 121-hectares farm in the Baix Ter rice irrigation district in Spain. The model was then used to explore the impact of alternative irrigation strategies compared to the traditional practice. Ten-days fixed-turn irrigation resulted in the greatest water savings, accounting for 30% compared to continuous irrigation. Early cut-off and DFL also resulted in relevant water savings, being of 17% and 15%, respectively, compared to irrigation until harvest and WFL. Finally, the no-runoff strategy only accounted for 6% reduction in irrigation water use. However, this practice’s water-saving potential might have been greater if the reference scenario had been continuous runoff (a common strategy in other rice-growing areas) rather than punctual runoff after pesticide treatments. The water-saving potential of fixed-turn irrigation, DFL, and early cut-off was mainly driven by their lower water storage (soil water storage plus ponding water depth) compared to traditional irrigation, which indicates that proper management of the ponding water height is critical for the overall irrigation efficiency in paddy areas. Given the water-scarcity situation of the study area and the high-water volumes required for traditional rice irrigation (scenarios A and B), it is critical to adopt water-saving strategies in rice cultivation. The most viable strategy given the actual water availability and cultivated surface is the adoption of at least two of the following water-saving strategies: DFL, early cut-off, and fixed-turn irrigation. Otherwise, the only solution to cultivate rice would be to reduce the irrigated area, but this situation would probably result in significant economic and social impact in the region. Future studies should focus on the specific impact of these water-saving irrigation practices on crop stress and final yield in the study area, since the simulation outcomes show that they may occasionally result in low soil water content and matric potential values.
Author Contributions
Conceptualization, S.C., G.A., J.M.V. and F.R.d.C.; methodology, S.C., G.A., B.C.-A., F.D. and F.R.d.C.; software, S.C. and B.C.-A.; validation, S.C. and F.D.; formal analysis, S.C., B.C.-A. and F.D.; investigation, S.C., G.A., J.P. and F.R.d.C.; resources, S.C., G.A., J.P. and F.R.d.C.; data curation, S.C. and G.A.; writing—original draft preparation, S.C. and F.R.d.C.; writing—review and editing, G.A., J.P., B.C.-A., A.F., J.M.V., F.D. and F.R.d.C.; visualization, S.C.; supervision, G.A., B.C.-A., A.F., J.M.V., F.D. and F.R.d.C.; project administration, G.A., J.P., A.F. and F.R.d.C.; funding acquisition, G.A., J.P., A.F. and F.R.d.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was carried out within the framework of MEDWATERICE and PROMEDRICE projects. Both projects are part of the PRIMA program supported by the European Union, and received funding from the Spanish Agencia Estatal de Investigación under grant agreements PCI2019-103738 and PCI2023-143435, respectively, as part od PRIMA program. This work was also supported by the Ministerio de Ciencia, Innovación y Universidades of Spain through an FPU predoctoral grant, under the grant agreement FPU20/01123.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
In memory of Luciano Mateos, without whose enthusiastic advice, guidance, and friendship this work could not have been developed.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study, collection, analyses, or interpretation of data, the writing of the manuscript, or the decision to publish the results.
References
- Gangopadhyay, S.; Banerjee, R.; Batabyal, S.; Das, N.; Mondal, A.; Pal, S.C.; Mandal, S. Carbon sequestration and greenhouse gas emissions for different rice cultivation practices. Sustain. Prod. Consum. 2022, 34, 90–104. [Google Scholar] [CrossRef]
- Picazo-Tadeo, A.J.; Reig-Martínez, E.; Estruch, V. Farming efficiency and the survival of valuable agro-ecosystems: A case study of rice farming in European Mediterranean wetlands. Open Environ. Sci. 2009, 3, 42–51. [Google Scholar] [CrossRef]
- Anan, M.; Yuge, K.; Nakano, Y.; Saptomo, S.; Haraguchi, T. Quantification of the effect of rice paddy area changes on recharging groundwater. Paddy Water Environ. 2007, 5, 41–47. [Google Scholar] [CrossRef]
- Gharsallah, O.; Rienzner, M.; Mayer, A.; Tkachencko, D.; Corsi, S.; Vuciterna, R.; Romani, M.; Ricciardelli, A.; Cadei, E.; Trevisan, M.; et al. Economic, environmental and social sustainability of Alternate Wetting and Drying irrigaiton for rice in northern Italy. Front. Water 2023, 5, 1213047. [Google Scholar] [CrossRef]
- Singh, R.; van Dam, J.C.; Jhorar, R.K. Water and salt balance at farmer fields. In Water Productivity of Irrigated Crops in Sirsa District, India; van Dam, J.C., Malik, R.S., Eds.; Wageningen University & Research: Wageningen, The Netherlands, 2003; pp. 41–58. [Google Scholar]
- Tuong, T.P.; Bouman, B.A.M.; Mortimer, M. More rice, less water—Integrated approaches for increasing water productivity in irrigated rice-based systems in Asia. Plant Prod. Sci. 2005, 8, 231–241. [Google Scholar] [CrossRef]
- Linquist, B.; Snyder, R.; Anderson, F.; Espino, L.; Inglese, G.; Marras, S.; Moratiel, R.; Mutters, R.; Nicolosi, P.; Rejmanek, H.; et al. Water balances and evapotranspiration in water- and dry-seeded rice systems. Irrig. Sci. 2015, 33, 375–385. [Google Scholar] [CrossRef]
- Zhuang, Y.; Zhang, L.; Li, S.; Liu, H.; Zhai, L.; Zhou, F.; Ye, Y.; Ruan, S.; Wen, W. Effects and potential of water-saving irrigation for rice production in China. Agric. Water Manag. 2019, 217, 374–382. [Google Scholar] [CrossRef]
- Ariani, M.; Hanudin, E.; Haryono, E. The effect of contrasting soil textures on the efficiency of alternate wetting-drying to reduce water use and global warming potential. Agric. Water Manag. 2022, 274, 107970. [Google Scholar] [CrossRef]
- Surendran, U.; Raja, P.; Jayakumar, M.; Rama Subramoniam, S. Use of efficient water saving techniques for production of rice in India under climate change scenario: A critical review. J. Clean. Prod. 2021, 309, 127–272. [Google Scholar] [CrossRef]
- Aurona, A.; Dzomeku, I.K.; Shaibu, A.G.; Nurudeen, A.R. Water management for sustainable irrigation in rice (Oryza sativa L.) production: A review. Agronomy 2023, 13, 1522. [Google Scholar] [CrossRef]
- Mallareddy, M.; Thirumalaikumar, R.; Balasubramanian, P.; Naseerddin, R.; Nithya, N.; Mariadoss, A.; Eazhilkrishna, N.; Choudhary, A.K.; Deiveegan, M.; Subramanian, E.; et al. Maximizing water use efficiency in rice farming: A comprehensive review of innovative irrigation management technologies. Water 2023, 15, 1802. [Google Scholar] [CrossRef]
- Peyron, M.; Bertora, C.; Pelissetti, S.; Said-Pullicino, D.; Celi, L.; Miniotti, E.; Romani, M.; Sacco, D. Greenhouse gas emissions as affected by different water management practices in temperate rice paddies. Agric. Ecosyst. Environ. 2016, 232, 17–28. [Google Scholar] [CrossRef]
- Cesari de Maria, S.; Bischetti, G.B.; Chiaradia, E.A.; Facchi, A.; Miniotti, E.F.; Rienzner, M.; Romani, M.; Tenni, D.; Gandolfi, C. The role of water management and environmental factors on field irrigation requirements and water productivity of rice. Irrig. Sci. 2017, 35, 11–26. [Google Scholar] [CrossRef]
- Arbat, G.; Cufí, S.; Duran-Ros, M.; Pinsach, J.; Puig-Bargués, J.; Pujol, J.; Ramírez de Cartagena, F. Modeling approaches for determining dripline depth and irrigation frequency of subsurface drip irrigated rice on different soil textures. Water 2020, 12, 1724. [Google Scholar] [CrossRef]
- Zhao, Y.; De Maio, M.; Vidotto, F.; Sacco, D. Influence of wet-dry cycles on the temporal infiltration dynamic in temperate rice paddies. Soil Tillage Res. 2015, 154, 14–21. [Google Scholar] [CrossRef]
- Gilardi, G.L.C.; Mayer, A.; Rienzner, M.; Romani, M.; Facchi, A. Effect of Alternate Wetting and Drying (AWD) and other irrigation management strategies on water resources in rice-producing areas of northern Italy. Water 2023, 15, 2150. [Google Scholar] [CrossRef]
- Cuadrado-Alarcón, B.; Mateos, L.; Guéry, S.; Gomez-Macpherson, H. Circulation and solute mass balance model for the rice growing area on the right bank of the lower Guadalquivir River valley. Agric. Water Manag. 2025, 313, 109453. [Google Scholar] [CrossRef]
- Burt, C.M. Irrigation water balance fundamentals. In Proceedings of the Conference on Benchmarking Irrigation System Performance Using Water Measurement and Water Balances, San Luis Obispo, CA, USA, 10–13 March 1999; Available online: https://digitalcommons.calpoly.edu/bae_fac/53 (accessed on 5 August 2025).
- Guidance document on the Application of Water Balances for Supporting the Implementation of the WFD, Final Version 6.1. In Technical Report; Office for Official Publications of the European Communities: Brussels, Belgium, 2015. [CrossRef]
- Merchán, D.; Causapé, J.; Abrahão, R.; García-Garizábal, I. Assessment of a newly implemented irrigated area (Lerma Basin, Spain) over a 10-year period. II: Salts and nitrate exported. Agric. Water Manag. 2015, 158, 288–296. [Google Scholar] [CrossRef]
- Mateos, L.; Young, C.A.; Wallender, W.W.; Carlson, H.L. Simulating spatially distributed water and salt balances. J. Irrig. Drain. Eng. 2000, 126, 288–295. [Google Scholar] [CrossRef]
- Lana, X.; Serra, C.; Casas-Castillo, M.C.; Rodríguez-Solà, R.; Prohom, M. Two centuries of monthly rainfall in Barcelona (NE Spain): Disparity trends, correlation of autumnal rainfall with the WeMO Index and its contribution to anual amounts. Climate 2024, 12, 166. [Google Scholar] [CrossRef]
- Staff, S.S. Keys to Soil Taxonomy, 13th ed.; Natural Resources Conservation Service—USDA: Washington, USA, 2022. [Google Scholar]
- Ayers, R.S.; Westcot, D.W. Water Quality for Agriculture. In FAO Irrigation and Drainage, Paper 29; FAO: Rome, Italy, 1985. [Google Scholar]
- Margarit, J.; Boixadera, J.; Muñoz, P.; Usón, A. Mapa de sòls detallat (E 1:25,000) del Marge Esquerre del Baix Ter (Alt i Baix Empordà). Generalitat de Catalunya; Departament d’Agricultura, Alimentació i Acció Rural: Catalonia, Spain, 1995. [Google Scholar]
- Allen, R.G.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements. In FAO Irrigation and Drainage, Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Simunek, J.M.; Sejna, M.T.; van Genuchten, M.T. Hydrus 1D for Windows, Version 4.17; U.S. Salinity Laboratory, USDA-ARS: Riverside, CA, USA, 2019; Available online: https://www.pc-progress.com/en/Default.aspx?hydrus-1d. (accessed on 9 May 2025).
- Pereira, L.S.; Paredes, P.; Hunsaker, D.J.; López-Urrea, R.; Mohammadi Shad, Z. Standard single and basal crop coefficients for field crops. Uptadtes and advances to the FAO56 crop water requirements method. Agric. Water Manag. 2021, 243, 106466. [Google Scholar] [CrossRef]
- Patrignani, A.; Ochsner, T.E. Canopeo: A powerful new tool for measuring fractional green canopy cover. Agron. J. 2015, 107, 2312–2320. [Google Scholar] [CrossRef]
- Meteocat. Dades de l’Estació Automàtica la Tallada d’Empordà. Generalitat de Catalunya. 2025. Available online: https://www.meteo.cat/observacions/xema/dades?codi=UB&dia=2024-12-31T00:00Z (accessed on 30 September 2025).
- Van Genuchten, M.T. A closed form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.E. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydr. Engin. ASCE 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. J. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Jovanovic, N. Soil water balance models for determining crop water and irrigation requirements and irrigaiton scheduling focusing on the FAO56 method and the dual Kc approach. Agric. Water Manag. 2020, 241, 106357. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- IRRI. How to Manage Water. Rice Knowledge Bank. 2025. Available online: http://www.knowledgebank.irri.org/step-by-step-production/growth/water-management#for-continuous-flooding (accessed on 30 September 2025).
- Playán, E.; Pérez-Coveta, O.; Martínez-Cob, A.; Herrero, J.; García-Navarro, P.; Latorre, B.; Brufau, P.; Garcés, J. Overland water and salt flows in a set of rice paddies. Agric. Water Manag. 2008, 95, 645–658. [Google Scholar] [CrossRef]
- Facchi, A.; Rienzner, M.; Cesari de Maria, S.; Mayer, A.; Chiaradia, E.A.; Masseroni, D.; Silvestri, S.; Romani, M. Exploring scale-effects on water balance components and water use efficiency of toposequence rice fields in Northern Italy. Hydrol. Res. 2018, 49, 1711–1723. [Google Scholar] [CrossRef]
- Walker, S.H.; Rushton, K.R. Verification of lateral percolation losses from irrigated rice fields by a numerical model. J. Hydrol. 1984, 71, 335–351. [Google Scholar] [CrossRef]
- Liang, X.Q.; Li, H.; Chen, Y.X.; He, M.M.; Tian, G.M.; Zhang, Z.J. Nitrogen loss through lateral seepage in near-trench paddy fields. J. Environ. Qual. 2008, 37, 712–717. [Google Scholar] [CrossRef]
- Liang, X.Q.; Li, H.; Chen, Y.X.; Li, H.; He, M.M.; Ye, Y.S.; Tian, G.M.; Lundy, M. Dissolved phosphorus losses by lateral seepage from swine manure amendments for organic rice production. Soil Chem. 2013, 77, 765–773. [Google Scholar] [CrossRef]
- Janssen, M.; Lennartz, B.; Wöhling, T. Percolation losses in paddy fields with a dynamic soil structure: Model development and applications. Hydrol. Proc. 2010, 24, 813–824. [Google Scholar] [CrossRef]
- Carrijo, D.R.; Lundy, M.E.; Linquist, B.A. Rice yields and water use under alternate wetting and drying irrigation: A meta-analysis. Field Crops Res. 2017, 203, 173–180. [Google Scholar] [CrossRef]
- Cesari de Maria, S.; Rienzner, M.; Facchi, A.; Chiaradia, E.A.; Romani, M.; Gandolfi, C. Water balance implications of switching from continuous submergence to flush irrigation in a rice-growing district. Agric. Water Manag. 2016, 171, 108–119. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).