Simulation and Experiment on Parameters of an Airflow-Guiding Device for a Centrifugal Air-Assisted Sprayer
Abstract
1. Introduction
2. Materials and Methods
2.1. Working Principle of Centrifugal Air-Assisted Sprayer
2.2. Structural Analysis of Flow-Guiding Device
2.3. Selection of Key Parameters for the Flow-Guiding Device
2.4. Airflow Field Simulation Based on CFD Technology
2.4.1. Governing Equations
- (1)
- The mass conservation equation is as follows:
- (2)
- The momentum conservation equation is as follows:
- (3)
- The energy conservation equation is as follows:
- (4)
- The turbulent kinetic energy equation is as follows:
- (5)
- The turbulent dissipation rate equation is as follows:
2.4.2. Evaluation Indicators
3. Results
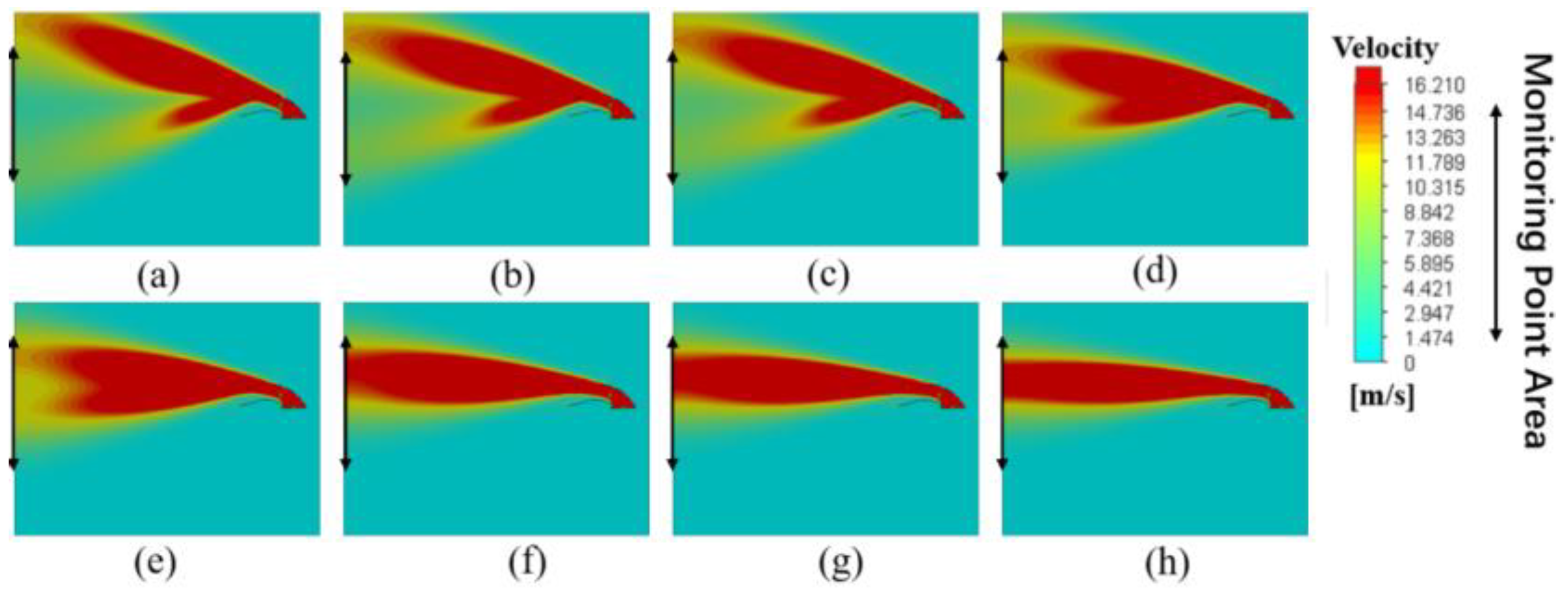
3.1. Single-Factor Experiment
3.1.1. Influence of Upper Edge Inclination Angle on Airflow Field
3.1.2. Influence of Lower Edge Inclination Angle on Airflow Field
3.1.3. Influence of Upper Air Outlet Position on Airflow Field
3.1.4. Influence of Upper Air Outlet Length on Airflow Field
3.1.5. Influence of Upper Air Outlet Width on Airflow Field
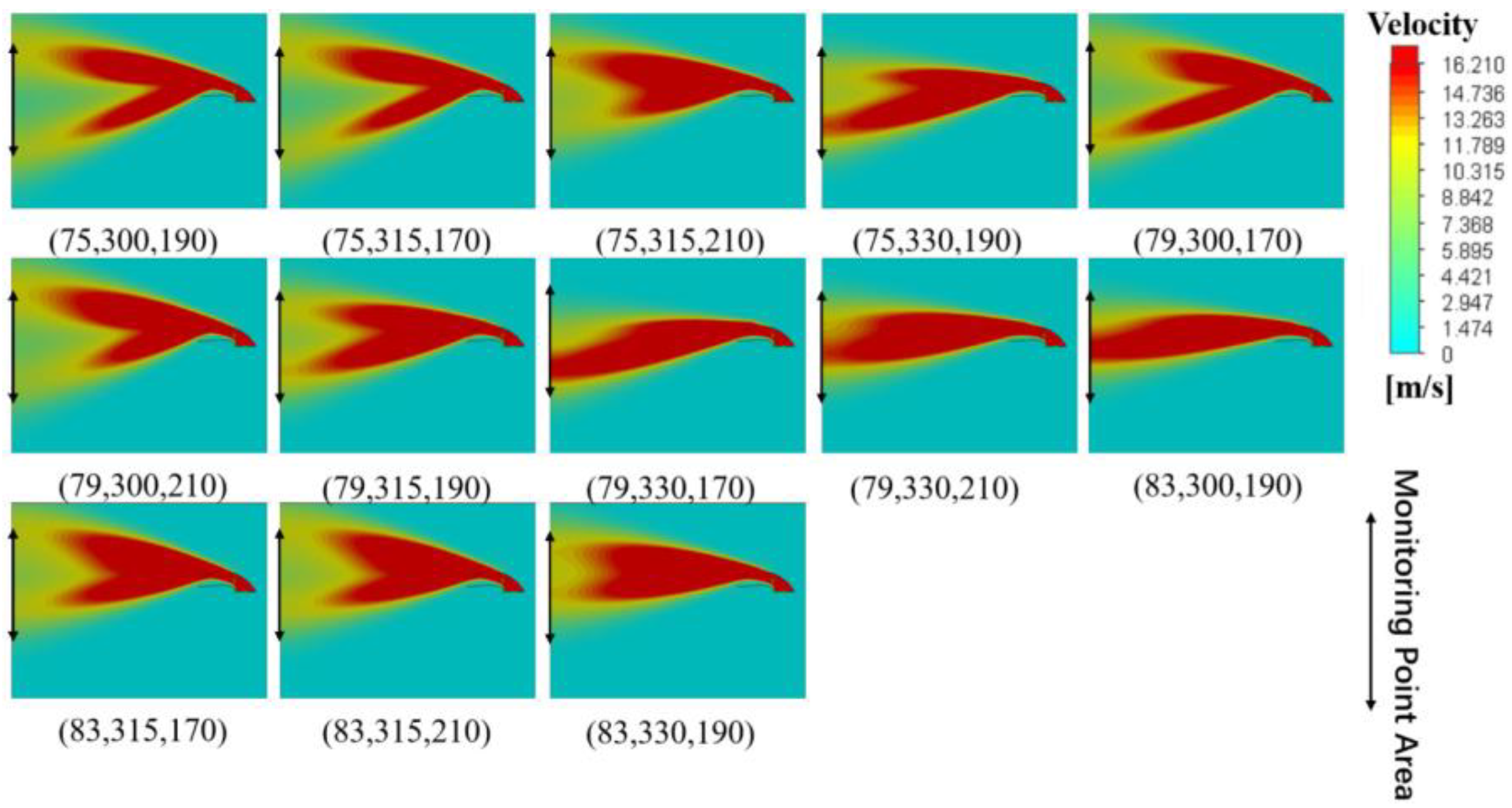
3.2. Multi-Factor Experiment
3.2.1. Test Results and Analysis of Variance
3.2.2. Influence of Interaction Between Experimental Factors on Velocity Unevenness Coefficient
3.3. Optimization of Air Outlet Parameters Based on the Itertools Library
4. Experimental Verification and Result Analysis
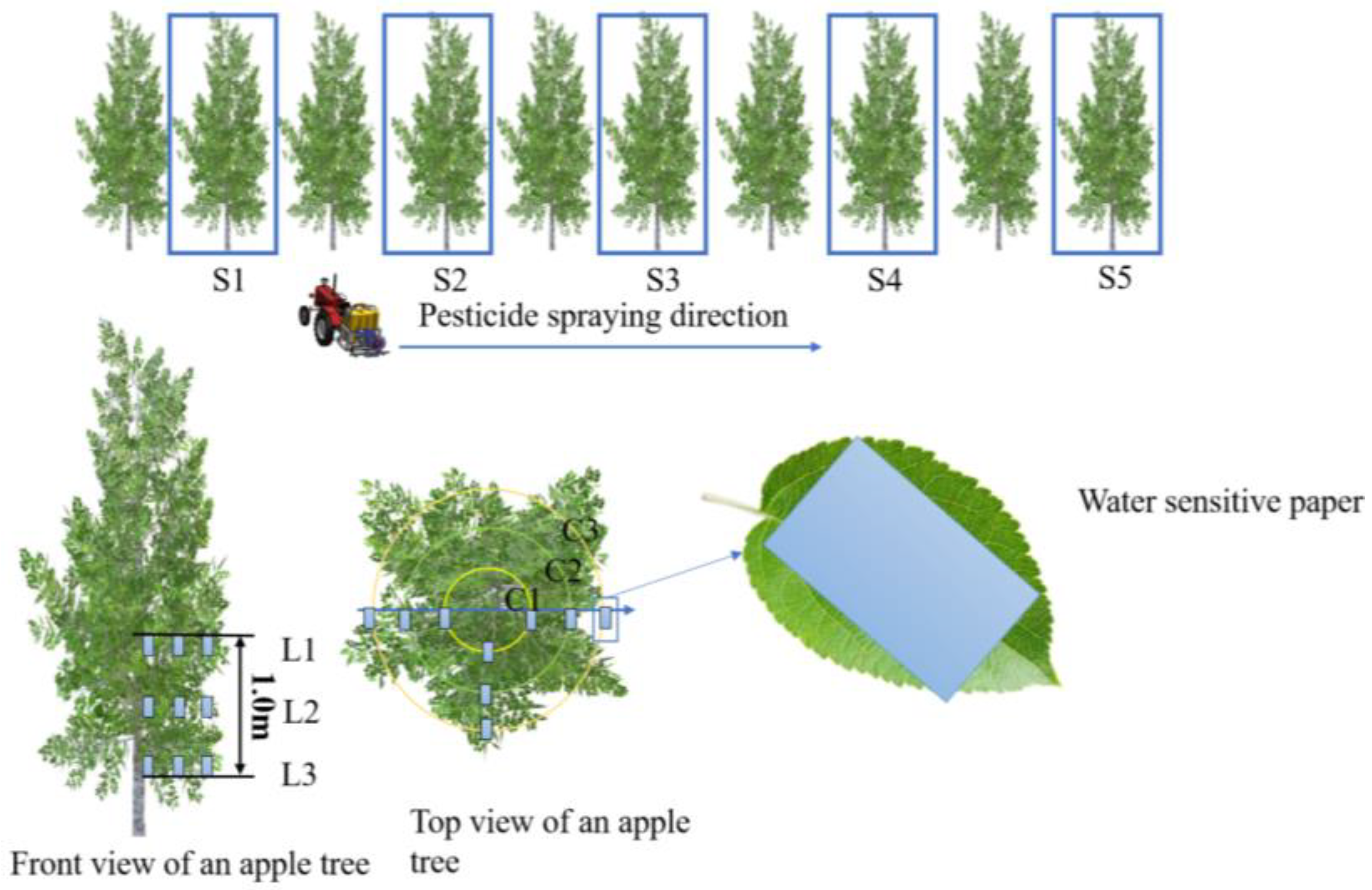
4.1. Test Materials and Equipment
4.2. Verification and Analysis of the Diversion Device Model
4.3. Droplet Deposition Test
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Cheng, J.; Yu, J.; Tan, D.; Wang, Q.; Zhao, Z. Life Cycle Assessment of Apple Production and Consumption under Different Sales Models in China. Sustain. Prod. Consum. 2025, 55, 100–116. [Google Scholar] [CrossRef]
- Boualleg, N.J.; Salomon, M.V.; Vilardell, P.; Aramburu, B.; Cabrefiga, J. Control of Apple Scab in Commercial Orchards Through Primary Inoculum Management. Agriculture 2024, 14, 2125. [Google Scholar] [CrossRef]
- Li, B.-H.; Zhang, Z.-F.; Xu, X.-M. Developing and Implementing an Integrated Pest/Disease Management in Apple for Smallholder Farms in Yantai, China. Crop Prot. 2024, 182, 106668. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Chen, B.T.; Lyu, H.T.; Kang, F.; Jiang, S.J. Research Progress of Orchard Plant Protection Mechanization Technology and Equipment in China. Trans. Chin. Soc. Agric. Eng 2020, 36, 110–124. [Google Scholar]
- Zhou, L.; Xue, X.; Zhou, L.; Zhang, L.; Ding, S.; Chang, C.; Zhang, X.; Chen, C. Research Situation and Progress Analysis on Orchard Variable Rate Spraying Technology. Trans. Chin. Soc. Agric. Eng. 2017, 33, 80–92. [Google Scholar]
- Liu, T.; Zhang, S.; Sun, T.; Ma, C.; Xue, X. Review of Active Plant Frost Protection Equipment and Technologies: Current Status, Challenges, and Future Prospects. Agronomy 2025, 15, 1164. [Google Scholar] [CrossRef]
- Bahlol, H.Y.; Chandel, A.K.; Hoheisel, G.-A.; Khot, L.R. The Smart Spray Analytical System: Developing Understanding of Output Air-Assist and Spray Patterns from Orchard Sprayers. Crop Prot. 2020, 127, 104977. [Google Scholar] [CrossRef]
- Jing, S.; Ren, L.; Zhang, Y.; Han, X.; Gao, A.; Liu, B.; Song, Y. A Simulation and Experiment on the Optimization Design of an Air Outlet Structure for an Air-Assisted Sprayer. Agriculture 2023, 13, 2277. [Google Scholar] [CrossRef]
- Qiu, W.; Sun, H.; Sun, Y.H.; Liao, Y.Y.; Zhou, L.F.; Wen, Z.J. Design and Test of Circulating Air-Assisted Sprayer for Dwarfed Orchard. Trans. CSAE 2021, 37, 18–25. [Google Scholar]
- Endalew, A.M.; Debaer, C.; Rutten, N.; Vercammen, J.; Delele, M.A.; Ramon, H.; Nicolaï, B.M.; Verboven, P. A New Integrated CFD Modelling Approach towards Air-Assisted Orchard Spraying. Part I. Model Development and Effect of Wind Speed and Direction on Sprayer Airflow. Comput. Electron. Agric. 2010, 71, 128–136. [Google Scholar] [CrossRef]
- Hong, S.-W.; Zhao, L.; Zhu, H. CFD Simulation of Airflow inside Tree Canopies Discharged from Air-Assisted Sprayers. Comput. Electron. Agric. 2018, 149, 121–132. [Google Scholar] [CrossRef]
- Badules, J.; Vidal, M.; Boné, A.; Llop, J.; Salcedo, R.; Gil, E.; García-Ramos, F.J. Comparative Study of CFD Models of the Air Flow Produced by an Air-Assisted Sprayer Adapted to the Crop Geometry. Comput. Electron. Agric. 2018, 149, 166–174. [Google Scholar] [CrossRef]
- Yanxiang, P.; Hua, Z.; Guicheng, H.E. Prediction of Spray Droplet Size Distribution Based on Maximum Entropy. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2023, 54. [Google Scholar] [CrossRef]
- Ding, S.; Xue, X.; Dong, X.; Gu, W.; Zhou, Q.Q. Effects of Spraying Parameters on Droplet Deposition Performance. Trans. Chin. Soc. Agric. Mach. 2020, 5, 308–315. [Google Scholar]
- Li, J.P.; Li, S.B.; Yu, S.M.; Wang, P.; Yang, X.; Liu, H. Deposition Characteristics of Umbrella Wind Field Type Anti-Drift Spray Device. Trans. Chin. Soc. Agric. Mach. 2023, 54, 80–91. [Google Scholar]
- Li, T.; Qi, P.; Wang, Z.; Xu, S.; Huang, Z.; Han, L.; He, X. Evaluation of the Effects of Airflow Distribution Patterns on Deposit Coverage and Spray Penetration in Multi-Unit Air-Assisted Sprayer. Agronomy 2022, 12, 944. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Chen, L.; Wang, K. CFD-Based Flow Field Characteristics of Air-Assisted Sprayer in Citrus Orchards. Agriculture 2025, 15, 1103. [Google Scholar] [CrossRef]
- Khot, L.R.; Ehsani, R.; Albrigo, G.; Larbi, P.A.; Landers, A.; Campoy, J.; Wellington, C. Air-Assisted Sprayer Adapted for Precision Horticulture: Spray Patterns and Deposition Assessments in Small-Sized Citrus Canopies. Biosyst. Eng. 2012, 113, 76–85. [Google Scholar] [CrossRef]
- Xu, S.; Feng, Y.; Han, L.; Ran, X.; Zhong, Y.; Jin, Y.; Song, J. Evaluation of the Wind Field and Deposition Effect of a Novel Air-Assisted Strawberry Sprayer. Agriculture 2023, 13, 230. [Google Scholar] [CrossRef]
- Lee, I.-B.; Bitog, J.P.P.; Hong, S.-W.; Seo, I.-H.; Kwon, K.-S.; Bartzanas, T.; Kacira, M. The Past, Present and Future of CFD for Agro-Environmental Applications. Comput. Electron. Agric. 2013, 93, 168–183. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, Y.; Wei, W.; Hu, Z.; Li, P. Optimization Design of Spray Cooling Fan Based on CFD Simulation and Field Experiment for Horticultural Crops. Agriculture 2021, 11, 566. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Z.; Wang, S.; Chen, R.; Wang, Y.; Liao, Q.; Yang, J.; Yang, C.; Zhang, Q. Simulation Study on the Spraying Performance of a Sprayer for the Middle and Lower Leaves of Cigar Tobacco Plants Based on CFD-DPM. Comput. Electron. Agric. 2025, 238, 110787. [Google Scholar] [CrossRef]
- Li, W.; Wu, B. Computational Fluid Dynamics Investigation of Pesticide Spraying by Agricultural Drones. Comput. Electron. Agric. 2024, 227, 109506. [Google Scholar] [CrossRef]
- Cui, H.; Wang, C.; Yu, S.; Xin, Z.; Liu, X.; Yuan, J. Two-Stage CFD Simulation of Droplet Deposition on Deformed Leaves of Cotton Canopy in Air-Assisted Spraying. Comput. Electron. Agric. 2024, 224, 109228. [Google Scholar] [CrossRef]
- Lü, X.; Zhang, M.; Chang, Y.; Lei, X.; Yang, Q. Influence of Deflector Angles for Orchard Air-Assisted Sprayer on 3D Airflow Distribution. Trans. Chin. Soc. Agric. Eng. 2017, 33, 81–87. [Google Scholar]
- Hong, S.-W.; Zhao, L.; Zhu, H. CFD Simulation of Pesticide Spray from Air-Assisted Sprayers in an Apple Orchard: Tree Deposition and off-Target Losses. Atmos. Environ. 2018, 175, 109–119. [Google Scholar] [CrossRef]
- Guo, J.; Wang, P.; Li, X.; Yang, X.; Li, J.; Bian, Y.; Xue, C. Design Optimization and Test of Air Supply System for Multi-Duct Sprayer. Smart Agric. 2022, 4, 75. [Google Scholar]
- Zhang, Z.; Wang, D.; Li, J.; Wang, P.; Guo, Y.; Tian, S. Design and Experiment of Dual Flexible Air Duct Spraying Device for Orchards. Agriculture 2025, 15, 1031. [Google Scholar] [CrossRef]
- Chen, J.; Song, S.; Sun, D.; Hong, T.; Zhang, L. Test on Airflow Field and Spray Characteristics for Long-Range Air-Blast Sprayer. Trans. Chin. Soc. Agric. Eng. 2017, 33, 72–79. [Google Scholar]
- Jiang, H.; Niu, Z.; Liu, L.; Wang, W.; Wang, J.; Mao, J. Design and Experiment of Air Volume Control System of Orchard Multi-Pipe Air Sprayer. Trans. Chin. Soc. Agric. Mach. 2020, 51, 298–307. [Google Scholar]
- Qi, F.; Zhao, X.; Shi, Z.; Rong, L.; Zhang, G.; Li, H. Applicability Evaluation of Innovative Simplified Methods of Slatted Floor in Pig Houses—A CFD Study. Comput. Electron. Agric. 2024, 216, 108532. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Ma, Y.; Cui, H.; Yang, Z.; Lu, H. Effects of Leaf Response Velocity on Spray Deposition with an Air-Assisted Orchard Sprayer. Int. J. Agric. Biol. Eng. 2021, 14, 123–132. [Google Scholar] [CrossRef]



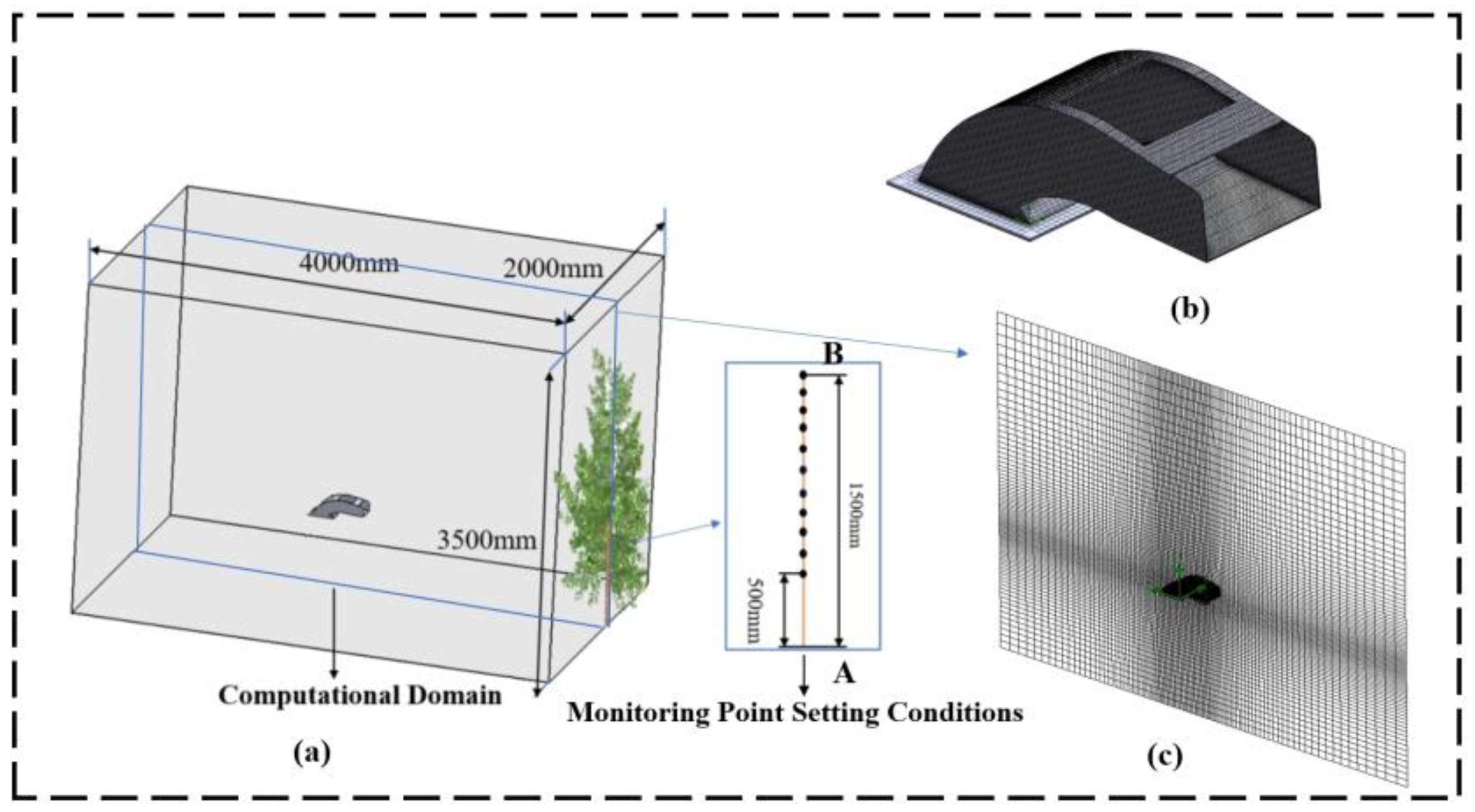
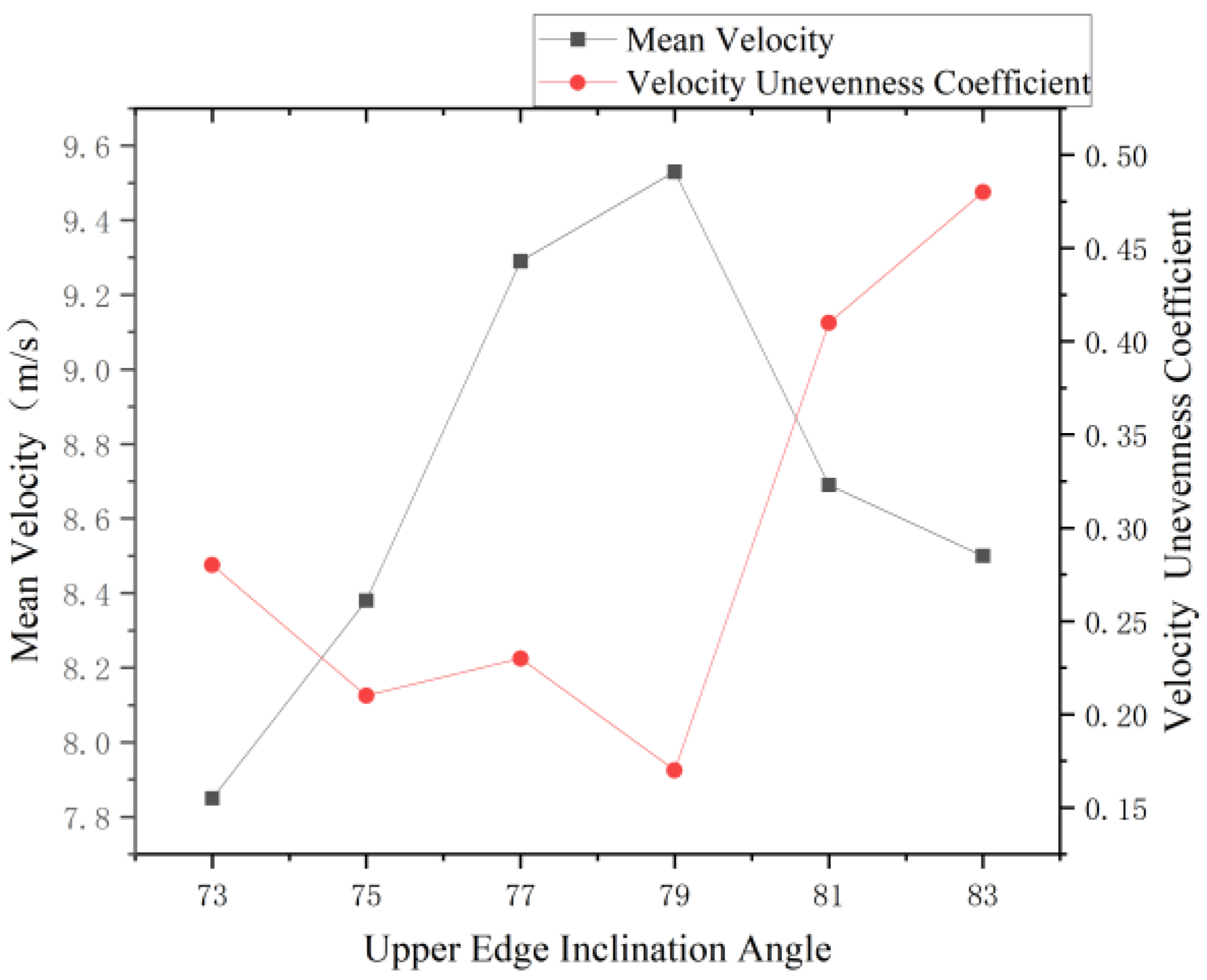

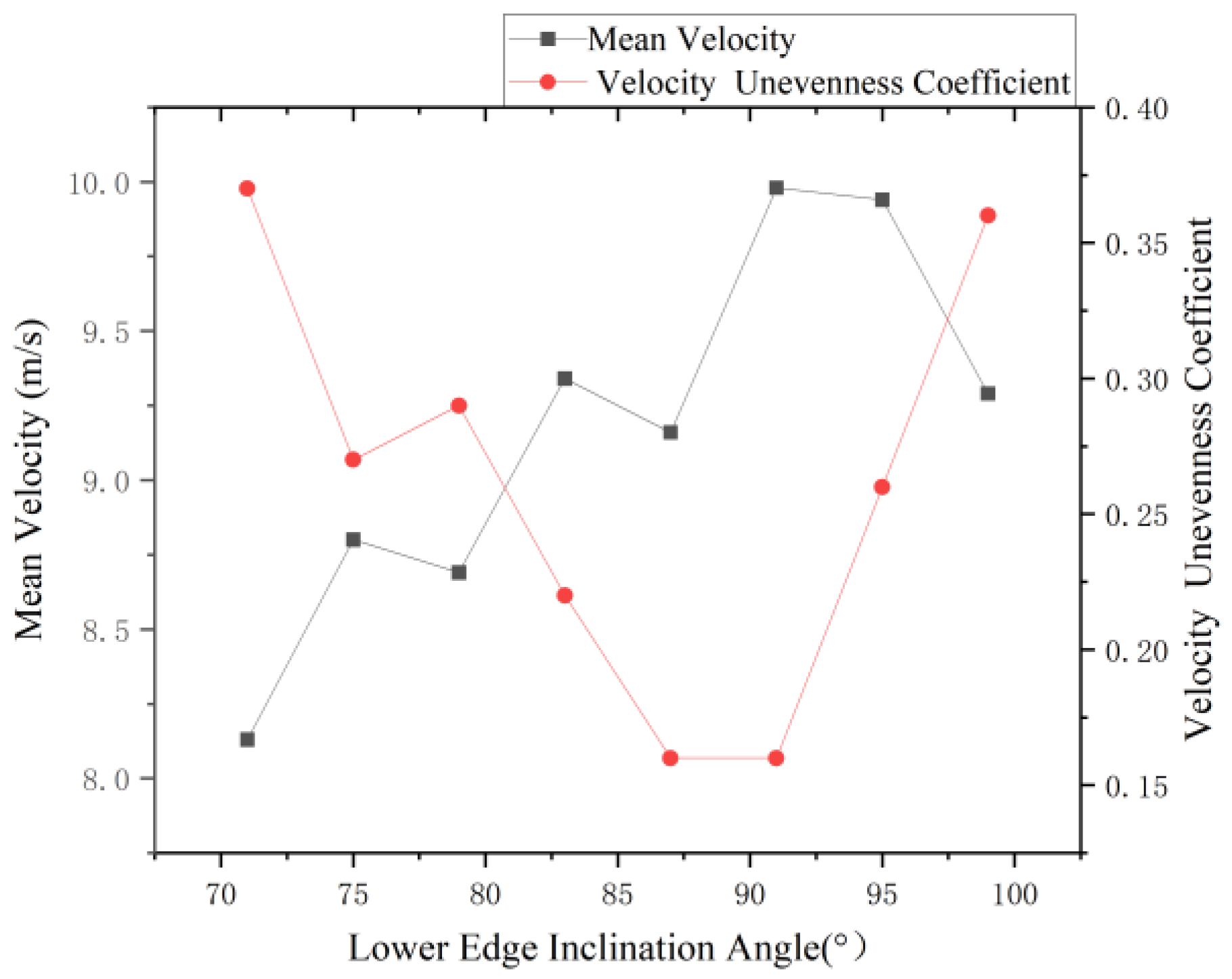

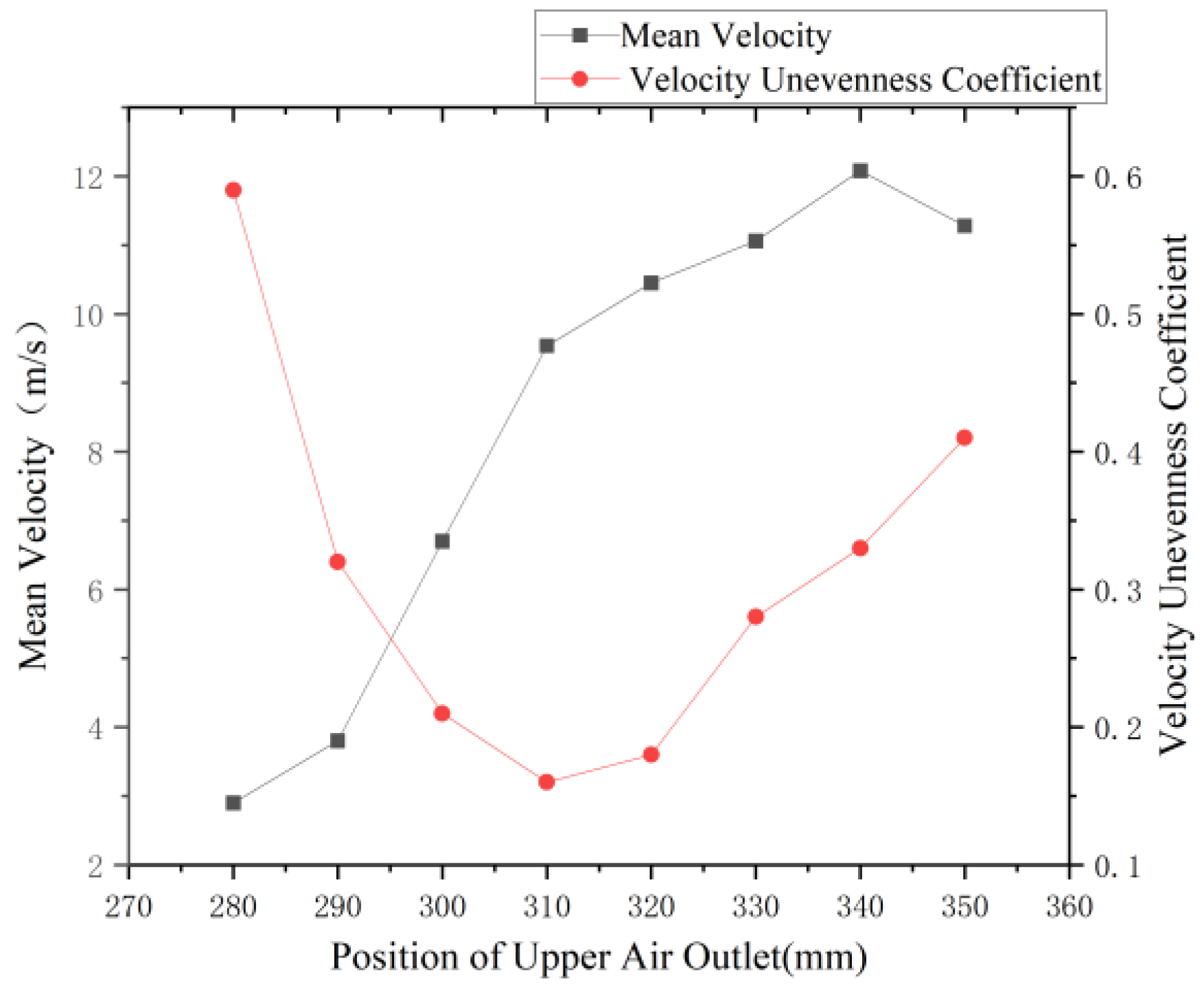











| Technical Parameters | Numerical Value |
|---|---|
| Hitching type | Suspended |
| Power input | PTO |
| Air volume of centrifugal fan | 4270 m3/h |
| Rotation speed of centrifugal fan | 1450 r/min |
| Power of centrifugal fan | 1.5 kW |
| Overall dimension (length × width × height) | 1600 × 1400 × 1500 mm |
| Medicine tank capacity | 400 L |
| Diaphragm pump pressure | 1–4.5 Mpa |
| Coding | Factors | ||
|---|---|---|---|
| X1, Upper Edge Inclination Angle/° | X2, Position of Upper Air Outlet/mm | X3, Length of Upper Air Outlet/mm | |
| −1 | 75 | 300 | 170 |
| 0 | 79 | 315 | 190 |
| 1 | 93 | 330 | 210 |
| Serial Number | Factor Levels | ||||
|---|---|---|---|---|---|
| X1 | X2 | X3 | |||
| 1 | −1 | −1 | 0 | 7.19 | 0.29 |
| 2 | 1 | −1 | 0 | 8.48 | 0.18 |
| 3 | −1 | 1 | 0 | 10.66 | 0.20 |
| 4 | 1 | 1 | 0 | 10.27 | 0.45 |
| 5 | −1 | 0 | −1 | 9.58 | 0.26 |
| 6 | 1 | 0 | −1 | 10.52 | 0.26 |
| 7 | −1 | 0 | 1 | 10.57 | 0.20 |
| 8 | 1 | 0 | 1 | 9.54 | 0.34 |
| 9 | 0 | −1 | −1 | 8.64 | 0.21 |
| 10 | 0 | 1 | −1 | 10.74 | 0.38 |
| 11 | 0 | −1 | 1 | 8.14 | 0.21 |
| 12 | 0 | 1 | 1 | 10.45 | 0.30 |
| 13 | 0 | 0 | 0 | 10.23 | 0.12 |
| 14 | 0 | 0 | 0 | 10.15 | 0.11 |
| 15 | 0 | 0 | 0 | 10.12 | 0.08 |
| 16 | 0 | 0 | 0 | 9.98 | 0.09 |
| 17 | 0 | 0 | 0 | 10.14 | 0.1 |
| Source | Square Sum | Degrees of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 16.30 | 9 | 1.81 | 39.81 | <0.0001 |
| X1 | 0.0820 | 1 | 0.0820 | 1.79 | 0.2260 |
| X2 | 11.69 | 1 | 11.69 | 251.18 | <0.0001 |
| X3 | 0.0761 | 1 | 0.0761 | 1.63 | 0.2419 |
| X1X2 | 0.7056 | 1 | 0.7056 | 15.16 | 0.0059 |
| X1X3 | 0.9702 | 1 | 0.9702 | 20.85 | 0.0059 |
| X2X3 | 0.0110 | 1 | 0.0110 | 0.2469 | 0.6412 |
| 0.1804 | 1 | 0.1804 | 3.88 | 0.0986 | |
| 2.48 | 1 | 2.48 | 58.23 | 0.0002 | |
| 0.0773 | 1 | 0.0773 | 1.66 | 0.2384 | |
| Lack of Fit | 0.2928 | 3 | 0.0976 | 11.86 | 0.0185 |
| Pure error | 0.0329 | 4 | 0.0082 | ||
| Sum | 16.62 | 16 |
| Source | Square Sum | Degrees of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 0.1799 | 9 | 0.0200 | 45.86 | <0.0001 |
| X1 | 0.0098 | 1 | 0.0098 | 22.49 | 0.0021 |
| X2 | 0.0242 | 1 | 0.0242 | 55.54 | 0.0001 |
| X3 | 0.0005 | 1 | 0.0005 | 1.03 | 0.3433 |
| X1X2 | 0.0324 | 1 | 0.0324 | 74.36 | <0.0001 |
| X1X3 | 0.0049 | 1 | 0.0049 | 11.25 | 0.0122 |
| X2X3 | 0.0016 | 1 | 0.0016 | 3.67 | 0.0969 |
| 0.0304 | 1 | 0.0304 | 69.86 | <0.0001 | |
| 0.0380 | 1 | 0.0380 | 87.21 | <0.0001 | |
| 0.0269 | 1 | 0.0269 | 61.85 | 0.0001 | |
| Lack of Fit | 0.0021 | 3 | 0.0007 | 2.73 | 0.1780 |
| Pure error | 0.0010 | 4 | 0.0002 | ||
| Sum | 0.1829 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, S.; Guo, H.; Li, J.; Li, Y.; Zhang, Z.; Wang, P. Simulation and Experiment on Parameters of an Airflow-Guiding Device for a Centrifugal Air-Assisted Sprayer. Agriculture 2025, 15, 1969. https://doi.org/10.3390/agriculture15181969
Tian S, Guo H, Li J, Li Y, Zhang Z, Wang P. Simulation and Experiment on Parameters of an Airflow-Guiding Device for a Centrifugal Air-Assisted Sprayer. Agriculture. 2025; 15(18):1969. https://doi.org/10.3390/agriculture15181969
Chicago/Turabian StyleTian, Sibo, Hao Guo, Jianping Li, Yang Li, Zhu Zhang, and Peng Wang. 2025. "Simulation and Experiment on Parameters of an Airflow-Guiding Device for a Centrifugal Air-Assisted Sprayer" Agriculture 15, no. 18: 1969. https://doi.org/10.3390/agriculture15181969
APA StyleTian, S., Guo, H., Li, J., Li, Y., Zhang, Z., & Wang, P. (2025). Simulation and Experiment on Parameters of an Airflow-Guiding Device for a Centrifugal Air-Assisted Sprayer. Agriculture, 15(18), 1969. https://doi.org/10.3390/agriculture15181969






