Research Progress on Path Planning and Tracking Control Methods for Orchard Mobile Robots in Complex Scenarios
Abstract
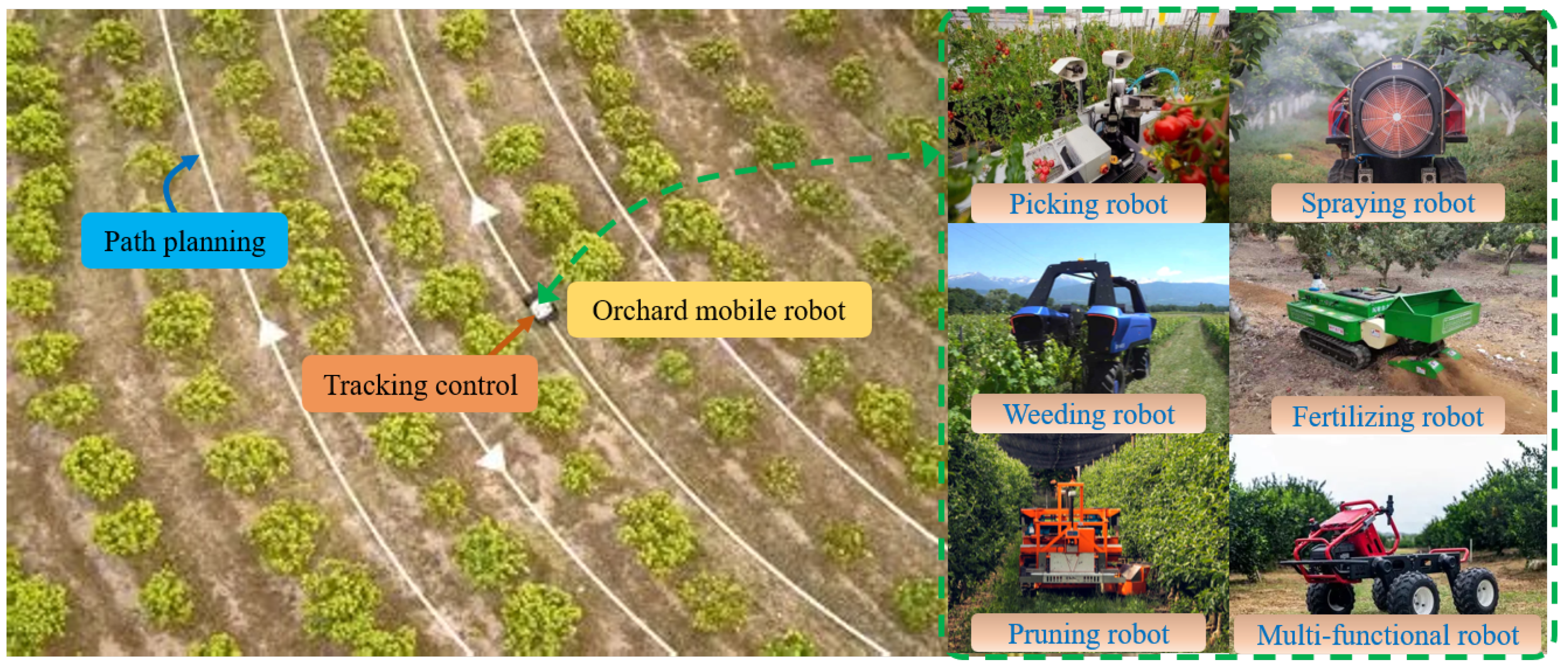
1. Introduction
1.1. Research Background and Objectives
1.2. The Composition of This Paper
2. Path Planning Method for OMR in Complex Scenarios
2.1. Global Path Planning Methods
2.1.1. Path Planning Method Based on Graph Search
2.1.2. Path Planning Method Based on Point Sampling
2.1.3. Path Planning Method Based on Intelligent Algorithms
2.2. Local Path Planning Methods
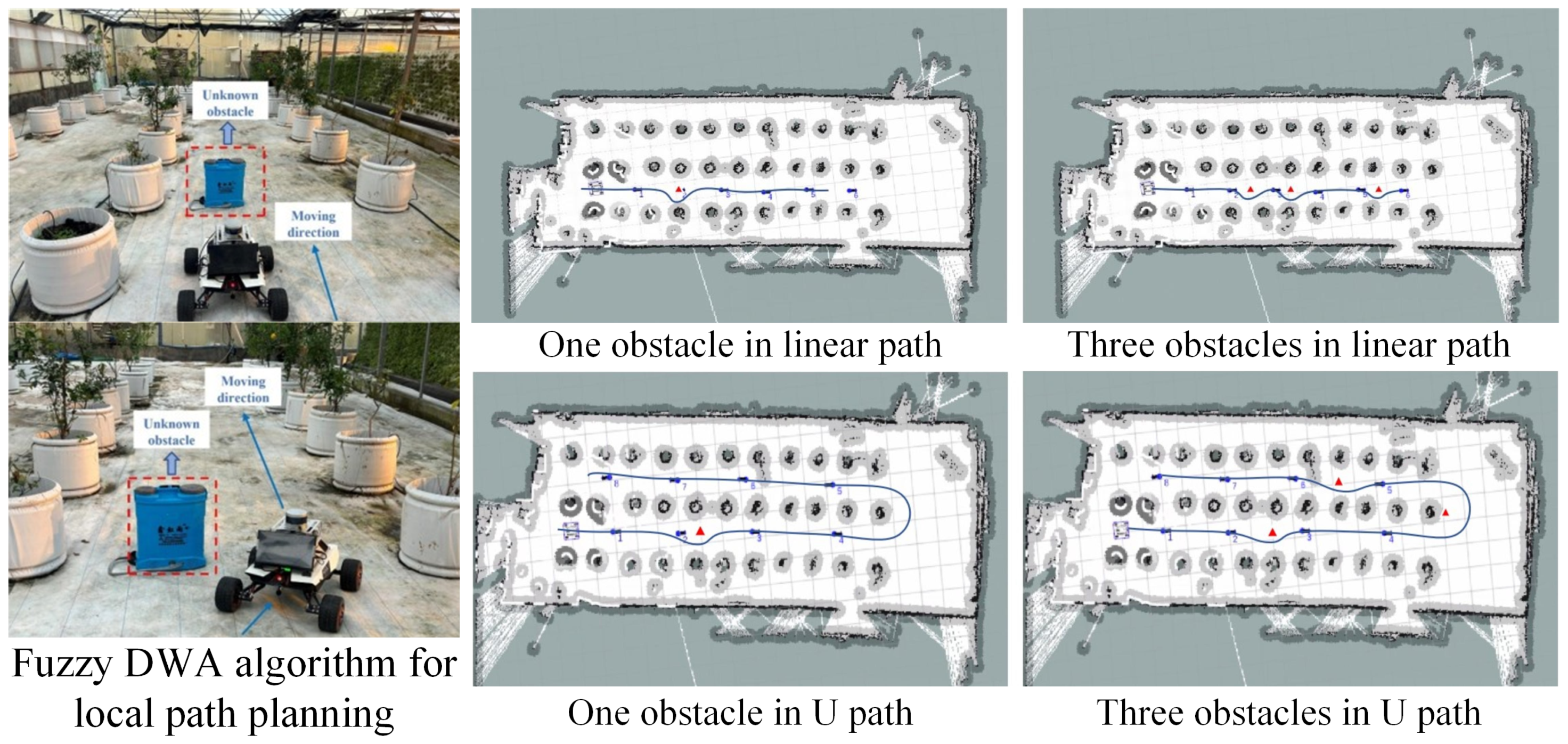
2.2.1. Trajectory Planning Method Based on Velocity Space
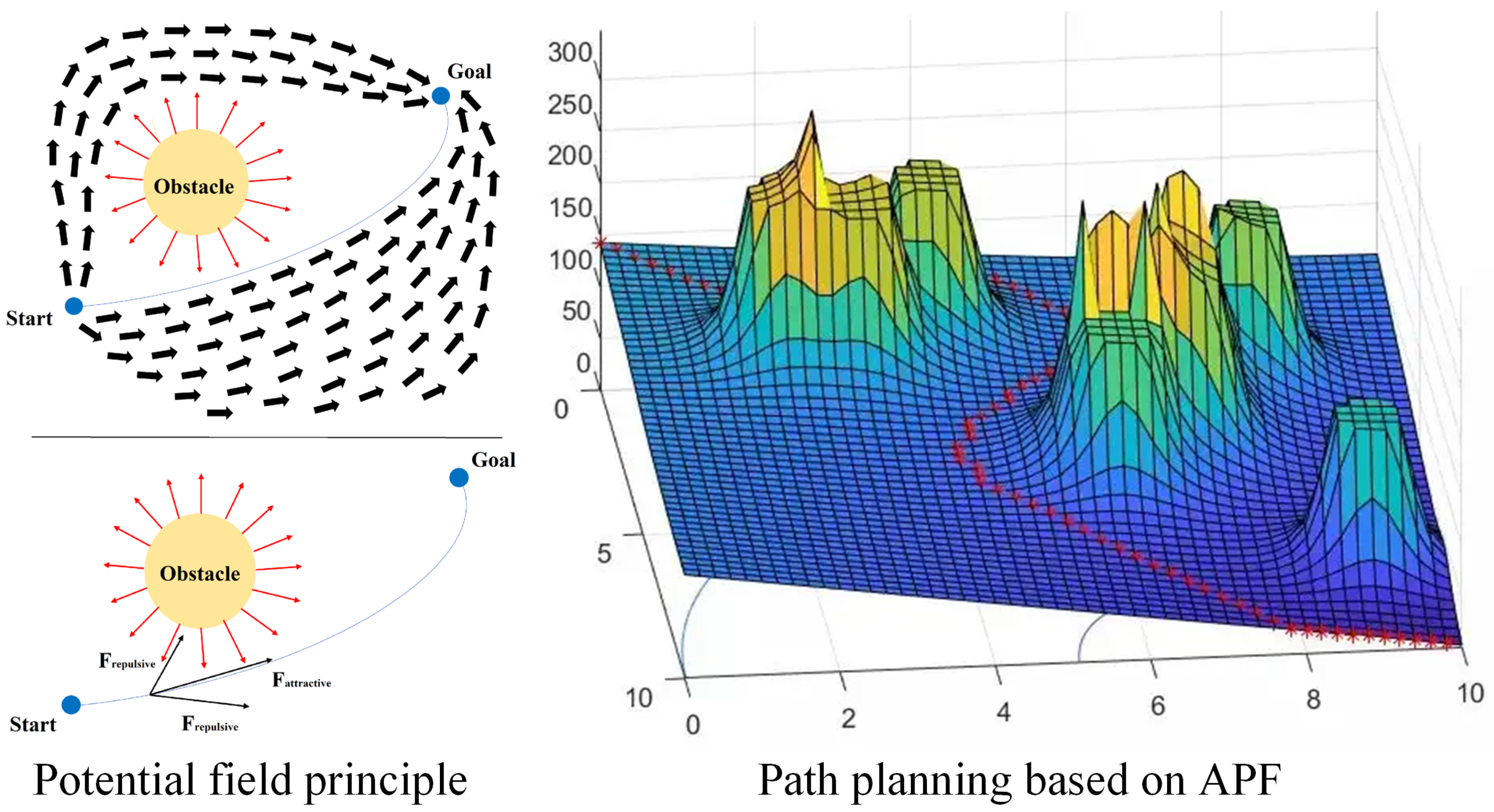
2.2.2. Trajectory Planning Method Using Artificial Potential Field
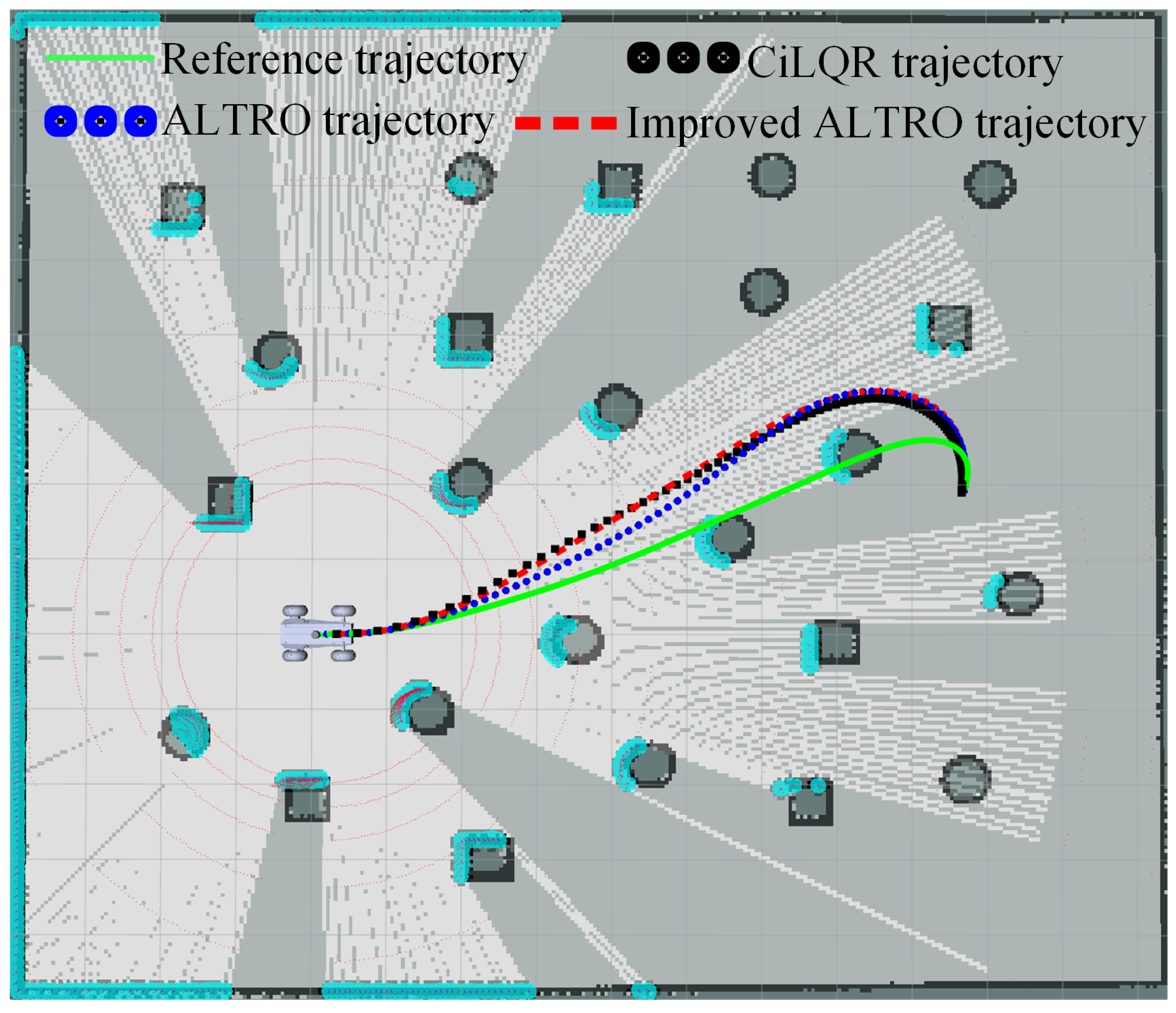
2.2.3. Trajectory Optimization Method Based on Optimal Control
2.3. Summary
3. Tracking Control Method for OMR in Complex Scenarios
3.1. Control Methods Based on Geometry Model
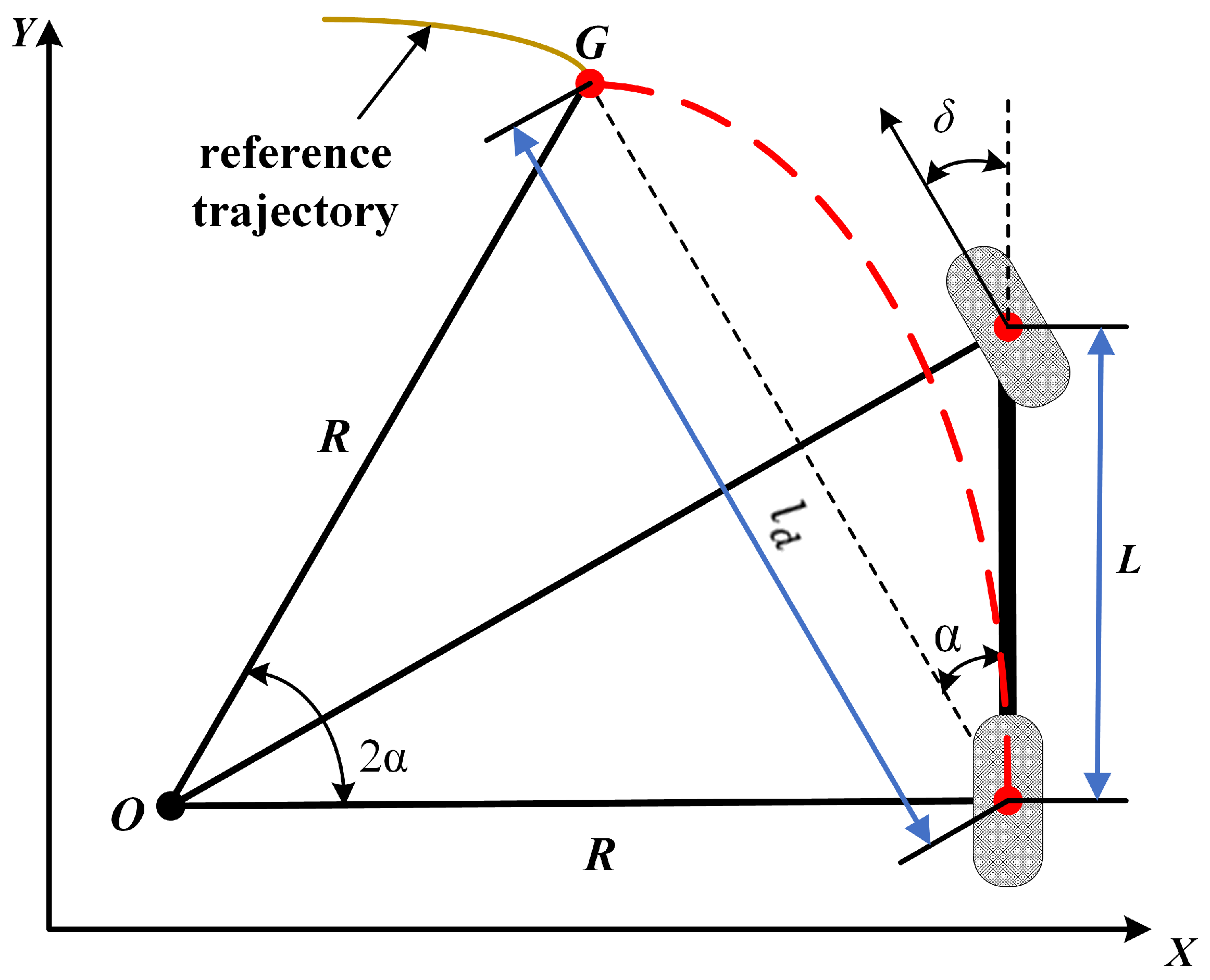
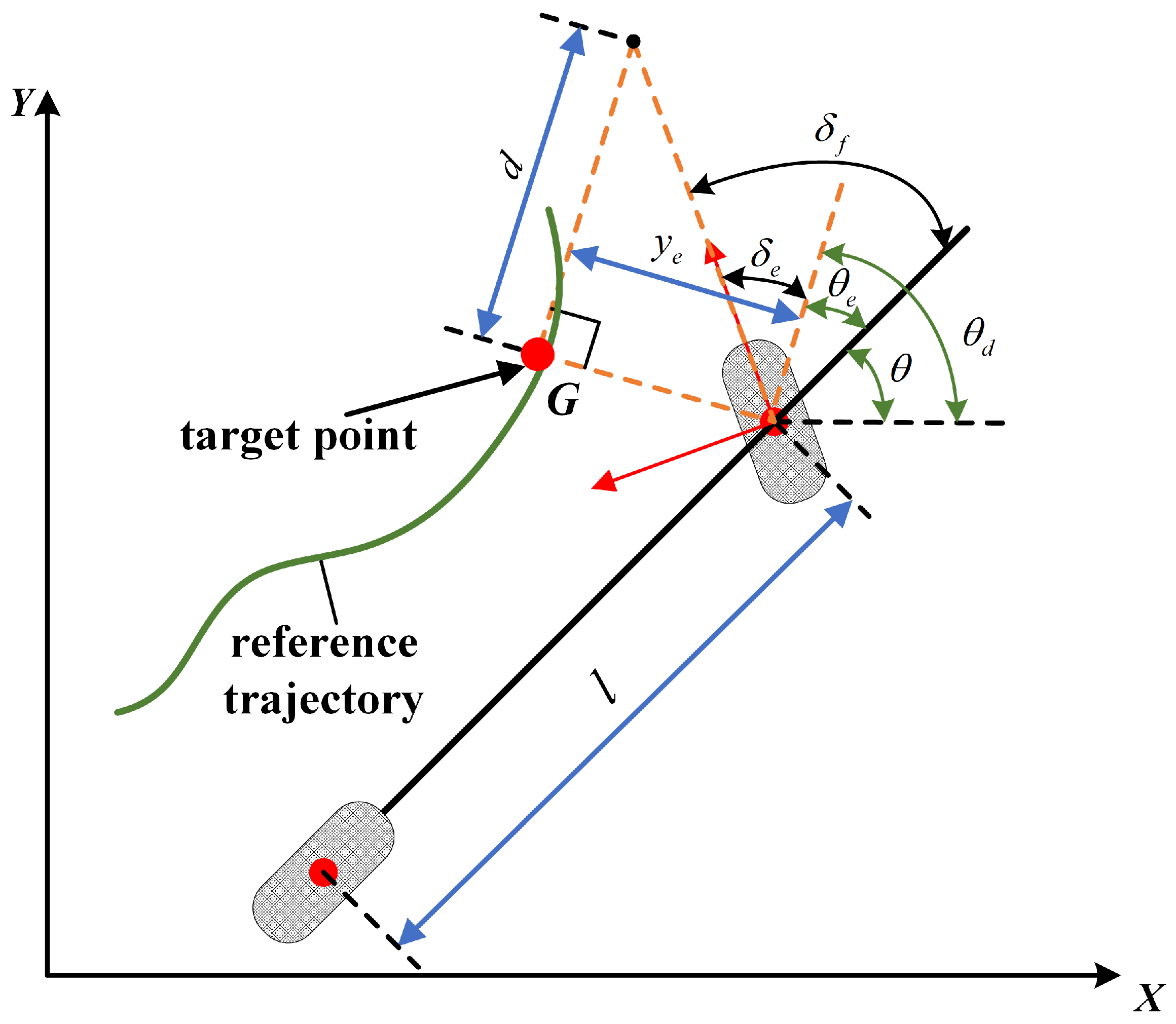
3.1.1. Pure Pursuit Control
3.1.2. Stanley Control
3.2. Control Methods Based on Kinematic Model
3.2.1. Construction of OMR Kinematic Model
3.2.2. PID Control
3.2.3. Model Predictive Control
3.2.4. Sliding Mode Control
3.3. Model-Free Intelligent Control Methods
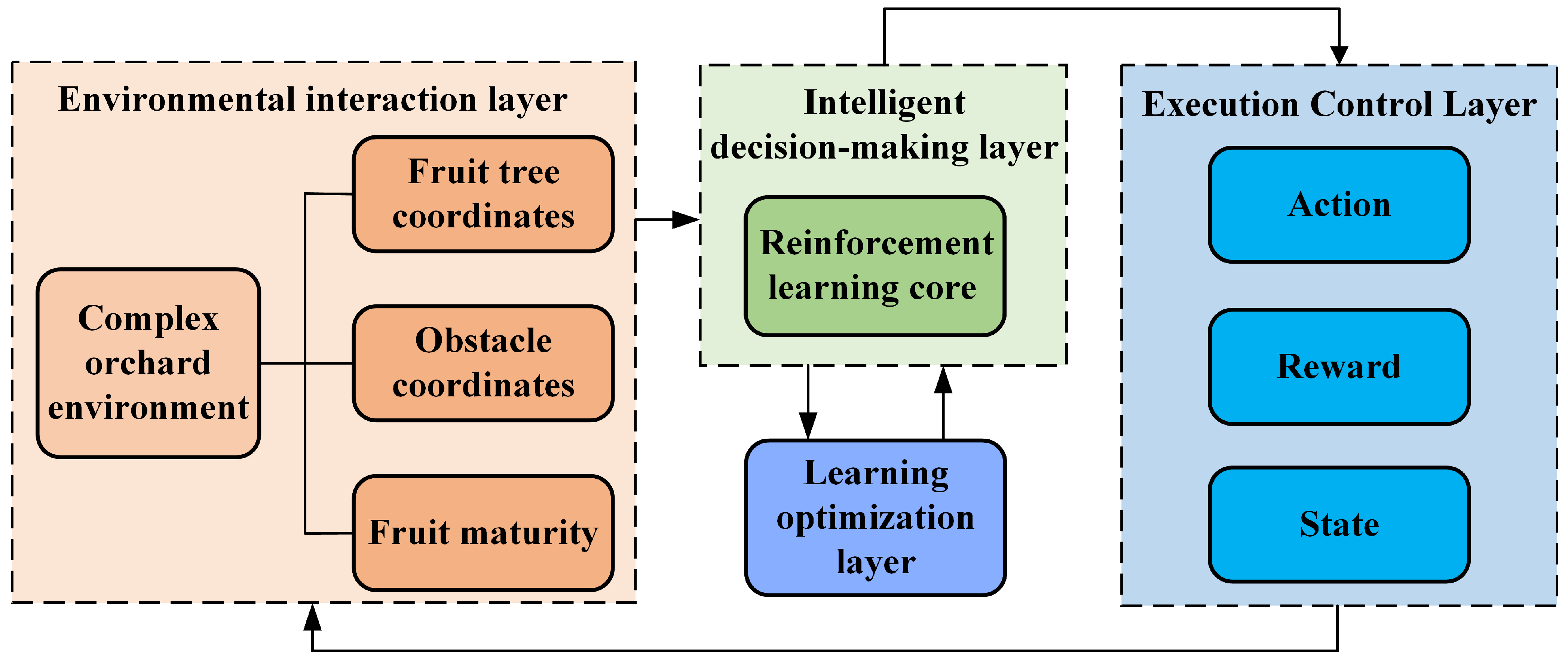
3.3.1. Control Strategy Based on Reinforcement Learning
3.3.2. Perception and Control Strategy Based on Transfer Learning
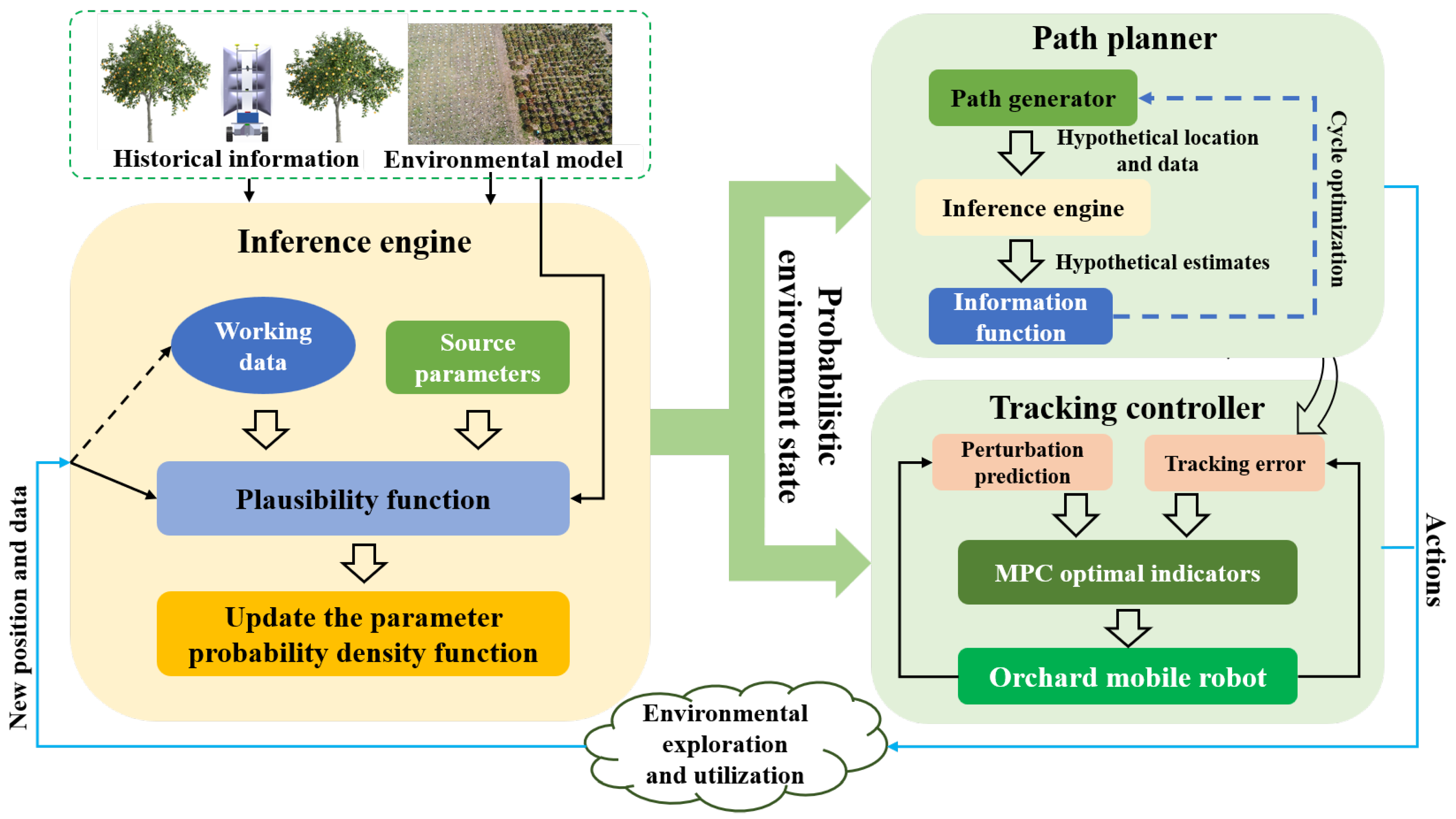
3.3.3. Learning and Control Strategy Based on DCEE
3.4. Summary
4. Challenges and Future Trends
- The existing OMR autonomous navigation control system adopts a hierarchical architecture combining path planning and tracking control, directly decoupling global decision-making from local execution. This facilitates separate algorithm optimization for varying levels of complexity. However, autonomous navigation systems with such hierarchical structures are highly susceptible to cumulative errors between layers; while deep learning and RL can learn complex control strategies through data-driven methods, they face challenges such as low sample efficiency, high training costs, and the complexity of state spaces in outdoor environments. Therefore, deeply integrating TL with RL or DCEE control strategies represents a key future research direction. Accelerating RL training using sparse expert demonstration data, coupled with a simulation-to-reality transfer learning framework, enables the safe and efficient transfer of strategies trained in high-fidelity virtual orchards to physical robots. Furthermore, frontier research is carried out to explore AI and end-to-end models, empowering robots to predict environmental changes and adaptively adjust control parameters using minimal online interaction data. This ultimately achieves strong generalization and high-robustness autonomous operations across crops and seasons.
- The complex terrain and continuous operational tasks in orchard environments lead to a significant increase in robotic energy consumption; while traditional global path planning algorithms can identify the shortest path, they do not necessarily yield the most energy-efficient route and fail to adequately account for the energy costs associated with actuator start-stop cycles and steering maneuvers. Development trends focus on developing multi-objective optimized energy-saving navigation strategies. The core lies in constructing a refined energy consumption model that integrates terrain elevation, soil hardness, steering angle, and motor efficiency. This model is then incorporated into a model predictive control framework for rolling optimization, achieving the optimal balance between path length and energy consumption. Simultaneously, integrating SLAM technology enables real-time identification of navigable areas, avoiding high-energy-consumption zones. This significantly extends the operational duration per charge, enhancing the economic viability and sustainability of orchard operations.
- Single-robot operation modes have limited efficiency in large-scale orchards, making multi-robot collaboration a key development direction for high-efficiency operations. However, coordinating and controlling multi-robot systems is highly complex. Existing centralized scheduling systems carry the risk of single points of failure, while fully distributed coordination faces challenges of communication latency and data consistency. The future trend lies in adopting a hierarchical hybrid architecture that integrates top-level task planning with bottom-level distributed real-time obstacle avoidance. By incorporating highly robust communication technologies such as Ultra-Wideband (UWB) and 5G to establish self-organizing networks and leveraging digital twin technology for virtual mapping and collaborative simulation of orchard environments and robot states, the overall operational efficiency and resource utilization of robot clusters can be maximized while ensuring safety.
- Multi-sensor fusion currently serves as the primary method for processing perception information in OMR. However, constrained by the conflict between the volume of perception data requiring processing and limited onboard computational resources, OMR cannot process vast amounts of environmental information data in real-time on the vehicle itself. The developmental trend is to establish a collaborative “end-edge-cloud” intelligent computing paradigm: deploying lightweight neural networks on the robot edge to handle low-latency tasks such as real-time obstacle avoidance and navigation. Edge servers deployed within orchards handle multi-robot data fusion, large-scale semantic mapping, offline computation for precision operations, and model updates. The cloud manages global data and conducts iterative algorithm training. This architecture achieves an optimal balance of computational resources, communication overhead, and system responsiveness through task offloading and collaborative reasoning.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chakraborty, S.; Elangovan, D.; Govindarajan, P.L.; ELnaggar, M.F.; Alrashed, M.M.; Kamel, S. A comprehensive review of path planning for agricultural ground robots. Sustainability 2022, 14, 9156. [Google Scholar] [CrossRef]
- Binbin, X.; Jizhan, L.; Meng, H.; Jian, W.; Zhujie, X. Research progress on autonomous navigation technology of agricultural robot. In Proceedings of the 2021 IEEE 11th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Jiaxian, China, 27–31 July 2021; pp. 891–898. [Google Scholar]
- Mhamed, M.; Zhang, Z.; Yu, J.; Li, Y.; Zhang, M. Advances in apple’s automated orchard equipment: A comprehensive research. Comput. Electron. Agric. 2024, 221, 108926. [Google Scholar] [CrossRef]
- Jiangyi, H.; Fan, W. Design and testing of a small orchard tractor driven by a power battery. Eng. Agrícola 2023, 43, e20220195. [Google Scholar] [CrossRef]
- Wu, M.; Ou, M.; Zhang, Y.; Jia, W.; Dai, S.; Wang, M.; Dong, X.; Wang, X.; Jiang, L. Development and Evaluation of a Monodisperse Droplet-Generation System for Precision Herbicide Application. Agriculture 2024, 14, 1885. [Google Scholar] [CrossRef]
- Zhu, C.; Hao, S.; Liu, C.; Wang, Y.; Jia, X.; Xu, J.; Guo, S.; Huo, J.; Wang, W. An Efficient Computer Vision-Based Dual-Face Target Precision Variable Spraying Robotic System for Foliar Fertilisers. Agronomy 2024, 14, 2770. [Google Scholar] [CrossRef]
- Wang, G.; Li, Z.; Jia, W.; Ou, M.; Dong, X.; Zhang, Z. A Review on the Evolution of Air-Assisted Spraying in Orchards and the Associated Leaf Motion During Spraying. Agriculture 2025, 15, 964. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Jia, W.; Ou, M.; Dong, X.; Dai, S. A review of environmental sensing technologies for targeted spraying in orchards. Horticulturae 2025, 11, 551. [Google Scholar] [CrossRef]
- Liu, H.; Du, Z.; Shen, Y.; Du, W.; Zhang, X. Development and evaluation of an intelligent multivariable spraying robot for orchards and nurseries. Comput. Electron. Agric. 2024, 222, 109056. [Google Scholar] [CrossRef]
- Dong, X.; Kim, W.Y.; Yu, Z.; Oh, J.Y.; Ehsani, R.; Lee, K.H. Improved voxel-based volume estimation and pruning severity mapping of apple trees during the pruning period. Comput. Electron. Agric. 2024, 219, 108834. [Google Scholar] [CrossRef]
- Wu, P.; Lei, X.; Zeng, J.; Qi, Y.; Yuan, Q.; Huang, W.; Ma, Z.; Shen, Q.; Lyu, X. Research progress in mechanized and intelligentized pollination technologies for fruit and vegetable crops. Int. J. Agric. Biol. Eng. 2024, 17, 11–21. [Google Scholar] [CrossRef]
- Wu, S.; Liu, J.; Lei, X.; Zhao, S.; Lu, J.; Jiang, Y.; Xie, B.; Wang, M. Research progress on efficient pollination technology of crops. Agronomy 2022, 12, 2872. [Google Scholar] [CrossRef]
- Chen, K.; Li, T.; Yan, T.; Xie, F.; Feng, Q.; Zhu, Q.; Zhao, C. A soft gripper design for apple harvesting with force feedback and fruit slip detection. Agriculture 2022, 12, 1802. [Google Scholar] [CrossRef]
- Zhou, K.; Xia, L.; Liu, J.; Qian, M.; Pi, J. Design of a flexible end-effector based on characteristics of tomatoes. Int. J. Agric. Biol. Eng. 2022, 15, 13–24. [Google Scholar] [CrossRef]
- Zhou, Z.; Zahid, U.; Majeed, Y.; Nisha; Mustafa, S.; Sajjad, M.M.; Butt, H.D.; Fu, L. Advancement in artificial intelligence for on-farm fruit sorting and transportation. Front. Plant Sci. 2023, 14, 1082860. [Google Scholar] [CrossRef]
- He, Y.; Huang, Z.; Yang, N.; Li, X.; Wang, Y.; Feng, X. Research Progress and Prospects of Key Navigation Technologies for Facility Agricultural Robots. Smart Agric. 2024, 6, 1–19. [Google Scholar]
- Wu, M.; Liu, S.; Li, Z.; Ou, M.; Dai, S.; Dong, X.; Wang, X.; Jiang, L.; Jia, W. A review of intelligent orchard sprayer technologies: Perception, control, and system integration. Horticulturae 2025, 11, 668. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, J.; Wang, J.; Cai, L.; Jin, Y.; Zhao, S.; Xie, B. Realtime picking point decision algorithm of trellis grape for high-speed robotic cut-and-catch harvesting. Agronomy 2023, 13, 1618. [Google Scholar] [CrossRef]
- Liu, J.; Liang, J.; Zhao, S.; Jiang, Y.; Wang, J.; Jin, Y. Design of a virtual multi-interaction operation system for hand–eye coordination of grape harvesting robots. Agronomy 2023, 13, 829. [Google Scholar] [CrossRef]
- Ji, W.; He, G.; Xu, B.; Zhang, H.; Yu, X. A new picking pattern of a flexible three-fingered end-effector for apple harvesting robot. Agriculture 2024, 14, 102. [Google Scholar] [CrossRef]
- Yu, Y.; Xie, H.; Zhang, K.; Wang, Y.; Li, Y.; Zhou, J.; Xu, L. Design, development, integration, and field evaluation of a ridge-planting strawberry harvesting robot. Agriculture 2024, 14, 2126. [Google Scholar] [CrossRef]
- Jiang, L.; Xu, B.; Husnain, N.; Wang, Q. Overview of Agricultural Machinery Automation Technology for Sustainable Agriculture. Agronomy 2025, 15, 1471. [Google Scholar] [CrossRef]
- Ji, W.; Zhang, T.; Xu, B.; He, G. Apple recognition and picking sequence planning for harvesting robot in a complex environment. J. Agric. Eng. 2024, 55, 1549. [Google Scholar]
- Syed, T.N.; Zhou, J.; Lakhiar, I.A.; Marinello, F.; Gemechu, T.T.; Rottok, L.T.; Jiang, Z. Enhancing Autonomous Orchard Navigation: A Real-Time Convolutional Neural Network-Based Obstacle Classification System for Distinguishing ‘Real’and ‘Fake’Obstacles in Agricultural Robotics. Agriculture 2025, 15, 827. [Google Scholar] [CrossRef]
- Wang, Q.; He, J.; Lu, C.; Wang, C.; Lin, H.; Yang, H.; Li, H.; Wu, Z. Modelling and control methods in path tracking control for autonomous agricultural vehicles: A review of state of the art and challenges. Appl. Sci. 2023, 13, 7155. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, R.; Ding, R.; Sun, Z.; Jiang, Y.; Liu, W. Research Review of Agricultural Machinery Power Chassis in Hilly and Mountainous Areas. Agriculture 2025, 15, 1158. [Google Scholar] [CrossRef]
- Yao, Z.; Zhao, C.; Zhang, T. Agricultural machinery automatic navigation technology. Iscience 2024, 27, 108714. [Google Scholar] [CrossRef]
- Yu, S.; Zhu, J.; Zhou, J.; Cheng, J.; Bian, X.; Shen, J.; Wang, P. Key technology progress of plant-protection uavs applied to mountain orchards: A review. Agronomy 2022, 12, 2828. [Google Scholar] [CrossRef]
- Staff, A. Coming soon to an orchard near you: The Global Unmanned Spray System (GUSS). Resour. Mag. 2019, 26, 9–10. [Google Scholar]
- Gallou, J.; Lippi, M.; Galle, M.; Marino, A.; Gasparri, A. Modeling and Control of the Vitirover Robot for Weed Management in Precision Agriculture. In Proceedings of the 2024 10th International Conference on Control, Decision and Information Technologies (CoDIT), Valletta, Malta, 1–4 July 2024; pp. 2670–2675. [Google Scholar]
- Wu, T.; Liu, D.; Li, X. Designing Hybrid Mobility for Agricultural Robots: Performance Analysis of Wheeled and Tracked Systems in Variable Terrain. Machines 2025, 13, 572. [Google Scholar] [CrossRef]
- Xin, Q.; Luo, Q.; Zhu, H. Key issues and countermeasures of machine vision for fruit and vegetable picking robot. In Mechatronics and Automation Technology; IOS Press: Amsterdam, The Netherlands, 2024; pp. 69–78. [Google Scholar]
- Su, Z.; Zou, W.; Zhai, C.; Tan, H.; Yang, S.; Qin, X. Design of an Autonomous Orchard Navigation System Based on Multi-Sensor Fusion. Agronomy 2024, 14, 2825. [Google Scholar] [CrossRef]
- Liu, W.; Hu, J.; Liu, J.; Yue, R.; Zhang, T.; Yao, M.; Li, J. Method for the navigation line recognition of the ridge without crops via machine vision. Int. J. Agric. Biol. Eng. 2024, 17, 230–239. [Google Scholar] [CrossRef]
- Zhenyu, C.; Hanjie, D.; Yuanyuan, G.; Changyuan, Z.; Xiu, W.; Wei, Z. Research on an orchard row centreline multipoint autonomous navigation method based on LiDAR. Artif. Intell. Agric. 2025, 15, 221–231. [Google Scholar] [CrossRef]
- Pi, J.; Liu, J.; Zhou, K.; Qian, M. An octopus-inspired bionic flexible gripper for apple grasping. Agriculture 2021, 11, 1014. [Google Scholar] [CrossRef]
- Ji, W.; Qian, Z.; Xu, B.; Tang, W.; Li, J.; Zhao, D. Grasping damage analysis of apple by end-effector in harvesting robot. J. Food Process. Eng. 2017, 40, e12589. [Google Scholar] [CrossRef]
- Zhong, W.; Yang, W.; Zhu, J.; Jia, W.; Dong, X.; Ou, M. An Improved UNet-Based Path Recognition Method in Low-Light Environments. Agriculture 2024, 14, 1987. [Google Scholar] [CrossRef]
- Jia, W.; Zheng, Y.; Zhao, D.; Yin, X.; Liu, X.; Du, R. Preprocessing method of night vision image application in apple harvesting robot. INternational J. Agric. Biol. Eng. 2018, 11, 158–163. [Google Scholar] [CrossRef]
- Zhang, H.; Ji, W.; Xu, B.; Yu, X. Optimizing contact force on an apple picking robot end-effector. Agriculture 2024, 14, 996. [Google Scholar] [CrossRef]
- Cui, L.; Mao, H.; Xue, X.; Ding, S.; Qiao, B. Optimized design and test for a pendulum suspension of the crop spray boom in dynamic conditions based on a six DOF motion simulator. Int. J. Agric. Biol. Eng. 2018, 11, 76–85. [Google Scholar]
- Jin, Y.; Liu, J.; Xu, Z.; Yuan, S.; Li, P.; Wang, J. Development status and trend of agricultural robot technology. Int. J. Agric. Biol. Eng. 2021, 14, 1–19. [Google Scholar] [CrossRef]
- Katona, K.; Neamah, H.A.; Korondi, P. Obstacle avoidance and path planning methods for autonomous navigation of mobile robot. Sensors 2024, 24, 3573. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zeng, X.; Shen, Y.; Xu, J.; Khan, Z. A single-stage navigation path extraction network for agricultural robots in orchards. Comput. Electron. Agric. 2025, 229, 109687. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Y.; Yuan, Q. Application of Dijkstra algorithm in robot path-planning. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Inner Mongolia, China, 15–17 July 2011; pp. 1067–1069. [Google Scholar]
- Husain, Z.; Al Zaabi, A.; Hildmann, H.; Saffre, F.; Ruta, D.; Isakovic, A. Search and rescue in a maze-like environment with ant and dijkstra algorithms. Drones 2022, 6, 273. [Google Scholar] [CrossRef]
- Xu, Y.; Xue, X.; Sun, Z.; Gu, W.; Cui, L.; Jin, Y.; Lan, Y. Global path planning for navigating orchard vehicle based on fruit tree positioning and planting rows detection from UAV imagery. Comput. Electron. Agric. 2025, 236, 110446. [Google Scholar] [CrossRef]
- Liu, Z.; Fang, J.; Zhao, Y. DynaFusion-SLAM: Multi-Sensor Fusion and Dynamic Optimization of Autonomous Navigation Algorithms for Pasture-Pushing Robot. Sensors 2025, 25, 3395. [Google Scholar] [CrossRef]
- Jin, P.; Li, T.; Pan, Y.; Hu, K.; Xu, N.; Ying, W.; Jin, Y.; Kang, H. A Context-Aware Navigation Framework for Ground Robots in Horticultural Environments. Sensors 2024, 24, 3663. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Zeng, J.; Zhao, Y.; Lü, X. Research on global path planning algorithm for mobile robots based on improved A. Expert Syst. Appl. 2024, 243, 122922. [Google Scholar] [CrossRef]
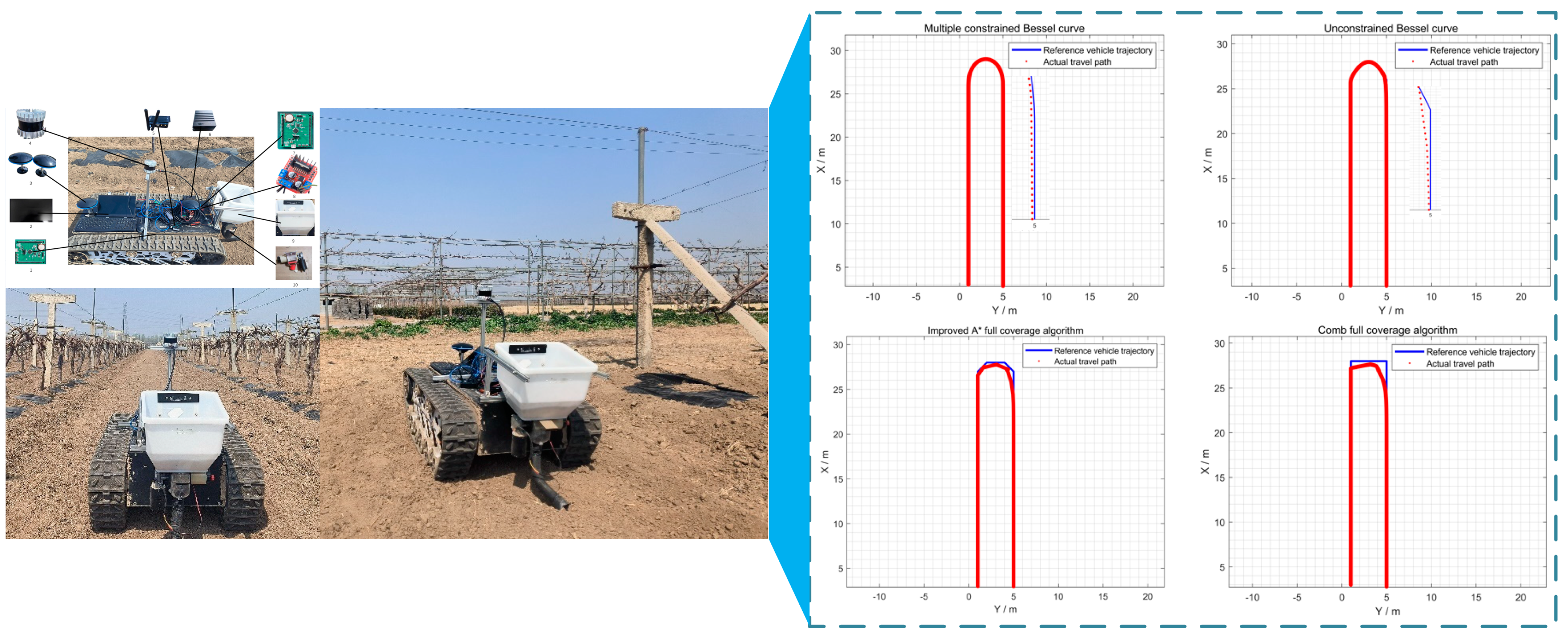
- Shen, Y.; Liu, Z.; Liu, H.; Du, W. Orchard spray robot planning algorithm based on multiple constraints. Trans. CSAM 2023, 54, 56–67. [Google Scholar]
- Hua, W.; Heinemann, P.; He, L. Multi-agent Path Planning in Apple Orchard with Tight Tree Rows Based on Improved A-Star Algorithm for Frost Protection. In Proceedings of the 2023 ASABE Annual International Meeting, Omaha, NE, USA, 9–12 July 2023; p. 1. [Google Scholar]
- Zhang, M.; Li, X.; Wang, L.; Jin, L.; Wang, S. A path planning system for orchard mower based on improved A* algorithm. Agronomy 2024, 14, 391. [Google Scholar] [CrossRef]
- Wang, M.; Xu, J.; Zhang, J.; Cui, Y. An autonomous navigation method for orchard rows based on a combination of an improved a-star algorithm and SVR. Precis. Agric. 2024, 25, 1429–1453. [Google Scholar] [CrossRef]
- Kong, F.; Liu, B.; Han, X.; Yi, L.; Sun, H.; Liu, J.; Liu, L.; Lan, Y. Path Planning Algorithm of Orchard Fertilization Robot Based on Multi-Constrained Bessel Curve. Agriculture 2024, 14, 979. [Google Scholar] [CrossRef]
- Chatzisavvas, A.; Dossis, M.; Dasygenis, M. Optimizing mobile robot navigation based on A-star algorithm for obstacle avoidance in smart agriculture. Electronics 2024, 13, 2057. [Google Scholar] [CrossRef]
- Chi, Z.; Yu, Z.; Wei, Q.; He, Q.; Li, G.; Ding, S. High-efficiency navigation of nonholonomic mobile robots based on improved hybrid A* algorithm. Appl. Sci. 2023, 13, 6141. [Google Scholar] [CrossRef]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Path planning for autonomous vehicles in unknown semi-structured environments. Int. J. Robot. Res. 2010, 29, 485–501. [Google Scholar] [CrossRef]
- Meng, T.; Yang, T.; Huang, J.; Jin, W.; Zhang, W.; Jia, Y.; Wan, K.; Xiao, G.; Yang, D.; Zhong, Z. Improved hybrid A-star algorithm for path planning in autonomous parking system based on multi-stage dynamic optimization. Int. J. Automot. Technol. 2023, 24, 459–468. [Google Scholar] [CrossRef]
- Schlapbach, J.; Schopferer, S. Time-Aware Probabilistic Roadmaps for Multi-Query Path Planning in Dynamic Environments. In Proceedings of the 2024 Eighth IEEE International Conference on Robotic Computing (IRC), Tokyo, Japan, 11–13 December 2024; pp. 9–16. [Google Scholar]
- Zeeshan, S.; Aized, T. Performance analysis of path planning algorithms for fruit harvesting robot. J. Biosyst. Eng. 2023, 48, 178–197. [Google Scholar] [CrossRef]
- Suravarapu, A.; Surampudi, S.S.; Potnuru, S.D.; Desai, R.P. Bidirectional Path Planning for Autonomous Robot Using Dijkstra Algorithm with PRM. In Proceedings of the 2024 IEEE 21st India Council International Conference (INDICON), Kharagpur, India, 19–21 December 2024; pp. 1–6. [Google Scholar]
- Tian, H.; Wang, J.; Huang, H.; Ding, F. Probabilistic roadmap method for path planning of intelligent vehicle based on artificial potential field model in off-roadenvironment. Acta Armamentarii 2021, 42, 1496. [Google Scholar]
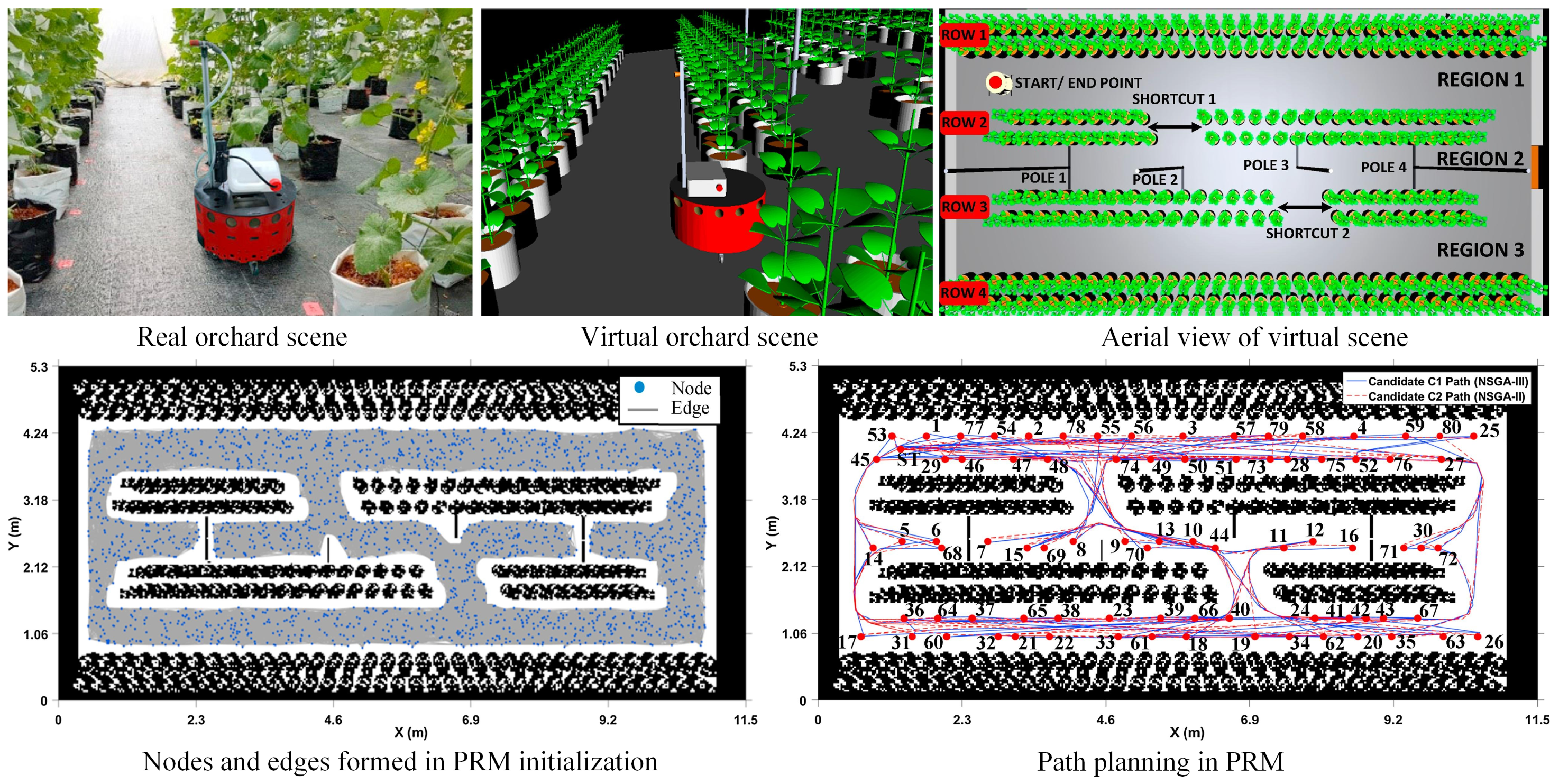
- Mahmud, M.S.A.; Abidin, M.S.Z.; Mohamed, Z.; Abd Rahman, M.K.I.; Iida, M. Multi-objective path planner for an agricultural mobile robot in a virtual greenhouse environment. Comput. Electron. Agric. 2019, 157, 488–499. [Google Scholar] [CrossRef]
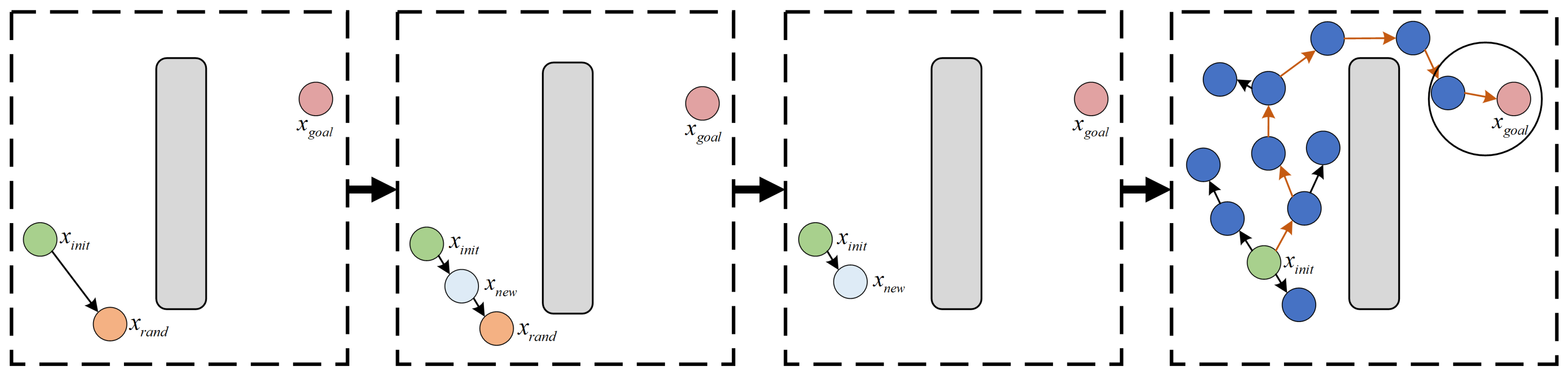
- LaValle, S.M.; Kuffner, J.J. Rapidly-exploring random trees: Progress and prospects: Steven m. lavalle, iowa state university, a james j. kuffner, jr., university of tokyo, tokyo, japan. In Algorithmic and Computational Robotics; A K Peters: Natick, MA, USA, 2001; pp. 303–307. [Google Scholar]
- Li, Y.; Ma, S.; Li, L.; Su, C.; Ding, Z. Path planning of apple tree pruning robot based on improved RRT algorithm. In Proceedings of the 2023 ASABE Annual International Meeting, Omaha, NE, USA, 9–12 July 2023; p. 1. [Google Scholar]
- Hu, M.; Huang, Q.; Cai, J.; Chen, Y.; Li, J.; Shi, L. HPS-RRT*: An Improved Path Planning Algorithm for a Nonholonomic Orchard Robot in Unstructured Environments. Agronomy 2025, 15, 712. [Google Scholar] [CrossRef]
- Li, Y.; Ma, S. Navigation of apple tree pruning robot based on improved RRT-connect algorithm. Agriculture 2023, 13, 1495. [Google Scholar] [CrossRef]
- Zhang, B.; Yin, C.; Fu, Y.; Xia, Y.; Fu, W. Harvest motion planning for mango picking robot based on improved RRT-Connect. Biosyst. Eng. 2024, 248, 177–189. [Google Scholar] [CrossRef]
- Chen, Y.; Fu, Y.; Zhang, B.; Fu, W.; Shen, C. Path planning of the fruit tree pruning manipulator based on improved RRT-Connect algorithm. Int. J. Agric. Biol. Eng. 2022, 15, 177–188. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Incremental sampling-based algorithms for optimal motion planning. Robot. Sci. Syst. VI 2010, 104, 267–274. [Google Scholar]
- Zeeshan, S.; Aized, T.; Riaz, F. In-depth evaluation of automated fruit harvesting in unstructured environment for improved robot design. Machines 2024, 12, 151. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, D.; Zhao, H.; Li, Y.; Song, W.; Liu, M.; Tian, L.; Yan, X. Rapid citrus harvesting motion planning with pre-harvesting point and quad-tree. Comput. Electron. Agric. 2022, 202, 107348. [Google Scholar] [CrossRef]
- Ye, L.; Li, J.; Li, P. Improving path planning for mobile robots in complex orchard environments: The continuous bidirectional Quick-RRT* algorithm. Front. Plant Sci. 2024, 15, 1337638. [Google Scholar] [CrossRef]
- Ye, L.; Wu, F.; Zou, X.; Li, J. Path planning for mobile robots in unstructured orchard environments: An improved kinematically constrained bi-directional RRT approach. Comput. Electron. Agric. 2023, 215, 108453. [Google Scholar] [CrossRef]
- Hui, L.; Shiyi, Z.; Yunpeng, D.; Weidong, J.; Yue, S. Orchard Robot Motion Planning Algorithm Based on Improved Bidirectional RRT. In Nongye Jixie Xuebao/Transactions of the Chinese Society of Agricultural Machinery; Chinese Society of Agricultural Machinery: Beijing, China, 2022; Volume 53. [Google Scholar]
- Lamini, C.; Benhlima, S.; Elbekri, A. Genetic algorithm based approach for autonomous mobile robot path planning. Procedia Comput. Sci. 2018, 127, 180–189. [Google Scholar] [CrossRef]
- Zhang, L.; He, Z.; Zhu, H.; Wei, Z.; Lu, J.; He, X. Adaptive SOM-GA Hybrid Algorithm for Grasping Sequence Optimization in Apple Harvesting Robots: Enhancing Efficiency in Open-Field Orchards. Agronomy 2025, 15, 1230. [Google Scholar] [CrossRef]
- Liao, T.; Deng, S. Research on Genetic Algorithm Optimization of Agricultural Robot Picking Task Planning. In Proceedings of the 2025 International Conference on Electrical Drives, Power Electronics & Engineering (EDPEE), Athens, Greece, 26–28 March 2025; pp. 810–815. [Google Scholar]
- Hizatate, T.; Noguchi, N. Work schedule optimization for electric agricultural robots in orchards. Comput. Electron. Agric. 2023, 210, 107889. [Google Scholar] [CrossRef]
- Li, S.; Zhang, M.; Wang, N.; Cao, R.; Zhang, Z.; Ji, Y.; Li, H.; Wang, H. Intelligent scheduling method for multi-machine cooperative operation based on NSGA-III and improved ant colony algorithm. Comput. Electron. Agric. 2023, 204, 107532. [Google Scholar] [CrossRef]
- Yu, Y.; Hao, S.; Guo, S.; Tang, Z.; Chen, S. Motor torque distribution strategy for different tillage modes of agricultural electric tractors. Agriculture 2022, 12, 1373. [Google Scholar] [CrossRef]
- Tian, H.; Mo, Z.; Ma, C.; Xiao, J.; Jia, R.; Lan, Y.; Zhang, Y. Design and validation of a multi-objective waypoint planning algorithm for UAV spraying in orchards based on improved ant colony algorithm. Front. Plant Sci. 2023, 14, 1101828. [Google Scholar] [CrossRef] [PubMed]
- Niu, J.; Shen, C.; Zhang, L.; Gao, G.; Zheng, J. Study on Multiobjective Path Optimization of Plant Protection Robots Based on Improved ACO-DWA Algorithm. Eng. Rep. 2025, 7, e70009. [Google Scholar] [CrossRef]
- Xu, Y.; Xue, X.; Sun, Z.; Cui, L.; Cai, C.; Zhou, Q.; Chen, C.; Gu, W. Path planning and scheduling of multiple unmanned Ground vehicles for orchard plant protection operations. Comput. Electron. Agric. 2025, 237, 110615. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Lv, L.; Shi, Y.; Yu, X. Study on modeling method of a multi-parameter control system for threshing and cleaning devices in the grain combine harvester. Agriculture 2022, 12, 1483. [Google Scholar] [CrossRef]
- Xu, L.; You, J.; Yuan, H. Real-time parametric path planning algorithm for agricultural machinery kinematics model based on particle swarm optimization. Agriculture 2023, 13, 1960. [Google Scholar] [CrossRef]
- Gao, R.; Zhou, Q.; Cao, S.; Jiang, Q. Apple-picking robot picking path planning algorithm based on improved PSO. Electronics 2023, 12, 1832. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path planning techniques for mobile robots: Review and prospect. Expert Syst. Appl. 2023, 227, 120254. [Google Scholar] [CrossRef]
- Wang, J.; Yang, L.; Cen, H.; He, Y.; Liu, Y. Dynamic obstacle avoidance control based on a novel dynamic window approach for agricultural robots. Comput. Ind. 2025, 167, 104272. [Google Scholar] [CrossRef]
- Huang, P.; Huang, P.; Wang, Z.; Wu, X.; Liu, J.; Zhu, L. Deep-learning-based trunk perception with depth estimation and DWA for robust navigation of robotics in orchards. Agronomy 2023, 13, 1084. [Google Scholar] [CrossRef]
- Zhu, F.; Chen, J.; Guan, Z.; Zhu, Y.; Shi, H.; Cheng, K. Development of a combined harvester navigation control system based on visual simultaneous localization and mapping-inertial guidance fusion. J. Agric. Eng. 2024, 55, 1583. [Google Scholar] [CrossRef]
- Vu, C.T.; Chen, H.C.; Liu, Y.C. Toward Autonomous Navigation for Agriculture Robots in Orchard Farming. In Proceedings of the 2024 IEEE International Conference on Recent Advances in Systems Science and Engineering (RASSE), IEEE, Taichung, Taiwan, 6–8 November 2024; pp. 1–8. [Google Scholar]
- Li, Y.; Li, J.; Zhou, W.; Yao, Q.; Nie, J.; Qi, X. Robot path planning navigation for dense planting red jujube orchards based on the joint improved A* and DWA algorithms under laser SLAM. Agriculture 2022, 12, 1445. [Google Scholar] [CrossRef]
- He, Q.; Wang, Z.; Li, K.; Zhang, Y.; Li, M. Research on autonomous navigation of mobile robots based on IA-DWA algorithm. Sci. Rep. 2025, 15, 2099. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, C.; Huang, R.; Tong, K.; He, Y.; Xu, L. Path planning for mobile robots in greenhouse orchards based on improved A* and fuzzy DWA algorithms. Comput. Electron. Agric. 2024, 227, 109598. [Google Scholar] [CrossRef]
- Zhang, W.; Zeng, Y.; Wang, S.; Wang, T.; Li, H.; Fei, K.; Qiu, X.; Jiang, R.; Li, J. Research on the local path planning of an orchard mowing robot based on an elliptic repulsion scope boundary constraint potential field method. Front. Plant Sci. 2023, 14, 1184352. [Google Scholar] [CrossRef]
- Tang, Z.; Xu, L.; Wang, Y.; Kang, Z.; Xie, H. Collision-free motion planning of a six-link manipulator used in a citrus picking robot. Appl. Sci. 2021, 11, 11336. [Google Scholar] [CrossRef]
- Yang, D.; Dong, L.; Dai, J.K. Collision avoidance trajectory planning for a dual-robot system: Using a modified APF method. Robotica 2024, 42, 846–863. [Google Scholar] [CrossRef]
- Das, M.S.; Sanyal, S.; Mandal, S. Navigation of multiple robots in formative manner in an unknown environment using artificial potential field based path planning algorithm. Ain Shams Eng. J. 2022, 13, 101675. [Google Scholar] [CrossRef]
- Zhuang, M.; Li, G.; Ding, K. Obstacle avoidance path planning for apple picking robotic arm incorporating artificial potential field and A* algorithm. IEEE Access 2023, 11, 100070–100082. [Google Scholar] [CrossRef]
- Wei, Y.; Lee, K.; Lee, K. Autonomous field navigation of mobile robots for data collection and monitoring in agricultural crop fields. In Proceedings of the 2024 21st International Conference on Ubiquitous Robots (UR), New York, NY, USA, 24–27 June 2024; pp. 707–712. [Google Scholar]
- Wu, H.; Zhang, Y.; Huang, L.; Zhang, J.; Luan, Z.; Zhao, W.; Chen, F. Research on vehicle obstacle avoidance path planning based on APF-PSO. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 1391–1405. [Google Scholar] [CrossRef]
- Rösmann, C.; Feiten, W.; Wösch, T.; Hoffmann, F.; Bertram, T. Trajectory modification considering dynamic constraints of autonomous robots. In Proceedings of the ROBOTIK 2012; 7th German Conference on Robotics, VDE, Munich, Germany, 21–22 May 2012; pp. 1–6. [Google Scholar]
- Inoue, K.; Kaizu, Y.; Igarashi, S.; Furuhashi, K.; Imou, K. Autonomous navigation and obstacle avoidance in an orchard using machine vision techniques for a robotic mower. Eng. Agric. Environ. Food 2022, 15, 87–99. [Google Scholar] [CrossRef]
- Zhang, M.; Pengcheng, L.; Jie, L.; Lei, L.; Huibin, Z.; Lili, Y. Local path planning method based on smooth time elastic band algorithm for orchard robotic lawn mower. INMATEH-Agric. Eng. 2024, 73, 249–262. [Google Scholar] [CrossRef]
- Han, W.; Gu, Q.; Gu, H.; Xia, R.; Gao, Y.; Zhou, Z.; Luo, K.; Fang, X.; Zhang, Y. Design of Chili Field Navigation System Based on Multi-Sensor and Optimized TEB Algorithm. Agronomy 2024, 14, 2872. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Wang, H.; Song, J.; Xie, F.; Wang, K. Research on robot path planning based on point cloud map in orchard environment. IEEE Access 2024, 12, 54853–54865. [Google Scholar] [CrossRef]
- Li, W.; Todorov, E. Iterative linear quadratic regulator design for nonlinear biological movement systems. In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, Setúbal, Portugal, 25–28 August 2004; Volume 2, pp. 222–229. [Google Scholar]
- Pinto, F.A.; Tommaselli, F.A.G.; Gasparino, M.V.; Becker, M. Navigating with finesse: Leveraging neural network-based lidar perception and ilqr control for intelligent agriculture robotics. In Proceedings of the 2023 Latin American Robotics Symposium (LARS), 2023 Brazilian Symposium on Robotics (SBR), and 2023 Workshop on Robotics in Education (WRE), Salvador, Bahia, Brazil, 9–11 October 2023; pp. 502–507. [Google Scholar]
- Howell, T.A.; Jackson, B.E.; Manchester, Z. Altro: A fast solver for constrained trajectory optimization. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hangzhou, China, 19–25 October 2025; pp. 7674–7679. [Google Scholar]
- Li, T.; Guo, Y.; Liu, H.; Shen, Y.; Yayun, S. Real-time local trajectory optimization of an orchard robot using improved ALTRO. Trans. Chin. Soc. Agric. Eng. 2025, 41, 1–10. [Google Scholar]
- Wu, H.; Wang, X.; Chen, X.; Zhang, Y.; Zhang, Y. Review on Key Technologies for Autonomous Navigation in Field Agricultural Machinery. Agriculture 2025, 15, 1297. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Wen, X.; Zhang, G.; Ma, Q.; Cheng, S.; Qi, J.; Xu, L.; Chen, L. An optimal goal point determination algorithm for automatic navigation of agricultural machinery: Improving the tracking accuracy of the Pure Pursuit algorithm. Comput. Electron. Agric. 2022, 194, 106760. [Google Scholar] [CrossRef]
- Li, B.; Wang, Y.; Ma, S.; Bian, X.; Li, H.; Zhang, T.; Li, X.; Zhang, Y. Adaptive pure pursuit: A real-time path planner using tracking controllers to plan safe and kinematically feasible paths. IEEE Trans. Intell. Veh. 2023, 8, 4155–4168. [Google Scholar] [CrossRef]
- Raikwar, S.; Fehrmann, J.; Herlitzius, T. Navigation and control development for a four-wheel-steered mobile orchard robot using model-based design. Comput. Electron. Agric. 2022, 202, 107410. [Google Scholar] [CrossRef]
- Song, Y.; Xue, J.; Zhang, T.; Sun, X.; Sun, H.; Gao, W.; Chen, Q. Path tracking control of crawler tractor based on adaptive adjustment of lookahead distance using sparrow search algorithm. Comput. Electron. Agric. 2025, 234, 110219. [Google Scholar] [CrossRef]
- Hu, C.; Ru, Y.; Li, X.; Fang, S.; Zhou, H.; Yan, X.; Liu, M.; Xie, R. Path tracking control for brake-steering tracked vehicles based on an improved pure pursuit algorithm. Biosyst. Eng. 2024, 242, 1–15. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, J.; Liu, Y.; Zhang, T.; Yan, M.; Chen, J.; Zhou, C.; Hu, J.; Chen, X. An ultrasonic ridge-tracking method based on limiter sliding window filter and fuzzy pure pursuit control for ridge transplanter. Agriculture 2024, 14, 1713. [Google Scholar] [CrossRef]
- Huang, P.C.; Luo, X.W.; Zhang, Z.G. Control method of headland turning based on improved pure pursuit model for agricultural machine. Jisuanji Gongcheng yu Yingyong (Comput. Eng. Appl.) 2010, 46, 216–219. [Google Scholar]
- Wang, X.; Zhang, B.; Du, X.; Hu, X.; Wu, C.; Cai, J. An Adaptive Path Tracking Controller with Dynamic Look-Ahead Distance Optimization for Crawler Orchard Sprayers. Actuators 2025, 14, 154. [Google Scholar] [CrossRef]
- Wen, J.; Yao, L.; Zhou, J.; Yang, Z.; Xu, L.; Yao, L. Path Tracking Control of Agricultural Automatic Navigation Vehicles Based on an Improved Sparrow Search-Pure Pursuit Algorithm. Agriculture 2025, 15, 1215. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, J.; Yao, L.; Yang, Z.; Xu, L.; Yao, L. Agricultural machinery path tracking with varying curvatures based on an improved pure-pursuit method. Agriculture 2025, 15, 266. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, B.; Du, X.; Chen, H.; Zhu, T.; Wu, C. Self-Adjusting Look-Ahead Distance of Precision Path Tracking for High-Clearance Sprayers in Field Navigation. Agronomy 2025, 15, 1433. [Google Scholar] [CrossRef]
- Al-Jumaili, M.H.; Özok, Y.E. New control model for autonomous vehicles using integration of Model Predictive and Stanley based controllers. Sci. Rep. 2024, 14, 19872. [Google Scholar] [CrossRef]
- Fu, W.; Liu, Y.; Zhang, X. Research on accurate motion trajectory control method of four-wheel steering AGV based on stanley-PID control. Sensors 2023, 23, 7219. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Xu, S.; Rai, R. Trailer-referenced autonomous navigation of agricultural tractor–trailer systems. Comput. Electron. Agric. 2025, 237, 110514. [Google Scholar] [CrossRef]
- Huang, S.; Pan, K.; Wang, S.; Zhu, Y.; Zhang, Q.; Su, X.; Yu, H. Design and test of an automatic navigation fruit-picking platform. Agriculture 2023, 13, 882. [Google Scholar] [CrossRef]
- Wang, L.; Zhai, Z.; Zhu, Z.; Mao, E. Path tracking control of an autonomous tractor using improved Stanley controller optimized with multiple-population genetic algorithm. Actuators 2022, 11, 22. [Google Scholar] [CrossRef]
- Cui, B.; Cui, X.; Wei, X.; Zhu, Y.; Ma, Z.; Zhao, Y.; Liu, Y. Design and Testing of a Tractor Automatic Navigation System Based on Dynamic Path Search and a Fuzzy Stanley Model. Agriculture 2024, 14, 2136. [Google Scholar] [CrossRef]
- Sun, Y.; Cui, B.; Ji, F.; Wei, X.; Zhu, Y. The full-field path tracking of agricultural machinery based on PSO-enhanced fuzzy stanley model. Appl. Sci. 2022, 12, 7683. [Google Scholar] [CrossRef]
- Jiang, A.; Ahamed, T. Navigation of an autonomous spraying robot for orchard operations using LiDAR for tree trunk detection. Sensors 2023, 23, 4808. [Google Scholar] [CrossRef] [PubMed]
- Shih, C.H.; Lin, C.J.; Jhang, J.Y. Ackerman unmanned mobile vehicle based on heterogeneous sensor in navigation control application. Sensors 2023, 23, 4558. [Google Scholar] [CrossRef]
- Lu, E.; Ma, Z.; Li, Y.; Xu, L.; Tang, Z. Adaptive backstepping control of tracked robot running trajectory based on real-time slip parameter estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Farkh, R.; Aljaloud, K. Vision navigation based PID control for line tracking robot. Intell. Autom. Soft Comput. 2023, 35, 901–911. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Wang, G.; Gu, K.; Che, H. Discrete open-closed-loop PID-type iterative learning control for trajectory tracking of tracked mobile robots. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221137247. [Google Scholar] [CrossRef]
- Li, Y.; Feng, Q.; Ji, C.; Sun, J.; Sun, Y. GNSS and LiDAR Integrated Navigation Method in Orchards with Intermittent GNSS Dropout. Appl. Sci. 2024, 14, 3231. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Pan, X.; Dou, H.; Zhao, X.; Gao, Y.; Yang, S.; Zhai, C. Design and experiment of a breakpoint continuous spraying system for automatic-guidance boom sprayers. Agriculture 2023, 13, 2203. [Google Scholar] [CrossRef]
- Yuexia, C.; Long, C.; Ruochen, W.; Xing, X.; Yujie, S.; Yanling, L. Modeling and test on height adjustment system of electrically-controlled air suspension for agricultural vehicles. Int. J. Agric. Biol. Eng. 2016, 9, 40–47. [Google Scholar]
- Zou, T.; Angeles, J.; Hassani, F. Dynamic modeling and trajectory tracking control of unmanned tracked vehicles. Robot. Auton. Syst. 2018, 110, 102–111. [Google Scholar] [CrossRef]
- Peicheng, S.; Li, L.; Ni, X.; Yang, A. Intelligent vehicle path tracking control based on improved MPC and hybrid PID. IEEE Access 2022, 10, 94133–94144. [Google Scholar] [CrossRef]
- Zhu, Y.; Cui, B.; Yu, Z.; Gao, Y.; Wei, X. Tillage Depth Detection and Control Based on Attitude Estimation and Online Calibration of Model Parameters. Agriculture 2024, 14, 2130. [Google Scholar] [CrossRef]
- Wan, C.; Yang, J.; Zhou, L.; Wang, S.; Peng, J.; Tan, Y. Fertilization control system research in orchard based on the PSO-BP-PID control algorithm. Machines 2022, 10, 982. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Zhang, W.; Li, H.; Zeng, Y.; Wang, T.; Fei, K.; Qiu, X.; Jiang, R.; Mai, C.; et al. Research on Path Tracking for an Orchard Mowing Robot Based on Cascaded Model Predictive Control and Anti-Slip Drive Control. Agronomy 2023, 13, 1395. [Google Scholar] [CrossRef]
- Zhang, S.; Wei, X.; Liu, C.; Ge, J.; Cui, X.; Wang, F.; Wang, A.; Chen, W. Adaptive path tracking and control system for unmanned crawler harvesters in paddy fields. Comput. Electron. Agric. 2025, 230, 109878. [Google Scholar] [CrossRef]
- Stano, P.; Montanaro, U.; Tavernini, D.; Tufo, M.; Fiengo, G.; Novella, L.; Sorniotti, A. Model predictive path tracking control for automated road vehicles: A review. Annu. Rev. Control. 2023, 55, 194–236. [Google Scholar] [CrossRef]
- Wang, S.; Guo, J.; Mao, Y.; Wang, H.; Fan, J. Research on the model predictive trajectory tracking control of unmanned ground tracked vehicles. Drones 2023, 7, 496. [Google Scholar] [CrossRef]
- Liu, H.; Yan, S.; Shen, Y.; Li, C.; Zhang, Y.; Hussain, F. Model predictive control system based on direct yaw moment control for 4WID self-steering agriculture vehicle. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- Hu, K.; Cheng, K. Trajectory planning for an articulated tracked vehicle and tracking the trajectory via an adaptive model predictive control. Electronics 2023, 12, 1988. [Google Scholar] [CrossRef]
- Villemazet, A.; Durand-Petiteville, A.; Cadenat, V. Autonomous navigation strategy for orchards relying on sensor-based nonlinear model predictive control. In Proceedings of the 2022 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Sapporo, Hokkaido, Japan, 11–15 July 2022; pp. 744–749. [Google Scholar]
- Liu, G.; Li, C.; Shen, Y. Trajectory tracking and fuzzy adaptive model predictive control of high clearance synchronous-steering sprayer. Trans. Chin. Soc. Agric. Mach. 2021, 52, 389–399. [Google Scholar]
- Sperti, M.; Ambrosio, M.; Martini, M.; Navone, A.; Ostuni, A.; Chiaberge, M. Non-linear Model Predictive Control for Multi-task GPS-free Autonomous Navigation in Vineyards. In Proceedings of the 2024 IEEE 20th International Conference on Automation Science and Engineering (CASE), Bari, Italy, 28 August–1 September 2024; pp. 96–101. [Google Scholar]
- Zhou, B.; Su, X.; Yu, H.; Guo, W.; Zhang, Q. Research on path tracking of articulated steering tractor based on modified model predictive control. Agriculture 2023, 13, 871. [Google Scholar] [CrossRef]
- Xu, J.; Lai, J.; Guo, R.; Lu, X.; Xu, L. Efficiency-oriented MPC algorithm for path tracking in autonomous agricultural machinery. Agronomy 2022, 12, 1662. [Google Scholar] [CrossRef]
- Wang, P.; Gao, S.; Li, L.; Cheng, S.; Zhao, L. Automatic steering control strategy for unmanned vehicles based on robust backstepping sliding mode control theory. IEEE Access 2019, 7, 64984–64992. [Google Scholar] [CrossRef]
- Sekban, H.T.; Basci, A. Designing new model-based adaptive sliding mode controllers for trajectory tracking control of an unmanned ground vehicle. IEEE Access 2023, 11, 101387–101397. [Google Scholar] [CrossRef]
- Lu, E.; Xue, J.; Chen, T.; Jiang, S. Robust trajectory tracking control of an autonomous tractor-trailer considering model parameter uncertainties and disturbances. Agriculture 2023, 13, 869. [Google Scholar] [CrossRef]
- Ma, B.; Pei, W.; Zhang, Q. Trajectory tracking control of autonomous vehicles based on an improved sliding mode control scheme. Electronics 2023, 12, 2748. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Z.; Ding, S.; Xia, J.; Xing, G. Adaptive disturbance observer-based fixed time nonsingular terminal sliding mode control for path-tracking of unmanned agricultural tractors. Biosyst. Eng. 2024, 246, 96–109. [Google Scholar] [CrossRef]
- Yan, X.; Wang, S.; He, Y.; Ma, A.; Zhao, S. Autonomous Tracked Vehicle Trajectory Tracking Control Based on Disturbance Observation and Sliding Mode Control. Actuators 2025, 14, 51. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Xie, J.; Wang, X.; Liu, H.; Li, J.; Wang, P.; Yang, X. Path planning and tracking control of orchard wheel mower based on BL-ACO and GO-SMC. Comput. Electron. Agric. 2025, 228, 109696. [Google Scholar] [CrossRef]
- Ding, C.; Ding, S.; Wei, X.; Mei, K. Output feedback sliding mode control for path-tracking of autonomous agricultural vehicles. Nonlinear Dyn. 2022, 110, 2429–2445. [Google Scholar] [CrossRef]
- Mancini, M.; Trombetta, E.I.; Carminati, D.; Capello, E. Adaptive sliding mode control with artificial potential field for ground robots in precision agriculture. In Proceedings of the 2023 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Pisa, Italy, 6–8 November 2023; pp. 325–330. [Google Scholar]
- Ji, X.; Wang, A.; Wei, X. Precision control of spraying quantity based on linear active disturbance rejection control method. Agriculture 2021, 11, 761. [Google Scholar] [CrossRef]
- Ma, J.; Xie, H.; Song, K.; Liu, H. Self-optimizing path tracking controller for intelligent vehicles based on reinforcement learning. Symmetry 2021, 14, 31. [Google Scholar] [CrossRef]
- BAI, Q. Deep reinforcement learning-driven decision support system design for precision agriculture: Optimizing farming and resource use. Turk. J. Agric. For. 2025, 49, 598–611. [Google Scholar] [CrossRef]
- Guo, Z.; Fu, H.; Wu, J.; Han, W.; Huang, W.; Zheng, W.; Li, T. Dynamic Task Planning for Multi-Arm Apple-Harvesting Robots Using LSTM-PPO Reinforcement Learning Algorithm. Agriculture 2025, 15, 588. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Cao, D.; Ma, L.; Li, K.; Jia, L.; Cui, Y. Coverage path planning for kiwifruit picking robots based on deep reinforcement learning. Comput. Electron. Agric. 2023, 205, 107593. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, S.; Zhang, B.; Wang, A.; Zhang, L.; Zhu, Q. Research Status and Development Trends of Deep Reinforcement Learning in the Intelligent Transformation of Agricultural Machinery. Agriculture 2025, 15, 1223. [Google Scholar] [CrossRef]
- Zhu, H. Reinforcement learning-based state space dimensionality reduction and optimal control strategy design in robot navigation systems. J. Combin. Math. Combin. Comput. 2025, 127, 9239–9261. [Google Scholar]
- Vashisth, A.; Rückin, J.; Magistri, F.; Stachniss, C.; Popović, M. Deep reinforcement learning with dynamic graphs for adaptive informative path planning. IEEE Robot. Autom. Lett. 2024, 9, 7747–7754. [Google Scholar] [CrossRef]
- Navone, A.; Martini, M.; Ambrosio, M.; Ostuni, A.; Angarano, S.; Chiaberge, M. GPS-free autonomous navigation in cluttered tree rows with deep semantic segmentation. Robot. Auton. Syst. 2025, 183, 104854. [Google Scholar] [CrossRef]
- Martini, M.; Cerrato, S.; Salvetti, F.; Angarano, S.; Chiaberge, M. Position-agnostic autonomous navigation in vineyards with deep reinforcement learning. In Proceedings of the 2022 IEEE 18th International Conference on Automation Science and Engineering (CASE), Mexico City, Mexico, 22–26 August 2022; pp. 477–484. [Google Scholar]
- Zhang, L.; Zhang, R.; Zhang, D.; Yi, T.; Ding, C.; Chen, L. Path curvature incorporated reinforcement learning method for accurate path tracking of agricultural vehicles. Comput. Electron. Agric. 2025, 234, 110243. [Google Scholar] [CrossRef]
- Fukada, K.; Hara, K.; Cai, J.; Teruya, D.; Shimizu, I.; Kuriyama, T.; Koga, K.; Sakamoto, K.; Nakamura, Y.; Nakajo, H. An automatic tomato growth analysis system using YOLO transfer learning. Appl. Sci. 2023, 13, 6880. [Google Scholar] [CrossRef]
- Attri, I.; Awasthi, L.K.; Sharma, T.P.; Rathee, P. A review of deep learning techniques used in agriculture. Ecol. Inform. 2023, 77, 102217. [Google Scholar] [CrossRef]
- Hossen, M.I.; Awrangjeb, M.; Pan, S.; Mamun, A.A. Transfer learning in agriculture: A review. Artif. Intell. Rev. 2025, 58, 97. [Google Scholar] [CrossRef]
- Bai, Y.; Guo, Y.; Zhang, Q.; Cao, B.; Zhang, B. Multi-network fusion algorithm with transfer learning for green cucumber segmentation and recognition under complex natural environment. Comput. Electron. Agric. 2022, 194, 106789. [Google Scholar] [CrossRef]
- Devanna, R.P.; Milella, A.; Marani, R.; Garofalo, S.P.; Vivaldi, G.A.; Pascuzzi, S.; Galati, R.; Reina, G. In-field automatic identification of pomegranates using a farmer robot. Sensors 2022, 22, 5821. [Google Scholar] [CrossRef]
- Xue, X.; Luo, Q.; Bu, M.; Li, Z.; Lyu, S.; Song, S. Citrus tree canopy segmentation of orchard spraying robot based on RGB-D image and the improved DeepLabv3+. Agronomy 2023, 13, 2059. [Google Scholar] [CrossRef]
- Cao, B.; Zhang, B.; Zheng, W.; Zhou, J.; Lin, Y.; Chen, Y. Real-time, highly accurate robotic grasp detection utilizing transfer learning for robots manipulating fragile fruits with widely variable sizes and shapes. Comput. Electron. Agric. 2022, 200, 107254. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.H.; Yang, J.; Yan, Y. Dual control of exploration and exploitation for auto-optimization control with active learning. IEEE Trans. Autom. Sci. Eng. 2024, 22, 2145–2158. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.H.; Yang, J.; Liu, C. Cooperative active learning-based dual control for exploration and exploitation in autonomous search. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 2221–2233. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.H. Perspective view of autonomous control in unknown environment: Dual control for exploitation and exploration vs reinforcement learning. Neurocomputing 2022, 497, 50–63. [Google Scholar] [CrossRef]
- Chen, W.H.; Rhodes, C.; Liu, C. Dual control for exploitation and exploration (DCEE) in autonomous search. Automatica 2021, 133, 109851. [Google Scholar] [CrossRef]









| Type | Methods | Advantages | Disadvantages | References |
|---|---|---|---|---|
| Global path Planning | Dijkstra | Global optimal solution, Simple algorithm | High computational complexity and low efficiency | [46,47,48,49] |
| A* | Shortest path, completeness | Large computational load, complex implementation | [50,51,52,53,54,55,56,57,58,59] | |
| PRM | High dimensionality for handling complex spaces | Static-only; non-optimal; time-consuming | [60,61,62,63,64] | |
| RRT | Simple structure, strong applicability | Non-optimal paths, slow convergence | [66,67,68,69,70,72,73,74,75,76] | |
| GA | Suitable for nonlinear systems with strong parallelism | Complex parameter tuning, slow convergence | [77,78,79,80] | |
| ACO | Suitable for discrete path optimization | Prone to local optimality, slow initial convergence | [81,82,83,84] | |
| PSO | Simple implementation, fast convergence | Premature convergence in high-dimensional problems | [85,86,87,88] | |
| Local path Planning | DWA | Strong real-time performance, consider constraints | Short-sightedness, sensitive to parameters | [90,91,92,93,94,95,96] |
| APF | Low complexity, small computational load | Prone to local minima, unstable dynamic spaces | [97,98,99,100,101,102,103] | |
| TEB | Adaptability to dynamic environments | Sensitive to initialization | [105,106,107,108] | |
| iLQR | Iterative approximation of optimal solution | Model dependence and large computational load | [110,111,112] |
| Methods | Advantages | Disadvantages | References |
|---|---|---|---|
| Pure Pursuit | Simple and intuitive with few parameters | Sensitive to path curvature, without considering constraints | [117,118,119,120,121,122,123,124] |
| Stanley | Adjustable parameters, heading deviation considered | Incapable of handling complex constraints | [127,128,129,130,131] |
| PID | Simple to implement, low computational load | Relies on parameter tuning, cannot handle nonlinear systems | [78,138,139,140,141,142,143,144] |
| MPC | Multi-objective optimization, predicts future states | Depends on accurate models, high computational complexity | [147,148,149,150,151,152,153,154] |
| SMC | Strong robustness, fast convergence | Chattering issues, complex parameter tuning | [155,156,157,158,159,160,161,162,163] |
| RL | Model-free learning, adapts to high-dimensional spaces | High training cost, limited real-time performance | [168,169,170,171,172,173,174] |
| TL | High data utilization efficiency and learning rate | Risk of negative migration, high computational overhead | [175,176,177,178,179,180,181] |
| DCEE | Strong adaptability, multi-objective optimization | Depends on environment information | [182,183,184,185] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Shen, Y.; Zhang, Y.; Huo, C.; Shen, Z.; Su, W.; Liu, H. Research Progress on Path Planning and Tracking Control Methods for Orchard Mobile Robots in Complex Scenarios. Agriculture 2025, 15, 1917. https://doi.org/10.3390/agriculture15181917
Shen Y, Shen Y, Zhang Y, Huo C, Shen Z, Su W, Liu H. Research Progress on Path Planning and Tracking Control Methods for Orchard Mobile Robots in Complex Scenarios. Agriculture. 2025; 15(18):1917. https://doi.org/10.3390/agriculture15181917
Chicago/Turabian StyleShen, Yayun, Yue Shen, Yafei Zhang, Chenwei Huo, Zhuofan Shen, Wei Su, and Hui Liu. 2025. "Research Progress on Path Planning and Tracking Control Methods for Orchard Mobile Robots in Complex Scenarios" Agriculture 15, no. 18: 1917. https://doi.org/10.3390/agriculture15181917
APA StyleShen, Y., Shen, Y., Zhang, Y., Huo, C., Shen, Z., Su, W., & Liu, H. (2025). Research Progress on Path Planning and Tracking Control Methods for Orchard Mobile Robots in Complex Scenarios. Agriculture, 15(18), 1917. https://doi.org/10.3390/agriculture15181917







