Research on Layered Fertilization Method of Fertilizer Applicator and Optimization of Key Parameters

Abstract

To address the challenges of layered fertilization in orchards and the lack of dedicated equipment, this study proposes a layered fertilization technique based on the three-dimensional distribution characteristics of jujube root systems and develops an orchard layered fertilizer applicator. First, the agronomic advantages of layered fertilization were systematically elucidated by analyzing the spatial distribution patterns of jujube roots, as well as the mechanisms of fertilizer nutrient transport and uptake. Second, parametric design was conducted for key components (e.g., trenching–fertilizing unit), with emphasis on the structural design of the fertilizer-dividing box and the augerless spiral conveying mechanism. A three-factor, three-level experiment based on response surface methodology was implemented, where the coefficient of variation (CV) of fertilization uniformity and row consistency were selected as evaluation indices to optimize key parameters (forward speed, augerless spiral speed, and fertilizer gate opening). The optimal operational combination was determined as follows: forward speed of 2.62 km/h, augerless spiral speed of 29.87 r/min, and fertilizer gate opening of 3.49 cm. Field tests demonstrated that the CVs of fertilization uniformity and row consistency reached 7.77% and 8.46%, respectively, meeting the agronomic requirements for orchard fertilization. This study provides a reference for the development of orchard fertilization technologies and machinery.

1. Introduction

Jujube (Ziziphus jujuba Mill.) is a characteristic and economically dominant fruit tree in Xinjiang [1]. Its cultivation area has consistently expanded in recent years, exceeding 410,000 hectares currently, serving as a pivotal industry for local fruit growers’ income growth. Rational fertilization during cultivation enhances jujube tree growth, improves fruit quality, and increases yield [2]. Root system distribution significantly affects crop nutrient uptake, water utilization, and soil anchorage [3]. Similarly, crop yield is closely correlated with the spatial distribution of roots [4]. Fertilization position and depth directly influence root absorption of soil nutrients [5]. Cheng Hongsheng et al. [6] employed a layered near-root fertilization shovel to deliver liquid manure adjacent to plant roots, effectively reducing the distance between fertilizer diffusion centers and root centers. Root-proximal fertilization can significantly improve fertilizer use efficiency [7]. As a root-proximal fertilization method, stratified fertilization remarkably enhances root system development and downward growth [8]. Stratified fertilization stimulates both taproots and lateral roots, increasing yield, nitrogen use efficiency (NUE), and phosphorus uptake efficiency by 7.8–24.6%, 11.1–43.5%, and 16.8–42.8%, respectively [9]. This method effectively improves nutrient uptake efficiency. However, current orchard fertilization technologies and equipment still have limitations. The high-efficiency stratified fertilization technique has not been widely adopted in orchard management. Existing orchard fertilization equipment cannot effectively achieve stratified fertilization. Due to poor adaptability of current tools to stratified root architectures, developing efficient and precise orchard fertilization technologies and equipment is of great significance.

The essence of precision orchard fertilization lies in the accurate and efficient application of appropriate fertilizer quantities to root distribution zones [10]. However, mechanized technologies and equipment meeting these criteria remain scarce. Traditional manual fertilization methods (broadcasting, hole application, and trench application) exhibit distinct limitations: Broadcasting (surface application with shallow tillage irrigation) tends to cause nutrient accumulation in topsoil, inducing root upward shift. Hole application (localized digging fertilization) enables rapid nutrient availability but increases risks of fertilizer burn and root damage [10,11]. Variations in fertilizer-application depth can alter root spatial distribution in soil [12]. Fertilizer-use efficiency increases significantly as the distance between the application zone and root absorption area decreases [5,13]. Layered fertilization regulates fertilizer allocation ratios across soil layers based on root distribution patterns, enhancing both subsoil nutrient content [9] and root architecture optimization [8]. Such root optimization indirectly improves yield and enhances lodging resistance [14]. Although China has developed various orchard fertilizer applicators to advance mechanization, most inadequately account for the spatial distribution characteristics of fruit tree roots. The circular-trench fertilizer applicator developed by Zhu Xinhua et al. [10] reduces nutrient migration distance, yet its applicability is restricted to dwarf high-density apple orchards. Han Bing’s spiral hole-digging applicator [15] and Shen Congju’s gas-explosion subsoiling applicator [16], respectively, integrate hole-digging/fertilization and subsoiling/fertilization operations. However, such hole-application machinery suffers from intermittent operation and low efficiency [10]. Trench-application method (along trunk periphery [17]): Chen Pinglu’s vertical spiral trencher [18] achieves efficient trenching–fertilizing–covering integration, while Han et al.’s deep orchard applicator [19] enables manure deep placement. Both systems retain technical constraints of single-row operation and inability to achieve layered fertilization. Given the differential nutrient uptake characteristics among distinct root layers [20], stratified fertilization (differential fertilization based on root distribution patterns) has been extensively studied in grain crops [9,21]. However, specialized fertilization equipment for stratified fertilization in fruit trees remains non-existent. Therefore, it is imperative to develop efficient and precise fertilization technologies and equipment tailored for Xinjiang orchards. Meanwhile, analysis of fruit tree root architecture must be conducted prior to design optimization, which establishes the foundation for improving layered fertilization equipment.

To address the technical bottlenecks and equipment gaps in mechanized layered fertilization for Xinjiang orchards, this study proposes an innovative mechanized layered fertilization solution through agronomic theoretical analysis, developing a dedicated layered fertilizer applicator and conducting field trials to achieve precise and efficient fertilizer application in Xinjiang orchards.

2. Materials and Methods

2.1. Agronomic Analysis

Fertilizers not only supply essential nutrients to fruit trees, but also effectively improve the soil structure in orchards. It is noteworthy that the spatial distribution of fertilizers in the root zone directly affects nutrient uptake efficiency and root system development [9].

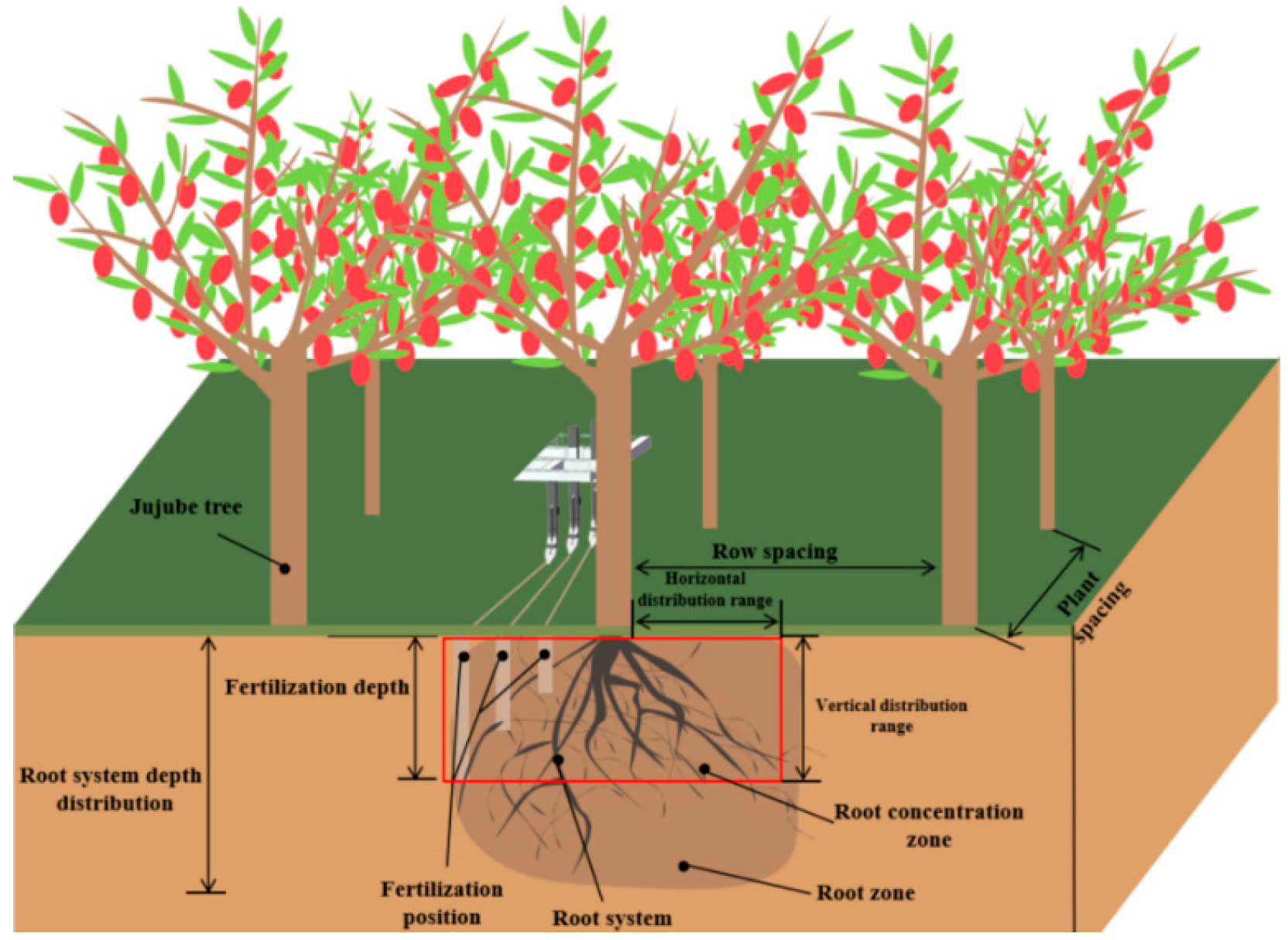
2.1.1. Root Distribution Characteristics and the Influence of Fertilization Position

The root system distribution characteristics constitute one of the fundamental bases for precision fertilization in orchards. These distribution patterns are illustrated in Figure 1. Studies indicate that although fruit tree root systems possess extensive expansion potential and actual range, high-density roots are concentrated within a relatively small area [10]. Depending on trunk diameter and soil type, this zone ranges horizontally from 0 to 150 cm and vertically from 0 to 160 cm in soil depth [20,22]. Research on biomass distribution of jujube trees with basal diameters of 3 cm, 6 cm, 9 cm, and 12 cm revealed that their root systems predominantly inhabit the 0–40 cm soil layer. Specifically, jujube trees measuring 12 cm in diameter exhibit 71.26% of root biomass within 0–50 cm horizontally from the trunk, while 81.12% of their root biomass vertically concentrates in the 0–40 cm soil layer [20]. Fine roots, as the primary nutrient-absorbing organs, demonstrate growth depths consistent with the overall root biomass distribution pattern [22].

Jujube trees exhibit root systems characterized by concentrated biomass and shallow distribution, making timely nutrient supplementation during growth phases particularly crucial. Rational fertilization not only rapidly replenishes soil nutrients but also enhances microbial diversity and maintains soil nutrient equilibrium. Soil nutrients primarily migrate to roots through diffusion and mass flow, with the diffusion process being exceptionally slow at approximately 0.3 mm per day [23]. Consequently, proximal root fertilization maximizes fertilizer efficacy [7], enhances root nutrient uptake, and more effectively improves fertilizer availability to guide root development and boost fruit tree nutrient absorption [24]. While proximal root fertilization inevitably severs some root systems, removing a small proportion proves non-detrimental and may even be beneficial to tree growth. Studies confirm that excising 10% of roots causes negligible impact, with significant damage occurring only when removal reaches 30% [25,26]. Moderate root pruning stimulates root regeneration and enhances root vitality and density, thereby improving the root system’s soil nutrient absorption capacity [25,27]. This practice promotes fruit tree root development and improves fruit quality.

In summary, proximal root fertilization offers the following advantages: (1) reduces the distance between fertilizer and roots, decreasing nutrient delivery time; (2) directly targets the root absorption zone, enhancing nutrient uptake; and (3) decreases soil nutrient fixation, thereby improving fertilizer use efficiency. The root distribution characteristics of jujube trees and corresponding fertilization positions are illustrated in Figure 1.

2.1.2. Stimulatory Effects of Stratified Fertilization on Fruit Tree Root Systems

The subterranean spatial distribution of fruit tree roots approximates an umbrella shape. Proximal root fertilization based on this distribution pattern requires stratified fertilization techniques, which effectively deliver nutrients to the root zone. Research demonstrates that precise fertilizer placement in adjacent zones to densely rooted areas [28] significantly enhances nutrient uptake efficiency in jujube root systems. In contrast, traditional deep-trench fertilization concentrates fertilizers at trench/pit bottoms, thus impairing root nutrient absorption and delaying the optimization of root zone environments [10]. Fruit trees exhibit stage-specific nutrient requirements, with significant variation in soil mobility rates among different nutrients. Phosphorus fertilizers, for instance, show limited soil mobility, making stratified fertilization particularly effective for regulating vertical phosphorus distribution [21]. This method’s advantage lies in targeted nutrient delivery to root zones, overcoming the over-concentration issues of conventional methods [12]. It enhances fertilizer efficacy, promotes tree growth, and allows for root distribution modulation through adjustable application depths.

Stratified fertilization further achieves balanced soil nutrient distribution by precisely applying fertilizers to root-dense layers, synchronizing nutrient release patterns with crop growth demands. This prolongs nutrient availability, ensures adequate nutrition supply, and partially accomplishes deep fertilizer placement. Deep fertilization not only stimulates root extension into deeper soil layers but also increases total root length throughout the soil profile, thereby optimizing root spatial distribution and creating favorable conditions for root development. Field evidence demonstrates that scientifically designed one-time-stratified fertilization can significantly increase crop yield while achieving the goal of reduced application with enhanced efficiency [29]. Based on root distribution characteristics, the stratified fertilization method systematically places fertilizers in layered trenches at root zone margins. This approach substantially reduces nutrient transport distance to roots, markedly improves nutrient content and buffering capacity in rhizosphere soil, and rapidly optimizes root growth environment. Compared with conventional trench fertilization, stratified fertilization significantly increases root–fertilizer contact area, enabling more efficient nutrient uptake and consequently improving fertilizer use efficiency.

Therefore, stratified fertilization enables proximal root fertilization, effectively reducing nutrient transport distance. Promoting mechanized stratified fertilization in Xinjiang orchards can enhance fertilizer efficacy, improve root zone soil environment, and stimulate fruit tree development.

2.2. Determination of Jujube Root System Distribution

2.2.1. Root System Excavation

The root distribution measurement experiment was conducted in the orchard experimental field of Tarim University. Methodology: Soil core sampling was performed at 10 cm intervals within 10–100 cm radial distances from jujube tree trunks of 3-, 5-, and 7-year-old trees, following the root distribution patterns of jujube trees [20], with maximum sampling depth reaching 90 cm, totaling 600 samples collected. A sampling schematic diagram using an individual tree as an example is illustrated in Figure 2a.

2.2.2. Root System Sieving

The collected soil samples were sieved through a 0.85 mm (20-mesh) sieve to separate roots from soil matrix. The isolated roots were temporarily stored in fresh-keeping bags. Subsequently, roots were rinsed with deionized water to remove adhering soil and impurities. Living roots of jujube plants were identified based on morphological characteristics, coloration, and elasticity, with dead roots being discarded. The selected living roots were stored in sealed bags for root length density measurement [20]. Subsequently, the removed dead roots underwent secondary screening, and the selected living roots were used to calculate root length density according to Formula (1), followed by statistical error calculation of the proportion of living roots. The root length density was calculated as follows [20]:

$$\rho ={\displaystyle \frac{l}{v}}$$

(1)

where ρ—root length density (RLD), cm/cm³; l—root length, cm; and v—container volume, cm³.

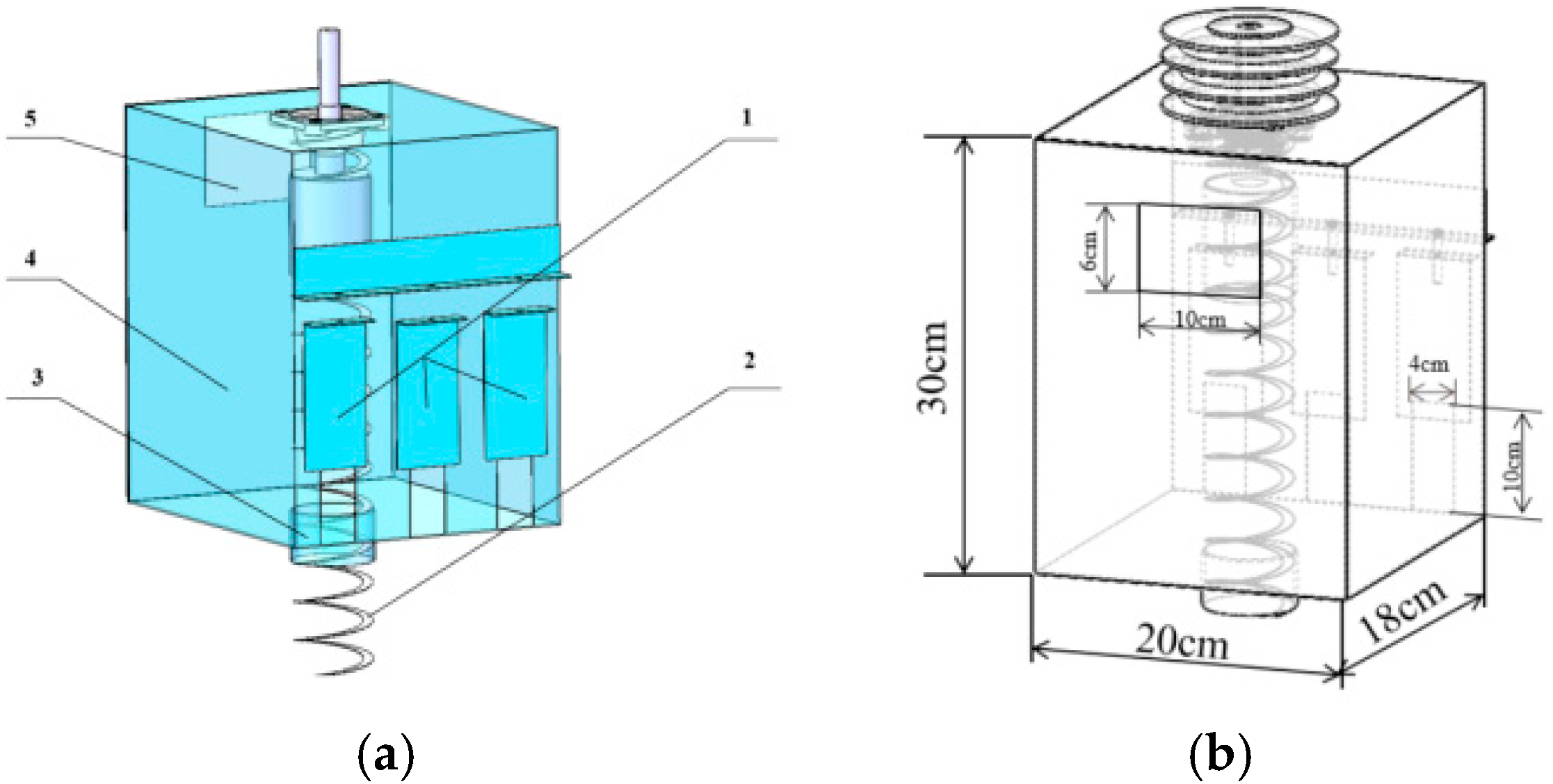
2.3. Fertilizer Applicator Structural Design

2.3.1. Structure and Working Principle of Layered Fertilizer Applicator

The complete machine structure is shown in Figure 3. The fertilizer applicator (Hongtian Metal Products Factory, Yanguan Town, Haining City, Zhejiang Province, China) consists of six main components: layered fertilizer shanks, frame, fertilizer hopper, transmission mechanism, fertilizer delivery system, and hydraulic drive unit. During operation, the tractor-pulled implement advances while ground wheels drive the shaftless auger to transport fertilizer from the hopper to distribution chambers; the distributed fertilizer is then delivered through discharge tubes and layered shanks into different soil strata within the jujube root zone.

2.3.2. Structural Design of Key Components

(1) Structural Parameters of the Fertilizer Distribution Chamber

The fertilizer distribution chamber performs fertilizer partitioning and reflux functions. As shown in Figure 4, the chamber dimensions are 20 × 30 × 18 cm, featuring three discharge gates connected to three layered fertilizer shanks, with maximum gate opening of 10 cm and overflow port dimensions of 10 × 6 cm. The gate opening shows a positive correlation with discharge quantity, enabling precise fertilizer dosage control across soil strata through opening adjustment.

(2) Shaftless Auger Flight Structure

The structure of the shaftless spiral blade is illustrated in Figure 5. According to the agronomic cultivation requirements for orchards in Alar, Xinjiang (the fertilizer application rate in jujube orchards is 3510 kg/ha), the flight diameter (D) and pitch (S) of the auger were designed and determined. The specific formulas are as follows [30]:

$$D=K({\displaystyle \frac{Q_C}{\theta \lambda \epsilon }}{)}^{{\displaystyle \frac{2}{5}}}$$

(2)

where D—auger flight diameter, mm; K—material comprehensive coefficient; Q_C—fertilizer discharge rate; θ—helical fertilizer discharge fill coefficient; λ—fertilizer bulk density, g/mm³; and ε—inclined conveying coefficient.

$$S=K_{1}D$$

(3)

In the formula, S—screw pitch (S), mm; K₁—helix pitch coefficient; and D—helical blade diameter.

The helical blade diameter (D) and pitch (S) are determined to be 80 mm and 64 mm, respectively.

Figure 5. Scheme of shaftless spiral structure.

Figure 5. Scheme of shaftless spiral structure.

2.4. Bench Test

2.4.1. Structural Composition of Fertilizer Delivery Mechanism

A fertilizer conveying system test bench was constructed, consisting of a fertilizer hopper, power system, distribution box, shaftless spiral, and dynamic simulation system. The power system incorporates a 2.2 kW variable-frequency speed-regulating motor with a speed range of 0–1440 r/min, enabling different operational speeds for the spiral conveyor. The distribution box features an adjustable fertilizer discharge outlet with 0–10 gear settings for precise control of fertilizer requirements across different soil layers. The shaftless spiral has a blade diameter of 80 mm and pitch of 64 mm, with a total length of 1500 mm. The dynamic simulation system is equipped with a 500 mm continuously variable transmission belt (speed range: 0.3–1.2 m/s) to simulate field operating speeds. The schematic diagram of the structure is shown in Figure 6.

2.4.2. Experimental Design and Protocol

Based on preliminary experiments, travel speed, auger rotation speed, and fertilizer gate opening were coded as A, B, and C, respectively, for conducting multifactorial combination trials. With three experimental replicates, the optimal parameters were determined as follows: travel speed of 2–3.4 km/h, auger rotation speed of 10–40 r/min, and valve opening of 3–9 cm. The experimental design was conducted using Design-Expert 13 software, and the data results were analyzed by multifactorial ANOVA, using IBM SPSS Statistics 26.0. The coded factors and levels are shown in

Table 1. Coded factors and levels.

Encoding	Implement Travel Speed (A) km/h	Screw Rotational Speed (B) r/min	Fertilizer Gate Opening (C) cm
1	2	10	3
0	2.7	25	6
−1	3.4	40	9

.

The constraint intervals of design factors were set (using extreme values of test factors), with the objectives of minimizing both fertilizer uniformity coefficient and row-to-row consistency coefficient. Constrained optimization was performed using Design-Expert software to find optimal solutions for all factors within their value ranges.

Objective function [31]:

$$\left\{\begin{array}{l}\min \alpha (A,B,C)\\ \min CV(A,B,C)\end{array}\right.$$

(4)

Constraint function:

$$\left\{\begin{array}{l}-1\le A\le 1\\ -1\le B\le 1\\ -1\le C\le 1\end{array}\right.$$

(5)

In the functions, A, B, and C represent travel speed, auger rotation speed, and fertilizer gate opening, respectively.

The optimization yields the global optimal solution.

2.4.3. Fertilization Performance Evaluation

According to Standard GB/T20346.2-2022 Fertilizer Spreaders [32], fertilizer uniformity and row-to-row consistency were selected as evaluation metrics. Row-to-row consistency is characterized by the coefficient of variation (CV), while fertilizer uniformity is quantified by the uniformity variation coefficient (α). Lower values of both variation coefficients indicate better spreader performance.

The calculation formula for fertilizer uniformity variation coefficient is as follows [32]:

$$\overline{x}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^{n_i}{x}_i}$$

(6)

$$S=\sqrt{{\displaystyle \frac{1}{n-1}}{\displaystyle \sum _{i=1}^{n_i}{\left(x_i-\overline{x}\right)}^2}}$$

(7)

$$CV={\displaystyle \frac{S}{\overline{x}}}\times 100\%$$

(8)

where $\overline{x}$—absolute mean, g; S—standard deviation (S), g; x_i—fertilizer mass collected per receptacle, g; n—number of fertilizer collection receptacles; and CV—uniformity variation coefficient.

The calculation formula for row-to-row consistency variation coefficient is as follows:

$$\overline{x}={\displaystyle \frac{{\displaystyle \sum _{i=1}^{n_i}{x}_i}}{n_i}}$$

(9)

$$S=\sqrt{{\displaystyle \frac{1}{n-1}}{\displaystyle \sum _{i=1}^{n_i}{(x_i-\overline{x})}^2}}$$

(10)

$$\alpha ={\displaystyle \frac{S}{\overline{x}}}\times 100\%$$

(11)

where $\overline{x}$—mean value of average discharge per row, per pass, g; n—number of fertilizer discharge outlets; S—standard deviation (S), g; x_i—average discharge per row, g; and α—average discharge per row, per pass.

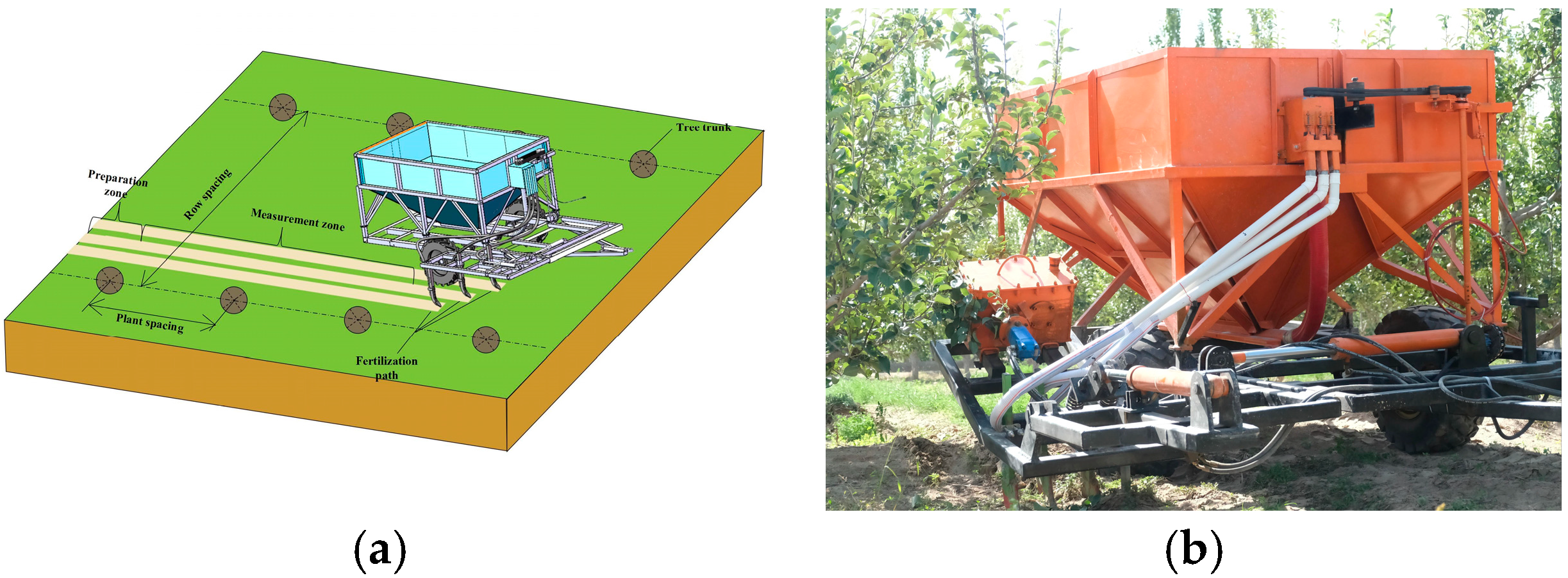
2.5. Field Trials

2.5.1. Field Trial Conditions

The field trials were conducted at the Modern Organic Orchard Demonstration Base of the 12th Regiment, First Division, Xinjiang Production and Construction Corps in Alar City. The experimental plot measured 500 m in length and 100 m in width, with sandy loam soil characterized by a bulk density of 0.0024 g/mm³, moisture content of 12%, and soil compaction of 3923 kPa. The planting configuration consisted of 6 m row spacing and 1.5 m plant spacing. Figure 7a illustrates the schematic diagram of field fertilization operations, while Figure 7b demonstrates the prototype operation of the orchard layered fertilizer applicator.

2.5.2. Experimental Protocol

During operation, the fertilizer applicator performed layered fertilization adjacent to one side of tree trunks, with the working area divided into a 10 m preparation zone and 50 m measurement zone. The forward speed, gate opening, and screw rotation speed were set according to the optimal parameters determined in Section 2.3.2. Three layered fertilizer shanks maintained fixed trench depths at 20 cm, 30 cm, and 40 cm, respectively, arranged sequentially from nearest to farthest from the tree trunk at 20 cm, 30 cm, and 40 cm intervals. Fertilizer granules in the measurement zone were collected post-application, with soil particles sieved out before gravimetric analysis. The experiment comprised two 50 m measurement passes. Time and speed parameters recorded during the experimental process are presented in

Table 2. Working speed measurement record sheet.

Stroke	Measurement Zone Length (m)	Time (s)	Velocity (km/h)
First stroke	50	56″95	3.2
Second stroke	50	50″90	3.2

.

2.5.3. Test Equipment and Evaluation Metrics

An electronic precision balance was employed for weighing. The device measures the net fertilizer mass applied over a fixed working length, with field validation conducted using the optimal parameter combination from Section 2.4.3’s evaluation metrics.

Measurement Method for Fertilizer Uniformity Coefficient

After reaching 10 m of fertilization distance, all fertilizer granules in the trench were collected, starting from the 11 m mark, and weighed in collection boxes, with a measurement zone length of 50 m; the test was repeated 5 times; the average value was calculated independently for each dataset, and the fertilizer uniformity coefficient was derived using Equations (6)–(8).

Measurement Method for Row-to-Row Consistency Coefficient

After the fertilization distance reaches 10 m, collect all fertilizer granules in the trench from the 11 m mark and weigh them in collection boxes, with 3 collection boxes per measurement zone, with the measurement zone length being 50 m; repeat the test 5 times; calculate the average value independently for each dataset; and derive the fertilizer uniformity coefficient using Equations (9)–(11).

3. Results and Discussion

3.1. Distribution Results of Jujube Root System Measurement

Measurement results indicate that the root length density (RLD) of jujube trees decreases with increasing horizontal distance from the trunk. Approximately 70% of the root system was distributed within the 0–50 cm range. Vertically, RLD initially increased and then decreased with soil depth, peaking at 20–30 cm. In total, 80% of the roots were concentrated in the 0–40 cm soil layer, consistent with the findings in Reference [20]. As shown in Figure 8a, root distribution was positively correlated with tree age: older trees exhibited greater lateral expansion and vertical penetration. For trees of three age groups (3-, 5-, and 7-year-old trees), roots were predominantly concentrated within 0–50 cm horizontally. Within this zone, RLD accounted for 100%, 98.14 ± 0.1%, and 99.64 ± 0.1% of the total for 3-, 5-, and 7-year-old trees, respectively. At 0–60 cm, the proportions were 98.92 ± 0.1% (5-year-old trees) and 95.85 ± 0.1% (7-year-old trees). Root distribution patterns were strongly age-dependent: older trees showed broader spatial occupation, higher RLD proportions, and pronounced lateral expansion. Figure 8b demonstrates that the RLD for all age groups followed a unimodal curve along the soil profile. The 0–40 cm layer harbored the highest RLD, with maximum values at 20–40 cm. Within this layer, RLD constituted 80.28 ± 0.5%, 82.94 ± 0.5%, and 83.23 ± 0.5% for 3-, 5-, and 7-year-old trees, averaging 82.13 ± 0.5%. Furthermore, advancing age progressively increased root density in deeper soils, reflecting vertical proliferation and densification. This pattern reveals age-dependent vertical plasticity in jujube root systems. Based on these findings, the layered fertilizer applicator was designed to operate at a 20–40 cm depth.

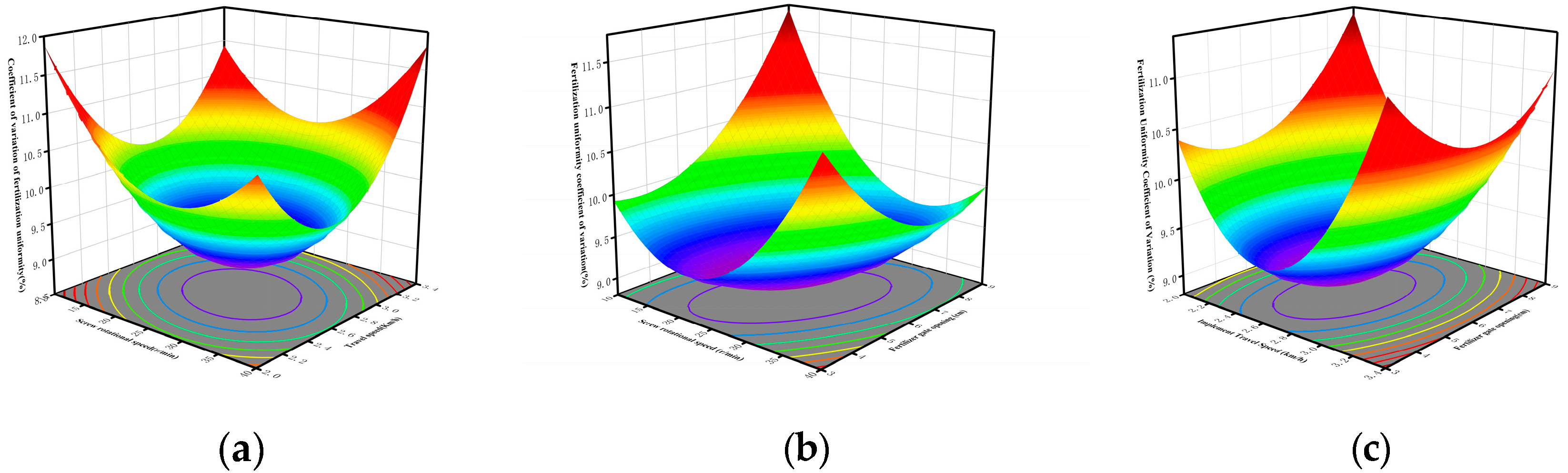
3.2. Analysis of Factors Affecting Fertilization Performance

The Design-Expert experimental results indicated that the minimum CV for uniformity was achieved at either 25 r/min screw speed, 2 km/h forward speed, and 3 cm gate opening or 10 r/min, 2 km/h, and 6 cm, while the minimum CV for consistency occurred at 25 r/min, 2.7 km/h, and 6 cm. The detailed experimental design and results are presented in

Table 3. Experimental results.

Test Serial Number	Experimental Factor			Experimental Index
	Screw Rotational Speed A	Implement Travel Speed B	Fertilizer Gate Opening C	Uniformity Coefficient of Variation (%)	Consistency Coefficient of Variation (%)
1	25	2	3	5.1	8.89
2	25	3.4	9	7.9	8.08
3	40	2.7	9	8.5	8.69
4	25	3.4	3	7	9.97
5	40	3.4	6	7.8	8.82
6	10	2	6	5.1	9.97
7	25	2.7	6	6	7.23
8	40	2.7	3	6.8	9.88
9	10	3.4	6	6.7	10
10	10	2.7	9	7.2	10.05
11	25	2.7	6	6.1	6.95
12	25	2.7	6	5.9	7.05
13	25	2	9	7.5	9.98
14	10	2.7	3	5.3	9.56
15	40	2	6	7.4	9.37

.

Multivariate analysis of variance (MANOVA) was performed on the tabulated data using IBM SPSS Statistics. The results demonstrated statistically significant predictions for both indices (CV: F = 132.644, p = 0.008; α: F = 75.484, p = 0.013). Main effect analysis revealed that auger rotation speed (A) exerted significant positive effects on both CV (p = 0.002) and α (p = 0.020), indicating that increased speed concurrently optimizes uniformity and consistency. Travel speed (B) showed a significant effect only on CV (p = 0.004), with marginal significance on α (p = 0.079), suggesting the need for cautious adjustment. Gate opening (C) significantly improved CV (p = 0.002) but showed no significant effect on α (p = 0.065), reflecting parameter-specific influences. Interaction analysis identified significant synergistic effects between rotation speed and travel speed (A × B) on CV (p = 0.027), demonstrating their coordinated control requirement for uniformity optimization. The A × C interaction significantly affected α (p = 0.027), indicating compensatory effects between these parameters. The B × C interaction showed significance for both indices (CV: p = 0.017; α: p = 0.009), confirming the necessity for synergistic control.

Response surface methodology (RSM) was employed to analyze the main and interaction effects of independent variables. By evaluating the gradient variations in response surface plots, the significance of three factors on fertilization uniformity and row consistency coefficients could be precisely identified and quantified. Notably, steeper gradients indicated stronger interaction effects between corresponding variables, demonstrating more pronounced impacts on experimental outcomes.

Figure 9 illustrates the effects of screw speed, forward speed, and gate opening on the CV for fertilization uniformity. Figure 9a demonstrates that when screw speed was constant, the CV initially decreased and then increased with rising forward speed, while maintaining the same trend when forward speed was fixed and screw speed increased. The optimal ranges were determined to be 25–35 r/min for screw speed and 2.4–3.0 km/h for forward speed. Figure 9b reveals that the CV followed a concave parabolic pattern versus gate opening at a fixed screw speed, with an identical response pattern observed when examining screw speed effects at constant gate openings. The analysis identified optimal parameter ranges of 15–30 r/min for screw speed and 4–8 cm for gate opening. Figure 9c indicates that under constant forward speed conditions, the CV exhibited a convex response to gate-opening variations, mirroring the same response pattern when examining forward speed effects at fixed gate openings. The corresponding optimal operational windows were 2.4–2.8 km/h for forward speed and 4–7 cm for gate opening.

Figure 10 presents the effects of screw speed, travel speed, and gate opening on the row-to-row consistency CV. Panel (a) demonstrates that at fixed screw speeds, the CV first decreased and then increased with increasing travel speed, while exhibiting the same trend when examining screw speed effects at constant travel speeds. The optimal parameter ranges were determined to be 25–30 r/min for screw speed and 2.4–2.8 km/h for travel speed. Panel (b) shows that the CV followed a concave response to gate-opening variations at fixed screw speeds, with similar patterns observed when analyzing screw speed effects at constant gate openings. The corresponding optimal values were 25–30 r/min for screw speed and 4 cm for gate opening. Panel (c) indicates that the CV decreased monotonically with gate opening at fixed travel speeds, but it showed a convex response to travel speed variations at constant gate openings. The optimal operating ranges were 2.6–3.0 km/h for travel speed and 4–8 cm for gate opening.

Design-Expert optimization with constrained objectives yielded the following optimal parameters within defined ranges: travel speed of 2.62 km/h, screw rotation speed of 29.87 r/min, and gate opening of 3.49 cm, achieving a fertilization uniformity CV of 6.86% and row-to-row consistency CV of 8.09%.

3.3. Field Fertilization Experiment Results

As presented in

Table 4. Field fertilization test results.

Serial Number	Uniformity Coefficient of Variation (%)	Consistency Coefficient of Variation (%)
1	8.90	8.31
2	8.25	7.18
3	7.64	8.02
4	6.86	9.77
5	7.20	9.01
Mean value	7.77	8.46
Predicted value	6.86	8.09
Relative error (%)	0.91	0.36

, the field tests (five replicates) showed mean CV of 7.77% for fertilization uniformity and 8.46% for row-to-row consistency. The predicted optimal values from bench test response surface analysis were 6.86% and 8.09%, respectively. This resulted in relative errors of 0.91% and 0.36% between predicted and actual field measurements.

As a non-standardized working environment, jujube orchards are susceptible to multiple interfering factors during layered fertilization, including soil dynamics and topographic variations. Specifically, soil fluidity [33] causes particle displacement during field sample collection, introducing measurement errors through soil disturbance. Simultaneously, micro-terrain variations induce equipment vibration and speed fluctuations during operation, resulting in unstable instantaneous discharge rates from the fertilizer mechanism [34]. The CV values for fertilization uniformity and row-to-row consistency are quantitatively characterized by Equations (8) and (11), respectively, with both standard deviation and mean parameters in the calculations showing significant positive correlations with fertilization quantity. Notably, the mean value reflects the direct linear influence of fertilization amount, whereas the standard deviation amplifies the ultimate effect of fertilization fluctuations through nonlinear transformations involving deviation accumulation and squaring operations.

Although the aforementioned factors introduced deviations between predicted and measured CV values, all fell within acceptable experimental errors of margin. To enhance fertilization accuracy, improvements should focus on two aspects: (1) mechanical stability optimization and (2) incorporation of fertilizer mass monitoring systems [35]. Specifically, vibration damping systems and speed control mechanisms should be upgraded to mitigate mechanical oscillations. Additionally, real-time monitoring with feedback control should be implemented, including inertial measurement units (IMUs) [36] for terrain compensation combined with algorithmic processing, and pressure and volume (P&V) systems [37] for precise fertilizer mass calculation, thereby establishing a multi-source data framework for precision fertilization in complex field conditions.

4. Conclusions

The three-dimensional distribution characteristics of jujube root systems were analyzed, leading to the development of a stepped layered fertilization technique and corresponding machinery. Theoretical modeling and experimental measurements revealed that root length density (RLD) exhibited (a) a negative correlation with horizontal distance from the trunk; and (b) unimodal distribution along soil depth, peaking at 20–30 cm (32% concentration). The concentrated root distribution zone of jujube trees was determined to be 0–50 cm horizontally and 0–40 cm vertically. Root length density (RLD) analysis indicated that a trench depth of 20–40 cm was optimal.

Optimization of key operational parameters (travel speed, shaftless screw rotation speed, and gate opening) yielded minimum coefficients of variation at 2.62 km/h, 29.87 r/min, and 3.49 cm configuration, achieving 6.86% uniformity CV and 8.09% row-to-row consistency CV.

Field tests under optimal conditions demonstrated CV of 7.77% for fertilization uniformity and 8.46% for row-to-row consistency, showing relative errors of 0.91% and 0.36%, respectively, compared to bench test results, which comply with orchard fertilization standards.

The orchard layered fertilizer applicator developed in this study features a simple and reliable structure. Compared to conventional fertilization equipment typically equipped with metering systems [38] (plunger pumps, control valves, distributors, etc.) and monitoring systems [39], this design significantly reduces both manufacturing and operational costs. With root architectures similar to jujube trees, apple trees only require minor adjustments in fertilization depth for effective application in apple orchards. The wider row and plant spacing in apple and pear orchards compared to jujube orchards can fully accommodate the operational requirements of this fertilizer applicator.

Based on the root architecture distribution characteristics of jujube trees, this study designed an orchard layered fertilizer applicator whose trenching depth was determined according to the root distribution pattern. Key design parameters were optimized according to fertilizer application machinery standards, ultimately developing a compliant orchard layered fertilizer applicator. A limitation of this study is its exclusive focus on jujube tree roots; application to other orchards would require supplementary experiments to adjust operational parameters. Compared with conventional methods, the layered fertilization technique provides a novel approach for improving fertilizer use efficiency in orchards.