Intelligent Optimization-Based Decision-Making Framework for Crop Planting Strategy with Total Profit Prediction
Abstract
1. Introduction
2. Data and Methods
2.1. Data and Preprocessing
2.1.1. Data on Cultivated Land Plots and Greenhouses in Rural Areas
2.1.2. Data on the Types of Crops with Diverse Preferences
2.1.3. Data on the Cultivated Areas in 2023
2.1.4. Data on the Yields, Costs, and Prices in 2023
2.2. Problems and Methods
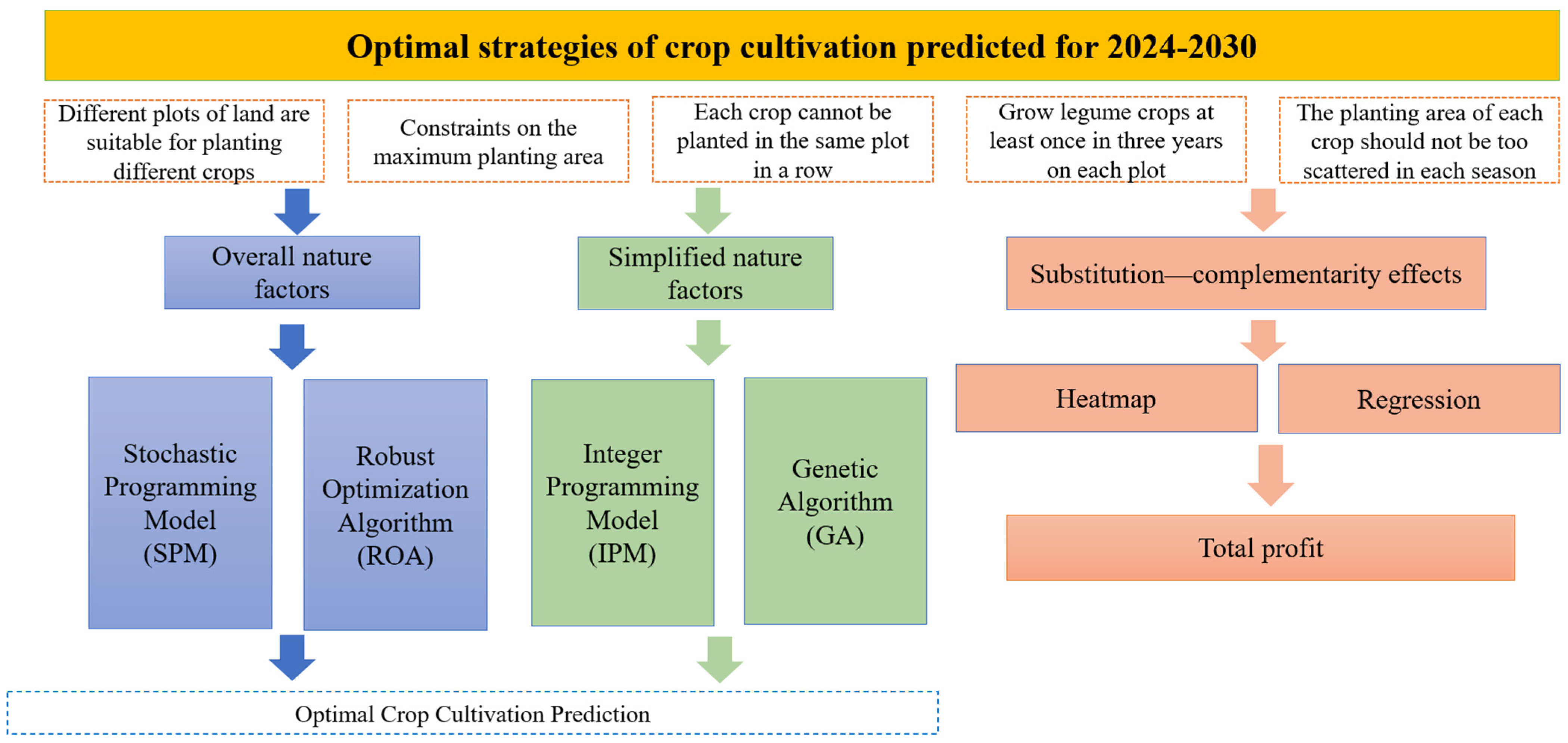
2.2.1. Optimized Planting Strategy with Overall Nature Factors
2.2.2. Optimized Planting Strategy with Restricted Natural Factors
2.2.3. Correlation Analysis and Multi-Objective Optimization
3. Models and Algorithms
3.1. Research Problem Overview
3.2. Construction of the Crop Planning Prediction Model
3.2.1. Stochastic Programming Model (SPM)
- 1.
- To mitigate yield reduction caused by consecutive planting of the same crop on the same plot, i.e., continuous cropping, the following constraint is enforced as
- 2.
- To leverage the soil-enriching benefits of legume root nodules (rhizobia) for subsequent crops, the constraint is imposed starting from 2023 that each land plot must cultivate legumes at least once within any consecutive three-year period and is denoted as
- 3.
- To ensure rational land utilization and avoid undersized cultivation, we assume that the total cultivation area allocated to crops on any land plot is deemed reasonable if and only if the sum of planted areas exceeds half of the plot’s fixed total area. The constraint is denoted as
- 4.
- Due to variations in land plot types and seasonal conditions, the variety of crops that can be cultivated on each plot is restricted. It necessitates the constraint that is denoted as
3.2.2. Integer Programming Models (IPMs)
- Scenario A: The crop surplus will be unsold, resulting in waste.
- Scenario B: The crop surplus is sold at a 50% discount of the selling price.
3.3. Algorithms
3.3.1. Hybrid Stochastic–Robust Optimization Algorithm
- Robust Fluctuation Variation: The parameters are set to maximize positive impacts on total profit as follows: (a) Projected Sales Volumes: Wheat and maize maintain a high annual growth rate of 10%. Other crops sustain a growth rate of 5%. (b) Yield per Acre: Annual yield increases by 10% for all crops. (c) Cultivation Costs: Annual cost growth averages 5%, but under robust fluctuation, the rate is set to the lower bound of its fluctuation range around 3%. (d) Market Prices: The sales prices of grain crops fluctuate within −2% to 2% and increase by 2% annually. The sales prices of vegetable crops fluctuate in the range from 3% to 7% with 7% annual growth. The sales prices of edible fungi decline by 1% annually, with only morel mushrooms experiencing a 3% annual decrease.
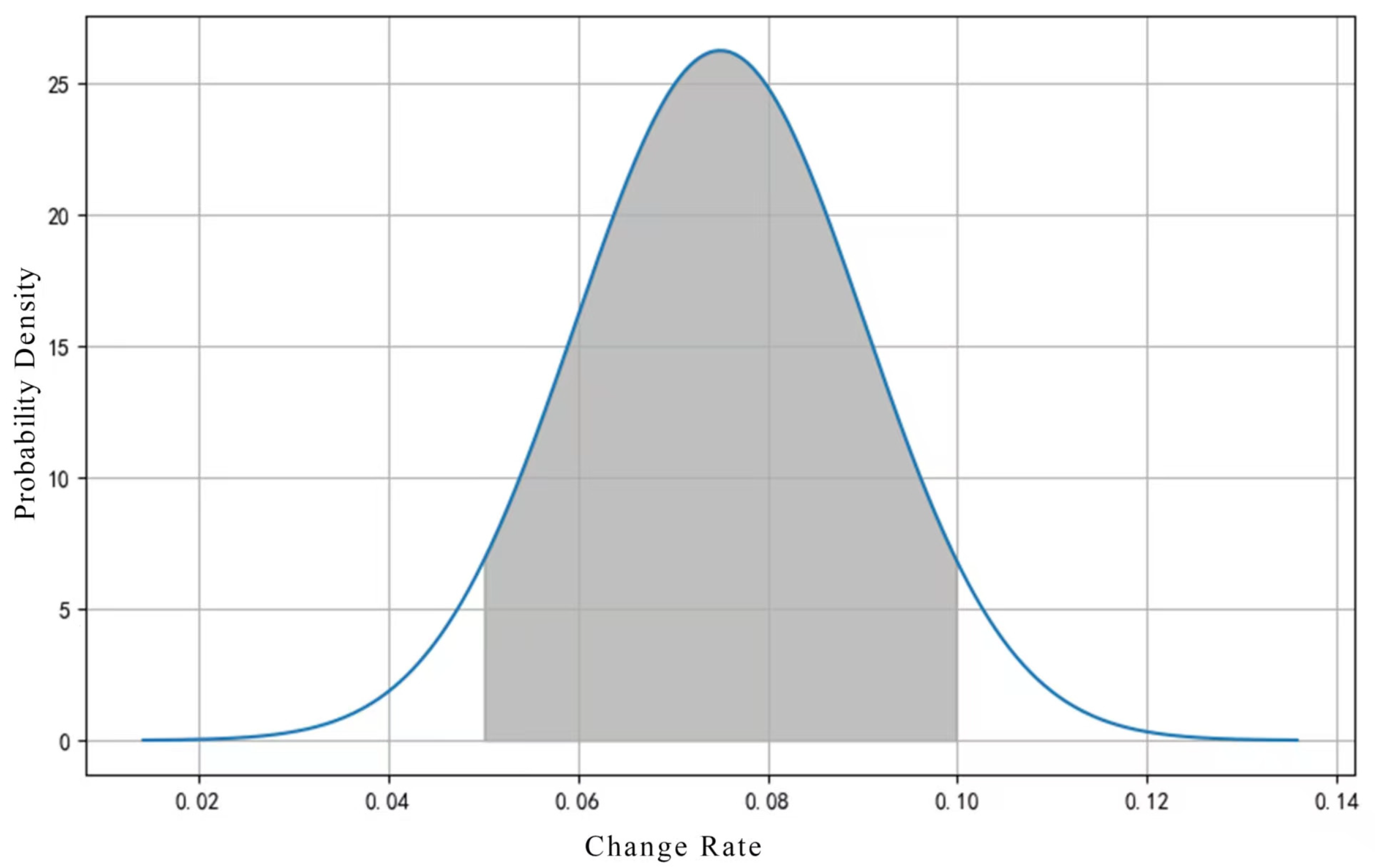
- Normal Fluctuation Variation: It is assumed that all parameter fluctuations adhere to a normal distribution. For instance, the statistical distribution of the annual change rate in the expected sales volume of wheat and corn is illustrated in Figure 4. The grey block indicates that the most likely range for the anticipated annual growth rate of sales volume for wheat and corn is between 5% and 10%.
- The Worst-Case Fluctuation Variation: the expected annual growth rate of sales volume for wheat and corn is 5%, whereas the sales volume of other crops decreases by 5% annually. Additionally, the crop yield per acre decreases by 10% annually, while the planting cost of crops increases by 7% annually. Furthermore, the selling price of edible fungi is estimated to decrease by 5% each year, with the price of morel mushrooms declining by 7% annually.
| Algorithm 1 Proposed ROA to Solve (9) in SPM |
| 1: , iteration index i = 0, and convergence accuracy ϵ. |
| 2: repeat |
| 3: Set i = i + 1. |
| 4: }. |
|
5: To solve (6): } according to (13). |
| 6: under (16). |
| 7: until convergence. |
| 8: . |
3.3.2. Hybrid Integer-Programming–Genetic-Optimization Algorithm
| Algorithm 2 Proposed Genetic Algorithm (GA) to Solve (19) |
| 1: , Set GA parameters: population size K, max generations G. |
| 2: repeat |
| 3: Set i = i + 1. |
| 4: , calculate yield and costs according to (17) and (18), respectively. |
|
5: according to (20). according to (25). |
| 6: . |
| 7: , solve IP subproblem. Compute (25) under (14). |
| 8: until Convergence. |
| 9: . |
4. Results
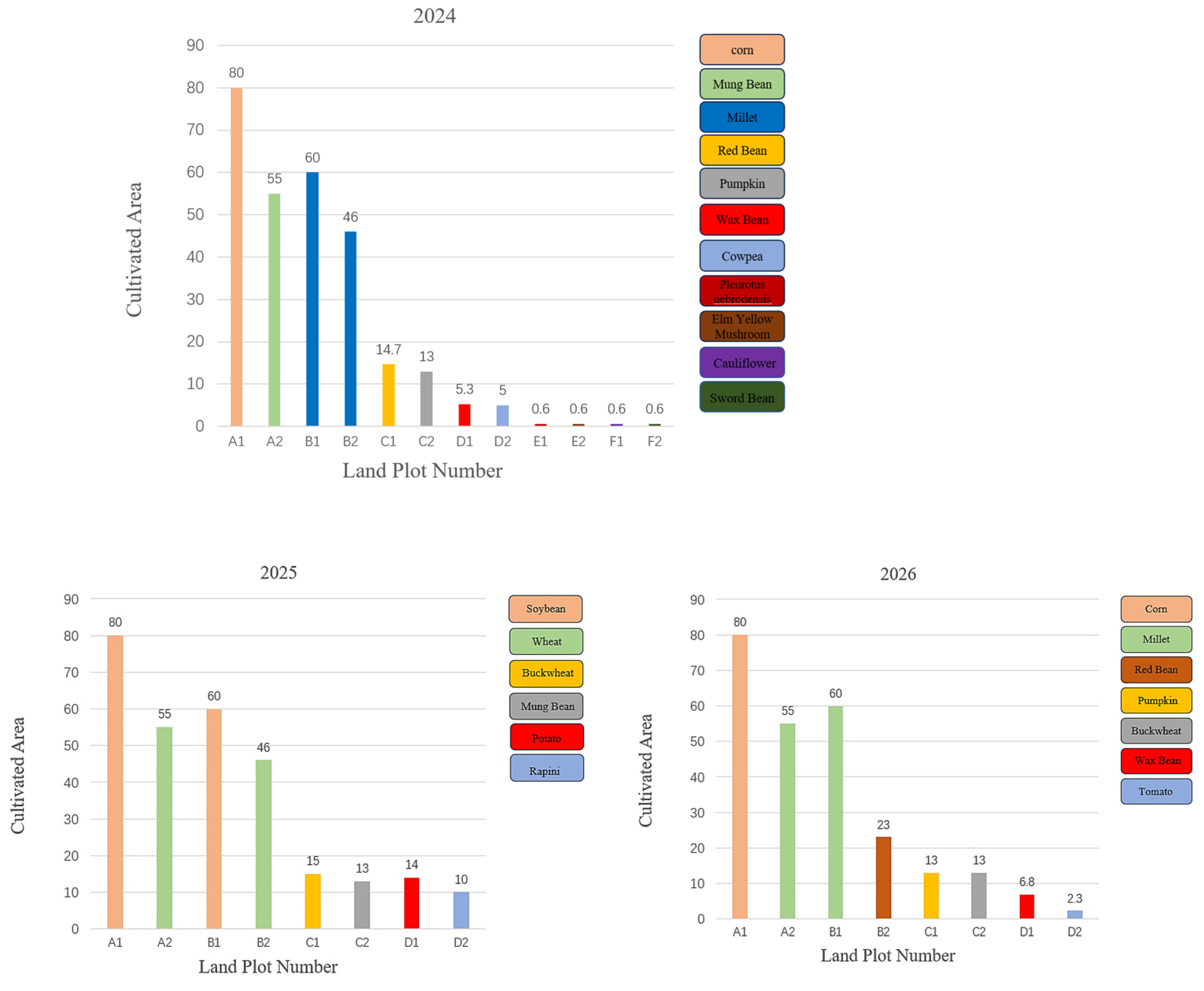
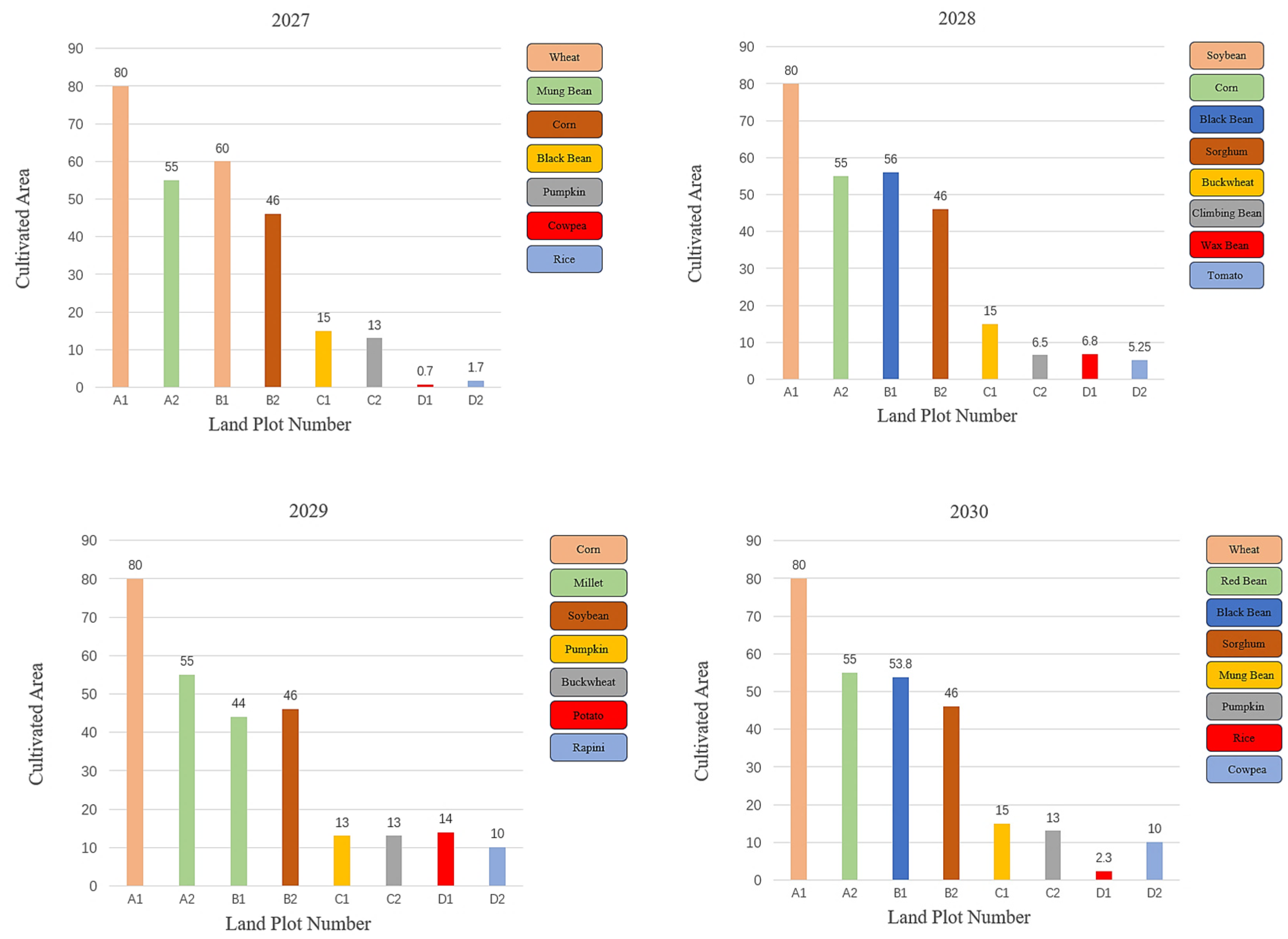
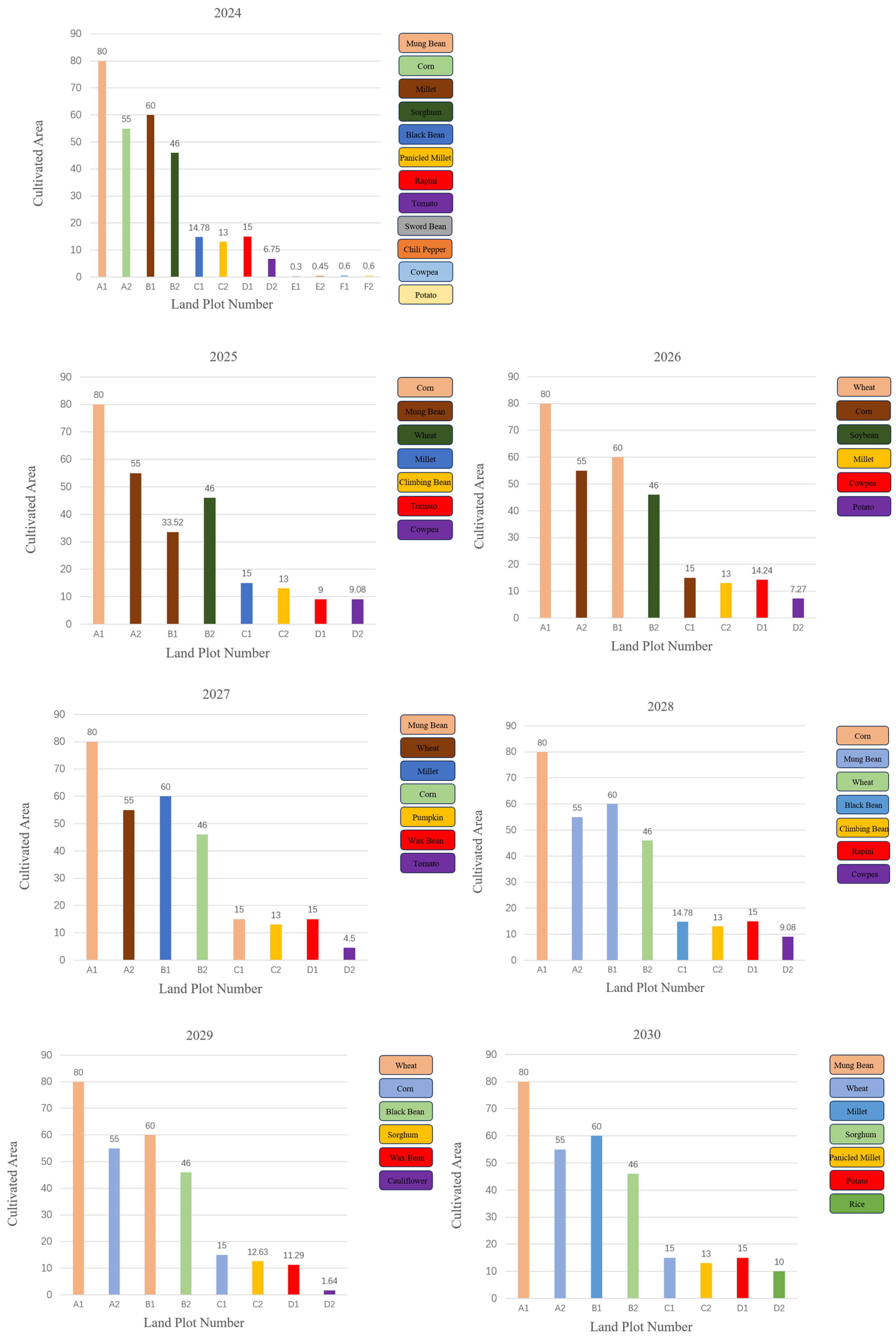
4.1. Optimal Crop Planting Results with Multi-Factor Constraints
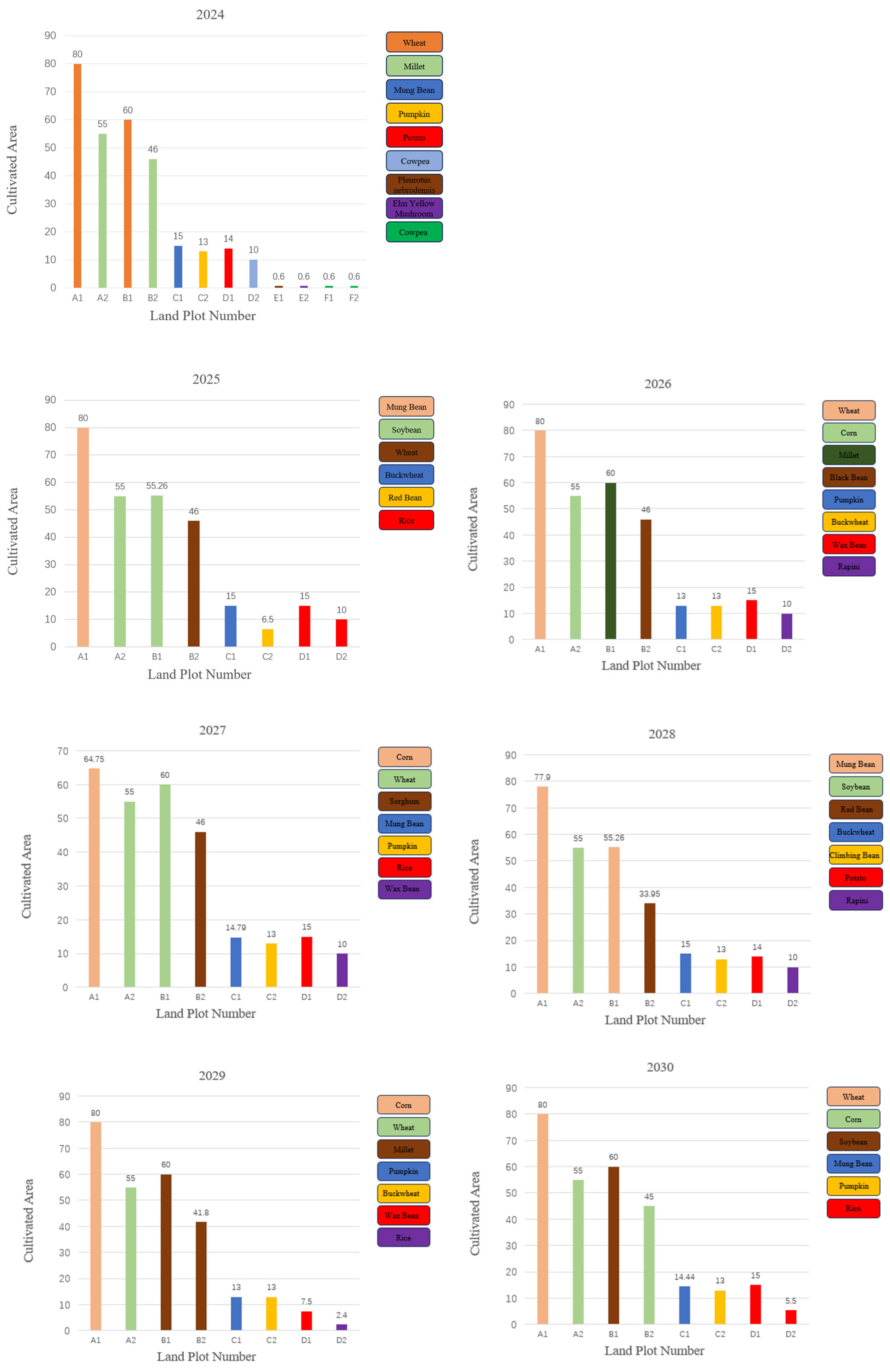
4.2. Optimal Crop Planting Results with Restricted Constraints
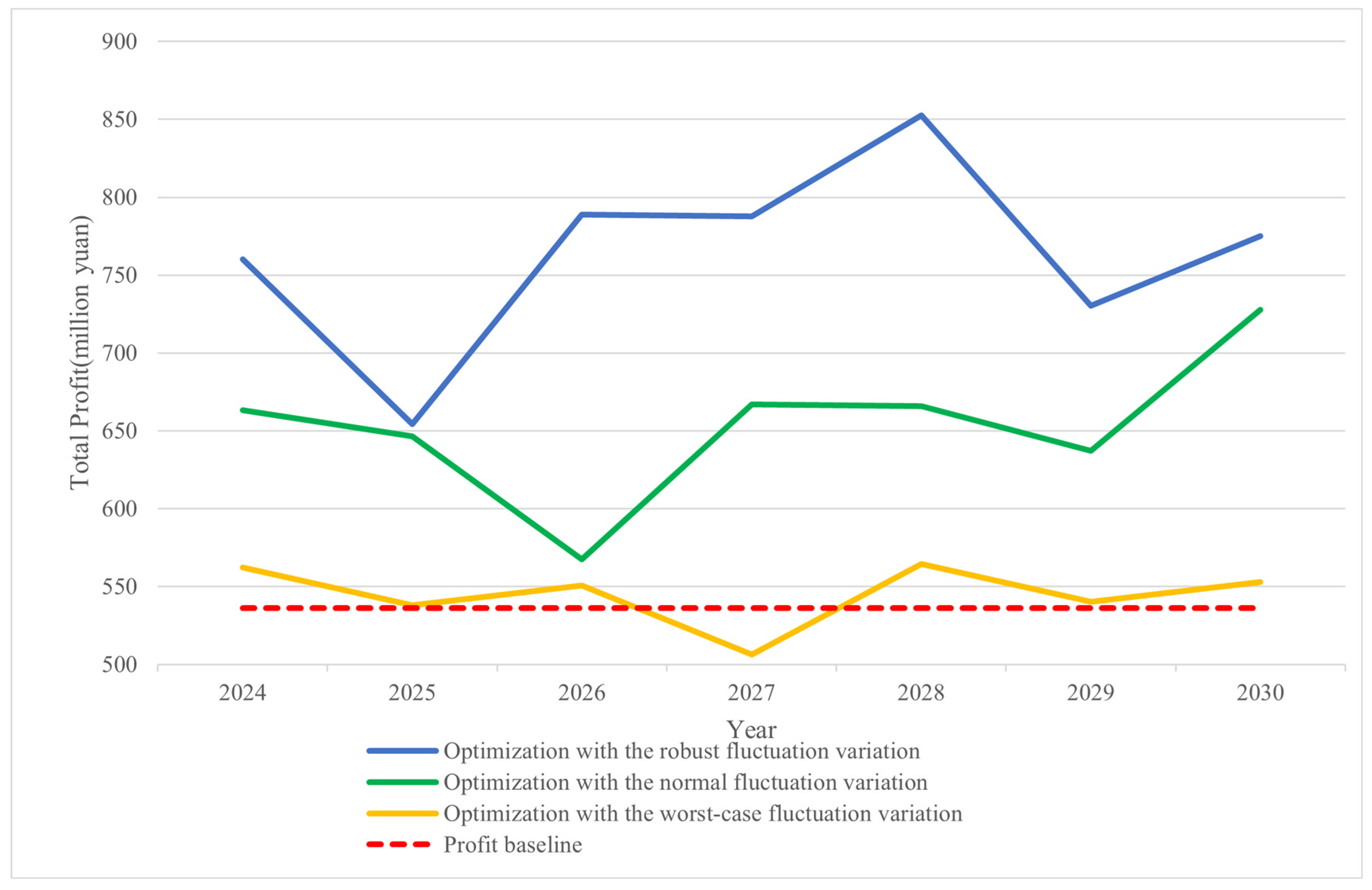
4.3. Sensitivity Analysis
5. Discussion
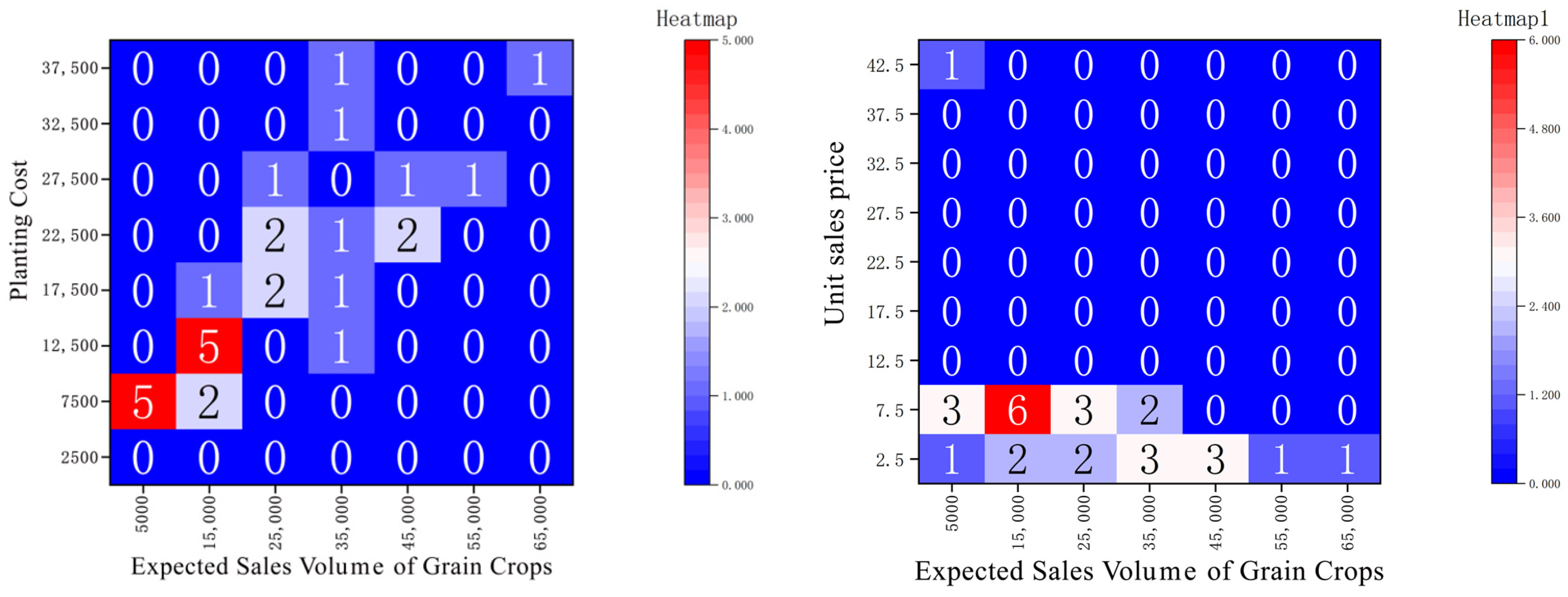
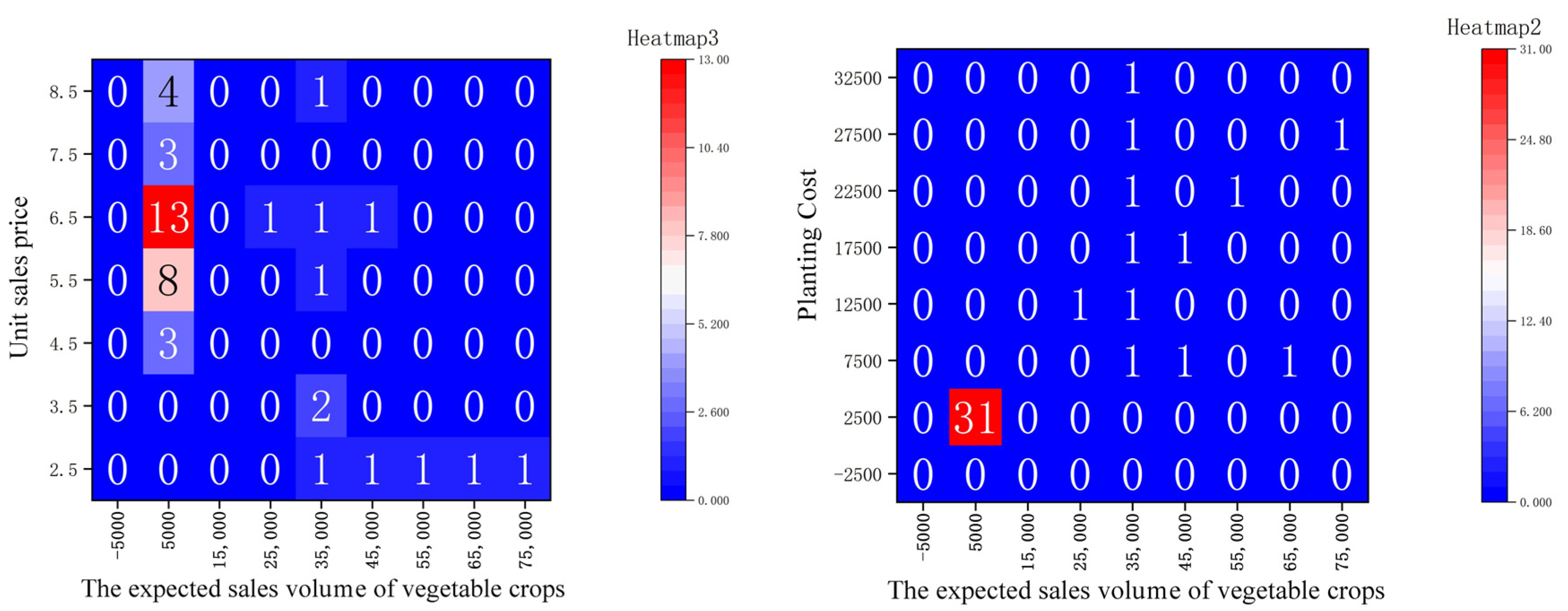
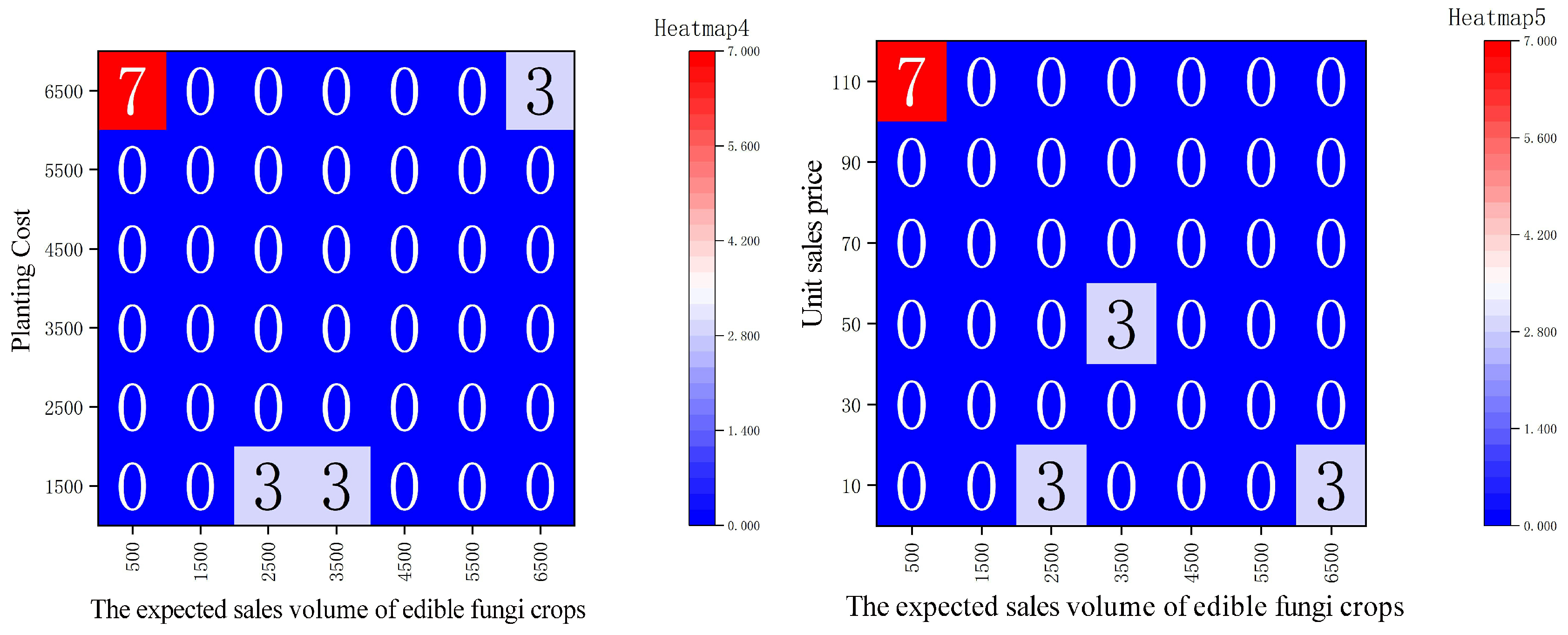
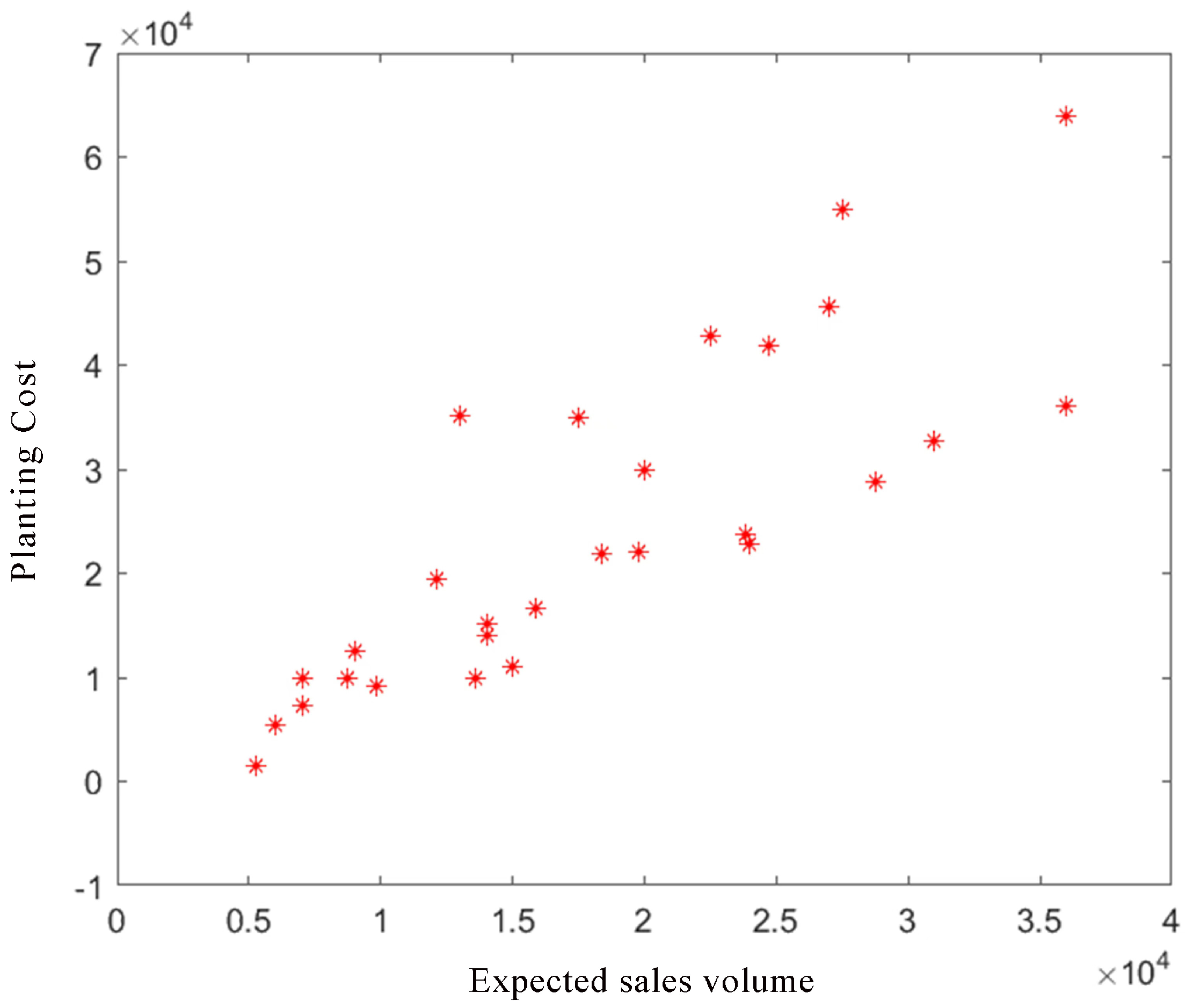
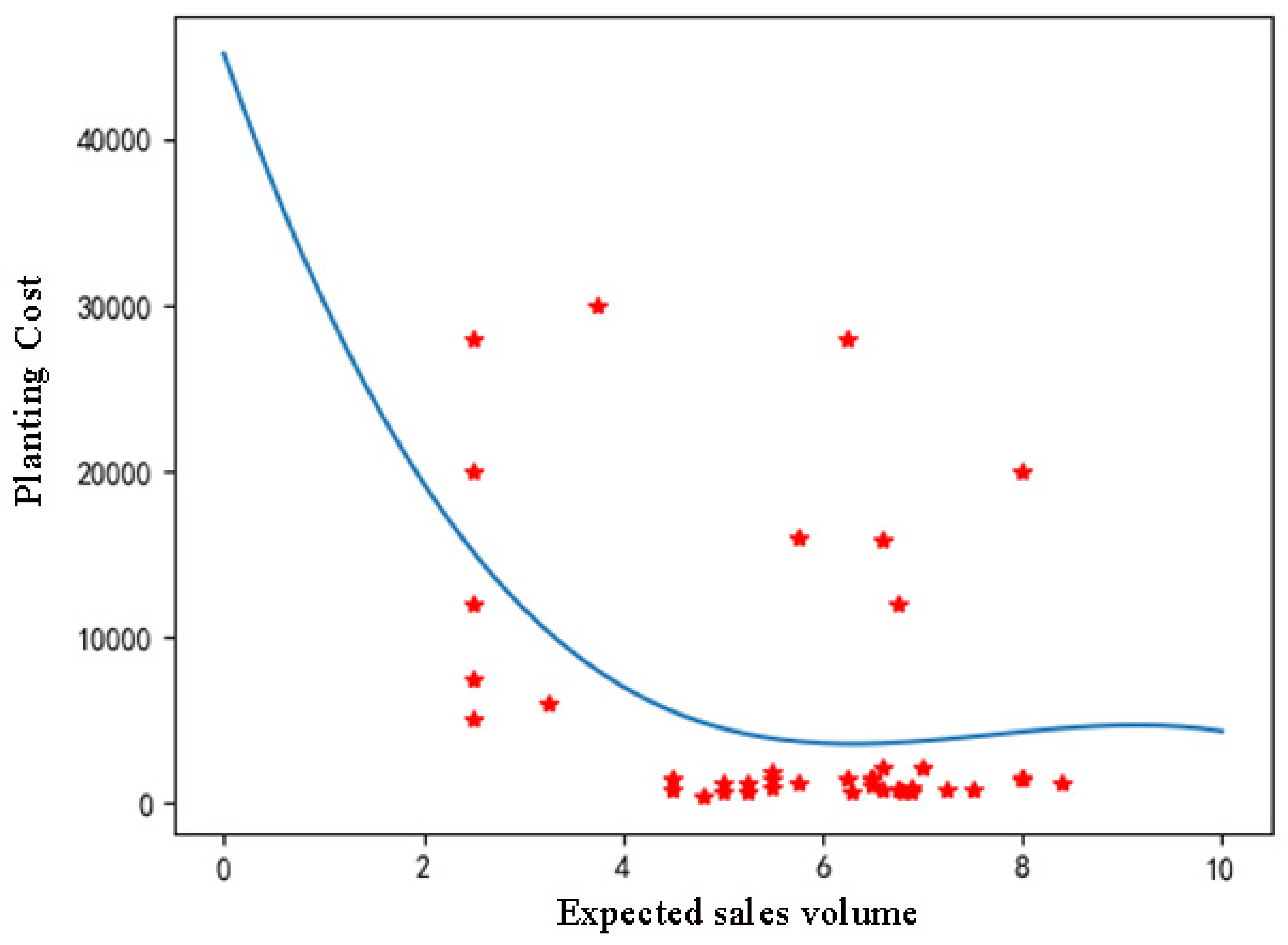
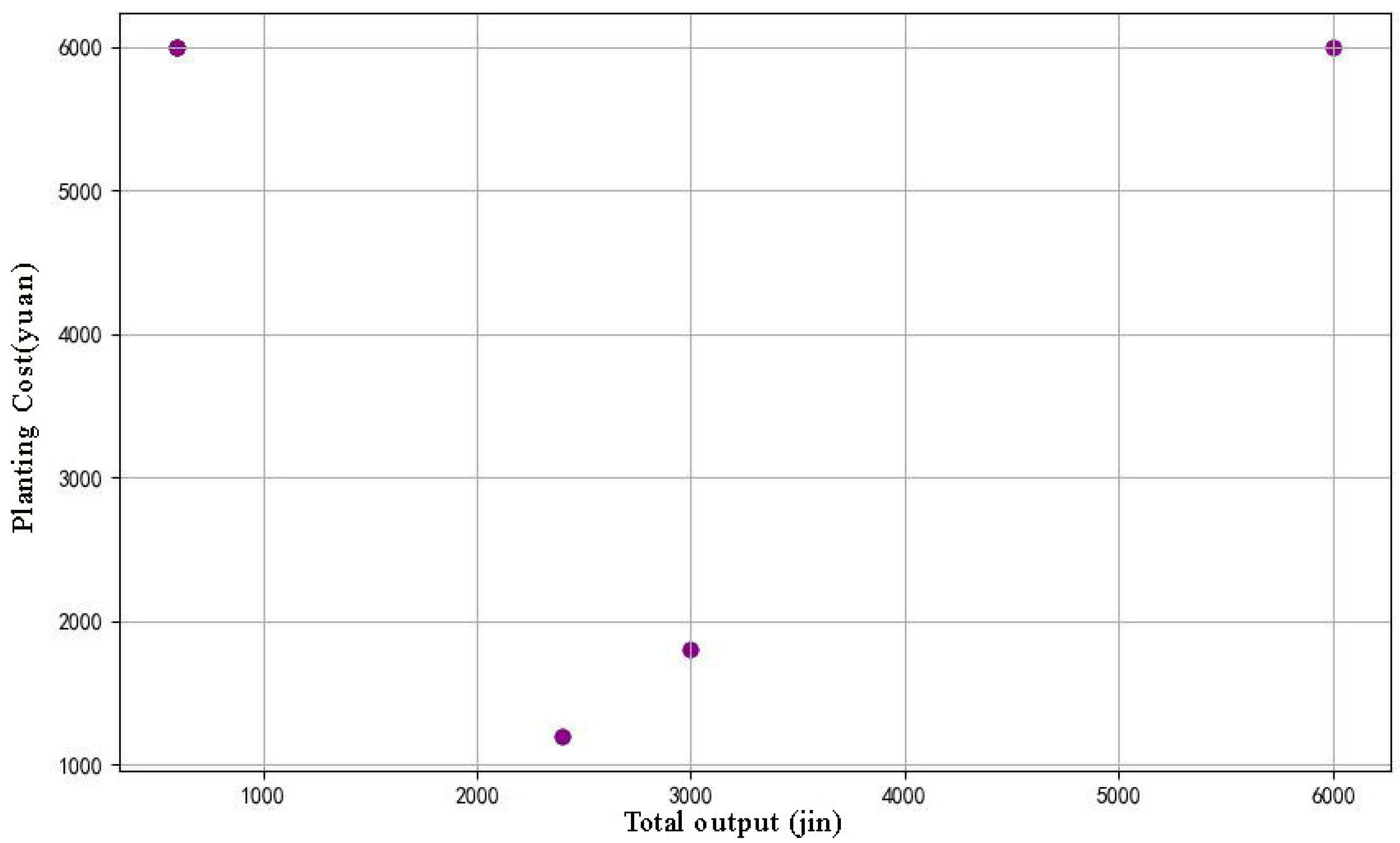
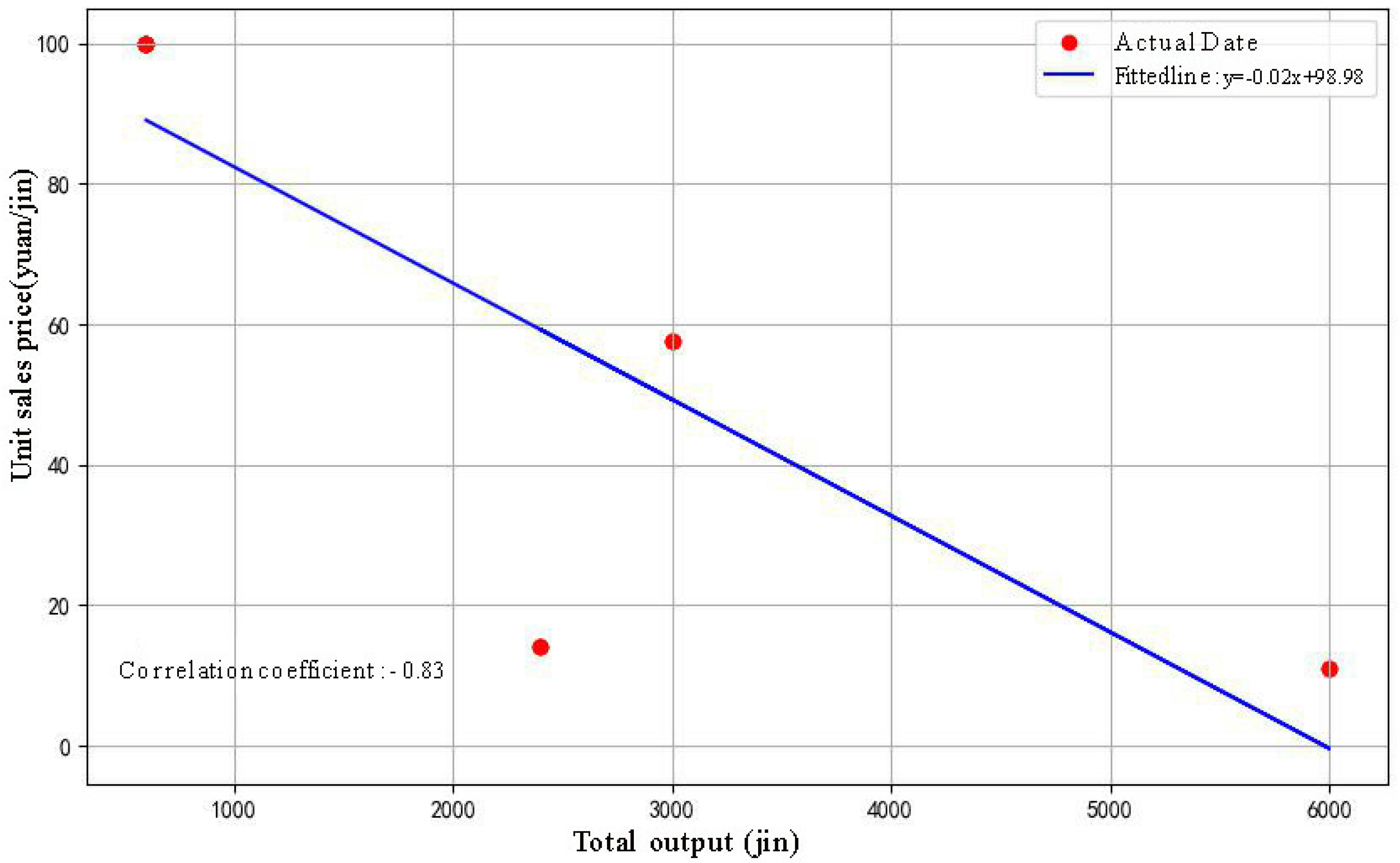
5.1. Correlation Analysis with Heatmap
5.2. Regression Analysis
- (a)
- Grain crops:
- (b)
- Vegetable crops:
- (c)
- Edible fungi crops:
5.3. Related Works
5.4. Extension of the Proposed Methods
5.5. Agricultural Resilience Analysis
5.6. Trade-Offs Between Profit, Soil Health, Biodiversity, and Climate
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SPM | Stochastic programming model |
| IPM | Integer programming model |
| ROA | Robust optimization algorithm |
| GA | Genetic algorithm |
References
- Chen, J. Research on the Protection of Agricultural Ecological Environment and Sustainable Development Path. World Trop. Agric. Inf. 2025, 5, 72–74. [Google Scholar]
- Wang, C.; Dong, W.; Wang, X. Research on the Coupling and Adaptation of Agricultural Sustainable Development Strategy and Rural Revitalization Strategy. J. Anyang Norm. Univ. 2019, 4, 31–35. [Google Scholar] [CrossRef]
- Deng, R.; Guo, W.; Chen, W.; Zhao, C. Multi-Agricultural Machinery Collaborative Task Planning Based on Non-dominated Sorting Genetic Algorithm. J. Chin. Agric. Mech. 2025, 46, 113-119+149. [Google Scholar] [CrossRef]
- Tian, M.; Ni, W.; Hu, W.; Ru, H.; Zhao, W. Optimization of Crop Planting Strategies in North China Mountainous Areas Based on Linear Programming. South. Agric. 2025, 19, 73–81. [Google Scholar] [CrossRef]
- Tang, S.; Wang, W.; Zhang, H.; Jiang, G. Analysis of Crop Planting Strategies Based on Two-Stage Optimization. J. Smart Agric. 2025, 5, 68-74+79. [Google Scholar] [CrossRef]
- Meng, Z.; Wang, J. Innovation in the Path of Agricultural Sustainable Development Under the Implementation of the Rural Revitalization Strategy. Agric. Econ. 2024, 10, 15–17. [Google Scholar]
- Li, B. Exploration and Practice of Agricultural Sustainable Development Models under the Rural Revitalization Strategy. Hebei Agric. Mach. 2025, 4, 162–164. [Google Scholar] [CrossRef]
- Wang, X. Analysis of the Advantages of Intercropping and Relay Cropping in Crop Planting. Seed Technol. 2025, 43, 194–196. [Google Scholar] [CrossRef]
- Sacks, W.J.; Deryng, D.; Foley, J.A.; Ramankutty, N. Crop planting dates: An analysis of global patterns. Glob. Ecol. Biogeogr. 2010, 19, 607–620. [Google Scholar] [CrossRef]
- Zhao, Y. Analysis of Greenhouse Vegetable Planting Techniques and Pest and Disease Control Strategies. Agric. Mach. Mark. 2025, 5, 65–67. [Google Scholar]
- Han, E. Exploration of Crop Planting Structure Optimization. Heilongjiang Grain 2024, 12, 23–25. [Google Scholar]
- Kambli, A.; McGarvey, R.G. Network design for local agriculture using robust optimization. Inf. Process. Agric. 2021, 8, 469–483. [Google Scholar] [CrossRef]
- Xia, J.Y.; Li, S.; Huang, J.J.; Yang, Z.; Jaimoukha, I.M.; Gündüz, D. Metalearning-based alternating minimization algorithm for nonconvex optimization. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 5366–5380. [Google Scholar] [CrossRef]
- Yin, Y.; Gong, H.; Chen, Z.; Tian, X.; Wang, Y.; Wang, Z.; He, K.; Miao, Q.; Chu, Y.; Xue, Y.; et al. Underestimated sequestration of soil organic carbon in China. Environ. Chem. Lett. 2025, 23, 373–379. [Google Scholar] [CrossRef]
- Xu, M.; Meng, X.; Liu, H. The Impact of Urbanization on Crop Planting Structure in China. Lanzhou Acad. J. 2013, 2, 141–146. [Google Scholar]
- Liu, F. Some Suggestions on Adjusting Crop Planting Structure. Agric. Econ. 2001, 5, 44. [Google Scholar]
- Zhang, Y. The Evolution of Crop Planting Structure and Rural Social Change: A Case Study of Central Hubei Rural Areas. Agric. Past Present 2005, 1, 9–14. [Google Scholar]
- Wang, W.H.; Zheng, J.H.; Liu, Z.; Fang, J.; Li, Z.; Wu, Q.H. Hierarchical demand response considering dynamic competing interaction based on multi-agent deep deterministic policy gradient. CSEE J. Power Energy Syst. 2025. [CrossRef]
- Li, J.; Zu, L.Y.; Zhong, X.L. Comparative Advantage Analysis of Crop Planting: A Case Study of Sichuan Province. Rural. Econ. 2005, 9, 47–49. [Google Scholar]
- Wieme, R.A.; Carpenter-Boggs, L.A.; Crowder, D.W.; Murphy, K.M.; Reganold, J.P. Agronomic and economic performance of organic forage, quinoa, and grain crop rotations in the Palouse region of the Pacific Northwest, USA. Agric. Syst. 2020, 177, 102709. [Google Scholar] [CrossRef]
- Wang, X.; Wang, W. Comparative Advantage Analysis of Major Agricultural Products in Yunnan’s Organic Agriculture. Contemp. Econ. 2014, 18, 72–73. [Google Scholar]
- Du, H.; Zhao, Y. A Review of Intelligent Algorithms for Solving Integer Programming Problems. J. Comput. Appl. Res. 2010, 27, 408–412. [Google Scholar]
- Zhu, H.; Liu, J.; Liu, F.; Li, T.; Wang, H. Adaptive Genetic Algorithm for Optimizing Crop Planting Structure and Resource Allocation. J. Liaoning Univ. Technol. 2019, 39, 393–396. [Google Scholar] [CrossRef]
- Zhang, D. Application of Genetic Algorithms in Multi-Constraint Combinatorial Optimization. J. Equip. Command. Technol. Coll. 2005, 3, 112–113. [Google Scholar]
- Zhang, A.; He, J. The Impact of Climate Change on Crop Growth and Coping Strategies. Rural. Sci. Exp. 2025, 5, 193–195. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, S. Exploring the Impact of Climate Change on Crop Breeding Strategies. Hebei Agric. Mach. 2024, 9, 94–96. [Google Scholar] [CrossRef]
- Zhang, H. Research on the Impact of Climate Change on Ecosystems and Agricultural Production. Agric. Disaster Res. 2023, 13, 201–203. [Google Scholar]
- Wang, Y. The Impact of Climate Change on Agricultural Meteorological Disasters and Pests and Coping Measures. Agric. Eng. Technol. 2021, 41, 92–93. [Google Scholar] [CrossRef]
- Feng, X.; Liu, D.; Zhao, J.; Si, W.; Fan, S. Impact of climate change on farmers’ crop production in China: A panel Ricardian analysis. Humanit. Soc. Sci. Commun. 2025, 12, 250. [Google Scholar] [CrossRef]
- Orke, A.Y.; Shanka, S.A. Analyzing the Impact of Climate Change on Crop Water Demand in the Semi-Arid Bilate Watershed, Ethiopia. Adv. Meteorol. 2025, 2025, 9466355. [Google Scholar] [CrossRef]
- Fan, M. The Impact of Climate Change on Crop Planting Patterns and Adaptive Strategies. Agric. Dev. Equip. 2025, 2, 160–162. [Google Scholar]
- Liu, J. The Impact of Climate Factors on Crop Growth and Solutions. Agric. Technol. Serv. 2017, 34, 141. [Google Scholar]
- Qi, L.; Zhang, M. The Impact of Agricultural Meteorological Changes on the Growth and Development of Crops in Jilin Province and Coping Measures. South. Agric. 2023, 17, 218-220+230. [Google Scholar] [CrossRef]
- Yu, P. Correctly Evaluating the Impact of Climate Change on Agriculture to Provide a Basis for Healthy and Stable Agricultural Development. Jilin Agric. 2016, 16, 113. [Google Scholar] [CrossRef]
- Li, C.; Dong, X.; Zong, Y. Analysis of Vegetable Price Trends in Hebei Province and Market Forecast for 2024. Vegetables 2024, 6, 21–27. [Google Scholar]
- Sabouni, M.S.; Mardani, M. Application of robust optimization approach for agricultural water resource management under uncertainty. J. Irrig. Drain. Eng. 2013, 139, 571–581. [Google Scholar] [CrossRef]
- Yuan, M.; Zheng, N.; Yang, Y.; Liu, C. Robust optimization for sustainable agricultural management of the water-land-food nexus under uncertainty. J. Clean. Prod. 2023, 403, 136846. [Google Scholar] [CrossRef]
- Mardani Najafabadi, M.; Taki, M. Robust data envelopment analysis with Monte Carlo simulation model for optimization the energy consumption in agriculture. Energy Sources Part A Recovery Util. Environ. Eff. 2024, 46, 9436–9450. [Google Scholar] [CrossRef]
- Ge, J.; Qiu, Y.; Wu, C.; Pu, G. A Review of Genetic Algorithms. J. Comput. Appl. Res. 2008, 25, 2911–2916. [Google Scholar]
- Yan, Z.; Li, M. A stochastic optimization model for agricultural irrigation water allocation based on the field water cycle. Water 2018, 10, 1031. [Google Scholar] [CrossRef]
- Ratanakuakangwan, S.; Morita, H. Hybrid stochastic robust optimization and robust optimization for energy planning–A social impact-constrained case study. Appl. Energy 2021, 298, 117258. [Google Scholar] [CrossRef]
- Usman, M.; Hameed, G.; Saboor, A.; Almas, L.K.; Hanif, M. R&d innovation adoption, climatic sensitivity, and absorptive ability contribution for agriculture TFP growth in Pakistan. Agriculture 2021, 11, 1206. [Google Scholar] [CrossRef]
- El Chami, D.; Daccache, A.; El Moujabber, M. How can sustainable agriculture increase climate resilience? A systematic review. Sustainability 2020, 12, 3119. [Google Scholar] [CrossRef]
- Cámara, J.; de Lemos, R.; Vieira, M.; Almeida, R.; Ventura, R. Architecture-based resilience evaluation for self-adaptive systems. Computing 2013, 95, 689–722. [Google Scholar] [CrossRef]
- Hellin, J.; Fisher, E.; Taylor, M.; Bhasme, S.; Loboguerrero, A.M. Transformative adaptation: From climate-smart to climate-resilient agriculture. CABI Agric. Biosci. 2023, 4, 30. [Google Scholar] [CrossRef]
- Asadzadeh, A.; Khavarian-Garmsir, A.R.; Sharifi, A.; Salehi, P.; Kötter, T. Transformative resilience: An overview of its structure, evolution, and trends. Sustainability 2022, 14, 15267. [Google Scholar] [CrossRef]
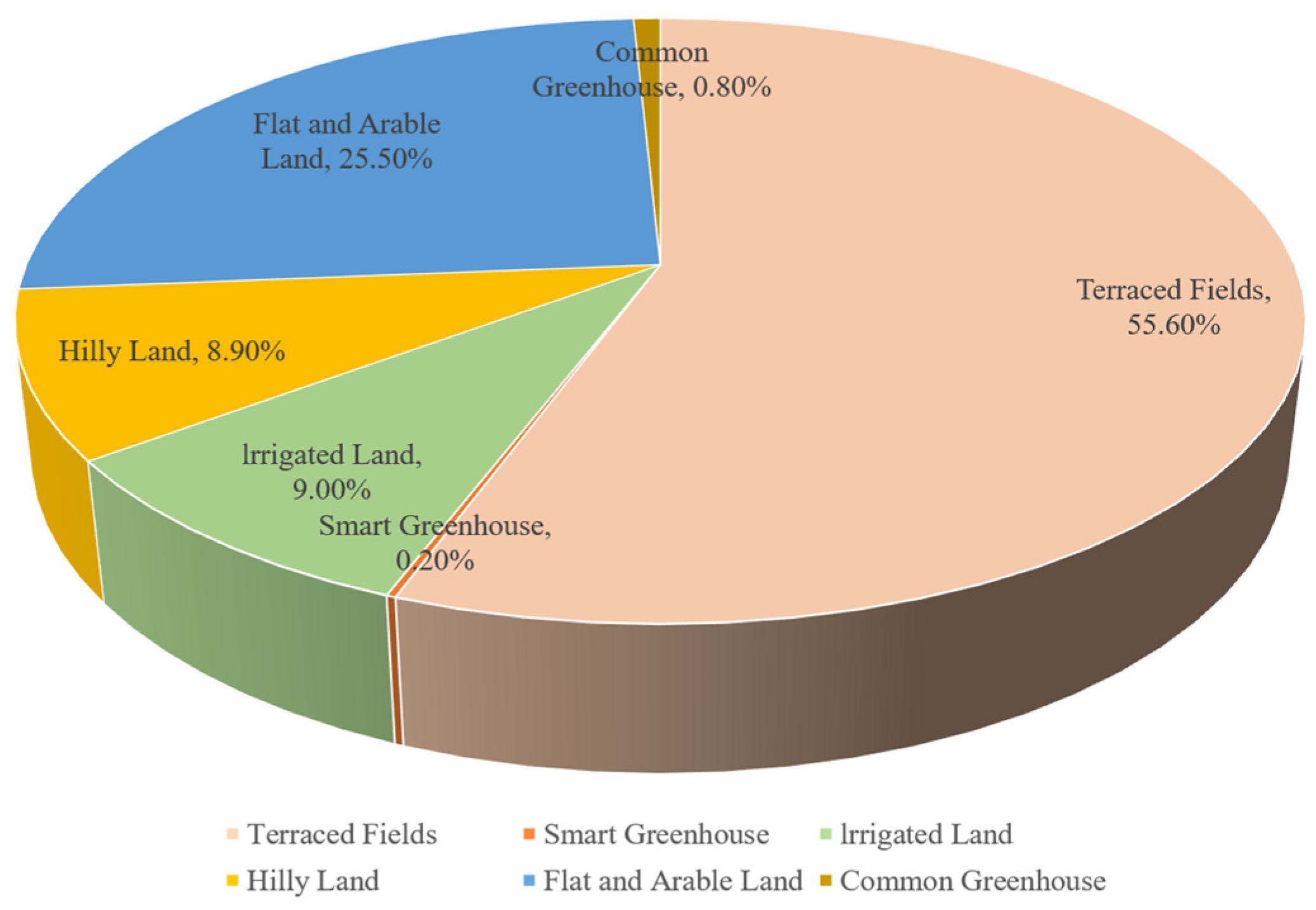
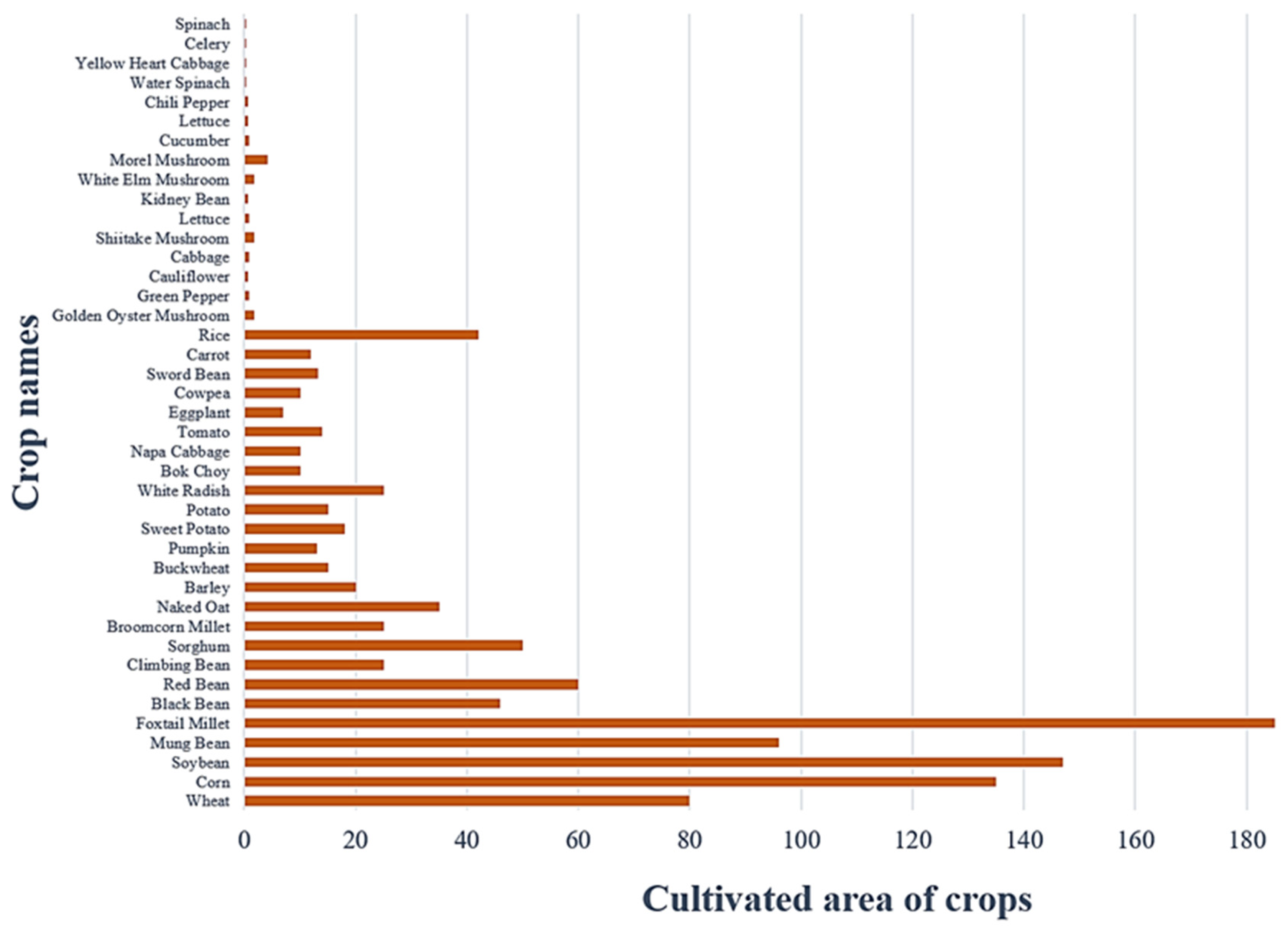
| Plot ID | Crop Code | Crop Name | Total Yield |
|---|---|---|---|
| A4 | 1 | Soybean | 28,800 |
| B11 | 1 | Soybean | 22,800 |
| C3 | 1 | Soybean | 5400 |
| B2 | 2 | Black soybean | 21,850 |
| B3 | 3 | Red bean | 15,200 |
| C6 | 3 | Red bean | 7200 |
| A5 | 4 | Mung bean | 23,800 |
| B4 | 4 | Mung bean | 9240 |
| B5 | 5 | Cowpea | 9875 |
| A1 | 6 | Wheat | 64,000 |
| Symbol | Description |
|---|---|
| The area planted with the -th crop in the -th plot | |
| The area of the -th plot | |
| The unit selling price of the -th crop | |
| A binary variable indicating whether the -th crop can be planted in the -th plot (0 = no, 1 = yes) | |
| The planting cost per unit area for the -th crop | |
| The yield per unit area of the -th crop | |
| The area planted with the -th crop in the -th plot during year | |
| The expected sales volume of the -th crop | |
| The yield of the -th crop in the -th plot | |
| The yield of the -th crop in the -th plot during year | |
| Total revenue over the seven-year period 2024–2030 |
| Fluctuation Scenarios | Robust Fluctuation Variation | Normal Fluctuation Variation | Worst-Case Fluctuation Variation | |
|---|---|---|---|---|
| Parameters | ||||
| The annual change rate of the expected sales volume for wheat and corn | 10% | 7.5% | 5% | |
| The annual change rate of the expected sales volume for other crops | 5% | 0 | −5% | |
| The annual change rate of crop yield per acre | 10% | 0 | −10% | |
| The annual change rate of planting costs | 3% | 5% | 7% | |
| The annual change rate of grain crop sales prices | 2% | 0 | −2% | |
| The annual change rate of vegetable crop sales prices | 7% | 5% | 3% | |
| The annual change rate of edible fungus prices | −1% | −3% | −5% | |
| The First Season | ||
|---|---|---|
| Field Name | Crop Type | Planting Area |
| A1 | Wheat | 80 |
| A2 | Red beans | 55 |
| A3 | Wheat | 35 |
| A4 | Wheat | 72 |
| A5 | Corn | 68 |
| A6 | Corn | 55 |
| B1 | Black beans | 53.8 |
| B2 | Sorghum | 46 |
| B3 | Millet | 40 |
| B4 | Mung beans | 28 |
| B5 | Sorghum | 25 |
| The Second Season | ||
|---|---|---|
| Field Name | Crop Type | Planting Area |
| D1 | Chinese cabbage | 15 |
| D2 | Chinese cabbage | 10 |
| D3 | White radish | 14 |
| D4 | Chinese cabbage | 5 |
| D5 | — | — |
| D6 | Carrot | 12 |
| D7 | — | — |
| D8 | White radish | 11 |
| E1 | — | — |
| E2 | — | — |
| E3 | — | — |
| The First Season | ||
|---|---|---|
| Field Name | Crop Type | Planting Area |
| A1 | Wheat | 80 |
| A2 | Millet | 55 |
| A3 | Millet | 35 |
| A4 | Wheat | 72 |
| A5 | Corn | 68 |
| A6 | Mung beans | 55 |
| B1 | Wheat | 60 |
| B2 | Millet | 46 |
| B3 | Buckwheat | 35 |
| B4 | Red beans | 28 |
| B5 | Sorghum | 25 |
| The Second Season | ||
|---|---|---|
| Field Name | Crop Type | Planting Area |
| D1 | White radish | 15 |
| D2 | Chinese cabbage | 10 |
| D3 | Chinese cabbage | 14 |
| D4 | Chinese cabbage | 6 |
| D5 | White radish | 10 |
| D6 | Carrot | 12 |
| D7 | — | — |
| D8 | — | — |
| E1 | — | — |
| E2 | — | — |
| E3 | — | — |
| The First Season | ||
|---|---|---|
| Field Name | Crop Type | Planting Area |
| A1 | Mung beans | 80 |
| A2 | Corn | 55 |
| A3 | Climbing beans | 35 |
| A4 | Wheat | 72 |
| A5 | Corn | 68 |
| A6 | Wheat | 55 |
| B1 | Millet | 60 |
| B2 | Sorghum | 46 |
| B3 | Wheat | 40 |
| B4 | Sorghum | 28 |
| B5 | Corn | 25 |
| The Second Season | ||
|---|---|---|
| Field Name | Crop Type | Planting Area |
| D1 | White radish | 15 |
| D2 | Carrot | 4 |
| D3 | Carrot | 14 |
| D4 | Chinese cabbage | 6 |
| D5 | Chinese cabbage | 8 |
| D6 | Chinese cabbage | 11 |
| D7 | White radish | 22 |
| D8 | Chinese cabbage | 20 |
| E1 | — | — |
| E2 | — | — |
| E3 | — | — |
| Scenarios | SPM with ROA Methods | IPM with GA Methods | ||||
|---|---|---|---|---|---|---|
| Key Metrics | Optimal | Normal | Worst | A | B | |
| Profit increase | 42.5% | 21.8% | 2.6% | 13.7% | 24.1% | |
| Land utilization | 100% | 80.7% | 60.2% | 77.4% | 82.3% | |
| Risk mitigation | 40.2% | 20% | —— | 11.9% | 22.1% | |
| Key Parameters | Fluctuation Ranges | |
|---|---|---|
| Expected sales volume | Wheat and corn annual growth rates | 5~10% |
| Other crops annual change rate | −5~5% | |
| Yield per acre | All crops annual change rate | −10~10% |
| Planting cost | All crops annual growth rate | 5% |
| Selling price | Annual growth rate of vegetable crops | 5% |
| Annual decline rate of edible mushroom crops | 1~5% | |
| Annual decline rate for morel mushrooms | 5% | |
| Key Parameters | Baseline Values | |
|---|---|---|
| Expected sales volume | Wheat and corn annual growth rates | 7.5% |
| Other crops annual change rate | 0% | |
| Yield per acre | All crops annual change rate | 0% |
| Planting cost | All crops annual growth rate | 5% |
| Selling price | Annual growth rate of vegetable crops | 5% |
| Annual decline rate of edible mushroom crops | 3% | |
| Annual decline rate for morel mushrooms | 5% | |
| Baseline total profit (million yuan) | 45.746 | |
| Key Parameters | Parameter Fluctuation | Sensitivity Analysis of Profit (Million Yuan) | Sensitivity Elasticity Coefficient | |
|---|---|---|---|---|
| Expected sales volume | Wheat and corn annual growth rates | 5% | Falls to 39.812 | 6.8 |
| 10% | Rises to 53.491 | |||
| Other crops annual change rate | −5% | Falls to 43.369 | 1.04 | |
| 5% | Rises to 48.123 | |||
| Yield per acre | All crops annual change rate | −10% | Falls to 40.258 | 1.2 |
| 10% | Rises to 51.234 | |||
| Planting cost | All crops annual growth rate | −2% | Falls to 43.369 | 2.6 |
| 2% | Rises to 48.123 | |||
| Selling price | Annual growth rate of vegetable crops | −2% | Falls to 43.369 | 2.6 |
| 2% | Rises to 48.123 | |||
| Annual decline rate of edible mushroom crops | −2% | Rises to 48.123 | −2.6 | |
| 2% | Falls to 43.369 | |||
| Crop Categories | High Substitution Complementary Combination | Substitution Coefficients | Substitution and Complementary Logic |
|---|---|---|---|
| Grains | Black beans↔Red beans ↔Climb beans | 0.92 | The yield is similar, and the nutritional function is similar |
| Wheat↔Barley ↔Millet | 0.85 | Dry land production capacity is similar | |
| Vegetables | Sweet potato↔Potato ↔Pumpkin | 0.78 | High-yield filler crops |
| Spinach↔Lettuce ↔Small greens | 0.95 | The growth cycle is short, and the annual output of the greenhouse exceeds 4000 catties | |
| fungi | Elm yellow mushroom ↔Lentinula edodes ↔White spirit mushroom | 0.65 | Exclusive to greenhouses, but the yield varies greatly |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhang, J.; Wang, T.; Zeng, B.; Wang, B.; Chen, Y.; Chen, Y. Intelligent Optimization-Based Decision-Making Framework for Crop Planting Strategy with Total Profit Prediction. Agriculture 2025, 15, 1736. https://doi.org/10.3390/agriculture15161736
Wang C, Zhang J, Wang T, Zeng B, Wang B, Chen Y, Chen Y. Intelligent Optimization-Based Decision-Making Framework for Crop Planting Strategy with Total Profit Prediction. Agriculture. 2025; 15(16):1736. https://doi.org/10.3390/agriculture15161736
Chicago/Turabian StyleWang, Chongyuan, Jinjuan Zhang, Ting Wang, Bowen Zeng, Bi Wang, Yishan Chen, and Yang Chen. 2025. "Intelligent Optimization-Based Decision-Making Framework for Crop Planting Strategy with Total Profit Prediction" Agriculture 15, no. 16: 1736. https://doi.org/10.3390/agriculture15161736
APA StyleWang, C., Zhang, J., Wang, T., Zeng, B., Wang, B., Chen, Y., & Chen, Y. (2025). Intelligent Optimization-Based Decision-Making Framework for Crop Planting Strategy with Total Profit Prediction. Agriculture, 15(16), 1736. https://doi.org/10.3390/agriculture15161736






