Design and Experiment of DEM-Based Layered Cutting–Throwing Perimeter Drainage Ditcher for Rapeseed Fields
Abstract
1. Introduction
2. Materials and Methods
2.1. Overall Structure and Working Principle
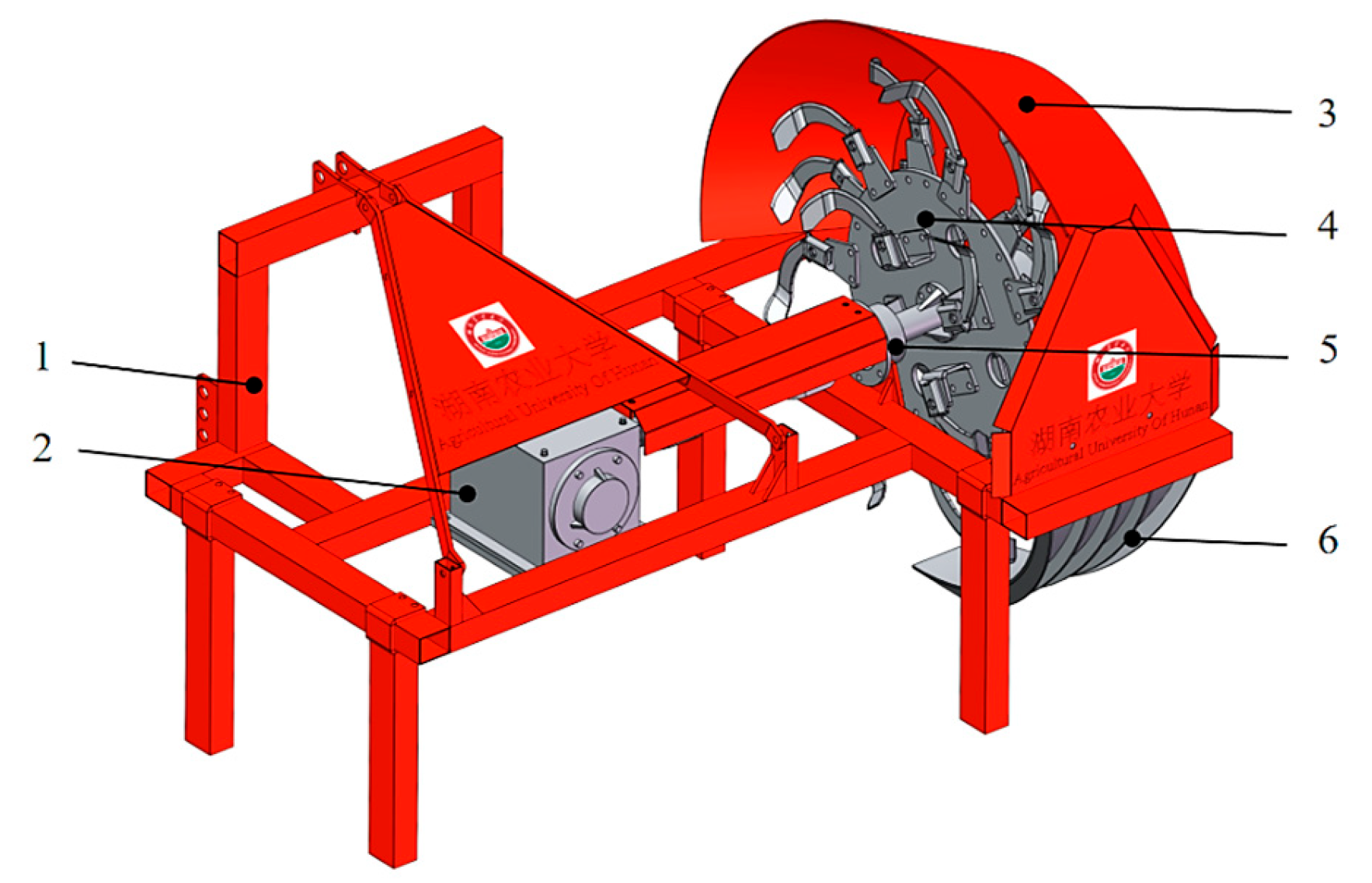
2.1.1. Overall Structure
2.1.2. Working Principle
2.2. Design of Ditching Components for Rapeseed Field Perimeter Ditch Discarding Machine Agricultural Engineering
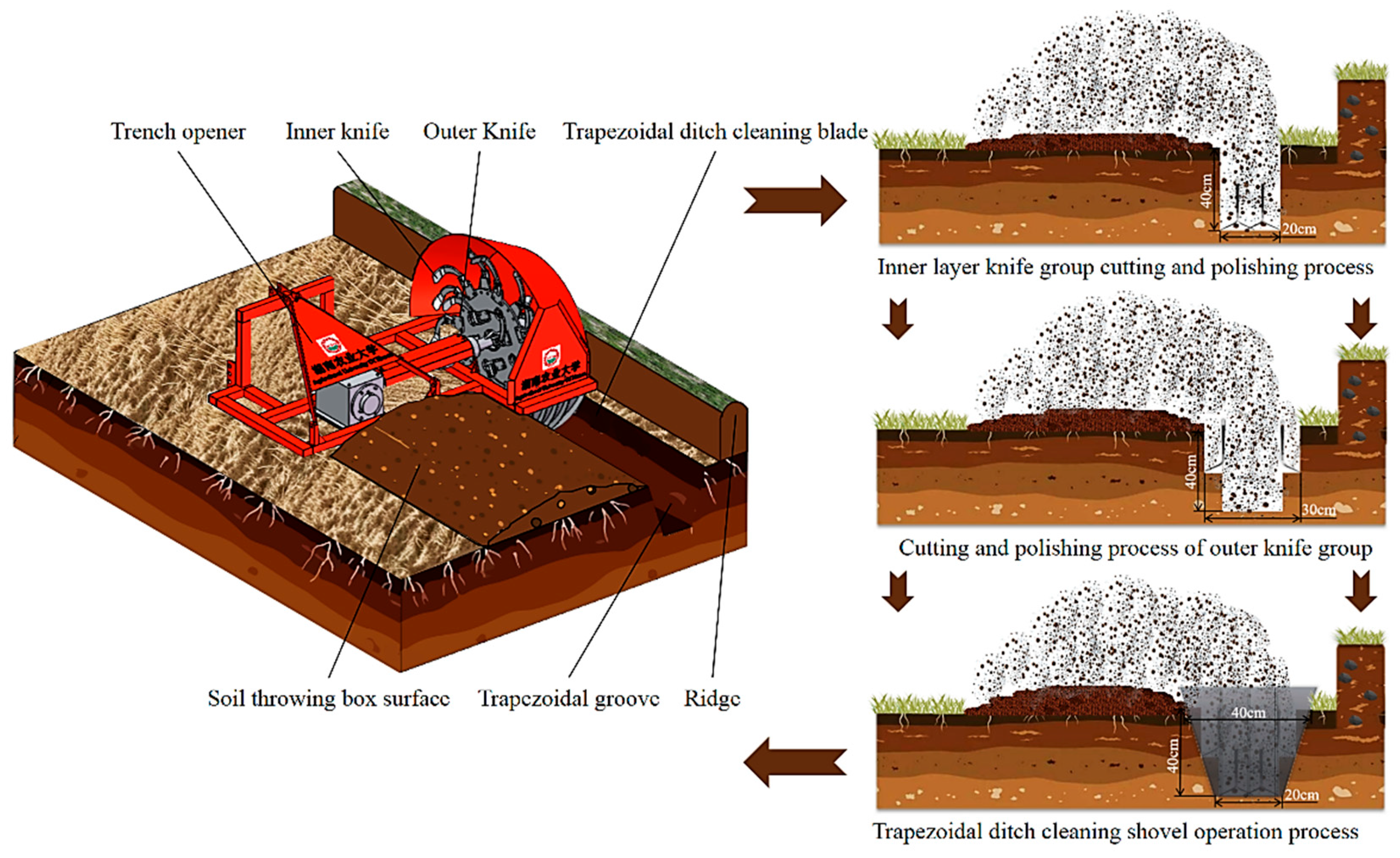
2.2.1. Ditching Unit Working Process
2.2.2. Soil-Cutting Pitch Design
2.2.3. Stepped Cutter Head Layout
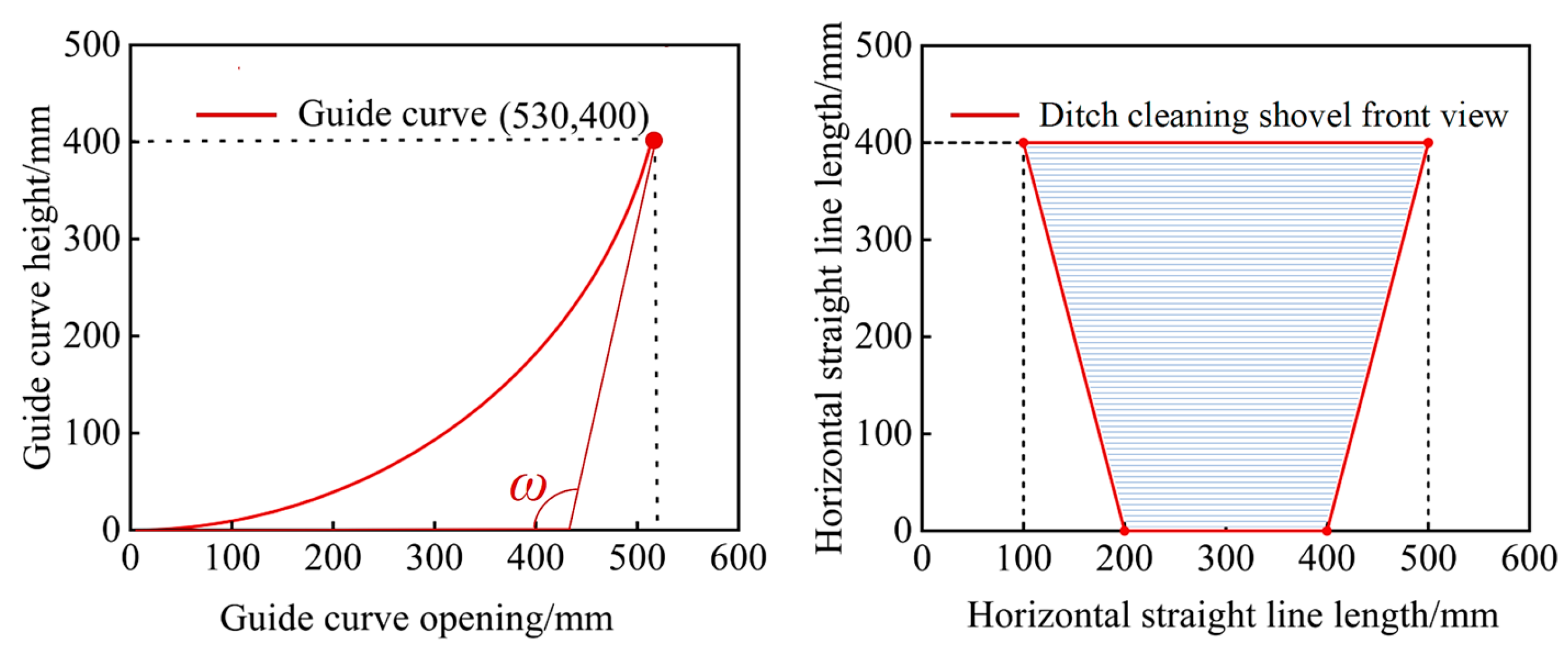
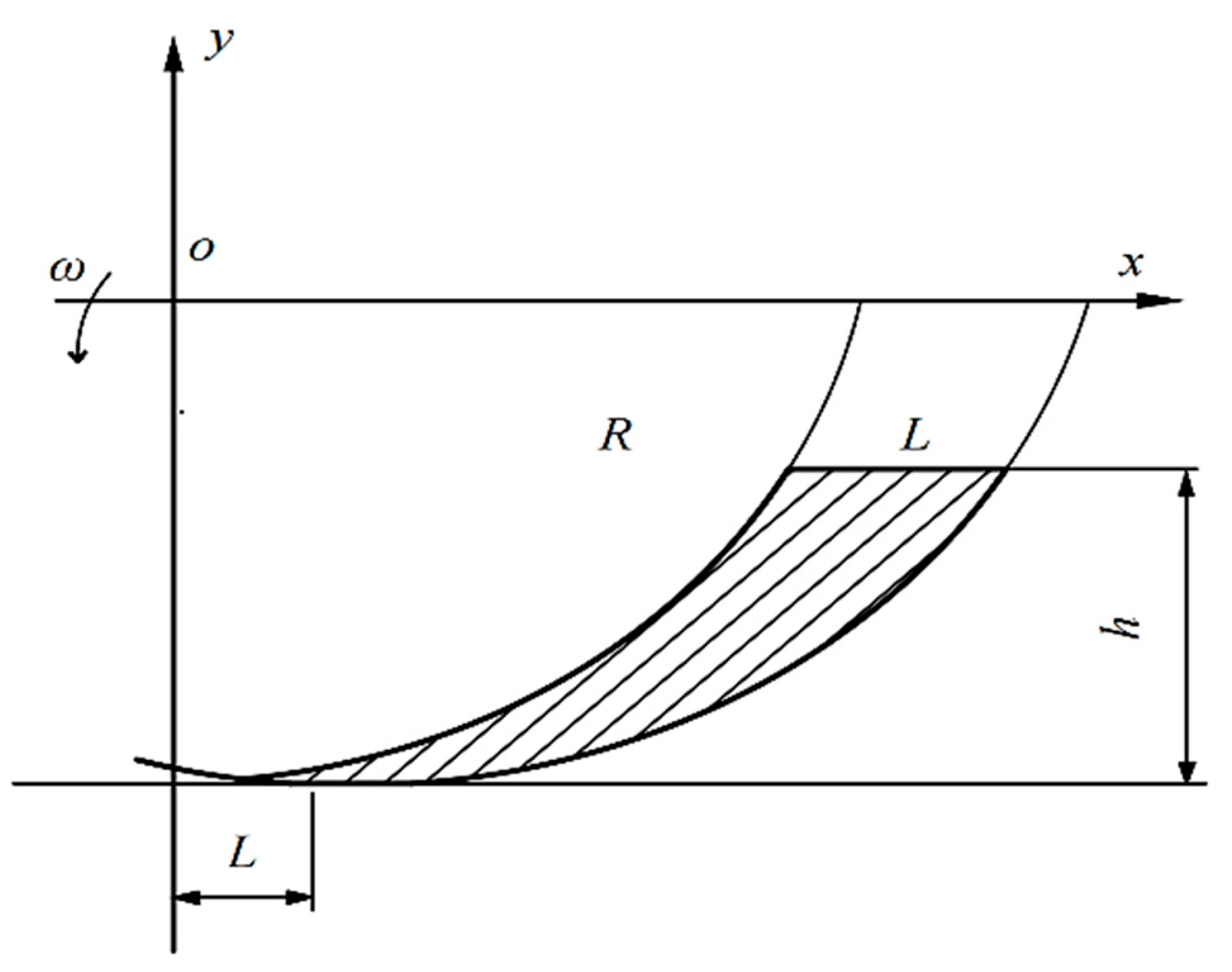
2.2.4. Curved Surface Design of Ditch-Cleaning Shovel
2.3. Identifying Key Parameters
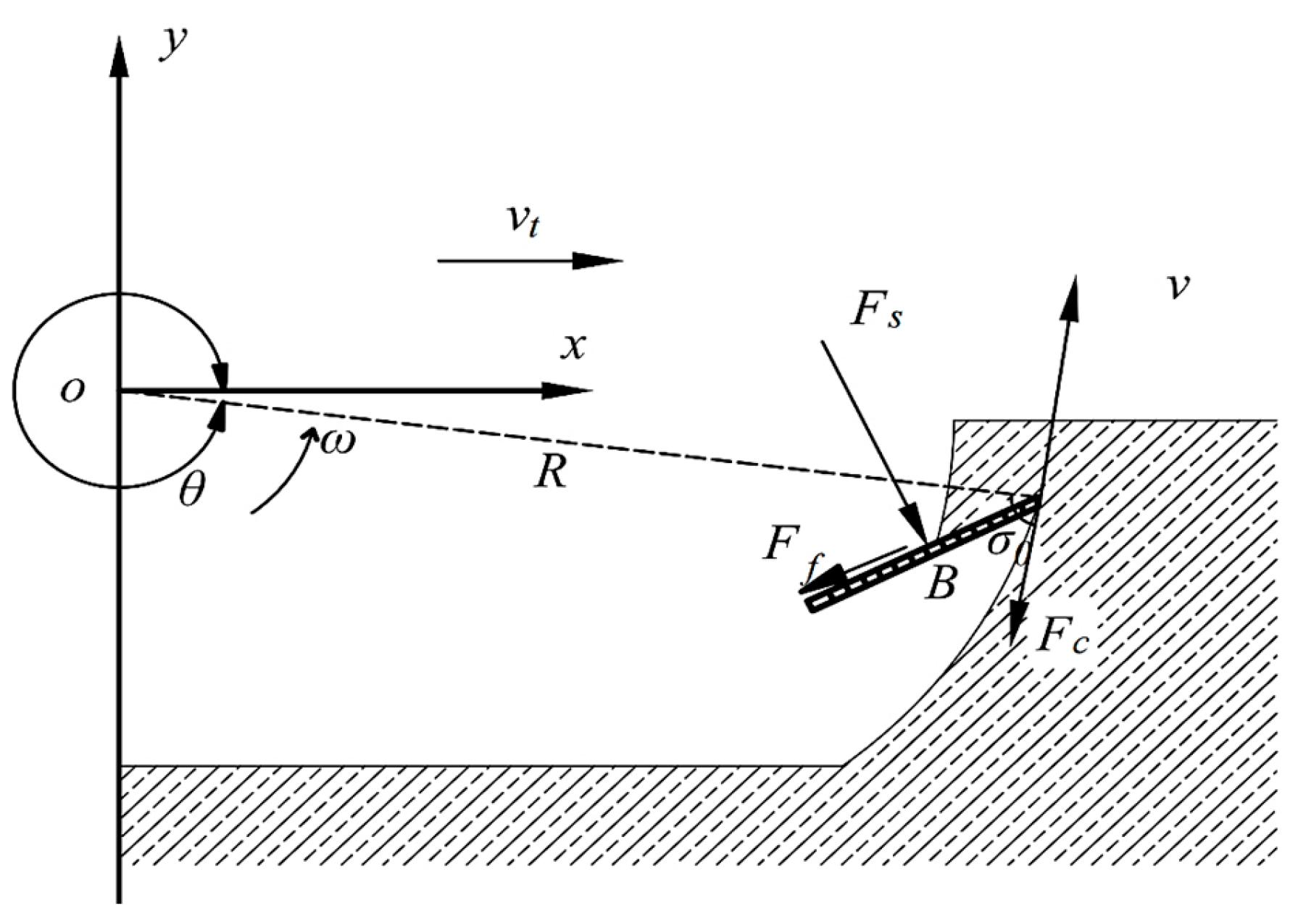
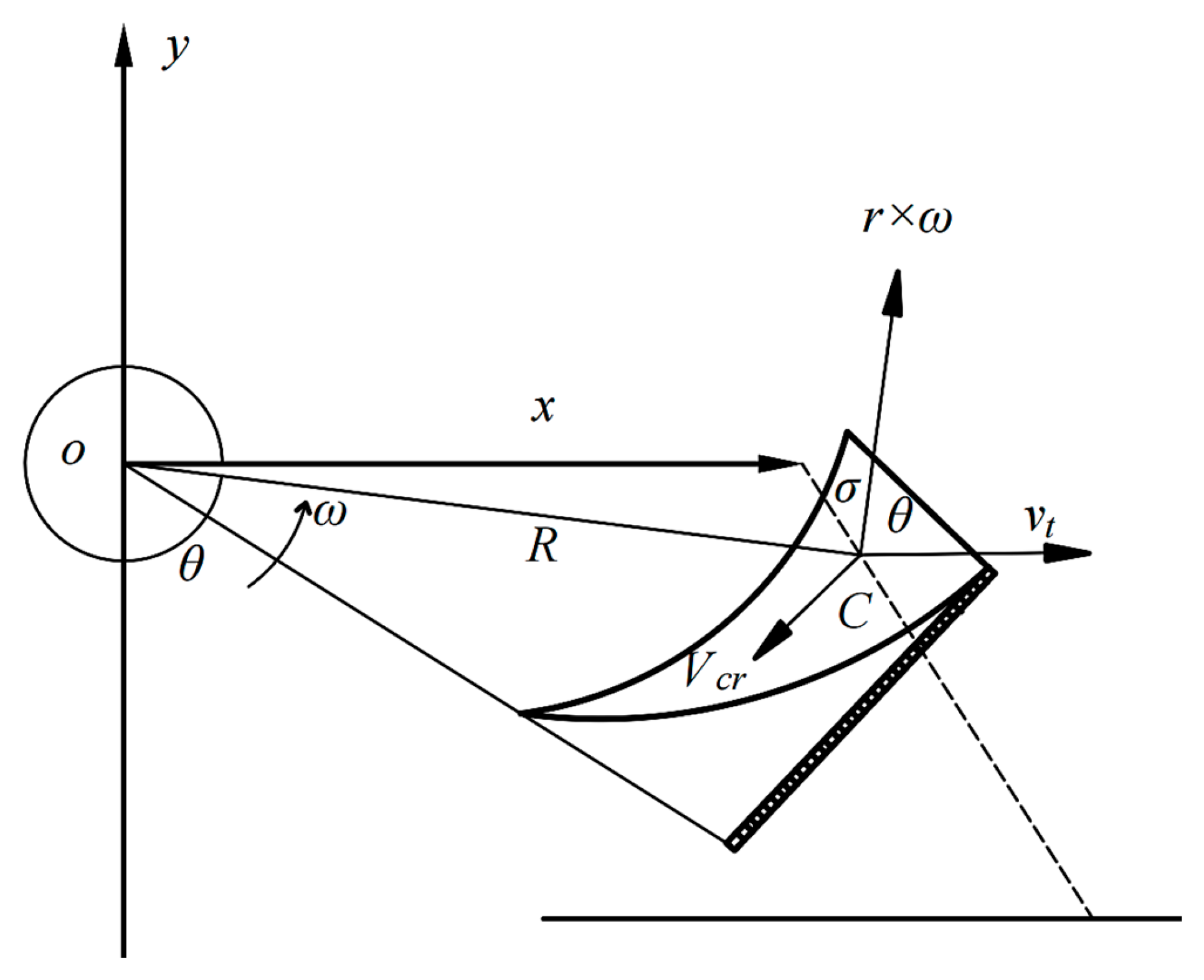
2.3.1. Factors Affecting Power Consumption in Soil Cutting by Disc Cutters
2.3.2. Factors Influencing Soil-Conveying and -Throwing Power by Disc Cutters
- (1)
- Power Consumption for Direct Soil Conveying and Throwing
- (2)
- Power Consumption for Indirect Soil Conveying and Throwing
2.3.3. Factors Affecting Tractive Power Consumption of Ditch-Cleaning Shovel
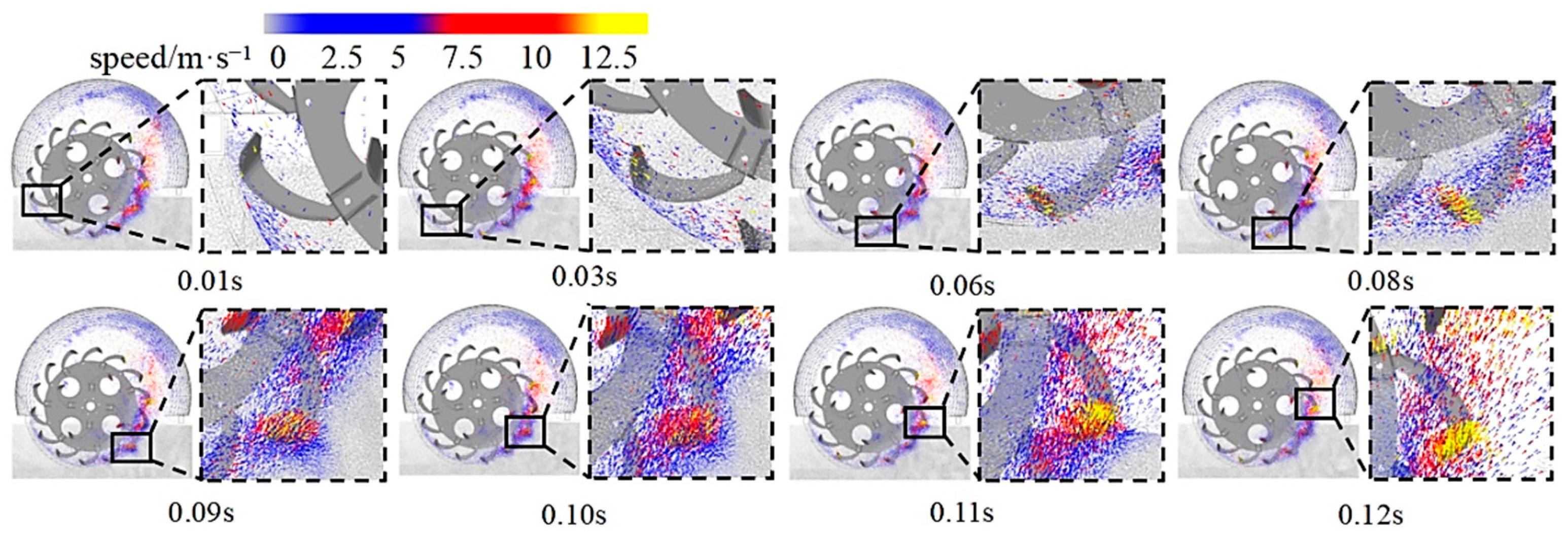
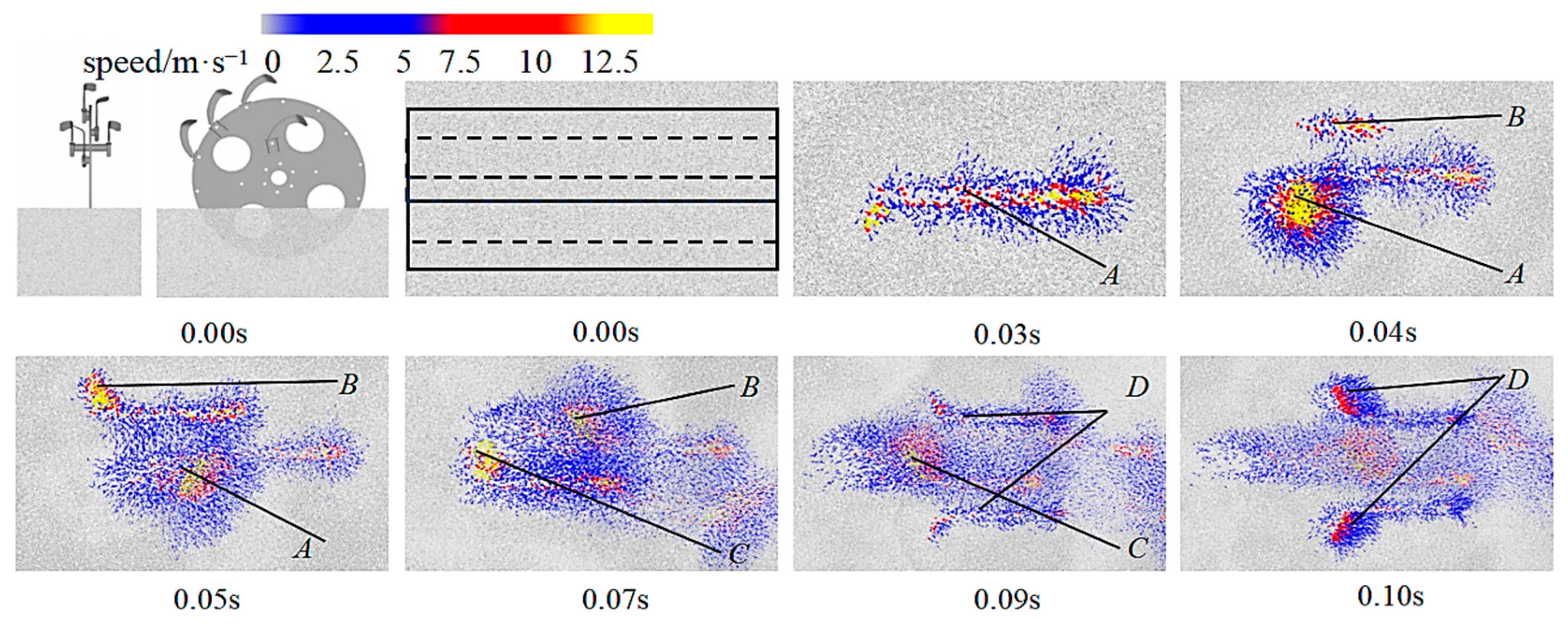
2.4. Operational Simulation of Ditching Unit
2.4.1. Discrete Element Model
2.4.2. Evaluation Metrics and Methods
2.5. Field Experiments
2.5.1. Test Conditions and Equipment
2.5.2. Test Methods and Evaluation Metrics
3. Results and Discussion
3.1. Single-Factor Experiments and Result Analysis
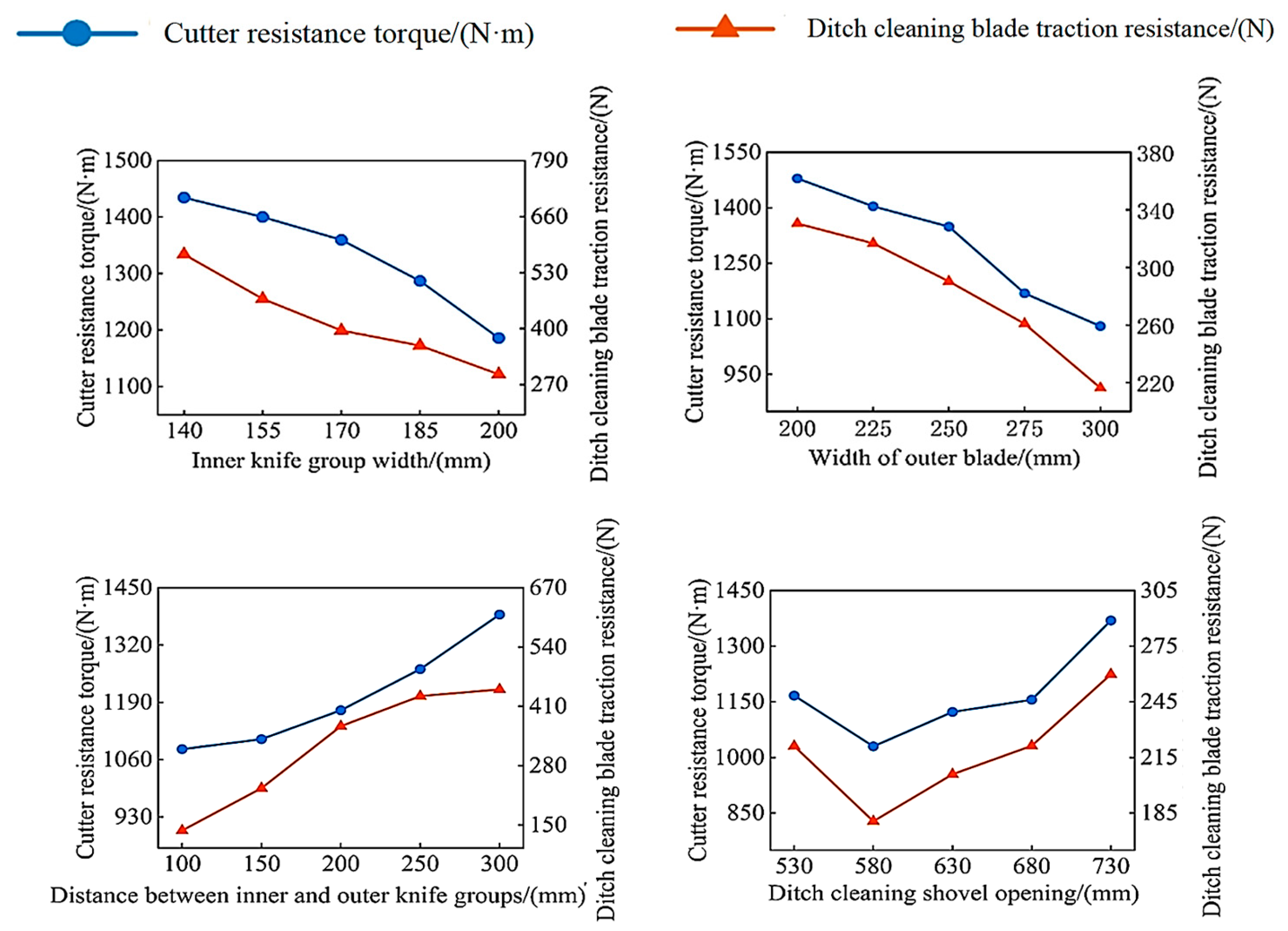
3.1.1. Influence of Inner Blade Group Width on Ditching Power Consumption
3.1.2. Influence of Outer Blade Group Width on Ditching Power Consumption
3.1.3. Influence of Distance Between Blade Groups on Ditching Power Consumption
3.1.4. Influence of Cleaning Blade Opening Width on Ditching Power Consumption
3.2. Box–Behnken Optimization Experiment
3.2.1. Experimental Design
3.2.2. Results and Analysis
- (1)
- Regression Model and Analysis of Variance (ANOVA)
- (2)
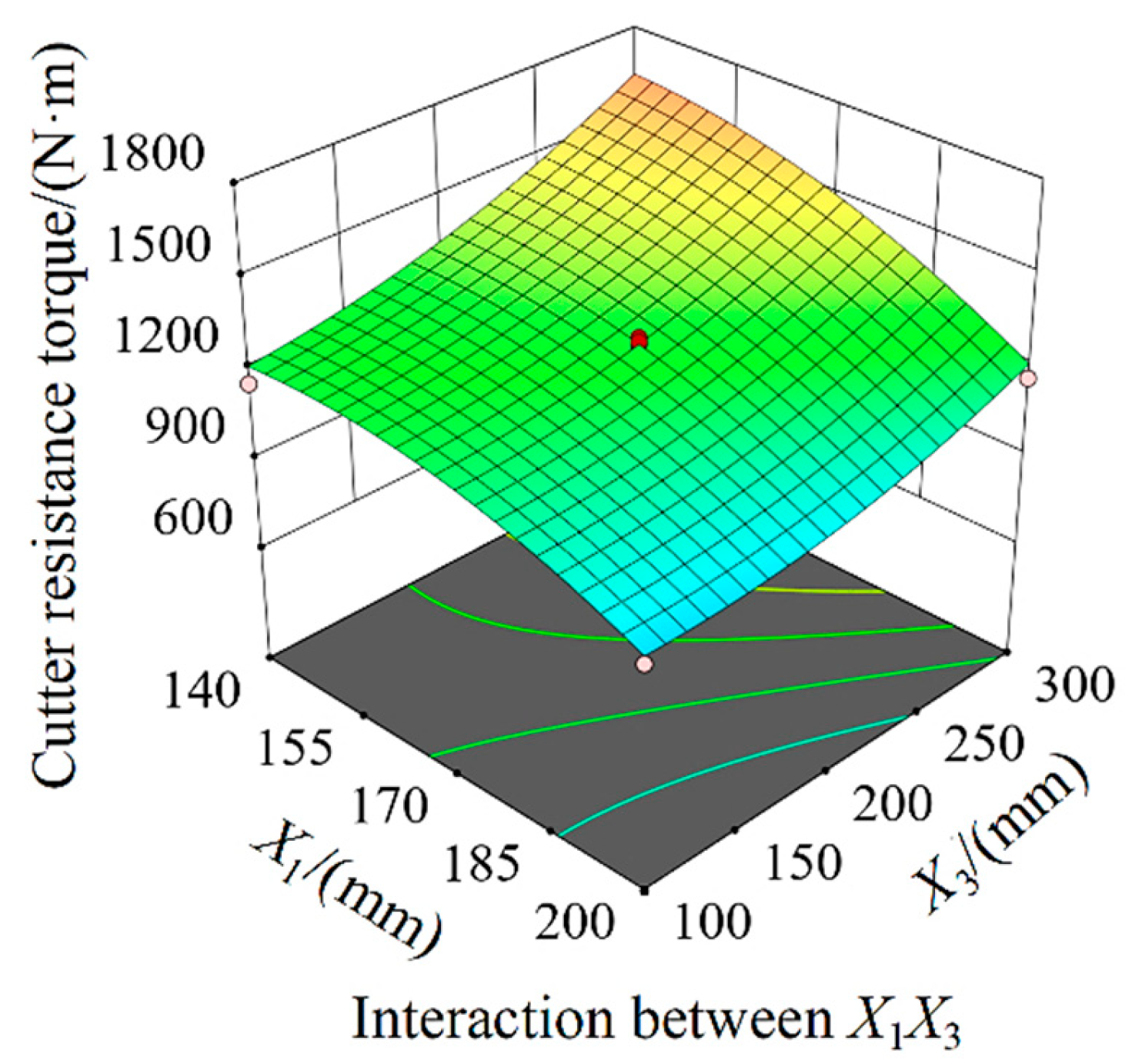
- Analysis of Interaction Effect Influence
- (3)
- Multi-Objective Optimization Based on Genetic Algorithm
3.3. Test Results
3.3.1. Operational Power Consumption
3.3.2. Operational Quality
4. Discussion of Limitations and Prospects
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, M.L.; Zhou, J.; Tian, T.; Wu, Y.Y.; Zhao, C.; Zhang, Y. Study on China’s oilseed self-sufficiency rate and its influencing factors. Trans. China Oils Fats 2025, 50, 1–13. [Google Scholar]
- Cao, C.; Yang, J.; Yuan, G.J. Import dependence and import safety of oilseeds in China. Trans. China Oils Fats 2025, 50, 1–8. [Google Scholar]
- Xiong, Q.Q. Size of grain net import and its self-sufficiency rate in China. J. China Agric. Univ. Soc. Sci. Ed. 2022, 21, 85–101. [Google Scholar]
- Peng, D.Z.; Dai, Y.; Zhang, Q.; Chen, H.; Yang, L.; Zhang, Z. Study on difference of seedling growth and physiological characteristics between three-way cross rapeseed and its parents under different water stress. Chin. Agric. Sci. Bull. 2024, 40, 20–26. [Google Scholar]
- Peng, Q.J.; Kang, J.M.; Jian, S.C.; Yang, X.J.; Liu, L.J. Parameter optimization and power consumption and kinematics analyses of clockwise and counterclockwise ditching. J. China Agric. Univ. 2018, 23, 151–159. [Google Scholar]
- Qin, K.; Liang, X.; Cao, C.; Ding, W.; Wu, Z.; Fang, L. Design and experiment of combined cutting and throwing ditching blade for tea garden. Trans. Chin. Soc. Agric. Mach. 2021, 52, 74–82. [Google Scholar]
- Liu, M.Z.; Xie, F.P.; Liu, D.W.; Wang, X. Analysis and experiment of the power of blade roller in reverse-rotary ditching machine based on the granular scale effect. Trans. Chin. Soc. Agric. Eng. 2024, 40, 83–92. [Google Scholar]
- Kang, J.M.; Li, S.J.; Yang, X.J.; Liu, L.; Wang, C. Virtual simulation and power test of disc type ditcher based on multi-body dynamics. Trans. Chin. Soc. Agric. Mach. 2017, 48, 57–63. [Google Scholar]
- Wang, L.Z.; Liao, Q.X.; Li, M.L.; Shan, Y.; Li, X.; Zhang, Q.; Liao, Y. Drive-type ditching device of the high-speed no-tillage direct seeder for rapeseed. Trans. Chin. Soc. Agric. Eng. 2023, 39, 15–26. [Google Scholar]
- Niu, M.M.; Yang, H.W.; Zhang, Q.Y.; Qi, P.; Wang, S.; Fang, H.; Wen, H. Experimental and simulation study on the ditching and backfilling characteristics of a 3DGZ-50A self-propelled orchard ditching machine. Horticulturae 2025, 11, 171. [Google Scholar] [CrossRef]
- Wang, L.J.; Zhou, B.; Wan, C.; Zhou, L. Structural parameter optimization of a furrow opener based on EDEM software. Int. J. Agric. Biol. Eng. 2024, 17, 115–120. [Google Scholar] [CrossRef]
- Liu, D.W.; Xie, F.P.; Ye, Q.; Ren, S.; Li, X.; Liu, M. Analysis and experiment on influencing factors on power of ditching parts for 1K-50 orchard ditching. Trans. Chin. Soc. Agric. Eng. 2019, 35, 20–29. [Google Scholar]
- Zeng, Y.; Jiang, X.H.; Wu, M.L.; Zhao, Z.; Tang, L.; Li, P. Development of the layered cut and throw ditching blade groups for oil tea forest based on DEM-MBD. Trans. Chin. Soc. Agric. Eng. 2024, 40, 30–42. [Google Scholar]
- Yang, Q.Z.; Yang, X.Y.; He, M.S.; Zhang, R.; Wen, T.; Shi, A. Design and experiment of the rotary throwing knife of wine grape cleaning machine. Trans. Chin. Soc. Agric. Eng. 2022, 38, 44–51. [Google Scholar]
- Wang, L.Z.; Liao, Q.X.; Zhang, Z.L.; Li, M.; Zhang, Q.; Wang, L.; Liao, Y. Optimization and experiments of the blade group of ditching devices in rapeseed direct seeder. Trans. Chin. Soc. Agric. Eng. 2024, 40, 37–49. [Google Scholar]
- Zhang, Q.S.; Qi, T.; Ao, Q.; Shu, C.; Liao, Y.; Liao, Q. Design and experiment of rapeseed direct seeding machine with furrow opener and shallow plowing. Trans. Chin. Soc. Agric. Mach. 2023, 54, 52–63. [Google Scholar]
- Zeng, Y.; Li, J.; Li, H.C.; Zhang, Q.; Li, C.; Li, Z.; Jiang, R.; Mai, C.; Ma, Z.; He, H. Research on the ditching resistance reduction of self-excited vibrations ditching device based on MBD-DEM coupling simulation. Front. Plant Sci. 2024, 15, 1372585. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, I. A torque calculator for rotary tiller using the laws of classical mechanics. Soil Tillage Res. 2017, 165, 137–143. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, M.; Chen, W.; Yuan, D.; Wu, C.; Zhu, J. Simulation analysis and experiments for blade-soil-straw interaction under deep ploughing based on the discrete element method. Agriculture 2023, 13, 136. [Google Scholar] [CrossRef]
- Ucgul, M.; Saunders, C.; Li, P.; Lee, S.-H.; Desbiolles, J.M. Analyzing the mixing performance of a rotary spader using digital image processing and discrete element modelling (DEM). Comput. Electron. Agric. 2018, 151, 1–10. [Google Scholar] [CrossRef]
- Tekeste, M.Z.; Way, T.R.; Syed, Z.; Schafer, R.L. Modeling soil-bulldozer blade interaction using the discrete element method (DEM). J. Terramechanics 2020, 88, 41–52. [Google Scholar] [CrossRef]
- Zhang, X.A. Agricultural Machinery Design Handbook; China Agriculture Press: Beijing, China, 2007. [Google Scholar]
- Liao, Q.X.; Zhang, J.Q.; Zhang, Q.S.; Du, W.; Lin, J.; Wang, L. Design and test of rapeseed seed bed preparation device combined with parallel plow group turnbuckle and rotary tillage. Trans. Chin. Soc. Agric. Mach. 2024, 55, 190–201. [Google Scholar]
- Song, J.N.; Li, Z.H. Theoretical studies of reverse rotary tillage. J. Beijing Agric. Eng. Univ. 1990, 10, 15–22. [Google Scholar]
- Zhang, C.L.; Xu, J.; Zheng, Z.H.; Wang, W.W.; Liu, L.C.; Chen, L.Q. Three-dimensional DEM tillage simulation: Validation of a suitable contact model for a sweep tool operating in cohesion and adhesion soil. J. Terramech. 2023, 108, 59–67. [Google Scholar] [CrossRef]
- Yang, Q.Z.; Shi, L.; Shi, A.P.; He, M.; Zhao, X.; Zhang, L.; Addy, M. Determination of key soil characteristic parameters using angle of repose and direct shear stress test. Int. J. Agric. Biol. Eng. 2023, 16, 143–150. [Google Scholar] [CrossRef]
- Xiang, W.; Wu, M.L.; Lu, J.N.; Quan, W.; Ma, L.; Liu, J. Calibration of simulation physical parameters of clay loam based on soil accumulation test. Trans. Chin. Soc. Agric. Eng. 2019, 35, 116–123. [Google Scholar]
- Zhao, Z.H.; Wu, M.L.; Xie, S.P.; Luo, H.; Li, P.; Zeng, Y.; Jiang, X. Parameter calibration for the discrete element simulation of soil-preceding rice stubble and its rotary tillage trajectory. Trans. Chin. Soc. Agric. Eng. 2024, 40, 72–82. [Google Scholar]
- Zhao, Z.; Wu, M.L.; Jiang, X. A review of contact models’ properties for discrete element simulation in agricultural engineering. Agriculture 2024, 14, 238. [Google Scholar] [CrossRef]
- Zeng, Z.W.; Ma, X.; Cao, X.L.; Li, Z.; Wang, X. Critical review of applications of discrete element method in agricultural engineering. Trans. Chin. Soc. Agric. Mach. 2021, 52, 1–20. [Google Scholar]
- Xiao, M.H.; Niu, Y.; Wang, K.X.; Zhu, Y.; Zhou, J.; Ma, R. Design of self-excited vibrating rotary tiller and analysis of its performance in reducing torsion and consumption. Trans. Chin. Soc. Agric. Mach. 2022, 53, 52–63. [Google Scholar]
- Cheng, J.; Zheng, K.; Xia, J.; Liu, G.; Jiang, L.; Li, D. Analysis of adhesion between wet clay soil and rotary tillage part in paddy field based on discrete element method. Processes 2021, 9, 845. [Google Scholar] [CrossRef]
- Zeng, Y.; Chen, C.; Wu, Q. Calibration parameter of soil discrete element based on area difference method. Agriculture 2023, 13, 648. [Google Scholar] [CrossRef]
- JB/T 11908-2014; Agricultural Disc Ditching Machine. Ministry of Industry and Information Technology of the People’s Republic of China, Machine Press: Beijing, China, 2014.
- Shi, Z. Research on Lifting Foldable Double-Sided Disc-Type Orchard Ditcher. Master’s Thesis, Huazhong Agricultural University, Wuhan, China, 2019. [Google Scholar]




| Parameter | Value |
|---|---|
| Overall Dimensions (L × W × H) (mm) | 2480 × 1800 × 1600 |
| Working Width (mm) | 2480 |
| Required Power (kW) | ≥66.2 |
| Operating Speed (km/h) | 1.8–5.4 |
| Total Transmission Ratio | 3:1 |
| Max. Radius of Trapezoidal Disc (mm) | 550 |
| Ditch Profile | Trapezoidal |
| Top Width of Perimeter Ditch (mm) | 400 |
| Bottom Width of Perimeter Ditch (mm) | 200 |
| Depth of Perimeter Ditch (mm) | 400 |
| Width of Seedbed Surface (mm) | ≥1000 |
| Name | Guide Curve Type | Guide Curve Height (h/mm) | Guide Curve Opening (L/mm) | Tangent Angle Between Two End Points (ω/(°)) |
|---|---|---|---|---|
| 1KX-40 | ||||
| Rapeseed Field Perimeter Ditch Discarding Machine | Arc | 400 | 530 | 108 |
| Category | Parameter | Value |
|---|---|---|
| Steel | Density/(kg·m−3) | 7850 |
| Poisson’s ratio | 0.3 | |
| Shear modulus/(Pa) | 7 × 1010 | |
| Soil | Particle density/(kg·m−3) | 2680 |
| Poisson’s ratio | 0.38 | |
| Shear modulus/(Pa) | 1.2 × 106 | |
| JKR surface energy/(J·m2) | 12.73 | |
| Particle size/mm | 5 | |
| Soil–soil | Static friction coefficient | 0.84 |
| Rolling friction coefficient | 0.1 | |
| Collision restitution coefficient | 0.55 | |
| Soil–steel | Static friction coefficient | 0.6 |
| Rolling friction coefficient | 0.1 | |
| Collision restitution coefficient | 0.3 |
| Levels | Inner Knife Group Width/(mm) | Outer Knife Group Width/(mm) | Distance Between Inner and Outer Knife Groups/(mm) | Ditch-Cleaning Shovel Opening/(mm) |
|---|---|---|---|---|
| 1 | 140 | 200 | 100 | 530 |
| 2 | 155 | 225 | 150 | 580 |
| 3 | 170 | 250 | 200 | 630 |
| 4 | 185 | 275 | 250 | 680 |
| 5 | 200 | 300 | 300 | 730 |
| Code Value | Inner Knife Group Width/(mm) | Outer Knife Group Width/(mm) | Distance Between Inner and Outer Knife Groups/(mm) | Ditch-Cleaning Shovel Opening/(mm) |
|---|---|---|---|---|
| −1 | 140 | 200 | 100 | 530 |
| 0 | 170 | 250 | 200 | 580 |
| 1 | 200 | 300 | 300 | 630 |
| Type | Average Power Consumption of Trenching Machine/kW | |
|---|---|---|
| Field Test | Simulation Test | |
| Control Group | 34.75 ± 0.5 | 32.78 |
| Experimental Group | 28.73 ± 0.3 | 27.07 |
| Power Consumption Reduction Rate | 17.3 ± 0.5% | 17.4% |
| Type | Control Group | Experimental Group | ||
|---|---|---|---|---|
| Test 1 | Simulation 1 | Test 2 | Simulation 2 | |
| Average furrow depth/cm | 41.6 ± 0.5 | 40.5 | 41.1 ± 0.5 | 40.5 |
| Stability coefficient of furrow depth/% | 88.2 ± 1.1 | 91.3 | 95.9 ± 1.2 | 96.8 |
| Average upper top width/cm | 44.3 ± 0.6 | 42.5 | 41.7 ± 0.5 | 40.8 |
| Stability coefficient of upper top width/% | 85.7 ± 1 | 90.1 | 94.2 ± 1.1 | 95.6 |
| Average bottom width/cm | 22.8 ± 0.3 | 20.9 | 21.5 ± 0.3 | 20.3 |
| Bottom width stability coefficient/% | 89.2 ± 1.2 | 92.9 | 96.4 ± 1.3 | 97.4 |
| Average backfill thickness/cm | 4.5 ± 0.1 | 4.1 | 1.8 ± 0.1 | 1.5 |
| Backfill rate/% | 11.3 ± 0.2 | 10.3 | 4.5 ± 0.3 | 3.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Kang, Z.; Wu, M.; Zhao, Z.; Peng, Z.; Ouyang, Y.; Luo, H.; Quan, W. Design and Experiment of DEM-Based Layered Cutting–Throwing Perimeter Drainage Ditcher for Rapeseed Fields. Agriculture 2025, 15, 1706. https://doi.org/10.3390/agriculture15151706
Jiang X, Kang Z, Wu M, Zhao Z, Peng Z, Ouyang Y, Luo H, Quan W. Design and Experiment of DEM-Based Layered Cutting–Throwing Perimeter Drainage Ditcher for Rapeseed Fields. Agriculture. 2025; 15(15):1706. https://doi.org/10.3390/agriculture15151706
Chicago/Turabian StyleJiang, Xiaohu, Zijian Kang, Mingliang Wu, Zhihao Zhao, Zhuo Peng, Yiti Ouyang, Haifeng Luo, and Wei Quan. 2025. "Design and Experiment of DEM-Based Layered Cutting–Throwing Perimeter Drainage Ditcher for Rapeseed Fields" Agriculture 15, no. 15: 1706. https://doi.org/10.3390/agriculture15151706
APA StyleJiang, X., Kang, Z., Wu, M., Zhao, Z., Peng, Z., Ouyang, Y., Luo, H., & Quan, W. (2025). Design and Experiment of DEM-Based Layered Cutting–Throwing Perimeter Drainage Ditcher for Rapeseed Fields. Agriculture, 15(15), 1706. https://doi.org/10.3390/agriculture15151706




