Author Contributions
Conceptualization, H.H. and Z.L.; methodology, H.H. and Z.L.; project administration, H.H. and Z.L.; funding acquisition, H.H. and Z.L.; software, Y.Z. (Yan Zhang); validation, Y.Z. (Yan Zhang); formal analysis, Y.Z. (Yan Zhang); writing—original draft, Y.Z. (Yan Zhang); writing—review and editing, G.H., B.S., H.Y., Z.F., Y.Z. (Yangfan Zhuang), H.T. and L.L.; supervision, G.H., B.S., H.Y., Z.F., Y.Z. (Yangfan Zhuang), H.T. and L.L. All authors have read and agreed to the published version of the manuscript.
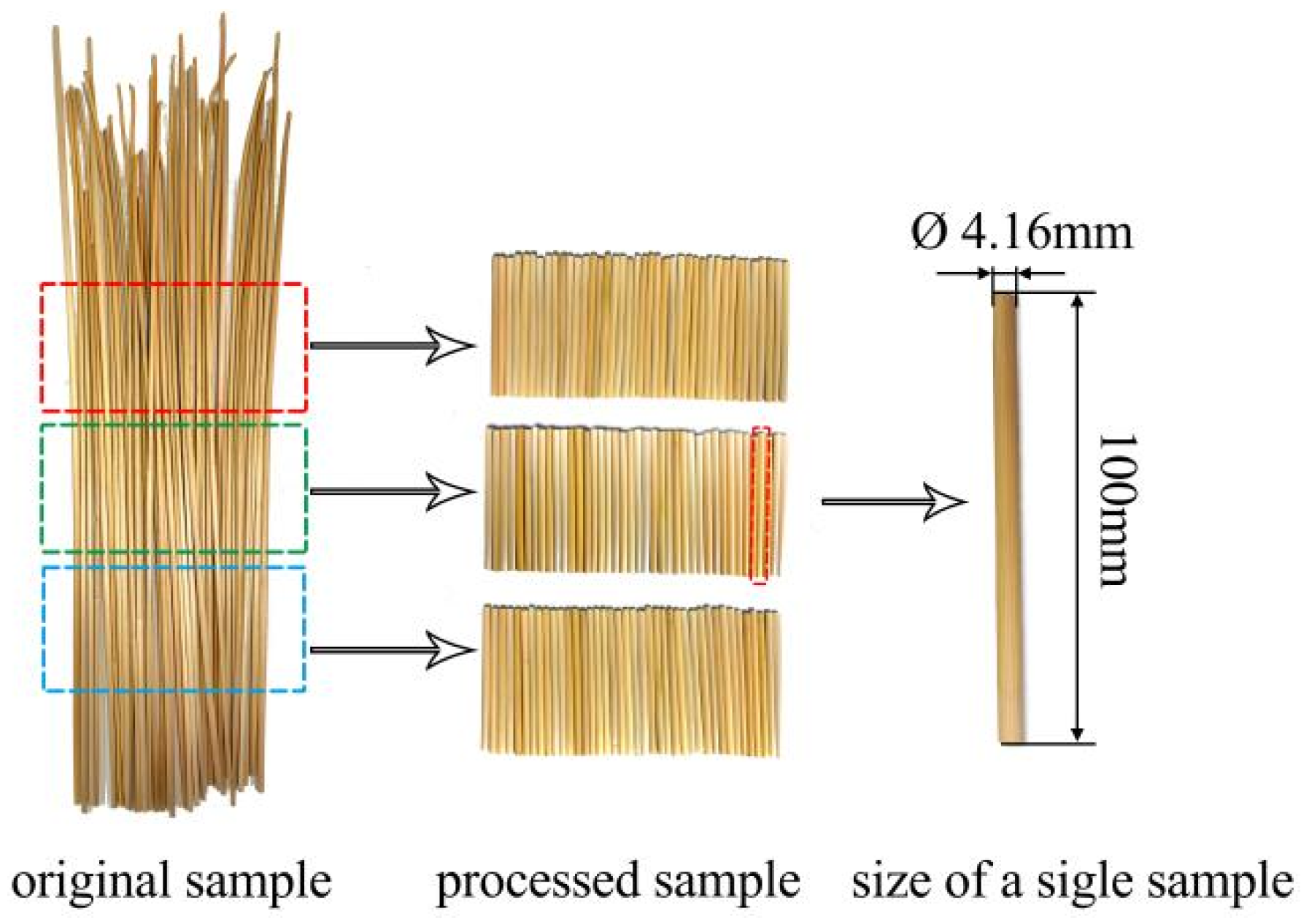
Figure 1.
Wheat straw selection and treatment.
Figure 1.
Wheat straw selection and treatment.
Figure 2.
Geometric size measurement of wheat straw: (a) determination of outer diameter of wheat straw; (b) determination of wall thickness.
Figure 2.
Geometric size measurement of wheat straw: (a) determination of outer diameter of wheat straw; (b) determination of wall thickness.
Figure 3.
The frequency distribution of geometric characteristics of wheat straw: (a) outer diameter distribution; (b) wall thickness distribution.
Figure 3.
The frequency distribution of geometric characteristics of wheat straw: (a) outer diameter distribution; (b) wall thickness distribution.
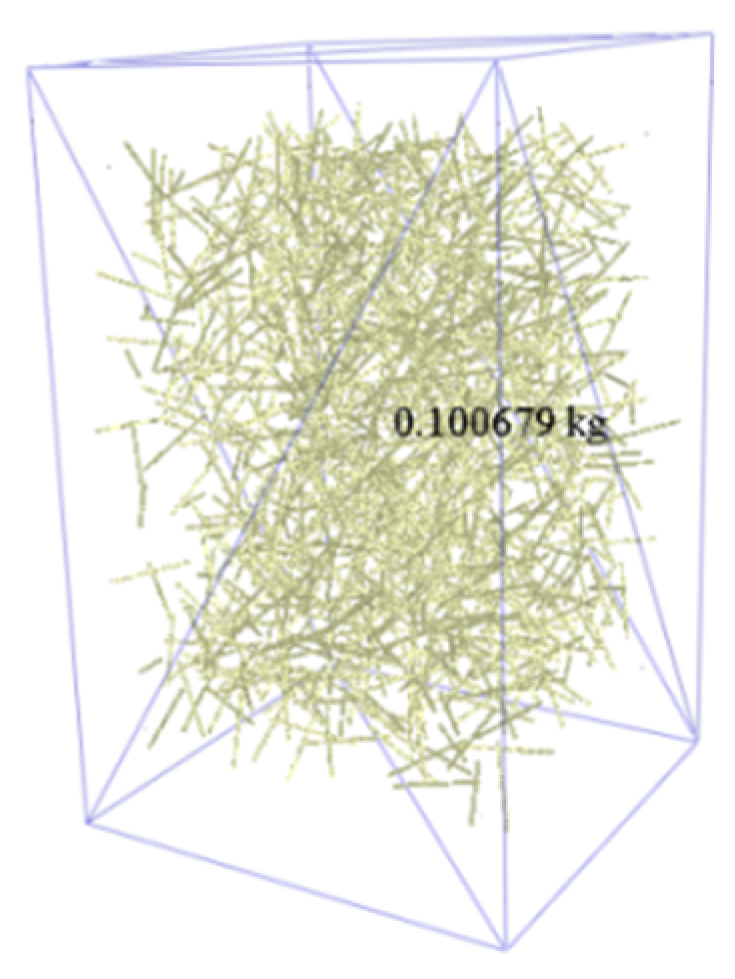
Figure 4.
Mass determination of wheat straw.
Figure 4.
Mass determination of wheat straw.
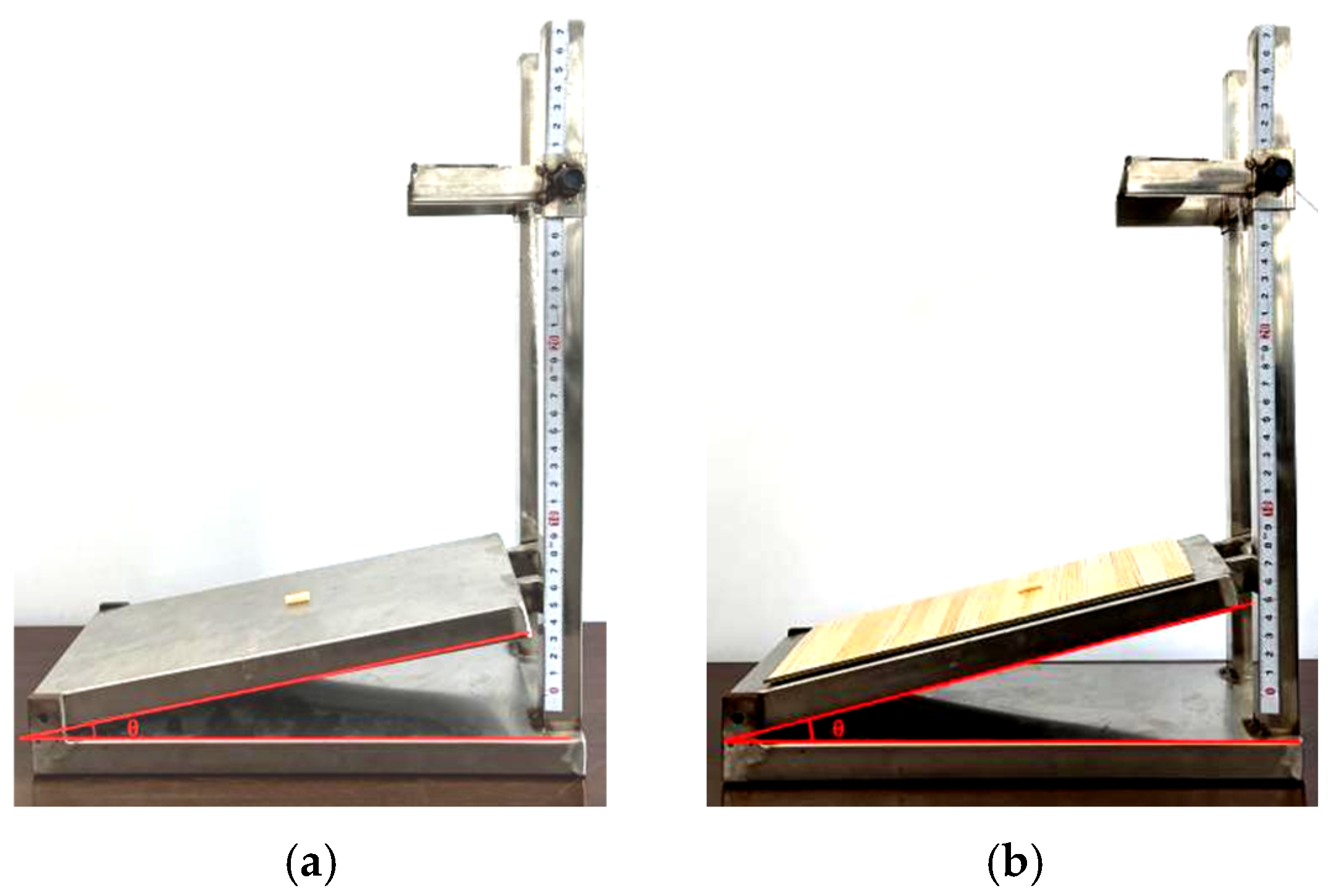
Figure 5.
The test platform for the frictional properties: (a) the coefficients of static friction between wheat straw and steel; (b) the coefficients of static friction between wheat straw.
Figure 5.
The test platform for the frictional properties: (a) the coefficients of static friction between wheat straw and steel; (b) the coefficients of static friction between wheat straw.
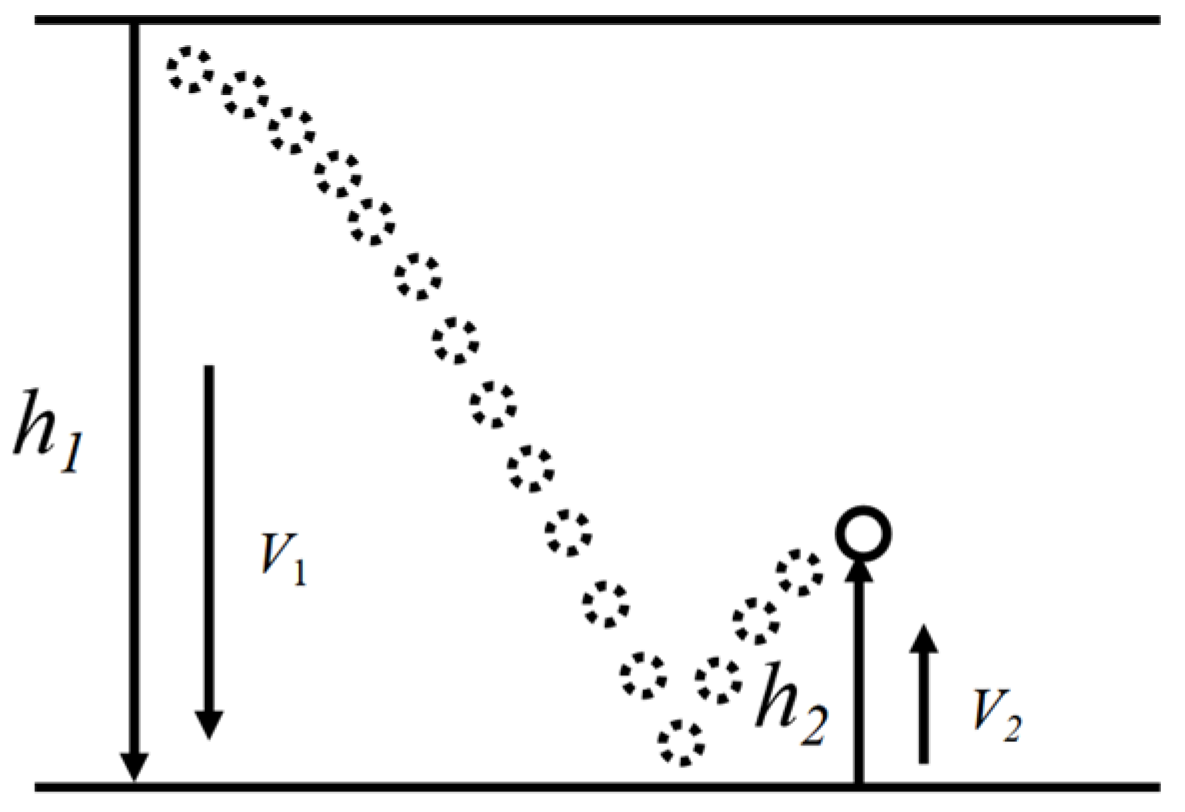
Figure 6.
Determination principle of coefficient of restitution.
Figure 6.
Determination principle of coefficient of restitution.
Figure 7.
Test measurement of the AOR: (a) the test platform for measuring the AOR; (b) single-side images of the pile of wheat straw; (c) images of grey-scale; (d) binarization diagram; (e) fitted lines.
Figure 7.
Test measurement of the AOR: (a) the test platform for measuring the AOR; (b) single-side images of the pile of wheat straw; (c) images of grey-scale; (d) binarization diagram; (e) fitted lines.
Figure 8.
Device of extrusion tests for wheat straw. 1. Universal testing machine; 2. Base plate for compression; 3. Top plate for compression; 4. PC data acquisition device; 5. Camera.
Figure 8.
Device of extrusion tests for wheat straw. 1. Universal testing machine; 2. Base plate for compression; 3. Top plate for compression; 4. PC data acquisition device; 5. Camera.
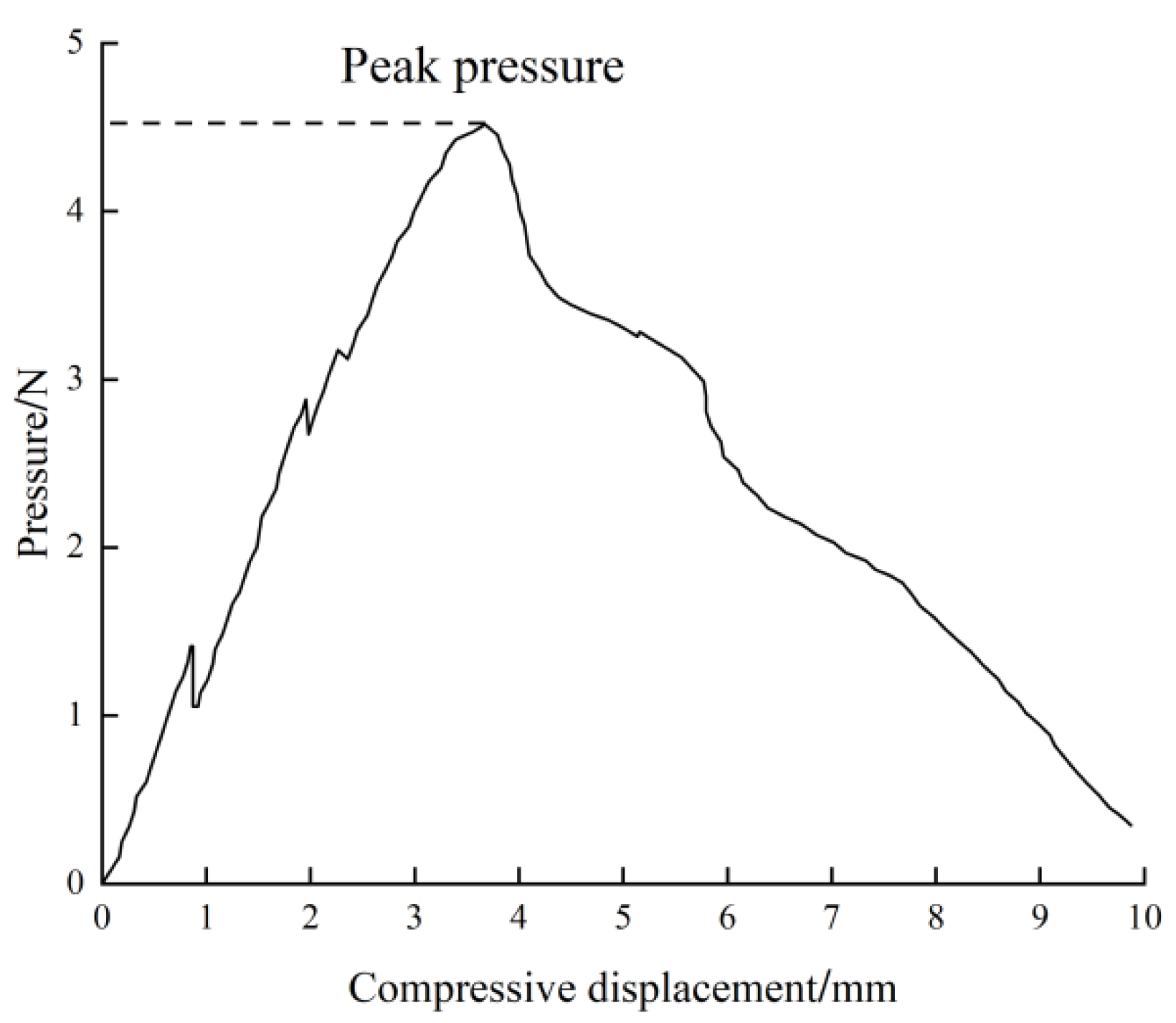
Figure 9.
Extrusion test image: (a) relationship diagram of extrusion force-compressive displacement; (b) the stage of elastic deformation; (c) the early and middle stage of plastic deformation (four pieces); (d) late plastic deformation (flattened).
Figure 9.
Extrusion test image: (a) relationship diagram of extrusion force-compressive displacement; (b) the stage of elastic deformation; (c) the early and middle stage of plastic deformation (four pieces); (d) late plastic deformation (flattened).
Figure 10.
Bending tests device. 1. Universal testing machine; 2. Extrusion tool; 3. Wheat straw; 4. U-shaped groove; 5. The bottom fixing base.
Figure 10.
Bending tests device. 1. Universal testing machine; 2. Extrusion tool; 3. Wheat straw; 4. U-shaped groove; 5. The bottom fixing base.
Figure 11.
Relationship diagram of bending pressure-compressive displacement.
Figure 11.
Relationship diagram of bending pressure-compressive displacement.
Figure 12.
Discrete element simulation model of wheat straw: (a) the interleaved arrangement of type-P1 fiber monomer and type-P2 fiber monomer and the two Bonding V2 generated between them; (b) key size description of wheat straw model.
Figure 12.
Discrete element simulation model of wheat straw: (a) the interleaved arrangement of type-P1 fiber monomer and type-P2 fiber monomer and the two Bonding V2 generated between them; (b) key size description of wheat straw model.
Figure 13.
Mass statistics of wheat straw model under 104.674 m length.
Figure 13.
Mass statistics of wheat straw model under 104.674 m length.
Figure 14.
Simulation test model of AOR.
Figure 14.
Simulation test model of AOR.
Figure 15.
Response surface diagrams for BBD tests of the AOR. (a) The influence of the coefficients of static friction between wheat straw and steel and the rolling friction between wheat straws on AOR. (b) The influence of the static friction between wheat straws and the static friction between wheat straw and steel on AOR. (c) The influence of the static friction between wheat straws and the rolling friction between wheat straws on the impurity rate.
Figure 15.
Response surface diagrams for BBD tests of the AOR. (a) The influence of the coefficients of static friction between wheat straw and steel and the rolling friction between wheat straws on AOR. (b) The influence of the static friction between wheat straws and the static friction between wheat straw and steel on AOR. (c) The influence of the static friction between wheat straws and the rolling friction between wheat straws on the impurity rate.
Figure 16.
Extrusion simulation test: (a) extrusion simulation test model; (b) wheat straw deformation in different extrusion stages.
Figure 16.
Extrusion simulation test: (a) extrusion simulation test model; (b) wheat straw deformation in different extrusion stages.
Figure 17.
Bending simulation test model.
Figure 17.
Bending simulation test model.
Figure 18.
Compression verification test of wheat straw group: (a) cubic cavity simulation model; (b) compression and bending posture of wheat straw.
Figure 18.
Compression verification test of wheat straw group: (a) cubic cavity simulation model; (b) compression and bending posture of wheat straw.
Table 1.
Geometric size characteristics of wheat straw.
Table 1.
Geometric size characteristics of wheat straw.
| Parameter | Min Value | Max Value | Average | Standard Deviation |
|---|
Outer diameter
D/mm | 3.30 | 4.70 | 4.045 | 0.2913 |
| Wall thickness h/mm | 0.65 | 1.05 | 0.416 | 0.0756 |
Table 2.
The results of total length of 100 g wheat straw.
Table 2.
The results of total length of 100 g wheat straw.
| Test Number | Length of 100 g Wheat Straw/m |
|---|
| 1 | 102.650 |
| 2 | 107.690 |
| 3 | 100.740 |
| 4 | 104.033 |
| 5 | 108.258 |
| Average | 104.674 |
Table 3.
Measurement result of the AOR.
Table 3.
Measurement result of the AOR.
| Index | Test Number |
|---|
| 1 | 2 | 3 | 4 | 5 |
|---|
| AOR/° | 18.05 | 18.28 | 18.70 | 18.32 | 18.40 |
| Average | 18.35° |
| Standard Deviation | 0.2 |
Table 4.
Value of peak extrusion force.
Table 4.
Value of peak extrusion force.
| Test Number | Peak/N | Test Number | Peak/N | Test Number | Peak/N | Test Number | Peak/N | Test Number | Peak/N |
|---|
| 1 | 23.66 | 2 | 20.58 | 3 | 28.41 | 4 | 21.55 | 5 | 24.32 |
| 6 | 26.07 | 7 | 20.45 | 8 | 21.89 | 9 | 28.34 | 10 | 24.53 |
| Average | 23.98 N |
Table 5.
Value of peak bending pressure.
Table 5.
Value of peak bending pressure.
| Test Number | Peak/N | Test Number | Peak/N | Test Number | Peak/N | Test Number | Peak/N | Test Number | Peak/N |
|---|
| 1 | 3.24 | 2 | 4.46 | 3 | 4.78 | 4 | 3.36 | 5 | 3.04 |
| 6 | 4.12 | 7 | 3.92 | 8 | 3.76 | 9 | 3.08 | 10 | 4.08 |
| Average | 3.784 N |
Table 6.
Simulation parameter setting of AOR.
Table 6.
Simulation parameter setting of AOR.
| Parameters | Values |
|---|
| Density of wheat straw ρ1/(kg·m−3) | 300 |
| Density of steel ρ2/(kg·m−3) | 7850 |
| Poisson’s ratio of wheat straw µ1 | 0.30 |
| Poisson’s ratio of steel µ2 | 0.30 |
| Shear modulus of wheat straw G1/Pa | 4,000,000 |
| Shear modulus of steel G1/Pa | 4,000,000 |
| Straw-steel static friction A | 0.13~0.53 |
| Straw-steel rolling friction B | 0.043~0.143 |
| Straw-steel restitution coefficient C | 0.382~0.582 |
| Straw-straw static friction D | 0.15~0.55 |
| Straw-straw rolling friction E | 0.060~0.160 |
| Straw-straw restitution coefficient F | 0.379~0.579 |
Table 7.
The levels and codes of Plackett–Burman test.
Table 7.
The levels and codes of Plackett–Burman test.
| Factors | Levels |
|---|
| −1 | 0 | 1 |
|---|
| A | 0.13 | 0.33 | 0.53 |
| B | 0.043 | 0.093 | 0.143 |
| C | 0.382 | 0.482 | 0.582 |
| D | 0.15 | 0.35 | 0.55 |
| E | 0.060 | 0.110 | 0.160 |
| F | 0.379 | 0.479 | 0.579 |
Table 8.
Plackett–Burman experimental design and results.
Table 8.
Plackett–Burman experimental design and results.
| Test Number | Test Factors | Y/° |
|---|
| A | B | C | D | E | F |
|---|
| 1 | −1 | 1 | 1 | −1 | 1 | 1 | 9.50 |
| 2 | 1 | −1 | −1 | −1 | 1 | −1 | 19.25 |
| 3 | −1 | −1 | −1 | 1 | −1 | 1 | 18.25 |
| 4 | −1 | 1 | 1 | 1 | −1 | −1 | 19.00 |
| 5 | 1 | 1 | 1 | −1 | −1 | −1 | 17.50 |
| 6 | 1 | 1 | −1 | −1 | −1 | 1 | 17.50 |
| 7 | 1 | −1 | 1 | 1 | −1 | 1 | 29.00 |
| 8 | −1 | −1 | −1 | −1 | −1 | −1 | 9.75 |
| 9 | −1 | −1 | 1 | −1 | 1 | 1 | 10.00 |
| 10 | −1 | 1 | −1 | 1 | 1 | −1 | 23.75 |
| 11 | 1 | 1 | −1 | 1 | 1 | 1 | 32.75 |
| 12 | 1 | −1 | 1 | 1 | 1 | −1 | 30.75 |
Table 9.
Significance analysis of test parameters.
Table 9.
Significance analysis of test parameters.
| Parameters | DOF | Sum of Squares | F-Value | p-Value |
|---|
| Model | 6 | 116.19 | 74.96 | <0.0001 ** |
| A | 1 | 266.02 | 171.63 | <0.0001 ** |
| B | 1 | 0.7500 | 0.4839 | 0.5177 |
| C | 1 | 2.52 | 1.63 | 0.2582 |
| D | 1 | 408.33 | 263.44 | <0.0001 ** |
| E | 1 | 18.75 | 12.10 | 0.0177 * |
| F | 1 | 0.7500 | 0.4839 | 0.5177 |
Table 10.
The levels and codes of BBD test parameters.
Table 10.
The levels and codes of BBD test parameters.
| Parameters | Levels |
|---|
| −1 | 0 | 1 |
|---|
| A | 0.18 | 0.28 | 0.38 |
| D | 0.20 | 0.30 | 0.40 |
| E | 0.060 | 0.110 | 0.160 |
Table 11.
Results of AOR in BBD test.
Table 11.
Results of AOR in BBD test.
| Test Number | Test Factors | Y2/° |
|---|
| A | D | E |
|---|
| 1 | 0.18 | 0.3 | 0.14 | 20.100 |
| 2 | 0.28 | 0.4 | 0.08 | 29.450 |
| 3 | 0.28 | 0.2 | 0.14 | 17.250 |
| 4 | 0.28 | 0.3 | 0.11 | 23.490 |
| 5 | 0.28 | 0.3 | 0.11 | 21.825 |
| 6 | 0.28 | 0.4 | 0.14 | 26.025 |
| 7 | 0.38 | 0.2 | 0.11 | 20.500 |
| 8 | 0.18 | 0.2 | 0.11 | 14.900 |
| 9 | 0.28 | 0.3 | 0.11 | 23.500 |
| 10 | 0.38 | 0.4 | 0.11 | 26.800 |
| 11 | 0.28 | 0.3 | 0.11 | 22.300 |
| 12 | 0.28 | 0.2 | 0.08 | 16.875 |
| 13 | 0.18 | 0.3 | 0.08 | 19.825 |
| 14 | 0.38 | 0.3 | 0.14 | 23.800 |
| 15 | 0.28 | 0.3 | 0.11 | 22.450 |
| 16 | 0.38 | 0.3 | 0.08 | 22.500 |
| 17 | 0.18 | 0.4 | 0.11 | 26.425 |
Table 12.
Analysis of variance of BBD-RSM optimization tests for AOR.
Table 12.
Analysis of variance of BBD-RSM optimization tests for AOR.
| Source of Variation | DOF | Mean Square | F-Value | p-Value |
|---|
| Model | 3 | 70.39 | 45.04 | <0.0001 ** |
| A | 1 | 19.07 | 12.2 | 0.004 ** |
| D | 1 | 191.84 | 122.76 | <0.0001 ** |
| E | 1 | 0.272 | 0.174 | 0.6834 |
| Residual | 13 | 1.56 | | |
| Lack-of-fit | 9 | 2.01 | 3.57 | 0.1166 |
| Pure error | 4 | 0.5628 | | |
| Cor total | 16 | | | |
Table 13.
Simulation parameter setting of extrusion test for wheat straw.
Table 13.
Simulation parameter setting of extrusion test for wheat straw.
| Parameters | Values |
|---|
| A | 0.271 |
| B | 0.093 |
| C | 0.482 |
| D | 0.227 |
| E | 0.136 |
| F | 0.479 |
| contact radius/mm | 0.260 |
| Bonding V2-B1 | The normal stiffness per unit area H2/(N/m3) | 3.0 × 1011~5.0 × 1011 |
| The shear stiffness per unit area I2/(N/m3) | 1.1 × 1013~2.1 × 1013 |
| The normal strength J2/Pa | 6.0 × 1010~1.2 × 1011 |
| The shear strength K2/Pa | 1.6 × 1012~2.8 × 1012 |
| Bonded Disk Scale | 3 |
| Bonding V2-B2 | The normal stiffness per unit area H3/(N/m3) | 1.0 × 1012 |
| The shear stiffness per unit area I3/(N/m3) | 7.5 × 1011 |
| The normal strength J3/Pa | 9.0 × 109 |
| The shear strength K3/Pa | 1.2 × 109 |
| Bonded Disk Scale | 1 |
Table 14.
The levels and codes of BBD test parameters for Bonding V2-B1 model.
Table 14.
The levels and codes of BBD test parameters for Bonding V2-B1 model.
| Parameters of Bonding V2-B1 | Levels |
|---|
| −1 | 0 | 1 |
|---|
| H2 | 3.0 × 1011 | 4.0 × 1011 | 5.0 × 1011 |
| I2 | 1.1 × 1013 | 1.6 × 1013 | 2.1 × 1013 |
| J2 | 6.0 × 1010 | 9.0 × 1010 | 1.2 × 1011 |
| K2 | 1.6 × 1012 | 2.2 × 1012 | 2.8 × 1012 |
Table 15.
Design and results of BBD extrusion test.
Table 15.
Design and results of BBD extrusion test.
| Test Number | Test Factors | Y4/N |
|---|
| H2 | I2 | J2 | K2 |
|---|
| 1 | 5.00 × 1011 | 1.60 × 1013 | 6.00 × 1010 | 2.20 × 1012 | 25.00 |
| 2 | 3.00 × 1011 | 1.60 × 1013 | 1.20 × 1011 | 2.20 × 1012 | 26.25 |
| 3 | 4.00 × 1011 | 2.10 × 1013 | 9.00 × 1010 | 1.60 × 1012 | 32.70 |
| 4 | 4.00 × 1011 | 1.60 × 1013 | 6.00 × 1010 | 1.60 × 1012 | 23.00 |
| 5 | 5.00 × 1011 | 2.10 × 1013 | 9.00 × 1010 | 2.20 × 1012 | 29.75 |
| 6 | 5.00 × 1011 | 1.60 × 1013 | 9.00 × 1010 | 2.80 × 1012 | 27.35 |
| 7 | 5.00 × 1011 | 1.60 × 1013 | 1.20 × 1011 | 2.20 × 1012 | 25.50 |
| 8 | 4.00 × 1011 | 1.60 × 1013 | 1.20 × 1011 | 1.60 × 1012 | 26.45 |
| 9 | 3.00 × 1011 | 2.10 × 1013 | 9.00 × 1010 | 2.20 × 1012 | 31.00 |
| 10 | 5.00 × 1011 | 1.10 × 1013 | 9.00 × 1010 | 2.20 × 1012 | 20.43 |
| 11 | 4.00 × 1011 | 1.60 × 1013 | 9.00 × 1010 | 2.20 × 1012 | 25.15 |
| 12 | 4.00 × 1011 | 1.60 × 1013 | 6.00 × 1010 | 2.80 × 1012 | 22.55 |
| 13 | 4.00 × 1011 | 1.60 × 1013 | 1.20 × 1011 | 2.80 × 1012 | 25.40 |
| 14 | 4.00 × 1011 | 1.10 × 1013 | 1.20 × 1011 | 2.20 × 1012 | 20.20 |
| 15 | 4.00 × 1011 | 1.10 × 1013 | 9.00 × 1010 | 2.80 × 1012 | 21.10 |
| 16 | 4.00 × 1011 | 2.10 × 1013 | 9.00 × 1010 | 2.80 × 1012 | 33.95 |
| 17 | 4.00 × 1011 | 1.10 × 1013 | 9.00 × 1010 | 1.60 × 1012 | 21.00 |
| 18 | 4.00 × 1011 | 1.60 × 1013 | 9.00 × 1010 | 2.20 × 1012 | 23.70 |
| 19 | 3.00 × 1011 | 1.60 × 1013 | 9.00 × 1010 | 1.60 × 1012 | 26.95 |
| 20 | 3.00 × 1011 | 1.60 × 1013 | 9.00 × 1010 | 2.80 × 1012 | 25.95 |
| 21 | 4.00 × 1011 | 1.60 × 1013 | 9.00 × 1010 | 2.20 × 1012 | 25.05 |
| 22 | 4.00 × 1011 | 2.10 × 1013 | 6.00 × 1010 | 2.20 × 1012 | 30.35 |
| 23 | 3.00 × 1011 | 1.10 × 1013 | 9.00 × 1010 | 2.20 × 1012 | 18.29 |
| 24 | 3.00 × 1011 | 1.60 × 1013 | 6.00 × 1010 | 2.20 × 1012 | 24.40 |
| 25 | 4.00 × 1011 | 1.10 × 1013 | 6.00 × 1010 | 2.20 × 1012 | 20.25 |
| 26 | 4.00 × 1011 | 1.60 × 1013 | 9.00 × 1010 | 2.20 × 1012 | 25.10 |
| 27 | 4.00 × 1011 | 1.60 × 1013 | 9.00 × 1010 | 2.20 × 1012 | 24.30 |
| 28 | 5.00 × 1011 | 1.60 × 1013 | 9.00 × 1010 | 1.60 × 1012 | 25.80 |
| 29 | 4.00 × 1011 | 2.10 × 1013 | 1.20 × 1011 | 2.20 × 1012 | 31.10 |
Table 16.
Analysis of variance of BBD-RSM extrusion tests.
Table 16.
Analysis of variance of BBD-RSM extrusion tests.
| Source of Variation | DOF | Mean Square | F-Value | p-Value |
|---|
| Model | 4 | 96.99 | 57.88 | <0.0001 ** |
| H2 | 1 | 0.0817 | 0.0487 | 0.8271 |
| I2 | 1 | 380.59 | 227.13 | <0.0001 ** |
| J2 | 1 | 7.29 | 4.35 | 0.0479 * |
| K2 | 1 | 0.0133 | 0.008 | 0.9297 |
| Residual | 24 | 1.68 | | |
| Lack-of-fit | 20 | 1.93 | 4.71 | 0.0714 |
| Pure error | 4 | 0.4093 | | |
| Cor total | 28 | | | |
Table 17.
Simulation parameter setting of bending test.
Table 17.
Simulation parameter setting of bending test.
| Parameters | Values |
|---|
| Bonding V2-B1 | The normal stiffness per unit area H2/(N/m3) | 4.00 × 1011 |
| The shear stiffness per unit area I2/(N/m3) | 1.53 × 1013 |
| The normal strength J2/Pa | 6.27 × 1010 |
| The shear strength K2/Pa | 2.20 × 1012 |
| Bonding V2-B2 | The normal stiffness per unit area H3/(N/m3) | 5.0 × 1011~1.5 × 1012 |
| The shear stiffness per unit area I3/(N/m3) | 5.0 × 1011~1.0 × 1012 |
| The normal strength J3/Pa | 6.0 × 109~1.2 × 1010 |
| The shear strength K3/Pa | 8.0 × 108~1.6 × 109 |
Table 18.
The levels and codes of BBD test parameters for Bonding V2-B2 model.
Table 18.
The levels and codes of BBD test parameters for Bonding V2-B2 model.
| Parameters of Bonding V2-B2 Model | Levels |
|---|
| −1 | 0 | 1 |
|---|
| H3 | 5.0 × 1011 | 1.0 × 1012 | 1.5 × 1012 |
| I3 | 5.0 × 1011 | 7.5 × 1011 | 1.0 × 1012 |
| J3 | 6.0 × 109 | 9.0 × 109 | 1.2 × 1010 |
| K3 | 8.0 × 108 | 1.2 × 109 | 1.6 × 109 |
Table 19.
Design and results of BBD-RSM bending tests.
Table 19.
Design and results of BBD-RSM bending tests.
| Test Number | Test Factors | Y5/N |
|---|
| H3 | I3 | J3 | K3 |
|---|
| 1 | 1.00 × 1012 | 7.50 × 1011 | 1.20 × 1010 | 8.00 × 108 | 3.63 |
| 2 | 1.50 × 1012 | 1.00 × 1012 | 9.00 × 109 | 1.20 × 109 | 4.08 |
| 3 | 1.00 × 1012 | 5.00 × 1011 | 6.00 × 109 | 1.20 × 109 | 3.34 |
| 4 | 1.00 × 1012 | 1.00 × 1012 | 1.20 × 1010 | 1.20 × 109 | 3.50 |
| 5 | 1.50 × 1012 | 7.50 × 1011 | 9.00 × 109 | 8.00 × 108 | 4.09 |
| 6 | 1.00 × 1012 | 7.50 × 1011 | 9.00 × 109 | 1.20 × 109 | 3.50 |
| 7 | 1.00 × 1012 | 7.50 × 1011 | 9.00 × 109 | 1.20 × 109 | 3.50 |
| 8 | 1.50 × 1012 | 7.50 × 1011 | 1.20 × 1010 | 1.20 × 109 | 4.80 |
| 9 | 1.50 × 1012 | 7.50 × 1011 | 9.00 × 109 | 1.60 × 109 | 4.19 |
| 10 | 1.50 × 1012 | 5.00 × 1011 | 9.00 × 109 | 1.20 × 109 | 4.36 |
| 11 | 1.00 × 1012 | 5.00 × 1011 | 9.00 × 109 | 1.60 × 109 | 3.59 |
| 12 | 1.00 × 1012 | 1.00 × 1012 | 9.00 × 109 | 8.00 × 108 | 3.36 |
| 13 | 1.00 × 1012 | 7.50 × 1011 | 9.00 × 109 | 1.20 × 109 | 3.49 |
| 14 | 5.00 × 1011 | 7.50 × 1011 | 9.00 × 109 | 1.60 × 109 | 2.53 |
| 15 | 5.00 × 1011 | 1.00 × 1012 | 9.00 × 109 | 1.20 × 109 | 2.97 |
| 16 | 1.00 × 1012 | 7.50 × 1011 | 6.00 × 109 | 1.60 × 109 | 3.57 |
| 17 | 1.00 × 1012 | 7.50 × 1011 | 9.00 × 109 | 1.20 × 109 | 3.51 |
| 18 | 1.00 × 1012 | 5.00 × 1011 | 1.20 × 1010 | 1.20 × 109 | 3.90 |
| 19 | 1.00 × 1012 | 5.00 × 1011 | 9.00 × 109 | 8.00 × 108 | 3.24 |
| 20 | 1.00 × 1012 | 1.00 × 1012 | 6.00 × 109 | 1.20 × 109 | 3.47 |
| 21 | 1.00 × 1012 | 1.00 × 1012 | 9.00 × 109 | 1.60 × 109 | 3.42 |
| 22 | 1.00 × 1012 | 7.50 × 1011 | 1.20 × 1010 | 1.60 × 109 | 3.66 |
| 23 | 5.00 × 1011 | 7.50 × 1011 | 9.00 × 109 | 8.00 × 108 | 2.78 |
| 24 | 1.00 × 1012 | 7.50 × 1011 | 6.00 × 109 | 8.00 × 108 | 3.75 |
| 25 | 5.00 × 1011 | 5.00 × 1011 | 9.00 × 109 | 1.20 × 109 | 2.67 |
| 26 | 1.00 × 1012 | 7.50 × 1011 | 9.00 × 109 | 1.20 × 109 | 3.33 |
| 27 | 1.50 × 1012 | 7.50 × 1011 | 6.00 × 109 | 1.20 × 109 | 4.10 |
| 28 | 5.00 × 1011 | 7.50 × 1011 | 6.00 × 109 | 1.20 × 109 | 2.72 |
| 29 | 5.00 × 1011 | 7.50 × 1011 | 1.20 × 1010 | 1.20 × 109 | 2.76 |
Table 20.
Analysis of variance of BBD-RSM bending tests.
Table 20.
Analysis of variance of BBD-RSM bending tests.
| Source of Variation | DOF | Mean Square | F-Value | p-Value |
|---|
| Model | 14 | 0.5488 | 27.78 | <0.0001 ** |
| H3 | 1 | 7.04 | 356.23 | <0.0001 ** |
| I3 | 1 | 0.0075 | 0.3796 | 0.5477 |
| J3 | 1 | 0.1408 | 7.13 | 0.0183 * |
| K3 | 1 | 0.001 | 0.051 | 0.8245 |
| H3I3 | 1 | 0.0841 | 4.26 | 0.0582 |
| H3J3 | 1 | 0.1089 | 5.51 | 0.0341 * |
| H3K3 | 1 | 0.0306 | 1.55 | 0.2336 |
| I3J3 | 1 | 0.0702 | 3.55 | 0.0803 |
| I3K3 | 1 | 0.021 | 1.06 | 0.3198 |
| J3K3 | 1 | 0.011 | 0.558 | 0.4674 |
| H32 | 1 | 0.0001 | 0.0035 | 0.9539 |
| I32 | 1 | 0.0016 | 0.0789 | 0.7829 |
| J32 | 1 | 0.1402 | 7.09 | 0.0185 * |
| K32 | 1 | 0.0046 | 0.2349 | 0.6354 |
| Residual | 14 | 0.0198 | | |
| Lack-of-fit | 10 | 0.0253 | 4.34 | 0.0848 |
| Pure error | 4 | 0.0058 | | |
| Cor total | 28 | | | |
Table 21.
Determination results of verification test.
Table 21.
Determination results of verification test.
| Times | Test Indexes |
|---|
| Peak Extrusion Force/N | Peak Bending Pressure/N |
|---|
| 1 | 22.70 | 4.31 |
| 2 | 23.40 | 3.95 |
| 3 | 23.50 | 3.50 |
| Average | 23.20 | 3.92 |