Design and Experimentation of Comb-Spiral Impact Harvesting Device for Camellia oleifera Fruit
Abstract
1. Introduction
2. Materials and Methods
2.1. Camellia oleifera Fruit and Flower Bud Material
2.2. Overall Structure and Working Principle
2.3. Design of Key Components
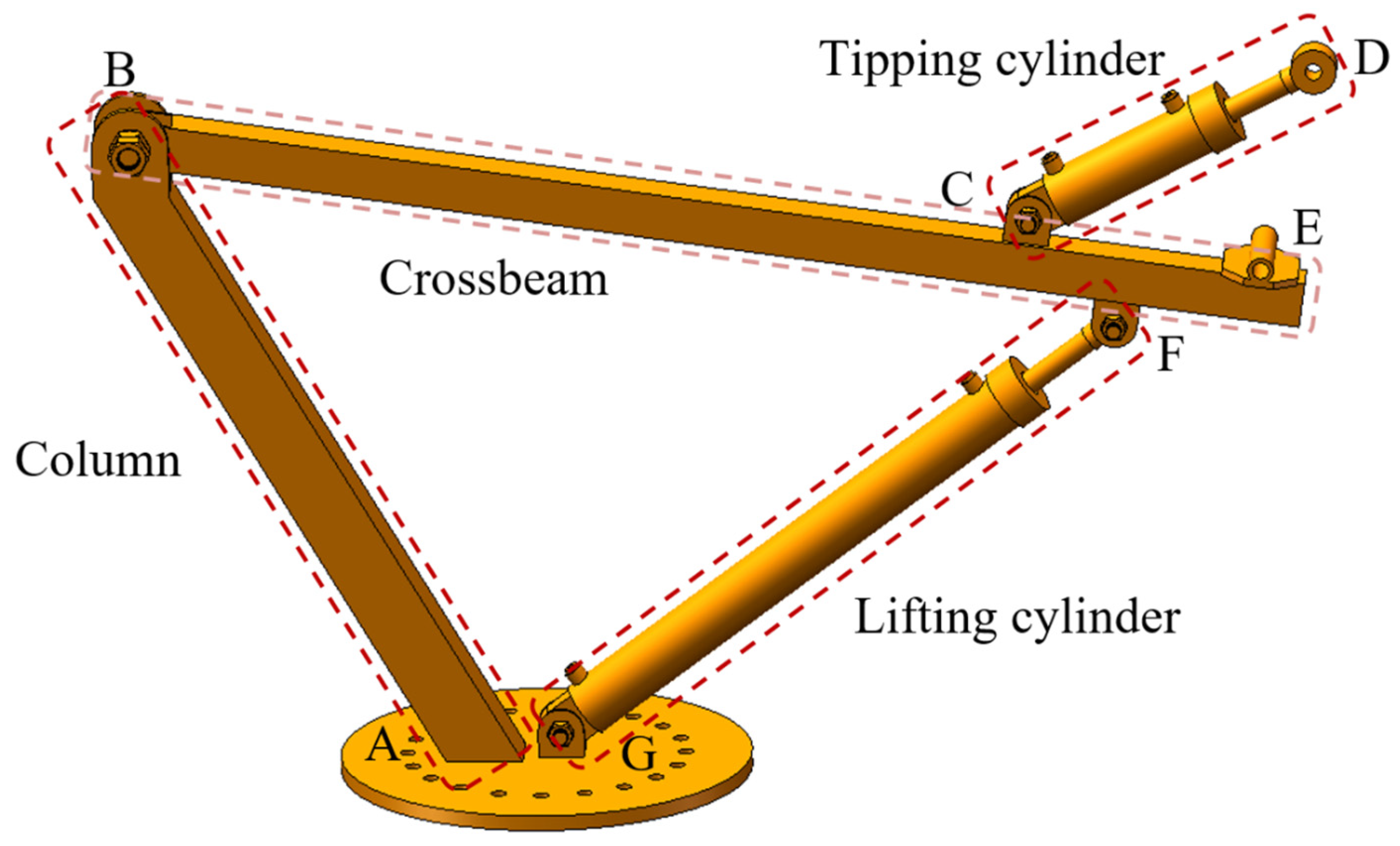
2.3.1. Design of the Lifting Mechanism
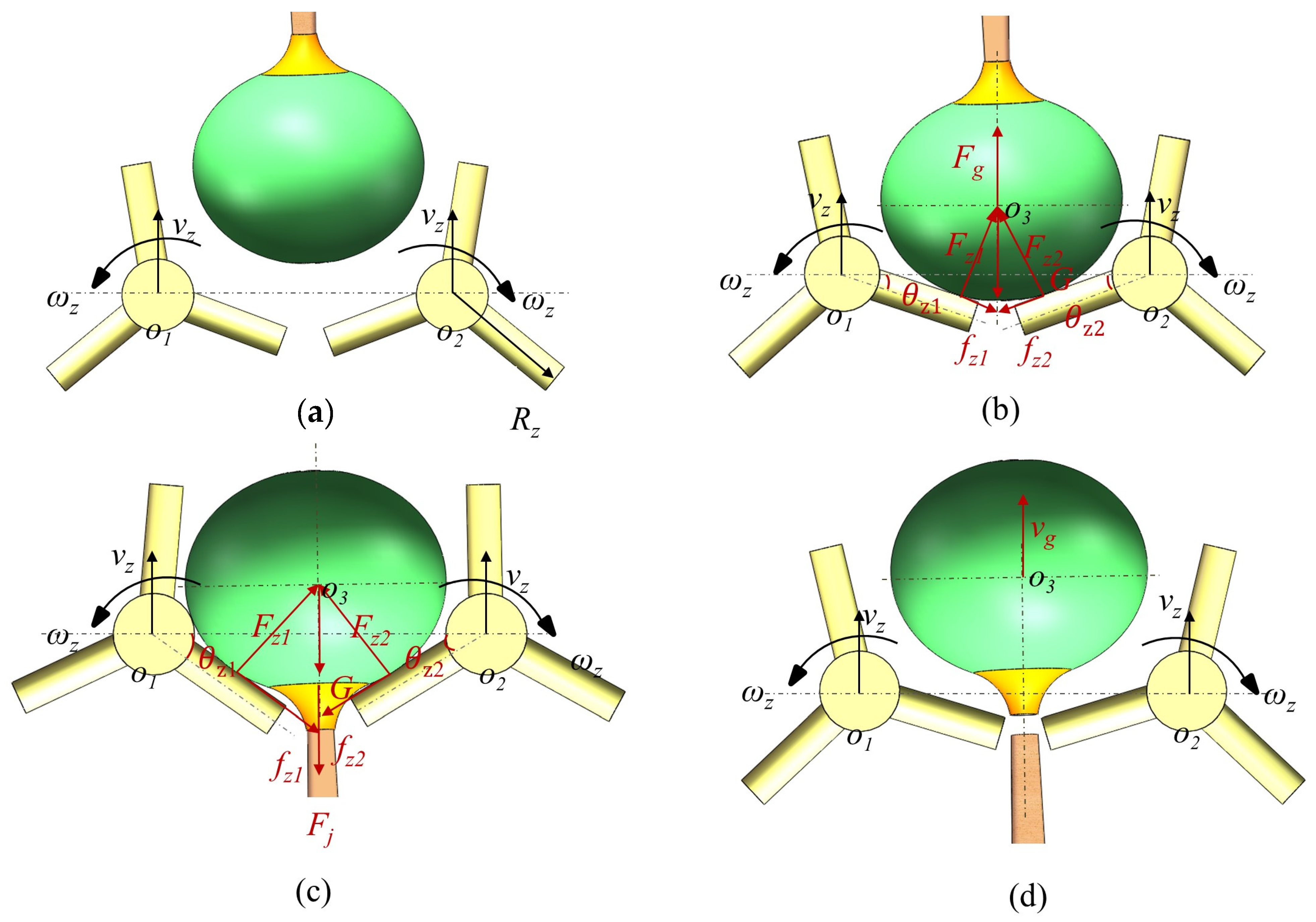
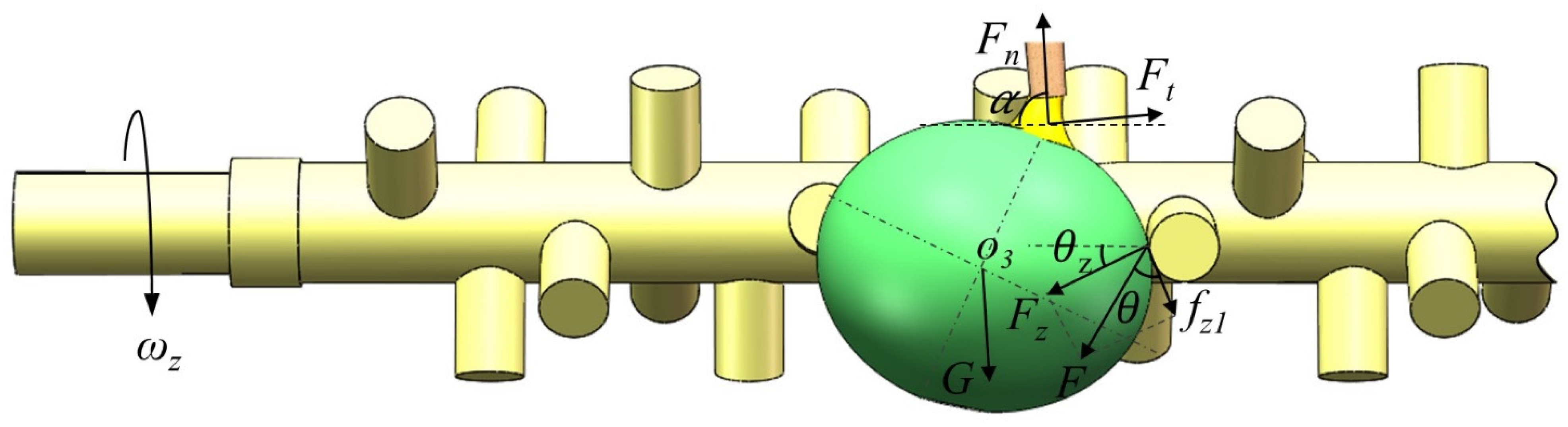
2.3.2. Design of Picking Finger
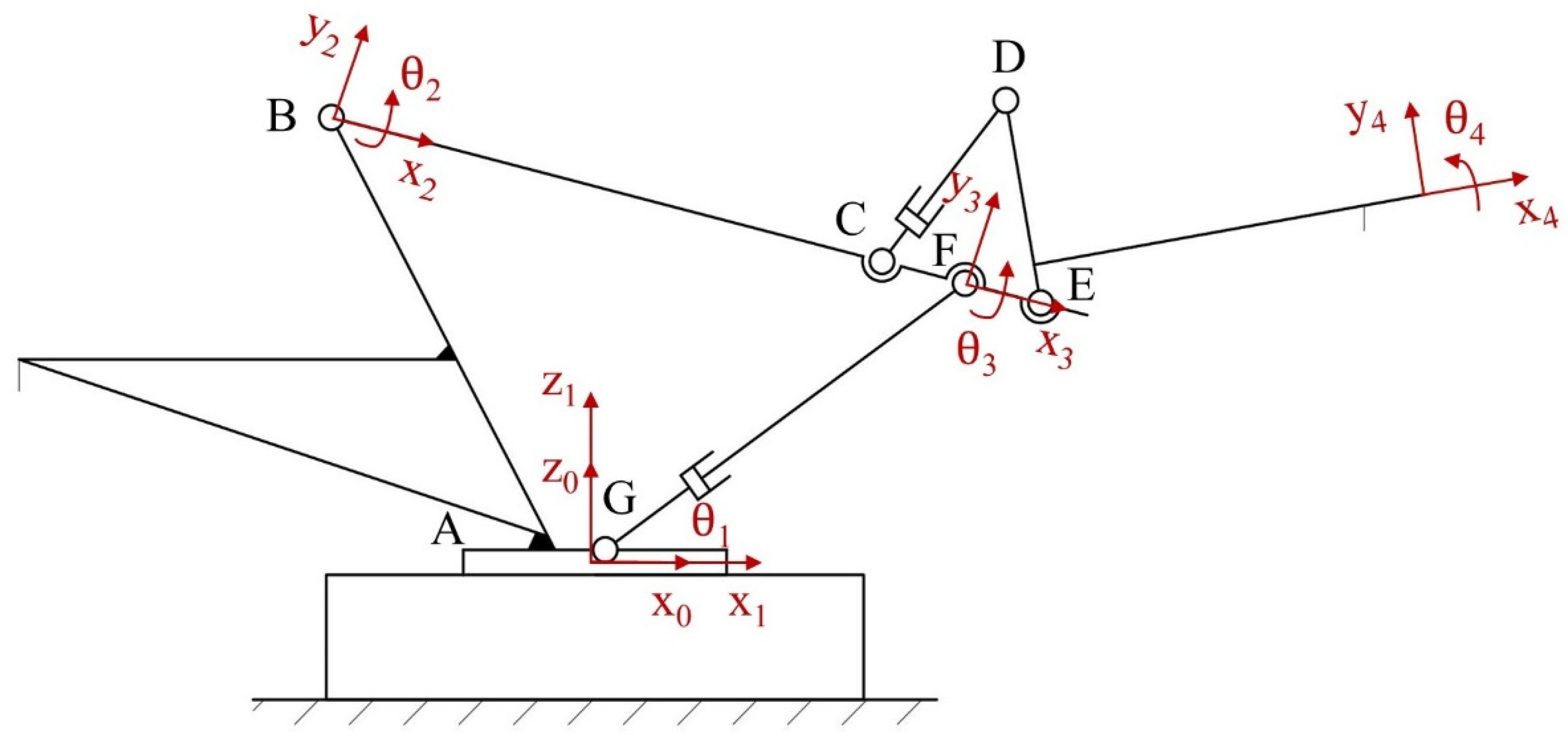
2.4. Kinematic Analysis of the Lifting Mechanism
2.4.1. Forward and Reverse Kinematic Analysis
2.4.2. Workspace Analysis
2.4.3. Optimization Method
2.4.4. Single-Factor Experiment and Orthogonal Experimental Design of Structural Parameters of the Picking Finger
2.5. Field Validation Experiment Design
3. Results
3.1. Workspace Analysis of the Lifting Mechanism
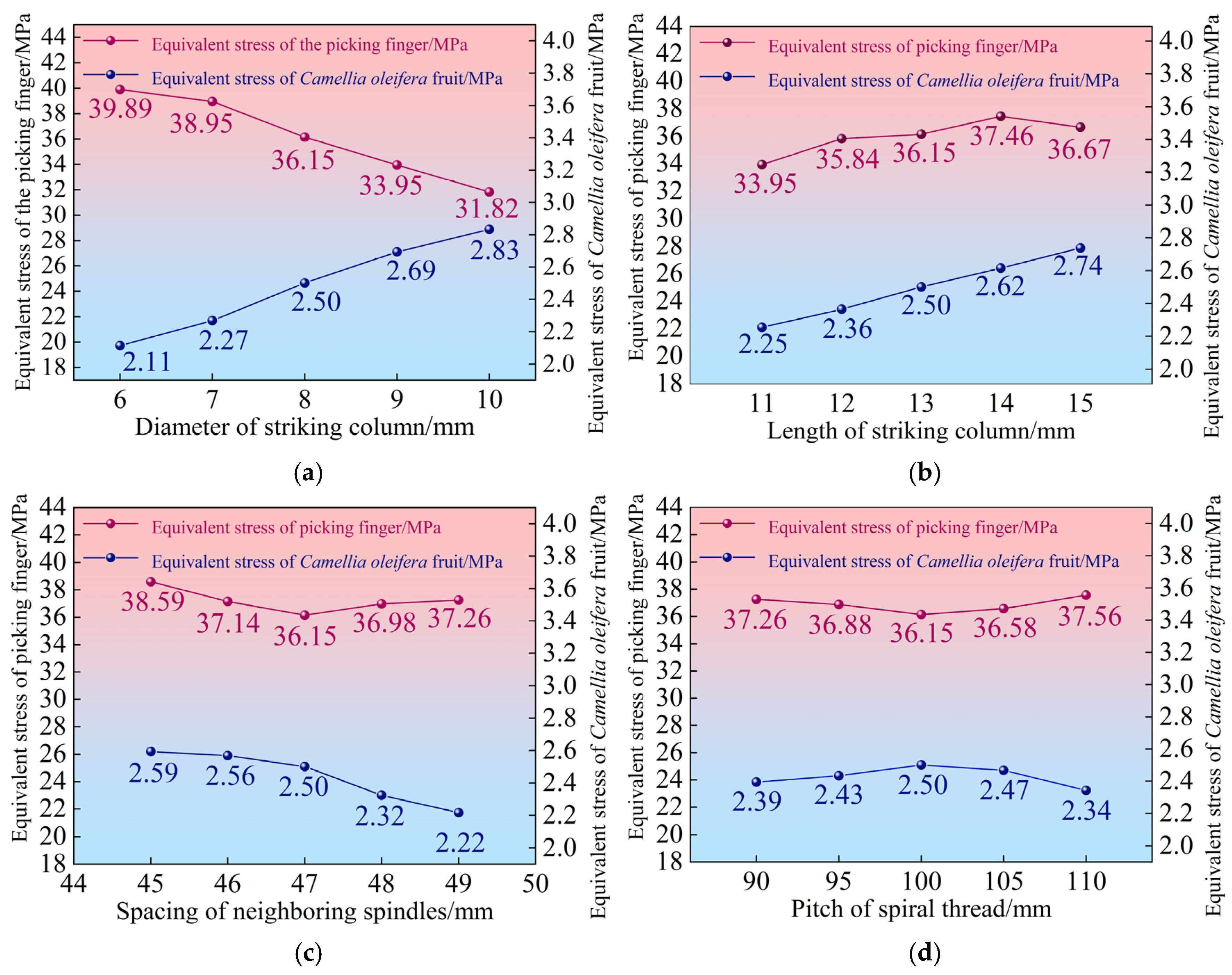
3.2. Determination of the Structural Parameters of the Picking Finger
3.2.1. Simulation Results
3.2.2. Results of the Single-Factor Experiment and Orthogonal Experiment of Structural Parameters of the Picking Finger
3.3. Results of Optimization of Operating Parameters Experiment
3.3.1. Results of Single-Factor Experiment for Optimization of Operating Parameters
3.3.2. Results of Response Surface Experiment for Optimization of Operating Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, X.C.; Ning, R.X.; Li, P.F.; Zhang, F.L.; Wang, K.; Jiang, J.X. Structural variations of lignin and lignin-carbohydrate complexes from the fruit shells of Camellia oleifera during ripening. Int. J. Biol. Macromol. 2023, 253, 126946. [Google Scholar] [CrossRef] [PubMed]
- Luan, F.; Zeng, J.S.; Yang, Y.; He, X.R.; Wang, B.J.; Gao, Y.B.; Zeng, N. Recent advances in Camellia oleifera Abel: A review of nutritional constituents, biofunctional properties, and potential industrial applications. J. Funct. Foods 2020, 75, 104242. [Google Scholar] [CrossRef]
- Shi, T.; Wu, G.C.; Jin, Q.Z.; Wang, X.G. Camellia oil authentication: A comparative analysis and recent analytical techniques developed for its assessment. A review. Trends Food Sci. Technol. 2020, 97, 88–99. [Google Scholar] [CrossRef]
- Zhu, F.; Wu, R.; Chen, B.L.; Zhang, F.; Chen, Y.Z.; Cao, F.L.; Yu, P.F.; Su, E.Z. Development of an efficient procedure for preparing high quality Camellia oleifera seed oil by enzymatic extraction and demulsification. Ind. Crops Prod. 2024, 212, 118392. [Google Scholar] [CrossRef]
- Wang, J.F.; Tan, X.J.; Wu, X.C.; Li, Q.P.; Zhong, Q.P.; Yan, C.; Guo, H.Y.; Ge, X.N. Development Status and Suggestions of camellia Industry in China. World For. Res. 2020, 33, 80–85. [Google Scholar]
- Yuan, Y.W.; Bai, S.H.; Niu, K.; Zhou, L.M.; Zhao, B.; Wei, L.G.; Xiong, S.; Liu, L.J. Research progress on mechanized harvesting technology and equipment for forest fruit. Trans. Chin. Soc. Agric. Eng. 2022, 38, 53–63. [Google Scholar]
- Zhuo, P.; Li, Y.X.; Wang, B.S.; Jiao, H.B.; Wang, P.; Li, C.S.; Niu, Q.; Wang, L.H. Analysis and experimental study on vibration response characteristics of mechanical harvesting of jujube. Comput. Electron. Agric. 2022, 203, 107446. [Google Scholar] [CrossRef]
- Zhen, Q.G.; He, M.; Wang, J.P.; Chen, Q.; Zhou, H.P.; Jiang, X.S. Research Progress in China’s Camellia oleifera fruit Picking Equipment. World For. Res. 2023, 36, 101–106. [Google Scholar]
- Cui, W.B.; Zhou, H.P.; Xu, L.Y.; Wang, Y.Y. Research Progress in Mechanically Vibratory Harvesting Equipment of Forest Fruit and Its Theory in China. World For. Res. 2023, 36, 64–70. [Google Scholar]
- Du, X.Q.; Ning, C.; He, Y.L.; Qian, Y.; Zhang, G.F.; Yao, X.H. Design and Test of Crawler-type High Clearance Camellia oleifera fruit Vibratory Harvester. Trans. Chin. Soc. Agric. Mach. 2022, 53, 113–121. [Google Scholar]
- Wu, D.L.; Li, C.; Cao, C.M.; Fan, E.B.; Wang, Q. Analysis and experiment of the operation process of branch-shaking type Camellia oleifera fruit picking device. Trans. Chin. Soc. Agric. Eng. 2020, 36, 56–62. [Google Scholar]
- Wang, D.; Tang, J.Y.; Fan, Z.Y.; Qu, Z.X. Design and Experiment of a Vibratory Camellia oleifera Fruit Harvester. For. Mach. Woodwork. Equip. 2020, 14, 4–7. [Google Scholar]
- Wu, D.L.; Zhao, E.L.; Jiang, S.; Wang, W.W.; Yuan, J.H.; Wang, K. Optimization and Experiment of Canopy Vibration Parameters of Camellia oleifera Based on Energy Transfer Characteristics. Trans. Chin. Soc. Agric. Mach. 2022, 53, 23–33. [Google Scholar]
- Liu, T.H.; Luo, G.; Ehsani, R.; Toudeshki, A.; Zou, X.J.; Wang, H.J. Simulation study on the effects of tine-shaking frequency and penetrating depth on fruit detachment for citrus canopy-shaker harvesting. Comput. Electron. Agric. 2018, 148, 54–62. [Google Scholar] [CrossRef]
- Castro-Garcia, S.; Aragon-Rodriguez, F.; Arias-Calderón, R.; Sola-Guirado, R.R.; Gil-Ribes, J.A. The contribution of fruit and leaves to the dynamic response of secondary branches of orange trees. Biosyst. Eng. 2020, 193, 149–156. [Google Scholar] [CrossRef]
- Yan, D.; Luo, L.F.; Zhang, P.; Liu, W.T.; Wang, J.X.; Lu, Q.H.; Luo, S.M. Vibration analysis and experimental study of the effects of mechanized grape picking on the fruit-stem system. Biosyst. Eng. 2023, 227, 82–94. [Google Scholar] [CrossRef]
- Wang, R.Y.; Fang, D.; Wu, C.; Wang, B.Y.; Zhu, H.C.; Hu, T.; Wu, D.L. Dynamic response of Camellia oleifera fruit-branch based on a mathematical model and high-speed photography. Biosyst. Eng. 2024, 237, 232–241. [Google Scholar] [CrossRef]
- Du, X.Q.; Shen, T.F.; Zhao, L.J.; Zhang, G.F.; Hu, A.G.; Fang, S.G.; Cao, Y.Q.; Yao, X.H. Design and experiment of the comb-brush harvesting machine with variable spacing for oil-tea camellia fruit. Int. J. Agric. Biol. Eng. 2021, 14, 172–177. [Google Scholar] [CrossRef]
- Wu, D.L.; Yuan, J.H.; Li, C.; Jiang, S.; Ding, D.; Cao, C.M. Design and Experiment of Twist-comb End Effector for Picking Camellia Fruit. Trans. Chin. Soc. Agric. Mach. 2021, 52, 21–33. [Google Scholar]
- Rao, H.H.; Wang, Y.L.; Li, Q.S.; Wang, B.Y.; Yang, J.L.; Liu, M.H. Design and Experiment of camellia Fruit Layered Harvesting Device. Trans. Chin. Soc. Agric. Mach. 2021, 52, 203–212. [Google Scholar]
- Wang, Y.L.; Rao, H.H.; Wang, B.Y.; Li, Q.S.; Liu, M.H. Manufacture of Portable Electro-hydraulic Camellia oleifera fruit Harvester. J. Agric. Mech. Res. 2022, 44, 106–111. [Google Scholar]
- Wang, R.Y.; Zheng, Z.A.; Lu, X.F.; Gao, L.; Jiang, D.L.; Zhang, Z.M. Design, simulation, and experiment of roller comb type Chrysanthemum (Dendranthema morifolium Ramat) picking machine. Comput. Electron. Agric. 2021, 187, 106295. [Google Scholar] [CrossRef]
- Cao, X.M.; Zou, X.J.; Jia, C.Y.; Chen, M.Y.; Zeng, Z.Q. RRT-based path planning for an intelligent litchi-picking manipulator. Comput. Electron. Agric. 2019, 156, 105–118. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, K.; Yang, L.; Zhang, D.; Cui, T.; Yu, Y.; Liu, H. Design and simulation experiment of ridge planting strawberry picking manipulator. Comput. Electron. Agric. 2023, 208, 107690. [Google Scholar] [CrossRef]
- Tsai, M.Y.; Cheng, M.Y.; Liao, H.C.; Lan, C.C. Kinematics and compliance analyses of a 3T1R parallel manipulator with rotational symmetry. Mech. Mach. Theory 2024, 193, 105544. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, J.F.; Yang, C.J.; Niu, B. The workspace mapping with deficient-DOF space for the PUMA 560 robot and its exoskeleton arm by using orthogonal experimental design method. Robot. Comput.-Integr. Manuf. 2007, 23, 478–487. [Google Scholar] [CrossRef]
- Hu, G.R.; Chen, C.; Chen, J.; Sun, L.J.; Sugirbay, A.; Chen, Y.; Jin, H.L.; Zhang, S.; Bu, L.X. Simplified 4-DOF manipulator for rapid robotic apple harvesting. Comput. Electron. Agric. 2022, 199, 107177. [Google Scholar] [CrossRef]
- Bu, L.X.; Chen, C.K.; Hu, G.R.; Sugirbay, A.; Sun, H.X.; Chen, J. Design and evaluation of a robotic apple harvester using optimized picking patterns. Comput. Electron. Agric. 2022, 198, 107092. [Google Scholar] [CrossRef]
- Van Henten, E.J.; Schenk, E.J.; Van Willigenburg, L.G.; Meuleman, J.; Barreiro, P. Collision-free inverse kinematics of the redundant seven-link manipulator used in a cucumber picking robot. Biosyst. Eng. 2010, 106, 112–124. [Google Scholar] [CrossRef]
- Zhao, X.; Cao, G.; Zhang, P.; Ma, Z.; Zhao, L.; Chen, J. Dynamic Analysis and Lightweight Design of 3-DOF Apple Picking Manipulator. Trans. Chin. Soc. Agric. Mach. 2023, 54, 88–98. [Google Scholar]
- Shrey, S.; Patil, S.; Pawar, N.; Lokhande, C.; Dandage, A.; Ghorpade, R.R. Forward kinematic analysis of 5-DOF LYNX6 robotic arm used in robot-assisted surgery. Mater. Today Proc. 2023, 72, 858–863. [Google Scholar] [CrossRef]
- Fu, M.; Guo, S.K.; Chen, A.Y.; Cheng, R.X.; Cui, X.M. Design and experimentation of multifruit envelope-cutting kiwifruit picking robot. Front. Plant Sci. 2024, 15, 1338050. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.H.; Gong, L.; Yu, C.R.; Du, X.F.; Chen, J.H.; Xie, S.H.; Le, X.Y.; Li, Y.M.; Liu, C.L. Workspace decomposition based path planning for fruit-picking robot in complex greenhouse environment. Comput. Electron. Agric. 2023, 215, 108353. [Google Scholar] [CrossRef]
- Yan, F.X.; Li, X.J.; Yang, Y.X.; Huang, G.Q.; Zhang, Y.; Yang, F.Z. Design and Experiment of Hand-held Impacting Comb-type Camellia oleifera fruit Harvester. Trans. Chin. Soc. Agric. Mach. 2023, 54, 129–140. [Google Scholar]



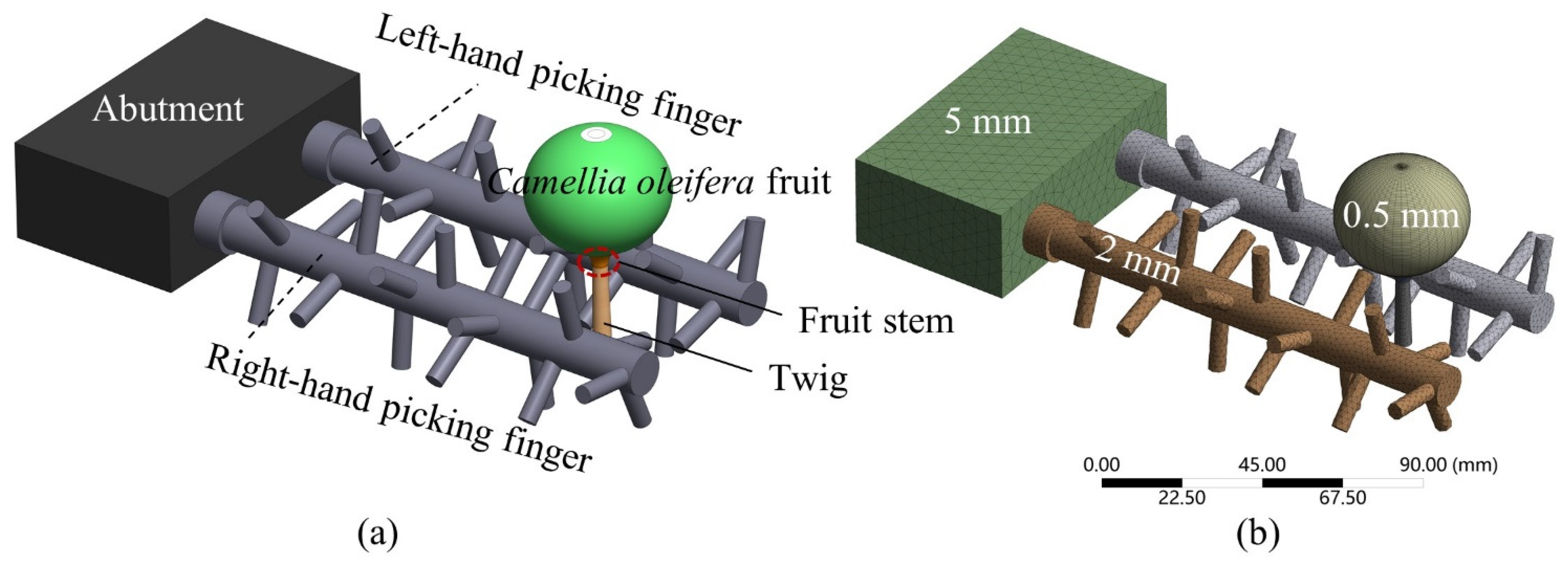






| Index | Crown Diameter (m) | Tree Height (m) | Minimum Result Height (m) | Result Layer Thickness (m) | Camellia oleifera Fruit Diameter (mm) | Bud Length Diameter (mm) | Short Diameter of Bud (mm) |
|---|---|---|---|---|---|---|---|
| Numerical range | 1.52~2.13 | 1.58~2.42 | 0.48 | 0.25~0.33 m | 18.99~58.78 | 13.43~19.85 | 7.29~9.67 |
| Standard Deviation | 0.10 | 0.14 | 0 | 0.013 | 6.63 | 1.07 | 0.40 |
| Index | Camellia oleifera | Bud Shedding Force (N) | ||
|---|---|---|---|---|
| Transversal Shedding Force (N) | Longitudinal Shedding Force (N) | Lateral Shedding Force (N) | ||
| Numerical range | 9.27~45.88 | 9.27~45.88 | 9.27~45.88 | 4.28~16.30 |
| Standard Deviation | 6.10 | 4.65 | 5.17 | 2.00 |
| Parameters | Range | Parameters | Range |
|---|---|---|---|
| Diameter of spindle (mm) | 12~16 | Pitch of spiral thread (mm) | 100~110 |
| Length of spindle (mm) | 330~360 | Spiral length (mm) | 300~330 |
| Diameter of striking pillar (mm) | 6~8 | Number of helix groups | 3~5 |
| Length of striking pillar (mm) | 10~15 | Spiral start interval (mm) | 8~10 |
| Clearance of two-strike pillar (mm) | 13.61~20.52 | Adjacent shaft clearance (mm) | 45~50 |
| Joint | (°) | (mm) | (°) | (mm) | Articulation Variable (°) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | (−45~45) | |
| 2 | −90 | 216 | 0 | (−15~30) | |
| 3 | 0 | 581 | 0 | −() | |
| 4 | 0 | 325 | 180 | (−10~60) |
| Level | Factors | |||
|---|---|---|---|---|
| Diameter of Striking Pillar (mm) | Length of Striking Pillar (mm) | Pitch of Spiral Thread (mm) | Neighboring Spindle Spacing (mm) | |
| 1 | 6 | 11 | 90 | 45 |
| 2 | 7 | 12 | 95 | 46 |
| 3 | 8 | 13 | 100 | 47 |
| 4 | 9 | 14 | 105 | 48 |
| 5 | 10 | 15 | 110 | 49 |
| Level | Factors | ||
|---|---|---|---|
| Brushing Speed (r/min) | Picking Finger Speed (r/min) | Picking Device Tilt Angle (°) | |
| 1 | 5 | 250 | −10 |
| 2 | 10 | 300 | −5 |
| 3 | 15 | 350 | 0 |
| 4 | 20 | 400 | 5 |
| 5 | 25 | 450 | 10 |
| Code | Factors | ||
|---|---|---|---|
| A (mm) | B (mm) | C (mm) | |
| −1 | 8 | 11 | 46 |
| 0 | 9 | 12 | 47 |
| 1 | 10 | 13 | 48 |
| Number | Factors | Evaluation Indicators | |||
|---|---|---|---|---|---|
| A (mm) | B (mm) | C (mm) | E1 (MPa) | E2 (MPa) | |
| 1 | 8 | 13 | 47 | 2.50 | 36.15 |
| 2 | 10 | 11 | 48 | 2.46 | 35.64 |
| 3 | 9 | 13 | 48 | 2.59 | 34.52 |
| 4 | 9 | 11 | 47 | 2.47 | 35.86 |
| 5 | 9 | 12 | 46 | 2.65 | 33.25 |
| 6 | 10 | 12 | 47 | 2.81 | 31.82 |
| 7 | 8 | 12 | 48 | 2.37 | 37.46 |
| 8 | 10 | 13 | 46 | 2.74 | 32.57 |
| 9 | 8 | 11 | 46 | 2.19 | 38.97 |
| Source | Degrees of Freedom | E1 | E2 | ||||
|---|---|---|---|---|---|---|---|
| Sum of Square | F Value | p Value | Sum of Square | F Value | p Value | ||
| Model | 6 | 0.048 | 623.429 | 0.002 ** | 7.216 | 114.767 | 0.009 ** |
| Intercept | 1 | 57.659 | 7413226.28 | 0.0001 ** | 11111.97 | 176723.33 | 0.0001 ** |
| A | 2 | 0.079 | 1010.714 | 0.001 ** | 13.920 | 221.386 | 0.004 ** |
| B | 2 | 0.056 | 720.143 | 0.001 ** | 6.434 | 102.333 | 0.010 * |
| C | 2 | 0.011 | 139.429 | 0.007 ** | 1.294 | 20.582 | 0.046 * |
| Inaccuracy | 2 | 7.778 × 10−5 | 0.063 | ||||
| Total | 9 | ||||||
| R2 | 99.8% | 99.7% | |||||
| Amended total | 8 | ||||||
| Number | E1 Average k1 | E1 Average k2 | E1 Average k3 | E1 Range R | E2 Average k1 | E2 Average k2 | E2 Average k3 | E2 Range R |
|---|---|---|---|---|---|---|---|---|
| A (mm) | 2.35 | 2.57 | 1.85 | 0.72 | 37.53 | 34.54 | 33.34 | 4.18 |
| B (mm) | 2.37 | 2.61 | 1.78 | 0.83 | 36.82 | 34.18 | 34.41 | 2.65 |
| C (mm) | 2.53 | 1.76 | 1.65 | 0.87 | 34.93 | 34.61 | 35.87 | 1.26 |
| Serial Number | Factors | Evaluation Indicators | ||||
|---|---|---|---|---|---|---|
| Y1 (r min−1) | Y2 (r min−1) | Y3 (°) | T1 (kg h−1) | T2 (%) | T3 (%) | |
| 1 | 19 | 330 | −2 | 108.07 | 89.68 | 8.69 |
| 2 | 22 | 340 | −2 | 120.64 | 90.73 | 8.84 |
| 3 | 22 | 340 | 1 | 122.85 | 94.25 | 9.23 |
| 4 | 16 | 330 | −0.5 | 97.08 | 89.21 | 8.78 |
| 5 | 19 | 340 | −0.5 | 109.06 | 93.24 | 9.08 |
| 6 | 19 | 340 | −0.5 | 113.94 | 93.96 | 9.14 |
| 7 | 19 | 340 | −0.5 | 110.49 | 92.47 | 9.11 |
| 8 | 19 | 330 | 1 | 108.99 | 91.31 | 8.97 |
| 9 | 19 | 340 | −0.5 | 110.25 | 92.62 | 9.12 |
| 10 | 19 | 350 | 1 | 118.63 | 94.56 | 9.47 |
| 11 | 22 | 330 | −0.5 | 110.52 | 90.26 | 9.09 |
| 12 | 16 | 350 | −0.5 | 99.34 | 91.74 | 9.37 |
| 13 | 19 | 340 | −0.5 | 112.10 | 93.83 | 9.06 |
| 14 | 16 | 340 | −2 | 100.33 | 89.98 | 8.73 |
| 15 | 16 | 340 | 1 | 104.52 | 91.89 | 9.02 |
| 16 | 19 | 350 | −2 | 110.97 | 92.27 | 9.25 |
| 17 | 22 | 350 | −0.5 | 130.02 | 94.86 | 9.65 |
| Source | Degrees of Freedom | T1 | T2 | T3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sum of Square | F Value | p Value | Sum of Square | F Value | p Value | Sum of Square | F Value | p Value | ||
| Model | 9 | 126.32 | 30.21 | <0.0001 ** | 5.41 | 15.29 | 0.0008 ** | 0.115 | 44.11 | <0.0001 ** |
| Y1 | 1 | 856.15 | 204.7 | <0.0001 ** | 6.62 | 18.73 | 0.0034 ** | 0.1035 | 39.69 | 0.0004 ** |
| Y2 | 1 | 147.06 | 35.17 | 0.0006 ** | 21.03 | 59.45 | 0.0001 ** | 0.6105 | 234.1 | <0.0001 ** |
| Y3 | 1 | 28.05 | 6.71 | 0.0359 * | 10.93 | 30.89 | 0.0009 ** | 0.1741 | 66.74 | <0.0001 ** |
| Y1Y2 | 1 | 74.30 | 17.77 | 0.0040 ** | 1.07 | 3.03 | 0.1254 | 0.0002 | 0.086 | 0.7775 |
| Y1Y3 | 1 | 0.98 | 0.234 | 0.6431 | 0.648 | 1.83 | 0.2180 | 0.0025 | 0.959 | 0.3601 |
| Y2Y3 | 1 | 11.36 | 2.72 | 0.1434 | 0.109 | 0.308 | 0.5963 | 0.0009 | 0.345 | 0.5753 |
| 1 | 2.39 | 0.572 | 0.4740 | 4.00 | 11.30 | 0.0120 * | 0.0004 | 0.1535 | 0.7069 | |
| 1 | 5.80 | 1.39 | 0.2773 | 2.26 | 6.38 | 0.0395 * | 0.0714 | 27.39 | 0.0012 ** | |
| 1 | 11.76 | 2.81 | 0.1375 | 1.21 | 3.43 | 0.1063 | 0.0793 | 30.41 | 0.0009 ** | |
| Residual | 7 | 4.18 | 0.354 | 0.0026 | ||||||
| Lack of fit | 3 | 4.99 | 1.40 | 0.3661 | 0.211 | 0.458 | 0.726 | 0.0047 | 4.63 | 0.0864 |
| Pure error | 4 | 3.57 | 0.461 | 0.0010 | ||||||
| R2 | 97.49% | 95.16% | 98.27% | |||||||
| Coefficient of variation | 1.84% | 6.45% | 0.561% | |||||||
| Area | Total Number of Fruits | Total Number of Buds | Number of Fruit Shedding | Number of Buds Shedding | Mass of Shed Fruit/g | Operating Time (s) | Picking Rate(kg/h) | Fruit Shedding Rate (%) | Bud Shedding Rate (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 85 | 356 | 79 | 32 | 2310.09 | 70 | 118.8 | 92.94 | 8.99 |
| 2 | 83 | 364 | 76 | 35 | 2236.26 | 65 | 123.85 | 91.57 | 9.62 |
| 3 | 79 | 351 | 74 | 33 | 2052.70 | 63 | 117.29 | 93.67 | 9.40 |
| 4 | 68 | 347 | 63 | 32 | 2003.18 | 60 | 120.19 | 92.65 | 9.22 |
| 5 | 75 | 338 | 68 | 29 | 2042.89 | 62 | 118.62 | 90.67 | 8.58 |
| Average value | 78 | 351.20 | 72 | 32.20 | 2129.02 | 64 | 119.75 | 92.30 | 9.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, F.; Zhu, Y.; Li, X.; Zhang, Y.; Astanakulov, K.; Alisher, N. Design and Experimentation of Comb-Spiral Impact Harvesting Device for Camellia oleifera Fruit. Agriculture 2025, 15, 1616. https://doi.org/10.3390/agriculture15151616
Yan F, Zhu Y, Li X, Zhang Y, Astanakulov K, Alisher N. Design and Experimentation of Comb-Spiral Impact Harvesting Device for Camellia oleifera Fruit. Agriculture. 2025; 15(15):1616. https://doi.org/10.3390/agriculture15151616
Chicago/Turabian StyleYan, Fengxin, Yaoyao Zhu, Xujie Li, Yu Zhang, Komil Astanakulov, and Naimov Alisher. 2025. "Design and Experimentation of Comb-Spiral Impact Harvesting Device for Camellia oleifera Fruit" Agriculture 15, no. 15: 1616. https://doi.org/10.3390/agriculture15151616
APA StyleYan, F., Zhu, Y., Li, X., Zhang, Y., Astanakulov, K., & Alisher, N. (2025). Design and Experimentation of Comb-Spiral Impact Harvesting Device for Camellia oleifera Fruit. Agriculture, 15(15), 1616. https://doi.org/10.3390/agriculture15151616






