Automatic Vibration Balancing System for Combine Harvester Threshing Drums Using Signal Conditioning and Optimization Algorithms
Abstract
1. Introduction
2. Materials and Methods
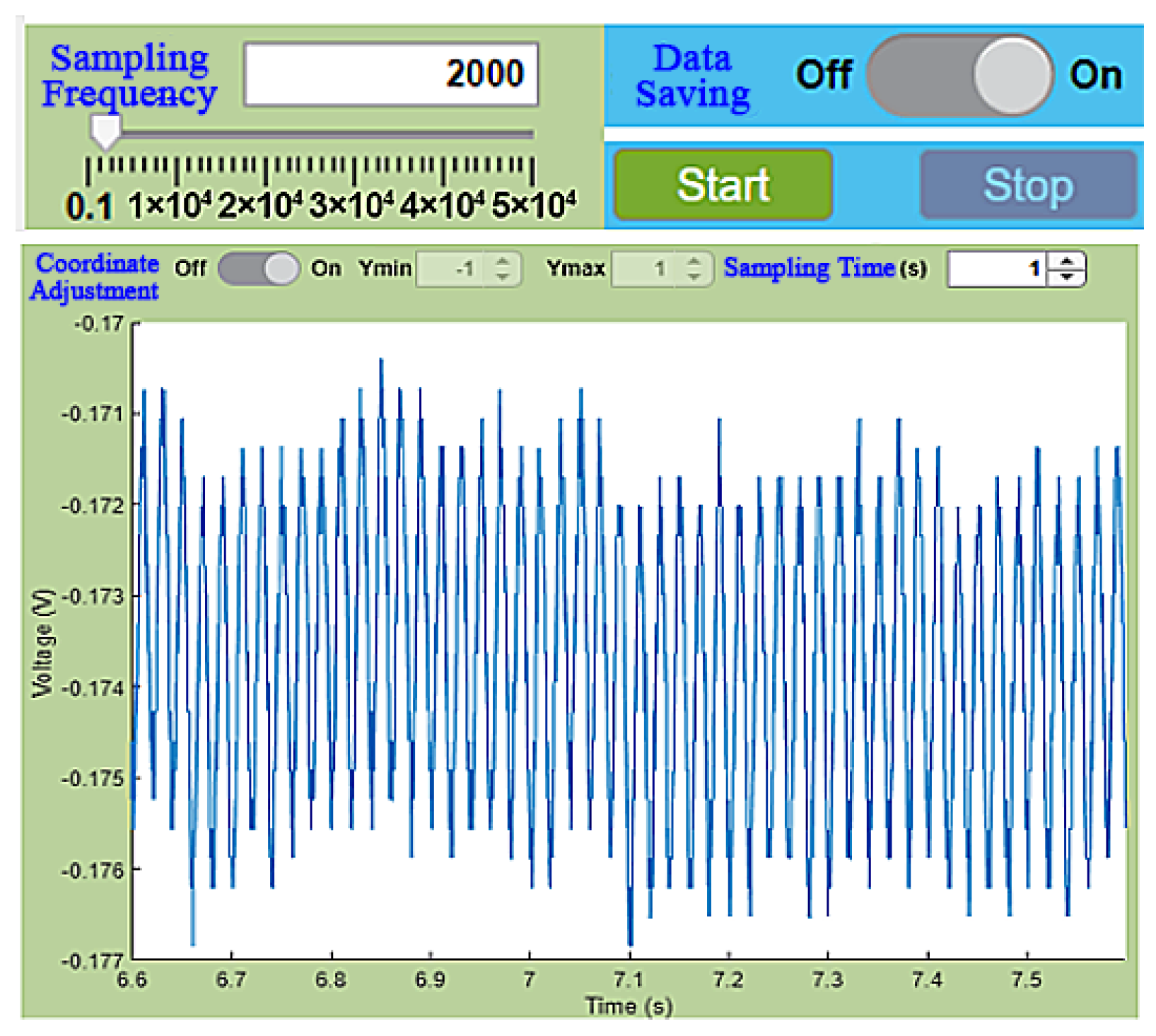
2.1. Signal Acquisition of Unbalanced Vibration in the Threshing Drum
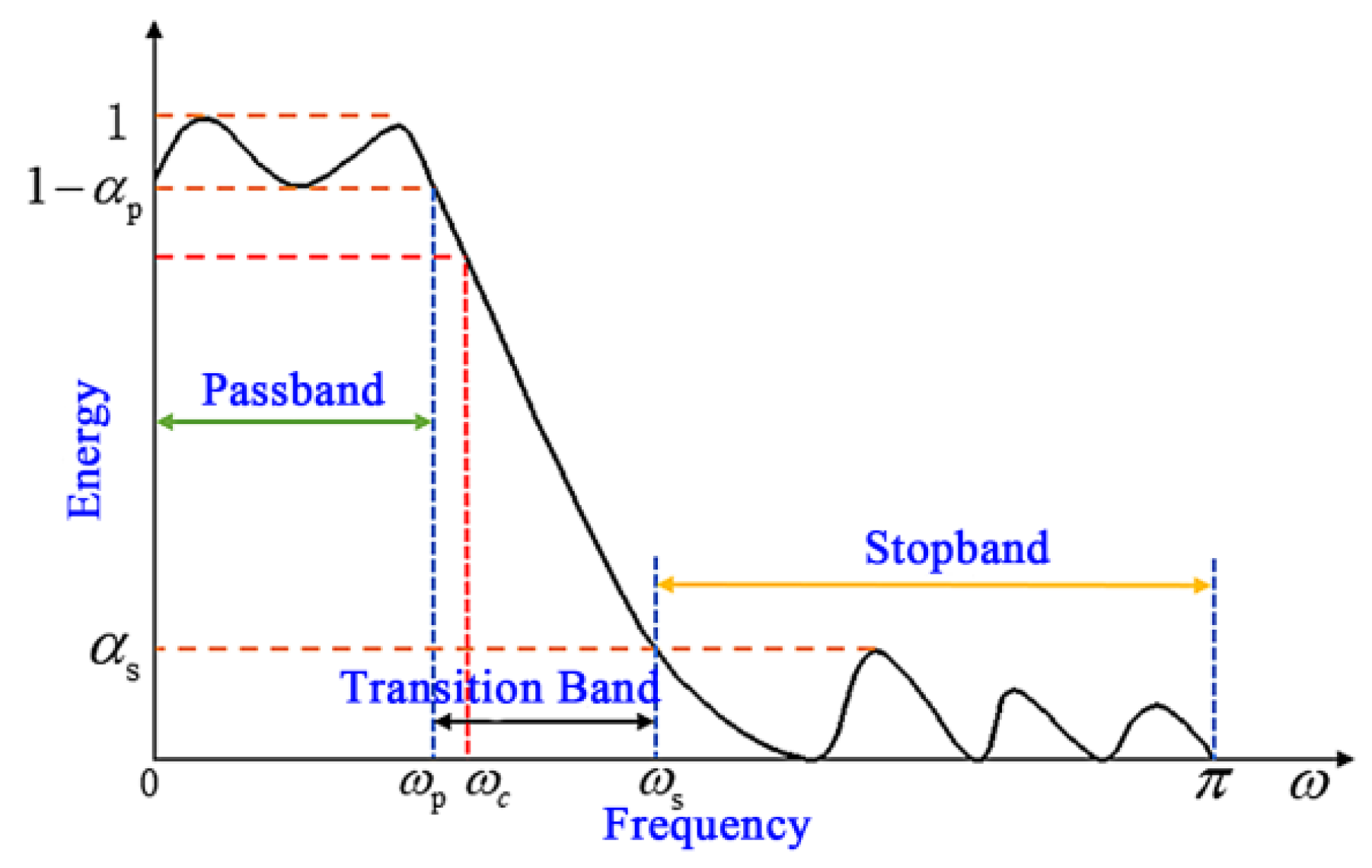
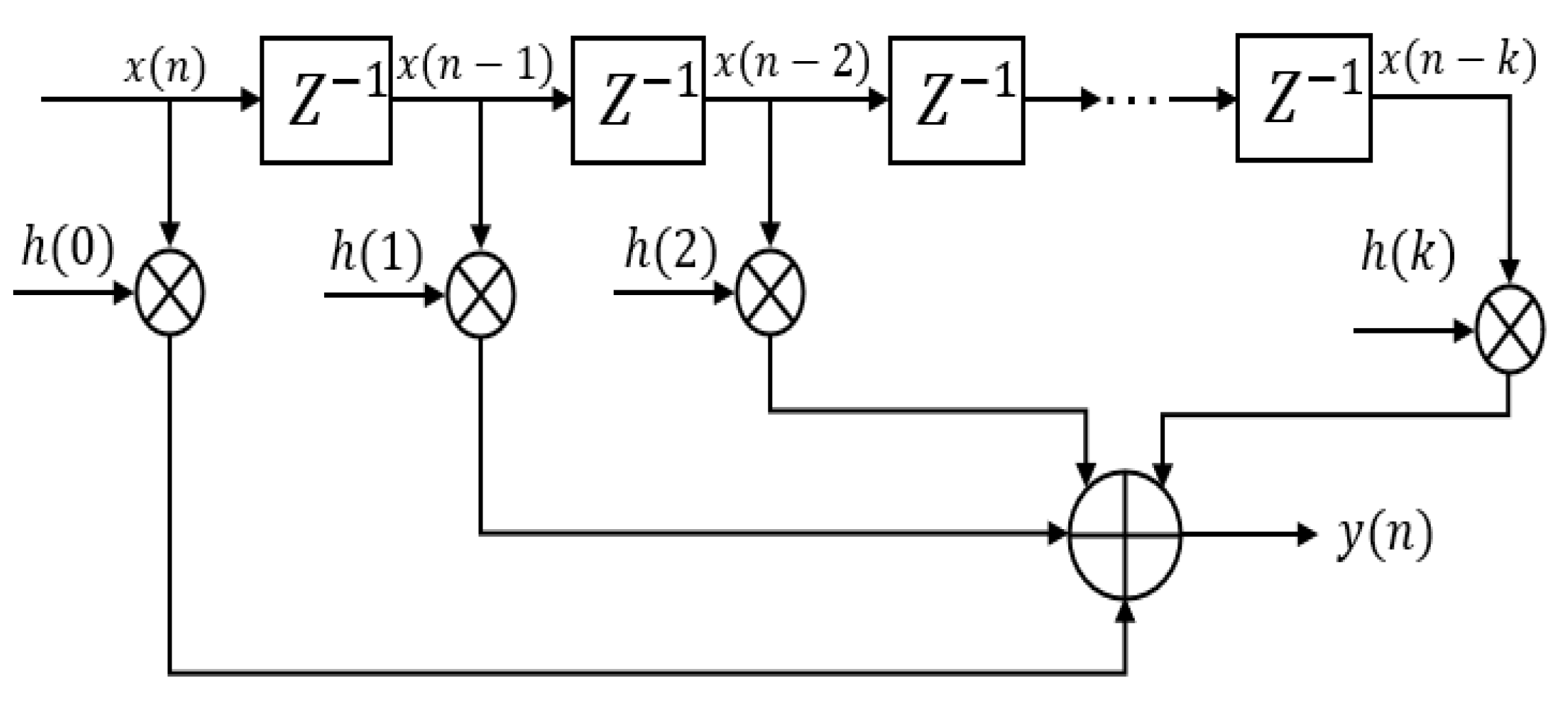
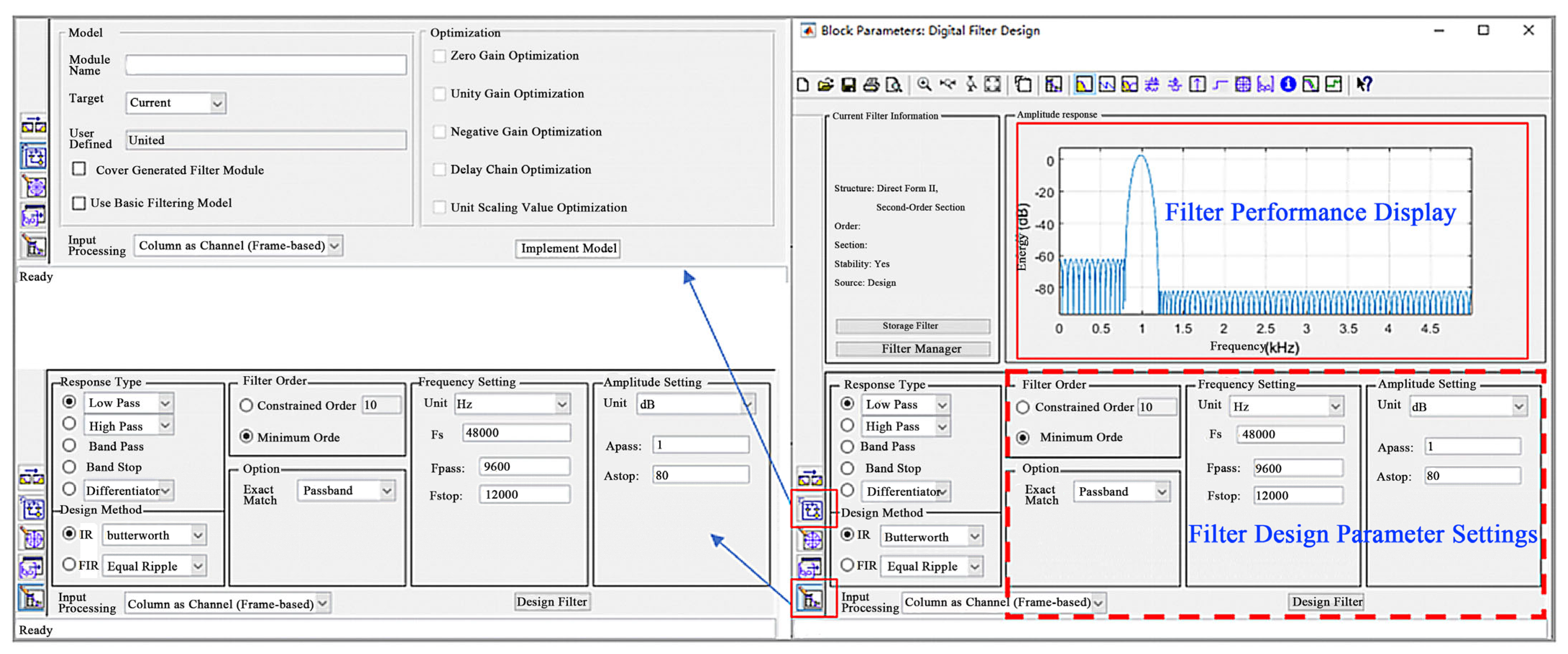
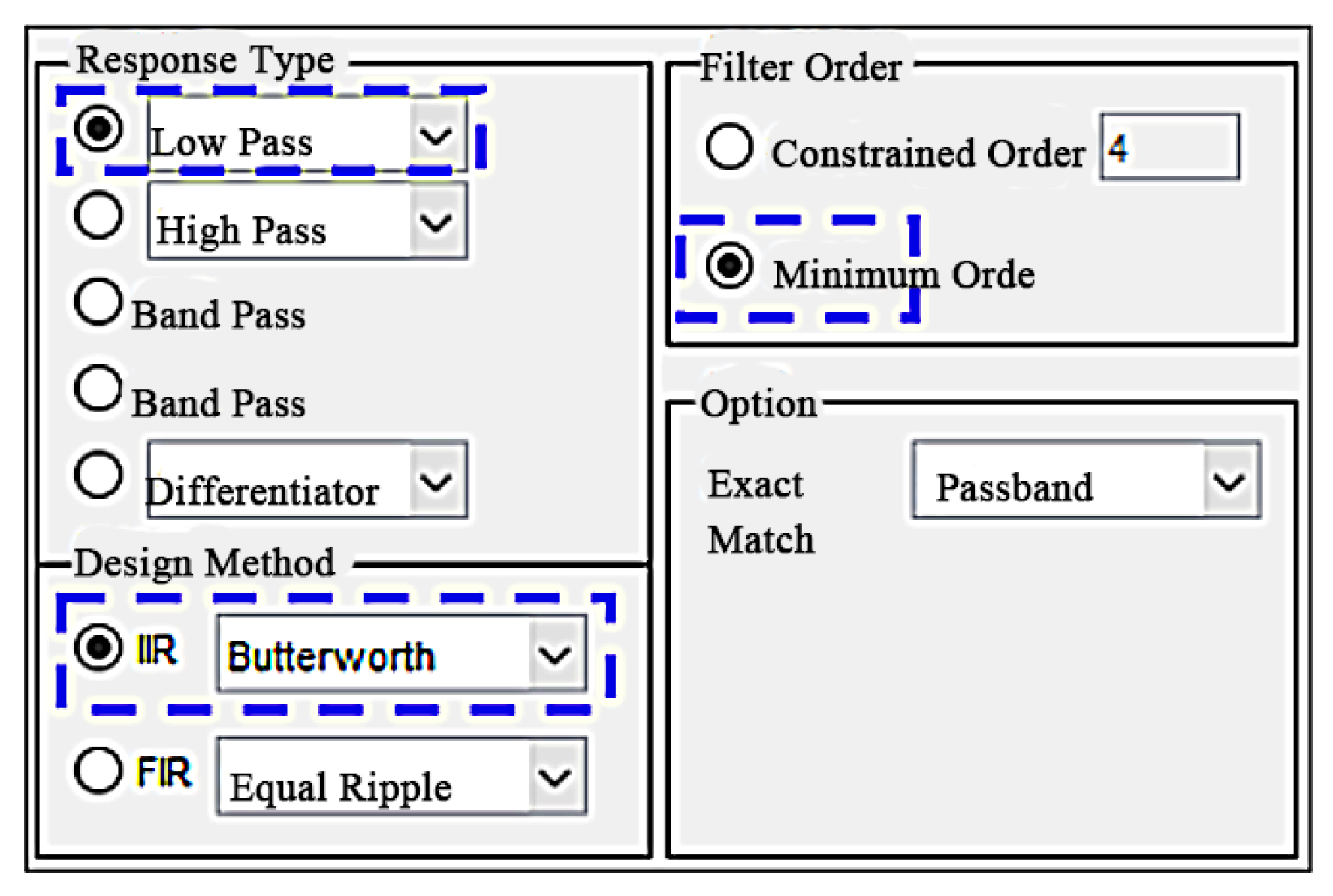
2.2. Signal Conditioning of Unbalanced Vibration in the Threshing Drum
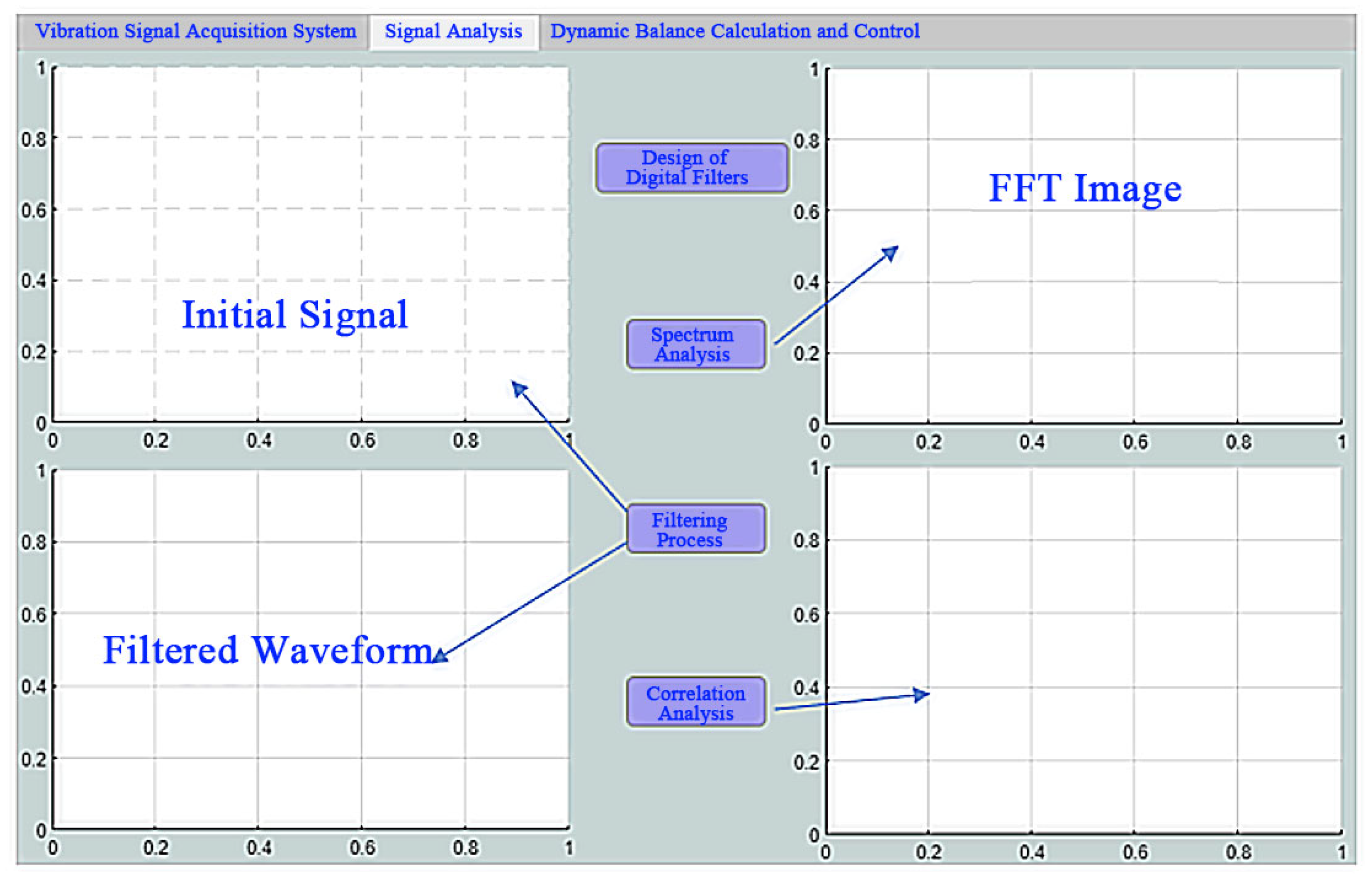
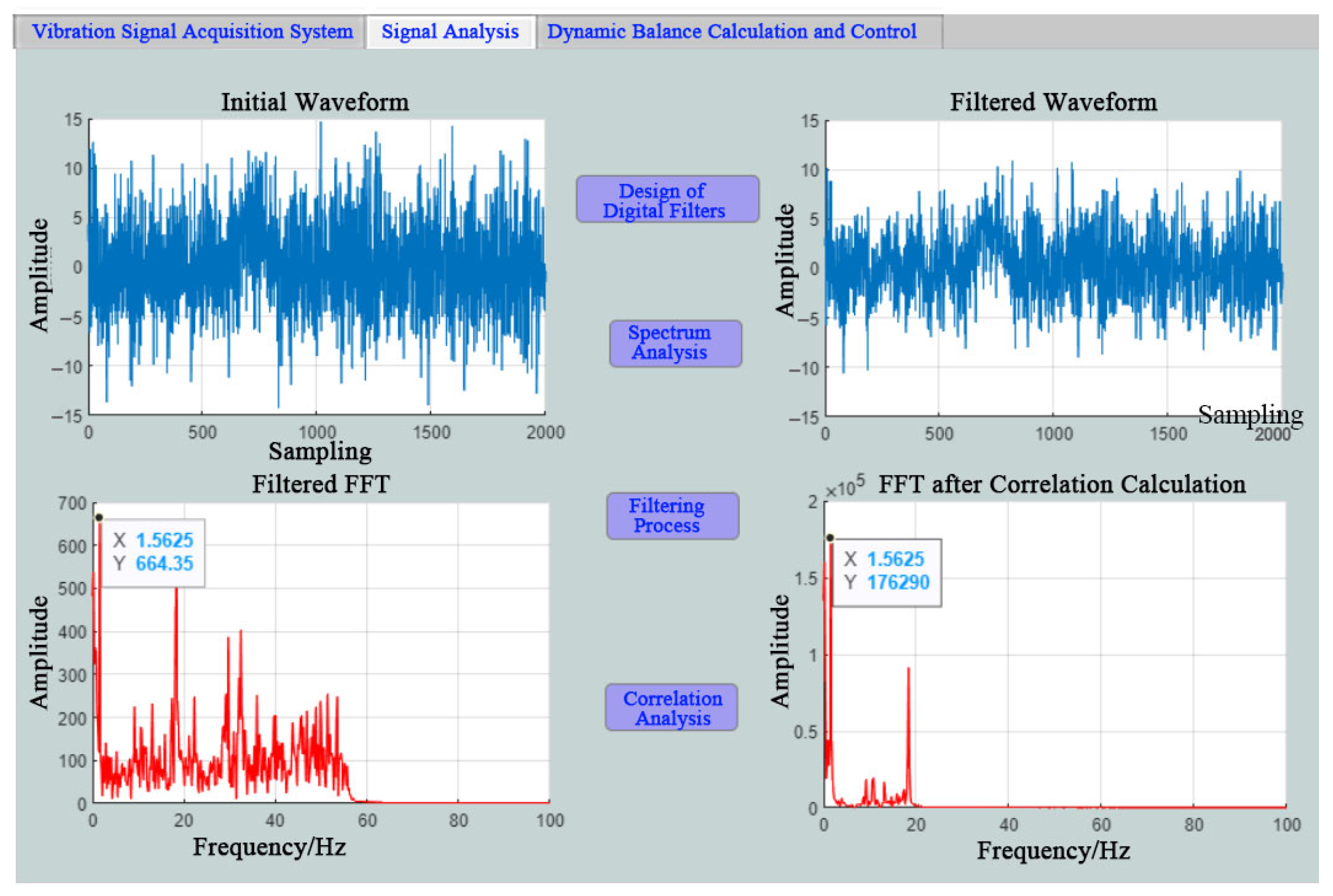
2.3. Method for Extracting Features of Unbalanced Vibration Signals
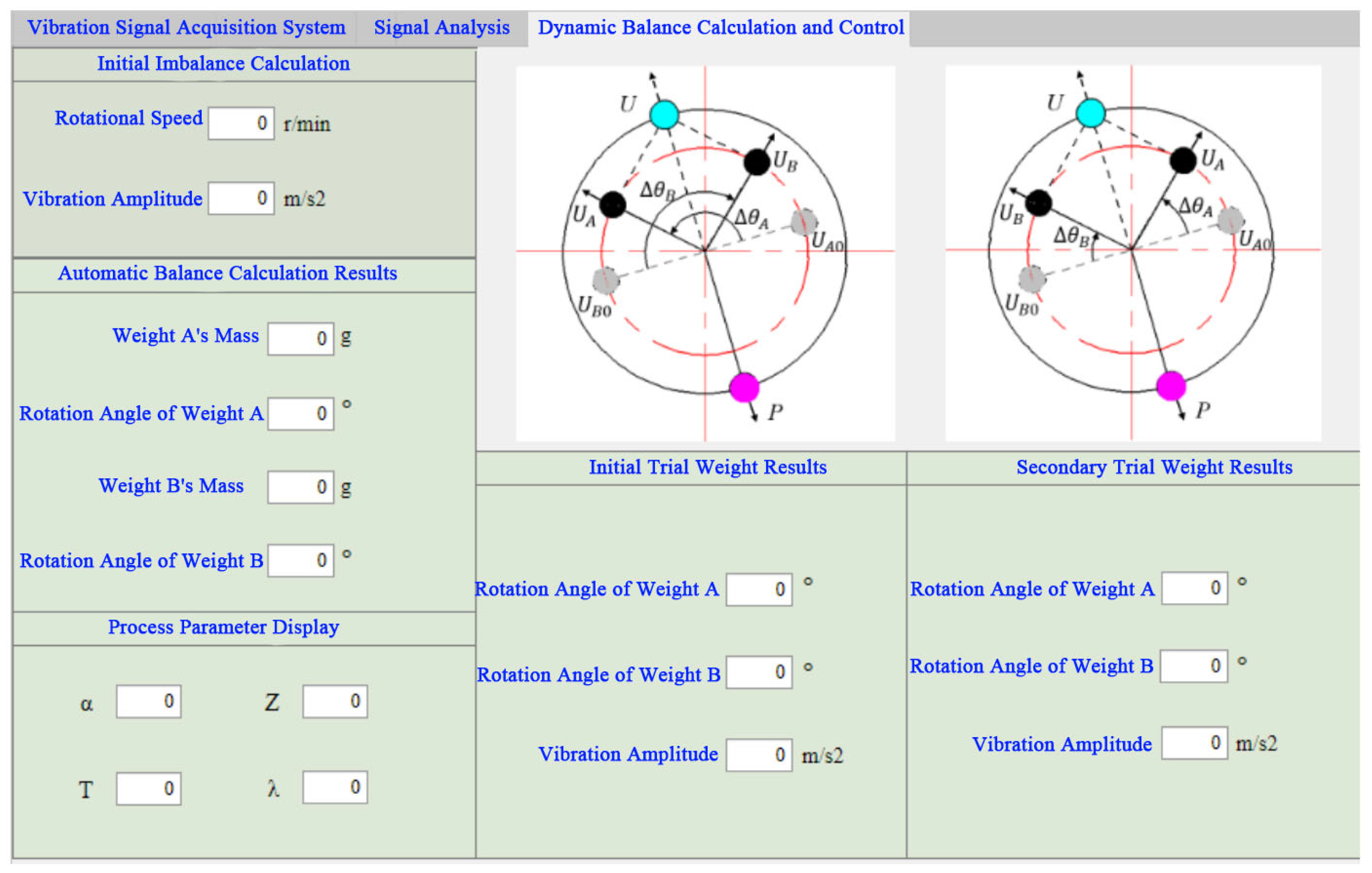
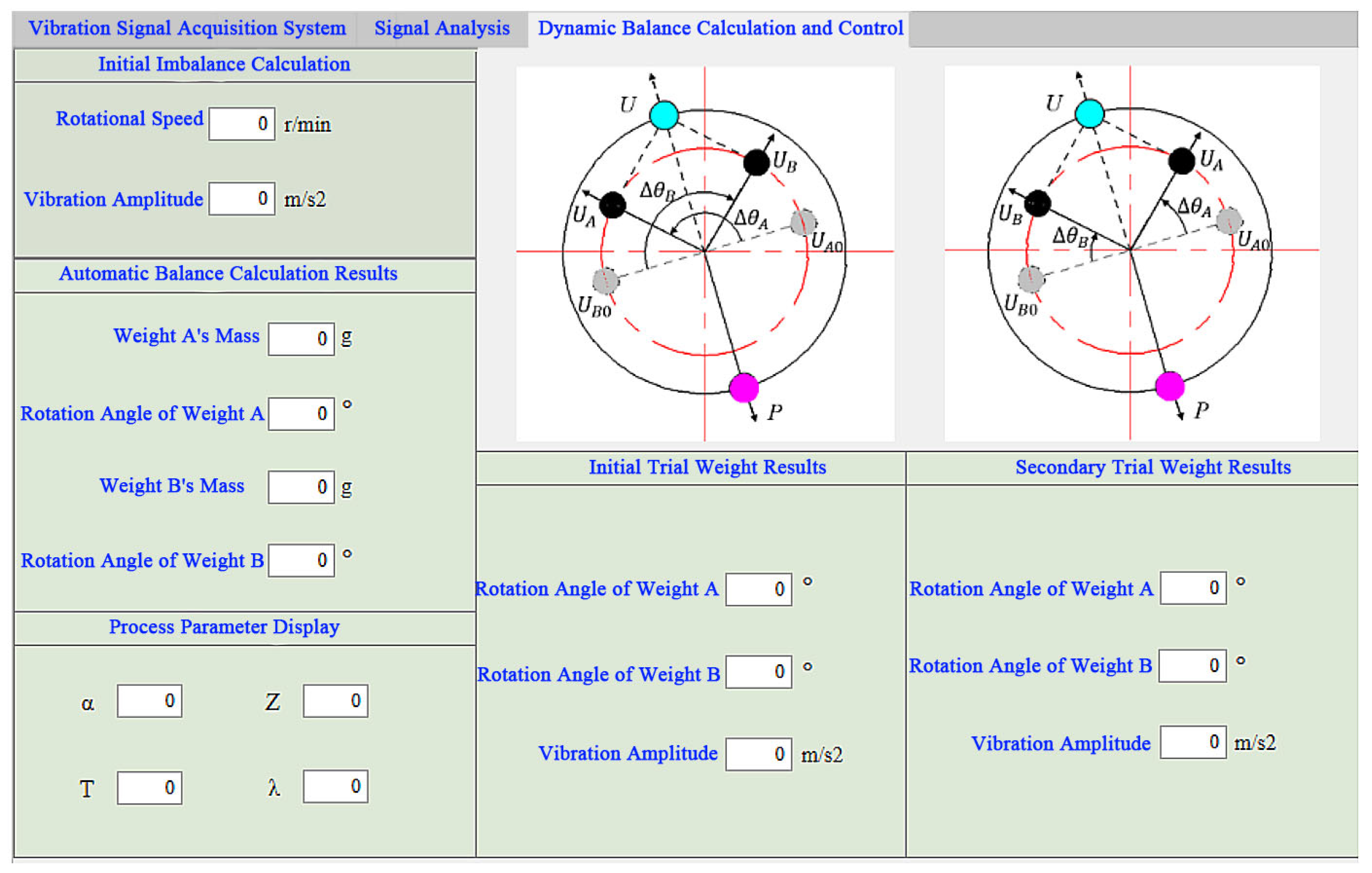
2.4. Dual-Sided Iterative Optimization Counterweight Strategy
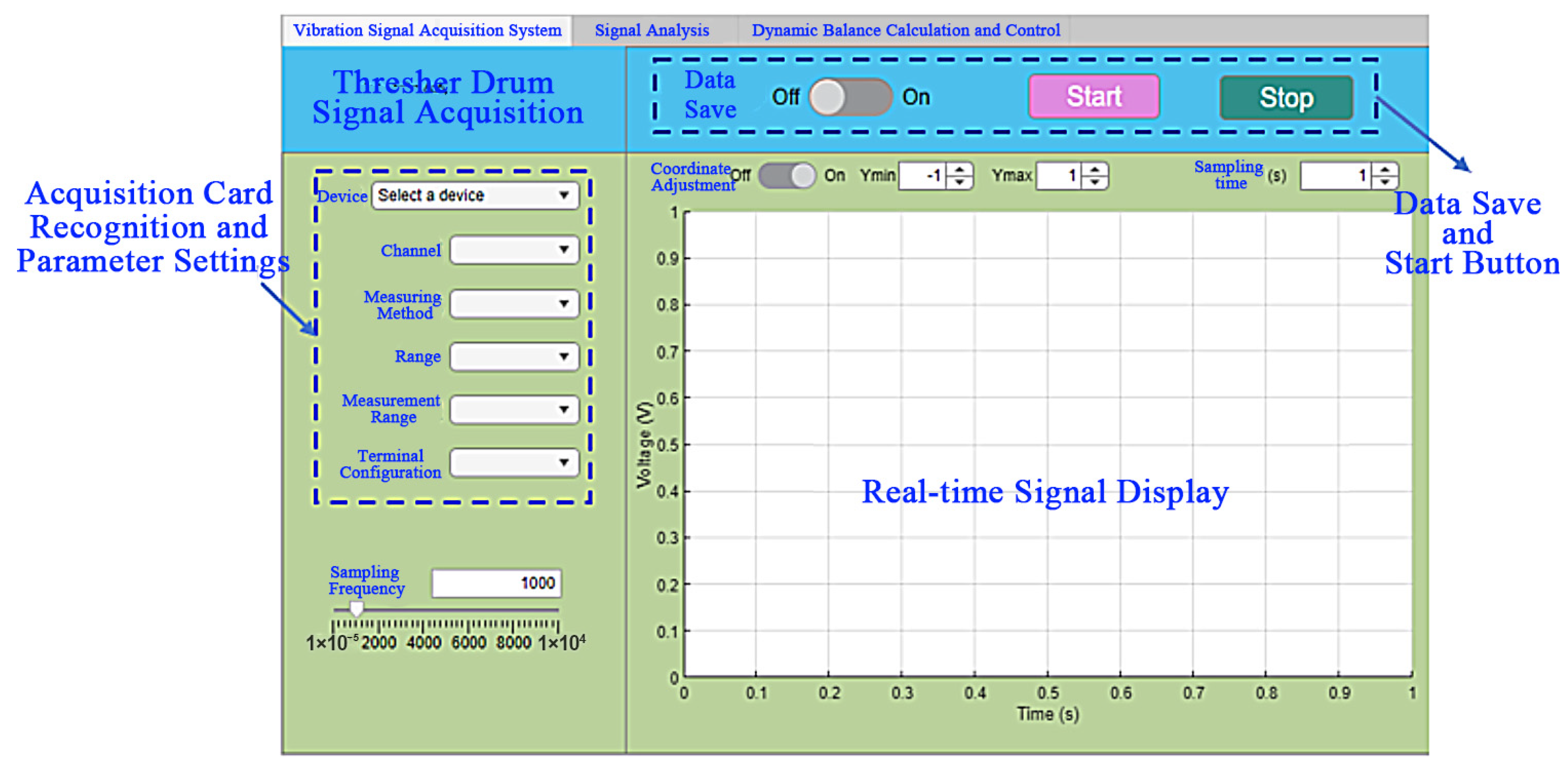
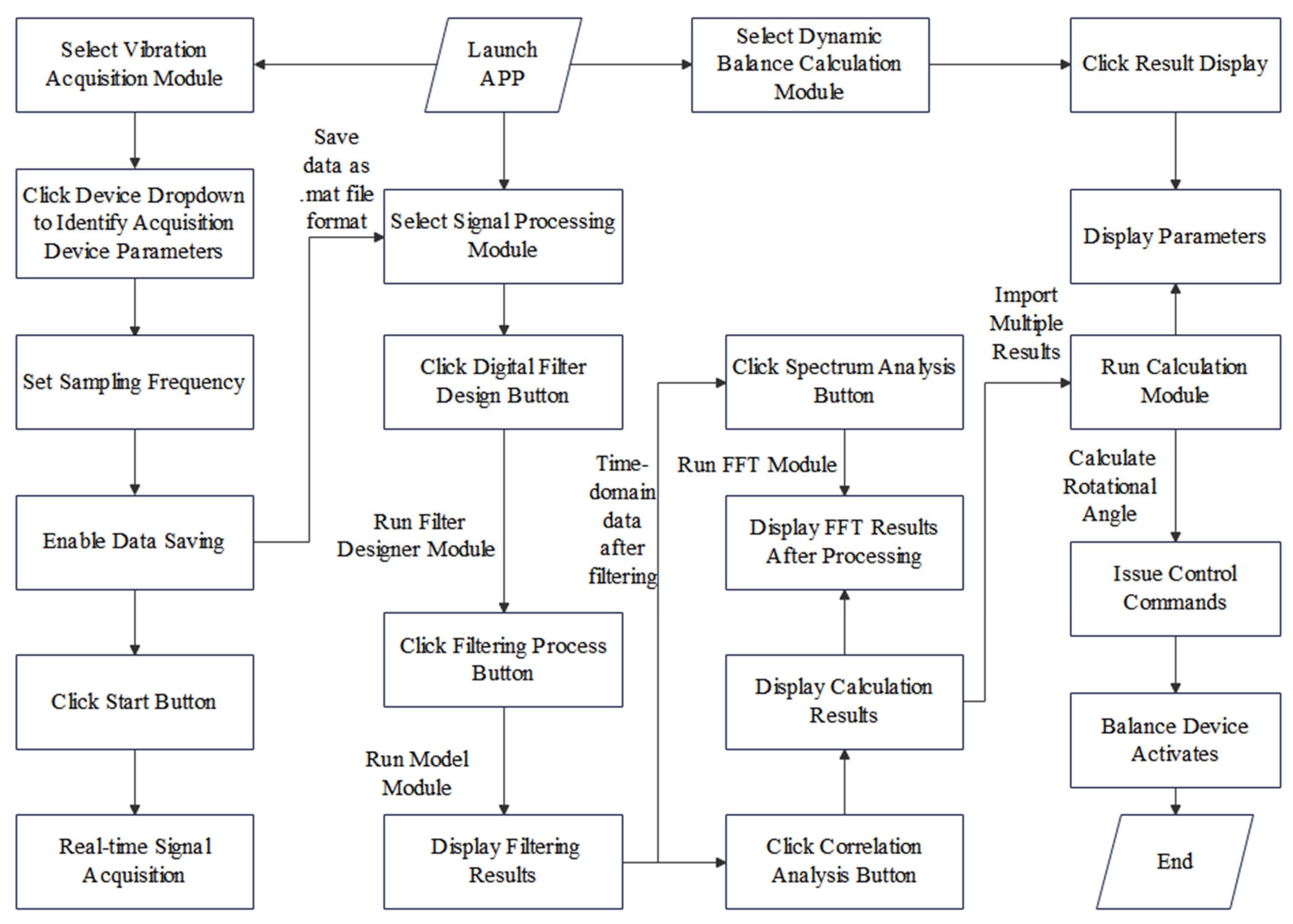
2.5. Integrated System for Self-Balancing Testing and Control of the Threshing Drum
3. Results and Discussion
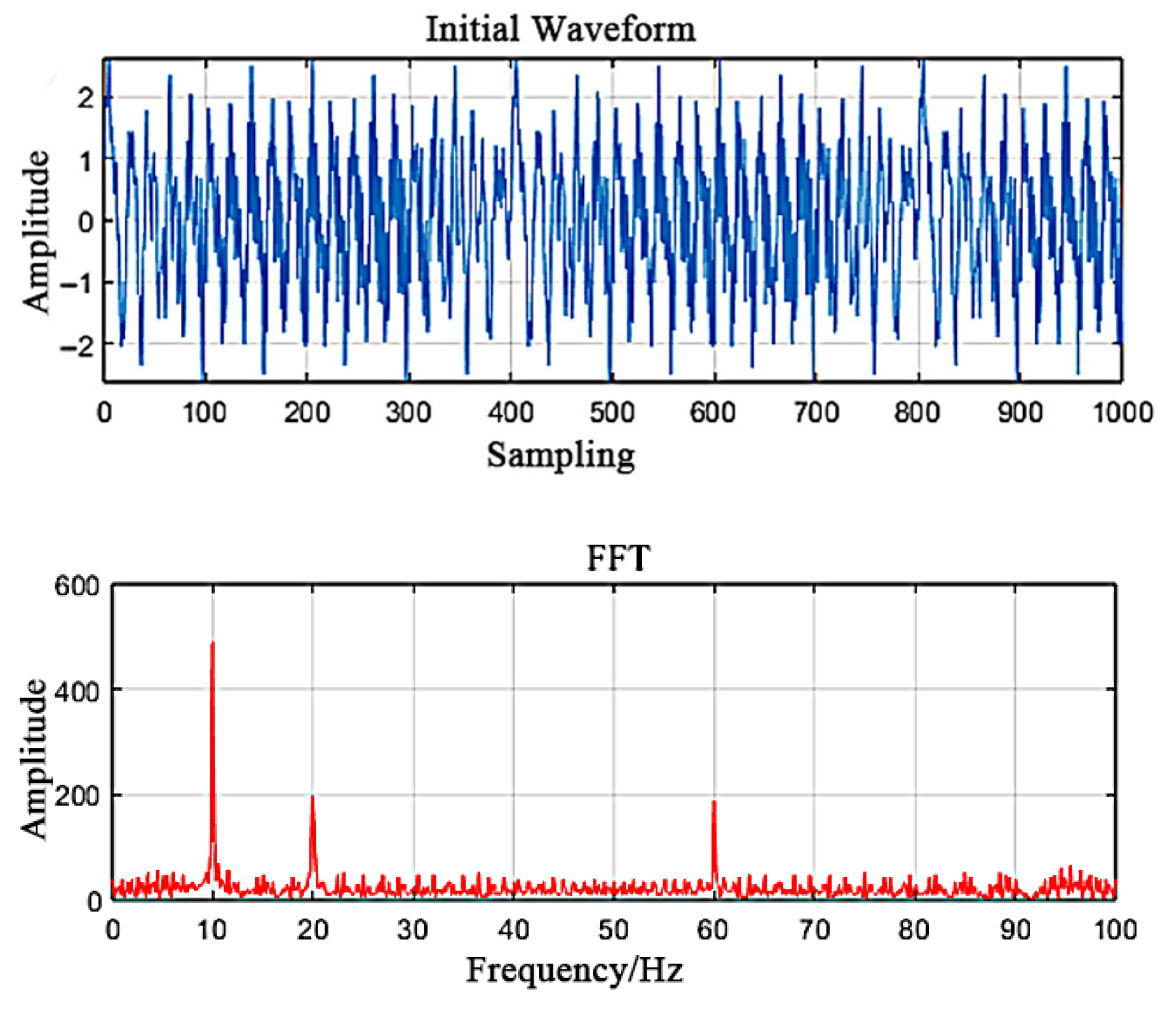
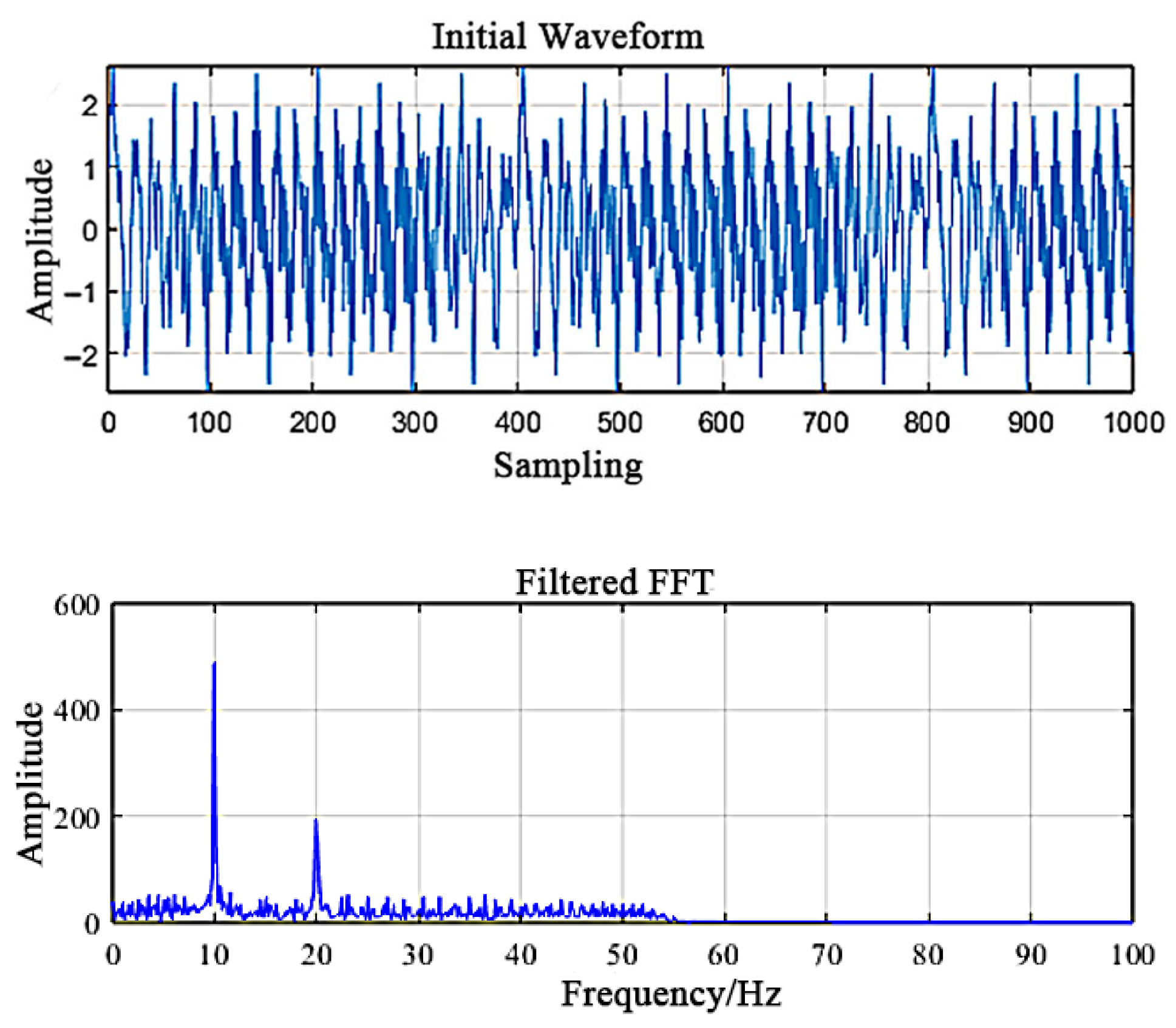
3.1. Testing for Feature Extraction of Unbalanced Vibration Signals
3.2. Dynamic Balance Testing and Online Automatic Balancing Trials of the Threshing Drum
4. Conclusions
- (1)
- The dynamic balance testing module has been designed and implemented to serve as the foundational component of an automatic balancing system for combine harvester threshing drums. The module’s design enables the real-time acquisition of unbalanced vibration signals and dictates the appropriate hardware configuration. Because excessive interference signals in operation often obscure fundamental frequency characteristics, a specialized signal conditioning process was developed. This process integrates a meticulously designed low-pass filter, supported by detailed parameter calculations and modeling, with correlation calculations and FFT transformations. This comprehensive signal processing chain achieves effective interference suppression and accurate extraction of the true signal amplitude at the operating frequency, thereby establishing a robust and precise basis for subsequent dynamic balancing calculations.
- (2)
- The design of a complete automatic dynamic balancing system for the threshing drum, along with its experimental validation, is systematically detailed. An online dynamic balance testing platform was constructed to facilitate real-time operation and balancing. Central to this platform is a novel automatic balance control method, which features a dual-sided iterative optimization counterweight strategy specifically developed for this application. The seamless integration of vibration testing, signal processing, and automatic balance control functionalities within a user-friendly visual interface enables the continuous online acquisition of unbalanced data and automated balancing. Experimental results demonstrate that the proposed balance control strategy accurately calculates the required rotation angles of the counterweight disks from online vibration measurements, confirming the system’s integrated capability for online testing, signal processing, and balance calculation.
- (3)
- The online dynamic balance testing and automatic balancing capabilities of the integrated system were validated through direct experimental trials on the threshing drum. Under test conditions of 100 r/min (the 1.5625 Hz operating frequency), the automatic balancing system achieved precise measurement of the unbalanced vibration. Its dynamic balance calculations then accurately determined the required counterweight disk angles for balancing to be 6.938° and −6.414°. These experimental findings provide compelling evidence for the effectiveness and feasibility of the designed system in achieving accurate online testing, sophisticated signal processing, and reliable balance calculations. The results offer valuable theoretical support and significant practical potential for addressing the critical issue of imbalance in combine harvesters—a problem frequently aggravated by material impacts and stem wrapping—ultimately enhancing machinery performance and longevity.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, R.; Dai, F.; Zhao, W.; Yang, F.; Zhang, F.; Zhao, Y.; Qu, H.; Wang, T.; Guo, J. Design and experiments of self-propelled quinoa combine harvester. J. Jilin University. Eng. Technol. Ed. 2023, 53, 2686–2694. [Google Scholar]
- Li, Y.; Xu, L.; Lv, L.; Shi, Y.; Yu, X. Study on Modeling Method of a Multi-Parameter Control System for Threshing and Cleaning Devices in the Grain Combine Harvester. Agriculture 2022, 12, 1483. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.Z.; Li, Y.M.; Lv, L.Y.; Shi, M.L. Modeling and control methods of a multi-parameter system for threshing and cleaning in grain combine harvesters. Comput. Electron. Agric. 2024, 225, 15. [Google Scholar] [CrossRef]
- Fu, J.; Wang, C.; Cai, F.; Niu, W. Comparative Study on Frequency Domain Fatigue Analysis Methods for Half Axle of Combine Harvester. J. Mech. Strength 2022, 44, 203–214. [Google Scholar]
- Liu, W.J.; Chen, X.G.; Zeng, S. Design and Parameter Optimization of a Rigid-Flexible Coupled Rod Tooth Threshing Device for Ratoon Rice Based on MBD-DEM. Agriculture 2024, 14, 2083. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, Z.P.; Li, Y.F.; Song, Z.Q.; Yu, J.; Li, Y.M.; Xu, L.Z. Study of the grain particle-conveying performance of a bionic non-smooth-structure screw conveyor. Biosyst. Eng. 2024, 238, 94–104. [Google Scholar] [CrossRef]
- Xu, L.Z.; Chai, X.Y.; Gao, Z.P.; Li, Y.M.; Wang, Y.D. Experimental study on driver seat vibration characteristics of crawler-type combine harvester. Int. J. Agric. Biol. Eng. 2019, 12, 90–97. [Google Scholar] [CrossRef]
- Yu, Z.; Li, Y.; Du, X.; Liu, Y. Threshing cylinder unbalance detection using a signal extraction method based on parameter-adaptive variational mode decomposition. Biosyst. Eng. 2024, 244, 26–41. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Chen, L.; Zhang, T.; Liang, Z.; Huang, M.; Su, Z. Study on Performance of Concentric Threshing Device with Multi-Threshing Gaps for Rice Combines. Agriculture 2021, 11, 1000. [Google Scholar] [CrossRef]
- Su, Z.; Li, Y.; Dong, Y.; Tang, Z.; Liang, Z. Simulation of rice threshing performance with concentric and non-concentric threshing gaps. Biosyst. Eng. 2020, 197, 270–284. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Y.; Li, Y.; Ji, K. Research and Experiment on Variable-Diameter Threshing Drum with Movable Radial Plates for Combine Harvester. Agriculture 2023, 13, 1487. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Ji, K.; Yu, Z.; Ma, Z.; Xu, L.; Niu, C. Development of a hydraulic variable-diameter threshing drum control system for combine harvester part I: Adaptive monitoring method. Biosyst. Eng. 2025, 250, 174–182. [Google Scholar] [CrossRef]
- Shi, R.; Chang, L.; Zhao, W.; Dai, F.; Liang, Z. Simulation of Flax Threshing Process by Different Forms of Threshing Drums in Combined Harvesting. Agronomy 2025, 15, 36. [Google Scholar] [CrossRef]
- Wang, Z.P.; Zuo, Y.Y.; Sun, L.M. The Impact of Sound Pressure Level, Loudness, Roughness, Sharpness, Articulation Index, Hand Vibration, and Seat Vibration on Subjective Comfort Perception of Tractor Drivers. Symmetry 2023, 15, 16. [Google Scholar] [CrossRef]
- Wang, X.Z.; Cao, Y.H.; Fang, W.Q.; Sheng, H.R. Vibration Test and Analysis of Crawler Pepper Harvester under Multiple Working Conditions. Sustainability 2023, 15, 16. [Google Scholar] [CrossRef]
- Wang, L.; Wang, G.Q.; Zhai, X.J.; Tang, Z.; Wang, B.Z.; Li, P.C. Response Characteristics of Harvester Bolts and the Establishment of the Strongest Response Structure’s Kinetic Model. Agriculture 2024, 14, 1174. [Google Scholar] [CrossRef]
- Gu, X.Y.; Zhang, B.; Tang, Z.; Zhang, H.; Wang, H.Y. Structural Optimization of Combine Harvester Plate-Shell Undergoing Multi-Source Excitation. Appl. Sci. 2022, 12, 20. [Google Scholar] [CrossRef]
- Yu, Z.W.; Li, Y.M.; Xu, L.Z.; Du, X.X.; Ji, K.Z. Unbalanced variation after assembly and double-speed influence coefficient method in the threshing drum. Int. J. Agric. Biol. Eng. 2023, 16, 1–10. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, H.; Wang, X.Z.; Gu, X.Y.; Zhang, B.; Liu, S.F. Rice threshing state prediction of threshing cylinder undergoing unbalanced harmonic response. Comput. Electron. Agric. 2023, 204, 11. [Google Scholar] [CrossRef]
- Li, H.B.; Chen, L.W.; Zhang, Z.Y. A Study on the Utilization Rate and Influencing Factors of Small Agricultural Machinery: Evidence from 10 Hilly and Mountainous Provinces in China. Agriculture 2023, 13, 25. [Google Scholar] [CrossRef]
- Bian, X.Y.; Shi, Z.G.; Sun, Z.; Shi, L.; Yan, X.S.; Mo, N. Automatic Balancing for AMB-Rotor System Using Adaptive Period Iteration Control with a Novel Rotating Speed Estimator. IEEE Sens. J. 2023, 23, 17173–17186. [Google Scholar] [CrossRef]
- Han, W.J.; Cai, Y.W.; Han, W.T.; Yin, Z.Y.; Ren, Y.; Wang, W.J.; Yu, C.M. A Method for Suppressing Mass Imbalance Vibration of Magnetically Suspended Rotor-Based on Multifrequency Adaptive Estimation. IEEE Sens. J. 2022, 22, 23793–23805. [Google Scholar] [CrossRef]
- Pang, J.; Li, Y.; Ji, J.; Xu, L. Vibration excitation identification and control of the cutter of a combine harvester using triaxial accelerometers and partial coherence sorting. Biosyst. Eng. 2019, 185, 25–34. [Google Scholar] [CrossRef]
- Faheem, M.; Liu, J.; Chang, G.; Abbas, I.; Xie, B.; Shan, Z.; Yang, K. Experimental Research on Grape Cluster Vibration Signals during Transportation and Placing for Harvest and Post-Harvest Handling. Agriculture 2021, 11, 902. [Google Scholar] [CrossRef]
- Cole, M.O.T.; Keogh, P.S.; Burrows, C.R. Control of multifrequency rotor vibration components. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2002, 216, 165–177. [Google Scholar] [CrossRef]
- Dai, D.; Chen, D.; Wang, S.; Li, S.; Mao, X.; Zhang, B.; Wang, Z.; Ma, Z. Compilation and Extrapolation of Load Spectrum of Tractor Ground Vibration Load Based on CEEMDAN-POT Model. Agriculture 2023, 13, 125. [Google Scholar] [CrossRef]
- Patil, S.S.; Gaikwad, J.A. Vibration Analysis of Electrical Rotating Machines using FFT A method of predictive maintenance. In Proceedings of the 4th International Conference on Computing, Communications and Networking Technologies (ICCCNT), Tiruchengode, India, 4–6 July 2013. [Google Scholar]
- Gao, Y.; Yang, Y.; Fu, S.; Feng, K.; Han, X.; Hu, Y.; Zhu, Q.; Wei, X. Analysis of Vibration Characteristics of Tractor–Rotary Cultivator Combination Based on Time Domain and Frequency Domain. Agriculture 2024, 14, 1139. [Google Scholar] [CrossRef]
- Klausen, A.; Robbersmyr, K.G. Cross-correlation of whitened vibration signals for low-speed bearing diagnostics. Mech. Syst. Signal Process. 2019, 118, 226–244. [Google Scholar] [CrossRef]
- Gan, M.; Wang, C.; Zhu, C.A. Fault feature enhancement for rotating machinery based on quality factor analysis and manifold learning. J. Intell. Manuf. 2018, 29, 463–480. [Google Scholar] [CrossRef]
- Stander, C.J.; Heyns, P.S. Transmission path phase compensation for gear monitoring under fluctuating load conditions. Mech. Syst. Signal Process. 2006, 20, 1511–1522. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, Z.; Zhang, Z.; Song, Z.; Liu, Y.; Li, Y.; Xu, L. Durable Testing and Analysis of a Cleaning Sieve Based on Vibration and Strain Signals. Agriculture 2023, 13, 2232. [Google Scholar] [CrossRef]
- Xin, Y.; Li, S.M.; Zhang, Z.Z. Adaptive Reinforced Empirical Morlet Wavelet Transform and Its Application in Fault Diagnosis of Rotating Machinery. IEEE Access 2019, 7, 65150–65162. [Google Scholar] [CrossRef]
- Qin, Q.; Zhu, F.; Yang, F.; Yin, L. Fault Feature Extraction of Rolling Bearings Based on Full Vector Improved Continuous Harmonic Wavelet Packet. Mech. Sci. Technol. Aerosp. Eng. 2023, 42, 2040–2046. [Google Scholar]
- Carassale, L. Analysis of the Synchronous Response of Rotor Components by Wavelet Transform and Wavelet Probing. J. Eng. Gas Turbines Power 2024, 146, 041017. [Google Scholar] [CrossRef]
- Gao, Y.; Hu, Y.; Yang, Y.; Feng, K.; Han, X.; Li, P.; Zhu, Y.; Song, Q. Optimization of Operating Parameters for Straw Returning Machine Based on Vibration Characteristic Analysis. Agronomy 2024, 14, 2388. [Google Scholar] [CrossRef]
- Khatua, P.; Ray, K.C. An Efficient DCT-II Based Harmonic Wavelet Transform for Time-Frequency Analysis. J. Signal Process. Syst. Signal Image Video Technol. 2022, 94, 1381–1394. [Google Scholar] [CrossRef]
- Ji, K.; Li, Y.; Liu, Y.; Yu, Z.; Cheng, J. Vibration Signal Extraction and Analysis of Combine Harvester Based on Low-Pass Filter-Eemd Combination. Eng. Agric. 2025, 44, e20240006. [Google Scholar] [CrossRef]
- Hang, X.C.; Lu, Z.R.; Yao, Q.W.; Jiang, D. A novel unbalanced signal extraction method based on quadratic SSA-VMD for micro-motor rotor. J. Mech. Sci. Technol. 2024, 38, 3327–3338. [Google Scholar] [CrossRef]
- Keji, Y. Application of an Adaptive Filtering Method Based on Harmonic Wavelet for High Precision Dynamic Balancing Measurement. Chin. J. Sci. Instrum. 2005, 26, 1013–1015. [Google Scholar]
- Danthez, J.M.; Giroussens, C.; Aquilina, R. The Autocoherent Spectrum: A Useful Spectral Estimator For Vibration Analysis Of Rotating Machinery Accurate Estimation and Cancellation of Pure Tones. Mech. Syst. Signal Process. 1998, 12, 753–768. [Google Scholar] [CrossRef]
- Zeng, S.; Wang, X.X. Unbalance Identification and Field Balancing of Dual Rotors System with Slightly Different Rotating Speeds. J. Sound Vib. 1999, 220, 343–351. [Google Scholar] [CrossRef]
- Zhang, S.H.; Cai, Y.J. A new double-face online dynamic balance device and its control system for high speed machine tool spindle. J. Vib. Control 2016, 22, 1037–1048. [Google Scholar] [CrossRef]
- Srivastava, S.; Sahu, S.N.; Sekar, A.; Sundaram, N.S.; Kumar, S.S.; Hariharan, V.K. Low frequency high sensitive velocity pickup transducer for vertical dynamic balancing machine (VDBM). Ferroelectrics 2017, 519, 194–199. [Google Scholar] [CrossRef]
- Wang, T.Z.; Ding, Q. Modal balancing for ball bearing-rotor system using nonlinear normal modes. J. Sound Vib. 2023, 547, 20. [Google Scholar] [CrossRef]
- Li, Y.; Cui, Y.C.; Deng, S.R. Research on Sudden Unbalance Response of Rigid-Elastic-Oil Coupled Ball Bearings. Lubricants 2024, 12, 22. [Google Scholar] [CrossRef]
- Wu, D.H.; Wu, X. Research on the Influence of Noise to Weak Signal Detection Based on Duffing Equation. In Proceedings of the International Conference on Mechatronic Systems and Automation Systems (MSAS 2011), Xi’an, China, 23–24 July 2011. [Google Scholar]
- Pancóatl-Bortolotti, P.; Costa, A.H.; Enríquez-Caldera, R.A.; Guerrero-Castellanos, J.F.; Tello-Bello, M. Time-frequency high-resolution for weak signal detection using chaotic intermittence. Digit. Signal Process. 2023, 141, 11. [Google Scholar] [CrossRef]
- Su, L.; Yang, J. Weak Pulse Signal Detection Based on the Broad Learning Method under the Chaotic Background. J. Commun. Technol. Electron. 2022, 67, 430–442. [Google Scholar] [CrossRef]
- Wang, X.; Hong, T.; Fang, W.; Chen, X. Optimized Design for Vibration Reduction in a Residual Film Recovery Machine Frame Based on Modal Analysis. Agriculture 2024, 14, 543. [Google Scholar] [CrossRef]
- Jian, Y.; Qing, Y.; Jia, W. A New Vibration Phase Solution Method and Its Application in Dynamic Balance Analysis. Noise Vib. Control 2022, 42, 241–246. [Google Scholar]


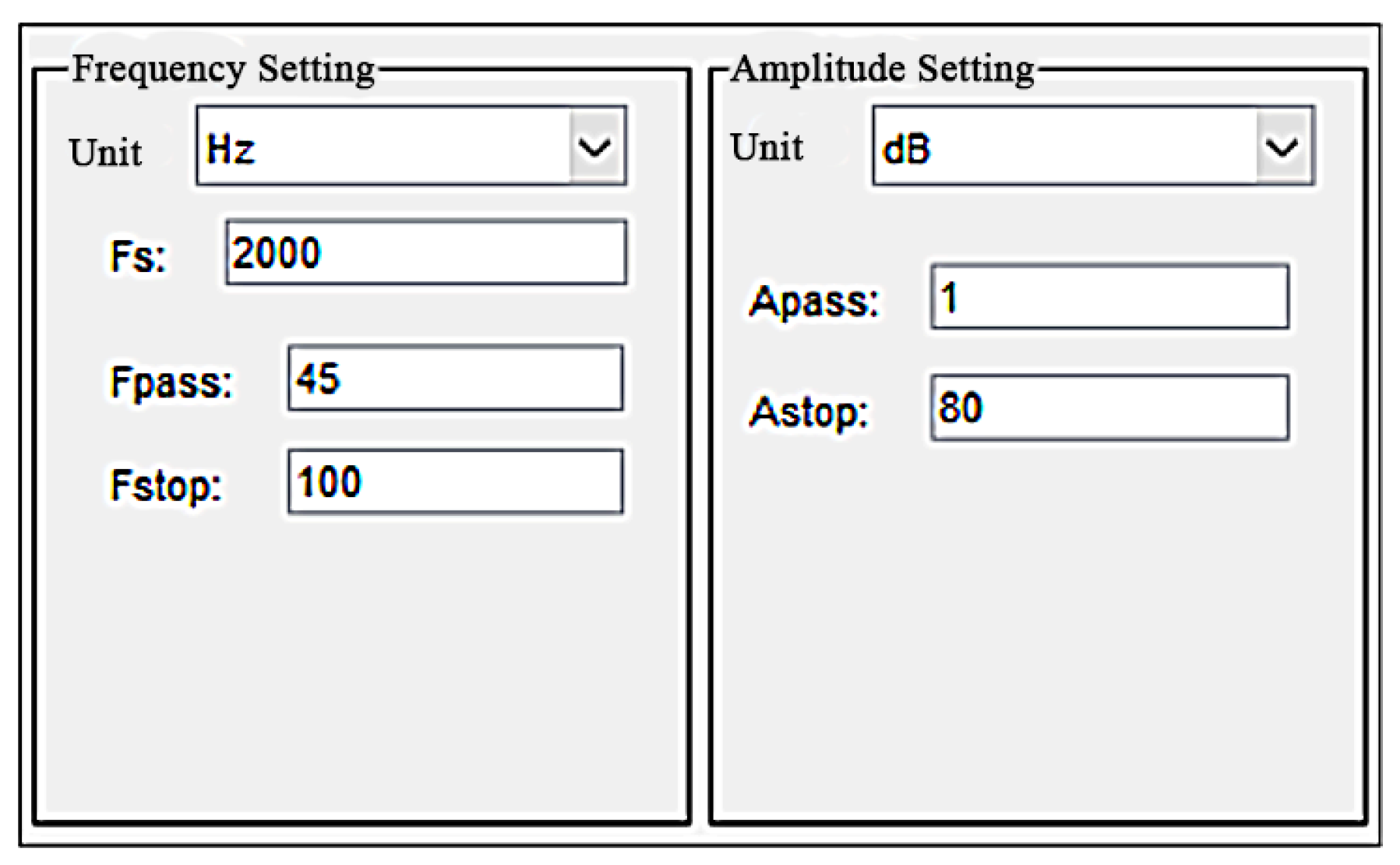
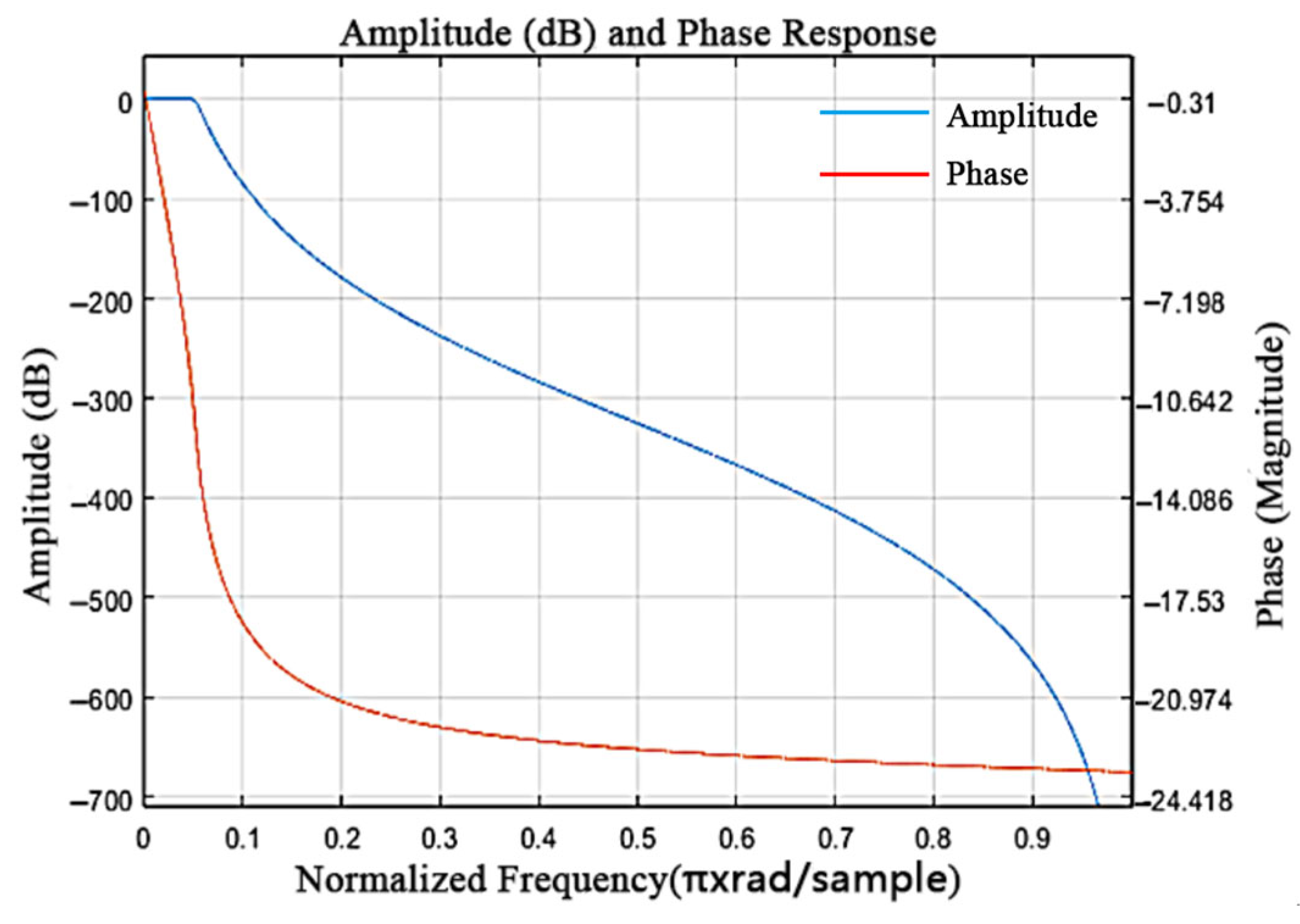
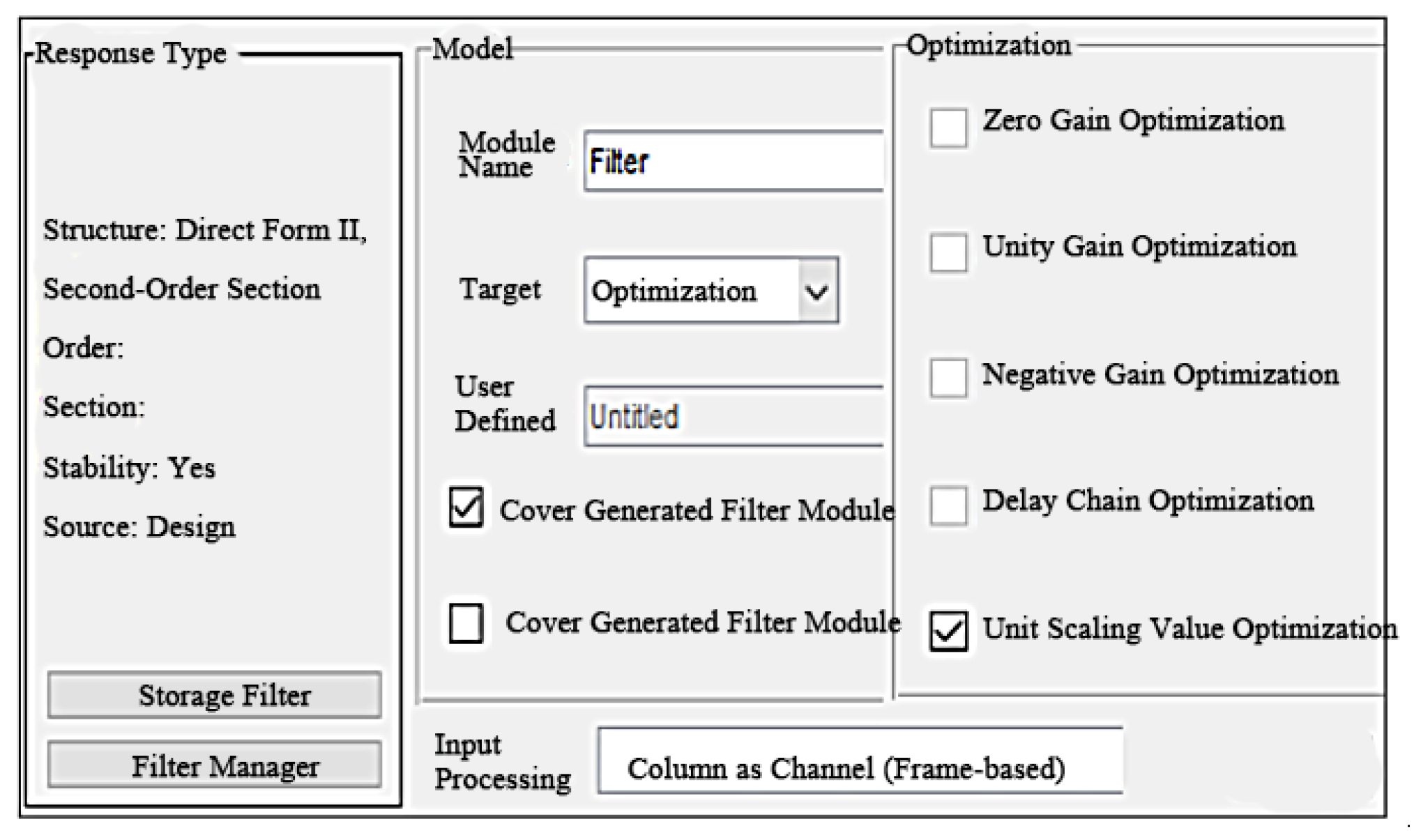
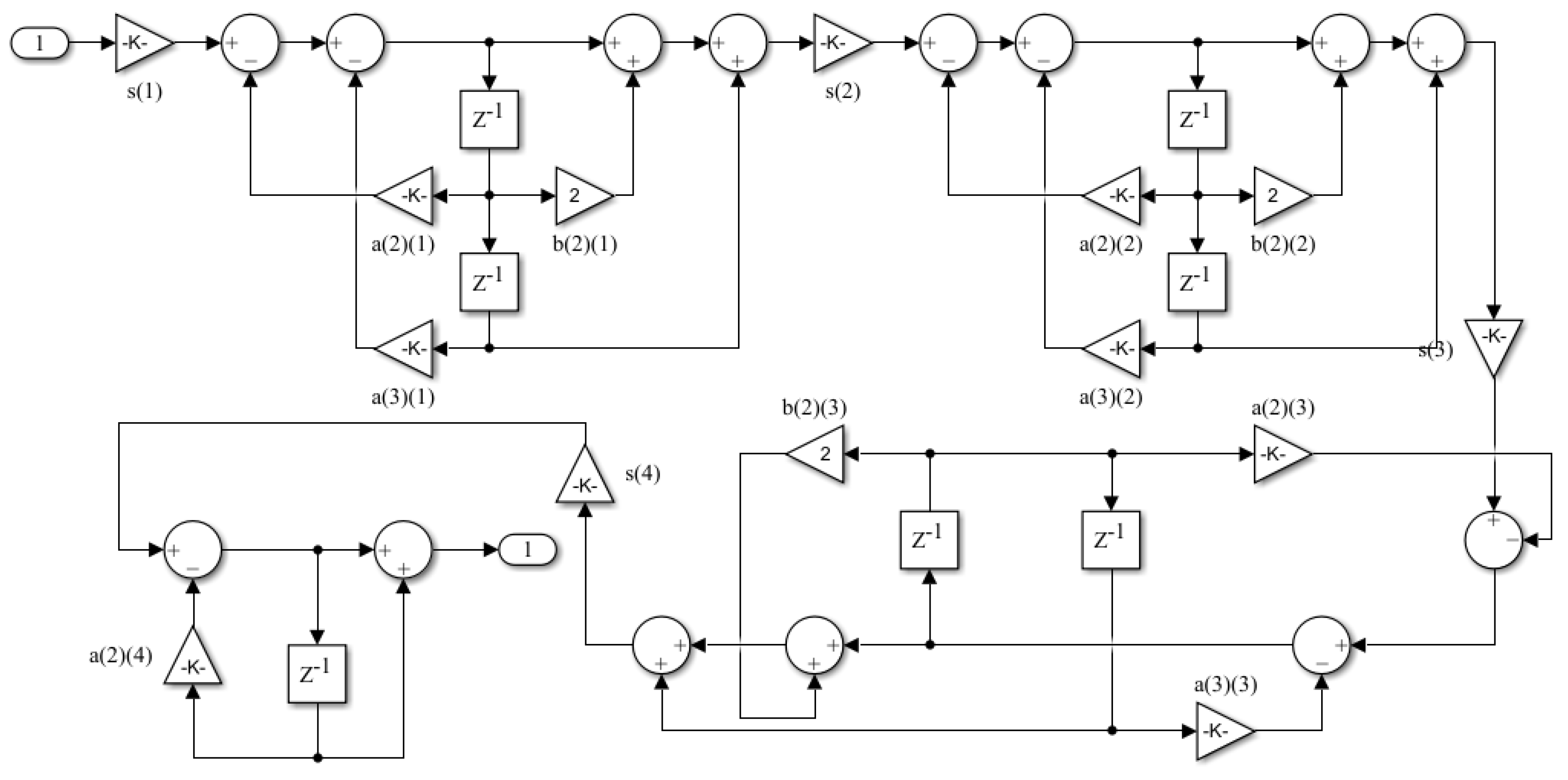

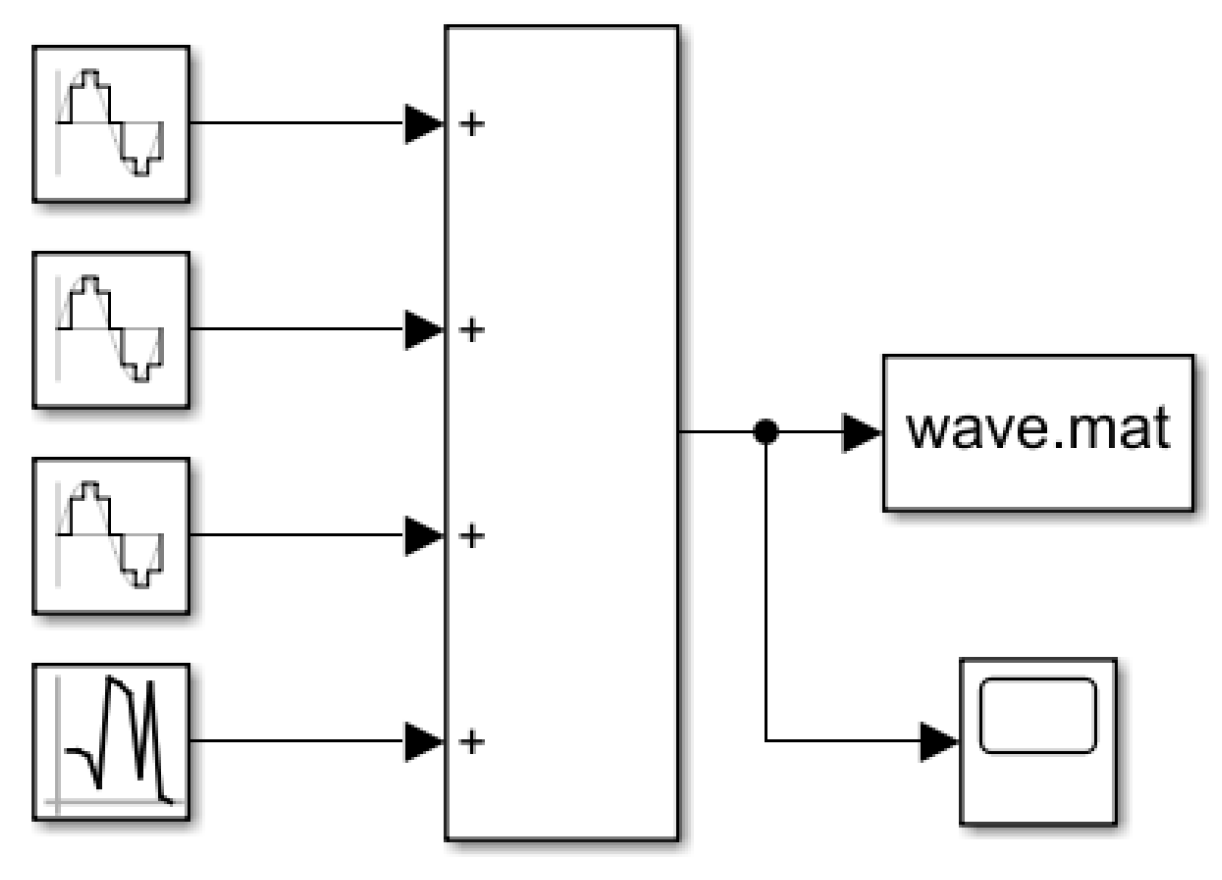



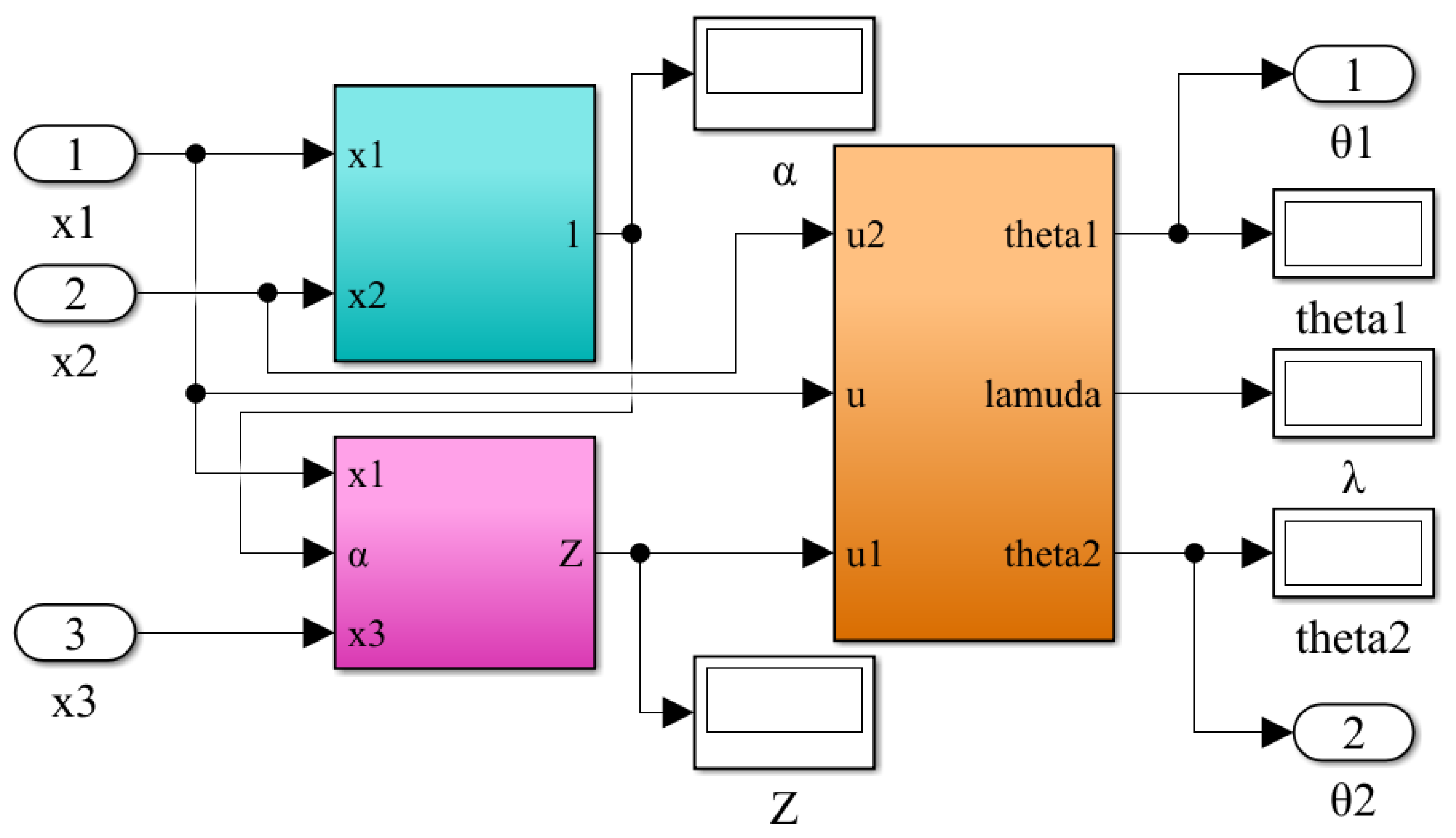

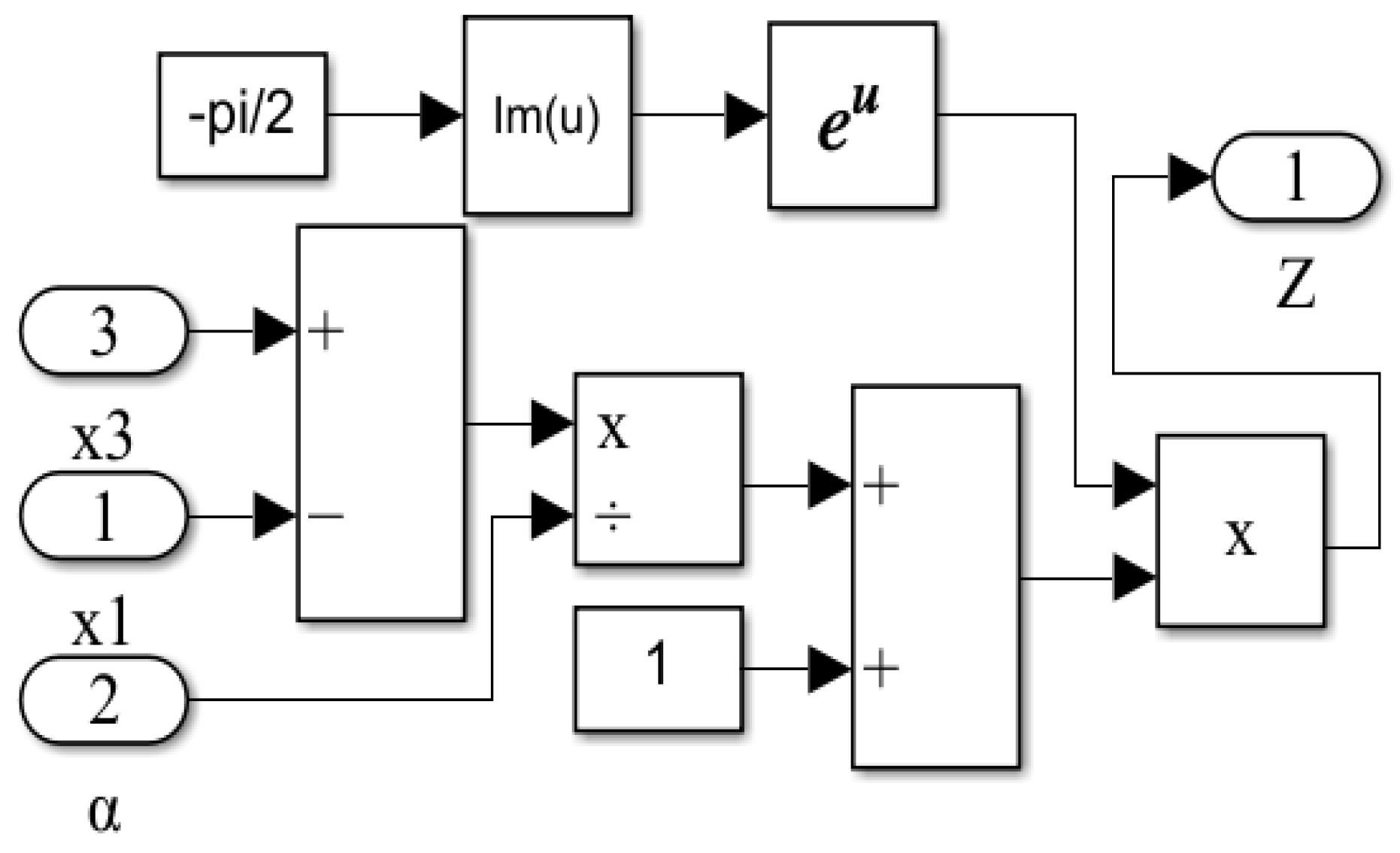
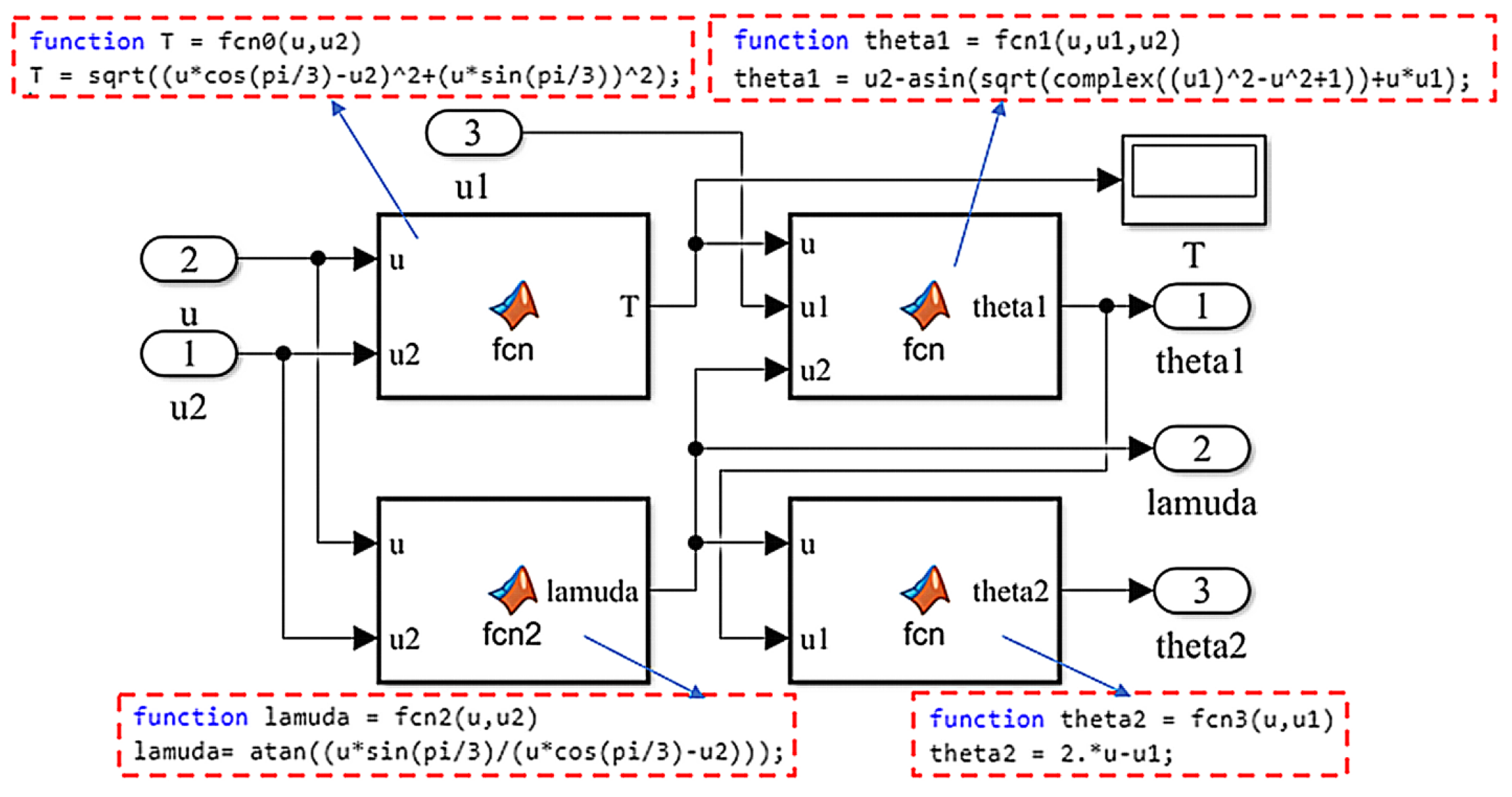

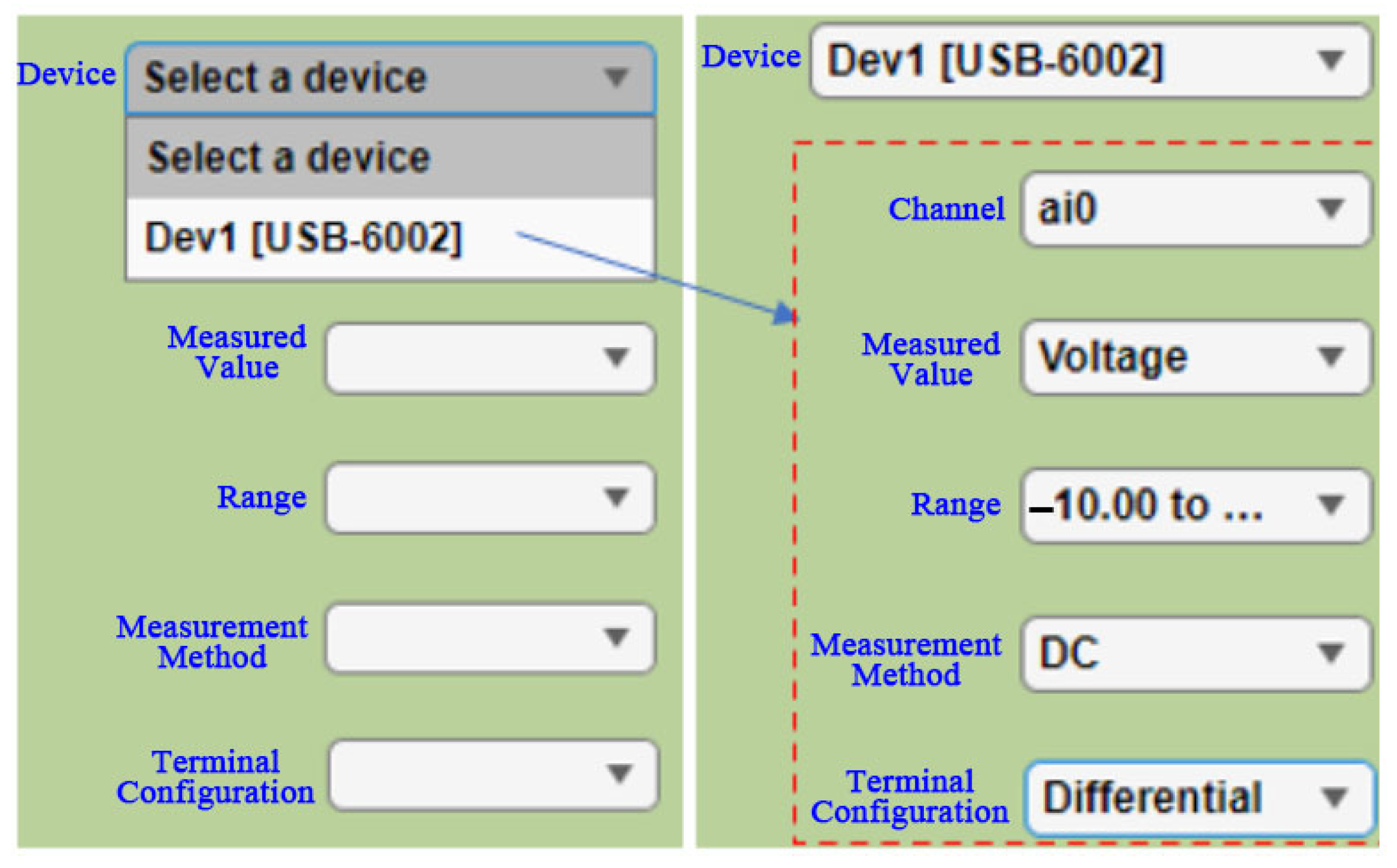
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Model | USB-6002 | Maximum transfer speed | 480 Mb/s |
| Resolution | 24-bit | Voltage input channel | 4-channel |
| Data bus interface | USB | IEPE input channel | 4-channel |
| Maximum sampling rate | 128 K | Input range | ±10 V |
| Number | Parameter | Value |
|---|---|---|
| 1 | Model | MPS-ACC01X ICP |
| 2 | Voltage sensitivity (mV/g) | 1008 |
| 3 | Transverse sensitivity (%) | ≤3 |
| 4 | Frequency range (Hz) | 0.1~8000 |
| 5 | Acceleration range (g) | ±5 |
| 6 | Amplitude nonlinearity (%) | 1 |
| Counterweight disc I | Parameters | Value | Counterweight disc II | Parameters | Value |
| Mass/g | 448.5 | Mass/g | 448.5 | ||
| Angle/° | 6.938 | Angle/° | −6.411 | ||
| Initial Test Weight | Parameters | Value | Secondary Test Weight | Parameters | Value |
| The rotation angle of counterweight disc I/° | 60 | The rotation angle of counterweight disc I/° | −60 | ||
| The rotation angle of counterweight disc II/° | 60 | The rotation angle of counterweight disc II/° | 120 | ||
| Vibration amplitude/m/s2 | 55.41 | Vibration amplitude/m/s2 | 20 | ||
| Process parameters | α | Z | T | λ | |
| 5.406 | 7 | 45.83 | −1.237 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, X.; Wang, B.; Tang, Z.; Zhang, H.; Zhang, H. Automatic Vibration Balancing System for Combine Harvester Threshing Drums Using Signal Conditioning and Optimization Algorithms. Agriculture 2025, 15, 1564. https://doi.org/10.3390/agriculture15141564
Gu X, Wang B, Tang Z, Zhang H, Zhang H. Automatic Vibration Balancing System for Combine Harvester Threshing Drums Using Signal Conditioning and Optimization Algorithms. Agriculture. 2025; 15(14):1564. https://doi.org/10.3390/agriculture15141564
Chicago/Turabian StyleGu, Xinyang, Bangzhui Wang, Zhong Tang, Honglei Zhang, and Hao Zhang. 2025. "Automatic Vibration Balancing System for Combine Harvester Threshing Drums Using Signal Conditioning and Optimization Algorithms" Agriculture 15, no. 14: 1564. https://doi.org/10.3390/agriculture15141564
APA StyleGu, X., Wang, B., Tang, Z., Zhang, H., & Zhang, H. (2025). Automatic Vibration Balancing System for Combine Harvester Threshing Drums Using Signal Conditioning and Optimization Algorithms. Agriculture, 15(14), 1564. https://doi.org/10.3390/agriculture15141564







