Optimizing the Design of Soil-Mixing Blade Structure Parameters Based on the Discrete Element Method
Abstract
1. Introduction
2. Materials and Methods
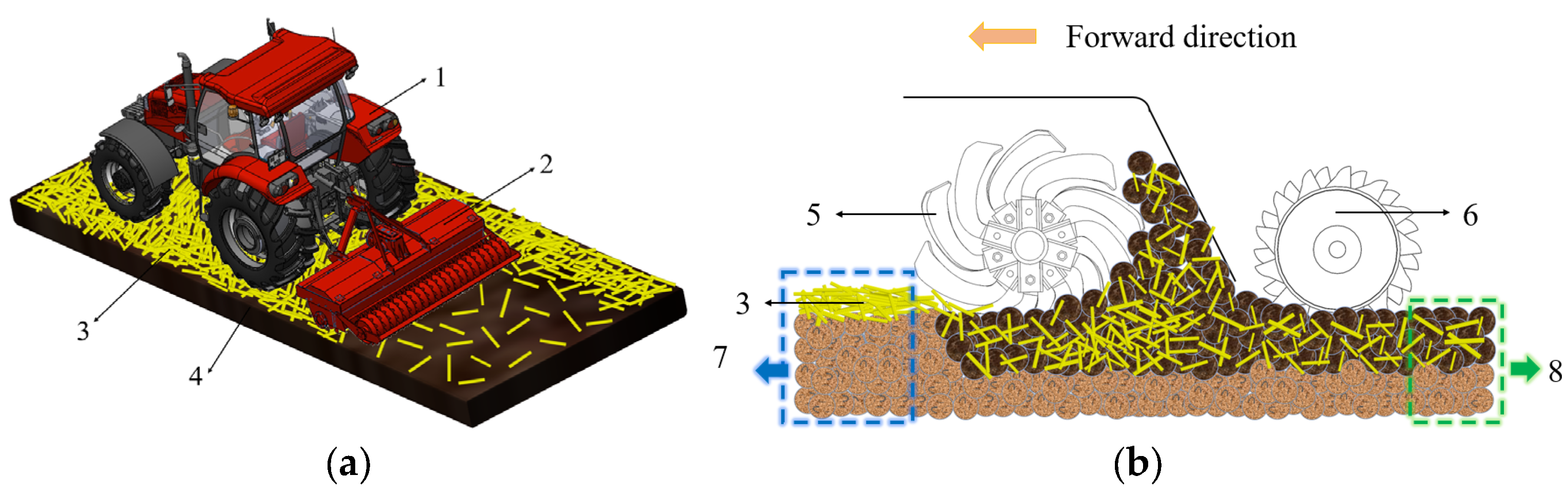
2.1. Design of the Soil-Mixing Blade
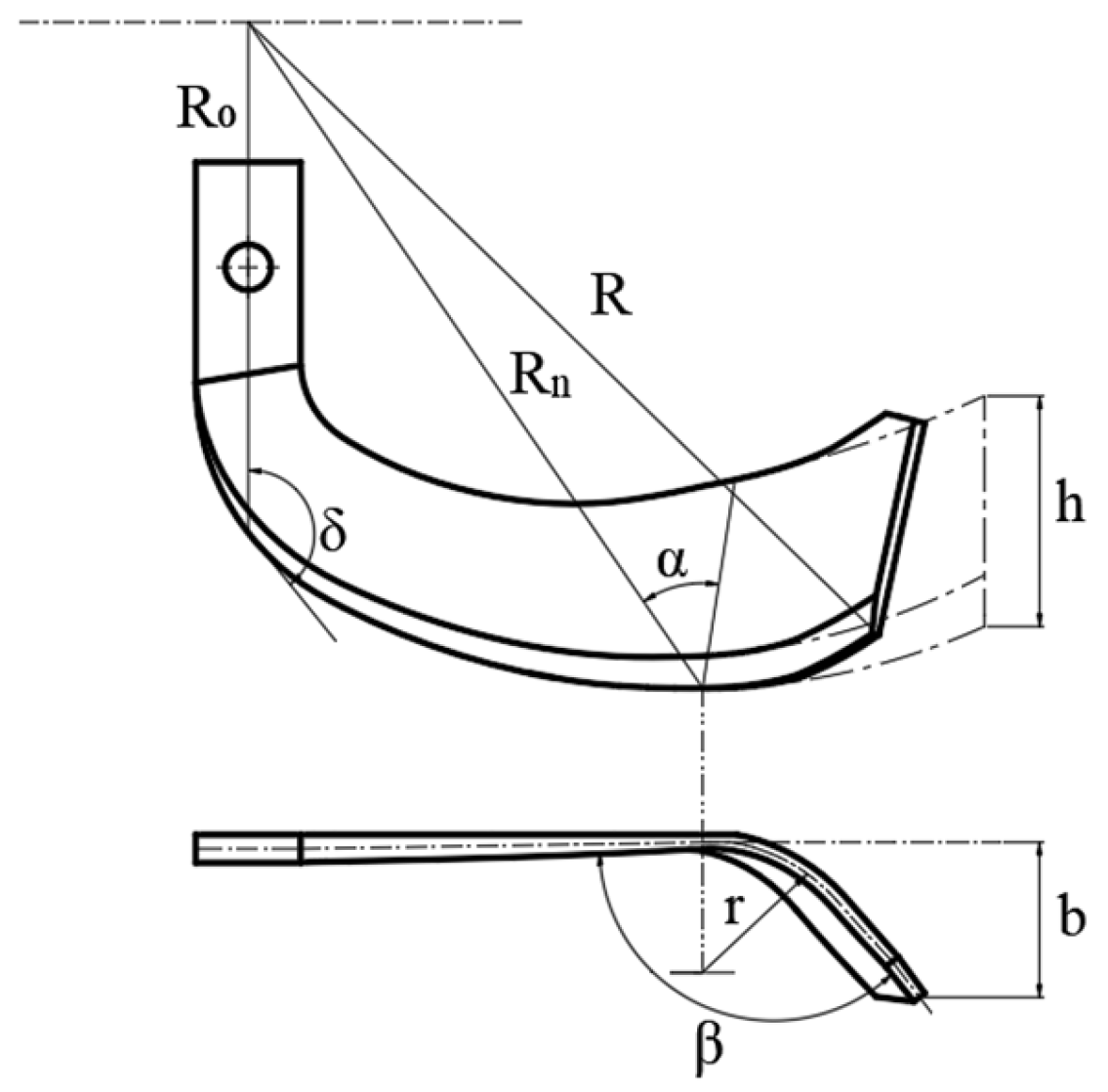
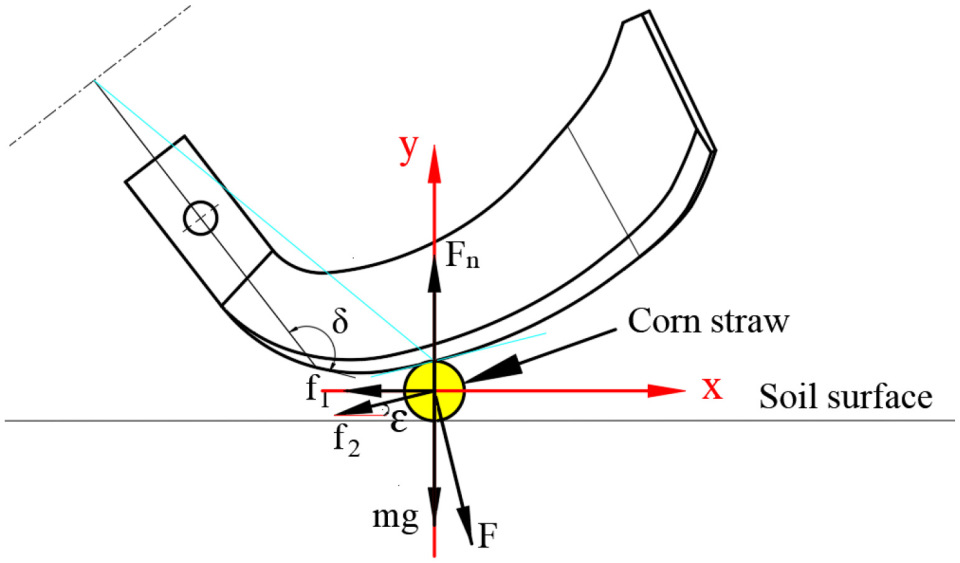
2.1.1. Soil-Mixing Blade Structure
- (1)
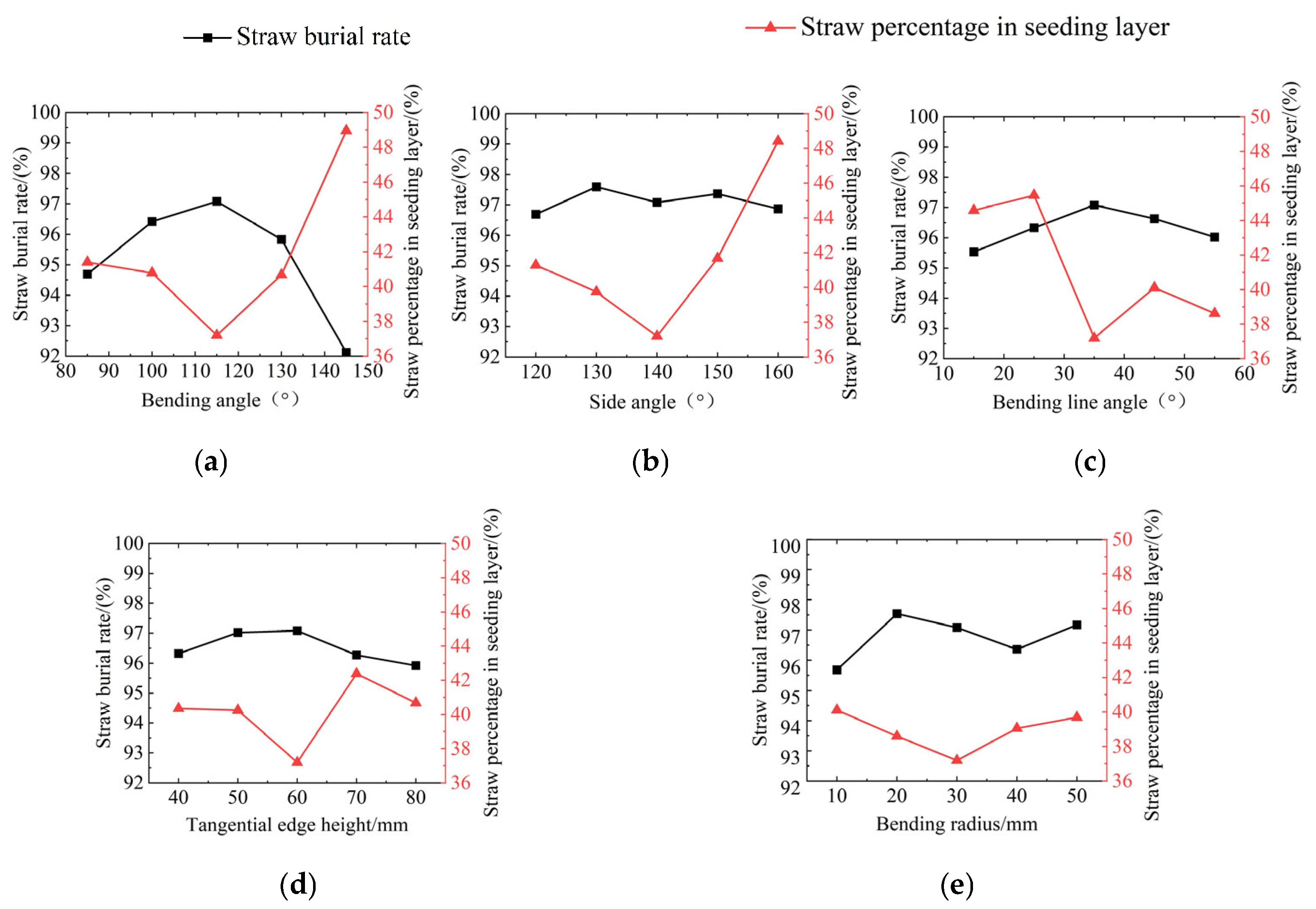
- The bending angle β, defined as the spatial angle between the tangential plane and the side-cutting plane of the soil-mixing blade, critically influences operational performance. Excessive values for β cause the blade tip to engage soil or root residues first, increasing mechanical stress and reducing service life. However, for insufficient β values, the bent section initially interacts with soil and corn stalks before they slide toward the side-cutting edge. This promotes clogging, elevates cutting resistance, and reduces straw incorporation efficiency [14,15].
- (2)
- The side angle δ is the angle between the side-cutting surface and the central line of the handle and affects the pressure exerted by the soil-mixing blade on the corn straw. When δ decreases appropriately, the pressure increases, promoting the rapid sliding of corn straw to the end of the side-cutting edge, which can reduce the carryback of straw.
- (3)
- The bending line angle α affects the relative acceleration between soil particles and the blade surface. A smaller α angle can enhance the soil acceleration effect but will increase the soil penetration resistance [16].
- (4)
- If the tangential edge height h is too small, the quality of soil throwing and crushing is poor. However, when it is too large, the cultivation resistance will increase and the bending part will be more prone to breakage [17].
- (5)
- A bending radius r that is too small will reduce the strength at the bending point of the soil-mixing blade, making it prone to sticking in soil and shortening its service life. However, a bending radius that is too large will increase the unevenness of the soil at the bottom of the trench [18].
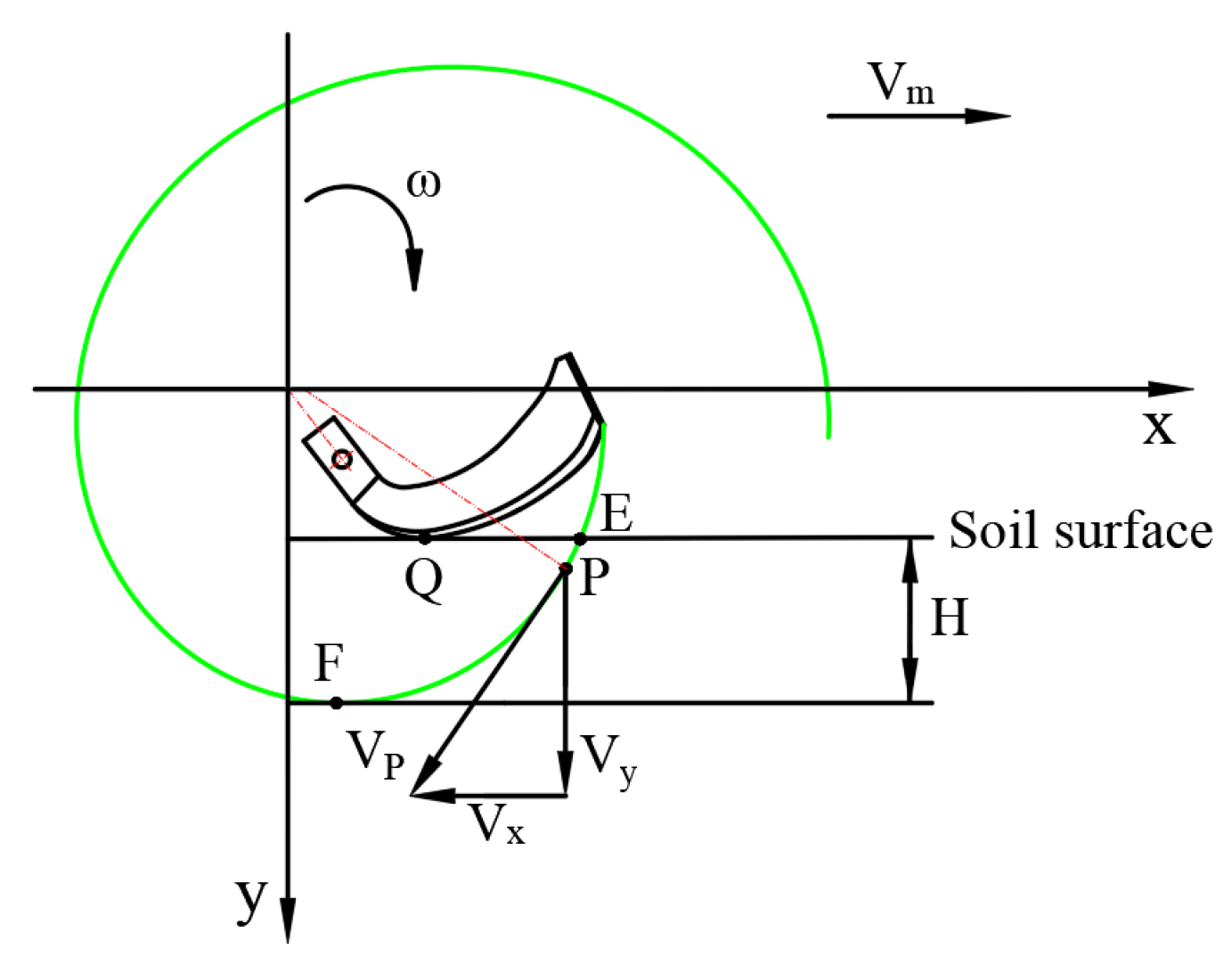
2.1.2. Motion Theory Analysis
2.1.3. Soil-Mixing Blade Tillage Depth
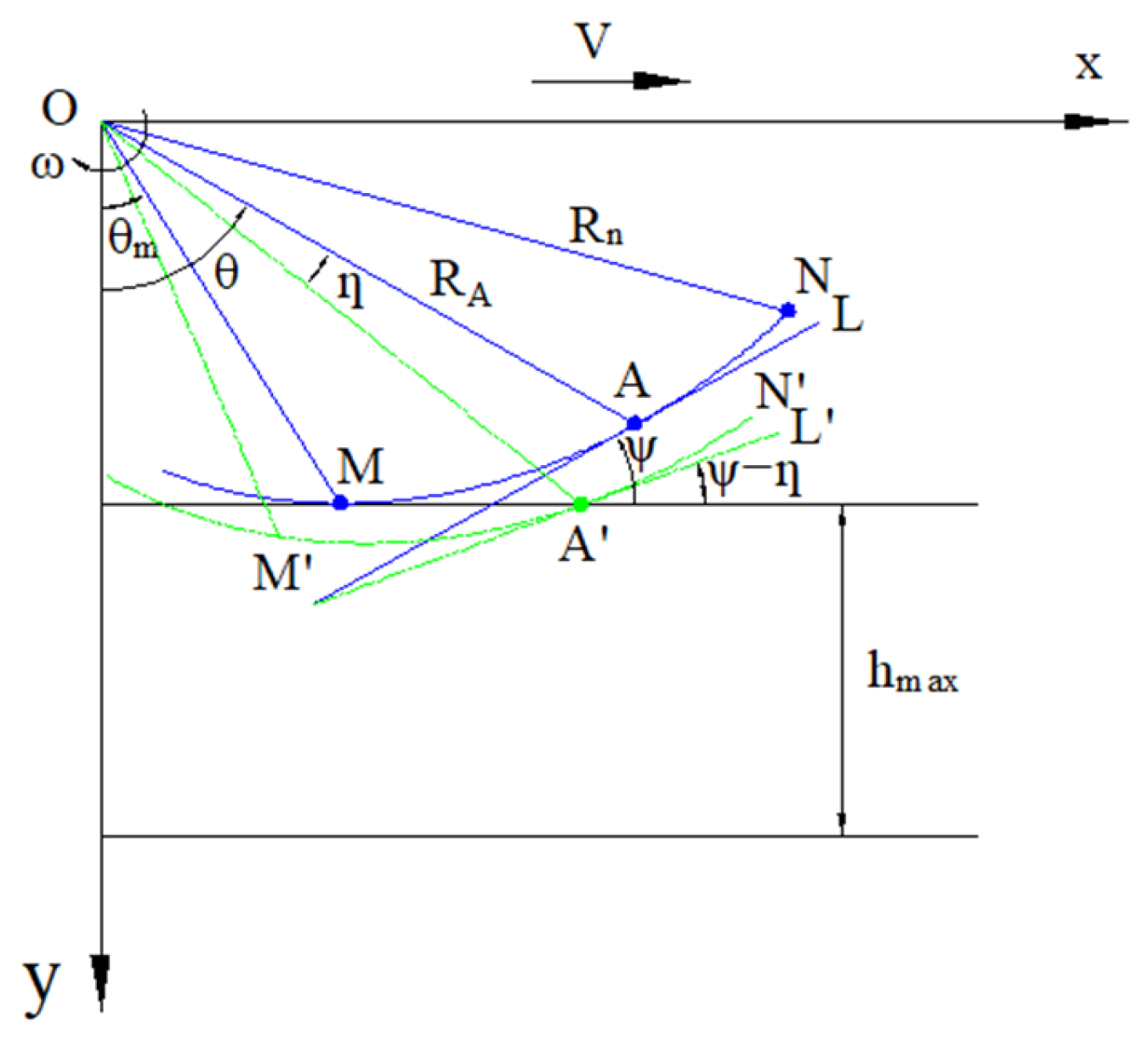
2.1.4. Conditions for the Soil-Mixing Blade to Minimize Straw Percentage in the Seeding Layer
2.1.5. Conditions for the Soil-Mixing Blade to Minimize Straw Back-Throwing
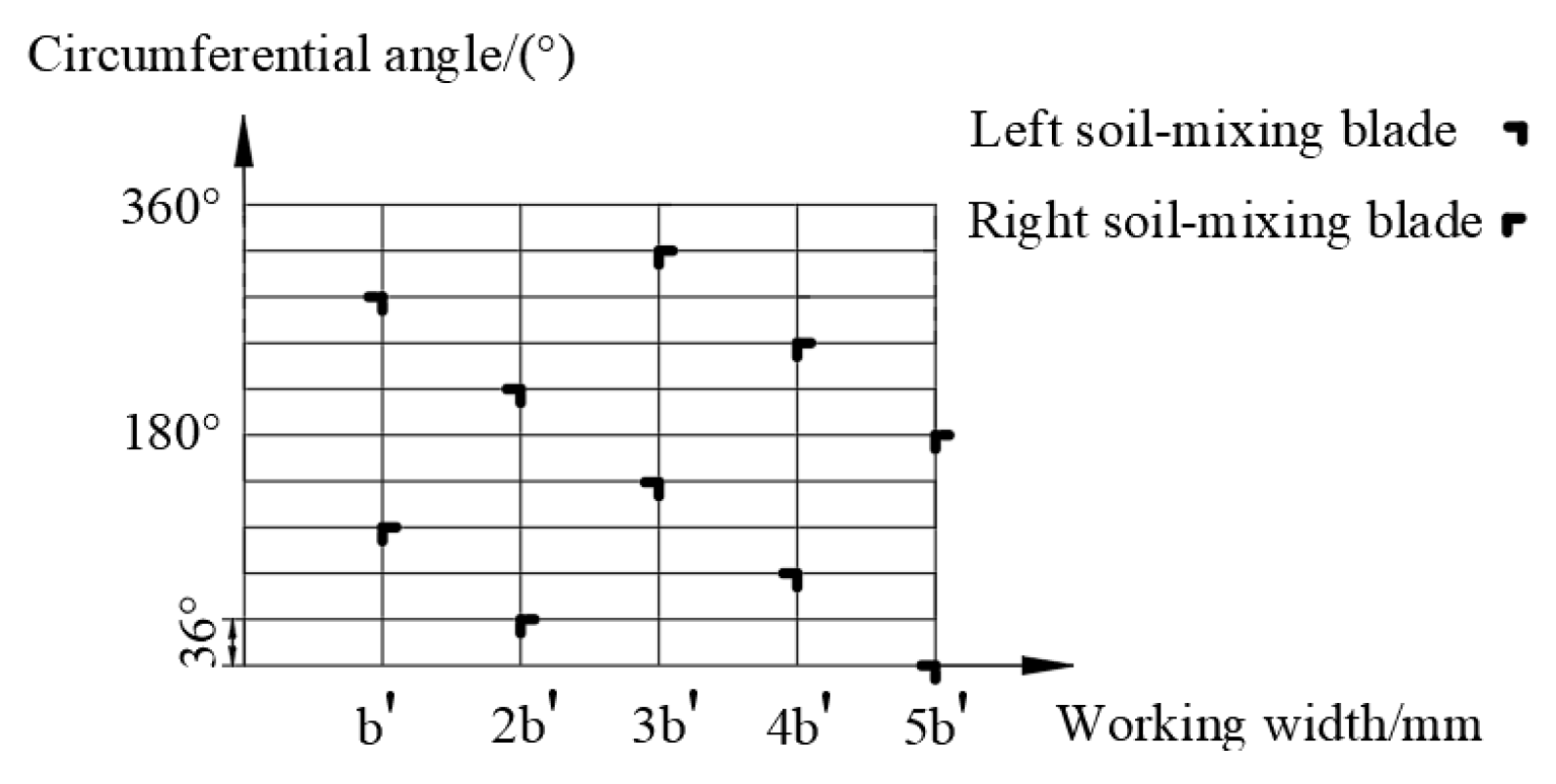
2.1.6. Soil-Mixing Blade Arrangement
2.2. Soil–Soil-Mixing Blade–Corn Straw Interaction Discrete Element Model Establishment
2.2.1. Soil-Mixing Blade Roller Model
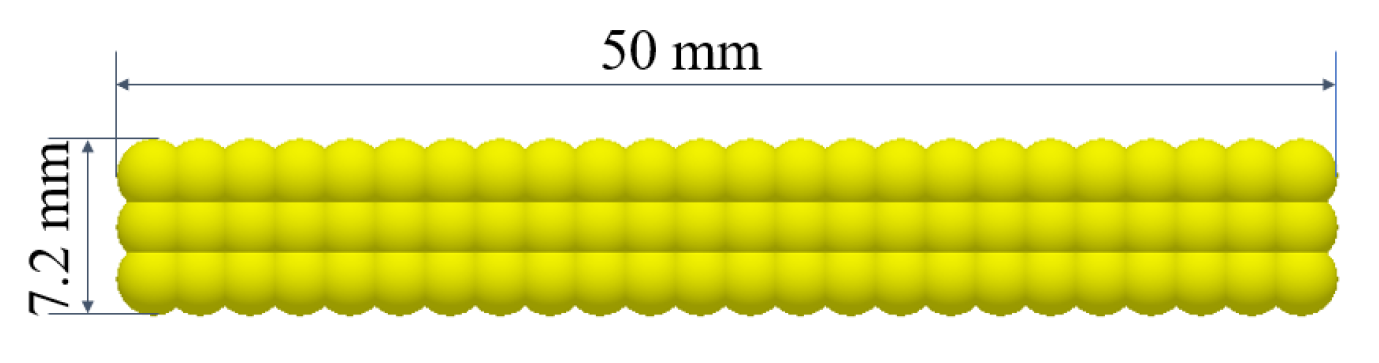
2.2.2. Soil and Corn Straw Model
2.2.3. Soil Contact Model
2.2.4. Overall Model
2.3. Data Collection and Processing
2.3.1. Straw Burial Rate
2.3.2. Straw Percentage in the Seeding Layer
3. Results and Discussion
3.1. Single-Factor Experiment
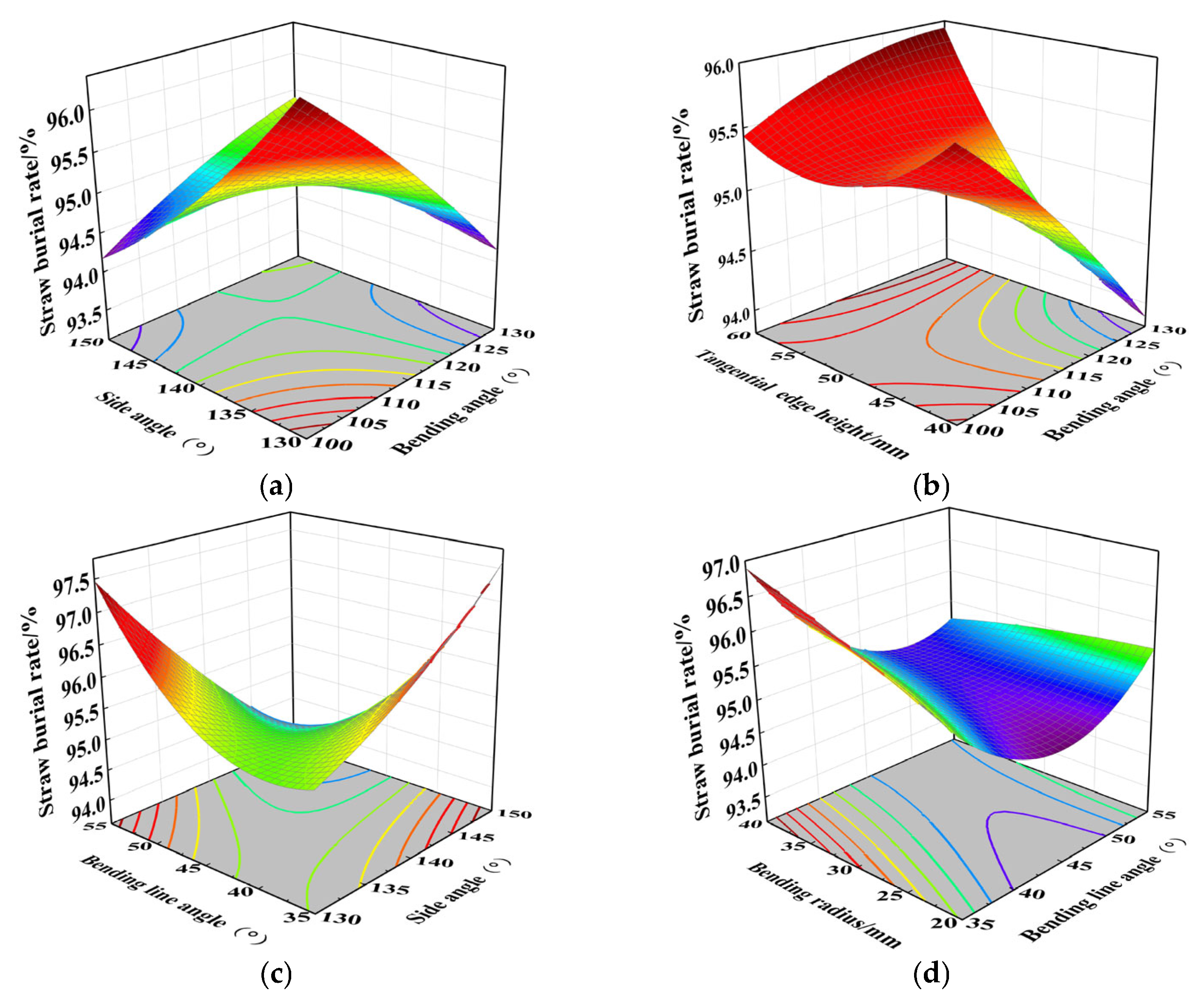
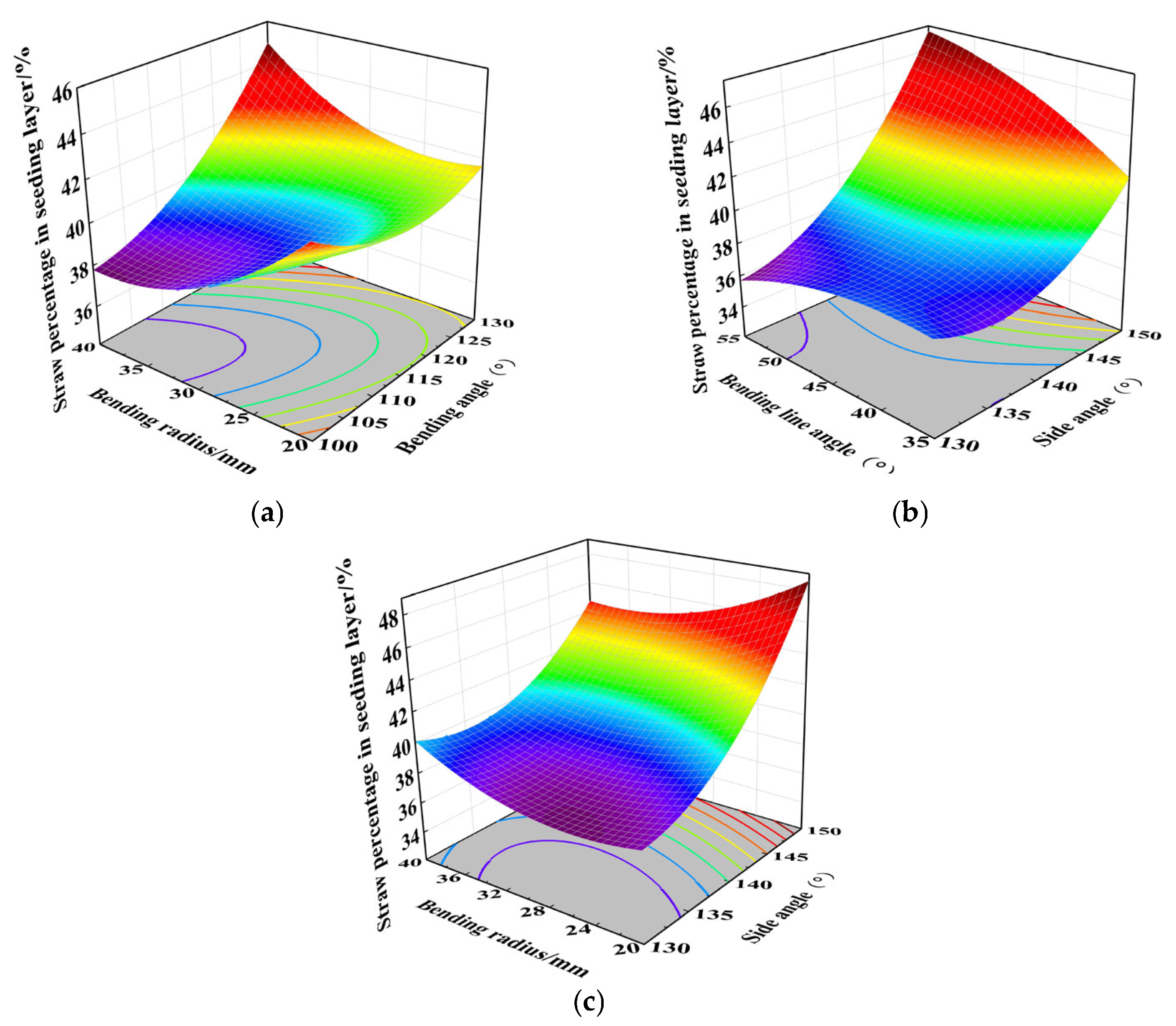
3.2. Box–Behnken Experiment
- (1)
- Straw burial rate regression model and response surface methodology analysis
- (2)
- Seeding layer straw percentage regression model and response surface methodology analysis
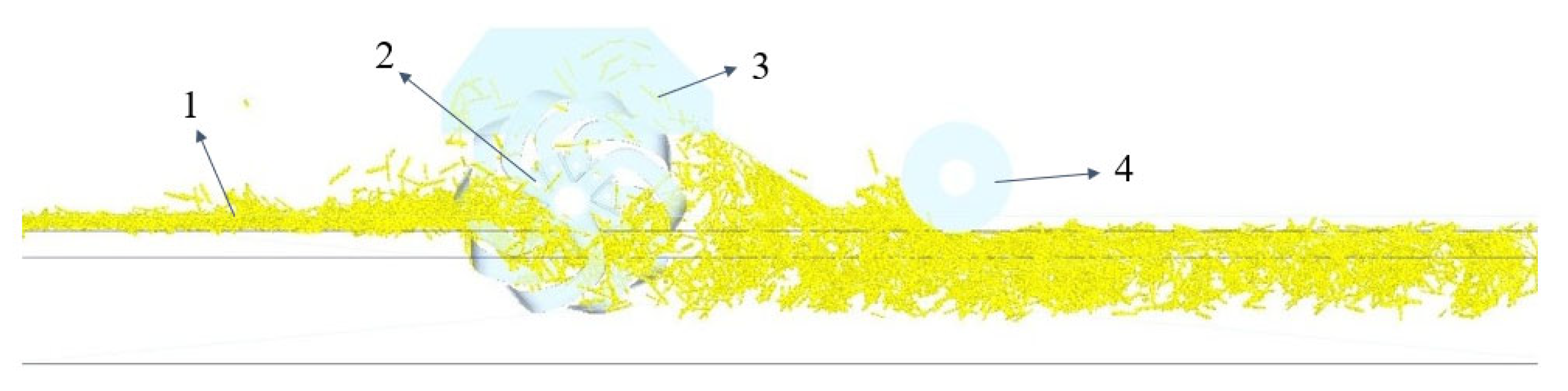
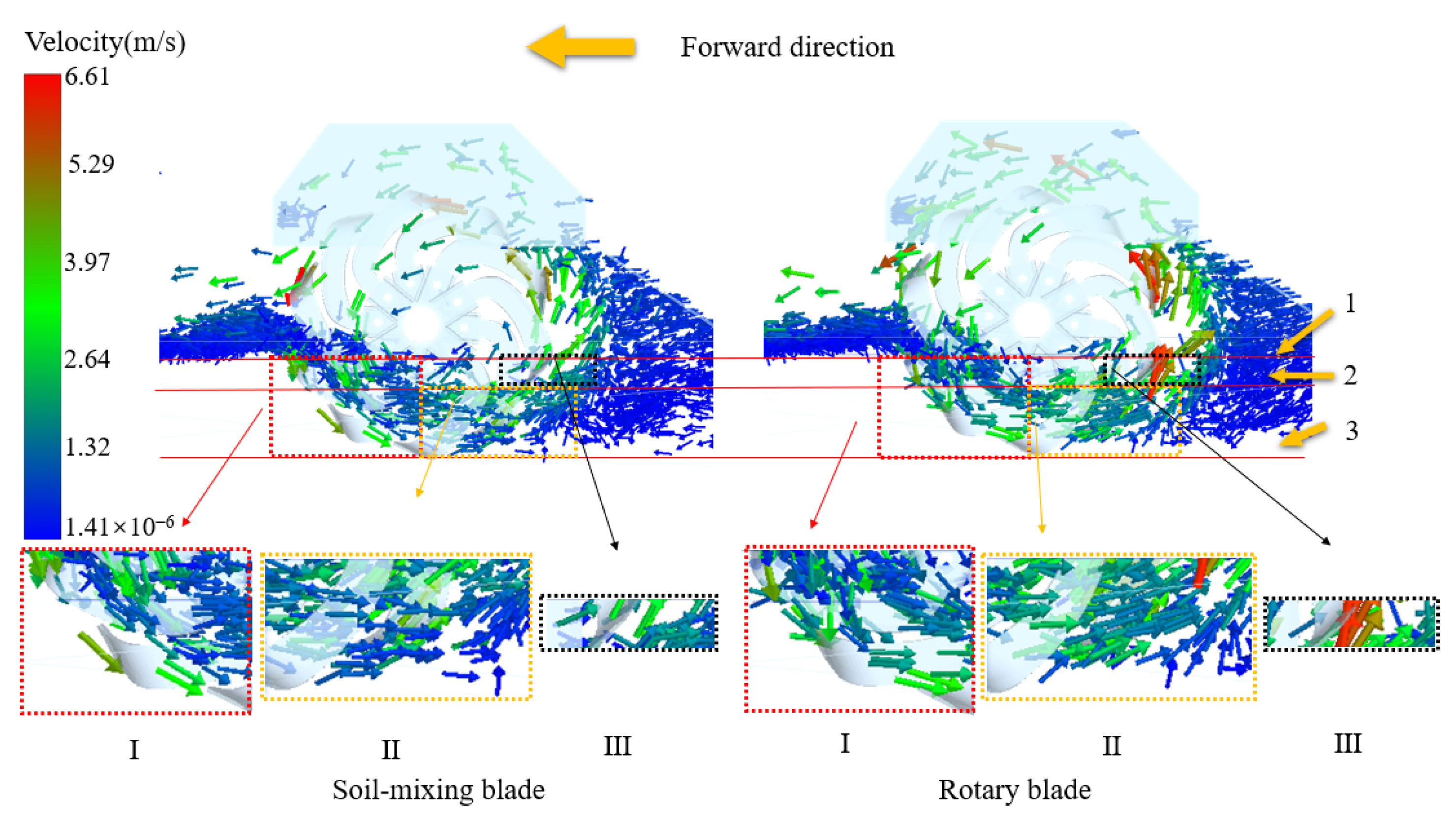
3.3. Spatial Motion Analysis of Corn Straw
3.3.1. Dynamic Analysis of Velocity Variation During the Corn Straw Burial Process
- I.
- During the stage of the cutter entering the soil to the maximum tillage depth, in the soil-mixing blade’s working area, approximately 82.6% of the corn straw particle movements are consistent with the rotational direction of the cutter as the soil-mixing blade moves deeper into the soil. However, during rotary blade operation, the movement of the corn straw exhibits a multi-directional distribution.
- II.
- During the soil penetration phase from the maximum tillage depth to the seeding layer, the straw’s velocity within the soil-mixing blade operation zone remained predominantly below 1 m/s, with velocity vectors maintaining <15° inclination relative to the horizontal plane. This kinematic behavior facilitated the stable retention of corn straw below the 50 mm soil depth. In contrast, a clear recirculation zone forms behind the rotary blade, where the average speed of the corn straw is greater than 1.5 m/s. The velocity vector forms an angle of 40° ± 6° with the horizontal plane, causing 31.7% of the straw particles to be carried back to the 0–50 mm sowing layer.
- III.
- From the sowing layer to the stage of detachment from the soil, the mixing blade maintained low straw velocities of <1.5 m/s for most of the corn straw particles, with only 5.3% exhibiting slight back-throwing (velocity vectors >30° to the horizontal plane). In contrast, the rotary blade generated a high-velocity straw flow, reaching peak velocities of 6.61 m/s and with near-vertical upward trajectories (with an angle > 80° to the horizontal plane), resulting in severe straw back-throwing.
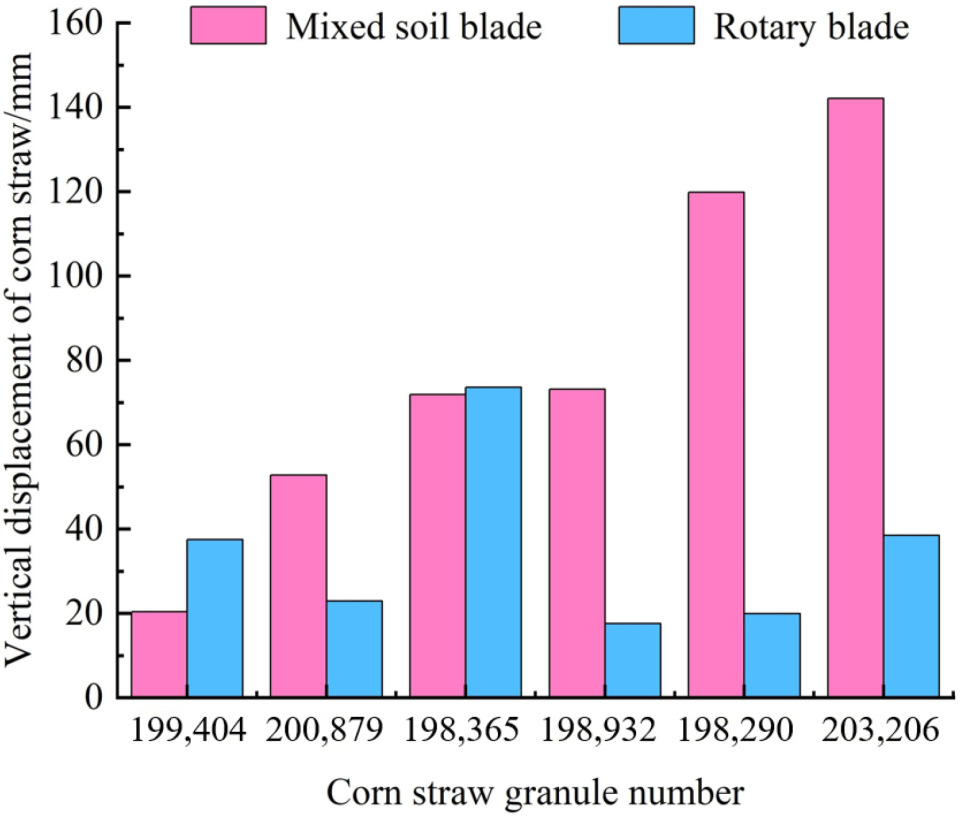
3.3.2. Comparative Analysis of the Vertical Motion Displacement of Corn Straw
3.4. Field Experiment
4. Conclusions
- (1)
- The mechanical structure of the soil-mixing blade was designed based on the characteristic parameters of its cutting-edge curve. Through the theoretical analysis of key operational factors—including the tillage depth, the conditions for the soil-mixing blade to minimize straw percentage in the seeding layer, and the conditions for the soil-mixing blade to minimize straw back-throwing—a mathematical model of the mixing blade’s working process was established.
- (2)
- A discrete element model of the soil-mixing blade–soil–corn straw interaction was developed, employing the Hertz–Mindlin with bonding contact model to simulate soil fragmentation dynamics. The corn straw morphology was represented by spherical particle assemblies, enabling the dynamic simulation of soil breakage and straw migration and burial during the operation of the soil-mixing blade. This provided an effective tool for analyzing blade performance.
- (3)
- Using the straw burial rate and straw percentage in the seeding layer as evaluation metrics, the Box–Behnken design yielded the soil-mixing blade’s optimal parameter combination, which was a bending line angle α of 55°, a bending angle β of 100.01°, a side angle δ of 130°, a tangential edge height h of 40.05 mm, and bending radius r of 28.67 mm. Simulation results predicted a straw burial rate of 96.04% and a straw percentage in the seeding layer of 35.25%, while field tests recorded a straw burial rate of 96.54% and a straw percentage in the seeding layer of 34.13%.
- (4)
- The velocity distribution of straw movement across different soil layers was analyzed during the operation of both the soil-mixing and rotary blades. By tracking motion trajectories, the vertical displacement of straw within the soil layer was quantified. From a kinematic perspective, this study elucidated the mechanism by which the soil-mixing blade reduces straw back-throwing and enhances straw transfer to deeper soil layers. These findings validate the experimental results and provide theoretical support for optimizing the operational performance of soil-mixing blades.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DEM | Discrete Element Method |
| RGB | Red Green Blue |
| HRC | Rockwell Hardness C Scale |
| ANOVA | Analysis of Variance |
References
- Guo, S.H. How does Straw Burning Affect Urban Air Quality in China? Am. J. Agric. Econ. 2021, 103, 1122–1140. [Google Scholar] [CrossRef]
- He, L.Y.; Duanmu, L.J.; Guo, L.; Qin, Y.; Shi, B.W.; Liang, L.; Chen, W.W. Determining an Optimal Combination of Meteorological Factors to Reduce the Intensity of Atmospheric Pollution During Prescribed Straw Burning. Agriculture 2025, 15, 279. [Google Scholar] [CrossRef]
- Li, Y.; Abalos, D.; Arthur, E.; Feng, H.; Siddique, K.H.M.; Chen, J. Different Straw Return Methods Have Divergent Effects on Winter Wheat Yield, Yield Stability, and Soil Structural Properties. Soil Tillage Res. 2024, 238, 105992. [Google Scholar] [CrossRef]
- Jiang, L.M.; Ning, A.R.; Liu, M.; Zhu, Y.H.; Huang, J.W.; Guo, Y.G.; Feng, W.Z.; Fu, D.P.; Wang, H.B.; Wang, J.L. Effects of Tillage Practices on Soil Properties and Maize Yield in Different Types of Soda Saline–Alkali Soils. Agriculture 2025, 15, 542. [Google Scholar] [CrossRef]
- Cui, H.; Luo, Y.; Chen, J.; Jin, M.; Li, Y.; Wang, Z.L. Straw Return Strategies to Improve Soil Properties and Crop Productivity in a Winter Wheat-summer Maize Cropping System. Eur. J. Agron. 2022, 133, 126436. [Google Scholar] [CrossRef]
- Li, S.; Li, X.S.; Zhu, W.L.; Chen, J.; Tian, X.H.; Shi, J.G. Does the Straw Return Strategy Influence Soil Carbon Sequestration and Labile Fractions? Agron. J. 2019, 111, 897–906. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Kushwaha, R.L. Effect of Tillage Speed and Straw Length on Soil and Straw Movement by a Sweep. Soil Tillage Res. 2010, 109, 9–17. [Google Scholar] [CrossRef]
- Akbolat, D.; Ekinci, K. Rotary Tiller Velocity Effects on the Distribution of Wheat (Triticum aestivum) Residue in The Soil Profile. N. Z. J. Crop Hortic. Sci. 2008, 36, 247–252. [Google Scholar] [CrossRef]
- Yang, Q.L.; Chen, G.B.; Xie, L.J.; Wang, Q.J.; He, J.; Li, H.W. Design and Experiment of Telescopic-Finger Corn Stalk Rotary Burying Machine. Trans. Chin. Soc. Agric. Mach. 2020, 51, 35–43. [Google Scholar]
- Wang, H.S. Design and Experiment of Rotary Blade-Finger Combination Straw Returning Machine. Master’s Thesis, Northeast Agricultural University, Harbin, China, 2023. [Google Scholar] [CrossRef]
- Liang, F.; Deng, W.H.; Luo, L.Q.; Wang, J.K.; Zhan, S.P. Design and Optimization of Counter-rotating Double-spiral Straw Burial Device for Rapeseed Straw Returning. Trans. Chin. Soc. Agric. Eng. 2023, 39, 10–17. [Google Scholar] [CrossRef]
- Wang, X.Z.; Gao, P.Y.; Yue, B.; Shen, H.; Fu, Z.L.; Zheng, Z.Q.; Zhu, R.X.; Huang, Y.X. Optimisation of Installation Parameters of Subsoiler’ Wing Using the Discrete Element Method. Comput. Electron. Agric. 2019, 162, 523–530. [Google Scholar] [CrossRef]
- Zeng, Z.W.; Ma, X.; Chen, Y.; Qi, L. Modelling Residue Incorporation of Selected Chisel Ploughing Tools Using The Discrete Element Method (DEM). Soil Tillage Res. 2020, 197, 14. [Google Scholar] [CrossRef]
- Zhao, Z.; Hou, J.; Guo, P.; Xia, C.; Yan, H.P.; Wang, D. Analysis of Soil–Straw Movement Behavior in Saline–Alkali Soil Under Dual-Axis Rotary Tillage Based on EDEM. Agriculture 2025, 15, 337. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Zhang, L.X.; Hu, X.; Wang, H.; Shi, X.B.; Ma, X. Simulation of Soil Cutting and Power Consumption Optimization of a Typical Rotary Tillage Soil Blade. Appl. Sci. 2022, 12, 8177. [Google Scholar] [CrossRef]
- Li, S.T.; Chen, X.B.; Chen, W.; Zhu, S.P.; Li, Y.W.; Yang, L.; Xie, S.Y.; Yang, M.J. Soil-cutting Simulation and Parameter Optimization of Handheld Tiller’s Rotary Blade by Smoothed Particle Hydrodynamics Modelling and Taguchi Method. J. Clean. Prod. 2018, 179, 55–62. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, M.; Chen, W.; Yuan, D.; Wu, C.Y.; Zhu, J.P. Simulation Analysis and Experiments for Blade-Soil-Straw Interaction Under Deep Ploughing Based on the Discrete Element Method. Agriculture 2023, 13, 136. [Google Scholar] [CrossRef]
- Du, J.; Heng, Y.F.; Zheng, K.; Luo, C.M.; Zhu, Y.H.; Zhang, J.; Xia, J.F. Investigation of The Burial and Mixing Performance of a Rotary Tiller Using Discrete Element Method. Soil Tillage Res. 2022, 220, 105349. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, D.W.; Shang, S.Q.; Guo, P.; Gao, Z.H.; Xia, C.; Yan, H.P.; Hou, J.L. Design and Test of a Dual-axis Layered Rotary Tillage Stubble Exterminator in Saline-alkali Land Based on Discrete Elements. Int. J. Agric. Biol. Eng. 2024, 17, 163–175. [Google Scholar] [CrossRef]
- Asaf, Z.; Rubinstein, D.; Shmulevich, I. Determination of Discrete Element Model Parameters Required for Soil Tillage. Soil Tillage Res. 2007, 92, 227–242. [Google Scholar] [CrossRef]
- Ono, I.; Nakashima, H.; Shimizu, H.; Miyasaka, J.; Ohdoi, K. Investigation of Elemental Shape for 3D DEM Modeling of Interaction Between Soil and a Narrow Cutting Tool. J. Terramech. 2013, 50, 265–276. [Google Scholar] [CrossRef]
- Guo, Q.; Xia, H.H. A Review of the Discrete Element Method/Modelling in Agricultural Engineering. J. Agric. Eng. 2023, 54, 1534. [Google Scholar] [CrossRef]
- Zeng, Z.W.; Chen, Y. Simulation of Straw Movement by Discrete Element Modelling of Straw-Sweep-Soil Interaction. Biosyst. Eng. 2019, 180, 25–35. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Wu, M.L.; Jiang, X.H. A Review of Contact Models’ Properties for Discrete Element Simulation in Agricultural Engineering. Agriculture 2024, 14, 238. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional Discrete Element Modelling (DEM) of Tillage: Accounting for Soil Cohesion and Adhesion. Biosyst. Eng. 2015, 129, 298–306. [Google Scholar] [CrossRef]
- Zhao, S.H.; Gao, L.L.; Yuan, Y.W.; Hou, L.T.; Zhang, X.; Yang, Y.Q. Movement Patterns of Corn Straw in Subsoiling Operations Based on Discrete Element Method. Trans. Chin. Soc. Agric. Eng. 2021, 37, 53–62. [Google Scholar] [CrossRef]
- Zhao, S.H.; Liu, H.P.; Yang, L.L.; Gao, L.L.; Yang, Y.Q. Design and Discrete Element Simulation of Interactive Layered Subsoiler for Rice Straw Returning. Trans. Chin. Soc. Agric. Mach. 2021, 52, 75–87. [Google Scholar] [CrossRef]
- Qi, L. Design and Experimental Study of Corn Stalk Furrow-Strip Mixing and Burying Machine. Master’s Thesis, Shenyang Agricultural University, Liaoning Province of China, Shenyang, China, 2019. [Google Scholar] [CrossRef]
- Liu, P.; He, J.; Zhang, Z.Q.; Zhang, Z.G.; Lin, H. Analysis and Experiment of Crushed Straw Motion Characteristics in Straw Returning Machine Based on CFD-DEM Coupling Method. Trans. Chin. Soc. Agric. Mach. 2020, 51, 244–253. [Google Scholar] [CrossRef]
- He, R.Y.; Duan, Q.F.; Chen, X.X. Discrete Element Analysis of Straw Spatial Distribution Quality in Rotary Tillage Straw Returning. Trans. Chin. Soc. Agric. Mach. 2022, 53, 44–53. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, C.; Zhang, W.; Yang, Q.; Li, D.; Liu, Z.; Xia, J. Evaluation of Straw Spatial Distribution After Straw Incorporation into Soil for Different Tillage Tools. Soil Tillage Res. 2020, 196, 104440. [Google Scholar] [CrossRef]
- Razavizadeh, N.; Zare, D.; Nassiri, S.M.; Karim, A.; Eslami, M.; Nematollahi, M.A. Experimental Study and Numerical Simulation of Resistance to Airflow in a Storage Bin of Rough Rice with Three Inlet Duct Configurations. Biosyst. Eng. 2023, 225, 118–131. [Google Scholar] [CrossRef]


| Symbol | Simulation Parameters | Value |
|---|---|---|
| Soil | Poisson’s ratio | 0.39 [27] |
| Density (kg·m−3) | 1450 [27] | |
| Shear modulus (Pa) | 1 × 106 [27] | |
| Particle diameter (mm) | 12 [27] | |
| Corn straw | Poisson’s ratio | 0.4 [28] |
| Density (kg·m−3) | 241 [28] | |
| Shear modulus (Pa) | 1.37 × 108 [29] | |
| Straw length (mm) | 50 | |
| 65Mn | Poisson’s ratio | 0.3 [26] |
| Density (kg·m−3) | 7865 [26] | |
| Shear modulus (Pa) | 7.9 × 1010 [30] |
| Simulation Parameters | Value |
|---|---|
| Coefficient of restitution of soil–soil | 0.6 |
| Coefficient of static friction of soil–soil | 0.57 [27] |
| Coefficient of rolling friction of soil–soil | 0.14 |
| Coefficient of restitution of soil–corn straw | 0.5 [30] |
| Coefficient of static friction of soil–corn straw | 0.5 [30] |
| Coefficient of rolling friction of soil–corn straw | 0.05 [30] |
| Coefficient of restitution of soil–65Mn | 0.729 [27] |
| Coefficient of static friction of soil–65Mn | 0.69 |
| Coefficient of rolling friction of soil–65Mn | 0.107 [27] |
| Coefficient of restitution of corn straw–corn straw | 0.182 [29] |
| Coefficient of static friction of corn straw–corn straw | 0.237 [29] |
| Coefficient of rolling friction of corn straw–corn straw | 0.0782 [29] |
| Coefficient of restitution of corn straw–65Mn | 0.729 [29] |
| Coefficient of static friction of corn straw–65Mn | 0.342 [29] |
| Coefficient of rolling friction of corn straw–65Mn | 0.01 [27] |
| Normal stiffness of bond (N·m−3) | 3.4 × 108 [26] |
| Shear stiffness of bond (N·m−3) | 1.5 × 108 [26] |
| Critical normal stress (Pa) | 2 × 105 [26] |
| Critical shear stress (Pa) | 6.8 × 104 [26] |
| Bond radius (mm) | 6.79 [27] |
| Code | β (°) | δ (°) | α (°) | h (mm) | r (mm) |
|---|---|---|---|---|---|
| 1 | 85 | 120 | 15 | 40 | 10 |
| 2 | 100 | 130 | 25 | 50 | 20 |
| 3 | 115 | 140 | 35 | 60 | 30 |
| 4 | 130 | 150 | 45 | 70 | 40 |
| 5 | 145 | 160 | 55 | 80 | 50 |
| Code | Factor | ||||
|---|---|---|---|---|---|
| Bending Angle A (°) | Side Angle B (°) | Bending Line Angle C (°) | Tangential Edge Height D (mm) | Bending Radius E (mm) | |
| −1 | 100 | 130 | 35 | 40 | 20 |
| 0 | 115 | 140 | 45 | 50 | 30 |
| +1 | 130 | 150 | 55 | 60 | 40 |
| No. | Factor | Straw Burial Rate Y1 (%) | Straw Percentage in the Seeding Layer Y2 (%) | ||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | |||
| 1 | −1 | −1 | 0 | 0 | 0 | 96.99 | 37.74 |
| 2 | 1 | −1 | 0 | 0 | 0 | 94.37 | 38.37 |
| 3 | −1 | 1 | 0 | 0 | 0 | 94.01 | 43.74 |
| 4 | 1 | 1 | 0 | 0 | 0 | 95.26 | 48.3 |
| 5 | 0 | 0 | −1 | −1 | 0 | 96.13 | 40.27 |
| 6 | 0 | 0 | 1 | −1 | 0 | 96.01 | 38.17 |
| 7 | 0 | 0 | −1 | 1 | 0 | 96.89 | 37.12 |
| 8 | 0 | 0 | 1 | 1 | 0 | 95.83 | 38.54 |
| 9 | 0 | −1 | 0 | 0 | −1 | 95.44 | 39.4 |
| 10 | 0 | 1 | 0 | 0 | −1 | 94.49 | 47.91 |
| 11 | 0 | −1 | 0 | 0 | 1 | 94.96 | 41.09 |
| 12 | 0 | 1 | 0 | 0 | 1 | 95.37 | 43.45 |
| 13 | −1 | 0 | −1 | 0 | 0 | 96.04 | 36.05 |
| 14 | 1 | 0 | −1 | 0 | 0 | 95.53 | 39.04 |
| 15 | −1 | 0 | 1 | 0 | 0 | 95.38 | 39.57 |
| 16 | 1 | 0 | 1 | 0 | 0 | 94.36 | 43.94 |
| 17 | 0 | 0 | 0 | −1 | −1 | 94.75 | 40.54 |
| 18 | 0 | 0 | 0 | 1 | −1 | 94.87 | 39.87 |
| 19 | 0 | 0 | 0 | −1 | 1 | 94.69 | 42.77 |
| 20 | 0 | 0 | 0 | 1 | 1 | 96.13 | 39.11 |
| 21 | 0 | −1 | −1 | 0 | 0 | 95.8 | 37.36 |
| 22 | 0 | 1 | −1 | 0 | 0 | 97.88 | 41.34 |
| 23 | 0 | −1 | 1 | 0 | 0 | 97.56 | 36.76 |
| 24 | 0 | 1 | 1 | 0 | 0 | 93.86 | 48.36 |
| 25 | −1 | 0 | 0 | −1 | 0 | 96.25 | 40.28 |
| 26 | 1 | 0 | 0 | −1 | 0 | 94.17 | 44.48 |
| 27 | −1 | 0 | 0 | 1 | 0 | 95.77 | 40.07 |
| 28 | 1 | 0 | 0 | 1 | 0 | 96.13 | 38.53 |
| 29 | 0 | 0 | −1 | 0 | −1 | 95.86 | 39.35 |
| 30 | 0 | 0 | 1 | 0 | −1 | 96.04 | 39.69 |
| 31 | 0 | 0 | −1 | 0 | 1 | 96.99 | 38.59 |
| 32 | 0 | 0 | 1 | 0 | 1 | 95.44 | 38.3 |
| 33 | −1 | 0 | 0 | 0 | −1 | 95.02 | 42.77 |
| 34 | 1 | 0 | 0 | 0 | −1 | 94.13 | 43.37 |
| 35 | −1 | 0 | 0 | 0 | 1 | 95.44 | 37.26 |
| 36 | 1 | 0 | 0 | 0 | 1 | 95.26 | 46.1 |
| 37 | 0 | −1 | 0 | −1 | 0 | 95.18 | 37.38 |
| 38 | 0 | 1 | 0 | −1 | 0 | 94.31 | 46.66 |
| 39 | 0 | −1 | 0 | 1 | 0 | 96.51 | 37.31 |
| 40 | 0 | 1 | 0 | 1 | 0 | 96.07 | 46.92 |
| 41 | 0 | 0 | 0 | 0 | 0 | 95.34 | 40.2 |
| 42 | 0 | 0 | 0 | 0 | 0 | 94.8 | 37.35 |
| 43 | 0 | 0 | 0 | 0 | 0 | 95.21 | 37.52 |
| 44 | 0 | 0 | 0 | 0 | 0 | 95.1 | 39.85 |
| 45 | 0 | 0 | 0 | 0 | 0 | 94.93 | 39.92 |
| 46 | 0 | 0 | 0 | 0 | 0 | 94.86 | 38.92 |
| Source of Variance | Mean Square | Degrees of Freedom | Sum of Squares | F Value | p Value |
|---|---|---|---|---|---|
| Model | 34.34 | 20 | 1.72 | 11.64 | <0.0001 *** |
| A | 2.02 | 1 | 2.02 | 13.72 | 0.0011 *** |
| B | 1.93 | 1 | 1.93 | 13.1 | 0.0013 *** |
| C | 2.76 | 1 | 2.76 | 18.69 | 0.0002 *** |
| D | 2.81 | 1 | 2.81 | 19.08 | 0.0002 *** |
| E | 0.8464 | 1 | 0.8464 | 5.74 | 0.0244 ** |
| AB | 3.74 | 1 | 3.74 | 25.39 | <0.0001 *** |
| AC | 0.065 | 1 | 0.065 | 0.4410 | 0.5172 * |
| AD | 1.49 | 1 | 1.49 | 10.09 | 0.0039 *** |
| AE | 0.126 | 1 | 0.126 | 0.8546 | 0.3641 |
| BC | 8.35 | 1 | 8.35 | 56.64 | <0.0001 *** |
| BD | 0.0462 | 1 | 0.0462 | 0.3135 | 0.5805 |
| BE | 0.4624 | 1 | 0.4624 | 3.14 | 0.0888 * |
| CD | 0.2209 | 1 | 0.2209 | 1.5 | 0.2324 |
| CE | 0.7482 | 1 | 0.7482 | 5.07 | 0.0333 ** |
| DE | 0.4356 | 1 | 0.4536 | 2.95 | 0.098 * |
| A2 | 0.1226 | 1 | 0.1226 | 0.8316 | 0.3705 |
| B2 | 0.3872 | 1 | 0.3872 | 2.63 | 0.1177 |
| C2 | 6.14 | 1 | 6.14 | 41.66 | <0.0001 *** |
| D2 | 1.05 | 1 | 1.05 | 7.1 | 0.0133 ** |
| E2 | 0.0258 | 1 | 0.0258 | 0.175 | 0.6793 |
| Residual | 3.69 | 25 | 0.1475 | ||
| Lack of fit | 3.46 | 20 | 0.1731 | 3.85 | 0.0701 |
| Pure error | 0.2246 | 5 | 0.0449 | ||
| Total | 38.03 | 45 |
| Source of Variance | Mean Square | Degrees of Freedom | Sum of Squares | F Value | p Value |
|---|---|---|---|---|---|
| Model | 451 | 20 | 22.55 | 10.68 | <0.0001 *** |
| A | 37.98 | 1 | 37.98 | 17.98 | 0.0003 *** |
| B | 234.63 | 1 | 234.63 | 111.11 | <0.0001 *** |
| C | 12.62 | 1 | 12.62 | 5.98 | 0.0219 ** |
| D | 10.69 | 1 | 10.69 | 5.06 | 0.0335 ** |
| E | 2.43 | 1 | 2.43 | 1.15 | 0.294 |
| AB | 3.86 | 1 | 3.86 | 1.83 | 0.1884 |
| AC | 0.4761 | 1 | 0.4761 | 0.2255 | 0.639 |
| AD | 8.24 | 1 | 8.24 | 3.9 | 0.0594 * |
| AE | 16.97 | 1 | 16.97 | 8.04 | 0.0089 *** |
| BC | 14.52 | 1 | 14.52 | 6.87 | 0.0147 ** |
| BD | 0.0272 | 1 | 0.0272 | 0.0129 | 0.9105 |
| BE | 9.46 | 1 | 9.46 | 4.48 | 0.0445 ** |
| CD | 3.1 | 1 | 3.1 | 1.47 | 0.2372 |
| CE | 0.0992 | 1 | 0.0992 | 0.047 | 0.8301 |
| DE | 2.24 | 1 | 2.24 | 1.06 | 0.3134 |
| A2 | 17.27 | 1 | 17.27 | 8.18 | 0.0084 *** |
| B2 | 52.25 | 1 | 52.25 | 24.74 | <0.0001 *** |
| C2 | 6.4 | 1 | 6.4 | 3.03 | 0.094 * |
| D2 | 1.7 | 1 | 1.7 | 0.8039 | 0.3785 |
| E2 | 17.19 | 1 | 17.19 | 8.14 | 0.0086 ** |
| Residual | 52.79 | 25 | 2.11 | ||
| Lack of fit | 44.87 | 20 | 2.24 | 1.42 | 0.3472 |
| Pure error | 7.92 | 5 | 1.58 | ||
| Total | 503.79 | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, H.; Wang, Q.; Wang, M.; Zhang, C.; Lin, H.; Jin, X.; Hong, H.; Dang, F. Optimizing the Design of Soil-Mixing Blade Structure Parameters Based on the Discrete Element Method. Agriculture 2025, 15, 1558. https://doi.org/10.3390/agriculture15141558
Ding H, Wang Q, Wang M, Zhang C, Lin H, Jin X, Hong H, Dang F. Optimizing the Design of Soil-Mixing Blade Structure Parameters Based on the Discrete Element Method. Agriculture. 2025; 15(14):1558. https://doi.org/10.3390/agriculture15141558
Chicago/Turabian StyleDing, Huiling, Qiaofeng Wang, Mengyang Wang, Chao Zhang, Han Lin, Xin Jin, Haizhou Hong, and Fengkui Dang. 2025. "Optimizing the Design of Soil-Mixing Blade Structure Parameters Based on the Discrete Element Method" Agriculture 15, no. 14: 1558. https://doi.org/10.3390/agriculture15141558
APA StyleDing, H., Wang, Q., Wang, M., Zhang, C., Lin, H., Jin, X., Hong, H., & Dang, F. (2025). Optimizing the Design of Soil-Mixing Blade Structure Parameters Based on the Discrete Element Method. Agriculture, 15(14), 1558. https://doi.org/10.3390/agriculture15141558






