Abstract
Lateritic soils in tropical regions feature cohesive textures and high specific resistance, driving up energy demands for tillage and harvesting machinery. However, current equipment designs lack discrete element models that account for soil moisture variations, and the microscopic effects of water content on lateritic soil deformation remain poorly understood. This study aims to calibrate and validate discrete element method (DEM) models of lateritic soil at varying moisture contents of 20.51%, 22.39%, 24.53%, 26.28%, and 28.04% by integrating the Hertz–Mindlin contact mechanics with bonding and JKR cohesion models. Key parameters in the simulations were calibrated through systematic experimentation. Using Plackett–Burman design, critical factors significantly affecting axial compressive force—including surface energy, normal bond stiffness, and tangential bond stiffness—were identified. Subsequently, Box–Behnken response surface methodology was employed to optimize these parameters by minimizing deviations between simulated and experimental maximum axial compressive forces under each moisture condition. The calibrated models demonstrated high fidelity, with average relative errors of 4.53%, 3.36%, 3.05%, 3.32%, and 7.60% for uniaxial compression simulations across the five moisture levels. Stress–strain analysis under axial loading revealed that at a given surface displacement, both fracture dimensions and stress transfer rates decreased progressively with increasing moisture content. These findings elucidate the moisture-dependent micromechanical behavior of lateritic soil and provide critical data support for DEM-based design optimization of soil-engaging agricultural implements in tropical environments.
1. Introduction
Lateritic soil, a predominant soil type in South China and Southeast Asia under tropical climates, is prone to compaction and acidification due to high temperature and excessive rainfall [1]. Increased moisture content in this soil significantly elevates adhesive resistance against soil-engaging implements during tillage operations, thereby leading to heightened energy consumption and accelerated component wear in agricultural machinery. In regions like Hainan and Yunnan, where lateritic soils are concentrated, strong interparticle cementation and significant mechanical heterogeneity between the topsoil and subsurface layers pose challenges for conventional discrete element method (DEM) models. These models, often parameterized with empirical values, frequently fail to accurately characterize the dynamic soil–tool interaction mechanisms [2,3]. Therefore, the precise calibration of DEM parameters for lateritic soil particles under different moisture conditions, along with a thorough investigation of microscopic deformation during soil compression, is essential for optimizing the design of soil-engaging components and improving tillage efficiency in tropical agro-ecosystems.
In recent years, the discrete element method (DEM) model proposed by Cundall et al. has been extensively applied in agricultural machinery design [4]. The objective of DEM parameter calibration is to ensure that the kinematic behavior of simulated particle assemblies closely approximates or matches that of real granular materials. Its accuracy is contingent upon the comprehensiveness of input parameters, the appropriateness of contact models, and the validity of calibration metrics [5]. DEM enables realistic simulations of microscopic and macroscopic interactions among soil particles, as well as between soil–crop and soil–implement systems, thereby providing critical insights for designing agricultural equipment that interacts with crops [6,7]. For instance, Qiu et al. utilized EDEM (2020) software to calibrate DEM parameters for cinnamon soil, establishing foundational data for reducing resistance between soil and soil-engaging tools [8]. Bo et al. integrated discrete element method (DEM) simulations with machine learning techniques, allowing for a more accurate prediction of material behavior under various loading conditions [9]. Similarly, Li et al. calibrated DEM parameters for cohesive black soil under two moisture levels, offering empirical support for optimizing adhesion reduction and resistance mitigation in northeastern China’s heavy clay soils [10].
Current research on soil particle contact parameters predominantly employs the Hertz–Mindlin model family within EDEM (2020) software [11]. For instance, Ding et al. developed a subsoiling DEM for paddy soil using the Hertz–Mindlin with bonding approach, which incorporates finite-sized “bonding agents” between particles. However, this method is more suitable for rigid media like rock rather than cohesive soils [12]. In contrast, Wang et al. advanced the Edinburgh Elasto-Plastic Cohesion Model (ECM), integrating soil strain hysteresis, cohesion, and van der Waals forces to establish a DEM surrogate model with sensitivity-optimized parameters [13]. While these contact models demonstrate robust applicability for low-cohesion soils with limited moisture content, they prove inadequate for lateritic soils prevalent in southern China. The strong interparticle bonding forces in such soils, coupled with their predominantly viscous–plastic behavior under deformation, challenge the fundamental assumptions of existing cohesive models.
As a complex multiphase mixture, soil undergoes intricate behaviors such as deformation and displacement during interactions with soil-engaging implements, demonstrating pronounced discrete characteristics [14]. Under low-moisture conditions, soil particles form rigid structures through physical bonds. As the moisture content increases, liquid bridge forces induced by interstitial water enhance interparticle cohesion [15]. Capillary action between soil particles and pore water enhances interparticle bonding by increasing cohesive forces. In EDEM (2020) simulations, the Bonding Model approximates rigid particle bonding via finite-sized “bonding agents”, effectively simulating structural bonding and fracture processes in low-moisture soils. Conversely, the Hertz–Mindlin with JKR contact model calculates adhesion forces based on surface energy, enabling accurate simulation of liquid bridge effects and cohesive behaviors in high-moisture soils [16].
Therefore, to address the unresolved issues of DEM parameter ambiguity and microscale deformation mechanisms during the compression of lateritic soil under varying moisture conditions in southern China, this study focuses on representative lateritic soil samples from Hainan Province. We systematically calibrated contact parameters for DEM models at five moisture levels (20.51%, 22.39%, 24.53%, 26.28%, and 28.04%). Uniaxial compression simulation tests were conducted to observe microscopic deformation characteristics, enabling the comprehensive parameter calibration and mechanistic analysis of soil behavior across different moisture regimes. The findings establish a theoretical foundation for energy-efficient design optimization of soil-engaging agricultural machinery in tropical southern China.
The remainder of the article is organized as follows. Section 2 elaborates on the materials and experimental methodologies employed in this study. The corresponding experimental results derived from systematic investigations are given in Section 3. Section 4 conducts a mechanistic analysis of phenomena observed during the experimental process. Finally, conclusions and the future research directions that can be studied in depth is presented in Section 5.
2. Materials and Methods
2.1. Preparation of Lateritic Soil Samples
The lateritic soil sampling area in this study was located in Lingao County, Hainan Province, a representative tropical region in southern China. The site exhibits stable climatic conditions, with an annual average temperature of 23–29 °C, annual precipitation exceeding 1100 mm, and annual sunshine duration of 1900–2400 h. The geographic coordinates are 109°44′50″ E longitude and 19°45′52″ N latitude.
The preparation process for lateritic soil samples with varying moisture contents is illustrated in Figure 1. Lateritic soil samples were oven-dried at 110 °C, ground, and then sieved using standardized soil sieves compliant with Test Sieves-Technical Requirements and Testing (GB/T 6003.1-2012) [17]. Mechanical shaking was applied for 10–15 min until no particles passed through the sieve, with triplicate measurements averaged to ensure repeatability. The plastic limit (PL) and liquid limit (LL) were determined using an LP-100D Liquid–Plastic Limit Tester, following the Standard for Geotechnical Testing Methods (GB/T 50123-2019) [18], where cone penetration depths of 2 mm and 10 mm corresponded to the plastic limit and liquid limit moisture contents, respectively.

Figure 1.
Preparation process for compacted lateritic soil samples.
Following the «T 0103-1993 Oven-Drying Method» [19], lateritic soil samples were dried at 105 °C until constant mass was achieved and subsequently distributed into five sealed containers. Precise volumes of water were uniformly sprayed into each container, followed by thorough mixing and sealing with plastic film for 24 h equilibration. The moisture contents of the prepared soil samples were measured using a QL-720A rapid halogen moisture analyzer, with the drying temperature set at 105 °C, the drying time set at 16 h, and the measurement deviations controlled within ±1%. The finalized moisture contents of the lateritic soil samples were determined as 20.51%, 22.39%, 24.53%, 26.28%, and 28.04%, respectively.
Field-collected intact lateritic soil samples often exhibit structural heterogeneity and moisture variability due to sampling disturbances [20], which compromises inter-sample consistency. To mitigate artificial excavation-induced artifacts, this study employed remolded lateritic soil for experimental investigations. As emphasized by Ding et al. [21], the Proctor compaction method produces specimens with superior mechanical representativeness compared to kneading techniques. Accordingly, cylindrical standard specimens (diameter × height: 50 mm × 32 mm) were prepared using the Proctor compaction approach. Following the protocol outlined in [21], preliminary compaction tests were conducted to determine the optimal lateritic soil mass (170 g). The total lateritic soil mass was divided into two equal layers, each subjected to 15 compaction blows using a standardized tamper, until the lateritic soil surface aligned with the sampler’s upper plane. Specimens were trimmed to achieve surface flatness deviations < 0.5 mm prior to testing. The compacted specimens were wrapped in plastic film and cured for 48 h to dissipate residual stresses. Figure 1 illustrates the finalized lateritic soil specimens across varying moisture contents.
2.2. Parameter Calibration Methodology for Discrete Element Method (DEM) Model of Lateritic Soil
All simulations in this study were performed using EDEM 2020 software. The bonding and JKR contact models were used to characterize interactions between lateritic soil particles, with the JKR model specifically simulating adhesive interactions between the soil and geometric entities. Key parameters for the discrete element modeling of lateritic soil compression tests include soil density, soil Poisson’s ratio, soil elastic modulus, soil-soil coefficient of restitution, soil–soil coefficient of static friction, and soil–soil coefficient of rolling friction. The parameter acquisition methods were implemented as follows: soil density was measured via the ring knife method; soil Poisson’s ratio and soil elastic modulus were derived from direct shear tests by correlating shear strength with normal stress; soil elastic modulus was calculated from load–displacement relationships under controlled uniaxial compression; and the soil–soil coefficient of static and rolling friction were quantified using a tribometer compliant with direct shear tests.
This study conducted uniaxial compression tests on lateritic soil samples with five moisture contents (20.51%, 22.39%, 24.53%, 26.28%, and 28.04%) using a Universal TA texture analyzer. The tests were performed at a compression rate of 60 mm/min, with a displacement limit of 30 mm. Displacement–load curves obtained from bench-scale tests served as target references for calibrating the discrete element models of lateritic soil under varying moisture conditions. A cylindrical lateritic soil DEM was established in EDEM 2020 software, maintaining geometric consistency with the bench-scale test setup (Figure 2). Particle radii were assigned according to the mass fractions of soil components: 63.76% sand (2 mm radius), 24.26% silt (1 mm radius), and 11.98% clay (0.5 mm radius). To optimize computational efficiency, the particle radii for sand, silt, and clay were set to 2 mm, 1 mm, and 0.5 mm, respectively, within EDEM 2020 software. Following particle packing stabilization, bonding and JKR model parameters were applied between lateritic soil particles. In accordance with the time step calculation methods established by Guo et al. [22], the time step for the uniaxial compression simulations was set to Δt = 9.6 × 10−7 s.
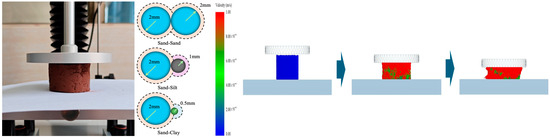
Figure 2.
Bonding and JKR coupled contact construction for discrete metamodeling of lateritic soil specimens.
The development of discrete element method (DEM) models for lateritic soil at five moisture content levels primarily involved calibrating five key parameters (Table 1).

Table 1.
Name and symbol of five key calibration parameters.
This study employed the average relative error of the axial maximum load (Δδ)—calculated from comparative simulations and bench-scale experiments as the calibration metric. Initial parameter ranges were established through single-factor experiments. Significant parameters were then screened using a Plackett–Burman design, followed by steepest ascent optimization to determine optimal parameter combinations. Finally, Box–Behnken response surface methodology was applied to refine the parameters to their optimal values.
2.3. Uniaxial Compression Test of Lateritic Soil
During interactions between lateritic soil and soil-engaging implements, compression dominates the mechanical behavior of the soil. Consequently, uniaxial compression tests were selected to calibrate model parameters for lateritic soil at varying moisture contents, with real-time measurement and recording of load–displacement curves. During the actual test, the cross-sectional area of the cylindrical soil specimen was 6.25 × 10−4 m2. The maximum loads obtained from the axial compression physical test of the five different moisture content lateritic soils and the corresponding calculated normal critical stresses of the five different moisture content lateritic soils are shown in Table 2. Since calibration was performed under purely axial compression, the critical tangential stresses retained identical magnitudes to the normal stresses.

Table 2.
Maximum loads and normal critical stresses in axial compression tests of lateritic soils with different water contents.
As Dai et al. emphasized [23], the particle contact radius serves as the triggering criterion for contact model activation, with the critical contact radius ranging from 1 to 1.732 times the particle radius. In constructing the discrete element model for lateritic soil, particle radii were set to 0.5 mm, 1 mm, and 2 mm, corresponding to contact radius ranges of 0.5–0.87 mm, 1–1.73 mm, and 2–3.46 mm, respectively. Consequently, the bonding radii were configured as 0.685 mm, 1.365 mm, and 2.73 mm to align with the critical thresholds.
In summary, three critical parameters remained to be calibrated: normal bond stiffness Sn, tangential bond stiffness St, and surface energy Ki. A Box–Behnken response surface design was therefore employed, with Analysis of Variance (ANOVA) used to identify the optimal parameter values. The average relative error (Δδ) of the axial maximum load—calculated from bench-scale experiments and numerical simulations—served as the calibration metric:
where n is the total number of data records; δi is the maximum axial compressive load in bench-scale tests, N; and δj is the maximum axial compressive load in simulation tests, N.
2.4. Data Statistics and Analysis Methods
Lateritic soil fissures originate from the lateral and longitudinal expansion of pores. The presence of these fissures leads to the degradation of soil strength, interparticle cohesion, and internal friction angle, ultimately compromising the structural integrity and stability of the soil matrix. The progressive initiation, propagation, and coalescence of microcracks under loading represent macroscopic manifestations of cumulative soil damage [24,25]. Given the challenges in directly quantifying internal fissures through physical experiments, this study employs the breakage of bonding bonds in the Discrete Element Method (DEM) model to characterize fissure evolution within lateritic soil [16]. A fissure ratio metric was introduced to quantitatively describe crack initiation and propagation, providing a micromechanical perspective on the destabilization mechanisms of lateritic soil. The fissure ratio is defined as follows:
where qi is the number of broken bonding bonds at time step i; and q is the total number of bonding bonds generated for lateritic soil aggregates.
During the data processing phase, Origin 2019 software was utilized to perform least squares method-based linear fitting of the fissure ratio under varying compressive displacements. The statistical significance of parameters for lateritic soil samples at different moisture contents under axial compression was analyzed using Duncan’s multiple range test in SPSS 26.0, with pairwise comparisons conducted through least significant difference (LSD) tests. This integrated analytical approach yielded mathematically robust fitting functions characterizing soil mechanical degradation.
3. Results
3.1. Measurement Results of Lateritic Soil Parameters
The lateritic soil samples underwent triplicate sieve analyses using standard soil sieves, with the averaged results showing mass fractions of clay particles (<0.002 mm): 47.53 ± 1.36%; silt particles (0.002–0.075 mm): 28.21 ± 1.89%; and sand particles (0.0075–2.36 mm): 24.26 ± 1.57%. Based on soil texture classification and comparative analysis with particle size distributions reported by Manuwa et al. [26] and Hoseinian et al. [27], the soil was classified as clay. Experimental measurements yielded a plastic limit (PL) of 17.74% and a liquid limit (LL) of 34.51%. Intrinsic and contact parameters of the lateritic soil, derived from direct measurements and literature references [28,29,30,31,32,33], are summarized in Table 3.

Table 3.
Material properties and parameters.
3.2. Axial Compression Simulation and Bench Testing Results of Lateritic Soil
Using lateritic soil with a moisture content of 24.53% as a case study, a Box–Behnken design (BBD) response surface methodology was implemented. The experimental factors, their corresponding levels, and the resultant data are detailed in Table 4 and Table 5, respectively.

Table 4.
Experimental factors and levels.

Table 5.
Response surface simulation results.
The Analysis of Variance (ANOVA) results are presented in Table 6, indicating that surface energy exerts a highly significant influence on the maximum axial compressive load of the lateritic soil, while both normal bond stiffness and tangential bond stiffness demonstrate significant effects. Utilizing the experimentally derived normal bond stiffness value of 458.03 N·m−3 as the optimization target, simulations revealed that the closest agreement between numerical and experimental results is achieved when parameters are set to normal bond stiffness (A) = 9.3 × 107 N·m−3, surface energy (B) = 32.26 J·m−2, and tangential bond stiffness (C) = 9.16 × 107 N·m−3.

Table 6.
Experimental ANOVA results.
3.3. Calibration Results of Discrete Element Model Parameters for Lateritic Soil with Varying Moisture Contents
Uniaxial compression simulation tests were conducted on lateritic soil samples with moisture contents of 20.51%, 22.39%, 24.53%, 26.28%, and 28.04%, using the parameters listed in Table 2. The average relative errors between simulated and experimentally measured maximum axial compressive loads were 4.53%, 3.36%, 3.05%, 3.32%, and 7.60%, respectively, for the corresponding moisture levels. These results validate that the calibrated discrete element method (DEM) model of lateritic soil is reliable for simulating soil–tool interactions in agricultural machinery applications. The calibration methodology remained consistent across all moisture content levels, with optimized parameters summarized in Table 7, enabling the successful establishment of DEM models for lateritic soil under varying hydration conditions.

Table 7.
Calibration results of contact parameters for soil with varying moisture contents.
4. Discussion
4.1. Characterization of Lateritic Soil
Compared to the loess from the middle and lower reaches of the Yellow River and the chernozem from northern China, lateritic soil exhibits distinct characteristics such as elevated clay content, iron–aluminum oxide enrichment, and complex pore structures [34]. As a typical product of intense tropical weathering, its high clay content (47.53 ± 1.36%) and iron–aluminum oxide-cemented microstructure confer pronounced hydrophilicity and adsorption capacity, leading to significant variations in its mechanical behavior. The experimental observations revealed that under low–moisture conditions, compressed lateritic soil specimens develop radially propagated fissures initiating from the top surface upon loading. With increasing compressive loads, annular secondary fissures continuously nucleate. Upon reaching the ultimate compressive strain, the specimens undergo complete lateral expansion, demonstrating a brittle-to-ductile transition in deformation mechanics. The compression process of the test lateritic soil is shown in Figure 3.

Figure 3.
Actual axial compression process of lateritic soil specimens.
Analysis of the aforementioned compression phenomena reveals that the radial distribution of initial fissures correlates with the spatial heterogeneity of the iron–aluminum oxide cementation network in lateritic soil. The enhanced lateral expansion during compression is attributed to interparticle interlaminar slip, a mechanism further validated by the coupled effects of bonding bond fracture energy and friction coefficient in the discrete element method (DEM) model, demonstrating the high consistency between simulation and experimental observations.
4.2. Comparative Analysis of Simulations and Physical Experiments
Comparative analysis between numerical simulations and bench-scale experiments revealed that under identical axial compressive displacements, the simulated lateritic soil exhibited more pronounced compressive deformation than physical specimens. This divergence primarily arises from morphological disparity: natural soil comprises aggregates of irregularly shaped particles, while computational constraints necessitate scaling-up particle models in DEM simulations to optimize computational efficiency. Consequently, the strain localization and interparticle rearrangement mechanisms observed in physical tests are partially homogenized in simulations, leading to amplified macroscopic deformation responses.
An in-depth analysis of the phenomenon shows that the morphology of the soil particles and the structure of the contact network have an impact on the strain localization in practical tests and the amplification of macroscopic deformations in numerical simulation tests. In physical tests, the diversity and irregularity of particle shapes allow for the non-uniform transfer of stress and strain through the force chain, leading to significant strain localization and complex rearrangements between particles. In numerical simulations, on the other hand, since the particle shapes are usually simplified to regular shapes, the contact force and strain distribution tends to be uniform and lacks the microscale irregularities of physical tests, which somewhat reduces the manifestation of strain localization phenomena. In addition, the scale effect of particles amplifies the macroscopic deformation response in numerical simulations (Figure 4).
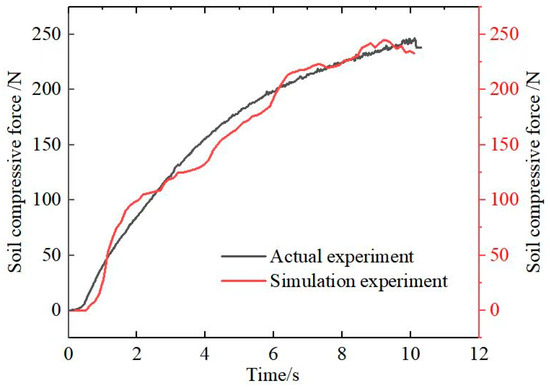
Figure 4.
Compression curves of lateritic soil with varying moisture contents.
In the future, in-depth studies on improved particle shape modeling and scale matching may be needed to capture the complex soil mechanical behavior more accurately.
4.3. Effect of Moisture Content on Compression Characteristics of Lateritic Soil
Increasing moisture content in lateritic soil leads to thickened interstitial water films between particles, which inhibits soil fragmentation and fracture during compression. At the peak moisture content of 28.04%, the texture analyzer recorded a minimal plunger displacement of 15.85 mm when compressing the specimen to its maximum sensing force. This phenomenon arises because elevated moisture levels saturate interparticle voids with water molecules, contrasting sharply with the highly porous structure of low-moisture soil. Consequently, equivalent compressive displacements induce substantially higher axial loads in hydrated specimens.
Experimental evidence suggests that as the moisture content of lateritic soil approaches its liquid limit, it transitions into a disturbed saturated state characterized by stress-independent yield behavior and a viscoelastic flow regime. Under such conditions, interactions between saturated soil and tillage tools result in elevated draught resistance, reduced trafficability, and increased power consumption of agricultural machinery. Notably, the mechanical complexity of saturated soil—encompassing compression, shear, and adhesion—exceeds the scope of the current DEM, which is validated only for lateritic soil within the moisture range of 20.51–28.04%.
In line with unsaturated soil mechanics, the reduction in strength and the shift in flow characteristics as the soil approaches saturation are governed by the soil’s capillary properties and the variation in matric suction. As the moisture content increases, the soil’s effective stress decreases, leading to greater deformability and a reduced frictional resistance to tillage tools. These changes are coupled with the transition from a predominantly elastic behavior at lower moisture levels to a more viscous and flow-dominated regime as the soil becomes increasingly saturated. Consequently, the ability of the current DEM to simulate these conditions is limited, as it was calibrated primarily for unsaturated soils within the specified moisture range and does not account for the complex mechanical behavior under fully saturated conditions.
5. Conclusions
This study calibrates discrete element method (DEM) models for tropical lateritic soil at moisture contents ranging from 20.51% to 28.04%, focusing on the soil’s stress–strain behavior under axial compression. It investigates the relationship between fissure development, moisture content, and compressive displacement. The findings show that under constant moisture content, compressive displacement initiates radial fissure propagation, while higher moisture content reduces the magnitude and speed of fissures. This study highlights the importance of moisture content in soil–tool interactions in tropical environments.
For the purposes of this post, the conclusion is divided into three main sections as follows. (1) The study utilized the Box–Behnken design (BBD) response surface methodology, which identified JKR surface energy, normal bond stiffness, and tangential bond stiffness as critical parameters for calibrating DEM for lateritic soils. The calibration was validated using axial compression simulations with EDEM (2020) software, demonstrating average relative errors between simulated and experimental axial compressive loads of 4.53%, 3.36%, 3.05%, 3.32%, and 7.60% for the respective test cases, confirming the accuracy and reliability of the DEM. (2) As the moisture content approaches higher levels, significant changes occur in the mechanical properties of lateritic soil. The results revealed that the magnitude and speed of fissure development are significantly influenced by moisture, with higher moisture contents reducing fissure propagation speed and strength. (3) It is important to highlight that the experimental validations in this study were confined to DEM models of lateritic soil within the moisture range of 20.51–28.04%. While the model provides accurate predictions within this range, its applicability to soils with moisture content beyond this range remains unexplored.
This study provides valuable insights into the mechanical behavior of lateritic soils in tropical environments. However, future research should expand the moisture range beyond 20.51–28.04%, exploring both single-contact and hybrid contact models. Further optimization of DEM parameters and the incorporation of factors like fissure formation and soil compaction will improve soil–tool interaction predictions and enhance agricultural machinery performance. These advancements will broaden the applicability of DEM models for tropical agriculture.
Author Contributions
Conceptualization, C.J. and W.L.; methodology, Y.W.; validation, B.Y.; formal analysis, P.C.; data curation, C.J.; writing—original draft preparation, C.J.; writing—review and editing, Y.D.; funding acquisition, Y.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Hainan Provincial Natural Science Foundation Youth Fund (Simulation of rotary furrowing process in orchards under lateritic soil conditions and study of power consumption influence law), grant number 521QN309 and Hainan Provincial Natural Science Foundation Youth Fund (Analysis of trenching process and optimization of high efficiency drag reduction of spiral trench opener), grant number 523QN285 and China Agriculture Research System (National Natural Rubber Industry Technology System Special Project of China), grant number CARS-33-JX1 and Hainan Provincial International Science and Technology Cooperation R&D Project (Demonstration and Promotion of Key Oil Palm Production Technologies in Indonesia), grant number GHYF2024019.
Data Availability Statement
Data are unavailable due to privacy or ethical restrictions.
Acknowledgments
The completion of this research paper would not have been possible without the assistance of Wanru Liu, to whom I extend my heartfelt gratitude. I would also like to acknowledge Yiguo Deng for his valuable guidance and insights provided during the preparation of this manuscript. My appreciation is extended to all contributing authors for their dedicated efforts.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ANOVA | Analysis of Variance |
| DEM | Discrete Element Method |
| ECM | Elasto-Plastic Cohesion Model |
References
- Zhang, J.; Sun, X.; Liu, Y.; Li, S.; Gao, C. Attribution of laterite of Danzhou, Hainan province in Chinese soil taxonomy. Guangdong Agric. Sci. 2015, 42, 46–52. [Google Scholar]
- Fang, M.; Yu, Z.; Zhang, W.; Cao, J.; Liu, W. Friction coefficient calibration of corn stalk particle mixtures using Plackett-Burman design and response surface methodology. Powder Technol. 2022, 39, 731–742. [Google Scholar] [CrossRef]
- Xing, J.; Zhang, R.; Wu, P.; Zhang, X.; Dong, X.; Chen, Y. Parameter calibration of discrete element simulation model for latosol particles in hot areas of Hainan Province. Trans. Chin. Soc. Agric. Eng. 2020, 36, 158–166. [Google Scholar]
- Cundall, P.; Strack, O. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Li, M.; Wang, L.; Liao, Q.; Liao, Y.; Xiao, W.; Zhang, Q. Calibration of Rototilled Soil Discrete Element Parameters After Rotary Tillage in The Preparation Process of Rapeseed Mechanized Direct Seeding Micro-Ridge Seed Bed. Trans. Chin. Soc. Agric. Eng. 2023, 20, 10–19. [Google Scholar]
- Zhang, B.; Yang, X.; Wang, J.; Chen, J.; Shen, W. Construction of a rheological model based on discrete element parameters calibration of clay from sugarcane cultivated land. Trans. Chin. Soc. Agric. Eng. 2024, 40, 36–44. [Google Scholar]
- Kan, Z.; Jin, H.; Hongwen, L.; Peisong, D.; Qingjie, W.; Hongbo, Z. Research on polyline soil breaking blade subsoiler based on subsoiling soil model using discrete element method. Trans. Chin. Soc. Agric. Mach. 2016, 47, 62–72. [Google Scholar]
- Qiu, Y.; Guo, Z.; Jin, X.; Zhang, P.; Si, S.; Guo, F. Calibration and verification test of cinnamon soil simulation parameters based on discrete element method. Agriculture 2022, 12, 1082. [Google Scholar] [CrossRef]
- Bo, L.; Weijun, C.; Guanxi, Y.; Alexander, S.; Changhai, Z.; Pei, Z. A machine learning-driven model for predicting macro-and micro-mechanical responses of rockfill materials considering particle breakage. Comput. Geotech. 2025, 185, 107349. [Google Scholar]
- Li, J.; Tong, J.; Hu, B.; Wang, H.; Mao, C.; Ma, Y. Calibration of parameters of interaction between clayey black soil with different moisture content and soil-engaging component in northeast China. Trans. Chin. Soc. Agric. Eng. 2019, 35, 130–140. [Google Scholar]
- Song, S.; Tang, Z.; Zheng, X.; Liu, J.; Meng, X.; Liang, Y. Calibration of the discrete element parameters for the soil model of cotton field after plowing in Xinjiang of China. Trans. Chin. Soc. Agric. Eng. 2021, 37, 63–70. [Google Scholar]
- Ding, Q.; Ren, J.; Belal, E.; Zhao, J.; Ge, S.; Li, Y. DEM analysis of subsoiling process in wet clayey paddy soil. Trans. Chin. Soc. Agric. Mach. 2017, 48, 38–48. [Google Scholar]
- Wang, X.; Hu, H.; Wang, Q.; Li, H.; He, J.; Chen, W. Calibration method of soil contact characteristic parameters based on DEM theory. Trans. Chin. Soc. Agric. Mach. 2017, 48, 78–85. [Google Scholar]
- Zeng, Z.W.; Ma, X.; Cao, X.L.; Li, Z.H.; Wang, X.C. Critical review of applications of discrete element method in agricultural engineering. Trans. Chin. Soc. Agric. Mach. 2021, 52, 1–20. [Google Scholar]
- Freeman, A.; Van, Z.; Klein, J.; Zebker, H.; Shen, Y. Calibration of Stokes and scattering matrix format polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1992, 30, 531–539. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, G.; Wang, H.; Liu, H.; Kang, Q.; Zhao, Z. Microscopic deformation and fragmentation energy consumption characteristics of soils with various moisture contents using discrete element method. Soil Tillage Res. 2024, 241, 106131. [Google Scholar] [CrossRef]
- GB/T 6003.1-2012; Test Sieves—Technical Requirements and Testing—Part 1: Test Sieves of Metal wire Cloth. National Standard of the People’s Republic of China: Beijing, China, 2013.
- GB/T 50123-2019; Standard for Geotechnical Testing Method. National Standard of the People’s Republic of China: Beijing, China, 2019.
- T 0103-1993; Drying Method. Ministry of Agriculture of the People’s Republic of China: Beijing, China, 1993.
- Gao, C.; Li, X.; Zhang, H.; Jiang, Y.; Xie, Y.; Liu, J. Effects of initial moisture and bulk density on the soil compression characteristics of black soil. Trans. Chin. Soc. Agric. Eng. 2023, 39, 102–111. [Google Scholar]
- Ding, Q.; Shen, F.; Ding, W.; Li, Y.; Pan, G.; Ji, C. Comparison of fragmentation properties and remolding techniques for clay soil. Trans. Chin. Soc. Agric. Mach. 2013, 44, 90–94. [Google Scholar]
- Guo, Y.; Wassgren, C.; Hancock, B.; Ketterhagen, W.; Curtis, J. Validation and time step determination of discrete element modeling of flexible fibers. Powder Technol. 2013, 249, 386–395. [Google Scholar] [CrossRef]
- Dai, E.; Wan, H.; Jian, B.; Hu, G. The Effect of Different Structures and Particles with Different Viscosity on the Performance of Double Screw Conveyors. Mach. Des. Manuf. 2020, 3, 118–122. [Google Scholar]
- Liu, C.; Chen, S.; Jang, C. Modelling water infiltration in cracked paddy field soil. Hydrol. Process. 2004, 18, 2503–2513. [Google Scholar] [CrossRef]
- Gallacher, D.; Roth, G.; McBratney, A. Interactive soil moisture interface of multi-depth change over time. Comput. Electron. Agric. 2023, 204, 107508. [Google Scholar] [CrossRef]
- Manuwa, S. Performance evaluation of tillage tines operating under different depths in a sandy clay loam soil. Soil Tillage Res. 2009, 103, 399–405. [Google Scholar] [CrossRef]
- Hoseinian, S.; Hemmat, A.; Esehaghbeygi, A.; Shahgoli, G.; Baghbanan, A. Development of a dual sideway-share subsurface tillage implement: Part 1. Modeling tool interaction with soil using DEM. Soil Tillage Res. 2022, 215, 105201. [Google Scholar] [CrossRef]
- Guo, L.; Fang, Q.; Li, M.; Wang, Z.; Wang, C.; Zhang, L. Parameter Calibration for Discrete Element Simulation of Red Clay Soils in Sloping Cropland in Central Yunnan. Trans. Chin. Soc. Agric. Mach. 2024, 55, 185–285. [Google Scholar]
- Zhao, Y.; Li, S.; Xie, Y.; Zhao, W.; Chen, Z.; Zhang, Y. Calibration of Yunnan Red Soil Simulation Parameters Based on Discrete Element Method. J. Shenyang Agric. Univ. 2024, 55, 465–473. [Google Scholar]
- Chen, Y.; Munkholm, L.; Nyord, T. A discrete element model for soil–sweep interaction in three different soils. Soil Tillage Res. 2013, 126, 34–41. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.; Yang, L.; Cui, T.; Jing, H.; Zhong, X. Modeling the interaction of soil and a vibrating subsoiler using the discrete element method. Comput. Electron. Agric. 2020, 174, 105518. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Liu, D.; Xie, F.; Ashwehmbom, L.; Zhang, Z. Calibration of discrete element parameters and experimental verification for modelling subsurface soils. Biosyst. Eng. 2021, 212, 215–227. [Google Scholar] [CrossRef]
- Zhou, L.; Lan, Y.; Yu, J.; Wang, Y.; Yan, D.; Sun, K. Validation and calibration of soil parameters based on EEPA contact model. Comput. Part. Mech. 2023, 10, 1295–1307. [Google Scholar] [CrossRef]
- Yan, X.; Wang, C.; Li, M.; Fu, S.; Wei, L.; Zhang, P. Design and experiment on the chisel-shape deep-shovel in red loam. J. Agric. Mech. Res. 2019, 41, 135–142. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).