Investigation on Seed-Filling Effect of Quantitative Precision Filling High-Speed Seed-Metering Device for Maize
Abstract
1. Introduction
2. Materials and Methods
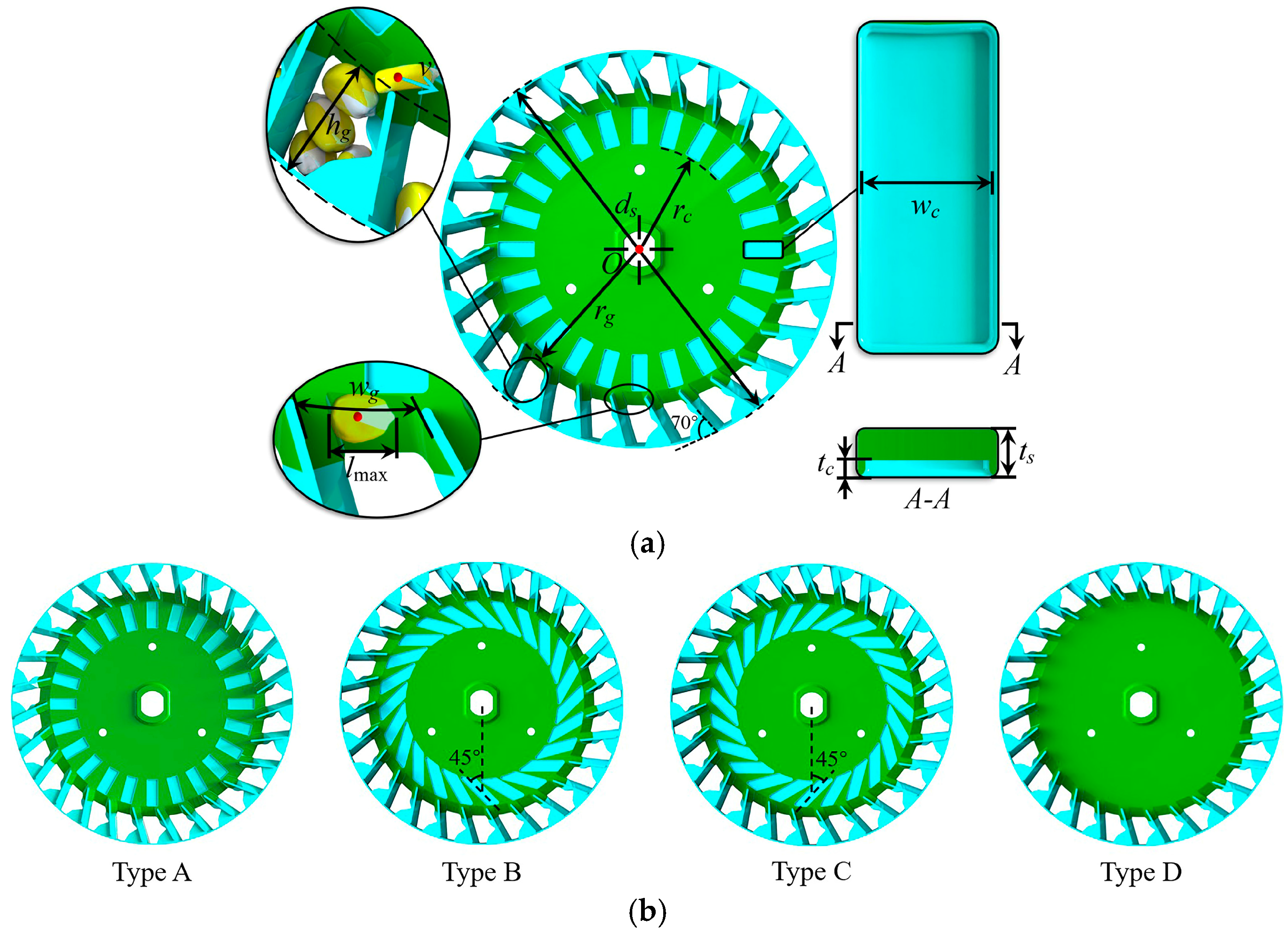
2.1. The Fundamental Structure and Principle
2.2. Design and Analysis of Key Component Structure
2.2.1. Seed Barrier and Infeed Groove
2.2.2. Seed Grid and Grooved Teeth
2.2.3. Seed Dispenser
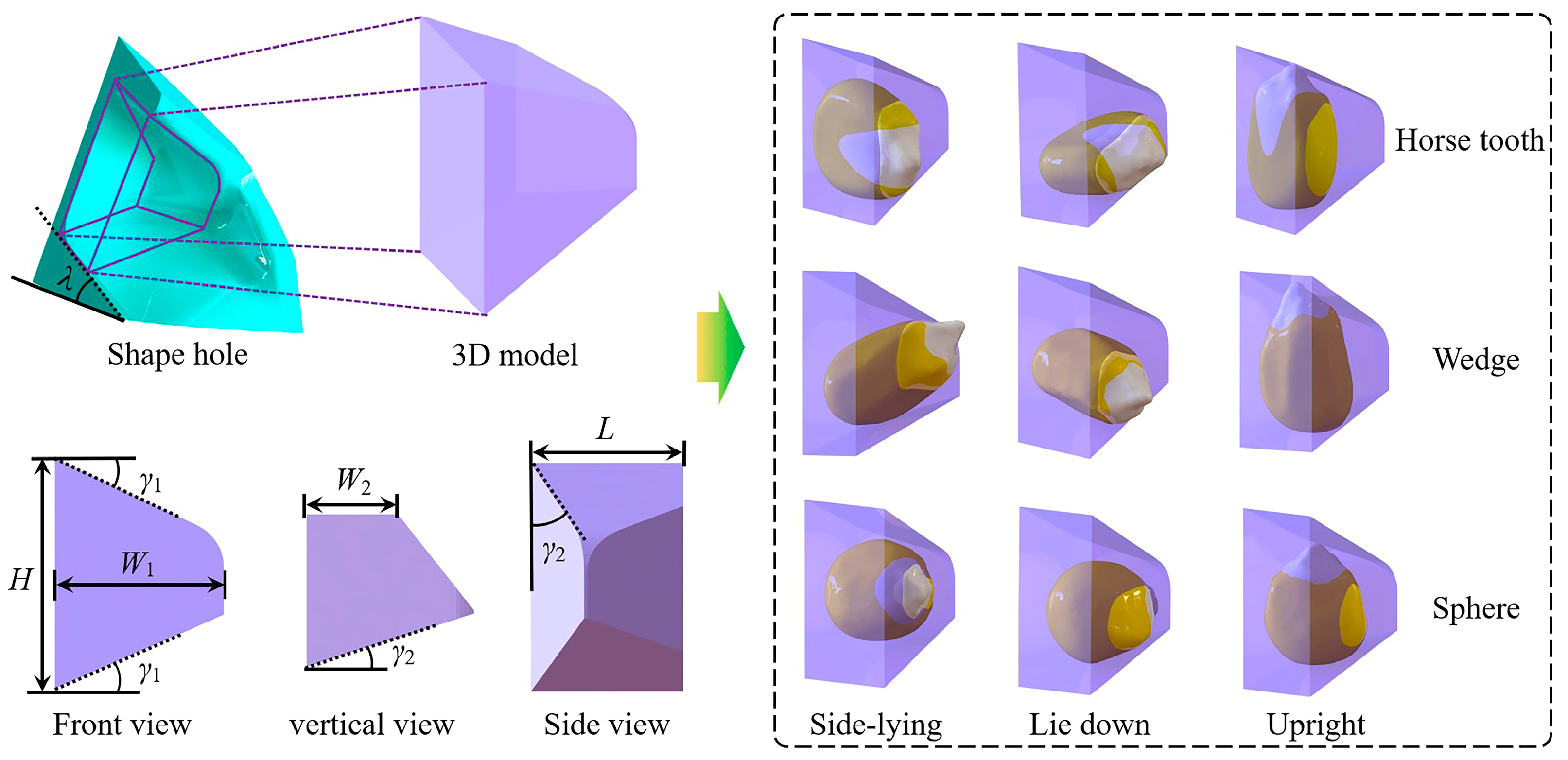
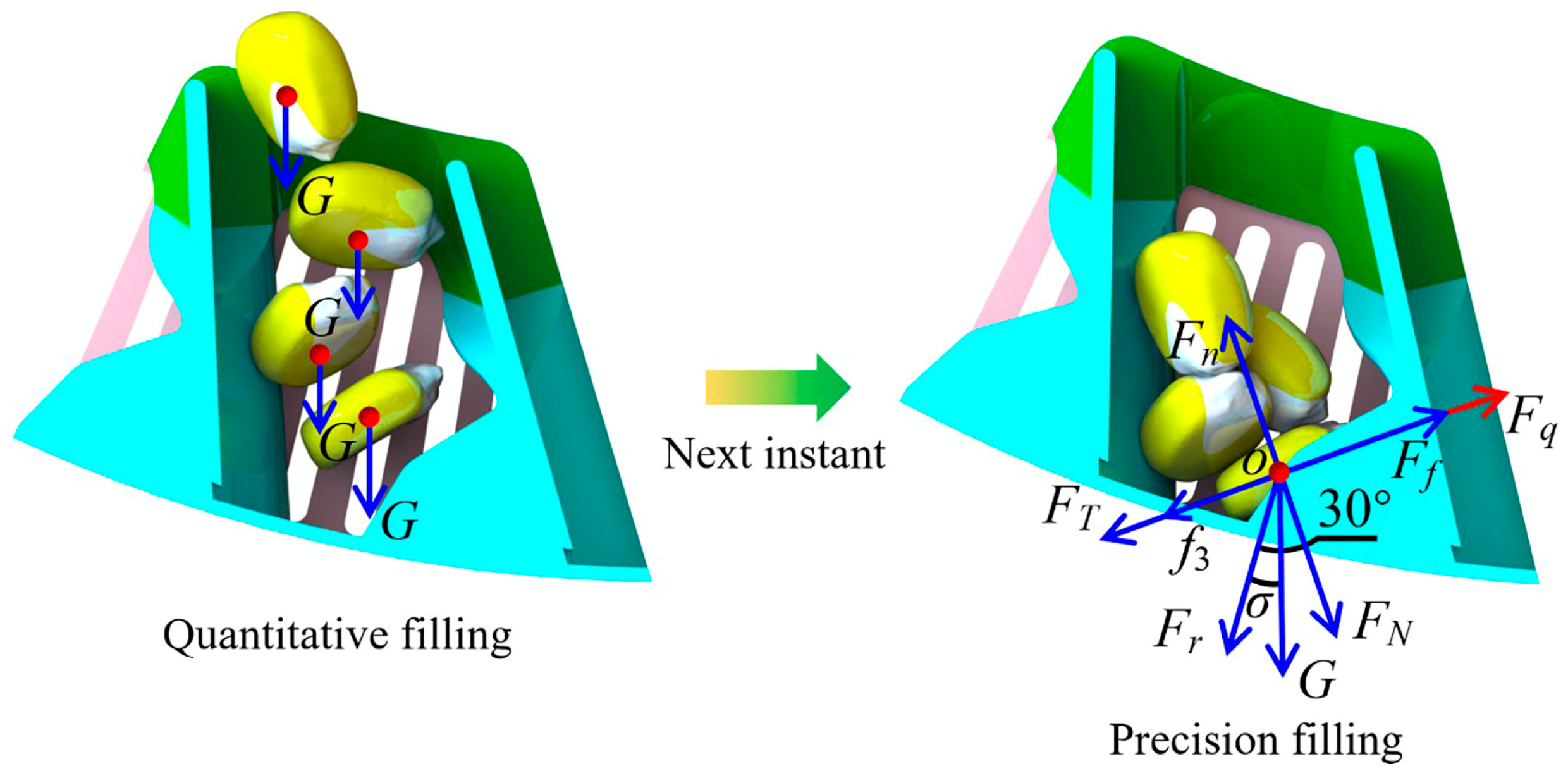
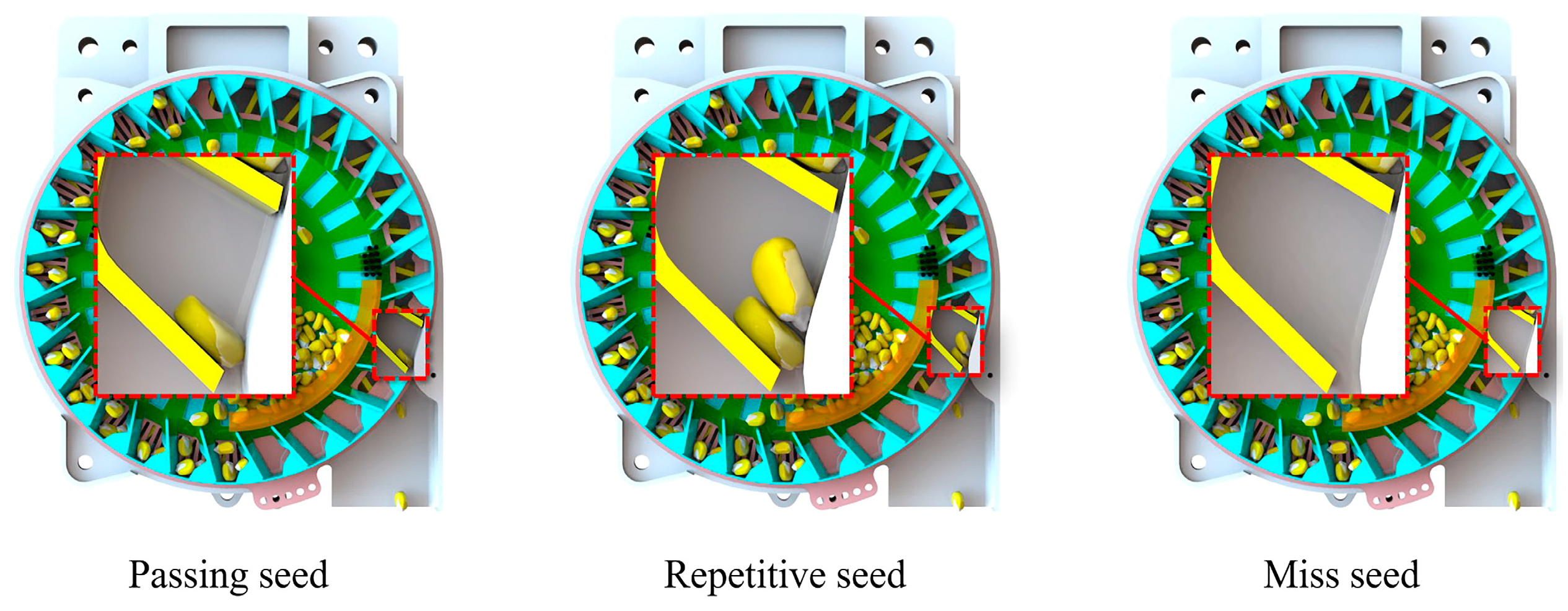
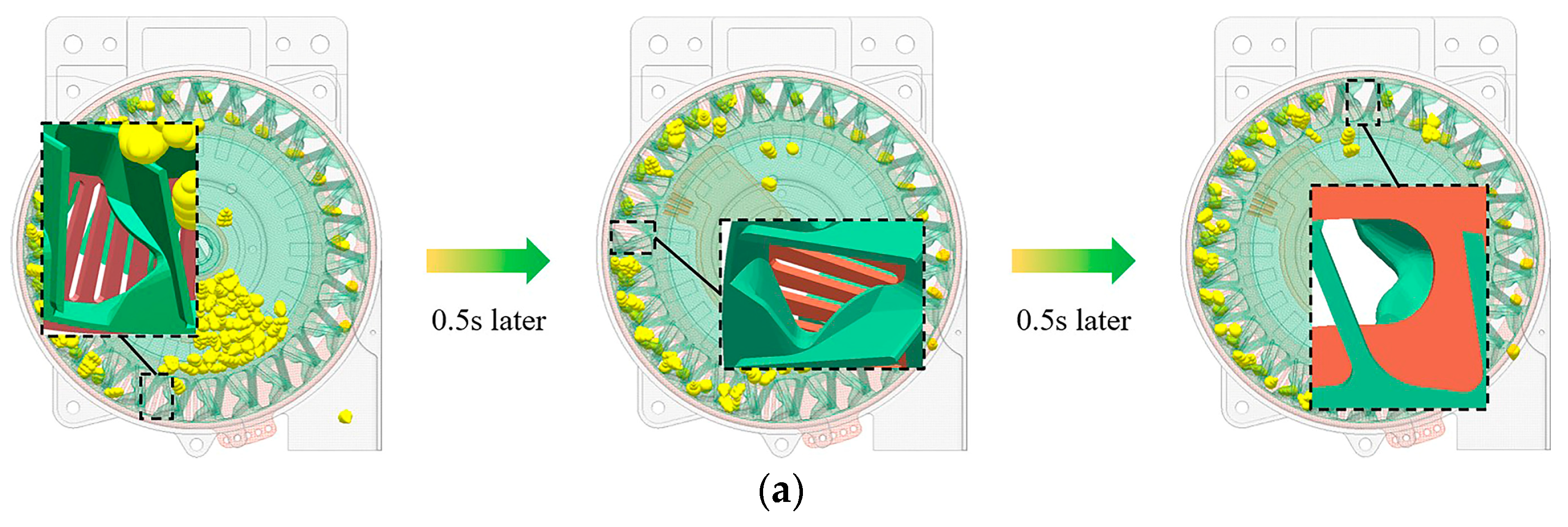
2.2.4. Analysis of Seed-Filling Process
2.3. Experiments and Methods
2.3.1. Simulation Experiment
2.3.2. Simulation Modeling
2.3.3. Bench Validation Experiment
2.3.4. Experiment Equipment and Materials
3. Results and Discussion
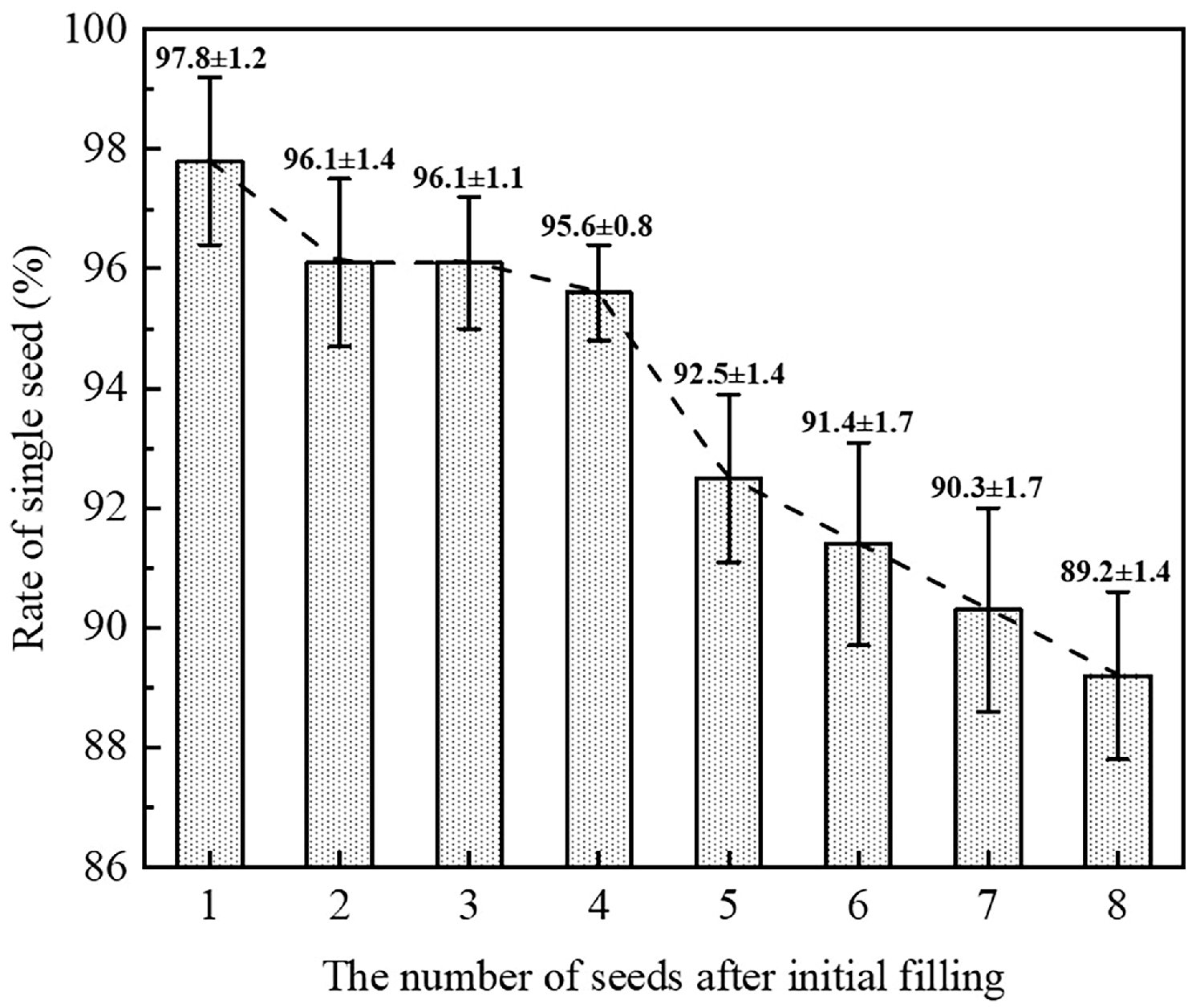
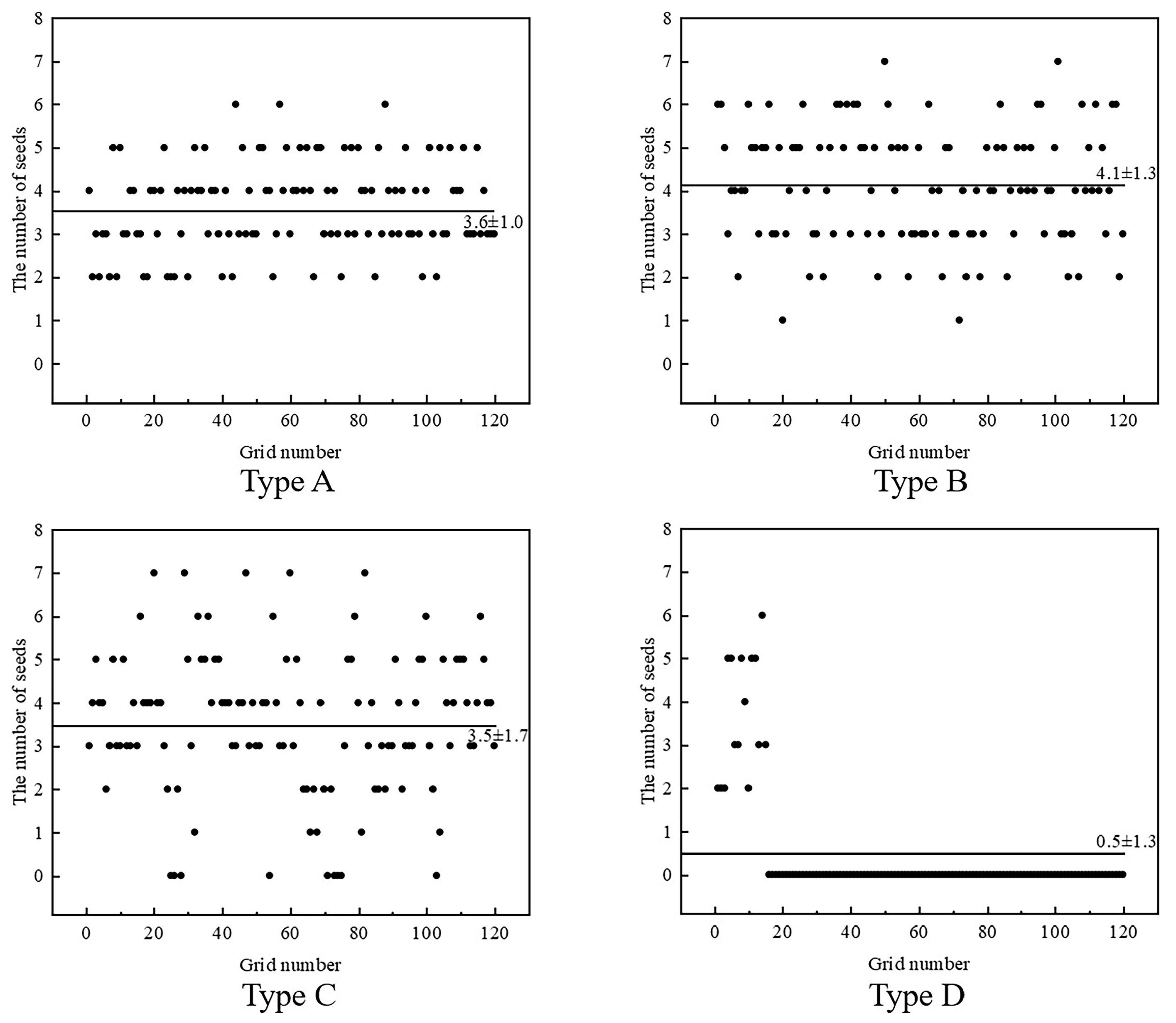
3.1. Simulation Comparison Experiment
3.1.1. Influence of Grooved Teeth Type on Seed Supply Capacity
3.1.2. Influence of Grooved Teeth Type on Seed-Filling Effect
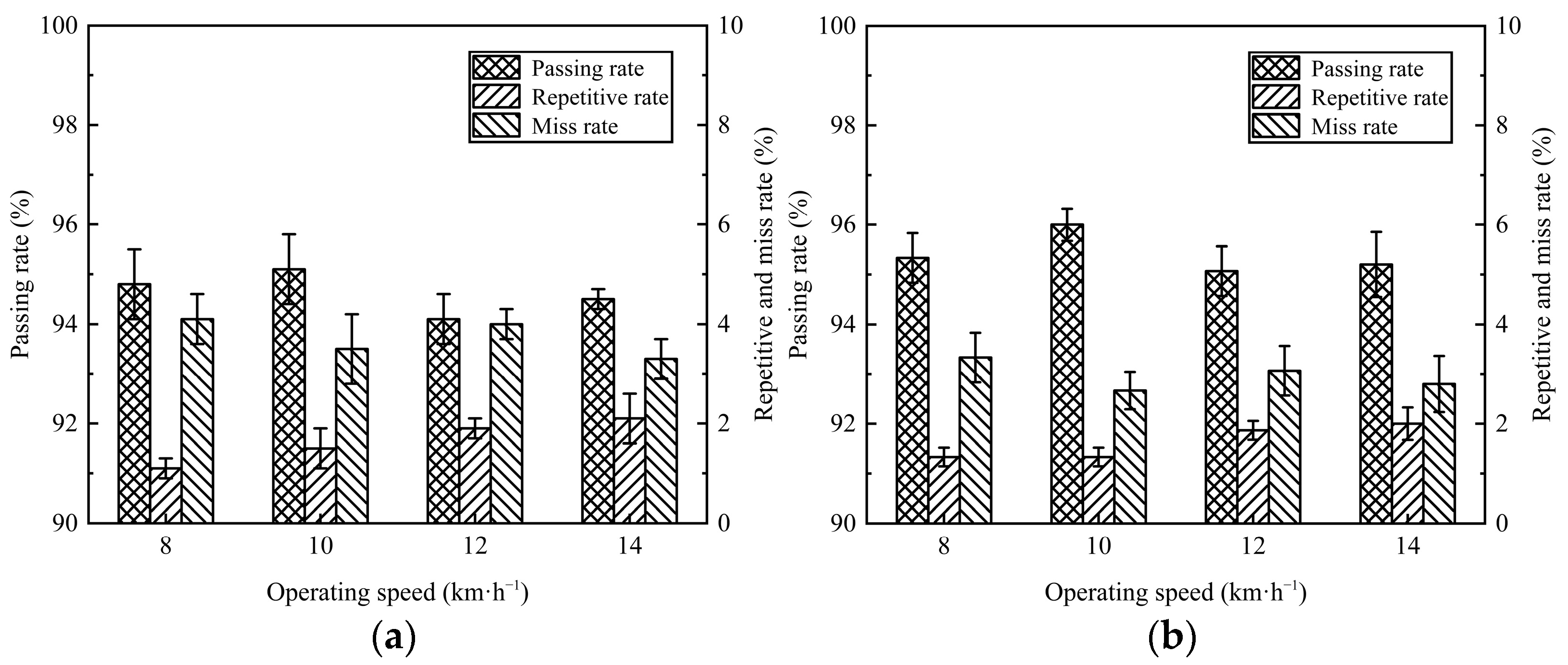
3.2. Simulation Optimization Experiment
3.3. Results of the Bench Validation Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anantachar, M.; Kumar, P.G.V.; Guruswamy, T. Neural network prediction of performance parameters of an inclined plate seed metering device and its reverse mapping for the determination of optimum design and operational parameters. Comput. Electron. Agric. 2010, 72, 87–98. [Google Scholar] [CrossRef]
- Dzvene, A.R.; Tesfuhuney, W.A.; Walker, S.; Ceronio, G. Optimizing the planting time and stand density of sunn hemp intercropping for biomass productivity and competitiveness in a maize-based system. Field Crops Res. 2023, 304, 109179. [Google Scholar] [CrossRef]
- Cay, A.; Kocabiyik, H.; May, S. Development of an electro-mechanic control system for seed-metering unit of single seed corn planters Part II: Field performance. Comput. Electron. Agric. 2018, 145, 11–17. [Google Scholar] [CrossRef]
- Pareek, C.M.; Tewari, V.K.; Machavaram, R.; Nare, B. Optimizing the seed-cell filling performance of an inclined plate seed metering device using integrated ANN-PSO approach. Artif. Intell. Agric. 2021, 5, 1–12. [Google Scholar] [CrossRef]
- Wang, J.; Tang, H.; Guan, R.; Li, X.; Bai, H.; Tian, L. Optimization design and experiment on clamping static and dynamic finger-spoon maize precision seed metering device. Trans. Chin. Soc. Agric. Mach. 2017, 48, 48–57. [Google Scholar] [CrossRef]
- Guzman, L.J.; Chen, Y.; Landry, H. Discrete element modeling of seed metering as affected by roller speed and damping coefficient. Trans. ASABE 2020, 63, 189–198. [Google Scholar] [CrossRef]
- Karayel, D.; Wiesehoff, M.; Özmerzi, A.; Müller, J. Laboratory measurement of seed drill seed spacing and velocity of fall of seeds using high-speed camera system. Comput. Electron. Agric. 2006, 50, 89–96. [Google Scholar] [CrossRef]
- Xue, P.; Xia, X.; Gao, P.; Ren, D.; Hao, Y.; Zheng, Z.; Zhang, J.; Zhu, R.; Hu, B.; Huang, Y. Double-Setting seed-metering device for precision planting of soybean at high Speeds. Trans. ASABE 2019, 62, 187–196. [Google Scholar] [CrossRef]
- BARUT, Z.B. Effect of different operating parameters on seed holding in the single seed metering unit of a pneumatic planter. Turk. J. Agric. For. 2004, 28, 435–441. [Google Scholar]
- Virk, S.S.; Porter, W.M.; Fulton, J.P.; Pate, G.L. Field validation of seed meter performance at varying seeding rates and ground speeds. Appl. Eng. Agric. 2019, 35, 937–948. [Google Scholar] [CrossRef]
- Yang, L.; Yan, B.; Cui, T.; Yu, Y.; He, X.; Liu, Q.; Liang, Z.; Yin, X.; Zhang, D. Global overview of research progress and development of precision maize planters. Int. J. Agric. Biol. Eng. 2016, 9, 9–26. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, J.; Chen, X.; Dong, J.; Huang, Y.; Shi, J. Development of a guiding-groove precision metering device for high-speed planting of soybean. Trans. ASABE 2021, 64, 1113–1122. [Google Scholar] [CrossRef]
- Liu, C.; Du, X.; Zhang, F.; Ma, T.; Zhang, H.; Li, Y. Design and test of cone diversion type horizontal plate wheat precision seed-metering device. Trans. Chin. Soc. Agric. Mach. 2018, 49, 56–65. [Google Scholar] [CrossRef]
- Du, X.; Liu, C.; Jiang, M.; Zhang, F.; Yuan, H.; Yang, H. Design and experiment of self-disturbance inner-filling cell wheel maize precision seed-metering device. Trans. Chin. Soc. Agric. Eng. 2019, 35, 23–34. [Google Scholar] [CrossRef]
- Kinze. Finger Pick-Up Meter. Available online: https://www.kinze.com/planter-performance/meters/finger-pick-up-meter/ (accessed on 18 June 2025).
- Embreparts. Plantsystem MAX. Available online: https://plantsystem.com.br/produto/pipoqueira (accessed on 18 June 2025).
- Singh, R.C.; Singh, G.; Saraswat, D.C. Optimisation of design and operational parameters of a pneumatic seed metering device for planting cottonseeds. Biosyst. Eng. 2005, 92, 429–438. [Google Scholar] [CrossRef]
- Jia, H.; Chen, Y.; Zhao, J.; Wang, J.; Guo, M.; Zhuang, X. Design and experiment of pneumatic-mechanical combined precision metering device for soybean. Trans. Chin. Soc. Agric. Mach. 2018, 49, 75–86, 139. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, J.; Li, B.; Ma, T.; Song, J.; Tian, Y. Design and experiment of horizontal disc seed metering device for maize seeder. Trans. Chin. Soc. Agric. Eng. 2017, 33, 37–46. [Google Scholar] [CrossRef]
- Maleki, M.R.; Mouazen, A.M.; De Ketelaere, B.; De Baerdemaeker, J. A New index for seed distribution uniformity evaluation of grain drills. Biosyst. Eng. 2006, 94, 471–475. [Google Scholar] [CrossRef]
- Li, C.; Cui, T.; Zhang, D.; Yang, L.; He, X.; Jing, M.; Dong, J.; Wu, D.; Wang, Z. Design shaped hole inserts by simulating and analysing the high-speed filling posture of maize seed particles. Biosyst. Eng. 2023, 232, 29–50. [Google Scholar] [CrossRef]
- Yang, L.; Li, Z.; Zhang, D.; Li, C.; Cui, T.; He, X. Design and test of the T-shaped hole of centrifugal high-speed maize precision seed metering device. Trans. Chin. Soc. Agric. Eng. 2024, 40, 50–60. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, S.; Zheng, Z.; Wu, J.; Huang, Y.; Gao, X. Development of a novel perforated type precision metering device for efficient and cleaner production of maize. J. Clean. Prod. 2024, 443, 140928. [Google Scholar] [CrossRef]
- Chinese Academy of Agricultural Mechanization Sciences. Agricultural Machinery Design Manual; China Agricultural Science and Technology Press: Beijing, China, 2007. [Google Scholar]
- St Jack, D.; Hesterman, D.C.; Guzzomi, A.L. Precision metering of Santalum spicatum (Australian Sandalwood) seeds. Biosyst. Eng. 2013, 115, 171–183. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, J.; Xue, D.; Wang, Y.; Zhang, Q.; Ren, L. An approach to and validation of maize-seed-assembly modelling based on the discrete element method. Powder Technol. 2018, 328, 167–183. [Google Scholar] [CrossRef]
- Li, Z.; He, S.; Zhong, J.; Han, J.; Chen, Y.; Song, Y. Parameter optimization and experiment of the disturbance pneumatic plate hole metering device for rapeseed. Trans. Chin. Soc. Agric. Eng. 2021, 37, 1–11. [Google Scholar] [CrossRef]
- GB/T20865-2017; No or Little-Tillage Fertilizers-Seeder. Standards Press of China: Beijing, China, 2018.
- Adilet, S.; Zhao, J.; Sayakhat, N.; Chen, J.; Nikolay, Z.; Bu, L.; Sugirbayeva, Z.; Hu, G.; Marat, M.; Wang, Z. Calibration strategy to determine the interaction properties of fertilizer particles using two laboratory tests and DEM. Agriculture 2021, 11, 592. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, R.; Liu, F.; Bai, H.; Dong, W. Research on the cluster hole effect and performance testing of air-suction quinoa seed metering device. Agriculture 2024, 14, 1391. [Google Scholar] [CrossRef]



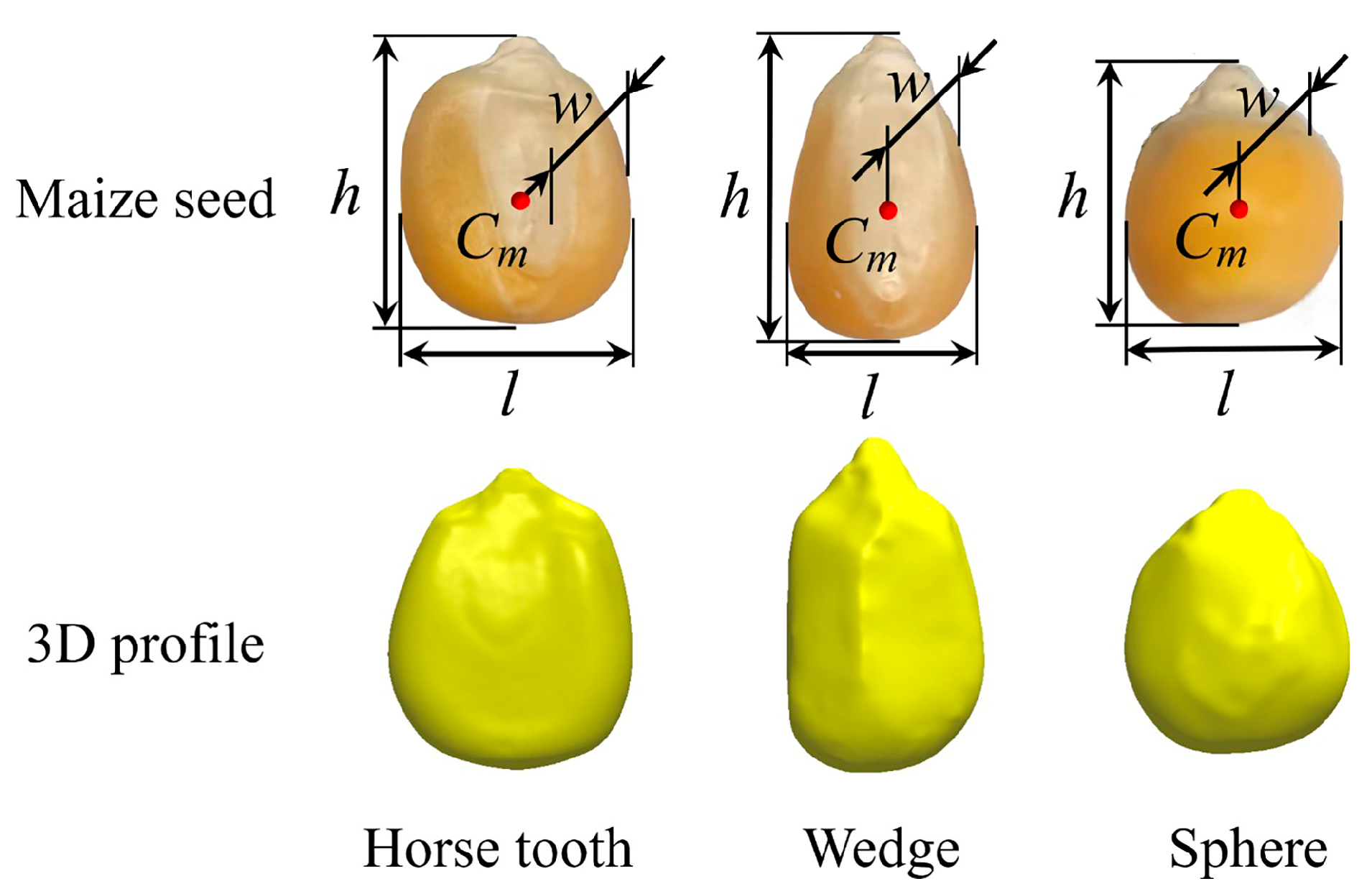
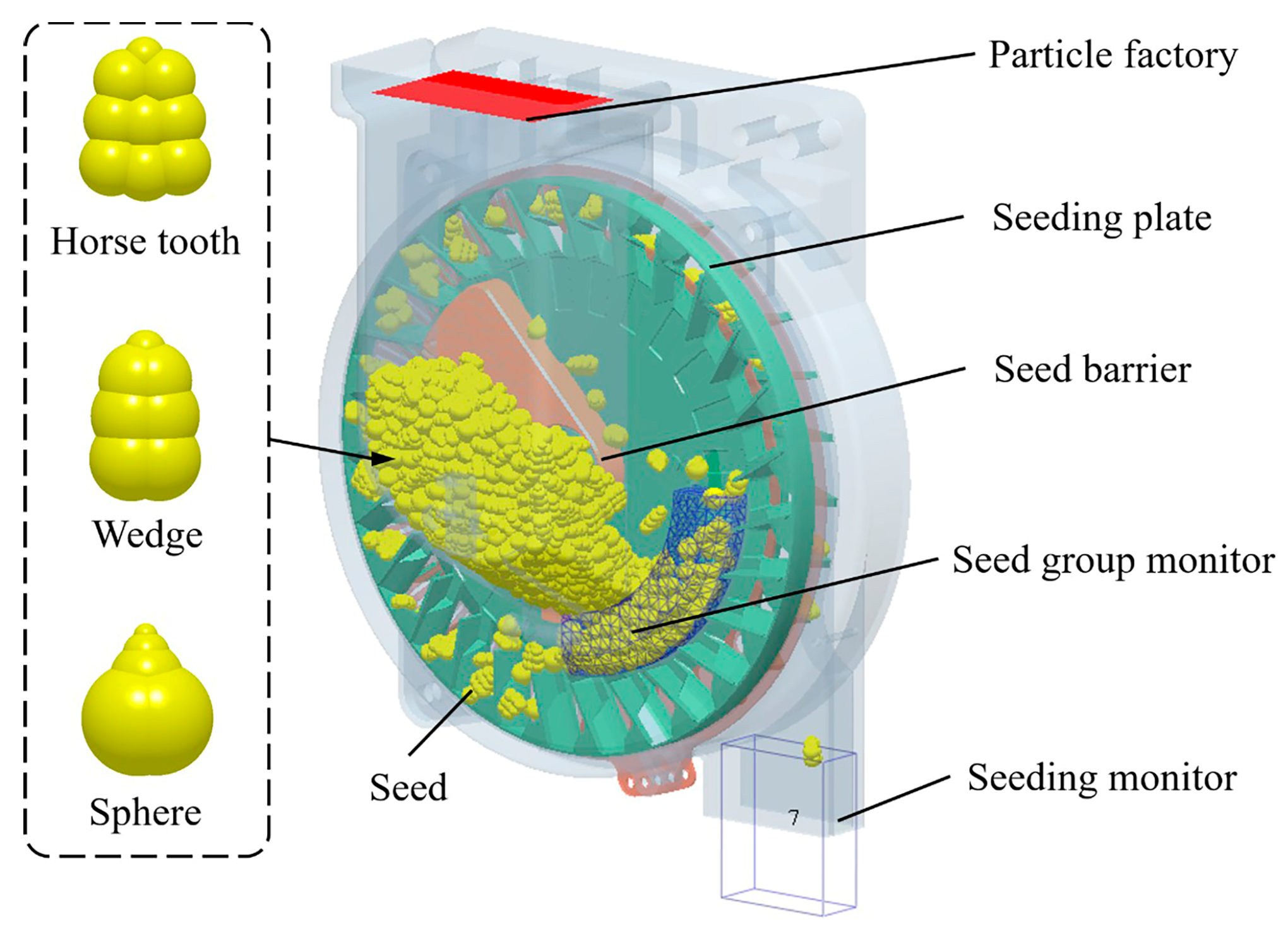




| Triaxial Dimensions | Horse Tooth | Wedge | Sphere |
|---|---|---|---|
| l (mm) | 10.8–13.5 | 11.0–14.0 | 6.7–10.5 |
| w (mm) | 7.5–10.7 | 5.9–9.5 | 7.4–10.9 |
| t (mm) | 3.8–6.3 | 4.3–8.4 | 5.7–10.7 |
| Parameters | Maize Seed | Seed-Metering Device |
|---|---|---|
| Density (kg·m−3) | 1197 | 2700 |
| Poisson’s ratio | 0.4 | 0.33 |
| Shear modulus (Pa) | 1.37 × 108 | 2.7 × 1010 |
| Restitution coefficient | 0.182 | 0.62 |
| Static friction coefficient | 0.07 | 0.3 |
| Sliding friction coefficient | 0.02 | 0.09 |
| Codes | Opening Height of the Seed Barrier X1 (mm) | The Depth of the Grooved Teeth X2 (mm) | Operating Speed X3 (km·h−1) |
|---|---|---|---|
| 1 | 25 | 1.5 | 14 (35 r·min−1) |
| 0 | 20 | 1.0 | 11 (27.5 r·min−1) |
| −1 | 15 | 0.5 | 8 (20 r·min−1) |
| No. | X1 (mm) | X2 (mm) | X3 (km·h−1) | Y1 (%) | Y2 (%) | Y3 (%) |
|---|---|---|---|---|---|---|
| 1 | 15 | 0.5 | 11 | 60.9 | 0.9 | 38.2 |
| 2 | 25 | 0.5 | 11 | 94.1 | 3.1 | 2.8 |
| 3 | 15 | 1.5 | 11 | 93.3 | 0.9 | 5.8 |
| 4 | 25 | 1.5 | 11 | 90.1 | 3.7 | 6.2 |
| 5 | 15 | 1.0 | 8 | 78.8 | 2 | 19.2 |
| 6 | 25 | 1.0 | 8 | 93.1 | 2.1 | 4.8 |
| 7 | 15 | 1.0 | 14 | 80.1 | 0.8 | 19.1 |
| 8 | 25 | 1.0 | 14 | 94.8 | 4.4 | 0.8 |
| 9 | 20 | 0.5 | 8 | 80 | 2.1 | 17.9 |
| 10 | 20 | 1.5 | 8 | 93.1 | 2 | 4.9 |
| 11 | 20 | 0.5 | 14 | 82.9 | 2.1 | 15.0 |
| 12 | 20 | 1.5 | 14 | 93.1 | 3.2 | 3.7 |
| 13 | 20 | 1.0 | 11 | 96.1 | 0.9 | 3.0 |
| 14 | 20 | 1.0 | 11 | 95.6 | 1.5 | 2.9 |
| 15 | 20 | 1.0 | 11 | 94.9 | 0.8 | 4.3 |
| 16 | 20 | 1.0 | 11 | 94.8 | 1.3 | 3.9 |
| 17 | 20 | 1.0 | 11 | 95.2 | 0.9 | 3.9 |
| Source | Passing Rate Y1 (%) | Repetitive Rate Y2 (%) | Miss Rate Y3 (%) | |||
|---|---|---|---|---|---|---|
| F | p | F | p | F | p | |
| Model | 243.52 | <0.0001 ** | 24.73 | 0.0002 ** | 236.35 | <0.0001 ** |
| X1 | 673.05 | <0.0001 ** | 110.29 | <0.0001 ** | 811.41 | <0.0001 ** |
| X2 | 516.80 | <0.0001 ** | 3.73 | 0.0947 | 502.94 | <0.0001 ** |
| X3 | 6.73 | 0.0357 * | 7.71 | 0.0274 * | 11.90 | 0.0107 * |
| X1 X2 | 512.36 | <0.0001 ** | 1.05 | 0.3398 | 453.79 | <0.0001 ** |
| X1 X3 | 0.062 | 0.8107 | 35.70 | 0.0006 ** | 5.39 | 0.0533 |
| X2 X3 | 3.25 | 0.1143 | 4.20 | 0.0797 | 1.02 | 0.3454 |
| X12 | 207.72 | <0.0001 ** | 13.40 | 0.0081 ** | 156.63 | <0.0001 ** |
| X22 | 167.58 | <0.0001 ** | 14.71 | 0.0064 ** | 122.10 | <0.0001 ** |
| X32 | 57.55 | 0.0001 ** | 25.62 | 0.0015 ** | 30.19 | 0.0009 ** |
| Lack of fit | 3.92 | 0.1099 | 0.84 | 0.5376 | 3.00 | 0.1580 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Wu, J.; Zhu, Y.; Gao, X. Investigation on Seed-Filling Effect of Quantitative Precision Filling High-Speed Seed-Metering Device for Maize. Agriculture 2025, 15, 1517. https://doi.org/10.3390/agriculture15141517
Dong J, Wu J, Zhu Y, Gao X. Investigation on Seed-Filling Effect of Quantitative Precision Filling High-Speed Seed-Metering Device for Maize. Agriculture. 2025; 15(14):1517. https://doi.org/10.3390/agriculture15141517
Chicago/Turabian StyleDong, Jianxin, Jingtao Wu, Yu Zhu, and Xiaojun Gao. 2025. "Investigation on Seed-Filling Effect of Quantitative Precision Filling High-Speed Seed-Metering Device for Maize" Agriculture 15, no. 14: 1517. https://doi.org/10.3390/agriculture15141517
APA StyleDong, J., Wu, J., Zhu, Y., & Gao, X. (2025). Investigation on Seed-Filling Effect of Quantitative Precision Filling High-Speed Seed-Metering Device for Maize. Agriculture, 15(14), 1517. https://doi.org/10.3390/agriculture15141517







