Abstract
With the advancement of Agriculture 4.0, intelligent systems and data-driven technologies offer new opportunities for pork supply-demand balance regulation, while also confronting challenges such as production cycle fluctuations and epidemic outbreaks. This paper introduces a knowledge-driven smart system for pork supply-demand regulation, which integrates essential components including a knowledge base, a mathematical-model-based expert system, an enhanced optimization framework, and a real-time feedback mechanism. Around the core of the system, a nonlinear constrained optimization model is established, which uses adjustments to newly retained gilts as decision variables and minimizes supply-demand squared errors as its objective function, incorporating multi-dimensional factors such as pig growth dynamics, epidemic impacts, consumption trends, and international trade into its analytical framework. By harnessing dynamic decision-making capabilities of reinforcement learning (RL), we design an optimization architecture centered on the Q-learning mechanism and dual-strategy pools, which is integrated into the honey badger algorithm to form the RL-enhanced honey badger algorithm (RLEHBA). This innovation achieves an efficient balance between exploration and exploitation in model solving and improves system adaptability. Numerical experiments demonstrate RLEHBA’s superior performance over State-of-the-Art algorithms on the CEC 2017 benchmark. A case study of China’s 2026 pork regulation confirms the system’s practical value in stabilizing the supply-demand balance and optimizing resource allocation. Finally, some targeted managerial insights are proposed. This study constructs a replicable framework for intelligent livestock regulation, and it also holds transformative significance for sustainable and adaptive supply chain management in global agri-food systems.
1. Introduction
The emergence of Agriculture 4.0, characterized by intelligent systems, data-driven automation, and decision-making frameworks [1,2], has driven transformative progress in agricultural productivity and supply chain management. This transformation holds profound significance for food security and socioeconomic stability in livestock farming, particularly pork production. China, the world’s largest producer, consumer, and importer of pork, faces critical challenges in balancing pork supply and demand. Over the past decade, pork production has fluctuated dramatically, from 50.71 million tons in 2010 to 55.41 million tons in 2022 [3], while imports surged from 0.1995 million tons to 1.7579 million tons during the same period, peaking at 4.39 million tons in 2020 [4]. External shocks such as the African swine fever outbreak in 2018 and the COVID-19 pandemic exacerbated these fluctuations, causing production to plummet to 41.133 million tons in 2020 [3]. In line with the fundamental principles of the market economy, prices are influenced by the interplay between supply and demand. When a substantial supply-demand gap exists, it results in notable fluctuations in pork prices, as observed in 2019 and 2020, when China experienced an average annual pork price surge to 52.42 CNY/kg, significantly higher than in non-pandemic years [3]. Such fluctuation disrupts the market equilibrium and harms farmer profitability, consumer affordability, and interlinked industries. These challenges highlight an urgent need for a smart pork regulation system, where the system is capable of coordinating biological production cycles, epidemic resilience, and market dynamics in real time. Existing models for pork supply-demand regulation predominantly rely on qualitative analysis and empirical adjustments [5]. While these methods offer basic functionality, they suffer from certain limitations. Therefore, it is necessary to design a quantitative regulation system that utilizes knowledge and mathematical models, combined with artificial intelligence technology, to facilitate the intelligent management of pork supply and demand.
The integration of reinforcement learning (RL) [6] and intelligent optimization algorithms provides a potential solution to the challenges in pork supply-demand regulation under Agriculture 4.0. RL performs well in decision-making, enabling agents to autonomously learn adaptive strategies through iterative interactions with complex environments. The decision process is consistent with the growth cycle of pigs, external factors such as epidemics, and the nature of market feedback loops, allowing for the timely adjustment of pork supply-demand supply-demand regulation plans based on knowledge and data information. Crucially, the reward-driven mechanism of RL aligns with the goal of optimizing the pork supply chain, which is to minimize the gap between the pork supply and demand while reducing market volatility, as demonstrated by the successful application in industrial scheduling [7] and resource allocation [8,9]. Intelligent optimization algorithms, such as the Honey Badger Optimization Algorithm [10] and Slime mold algorithm [11], possess advantages in addressing complicated optimization problems, such as a simple structure, strong robustness, and an outstanding global search ability [12]. They provide solutions for high-dimensional and nonlinear scenarios, particularly for solving mathematical models of pork supply-demand balance regulation. Combining RL with intelligent optimization algorithms can further improve the quality and efficiency of solutions. Intelligent optimization algorithms offer a global optimization framework, whereas RL achieves adaptive exploration–exploitation trade-offs through policy adjustments, delivering decision support driven by both data and knowledge for supply and demand regulation. Their application to agricultural supply chain regulation remains underexplored, which also forms the motivation for this study.
To bridge these gaps, a knowledge-driven smart system was proposed to regulate the pork supply and demand balance. The main contributions are summarized as follows:
- A knowledge-driven smart system was designed to regulate the pork supply and demand balance, which includes a knowledge base for some information like pork prices, pig quantities, pork import and export volumes, an expert system that is a rule-based decision-making module that utilizes mathematical models to analyze data and simulate scenarios, an optimizer using the reinforcement learning-enhanced honey badger algorithm (RLEHBA), and a real-time feedback mechanism for each module. The system achieves the full-cycle optimization and regulation of the pork supply and demand through the deep integration of multiple technologies;
- As the core of the regulation system, the expert system based on a quantitative mathematical model was developed to regulate the balance of the pork supply–demand. This model takes the adjustment amount of newly retained gilts as the decision variable and aims to minimize the sum of squares of the errors between the pork demand and supply. This model consists of four parts: pork production, pork consumption, pork import and export volumes, and comprehensively considers the growth characteristics of pigs, epidemic factors, consumption, and international trade;
- Given the nonlinearity and complexity of the proposed regulation model, a customized RLEHBA was proposed, providing a promising optimization framework for the regulation system. The proposed RLEHBA introduces two different position update strategies, forming strategy pools to help the algorithm break out of local stagnation. It also incorporates the Q-learning mechanism in RL to help the algorithm achieve intelligent strategy selection based on historical experience and information feedback. The proposed RLEHBA also offers a sound methodology for solving the complex and non-linear problems;
- A series of experiments were conducted to verify the effectiveness and superiority of the proposed regulation system. Firstly, the proposed RLEHBA and other comparative algorithms were tested on the CEC 2017 test set, verifying the superiority of the RLEHBA in solving complex optimization problems. Secondly, the inference and equilibrium process of the pork supply and demand balance were simulated, and the supply and demand of pork in China in 2025 and 2026 were predicted. On this basis, a pork regulation model for 2026 was established, and the RLEHBA was employed to address this model and obtain the optimal regulation strategy. Finally, relevant countermeasures and suggestions were provided;
- A significant contribution is the provision of feasible and rational grounds for the formulation of production plans by various departments and pig farmers based on the obtained optimal regulatory strategies. This contributes to the sustainable growth of the pig sector, aligning with stable pork prices and food security goals.
The remaining sections of this paper are organized as follows: Section 2 reviews previous studies; Section 3 presents the details of our proposed regulation system and the proposed RLEHBA; Section 4 validates the performance of the RLEHBA; Section 5 focuses on the application of the proposed system; and Section 6 addresses the main conclusions and future directions.
2. Literature Review
Recently, research on pork supply-demand supply-demand regulation has grown increasingly complex due to economic fluctuations, epidemic shocks, and upgraded consumption patterns, prompting a shift from single-market analysis to interdisciplinary integrated systemic regulation frameworks. This paper primarily outlines the following five aspects:
2.1. Pork Supply Prediction
The existing research has gradually evolved from traditional statistical and economic models to machine learning algorithms, intelligent optimization algorithms, and other technologies. While capturing supply cycle patterns and nonlinear trends, research has begun to integrate exogenous shock variables such as African swine fever to enhance the response capability of supply fluctuations during sudden epidemics.
For traditional statistical and economic model research, Coase and Fowler [13] pointed out that under the assumption that pork prices and breeding costs remain constant, any changes in supply and demand conditions will lead to sustained fluctuations and imbalances. Kim et al. [14] found through canonical correlation analysis that South Korea’s meat production has the strongest correlation with pork imports and the weakest correlation with domestic production, highlighting the dominant role of domestic production in local meat consumption. This study systematically analyzed the impact of domestic production and import/export factors on pork. Zhang et al. [15] developed a pig population prediction model based on discrete population quantities, forecasting the monthly pork supply in the Heilongjiang Province of China. Despite achieving satisfactory results, the model did not consider factors such as African swine fever outbreaks and the influence of imported pork. If epidemic factors were incorporated, the predictive accuracy of the model would be uncertain. Zielinska-Sitkiewicz et al. [16] considered the fluctuations in pork supply and demand by constructing creep trend model and ARIMA models to forecast pork prices.
The advancement of artificial intelligence has facilitated the utilization of machine learning, intelligent optimization algorithms, and other technologies in research to evaluate the impact of more factors on pork supply. Wang et al. [17] proposed an improved mayfly optimization algorithm (AVC-IMOA) along with a Back-Propagation Artificial Neural Network (BPANN) to predict the pork supply. However, this method utilizes historical data for prediction without considering the principle of pig age transfer and the impact of external factors such as epidemics, making it difficult to adapt to the complex effects of sudden exogenous shocks. Song et al. [18] introduced a prediction model for the number of breeding sows using an improved flower pollination algorithm and backpropagation neural network while considering the principle of pig age transfer and external factors such as epidemics. They introduced random disturbance terms into the model to simulate the impact of external factors on the pig herd system, providing a new idea for predicting the pork supply. On this basis, Song et al. [19] established a pork supply prediction model considering the growth characteristics of pigs and epidemic factors, laying the basis for the next step of pork supply-demand regulation. Chuluunsaikhann [20] proposed a Stacking Forest Ensemble method (SFE-NET) to predict the pork supply by incorporating internal and external factors, thus enhancing sustainable pork production.
2.2. Pork Demand Analysis
The research on pork demand mainly emphasizes the analysis of multi-dimensional influencing factors, but there are relatively few related studies. Fousekis et al. [21] contributed a methodological advancement by deriving a second-order differential demand system to analyze the pork demand. Bekkerman et al. [22] designed an alternative method to measure changes in the meat market demand, aiming for a more accurate and cost-effective evaluation of demand fluctuations over time. Yu et al. [23] carried out a global study on the influence of global pork demand growth on global trade, as well as the environmental challenges associated with increased pork production.
International institutions’ predictive research on meat consumption in China indicated that with the growth of per capita income and urbanization, the meat demand will continue to rise. Rabobank pointed out that China’s pork consumption will maintain high-speed growth, and that demand will gradually approach the level of developed countries [24]. The joint research agency of FAO predicted that the annual growth rate of the per capita meat consumption in China from 1997 to 2020 will reach 3.0%, and the per capita meat consumption will reach 71 kg [25].
2.3. Pork Supply and Demand Regulation
For the study of the regulation of the supply and demand balance, fruitful results have emerged in fields such as flood regulation ecosystems [26], Internet of Things systems [27], and energy supply-demand interactions [28], but there are few studies on the balance of the supply and demand of pork or food, and there is a lack of quantitative models for pork supply-demand regulation. Wang et al. [5] investigated the impact of import pork on the supply-demand relationship in China’s pork market during the outbreaks of African swine fever and COVID-19. The results show that imported pork helped to bridge the supply gap resulting from the epidemics, providing new ideas for regulating the pork supply and demand. Wang et al. [29] established a supply and demand-based price model to offer optimal breeding strategies for animal husbandry farmers, enabling them to maximize profits and adjust the supply-demand balance. Yao et al. [30] explored strategies to guarantee food security and maintain a stable pork supply amidst the simultaneous effects of African swine fever and COVID-19. This study considers the impact of emergencies such as epidemics on the pork supply. Pang et al. [31] employed the structural vector autoregressive model to examine the primary factors affecting pork price fluctuations. The findings demonstrate that pork prices have the greatest impact on pork price fluctuations. Sarttra et al. [32] solved the supply chain management problem of a dairy cooperative in Thailand by establishing a mixed integer linear programming model to meet the product demand at any given time and simplify cattle herd structure management. Although this model does not have the advantage of dynamic adjustment, it provides a new idea for regulating the supply-demand balance of pork.
2.4. The Application of RL in Agriculture
Recently, RL technology has been widely applied in the field of agriculture. Pamuklu et al. [33] proposed a multi-agent risk sensitive RL method suitable for task scheduling in intelligent agricultural aerial base stations, and verified that the proposed method is superior to several heuristics methods and the classical Q-learning approach. Chen et al. [34] applied RL to a solar sensor-based smart farm system to optimize the monitoring quality, extend the system life, and ensure the best strategy for energy security. Ali et al. [35] innovatively applied the Q-learning method to battery management in dairy farms, providing new technological ideas for the industry. Lu et al. [36] proposed a dual-mode grey wolf optimizer based on RL, and used RL to enhance information feedback to optimize the hyperparameters of convolutional neural networks. This technique was successfully applied to the automatic detection of crop diseases and pests. Farid et al. [37] combined RL with real-time wind data to solve the technical problem that the traditional UAV spray is disturbed by wind in precision agriculture. Although significant progress has been made in these studies, the effectiveness of RL in regulating the pork supply and demand balance has not yet been explored.
2.5. Research Gaps
Although the existing research has achieved fruitful results, several research gaps are summarized below:
- Existing research on pork supply-demand balance regulation is predominantly grounded in market theory and relies on historical data to predict future supply and demand. The regulation strategies are qualitative analyses derived from market theories; they lack systematic and quantitative model analysis. Therefore, it is not feasible to formulate production plans and scientifically reasonable regulations based on the quantitative analysis results of supply and demand balance. The purpose of pork supply-demand balance regulation is to effectively manage the supply and demand of pork to achieve a relatively balanced state in terms of quantity, so as to reconcile supply and demand gaps and stabilize pork prices. The current approaches fail to establish a closed-loop feedback mechanism between regulation decisions and market responses, particularly lacking adaptive learning capabilities for emergent scenarios like African swine fever outbreaks. Therefore, a scientific and rational regulation system needs to be designed to formulate matching regulation strategies based on the regulation results.
- The existing research exhibits insufficient environmental adaptability to the effects of multiple factors. Firstly, regarding the intrinsic factor of pig growth characteristics, the research [17] adopts simplified processing and directly extrapolates yield predictions from historical data. Although short-term statistical significance can be obtained, the biological temporal patterns of pig population age transfer are ignored. It is not conducive to formulating specific production plans based on the results, hence demonstrating limited practical application. Secondly, when considering external factors such as the pandemic, the model [15] that takes into account growth characteristics fails to effectively integrate the nonlinear effects of pandemic shocks on the pig inventory and fattening success rates. Thirdly, the existing research [5] only analyzes how the pork import volume affects the pork supply and demand relationship during the epidemic period, and there is no reported research on incorporating the pork import and export volume into the model for regulating the pork supply and demand. This omission becomes particularly critical given the increasing globalization of agricultural markets, where trade policy changes can induce supply shocks in regional markets. The approach of considering only a single factor makes it difficult for current models to adapt to the multi-dimensional dynamic environment of the Agriculture 4.0 era. It cannot establish a relationship between the growth stage of pig herds and market demand fluctuations, nor can it achieve the collaborative optimization of supply and demand parameters in sudden epidemics and international trade changes, ultimately limiting the model’s decision support capabilities in complex real-world scenarios.
Based on the above analysis, we attempt to provide a knowledge-driven system for regulating the pork supply and demand, taking into account multiple factors, such as pig growth characteristics, epidemics, and pork import and export trade. RL and the honey badger algorithm are integrated to enhance the environmental adaptability and solution quality of the proposed system.
3. Proposed Regulation System
In this section, we first propose a mathematical model for regulating the pork supply–demand, which is the core of the proposed regulation system. Then, we provide an optimization framework for this system, namely the RLEHBA. Finally, the knowledge-driven regulation system framework is presented.
3.1. Supply-Demand Balance Regulation Model
3.1.1. Problem Description
From a comprehensive perspective, the balance of the pork supply and demand mainly consists of four aspects: pork production, consumption, imports, and exports. Domestic pork production and pork imports together constitute the total pork supply. In addition, depending on the different uses of pork, the pork demand includes the demand for pork for consumption, the demand for pork for processing, and the demand for pork for export [38]. Therefore, we consider pork consumption and pork exports together as the total pork demand. Taking the historical data of the pork supply and demand in China as an example (as shown in Figure 1), the outbreaks of porcine reproductive and respiratory syndrome occurred in some regions of China during 2015 and 2016, leading to a decrease in domestic pork production and a supply shortage. Despite an increase in pork imports, there was still a significant gap between the pork supply and demand. In the scenarios of African swine fever at the end of 2018 and the outbreak of the COVID-19 pandemic from 2020 to 2021, pork production decreased. To ensure an adequate domestic pork supply, the pork import volume increased substantially, thus guaranteeing the pork supply. Therefore, when regulating the balance of the pork supply and demand, we cannot overlook the impact of pork imports and exports on the adjustment process. Based on the aforementioned analysis, the key factors in the proposed model for regulating the pork supply and demand balance are illustrated in Figure 2.
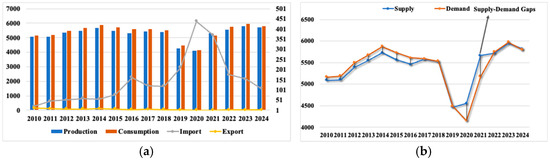
Figure 1.
The pork supply-demand gaps in China: (a) The pork volumes; (b) supply and demand gaps.
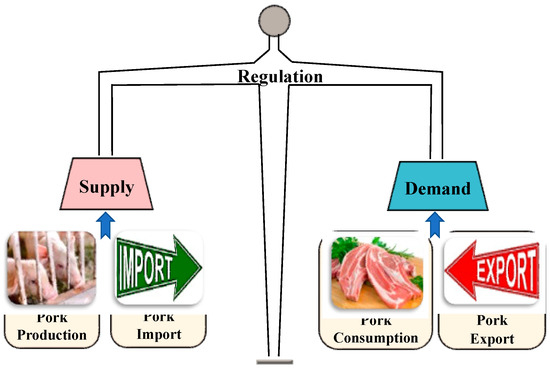
Figure 2.
Structural diagram of pork supply and demand balance regulation.
3.1.2. Model Formulation
For the convenience of formal description, the following symbols are defined, as presented in Table 1.

Table 1.
Related parameters and definitions.
The mathematical model of the pork supply-demand balance regulation is presented below:
- Objective function
The purpose of the pork supply-demand balance regulation proposed in this paper is to achieve a relative balance in the quantity of the pork supply and demand; hence, the goal is to minimize the error between the pork demand and supply for all the years to be regulated. The objective function is represented in Equation (1).
- Decision variables
In the prediction of pork production, the quantity of newly retained gilts will influence the quantities of breeding sows and hogs, thus affecting pork production. Therefore, the essence of the supply-demand balance regulation model lies in adjusting the quantity of newly retained gilts. Taking into account the temporal impact of factors such as epidemics on the pig population, let the quantity of newly retained gilts before adjustment be gilt(t) (t = 1, 2, …, 12), with the adjustment quantity of newly retained gilts as the decision variable x(t) (t = 1, 2, …, 12). In the regulation model, the adjustment quantity of newly retained gilts in the T-th year, namely, the decision variable, is expressed as follows:
The number of newly retained gilts in the T-th year is as follows:
- Constraints
When adjusting the quantity of newly retained gilts, efforts should be made to respect the market rules while minimizing fluctuations in the pig herd system and avoiding unlimited increases or decreases. Therefore, the decision variables should fall within the following range:
where represents a threshold value that serves as a cautionary limit, constraining the adjustment amount of newly retained gilts to a rational and manageable range.
- Prediction of annual total pork production PorkP(T)
The prediction of the annual total pork production, PorkP(T), is a key aspect of the regulation model. The prediction steps for PorkP(T) based on the approach in reference [18,19] are outlined below:
- (1)
- The calculation method for determining the number of newly retained gilts is below.where f1, f2, f3, and f4 are the parameters to be solved, which are obtained by using the method in reference [19] and the proposed RLEHBA algorithm. We will provide a detailed description of the RLEHBA algorithm in Section 3.2.
- (2)
- The number of monthly breeding sows is determined based on the principle of sow age transfer [18,19]. Considering the impact of external factors such as the epidemic on live pigs, we introduce a random disturbance term in the recursive formula for the status of sows to simulate the impact of external factors. The calculation method for the number of breeding sows is summarized as follows:
- (3)
- Similarly, we incorporate the random disturbance term into the recursive formula to calculate the number of newborn piglets:
- (4)
- Calculate the quantity of boars and hogs separately by employing the following calculation method:
- (5)
- The SMERs of hogs are adjusted using random disturbance terms to obtain the quantity of slaughtered hogs, as formulated in Equation (12).
- (6)
- Based on the average meat production of each slaughtered hog, Meat, over the years, we can calculate the pork production in the t-th month. The calculation method is as follows:
By summing up the pork production of the T-th year obtained in Equation (13), we can obtain the total annual pork production, PorkP(T), in the T-th year.
Disturbance1 and Disturbance3 are random disturbance terms used to correct the impact of external factors on the pig population. In the years affected by outbreaks, the SMER of sows and hogs tends to be higher compared to in normal years, while the provided SMER remains at normal levels. In such cases, this may lead to an overestimation of the predicted numbers of various categories of pigs. Therefore, the SMER values for breeding sows and hogs are calibrated using Disturbance1 and Disturbance3, respectively. For example, Disturbance1(T) in the T-th year is derived from the relative error between the observed and predicted values of the number of breeding sows at the end of each year, as shown in Equation (14). A similar approach applies to Disturbance 3 for hogs.
where SN(T) represents the actual number of breeding sows at the end of the T-th year, denotes the predicted number of breeding sows at the end of the T-th year.
A negative Disturbance1(T) indicates overestimation due to unmodeled epidemic effects that increase the SMER of sows, thus requiring a +Disturbance1 adjustment in Equation (6). Conversely, a positive Disturbance1(T) reflects underestimation during normal years with a lower SMER of sows, necessitating a −Disturbance1 adjustment.
The random disturbance term Disturbance2, which affects the average monthly litter size of each breeding sow (AMLSBS), is affected by various factors such as farms, breeds, parities, and seasons, leading to fluctuations in the annual total of piglets born to sows [39,40,41]. Positive Disturbance2 denotes underestimation, necessitating litter size increases above the mean level; negative Disturbance2 indicates overestimation, requiring reductions below the mean level, thereby calibrating newborn piglet numbers through systematic adjustments.
- Prediction of pork consumption, PorkC(T), and import and export volumes, PorkI(T) and PorkE(T)
Based on historical data, we employed an improved BPNN to forecast the pork consumption, import and export volume, and random disturbance terms. Due to the defects of the gradient descent method, a standard BPNN is prone to falling into local optima and insufficient prediction accuracy, which directly affects the prediction performance of key parameters in the pork regulation model [42]. The combination of intelligent optimization algorithms with a BPNN to optimize the weights and thresholds can significantly improve the prediction accuracy of the algorithm. Various similar variants such as the GA-BPNN [43], ADE-BPNN [44], and GWO-BPNN [45] have been successfully applied to predictive problems in practical production, yielding favorable predictive results. Inspired by these successful applications, this study applies the RLEHBA to optimize the weights and thresholds of the BPNN, presenting a new prediction model based on the RLEHBA and BPNN. This model is utilized for predicting relevant parameters in the pork supply-demand balance regulation model, thereby enhancing prediction accuracy. For brevity, the proposed prediction model is referred to as the RLEHBA-BPNN. For the derivation principles of the BPNN, please refer to the literature [17,44].
In the proposed regulation model, the dimension of decision variables is determined by the regulated year. For instance, when trying to regulate the pork supply and demand for China in 2026, the nonlinearity of this optimization problem, coupled with many parameters and the complexity of the solution process, makes it hard to obtain the optimal solution for this model. Therefore, this paper presents a tailored reinforcement learning-enhanced honey badger algorithm (RLEHBA) for solving the pork supply-demand balance regulation model. Furthermore, we used the RLEHBA-BPNN to forecast the crucial parameters in the model, including random disturbance terms and pork import and export volumes.
3.2. RLEHBA for Optimization
The honey badger algorithm (HBA) is a swarm intelligence optimization algorithm proposed by Fatma A. Hashim in 2022, inspired by the foraging behavior of honey badgers [10]. Due to its simple structure, ease of implementation, and excellent optimization performance, the algorithm has found extensive application in addressing real-world challenges, including medical diagnosis [46], feature selection [47], power systems [48], and unmanned aerial vehicle path planning [49]. The foraging behavior of honey badgers involves two modes of movement: the digging mode and honey mode. In the digging mode, the honey badger utilizes its olfactory abilities to approach the location of its prey, namely, the optimal solution’s location. Once it reaches this location, the honey badger moves around the prey, carefully selecting suitable spots for digging and capturing them. In the honey mode, the honey badger directly follows the guidance of honey guide birds to the beehive. With the assistance of these two modes, the algorithm combines global exploration and local exploitation search strategies to find the global optimal solution.
Despite numerous variants of HBA, including LFHBA [50], T-pHBGO [51] and HHB-WCA [52], which have demonstrated the efficacy and superiority of the HBA in addressing global optimization challenges, persistent issues remain, such as entrapment in local optima and poor solution quality in high-dimensional contexts. On the one hand, the HBA incorporates guidance from the global optimum individual Xprey during both the digging phase and honey phase to accelerate convergence; however, this approach hinders the algorithm from exploring the search space effectively. On the other hand, different search strategies may be required at different stages in the optimization process, and the random approach in the original HBA cannot effectively adapt to the needs of different stages. Therefore, this paper introduces the Q-learning mechanism in RL into the HBA, endowing the algorithm with environmental adaptability. Q-learning, a model-free, off-policy, and temporal difference learning approach in RL, is employed to learn the optimal policies by estimating the action value function [6], and it can achieve intelligent strategy selection based on historical experience and information feedback. In addition, new position update strategies are incorporated for different search stages to avoid local stagnation. The proposed variant of the HBA is called the reinforcement learning-enhanced honey badger algorithm (RLEHBA), with the goal of improving the solution quality for the pork supply-demand regulation problem.
3.2.1. Improved HBA with Q-Learning Mechanism
For the convenience of expression, we provide a unified definition for the following variables: Xi represents the i-th individual in the population, and Xnew is the updated position of the honey badger. Xprey denotes the prey, which is the position of the global best solution. Xj and Xk are randomly selected individuals different from Xi in the population. rand is a random number between [0, 1]. L represents a learning factor, and it is a random vector between [0, 1].
The mathematical description of the RLEHBA is provided below:
- Population initialization
Like other intelligent optimization algorithms, the RLEHBA requires the initialization of a population at the beginning of the optimization process, namely, generating initial individuals within the search space. Assuming a population size of N and a problem dimension of D, the generation method for the i-th individual of the j-th component is as shown in Equation (15).
- 2.
- Defining intensity (I)
The honey badger detects its prey using its sense of smell, and the intensity of the prey’s odor I is determined by the concentration of the prey and the distance between it and the honey badger. A higher value of I indicates a stronger odor of the prey, prompting the honey badger to accelerate its search, and vice versa. Equation (16) provides the definition of I.
where di represents the distance between Xprey and Xi, and r2 is a random number ranging from [0, 1].
- 3.
- Update density factor
The density factor α controls time-varying randomization to facilitate a seamless transition from exploration to exploitation. α can be mathematically represented as follows:
where C is a constant with a value of 2. runtime is the current runtime of the algorithm, and Maxruntime is the maximum runtime of the algorithm.
- 4.
- Digging phase
At this stage, the honey badger performs a global search to locate the food source, which is the global exploration of the algorithm using trigonometric perturbation. This behavior can be simulated in Equation (20).
where α is the density factor, and its update method is described in Equation (19). β is the ability of the honey badger to obtain food, typically taking a value of 6. di is the distance between Xprey and Xi, which can be calculated using Equation (18). r3, r4, and r5 are three distinct random numbers between the range of [0, 1]. The flag direction operator (±) provides the flexibility to increment or decrement the positions of solutions, enabling more opportunities for individuals to change direction. This feature facilitates a comprehensive exploration of the search space in multiple directions, helping the algorithm escape from local optima.
Due to the limited global search capability of the HBA in the early optimization stage, it cannot effectively explore the entire search space. To address this issue, we provide a learning strategy for the RLEHBA, where it learns from other individuals within the entire search space based on the position update methods provided in Equations (21) and (22). The learning mechanism operates as follows:
This position update strategy in Equation (21) introduces differential information between individuals through differential items and random perturbations, promoting the transfer and sharing of knowledge within the population, thereby enhancing the algorithm’s global search capability.
- 5.
- Honey phase
At this stage, the badger finds the hive with the assistance of the honey guide bird, which is the local exploitation of the algorithm. This behavior can be represented as follows:
where r7 is a random number between [0, 1], and the calculation methods for di and α are outlined in Equations (18) and (19).
In the position update mechanism described in Equation (23), although the local exploitation is achieved by combining the prey position with random factors, the update process only relies on a single prey individual and fixed parameters, resulting in insufficient diversity and the dynamic adjustment ability of the search direction. Therefore, a position update strategy with relatively balanced global and local search capabilities was introduced, as shown in Equation (24).
- 6.
- Q-learning mechanism
In the optimization process of metaheuristic algorithms, different evolutionary stages often have differentiated requirements for search strategies: early stages emphasize global exploration to escape local optima, while later stages focus on local exploitation to enhance convergence efficiency. Therefore, dynamically selecting a position update strategy that is adapted to the current evolutionary stage has become the key to improving the search efficiency of the algorithm. This requirement is highly compatible with the interactive learning mechanism of RL, which effectively captures the evolutionary characteristics of algorithms at different stages by constructing a feedback system between agents and solution spaces. The remarkable RL technique known as Q-learning [53] aims to interact with the environment through the agent and then accumulate the maximum reward to obtain the optimal policy, and it is used in this paper to allow the RLEHBA to adaptively select the optimal strategy from the possible actions.
The Q-learning mechanism is mainly composed of a learning agent, environment, states S = {s1, s2, …, sm}, actions A = {a1, a2, …, an}, and rewards R. In Q-learning, the reward Q-table is a matrix used to penalize and reward the combination of the behavior and state of the agent, and continuously learns the long-term benefits of each state–action pair during iteration, forming an experience base for problem solving [54]. The agent attempts to update its state by considering the corresponding Q value, and all possible actions it can take in order to select the best action. Each agent gains experience by exploring the environment in a specific iteration (t) and updating the corresponding Q value according to the Bellman equation [55,56] in Equation (25):
where Q(st+1, at+1) is the cumulative reward of a new action at+1 in the new state of st+1, Q(st, at) is the cumulative reward of action at in the state of st. Q(st+1, a) is the maximum expected Q value for all possible actions in the next state st+1. rt+1 is the immediate reward obtained by the action at in the state of st. λ is the learning rate between [0, 1], which controls the degree to which new information updates the existing Q value. γ is the discount factor between 0 and 1, and it is used to balance the relationship between immediate rewards and future rewards.
The main components of the Q-learning mechanism in the proposed RLEHBA are as follows:
- (1)
- State
The state describes the key component of the environment related to the problem to be solved, and it should provide sufficient information for the agent to support behavioral decisions in each iteration. For the RLEHBA, there are two states S = {s1, s2}: the digging phase (s1) and the honey phase (s2), corresponding to exploration and exploitation search, respectively.
- (2)
- Action
In each iteration of the algorithm, the agent needs to decide the next action based on the current state, namely, choose different position update strategies. For each state in the RLEHBA, there are two different actions, A = {a1, a2}. The action space defined in this study is as follows:
In the exploration state (s1), the action (a1) in Equation (21) is based on random perturbations of population differences, which is suitable for large-scale global exploration; the action (a2) in Equation (20) expands the search range through nonlinear perturbations, enhancing the diversity of the population. The two global update strategies jointly aim to extensively search the solution space and avoid local stagnation. In the exploitation state (s2), the action (a1) in Equation (24) serves as a neutral action, allowing for a certain degree of exploitation but not dominating global exploration. The action (a2) in Equation (23) directly moves towards the current optimal solution along the gradient direction. The two position update strategies work together towards fine search, endowing the algorithm with relatively balanced global and local search capabilities, avoiding premature convergence caused by a single local search.
- (3)
- Reward
Reward serves as feedback from the environment on the execution of the agent’s actions, guiding the agent to choose the best actions. A good action means that updating the candidate solution can effectively improve the quality of the original solution. Due to the fact that the mathematical model for the pork supply-demand balance regulation is a minimization problem, solutions with lower fitness values are better. Therefore, if the agent chooses an update action that reduces fitness, it will be rewarded, and if it increases the original fitness, it will be punished. Otherwise, the reward value will be assigned as 0. Therefore, the reward can be defined as follows:
where f(X(t + 1)) and f(X(t)) represent the fitness values obtained from the t + 1 and t iterations, respectively, after taking action.
- (4)
- Adaptive ε-greedy strategy
In the RL framework, employing a pure greedy strategy that consistently selects actions with a maximum Q value may lead to premature convergence due to insufficient early-stage experience. Conversely, relying entirely on random exploration significantly degrades convergence efficiency. Therefore, we introduced an adaptive ε-greedy strategy in the RLEHBA to optimize the action selection process. Set the exploration rate ε for nonlinear decreasing changes, as formalized in Equation (27).
where εinitial is the initial exploration rate, with a value of 0.3; d is the decay coefficient, with a value of 0.01; εmin is the minimum exploration rate, with a value of 0.1; and runtime is the running time of the algorithm.
The adaptive ε-greedy strategy is implemented with the following mechanism: a random number r between [0, 1] is generated for each decision step. When r < ε, the agent randomly selects an action; otherwise, it selects the action with the highest current Q value. During the initial optimization phase, a higher initial exploration rate prompts the agent to have a 30% probability of randomly selecting actions, fully exploring the solution space, and avoiding premature convergence. The remaining 70% probability leverages the current optimal actions from the Q-table to accelerate convergence. As the learning process progresses, the exploration rate undergoes systematic decay, gradually shifting the algorithm’s focus from global exploration to local exploitation. Notably, a predefined minimum exploration rate εmin prevents the complete termination of exploratory behavior in later stages.
The adaptive ε-greedy strategy ensures the adequacy of the global search and improves the convergence efficiency through a phased mechanism of “initial random exploration followed by directed exploitation”. In the regulation model, a high exploration rate in the early stage can traverse different production strategy combinations, while a low exploration rate in the later stage focuses on fine adjustment, ultimately achieving the optimal supply-demand balance goal.
3.2.2. The Flowchart and Pseudo-Code of the Proposed RLEHBA
To provide a clearer illustration of the evolutionary strategy and optimization process of the RLEHBA, we present a flowchart of the RLEHBA, as depicted in Figure 3.
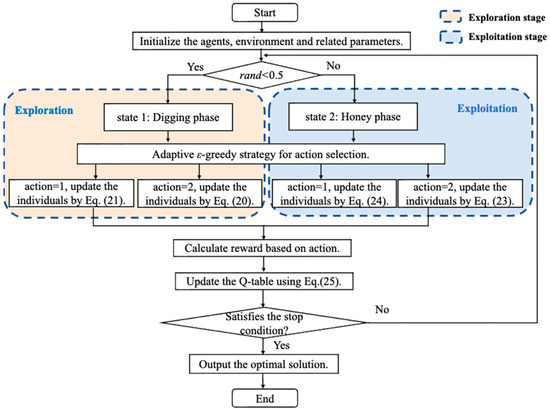
Figure 3.
The flowchart of RLEHBA.
As shown in Figure 3, the RLEHBA algorithm first initializes the agent, environment, and related parameters. Through the deep integration of RL and metaheuristic optimization techniques, it has entered the stage of exploration and exploitation, and adaptively selects different states and actions based on probability. After executing the action, it calculates the reward and updates the Q-table. This iterative process of state switching, action execution, reward feedback, and Q-table updates enables autonomous collaboration and the generalization of multiple strategies. By continuously iterating until the termination condition is met, the optimal solution is ultimately output, thus constructing the optimization framework for pork supply-demand regulation.
Taking the minimization of the objective function as an example, the runtime refers to the algorithm’s running time, and Maxruntime represents the maximum allowable runtime. When the algorithm reaches Maxruntime, the iteration stops, and the optimal result is output. The pseudo-code for the RLEHBA is presented in Algorithm 1.
| Algorithm 1: The pseudocode of RLEHBA |
| 1: Initialize the population and related parameters (N, D, runtime, Maxruntime, α, γ, Q-table, εinitial, d, εmin). |
| 2: Evaluate the fitness values and find the best solution Xprey. |
| 3: While runtime < Maxruntime do |
| 4: For i = 1:N |
| 5: Update the density factor α using Equation (19). |
| 6: Calculate the intensity I using Equation (16). |
| 7: Calculate the exploration rate ε using Equation (27). |
| 8: If rand < 0.5 |
| 9: current_state = 1(Digging phase). |
| 10: else |
| 11: current_state = 2 (Honey phase). |
| 12: End |
| 13: If rand < ε |
| 14: Randomly select action a∈{1,2}. |
| 15: else |
| 16: Select the action corresponding to the highest Q value, namely, a = argmax Q(current_state, :). |
| 17: End |
| 18: If current_state = 1 |
| 19: If a = 1 |
| 20: Update the individuals using Equation (21). |
| 21: elseif a = 2 |
| 22: Update the individuals using Equation (20). |
| 23: End |
| 24: elseif current_state = 2 |
| 25: If a = 1 |
| 26: Update the individuals using Equation (24). |
| 27: elseif a = 2 |
| 28: Update the individuals using Equation (23). |
| 29: End |
| 30: End |
| 31: Evaluate the fitness values of the updated individuals |
| 32: If temFitness < fitness(i) |
| 33: Reward = 1; |
| 34: elseif temFitness > fitness(i) |
| 35: Reward = −1; |
| 36: else |
| 37: Reward = 0. |
| 38: End |
| 39: Update the individuals in the population. |
| 40: Update the Q-table based on Equation (25). |
| 41: End for |
| 42: Update the global optimal solution. |
| 43: End while |
| 44: Output the best solution Xprey and fprey. |
The time complexity of an algorithm is a critical metric for evaluating its performance. In this paper, the iteration termination condition of the algorithm is the maximum running time. We use the Big O notation to present the time complexity of the RLEHBA at each iteration. Assuming that N represents the population size and D represents the dimensions of the given problem, the complexity of each component in the RLEHBA is as follows: the complexity of population initialization is O(N × D), the complexity of the position update is O(N × D), and the complexity of adopting Q-learning is O(N). Subsequently, the overall complexity of the algorithm is O(N × D). Compared with the standard HBA [10], the RLEHBA does not increase the algorithm’s complexity while improving the original algorithm.
3.3. Knowledge Base
The proposed regulation system is knowledge driven and mainly includes two aspects: data integration and supply and demand prediction knowledge, which enable the system to not only trace the operating rules of the industry, but also respond to market fluctuations, ultimately achieving the regulation of the pork supply chain.
3.3.1. Data Integration
In the data integration module, the system aggregates multi-dimensional historical data sources such as production, consumption, and international trade. Among them, the production data includes the monthly pork prices, breeding sow inventory at the end of each year, pork production, and slaughtered hogs inventory, where the data is sourced from the “China Animal Husbandry and Veterinary Yearbook” [3] and “China Statistical Yearbook” [57]. The consumer data includes the annual pork consumption, sourced from the USDA [58], while the trade data includes the pork import and export volume, sourced from the General Administration of Customs of the People’s Republic of China [4]. Other indirect data are obtained through consulting experts and the production practice experience of pig breeders, as described below:
- The SMER of pigs
In the model of pork production prediction, the SMER of pigs at different ages is a crucial parameter. According to the data and expert consultation, the annual SMER of boars and sows is 40%. Supplementary Material Tables SB1–SB3 list the SMER of pigs at different ages.
- 2.
- The value of the AMLSBS
Due to the complexity and slight fluctuations in determining the AMLSBS, this paper adjusts this value based on a mean level of 1.68, incorporating modifications based on the random disturbance term Disturbance2.
- 3.
- The retention ratio of sows and boars
Based on expert consultation, it is generally recognized that a boar can be effectively mated with twenty sows for breeding purposes. Therefore, in theory, the retention ratio of sows to boars in a pig farm can be 20:1, denoted as k = 20.
- 4.
- The average meat production of each slaughtered hog
It should be noted that the pork production mentioned in this paper refers to the weight after slaughter. The calculation method is given in Equation (28).
Meat = pork production/slaughtered hog
Based on the above analysis, the production data provides data support for predicting pork production, the consumption data indicates market demand characteristics, the import and export data reflects trade fluctuations, and indirect data such as the SMER can analyze pig growth patterns and market cycle characteristics, quantitatively evaluating the impact of external shocks on production capacity. These data form a database, providing a quantitative basis for timely monitoring and trend analysis for the system.
3.3.2. Supply and Demand Prediction Knowledge
In the mathematical model for pork supply-demand regulation, the prediction knowledge of the pork supply and demand is the core foundation for the system to achieve equilibrium. The prediction of the supply side relies on a recursive model of the pig herd system, which categorizes the types of live pigs (newly retained gilts, breeding sows, boars, hogs, and slaughtered hogs) and quantifies their month–age transition patterns. Based on parameters such as mortality and elimination rates and growth cycles at each age stage, it simulates the quantity status of the pig herd. The supply knowledge is directly related to the allocation of production resources, and also affects government regulation. Due to space limitations, detailed explanations of the categories of pigs, the month–age transfer, and the recursive formula for the quantity status of pigs in various categories can be referred to in the literature [18,19]. The prediction of demand provides data support for the calculation of the supply-demand gap from the domestic pork consumption and pork exports.
This knowledge system deeply integrates biological laws, market dynamics, and mathematical models. Based on the predicted data of supply and demand, it can update the supply and demand gap of pork in real time, laying the basis for the next step of pork regulation.
3.4. The Framework of the Regulation System
The framework of the proposed smart pork supply-demand regulation system is provided, as depicted in Figure 4.
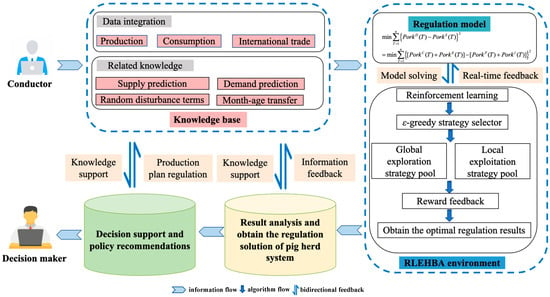
Figure 4.
The framework of the proposed regulation system.
As illustrated in Figure 4, the proposed knowledge-driven system integrates a knowledge base, mathematical model-based expert system, RL-enhanced optimizer, decision support module, and real-time feedback mechanism. Taking the pork supply-demand regulation in China as an example, the knowledge base stores information, including pork price trends, livestock inventory levels, import/export volumes, supply-demand prediction models, and random disturbance terms, providing essential data support and a theoretical foundation for the system. Based on these historical data and the relevant predictive knowledge, the supply and demand of pork can be obtained. Secondly, a quantitative regulation model is established, and the RLEHBA optimizer is employed to solve the model and deliver optimal solutions through its efficient optimization capabilities. Next, the result analysis can be conducted and the regulation solution of the pig herd system is updated. Finally, the decision support module analyzes the computational results, generating targeted recommendations and regulation strategies for decision-makers. The feedback mechanism enables real-time data updates, continuous system monitoring, and dynamic parameter adjustments, thus achieving the adaptive and efficient regulation of the pork supply-demand balance. This integrated architecture significantly enhances the operational efficiency and regulatory accuracy of the system.
4. Performance Validation of the RLEHBA
Due to the significant impact of the RLEHBA’s optimization performance on the regulation system, a series of simulation experiments were conducted to verify the performance of the proposed algorithm.
4.1. Experimental Setup
Since the mathematical model for regulating the pork supply and demand is a nonlinear optimization model, the solution quality has a significant impact on the regulation effect. Therefore, we conducted performance tests using 10-dimensional (10D) and 30-dimensional (30D) CEC 2017 global optimization problems (GOPs). The performance of the RLEHBA was compared with that of five other State-of-the-Art intelligent optimization algorithms. The simulations in this paper were executed on a computer equipped with a Core i5-1135G7 processor operating at 2.40 GHz and 16 GB RAM, using MATLAB 2022a. For detailed specifications of CEC 2017, please refer to the literature [59]. To evaluate the algorithmic performance, the average value (Avg) and standard deviation (Std) [60] were adopted as assessment metrics, with overall comparisons conducted through Friedman tests [61]. Since the CEC 2017 GOP is a minimization problem, the smaller the value of the Avg, the higher the accuracy of the algorithm’s solution, and the smaller the value of the Std, the better the stability of the algorithm. Similarly, in the Friedman test, the smaller the mean rank, the better the overall performance of the algorithm. To ensure fairness in the comparison, the maximum runtime for each algorithm on each test function was limited to 30 s. The Avg and Std values were calculated and recorded over 20 independent runs.
The algorithms involved in the comparison are the Mountain Gazelle Optimizer (MGO) [62], whale optimization algorithm with combined mutation and removing similarity (CRWOA) [63], Modified Grasshopper Optimization Algorithm (MGOA) [64], Dream Optimization Algorithm (DOA) [65], and honey badger algorithm (HBA) [10]. The parameter settings of the comparison algorithms are presented in Table 2.

Table 2.
Parameter settings for all comparison algorithms.
4.2. Results and Discussion
The comparison algorithms in Table 2 were used to address the 10D and 30D CEC 2017 GOPs, and the Avg and Std values of the optimal objective function values were recorded. Supplementary Material Tables SA1 and SA2 summarize the results. The optimal results are highlighted in bold. Furthermore, the Friedman test was conducted on the statistical results for the whole performance, the Friedman mean rank results are visualized in Figure 5, and the statistical results of the Friedman test are displayed in Table 3.
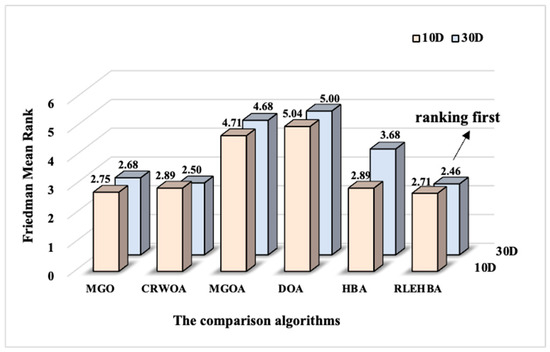
Figure 5.
The Friedman mean rank of comparison algorithms.

Table 3.
The results of Friedman statistic test for 10D and 30D CEC 2017 GOPs.
In terms of the convergence accuracy for the 10D problems presented in Supplementary Material Table SA1, the proposed RLEHBA, HBA, and CRWOA exhibit superior performance, achieving the smallest Avg values on eight benchmark functions. In contrast, the MGO, MGOA, and DOA demonstrate relatively inferior performance. Notably, the proposed RLEHBA does not underperform compared to other competing algorithms. As the dimensionality increases, the algorithm requires an increased ability to resist the curse of dimensionality. For the 30D results summarized in Supplementary Material Table SA2, the RLEHBA demonstrates exceptional performance, obtaining optimal results on 11 functions. In comparison, the original HBA achieves the smallest Avg values on only three functions, confirming the effectiveness of the proposed improvements to the HBA. By incorporating RL, the RLEHBA effectively utilized population information and feedback mechanisms, thereby showing enhanced adaptability and scalability when solving problems of varying dimensions. Although the CRWOA performs well on nine functions, its solution quality for high-dimensional problems was inferior to that of the RLEHBA. Across both 10D and 30D GOPs, the MGO, MGOA, and DOA exhibit mediocre performance overall.
Regarding stability, for 10D problems, the RLEHBA and HBA achieve the smallest Std values on five functions, indicating strong stability. However, the CRWOA attains the smallest Std values on only three functions, sacrificing stability while improving the accuracy of the algorithm. As the dimensionality increases, the RLEHBA maintains robust performance, obtaining the smallest Std values on eight functions for 30D problems, whereas the HBA achieves this on only one function. These results highlight the RLEHBA’s strong robustness and cross-dimensional scalability in high-dimensional optimization scenarios.
From the statistical analysis in Figure 5, the Friedman mean rank values obtained by the RLEHBA at 10D and 30D GOPs are 2.71 and 2.46, respectively, ranking first among all competing algorithms, indicating that the performance of the RLEHBA is superior to that of the other compared algorithms. From the statistical values in Table 3, it can be concluded that the p-values of 10D and 30D are 9.08 × 10−9 and 7.34 × 10−10, respectively, which are less than 0.05, confirming the statistical significance of the results and significant differences in the algorithm performance.
Based on the above analysis, the proposed RLEHBA performs well in solving optimization problems and can provide an efficient optimization framework for the proposed regulation system, as evidenced by the statistically significant results. In the next section, we will further validate the effectiveness of the proposed regulation system.
5. Case Study
In this section, the effectiveness and superiority of the proposed regulation system were validated using China’s pork supply and demand as an empirical study. First, the quantity status of different pig categories was derived through historical data and the knowledge of supply and demand forecasting, and the supply and demand of pork in 2025 and 2026 were predicted. Subsequently, a mathematical model for pork supply-demand regulation in 2026 was established and optimized using the RLEHBA algorithm, demonstrating the process of the smart regulation system. Finally, targeted recommendations and management implications were proposed.
5.1. Data Collection and Related Settings
By consulting the “China Animal Husbandry and Veterinary Yearbook” [3], “China Statistical Yearbook” [59], the General Administration of Customs of the People’s Republic of China [4], and the USDA [60], we obtained the monthly pork prices, the number of breeding sows at the end of each year, the pork production, the inventory of slaughtered hogs, the domestic pork consumption, and the international trade. The value of Meat was calculated using Equation (28). For detailed data, please refer to the Supplementary Material Tables SB1–SB7. In the subsequent sections, the quantities of different categories of pigs are expressed in tens of thousands, while the quantities of pork production, consumption, and import/export are given in ten thousand tons, and the monthly pork prices are measured in CNY/kg.
When predicting random disturbance terms and pork demand, the RLEHBA-BPNN adopts a network structure of 3-5-1 and employs the Mean Squared Error (MSE) as the loss function, with the Bipolar Sigmoid function as the activation function. In the RLEHBA and RLEHBA-BPNN, the maximum runtime of the algorithm is set to 60 s. The iterative optimization process automatically terminates when this time limit is reached. To ensure statistical reliability, the experimental protocol repeats each algorithm 20 independent times, with optimal outcomes recorded during multiple executions.
For the performance evaluation of the prediction part in the regulation model, we selected the Relative Error (RE) and Mean Relative Absolute Error (MRAE) as evaluation indicators to help determine the random disturbance terms. It should be noted that the accuracy of the pork supply prediction model based on the principle of pig age transfer and random disturbance terms has been verified in previous studies [18,19]. Therefore, this paper directly derived the status and random disturbance terms of various types of pigs using this model and predicted the pork supply for China in 2025 and 2026.
5.2. Prediction of Pork Supply and Demand
5.2.1. The Quantity Status of the Pig Herd System
Firstly, using the method described in reference [19], the quantity status of various types of pigs was obtained. The prediction results are as follows:
- (1)
- The RLEHBA was employed to resolve the unknown parameters in Equation (5), and the optimal parameter combination was obtained as follows: f1 = 0.0069674, f2 = −0.6721457, f3 = 19.0208246, and f4 = 47.8363813. For the method of solving parameters (f1–f4), reference [19] provides detailed mechanism derivation, a model establishment process, and effectiveness verification. In order to reduce repetition and focus more on the validation of the proposed pork supply and demand regulation model, we have included the fitting results of the parameter solving model (f1–f4) in Supplementary Material Section C. Subsequently, the calculation method for the newly retained gilts can be obtained, as formulated in Equation (29).
- (2)
- By substituting the pork prices into Equation (29), the quantity of newly retained gilts was calculated, as shown in Table 4. According to the formulas in Equation (6), the number of monthly breeding sows was calculated, as presented in Table 5. The results of the RE and MRAE are also given in Table 5.
 Table 4. Quantity status of newly retained gilts from 2005 to 2024 (Unit: 10,000 heads).
Table 4. Quantity status of newly retained gilts from 2005 to 2024 (Unit: 10,000 heads). Table 5. Quantity status of breeding sows from 2010 to 2024 (Unit: 10,000 heads).
Table 5. Quantity status of breeding sows from 2010 to 2024 (Unit: 10,000 heads).
Table 5 shows that in scenarios such as the outbreak of swine flu in 2009, porcine reproductive and respiratory syndrome in 2016, African swine fever in 2018, and the COVID-19 pandemic in 2020, the RE values are notably high, indicating the substantial impact of epidemic factors on the pig herd. Therefore, the RE values from Table 5 were utilized as random disturbance terms to adjust the SMER of sows, and the results are presented in Table 6. Table 6 reveals that the RE values between the predicted and actual values of breeding sow numbers after adjustment are small. The MRAE of 0.0544240 further indicates a minor deviation. These findings demonstrate that the predictive model for the quantity of breeding sows by considering random disturbance terms is effective.

Table 6.
Quantity status of breeding sows from 2010 to 2024 after adjusting the SMER of sows (Unit: 10,000 heads).
- (3)
- Based on the results in Table 4 and Table 6, the quantity status of newborn piglets can be calculated using Equations (7)–(9). Subsequently, the monthly slaughtered hogs and the total annual slaughtered hogs from 2010 to 2024 can be obtained according to Equations (10)–(12), as displayed in Table 7.
 Table 7. Quantity status of slaughtered hogs from 2010 to 2024 (Unit: 10,000 heads).
Table 7. Quantity status of slaughtered hogs from 2010 to 2024 (Unit: 10,000 heads).
Similarly, the RE values in Table 7 were used as random disturbance terms to adjust the SMER of hogs using Equation (12), and the adjusted number of slaughtered hogs was obtained, as presented in Table 8.

Table 8.
Quantity status of slaughtered hogs from 2010 to 2024 after adjusting the SMER of hogs (Unit: 10,000 heads).
Considering that the AMLSBS serves as an average level and may exhibit slight variations from year to year, we incorporated the RE values in Table 8 as random disturbance terms to modify this value. The quantity status of slaughtered hogs from 2010 to 2024 after adjustment is provided in Table 9.

Table 9.
Quantity status of slaughtered hogs from 2010 to 2024 after adjusting the AMLSBS (Unit: 10,000 heads).
- (4)
- According to Equation (28), the monthly pork production for each year was obtained, as presented in Table 10.
 Table 10. China’s pork production prediction from 2010 to 2024 (Unit: 10,000 tons).
Table 10. China’s pork production prediction from 2010 to 2024 (Unit: 10,000 tons).
From Table 10, it can be observed that the MRAE value is 0.0046525, confirming the scientific effectiveness of the pork production prediction model. Based on the above analysis, we have obtained the quantity status of the pig herd system and stored it in the regulation system as relevant data and knowledge.
5.2.2. Pork Supply and Demand Prediction for 2025 and 2026
According to the quantity status of the pig herd, the pork supply and demand in 2025 and 2026 were predicted. Since the newly retained hogs take six months to mature into slaughtered hogs, the newly retained gilts from July to December 2024 will impact the pork supply from January to June 2025. Similarly, the newly retained hogs from January to June 2025 will affect the pork supply from July to December 2025. Likewise, the newly retained hogs from July to December 2025 will influence the pork supply from January to June 2026, and the newly retained hogs from January to June 2026 will impact the pork supply from July to December 2026. Since there is a lack of pork price data for 2025 and 2026, the pork prices from January 2005 to December 2024 in Supplementary Material Table SB4 were used as a time series. The RLEHBA-BPNN was used to forecast the pork prices. Using this information, the monthly newly retained gilts were calculated using Equation (29). Subsequently, the quantity status of breeding sows can be calculated. Furthermore, based on the RE values in Table 5, the random disturbance terms for 2025 and 2026 were predicted to be −0.1881650 and −0.1626110, respectively. By adjusting the SMER of sows with the random disturbance terms, we obtained the adjusted numbers of breeding sows. The results are presented in Table 11.

Table 11.
Quantity status of newly retained gilts and breeding sows in China from July 2024 to July 2026 (Unit: 10,000 heads).
Based on the adjusted quantity of breeding sows in Table 11, the monthly slaughtered hogs can be calculated using Equation (12), as displayed in Table 12. Similarly, using the RE values from Table 7 as a time series for the random disturbance terms, the RLEHBA-BPNN was utilized to forecast the random disturbance terms for slaughtered hogs in 2025 and 2026, yielding values of 0.0871985 and 0.0548342, respectively. Furthermore, considering the variation in the AMLSBS, the RE values from Table 8 were used as a time series to forecast the disturbance terms for the AMLSBS in 2025 and 2026. The forecasted random disturbance terms are 0.1286805 and 0.1249850, respectively. Then, the quantity of slaughtered hogs after adjustment can be obtained. Afterwards, utilizing the historical data of Meat in the Supplementary Material Table SB6, the values of Meat in 2025 and 2026 were predicted to be 0.0809227 and 0.0811098, respectively. By applying Equation (13), the pork production for 2025 and 2026 were calculated. The results are presented in Table 12.

Table 12.
Prediction results of slaughtered hogs and pork production.
Based on the statistical data provided in Supplementary Material Table SB7, the RLEHBA-BPNN was used to forecast the pork consumption and import and export volumes in China for the years 2025 and 2026. The predicted results are as follows: the pork consumption volumes for 2025 and 2026 are 5617.50 and 5703.78 thousand tons, respectively, with pork import volumes of 124.26 and 151.77 thousand tons, and pork export volumes of 2.99 and 2.42 thousand tons, respectively.
According to the predicted results, the predicted value of China’s pork supply in 2025 is 5593.12 thousand tons, and the predicted value of pork demand in 2025 is 5620.49 thousand tons. For 2026, the predicted pork supply is 5690.26 thousand tons, while the predicted pork demand remains at 5706.21 thousand tons. There is a gap between the pork supply and demand in 2026, with a shortage of 15.95 thousand tons. Therefore, it is very necessary to regulate the pork supply-demand balance, so as to better stabilize pork prices. In the next section, we will establish a pork supply-demand balance regulation model for 2026 based on the prediction results.
5.3. Regulation Results
In this section, the supply-demand balance regulation model for 2026 was established, and the model was solved using the proposed RLEHBA to obtain the optimal regulation strategy. The regulation process of the proposed system has been demonstrated.
5.3.1. Model Establishment and Solution
According to the growth characteristics of pigs, the newly retained gilts grow into breeding sows after 12 months. After the breeding sow gives birth, the newborn piglets are classified according to their functions after reaching one month of age, including the newly retained gilts, the newly retained boars, and the newly retained hogs. After six months of growth, the slaughtered hogs provide pork for the market. Therefore, it is essential to regulate the number of newly retained gilts at least 18 months in advance to achieve long-term production planning. If the supply and demand of pork in 2026 are to be regulated, the essence is to regulate the pork production in 2026 to make up for the supply-demand gap of 15.95 thousand tons. In other words, the newly retained gilts from August 2024 to July 2025 will be adjusted. Due to the known status of the number of newly retained gilts in 2024, it is necessary to adjust the newly retained gilts from January to July 2025, namely, S1(T) = [206.65 + x(1), 206.81 + x(2), 209.12 + x(3), 210.69 + x(4), 211.46 + x(5), 211.54 + x(6), and 211.43 + x(7)], which will affect the number of breeding sows from December 2025 to June 2026. When adjusting newly retained gilts, it is necessary to minimize the fluctuation of the pig herd system while respecting the market rules. The threshold value is set to 8, which means that the adjustment amount for newly retained gilts is [−8, 8].
Based on the knowledge base for the quantity status and prediction results of the pig herd system in Section 5.2, the relevant parameters in the regulation model are obtained as follows: PorkC(T)= 5703.78, PorkI(T) = 151.77, and PorkE(T) = 2.42. It should be noted that since the growth of sows needs to go through the time spans of 2025 and 2026, the values of Disturbance1 for adjusting the SMER of sows are −0.1881650 and −0.1626110, respectively. Similarly, the values of Disturbance2 for adjusting the AMLSBS are 0.1286805 and 0.1249850, respectively, and the value of Disturbance3 for adjusting the SMER of hogs is 0.0548342. The predicted value of Meat in 2026 is 0.0811098. By substituting these parameters into the model described in Section 3.1.2, the mathematical model for pork supply-demand regulation in 2026 can be obtained. The specific content can be found in the Supplementary Material Section D.
The proposed RLEHBA was used to solve the regulation model. The optimal solution is 4.23 × 10−13, with x(1) = 6.98, x(2) = 7.20, x(3) = 7.84, x(4) = 7.25, x(5) = 7.68, x(6) = 7.32, and x(7) = 5.24, which is the adjustment amount for the newly retained gilts from January to July 2025.
5.3.2. Optimal Regulation Strategy
According to the optimal solution, the quantity status of various types of pigs after regulation can be obtained so that the supply and demand of pork can reach a balanced state. The results are provided in Table 13. Among them, “Before” represents before regulation, and “After” represents after regulation.

Table 13.
The quantity state of various categories and pork production in China (Unit: 10,000 heads).
As shown in Table 13, implementing small-scale regulation in the quantity of newly retained gilts in advance can effectively adjust pork production. The regulated total pork production in 2026 reaches 5554.43 thousand tons, while the predicted pork consumption in Section 5.2 stands at 5703.78 thousand tons, with pork imports and exports reaching 151.77 thousand tons and 2.42 thousand tons, respectively. Consequently, the post-regulation pork supply amounts to 5706.20 thousand tons, perfectly matching the equivalent pork demand. The sum of squared errors between the pork demand and supply is calculated as 4.23 × 10−13, demonstrating negligible deviation. This indicates that the pork supply-demand regulation model achieves satisfactory performance, successfully establishing a relatively balanced state between the pork supply and demand in 2026.
Based on the optimal regulation results, decision-makers can comprehensively evaluate the overall situation of the pig herd system, formulate production plans in advance, and encourage them to retain a reasonable quantity of newly retained gilts through diversified measures such as providing special subsidies, human oversight, and technical guidance, thereby effectively guiding pig production and ensuring a stable and long-term supply of pork from the source. In addition, the adjustment of production plans also enables the updating of the relevant information in the knowledge database. These accurate data can provide data support for the formulation and adjustment of the next round of production plans, forming a closed-loop feedback mechanism. This enables the pork production system to continuously adapt to market changes and enhance the overall competitiveness and risk resistance of the industry through iterative optimization.
5.4. Managerial Insights
This work provides valuable managerial insights for decision-makers:
- The proposed smart regulation system provides a robust theoretical basis for the sustainable development of the swine industry chain while facilitating enhanced information exchange and sharing. By integrating real-time data across the entire industrial chain, the system establishes a knowledge-driven database and theoretical framework. It develops a quantitative analysis-based regulation model to support decision-making, thereby creating a closed-loop intelligent regulation system characterized by “data monitoring—model analysis—expert decision-making—timely feedback”. This architecture achieves an equilibrium that considers multifactorial interactions from production to consumption ends. Decision-makers can utilize this system framework to implement multiple functions and facilitate long-term development, such as market monitoring and early warning, emergency risk simulation, flexible production planning, and market information sharing;
- The proposed regulation model comprehensively incorporates multi-dimensional factors, including the growth characteristics of pigs, external influences such as epidemic risks, and import–export trade. The derived optimal solutions are reasonable and feasible, providing practical guidance for optimizing the governance of the swine industry chain. On the one hand, decision-makers can develop differentiated subsidy policies to incentivize breeders in maintaining optimal gilt retention levels for supply-demand equilibrium. On the other hand, an emergency management mechanism for pig production can be established. By simulating, predicting, and analyzing random disturbance terms, the impact of external factors can be deeply analyzed. Based on the different influencing factors, corresponding regulation measures and emergency management mechanisms can be established. The immediate market stabilization protocols when abnormal fluctuations exceed the predefined tolerance ranges effectively minimize losses and adverse impacts;
- The proposed RLEHBA provides an efficient and flexible optimization framework for addressing complex system optimization and prediction challenges. This framework enables the transformation of algorithms from static tools into intelligent decision-making partners, providing robust technical support for managers to gain strategic advantages in uncertain environments. Managers can deploy the RLEHBA in high-dimensional, nonlinear problem domains such as production scheduling and multi-objective supply chain management, particularly excelling in scenarios involving non-differentiable objective functions or complex constraints. They can also customize different metaheuristic algorithms according to their actual needs to improve the adaptability and solution quality of the algorithm when tackling similar problems, and simultaneously minimize unnecessary costs.
6. Conclusions and Future Research
This paper proposed a knowledge-driven quantitative regulation system for pork supply-demand balance in the Agriculture 4.0 era, which integrates multi-dimensional factors including production cycles, consumption demands, and international trade. Using the adjustment quantity of the newly retained gilts inventory as the decision variable, we established a nonlinear constrained optimization model with the objective function of minimizing the sum of squared errors between the pork supply and demand quantities, serving as the core component of the proposed system. To address the model’s complexity and high solution quality requirements, the RLEHBA was developed to provide technical support for the regulation system. New position update strategies were introduced for different search stages to avoid local stagnation. The Q-learning mechanism was incorporated to achieve intelligent strategy selection based on historical experience and information feedback. These improvements work together to achieve a balance between exploration and exploitation, thereby improving the solution accuracy and robustness of the RLEHBA.
Given the major impact of the RLEHBA’s performance on regulation effectiveness, a series of experiments were conducted to validate its efficacy and superiority. The RLEHBA and other comparison algorithms were tested on CEC 2017 GOPs, with results systematically compared. Statistical analysis demonstrates that the RLEHBA achieves the top Friedman rank for both low-dimensional and high-dimensional problems, showcasing exceptional solution quality, stability, and scalability. On this basis, a case study on China’s pork supply-demand regulation was investigated to verify the adaptive capabilities and practical effectiveness of the proposed system. Firstly, the quantity status of the pig herd system was derived through historical data and supply-demand prediction knowledge, providing data support for the regulation of pork supply and demand. Subsequently, a mathematical model for pork supply-demand regulation in 2026 was formulated and solved using the RLEHBA, yielding optimal regulatory strategies. Management recommendations were further proposed for stabilizing pork prices and ensuring food security.
This work also has certain limitations. Due to the unavailability or high dispersion of key parameters in the public data of other major pork-producing countries, a comparable verification of the pork supply-demand balance in other countries could not be achieved. Additionally, the inability to rigorously test the model’s sensitivity to parameter settings across diverse international contexts limits the model’s application in scenarios outside China or across multiple nations. For future research, there are numerous appealing research directions. Multi-objective optimization models can be developed to incorporate more practical factors into the regulation system, such as animal welfare, biosecurity and infectious disease risks, geopolitics, trade disruptions, and human oversight. Based on game theory, the feedback and interactions between governments and profit-related stakeholders for pork regulation can be explored in depth. Additionally, the proposed RLEHBA optimization framework is highly recommended for other livestock industries, providing universal technical support for intelligent supply chain management.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/agriculture15141484/s1, Table SA1. The results of comparison algorithms on 10D CEC 2017 GOPs; Table SA2. The results of comparison algorithms on 30D CEC 2017 GOPs; Table SB1. The SMER of newborn piglets at different ages (%); Table SB2. The SMER of sows/boars at different ages (%); Table SB3. The SMER of hogs at different month-age (%); Table SB4. Monthly pork prices in China from 2005 to 2024 (Unit: CNY/kg); Table SB5. The quantity of breeding sows at the end of each year in China (Unit: 10,000 heads); Table SB6. Average pork production of each slaughtered hog in China; Table SB7. China’s pork consumption, import and export volume from 2007 to 2024 (Unit: 10,000 tons); Table SC1. Prediction results for the quantity of breeding sows at the end of the year considering the principle of month-age transfer of pigs and the random disturbance terms [19].
Author Contributions
H.S.: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing—original draft, and Writing–review and editing. J.W.: Conceptualization, Formal analysis, Supervision, Investigation, Methodology, Resources, Software, Project administration, and Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Fund of China, grant number 21BGL174.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data will be made available on request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Wu, Y.; Duan, Y.; Wei, Y.; An, D.; Liu, J. Application of intelligent and unmanned equipment in aquaculture: A review. Comput. Electron. Agric. 2022, 199, 107201. [Google Scholar] [CrossRef]
- Walter, A.; Finger, R.; Huber, R.; Buchmann, N. Smart farming is key to developing sustainable agriculture. Proc. Natl. Acad. Sci. USA 2017, 114, 6148–6150. [Google Scholar] [CrossRef]
- China Animal Husbandry and Veterinary Yearbook. Available online: https://www.shujuku.org/china-animal-husbandry-and-veterinary-yearbook.html (accessed on 1 November 2024).
- General Administration of Customs of the People’s Republic of China. Available online: http://www.customs.gov.cn (accessed on 1 July 2025).
- Wang, J.; Wang, G.; Cui, Y.; Zhang, J. How does imported pork regulate the supply and demand of China’s pig market during the epidemic?—Based on the analysis of African swine fever and COVID-19. Front. Vet. Sci. 2022, 9, 1028460. [Google Scholar] [CrossRef] [PubMed]
- Li, X.K.; Ma, J.X.; Li, X.Y.; Hu, J.J.; Ding, C.Y.; Han, F.K.; Jin, X.M. High-efficiency reinforcement learning with hybrid architecture photonic integrated circuit. Nat. Commun. 2024, 15, 10. [Google Scholar] [CrossRef] [PubMed]
- Shu, T.; Pan, Z.J.; Ding, Z.H.; Zu, Z.Q. Resource scheduling optimization for industrial operating system using deep reinforcement learning and WOA algorithm. Expert Syst. Appl. 2024, 255, 25. [Google Scholar] [CrossRef]
- Zong, K.; Luo, C.C. Reinforcement learning based framework for COVID-19 resource allocation. Comput. Ind. Eng. 2022, 167, 10. [Google Scholar] [CrossRef]
- He, Y.; Wang, Y.H.; Lin, Q.Z.; Li, J.Q. Meta-Hierarchical Reinforcement Learning (MHRL)-Based Dynamic Resource Allocation for Dynamic Vehicular Networks. IEEE Trans. Veh. Technol. 2022, 71, 3495–3506. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Bei, J.L.; Wang, J.Q.; Song, H.H.; Liu, H.L. Slime mould algorithm with mechanism of leadership and self-phagocytosis for multilevel thresholding of color image. Appl. Soft Comput. 2024, 163, 28. [Google Scholar] [CrossRef]
- Song, H.H.; Bei, J.L.; Zhang, H.Y.; Wang, J.Q.; Zhang, P.L. Hybrid algorithm of differential evolution and flower pollination for global optimization problems. Expert Syst. Appl. 2024, 237, 34. [Google Scholar] [CrossRef]
- Coase, R.H.; Fowler, R.F. Bacon Production and the Pig-Cycle in Great Britain. Economica 1935, 2, 142–167. [Google Scholar] [CrossRef]
- Kim, T.W.; Kim, C.W.; Noh, C.W.; Kim, S.W.; Kim, I.S. Identification of Association between Supply of Pork and Production of Meat Products in Korea by Canonical Correlation Analysis. Korean J. Food Sci. Anim. Resour. 2018, 38, 794–805. [Google Scholar]
- Zhang, F.; Wang, F.L. Prediction of pork supply via the calculation of pig population based on population prediction model. Int. J. Agric. Biol. Eng. 2020, 13, 208–217. [Google Scholar] [CrossRef]
- Zielinska-Sitkiewicz, M.; Chrzanowska, M. Prediction of pork meat prices by selected methods as an element supporting the decision-making process. Oper. Res. Decis. 2021, 31, 137–152. [Google Scholar] [CrossRef]
- Wang, J.-Q.; Zhang, H.-Y.; Song, H.-H.; Zhang, P.-L.; Bei, J.-L. Prediction of Pork Supply Based on Improved Mayfly Optimization Algorithm and BP Neural Network. Sustainability 2022, 14, 16559. [Google Scholar] [CrossRef]
- Song, H.H.; Zhang, H.Y.; Yang, J.N.; Wang, J.Q. Forecasting Model for the Number of Breeding Sows Based on Pig’s Months of Age Transfer and Improved Flower Pollination Algorithm-Back Propagation Neural Network. Appl. Intell. 2024, 54, 5826–5858. [Google Scholar] [CrossRef]
- Song, H.H.; Wang, J.Q.; Xu, G.; Tian, Z.W.; Xu, F.; Deng, H. Novel Model for Pork Supply Prediction in China Based on Modified Self-Organizing Migrating Algorithm. Agriculture 2024, 14, 30. [Google Scholar] [CrossRef]
- Chuluunsaikhan, T.; Kim, J.H.; Park, S.H.; Nasridinov, A. Analyzing Internal and External Factors in Livestock Supply Forecasting Using Machine Learning: Sustainable Insights from South Korea. Sustainability 2024, 16, 21. [Google Scholar] [CrossRef]
- Fousekis, P.; Revell, B.J. Quadratic Differential Demand Systems and the Retail Demand for Pork in Great Britain. J. Agric. Econ. 2003, 54, 417–430. [Google Scholar] [CrossRef]
- Bekkerman, A.; Brester, G.W.; Tonsor, G.T. An alternative approach to measuring demand changes in meat markets. Int. Food Agribus. Manag. Rev. 2019, 22, 397–412. [Google Scholar] [CrossRef]
- Yu, W.S.; Jensen, J.D. Sustainability implications of rising global pork demand. Anim. Front. 2022, 12, 56–60. [Google Scholar] [CrossRef]
- Agricultural Outlook 2012–2021. Manag. Environ. Qual. 2012, 24. Available online: https://www.agriculture.gov.au/abares/research-topics/agricultural-outlook (accessed on 1 July 2025).
- Delgado, C.L.; Rosegrant, M.W.; Steinfeld, H.; Ehui, S.K.; Courbois, C. Livestock to 2020: The next food revolution. 2020 vision briefs. Outlook Agric. 1999, 30, 27–29. [Google Scholar] [CrossRef]
- Nedkov, S.; Burkhard, B. Flood regulating ecosystem services-Mapping supply and demand, in the Etropole municipality, Bulgaria. Ecol. Indic. 2012, 21, 67–79. [Google Scholar] [CrossRef]
- Cohen, E. Regulating Demand or Supply: Examining Israel’s Public Policy for Reducing Housing Prices During 2015–2019. Hous. Policy Debate 2022, 32, 533–548. [Google Scholar] [CrossRef]
- Zhou, K.L.; Chu, Y.B.; Hu, R. Energy supply-demand interaction model integrating uncertainty forecasting and peer-to-peer energy trading. Energy 2023, 285, 18. [Google Scholar] [CrossRef]
- Wang, L.S.; Li, M.T.; Pei, X.; Zhang, J. Optimal Breeding Strategy for Livestock with a Dynamic Price. Mathematics 2022, 10, 24. [Google Scholar] [CrossRef]
- Yao, H.Z.; Zang, C.F.; Zuo, X.X.; Xian, Y.Y.; Lu, Y.Q.; Huang, Y.T.; Li, X.B. Tradeoff analysis of the pork supply and food security under the influence of African swine fever and the COVID-19 outbreak in China. Geogr. Sustain. 2022, 3, 32–43. [Google Scholar] [CrossRef]
- Pang, J.; Yin, J.; Lu, G.C.; Li, S.M. Supply and Demand Changes, Pig Epidemic Shocks, and Pork Price Fluctuations: An Empirical Study Based on an SVAR Model. Sustainability 2023, 15, 16. [Google Scholar] [CrossRef]
- Sarttra, T.; Kittitanasak, K.; Wongwaitayakul, K.; Phaophu, C.; Kiatcharoenpol, T. An optimal approach for supply and demand management with the consideration of cattle herd structure management: A case study of medium-size dairy cooperative in Thailand. Comput. Ind. Eng. 2023, 182, 15. [Google Scholar] [CrossRef]
- Pamuklu, T.; Nguyen, A.C.; Syed, A.; Kennedy, W.S.; Erol-Kantarci, M. IoT-Aerial Base Station Task Offloading With Risk-Sensitive Reinforcement Learning for Smart Agriculture. IEEE Trans. Green Commun. Netw. 2023, 7, 171–182. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, Q.S.; Chen, I.R.; Ha, D.S.; Cho, J.H. Energy-Adaptive and Robust Monitoring for Smart Farms Based on Solar-Powered Wireless Sensors. IEEE Internet Things J. 2024, 11, 29781–29797. [Google Scholar] [CrossRef]
- Ali, N.; Wahid, A.; Shaw, R.; Mason, K. A reinforcement learning approach to dairy farm battery management using Q learning. J. Energy Storage 2024, 93, 13. [Google Scholar] [CrossRef]
- Lu, Y.C.; Yu, X.B.; Hu, Z.P.; Wang, X.M. Convolutional neural network combined with reinforcement learning-based dual-mode grey wolf optimizer to identify crop diseases and pests. Swarm Evol. Comput. 2025, 94, 24. [Google Scholar] [CrossRef]
- Farid, A.M.; Roshanian, J.; Mouhoub, M. Multiple aerial/ground vehicles coordinated spraying using reinforcement learning. Eng. Appl. Artif. Intell. 2025, 151, 11. [Google Scholar]
- Liu, X.; Chen, X.; Ding, X. Predictions on the Supply and Demand of Pig in China and the Supply and Demand Gap. Stat. Decis. 2008, 3, 109–111. [Google Scholar]
- He, Y. The Investigation and Analysis on the Difference of Sow Farrowing Level in a Pig Farm. Master’s Thesis, HUNAN Agricultural University, Changsha, China.
- Huang, Y.; Sun, H.; Shu, D. The Effect of Litter Number and Mating Season on Litter Size of Different Breed Pigs. Acta Agric. Univ. Jiangxiensis 2000, 22, 106–109. [Google Scholar]
- Ye, R.; Lv, M.; Li, A.; Yin, A.; Luo, W.; Gu, W. Reproductive performance and correlation regression analysis of different parity sows. Anim. Husb. Vet. Med. 2006, 38, 20–22. [Google Scholar]
- Wang, R.; Bi, H.Y. A predictive model for Chinese children with developmental dyslexia-Based on a genetic algorithm optimized back-propagation neural network. Expert Syst. Appl. 2022, 187, 115949. [Google Scholar] [CrossRef]
- Che, Z.G.; Chiang, T.A.; Che, Z.H. Feed-forward neural networks training: A comparison between genetic algorithm and back-propagation learning algorithm. Int. J. Innov. Comput. I 2011, 7, 5839–5850. [Google Scholar]
- Wang, L.; Zeng, Y.; Chen, T. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Syst. Appl. 2015, 42, 855–863. [Google Scholar] [CrossRef]
- Mian, Z.; Bin, W.; Chao, L.; Zhenhui, Y.; Liu, J.X. Process parameter optimization for ionic liquids as gas separation membranes based on a GWO-BPNN model. J. Appl. Polym. Sci. 2023, 141, e55068. [Google Scholar] [CrossRef]
- Abasi, A.K.; Aloqaily, M.; Guizani, M. Optimization of CNN using modified Honey Badger Algorithm for Sleep Apnea detection. Expert Syst. Appl. 2023, 229, 120484. [Google Scholar] [CrossRef]
- Alshathri, S.; Abd Elaziz, M.; Yousri, D.; Hassan, O.F.; Ibrahim, R.A. Quantum Chaotic Honey Badger Algorithm for Feature Selection. Electronics 2022, 11, 3463. [Google Scholar] [CrossRef]
- Chandrasekharan, S.; Subramaniam, S.; Veerakgoundar, V. Honey badger optimization algorithm based maximum power point tracking for solar photovoltaic systems. Electr. Power Syst. Res. 2023, 221, 109393. [Google Scholar] [CrossRef]
- Hu, G.; Zhong, J.; Wei, G. SaCHBA_PDN: Modified honey badger algorithm with multi-strategy for UAV path planning. Expert Syst. Appl. 2023, 223, 119941. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Mabrouk, A.; Dahou, A.; Chelloug, S.A. Medical Image Classification Utilizing Ensemble Learning and Levy Flight-Based Honey Badger Algorithm on 6G-Enabled Internet of Things. Comput. Intell. Neurosci. 2022, 2022, 5830766. [Google Scholar] [CrossRef]
- Karthika, K.P.; Priya, S.K. An integrated approach for depression diagnosis using 3S feature embeddings and G-BLS with T-pHBGO optimizer. Expert Syst. Appl. 2024, 235, 121189. [Google Scholar]
- Nagarajan, S.; Kayalvizhi, S.; Subhashini, R.; Anitha, V. Hybrid honey badger-world cup algorithm-based deep learning for malicious intrusion detection in industrial control systems. Comput. Ind. Eng. 2023, 180, 109166. [Google Scholar] [CrossRef]
- Dayan, P.; Watkins, C. Q-learning. In Machine Learning; Springer: Berlin/Heidelberg, Germany, 1992; Volume 8, pp. 279–292. [Google Scholar]
- Zhao, S.; Wu, Y.; Tan, S.; Wu, J.; Cui, Z.; Wang, Y.G. QQLMPA: A quasi-opposition learning and Q-learning based marine predators algorithm. Expert Syst. Appl. 2022, 213, 119246. [Google Scholar] [CrossRef]
- Ye, T.Y.; Zhang, P.; Wang, H.; Zeng, H.L.; Wang, J.H.; Zeng, T. Reinforcement learning-driven dual neighborhood structure artificial bee colony algorithm for continuous optimization problem. Appl. Soft Comput. 2025, 169, 17. [Google Scholar] [CrossRef]
- Yu, X.B.; Xu, P.P.; Wang, F.; Wang, X.M. Reinforcement learning-based differential evolution algorithm for constrained multi-objective optimization problems. Eng. Appl. Artif. Intell. 2024, 131, 17. [Google Scholar] [CrossRef]
- China Statistical Yearbook. Available online: http://www.stats.gov.cn/sj/ndsj/ (accessed on 1 July 2025).
- U.S. Department of Agriculture. Available online: https://www.usda.gov/ (accessed on 1 December 2024).
- Wu, G.; Mallipeddi, R.; Suganthan, P. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition and Special Session on Constrained Single Objective Real-Parameter Optimization. Tech. Report 2017, 1–18. Available online: https://www.researchgate.net/publication/317228117_Problem_Definitions_and_Evaluation_Criteria_for_the_CEC_2017_Competition_and_Special_Session_on_Constrained_Single_Objective_Real_Parameter_Optimization (accessed on 1 July 2025).
- Song, H.H.; Wang, J.Q.; Song, L.; Zhang, H.Y.; Bei, J.L.; Ni, J.; Ye, B. Improvement and application of hybrid real-coded genetic algorithm. Appl. Intell. 2022, 52, 17410–17448. [Google Scholar] [CrossRef]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Khodadadi, N.; Mirjalili, S. Mountain Gazelle Optimizer: A new Nature-inspired Metaheuristic Algorithm for Global Optimization Problems. Adv. Eng. Softw. 2022, 174, 34. [Google Scholar] [CrossRef]
- Wang, J.Q.; Bei, J.L.; Song, H.H.; Zhang, H.Y.; Zhang, P.L. A whale optimization algorithm with combined mutation and removing similarity for global optimization and multilevel thresholding image segmentation. Appl. Soft Comput. 2023, 137, 30. [Google Scholar] [CrossRef]
- Ingle, K.K.; Jatoth, R.K. Non-linear Channel Equalization using Modified Grasshopper Optimization Algorithm. Appl. Soft Comput. 2024, 153, 15. [Google Scholar] [CrossRef]
- Lang, Y.F.; Gao, Y.L. Dream Optimization Algorithm (DOA): A novel metaheuristic optimization algorithm inspired by human dreams and its applications to real-world engineering problems. Comput. Methods Appl. Mech. Eng. 2025, 436, 80. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).