Determination of Soft Partitioning Thresholds for Reservoir Drought Warning Levels Under Socio-Hydrological Drought
Abstract
1. Introduction
2. Materials and Methodology
2.1. Study Area
2.2. Data
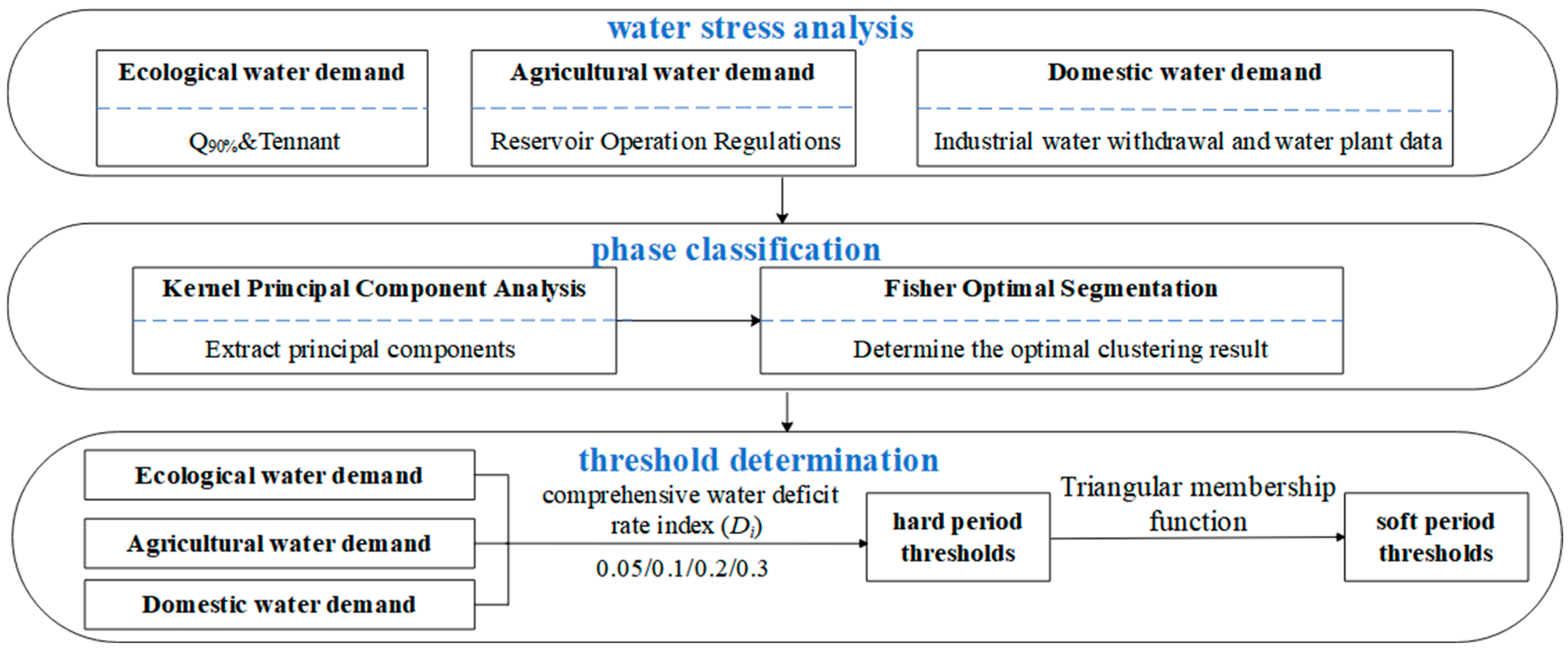
2.3. Method for Determining Staged and Graded Reservoir Drought Warning Water Levels
2.3.1. Water Stress Analysis
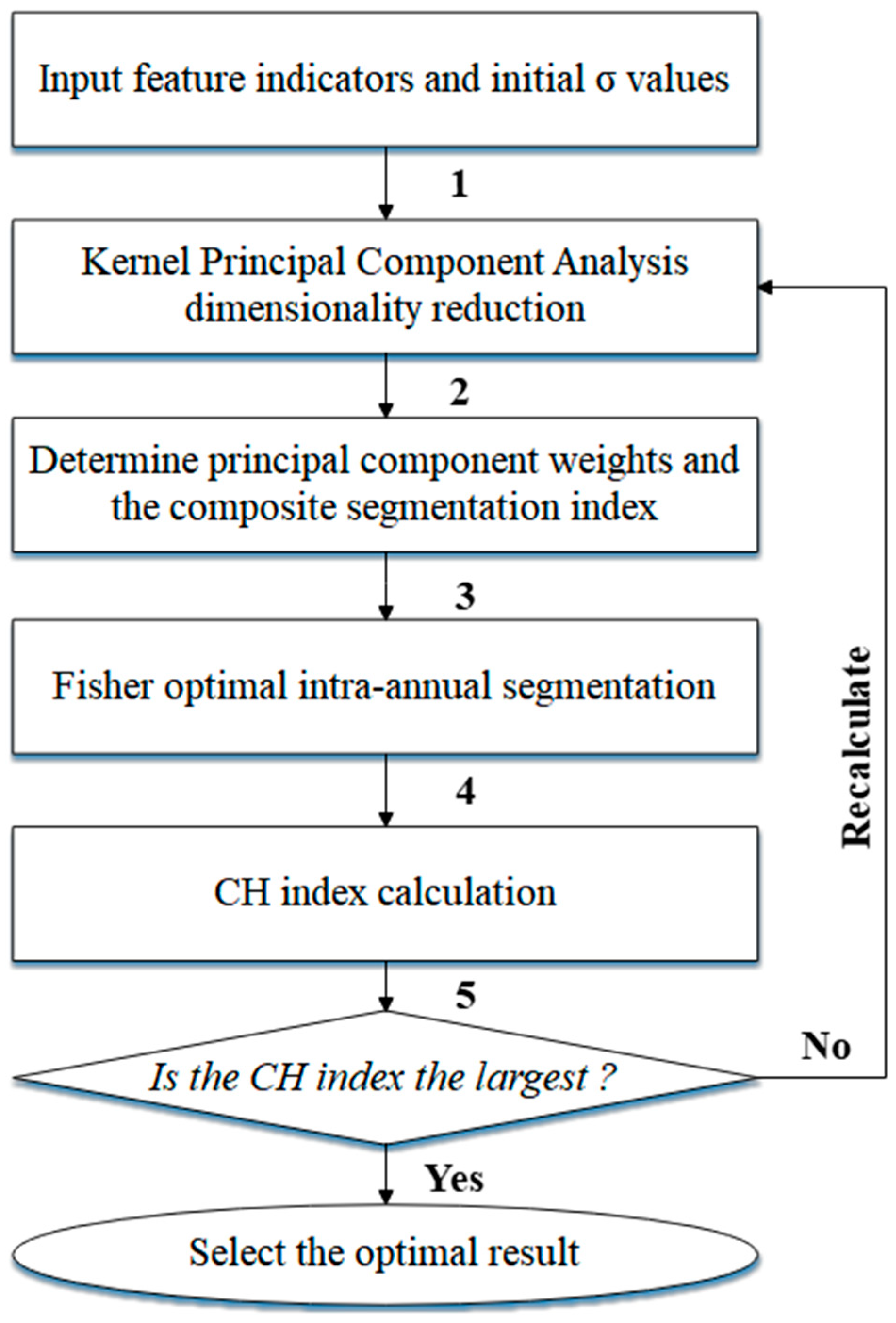
2.3.2. Semi-Supervised Phase Classification Based on KPCA-Fisher
2.3.3. Classification of Drought Warning Water Levels Based on Water Deficit Rate
3. Results
3.1. Agricultural, Ecological, and Domestic Water Demand Analysis
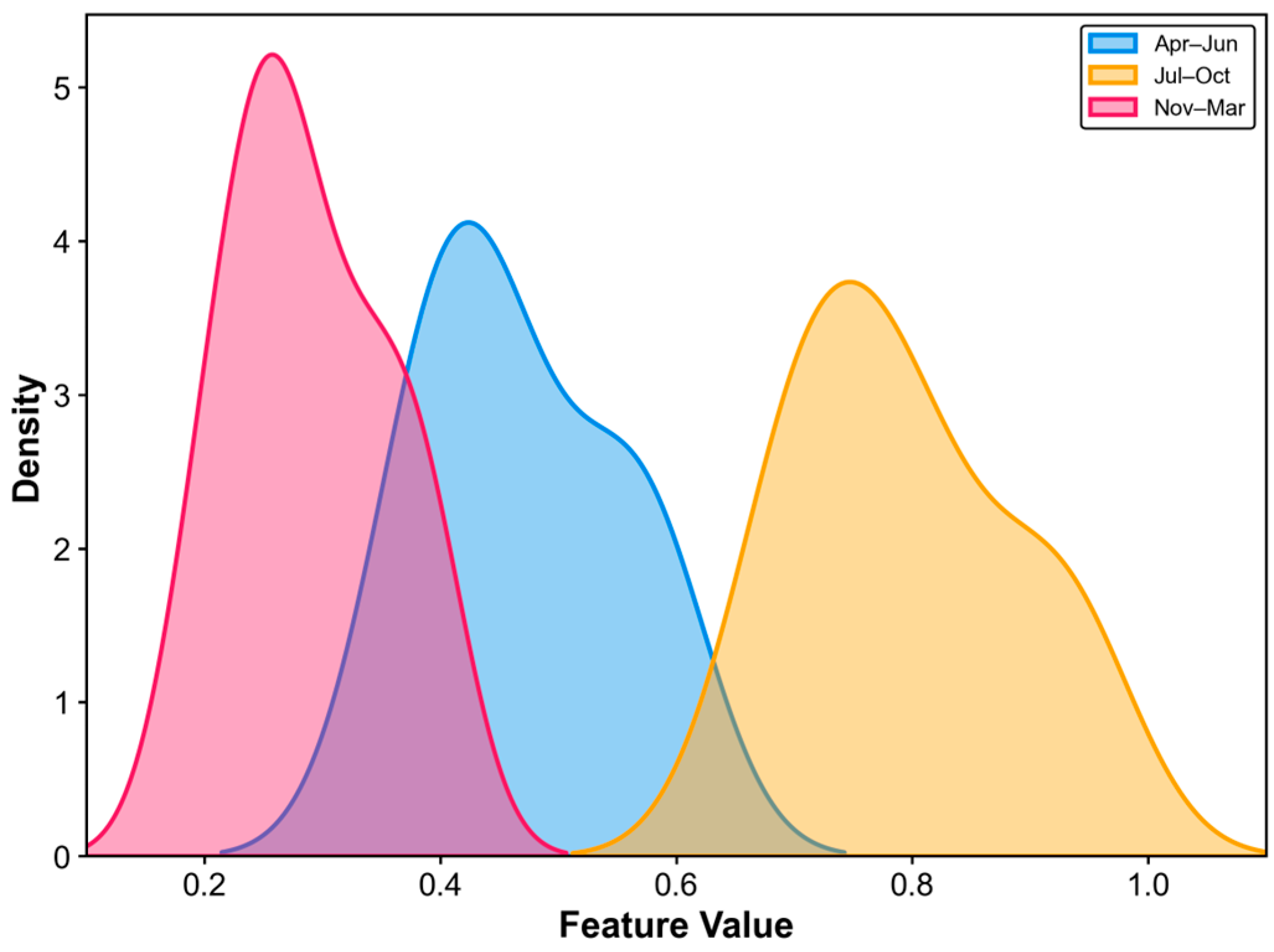
3.2. Phasing of Drought Warning Water Level Thresholds
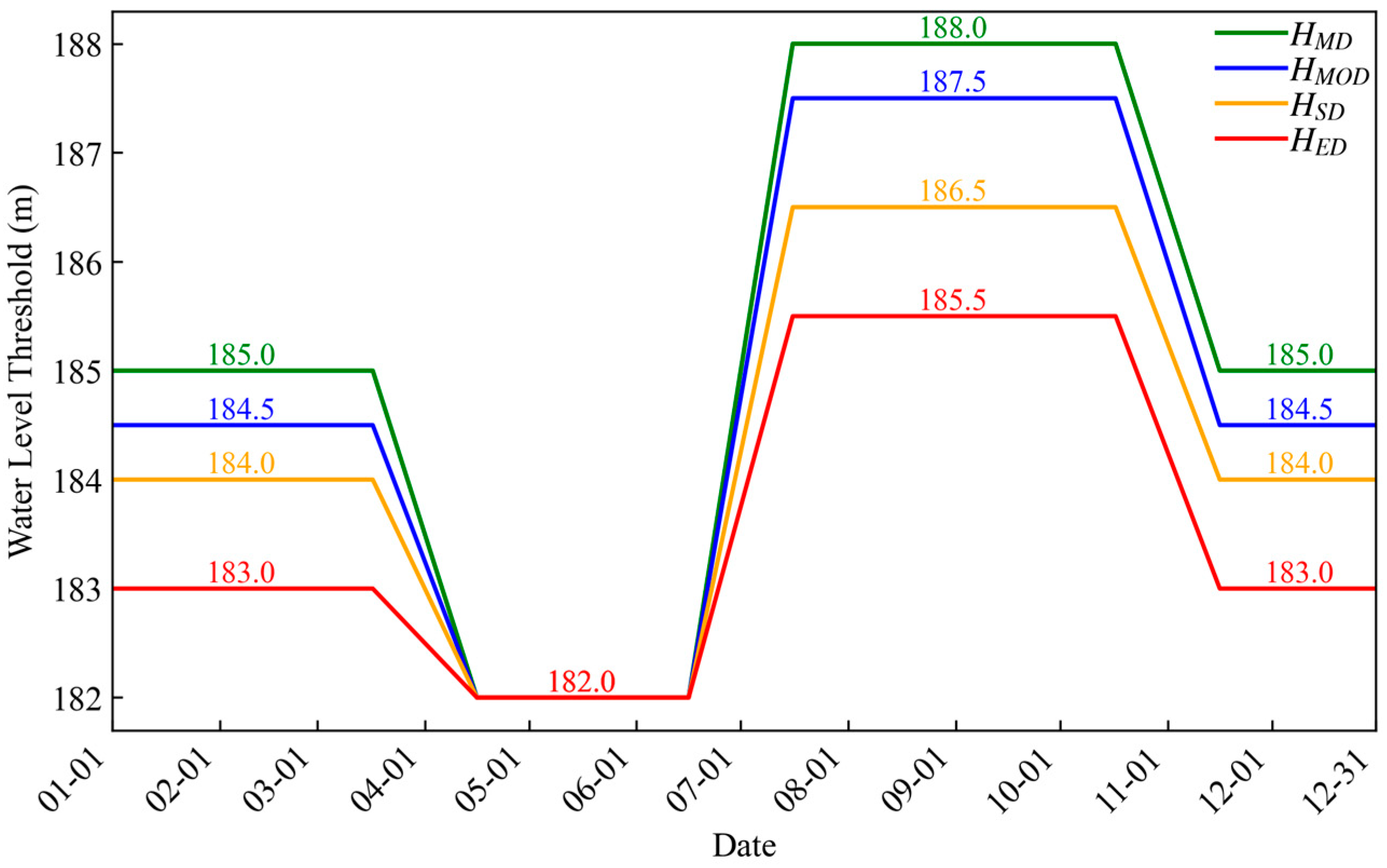
3.3. Determination of Drought Warning Water Level Thresholds
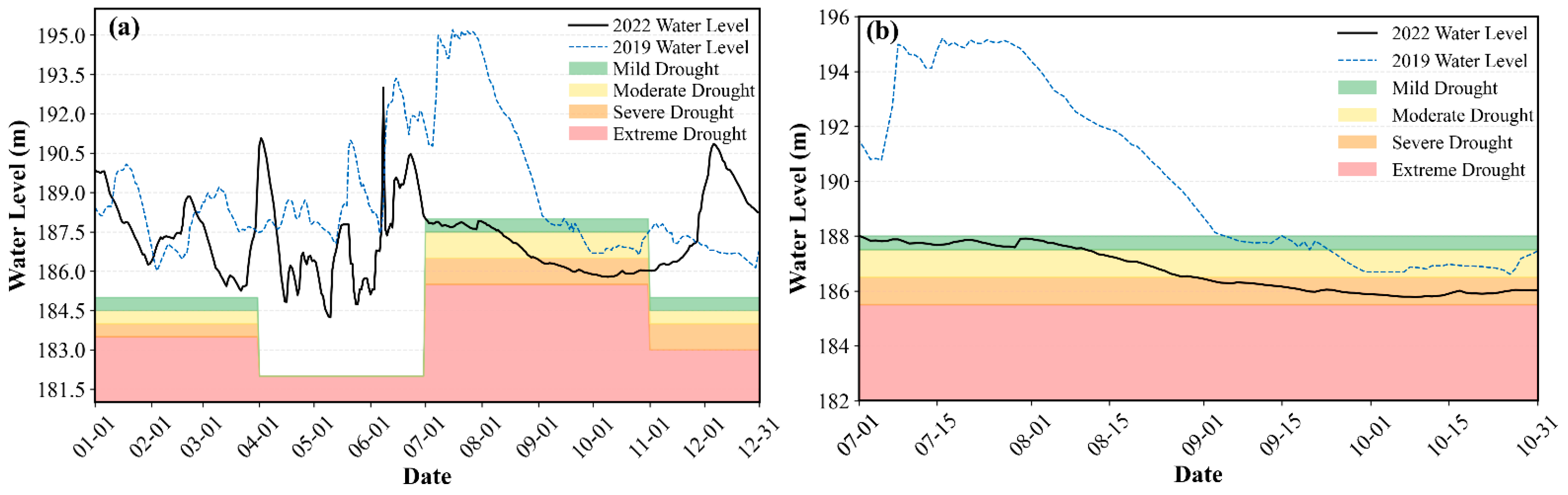
3.4. Rationality Analysis
4. Discussion
4.1. Impact Analysis of Threshold Smoothing on Drought Process Characterization
4.2. Sensitivity Analysis of Drought Warning Water Level Thresholds to Ecological Water Demand
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Min, S.-K.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human Contribution to More-Intense Precipitation Extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little Change in Global Drought over the Past 60 Years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef] [PubMed]
- Gu, X.; Zhang, Q.; Singh, V.P.; Shi, P. Changes in Magnitude and Frequency of Heavy Precipitation across China and Its Potential Links to Summer Temperature. J. Hydrol. 2017, 547, 718–731. [Google Scholar] [CrossRef]
- Cook, B.I.; Mankin, J.S.; Anchukaitis, K.J. Climate Change and Drought: From Past to Future. Curr. Clim. Change Rep. 2018, 4, 164–179. [Google Scholar] [CrossRef]
- Dai, A.; Zhao, T.; Chen, J. Climate Change and Drought: A Precipitation and Evaporation Perspective. Curr. Clim. Change Rep. 2018, 4, 301–312. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [Google Scholar]
- Vicente-Serrano, S.M.; Domínguez-Castro, F.; Murphy, C.; Hannaford, J.; Reig, F.; Peña-Angulo, D.; Tramblay, Y.; Trigo, R.M.; Donald, N.M.; Luna, M.Y.; et al. Long-Term Variability and Trends in Meteorological Droughts in Western Europe (1851–2018). Int. J. Climatol. 2020, 41, E690–E717. [Google Scholar] [CrossRef]
- Lei, S.; Shi, S.; Qu, Y.P.; Liu, Y.W.; Liao, J.Y.; Zhang, Y.; Zhang, Y.; Li, S.Y.; Dong, G.X. Characteristics of extreme drought in the Poyang Lake Basin in 2022 and implications for future response. J. Hydraul. Eng. 2023, 54, 333–346. (In Chinese) [Google Scholar] [CrossRef]
- He, S.; Guo, S.; Zhang, J.; Liu, Z.; Cui, Z.; Zhang, Y.; Zheng, Y. Multi-Objective Operation of Cascade Reservoirs Based on Short-Term Ensemble Streamflow Prediction. J. Hydrol. 2022, 610, 127936. [Google Scholar] [CrossRef]
- Van Loon, A.F. Hydrological Drought Explained. WIREs Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A Review of Drought Concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Tallaksen, L.; van Lanen, H.A.J. Hydrological Drought. Processes and Estimation Methods for Streamflow and Groundwater; Developments in Water Science; Elsevier: Amsterdam, The Netherlands, 2004; Volume 48, ISBN 978-0-444-51688-6. [Google Scholar]
- Van Loon, A.F.; Gleeson, T.; Clark, J.; Van Dijk, A.I.J.M.; Stahl, K.; Hannaford, J.; Di Baldassarre, G.; Teuling, A.J.; Tallaksen, L.M.; Uijlenhoet, R. Drought in the Anthropocene|Nature Geoscience. Nat. Geosci. 2016, 9, 89–91. [Google Scholar] [CrossRef]
- Wanders, N.; Wada, Y.; Van Lanen, H.A.J. Global Hydrological Droughts in the 21st Century under a Changing Hydrological Regime. Earth Syst. Dyn. 2015, 6, 1–15. [Google Scholar] [CrossRef]
- Sivapalan, M.; Konar, M.; Srinivasan, V.; Chhatre, A.; Wutich, A.; Scott, C.A.; Wescoat, J.L.; Rodríguez-Iturbe, I. Socio-Hydrology: Use-Inspired Water Sustainability Science for the Anthropocene. Earth’s Future 2014, 2, 225–230. [Google Scholar] [CrossRef]
- Sivapalan, M.; Savenije, H.H.G.; Blöschl, G. Socio-Hydrology: A New Science of People and Water. Hydrol. Process. 2012, 26, 1270–1276. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Sivapalan, M.; Rusca, M.; Cudennec, C.; Garcia, M.; Kreibich, H.; Konar, M.; Mondino, E.; Mård, J.; Pande, S.; et al. Sociohydrology: Scientific Challenges in Addressing the Sustainable Development Goals. Water Resour. Res. 2019, 55, 6327–6355. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Sun, S.; Yin, Y.; Wang, Y.; Zhao, X.; Wu, P. Evaluating Grain Virtual Water Flow in China: Patterns and Drivers from a Socio-Hydrology Perspective. J. Hydrol. 2022, 606, 127412. [Google Scholar] [CrossRef]
- Wada, Y.; Bierkens, M.F.P.; de Roo, A.; Dirmeyer, P.A.; Famiglietti, J.S.; Hanasaki, N.; Konar, M.; Liu, J.; Müller Schmied, H.; Oki, T.; et al. Human–Water Interface in Hydrological Modelling: Current Status and Future Directions. Hydrol. Earth Syst. Sci. 2017, 21, 4169–4193. [Google Scholar] [CrossRef]
- Rachunok, B.; Fletcher, S. Socio-Hydrological Drought Impacts on Urban Water Affordability. Nat. Water 2023, 1, 83–94. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Huang, P.-Y.; Hsu, S.-Y.; Tung, C.-P.; Liao, K.-W. Anthropogenic Drought Monitoring Using Socio-Hydrological Modeling for Surface Water Deficit: Lessons from Northern Taiwan. J. Hydrol. 2025, 647, 132298. [Google Scholar] [CrossRef]
- Ministry of Water Resources of the People’s Republic of China. Methods for Determining Drought Warning Water Levels and Flow Rates; Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2011.
- He, S.; Wang, D.; Sang, X.; Niu, G. Water Resource Regulation and Evaluation Method Based on Optimization of Drought-Limited Water Level in Reservoir Group. Sustainability 2024, 16, 7015. [Google Scholar] [CrossRef]
- Luo, C.; Xu, B.; Ding, W.; Zhang, C.; Du, E. Characteristics of Reservoirs to Mitigate Drought Effects with a Hedging Rule Triggered by Drought Limited Water Level. J. Hydrol. 2023, 617, 129106. [Google Scholar] [CrossRef]
- Wang, K.; Yan, Z.Q.; Chen, G.; Jiang, Y.; Zhou, Z.; Yan, D. Study on Multi-Level Optimization of Reservoir Drought-Limit Water Levels for Extreme Drought. J. Hydraul. Eng. 2024, 55, 1528–1538. (In Chinese) [Google Scholar] [CrossRef]
- Peng, Z.W.; Guo, A.J.; Chang, J.X.; Yan, D.H.; Yan, Z.Q.; Zhao, Z. Q Connotation and determination method of graded and staged drought warning water level for reservoir considering drought risks. J. Hydraul. Eng. 2024, 55, 1260–1269. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, L.B.; Bai, Y.C.; Jin, J.L.; Yue, H.; Zhou, Y.; Zhou, T. Optimization of Reservoir Drought-Limited Water Level and Water Supply Strategy in an Irrigation District Based on Fuzzy Set-Pair Analysis. J. Hydraul. Eng. 2022, 53, 1154–1167. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, L.; Kang, C.; Wu, C.; Yu, H.; Jin, J.; Zhou, Y.; Zhou, T. Optimization of Drought Limited Water Level and Operation Benefit Analysis of Large Reservoir. Water Resour. Manag. 2022, 36, 4677–4696. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO); Global Water Partnership (GWP). Handbook of Drought Indicators and Indices; World Meteorological Organization: Geneva, Switzerland, 2016. [Google Scholar]
- Shah, D.; Zhao, G.; Li, Y.; Singh, V.P.; Gao, H. Assessing Global Reservoir-Based Hydrological Droughts by Fusing Storage and Evaporation. Geophys. Res. Lett. 2024, 51, e2023GL106159. [Google Scholar] [CrossRef]
- Zhao, G.; Gao, H. Towards Global Hydrological Drought Monitoring Using Remotely Sensed Reservoir Surface Area. Geophys. Res. Lett. 2019, 46, 13027–13035. [Google Scholar] [CrossRef]
- Fung, K.F.; Huang, Y.F.; Koo, C.H. Investigation of Streamflow as a Seasonal Hydrological Drought Indicator for a Tropical Region. Water Supply 2020, 20, 609–620. [Google Scholar] [CrossRef]
- Yan, Z.Q.; Zhou, Z.H.; Yan, D.H.; Wei, R.S. An algorithm for grading and staged drought- limited water level (flow) of river sections. Adv. Water Sci. 2023, 34, 53–62. (In Chinese) [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Wen, Z.; Chen, Y.; Cao, Y.; Ren, J. Spatiotemporal Change and Trend Analysis of Potential Evapotranspiration over the Loess Plateau of China during 2011–2100. Agric. For. Meteorol. 2017, 233, 183–194. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.-R. Nonlinear Component Analysis as a Kernel Eigenvalue Problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.-R. Kernel Principal Component Analysis. In Proceedings of the Artificial Neural Networks—ICANN’97; Gerstner, W., Germond, A., Hasler, M., Nicoud, J.-D., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 583–588. [Google Scholar]
- Fisher, W.D. On Grouping for Maximum Homogeneity. J. Am. Stat. Assoc. 1958, 53, 789–798. [Google Scholar] [CrossRef]
- Tennant, D.L. Instream Flow Regimens for Fish, Wildlife, Recreation and Related Environmental Resources. Fisheries 1976, 1, 6–10. [Google Scholar] [CrossRef]
- A Dendrite Method for Cluster Analysis. Commun. Stat.-Theory Methods 1974, 3, 1–27. [CrossRef]
- Ministry of Water Resources of the People’s Republic of China. Technical Specification for Calculation of Ecological Environmental Water Requirements in Rivers and Lakes (SL/T712-2021); Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2021.
- Hotelling, H. Analysis of a Complex of Statistical Variables into Principal Components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Mika, S.; Schölkopf, B.; Smola, A.; Müller, K.-R.; Scholz, M.; Rätsch, G. Kernel PCA and De-Noising in Feature Spaces. In Proceedings of the 12th International Conference on Neural Information Processing Systems, Denver, CO, USA, 1 December 1998; MIT Press: Cambridge, MA, USA; pp. 536–542. [Google Scholar]
- Chen, W.; Wang, H.; Qin, Q.H. Kernel Radial Basis Functions. In Proceedings of the Computational Mechanics; Yao, Z.H., Yuan, M.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; p. 347. [Google Scholar]
- Chudzian, P. Radial Basis Function Kernel Optimization for Pattern Classification. In Proceedings of the Computer Recognition Systems 4; Burduk, R., Kurzyński, M., Woźniak, M., Żołnierek, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 99–108. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- GB/T 32135-2015; Regional Drought Classification. China Standards Press: Beijing, China, 2015.
- Yan, Z.; Zhou, Z.; Liu, J.; Wen, T.; Sang, X.; Zhang, F. Multiobjective Optimal Operation of Reservoirs Based on Water Supply, Power Generation, and River Ecosystem with a New Water Resource Allocation Model. J. Water Resour. Plan. Manag. 2020, 146, 05020024. [Google Scholar] [CrossRef]
- Yan, Z.; Zhou, Z.; Sang, X.; Wang, H. Water Replenishment for Ecological Flow with an Improved Water Resources Allocation Model. Sci. Total Environ. 2018, 643, 1152–1165. [Google Scholar] [CrossRef]
- Wang, W.; Van Gelder, P.H.; Vrijling, J.K.; Ma, J. Forecasting Daily Streamflow Using Hybrid ANN Models. J. Hydrol. 2006, 324, 383–399. [Google Scholar] [CrossRef]
- Yihuang County Water Bureau. Operation Regulation of Xianan Reservoir in Yihuang County, Jiangxi Province; Yihuang County Water Bureau: Fuzhou, China, 2023.
- Yihuang County Water Bureau. Jiangxi Province Yihuang County Xianan Reservoir Flood Control Emergency Plan; Yihuang County Water Bureau: Fuzhou, China, 2022.
- Wang, M.; Jiang, S.; Ren, L.; Xu, J.; Yuan, S.; Xu, C.-Y. An Integrated Framework for Non-Stationary Hydrological Drought Assessment Using Time-Varying Parameter Standardized Streamflow Index and Time-Varying Threshold Level Method. J. Hydrol. Reg. Stud. 2025, 59, 102329. [Google Scholar] [CrossRef]
- Milly, P.C.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Duan, L.; Liu, T.; Li, J.; Feng, P. A Non-Stationary Standardized Streamflow Index for Hydrological Drought Using Climate and Human-Induced Indices as Covariates. Sci. Total Environ. 2020, 699, 134278. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Su, X.; Wu, L.; Chu, J. Identification of Dynamic Drought Propagation from a Nonstationary Perspective and Its Application to Drought Warnings. J. Hydrol. 2023, 626, 130372. [Google Scholar] [CrossRef]
- Pastor, A.V.; Ludwig, F.; Biemans, H.; Hoff, H.; Kabat, P. Accounting for Environmental Flow Requirements in Global Water Assessments. Hydrol. Earth Syst. Sci. 2014, 18, 5041–5059. [Google Scholar] [CrossRef]
- Smakhtin, V.; Revenga, C.; Doell, P. A Pilot Global Assessment of Environmental Water Requirements and Scarcity. Water Int. 2004, 29, 307–317. [Google Scholar] [CrossRef]





| Data Types | Time Period | Sources |
|---|---|---|
| Monthly streamflow and Taopi Hydrological Station | January 1958 to December 2022 | Data provided by the Jiangxi Provincial Hydrological Monitoring Center. |
| Monthly precipitation and Xuxi and Yingfang Rain Gauge Stations | January 2015 to December 2024 | |
| Monthly initial water storage level and Xianan Reservoir | January 2000 to December 2022 | |
| Monthly potential evapotranspiration | January 1990 to December 2022 | [34] |
| Categories | Mild Drought | Moderate Drought | Severe Drought | Extremely Severe Drought |
|---|---|---|---|---|
| Agricultural Irrigation Deficit Rate | [0.05, 0.20) | [0.20, 0.35) | [0.35, 0.50) | [0.50, 1) |
| Urban Drought Deficit Rat | [0.05, 0.10) | [0.10, 0.20) | [0.20, 0.30) | [0.30, 1) |
| Ecological Water Demand Deficit Rate | [0.20, 0.40) | [0.40, 0.60) | [0.60, 0.80) | [0.80, 1) |
| Di | [0.05, 0.10) | [0.10, 0.20) | [0.20, 0.30) | [0.30, 1) |
| Month | Inflow (m3/s) | Precipitation (mm) | Evaporation (mm) | Agricultural Demand (104 m3) | Initial Water Level (m) |
|---|---|---|---|---|---|
| Jan | 2.93 | 88.3 | 39.1 | 24.5 | 188.04 |
| Feb | 4.25 | 121.2 | 49.0 | 24.5 | 186.92 |
| Mar | 6.85 | 201.3 | 76.3 | 22.4 | 187.12 |
| Apr | 10.2 | 218.3 | 98.2 | 113.1 | 186.92 |
| May | 11.3 | 346.8 | 119.2 | 95.8 | 187.27 |
| Jun | 14.5 | 354.4 | 122.0 | 104.1 | 188.82 |
| Jul | 7.69 | 199.2 | 159.8 | 487 | 191.04 |
| Aug | 4.89 | 137.7 | 147.2 | 388.2 | 190.17 |
| Sep | 4.44 | 143.1 | 121.7 | 250.8 | 190.29 |
| Oct | 3.46 | 72.8 | 94.1 | 532.9 | 189.68 |
| Nov | 3.46 | 140.5 | 62.6 | 24.5 | 189.34 |
| Dec | 2.91 | 69.5 | 46.7 | 24.5 | 188.89 |
| Month | Domestic Demand | Agricultural Demand | Ecological Demand | Total Demand | Design Inflow (p = 75%) | Evaporation |
|---|---|---|---|---|---|---|
| Jan | 350.4 | 24.5 | 372.3 | 747.2 | 448.8 | 6.6 |
| Feb | 350.4 | 24.5 | 411.3 | 786.2 | 593.2 | 7.5 |
| Mar | 408.8 | 22.4 | 527.6 | 958.8 | 1249.7 | 11.9 |
| Apr | 467.2 | 113.1 | 616.9 | 1197.2 | 1684.5 | 15.0 |
| May | 584.0 | 95.8 | 859.8 | 1539.6 | 1919.6 | 18.8 |
| Jun | 584.0 | 104.1 | 845.0 | 1533.1 | 2400.3 | 21.7 |
| Jul | 700.8 | 487.0 | 752.6 | 1940.4 | 1033.9 | 32.9 |
| Aug | 700.8 | 388.2 | 492.8 | 1581.8 | 819.7 | 28.7 |
| Sep | 525.6 | 250.8 | 422.5 | 1198.9 | 620.4 | 23.9 |
| Oct | 408.8 | 532.9 | 348.2 | 1289.9 | 584.8 | 17.8 |
| Nov | 408.8 | 24.5 | 349.9 | 783.2 | 472.1 | 11.5 |
| Dec | 350.4 | 24.5 | 342.8 | 717.7 | 406.9 | 8.3 |
| Phase | Months | Drought Warning Water Level (m) | |||
|---|---|---|---|---|---|
| Mild Drought | Moderate Drought | Severe Drought | Extremely Severe Drought | ||
| Main Flood Season | Apr–Jun | 182.0 | 182.0 | 182.0 | 182.0 |
| Critical Water Demand Period | Jul–Oct | 188.0 | 187.5 | 186.5 | 185.5 |
| Dry Season | Nov–Mar | 185.0 | 184.5 | 184.0 | 183.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Xu, X.; Lin, R.; Yang, W.; Yang, P.; Li, S.; Wang, H. Determination of Soft Partitioning Thresholds for Reservoir Drought Warning Levels Under Socio-Hydrological Drought. Agriculture 2025, 15, 1408. https://doi.org/10.3390/agriculture15131408
Liu Y, Xu X, Lin R, Yang W, Yang P, Li S, Wang H. Determination of Soft Partitioning Thresholds for Reservoir Drought Warning Levels Under Socio-Hydrological Drought. Agriculture. 2025; 15(13):1408. https://doi.org/10.3390/agriculture15131408
Chicago/Turabian StyleLiu, Yewei, Xiaohua Xu, Rencai Lin, Weifeng Yang, Peisheng Yang, Siying Li, and Hongxin Wang. 2025. "Determination of Soft Partitioning Thresholds for Reservoir Drought Warning Levels Under Socio-Hydrological Drought" Agriculture 15, no. 13: 1408. https://doi.org/10.3390/agriculture15131408
APA StyleLiu, Y., Xu, X., Lin, R., Yang, W., Yang, P., Li, S., & Wang, H. (2025). Determination of Soft Partitioning Thresholds for Reservoir Drought Warning Levels Under Socio-Hydrological Drought. Agriculture, 15(13), 1408. https://doi.org/10.3390/agriculture15131408





