Real-Time Energy-Efficient Control Strategy for Distributed Drive Electric Tractor Based on Operational Speed Prediction
Abstract
1. Introduction
2. Materials and Methods
2.1. Dynamic Analysis of Distributed Drive Electric Tractor
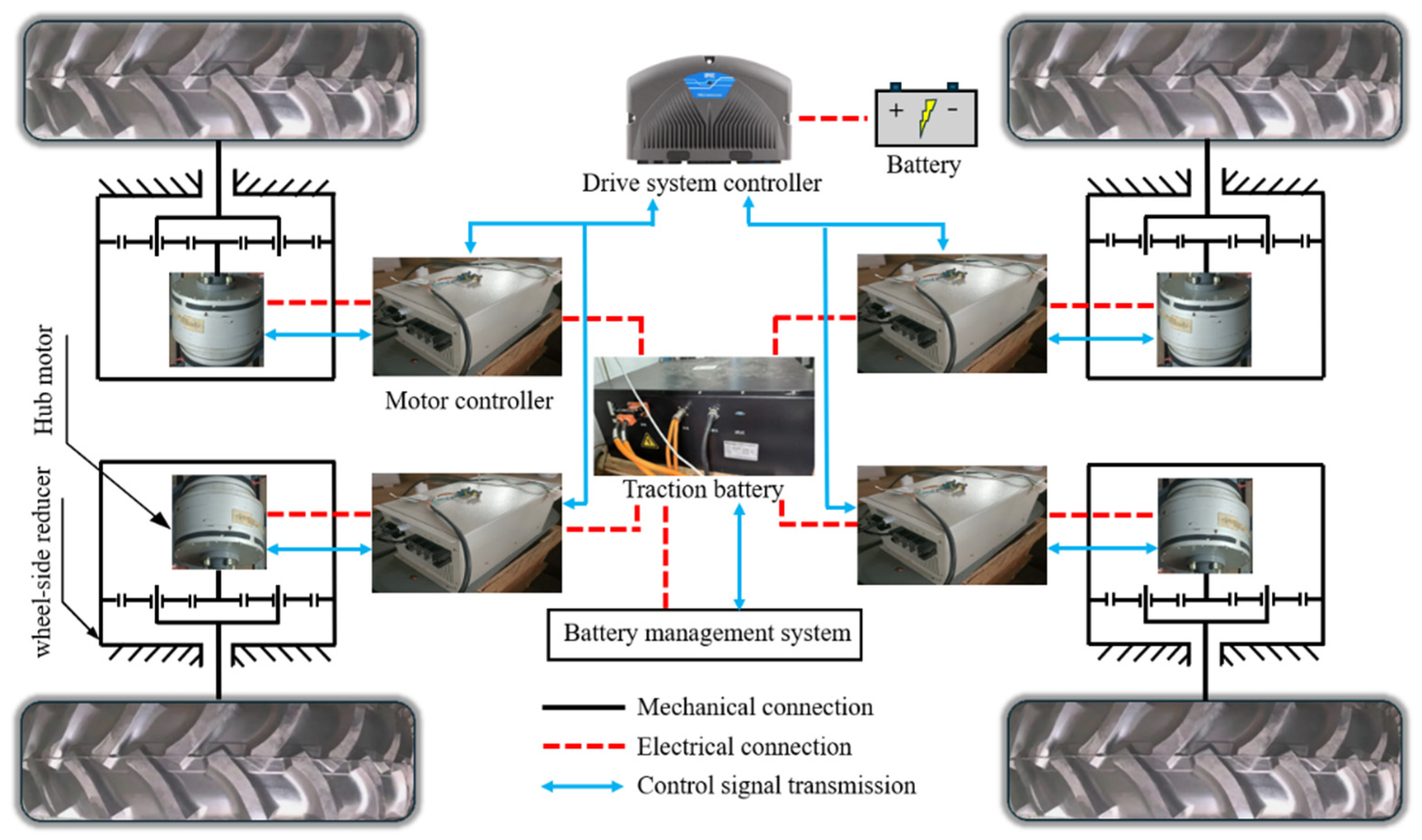
2.1.1. Structure of the Drive and Transmission System of the DDET
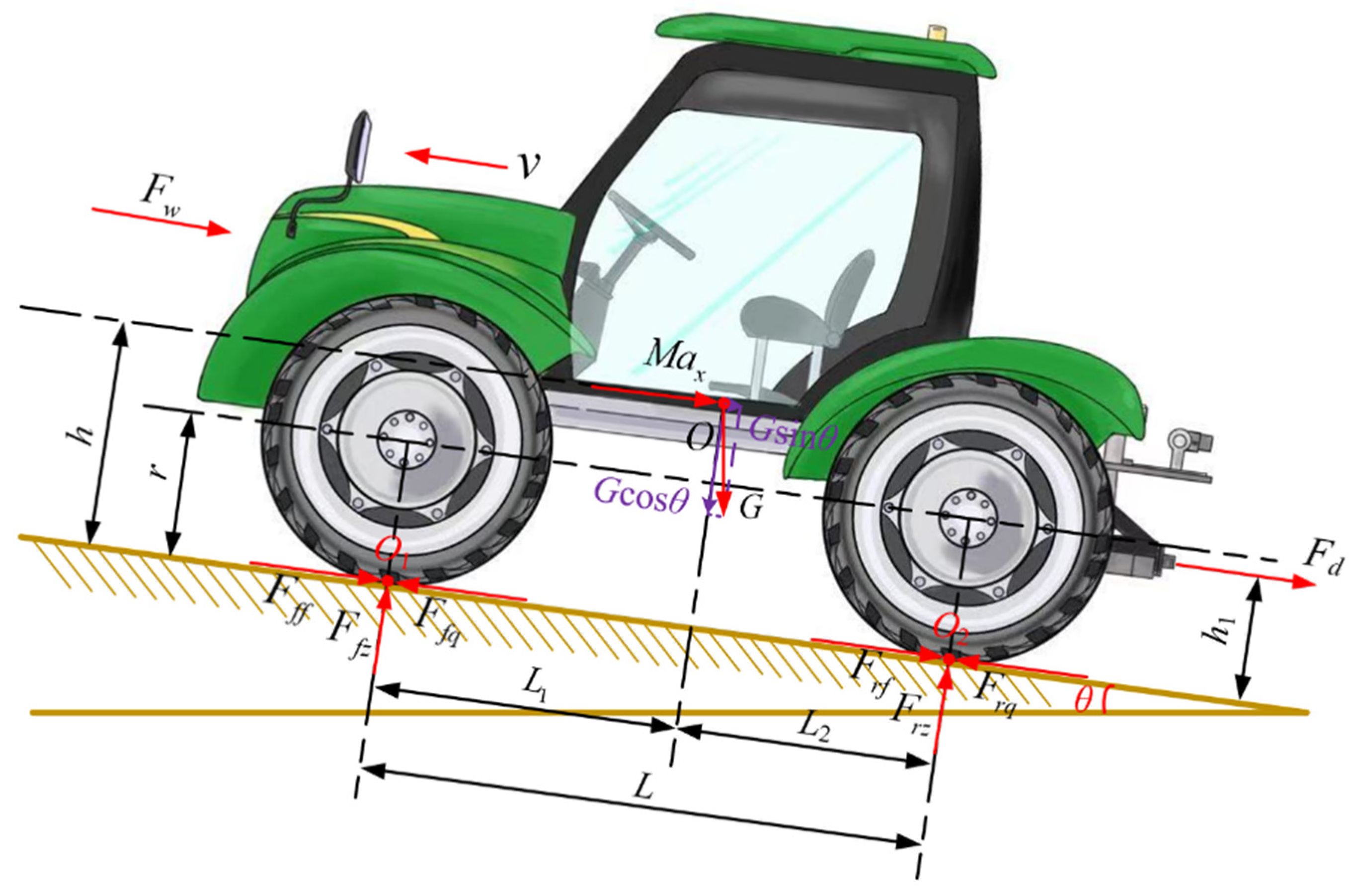
2.1.2. Dynamic Analysis of Traction Operations of Distributed Drive Electric Tractor
2.2. Modeling of Drive and Transmission Components for Distributed Drive Electric Tractor
2.2.1. Modeling of Hub Motor
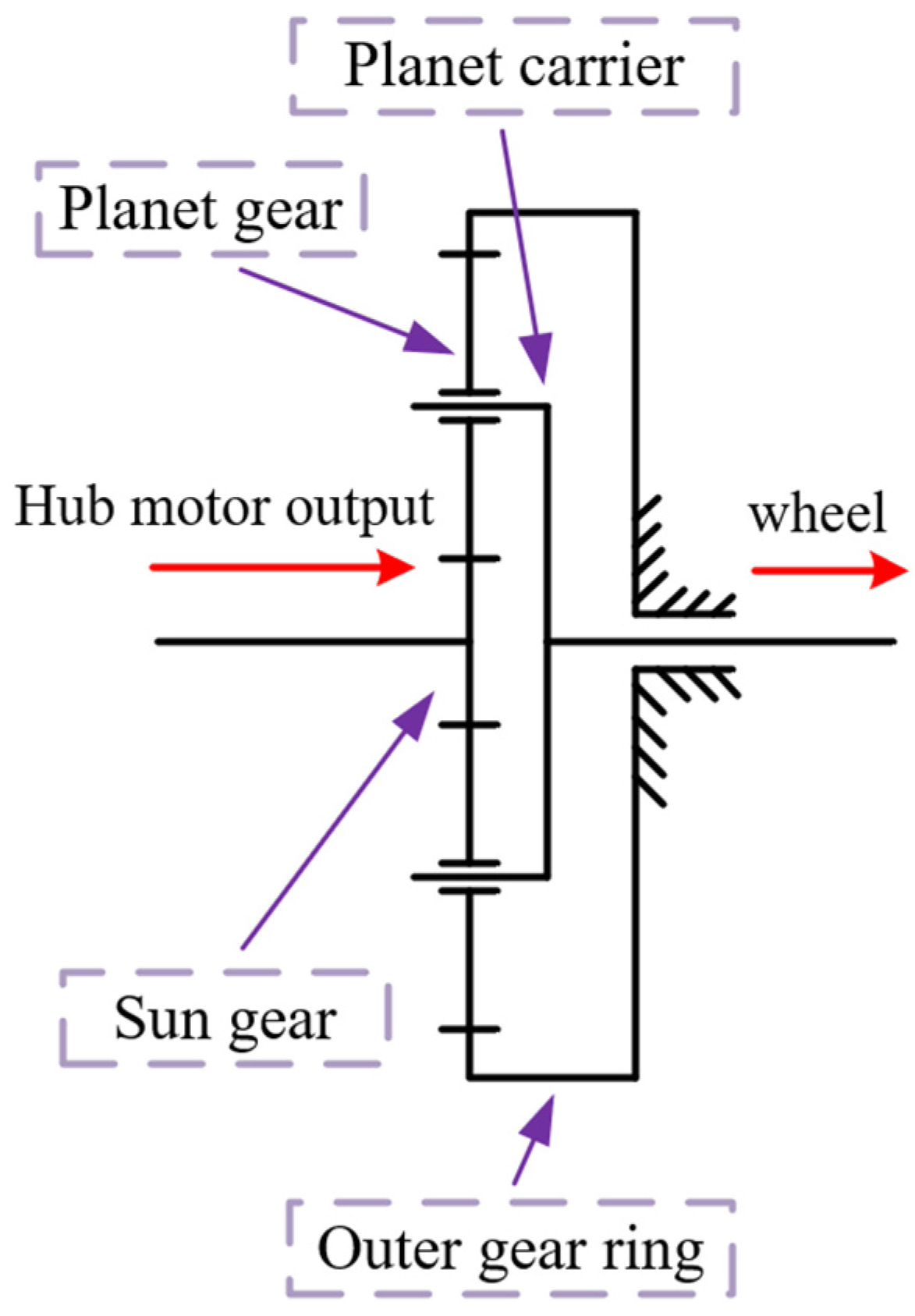
2.2.2. Modeling of Wheel-Side Reducer
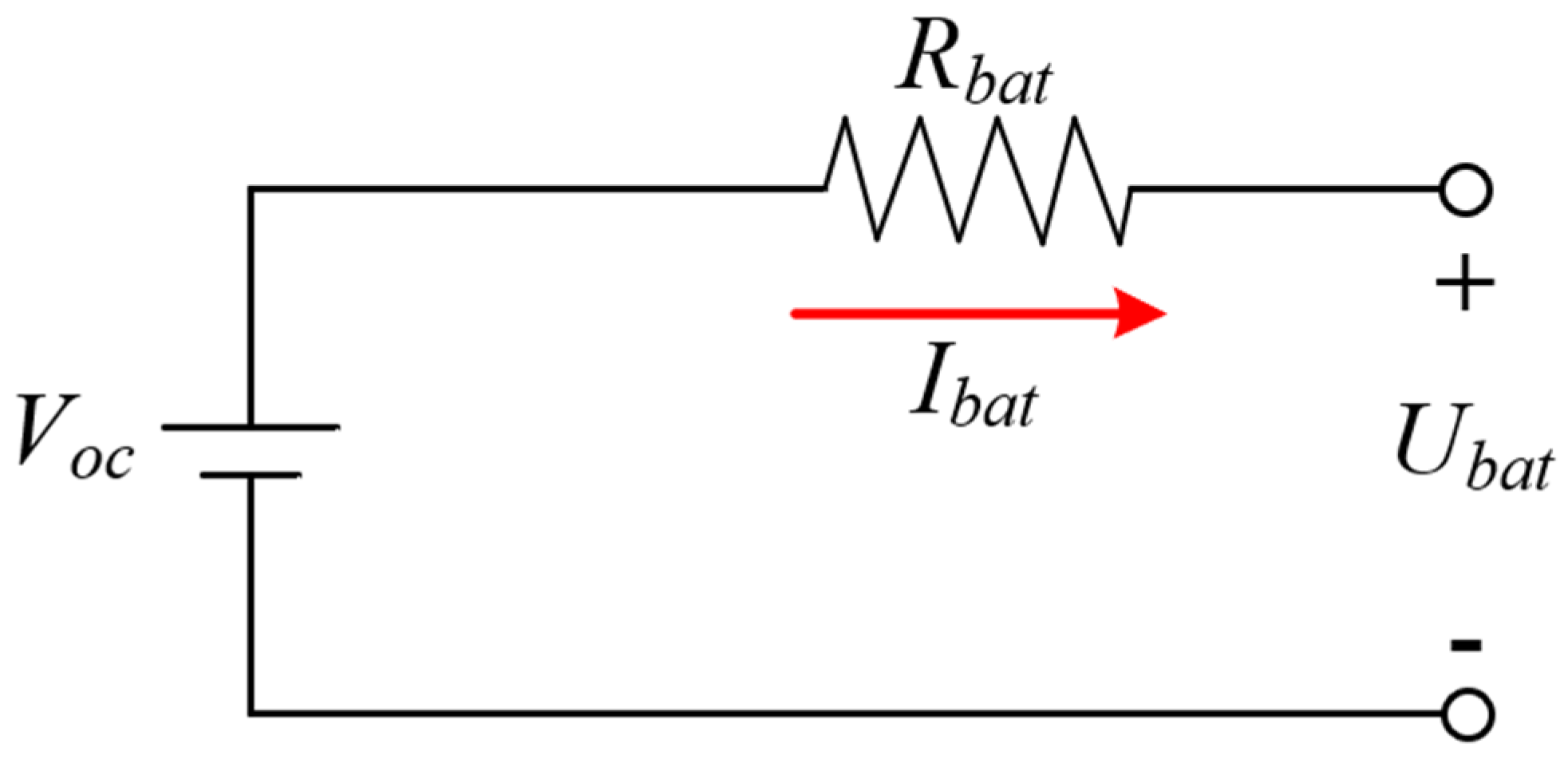
2.2.3. Modeling of Traction Battery
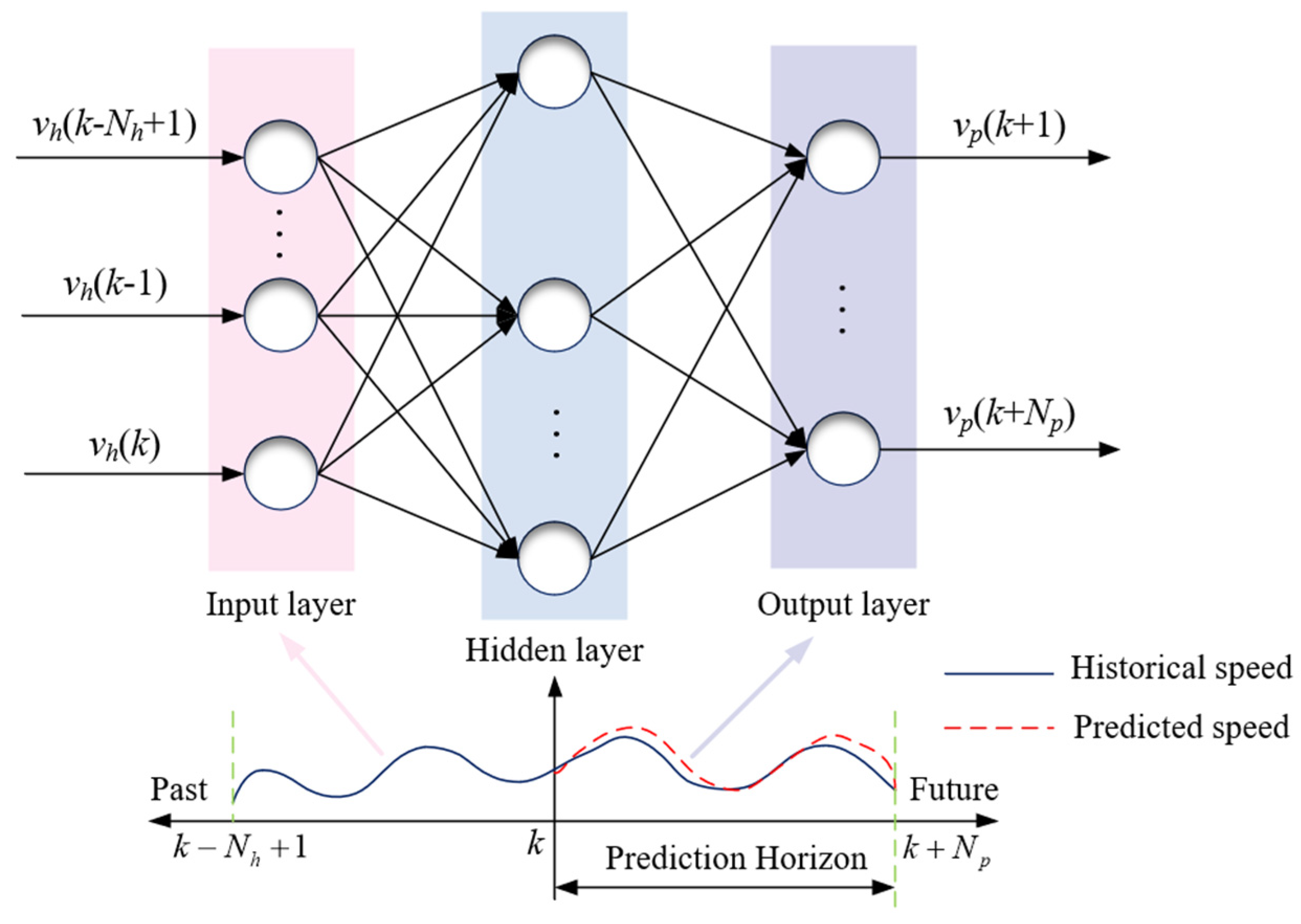
2.3. Tractor Operational Speed Prediction Model Based on Backpropagation Neural Network
2.3.1. Design of Backpropagation Neural Network
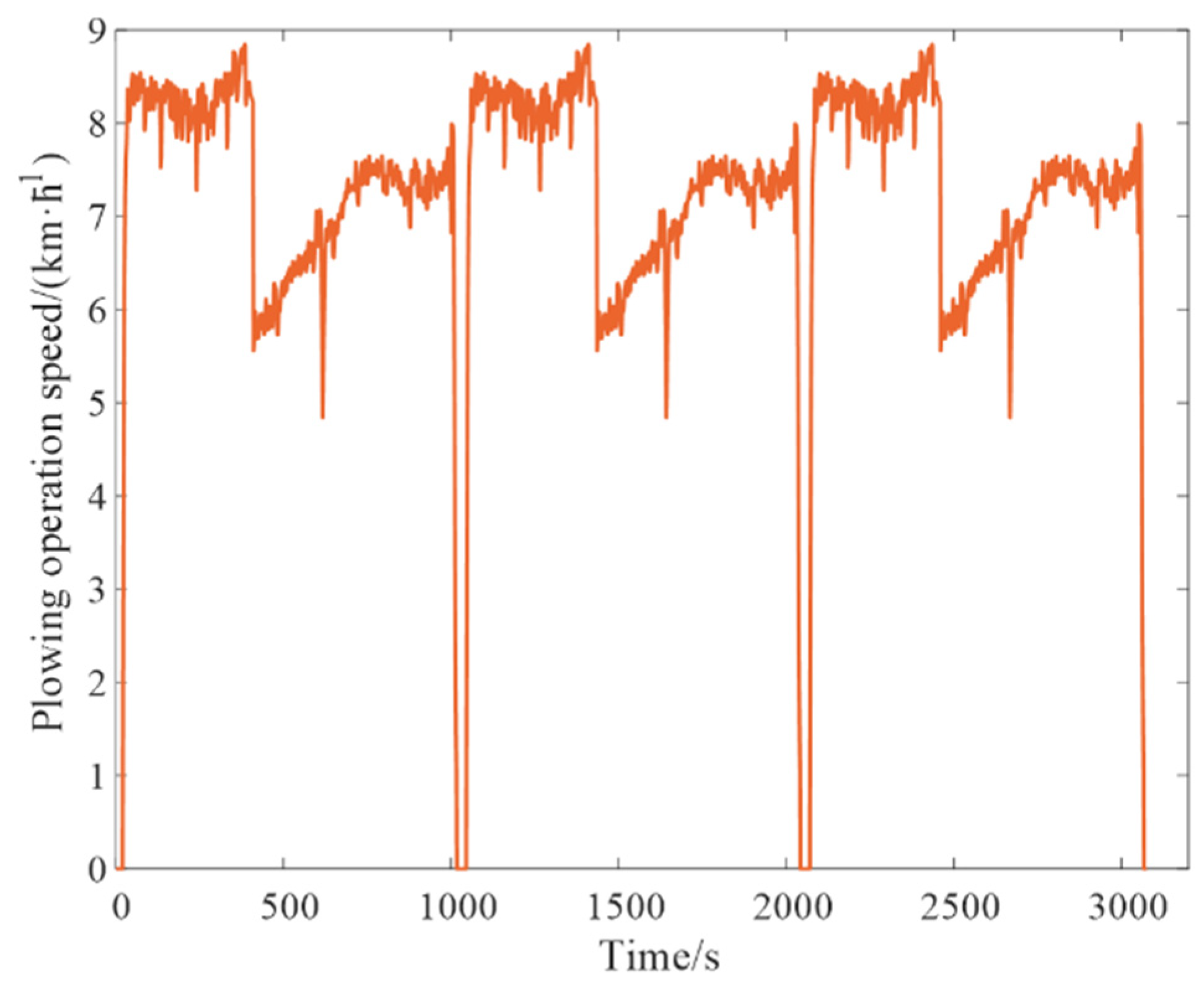
2.3.2. Tractor Plowing Operation Speed Acquisition Experiment
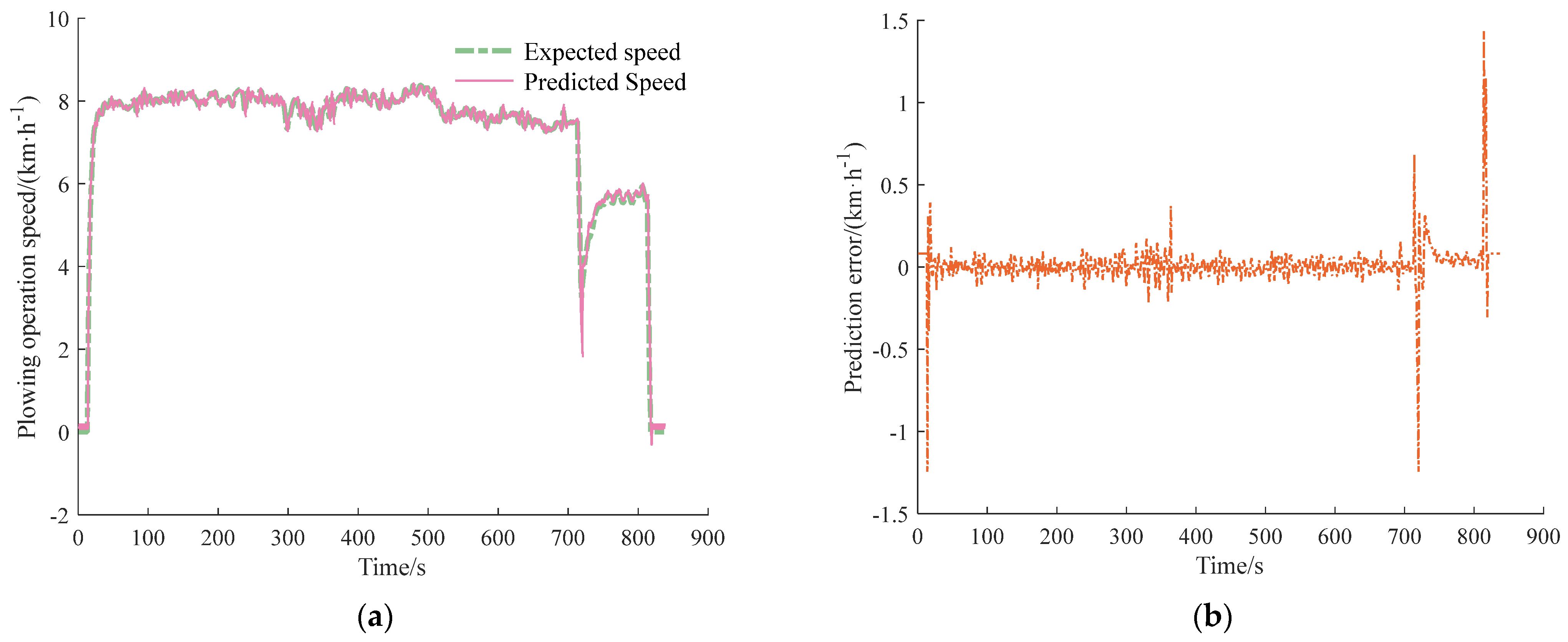
2.3.3. Prediction Results and Analysis of Tractor Operational Speed
2.4. Design of Real-Time Energy-Efficient Control Strategy Based on Model Predictive Control
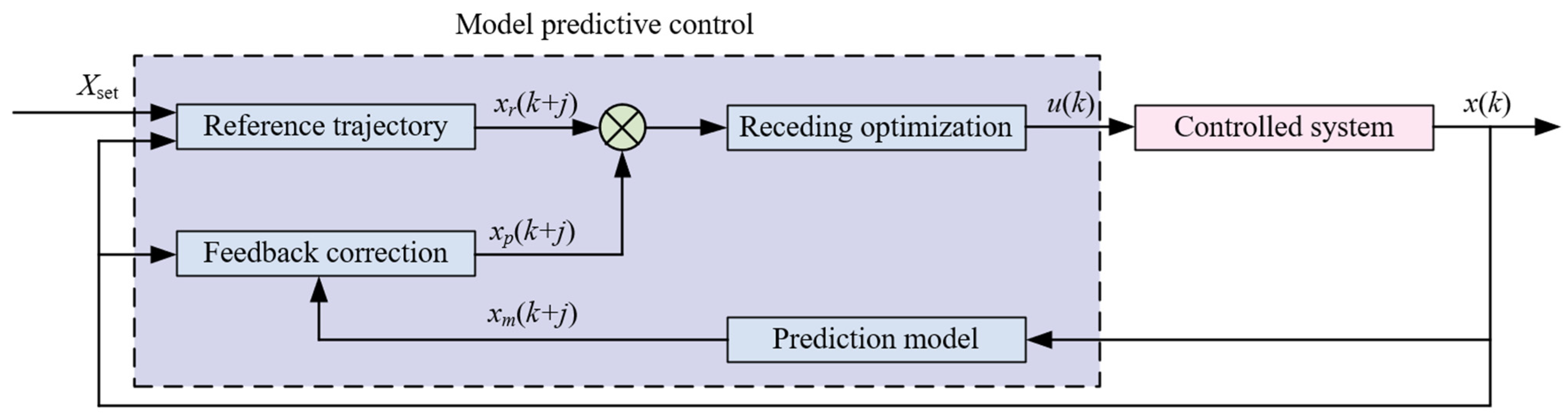
2.4.1. Principles of Model Predictive Control
2.4.2. Establishment of a Real-Time Energy-Efficient Control Strategy Framework
3. Results and Discussion
3.1. Establishment of Plowing Working Conditions
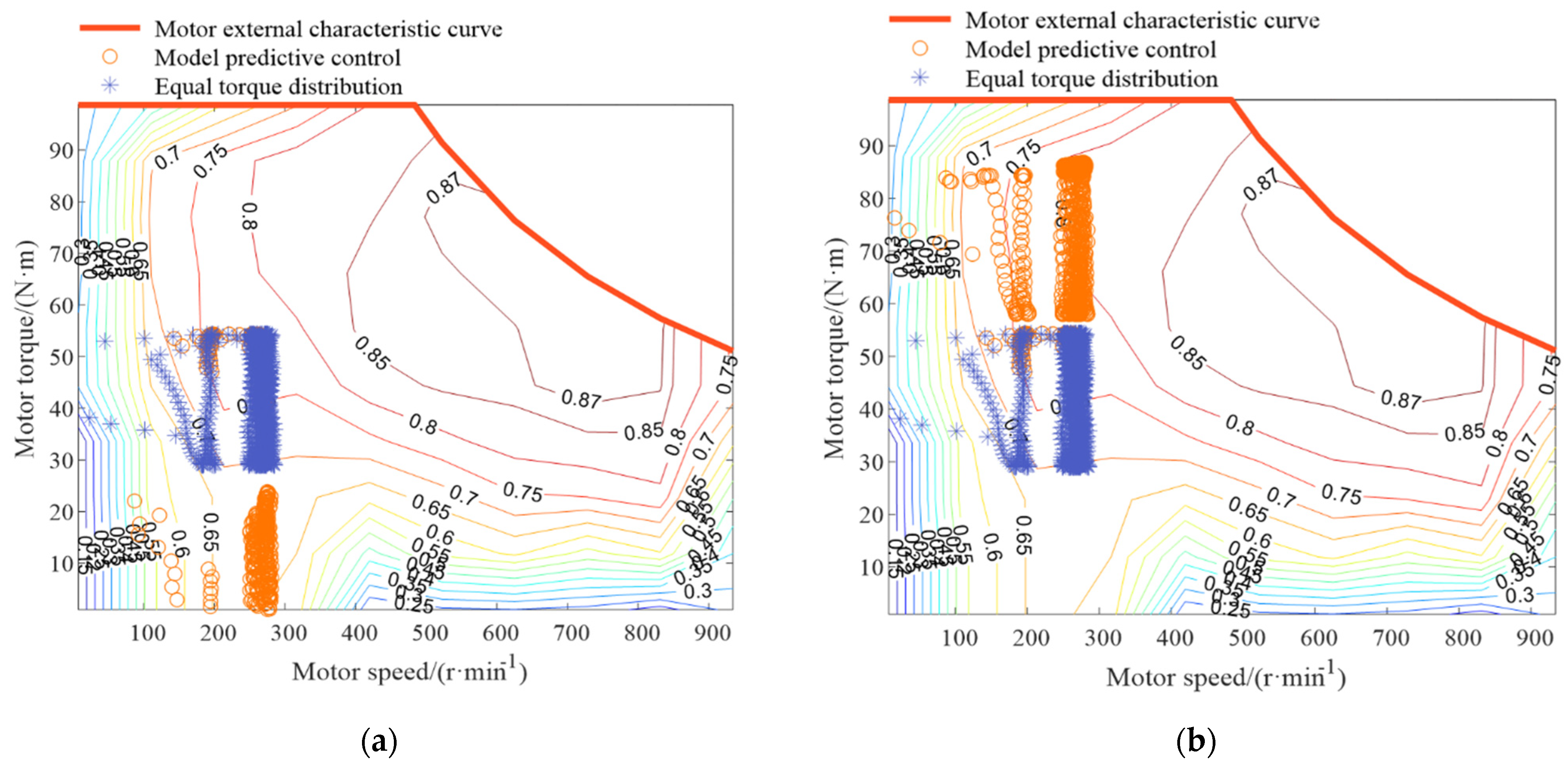
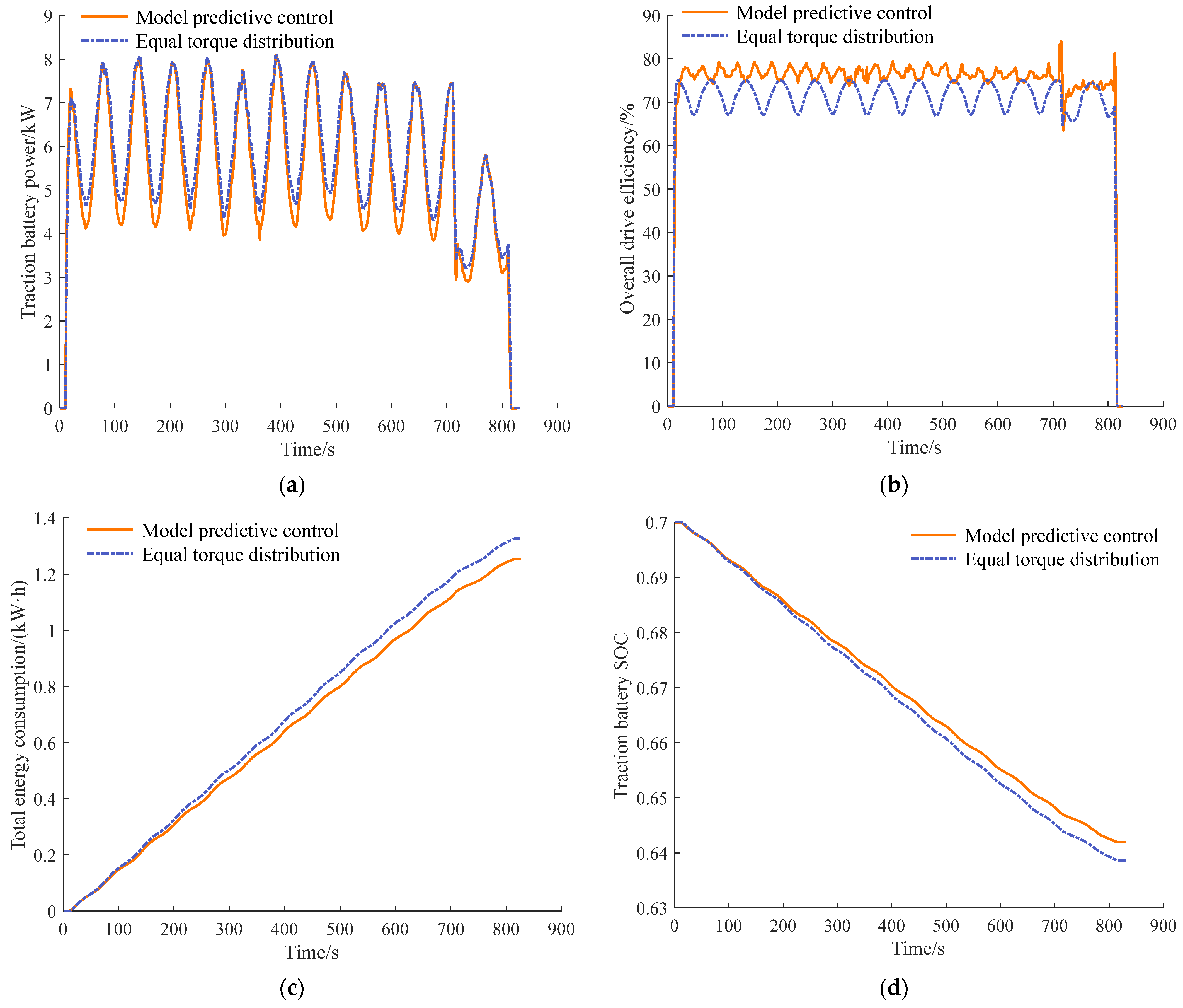
3.2. Simulation Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, B.; Wu, Z.B.; Mao, E.R. Development and Prospect of Key Technologies on Agricultural Tractor. Trans. Chin. Soc. Agric. Mach. 2018, 49, 1–17. [Google Scholar]
- Liu, M.N.; Lei, S.H.; Zhao, J.H.; Meng, Z.J.; Zhao, C.J.; Xu, L.Y. Review of Development Process and Research Status of Electric Tractors. Trans. Chin. Soc. Agric. Mach. 2022, 53 (Suppl. S1), 348–364. [Google Scholar]
- An, Y.H.; Wang, L.; Deng, X.T.; Chen, H.; Lu, Z.X.; Wang, T. Research on Differential Steering Dynamics Control of Four-Wheel Independent Drive Electric Tractor. Agriculture 2023, 13, 1758. [Google Scholar] [CrossRef]
- Yang, Y.P.; Shih, Y.C.; Chen, J.M. Real-time Torque Distribution Strategy for an Electric Vehicle with Multiple Traction Motors by Particle Swarm Optimization. In Proceedings of the Automatic Control Conference (CACS), 2013 CACS International, Nantou, Taiwan, 2–4 December 2013; pp. 233–238. [Google Scholar]
- Zhu, S.P.; Kuang, C.Y.; Chen, P.; Chen, H.P.; Wu, Z.Q. Economical Optimal Torque Distribution Control for Distributed Four-Wheel-Drive Electric Buses. Automob. Technol. 2022, 9, 15–22. [Google Scholar]
- Li, Q.; Li, Z.; Tang, J.M.; Wang, Y.; Zhang, B.Y.; He, D.Q. Multi-objective Torque Distribution Strategy for Distributed Drive Multi-objective Torque Distribution Strategy for Distributed Drive. Automot. Eng. 2025, 47, 489–498. [Google Scholar]
- Qiu, X.A. Research on Energy-saving Control Technology of Distributed Drive Pure Electric Bus. Master’s Thesis, Chongqing University, Chongqing, China, 2021. [Google Scholar]
- Zhang, Z.Y. Research on Optimal Torque Allocation Strategy for Distributed Drive Electric Vehicle. Master’s Thesis, Wuhan University of Science and Technology, Wuhan, China, 2019. [Google Scholar]
- Cheng, Y. Research on Torque Allocation Strategy Based on Energy Efficiency of Distributed Drive System. Master’s Thesis, Zhejiang University, Hangzhou, China, 2023. [Google Scholar]
- Lü, S.W. Research on Energy Management Strategy of Four-Wheel Drive Electric Vehicle Based on Energy Consumption Optimization. Master’s Thesis, Jilin University, Changchun, China, 2022. [Google Scholar]
- Xu, Y.; Jiang, L.Y.; Wei, B.; Qiu, L. An Optimal Torque Distribution Strategy for Four-Motorized-Wheel Electric Vehicle Considering Energy Conversation. IEEE Access 2020, 8, 135975–135988. [Google Scholar] [CrossRef]
- Dou, H.S.; Zhang, Y.T.; Fan, L.K. Design of Optimized Energy Management Strategy for All-Wheel-Drive Electric Vehicles. Appl. Sci. 2021, 11, 8218. [Google Scholar] [CrossRef]
- Kim, H.W.; Amarnathvarma, A.; Kim, E.; Hwang, M.H.; Kim, K.; Kim, H.; Choi, I.; Cha, H.R. A Novel Torque Matching Strategy for Dual Motor-Based All-Wheel-Driving Electric Vehicles. Energies 2022, 15, 2717. [Google Scholar] [CrossRef]
- Zhou, H.D.; Lu, Z.X.; Deng, X.T.; Zhang, C.; Luo, G.J.; Zhou, R.D. Study on torque distribution of traction operation of four wheel independent driven electric tractor. J. Nanjing Agric. Univ. 2018, 41, 962–970. [Google Scholar]
- Deng, X.T.; Sun, H.L.; Lu, Z.X.; Cheng, Z.; An, Y.H.; Chen, H. Research on Dynamic Analysis and Experimental Study of the Distributed Drive Electric Tractor. Agriculture 2023, 13, 40. [Google Scholar] [CrossRef]
- Li, X.Z.; Zhang, M.Z.; Liu, M.N.; Xu, L.Y.; Yan, X.H.; Lei, S.H. Optimized Design and Validation of Distributed Drive System for Electric Tractor Based on Multi-Island Genetic Algorithm. Trans. Chin. Soc. Agric. Mach. 2024, 55, 401–411. [Google Scholar]
- Xie, B.; Zhang, C.; Chen, S.; Mao, E.R.; Du, Y.F. Transmission Performance of Two-Wheel Drive Electric Tractor. Trans. Chin. Soc. Agric. Mach. 2015, 46, 8–13. [Google Scholar]
- Sun, H.L. Structural Design and Experimental Research of Distributed Drive Electric Tractor. Master’s Thesis, Nanjing Agricultural University, Nanjing, China, 2022. [Google Scholar]
- Zhang, K.; Lu, Z.X.; Wang, L.; Deng, X.T.; Zhang, B.; Sun, X.X. ECVT Configuration Design and Energy-Saving Control of Hybrid Tractor Based on Lever Topology Method. Trans. Chin. Soc. Agric. Mach. 2024, 55, 505–518+538. [Google Scholar]
- Li, S.P. Research on Driving Cycle Prediction and Energy Management Strategy Optimization of Plug-In Hybrid Electric Vehicle. Master’s Thesis, Shandong University of Technology, Zibo, China, 2023. [Google Scholar]
- Yang, M.; Sun, X.X.; Deng, X.T.; Lu, Z.X.; Wang, T. Extrapolation of Tractor Traction Resistance Load Spectrum and Compilation of Loading Spectrum Based on Optimal Threshold Selection Using a Genetic Algorithm. Agriculture 2023, 13, 1133. [Google Scholar] [CrossRef]
- Wang, S.Y. Fuel Cell Hybrid Vehicle Energy Management Strategy Based on Vehicle Speed Prediction. Master’s Thesis, Jilin University, Changchun, China, 2023. [Google Scholar]
- Yan, D.C. Research on Energy Management Strategy of Four-Wheel Drive PHEV Based on Multi-Source Information Fusion. Master’s Thesis, Shandong University of Technology, Zibo, China, 2022. [Google Scholar]
- Li, T.H.; Xie, B.; Wang, D.Q.; Zhang, S.L.; Wu, L.P. Real-time Adaptive Energy Management Strategy for Dual-Motor-Driven Electric Tractors. Trans. Chin. Soc. Agric. Mach. 2020, 51 (Suppl. S2), 530–543. [Google Scholar]
- Li, T.H.; Xie, B.; Li, Z.; Li, J.K. Design and Optimization of a Dual-Input Coupling Powertrain System: A Case Study for Electric Tractors. Appl. Sci. 2020, 10, 1608. [Google Scholar] [CrossRef]
- Zhang, B. Research on Energy Management Strategy of Hybrid Electric Vehicle Based on Speed Prediction. Master’s Thesis, Shenyang University Of Technology, Shenyang, China, 2024. [Google Scholar]
- Zhou, R.D.; Wang, L.; Deng, X.T.; Su, C.; Fang, S.; Lu, Z.X. Research on Energy Distribution Strategy of Tandem Hybrid Tractor Based on the Pontryagin Minimum Principle. Agriculture 2024, 14, 440. [Google Scholar] [CrossRef]
- Miao, H.N.; Yin, B.F.; Huang, Y.L.; Zhu, Y.H.; Xie, X.; Yun, L. Research on Power System Design and Energy Management of Series-Connected Hybrid Tractor Based on Dynamic Programming Algorithm. J. Chin. Agric. Mech. 2024, 45, 147–153. [Google Scholar]
- Zhu, Z.; Zeng, L.X.; Lin, Y.G.; Chen, L.; Zou, R.; Cai, Y.F. Adaptive Energy Management Strategy for Hybrid Tractors Based on Condition Prediction. J. Xi’an Jiaotong Univ. 2023, 57, 201–210. [Google Scholar]
- Zhang, K.; Deng, X.T.; Lu, Z.X.; Wang, T. Research on the Energy Management Strategy of a Hybrid Tractor OS-ECVT Based on a Dynamic Programming Algorithm. Agriculture 2024, 14, 1658. [Google Scholar] [CrossRef]
- Dou, H.S.; Wei, H.Q.; Ai, Q.; Zhang, Y.T. Control Strategy for Rotary Tillage Condition of Hybrid Electric Tractor with Coupled-split Dynamic Configuration. Trans. Chin. Soc. Agric. Mach. 2024, 55, 393–400+414. [Google Scholar]
- Wu, X.; Quan, L.; Zhu, X.Y.; Zhang, C. Torque Control Strategy of Electric Tractor Based on Optimal Energy Consumption. J. Agric. Mech. Res. 2025, 47, 266–272. [Google Scholar]








| Hub Motor Parameters | Values |
|---|---|
| Rated voltage | 200 V |
| Rated power | 5 kW |
| Maximum output torque | 100 N∙m |
| Control signal voltage | 0.8~3.4 V |
| Prediction Horizon (s) | RMSE (km∙h−1) | RMSE Increment |
|---|---|---|
| 2 | 0.1382 | - |
| 5 | 0.2474 | 0.1092 |
| 8 | 0.4190 | 0.1716 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, X.; Wang, Z.; Lu, Z.; Zhang, K.; Sun, X.; Huang, X. Real-Time Energy-Efficient Control Strategy for Distributed Drive Electric Tractor Based on Operational Speed Prediction. Agriculture 2025, 15, 1398. https://doi.org/10.3390/agriculture15131398
Deng X, Wang Z, Lu Z, Zhang K, Sun X, Huang X. Real-Time Energy-Efficient Control Strategy for Distributed Drive Electric Tractor Based on Operational Speed Prediction. Agriculture. 2025; 15(13):1398. https://doi.org/10.3390/agriculture15131398
Chicago/Turabian StyleDeng, Xiaoting, Zheng Wang, Zhixiong Lu, Kai Zhang, Xiaoxu Sun, and Xuekai Huang. 2025. "Real-Time Energy-Efficient Control Strategy for Distributed Drive Electric Tractor Based on Operational Speed Prediction" Agriculture 15, no. 13: 1398. https://doi.org/10.3390/agriculture15131398
APA StyleDeng, X., Wang, Z., Lu, Z., Zhang, K., Sun, X., & Huang, X. (2025). Real-Time Energy-Efficient Control Strategy for Distributed Drive Electric Tractor Based on Operational Speed Prediction. Agriculture, 15(13), 1398. https://doi.org/10.3390/agriculture15131398






