Influence Mechanism and Optimal Design of Flexible Spring-Tooth Reel Mechanism for Soybean Pod-Shattering Reduction
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Materials
2.2. Experimental Equipment
2.3. Experimental Methods
2.3.1. Pod Moisture Content Test
2.3.2. Investigation of Pod-Shattering Force Under Different Loading Directions
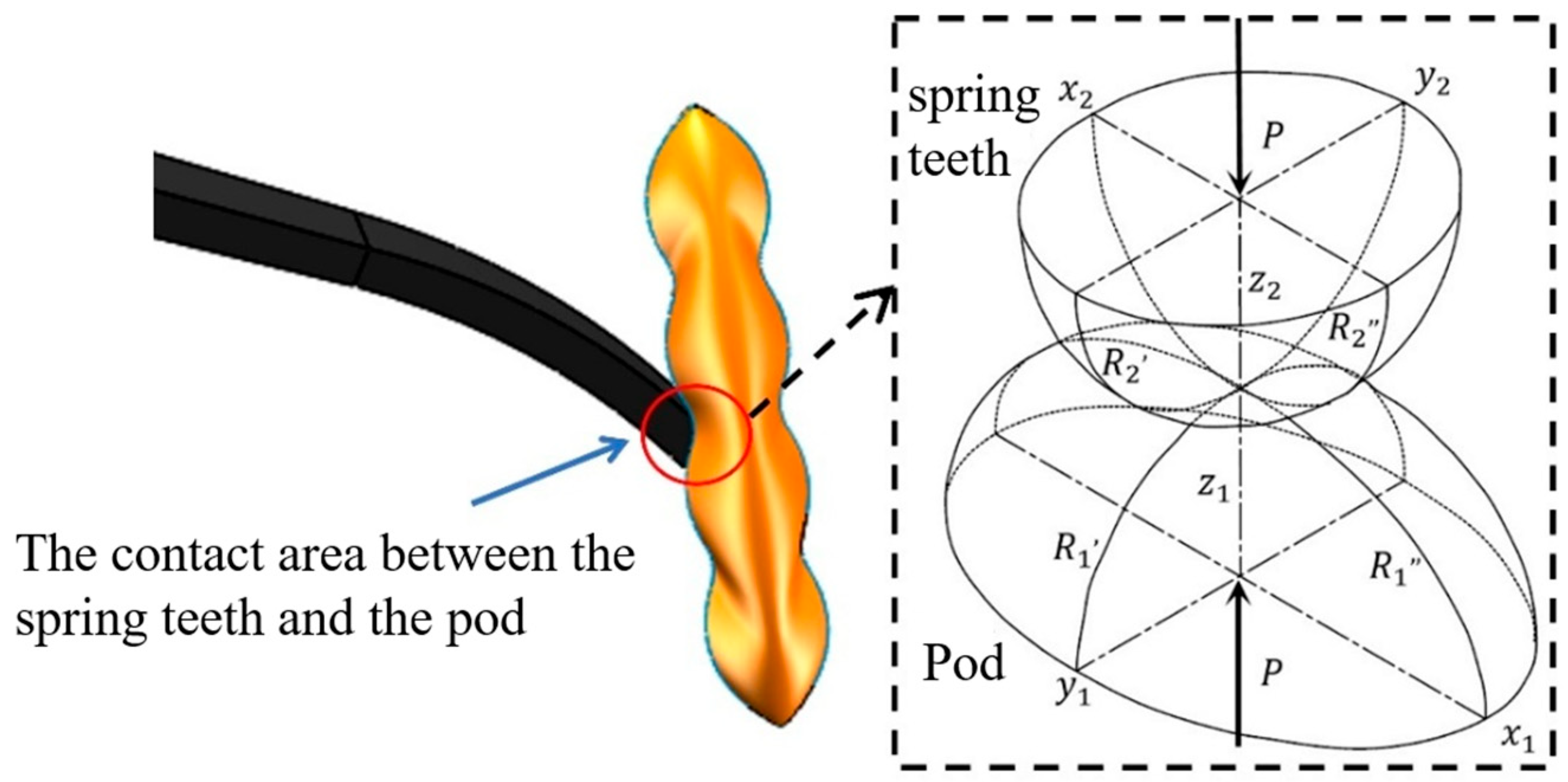
2.3.3. Mechanical Analysis of Pod-Spring Tooth Collision
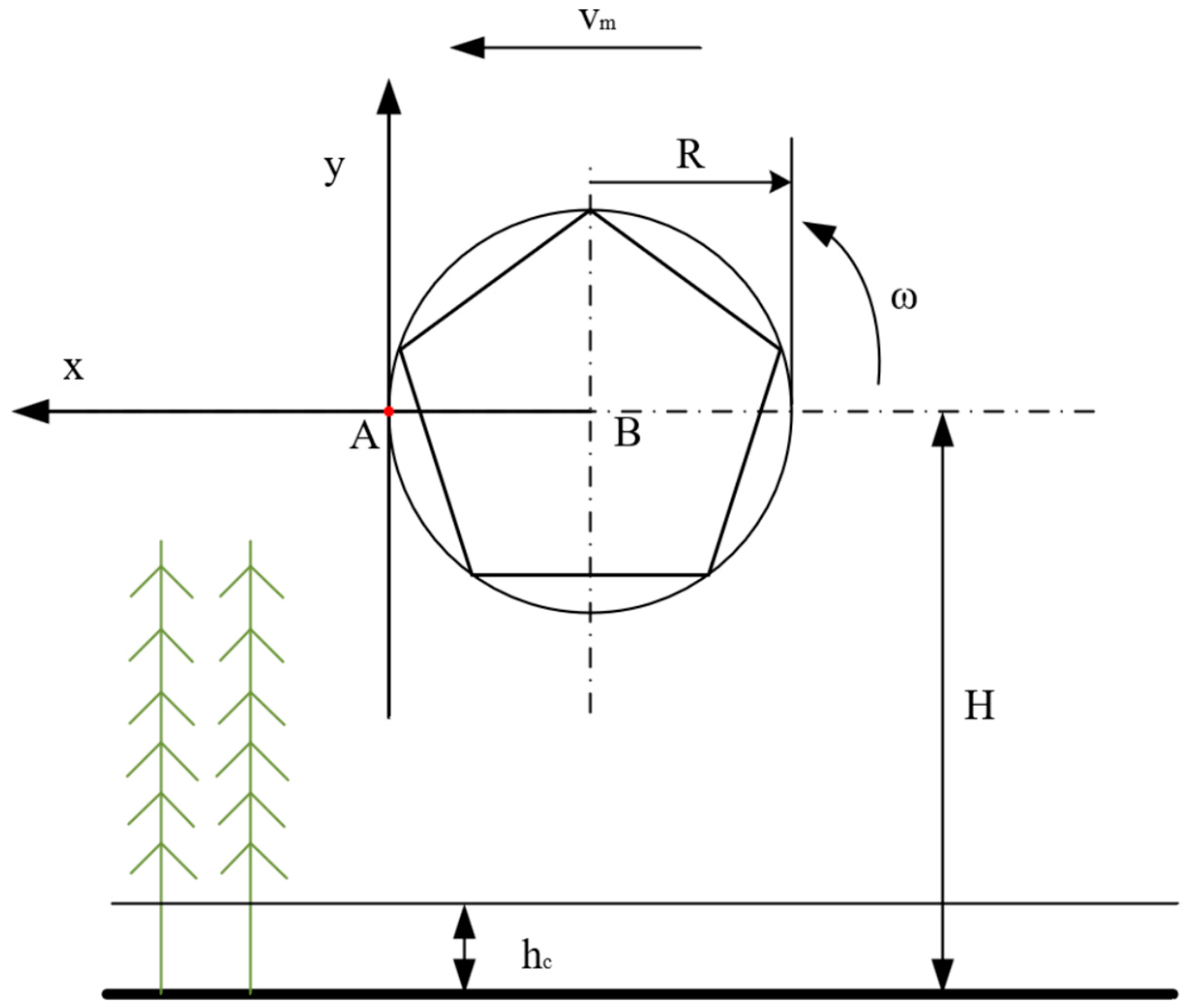
2.3.4. Study on the Motion Trajectory of Spring Tooth Tip
- (1)
- The reel rotates counterclockwise at constant speed around fixed center point B.
- (2)
- The combine harvester moves forward at a constant speed.
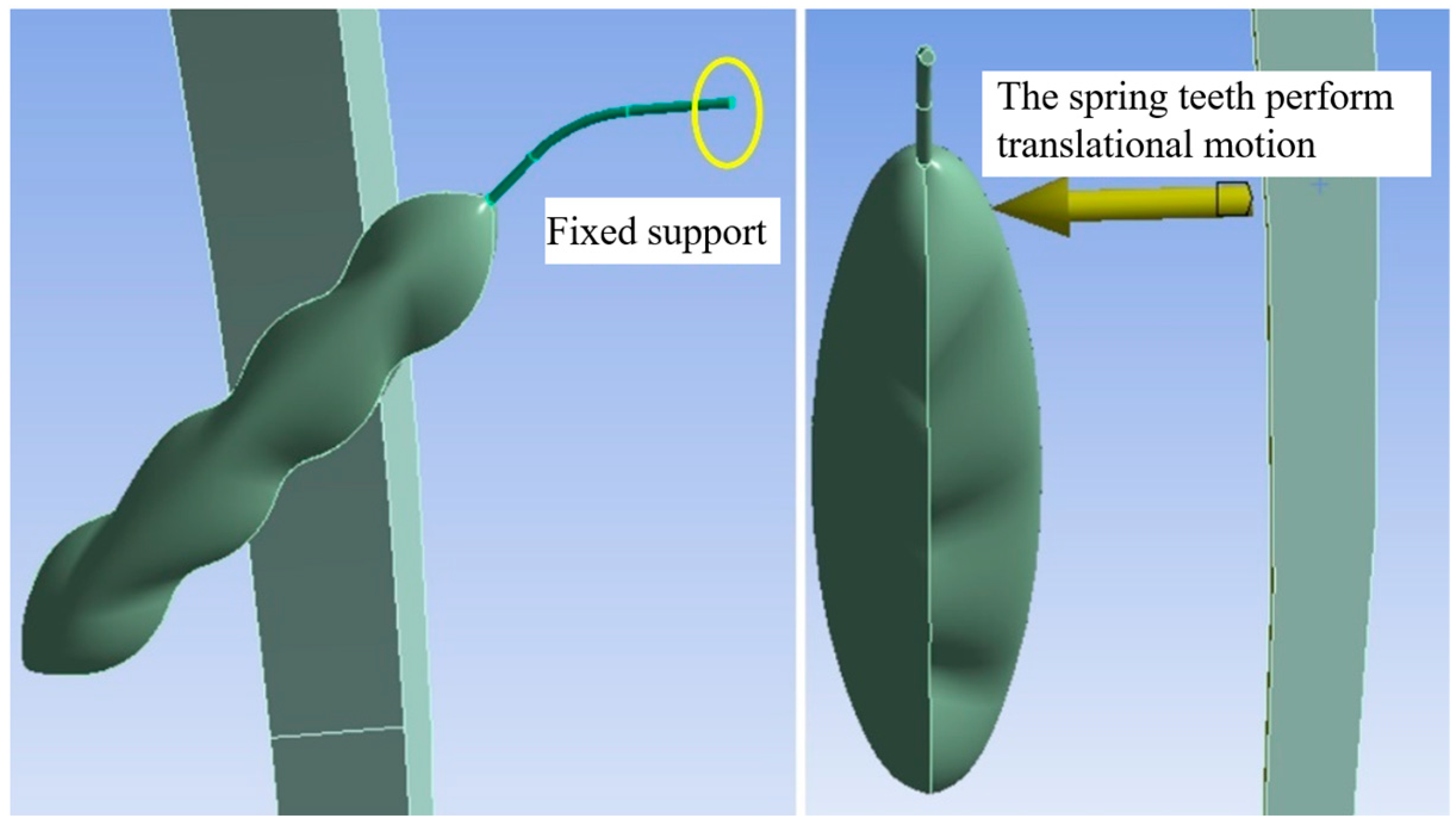
2.3.5. Investigation of Pod-Spring Tooth Collision with Different Parameters
2.3.6. Field Harvesting Test of Flexible Spring Tooth
3. Results and Discussion
3.1. Test Results of Moisture Content in Pods
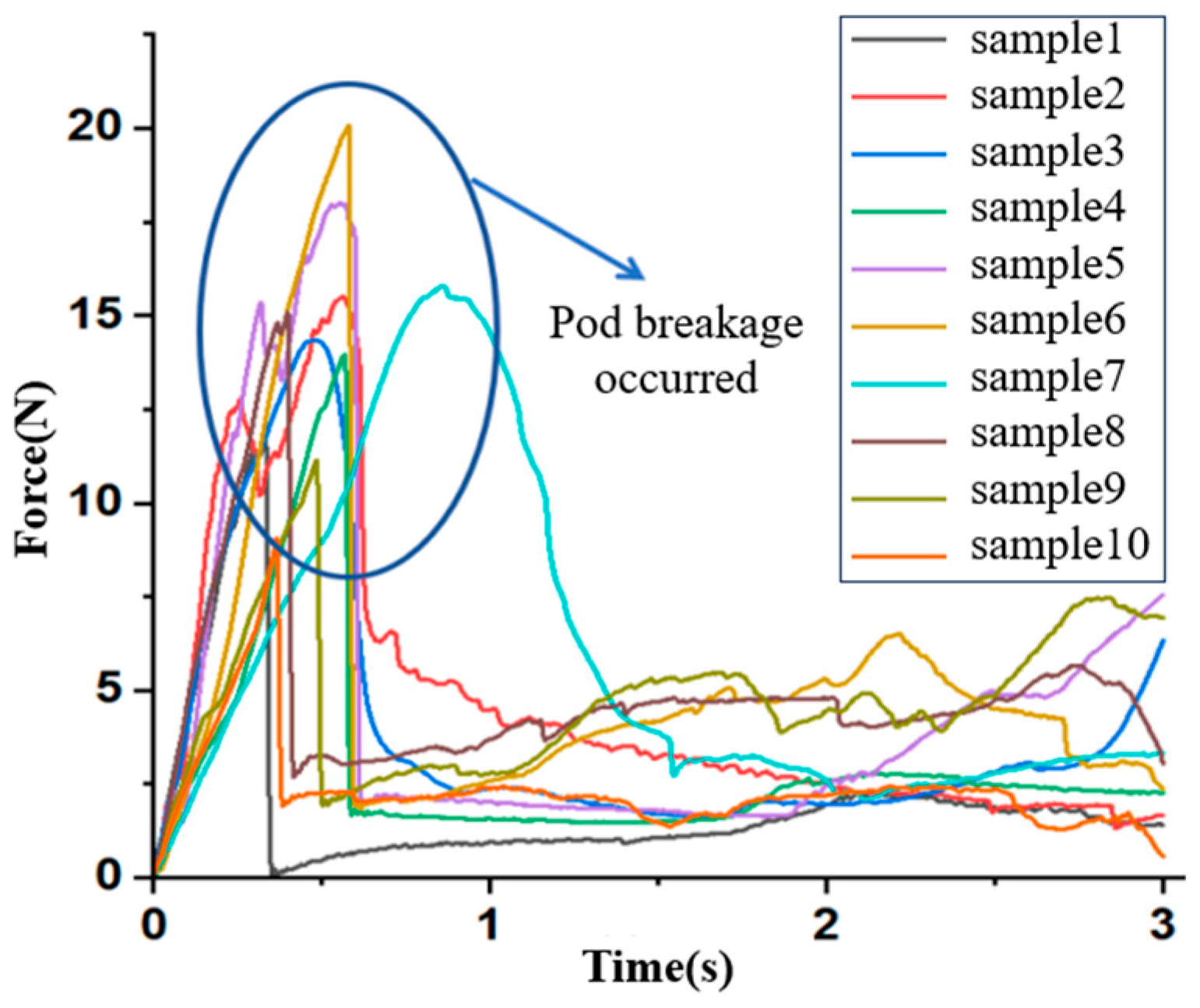
3.2. Experimental Results of Pod Shattering Force Under Different Loading Directions
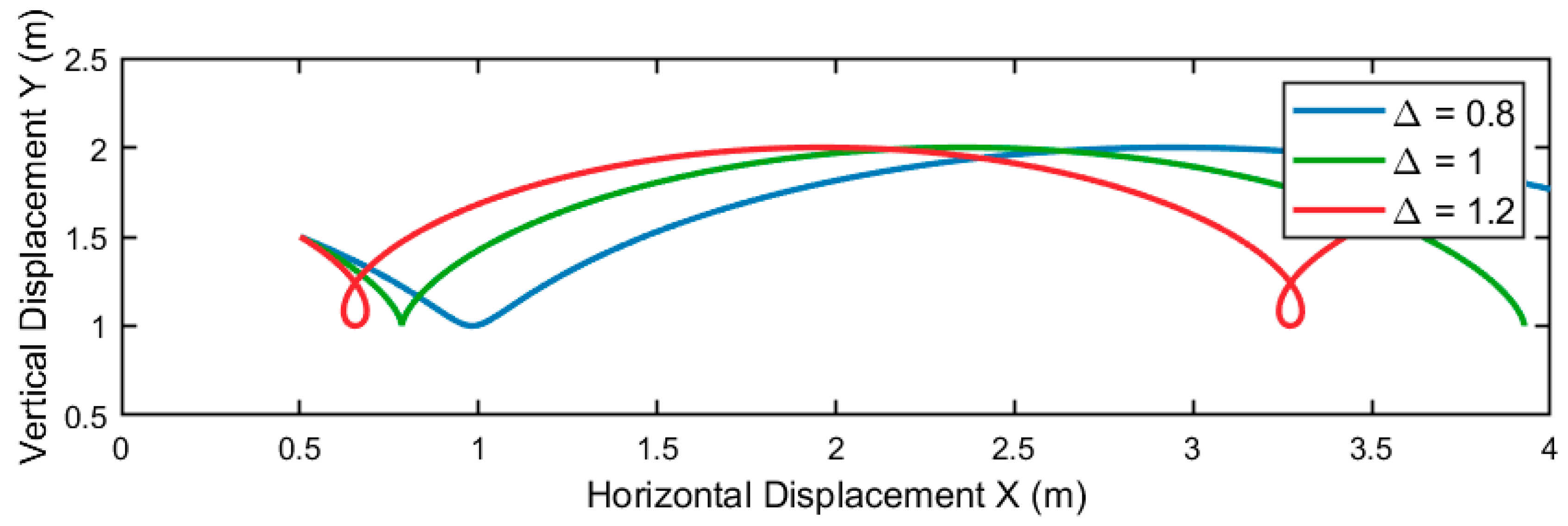
3.3. Analysis of Spring Tooth Tip Trajectory Simulation Results
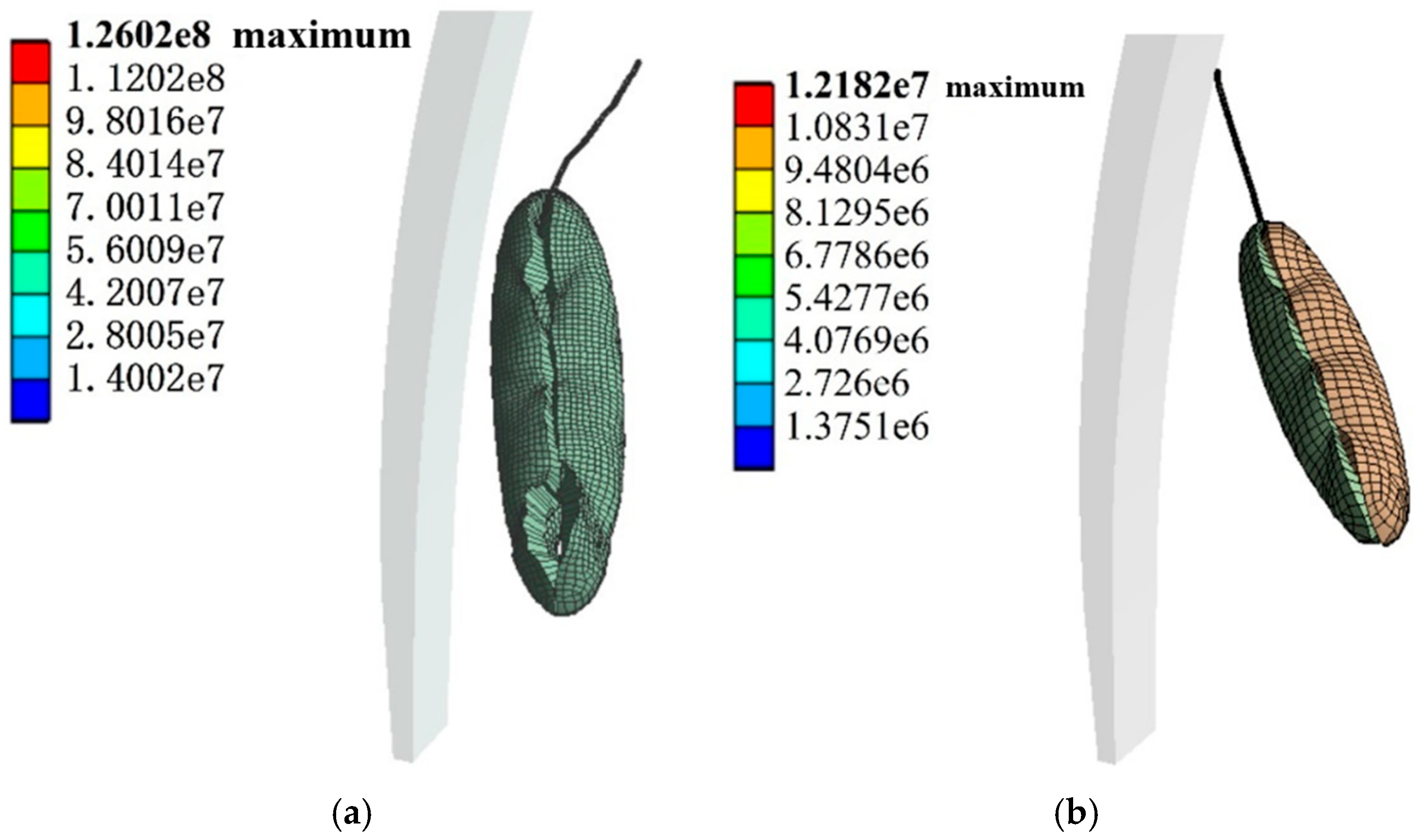
3.4. Simulation Results of Spring Tooth Effects on Pods Under Different Parameters
3.5. Field Test Results of Flexible Spring Tooth
3.5.1. Test Results of Soybean Grain Mass per Unit Area
3.5.2. Thousand-Grain Weight of Soybean Seeds
3.5.3. Natural Grain Loss per Unit Area
3.5.4. Header Loss Test per Unit Area
4. Conclusions
- (1)
- The mechanical properties of soybean pods from Xinjiang, with an average moisture content of 9.267%, exhibit significant anisotropy. The results of compression tests in different loading directions revealed that the average shattering force of these pods reached 14.3271 N under vertical compression, which posed the highest risk of pod shattering. This finding provides theoretical guidance for optimizing the operational parameters of harvesting mechanisms for soybeans under these specific conditions.
- (2)
- The collision damage mechanism between reel spring teeth and soybean pods is significantly influenced by the elastic modulus and contact area of the spring teeth. Based on Hertzian contact theory and finite element simulation, increasing the contact area and decreasing the elastic modulus of the spring teeth effectively reduced the maximum equivalent stress on the pods by 90.3%, thereby mitigating mechanical damage during harvesting.
- (3)
- The reel spring tooth tip trajectory analysis indicated that a spring tooth speed ratio (Δ) greater than 1 is necessary to achieve effective crop gathering. Simulation results demonstrated that only when Δ > 1.0 did the spring tooth tip trajectory form a looping path, enabling the backward hooking motion essential for efficient plant lifting and gathering.
- (4)
- Field trials confirmed the practical effectiveness of flexible PVC spring teeth in reducing harvest losses. The optimized flexible spring tooth reel achieved 1.371%, which is significantly lower than that of conventional rigid steel spring teeth, thus verifying the reliability of the theoretical and simulation-based design improvements in actual field operations.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Dai, C.; Hou, Y.; Xu, H.; Huang, L.; Dabbour, M.; Mintah, B.K.; He, R.; Ma, H. Effect of solid-state fermentation by three different Bacillus species on composition and protein structure of soybean meal. J. Sci. Food Agric. 2022, 102, 557–566. [Google Scholar] [CrossRef] [PubMed]
- Dai, C.; Hou, Y.; Xu, H.; Umego, E.C.; Huang, L.; He, R.; Ma, H. Identification of a thermophilic protease-producing strain and its application in solid-state fermentation of soybean meal. J. Sci. Food Agric. 2022, 102, 2359–2370. [Google Scholar] [CrossRef] [PubMed]
- Heng, X.; Chen, H.; Lu, C.; Feng, T.; Li, K.; Gao, E. Study on synergistic fermentation of bean dregs and soybean meal by multiple strains and proteases. LWT-Food Sci. Technol. 2022, 154, 112626. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, J.; He, Z.; Hao, W.; Liu, J.; Kwek, E.; Zhao, Y.; Ma, K.Y.; He, W.-S.; Chen, Z.-Y. Soybean germ oil reduces blood cholesterol by inhibiting cholesterol absorption and enhancing bile acid excretion. Food Funct. 2019, 10, 1836–1845. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, J.; Zhao, X.; Zhang, L.; Zhou, D.; Yu, C.; Hu, W.; Zhang, Q. Optimising maize threshing by integrating DEM simulation and interpretive enhanced predictive modelling. Biosyst. Eng. 2024, 244, 93–106. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, J.; Zhao, X.; Zhang, Q.; Zhang, L.; Zhou, D.; Yu, C.; Hu, W.; Wang, H. Maize kernel damage dynamic prediction in threshing through PSO-LSTM and discrete element modelling. Biosyst. Eng. 2024, 242, 179–195. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Ji, K.; Yu, Z.; Ma, Z.; Xu, L.; Niu, C. Development of a hydraulic variable-diameter threshing drum control system for combine harvester part I: Adaptive monitoring method. Biosyst. Eng. 2025, 250, 174–182. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Ji, K.; Yu, Z.; Ma, Z.; Xu, L.; Niu, C. Development of a hydraulic variable-diameter threshing drum control system for combine harvester part II: Controller design and field performance. Biosyst. Eng. 2025, 254, 104160. [Google Scholar] [CrossRef]
- Qian, Z.; Jin, C.; Ni, Y.; Zhang, D. Modelling threshing using an entropy regularisation approach with frictional contact dynamics and a flexible threshing mechanism. Biosyst. Eng. 2023, 226, 144–154. [Google Scholar] [CrossRef]
- Zhang, Q.; Fang, X.; Gao, X.; Zhang, J.; Zhao, X.; Yu, L.; Yu, C.; Zhou, D.; Zhou, H.; Zhang, L.; et al. Optimising maize threshing process with temporal proximity soft actor-critic deep reinforcement learning algorithm. Biosyst. Eng. 2024, 248, 229–239. [Google Scholar] [CrossRef]
- Cao, Z.; Li, Q.; Chen, L.; Zhou, Y.; Nie, J.; Chen, Q.; Xiao, Y.; Zhou, S.; Zhang, L. Structural Design and Testing of a Corn Header for Soybean-Corn Intercropping. Agriculture 2025, 15, 123. [Google Scholar] [CrossRef]
- Luo, H.; Wang, J.; Lian, X.; Geng, B.; Li, F. Design and experiment of small narrow range segmented soybean harvester in hilly area. Agric. Res. Arid Areas 2024, 42, 283–293. [Google Scholar]
- Wang, S.; Li, B.; Chen, S.; Tang, Z.; Zhou, W.; Guo, X. Design and Performance Test of Soybean Profiling Header Suitable for Harvesting Bottom Pods on Film. Agriculture 2024, 14, 1058. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, R.; Xi, X.; Zhang, X.; Ding, W.; Liu, J.; Xiao, S.; Lin, M.; Xing, J.; Yang, S.; et al. Numerical simulation and optimisation of depodding performance in a fresh green soybean harvester. Biosyst. Eng. 2025, 253, 104127. [Google Scholar] [CrossRef]
- Cong, C.; Guangqiao, C.; Jinlong, Z.; Jianping, H. Dynamic Monitoring of Harvester Working Progress Based on Traveling Trajectory and Header Status. Eng. Agric. 2023, 43, e20220196. [Google Scholar] [CrossRef]
- Liu, H.; Han, X.; Fadiji, T.; Li, Z.; Ni, J. Prediction of the cracking susceptibility of tomato pericarp: Three-point bending simulation using an extended finite element method. Postharvest Biol. Technol. 2022, 187, 111876. [Google Scholar] [CrossRef]
- Pang, J.; Li, Y.; Ji, J.; Xu, L. Vibration excitation identification and control of the cutter of a combine harvester using triaxial accelerometers and partial coherence sorting. Biosyst. Eng. 2019, 185, 25–34. [Google Scholar] [CrossRef]
- Nie, J.; Luo, H.; Zhou, Y.; Li, Q.; Qiu, Q.; Zhang, L. Design and Test of a Low-Loss Soybean Header Based on Synchronous Profiling. Agriculture 2023, 13, 1580. [Google Scholar] [CrossRef]
- Tong, W.; Zhang, J.; Cao, G.; Song, Z.; Ning, X. Design and Experiment of a Low-Loss Harvesting Test Platform for Cabbage. Agriculture 2023, 13, 1204. [Google Scholar] [CrossRef]
- Xie, B.; Wang, J.; Jiang, H.; Zhao, S.; Liu, J.; Jin, Y.; Li, Y. Multi-feature detection of in-field grain lodging for adaptive low-loss control of combine harvesters. Comput. Electron. Agric. 2023, 208, 107772. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, M.; Xing, Z.; Liu, X. Design and Test of Double-acting Opposite Direction Cutting End Effector for Safflower Harvester. Trans. Chin. Soc. Agric. Mach. 2022, 53, 160–170. [Google Scholar]
- Zhao, Y.; Dai, F.; Shi, R.; Chen, J.; Xin, S.; Zhao, W.; Zhang, F. Design and Experiment of Self-propelled Seed Corn Combine Harvester. Trans. Chin. Soc. Agric. Mach. 2024, 55, 121–134. [Google Scholar]
- Li, D.; Wang, Z.; Liang, Z.; Zhu, F.; Xu, T.; Cui, X.; Zhao, P. Analyzing Rice Grain Collision Behavior and Monitoring Mathematical Model Development for Grain Loss Sensors. Agriculture 2022, 12, 839. [Google Scholar] [CrossRef]
- Liang, Z.; Huang, Y.; Li, D.; Wada, M.E. Parameter determination of a viscoelastic-plastic contact model for potatoes during transient collisions. Biosyst. Eng. 2023, 234, 156–171. [Google Scholar] [CrossRef]
- Wang, G.; He, B.; Han, D.; Zhang, H.; Wang, X.; Chen, Y.; Chen, X.; Zhao, R.; Li, G. Investigation of Collision Damage Mechanisms and Reduction Methods for Pod Pepper. Agriculture 2024, 14, 117. [Google Scholar] [CrossRef]
- Ding, B.; Liang, Z.; Qi, Y.; Ye, Z.; Zhou, J. Improving Cleaning Performance of Rice Combine Harvesters by DEM-CFD Coupling Technology. Agriculture 2022, 12, 1457. [Google Scholar] [CrossRef]
- Hu, J.; Pan, J.; Dai, B.; Chai, X.; Sun, Y.; Xu, L. Development of an Attitude Adjustment Crawler Chassis for Combine Harvester and Experiment of Adaptive Leveling System. Agronomy 2022, 12, 717. [Google Scholar] [CrossRef]
- Huang, J.; Tan, L.; Tian, K.; Zhang, B.; Ji, A.; Liu, H.; Shen, C. Formation mechanism for the laying angle of hemp harvester based on ANSYS-ADAMS. Int. J. Agric. Biol. Eng. 2023, 16, 109–115. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Ji, K.; Zhu, R. A Fault Diagnosis Method for a Differential Inverse Gearbox of a Crawler Combine Harvester Based on Order Analysis. Agriculture 2022, 12, 1300. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.Z.; Li, Y.; Lv, L.; Shi, M. Modeling and control methods of a multi-parameter system for threshing and cleaning in grain combine harvesters. Comput. Electron. Agric. 2024, 225, 109251. [Google Scholar] [CrossRef]
- Lian, Y.; Chen, J.; Guan, Z.; Song, J. Development of a monitoring system for grain loss of paddy rice based on a decision tree algorithm. Int. J. Agric. Biol. Eng. 2021, 14, 224–229. [Google Scholar] [CrossRef]
- Bertin, V. Similarity solutions in elastohydrodynamic bouncing. J. Fluid Mech. 2024, 986, A13. [Google Scholar] [CrossRef]
- Cai, S.L.; Ding, G.; Duan, G.H.; Jing, X.H.; Dai, L.H.; Jiang, M.Q. Scaling laws for two-metallic spheres in a head-on collision. Int. J. Impact Eng. 2025, 200, 105257. [Google Scholar] [CrossRef]
- Gorin, B.; Ribe, N.M.; Bonn, D.; Kellay, H. Impacts of poroelastic spheres. Commun. Phys. 2025, 8, 104. [Google Scholar] [CrossRef]
- He, J.; Zhu, W.; Pang, Z.; Zhao, Z.; Du, Z. Parameter Feasible Region Analysis of the Tethered Net Shooting Error Aiming at UAV. J. Astronaut. 2024, 45, 711–719. [Google Scholar]
- Lin, S.; Shi, D.; Zhou, L.; Chen, L.; Li, Z. Probing the contact time of droplet impacts: From the Hertz collision to oscillation regimes. Phys. Rev. E 2024, 110, L053101. [Google Scholar] [CrossRef]
- Wang, P.; Liu, Y.; Zhu, R.; Qin, L.; Deng, J.; Yang, Z.; Qin, Z.; Chu, F. Dynamic analysis of vibro-impact energy harvester with acoustic black hole. Int. J. Mech. Sci. 2025, 291, 110193. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Xu, X.; Wei, W.; Shang, K. Research on the Contact Dynamics of Binary Non-Spherical Particles Based on Hertz Theory. J. Food Process Eng. 2025, 48, e70070. [Google Scholar] [CrossRef]
- Liang, Z.; Li, J.; Liang, J.; Shao, Y.; Zhou, T.; Si, Z.; Li, Y. Investigation into Experimental and DEM Simulation of Guide Blade Optimum Arrangement in Multi-Rotor Combine Harvesters. Agriculture 2022, 12, 435. [Google Scholar] [CrossRef]
- Liang, Z.; Wada, M.E. Development of cleaning systems for combine harvesters: A review. Biosyst. Eng. 2023, 236, 79–102. [Google Scholar] [CrossRef]
- Luo, Y.; Wei, L.; Xu, L.; Zhang, Q.; Liu, J.; Cai, Q.; Zhang, W. Stereo-vision-based multi-crop harvesting edge detection for precise automatic steering of combine harvester. Biosyst. Eng. 2022, 215, 115–128. [Google Scholar] [CrossRef]
- Chen, X.; Chen, R.; Wang, J.; Li, H.; Zhang, W. Evaluation of water distribution and uniformity of sprinkler irrigation based on harmonic analysis and finite element method. Biosyst. Eng. 2024, 248, 308–320. [Google Scholar] [CrossRef]
- Li, W.; Shi, Y.; Huang, X.; Li, Z.; Zhang, X.; Zou, X.; Hu, X.; Shi, J.; Tomovic, V. Study on the Diffusion and Optimization of Sucrose in Gaido Seak Based on Finite Element Analysis and Hyperspectral Imaging Technology. Foods 2024, 13, 249. [Google Scholar] [CrossRef]
- Wang, J.; Chen, R. An improved finite element model for the hydraulic analysis of drip irrigation subunits considering local emitter head loss. Irrig. Sci. 2020, 38, 147–162. [Google Scholar] [CrossRef]
- Wang, W.; Lv, X.; Yi, Z. Parameter Optimization of Reciprocating Cutter for Chinese Little Greens Based on Finite Element Simulation and Experiment. Agriculture 2022, 12, 2131. [Google Scholar] [CrossRef]
- Hao, C.; Yang, D.; Zhao, L.; Yang, J.; Wang, T.; He, J. Compressive Characteristics and Fracture Simulation of Cerasus Humilis Fruit. Agriculture 2025, 15, 88. [Google Scholar] [CrossRef]
- Liu, C.; Li, B.; Xu, C. Analysis of Bruising Characteristics of Large-Stone Fruits upon Impact Using Finite Element Method-A Case Study of Postharvest Loquats. Horticulturae 2025, 11, 440. [Google Scholar] [CrossRef]
- Looh, G.A.; Xie, F.; Wang, X.; Looh, A.N.; Hind, H. Grain kernel damage during threshing: A comprehensive review of theories and models. J. Agric. Eng. 2025, 56. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Q.; Fang, X.; Zhang, J.; Feng, W.; Zhang, L.; Zhou, D.; Yu, C.; Wang, H.; Gao, X.; et al. Finite element analysis of corn kernel damage: A viscoelastic model approach for impact-induced damage prediction. J. Sci. Food Agric. 2025, 105, 3993–4004. [Google Scholar] [CrossRef]
- Aina, A.M.; Harith, H.H.; Hashim, N.; Shukery, M.F.M. Finite element modelling of the mechanical behavior of papaya fruit under compression. Postharvest Biol. Technol. 2025, 226, 113565. [Google Scholar] [CrossRef]
- Chen, H.; Guo, T.; Jin, L.; Wang, J.; Zhu, Y.; Ban, Z.; Di, J. Prediction of damage characteristics of apple fruit based on test and finite element method. J. Stored Prod. Res. 2025, 111, 102543. [Google Scholar] [CrossRef]








| The Quality of the Pod Before Drying/g | The Quality of the Pod After Drying/g | |||||
|---|---|---|---|---|---|---|
| 10 | 10 | 10 | 8.97 | 9.21 | 9.04 | 9.267 |
| Test Number | Shattering Force Under Side Compression/N | Shattering Force Under Vertical Compression/N |
|---|---|---|
| 1 | 16.7274 | 11.6102 |
| 2 | 9.0234 | 15.5062 |
| 3 | 21.8909 | 14.3449 |
| 4 | 10.3382 | 13.9600 |
| 5 | 10.8371 | 18.0061 |
| 6 | 12.3777 | 20.0636 |
| 7 | 14.9227 | 15.4701 |
| 8 | 12.8980 | 15.0751 |
| 9 | 12.6057 | 10.1746 |
| 10 | 12.0425 | 9.0606 |
| Testing Number | Plot 1 Mass/kg | Plot 2 Mass/kg | Plot 3 Mass/kg | Plot 4 Mass/kg | Plot 5 Mass/kg | Plot 6 Mass/kg | Plot 7 Mass/kg | Plot 8 Mass/kg | Plot 9 Mass/kg | Plot 10 Mass/kg | Mean Mass/kg |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.48 | 4.20 | 3.95 | 4.15 | 4.31 | 4.26 | 4.19 | 4.20 | 4.49 | 4.37 | 4.260 |
| 2 | 4.29 | 4.36 | 4.31 | 4.21 | 4.05 | 3.94 | 4.35 | 4.15 | 4.19 | 4.28 | 4.213 |
| 3 | 4.13 | 4.06 | 3.93 | 4.34 | 4.37 | 4.45 | 4.09 | 4.06 | 4.25 | 4.30 | 4.198 |
| Testing Number | Soybean 1000-Grain Weight (Test One)/g | Soybean 1000-Grain Weight (Test Two)/g | Soybean 1000-Grain Weight (Test Three)/g |
|---|---|---|---|
| 1 | 262.58 | 274.61 | 265.12 |
| 2 | 267.40 | 262.10 | 267.03 |
| 3 | 274.32 | 264.51 | 264.35 |
| 4 | 263.21 | 271.21 | 269.33 |
| 5 | 269.85 | 265.37 | 271.61 |
| 6 | 271.56 | 261.44 | 274.00 |
| 7 | 264.79 | 265.34 | 264.55 |
| 8 | 268.51 | 261.55 | 261.94 |
| 9 | 264.91 | 262.07 | 262.16 |
| 10 | 263.33 | 262.43 | 264.44 |
| average value | 267.05 | 265.06 | 266.45 |
| Mass of a single grain/g | 0.26704 | 0.26506 | 0.26645 |
| Average mass of a single grain/g | 0.26619 | ||
| Testing Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Grains | 7 | 6 | 5 | 6 | 7 | 4 | 3 | 4 | 6 | 4 |
| Grain mass/g | 1.86333 | 1.59714 | 1.33095 | 1.59714 | 1.86333 | 1.06476 | 0.79857 | 1.06476 | 1.59714 | 1.06476 |
| Parts per thousand of the total mass/per thousand | 0.44 | 0.38 | 0.32 | 0.38 | 0.44 | 0.25 | 0.19 | 0.25 | 0.38 | 0.25 |
| Test One | Test Two | Test Three | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Testing Number | Grains | Grain Mass/g | Percentage of the Total Mass (%) | Grains | Grain Mass/g | Percentage of the Total Mass (%) | Grains | Grain Mass/g | Percentage of the Total Mass (%) |
| 1 | 253 | 67.34607 | 1.59 | 276 | 73.46844 | 1.74 | 263 | 70.00797 | 1.66 |
| 2 | 178 | 47.38182 | 1.12 | 253 | 67.34607 | 1.59 | 246 | 65.48274 | 1.55 |
| 3 | 234 | 62.28846 | 1.47 | 215 | 57.23085 | 1.35 | 223 | 59.36037 | 1.41 |
| 4 | 167 | 44.45373 | 1.05 | 246 | 65.48274 | 1.55 | 214 | 56.96466 | 1.35 |
| 5 | 154 | 40.99326 | 0.97 | 149 | 39.66231 | 0.94 | 193 | 51.37467 | 1.22 |
| 6 | 196 | 52.17324 | 1.24 | 198 | 52.70562 | 1.25 | 167 | 44.45373 | 1.05 |
| 7 | 264 | 70.27416 | 1.66 | 236 | 62.82084 | 1.49 | 284 | 75.59796 | 1.79 |
| 8 | 186 | 49.51134 | 1.17 | 225 | 59.89275 | 1.42 | 264 | 70.27416 | 1.66 |
| 9 | 177 | 47.11563 | 1.12 | 264 | 70.27416 | 1.66 | 219 | 58.29561 | 1.38 |
| 10 | 212 | 56.43228 | 1.34 | 173 | 46.05087 | 1.09 | 199 | 52.97181 | 1.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, S.; Li, B.; Liu, Y.; Tang, Z.; He, X.; Jing, J.; Zhou, W. Influence Mechanism and Optimal Design of Flexible Spring-Tooth Reel Mechanism for Soybean Pod-Shattering Reduction. Agriculture 2025, 15, 1378. https://doi.org/10.3390/agriculture15131378
Chen Y, Wang S, Li B, Liu Y, Tang Z, He X, Jing J, Zhou W. Influence Mechanism and Optimal Design of Flexible Spring-Tooth Reel Mechanism for Soybean Pod-Shattering Reduction. Agriculture. 2025; 15(13):1378. https://doi.org/10.3390/agriculture15131378
Chicago/Turabian StyleChen, Yuxuan, Shiguo Wang, Bin Li, Yang Liu, Zhong Tang, Xiaoying He, Jianpeng Jing, and Weiwei Zhou. 2025. "Influence Mechanism and Optimal Design of Flexible Spring-Tooth Reel Mechanism for Soybean Pod-Shattering Reduction" Agriculture 15, no. 13: 1378. https://doi.org/10.3390/agriculture15131378
APA StyleChen, Y., Wang, S., Li, B., Liu, Y., Tang, Z., He, X., Jing, J., & Zhou, W. (2025). Influence Mechanism and Optimal Design of Flexible Spring-Tooth Reel Mechanism for Soybean Pod-Shattering Reduction. Agriculture, 15(13), 1378. https://doi.org/10.3390/agriculture15131378







