Effects of Different Excitation Parameters on Mechanized Harvesting Performance and Postharvest Quality of First-Crop Organic Goji Berries in Saline–Alkali Land
Abstract
1. Introduction
2. Vibration Model
2.1. Modeling the Vibration of Fruit-Bearing Branches of Goji Berry
2.2. Determination of Vibration Model Parameters
3. Simulation Analysis
3.1. Simulation Parameters
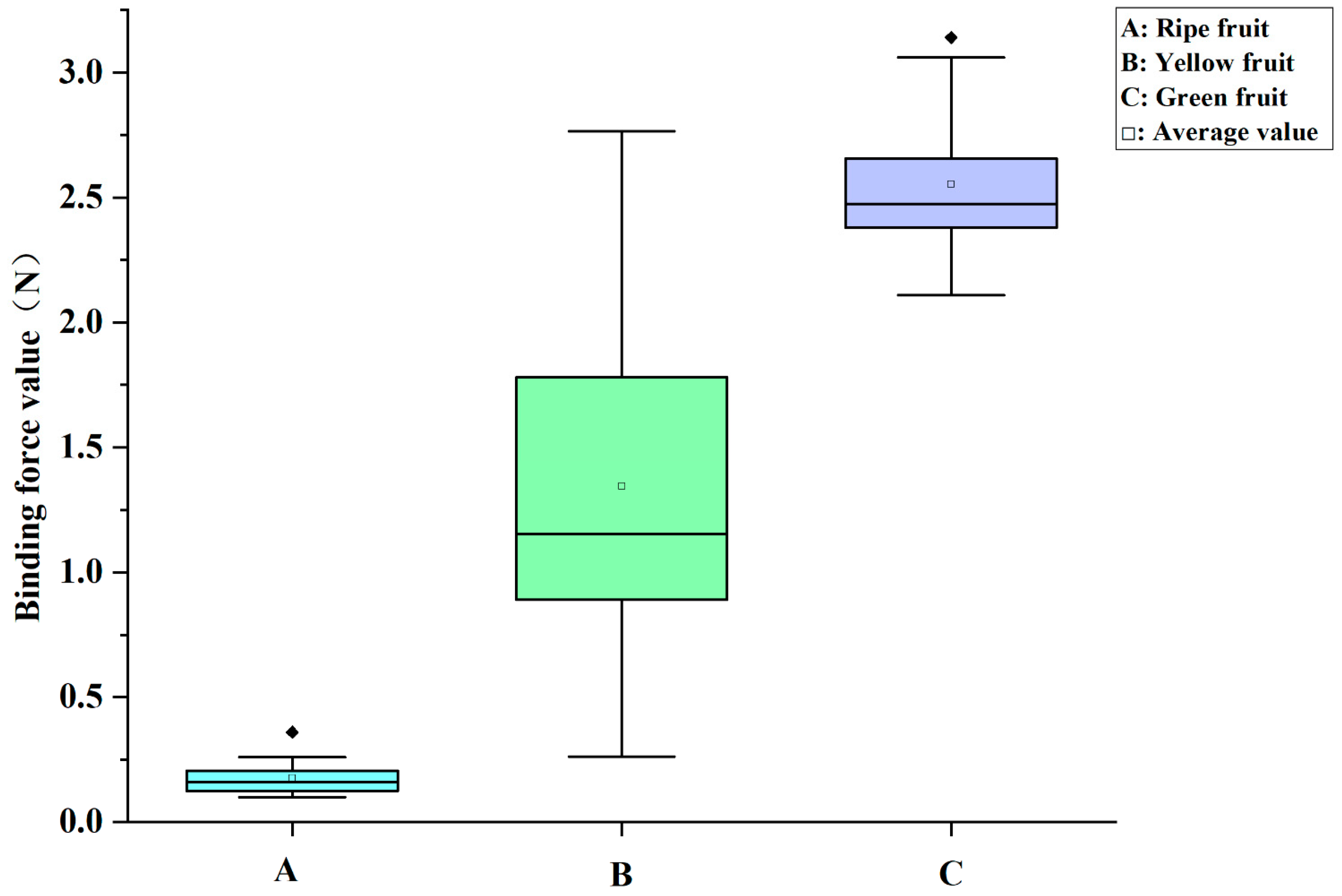
3.2. Determination of the Binding Capacity of Goji Berry
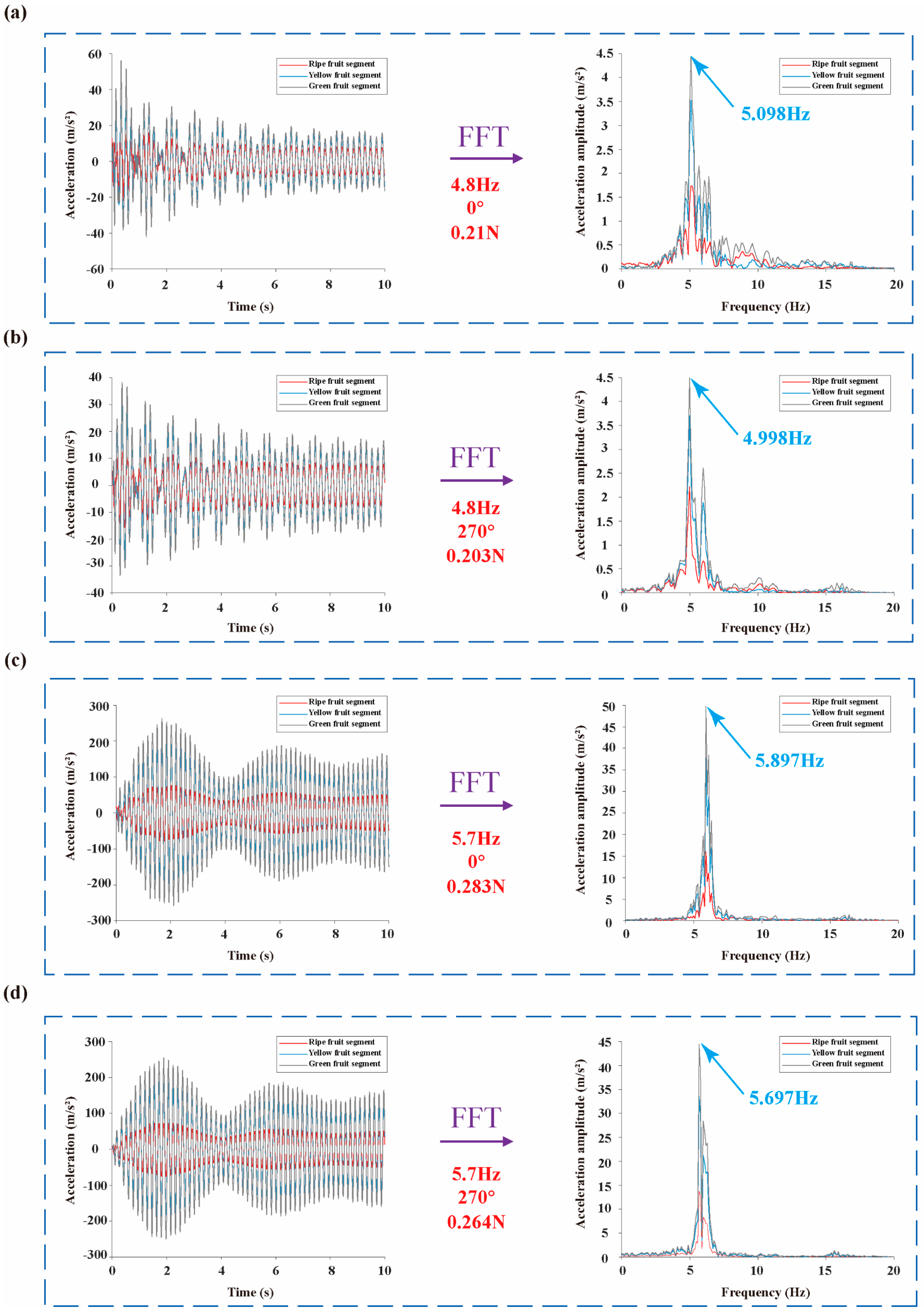
3.3. Analysis of Vibration Response Simulation Results
4. Vibration Experiment
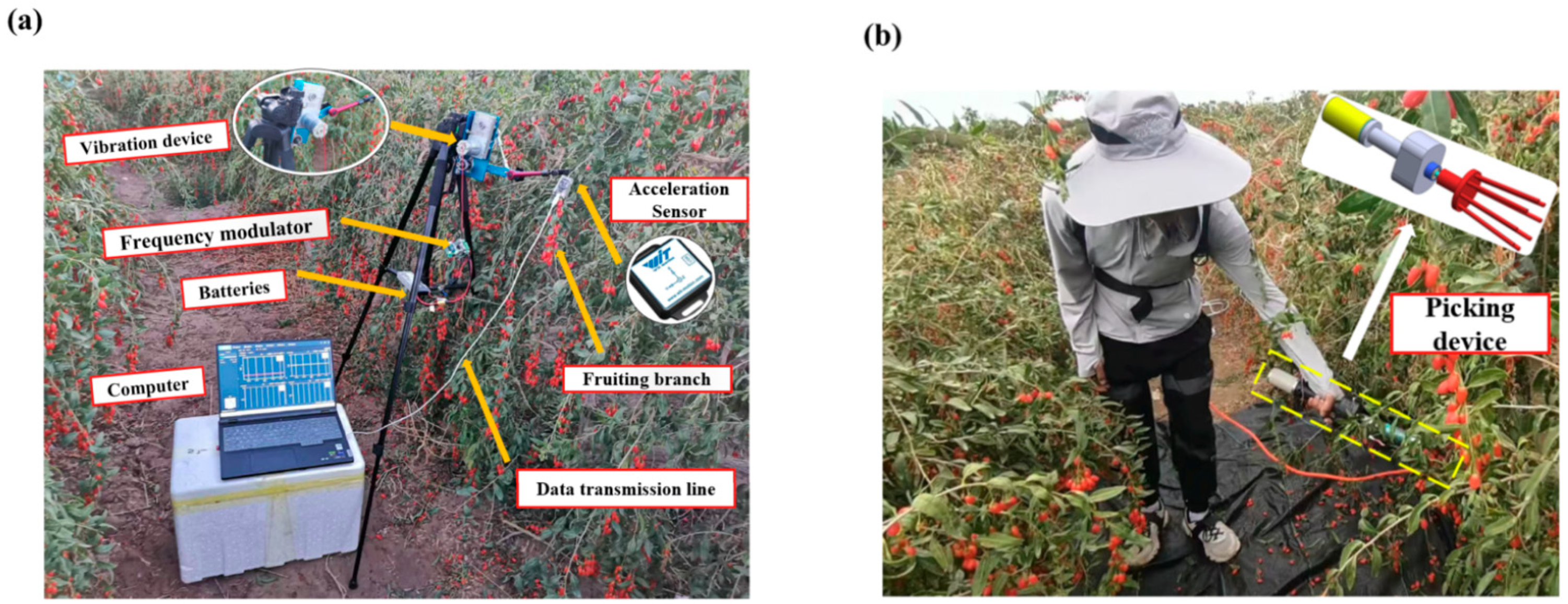
4.1. Design of the Experiment
4.2. Analysis of Regression Variance
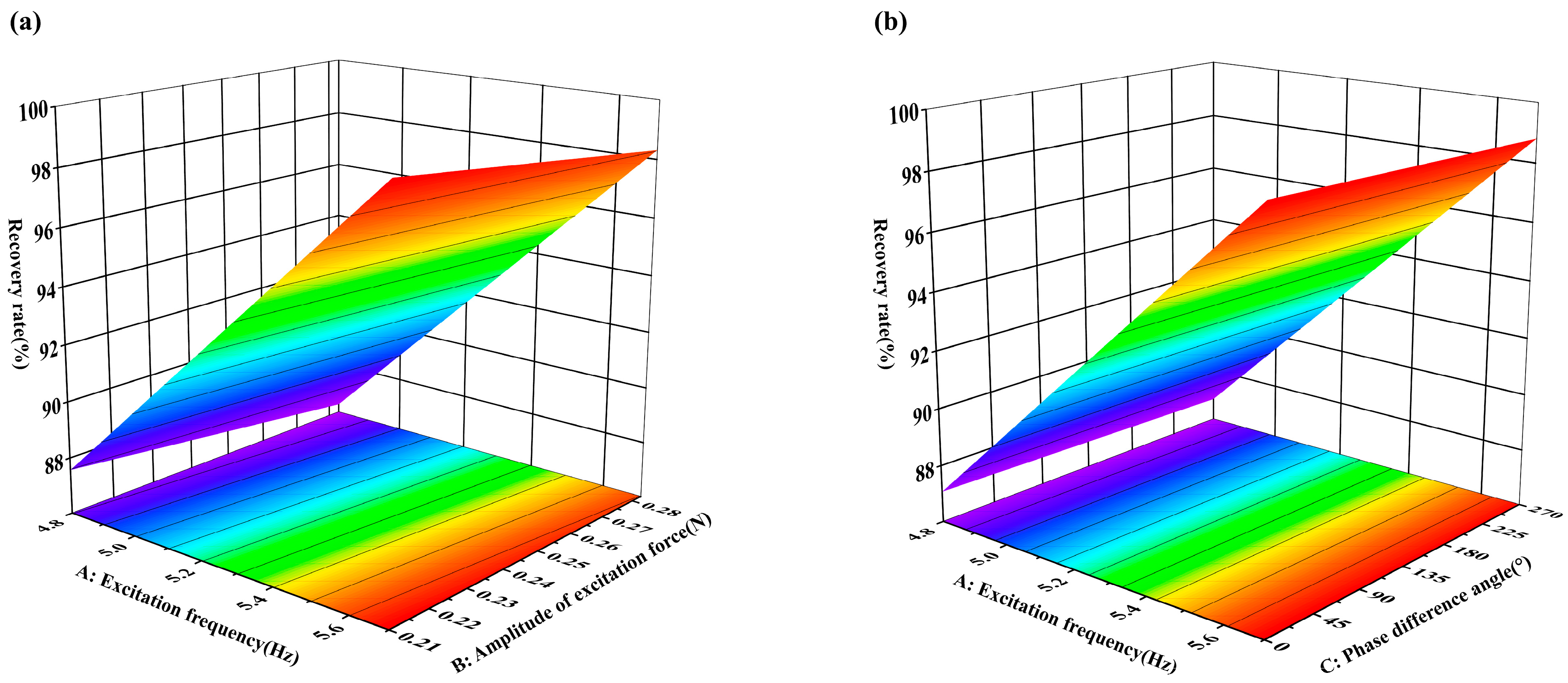
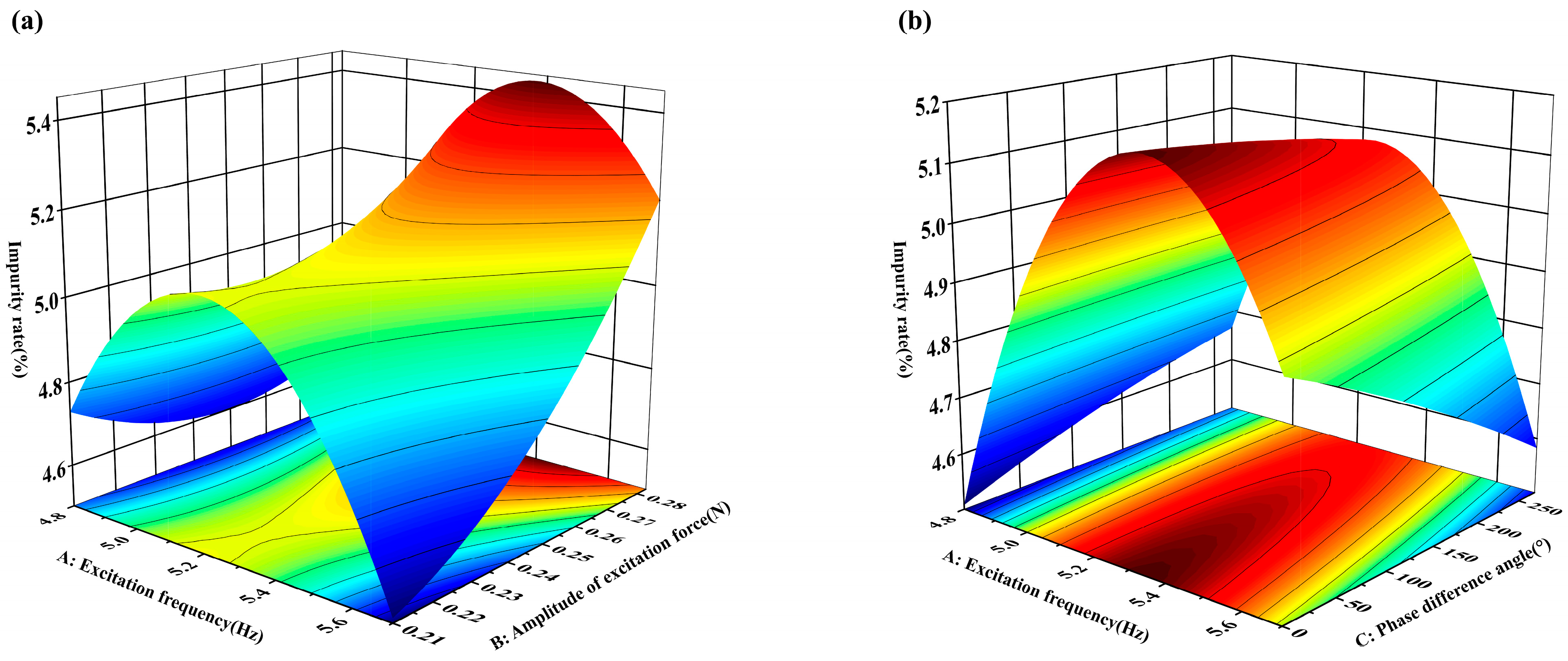
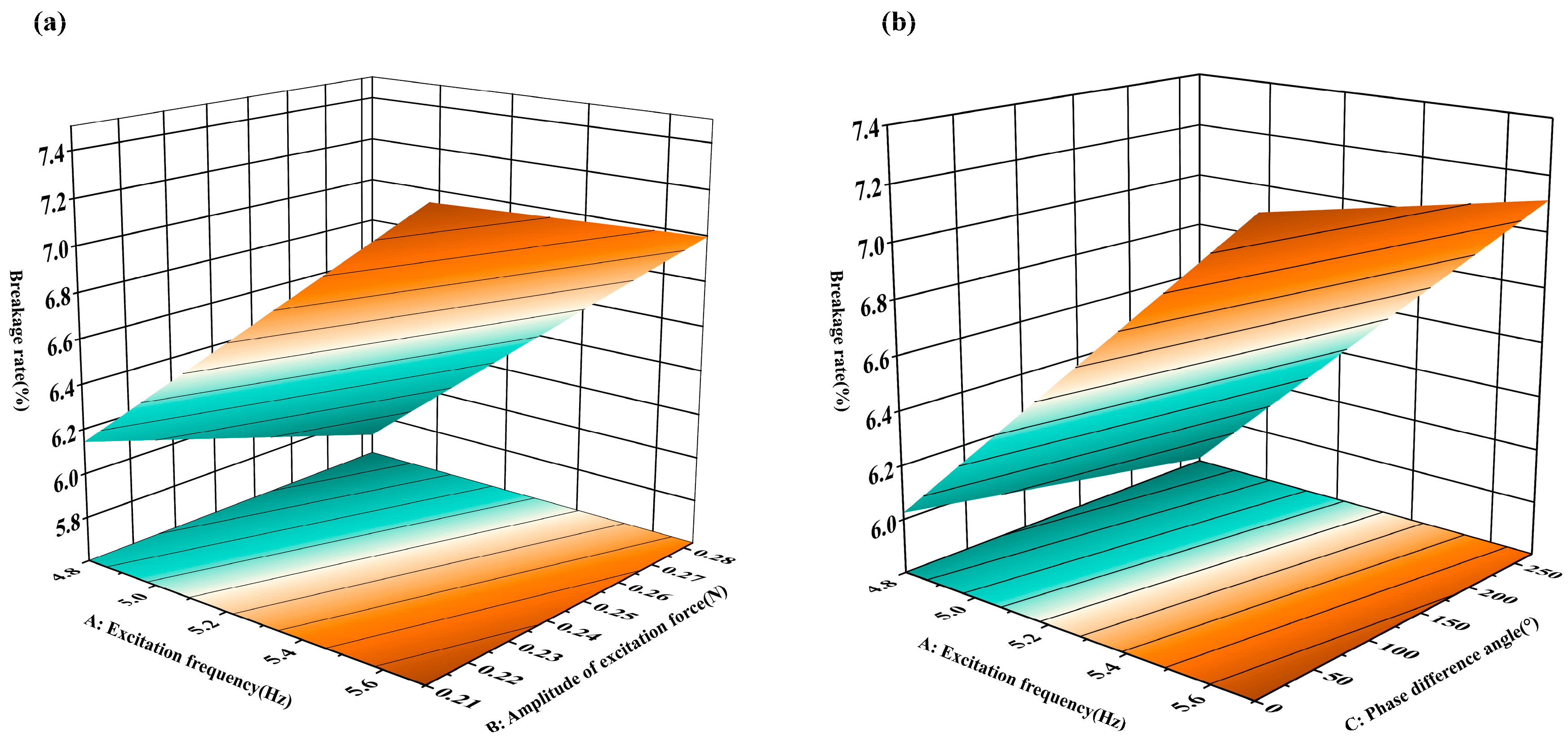
4.3. Response Surface Analysis
4.4. Optimization of Optimal Working Parameters
5. Field Trial Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- He, J.W.; Wang, T.S.; Yan, H.; Guo, S.; Hu, K.F.; Yang, X.C.; Ma, C.L.; Duan, J.A. Intelligent Identification Method of Geographic Origin for Chinese Wolfberries Based on Color Space Transformation and Texture Morphological Features. Foods 2023, 12, 2541. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, X.; Kong, H.; Zhang, D. Characterizing Aqueous Cd2+ Removal by Plant Biochars from Qinghai–Tibet Plateau. Water 2022, 14, 4085. [Google Scholar] [CrossRef]
- Peng, Q.; Huang, J.; Li, S.; Massou, B.B.; Chen, Z.; Zhu, Q.; Xie, G. Comprehensive origin authentication of wolfberry pulp (Lycium barbarum L.) using multimodal sensory analysis and chemometrics. Ind. Crops Prod. 2024, 219, 119023. [Google Scholar] [CrossRef]
- Wang, Y.J.; Liang, X.J.; Guo, S.J.; Li, Y.K.; Zhang, B.; Yin, Y.; An, W.; Cao, Y.L.; Zhao, J.H. Evaluation of nutrients and related environmental factors for wolfberry (Lycium barbarum L.) fruits grown in the different areas of China. Biochem. Syst. Ecol. 2019, 86, 103916. [Google Scholar] [CrossRef]
- Yin, W.X.; Zhang, C.; Zhu, H.Y.; Zhao, Y.R.; He, Y. Application of near-infrared hyperspectral imaging to discriminate different geographical origins of Chinese wolfberries. PLoS ONE 2017, 12, e0180534. [Google Scholar] [CrossRef]
- Yang, T.; Zhou, S.X.; Fang, S.T.; Qin, W.Y.; Inman, D.J. Nonlinear vibration energy harvesting and vibration suppression technologies: Designs, analysis, and applications. Appl. Phys. Rev. 2021, 8, 031317. [Google Scholar] [CrossRef]
- Polat, M.; Mertoglu, K.; Eskimez, I.; Okatan, V. Effects of the fruiting period and growing seasons on market quality in goji berry (Lycium barbarum L.). Folia Hortic. 2020, 32, 229–239. [Google Scholar] [CrossRef]
- Bolat, F.C.; Sugec, A.; Ozdemir, A. Design, numerical analysis and experiments of different types auxetic beams for vibration based energy harvester. Mech. Syst. Signal. Process. 2024, 210, 111170. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, J.; Hu, G.; Chen, J. Design and testing of a pneumatic oscillating Chinese wolfberry harvester. Horticulturae 2021, 7, 214. [Google Scholar] [CrossRef]
- So, J. Vibration characteristics of boxthorn (Lycium chinense Mill) branches. Appl. Eng. Agric. 2001, 17, 755. [Google Scholar] [CrossRef]
- So, J. Vibratory harvesting machine for boxthorn (Lycium chinense Mill) berries. Trans. ASAE 2003, 46, 211. [Google Scholar] [CrossRef]
- Jinpeng, W.; Song, M.; Hongru, X.; Ying, Z.; Hongping, Z. Research on mechanized harvesting methods of Lycium barbarum fruit. IFAC-Pap. 2018, 51, 223–226. [Google Scholar] [CrossRef]
- Tang, X.; Ren, J.; Liu, C.; Xiao, D. Simulation of vibration harvesting mechanism for wolfberry. Am. Soc. Agric. Biol. Eng. 2011, 1. [Google Scholar] [CrossRef]
- Zhao, J.; Tsuchikawa, S.; Ma, T.; Hu, G.; Chen, Y.; Wang, Z.; Chen, Q.; Gao, Z.; Chen, J. Modal analysis and experiment of a Lycium barbarum L. Shrub for efficient vibration harvesting of fruit. Agriculture 2021, 11, 519. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, J.; Chen, Q.Y.; Chen, J. Simulation for Fitting the Bending Shape of Fruit Branches of Based on the Finite Element Method. Horticulturae 2021, 7, 434. [Google Scholar] [CrossRef]
- Mei, S.; Wang, J.P.; Song, Z.Y.; Tang, D.B.; Shen, C. Mechanism and experimental study on the fruit detachment of Chinese wolfberry through reciprocating vibration. Int. J. Agr. Biol. Eng. 2024, 17, 47–58. [Google Scholar] [CrossRef]
- Zhuo, P.; Li, Y.X.; Jiao, H.B.; Wang, P.; Li, C.S.; Niu, Q.; Wang, L.H. Analysis and experimental study on vibration response characteristics of mechanical harvesting of jujube. Comput. Electron. Agr. 2022, 203, 107446. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, L.Y.; Zhang, A.Q.; Hang, X.C. Finite element explicit dynamics simulation of motion and shedding of jujube fruits under forced vibration. Comput. Electron. Agr. 2022, 198, 107009. [Google Scholar] [CrossRef]
- Hu, Y.; Zheng, Z.; Yu, C.; Feng, J.; Qiao, Y. Vibration response characteristics of Jujube trees based on finite element method and structure-from-motion. Sci. Hortic. 2024, 331, 113125. [Google Scholar] [CrossRef]
- Cao, J.; An, J.; Xu, D.; Bai, X.; Li, W.; Chen, C. Test and analysis of walnut (Juglans regia L.) tree vibration transfer based on a low-frequency shaking table. Ind. Crops Prod. 2024, 216, 118797. [Google Scholar] [CrossRef]
- Cao, J.; Bai, X.; Xu, D.; Li, W.; Chen, C. Experiment and analysis on walnut (Juglans regia L.) Shedding force based on low-frequency vibration response. Ind. Crops Prod. 2023, 204, 117242. [Google Scholar] [CrossRef]
- Wang, Y.F.; Wang, W.Z.; Fu, H.; Yang, Z.; Lu, H.Z. Detachment patterns and impact characteristics of litchi fruit during vibrational harvesting. Sci. Hortic. 2022, 295, 110836. [Google Scholar] [CrossRef]
- Du, X.; Shen, T.; Zhao, L.; Zhang, G.; Hu, A.; Fang, S.; Cao, Y.; Yao, X. Design and experiment of the comb-brush harvesting machine with variable spacing for oil-tea camellia fruit. Int. J. Agr. Biol. Eng. 2021, 14, 172–177. [Google Scholar] [CrossRef]
- Lyu, X.; Wang, H.; Xu, G.; Chu, C. Research on fruit picking test of blueberry harvesting machinery under transmission clearance. Heliyon 2024, 10, e34740. [Google Scholar] [CrossRef] [PubMed]
- Hou, J.M.; Hu, W.X.; Wang, W.; Zhu, H.J.; Zhi, R.D. Fruit Vibration Harvesting Technology and Its Damage. A Review. Inmateh-Agric. Eng. 2021, 63, 155–168. [Google Scholar] [CrossRef]
- Jin, Y.; Hou, S.A.; Yang, T.Z. Cascaded essential nonlinearities for enhanced vibration suppression and energy harvesting. Nonlinear. Dynam. 2021, 103, 1427–1438. [Google Scholar] [CrossRef]
- Liu, C.Y.; Xu, D.C.; Cao, J.L. Vibration Response of Walnuts under Vibration Harvesting. Agronomy 2023, 13, 461. [Google Scholar] [CrossRef]
- Sun, X.D.; Wu, W.D.; Cao, C.M.; Xu, L.Y.; Jiang, R.; Fang, L.F.; Sheng, Z.L.; Lu, X.Y. Research on vibration response characteristics and separation deformation law of fruit-branch system. Aip. Adv. 2023, 13, 065306. [Google Scholar] [CrossRef]
- Ferreira, L.D.; da Silva, F.M.; Ferreira, D.D.; de Souza, C.E.P.; Pinto, A.W.M.; Borges, F.E.D. Dynamic behavior of coffee tree branches during mechanical harvest. Comput. Electron. Agr. 2020, 173, 105415. [Google Scholar] [CrossRef]
- Delin, W.; Enlong, Z.; Shan, J.; Weiwei, W.; Jiahao, Y.; Kui, W. Optimization and Experiment of Canopy Vibration Parameters of Camellia oleifera Based on Energy Transfer Characteristics. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2022, 53, 23–33. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, L.; Zhang, Y.; Zhu, Y.; Zhou, H.; Cui, W.; Zhang, A. Study of vibration patterns and response transfer relationships in walnut tree trunks. Sci. Hortic. 2024, 337, 113567. [Google Scholar] [CrossRef]
- Xuan, Y.; Xu, L.; Liu, G.; Zhou, J. The vibrational response of simulated Ginkgo biloba fruit based on their frequency spectrum characteristics. PLoS ONE 2020, 15, e0235494. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Chen, X. The Phenomenon of Bistable Phase Difference Intervals in the Times-Frequency Vibration Synchronization System Driven by Two Homodromy Exciters. Math. Probl. Eng. 2020, 2020, 1430531. [Google Scholar] [CrossRef]
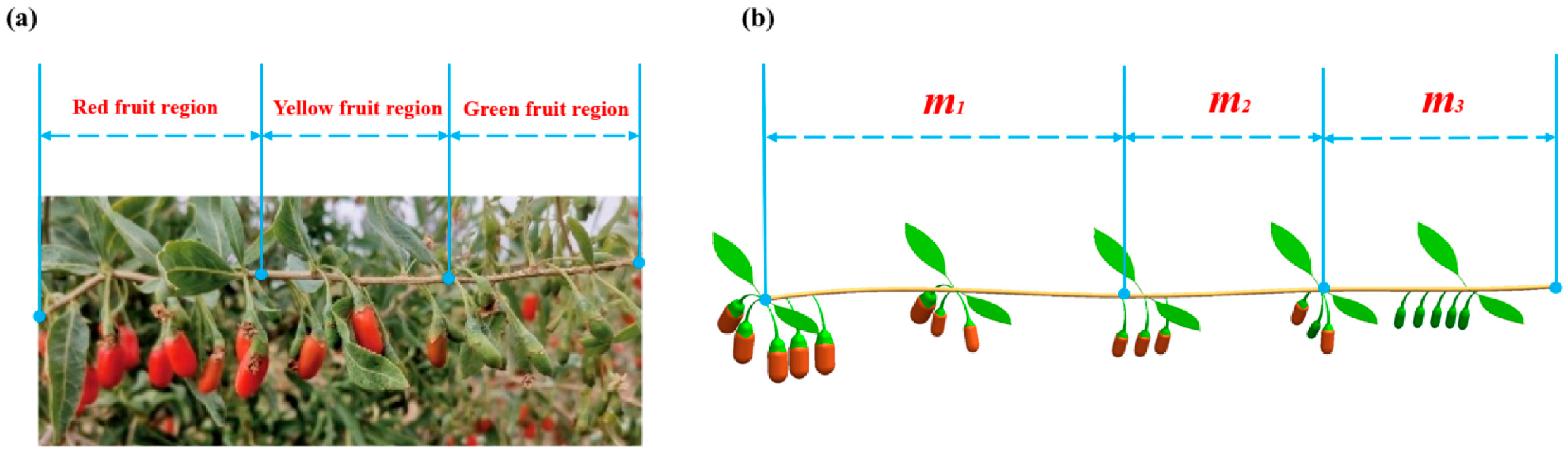
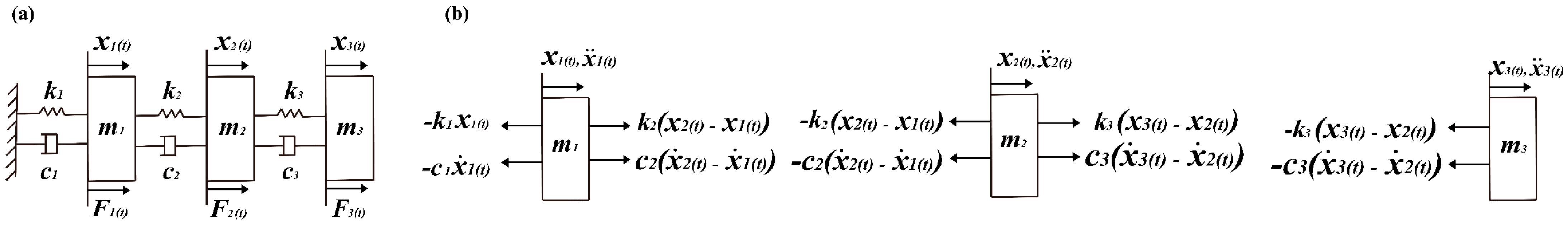

| Name | Ripe Fruit Segment | Yellow Fruit Segment | Green Fruit Segment |
|---|---|---|---|
| Mass | |||
| Damping | |||
| Stiffness | |||
| Displacement | |||
| Excitation force |
| Excitation Point | Equivalent Mass (Kg) | Equivalent Damping (Ns/m) | Equivalent Stiffness (N/m) |
|---|---|---|---|
| Ripe fruit segment | 0.093 | 0.2 | 284.03 |
| Yellow fruit segment | 0.025 | 0.01 | 87 |
| Green fruit segment | 0.011 | 0.01 | 58 |
| Excitation Point | Excitation Frequency (Hz) | Phase Angle (°) | Amplitude of Excitation Force (N) |
|---|---|---|---|
| Ripe fruit segment | 4.8 | 0 | 0.21 |
| 4.8 | 90 | 0.203 | |
| 4.8 | 180 | 0.21 | |
| 4.8 | 270 | 0.203 | |
| 5.7 | 0 | 0.283 | |
| 5.7 | 90 | 0.264 | |
| 5.7 | 180 | 0.283 | |
| 5.7 | 270 | 0.264 | |
| Yellow fruit segment | 4.8 | 0 | 0.23 |
| 4.8 | 90 | 0.21 | |
| 4.8 | 180 | 0.23 | |
| 4.8 | 270 | 0.21 | |
| 5.7 | 0 | 0.3 | |
| 5.7 | 90 | 0.27 | |
| 5.7 | 180 | 0.3 | |
| 5.7 | 270 | 0.27 | |
| Green fruit segment | 4.8 | 0 | 0.67 |
| 4.8 | 90 | 0.64 | |
| 4.8 | 180 | 0.67 | |
| 4.8 | 270 | 0.64 | |
| 5.7 | 0 | 0.67 | |
| 5.7 | 90 | 0.64 | |
| 5.7 | 180 | 0.67 | |
| 5.7 | 270 | 0.64 |
| Experiment No. | Influencing Factor | Evaluation Indicators | ||||
|---|---|---|---|---|---|---|
| Excitation Frequency A (Hz) | Amplitude of Excitation Force B (N) | Phase Angle C (°) | Recovery Rate Y1 (%) | Impurity Rate Y2 (%) | Breakage Rate Y3 (%) | |
| 1 | 5.25 | 0.283 | 270 | 89 | 5.47 | 5.84 |
| 2 | 5.25 | 0.2465 | 135 | 90 | 5.39 | 5.73 |
| 3 | 4.8 | 0.21 | 135 | 83 | 4.66 | 5.67 |
| 4 | 5.25 | 0.2465 | 135 | 91 | 5.13 | 6.69 |
| 5 | 5.25 | 0.21 | 0 | 94 | 5.21 | 6.98 |
| 6 | 5.25 | 0.283 | 0 | 92 | 5.19 | 6.91 |
| 7 | 4.8 | 0.283 | 135 | 87 | 4.73 | 5.73 |
| 8 | 4.8 | 0.2465 | 270 | 89 | 4.62 | 5.81 |
| 9 | 5.7 | 0.283 | 135 | 100 | 5.27 | 7.12 |
| 10 | 4.8 | 0.2465 | 0 | 90 | 4.58 | 6.67 |
| 11 | 5.25 | 0.2465 | 135 | 95 | 5.03 | 6.72 |
| 12 | 5.7 | 0.2465 | 0 | 98 | 4.93 | 6.59 |
| 13 | 5.25 | 0.21 | 270 | 96 | 5.02 | 7.01 |
| 14 | 5.25 | 0.2465 | 135 | 97 | 4.82 | 5.64 |
| 15 | 5.7 | 0.21 | 135 | 100 | 4.47 | 7.73 |
| 16 | 5.7 | 0.2465 | 270 | 99 | 4.51 | 7.64 |
| 17 | 5.25 | 0.2465 | 135 | 90 | 5.28 | 7.19 |
| Source | Square Sum | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Mold | 291.25 | 3 | 97.08 | 12.92 | 0.0003 |
| A | 288.00 | 1 | 288.00 | 38.32 | <0.0001 (significant) |
| B | 3.13 | 1 | 3.13 | 0.42 | 0.5302 |
| C | 0.13 | 1 | 0.13 | 0.017 | 0.8994 |
| Residual | 97.69 | 13 | 7.51 | ||
| Lack of Fit | 56.49 | 9 | 6.28 | 0.61 | 0.7536 (not significant) |
| Pure Error | 41.2 | 4 | 10.30 | ||
| Cor Total | 388.94 | 16 |
| Source | Square Sum | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Mold | 1.41 | 9 | 0.16 | 4.4 | 0.0317 (significant) |
| A | 0.044 | 1 | 0.044 | 1.22 | 0.3058 |
| B | 0.21 | 1 | 0.21 | 5.93 | 0.0451 |
| C | 0.011 | 1 | 0.011 | 0.29 | 0.6039 |
| AB | 0.13 | 1 | 0.13 | 3.74 | 0.0945 |
| AC | 0.053 | 1 | 0.053 | 1.48 | 0.2626 |
| BC | 0.055 | 1 | 0.055 | 1.55 | 0.2533 |
| A2 | 0.87 | 1 | 0.87 | 24.45 | 0.0017 |
| B2 | 0.049 | 1 | 0.049 | 1.37 | 0.2809 |
| C2 | 0.0009474 | 1 | 0.0009474 | 0.027 | 0.8751 |
| Residual | 0.25 | 7 | 0.036 | ||
| Lack of Fit | 0.053 | 3 | 0.018 | 0.36 | 0.7847 (not significant) |
| Pure Error | 0.2 | 4 | 0.049 | ||
| Cor Total | 1.66 | 16 |
| Source | Square Sum | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Mold | 3.87 | 3 | 1.29 | 4.16 | 0.0285 (significant) |
| A | 3.38 | 1 | 3.38 | 10.91 | 0.0057 |
| B | 0.40 | 1 | 0.40 | 1.29 | 0.2761 |
| C | 0.090 | 1 | 0.090 | 0.29 | 0.5984 |
| Residual | 4.03 | 13 | 0.31 | ||
| Lack of Fit | 2.19 | 9 | 0.24 | 0.53 | 0.8029 (not significant) |
| Pure Error | 1.84 | 4 | 0.46 | ||
| Cor Total | 7.9 | 16 |
| Number of Groups | Recovery Rate (%) | Impurity Rate (%) | Breakage Rate (%) |
|---|---|---|---|
| 1 | 92.86 | 5.17 | 7.69 |
| 2 | 98.41 | 6.44 | 9.68 |
| 3 | 97.06 | 4.83 | 10.61 |
| 4 | 100 | 5.30 | 6.58 |
| 5 | 98.04 | 4.84 | 8 |
| 6 | 94.59 | 4.95 | 8.57 |
| 7 | 98.28 | 4.03 | 7.02 |
| 8 | 91.53 | 4.65 | 7.41 |
| 9 | 100 | 6.17 | 6.76 |
| 10 | 98.61 | 4.79 | 8.45 |
| 11 | 98.55 | 5.33 | 5.88 |
| 12 | 100 | 4.87 | 5.77 |
| 13 | 97.14 | 4.96 | 8.82 |
| 14 | 96.72 | 4.12 | 6.78 |
| 15 | 97.26 | 4.58 | 7.04 |
| 16 | 96.77 | 4.60 | 6.67 |
| 17 | 100 | 4.41 | 8.77 |
| 18 | 98.53 | 4.90 | 10.45 |
| 19 | 98.63 | 6.30 | 8.33 |
| 20 | 98.53 | 7.20 | 5.97 |
| Average value (%) | 97.58 | 5.12 | 7.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, J.; Zhao, J.; Wang, F.; Zhang, H.; Su, X.; Sun, Y.; Liu, J.; Zhao, D. Effects of Different Excitation Parameters on Mechanized Harvesting Performance and Postharvest Quality of First-Crop Organic Goji Berries in Saline–Alkali Land. Agriculture 2025, 15, 1377. https://doi.org/10.3390/agriculture15131377
Liu Y, Liu J, Zhao J, Wang F, Zhang H, Su X, Sun Y, Liu J, Zhao D. Effects of Different Excitation Parameters on Mechanized Harvesting Performance and Postharvest Quality of First-Crop Organic Goji Berries in Saline–Alkali Land. Agriculture. 2025; 15(13):1377. https://doi.org/10.3390/agriculture15131377
Chicago/Turabian StyleLiu, Yuchuang, Jiahui Liu, Jian Zhao, Fanyu Wang, Hongye Zhang, Xiaokang Su, Yichun Sun, Jia Liu, and Dong Zhao. 2025. "Effects of Different Excitation Parameters on Mechanized Harvesting Performance and Postharvest Quality of First-Crop Organic Goji Berries in Saline–Alkali Land" Agriculture 15, no. 13: 1377. https://doi.org/10.3390/agriculture15131377
APA StyleLiu, Y., Liu, J., Zhao, J., Wang, F., Zhang, H., Su, X., Sun, Y., Liu, J., & Zhao, D. (2025). Effects of Different Excitation Parameters on Mechanized Harvesting Performance and Postharvest Quality of First-Crop Organic Goji Berries in Saline–Alkali Land. Agriculture, 15(13), 1377. https://doi.org/10.3390/agriculture15131377






