Design and Experimental Evaluation of a Rotary Knife-Type Device for Chopping Film-Mixed Residues

Abstract

To address the resource utilization challenges of residual plastic film in Xinjiang and the issues of low reliability, poor cutting length qualification rates, and high energy consumption in existing film-mixed residue choppers, a rotary knife-type mixed film residue chopper was designed based on the “single support cutting + sliding cutting” principle. The device primarily consists of an adaptive feeding mechanism, a chopping mechanism, and a transmission system. The main structural and motion parameters of the mechanisms were determined through the analysis of feeding and chopping conditions. The primary factors affecting the cotton stalk chopping length qualification rate (CLCR-CS), residual film chopping length qualification rate (CFCR-RF), and specific energy consumption (SEC) were identified as the feeding roller speed, chopper speed, and the gap between the moving and fixed blades. Vibration characteristic analysis of the chopper was conducted using ANSYS software. The first six natural frequencies of the chopper were found to range from 112.54 to 186.65 Hz, with maximum deformation ranging from 0.885 to 1.237 mm. The excitation frequency was significantly lower than the first natural frequency, ensuring that the chopper met reliability and operational performance standards. A prototype was fabricated, and a second-order rotational orthogonal experiment was performed with CLCR-CS, CFCR-RF, and SEC as the test indicators and feeding roller speed, chopper speed, and the gap between the moving and fixed blades as the experimental factors. Variance and response surface analyses were conducted using Design-Expert software to clarify the effects and interactions of experimental factors on the test indicators. The second-order polynomial response surface model was optimized, and the optimal factor values were derived based on practical operational conditions. Verification experiments confirmed that the optimal operating parameters were a feeding roller speed of 32.40 r/min, a chopper speed of 222.0 r/min, and a blade gap of 1.0 mm. Under these conditions, CLCR-CS was 89.96%, CFCR-RF was 91.62%, and SEC was 5.36 kJ/kg, meeting the design specifications of the mixed film residue chopper.

1. Introduction

In 2024, the cotton planting area in Xinjiang was approximately 35.5 million acres, representing 84.8% of the total cotton planting area in China [1]. Cotton in Xinjiang is grown with plastic film mulch, with an estimated usage of 112,400 tons of plastic film. However, delayed recovery of this film has led to severe plastic film residue pollution in the region [2]. Although the development of plastic film residue recovery machinery has significantly alleviated this issue, improper handling of the mixed film residues after recovery can still cause secondary environmental pollution [3,4]. Resource utilization of these residues is the primary solution to prevent secondary pollution from plastic film residues. However, due to the entanglement of cotton stalks with the soft, coiled plastic film in the mixed residues, achieving resource utilization requires effective shredding and separation of the mixed film residues [5].

In recent years, research on mixed film residue chopping technology has expanded. Pan et al. [6] developed a V-type moving knife mixed film residue chopping device, analyzing the structural characteristics and working principles of the V-type knife. Through experimental testing, the optimal working parameters and chopping performance of the device were determined. Liang et al. [7] designed a multi-blade toothed knife mixed film residue chopping device and established relationships between the working parameters, chopping performance, and specific energy consumption. Guo et al. [8] developed a sliding-cut knife mixed film residue chopping device, optimizing key parameters to determine the best structural configuration. Yuan et al. [9] proposed a new method for cyclone sedimentation and film filtration under negative pressure transport, revealing the correlation between the shear separation device’s working parameters and the qualified chopped film rate. Yan et al. [10] introduced a two-step shredding process for mixed film residues, which involves breaking the bales first, followed by crushing. They designed a multi-stage crusher for mixed film residue bales, achieving a crushing qualification rate of 75.15%. Despite advances in mixed film residue chopping technology, common challenges such as low reliability (e.g., material jamming and shaft entanglement), low chopping length qualification rates, and high specific energy consumption persist, hindering the effective resource utilization of plastic film residues. Therefore, exploring new mixed film residue chopping technologies and optimizing the structure of key components to enhance performance is critical.

This paper presents the design of a rotary knife-type mixed film residue chopping device based on the “single support cutting + sliding cutting” principle. The study focuses on the structure and working parameters of two key components: the feeding mechanism and the chopping mechanism. The interactions between these key structures and working parameters, and their impact on chopping length qualification rates and specific energy consumption, are analyzed. The paper also validates the optimized parameter combinations and the chopping performance under these optimal conditions, aiming to provide theoretical insights and technical support for the development of mixed film residue chopping technology.

2. Materials and Methods

2.1. Machine Structure and Working Principle

2.1.1. Machine Structure

The rotary knife-type film-mixed residue chopping device consists primarily of an adaptive feeding mechanism, a chopping mechanism, a transmission system, and a frame. The adaptive feeding mechanism includes a conveyor belt, feeding components, and a gap adjustment system. The feeding components are positioned above the conveyor belt and connected to the rear of the chopping mechanism. The overall structure of the device is shown in Figure 1a.

2.1.2. Working Principle and Technical Parameters

As shown in Figure 1b, during operation, all motors are activated, and the mixed film residues are loaded onto the conveyor belt. Upon reaching the feeding mechanism, the feeding roller evenly and smoothly feeds the fluctuating, large-volume mixed film residues into the chopping mechanism, effectively addressing material jamming in the chopping chamber caused by fluctuations in the feeding rate. Simultaneously, the feeding roller compresses the mixed film residues and exerts positive pressure. The rotary knife chopper rotates rapidly, with the moving and fixed blades operating in unison. Under the positive pressure from the feeding roller, the “single support cutting + sliding cutting” principle is applied to chop the mixed film residues. The chopped mixed film residues, meeting the required length, pass through the screen under the combined effect of airflow and centrifugal force generated by the rotation of the chopper. Any mixed film residues not meeting the length requirements are repeatedly sheared by the fixed blade in the chopping chamber, thus completing the chopping operation. The main design parameters of the device are summarized in

Table 1. Main parameters of device.

Parameters	Value
Structure size (length × width × height) (mm)	4810 × 1240 × 2450
Productivity (kg·h−1)	600
Working width(mm)	800
Matched power of chopping mechanism (kW)	18.5
Matched power of feeding mechanism (kW)	5.0
Matched power of conveyor belt (kW)	1.5
Conveying speed (m·s−1)	0.2
Feeding roller speed (r·min−1)	25–40
Gap between moving and fixed blades (mm)	0.5–2.0
Chopping roller speed (r·min−1)	120–320

.

2.2. Design and Analysis of Key Components

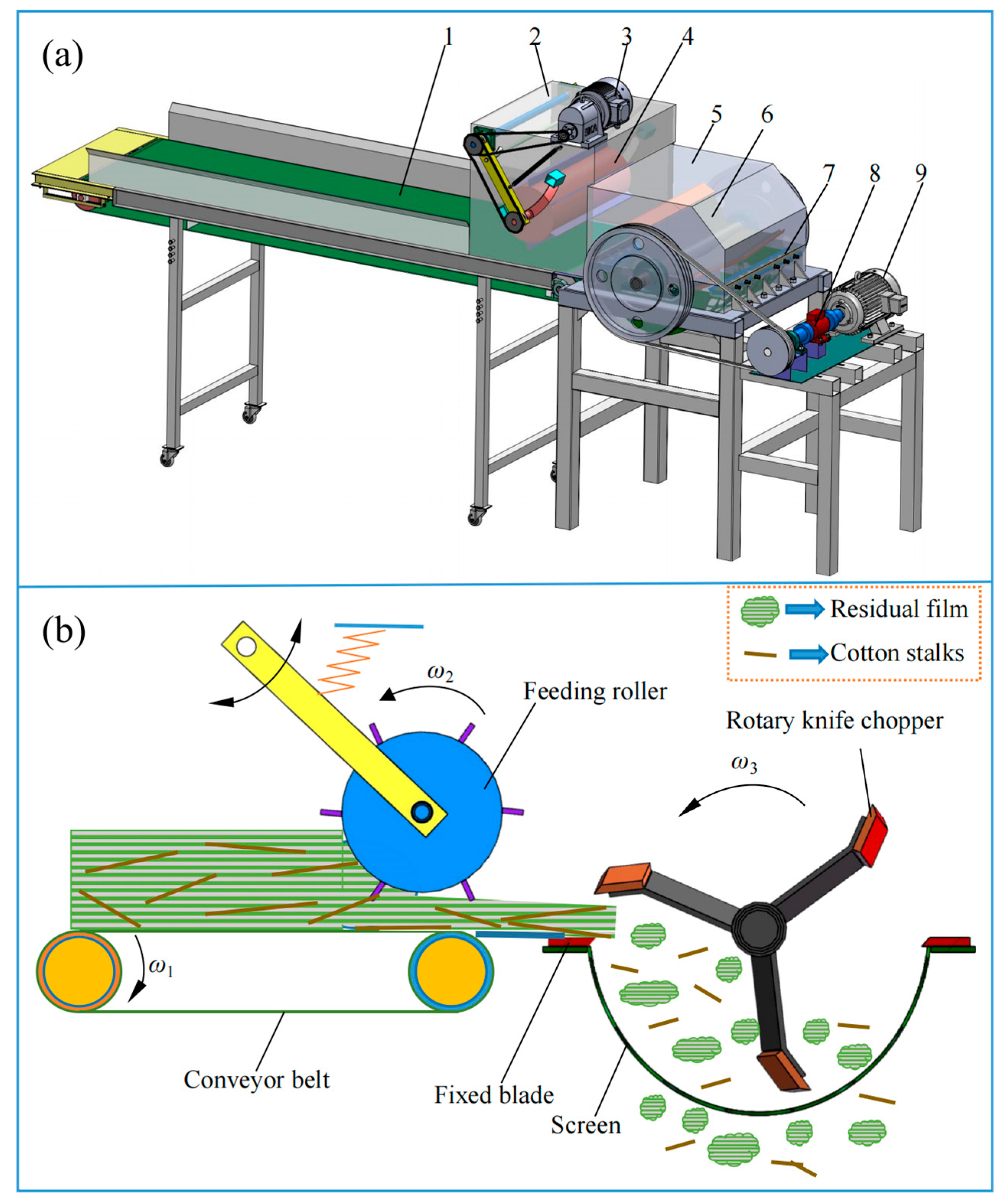
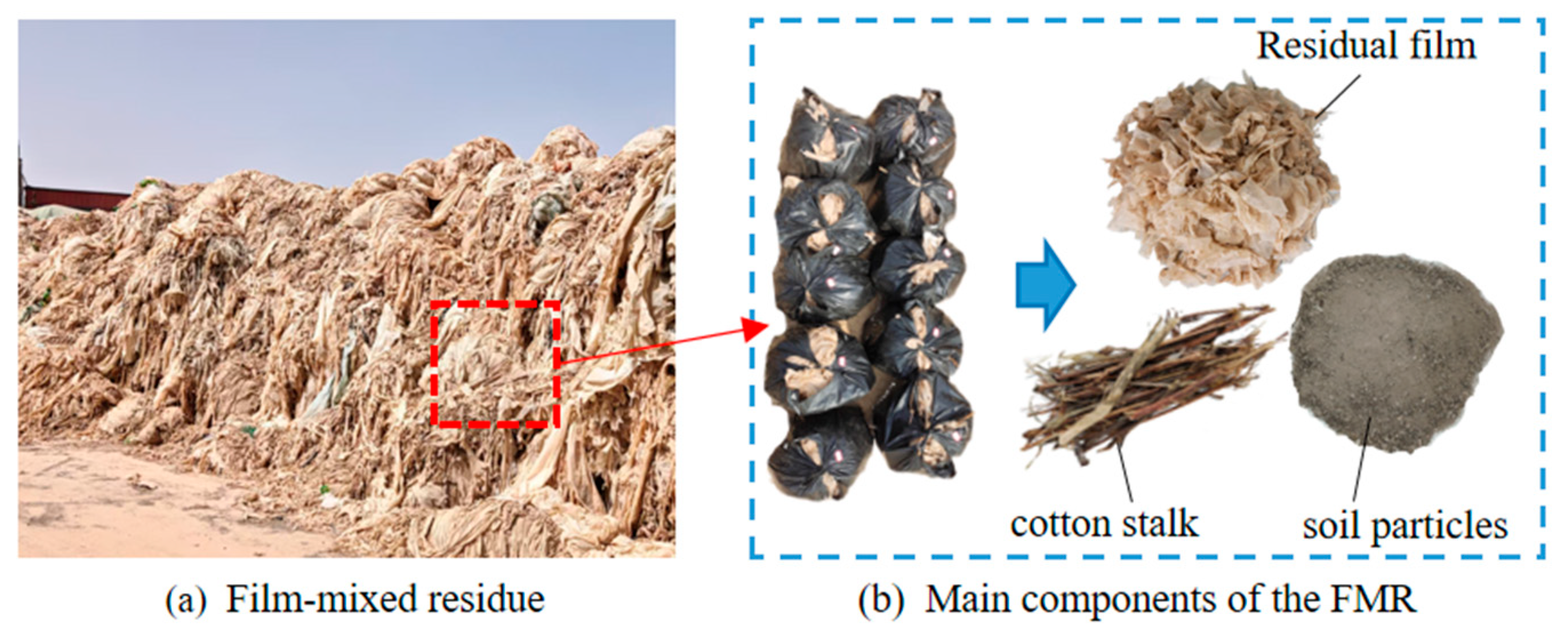
2.2.1. Adaptive Feeding Mechanism

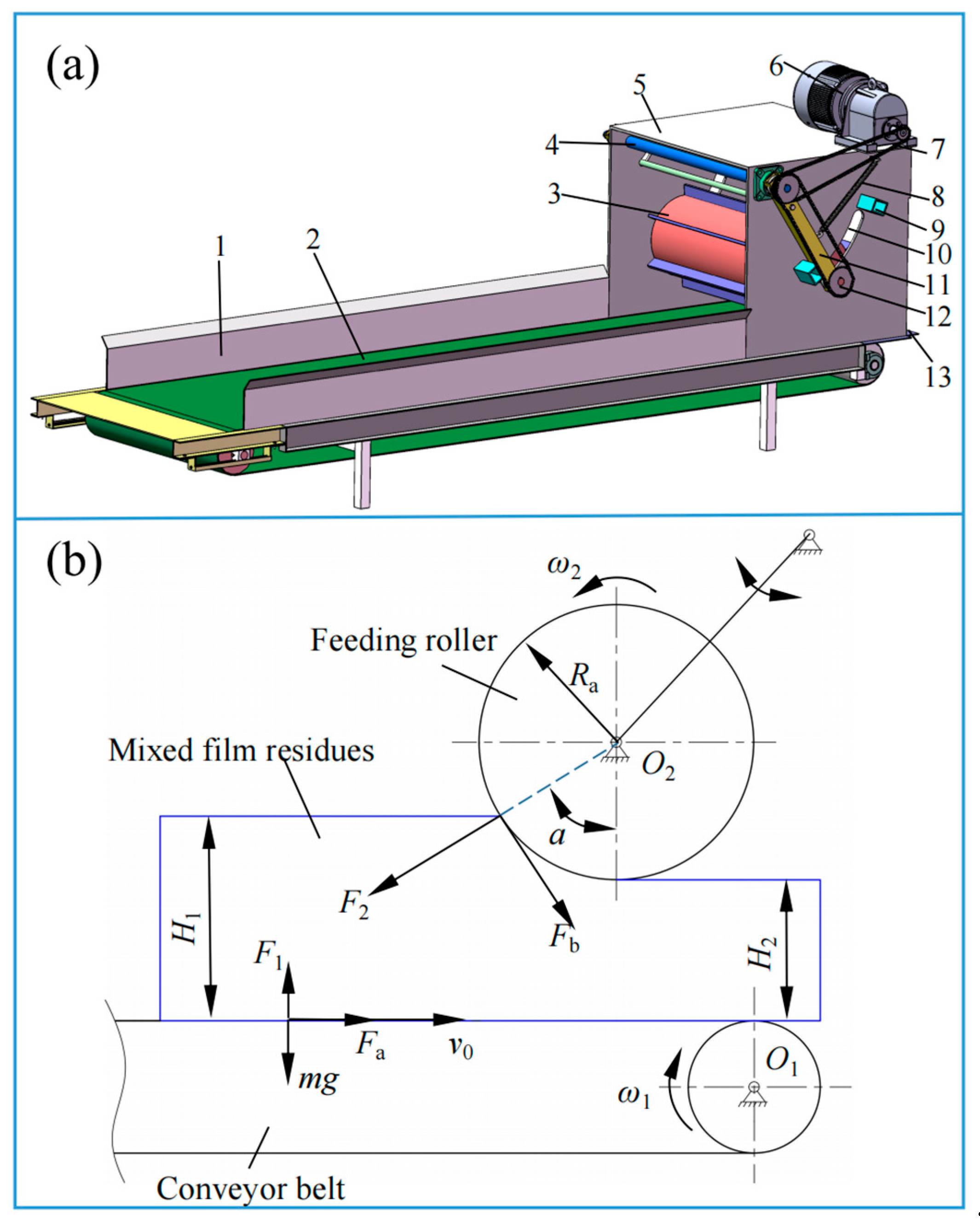
As shown in Figure 2a, the feeding mechanism consists of a feeding motor, a first chain wheel assembly, a second chain wheel assembly, a frame, and a feeding roller. The feeding motor drives the rotation of the feeding roller via the first and second chain wheel assemblies. The gap adjustment component includes a rotary shaft, a tension spring, a rotating arm, a guide slot, and a limit block. During operation, the linear rotational speed at the lower end of the feeding roller aligns with the conveyor belt’s direction of movement. As fluctuations in mixed film residues feeding volume occur, the feeding roller moves adaptively up and down along the guide slot around the rotary shaft. This enables real-time, automatic adjustment of the gap between the feeding roller and the conveyor belt, ensuring that the mixed film residues are always subjected to a specific amount of pressure.

The feeding mechanism facilitates the feeding of mixed film residues through the applied force from the feeding roller and conveyor belt. Based on the theory of stalk rupture and fracture under directional feeding conditions [11,12], an analysis of the forces and motion acting on the mixed film residues during the feeding process is conducted to ensure smooth feeding and prevent blockages, as shown in Figure 2b.

As shown in Figure 2b, the necessary condition for stable and uniform feeding of the mixed film residues is that the frictional force acting on it must be greater than or equal to the component of the normal force, as expressed by:

$$F_{\mathrm{a}}+F_{\mathrm{b}}\cos \alpha \ge F_2\sin a$$

(1)

where

$$\left\{\begin{array}{l}{F}_1=mg+F_2\cos a+F_{\mathrm{b}}\sin a\hfill \\ F_{\mathrm{a}}=F_1{\mu }_{\mathrm{a}}\hfill \\ F_{\mathrm{b}}=F_2{\mu }_{\mathrm{b}}\hfill \end{array}\right.$$

(2)

In Equations (1) and (2), F₁ represents the supporting force exerted by the conveyor belt on the film-mixed residues, N; F₂ represents the normal force applied by the feeding roller on the mixed film residues, N; F_a represents the static frictional force exerted by the conveyor belt on the mixed film residues, N; F_b represents the static frictional force exerted by the feeding roller on the mixed film residues, N; ɑ represents the feeding angle, in degrees (°); μ_a represents the coefficient of static friction between the conveyor belt and the mixed film residues; μ_b represents the coefficient of friction between the feeding roller and the mixed film residues; m represents the mass of the mixed film residues, kg; and g represents the acceleration due to gravity, m·s⁻².

By combining Equations (1) and (2), the following result can be obtained:

$${\displaystyle \frac{{\mu }_{\mathrm{a}}mg}{F_1}}+\left({\mu }_{\mathrm{a}}+{\mu }_{\mathrm{b}}\right)\cos a+{\mu }_{\mathrm{a}}{\mu }_{\mathrm{b}}\sin a⩾\sin a$$

(3)

Since μ_amg/F₁ + (μ_a + μ_b) ≥ 0 holds true in Equation (3), it is sufficient for the inequality (μ_a + μ_b)cosθ ≥ (1 − μ_aμ_b)sinɑ to be satisfied for Equation (3) to be valid. According to the relevant literature [13], the coefficient of static friction between the conveyor belt and the film-mixed residue (μ_a) is 0.44, and the coefficient of static friction between the feeding roller and the mixed film residues (μ_b) is 0.34. By solving this inequality, the feeding angle α is found to be ≤42°. This ensures that a feeding angle α ≤ 42° facilitates uniform and effective feeding of the mixed film residues while applying a sufficient compressive force.

The conveyor belt width, feeding roller diameter, and rotational speed are directly related to the grabbing, conveying performance, and productivity of the mixed film residues. To ensure stable feeding of the mixed film residues and meet the productivity requirements, it is necessary to appropriately set the conveyor belt width, feeding roller diameter, and rotational speed. As shown in Figure 2b, the following occurs:

$$\left\{\begin{array}{l}Q=3600\mathsf{\eta }B{H}_2{v}_{\mathrm{a}}{\kappa }_a\hfill \\ \begin{array}{l}{H}_1-H_2=R_a\left(1-\cos 2a\right)\\ n_a\ge {\displaystyle \frac{30v_a}{\pi R_a}}\end{array}\hfill \end{array}\right.$$

(4)

In Equation (4), Q represents the productivity, kg/h; η represents the material fill coefficient, set at 0.2 [14]; v_a represents the feeding speed, m/s; κ_a represents the bulk density of the mixed film residues, t/m³; B represents the conveyor belt width, mm; H₁ represents the height of the mixed film residues before feeding, mm; H₂ represents the height of the mixed film residues after feeding, mm; R_a represents the radius of the feeding roller, mm; and n_a represents the rotational speed of the feeding roller, r/min.

Assuming that the mixed film residues’ height before feeding (H₁) is 230 mm and after feeding (H₂) is 80 mm, the radius of the feeding roller (R_a) is calculated to be 200 mm, with a length of 800 mm, based on Equation (4). To improve the feeding roller’s grip and reduce the risk of residual film entangling the shaft, rectangular pressing plates are evenly installed along its circumference. The conveyor belt width (B) is set to 800 mm, matching the length of the feeding roller, with the total conveyor belt length set to 3000 mm. The conveyor belt speed (v_p) is set at 0.2 m/s. To ensure smoother feeding, the feeding roller speed (v_a) is typically required to be 3 to 4 times the conveyor belt speed (v_p) [15], resulting in a feeding speed (v_a) of 0.6 to 0.8 m/s. This translates to a feeding roller rotational speed (n_a) ranging from 28.66 to 38.22 r/min. Considering speed fluctuations during chain transmission, the feeding roller speed range is expanded, and n_a is set to 25 to 40 r/min. Experimental measurements show that the average bulk density of the mixed film residues (η) is 0.024 t/m³, and the theoretical chopping productivity is calculated to be 663.5 kg/h, which meets the design requirement of 600 kg/h.

2.2.2. Rotary Knife Chopping Mechanism

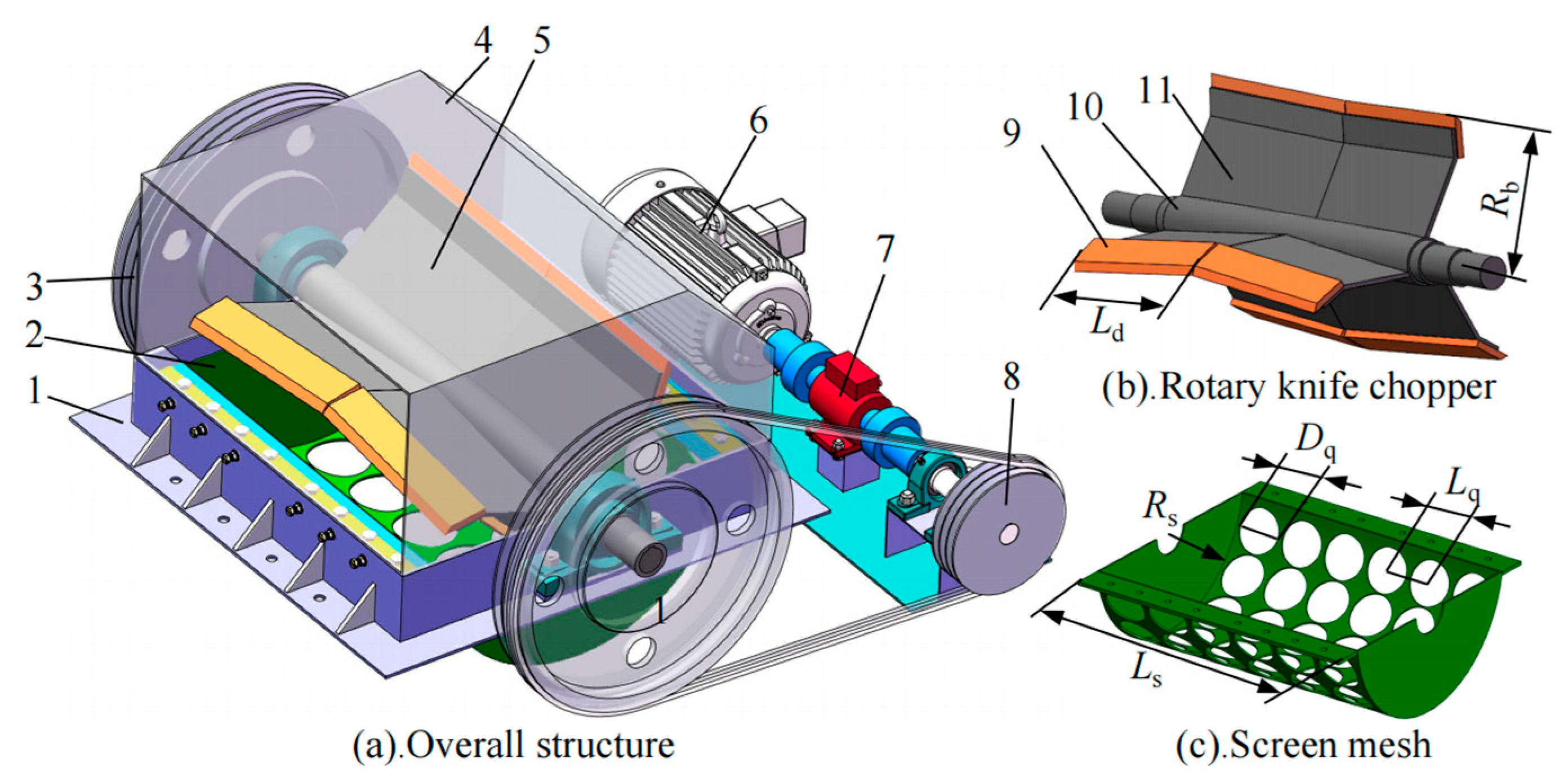
The structure of the rotary knife-type chopping mechanism is illustrated in Figure 3. It primarily consists of a chopping motor, a torque sensor, a rotary knife chopper, stationary knives, gap adjustment components, a screen, and a frame. The stationary knives are mounted on either side of the rotary knife chopper, with the screen positioned beneath it. The rotary knife chopper includes a drive shaft, a knife holder plate, and moving knives. In conventional rotary choppers, the hollow drive shaft and parallel-aligned, untilted moving knives permit long strips of residual film to wrap around the shaft—thereby increasing cutting resistance and undermining machine stability. To address these issues and enhance cutting performance, the design employs moving knives arranged in a three-section chevron pattern along the shaft, seamlessly integrated via the knife holder plate—eliminating gaps that could trap residual film.

• Configuration and structural parameters of moving blades

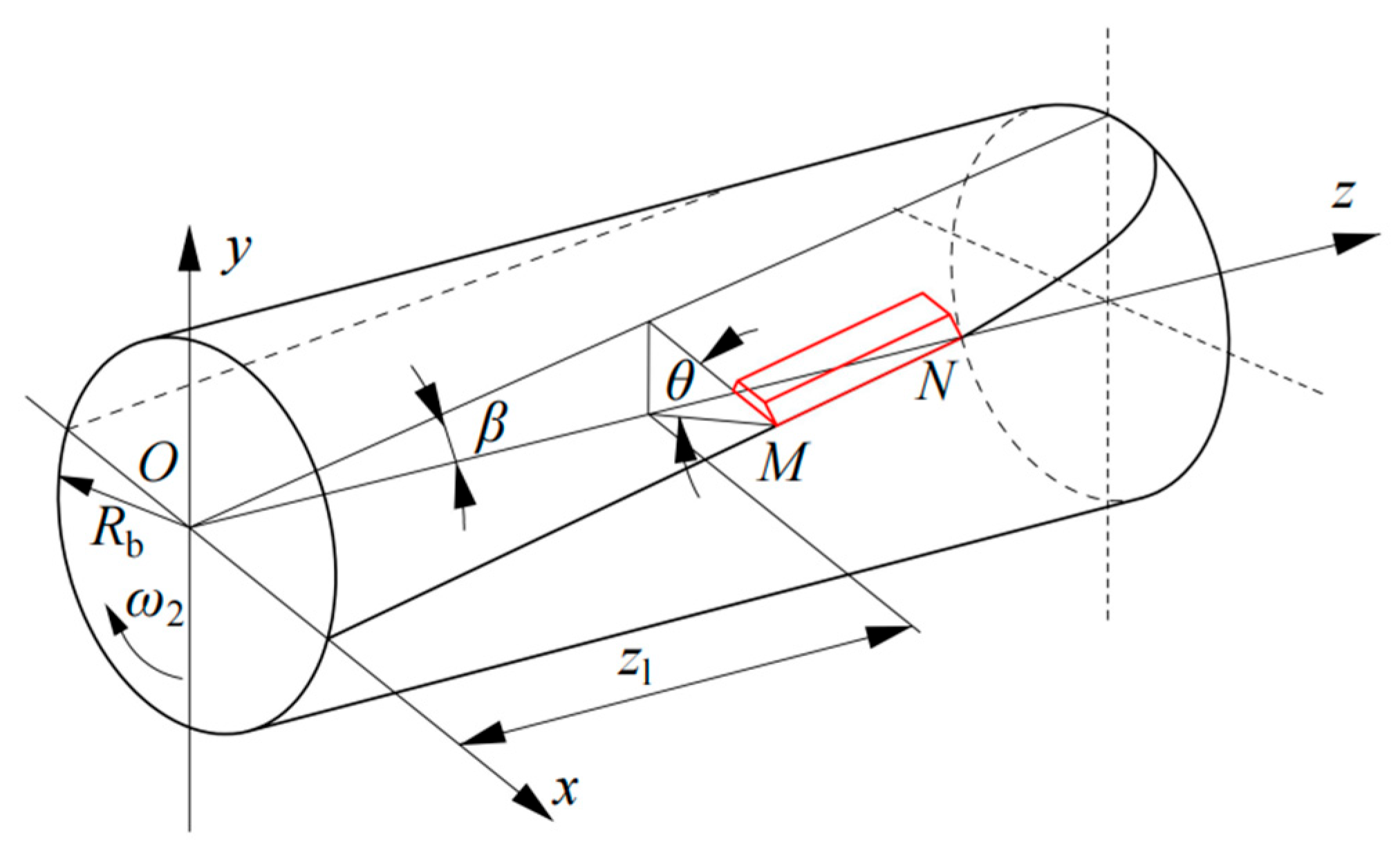
The configuration of the moving knives on the rotary knife chopper influences their sliding cutting performance, which in turn affects the chopping efficiency and operational power consumption of the mixed film residues [16]. The cutting edge of the moving knives can be approximated as a segment of an elliptical curve. This ellipse is formed by the intersection of the moving knife’s bottom surface and the drum’s centerline, which are inclined at a specific angle. The cutting edge curve is taken from the segment of the ellipse that is closest to a straight line, ensuring that the tip of the moving knife, point MN, follows a cylindrical path. The cutting edge curve of the moving knife is shown in Figure 4.

Given that the semi-major axis of the elliptical curve is R_b/sin β and the semi-minor axis is R_b, the equation for the cutting edge of the moving knife is derived in the xoz-coordinate system:

$${\displaystyle \frac{X^2}{{R_b}^2}}+{\displaystyle \frac{Z^2}{{\left(\frac{R_{\mathrm{b}}}{\sin \beta }\right)}^2}}=1$$

(5)

As shown in Figure 5, the installation angle θ of the moving knife is given by:

$$\left\{\begin{array}{l}X=R_b\cos \theta \hfill \\ Z\tan \beta =R_b\sin \theta \hfill \end{array}\right.$$

(6)

In Equations (5) and (6), X and Z represent the coordinates of any point on the cutting edge of the moving knife, mm; β represents the inclination angle of the elliptical plane of the moving knife relative to the central plane, (°); R_b represents the radius of the blade trajectory, mm; and θ represents the installation tilt angle of the cutting edge at point, M (°).

Based on the overall machine working width and the dimensions of the chopping chamber, the chopper width is set to 800 mm. Two sets of moving knives, totaling six knives, are symmetrically mounted on the chopper drum. Each moving knife has dimensions of 400 × 90 × 15 mm. Due to the small rotational radius of the chopper, the required material chopping length can only be achieved by increasing the rotational speed. However, increasing the speed demands higher stiffness, strength, and dynamic balance of the chopper. To address this, the rotational radius should be maximized within the available space in the chopping chamber. Therefore, the radius of the blade trajectory (R_b) is designed to be 265 mm. Experimental studies [17,18] indicate that increasing the installation tilt angle (θ) of the moving knives reduces the cutting edge angle (η), improving chopping performance but worsening discharge performance. To balance chopping and discharge performance, the relationship between the cutting edge angle (η) and installation tilt angle (θ) must satisfy η + θ < 90°. Thus, an installation tilt angle of θ = 30° and a cutting edge angle of η = 35° are chosen. The inclination angle (β), constrained by the chopper’s structure, is set to β = 5°.

The sliding cutting angle of the moving knife is a crucial factor influencing cutting resistance and specific energy consumption. An optimal sliding cutting angle can reduce both cutting resistance and the power required to process mixed film residues [18,19]. During operation, the moving knife moves in a circular motion around the drive shaft. The cutting process begins when the cutting edge MN reaches the starting point D of the mixed film residues (ABCD) and is completed when the moving knife reaches point B. 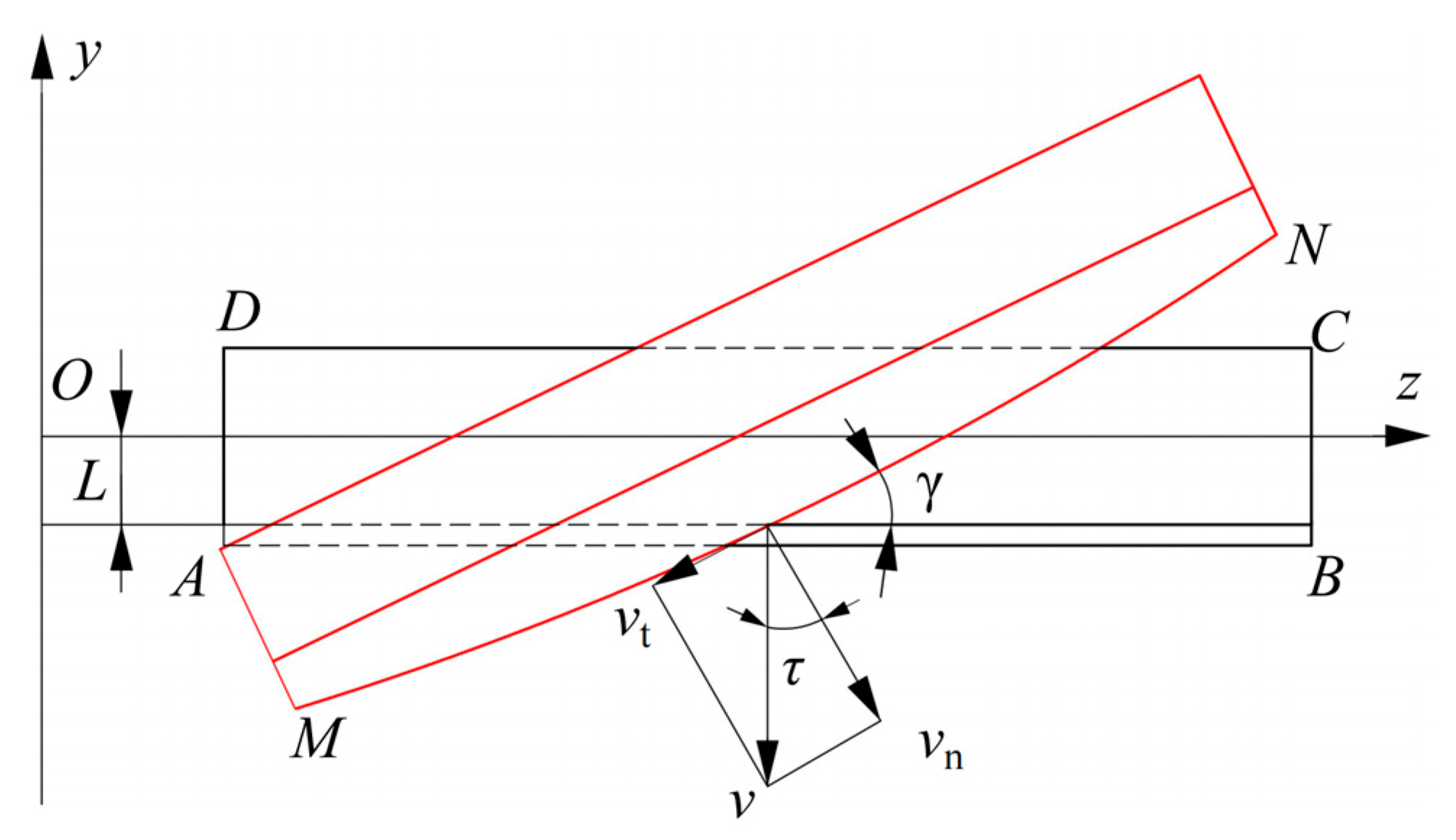Assuming that the moving knife MN intersects the stationary knife AB at point E, the velocity v at point E is decomposed into the tangential velocity v_n and the sliding velocity v_t. The angle between the tangential velocity v_n and the moving knife velocity v is defined as the sliding cutting angle (τ), and the angle between MN and AB is the thrust angle (γ). The cutting process of the moving knife is illustrated in Figure 5.

As illustrated in Figure 5, the sliding cutting angle (τ) and the thrust angle (γ) are related by the following equation:

$${\displaystyle \frac{L}{\sqrt{{R_b}^2-L^2}}}=\tan \left(\tau -\gamma \right)$$

(7)

In Equation (7), τ represents the sliding cutting angle, (°), γ represents the thrust angle, (°), and L represents the installation height of the stationary knife, mm.

As shown in Equation (7), the thrust angle (γ) is directly proportional to the sliding cutting angle (τ). An excessively large sliding cutting angle leads to an excessively large thrust angle, whereas selecting an appropriate sliding cutting angle can reduce chopping power consumption. According to the Agricultural Machinery Design Handbook, the sliding cutting angle should range from 10° to 18°, while the thrust angle should range from 4° to 8°. Given the low moisture content of the mixed film residues, a sliding cutting angle of τ = 12° and a thrust angle of γ = 5° are chosen for this design.

2.

Configuration and structural parameters of stationary blade

The structural dimensions of the stationary blade are identical to those of the moving blade, with a length of 400 mm, a width of 90 mm, and a thickness of 15 mm. The configuration parameters of the stationary blade include its installation height and the gap between the moving and stationary blades. The installation height refers to the relative position of the stationary blade with respect to the main axis of the chopping drum, as derived from Equation (8):

$$L={\displaystyle \frac{\tan \left(\tau -\gamma \right)R_b}{\sqrt{{\tan }^2\left(\tau -\gamma \right)+1}}}$$

(8)

In Equation (8), L represents the installation height of the stationary blade, mm.

Given the radius of the cutting edge trajectory of the moving knife (R_b = 265 mm), the installation height of the stationary blade (L) can be calculated using Equation (8), yielding L = 32.29 mm. A value of L = 32.0 mm is selected.

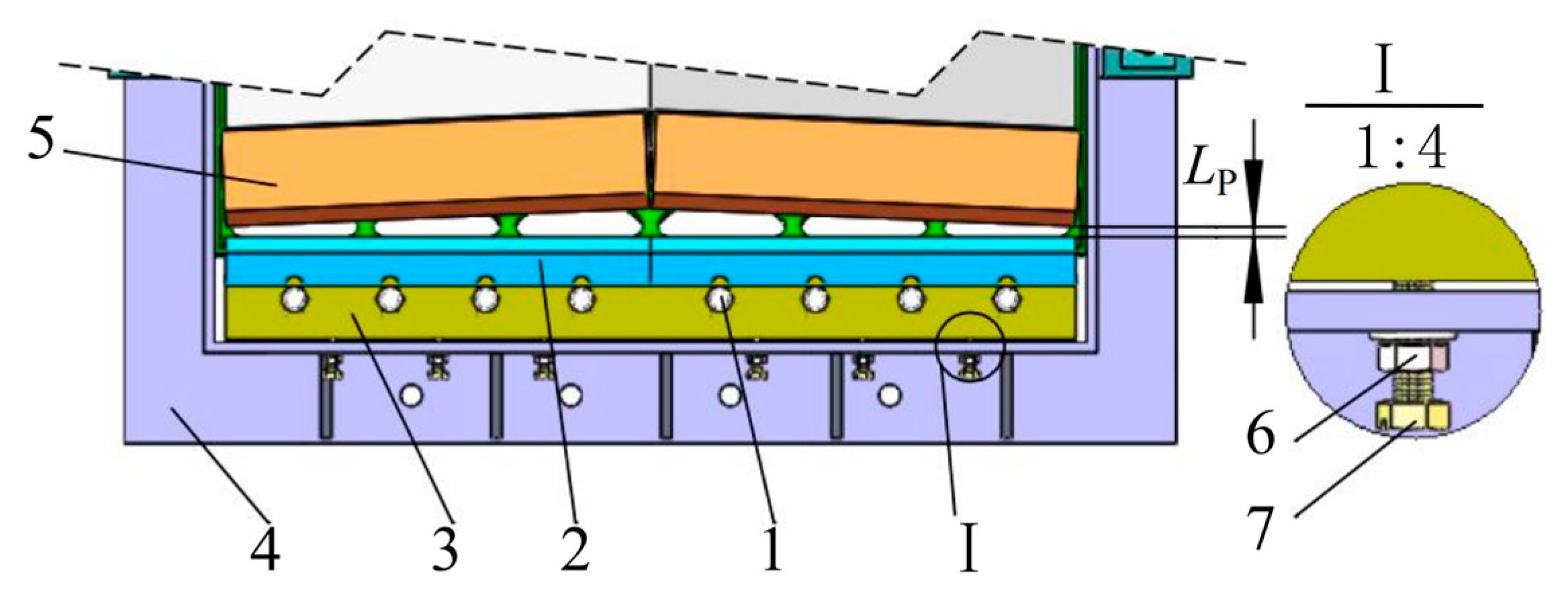
To precisely adjust the gap between the moving and stationary knives, a gap adjustment component was designed. This component primarily consists of a limit bolt, a fixing nut, and a stationary knife holder. The fixing nut is mounted on the outer side of the box-type frame, and the limit bolt passes through the nut to connect with the stationary knife holder, enabling movement. By rotating the limit bolt, the stationary knife can be adjusted, as shown in Figure 6.

During the installation of the stationary knife, the position of the chopper is first adjusted. The limit bolt is rotated to set the gap between the moving and stationary knives to zero. The limit bolt is then rotated in the opposite direction to move the stationary knife away from the moving knife, increasing the gap until the desired value is reached. Subsequently, the locking bolt is tightened to secure the stationary knife. The gap between the moving and stationary knives (L_p) can be calculated using Equation (9).

$$L_{\mathrm{p}}=P\times n$$

(9)

In Equation (9), P represents the pitch of the limit bolt, mm; n represents the number of rotations of the limit bolt.

The gap between the moving and stationary knives directly influences both material cutting length and operational power consumption [20]. Due to the soft texture of the residual film in the mixed film residues, an excessively large gap disperses the shear force, increasing shear resistance and leading to suboptimal chopping performance. A smaller gap improves chopping performance; however, an overly small gap increases the risk of knife collisions [21]. Based on preliminary shear force experiments with mixed film residues, the gap between the moving and stationary knives (L_p) is set between 0.5 and 2.0 mm.

3.

Rotational speed of rotary knife chopper

The rotational speed of the rotary knife chopper influences the theoretical cutting length of the material, defined as the feed length during the interval between two successive cutting actions of adjacent moving knives [22]. The rotational speed (n_b) of the rotary knife chopper is related to the following equation:

$$n_{\mathrm{b}}={\displaystyle \frac{60,000v_{\mathrm{a}}}{l_{1}Z}}$$

(10)

In Equation (10), v_a represents the feeding speed (ranging from 0.6 to 0.8 m/s); l₁ represents the theoretical cutting length of the material, mm; and Z represents the number of moving knives on the circumference (Z = 3).

As shown in Equation (10), the theoretical cutting length of the material is inversely proportional to the chopper’s rotational speed. The higher the rotational speed, the more cutting actions occur per unit of time, resulting in a smaller material cutting length. Excessively large or small pieces of residual film, as well as oversized cotton stalks, hinder the subsequent separation of film-mixed residues and the water-washing process for residual film [6,10,23,24]. Based on the GB/T 37821-2019 [25] Technical Specification for the Recycling of Waste Plastics and mixed film residue separation test results, the optimal cutting length range for residual film is 50–150 mm, while the optimal range for cotton stalks is 50–100 mm. Due to the unique ductility of residual film, under the same cutting conditions, its cutting size is always larger than that of cotton stalks. Therefore, the theoretical cutting length of the mixed film residues is designed based on the common qualified length range for both cotton stalks and residual film (50–100 mm). Substituting these parameters into Equation (10) yields a chopper rotational speed (n_b) between 120 and 320 r/min.

4.

Screen

As illustrated in Figure 3c, the screen is located beneath the rotary knife chopper and functions as a secondary sizing and discharge component for the chopped film residues. Common aperture geometries include circular, square, triangular, and oblong shapes. Circular apertures were selected for their enhanced screening performance, which improves both chopping efficiency and material discharge. The aperture diameter and open area ratio are two critical structural parameters that significantly influence both chopping quality and throughput. The relationship between the theoretical chopped length (l₁) of the mixed film residues and the aperture diameter (D_q) of the screen is expressed as follows [26]:

$$D_{\mathrm{q}}={\displaystyle \frac{l_1}{\left(0.75-0.85\right)}}$$

(11)

The open area ratio (K) of the screen is defined by the following equation:

$$K={\displaystyle \frac{0.91}{\left(\frac{L_{\mathrm{q}}}{D_{\mathrm{q}}}+0.1\right)}}\times 100\%$$

(12)

In Equation (12), D_q represents the diameter of the screen aperture, mm; and L_q represents the center-to-center spacing of adjacent apertures, mm.

Considering the overall design constraints and spatial requirements of the chopping mechanism, the screen was designed with a length L_s = 820 mm and a radius R_s = 315 mm. According to Equations (11) and (12), the calculated screen aperture diameter D_k falls within the range of 58.8–133.3 mm. Taking into account the practical requirements of the shredding operation, the aperture diameter was finalized as D_q = 120 mm, the center spacing to L_q = 130 mm, and the open area ratio to K = 76.9%.The apertures are uniformly arranged in a linear pattern to ensure stable discharge and reduce the risk of clogging during operation.

5.

Analysis of film-mixed residue cutting resistance

To better understand the mechanism of cutting resistance during mixed film residues processing, the composition of the cutting resistance force system at the moving knife’s cutting edge is analyzed from a microscopic perspective [27].

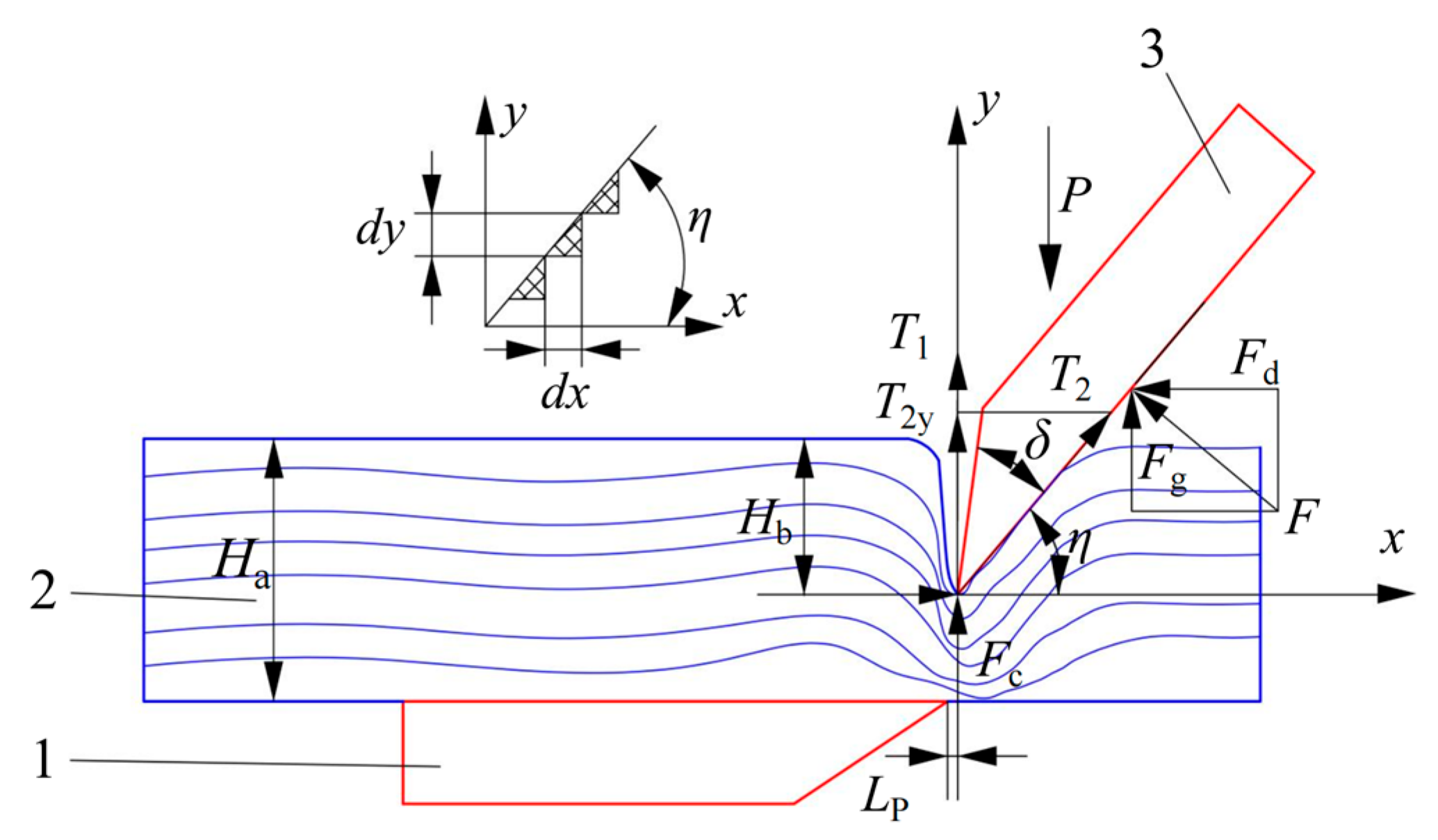
As shown in Figure 7, the reactive force (F) acting on the moving knife during the shearing process of the film-mixed residues is expressed as follows:

$$F=F_{\mathrm{g}}\sin \eta +F_{\mathrm{d}}\sin \eta$$

(13)

Under the influence of the reactive force (F), the vertical components of the frictional forces T₁ on the front edge and T₂ on the rear edge of the moving knife are given by T_2y:

$$\left\{\begin{array}{l}{T}_1=\mu F_{\mathrm{d}}\\ T_{2\mathrm{y}}=T_2\sin \eta =\mu \left(F_{\mathrm{g}}\cos \eta +F_{\mathrm{d}}\sin \eta \right)\sin \eta \end{array}\right.$$

(14)

After the film-mixed residues are compressed and deformed, the reactive force (F_c) acting on the moving knife is expressed as:

$$F_{\mathrm{c}}=m_{\mathrm{d}}{l}_{\mathrm{d}}{\sigma }_{\mathrm{c}}$$

(15)

In Equation (15), m_d represents the thickness of the moving knife’s cutting edge, mm; l_d represents the length of the moving knife’s cutting edge, mm; and σ_c represents the compressive stress of the film-mixed residues, MPa.

Based on the above analysis, it can be concluded that, to complete the cutting process, the vertical force (P) acting on the cutting edge of the moving knife must satisfy the following condition:

$$P\ge F_{\mathrm{c}}+F_{\mathrm{g}}+T_1+T_{2\mathrm{y}}$$

(16)

In Equation (16), F_c represents the reactive force exerted by the film-mixed residues on the moving knife, N; F_g represents the vertical reactive force applied by the mixed film residues to the moving knife after compression, N; F_d represents the horizontal reactive force applied by the mixed film residues to the moving knife after compression, N; and T_2y represents the horizontal component of the tangential frictional force T₂, N.

To determine F_c and F_d, it is essential to first analyze the differential forces dF_c and dF_d acting on the cutting edge. During the shear deformation process, assuming that the film-mixed residue unit only undergoes changes in the height direction and that its stress–strain relationship follows the generalized Hooke’s law, the stress–strain relationship during compression by the cutting edge is given by:

$$\epsilon ={\displaystyle \frac{\sigma }{E}}={\displaystyle \frac{H_{\mathrm{b}}}{H_{\mathrm{a}}}}$$

(17)

In Equation (17), ε represents the relative deformation; σ represents the normal stress exerted on the film-mixed residue, N/m²; E represents the elastic modulus of the mixed film residues, N/m²; H_b represents the total thickness of the mixed film residues, mm; and H_a represents the depth of compression of the mixed film residues under the cutting edge, mm.

The differential forces dF_g and dF_d acting on the cutting edge of the moving knife in the horizontal and vertical directions are expressed as follows:

$$\left\{\begin{array}{l}\mathrm{d}{F}_{\mathrm{g}}=E{\epsilon }_{1}dx=E\epsilon \tan \eta d{H}_{\mathrm{y}}\\ \mathrm{d}{F}_{\mathrm{d}}={\epsilon }_{2}Ed{H}_{\mathrm{b}}\end{array}\right.$$

(18)

By integrating both sides of Equation (16), we obtain:

$$\left\{\begin{array}{l}{F}_{\mathrm{g}}={\displaystyle \frac{E}{H_{\mathrm{a}}}}\tan \eta {\displaystyle {\int }_0^{H_{\mathrm{b}}}}{H}_{\mathrm{y}}d{H}_{\mathrm{y}}={\displaystyle \frac{E}{2H_{\mathrm{a}}}}{H_b}^2\tan \eta \\ F_{\mathrm{d}}={\displaystyle \frac{\mu E}{H_{\mathrm{a}}}}{\displaystyle {\int }_0^{H_{\mathrm{b}}}}{H}_{\mathrm{y}}d{H}_{\mathrm{y}}={\displaystyle \frac{E}{2H_{\mathrm{a}}}}{H_b}^2\mu \end{array}\right.$$

(19)

By substituting Equations (15) and (19) into Equation (16), the vertical force(P) acting on the moving knife in the horizontal direction is derived as follows:

$$P=m_d{l}_{\mathrm{d}}{\sigma }_{\mathrm{c}}+{\displaystyle \frac{E}{2H_{\mathrm{a}}}}{H_b}^2\tan \eta +{\displaystyle \frac{E\mu }{2}}{\displaystyle \frac{{H_b}^2}{H_{\mathrm{a}}}}+\mu ({\displaystyle \frac{E{H_b}^2}{2H_{\mathrm{a}}}}\tan \eta +{\sin }^2\eta +{\displaystyle \frac{E\mu }{2}}{\displaystyle \frac{{H_b}^2}{H_{\mathrm{a}}}}{\cos }^2\eta )$$

(20)

In summary, to achieve efficient chopping of film-mixed residues, the vertical force applied to the moving knife must surpass the cutting resistance force. Cutting resistance force is influenced not only by the physical properties of the mixed film residues (such as elastic modulus, compression/shear stress, Poisson’s ratio, and thickness), but also by the structural parameters of the cutting edge (such as edge thickness and the effective length of the moving knife). Additionally, it is affected by the speed of the moving knife and the gap between the moving and stationary knives. To minimize cutting resistance force and reduce operational power consumption, the mechanical model of cutting resistance force should be integrated with all influencing factors.

6.

Vibration characteristics analysis of chopper

During normal operation, the chopper is subjected to significant impact forces. If the frequency of the dynamic load from these impacts aligns with or closely matches the chopper’s natural frequency in a specific mode, resonance may occur, leading to variations in the gap between the moving and stationary knives and potentially causing structural fatigue. This can adversely affect the chopper’s performance, service life, and safety [28]. To evaluate its safety and design feasibility, a modal analysis of the chopper was performed using ANSYS 2022R2 software, which provided its natural frequencies and maximum displacement deformation. The chopper’s 3D model, created in SolidWorks 2021, was imported into ANSYS’s modal module. The moving knife material was set to 65Mn, and the transmission shaft and support plate were made from Q235, with material properties listed in

Table 2. Material parameters.

Parameters	Material
	65Mn	Q235
Density (kg·m−3)	7830	7850
Elastic modulus (MPa)	1.97 × 105	2.1 × 105
Shear modulus (MPa)	7.86 × 104	8.0 × 104
Poisson’s ratio	0.3	0.3
Tensile strength (MPa)	735	375
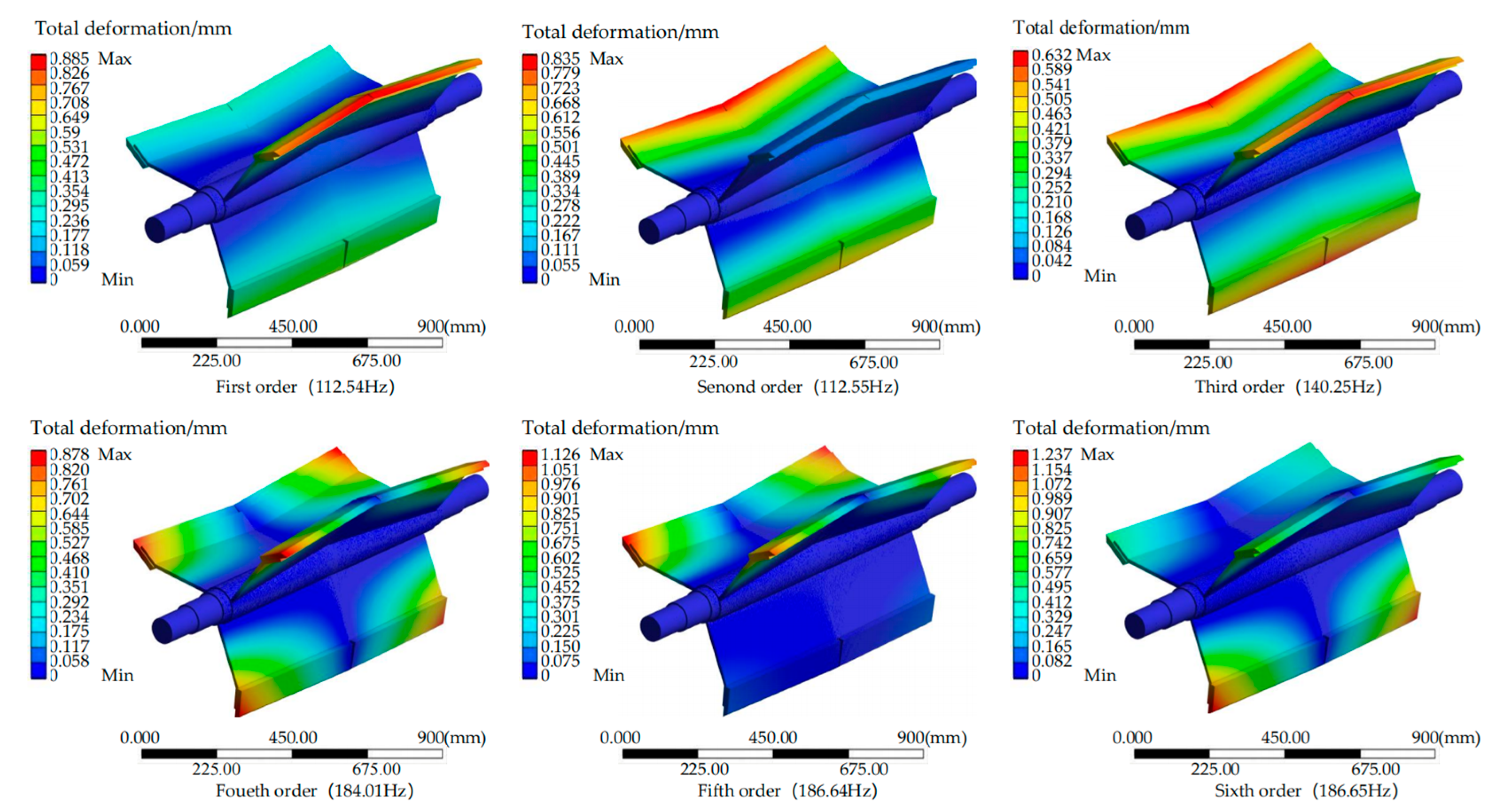
Yield strength (MPa)	430	235

. The SOLID92 mesh type was used for meshing, and fixed supports were applied at both ends of the chopper. The results of the first six vibration modes are presented in

Table 3. The results of the first six mode shape analyses of the chopper.

Order	Natural Frequency (Hz)	Maximum Deformation (mm)
1	112.54	0.885
2	122.55	0.835
3	140.25	0.632
4	184.01	0.878
5	186.64	1.126
6	186.65	1.237

and Figure 8.

As shown in Table 3, The results of the first six mode shape analyses of the chopper, the first six natural frequencies of the chopper range from 112.54 to 186.65 Hz, with the maximum deformation ranging from 0.885 to 1.237 mm. As the mode number increases, both the natural frequency and maximum deformation reach their highest values in the sixth mode. The first mode exhibits the lowest natural frequency, while the third mode shows the smallest maximum deformation. From Figure 8, it is evident that, in the first mode shape, the largest displacement deformation occurs in the first and second rows of the moving knives; in the second mode shape, the greatest deformation is seen in the second row; in the third mode shape, displacement deformation occurs across all rows from the first to the third, which explains the smallest deformation. In the fourth and fifth mode shapes, the maximum deformation occurs at the sides of the first and second rows of the moving knives. In the sixth mode shape, the maximum deformation is observed at the sides of the third row of the moving knives. The operational rotational speed of the chopper is set to 120–320 r/min, producing an excitation frequency range of 2 to 5.33 Hz, which is much lower than the first natural frequency of the chopper (112.54 Hz). Therefore, the designed chopper effectively avoids resonance.

2.3. Prototype Experiment

2.3.1. Experiment Materials and Equipment

The film-mixed residues used in this study were collected on 8 April 2024, from Malas County in the Xinjiang Uygur Autonomous Region, China. The material was recovered using a 1CMJ-2.0 combined residual film recovery and straw-crushing–returning machine manufactured by Guangda Agricultural Machinery Co., Ltd., Yuhuan, China, and was stored outdoors for approximately nine months prior to testing. The film-mixed residues were found to primarily consist of cotton stalks (approximately 35.5%), residual film (approximately 21.8%), and soil particles (approximately 42.7%). The cotton stalks had an average length of 24.31 ± 0.54 mm, an average diameter of 5.22 ± 0.17 mm, and an average moisture content of 7.83 ± 0.21%. The residual film had an average length of 536.45 ± 5.46 mm. Given the small particle size of the soil, which could contribute to environmental pollution but have minimal impact on the experimental results, the soil was excluded from the testing. The materials used in the experiment are shown in Figure 9.

The experiment was conducted in late April 2024 at the Xiaoweichuangye Industrial Park in Midong District, Urumqi, Xinjiang, as shown in Figure 10. The experimental setup included a prototype test machine, a JN-DN dynamic torque sensor (range: 0–500 N·m; accuracy: 0.1 N·m; manufacturer: Bengbu Sensor System Engineering Co., Ltd., Bengbu, China), measurement and control instruments, a Lenovo-R7000p computer (Lenovo Group Ltd., Beijing, China), and three frequency converters: A (model: WXQ-5.0KW-380V); Manufacturer: Foshan Yuqiang Electromechanical Co., Ltd., Foshan, China), B (VFD075M43A-7.5KW-380V); Manufacturer: Foshan Yuqiang Electromechanical Co., Ltd., Foshan, China), and C (model: ABE800A-18.5KW-380V); Manufacturer: Foshan Yuqiang Electromechanical Co., Ltd., Foshan, China). Additionally, an MTC008-C electronic balance (capacity: 0–500 g; accuracy: 0.001 g), AR925 laser tachometer (range: 0.5–19,999 r/min; accuracy: 0.1 r/min; Manufacturer: Shangyi Vibration Instrument (Suzhou) Co., Ltd., Suzhou, China), 100B32 feeler gauge (range: 0.1–2.0 mm; accuracy: 0.1 mm), vernier calipers, tape measures, and storage bags were used. Frequency converter A was employed for the stepless speed control of the conveyor belt, frequency converter B for the feeding roller, and frequency converter C for the chopper. The dynamic torque sensor, installed between the chopping motor and the chopper, measured the rotational speed and torque of the chopper. Data transmission was accomplished via a custom protocol or Modbus RTU protocol, using RS485 half-duplex master–slave communication. The speed and torque values, along with corresponding curves, were displayed in real-time on the human–machine interface or computer.

2.3.2. Experimental Indicators

The experimental indicators include the chopping length qualification rate of cotton stalks (CLQR-CS), the chopping length qualification rate of residual film (CLQR-RF), and specific energy consumption (SEC). To ensure scientific rigor and measurement accuracy, 2 kg of film-mixed residues was evenly distributed on the conveyor belt to form a continuous and uniform material layer of sufficient thickness, fully covering the working width of the system. All motors were then activated to begin the test. Upon completion of each experimental run, the motors were shut down, and the chopped materials were collected for sampling. Following the GB/T 26551-2011 [29] cross-sampling method, each sample weighed (300 ± 20) g. The cotton stalks in each sample were categorized and measured according to the following length ranges: 0–50 mm, 50–100 mm, and >100 mm. The maximum contour length of the residual film was classified based on the following ranges: 0–50 mm, 50–150 mm, and >150 mm. CLQR-CS, CLQR-RF, and SEC were then calculated using Equations (21)–(23).

(1)

The chopping length qualification rate of cotton stalks

$$Y_1={\displaystyle \frac{M_{\mathrm{g}}-M_1}{M_{\mathrm{g}}}}\times 100\%$$

(21)

In Equation (21), M_g represents the total mass of cotton stalks in the sample, g; and M₁ represents the mass of cotton stalks within the length range of 50–100 mm, g.

(2)

The chopping length qualification rate of residual film

$$Y_2={\displaystyle \frac{M_{\mathrm{m}}-\left(M_2+M_3\right)}{M_{\mathrm{m}}}}\times 100\%$$

(22)

In Equation (22), M_m represents the total mass of residual film in the sample, g; M₂ represents the mass of residual film with a length < 50 mm, g; and M₃ represents the mass of residual film with a length > 150 mm, g.

(3)

Specific energy consumption

The specific energy consumption (SEC) is measured using a torque power sensor installed on the chopper’s main shaft. After each experimental set, the torque sensor records the instantaneous torque, power, and operation time. The specific energy consumption per unit mass, Y₃, is then calculated based on the average power during the effective working period, the operation time, and the material mass for each test. The calculation formula is:

$$Y_3={\displaystyle \frac{{\displaystyle \int P\left(t\right)}\mathrm{d}{t}_{\mathrm{z}}}{m_{\mathrm{t}}}}$$

(23)

In Equation (23), P(t) represents the average power during the operation time, W; t_z represents the operation time, s; and m_t represents the material mass for each test, kg.

2.3.3. Experimental Plan

Based on theoretical analysis, the key factors affecting the experimental indicators were identified as the feeding roller speed, chopper speed, and the gap between the moving and stationary knives. To assess the impact of these factors on the experimental indicators (CLQR-CS, CLQR-RF, and SEC), a three-factor, five-level, second-order rotational orthogonal experimental design was implemented using Design-Expert 12 software. The feeding roller speed (X₁) was set within the range of 25–40 r/min, the chopper speed (X₂) was set within the range of 120–320 r/min, and the gap between the moving and stationary knives (X₃) was set between 0.5 and 2.0 mm, based on theoretical analysis and single-factor experimental results. The factor coding is provided in

Table 4. Experimental factors and coding.

Levels	Factors
	Feeding Roller Speed X1 (r·min−1)	Chopping Roller Speed X2 (r·min−1)	Gap Between Moving and Fixed Blades X3 (mm)
1.682	40	320	2.0
1	36.96 (370)	279.45 (280)	1.69 (1.7)
0	32.5	220	1.25
−1	28.04 (28)	160.55 (160)	0.80 (0.8)
−1.682	25	120	0.5

. A total of 20 experiments were performed, and the experimental plan and results are shown in

Table 5. Experimental plan and results.

Test No.	Factors			Y1/%	Y2/%	Y3/KJ·kg−1
	X1	X2	X3
1	−1	−1	−1	80.54	84.38	5.54
2	1	−1	−1	79.02	84.84	5.41
3	−1	1	−1	93.63	93.91	6.21
4	1	1	−1	86.37	90.72	5.82
5	−1	−1	1	78.05	84.29	5.38
6	1	−1	1	77.85	83.23	5.31
7	−1	1	1	86.45	89.81	5.81
8	1	1	1	76.83	80.17	5.53
9	−1.682	0	0	83.93	88.98	5.73
10	1.682	0	0	77.24	83.34	5.34
11	0	−1.682	0	74.18	77.05	5.58
12	0	1.682	0	82.22	86.15	6.15
13	0	0	−1.682	85.34	92.87	5.55
14	0	0	1.682	81.11	84.05	5.26
15	0	0	0	85.12	93.27	5.67
16	0	0	0	83.38	93.36	5.68
17	0	0	0	85.27	91.13	5.61
18	0	0	0	84.34	92.28	5.71
19	0	0	0	85.18	92.97	5.69
20	0	0	0	86.79	91.74	5.54

.

3. Results and Discussion

3.1. Analysis of Variance for Experimental Results

Variance analysis and significance testing were conducted on the regression models for CLQR-CS, CLQR-RF, and SEC using Design-Expert software. The relative importance of the influencing factors was assessed by comparing the partial regression coefficients. The results of the variance analysis for the experimental indicators are presented in

Table 6. Regression model analysis of variance.

Items	Source	Sum of Squares	Degree of Freedom	Mean Square	F	p	Significance
Y1	Model	527.53	9	58.61	22.73	<0.0001	**
	X1	39.08	1	39.08	15.15	0.003	**
	X2	91.1	1	91.1	35.33	0.0001	**
	X3	25.89	1	25.89	10.04	0.01	**
	X1X2	13.6	1	13.6	5.27	0.0445	*
	X1X3	7.13	1	7.13	2.76	0.1274
	X2X3	2.45	1	2.45	0.9514	0.3524
	$X_1^2$	131.66	1	131.66	51.06	<0.0001	**
	$X_2^2$	215.37	1	215.37	83.52	<0.0001	**
	$X_3^2$	62.9	1	62.9	24.39	0.0006	**
	Residual	25.79	10	2.58
	Lack of fit	16.62	5	3.32	1.81	0.2646
	Error	9.16	5	1.83
	Total	553.32	19
Y2	Model	362.89	9	40.32	38.42	<0.0001	**
	X1	20.26	1	20.26	19.31	0.0013	**
	X2	90.59	1	90.59	86.33	<0.0001	**
	X3	19.65	1	19.65	18.73	0.0015	**
	X1X2	7.28	1	7.28	6.93	0.025	*
	X1X3	4.46	1	4.46	4.25	0.0663
	X2X3	3.85	1	3.85	3.67	0.0844	**
	$X_1^2$	46.2	1	46.2	44.02	<0.0001	**
	$X_2^2$	184.64	1	184.64	175.95	<0.0001	**
	$X_3^2$	10.94	1	10.94	10.42	0.009	**
	Residual	10.49	10	1.05
	Lack of fit	6.45	5	1.29	1.59	0.3108
	Error	4.05	5	0.8092
	Total	373.38	19
Y3	Model	0.5574	9	0.0619	12.48	0.0002	**
	X1	0.0478	1	0.0478	9.62	0.0112	*
	X2	0.3457	1	0.3457	69.64	<0.0001	**
	X3	0.0697	1	0.0697	14.04	0.0038	**
	X1X2	0.0265	1	0.0265	5.33	0.0436	*
	X1X3	0.0041	1	0.0041	0.816	0.3876
	X2X3	0.0288	1	0.0288	5.8	0.0368	*
	$X_1^2$	0.0119	1	0.0119	2.39	0.1531
	$X_2^2$	0.0167	1	0.0167	3.36	0.0969
	$X_3^2$	0.0134	1	0.0134	2.69	0.1317
	Residual	0.0496	10	0.005
	Lack of fit	0.0409	5	0.0082	4.68	0.0577
	Error	0.0087	5	0.0017
	Total	0.6071	19

Note: 0.01 < p < 0.05 (significant *); p < 0.01 (highly significant **).

.

The variance analysis in Table 6 shows that the regression models for the cotton stalk chopping length qualification rate (Y₁), residual film chopping length qualification rate (Y₂), and specific energy consumption (Y₃) are all statistically significant (p < 0.001), while the lack of fit terms are not significant (p > 0.05). This indicates that the constructed models are robust, with regression equations that exhibit a good fit, as evidenced by correlation coefficients (R²) greater than 0.97. These results suggest that the predicted values from the models align closely with the experimental values, confirming their suitability for analyzing and optimizing Y₁, Y₂, and Y₃.

Additionally, the effects of the experimental factors on Y₁, Y₂, and Y₃ are all significant. By comparing the F-values, it can be observed that the experimental factors affect the cotton stalk chopping length qualification rate in the following order of importance: chopper speed (X₂), feeding roller speed (Y₃), and gap between the moving and stationary knives (X₃). For the residual film chopping length qualification rate (Y₂), the order is as follows: chopper speed (Y₃), feeding roller speed (X₁), and gap between the moving and stationary knives (X₃). For the specific energy consumption (Y₃), the order is as follows: chopper speed (X₂), gap between the moving and stationary knives (X₃), and feeding roller speed (X₁). After performing multiple regression fitting on the experimental results and eliminating the insignificant terms, the regression equations for the effects of the experimental factors on Y₁, Y₂, and Y₃ are as follows:

$$\begin{array}{l}{Y}_1=84.9554-2.0577X_1+2.9489X_2-1.7430X_3-1.9288X_1{X}_2\\ -1.1869{X_1}^2-2.0302{X_2}^2\end{array}$$

(24)

$$\begin{array}{l}{Y}_2=92.4196-1.2179X_1+2.5756X_2-1.1997X_3-0.9538X_1{X}_2\\ -1.7904{X_1}^2-3.5794{X_2}^2-0.8712{X_3}^2\end{array}$$

(25)

$$\begin{array}{l}{Y}_3=5.3549-0.0591X_1+0.1591X_2-0.0714X_3-0.0575X_1{X}_2\\ -0.06X_2{X}_3\end{array}$$

(26)

3.2. Response Surface Analysis of Experimental Results

Response surface analysis was conducted on the experimental results using Design-Expert software to assess the impact of significant interactions between the experimental factors on the experimental indicators. The effects of these interactions on the cotton stalk chopping length qualification rate (Y₁), residual film chopping length qualification rate (Y₂), and specific energy consumption (Y₃) are presented in Figure 11.

When the gap between the moving and stationary knives is set to 1.2 mm, the response surface illustrating the effects of feeding roller speed and chopper speed on the cotton stalk chopping length qualification rate is shown in Figure 11a. As depicted in Figure 11a, with constant feeding roller speed, the qualification rate initially increases and then decreases as chopper speed rises. Likewise, with constant chopper speed, the qualification rate first increases and then decreases as feeding roller speed increases. This behavior occurs because a decrease in feeding roller speed or an increase in chopper speed both lead to an increased number of cuts per unit time, which reduces the cotton stalk chopping length. The optimal chopping length for cotton stalks is in the range of 5–10 mm, with both excessively large and small sizes resulting in a lower qualification rate. Thus, the interaction between feeding roller speed and chopper speed significantly impacts the cotton stalk chopping length qualification rate.

When the gap between the moving and stationary knives is set to 1.2 mm, the response surface illustrating the effects of feeding roller speed and chopper speed on the residual film chopping length qualification rate is shown in Figure 11b. As depicted in Figure 11b, with constant feeding roller speed, the residual film chopping length qualification rate increases as chopper speed rises. Conversely, with constant chopper speed, the qualification rate initially increases and then decreases as feeding roller speed increases. This behavior is attributed to the fact that increasing the feeding roller speed accelerates the entry of the film-mixed residues into the chopper chamber, while increasing the chopper speed raises the number of cuts per unit time. The optimal chopping length for residual film ranges from 5 to 15 mm. Due to the mesh size limitation in the chopper chamber, longer residual film pieces are repeatedly cut, reducing the number of residual films longer than 15 mm and thereby improving the residual film chopping length qualification rate. Therefore, the interaction between feeding roller speed and chopper speed plays a significant role in affecting the residual film chopping length qualification rate.

When the gap between the moving and stationary knives is set to 1.2 mm, the response surface illustrating the effects of feeding roller speed and chopper speed on specific energy consumption (SEC) is shown in Figure 11c. As depicted in Figure 11c, with constant feeding roller speed, SEC increases as the chopper speed rises. Conversely, with constant chopper speed, SEC decreases as the feeding roller speed increases. According to theoretical analysis of the chopper’s power, the chopper speed is directly proportional to the operational power. A decrease in feeding roller speed or an increase in chopper speed both lead to an increased number of cuts per unit time, and when feeding roller speed is reduced and chopper speed is increased, SEC shows a noticeable upward trend. Therefore, the interaction between feeding roller speed and chopper speed significantly influences SEC.

When the feeding roller speed is set to 32.5 r/min, the response surface illustrating the effects of chopper speed and the gap between the moving and stationary knives on specific energy consumption (SEC) is shown in Figure 11d. As depicted in Figure 11d, with constant chopper speed, SEC increases as the gap between the moving and stationary knives increases. Conversely, with a constant gap between the knives, SEC decreases as the chopper speed rises. This behavior is due to the fact that cutting of the film-mixed residues is primarily driven by the interaction between the moving and stationary knives. As the gap between the moving and stationary knives widens, the mixed film residues fill the gap, leading to increased interactions such as friction and compression between the components, which elevates the cutting power consumption. Additionally, because of the soft, ductile nature of the residual film, some pieces are not completely cut and are repeatedly processed within the chopper chamber, increasing SEC. Therefore, the interaction between the chopper speed and the gap between the moving and stationary knives plays a significant role in affecting SEC.

3.3. Parameter Optimization and Experimental Validation

To optimize the prototype’s performance, multi-objective optimization was conducted on the cotton stalk chopping length qualification rate (CLQR-CS), residual film chopping length qualification rate (CLQR-RF), and specific energy consumption (SEC) using the Optimization module of the Design-Expert software. The optimization constraints for each factor were defined by the upper and lower limits of the experimental factors. The optimization objectives were to maximize CLQR-CS, maximize CLQR-RF, and minimize SEC. In line with the requirements of film-mixed residue recycling technology, CLQR-CS and CLQR-RF were prioritized over SEC. Accordingly, the importance of CLQR-CS and CLQR-RF was set to “++++”, while the importance of SEC was set to “+++”. The mathematical model for the constrained optimization conditions was formulated as follows:

$$\left\{\begin{array}{l}\mathrm{Max}{Y}_1\left(X_1,X_2,X_3\right)\\ \mathrm{Max}{Y}_2\left(X_1,X_2,X_3\right)\\ \mathrm{Min}{Y}_3\left(X_1,X_2,X_3\right)\\ \mathrm{s}.\mathrm{t}\left\{\begin{array}{l}25\mathrm{r}/\min \le X_1\le 40\mathrm{r}/\min \\ 120\mathrm{r}/\min \le X_2\le 320\mathrm{r}/\min \\ 0.5\mathrm{mm}\le X_3\le 2.0\mathrm{mm}\end{array}\right.\end{array}\right.$$

(27)

The optimized operating parameters were as follows: a feeding roller speed of 32.4 r/min, a chopper speed of 222 r/min, and a gap of 0.99 mm between the moving and stationary knives. The predicted cotton stalk chopping length qualification rate was 90.20%, the residual film chopping length qualification rate was 92.90%, and the specific energy consumption (SEC) was 5.34 kJ·kg⁻¹.

In late April 2024, a verification experiment was conducted at the Xiaoweichuangye Industrial Park in Midong District, Urumqi, Xinjiang. During the experiment, the feeding roller speed was set to 32.4 r/min, the chopper speed to 220 r/min, and the gap between the moving and stationary knives to 1.0 mm. The experiment was repeated three times, and the average values were calculated. The experimental results are summarized in

Table 7. Results of verification experiment.

Test No.	Evaluation Index
	Y1/(%)	Y2/(%)	Y3/(kJ·kg−1)
1	89.95	91.58	5.35
2	90.05	92.21	5.37
3	89.89	91.97	5.36
Average values	89.96	91.92	5.36

.

The experimental results indicated that the measured average values for the cotton stalk chopping length qualification rate, residual film chopping length qualification rate, and specific energy consumption (SEC) were 89.96%, 91.92%, and 5.36 kJ/kg, respectively. Comparison of the predicted and experimental results revealed that the relative errors for all performance indicators were below 3%, demonstrating strong agreement between the two. This confirms that the developed model is reliable, and the analysis results are credible, suggesting that the machine exhibits strong operational performance.

4. Conclusions

(1)

A novel film-mixed residue chopping method, based on the “single support cutting + sliding cutting” principle, was developed to address the resource utilization needs of mixed film residues and the physical characteristics of its components. A rotary knife-type chopper was designed, and the optimal feeding and chopping conditions were determined. The key design parameters for the chopper were established, including a feeding roller speed of 25–40 r/min, a chopper speed of 120–320 r/min, and a gap between the moving and stationary knives of 0.5–2.0 mm. Vibration characteristic analysis of the chopper, using ANSYS finite element software, showed that the first six natural frequencies ranged from 112.54 to 186.65 Hz, with maximum deformation ranging from 0.885 to 1.237 mm. The chopper’s excitation frequency ranged from 2 to 5.33 Hz, which is well below its first natural frequency, preventing resonance and ensuring the chopper’s reliability and operational performance.

(2)

A prototype was developed and tested. A second-order rotational orthogonal experimental design was employed to derive regression equations that describe the relationships between feeding roller speed, chopper speed, and the gap between the moving and stationary knives, as well as the cotton stalk chopping length qualification rate (CLQR-CS), residual film chopping length qualification rate (CLQR-RF), and specific energy consumption (SEC). The second-order response surface model was optimized using Design-Expert software, resulting in the optimal operating parameters for the chopper: a feeding roller speed of 32.40 r/min, a chopper speed of 222 r/min, and a gap between the moving and stationary knives of 0.99 mm.

(3)

A verification experiment was conducted using these optimal parameters. The experimental results showed that the cotton stalk chopping length qualification rate was 89.96%, the residual film chopping length qualification rate was 91.92%, and the specific energy consumption was 5.36 kJ/kg. When comparing the predicted and experimental results, the relative errors for all performance indicators were less than 3%, indicating that the experimental results were in good agreement with the model predictions, and the chopping device met the industry requirements for operational quality.