Methods for Constructing Soil Dynamic Models Under Intelligent Cultivation: Dynamic Interaction Mechanisms Between Farming Tools with Complex Structures and Soil
Abstract
1. Introduction
2. Materials and Methods
2.1. Establishment of Soil Constitutive Models
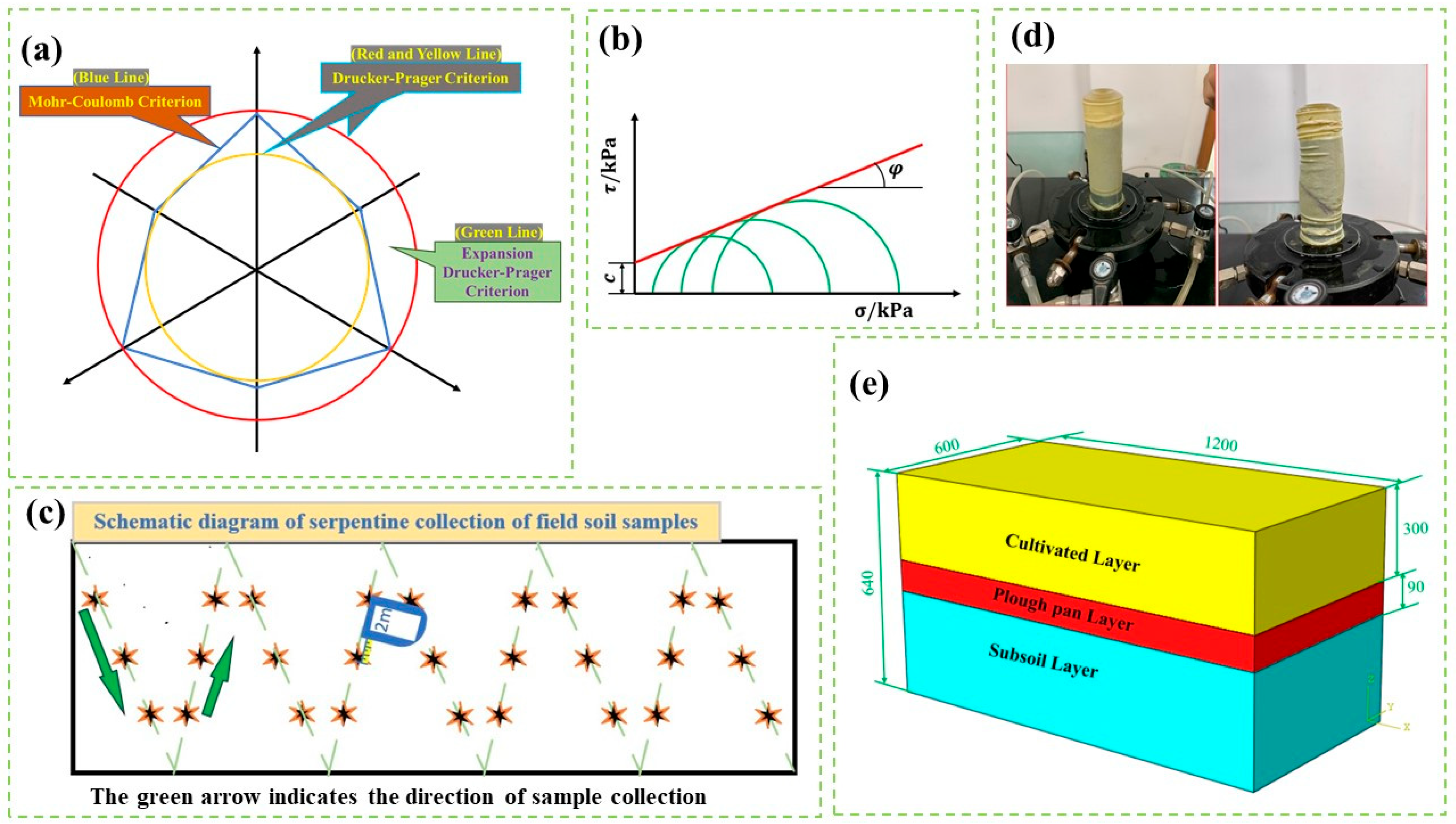
2.1.1. Mohr–Coulomb (M-C) Yield Criteria
2.1.2. Drucker–Prager (D-P) Yield Criteria
2.2. Determination of Field Soil Parameters
2.2.1. Soil Bulk Density—Ring Knife Sampling and Oven-Drying Method
2.2.2. Soil Moisture Content—Wet Weight Method
2.2.3. Soil Particle Size Distribution—Sieving and Laser Particle Size Analysis
2.2.4. Soil Cohesion and Internal Friction Angle—Triaxial Compression Test
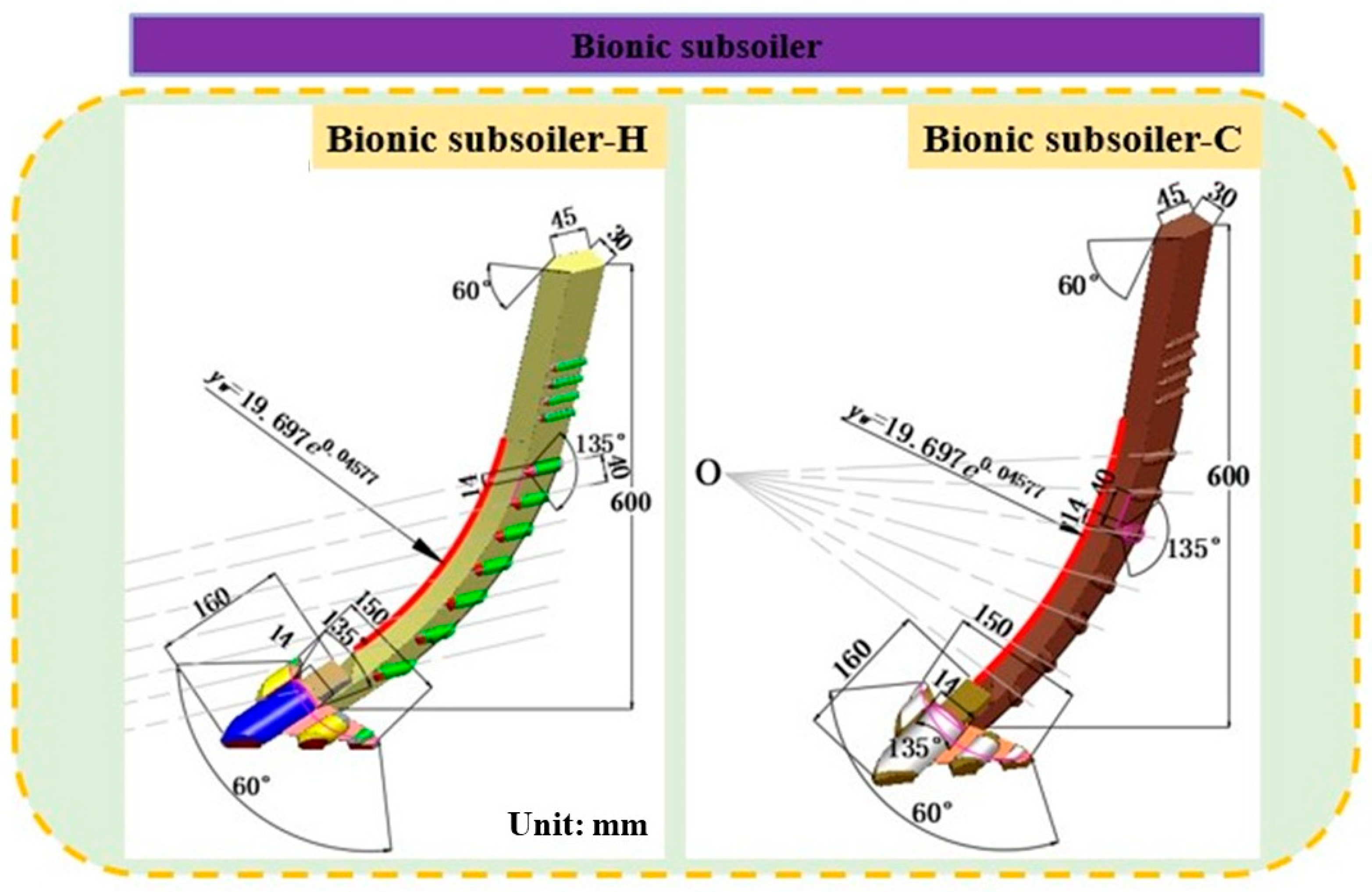
2.3. Establishment of the Soil Tillage Model
2.3.1. Material Properties and Boundary Conditions
2.3.2. Geometry and Mesh Density Optimization
2.4. Soil Bin Test
2.4.1. Experimental Setup
2.4.2. Data Acquisition
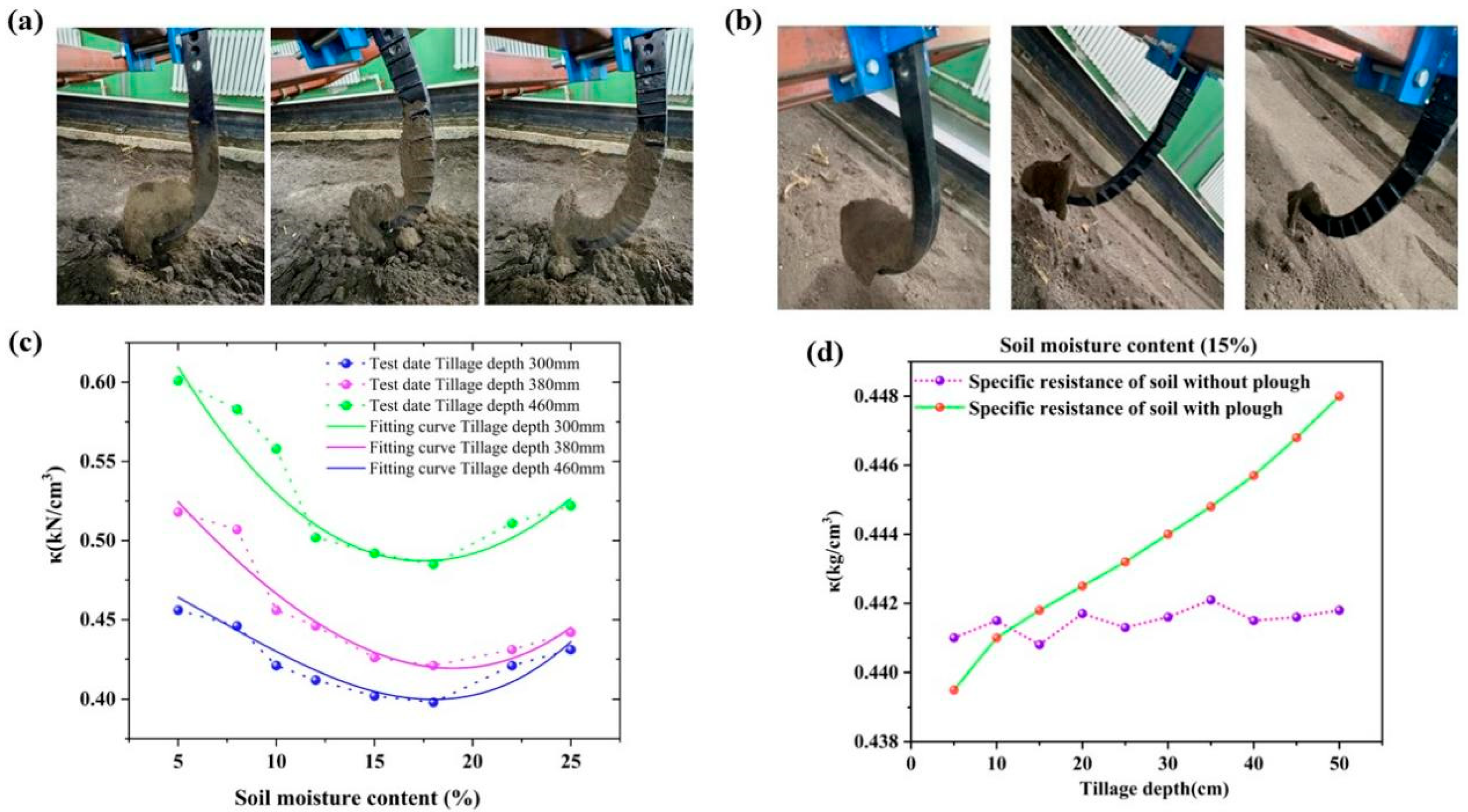
3. Results
3.1. Field Soil Properties
3.2. Farming Forces and Soil Failure
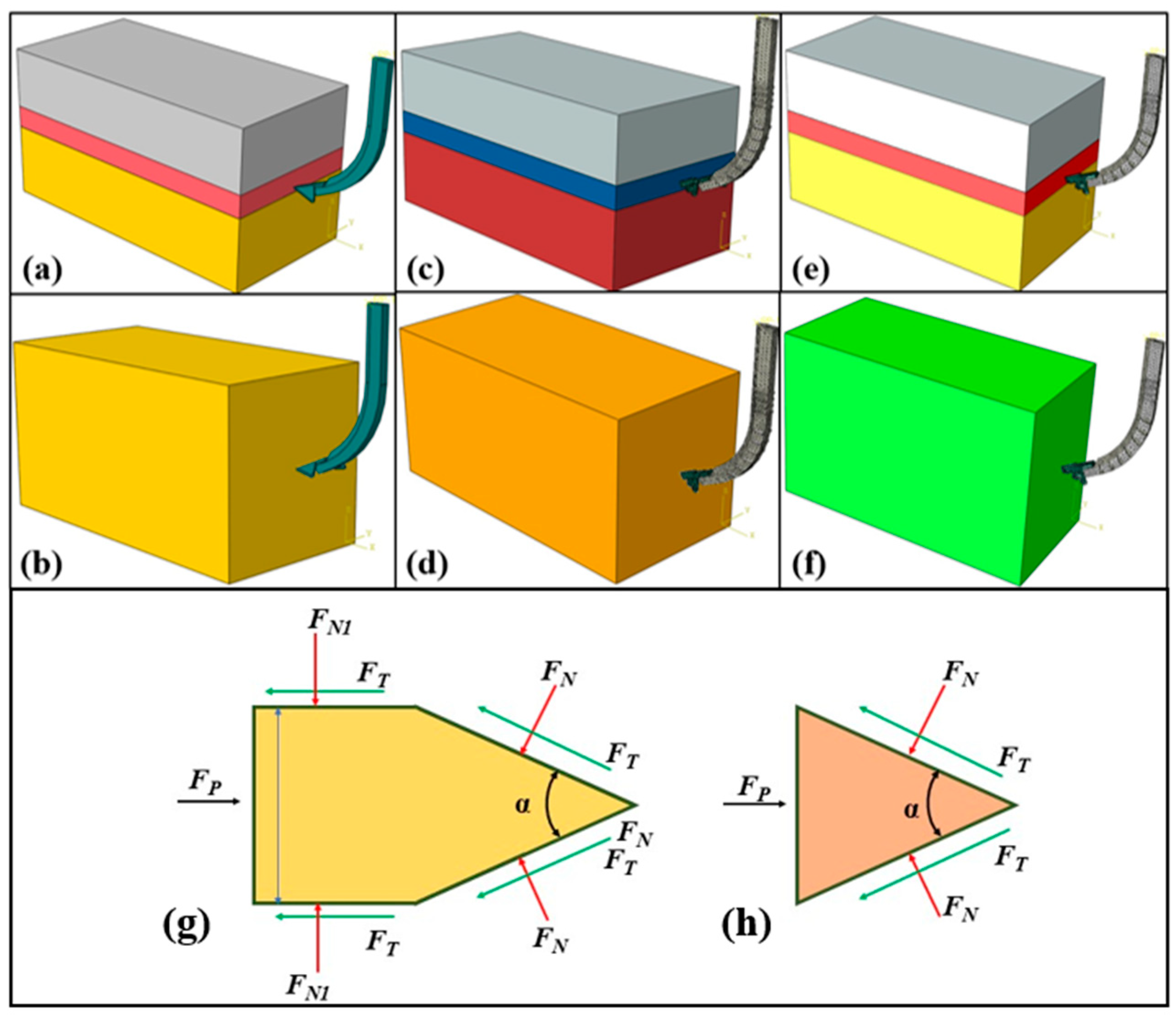
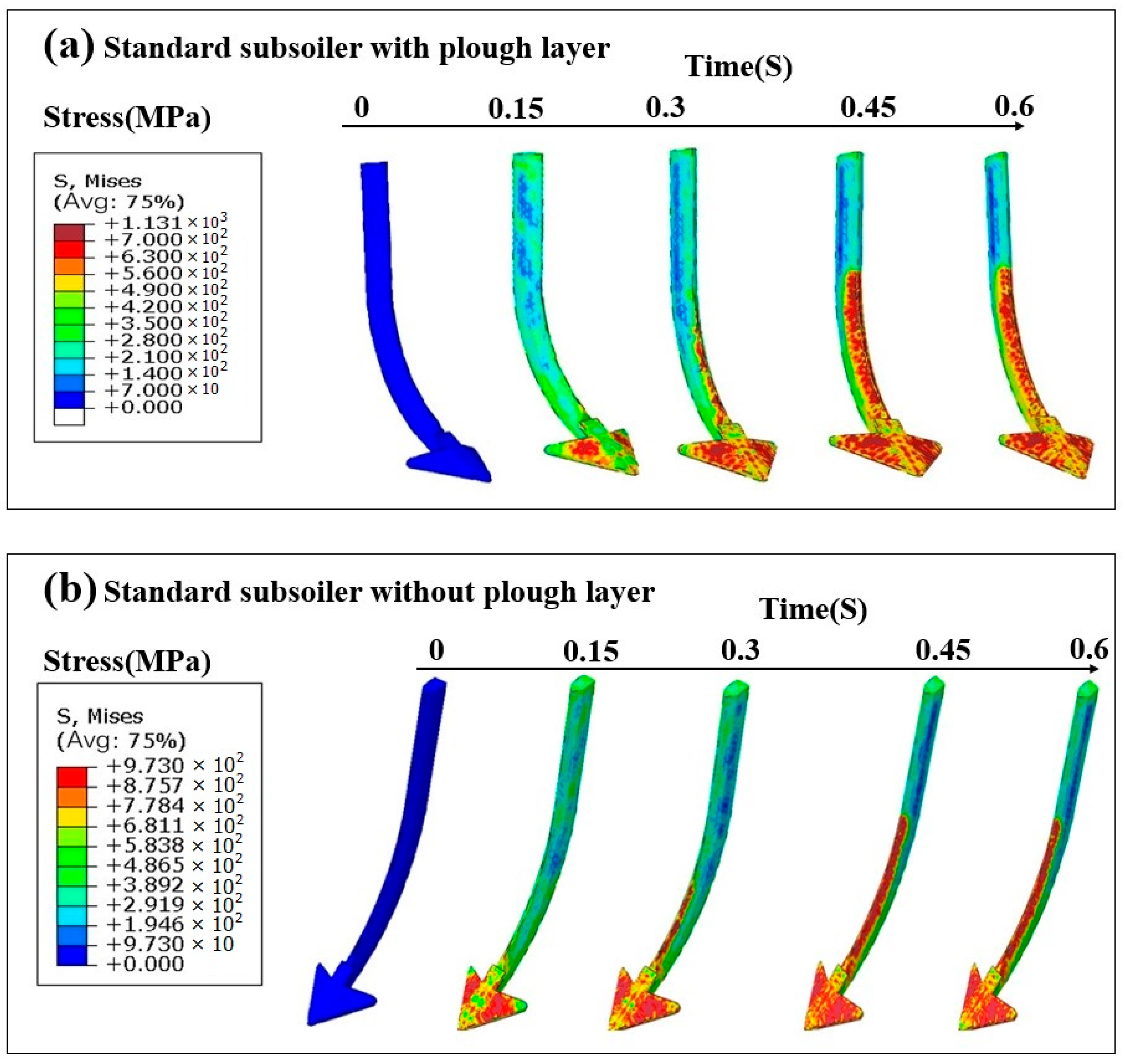
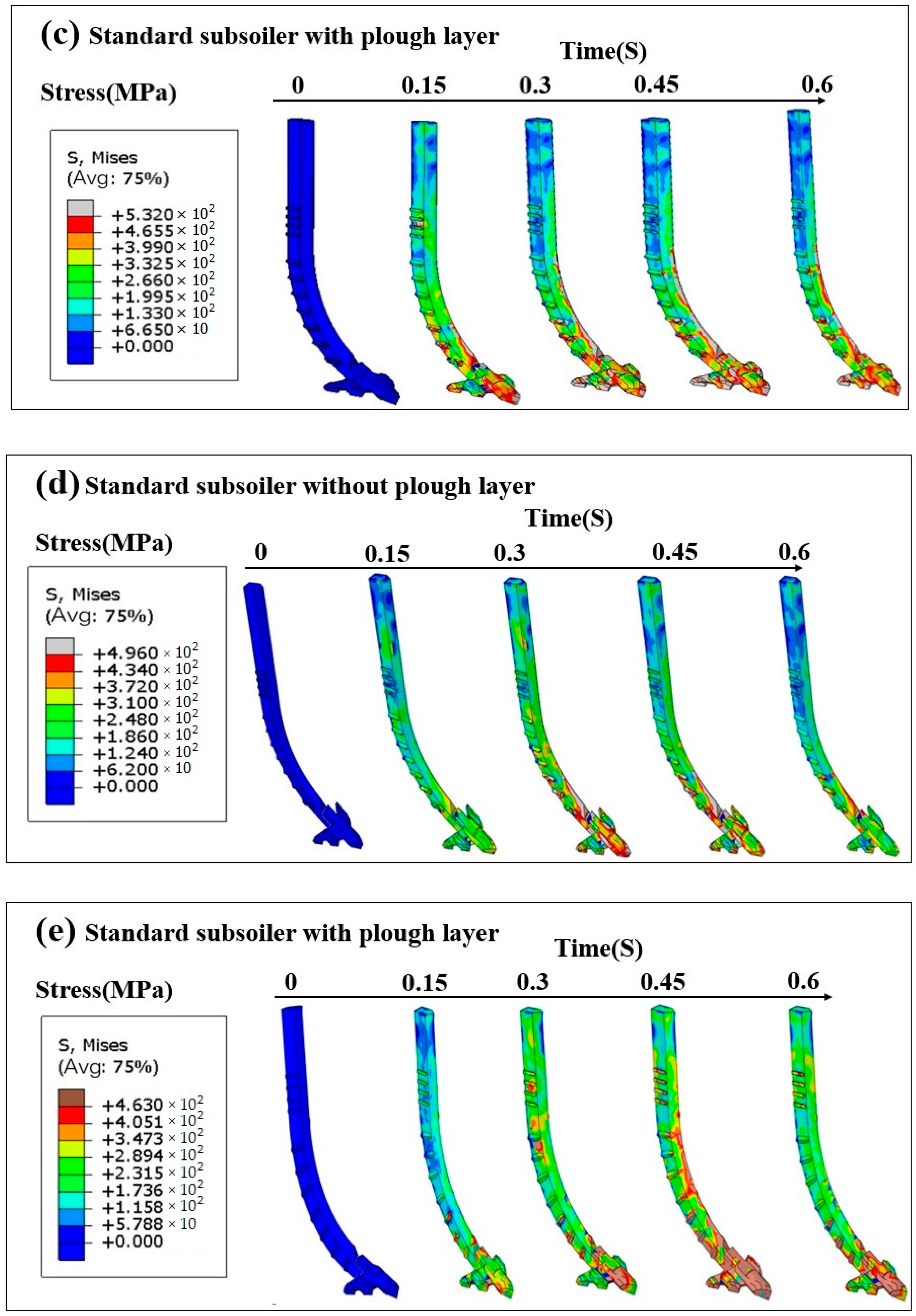
3.2.1. Stress of Subsoiler and Soil
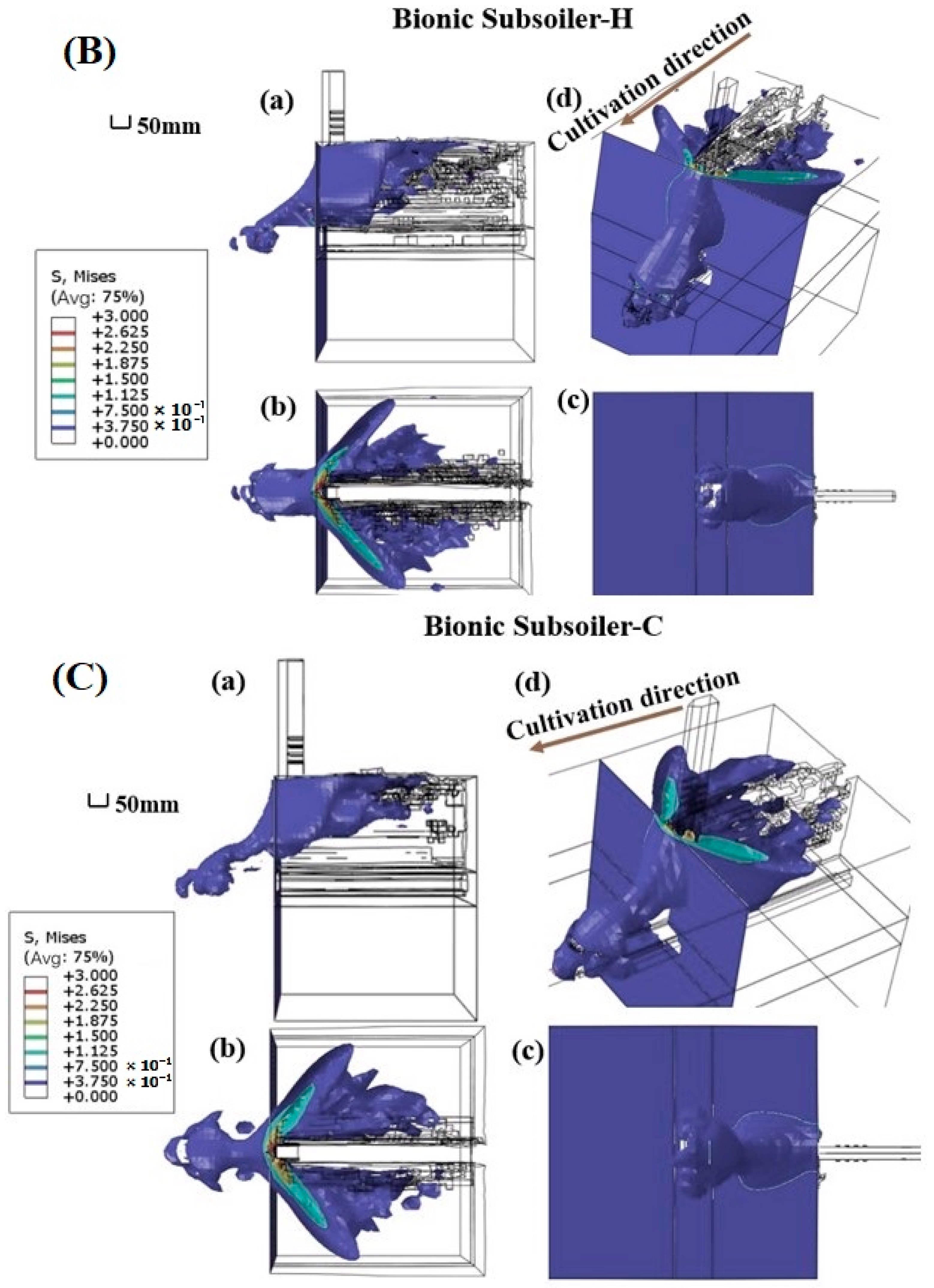
3.2.2. Soil Failure Analysis
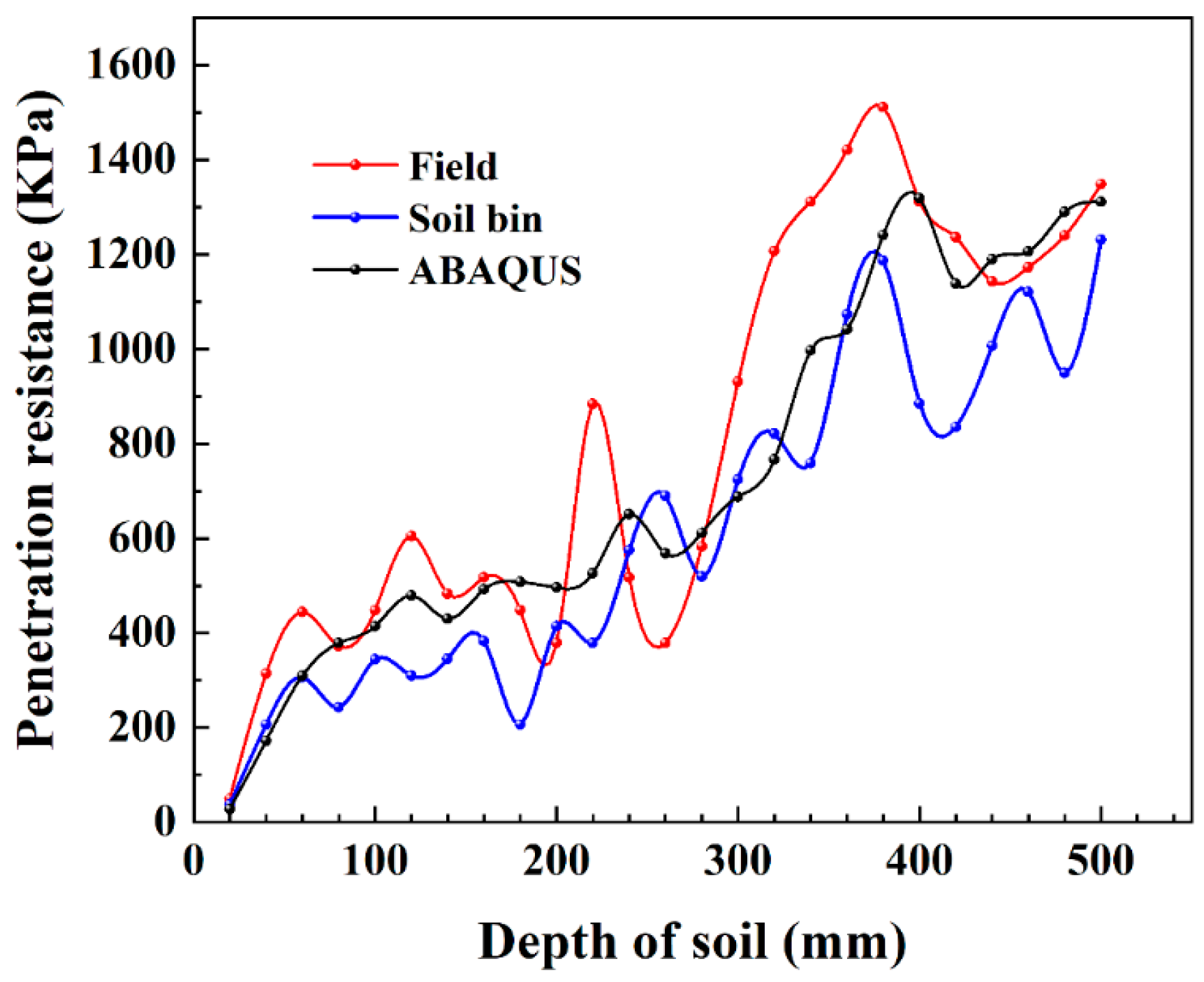
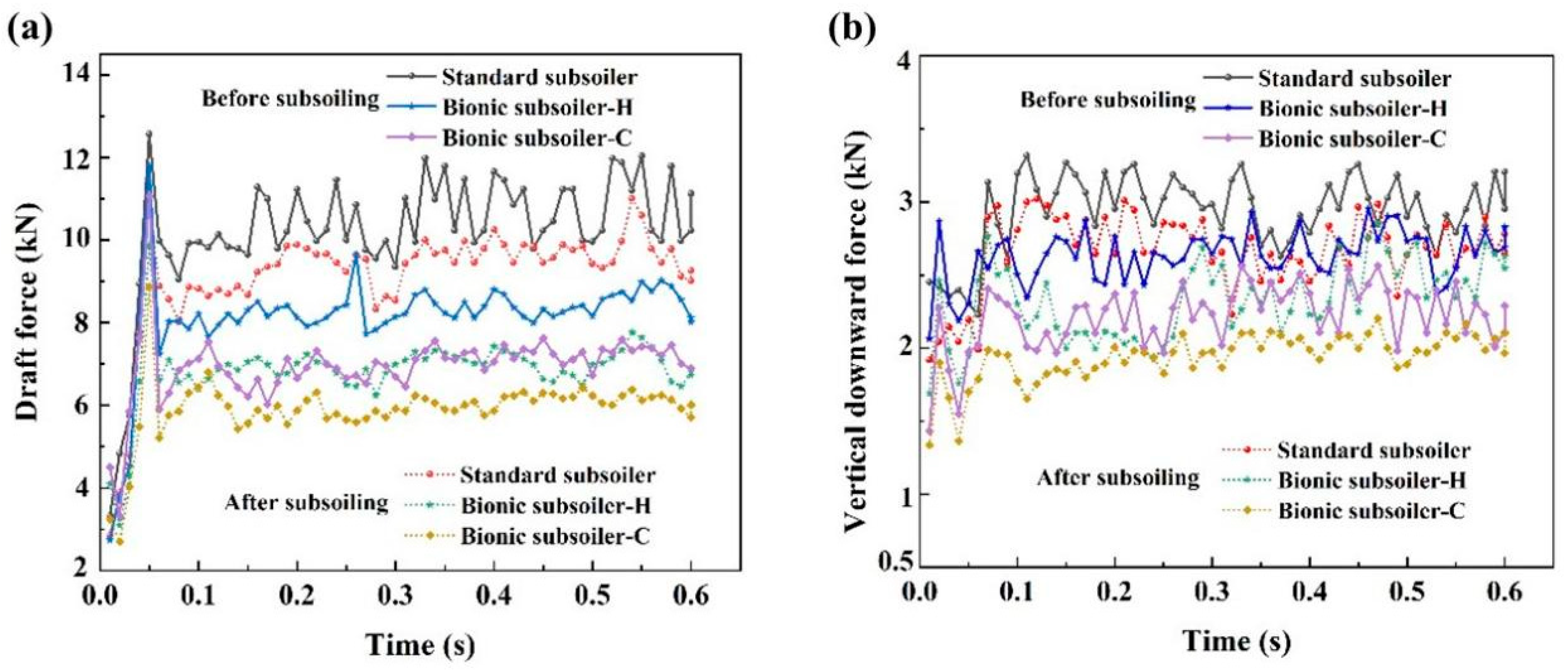
3.3. Verification of Model Accuracy Through Soil Bin Testing
4. Discussion
4.1. Stress Analysis of the Soil Tillage Dynamics Model
4.2. Soil Failure Analysis of the Soil Tillage Dynamics Model
4.3. Prediction of Soil Cultivability via the Soil FEM
4.4. Prediction of Potential Environmental Impacts of Subsoiling
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bai, H.; Zhou, X.; Zhao, Y.; Zhao, Y.; Han, Q. Soil CT image quality enhancement via an improved super-resolution reconstruction method based on GAN. Comput. Electron. Agric. 2023, 213, 108177. [Google Scholar] [CrossRef]
- Torotwa, I.; Ding, Q.; Makange, N.R.; Liang, L.; He, R. Performance evaluation of a biomimetically designed disc for dense-straw mulched conservation tillage. Soil Tillage Res. 2021, 212, 105068. [Google Scholar] [CrossRef]
- Ibrahmi, A.; Bentaher, H.; Hbaieb, M.; Maalej, A.; Mouazen, A.M. Study the effect of tool geometry and operational conditions on mouldboard plough forces and energy requirement: Part 1. Finite element simulation. Comput. Electron. Agric. 2015, 117, 258–267. [Google Scholar] [CrossRef]
- Patuk, I.; Hasegawa, H.; Borodin, I.; Whitaker, A.C.; Borowski, P.F. Simulation for Design and Material Selection of a Deep Placement Fertilizer Applicator for Soybean Cultivation. Open Eng. 2020, 10, 733–743. [Google Scholar] [CrossRef]
- Pulido-Moncada, M.; Katuwal, S.; Munkholm, L.J. Characterisation of soil pore structure anisotropy caused by the growth of bio-subsoilers. Geoderma 2022, 409, 115571. [Google Scholar] [CrossRef]
- Zhao, F.; Guo, Y.; Lai, S. Developed and test study on the subsoiler. In Proceedings of the 2011 International Conference on Electronic and Mechanical Engineering and Information Technology, Harbin, China, 12–14 August 2011. [Google Scholar] [CrossRef]
- Feng, T.; Xu, L.; Song, Y.; Li, F.; Song, Z. Design and Analysis of Bionic Rib Subsoiling Shovel Based on Hawaiian Shell. Proc. IOP Conf. Ser. Earth Environ. Sci. 2019, 267, 032048. [Google Scholar] [CrossRef]
- Qi, P.; Gao, F.; Qiu, L. The Finite Element Analysis and Simulation of the Gap Disc Trenching Based on ABAQUS. J. Agric. Mech. Res. 2016, 9, 64–73. [Google Scholar] [CrossRef]
- Kong, X.; Cai, G.; Cheng, Y.; Zhao, C. Numerical Implementation of Three-Dimensional Nonlinear Strength Model of Soil and Its Application in Slope Stability Analysis. Sustainability 2022, 14, 5127. [Google Scholar] [CrossRef]
- Anubhav; Wu, H. Modelling of Non-linear Shear Displacement Behaviour of Soil–Geotextile Interface. Int. J. Geosynth. Ground Eng. 2015, 1, 19. [Google Scholar] [CrossRef]
- Xu, X.; Dai, Z.H.; Chen, L.J.; Xu, X.T. Nonlinear Elastic-Perfectly Plastic Model of Soil and its Numerical Implementation and Application. Soil Mech. Found. Eng. 2022, 59, 215–224. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Wang, W.; Cao, Y. FEM Analysis and Experimental Research of Vibration Compaction Based on Drucker-Prager Mode. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2019, 38, 2–7. [Google Scholar] [CrossRef]
- Frenning, G. On the thermodynamic consistency of the Drucker–Prager Cap model: Modification of the plastic potential and analysis of unloading. Powder Technol. 2023, 423, 118503. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Z.; Yang, L. Accelerating fracture simulation with phase field methods based on Drucker-Prager criterion. Front. Phys. 2023, 11, 1159566. [Google Scholar] [CrossRef]
- Stopa, R.; Komarnicki, P.; Kuta, Ł.; Szyjewicz, D.; Słupska, M. Modeling with the finite element method the influence of shaped elements of loading components on the surface pressure distribution of carrot roots. Comput. Electron. Agric. 2019, 167, 105046. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Song, Y.; Zhang, R.; Wang, X. Finding the lowest damage picking mode for tomatoes based on finite element analysis. Comput. Electron. Agric. 2023, 204, 107536. [Google Scholar] [CrossRef]
- Hashiguchi, K.; Saitoh, K.; Okayasu, T.; Tsutsumi, S. Evaluation of typical conventional and unconventional plasticity models for prediction of softening behaviour of soils. Géotechnique 2002, 52, 561–578. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, H.; Yuan, L.; Zhang, B.; Wang, W.; Ma, Z.; Xue, Y.; Li, Y. A new test method and system for the circumferential deformation of cylindrical standard specimens in geotechnical mechanics and its application. Measurement 2020, 149, 107041. [Google Scholar] [CrossRef]
- Karmakar, S.; Lal Kushwaha, R. CFD simulation of soil forces on a flat tillage tool. In Proceedings of the 2005 ASAE Annual International Meeting, Tampa, FL, USA, 17–20 July 2005. [Google Scholar]
- Zeng, Z.; Ma, X.; Chen, Y.; Qi, L. Modelling residue incorporation of selected chisel ploughing tools using the discrete element method (DEM). Soil Tillage Res. 2020, 197, 104505. [Google Scholar] [CrossRef]
- Li, J.; Jiang, X.; Ma, Y.; Tong, J.; Hu, B. Bionic design of a potato digging shovel with drag reduction based on the discrete element method (Dem) in clay soil. Appl. Sci. 2020, 10, 7096. [Google Scholar] [CrossRef]
- Vilca, N.S.; Gómez-Amador, A.M.; Jiménez de Cisneros Fonfría, J.J. Soil–Structure Interaction Analysis Using the Finite Element Method in Thin-Walled Steel Pipes Buried under Haul Roads. Appl. Sci. 2024, 14, 167. [Google Scholar] [CrossRef]
- Pásthy, L.; József Farkas, Z.; Haba, T.; Tamás, K. Development of a multi-way coupled discrete-finite element method simulation procedure for modelling soil-passive vibration tool interaction. Comput. Electron. Agric. 2024, 216, 108459. [Google Scholar] [CrossRef]
- Song, W.; Jiang, X.; Li, L.; Ren, L.; Tong, J. Increasing the width of disturbance of plough pan with bionic inspired subsoilers. Soil Tillage Res. 2022, 220, 105356. [Google Scholar] [CrossRef]
- JB/T 9788-1999; Subsoiler and Share Shaft. Chinese Standard Press: Beijing, China, 1999.
- Arvidsson, J.; Keller, T.; Gustafsson, K. Specific draught for mouldboard plough, chisel plough and disc harrow at different water contents. Soil Tillage Res. 2004, 79, 221–231. [Google Scholar] [CrossRef]
- Abo-Elnor, M.; Hamilton, R.; Boyle, J.T. Simulation of soil-blade interaction for sandy soil using advanced 3D finite element analysis. Soil Tillage Res. 2004, 75, 61–73. [Google Scholar] [CrossRef]
- Wang, S.; Liu, X.; Qi, H.; Xu, Z.; Ma, Y. Determination of Biomechanical Parameters and Development of an Improved FEM Model for Perennial Alfalfa (Medicago sativa L.) Roots. Agronomy 2024, 14, 3033. [Google Scholar] [CrossRef]
- Wang, Y.; Li, N.; Ma, Y.; Tong, J.; Pfleging, W.; Sun, J. Field experiments evaluating a biomimetic shark-inspired (BioS) subsoiler for tillage resistance reduction. Soil Tillage Res. 2020, 196, 104432. [Google Scholar] [CrossRef]
- Torotwa, I.; Ding, Q.; Alele, J.O.; He, R. 3D Finite Element Analysis of the Tillage and Straw Cutting Performance of a Curved-Edged Toothed Disc. Eng. Agric. 2022, 42, 10–17. [Google Scholar] [CrossRef]
- Jiang, X.; Tong, J.; Ma, Y.; Sun, J. Development and verification of a mathematical model for the specific resistance of a curved subsoiler. Biosyst. Eng. 2020, 190, 107–119. [Google Scholar] [CrossRef]
- Tamás, K.; Jóri, I.J.; Mouazen, A.M. Modelling soil-sweep interaction with discrete element method. Soil Tillage Res. 2013, 134, 223–231. [Google Scholar] [CrossRef]
- He, C.; You, Y.; Wang, D.; Wang, G.; Lu, D.; Morris Togo Kaji, J. The effect of tine geometry during vertical movement on soil penetration resistance using finite element analysis. Comput. Electron. Agric. 2016, 130, 97–108. [Google Scholar] [CrossRef]
- Celik, H.K.; Caglayan, N.; Topakci, M.; Rennie, A.E.W.; Akinci, I. Strength-based design analysis of a Para-Plow tillage tool. Comput. Electron. Agric. 2020, 169, 105168. [Google Scholar] [CrossRef]
- Armin, A.; Fotouhi, R.; Szyszkowski, W. On the FE modeling of soil-blade interaction in tillage operations. Finite Elem. Anal. Des. 2014, 92, 1–11. [Google Scholar] [CrossRef]
- Tong, J.; Jiang, X.H.; Wang, Y.M.; Ma, Y.H.; Li, J.W.; Sun, J.Y. Tillage force and disturbance characteristics of different geometric-shaped subsoilers via DEM. Adv. Manuf. 2020, 8, 392–404. [Google Scholar] [CrossRef]
- Ibrahmi, A.; Bentaher, H.; Hamza, E.; Maalej, A.; Mouazen, A.M. Study the effect of tool geometry and operational conditions on mouldboard plough forces and energy requirement: Part 2. Experimental validation with soil bin test. Comput. Electron. Agric. 2015, 117, 268–275. [Google Scholar] [CrossRef]
- Bahrami, M.; Naderi-Boldaji, M.; Ghanbarian, D.; Keller, T. Simulation of soil stress under plate sinkage loading: A comparison of finite element and discrete element methods. Soil Tillage Res. 2022, 223, 105463. [Google Scholar] [CrossRef]
- Xu, L.; Peng, X.; Lu, G. Dynamic Response Analysis of Gas Pipeline under Land slide Based on DEM-FEM Coupling. Sci. Technol. Eng. 2022, 22, 3518–3524. [Google Scholar]
- Li, B.; Wang, C.; Li, Y.; Zhang, S. Dynamic Response Study of Impulsive Force of Debris Flow Evaluation and Flexible Retaining Structure Based on SPH-DEM-FEM Coupling. Adv. Civ. Eng. 2021, 2021, 9098250. [Google Scholar] [CrossRef]
- Wang, Q.; Cao, X.; Wang, C.; Li, H.; He, J.; Lu, C. Research Progress of No/Minimum Tillage Corn Seeding Technology andMachine in Northeast Black Land of China. Trans. Chin. Soc. Agric. Eng. 2021, 52, 1–15. [Google Scholar] [CrossRef]
- Cheng, H.; Tang, H.; Wu, Q.; Li, G. An elasto-plasticity extended Cam-clay model for unsaturated soils usingexplicit integration algorithm in FEM with hydraulic hysteresis. Rock Soil Mech. 2020, 41, 676–686+694. [Google Scholar] [CrossRef]
- Tolooiyan, A.; Gavin, K. Modelling the Cone Penetration Test in sand using Cavity Expansion and Arbitrary Lagrangian Eulerian Finite Element Methods. Comput. Geotech. 2011, 38, 482–490. [Google Scholar] [CrossRef]
- Ning, T.; Liu, Z.; Hu, H.; Li, G.; Kuzyakov, Y. Physical, chemical and biological subsoiling for sustainable agriculture. Soil Tillage Res. 2022, 223, 105490. [Google Scholar] [CrossRef]
- Jin, H.; Huang, S.; Shi, D.; Li, J.; Li, J.; Li, Y.; Zhu, H. Effects of Different Tillage Practices on Soil Stability and Erodibility for Red Soil Sloping Farmland in Southern China. Agronomy 2023, 13, 1310. [Google Scholar] [CrossRef]
- Higaki, D.; Karki, K.K.; Gautam, C.S. Soil erosion control measures on degraded sloping lands: A case study in Midlands of Nepal. Aquat. Ecosyst. Health Manag. 2005, 8, 243–249. [Google Scholar] [CrossRef]
- Qin, K.; Zhao, Y.; Zhang, Y.; Cao, C.; Shen, Z. Lateral stress and its transmission law caused by operation of a double-wing subsoiler in sandy loam soil. Front. Environ. Sci. 2022, 10, 986361. [Google Scholar] [CrossRef]
- Håkansson, I. Subsoil compaction caused by heavy vehicles-a long-term threat to soil productivity. Soil Tillage Res. 1994, 29, 105–110. [Google Scholar] [CrossRef]
- Possinger, A.R.; Weiglein, T.L.; Bowman, M.M.; Gallo, A.C.; Hatten, J.A.; Heckman, K.A.; Matosziuk, L.M.; Nave, L.E.; SanClements, M.D.; Swanston, C.W.; et al. Climate Effects on Subsoil Carbon Loss Mediated by Soil Chemistry. Environ. Sci. Technol. 2021, 55, 16224–16235. [Google Scholar] [CrossRef]
- Lou, S.; He, J.; Li, H.; Wang, Q.; Lu, C.; Liu, W.; Liu, P.; Zhang, Z.; Li, H. Current knowledge and future directions for improving subsoiling quality and reducing energy consumption in conservation fields. Agriculture 2021, 11, 575. [Google Scholar] [CrossRef]





| Parameter | Cultivated Layer | Plough Pan Layer | Subsoil Layer |
|---|---|---|---|
| ρ Volume density (mg·m−3) | 1.41 | 1.67 | 1.53 |
| E Young’s modulus (MPa) | 2.3 | 2.61 | 2.52 |
| β Friction angle (°) | 24.73 | 24.73 | 24.73 |
| Soil moisture content (%) | 10.21 | 15.13 | 10.62 |
| ν Poisson’s ratio | 0.3 | 0.3 | 0.3 |
| k Flow Stress ratio | 0.8668 | 0.8668 | 0.8668 |
| Ψ Dilation angle (°) | 0 | 0 | 0 |
| Measurement Items | Depth From Surface (mm) | |||
|---|---|---|---|---|
| Cultivated Layer | Plough Pan Layer | Subsoil Layer | ||
| 0–120 | 120–300 | 300–380 | 380–640 | |
| Soil particle density (g·cm−3) | 2.62 ± 0.01 a | 2.70 ± 0.02 b | 2.60 ± 0.01 a | 2.62 ± 0.02 a |
| Soil dry bulk density (g·cm−3) | 1.36 ± 0.01 a | 1.44 ± 0.01 b | 1.67 ± 0.01 d | 1.53 ± 0.01 c |
| Soil moisture content (%) | 5.31 ± 0.01 a | 10.2 ± 0.01 c | 13.6 ± 0.01 c | 9.1 ± 0.01 b |
| Measurement Items | Depth From Surface (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Cultivated Layer | Plough Pan Layer | Subsoil Layer | |||||||
| 0–300 | 300–380 | 380–640 | |||||||
| Soil texture classification | sand | silt | clay | sand | silt | clay | sand | silt | clay |
| Percentage of particle size | 47.8 | 39.1 | 13.1 | 48.6 | 39.3 | 12.1 | 47.2 | 39.2 | 13.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, W.; Ren, L.; Wang, J.; Ma, Y.; Guo, Y.; Han, M.; Zhao, H. Methods for Constructing Soil Dynamic Models Under Intelligent Cultivation: Dynamic Interaction Mechanisms Between Farming Tools with Complex Structures and Soil. Agriculture 2025, 15, 1355. https://doi.org/10.3390/agriculture15131355
Song W, Ren L, Wang J, Ma Y, Guo Y, Han M, Zhao H. Methods for Constructing Soil Dynamic Models Under Intelligent Cultivation: Dynamic Interaction Mechanisms Between Farming Tools with Complex Structures and Soil. Agriculture. 2025; 15(13):1355. https://doi.org/10.3390/agriculture15131355
Chicago/Turabian StyleSong, Wei, Lili Ren, Jingli Wang, Yunhai Ma, Yingjie Guo, Minglei Han, and Huaixiang Zhao. 2025. "Methods for Constructing Soil Dynamic Models Under Intelligent Cultivation: Dynamic Interaction Mechanisms Between Farming Tools with Complex Structures and Soil" Agriculture 15, no. 13: 1355. https://doi.org/10.3390/agriculture15131355
APA StyleSong, W., Ren, L., Wang, J., Ma, Y., Guo, Y., Han, M., & Zhao, H. (2025). Methods for Constructing Soil Dynamic Models Under Intelligent Cultivation: Dynamic Interaction Mechanisms Between Farming Tools with Complex Structures and Soil. Agriculture, 15(13), 1355. https://doi.org/10.3390/agriculture15131355









