Evaluating Coupling Security and Joint Risks in Northeast China Agricultural Systems Based on Copula Functions and the Rel–Cor–Res Framework
Abstract
1. Introduction
2. Materials and Methods
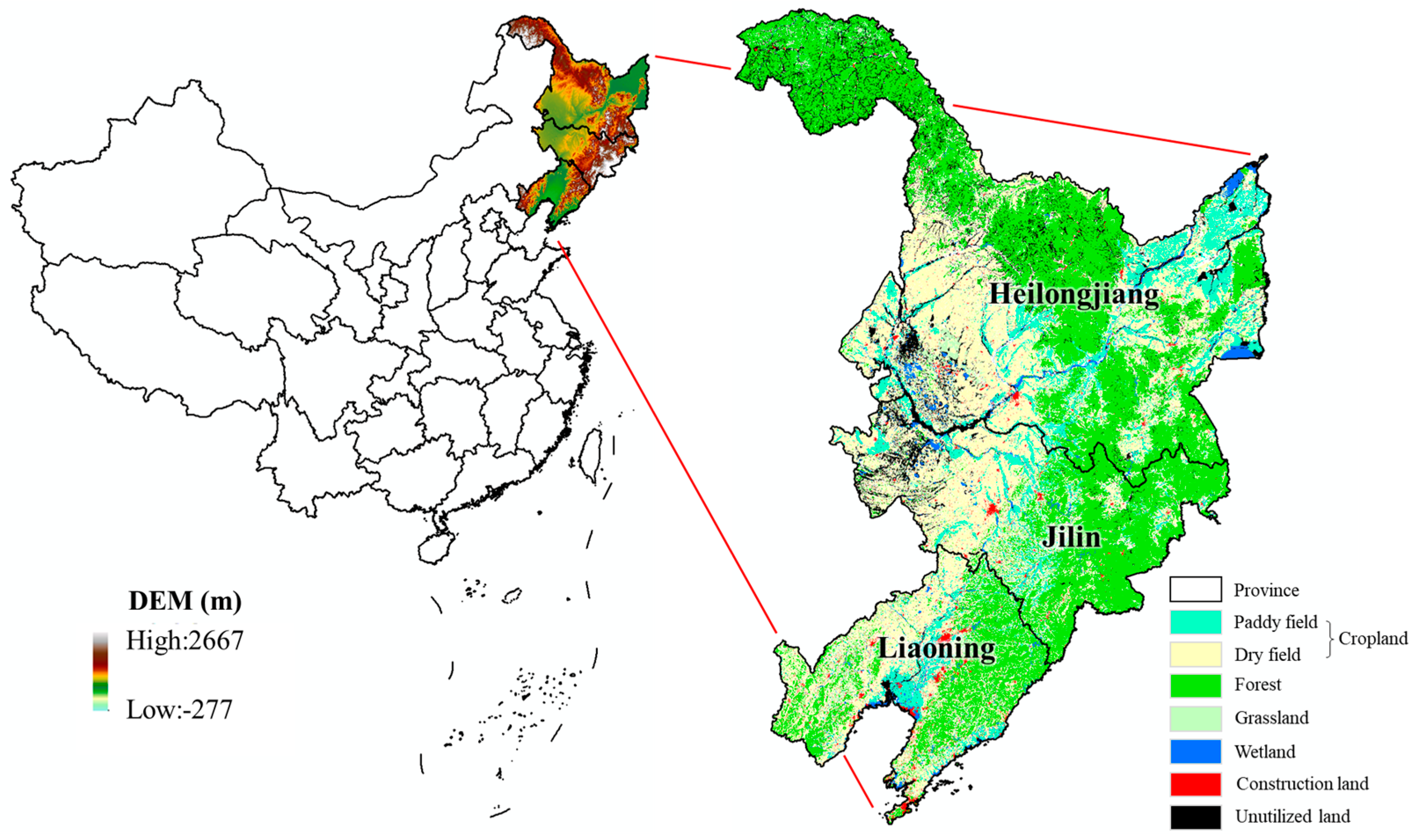
2.1. Study Area
2.2. Research Framework and Indicator System
2.2.1. Conceptual Framework of Agricultural System Coupling Security
2.2.2. Indicator System Construction and Data Sources
2.3. Comprehensive Evaluation Method
2.3.1. Indicator Normalization
2.3.2. Integrated Weighting Method
- (1)
- EWM
- (2)
- CRITIC Method
- (3)
- Integrated Weighting
2.3.3. Coupling Security Index Calculation
2.3.4. Security Level Classification
2.4. Obstacle Factor Diagnosis
2.5. Fitting Marginal Distributions for Rel, Cor, and Res
2.6. Multivariate Copula Modeling of Rel-Cor-Res
3. Results
3.1. Evaluation of Agricultural System Coupling Security
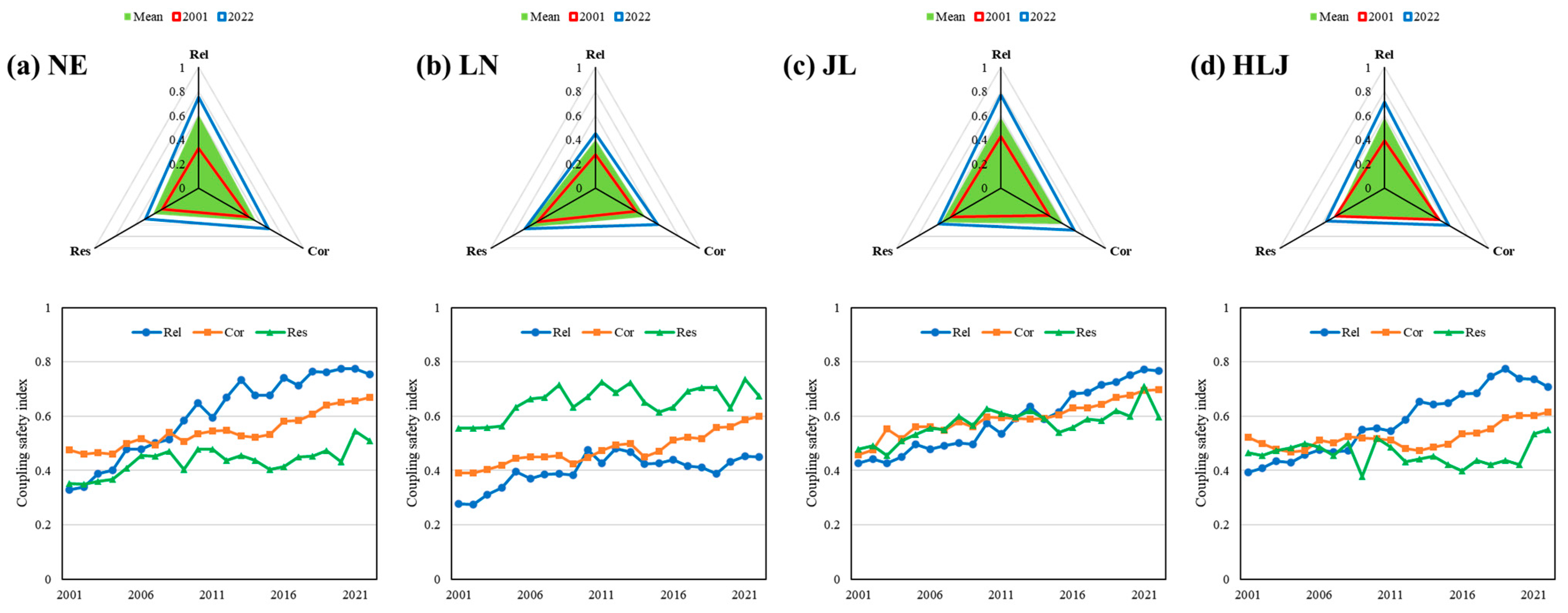
3.1.1. Spatiotemporal Evolution of Rel–Cor–Res
3.1.2. Spatiotemporal Evolution of Agricultural System Coupling Security Index
3.2. Obstacle Factor Analysis
3.3. Results of Copula Model Fitting
3.3.1. Determination of Marginal Distribution Models
3.3.2. Determination of Multivariate Joint Distribution Models
3.4. AS-CSI Risk Probability
3.4.1. Bivariate Joint Risk Probability
3.4.2. Trivariate Joint Risk Probability
4. Discussion
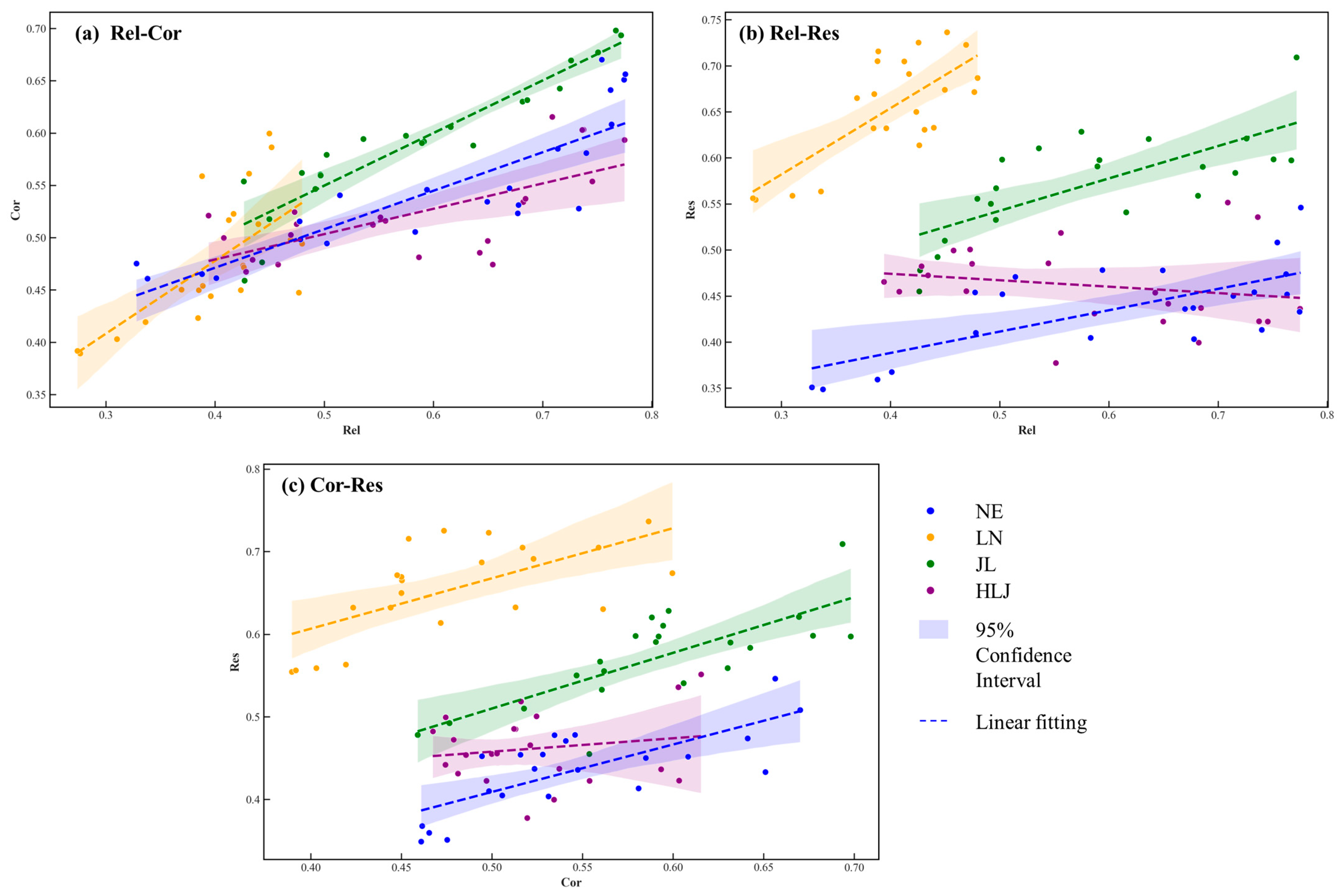
4.1. Relationships Among Rel–Cor–Res
4.2. Policy Implications
4.3. Comparison with Previous Studies
5. Conclusions
- (1)
- The Agricultural System Coupling Security Index (CSI) in Northeast China showed a significant upward trend, increasing from 0.38 in 2001 to 0.62 in 2022, indicating a shift from an insecure to a relatively secure state. Among the three provinces, Jilin had the highest multi-year average CSI (0.58), while Liaoning and Heilongjiang were slightly lower, at 0.51 and 0.52, respectively.
- (2)
- At the Northeast regional level, Rel increased rapidly over time, with a multi-year average of 0.60. Cor started at the highest initial level (0.48) but grew slowly between 2001 and 2015, averaging 0.55 over the study period. Res showed an initial increase followed by stabilization, with a relatively low average of 0.44.
- (3)
- Five key obstacle indicators—area under soil erosion control, reservoir storage capacity per capita, pesticide application amount, rural electricity consumption per capita, and proportion of agricultural water use—were identified as common and significant threats to agricultural system security across the region.
- (4)
- The bivariate joint probability of Rel–Cor reaching the relatively secure threshold (0.8) was the highest at 0.7643, reflecting strong reliability and coordination in the region. In contrast, the probabilities for Rel–Res and Cor–Res to reach the same threshold were lower, at 0.7164 and 0.7318, respectively.
- (5)
- The trivariate joint probability of Rel-Cor-Res reaching the relatively secure threshold (0.8) was the highest in Jilin (0.5538) and the lowest in Heilongjiang (0.5413). This highlights the importance of synergistic and balanced development across reliability, coordination, and resilience dimensions to enhance overall agricultural system coupling security.
- (6)
- This study introduces and operationalizes the concept of agricultural systems coupling security, which integrates the dimensions of reliability, coordination, and resilience to holistically assess the performance and stability of agricultural systems under complex environmental and socio-economic conditions. Although this term is not yet widely established in the existing literature, it offers a novel analytical lens for capturing the internal interdependence among critical resource subsystems and their collective response to external stressors. Moving forward, the Rel–Cor–Res framework and its coupling security index can serve as a foundational tool for cross-regional comparisons, scenario-based policy simulations, and long-term sustainability evaluations. It also provides a quantitative basis for studying macro-level properties of agricultural systems, such as systemic robustness, coupling dynamics, and risk transmission.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
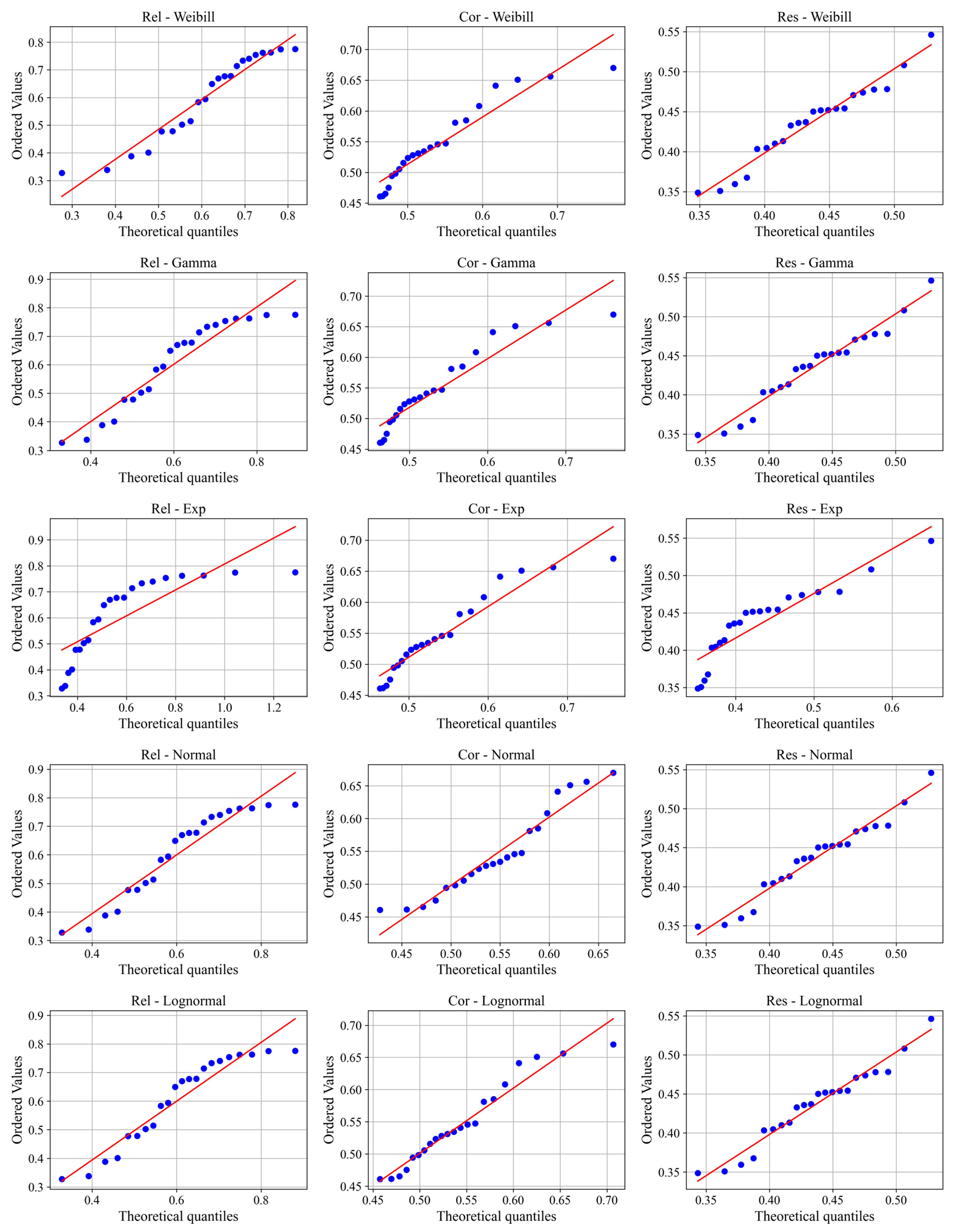

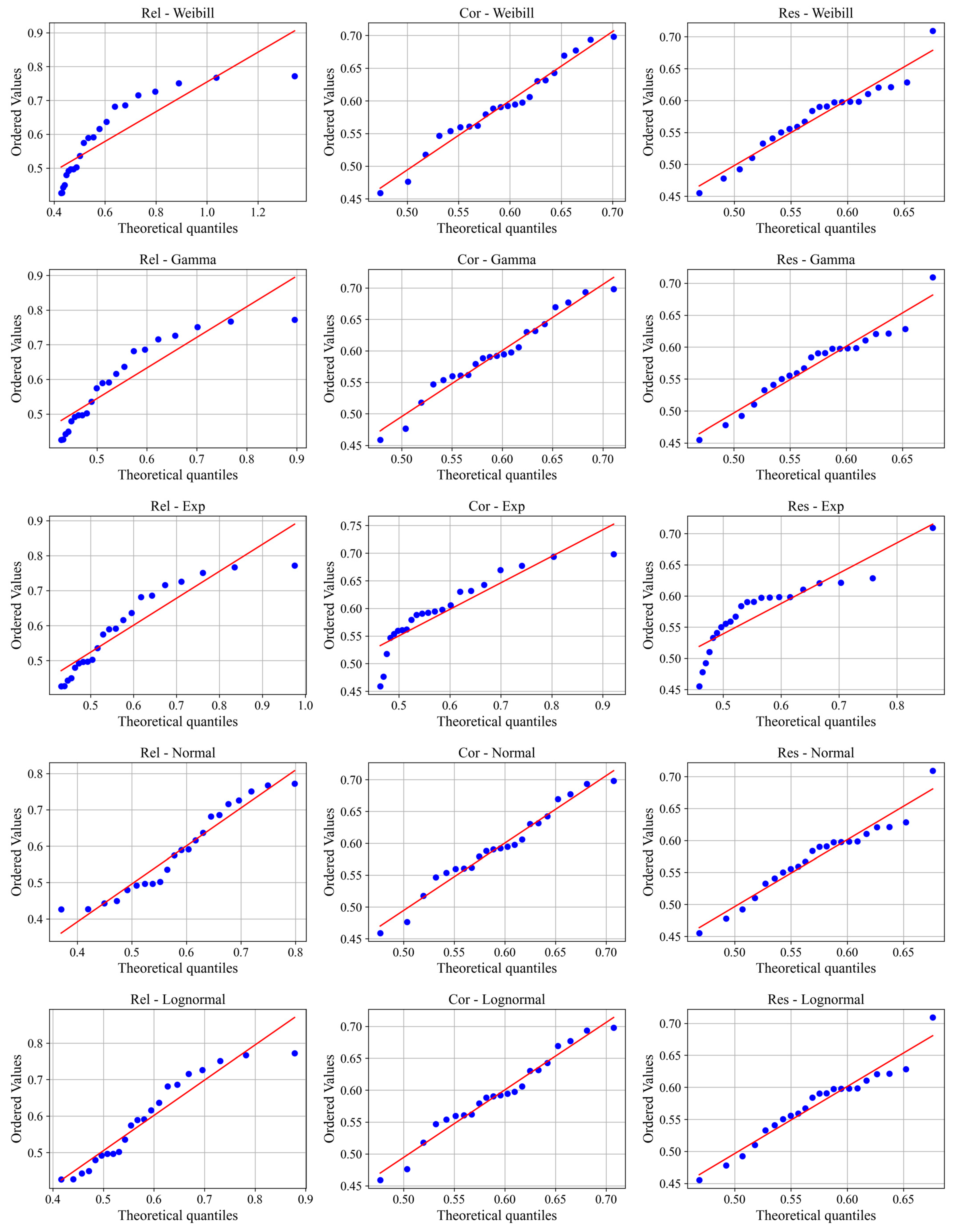

| Dimension | Marginal Distribution | Liaoning | Jilin | Heilongjiang | Northeast | ||||
|---|---|---|---|---|---|---|---|---|---|
| P | D | P | D | P | D | P | D | ||
| Rel | Weibill | / | / | 0.1797 | 0.4263 | 0.1767 | 0.447 | / | / |
| Gamma | 0.1764 | 0.4492 | 0.249 | 0.1092 | / | / | 0.1767 | 0.4471 | |
| Exp | 0.3546 | 0.0056 | 0.1547 | 0.6137 | 0.1886 | 0.3676 | 0.2393 | 0.1359 | |
| Normal | 0.1612 | 0.5628 | 0.1722 | 0.4791 | 0.1731 | 0.4726 | 0.1705 | 0.492 | |
| Lognormal | / | / | 0.1322 | 0.7899 | / | / | / | / | |
| Cor | Weibill | 0.1145 | 0.9039 | 0.1166 | 0.8927 | 0.1074 | 0.9382 | 0.1698 | 0.4968 |
| Gamma | 0.1141 | 0.906 | 0.0983 | 0.9695 | 0.1228 | 0.8548 | 0.2173 | 0.2161 | |
| Exp | 0.232 | 0.1593 | 0.3461 | 0.0074 | 0.1437 | 0.7016 | 0.1553 | 0.6092 | |
| Normal | 0.1577 | 0.5897 | 0.1015 | 0.9599 | 0.1688 | 0.5048 | 0.176 | 0.4518 | |
| Lognormal | 0.1073 | 0.9384 | / | / | 0.1103 | 0.9253 | 0.091 | 0.9854 | |
| Res | Weibill | 0.1128 | 0.9131 | 0.1268 | 0.8281 | 0.1006 | 0.963 | 0.1232 | 0.8523 |
| Gamma | 0.1345 | 0.773 | / | / | 0.0907 | 0.9858 | / | / | |
| Exp | 0.307 | 0.0245 | 0.3031 | 0.0273 | 0.3245 | 0.0146 | 0.2853 | 0.0445 | |
| Normal | 0.1288 | 0.8144 | 0.1289 | 0.8132 | 0.1015 | 0.9601 | 0.1166 | 0.8926 | |
| Lognormal | / | / | / | / | 0.0899 | 0.987 | / | / | |
| Region | Dimension | Weibill | Gamma | Exp | Normal | Lognormal | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| k | λ | α | θ | θ | μ | σ | σ | μ | ||
| Liaoning | Rel | / | / | 284.187 | 0.003 | 0.127 | 0.4 | 0.057 | / | / |
| Jilin | 0.722 | 0.163 | 0.816 | 0.152 | 0.158 | 0.584 | 0.115 | 0.422 | 0.265 | |
| Heilongjiang | 1.682 | 0.232 | / | / | 0.187 | 0.582 | 0.122 | / | / | |
| Northeast | / | / | 226.615 | 0.01 | 0.276 | 0.604 | 0.148 | / | / | |
| Liaoning | Cor | 1.618 | 0.108 | 3.142 | 0.036 | 0.089 | 0.478 | 0.059 | 0.318 | 0.18 |
| Jilin | 4.335 | 0.258 | 395.667 | 0.003 | 0.133 | 0.592 | 0.062 | / | / | |
| Heilongjiang | 1.189 | 0.06 | 1.226 | 0.046 | 0.056 | 0.523 | 0.044 | 0.647 | 0.059 | |
| Northeast | 0.944 | 0.084 | 0.79 | 0.099 | 0.085 | 0.546 | 0.064 | 0.447 | 0.134 | |
| Liaoning | Res | 24.853 | 1.156 | 237.219 | 0.004 | 0.1 | 0.654 | 0.056 | / | / |
| Jilin | 3.469 | 0.194 | / | / | 0.117 | 0.572 | 0.056 | / | / | |
| Heilongjiang | 2.714 | 0.12 | 35.35 | 0.007 | 0.084 | 0.461 | 0.043 | 0.107 | 0.393 | |
| Northeast | 3.055 | 0.152 | / | / | 0.087 | 0.436 | 0.049 | / | / | |
| Variable | Copula Function | Liaoning | Jilin | ||||
|---|---|---|---|---|---|---|---|
| θ | AIC | BIC | θ | AIC | BIC | ||
| Rel-Cor | Clayton | 2.125 | 31.2655 | 32.3565 | 10.8333 | 27.9354 | 29.0265 |
| Gumbel | 2.0625 | 17.14 | 18.2311 | 6.4167 | −38.4891 | −37.3981 | |
| Frank | 6.0187 | 23.1945 | 24.2855 | / | / | / | |
| Rel-Res | Clayton | 1.3971 | 17.2077 | 18.2988 | 2.62 | −21.5269 | −20.4359 |
| Gumbel | 1.6985 | 8.4586 | 9.5496 | 2.31 | −8.9757 | −7.8846 | |
| Frank | 4.3182 | 13.2361 | 14.3272 | 7.1113 | −13.5862 | −12.4952 | |
| Cor-Res | Clayton | 2.125 | −18.8902 | −17.7991 | 2.2778 | −9.3308 | −8.2397 |
| Gumbel | 2.0625 | −7.5409 | −6.4499 | 2.1389 | −9.8078 | −8.7167 | |
| Frank | 6.0187 | −9.4897 | −8.3987 | 6.3599 | −14.8109 | −13.7198 | |
| Rel-Cor-Res | Frank | 1.1481 | −48.7365 | −47.6454 | 1.4361 | −89.7175 | −88.6265 |
| Clayton | 1 | −5.618 | −4.527 | 1.1605 | −36.9292 | −35.8381 | |
| Variable | Copula function | Heilongjiang | Northeast | ||||
| θ | AIC | BIC | θ | AIC | BIC | ||
| Rel-Cor | Clayton | 1.6094 | 22.0027 | 23.0937 | 5.4516 | 104.8431 | 105.9341 |
| Gumbel | 1.8047 | 4.6171 | 5.7081 | 3.7258 | 52.1079 | 53.1989 | |
| Frank | 4.8302 | 10.0159 | 11.107 | 13.0205 | 66.1054 | 67.1964 | |
| Rel-Res | Clayton | / | / | / | 1.4478 | −17.5156 | −16.4245 |
| Gumbel | / | / | / | 1.7239 | −25.8198 | −24.7288 | |
| Frank | −1.8094 | 2.8289 | 3.9199 | 4.442 | −22.3164 | −21.2253 | |
| Cor-Res | Clayton | 0.0263 | 2.2636 | 3.3547 | 2.125 | 32.6501 | 33.7412 |
| Gumbel | 1.0132 | 1.696 | 2.787 | 2.0625 | 16.8557 | 17.9467 | |
| Frank | 0.1172 | 2.0353 | 3.1264 | 6.0187 | 23.9647 | 25.0557 | |
| Rel-Cor-Res | Frank | 1.0071 | −48.3442 | −47.2531 | 1.1263 | −12.8303 | −11.7393 |
| Clayton | 1 | 38.7812 | 39.8722 | 0.495 | −12.4066 | −11.3156 | |
References
- Viana, C.M.; Freire, D.; Abrantes, P.; Rocha, J.; Pereira, P. Agricultural land systems importance for supporting food security and sustainable development goals: A systematic review. Sci. Total Environ. 2022, 806, 150718. [Google Scholar] [CrossRef] [PubMed]
- Ben Hassen, T.; El Bilali, H. Impacts of the Russia-Ukraine war on global food security: Towards more sustainable and resilient food systems? Foods 2022, 11, 2301. [Google Scholar] [CrossRef] [PubMed]
- Krishnamurthy, R.P.K.; Fisher, J.B.; Choularton, R.J.; Kareiva, P.M. Anticipating drought-related food security changes. Nat. Sustain. 2022, 5, 956–964. [Google Scholar] [CrossRef]
- He, T.; Hu, Y.; Li, F.; Chen, Y.; Zhang, M.; Zheng, Q.; Jin, Y.; Ren, H. Mapping Land- and Offshore-Based Wind Turbines in China in 2023 with Sentinel-2 Satellite Data. Renew. Sustain. Energy Rev. 2025, 214, 115566. [Google Scholar] [CrossRef]
- Abbas, S.; Haider, A.; Kousar, S.; Lu, H.; Lu, S.; Liu, F.; Li, H.; Miao, C.; Feng, W.; Ahamad, M.I.; et al. Climate variability, population growth, and globalization impacting food security in Pakistan. Sci. Rep. 2025, 15, 4225. [Google Scholar] [CrossRef] [PubMed]
- Khatri, P.; Kumar, P.; Shakya, K.S.; Kirlas, M.C.; Tiwari, K.K. Understanding the intertwined nature of rising multiple risks in modern agriculture and food system. Environ. Dev. Sustain. 2024, 26, 24107–24150. [Google Scholar] [CrossRef]
- Maqbool, M.E.; Farhan, A.; Qamar, M.A. Global impact of COVID-19 on food safety and environmental sustainability: Pathways to face the pandemic crisis. Heliyon 2024, 10, 15. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Y.; Zhu, Y.; Li, Y.; Cui, J.; Yu, B. Multidimensional deconstruction and workable solutions for addressing China’s food security issues: From the perspective of sustainable diets. Land Use Policy 2025, 148, 107401. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations (FAO). The State of Food Security and Nutrition in the World (SOFI) Report 2023; FAO: Rome, Italy, 2023. [Google Scholar]
- United Nations (UN). Transforming Our World: The 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2015; Available online: https://sdgs.un.org/2030agenda (accessed on 10 May 2025).
- Noe, E.; Alrøe, H.F. Sustainable agriculture issues explained by differentiation and structural coupling using social systems analysis. Agron. Sustain. Dev. 2015, 35, 133–144. [Google Scholar] [CrossRef]
- Li, M.; Li, H.; Fu, Q.; Liu, D.; Yu, L.; Li, T. Approach for optimizing the water–land–food–energy nexus in agroforestry systems under climate change. Agric. Syst. 2021, 192, 103201. [Google Scholar] [CrossRef]
- Chang, H.; Zhao, Y.; Cao, Y.; He, G.; Wang, Q.; Liu, R.; Ren, H.; Yao, J.; Li, W. Evaluating Sustainability of Water–Energy–Food–Ecosystems Nexus in Water-Scarce Regions via Coupled Simulation Model. Agriculture 2025, 15, 1271. [Google Scholar] [CrossRef]
- De Haen, H.; Hemrich, G. The economics of natural disasters: Implications and challenges for food security. Agric. Econ. 2007, 37, 31–45. [Google Scholar] [CrossRef]
- Lin, B.; Wang, Y. How does natural disasters affect China agricultural economic growth? Energy 2024, 296, 131096. [Google Scholar] [CrossRef]
- Trusova, N.V.; Hryvkivska, O.V.; Kotvytska, N.M.; Nesterenko, S.A.; Yavorska, T.I.; Kotyk, O.V. Determinants of the innovative and investment development of agriculture. Int. J. Agric. Ext. 2021, 9, 81–100. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Song, J. Analysis of the threshold effect of agricultural industrial agglomeration and industrial structure upgrading on sustainable agricultural development in China. J. Clean. Prod. 2022, 341, 130818. [Google Scholar] [CrossRef]
- Van der Ploeg, J.D.; Barjolle, D.; Bruil, J.; Brunori, G.; Madureira, L.M.C.; Dessein, J.; Drąg, Z.; Fink-Kessler, A.; Gasselin, P.; de Molina, M.G.; et al. The economic potential of agroecology: Empirical evidence from Europe. J. Rural Stud. 2019, 71, 46–61. [Google Scholar] [CrossRef]
- Manikas, I.; Ali, B.M.; Sundarakani, B. A systematic literature review of indicators measuring food security. Agric. Food Secur. 2023, 12, 10. [Google Scholar] [CrossRef] [PubMed]
- Gutzler, C.; Helming, K.; Balla, D.; Dannowski, R.; Deumlich, D.; Glemnitz, M.; Knierim, A.; Mirschel, W.; Nendel, C.; Paul, C.; et al. Agricultural land use changes–a scenario-based sustainability impact assessment for Brandenburg, Germany. Ecol. Indic. 2015, 48, 505–517. [Google Scholar] [CrossRef]
- Ye, S.; Wang, J.; Jiang, J.; Gao, P.; Song, C. Coupling input and output intensity to explore the sustainable agriculture intensification path in mainland China. J. Clean. Prod. 2024, 442, 140827. [Google Scholar] [CrossRef]
- Liu, F.; Wang, C.; Zhang, Y.; Zhou, S.; Yang, Y.; Wu, X.; Hu, F.; Liu, C. Data-driven analysis and evaluation of regional agriculture for high-quality development of Anhui Province in the Yangtze River Delta. Environ. Sci. Pollut. Res. 2022, 29, 1–14. [Google Scholar]
- Wang, X. Managing land carrying capacity: Key to achieving sustainable production systems for food security. Land 2022, 11, 484. [Google Scholar] [CrossRef]
- Sami, M.; Shiekhdavoodi, M.J.; Pazhohanniya, M.; Pazhohanniya, F. Environmental comprehensive assessment of agricultural systems at the farm level using fuzzy logic: A case study in cane farms in Iran. Environ. Model. Softw. 2014, 58, 95–108. [Google Scholar] [CrossRef]
- Zhao, Y.; Talha, M. Evaluation of food safety problems based on the fuzzy comprehensive analysis method. Food Sci. Technol. 2021, 42, e47321. [Google Scholar] [CrossRef]
- Liu, D.; Qi, X.; Fu, Q.; Li, M.; Zhu, W.; Zhang, L.; Faiz, M.A.; Khan, M.I.; Li, T.; Cui, S. A resilience evaluation method for a combined regional agricultural water and soil resource system based on Weighted Mahalanobis distance and a Gray-TOPSIS model. J. Clean. Prod. 2019, 229, 667–679. [Google Scholar] [CrossRef]
- Li, D.; Chen, J.; Qiu, M. The evaluation and analysis of the entropy weight method and the fractional grey model study on the development level of modern agriculture in Huizhou. Math. Probl. Eng. 2021, 2021, 5543368. [Google Scholar] [CrossRef]
- Zhang, X.; Yao, G.; Vishwakarma, S.; Dalin, C.; Komarek, A.M.; Kanter, D.R.; Davis, K.F.; Pfeifer, K.; Zhao, J.; Zou, T.; et al. Quantitative assessment of agricultural sustainability reveals divergent priorities among nations. One Earth 2021, 4, 1262–1277. [Google Scholar] [CrossRef]
- Chen, Z.; Sarkar, A.; Rahman, A.; Li, X.; Xia, X. Exploring the drivers of green agricultural development (GAD) in China: A spatial association network structure approaches. Land Use Policy 2022, 112, 105827. [Google Scholar] [CrossRef]
- Sarkar, A.; Azim, J.A.; Al Asif, A.; Qian, L.; Peau, A.K. Structural equation modeling for indicators of sustainable agriculture: Prospective of a developing country’s agriculture. Land Use Policy 2021, 109, 105638. [Google Scholar] [CrossRef]
- Bathaei, A.; Štreimikienė, D. A systematic review of agricultural sustainability indicators. Agriculture 2023, 13, 241. [Google Scholar] [CrossRef]
- Cui, X.; Cai, T.; Deng, W.; Zheng, R.; Jiang, Y.; Bao, H. Indicators for evaluating high-quality agricultural development: Empirical study from Yangtze River Economic Belt, China. Soc. Indic. Res. 2022, 164, 1101–1127. [Google Scholar] [CrossRef]
- Yu, J.; Wu, G. Spatial disparities and dynamics in the high quality agricultural development in Heilongjiang Province of China. Sci. Rep. 2025, 15, 4765. [Google Scholar] [CrossRef]
- Cansino-Loeza, B.; Ponce-Ortega, J.M. Sustainable assessment of Water-Energy-Food Nexus at regional level through a multi-stakeholder optimization approach. J. Clean. Prod. 2021, 290, 125194. [Google Scholar] [CrossRef]
- Hao, L.; Wang, P.; Yu, J.; Ruan, H. An integrative analytical framework of water–energy–food security for sustainable development at the country scale: A case study of five Central Asian countries. J. Hydrol. 2022, 607, 127530. [Google Scholar] [CrossRef]
- Qin, J.; Duan, W.; Chen, Y.; Dukhovny, V.A.; Sorokin, D.; Li, Y.; Wang, X. Comprehensive evaluation and sustainable development of water–energy–food–ecology systems in Central Asia. Renew. Sustain. Energy Rev. 2022, 157, 112061. [Google Scholar] [CrossRef]
- Radmehr, R.; Ghorbani, M.; Ziaei, A.N. Quantifying and managing the water–energy–food nexus in dry regions food insecurity: New methods and evidence. Agric. Water Manag. 2021, 245, 106588. [Google Scholar] [CrossRef]
- Qian, X.Y.; Liang, Q.M. Sustainability evaluation of the provincial water–energy–food nexus in China: Evolutions, obstacles, and response strategies. Sustain. Cities Soc. 2021, 75, 103332. [Google Scholar] [CrossRef]
- Correa-Cano, M.; Salmoral, G.; Rey, D.; Knox, J.; Graves, A.; Melo, O.; Foster, W.; Naranjo, L.; Zegarra, E.; Johnson, C.; et al. A novel modelling toolkit for unpacking the Water-Energy-Food-Environment (WEFE) nexus of agricultural development. Renew. Sustain. Energy Rev. 2022, 159, 112182. [Google Scholar] [CrossRef]
- Mirzaei, A.; Abdeshahi, A.; Azarm, H.; Naghavi, S. New design of water–energy–food–environment nexus for sustainable agricultural management. Stoch. Environ. Res. Risk Assess. 2022, 36, 1861–1874. [Google Scholar] [CrossRef]
- Ren, H.; Liu, B.; Zhang, Z.; Li, F.; Pan, K.; Zhou, Z.; Xu, X. A water–energy–food–carbon nexus optimization model for sustainable agricultural development in the Yellow River Basin under uncertainty. Appl. Energy 2022, 326, 120008. [Google Scholar] [CrossRef]
- Yue, Q.; Wu, H.; Wang, Y.; Guo, P. Achieving sustainable development goals in agricultural energy–water–food nexus system: An integrated inexact multi-objective optimization approach. Resour. Conserv. Recycl. 2021, 174, 105833. [Google Scholar] [CrossRef]
- Bazzana, D.; Foltz, J.; Zhang, Y. Impact of climate smart agriculture on food security: An agent-based analysis. Food Policy 2022, 111, 102304. [Google Scholar] [CrossRef]
- Wang, W.; Li, K.; Liu, Y.; Lian, J.; Hong, S. A system dynamics model analysis for policy impacts on green agriculture development: A case of the Sichuan Tibetan Area. J. Clean. Prod. 2022, 371, 133562. [Google Scholar] [CrossRef]
- Walters, J.P.; Archer, D.W.; Sassenrath, G.F.; Hendrickson, J.R.; Hanson, J.D.; Halloran, J.M.; Vadas, P.; Alarcon, V.J. Exploring agricultural production systems and their fundamental components with system dynamics modelling. Ecol. Model. 2016, 333, 51–65. [Google Scholar] [CrossRef]
- Pasqualino, R.; Monasterolo, I.; Jones, A. An integrated global food and energy security system dynamics model for addressing systemic risk. Sustainability 2019, 11, 3995. [Google Scholar] [CrossRef]
- Qazi, A.; Al-Mhdawi, M.K.S. Sustainability and adaptation dynamics in global food security: A Bayesian belief network approach. J. Clean. Prod. 2024, 467, 142931. [Google Scholar] [CrossRef]
- Eyre, R.W.; House, T.; Gómez-Olivé, F.X.; Griffiths, F.E. Bayesian belief network modelling of household food security in rural South Africa. BMC Public Health 2021, 21, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Zou, J.; Long, H.L. The variation of farmland use and the security pattern of grain production in China since 1978. J. Nat. Resour. 2009, 24, 1366–1377. [Google Scholar]
- Yao, C.; Wei, Y.; Lin, H.; Cui, H. Spatial-temporal pattern and coupling coordination evolution of the vulnerability of food production and consumption ability in China. Econ. Geogr. 2019, 39, 147–156. [Google Scholar]
- Al Rashed, M.; Sefelnasr, A.; Sherif, M.; Murad, A.; Alshamsi, D.; Aliewi, A.; Ebraheem, A.A. Novel concept for water scarcity quantification considering nonconventional and virtual water resources in arid countries: Application in Gulf Cooperation Council countries. Sci. Total Environ. 2023, 882, 163473. [Google Scholar] [CrossRef]
- Luo, L.; Xing, Z.; Chu, B.; Zhang, H.; Wang, H. Virtual land trade and associated risks to food security in China. Environ. Impact Assess. Rev. 2024, 106, 107461. [Google Scholar] [CrossRef]
- Chen, L.; Chang, J.; Wang, Y.; Guo, A.; Liu, Y.; Wang, Q.; Zhu, Y.; Zhang, Y.; Xie, Z. Disclosing the future food security risk of China based on crop production and water scarcity under diverse socioeconomic and climate scenarios. Sci. Total Environ. 2021, 790, 148110. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.Y.; Pang, B.; He, J.J.; Guo, Y.; Zhu, L.Q. Coupling relationship and trend of cultivated land productivity and food security: A case study of Henan Province. Sci. Geogr. Sin. 2017, 37, 1392–1402. [Google Scholar]
- Yang, S.; Li, D.; Liao, H.; Zhu, L.; Zhou, M.; Cai, Z. Analysis of the balance between supply and demand of arable land in China based on food security. Sustainability 2023, 15, 5706. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y. Analysis of dynamic changes and main obstacle factors of grain supply and demand balance in northwest China. Sustainability 2023, 15, 10835. [Google Scholar] [CrossRef]
- Chen, L.; Xia, X.; Zhang, J.; Zhu, Y.; Long, C.; Chen, Y.; Guo, W.; Xu, L.; Jia, J. The food security risks in the Yangtze River Delta of China associated with water scarcity, grain production, and grain trade. Sci. Total Environ. 2024, 948, 174863. [Google Scholar] [CrossRef] [PubMed]
- Yao, C.S.; Yin, W.; Li, Z.T. The vulnerability assessment and driving mechanism analysis of China’s food security system. J. Nat. Resour. 2019, 34, 1720–1734. [Google Scholar] [CrossRef]
- Kalogiannidis, S.; Papadopoulou, C.I.; Loizou, E.; Chatzitheodoridis, F. Risk, vulnerability, and resilience in agriculture and their impact on sustainable rural economy development: A case study of Greece. Agriculture 2023, 13, 1222. [Google Scholar] [CrossRef]
- Das, S.; Goswami, K. Progress in agricultural vulnerability and risk research in India: A systematic review. Reg. Environ. Change 2021, 21, 24. [Google Scholar] [CrossRef]
- Shukla, R.; Gleixner, S.; Yalew, A.W.; Schauberger, B.; Sietz, D.; Gornott, C. Dynamic vulnerability of smallholder agricultural systems in the face of climate change for Ethiopia. Environ. Res. Lett. 2021, 16, 044007. [Google Scholar] [CrossRef]
- Liu, J.; Dietz, T.; Carpenter, S.R.; Alberti, M.; Folke, C.; Moran, E.; Pell, A.N.; Deadman, P.; Kratz, T.; Lubchenco, J.; et al. Complexity of coupled human and natural systems. Science 2007, 317, 1513–1516. [Google Scholar] [CrossRef]
- Chang, H.; Cao, Y.; Zhao, Y.; He, G.; Wang, Q.; Yao, J.; Ren, H.; Yang, H.; Hong, Z. Competitive and synergic evolution of the water–food–ecology system: A case study of the Beijing–Tianjin–Hebei region, China. Sci. Total Environ. 2024, 923, 171509. [Google Scholar] [CrossRef]
- Chang, H.; Zhang, B.; Han, J.; Zhao, Y.; Cao, Y.; Yao, J.; Shi, L. Evaluation of the coupling coordination and sustainable development of water–energy–land–food system on a 40-year scale: A case study of Hebei, China. Land 2024, 13, 1089. [Google Scholar] [CrossRef]
- Li, W.; Jiang, S.; Zhao, Y.; Li, H.; Zhu, Y.; He, G.; Xu, Y.; Shang, Y. A copula-based security risk evaluation and probability calculation for water–energy–food nexus. Sci. Total Environ. 2023, 856, 159236. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, L.; Sun, K.; Zhu, J. Synergistic security relationships and risk measurement of water resources–social economy–ecological environment in Beijing–Tianjin–Hebei region. Ecol. Indic. 2025, 175, 113512. [Google Scholar] [CrossRef]
- Li, W.; Jiang, S.; Zhao, Y.; Wang, Q.; He, F.; Li, H.; Zhu, Y.; He, G. Safety Evaluation of Water–Energy–Food Coupling System in Beijing–Tianjin–Hebei Region. Water Resour. Prot. 2023, 39, 39–48. (In Chinese) [Google Scholar]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of entropy weight method in decision-making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Žižović, M.; Miljković, B.; Marinković, D. Objective methods for determining criteria weight coefficients: A modification of the CRITIC method. Decis. Mak. Appl. Manag. Eng. 2020, 3, 149–161. [Google Scholar] [CrossRef]
- Chakraborty, S. TOPSIS and Modified TOPSIS: A comparative analysis. Decis. Anal. J. 2022, 2, 100021. [Google Scholar] [CrossRef]
- Zuo, Q. Harmony Theory: Theory Method and Application; Science Press: Beijing, China, 2012. (In Chinese) [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Scaillet, O. A Kolmogorov–Smirnov type test for positive quadrant dependence. Can. J. Stat. 2005, 33, 415–427. [Google Scholar] [CrossRef]
- Li, W.; Guo, J. Coupling Coordination and Obstacle Factors of Cultivated Land System Resilience and New Urbanization. Front. Sustain. Food Syst. 2025, 9, 1554797. [Google Scholar] [CrossRef]
- He, H.; Zhang, Z.; Ding, R.; Shi, Y. Multi-Driving Paths for the Coupling Coordinated Development of Agricultural Carbon Emission Reduction and Sequestration and Food Security: A Configurational Analysis Based on Dynamic fsQCA. Ecol. Indic. 2024, 160, 111875. [Google Scholar] [CrossRef]
- Magrini, A.; Giambona, F. A Composite Indicator to Assess Sustainability of Agriculture in European Union Countries. Soc. Indic. Res. 2022, 163, 1003–1036. [Google Scholar] [CrossRef]
- Kamali, F.P.; Borges, J.A.R.; Meuwissen, M.P.M.; de Boer, I.J.M.; Oude Lansink, A.G.J.M. Sustainability Assessment of Agricultural Systems: The Validity of Expert Opinion and Robustness of a Multi-Criteria Analysis. Agric. Syst. 2017, 157, 118–128. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Zhang, G.; Wang, Z. Evaluation of Agricultural Extension Service for Sustainable Agricultural Development Using a Hybrid Entropy and TOPSIS Method. Sustainability 2021, 13, 347. [Google Scholar] [CrossRef]
- Bera, D.; Dutta, D. A Comprehensive Evaluation of Agricultural Drought Vulnerability Using Fuzzy-AHP-Based Composite Index Integrating Sensitivity and Adaptive Capacity. Hydrol. Process. 2024, 38, e15331. [Google Scholar] [CrossRef]
- Stave, K.A.; Kopainsky, B. A System Dynamics Approach for Examining Mechanisms and Pathways of Food Supply Vulnerability. J. Environ. Stud. Sci. 2015, 5, 321–336. [Google Scholar] [CrossRef]
- Soliman, M.; Newlands, N.K.; Lyubchich, V.; Gel, Y.R. Multivariate Copula Modeling for Improving Agricultural Risk Assessment under Climate Variability. Variance 2023, 16, 1. [Google Scholar]
- Lei, H.; Yu, J.; Pan, H.; Li, J.; Leghari, S.J.; Shang, C.; Shi, L. A New Agricultural Drought Disaster Risk Assessment Framework: Coupled a Copula Function to Select Return Periods and the Jensen Model to Calculate Yield Loss. Sustainability 2023, 15, 3786. [Google Scholar] [CrossRef]
- Hou, W.; Yan, P.; Feng, G.; Zuo, D. A 3D Copula Method for the Impact and Risk Assessment of Drought Disaster and an Example Application. Front. Phys. 2021, 9, 656253. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, K. The Implication of Copula-Based Models for Crop Insurance and Reinsurance under Systemic Risk. Front. Environ. Sci. 2022, 10, 916494. [Google Scholar] [CrossRef]




| Target Layer | Criterion Layer | Subsystem | Indicator | Unit | Attribute | Code | Weight |
|---|---|---|---|---|---|---|---|
| AS-CSI | Reliability (0.328) | Water | Water resources per capita | m3 | + | Rel1 | 0.027 |
| Agricultural water use per capita | m3 | + | Rel2 | 0.032 | |||
| Water resources utilization rate | % | − | Rel3 | 0.031 | |||
| Reservoir storage capacity per capita | m3 | + | Rel4 | 0.038 | |||
| Land | Effective irrigated area per capita | m2 | + | Rel5 | 0.03 | ||
| Total sown area of foods per capita | m2 | + | Rel6 | 0.033 | |||
| Sown area of grain foods per capita | m2 | + | Rel7 | 0.034 | |||
| Energy | Total power of agricultural machinery per capita | kW | + | Rel8 | 0.027 | ||
| Rural electricity consumption per capita | kWh | + | Rel9 | 0.05 | |||
| Application amount of chemical fertilizers per capita | kg | + | Rel10 | 0.025 | |||
| Coordination (0.327) | Food Production Efficiency | Food yield per cubic meter of water | kg/m3 | + | Cor1 | 0.027 | |
| Food yield per hectare | kg/ha | + | Cor2 | 0.031 | |||
| Food yield per unit of fertilizer input | kg/kg | + | Cor3 | 0.031 | |||
| Food yield per unit of agricultural machinery power | kg/kW | − | Cor4 | 0.034 | |||
| Food self-sufficiency rate | % | + | Cor5 | 0.034 | |||
| Water–Land–Energy Synergy Efficiency | Water consumption per hectare | t/ha | − | Cor6 | 0.032 | ||
| Fertilizer use per hectare | t/ha | − | Cor7 | 0.037 | |||
| Machinery power per hectare | kW/ha | + | Cor8 | 0.033 | |||
| Multiple cropping index | % | + | Cor9 | 0.032 | |||
| Proportion of agricultural water use | % | − | Cor10 | 0.036 | |||
| Resilience (0.345) | Economy | GDP per capita | 104 CNY | + | Res1 | 0.034 | |
| GDP growth rate | % | + | Res2 | 0.039 | |||
| Proportion of agricultural GDP | % | − | Res3 | 0.035 | |||
| Water consumption per 104 CNY of agricultural GDP | % | − | Res4 | 0.03 | |||
| Social | Urbanization rate | % | + | Res5 | 0.031 | ||
| Proportion of agricultural employment | % | − | Res6 | 0.033 | |||
| Population growth rate | % | + | Res7 | 0.037 | |||
| Environment | Pesticide application amount | 104 t | − | Res8 | 0.036 | ||
| Area under soil erosion control | 103 ha | − | Res9 | 0.04 | |||
| Disaster-affected area | 103 ha | − | Res10 | 0.031 |
| Code | Characteristic Threshold Values | Code | Characteristic Threshold Values | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Worst (a) | Poor (b) | Moderate (c) | Good (d) | Optimal (e) | Worst (a) | Poor (b) | Moderate (c) | Good (d) | Optimal (e) | ||
| Rel1 | 474 | 1096 | 1351 | 2172 | 3029 | Cor6 | 2.93 | 2.44 | 2.11 | 1.86 | 1.52 |
| Rel2 | 193 | 238 | 340 | 473 | 885 | Cor7 | 0.46 | 0.41 | 0.31 | 0.22 | 0.16 |
| Rel3 | 68% | 47% | 37% | 27% | 21% | Cor8 | 2.49 | 3.55 | 4.8 | 6.19 | 7.56 |
| Rel4 | 238 | 732 | 847 | 1020 | 1326 | Cor9 | 201% | 223% | 249% | 296% | 369% |
| Rel5 | 352 | 446 | 607 | 825 | 1817 | Cor10 | 89% | 77% | 70% | 65% | 62% |
| Rel6 | 898 | 1542 | 1993 | 2609 | 4387 | Res1 | 0.87 | 1.57 | 3.22 | 4.46 | 5.87 |
| Rel7 | 730 | 1259 | 1776 | 2382 | 4235 | Res2 | 1% | 5% | 8% | 13% | 19% |
| Rel8 | 0.4 | 0.52 | 0.68 | 1.21 | 1.85 | Res3 | 23% | 16% | 14% | 11% | 9% |
| Rel9 | 88 | 155 | 250 | 434 | 913 | Res4 | 2847 | 1393 | 859 | 706 | 409 |
| Rel10 | 29 | 35 | 51 | 67 | 92 | Res5 | 49% | 53% | 59% | 64% | 69% |
| Cor1 | 1.63 | 2 | 2.41 | 3.3 | 4.57 | Res6 | 49% | 43% | 38% | 34% | 28% |
| Cor2 | 3557 | 4963 | 5691 | 6425 | 7176 | Res7 | −1.95% | −1.16% | −0.24% | 0.18% | 0.53% |
| Cor3 | 13 | 16 | 18 | 22 | 30 | Res8 | 19.36 | 8.83 | 5.82 | 4.56 | 2.96 |
| Cor4 | 1747 | 1343 | 1197 | 1029 | 825 | Res9 | 14,531 | 7458 | 5002 | 3608 | 2252 |
| Cor5 | 100% | 151% | 237% | 299% | 475% | Res10 | 7521 | 3513 | 1749 | 884 | 336 |
| AS-CSI | [0,0.2) | [0.2,0.4) | [0.4,0.6) | [0.6,0.8) | [0.8,1] |
|---|---|---|---|---|---|
| Security Level | Very Insecure | Insecure | Marginally Secure | Relatively Secure | Highly Secure |
| Distribution | Formula | Parameters |
|---|---|---|
| Weibill | Shape: k | |
| Gamma | ||
| Exp | ||
| Normal | ||
| Lognormal | Log-mean: Log-std. dev: |
| Distribution | Formula | Parameters |
|---|---|---|
| Gumbel | ||
| Frank | ||
| Clayton |
| Region | Rel | Cor | Rel-Cor | Rel | Res | Rel-Res | Cor | Res | Cor-Res |
|---|---|---|---|---|---|---|---|---|---|
| Liaoning | 0.8 | 0.8 | 0.7318 | 0.8 | 0.8 | 0.7149 | 0.8 | 0.8 | 0.688 |
| Jilin | 0.7799 | 0.6956 | 0.715 | ||||||
| Heilongjiang | 0.7206 | 0.6202 | 0.6426 | ||||||
| Northeast | 0.7643 | 0.7164 | 0.7318 |
| Region | Rel | Cor | Res | Rel-Cor-Res |
|---|---|---|---|---|
| Liaoning | 0.8 | 0.8 | 0.8 | 0.5454 |
| Jilin | 0.5538 | |||
| Heilongjiang | 0.5413 | |||
| Northeast | 0.5448 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.; Zhao, Y.; Cao, Y.; Ren, H.; Yao, J.; Liu, R.; Li, W. Evaluating Coupling Security and Joint Risks in Northeast China Agricultural Systems Based on Copula Functions and the Rel–Cor–Res Framework. Agriculture 2025, 15, 1338. https://doi.org/10.3390/agriculture15131338
Chang H, Zhao Y, Cao Y, Ren H, Yao J, Liu R, Li W. Evaluating Coupling Security and Joint Risks in Northeast China Agricultural Systems Based on Copula Functions and the Rel–Cor–Res Framework. Agriculture. 2025; 15(13):1338. https://doi.org/10.3390/agriculture15131338
Chicago/Turabian StyleChang, Huanyu, Yong Zhao, Yongqiang Cao, He Ren, Jiaqi Yao, Rong Liu, and Wei Li. 2025. "Evaluating Coupling Security and Joint Risks in Northeast China Agricultural Systems Based on Copula Functions and the Rel–Cor–Res Framework" Agriculture 15, no. 13: 1338. https://doi.org/10.3390/agriculture15131338
APA StyleChang, H., Zhao, Y., Cao, Y., Ren, H., Yao, J., Liu, R., & Li, W. (2025). Evaluating Coupling Security and Joint Risks in Northeast China Agricultural Systems Based on Copula Functions and the Rel–Cor–Res Framework. Agriculture, 15(13), 1338. https://doi.org/10.3390/agriculture15131338








