Abstract
Recent advancements in agricultural mobile robots (agribots) have enabled the execution of critical tasks such as crop inspection, precision spraying, and selective harvesting. While agribots show significant potential, conventional path-planning algorithms suffer from three limitations: (1) inadequate dynamic obstacle avoidance, which may compromise operational safety, (2) premature convergence to local optima, and (3) excessive energy consumption due to suboptimal trajectories. To overcome these challenges, this study proposes an enhanced Dynamic Genetic Algorithm—Ant Colony Optimization (DGA-ACO) framework. It integrates a 2D risk-penalty mapping model with dynamic obstacle avoidance mechanisms, improves max–min ant system pheromone allocation through adaptive crossover-mutation operators, and incorporates a hidden Markov model for accurately forecasting obstacle trajectories. A multi-objective fitness function simultaneously optimizes path length, energy efficiency, and safety metrics, while genetic operators prevent algorithmic stagnation. Simulations in different scenarios show that DGA-ACO outperforms Dijkstra, A*, genetic algorithm, ant colony optimization, and other state-of-the-art methods. It achieves shortened path lengths and improved motion smoothness while achieving a certain degree of dynamic obstacle avoidance in the global path-planning process.
1. Introduction
Agricultural mobile robots (agribots) have been widely used in agricultural operations, but autonomous obstacle avoidance and safe navigation indoors (Figure 1a) and outdoors (Figure 1b) remain challenging technical barriers in system implementation [1].

Figure 1.
Two typical working scenarios for agribots: (a) Indoor potted plant with controlled container arrangements. (b) Outdoor plantation featuring terrain variations.
Numerous studies have investigated path planning strategies for intelligent agricultural robotics (agribots) [2,3,4,5]. Comparative studies indicate that coverage path planning demonstrates inferior efficiency compared to point-to-point navigation in precision farming scenarios, with the latter exhibiting enhanced task-specific accuracy and reduced redundant path exploration [6,7,8,9,10]. Zhang et al. [11] developed a time-efficient dual pass algorithm for weed removal around identified maize plants, utilizing depth cameras for multi-target ranging and optimal herbicide application path generation. Kiani et al. [2] implemented metaheuristic algorithms to compute collision-free optimal paths between predefined coordinates, achieving a 55.56% success rate in large-scale crowded farmland trials.
Some scholars are also studying intelligent algorithms to solve the path-planning problem of agribots more quickly, among which genetic algorithms (GAs) and ant colony algorithms (ACOs) are representatives. GAs, originally proposed by J. Holland, simulate biological evolution to solve optimization problems through selection, crossover, and mutation operations [12]. However, conventional GAs suffer from premature convergence and local optima, prompting various improvements for robotic path planning [13,14]. Current enhancements focus on two directions: graph-based topological optimization [15,16,17,18,19], and hybridization with other algorithms [20,21]. Similarly, ACO, introduced by Dorigo et al., has undergone multiple modifications to address its limitations in agricultural path planning [22,23,24,25,26]. Hybrid GA-ACO approaches have emerged as a promising research direction [27,28,29,30]. Oleiwi et al. devised a GA-ACO fusion method that initializes GA populations with ACO-generated paths, incorporating specialized deletion operators for agribot optimization [27]. Châari et al. developed a wireless sensor network-integrated hybrid system where ACO enables rapid path selection while GA prevents local minima through enhanced crossover operations [30].
Agribots’ dynamic obstacle avoidance is crucial in agricultural scenarios [31]. Nasrinahar et al. used fuzzy control to avoid dynamic obstacles [32]. Gao et al. worked on implementing a deep deterministic policy gradient (DDPG) with long short-term memory (LSTM) network-based encoder to achieve dynamic obstacle avoidance for the agribot in stochastic working scenarios, which can encode the variable number of obstacles into a fixed-length representation [33]. Dong et al. proposed estimating the motion of dynamic obstacles by tracking targets through a Kalman filter [34]. Lee et al. proposed a novel obstacle avoidance algorithm for an agribot based on finite memory filtering (FMF) in unknown dynamic environments, overcoming the limitations of the existing dynamic window approach (DWA) [35].
Despite these advances, agricultural scenarios are complex. For indoor cases, such as in greenhouses, the passages between crops are narrow and the robot has limited turning space, which poses new challenges to safety. For outdoor cases, such as in fields, the terrain is complex and crops are arranged irregularly. It is difficult for robots to accurately distinguish between passable and impassable areas, requiring sophisticated path planning and dynamic obstacle avoidance capabilities to prevent collisions with plants or other equipment. This paper proposes a dynamic GA-ACO (DGA-ACO) framework, which is first used to solve the problem of safe obstacle avoidance for agribots in confined spaces in indoor and outdoor scenarios. It can predict dynamic obstacles in global path planning and has a certain global avoidance ability; the optimal path planned by the algorithm is as short as possible, smooth, and low in energy consumption.
2. Materials and Methods
The DGA-ACO algorithm workflow is shown in Figure 2. It is mainly divided into three parts: one is a more detailed modeling of agricultural scenarios, the second is the main improvement of the GA-ACO algorithm for agricultural scenarios, and the third is the post-processing of unsafe nodes on the path.
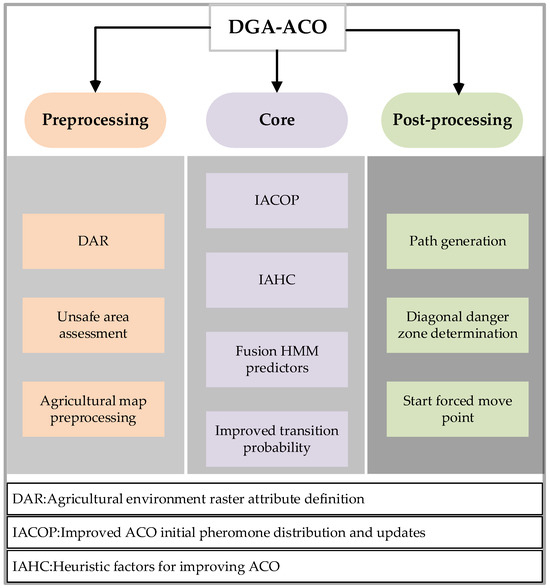
Figure 2.
The workflow of the DGA-ACO algorithm.
2.1. Environmental Modeling for Agricultural Scenarios
When the agribot starts global path planning, a suitable environment model will help to better understand the environmental variables in advance and reduce unnecessary planning computations. Common methods for environment modeling include the frame space method, free space method, unit layout method, topological method, probabilistic roadmap, and grid method [31]. This paper divides the grid map according to the characteristics of the agricultural scene. The rules are as follows: the original map is reduced to a given resolution, for which the height is and width is , where and are the height and width of the real scene and is the map resolution. Plants and other objects in the scene are defined as obstacles, and open areas are where the agribot can move. Figure 3 is used to illustrate how we can perform more detailed environmental modeling for agricultural scenes. The green plants, non-plant obstacles, and open areas in the scene are defined as the green grid, black grid, and white grid, as shown in Figure 3b. Considering the impact of grid size on the safety of the mobile agribot, the design of the unit grid sets the grid side length according to a certain ratio , where is the radius of the agribot, and ensures a tolerance distance from obstacles for safety. This method allows the robot to have a sufficient safety distance from obstacles when moving horizontally and vertically along the planned path.
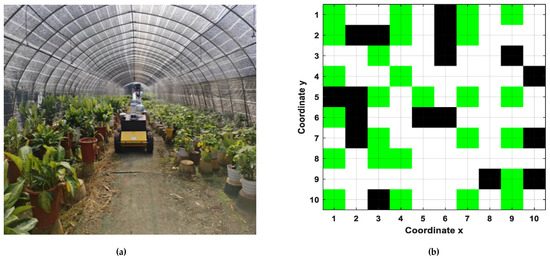
Figure 3.
Environmental modeling of agricultural scenes. (a) Scene image; (b) grid map (green, black and white colors represent plants, non-plant obstacles, and open space, respectively). For illustration purpose, (b) is not a strict mapping of (a).
2.2. Preprocessing of Narrow Spaces in Maps
The agribot may encounter narrow spaces during operation. Path planning in narrow spaces is a challenge. Few scholars have studied the problem of safe obstacle avoidance in narrow spaces [36,37]. The specific analysis is as follows: As shown in Figure 4a, the brown polygon represents the obstacle before expansion. The top of the obstacle intersects at the diagonal line and occupies two grids after expansion; however, as shown in Figure 4b, the global path planning algorithm may plan a path from to , resulting in a collision risk when the agribot moves diagonally.
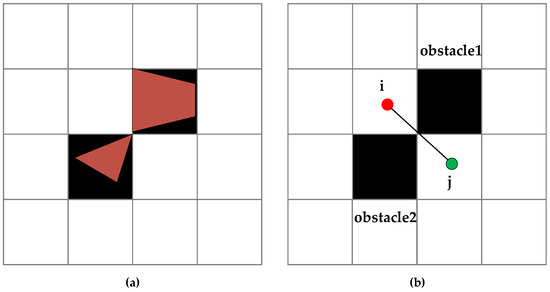
Figure 4.
Analysis of narrow spaces in maps. (a) Grid expansion in confined spaces; (b) path planning in narrow spaces.
To address the safety risk in Figure 4, the proposed solution consists of two consecutive steps: during the generation of the grid map of the planting environment, each grid cell is subjected to a four-corner line detection. For the configuration matching Figure 4b, diagonally adjacent navigable grids (i and j pairs), during the local path selection process, any waypoints present in dangerous areas are invalidated and removed from the options. When searching the map environment, we define the nodes in dangerous areas as absolute danger grids. After environment modeling, the following properties are found:
where is the index of the path grid in the map.
2.3. DGA-ACO Algorithm
The enhanced DGA-ACO algorithm is designed with three primary objectives: First, to address the slow initial convergence and stagnation issues of conventional ACO, genetic crossover and mutation operators are integrated for pheromone initialization and adaptive updates. Second, Hidden Markov Models (HMMs) are incorporated as dynamic scenario coefficients to predict obstacle trajectories. Finally, the algorithm’s capability is enhanced by redesigning the traditional ACO distance metric, introducing path smoothness and safety factors, while integrating dynamic prediction parameters into the fitness function. This multi-criteria optimization enables the selection of safer and more efficient nodes during state transitions, as governed by Equation (2) for pheromone allocation and Equation (18) for fitness evaluation.
2.3.1. Optimization of ACO Pheromone Initialization via Cross Entropy and Genetic Algorithm
The pheromone initialization mechanism is designed with dual components as formulated in Equation (2): one derived from conventional ACO distribution rules, and the other from GA optimized paths. The ACO-distributed pheromones adhere to Max–Min Ant System (MMAS) constraints, where post-iteration pheromone values are clamped to predefined bounds: if the pheromone level falls below the min , ; if it exceeds the max, , .
The proposed algorithm employs genetic crossover and mutation operations to initialize ACO pheromones; a crossover probability Pc governs the gene-like recombination of parent paths, generating offspring paths with potentially enhanced fitness through optimized segment exchanges, while a mutation probability strategically perturbs parent paths via probabilistic node-flipping operations, combined with crossover to yield adaptive offspring solutions. This dual mechanism enables a comprehensive exploration of feasible paths through mutation-driven diversity while retaining high performance traits via crossover-driven optimization, effectively escaping local optima to pursue globally optimal navigation trajectories. Specifically, elite paths identified through preliminary iterations initialize the pheromone distribution integrated into ACO’s framework, where adaptive mutations and dynamically adjust exploration intensity based on iteration progress , ensuring robust path diversity without compromising convergence efficiency in complex plantation environments.
where is the number of elite solutions generated by GA crossover mutation; is the path corresponding to the elite solution; is an indicator function, which takes the value 1 if the edge belongs to path , and 0 otherwise; is the objective function value of the elite path; and is the pheromone strength. The calculation steps are as follows:
- Step 1:
- Generate candidate solutions: Here, 100 ants perform 50 iterations of path optimization using the GA, and the top 10% of all iterations are selected as elite solutions.
- Step 2:
- Calculate initial pheromone: For each edge , count its appearance times in all elite solutions and sum them weighted by the path length.
2.3.2. Dynamic Obstacle Prediction Mechanism
For agribots, avoiding dynamic obstacles is crucial for human–robot safety. However, most current mainstream dynamic obstacle avoidance algorithms rely on complex kinetic modeling approaches, which are computationally intensive. We chose HMM [38] to make certain predictions about dynamic obstacles. On the one hand, there are fewer dynamic obstacles in agricultural scenes and the movement of obstacles is discrete. The hidden state of HMM can naturally simulate these discrete behaviors; some continuous state-based methods, such as Kalman filtering and end-to-end methods (such as LSTM), are not good at discretizing data. On the other hand, HMM prediction requires a small amount of data. Our goal in global path planning is to have a certain prediction ability. If we choose an algorithm with a lightweight model, the real-time prediction will be faster [39]. This models dynamic obstacle trajectories as a sequence of hidden states evolving through discrete time steps, leveraging sensor-derived observations (positional data, velocity profiles) to probabilistically infer future motion patterns based on state transition matrices A (Equation (3)) and observation probability distributions B (Equation (4)).
where is a hidden state representing the true motion state of the obstacle; , , and represent the position, speed, and direction, respectively; is the time step; and is the covariance matrix of motion uncertainty, reflecting the possible random turning of obstacles. For the convenience of the experiment, we assume that the speed is constant. It should be noted that our design supports the prediction of dynamic obstacles with variable speed.
where is the number of sensors; is the obstacle position detected by the sensor; and and are the mean and covariance of each sensor.
The HMM established based on this is , where is the probability of each state of the model appearing at the initial moment, assuming that the estimated value of the initial state is obtained through the first observation of the sensor, combined with the measurement error. The initial probability distribution is a multidimensional Gaussian distribution:
where is estimation based on first sensor observations, and is a diagonal matrix reflecting sensor measurement error and state uncertainty.
The state update of HMM needs to be combined with observation data, that is, sensor correction. We adopt the forward algorithm to update:
2.3.3. Hybrid Path Fitness Function Integrating GA and HMM Components
The path fitness function serves as a critical performance metric in the enhanced algorithm for agribot path planning, directly determining the solution quality and navigational safety of optimized trajectories. Simultaneously, the function’s design rationality profoundly impacts computational efficiency and memory utilization. This study holistically integrates four essential factors into the fitness function design—path length minimization, angular smoothness optimization, obstacle avoidance safety metrics, and dynamic obstacle prediction capability, as formulated below.
- Path Length Factor and Smoothness Factor
To objectively evaluate path length while minimizing robot energy consumption caused by suboptimal trajectory planning, an adaptive fitness function is designed to holistically integrate both local waypoint distances and global path continuity.
where is current position; is candidate waypoint; is the target position; and is weighting coefficient (empirically set to 0.5). Given the elevated energy consumption during turning maneuvers of the robot, we design an angular smoothness factor guided by candidate and target waypoints, incorporating both local trajectory curvature and global path continuity into a holistic optimization framework. The resultant fitness function formulation is expressed as
where is directional angle from waypoint to waypoint ; is angular deviation from waypoint to target ; and is smoothness gradient threshold (empirically set to 0.2).
- 2.
- Waypoint Safety Risk Assessment Factor
A risk penalty model is holistically constructed based on the proportional distribution of vegetation, non-vegetation obstacles, and static barriers within the environment, ensuring optimal safety assurance for the agribot through predictive hazard mitigation.
The safety risk assessment framework integrates three core components: is a risk-penalty model that aggregates nodal risks from eight adjacent grids, where escalating safety penalties correlate with cumulative hazard exposure; is the attribute value of candidate waypoint as defined in Equation (1); and is a safety risk weighting coefficient (empirically set to 0.2) that quantifies obstacle density impacts within the navigable neighborhood.
- 3.
- Dynamic Obstacle Prediction Factor
Building upon the HMM-based dynamic obstacle prediction framework established in Section 2.3.2, the forward algorithm computes the probability of dynamic obstacles intersecting the robot’s path at the next timestep. The agribot selects subsequent waypoints by minimizing this collision probability, with the dynamic avoidance factor formalized as
where is the next-step probability distribution for adjacent grids; denotes the probability of a sensor-detected robot at grid ; and is the dynamic obstacle prediction weighting coefficient (empirically set to 0.1). In the absence of dynamic obstacles, it is 0.
- 4.
- The Design of the Path Adaptation Function
This incorporates the path length factor, the path smoothness factor, the path safety risk factor, and the dynamic obstacle avoidance.
2.3.4. Enhanced Pheromone Updating via Genetic Operators
Traditional ACO only updates pheromones through the optimal path, which is prone to falling into local optimality. We introduce GA crossover and mutation operations to increase the diversity of pheromone updates:
where is the pheromone volatilization; is the pheromone increment of the optimal path; and and are adaptive weights. When is small, and are large, and the genetic operator dominates the exploration; as the iterations are heavily attenuated, it gradually returns to the traditional ACO utilization strategy.
The cross term is used to inherit the high-quality path fragments of the parent generation to avoid relying entirely on a single optimal solution.
The computation steps are as follows:
- Step 1:
- Select two parent paths from the path generated by the current ant (like roulette wheel selection).
- Step 2:
- Perform crossover operations on the parent path to generate child paths.
- Step 3:
- If an edge appears in the child path (), its pheromone increment is the average of the pheromones of the two parent generations.
We incorporate mutation factors to introduce small random perturbations to escape from local optimality:
The computation steps are as follows:
- Step 1:
- Randomly select a path for mutation.
- Step 2:
- Apply uniformly distributed random perturbations to the newly added edge () in the mutation operation.
2.3.5. State Transition Function of DGA-ACO
While conventional ACO selects paths via roulette wheel selection based on pheromone and distance factors, often leading to search stagnation during iterative optimization, the proposed DGA-ACO introduces crossover-mutation operators to refresh pheromone distributions upon stagnation detection, thereby enhancing state transition dynamics.
where the state transition parameters are defined as follows: denotes the probability of ant moving from node to ; represents the pheromone concentration between nodes node and ; corresponds to the path fitness function defined above; indicates the set of unvisited neighboring nodes for the ant; denotes the iteration count; specifies the weighting exponents (pheromone influence) and (heuristic distance priority); and sets the stagnation threshold (0.5) to activate genetic mutation operators when algorithm convergence variance falls below this empirically determined value.
2.4. Post-Processing of Dangerous Nodes in the Path
Some algorithms produce paths that are too close to obstacles when moving diagonally [31,32,33,34,35,36]. When the triangular obstacle ABC is expanded to the square obstacle AEDC, as shown in Figure 5a, the diagonal movement of the agricultural robot from to near point C still shows a considerable collision probability. We want to avoid this collision risk as much as possible in global path planning, which can simplify the time consumption of local path planning. In Section 2.1, we equated the robot to a circle with a radius of . Next, we added the center of mass of the circle to and constructed a safety buffer circle C (radius ) which is constructed around obstacle grid center . The designed diagonal safe movement mechanism is shown in Figure 5b. The diagonal forced movement point is the center position of the robot circle when it is a tangent to the obstacle’s safety circle C on the C- line (Equation (20)).
where and are the coordinates of point and robot centroid .
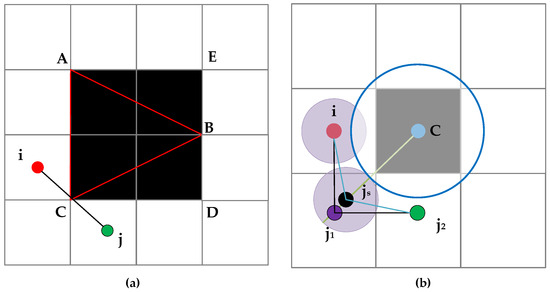
Figure 5.
The diagonal safe movement mechanism of agribots.
Figure 5b demonstrates that the agribot-enforced diagonal navigation path i→js→j2, though slightly longer than the direct diagonal path i → j2, ensures safe clearance distances from obstacles while being shorter than the orthogonal path i → j1 → j2. By strategically incorporating enforced navigation points, this methodology adapts to complex environments, balancing path efficiency and collision avoidance reliability without introducing external data or segmentations.
We named this the diagonal safe movement strategy, which is run in the post-processing stage of path data optimization, and can reduce the time and space complexity of the algorithm while maintaining the operating efficiency of the core algorithm.
3. Experiments and Results
To validate the path-planning efficacy, reliability, and safety of the DGA-ACO algorithm in agricultural environments, we conducted modular experiments across multi-scale agricultural grid maps. Comparative evaluations were performed against benchmark algorithms in scenarios featuring straight corridors, scattered obstacles, specialized U-shaped obstacle layouts, and dynamic obstacle environments. Performance was assessed using key metrics including optimal path length, average path length, path length variance, average turning count, path planning success rate, and path safety index.
3.1. Experimental Params’ Setting and Pseudocode
The computational platform for simulation experiments is configured with an Intel Core i7-14650HX processor, 16 GB RAM, Windows OS, and MATLAB R2021a for algorithm implementation. The parameter configurations of the ACO and GA algorithms proposed in this study were designed with reference to the literature [22,27,28,30]. To investigate the influence of different parameters on algorithm performance, eight parameter sets were prepared as shown in Table 1. For clarity and ease of reference in subsequent discussions, these parameter combinations are systematically labeled as params1 through params8 throughout this paper. The proposed hybrid optimization approach is based on an improved ant colony optimization framework integrated with genetic operators. The detailed steps are outlined in Algorithm 1.

Table 1.
Algorithm parameter table.
| Algorithm 1: Pseudocode of the DGA-ACO algorithm |
| Input: Max iterations K, Max Ant count M Output: 1. Initialize = 1, = 3, = 10, = 3, = 1, 2. for k = 1 to K do 3. for m = 1 to M do 4. while not reached destination do 5. if , then 6. according to the calculated transition probability , move the next node 7. else 8. enable crossover factor and mutation factor , move the next node 9. end if 10. end while 11. evaluate path fitness: , update pheromones locally: 12. end for 13. update global pheromone: 14. if , then 15. 16. end if 17. end for 18. return |
3.2. Algorithm Evaluation Metrics
To comprehensively evaluate the algorithm’s performance with reference to previous studies [22,28,36,40], we established seven key metrics: Optimal Path Length (OPL) and Average Path Length (APL) for path length evaluation, Path Length Variance (PLV) for path stability assessment, Number of Successful Planning (NSP) for solution quality measurement, Number of Turns (NT) for path smoothness evaluation, and two safety metrics—Number of Narrow Spaces (NNS), defined as the total count of path points meeting narrow space criteria in Section 2.2, and Number of Diagonal Potential Hazard Areas (NDHA), representing hazardous zone path points specified in Section 2.4, with detailed definitions provided below.
where represents the total number of valid paths from start to goal found by the algorithm; denotes the total number of search iterations performed; indicates the path length corresponding to the maximum fitness value; and refers to the length of the -th path connecting start to goal.
where is calculated using Equation (11), with statistical counting of occurrences where the angle exceeds 0 degrees.
3.3. Experiments on DGA-ACO Mechanism Effectiveness
3.3.1. Path Search and Planning Capability Experiments
To validate the path search and planning capabilities of DGA-ACO, we conducted four experimental groups (a–d) comparing it with ACO [22] in terms of (1) total search area, (2) failed planning search area, (3) successful planning search area, and (4) maximum fitness path. The tests were performed on a 10 × 10 agriculture-like grid map containing 36% obstacles (24% plant grids and 12% other obstacles). Algorithm parameters were selected from Table 1 (param1, param3, param8), with start point at (1.5,0.5) and goal point at (9.5,9.5).
As shown in Figure 6, where the start point is marked by a red snowflake symbol and the goal by a red dot symbol, with red circles highlighting narrow regions potentially hazardous to robots as discussed in Section 2.2, DGA-ACO demonstrates superior performance due to its GA elite population’s prior knowledge and design, concentrating the search area along the start–goal connection line (Figure 6a). The failed and successful planning search areas in Figure 6b,c reveal DGA-ACO’s broader exploration range, attributable to its improved pheromone allocation/update mechanism through GA crossover-mutation factors and well-designed distance/angle functions.
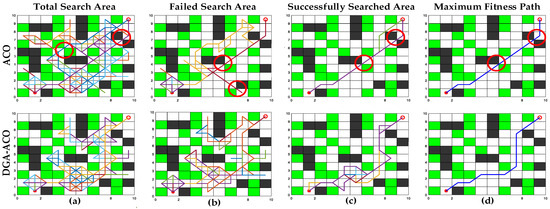
Figure 6.
Experiments on ACO and DGA-ACO search and planning capabilities in a 10 × 10 agricultural simulation map. (a) Total search area; (b) failed search area; (c) successful search area; (d) maximum fitness path.
The path planning results in Figure 6d show that DGA-ACO, benefiting from the risk map model (Section 2.2) and safety risk factors (Section 2.3), avoids planning optimal paths through narrow spaces like ACO does. Compared with ACO, DGA-ACO’s optimal paths maintain shorter lengths with fewer turns, verifying the advantages of our multi-factor improved fitness function in path planning.
3.3.2. Safety Experiments on an Optimized Path
To validate the safety of the algorithm’s optimized paths across the entire map, we conducted three experimental cases with different start and goal points. The testing environment was configured as a 20 × 20 grid map containing 35.5% obstacles (26% plant grids and 9.5% other obstacles), following the map design in JPIACO [36]. Parameters were selected from Table 1 (param7 and param8).
As shown in Figure 7, the start and goal points are marked by red snowflake and period symbols, respectively, with red circles indicating narrow areas (Section 2.2) and red rectangles marking potentially hazardous diagonal zones (Section 2.4). Blue circles and purple dashed lines represent DGA-ACO’s safety zones and forced diagonal movement paths.
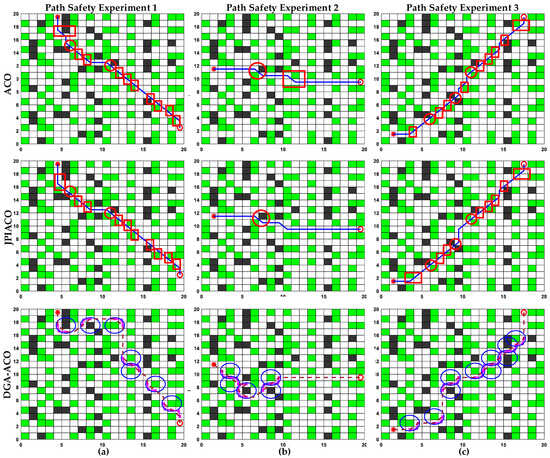
Figure 7.
Safety experiment of the final optimized path in a 20 × 20 agricultural simulation map. (a) Path safety experiment 1 with start (4.5,19.5) and end (19.5,2.5); (b) path safety experiment 2 with start (1.5,11.5) and end (19.5,9.5); (c) path safety experiment 3 with start (1.5,1.5) and end (17.5,19.5).
In Figure 7a (start: (4.5,19.5), goal: (19.5,2.5)), ACO’s optimal path passed through 2 narrow areas and 10 hazardous diagonal zones, while JPIACO [36] traversed 2 narrow areas and 10 hazardous diagonal zones. Figure 7b (start: (1.5,11.5), goal: (19.5,9.5)) shows ACO crossing one narrow area and one hazardous diagonal zone, versus JPIACO’s one narrow area. Figure 7c (start: (15,1.5), goal: (17.5,19.5)) recorded ACO passing three narrow areas and nine hazardous diagonal zones, compared to JPIACO’s three narrow areas and eight hazardous diagonal zones. Notably, DGA-ACO completely avoided these dangerous regions, demonstrating superior path safety.
For a fair comparison, we evaluated all results using metrics in JPIACO [36] (Table 2). While ACO and JPIACO produced seemingly shorter paths with fewer turns, they compromised safety by traversing hazardous zones. Conversely, DGA-ACO prioritizes safety over deceptive “shortcuts” while maintaining better convergence speed.

Table 2.
Evaluation of the paths planned by the three algorithms in the 20 × 20 agricultural simulation map using the evaluation metrics from reference [36].
3.4. Comparative Experiments of Multiple Algorithms in Agricultural Environments
To validate the advantages of our DGA-ACO algorithm across different parameter sets and maps, we conducted multiple experiments with varying start and goal points in agricultural map environments featuring straight corridors segments, scattered obstacles, U-shaped obstacles, and dynamic obstacles. The benchmark algorithms included graph-based Dijkstra, greedy heuristic-based A*, conventional ACO, and crossover-mutation-based GA.
3.4.1. Algorithm Comparison on Agricultural Maps with Straight Corridor Segments
Our straight-corridor agricultural map was designed as a 20 × 20 grid with 47.25% obstacle coverage (34% plant grids and 13.25% other obstacles) according to reference [40], featuring several straight-corridor free spaces. Using the unified parameters from Table 3 (param8 settings for maximum iterations and population size), we conducted three representative experiments with start–goal pairs covering the entire map region. As shown in Figure 8 (left: algorithm comparison; right: local path details), Dijkstra’s algorithm and A* produced longer paths with frequent 90° turns, while conventional ACO and GA algorithms generated paths through multiple narrow spaces and potentially hazardous diagonal zones. In contrast, our algorithm achieved safer paths with sub-90° turns and shorter lengths while completely avoiding hazardous areas, demonstrating superior performance in both safety and efficiency metrics.

Table 3.
Experiment setting of agricultural maps with straight corridor segments.
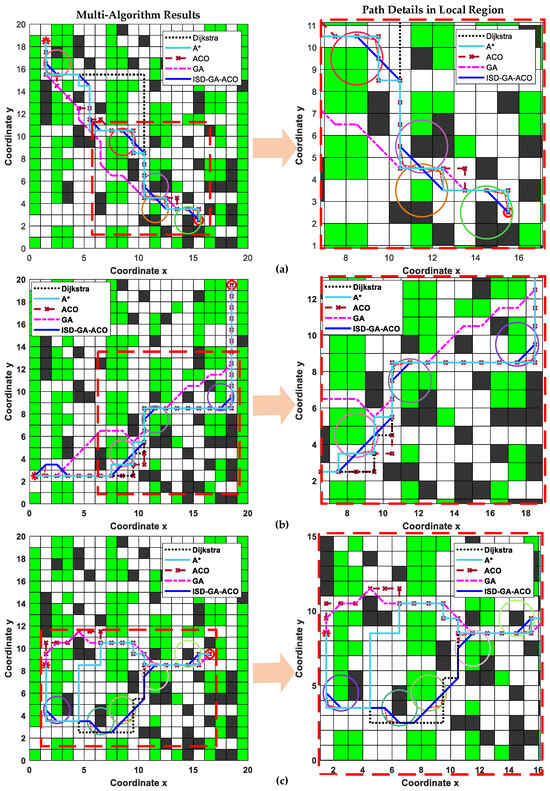
Figure 8.
Comparison of multiple algorithms in an agricultural environment containing straight corridor segments, circles of different colors represent safety circles at different locations (described in Section 2.4). (a) Experiment a with start (1.5,18.5) and end (15.5,2.5); (b) experiment b with start (0.5,2.5) and end (18.5,19.5); (c) experiment c with start (1.5,8.5) and end (16.5,9.5).
Figure 9 and Figure 10 present qualitative results, evaluated using the five metrics defined in Section 3.2. Figure 9 systematically evaluates the performance of five path planning algorithms, classical Dijkstra, A*, ACO, GA, and the proposed DGA-ACO, across three varying starts and goals, focusing on convergence speed, path optimality, solution stability, and feasible solution discovery capability. All experiments were conducted under standardized conditions with an iteration cap of 50 cycles and 50 independent trials per algorithm. Convergence was defined as <1% variation in path length over five consecutive iterations. DGA-ACO achieves the earliest convergence, requiring 24~55% and 16~35% fewer iterations than ACO and GA, respectively. DGA-ACO optimal paths outperformed GA/ACO by over 30% in solution quality. The average path length remained significantly lower than other heuristics, confirming the effectiveness of pheromone initialization and update via cross-entropy and GA. Solution stability analysis reveals that DGA-ACO reduces late-phase (40–50 iterations) path variance by approximately 50% compared to conventional methods, with minimal early-stage fluctuations indicating noise-resistant search behavior. Feasible solution discovery rates show that DGA-ACO achieves 100% success within 7–12 iterations across scenarios, versus 18–30 iterations for ACO/GA. The DGA-ACO framework demonstrates multidimensional superiority in convergence speed, path optimality, stability, and robustness. This advancement provides an efficient and reliable solution for real-time path planning in complex agricultural environments requiring safety assurance.
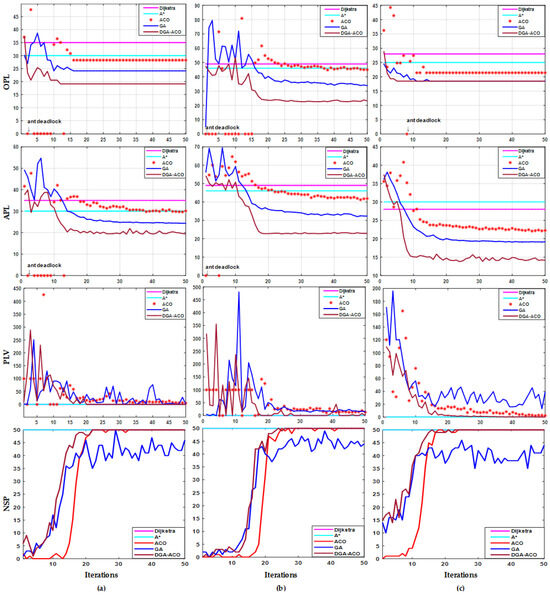
Figure 9.
Performance analysis of multiple algorithms in an agricultural environment containing straight corridor segments. (a) Experiment a with start (1.5,18.5) and end (15.5,2.5); (b) path safety experiment b with start (0.5,2.5) and end (18.5,19.5); (c) path safety experiment c with start (1.5,8.5) and end (16.5,9.5).
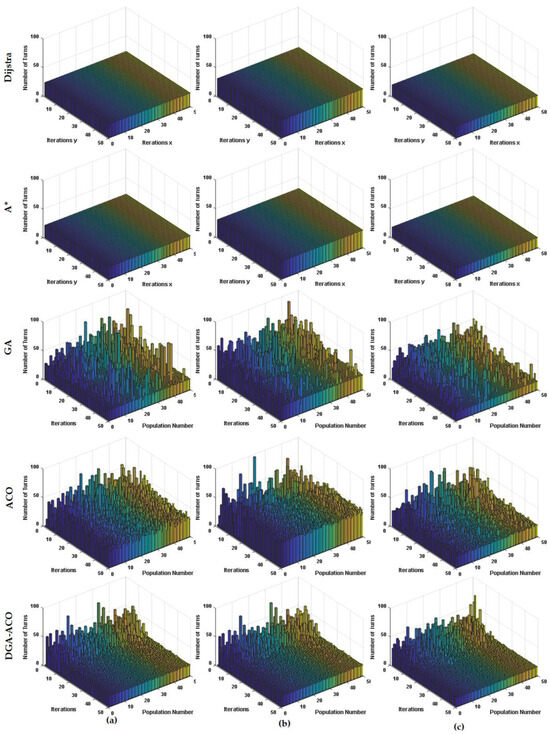
Figure 10.
Path smoothness analysis of multiple algorithms in an agricultural environment containing straight corridor segments. (a) Experiment a with start (1.5,18.5) and end (15.5,2.5); (b) experiment b with start (0.5,2.5) and end (18.5,19.5); (c) experiment c with start (1.5,8.5) and end (16.5,9.5).
In Figure 10, the horizontal axis denotes the iteration number (1–50), the vertical axis denotes the population index (1–50), and the height (bar) represents the number of turns in the resulting path. The classical Dijkstra and A* algorithms produce perfectly flat turns: 16 and 14 turns in Figure 10a, 18 and 15 in Figure 10b, and 12 and 10 in Figure 10c. This reflects their guaranteed global optimality but zero adaptability or diversity in path shape. By contrast, the pure metaheuristics (GA and ACO) display large, irregular peaks and valleys; in early- to mid-stage searches their average turn counts reach 42.3 ± 10.8 (GA) and 47.5 ± 9.2 (ACO) in Figure 10a, 50.1 ± 12.2/53.4 ± 10.7 in Figure 10b, and 32.7 ± 8.1/38.2 ± 7.5 in Figure 10c, with occasional spikes up to 75–85 turns. Such volatility not only slows convergence but also risks settling in high-turn local optima. The proposed DGA-ACO dramatically attenuates these instabilities; across all three environments its mean turn counts fall to 33.1 ± 8.1 in Figure 10a, 36.4 ± 9.0 in Figure 10b, and 25.3 ± 6.2 in Figure 10c, reducing by 21.7–27.3% versus GA and 30.4–33.7% versus ACO while the maximum observed turns never exceed 60. Its standard deviation over the full grid is 7.8, approximately 25% lower than that of either GA or ACO, indicating a far smoother search trajectory. Moreover, by the “five-iteration <1% turn-count-change” criterion, DGA-ACO stabilizes in an average of only 10 iterations, compared to 15–20 iterations for the standalone metaheuristics.
Together, these results demonstrate that DGA-ACO not only preserves the global optimal relevance of classical graph methods but also endows the search with diversity control, yielding consistently lower turn counts, diminished fluctuation, and accelerated convergence across heterogeneous path-planning scenarios.
3.4.2. Algorithm Comparison on Agricultural Maps with Scattered Obstacles
Path planning becomes significantly more challenging in large-scale maps. To address this, we designed a 40 × 40 agricultural map with scattered obstacles featuring 28.43% obstacle density (22.81% plant grids and 5.62% other obstacles) distributed uniformly across the entire area. Using parameters param2, param3, and param8 from Table 1, we conducted three representative experiments with start–goal pairs covering the full map region. As shown in Figure 11, the conventional ACO exhibited substantial path redundancy in this enlarged map, potentially due to its reliance solely on local path distance heuristics without global guidance. Dijkstra’s and A* algorithms produced longer paths with excessive turns due to their lack of population-based information sharing characteristic of intelligent algorithms. While GA generated shorter global paths, they traversed numerous narrow spaces and potentially hazardous diagonal zones. In contrast, DGA-ACO demonstrated superior comprehensive performance, achieving shorter paths with fewer turns than Dijkstra, A*, and conventional ACO, while maintaining higher safety than GA. Detailed quantitative analysis using the evaluation metrics proposed in Section 3.2 is presented in Table 4.
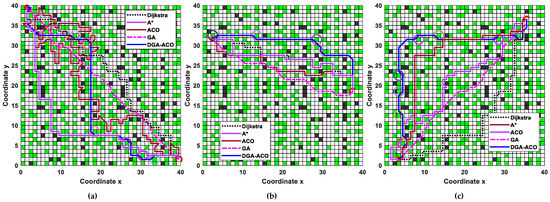
Figure 11.
Path planning results of various algorithms in agricultural maps with scattered obstacles. (a) Experiment with start (1.5,39.5) and end (39.5,1.5); (b) experiment with start (2.5,31.5) and end (37.5,18.5); (c) experiment with start (3.5,1.5) and end (36.5,36.5).

Table 4.
Experiment result of agricultural maps with scattered obstacles.
3.4.3. Algorithm Comparison on Agricultural Maps with U-Shaped Obstacles
Path planning in maps containing U-shaped obstacles serves as another critical performance metric for evaluation [41]. We designed a 50 × 50 agricultural map with over 30% U-shaped obstacle coverage, conducting three comparative experiments with different start–goal pairs using parameters param3, param4, and param8. The experimental results are presented in Figure 12, presenting three representative experimental cases, revealing that conventional GA and ACO exhibit localized path redundancy (41.48% and 67.34% redundancy rates, respectively) due to premature convergence in U-shaped traps caused by population stagnation and pheromone accumulation during node exploration. In contrast, DGA-ACO integrates genetic crossover-mutation operators into pheromone initialization/update mechanisms and incorporates obstacle proximity penalties in its path safety factor design, eliminating path redundancy while achieving 23–39% reductions in path length and 38–45% decreases in angular turns compared to Dijkstra/A* baselines. The quantitative analysis in Table 5 systematically confirms the algorithm’s effectiveness and operational efficiency in U-shaped obstacle-rich environments.
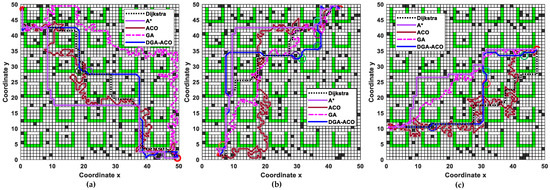
Figure 12.
Path-planning results of various algorithms in agricultural maps with U-shaped obstacles. (a) Experiment with start (0.5,48.5) and end (49.5,0.5); (b) experiment with start (5.5,1.5) and end (43.5,48.5); (c) experiment with start (1.5,10.5) and end (47.5,35.5).

Table 5.
Experiment result of agricultural maps with U-shaped obstacles.
3.4.4. Algorithm Comparison on Agricultural Maps with Dynamic Obstacles
The motion patterns of dynamic obstacles are theoretically probabilistic in nature, yet demonstrate non-random movement characteristics due to inherent purposiveness, typically following activity- or location-specific behavioral patterns [42]. To validate the standalone DGA-ACO’s dynamic obstacle avoidance capability in plantation environments without hybrid local planners, we configured a dynamic obstacle at (1.5,1.5) with 1 m/s velocity, ±45° stochastic angular deviation orthogonal to the start–goal axis, and eight-directional transition states (forward/stop/turn). Figure 13 presents randomized experimental results with red rectangles marking dynamic obstacles, showing conventional algorithms’ critical safety failures: Dijkstra and A* collisions were at (25.5,26.5) and (16.5,17.5), respectively, and ACO/GA collisions at (16.5,28.5). In contrast, DGA-ACO successfully avoided proximal obstacles at (16.5,17.5) and (16.5,20.5), empirically confirming its enhanced safety compliance in unstructured dynamic environments with 100% collision avoidance without auxiliary path correction modules.
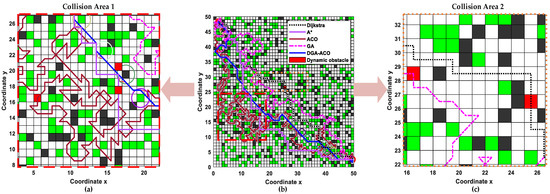
Figure 13.
Path-planning results of various algorithms in agricultural maps with dynamic obstacles. (a) Collision area 1; (b) global path planning on agricultural maps with dynamic obstacles; (c) collision area 2.
3.5. Algorithm Comparison in Other Environments
To further validate the superior performance of our enhanced algorithm in non-agricultural environments, we conducted comparative experiments against the advanced reinforcement learning method R-SAC [10] using param1 and param8 under identical experimental conditions, including a 600 × 600 grid map with matching obstacle configurations and three sets of consistent start–goal pairs for fair evaluation. As demonstrated in Figure 14 and Table 6, DGA-ACO exhibits significant advantages in both static and dynamic environments: in static scenarios (Figure 14a–c), it generates globally optimized paths with 23% fewer turns and shorter lengths while ensuring complete safety; in dynamic environments (Figure 14d–f), the integrated HMM prediction factor enables effective dynamic obstacle avoidance while the coordinated distance–angle optimization maintains safe clearance with 17% more efficient trajectories, collectively confirming DGA-ACO’s comprehensive superiority over R-SAC across all test conditions.
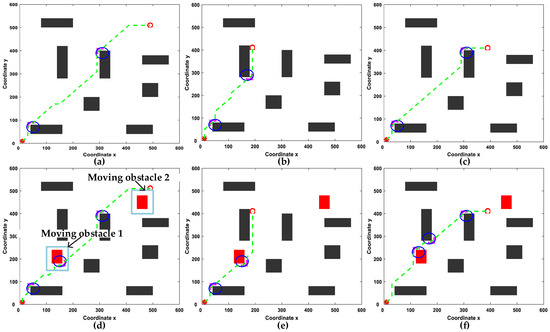
Figure 14.
Comparison of R-SAC and DGA-ACO using the map from reference [10]. (a) Static experiment with target (500,500); (b) static experiment with target (200,400); (c) static experiment with target (400,400); (d) dynamic experiment with target (500,500); (e) dynamic experiment with target (200,400); (f) dynamic experiment with target (400,400).

Table 6.
The results comparing R-SAC and DGA-ACO in both static and dynamic environments.
4. Discussion
Path planning for agribots plays a pivotal role in advancing precision agriculture. Previous research has investigated various path-planning methodologies for smart farming applications, including grid-based Dijkstra’s, grid-based A* algorithm, sampling-based Rapidly exploring Random Tree (RRT), and its optimized variant RRT* [6]. With the evolution of intelligent algorithms, metaheuristic approaches such as Genetic Algorithm (GA) and Ant Colony Optimization (ACO) have increasingly been adopted for robotic path planning. Notably, Wu et al. [43] developed an enhanced GA incorporating a multi-point mutation strategy, which demonstrated superior global optimization capabilities compared to conventional single-point mutation by effectively disrupting parental paths. This study systematically evaluates the safety and reliability of the proposed DGA-ACO across both static and dynamic environments, encompassing agricultural and non-agricultural scenarios. Through comprehensive simulations on diverse agricultural and non-agricultural maps with detailed comparative analyses against multiple benchmark algorithms, qualitative and quantitative results consistently demonstrate DGA-ACO’s unique advantage in ensuring high safety for agribot path planning. The dynamic obstacle prediction mechanism, being model-agnostic, ensures excellent generalizability to other robotic platforms. However, real-world deployment presents three key challenges: (1) Markov-based prediction requires substantial training data collection and annotation efforts; (2) real-time dynamic obstacle reasoning demands significant computational resources and power consumption, with requirements scaling proportionally to obstacle quantity and state transition complexity; (3) current safety and dynamic avoidance validations are limited to global path planning simulations, necessitating the further verification of system-level errors in physical robotic implementations. Our immediate future work will focus on experimental validation using actual robotic platforms.
5. Conclusions
This paper studies an enhanced DGA-ACO algorithm for agribot path planning in agricultural environments, with three key innovations. (1) Population Initialization Optimization: A GA-based elite cluster minimizes cross-entropy to initialize ACO pheromone distribution. A GA-driven crossover-mutation operator activates during stagnation phases, addressing slow early convergence and late-stage stagnation in conventional ACO. (2) Safety Assurance Mechanism: Static hazardous zones are constrained via a hazard penalty model, supplemented by post-processing with diagonal forced maneuver points to eliminate collision risks during diagonal node transitions. (3) Dynamic Adaptation Framework: HMM-based dynamic obstacle prediction is integrated with a multi-criteria fitness function balancing path length, smoothness, and safety compliance. Extensive experiments with qualitative and quantitative results consistently demonstrate that DGA-ACO outperforms multiple existing algorithms. It offers an innovative approach to path planning in agribots, which can make agribots more efficient and safer. It is a valuable contribution to precision agriculture technologies.
Author Contributions
Conceptualization, Z.Z. and Y.T.; Methodology, Z.Z. and Y.C.; Software, Z.Z., P.L. and S.C.; Validation, Z.Z., P.L. and S.C.; Investigation, Y.T.; Resources, Y.T.; Data curation, P.L.; Writing—original draft, Z.Z.; Writing—review & editing, S.C., Y.C. and Y.T.; Visualization, Z.Z.; Supervision, Y.T.; Funding acquisition, Y.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partially funded by the Key R&D Program of China (2024YFB4710600), the LingChuang Research Project of China National Nuclear Corporation (CNNC-LCKY-2024-072), the Shenzhen Talent Startup Funds (No. 827-000954), and Shenzhen University (No. 00000224).
Data Availability Statement
Data created or analyzed in this study are presented in the paper. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chakraborty, S.; Elangovan, D.; Govindarajan, P.L.; ELnaggar, M.F.; Alrashed, M.M.; Kamel, S. A Comprehensive Review of Path Planning for Agricultural Ground Robots. Sustainability 2022, 14, 9156. [Google Scholar] [CrossRef]
- Kiani, F.; Seyyedabbasi, A.; Nematzadeh, S.; Candan, F.; Çevik, T.; Anka, F.A.; Randazzo, G.; Lanza, S.; Muzirafuti, A. Adaptive Metaheuristic-Based Methods for Autonomous Robot Path Planning: Sustainable Agricultural Applications. Appl. Sci. 2022, 12, 943. [Google Scholar] [CrossRef]
- Pham, T.H.; Bestaoui, Y.; Mammar, S. Aerial robot coverage path planning approach with concave obstacles in precision agriculture. In Proceedings of the 2017 Workshop on Research, Education and Development of Unmanned Aerial Systems (RED-UAS), Linköping, Sweden, 3–5 October 2017; pp. 43–48. [Google Scholar] [CrossRef]
- Hameed, I.A.; Bochtis, D.; Sørensen, C.A. An Optimized Field Coverage Planning Approach for Navigation of Agricultural Robots in Fields Involving Obstacle Areas. Int. J. Adv. Robot. Syst. 2013, 10, 231. [Google Scholar] [CrossRef]
- Pour Arab, D.; Spisser, M.; Essert, C. Complete coverage path planning for wheeled agricultural robots. J. Field Robot. 2023, 40, 1460–1503. [Google Scholar] [CrossRef]
- Pak, J.; Kim, J.; Park, Y.; Son, H.I. Field Evaluation of Path-Planning Algorithms for Autonomous Mobile Robot in Smart Farms. IEEE Access 2022, 10, 60253–60266. [Google Scholar] [CrossRef]
- Lal, R.; Sharda, A.; Prabhakar, P. Optimal multi-robot path planning for pesticide spraying in agricultural fields. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, Australia, 12–15 December 2017; pp. 5815–5820. [Google Scholar] [CrossRef]
- Santos, L.C.; Santos, F.N.; Pires, E.J.S.; Valente, A.; Costa, P.; Magalhães, S. Path Planning for ground robots in agriculture: A short review. In Proceedings of the 2020 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Ponta Delgada, Portugal, 15–17 April 2020; pp. 61–66. [Google Scholar] [CrossRef]
- Noguchi, N.; Terao, H. Path planning of an agricultural mobile robot by neural network and genetic algorithm. Comput. Electron. Agric. 1997, 18, 187–204. [Google Scholar] [CrossRef]
- Yang, J.; Ni, J.; Li, Y.; Wen, J.; Chen, D. The Intelligent Path Planning System of Agricultural Robot via Reinforcement Learning. Sensors 2022, 22, 4316. [Google Scholar] [CrossRef]
- Zhang, L.; Li, R.; Li, Z.; Meng, Y.; Liang, J.; Fu, L.; Jin, X.; Li, S. A Quadratic Traversal Algorithm of Shortest Weeding Path Planning for Agricultural Mobile Robots in Cornfield. J. Robot. 2021, 2021, 6633139. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, S.X. A knowledge based genetic algorithm for path planning of a mobile robot. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Volume 5, pp. 4350–4355. [Google Scholar] [CrossRef]
- Tu, J.; Yang, S.X. Genetic algorithm based path planning for a mobile robot. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; Volume 1, pp. 1221–1226. [Google Scholar] [CrossRef]
- Nagib, G.; Gharieb, W. Path planning for a mobile robot using genetic algorithms. In Proceedings of the 2004 International Conference on Electrical, Electronic and Computer Engineering, Cairo, Egypt, 5–7 September 2004; pp. 185–189. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Sheng, L. A new genetic algorithm approach to smooth path planning for mobile robots. Assem. Autom. 2016, 36, 138–145. [Google Scholar] [CrossRef]
- Chen, H.; Xu, Z. Path Planning Based on A New Genetic Algorithm. In Proceedings of the 2005 International Conference on Neural Networks and Brain, Beijing, China, 13–15 October 2005; Volume 2, pp. 788–792. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Z.; Xie, Y. Path planning of mobile robot based on improved genetic algorithm. In Proceedings of the 2020 3rd International Conference on Electron Device and Mechanical Engineering (ICEDME), Suzhou, China, 1–3 May 2020; pp. 691–695. [Google Scholar] [CrossRef]
- Benavides, F.; Tejera, G.; Pedemonte, M.; Casella, S. Real path planning based on genetic algorithm and Voronoi diagrams. In Proceedings of the 2011 IEEE IX Latin American Robotics Symposium and IEEE Colombian Conference on Automatic Control, Bogota, Colombia, 1–4 October 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Ma, J.; Liu, Y.; Zang, S.; Wang, L. Robot Path Planning Based on Genetic Algorithm Fused with Continuous Bezier Optimization. Comput. Intell. Neurosci. 2020, 2020, 9813040. [Google Scholar] [CrossRef]
- Xin, D.; Hua-hua, C.; Wei-kang, G. Neural network and genetic algorithm based global path planning in a static environment. J. Zhejiang Univ. Sci. A 2005, 6, 549–554. [Google Scholar] [CrossRef]
- Zeng, C.; Zhang, Q.; Wei, X. Robotic Global Path-Planning Based Modified Genetic Algorithm and A* Algorithm. In Proceedings of the 2011 Third International Conference on Measuring Technology and Mechatronics Automation, Shanghai, China, 6–7 January 2011; Volume 3, pp. 167–170. [Google Scholar] [CrossRef]
- Chen, X.; Kong, Y.; Fang, X.; Wu, Q. A fast two-stage ACO algorithm for robotic path planning. Neural Comput. Appl. 2013, 22, 313–319. [Google Scholar] [CrossRef]
- Yen, C.-T.; Cheng, M.-F. A study of fuzzy control with ant colony algorithm used in mobile robot for shortest path planning and obstacle avoidance. Microsyst. Technol. 2018, 24, 125–135. [Google Scholar] [CrossRef]
- Liu, J.; Yang, J.; Liu, H.; Tian, X.; Gao, M. An improved ant colony algorithm for robot path planning. Soft Comput. 2017, 21, 5829–5839. [Google Scholar] [CrossRef]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Cui, J.; Wu, L.; Huang, X.; Xu, D.; Liu, C.; Xiao, W. Multi-strategy adaptable ant colony optimization algorithm and its application in robot path planning. Knowl. Based Syst. 2024, 288, 111459. [Google Scholar] [CrossRef]
- Oleiwi, B.K.; Roth, H.; Kazem, B.I. A Hybrid Approach Based on ACO and Ga for Multi Objective Mobile Robot Path Planning. Appl. Mech. Mater. 2014, 527, 203–212. [Google Scholar] [CrossRef]
- Li, G.; Liu, C.; Wu, L.; Xiao, W. A mixing algorithm of ACO and ABC for solving path planning of mobile robot. Appl. Soft Comput. 2023, 148, 110868. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, J.; Xu, L.; Wang, J. Cooperative path planning study of distributed multi-mobile robots based on optimised ACO algorithm. Robot. Auton. Syst. 2024, 179, 104748. [Google Scholar] [CrossRef]
- Châari, I.; Koubâa, A.; Bennaceur, H.; Trigui, S.; Al-Shalfan, K. smartPATH: A hybrid ACO-GA algorithm for robot path planning. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Tang, Y.; Zakaria, M.A.; Younas, M. Path Planning Trends for Autonomous Mobile Robot Navigation: A Review. Sensors 2025, 25, 1206. [Google Scholar] [CrossRef]
- Nasrinahar, A.; Chuah, J.H. Intelligent motion planning of a mobile robot with dynamic obstacle avoidance. J. Veh. Routing Algorithms 2018, 1, 89–104. [Google Scholar] [CrossRef]
- Gao, X.; Yan, L.; Li, Z.; Wang, G.; Chen, I.M. Improved deep deterministic policy gradient for dynamic obstacle avoidance of mobile robot. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 3675–3682. [Google Scholar] [CrossRef]
- Dong, H.; Weng, C.Y.; Guo, C.; Yu, H.; Chen, I.M. Real-time avoidance strategy of dynamic obstacles via half model-free detection and tracking with 2d lidar for mobile robots. IEEE/ASME Trans. Mechatron. 2020, 26, 2215–2225. [Google Scholar] [CrossRef]
- Lee, D.H.; Lee, S.S.; Ahn, C.K.; Shi, P.; Lim, C.C. Finite distribution estimation-based dynamic window approach to reliable obstacle avoidance of mobile robot. IEEE Trans. Ind. Electron. 2020, 68, 9998–10006. [Google Scholar] [CrossRef]
- Chen, T.; Chen, S.; Zhang, K.; Qiu, G.; Li, Q.; Chen, X. A jump point search improved ant colony hybrid optimization algorithm for path planning of mobile robot. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221127953. [Google Scholar] [CrossRef]
- Tao, Y.; Gao, H.; Ren, F.; Chen, C.; Wang, T.; Xiong, H.; Jiang, S. A mobile service robot global path planning method based on ant colony optimization and fuzzy control. Appl. Sci. 2021, 11, 3605. [Google Scholar] [CrossRef]
- Baum, L.E.; Petrie, T. Statistical Inference for Probabilistic Functions of Finite State Markov Chains. Ann. Math. Stat. 1966, 37, 1554–1563. [Google Scholar] [CrossRef]
- Tadayon, M.; Pottie, G. Comparative analysis of the hidden Markov model and LSTM: A simulative approach. arXiv 2020, arXiv:2008.03825. [Google Scholar]
- Ali, H.; Gong, D.; Wang, M.; Dai, X. Path planning of mobile robot with improved ant colony algorithm and MDP to produce smooth trajectory in grid-based environment. Front. Neurorobot. 2020, 14, 44. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, B.; Zhang, L.; Liu, J.; Han, H. Global path planning for mobile robots based on improved A-Star algorithm. Research Square 2024. [Google Scholar] [CrossRef]
- Bennewitz, M.; Burgard, W.; Cielniak, G.; Thrun, S. Learning motion patterns of people for compliant robot motion. Int. J. Robot. Res. 2005, 24, 31–48. [Google Scholar] [CrossRef]
- Wu, X.; Bai, J.; Hao, F.; Cheng, G.; Tang, Y.; Li, X. Field Complete Coverage Path Planning Based on Improved Genetic Algorithm for Transplanting Robot. Machines 2023, 11, 659. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).