Laser Scanning for Canopy Characterization in Hazelnut Trees: A Preliminary Approach to Define Growth Habitus Descriptor
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Acquisition
2.2. Point Cloud Generation and Geometrical Feature Extraction
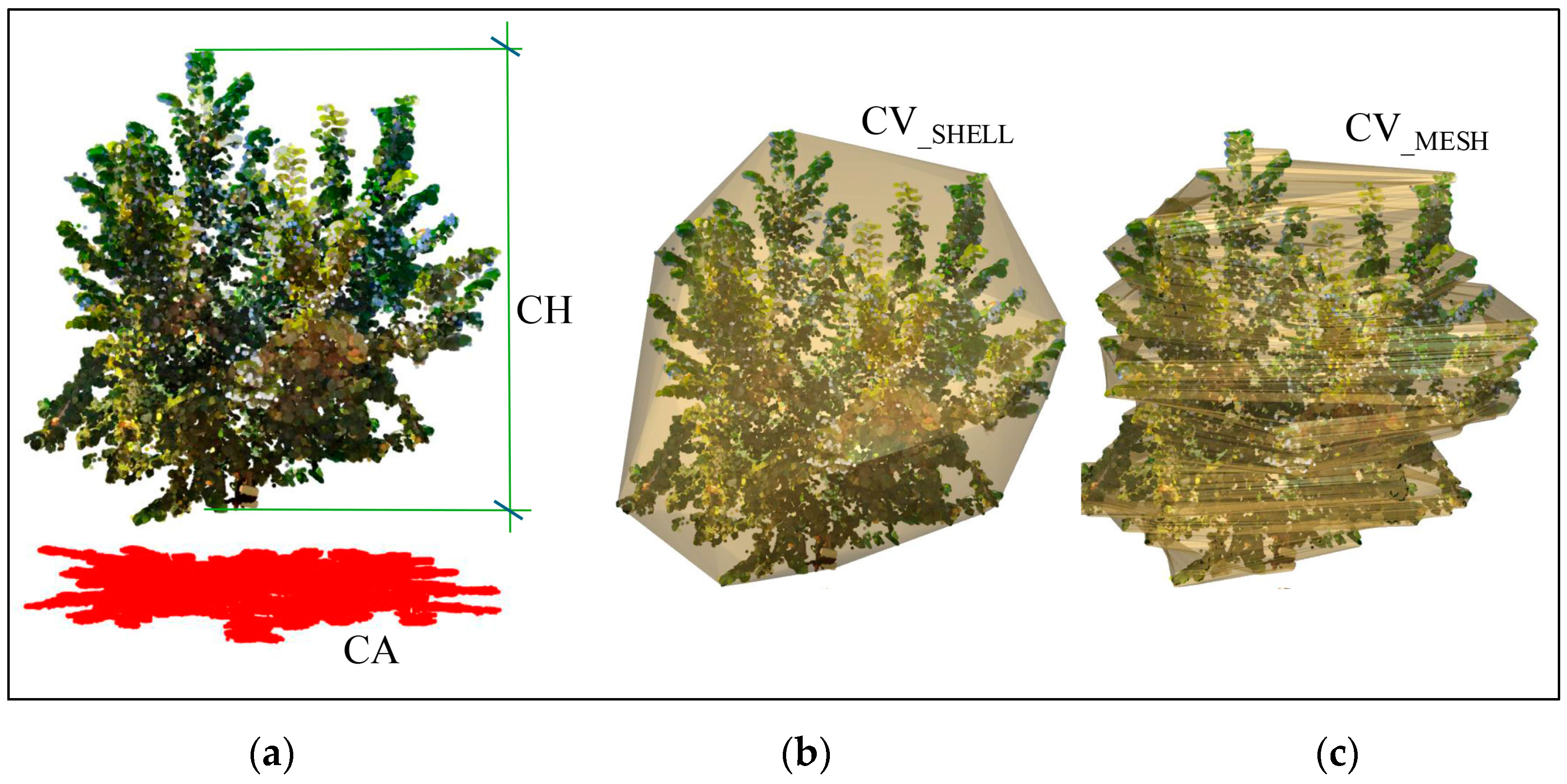
- Canopy height (CH), calculated as the difference between the maximum and the minimum elevation values of the point cloud (Figure 5a);
- Canopy area (CA), determined by measuring the area of the projected canopy point cloud onto a horizontal plane (Figure 5a);
- Canopy volume (CV), estimated using two different approaches: a shell (CVSHELL), a convex surface enclosing all the canopy points and accounting for the empty spaces between branches (Figure 5b) and a mesh (CVMESH) derived from the “tree meshing script” in Cyclone 3DR (Figure 5c), which uses horizontal slices with assigned depth at regular intervals in the Z direction;
- bmin and bmax, the minimum and maximum planimetric dimensions, respectively, of a bounding box (the yellow box in Figure 6a,b) around the canopy projection, obtained in a GIS environment;
- Canopy width (CW), the average dimension of the bounding box around the canopy.
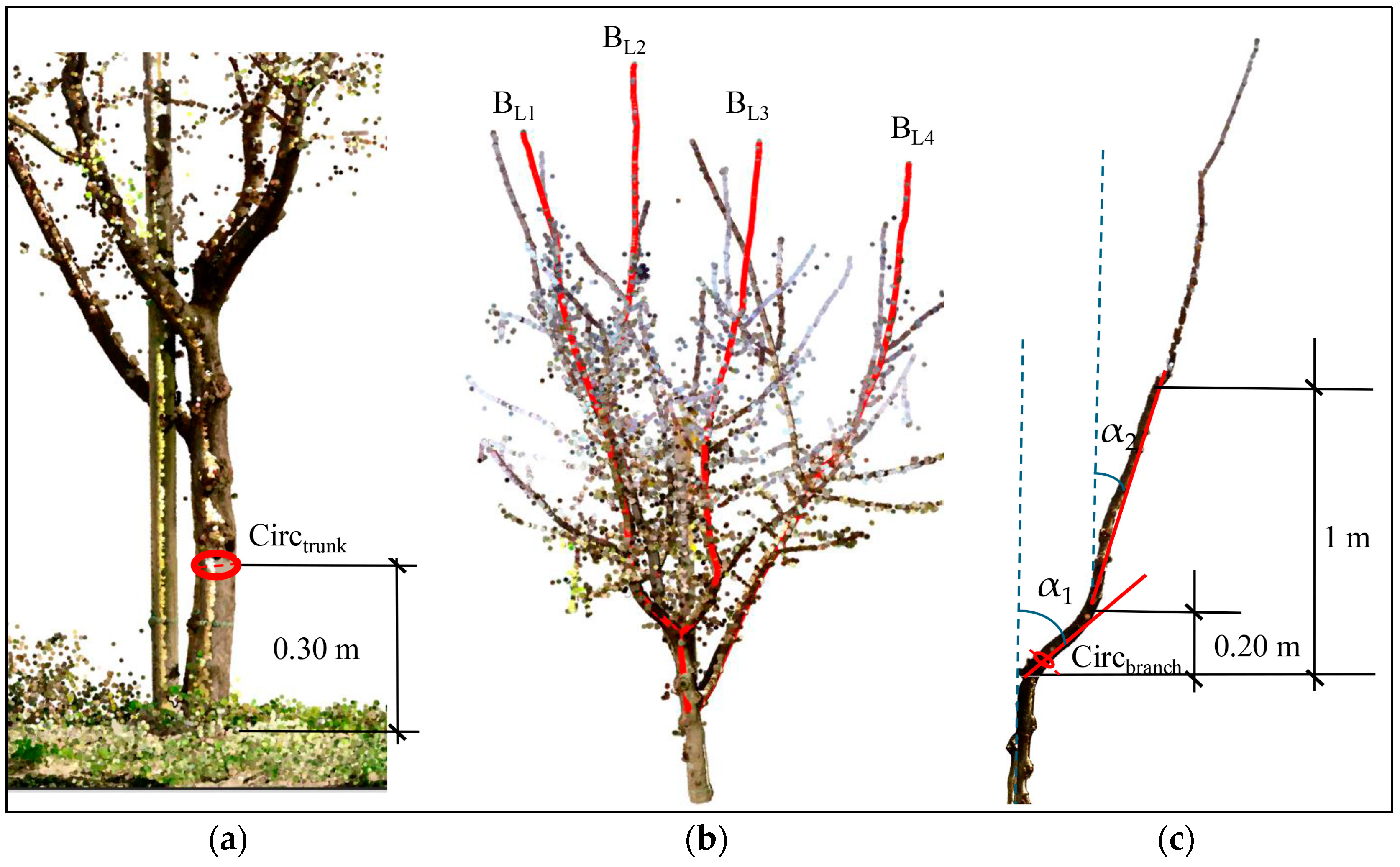
- Trunk circumference at 30 cm from the ground and the relative trunk section (TS) (Figure 7a);
- The number of the principal branches (BN) and the respective length (BL) (Figure 7b), where principal branches are defined as those that are inserted directly on the trunk and constituting the permanent constituent portion of the plant;
- The mean value of the branch length (BLm) and the total length of the branches (BLt) for each tree;
- The branch angles, including the attachment angle (α1, calculated over an ~20 cm segment from the trunk attachment) and the elevation angle (α2, calculated over an ~1 m segment from the trunk attachment), both measured with respect to the vertical direction (Figure 7c);
- The circumference of the principal branches (Figure 7c) and the corresponding branch basic diameter (BBD) and basal branch section (BBS);
- The branch volume (BVC) and the lateral surface (LSB) of each principal branch, considered as a cone with a base area equal to BBS and a height equal to BL;
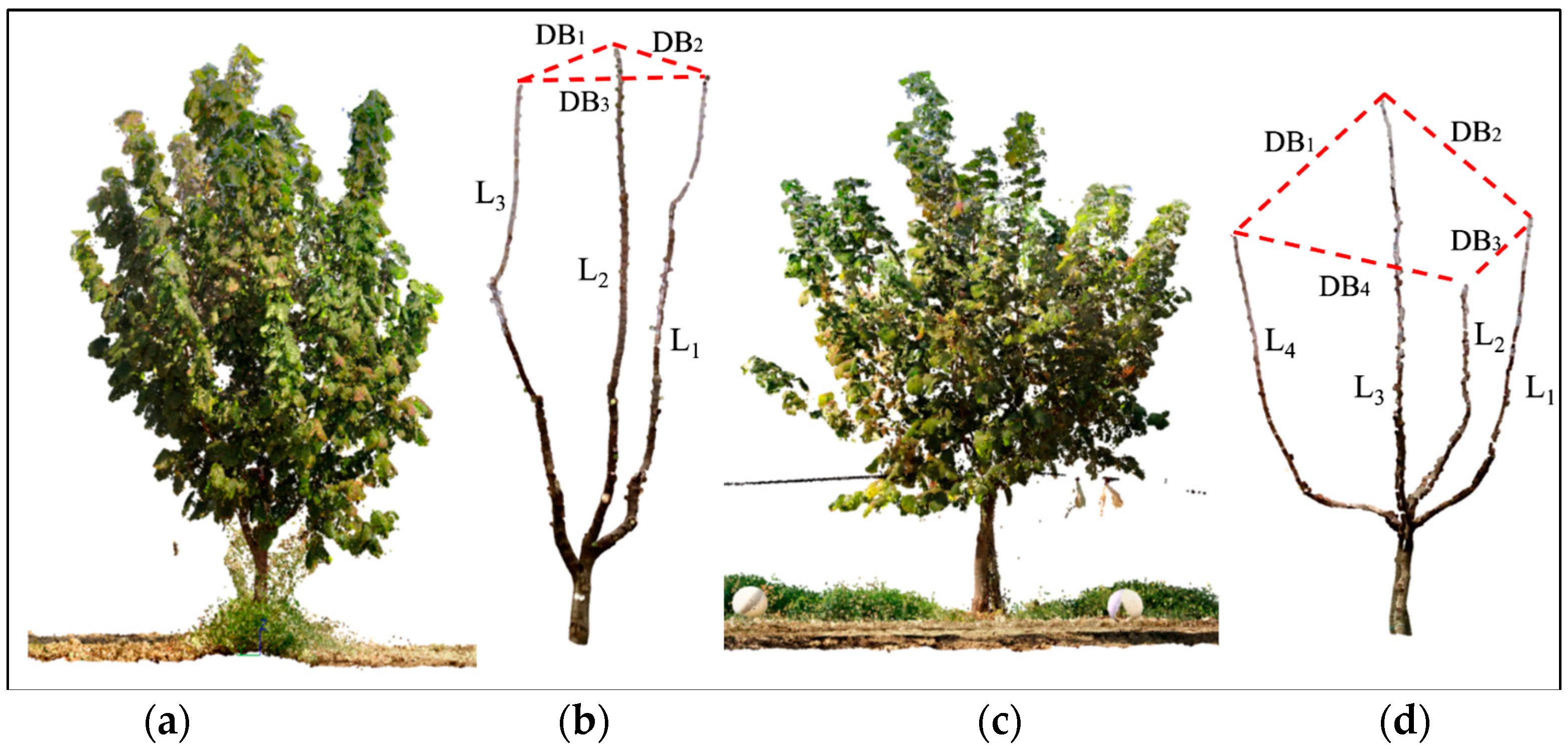
- The mean distance between principal branches (DBm) (Figure 8).
2.3. Morphological Indexes
- CS (Canopy Symmetry), defined as the ratio between the minimum and the maximum planimetric dimension of the canopy projection;
- CU (Canopy Uprightness), defined as the ratio between the canopy width (CW) and the canopy height (CH);
- C_HW, defined as the ratio between the height (CH) and width of the canopy (CW);
- C_AV, defined as the ratio between the area (CA) and volume of the canopy (CV);
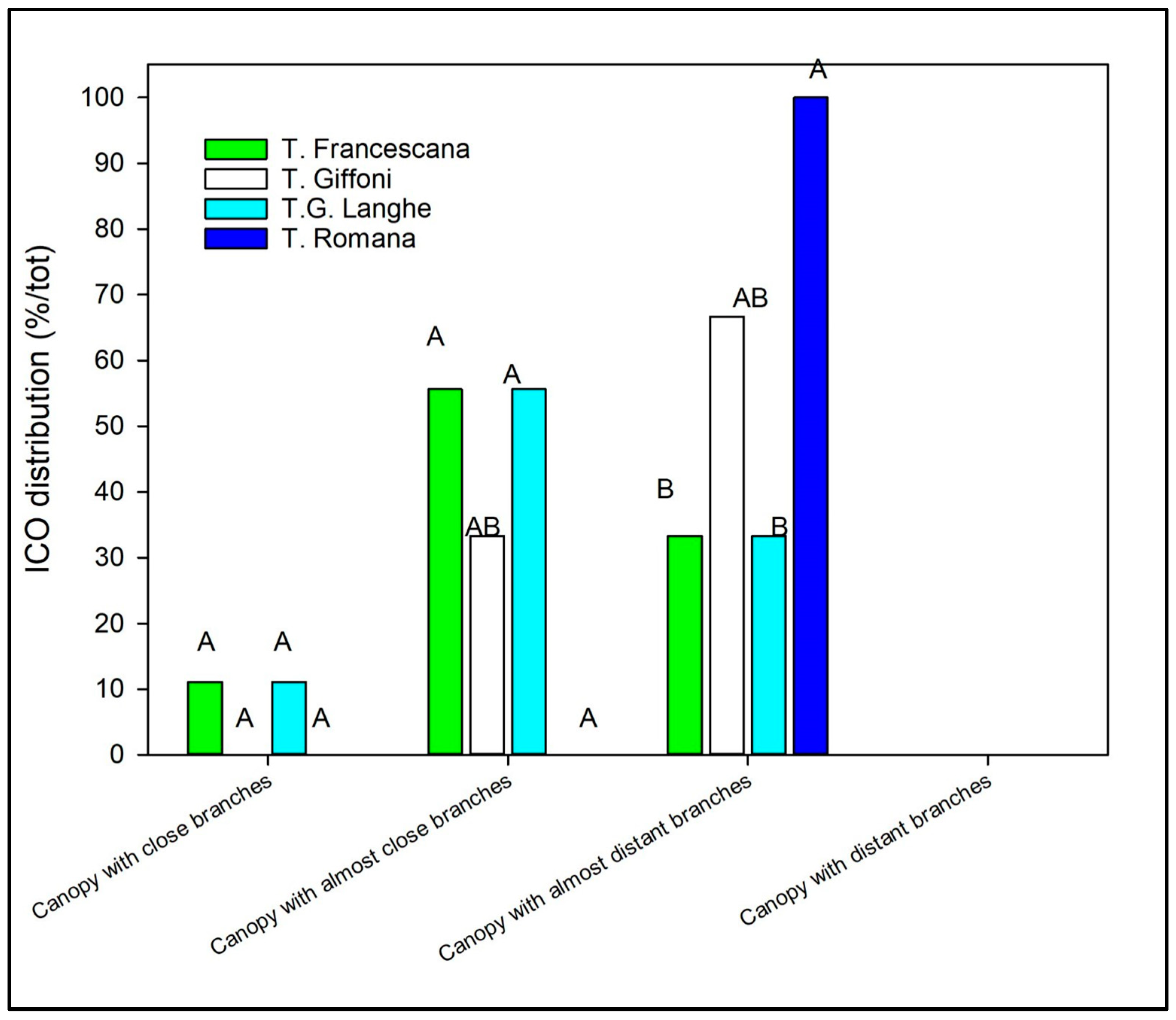
- ICO (Index of Canopy Opening), calculated as the ratio between the average distance between adjacent branches (DBm) and the average branch length (BLm);
- ICO was used to define the canopy habit, expressed as the number of branches falling in each class relative to the total. If ICO was <0.35, the canopy was classified as “canopy with close branches”; ICO between 0.35 and 0.45 indicated a “canopy with almost close branches”; ICO between 0.45 and 0.55 indicated “canopy with almost distant branches”; and ICO > 0.55 indicated a “canopy with distant branches”;
- BL_CV, calculated as the ratio between the total length of branches (BLt) and the canopy volume (CV);
- LSB_CV, calculated as the ratio between the lateral surface of all the branches (LSB) and the canopy volume (CV);
- BBS_CV, calculated as the ratio between the basal branches section (BBS) and the canopy volume (CV);
- BBS_TS, calculated as the ratio between the basal section of the branches (BBS-TS) and the trunk section (TS);
- BN_CA, calculated as the ratio between the number of branches (BN) and the canopy area (CA);
- BN_CV, calculated as the ratio between the number of branches (BN) and the canopy volume (CV);
- BVC_CV, calculated as the ratio between branch volume (BVC) and canopy volume (CV).
- CS values close to 1 indicate symmetry, while lower values reflect asymmetry in the canopy projection onto a horizontal plane;
- Higher CU values indicate a less compact canopy, while lower values reflect a more compact structure;
- Higher C_HW values indicate a more slender canopy, while values close to 1 indicate constant proportions between height and width;
- Larger C-AV values correspond to a less compact canopy, whereas smaller values indicate a denser structure;
- VPI values close to 1 indicate that the ideal solid closely approximates the canopy shape;
- Lower ICO values correspond to a more compact canopy with close branches;
- The values of BL_CV, LSB_CV, BBS_CV, BBS_TS, BN_CA, BN_CV, and BVC_CV provide information regarding branch density.
2.4. Statistical Analysis and Principal Component Analysis
3. Results and Discussion
3.1. Definition of the Hazelnut Plant Traits by the Application of Morphological Traits and Morphological Indexes
3.2. Assessment of Geometric Models of Canopy Volume That Best Reproduce TLS Estimates
3.3. Plant Traits to Be Used as Standard Descriptors of Hazelnut Cultivar
- BBD (branch basic diameter) allowed us to distinguish two groups of cultivars: one group composed of TF and TGL and one composed of TG and TR (Table 4). The BBD was different between a grafted plant and an own-rooted plant.
- BBS (basal branch section) also allowed us to differentiate two groups of cultivars: one group with greater BBS, and therefore greater vigour, composed of TF and TGL; and one group with smaller BBS, composed of TG and TR (Table 6). Thus, the BBS of the grafted plants was higher than that of the own-rooted plants (Table 6). Moreover, it can be used to determine the growth rate, based on the increment in branch size over the year.
- BLm (branch length mean per tree) was longest in the F cultivar, while the shortest branch was in TR (Table 6).
- BLt (branch total length per tree) allowed us to discriminate the TGL cultivar, showing the longest value, from TG and TF, and from TR, with the shortest value. Moreover, the grafted plants exhibited the longest total branch length compared to micropropagated and own-rooted plants (Table 6).
- BVC represents the branch volume (cone) and differentiated two groups of cultivars: one made from TF and TGL, with higher values; and the other from TG and TR, with lower values (Table 6).
- LSB (lateral surface of branches) revealed a difference between two groups of cultivars: the TF and TG cultivars, and TG and TR (Table 6).
- α1 (attachment angle of the branches, measured with respect to the vertical direction) allowed us to distinguish two groups of cultivars: one group with a narrow angle α1 composed of TGL and TG cultivars and one group with a wider angle α1, consisting of TF and TR cultivars (Table 4 and Figure 6). Moreover, the grafted plants showed a narrower angle.
- α2 (elevation angle of the branches, measured with respect to the vertical direction) allowed us to discriminate the TF and TGL cultivars (Figure 6 and Figure 12 and Table 4), confirming the growth habit of the TGL cultivar as erect, since α2 also proved to be narrow, similar to α1, and the growth habit of the TF cultivar is revealed as semi-erect.
- BBS_CV (ratio between the basal branches section (BBS) and the canopy volume (CV)), an expression of branch density, allowed us to distinguish the TF cultivar from TGL and TR cultivars (Table 7).
- BL_CV (ratio between the total branch length (BLt) and the canopy volume (CV)) may represent an evaluation of the canopy density and was different among the cultivars. The highest BL_CV was obtained by the TG and TGL cultivars, followed by the TR cultivar; the lowest BL_CV was in TF (Table 6).
- BN_CV (ratio between the branches number (BN) and the canopy volume (CV)), an expression of branch density, was highest in the TR and TG cultivars, significantly lowest in the TF cultivar (Table 7).
- BVC_CV (ratio between branches volume (BVC) and canopy volume (CV)), an expression of branch density, discriminated the TGL cultivar from the TF and TR cultivars (Table 7).
- C_AV (ratio between the area (CA) and volume of the canopy (CV)) was different among the cultivars, allowing us to distinguish the TG and TR cultivars, showing plants with less compact canopy. It was the index with the highest value in the TGL and TF cultivars, which had a denser canopy structure (Table 4).
- CU (canopy uprightness) is defined as the ratio between the canopy width (CW) and the canopy height (CH). The TGL cultivar showed the lowest value, which was significantly different from those of TF and TG, confirming that the TGL cultivar has a more compact structure compared to those of the other cultivars, since lower values reflect a more compact structure (Table 4).
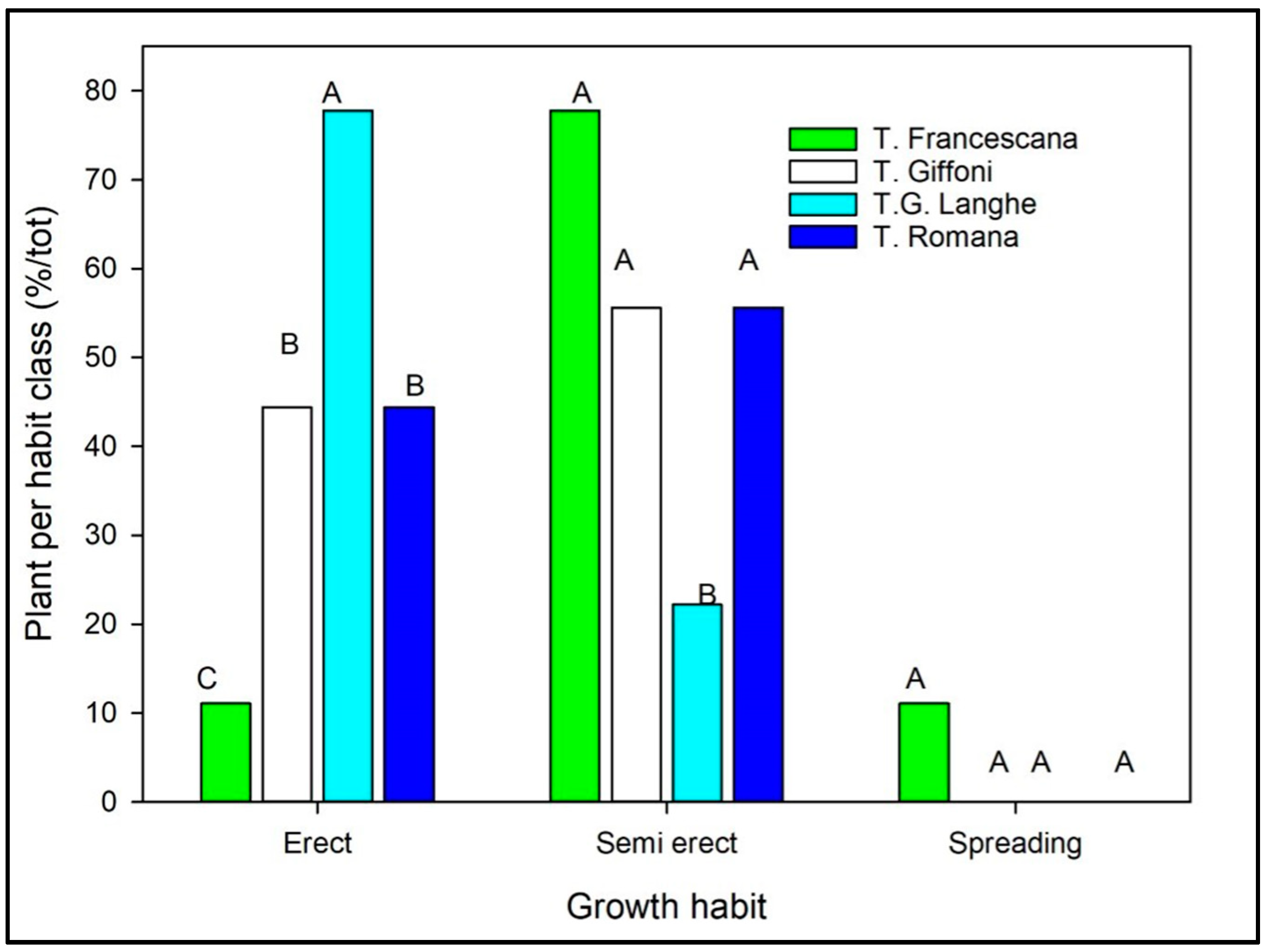
- ICO (Index of Canopy Opening) (ratio between the average distance between adjacent branches (DBm) and the average branch length (BLm)), defining the canopy habit, significantly varied among the cultivars, while it was similar among the three plant materials (Figure 9 and Table 4). The canopy habit, on average, resulted in a canopy with almost distant branches on TR and TG cultivars, with almost close branches on the TGL and TF cultivars.
- LSB_CV (ratio between the lateral surface of all the branches (LSB) and the canopy volume (CV)) allows us to differentiate TGL plants from TF plants (Table 6).
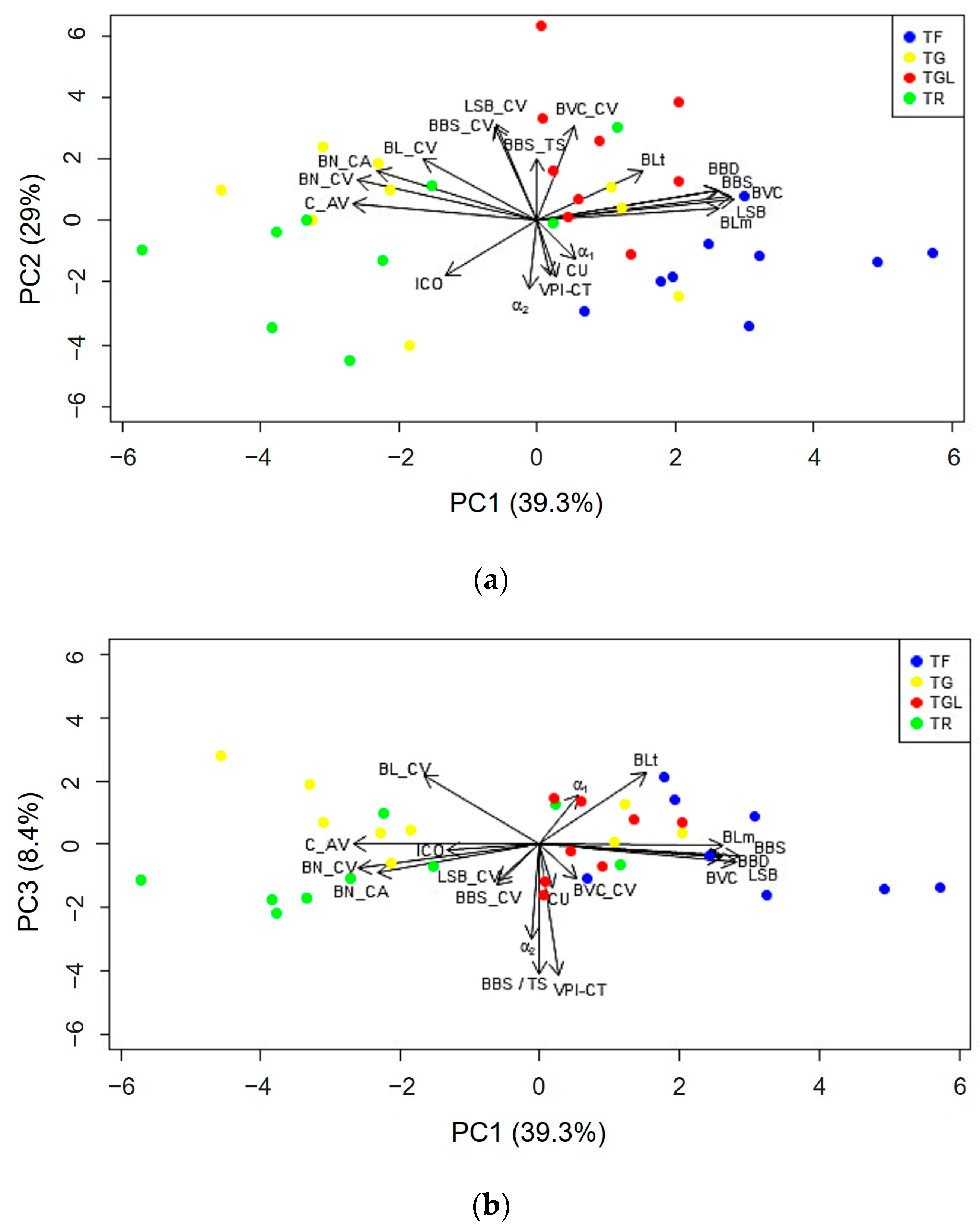
3.4. Principal Component Analysis to Discriminate the Cultivars
3.5. Strength and Weakness of TLS in Fruit Tree Applications
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Sinoquet, H.; Bruno, A. The geometrical structure of plant canopies: Characterization and direct measurement methods. In Crop Structure and Light Microclimate; INRA Editions: Paris, France, 1993; pp. 131–158. [Google Scholar]
- Valentini, N.; Caviglione, M.; Ponso, A.; Lovisolo, C.; Me, G. Physiological aspects of hazelnut trees grown in different training systems. Acta Hortic. 2009, 845, 233–238. [Google Scholar] [CrossRef]
- Portarena, S.; Proietti, S.; Moscatello, S.; Zadra, C.; Cinosi, N.; Traini, C.; Farinelli, D. Effect of Tree Density on Yield and Fruit Quality of the Grafted Hazelnut Cultivar ‘Tonda Francescana®’. Foods 2024, 13, 3307. [Google Scholar] [CrossRef]
- Costes, E.; Lauri, P.E.; Regnard, J.L. Analyzing fruit tree architecture: Implications for tree management and fruit production. Hortic. Rev. 2006, 32, 1–61. [Google Scholar]
- Martinez-Guanter, J.; Ribeiro, Á.; Peteinatos, G.G.; Pérez-Ruiz, M.; Gerhards, R.; Bengochea-Guevara, J.M.; Machleb, J.; Andújar, D. Low-cost three-dimensional modeling of crop plants. Sensors 2019, 19, 2883. [Google Scholar] [CrossRef]
- Walter, A.; Liebisch, F.; Hund, A. Plant phenotyping: From bean weighing to image analysis. Plant Methods 2015, 11, 14. [Google Scholar] [CrossRef] [PubMed]
- Pace, R.; Masini, E.; Giuliarelli, D.; Biagiola, L.; Tomao, A.; Guidolotti, G.; Agrimi, M.; Portoghesi, L.; De Angelis, P.; Calfapietra, C. Tree measurements in the urban environment: Insights from traditional and digital field instruments to smartphone applications. Arboric. Urban For. 2022, 48, 113–123. [Google Scholar] [CrossRef]
- Moorthy, I.; Miller, J.R.; Berni, J.A.J.; Zarco-Tejada, P.; Hu, B.; Chen, J. Field characterization of olive (Olea europaea L.) tree crown architecture using terrestrial laser scanning data. Agric. For. Meteorol. 2011, 151, 204–214. [Google Scholar] [CrossRef]
- Lodolini, E.M.; de Iudicibus, A.; Lucchese, P.G.; Las Casas, G.; Torrisi, B.; Nicolosi, E.; Giuffrida, A.; Ferlito, F. Comparison of canopy architecture of five olive cultivars in a high-density planting system in Sicily. Agriculture 2023, 13, 1612. [Google Scholar] [CrossRef]
- Costes, E.; Belouin, A.; Brouard, L.; Le Lezec, M. Development of young pear tree architecture and occurrence of first flowering: A varietal comparison. J. Hortic. Sci. Biotechnol. 2004, 79, 67–74. [Google Scholar]
- Dewar, R.C. The Correlation between Plant Growth and Intercepted Radiation: An Interpretation in Terms of Optimal Plant Nitrogen Content. Ann. Bot. 1996, 78, 125–136. [Google Scholar] [CrossRef]
- Hampson, C.R.; Azarenko, A.N.; Potter, J.R. Photosynthetic rate, flowering, and yield component alteration in hazelnut in response to different light environments. J. Am. Soc. Hortic. Sci. 1996, 121, 1103–1111. [Google Scholar] [CrossRef]
- Ghosh, A.; Dey, K.; Das, S.; Dutta, P. Effect of Light on Flowering of Fruit Crops. Adv. Life Sci. 2016, 5, 2597–2603. [Google Scholar]
- Singh, J.; Marboh Stone, E.; Singh, P.; Poojan, S. Light interception under different training system and high-density planting in fruit crops. J. Pharmacogn. Phytochem. 2020, 9, 611–616. [Google Scholar]
- Dorji, Y.; Schuldt, B.; Neudam, L.; Dorji, R.; Middleby, K.; Isasa, E.; Korber, K.; Ammer, C.; Annighofer, P.; Seidel, D. Three-dimensional quantification of tree architecture from mobile laser scanning and geometry analysis. Trees 2021, 35, 1385–1398. [Google Scholar] [CrossRef]
- Tombesi, S.; Farinelli, D. Modelling of pruning technique effects on branch architecture and subsequent year shoot flowering in hazelnut. Acta Hortic. 2017, 1160, 141–144. [Google Scholar] [CrossRef]
- Costes, E.; Crespel, L.; Denoyes, B.; Morel, P.; Demene, M.N.; Lauri, P.E.; Wenden, B. Bud structure, position and fate generate various branching patterns along shoots of closely related Rosaceae species: A review. Front. Plant Sci. 2014, 5, 666. [Google Scholar] [CrossRef]
- Montesinos, Á.; Thorp, G.; Grimplet, J.; Rubio-Cabetas, M.J. Phenotyping almond orchards for architectural traits influenced by rootstock choice. Horticulturae 2021, 7, 159. [Google Scholar] [CrossRef]
- Grisafi, F.; Tombesi, S.; Farinelli, D.; Boudon, F.; Durand, J.B.; Costes, E. Analysing the architecture of Corylus avellana and parametrizing L. Hazelnut FSPM. In Proceedings of the 10th International Conference on Functional-Structural Plant Models (FSPM2023), Berlin, Germany, 27–31 March 2023. [Google Scholar]
- Grisafi, F.; Farinelli, D.; Costes, E.; Boudon, F.; Durand, J.B.; Tombesi, S. Analysis of bud and sylleptic shoot distribution along one-year-old shoots of hazelnut (Corylus avellana). Acta Hortic. 2023, 1379, 283–290. [Google Scholar] [CrossRef]
- Grisafi, F.; Farinelli, D.; Costes, E.; Boudon, F.; Durand, J.B.; Tombesi, S. Architecture and yield relationship in hazelnut tree. Acta Hortic. 2023, 1366, 331–336. [Google Scholar] [CrossRef]
- Grisafi, F.; Tombesi, S.; Farinelli, D.; Costes, E.; Durand, J.B.; Boudon, F. Modelling the architecture of hazelnut (Corylus avellana) Tonda di Giffoni over two successive years. Silico Plants 2024, 6, diae004. [Google Scholar] [CrossRef]
- Vandendaele, B.; Martin-Ducup, O.; Fournier, R.A.; Pelletier, G.; Lejeune, P. Mobile Laser Scanning for Estimating Tree Structural Attributes in a Temperate Hardwood Forest. Remote Sens. 2022, 14, 4522. [Google Scholar] [CrossRef]
- Holopainen, M.; Kankare, V.; Vastaranta, M.; Liang, X.; Lin, Y.; Vaaja, M.; Yu, X.; Hyyppä, J.; Hyyppä, H.; Kaartinen, H.; et al. Tree mapping using airborne, terrestrial and mobile laser scanning–A case study in a heterogeneous urban forest. Urban For. Urban Green. 2013, 12, 546–553. [Google Scholar] [CrossRef]
- Stal, C.; Verbeurgt, J.; De Sloover, L.; De Wulf, A. Assessment of handheld mobile terrestrial laser scanning for estimating tree parameters. J. For. Res. 2021, 32, 1503–1513. [Google Scholar] [CrossRef]
- Estornell, J.; Hadas, E.; Martí, J.; López-Cortés, I. Tree extraction and estimation of walnut structure parameters using airborne LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102273. [Google Scholar] [CrossRef]
- Okura, F. 3D modeling and reconstruction of plants and trees: A cross-cutting review across computer graphics, vision, and plant phenotyping. Breed Sci. 2022, 72, 31–47. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Christoph, K.; Nölke, N. Assessing tree crown volume—A review. Forestry 2021, 94, 18–35. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Young-Pow, C.; Treitz, P. Assessing Forest metrics with a ground-based scanning LIDAR. Can. J. For. Res. 2004, 34, 573–583. [Google Scholar] [CrossRef]
- Rutzinger, M.; Pratihast, A.K.; Oude Elberink, S.; Vosselman, G. Detection and modelling of 3D trees from mobile laser scanning data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 520–525. [Google Scholar]
- Lin, Y.; Herold, M. Tree species classification based on explicit tree structure feature parameters derived from static terrestrial laser scanning data. Agric. For. Meteorol. 2016, 216, 105–114. [Google Scholar] [CrossRef]
- Reich, K.F.; Kunz, M.; von Oheimb, G. A new index of forest structural heterogeneity using tree architectural attributes measured by terrestrial laser scanning. Ecol. Indic. 2021, 133, 108412. [Google Scholar] [CrossRef]
- Brigante, R.; Calisti, R.; Marconi, L.; Proietti, P.; Radicioni, F.; Vinci, A. GNSS NRTK-UAV photogrammetry and LiDAR point clouds for geometric features extraction of olive orchard. In Proceedings of the 2024 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Padua, Italy, 29–31 October 2024; pp. 563–568. [Google Scholar] [CrossRef]
- Bogdanovich, E.; Perez-Priego, O.; El-Madany, T.S.; Guderle, M.; Pacheco-Labrador, J.; Levick, S.R.; Moreno, G.; Carrara, A.; Pilar Martín, M.; Migliavacca, M. Using terrestrial laser scanning for characterizing tree structural parameters and their changes under different management in a Mediterranean open woodland. For. Ecol. Manag. 2021, 486, 118945. [Google Scholar] [CrossRef]
- Vinci, A.; Brigante, R.; Traini, C.; Farinelli, D. Geometrical Characterization of Hazelnut Trees in an Intensive Orchard by an Unmanned Aerial Vehicle (UAV) for Precision Agriculture Applications. Remote Sens. 2023, 15, 541. [Google Scholar] [CrossRef]
- McGaughey, R.J.; Kruper, A.; Bobsin, C.R.; Bormann, B.T. Tree Species Classification Based on Upper Crown Morphology Captured by Uncrewed Aircraft System Lidar Data. Remote Sens. 2024, 16, 603. [Google Scholar] [CrossRef]
- Bioversity; FAO; CIHEAM. Descriptors for Hazelnut (Corylus avellana L.); Bioversity International: Rome, Italy; Food and Agriculture Organization of the United Nations: Rome, Italy; International Centre for Advanced Mediterranean Agronomic Studies: Zaragoza, Spain, 2008. [Google Scholar]
- UPOV. Available online: https://www.upov.int/meetings/en/doc_details.jsp?meeting_id=60592&doc_id=541353 (accessed on 20 March 2025).
- Coupel-Ledru, A.; Pallas, B.; Delalande, M.; Boudon, F.; Carrié, E.; Martinez, S.; Regnard, J.L.; Costes, E. Multi-scale high-throughput phenotyping of apple architectural and functional traits in orchard reveals genotypic variability under contrasted watering regimes. Hortic. Res. 2019, 6, 52. [Google Scholar] [CrossRef]
- Traini, C.; Facchin, S.L.; Brigante, R.; Vinci, A.; Persichetti, S.; Meneghini, M.; Micheli, M.; Famiani, F.; Portarena, S.; Dradi, G.; et al. Field performance of grafted, micropropagated, and own-rooted plants of three Italian hazelnut cultivars during the initial four seasons of development. Front. Plant Sci. 2024, 15, 1412170. [Google Scholar] [CrossRef]
- Portarena, S.; Gavrichkova, O.; Brugnoli, E.; Battistelli, A.; Proietti, S.; Moscatello, S.; Famiani, F.; Tombesi, S.; Zadra, C.; Farinelli, D. Carbon allocation strategies and water uptake in young grafted and own-rooted hazelnut (Corylus avellana L.). Tree Physiol. 2022, 42, 939–957. [Google Scholar] [CrossRef]
- Scorza, R.; Lightner, G.W.; Liverani, A. The pillar peach tree and growth habit analysis of compact × pillar progeny. J. Am. Soc. Hortic. Sci. 1989, 114, 991–995. [Google Scholar] [CrossRef]
- Pretzsch, H. Canopy space filling and tree crown morphology in mixed-species stands compared with monocultures. For. Ecol. Manag. 2014, 327, 251–264. [Google Scholar] [CrossRef]
- Owen, H.J.F.; Lines, E.R. Common field measures and geometric assumptions of tree shape produce consistently biased estimates of tree and canopy structure in mixed Mediterranean forests. Ecol. Indic. 2024, 165, 112219. [Google Scholar] [CrossRef]
- Asante, W.A.; Ahoma, G.; Gyampoh, B.; Kyereh, B.; Asare, R. Upper canopy tree crown architecture and its implications for shade in cocoa agroforestry systems in the western region of Ghana. Trees For. People 2021, 5, 100100. [Google Scholar] [CrossRef]
- Farinelli, D.; Portarena, S.; da Silva Fernandes, D.; Traini, C.; Menegazzo da Silva, G.; Costa da Silva, E.; Ferreira da Veiga, J.; Pollegioni, P.; Villa, F. Variability of Fruit Quality among 103 Acerola (Malpighia emarginata D.C.) Phenotypes from the Subtropical Region of Brazil. Agriculture 2021, 11, 1078. [Google Scholar] [CrossRef]
- Leposavić, A.; Ružić, D.; Karaklajić-Stajić, Z.; Cerović, R.; Vujović, T.; Žurawicz, E.; Mitrovic, O. Field performance of micropropagated Rubus species. Acta Sci. Pol. Hortorum Cultus 2016, 15, 3–14. [Google Scholar]
- Tarsha Kurdi, F.; Gharineiat, Z.; Lewandowicz, E.; Shan, J. Modeling the Geometry of Tree Trunks Using LiDAR Data. Forests 2024, 15, 368. [Google Scholar] [CrossRef]
- Fish, H.; Lieffers, V.J.; Silins, U.; Hall, R.J. Crown shyness in lodgepole pine stands of varying stand height, density, and site index in the upper foothills of Alberta. Can. J. For. Res. 2006, 36, 2104–2111. [Google Scholar] [CrossRef]
- Hashimoto, R. Canopy development in young sugi (Cryptomeria japonica) stands in relation to changes with age in crown morphology and structure. Tree Physiol. 1991, 8, 129–143. [Google Scholar] [CrossRef]
- Jatzek, V.A.; Menecheli Filho, H.; Rocha, G.N.; Silva, O.J.; Rodriguez, L.C.E.; Paula, R.C.D.; Silva, P.H.M.D. Comparative assessment of LiDAR and conventional methods in evaluating genetic parameters of eucalypt progeny trials. Crop Breed. Appl. Biotechnol. 2025, 25, e50382516. [Google Scholar] [CrossRef]
- Farinelli, D.; Boco, M.; Tombesi, A. Productive and organoleptic evaluation of new hazelnut crosses. Acta Hortic. 2009, 845, 651–656. [Google Scholar] [CrossRef]
- Walter, J.D.; Edwards, J.; McDonald, G.; Kuchel, H. Estimating biomass and canopy height with LiDAR for field crop breeding. Front. Plant Sci. 2019, 10, 1145. [Google Scholar] [CrossRef]
- Lindberg, E.; Johan, H. Individual tree crown methods for 3D data from remote sensing. Curr. For. Rep. 2017, 3, 19–31. [Google Scholar] [CrossRef]









| Laser Scanner | Range (m) | Measurement Speed (pts/s) | Ranging Error 1 (mm) | Ranging Noise 2 (mm) | Beam Divergence (mrad) | Point Distance 3 (mm/10 m) |
|---|---|---|---|---|---|---|
| Faro Focus 3D X130 | up to 130 | up to 976,000 | ±2 | 0.3–0.5 | 0.19 | 7.00 |
| Code | Traits | Measurement Method |
|---|---|---|
| CH | Canopy height (m) | Automatic from canopy point cloud |
| CA | Canopy area (m2) | Automatic from canopy point cloud projection |
| CV | Canopy volume (m3) | Automatic from canopy point cloud |
| bmin | Minimum planimetric dimension of the canopy projection (m) | Automatic from canopy point cloud projection |
| bmax | Maximum planimetric dimension of the canopy projection (m) | Automatic from canopy point cloud projection |
| CW | Canopy width (m) | Automatic from spreadsheet |
| TS | Trunk section (m2) | Automatic from a horizontal section of the trunk point cloud |
| BN | Branch number | Manual from tree point cloud |
| BL | Branch length (m) | Manual from branch point cloud |
| BLm | Branch length (mean per tree) (m) | Automatic from spreadsheet |
| BLt | Branch total length (per tree) (m) | Automatic from spreadsheet |
| α1 | Attachment angle of the branches (measured with respect to the vertical direction) | Manual from branch point cloud |
| α2 | Elevation angle of the branches (measured with respect to the vertical direction) | Manual from branch point cloud |
| BBD | Branch basic diameter (cm) | Manual from branch point cloud |
| BBS | Basal branch section (cm2) | Automatic from spreadsheet |
| BVC | Branch volume (cone) (cm3) | Automatic from spreadsheet |
| LSB | Lateral urface of branches (cm2) | Automatic from spreadsheet |
| DBm | Mean distance between principal branches (m) | Manual from branch point cloud |
| Code | Index | Equation |
|---|---|---|
| CS | Canopy symmetry | bmin/bmax |
| CU | Canopy uprightness | CW/CH |
| C_HW | Ratio between the height and width of the canopy | CH/CW |
| C_AV | Ratio between the area and volume of the canopy (m−1) | CA/CV |
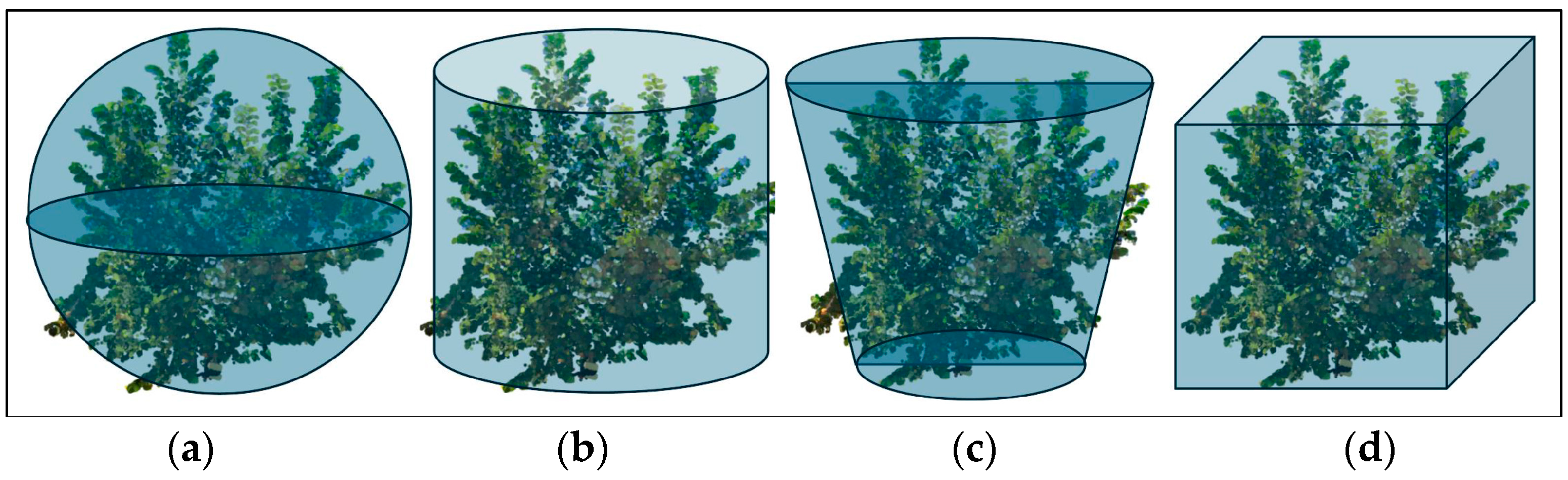
| VPI—E | Volumetric Projection Index—Ellipsoid | CV/Vellipsoid |
| VPI—C | Volumetric Projection Index—Cylinder | CV/Vcylinder |
| VPI—CT | Volumetric Projection Index—Cone Trunk | CV/Vcone_trunk |
| VPI—P | Volumetric Projection Index—Parallelepiped | CV/Vparallelepiped |
| ICO | Index of Canopy Opening | DBm/BLm |
| BL_CV | Ratio between the total branch length and the canopy volume (m−2) | BLt/CV |
| LSB_CV | Ratio between the lateral surface of all the branches and the canopy volume (cm−1) | LSB/CV |
| BBS_CV | Ratio between the basal section of the branches and the canopy volume (cm2/m3) | BBS/CV |
| BBS_TS | Ratio between the basal section of the branches and the trunk section | BBS/TS |
| BN_CA | Ratio between the number of branches and the canopy area (m−2) | BN/CA |
| BN_CV | Ratio between the number of branches and the canopy volume (m−3) | BN/CV |
| BVC_CV | Ratio between branch volume and canopy volume (cm3/m3) | BVC/CV |
| Cultivar/ Plant Type | BN (n) | BBD (cm) | α1 (°) | α2 (°) | C_HW | ICO | CS | CU | C_AV |
|---|---|---|---|---|---|---|---|---|---|
| TF | 3.7 A | 3.65 A | 46.4 A | 24.8 A | 1.32 A | 0.446 BC | 0.94 A | 0.90 A | 0.52 C |
| TG | 3.7 A | 3.16 B | 39.0 B | 21.7 AB | 1.28 A | 0.514 AB | 0.94 A | 0.89 A | 0.64 A |
| TGL | 3.8 A | 3.63 A | 39.1 B | 19.8 B | 1.36 A | 0.433 C | 0.96 A | 0.81 B | 0.60 B |
| TR | 3.3 A | 3.13 B | 41.2 AB | 23.1 AB | 1.34 A | 0.529 A | 0.91 A | 0.86 AB | 0.66 A |
| G | 3.7 a | 3.54 a | 38.0 b | 23.1 a | 1.29 a | 0.494 a | 0.95 a | 0.87 a | 0.60 a |
| M | 3.5 a | 3.42 ab | 41.0 ab | 21.4 a | 1.34 a | 0.444 a | 0.93 a | 0.86 a | 0.61 a |
| O | 3.7 a | 3.21 b | 45.2 a | 22.5 a | 1.34 a | 0.504 a | 0.94 a | 0.87 a | 0.61 a |
| Cultivar/ Plant Type | VPI—E | VPI—C | VPI—P | VPI—CT |
|---|---|---|---|---|
| TF | 1.18 A | 1.77 A | 2.25 A | 1.11 A |
| TG | 1.10 A | 1.65 A | 2.09 A | 0.91 B |
| TGL | 1.11 A | 1.67 A | 2.13 A | 0.94 B |
| TR | 1.14 A | 1.72 A | 2.17 A | 1.07 A |
| G | 1.11 a | 1.66 a | 2.11 a | 0.93 b |
| M | 1.13 a | 1.70 a | 2.16 a | 1.05 a |
| O | 1.16 a | 1.75 a | 2.22 a | 1.03 a |
| Cultivar/ Plant Type | BBS (cm2) | LSB (cm2) | BVC (cm3) | BLm (m) | BLt (m) | BL_CV (m/m3) | LSB_CV (cm2/cm3) |
|---|---|---|---|---|---|---|---|
| TF | 10.6 A | 1334 A | 825 A | 2.3 A | 7.8 B | 1.6 C | 0.00096 B |
| TG | 8.0 B | 976 B | 537 B | 1.9 B | 8.0 B | 2.6 A | 0.00112 AB |
| TGL | 10.6 A | 1191 A | 741 A | 2.1 B | 9.0 A | 2.5 A | 0.00123 A |
| TR | 7.9 B | 882 B | 478 B | 1.8 C | 5.3 C | 2.1 B | 0.00111 AB |
| G | 10.1 a | 1148 a | 700 a | 2.1 a | 8.3 a | 2.1 a | 0.0011 a |
| M | 9.4 ab | 1107 a | 653 a | 2.0 a | 7.4 b | 2.3 a | 0.0012 a |
| O | 8.4 b | 1031 a | 584 a | 2.0 a | 6.9 b | 2.1 a | 0.0011 a |
| Cultivar/ Plant Type | BN_CA (n./m2) | BN_CV (n./m3) | BBS_TS | BBS_CV (cm2/m3) | BVC_CV (cm3/m3) |
|---|---|---|---|---|---|
| TF | 1.4 B | 0.7 C | 1.1 B | 7.6 B | 587 B |
| TG | 1.9 A | 1.2 AB | 1.1 B | 9.1 AB | 630 AB |
| TGL | 1.7 A | 1.0 B | 1.6 A | 10.9 A | 767 A |
| TR | 2.0 A | 1.3 A | 1.2 AB | 10.0 A | 595 B |
| G | 1.6 a | 0.9 a | 1.0 b | 9.6 a | 659 a |
| M | 1.8 a | 1.1 a | 1.4 a | 10.0 a | 670 a |
| O | 1.8 a | 1.1 a | 1.3 ab | 8.7 a | 605 a |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brigante, R.; Marconi, L.; Facchin, S.L.; Famiani, F.; Sánchez Piñero, M.; Portarena, S.; De Vargas, R.J.; Villa, F.; Traini, C.; Vinci, A.; et al. Laser Scanning for Canopy Characterization in Hazelnut Trees: A Preliminary Approach to Define Growth Habitus Descriptor. Agriculture 2025, 15, 1251. https://doi.org/10.3390/agriculture15121251
Brigante R, Marconi L, Facchin SL, Famiani F, Sánchez Piñero M, Portarena S, De Vargas RJ, Villa F, Traini C, Vinci A, et al. Laser Scanning for Canopy Characterization in Hazelnut Trees: A Preliminary Approach to Define Growth Habitus Descriptor. Agriculture. 2025; 15(12):1251. https://doi.org/10.3390/agriculture15121251
Chicago/Turabian StyleBrigante, Raffaella, Laura Marconi, Simona Lucia Facchin, Franco Famiani, Marta Sánchez Piñero, Silvia Portarena, Rodrigo José De Vargas, Fabiola Villa, Chiara Traini, Alessandra Vinci, and et al. 2025. "Laser Scanning for Canopy Characterization in Hazelnut Trees: A Preliminary Approach to Define Growth Habitus Descriptor" Agriculture 15, no. 12: 1251. https://doi.org/10.3390/agriculture15121251
APA StyleBrigante, R., Marconi, L., Facchin, S. L., Famiani, F., Sánchez Piñero, M., Portarena, S., De Vargas, R. J., Villa, F., Traini, C., Vinci, A., Radicioni, F., & Farinelli, D. (2025). Laser Scanning for Canopy Characterization in Hazelnut Trees: A Preliminary Approach to Define Growth Habitus Descriptor. Agriculture, 15(12), 1251. https://doi.org/10.3390/agriculture15121251









