A Recognition Method for Adzuki Bean Rust Disease Based on Spectral Processing and Deep Learning Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of Adzuki Bean Samples
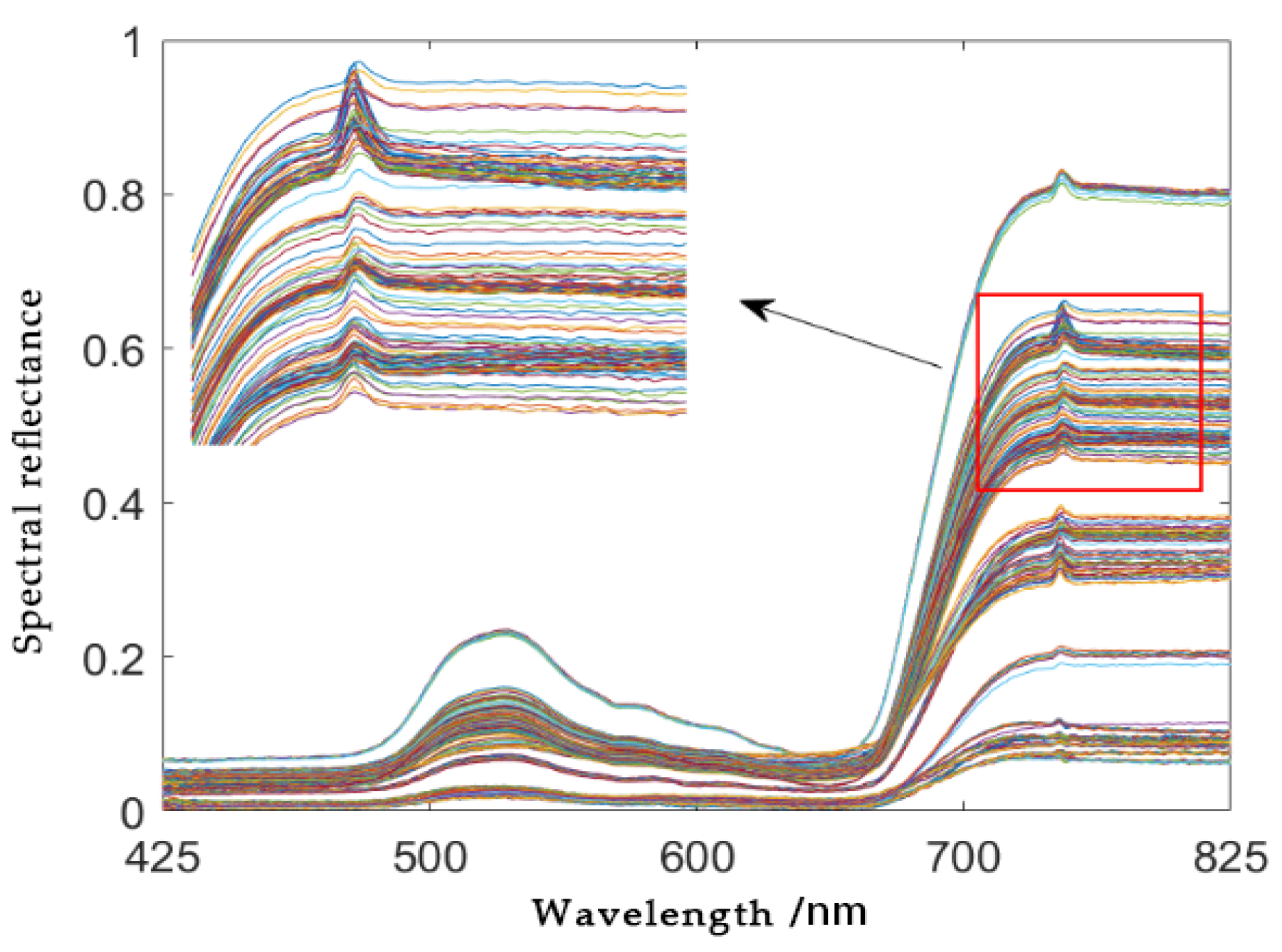
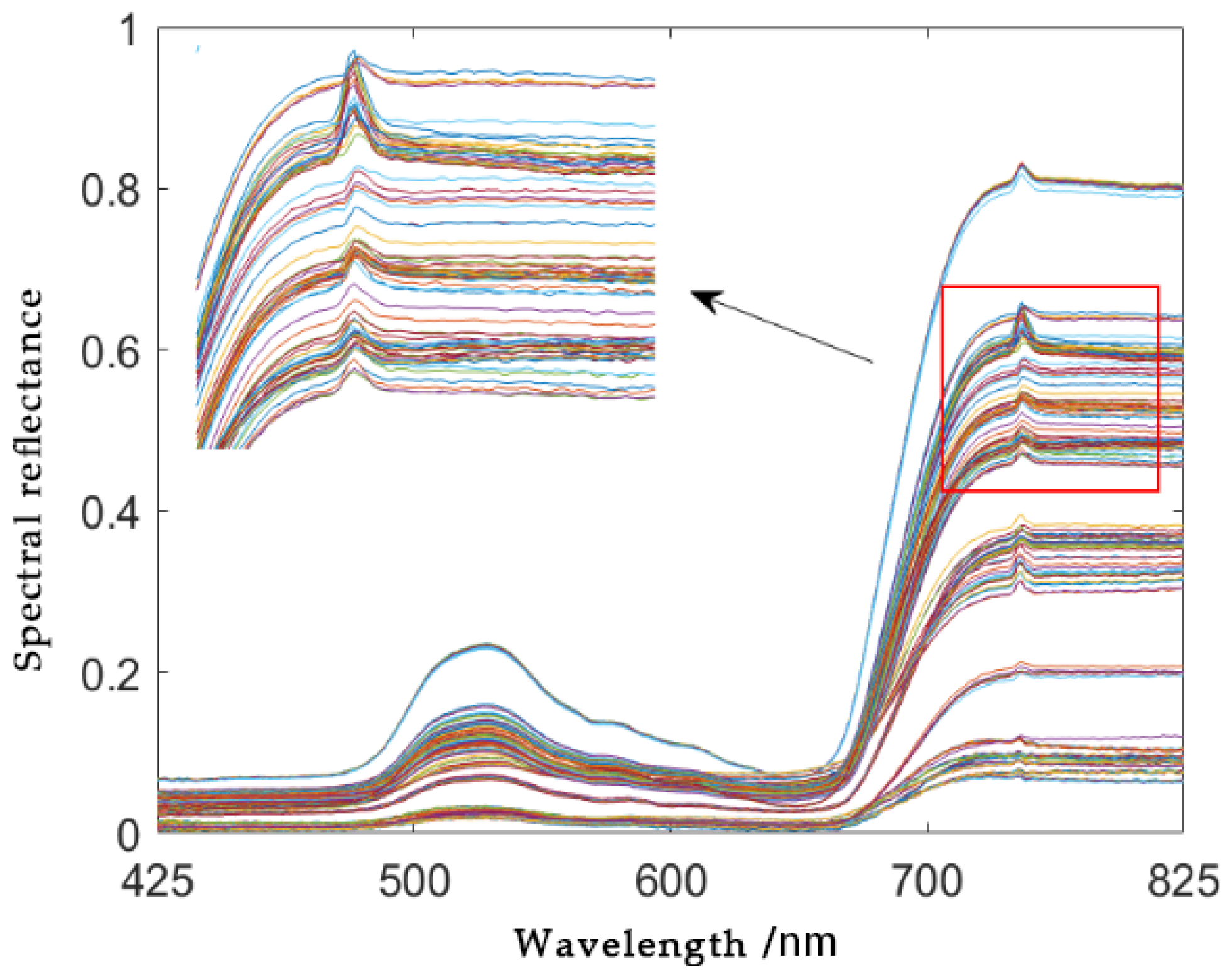
2.2. Spectral Data Acquisition for Adzuki Beans
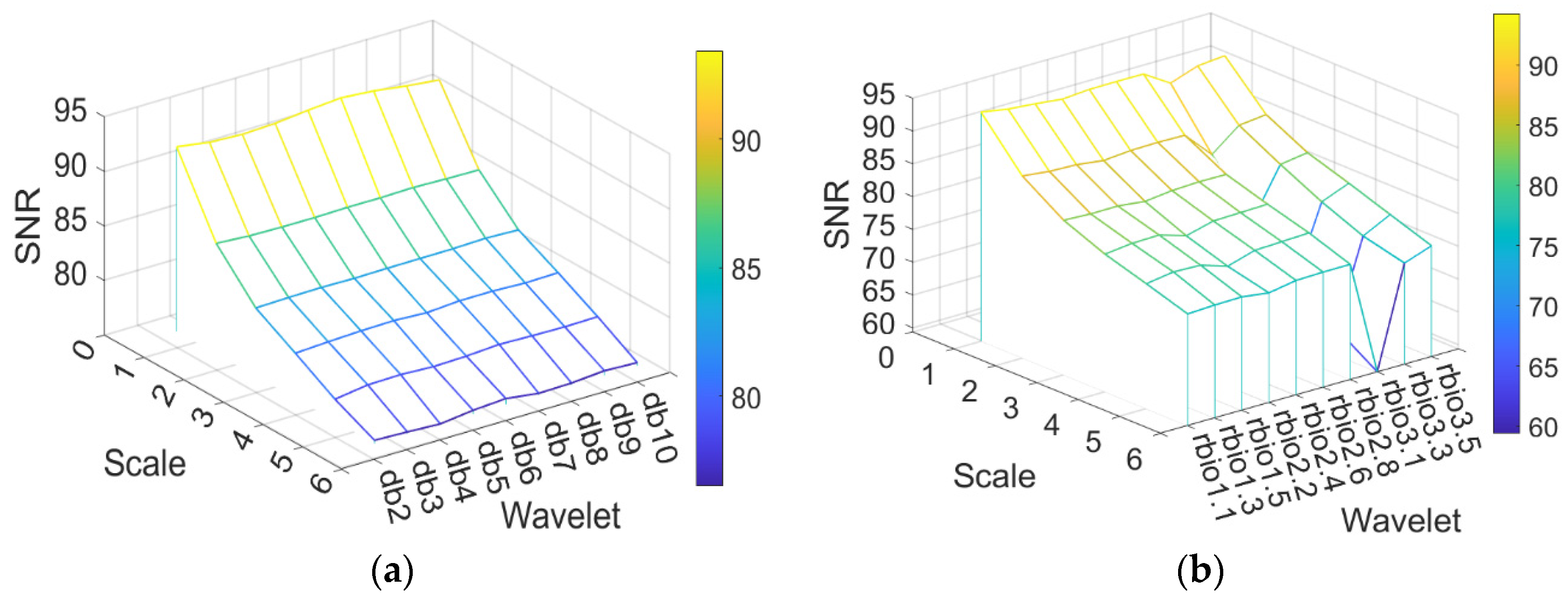
2.3. Spectral Data Preprocessing
- Wavelet Decomposition
- 2.
- Threshold Selection
- 3.
- Wavelet Coefficient Reconstruction
2.4. Extraction of Characteristic Wavenumberss
Competitive Adaptive Reweighted Sampling Algorithm
- Monte Carlo Sampling
- 2.
- Weight Calculation in the PLS Model
- 3.
- Exponential Decreasing Function (EDF) Filtering
- 4.
- Wavenumbers Selection Using the CARS Algorithm
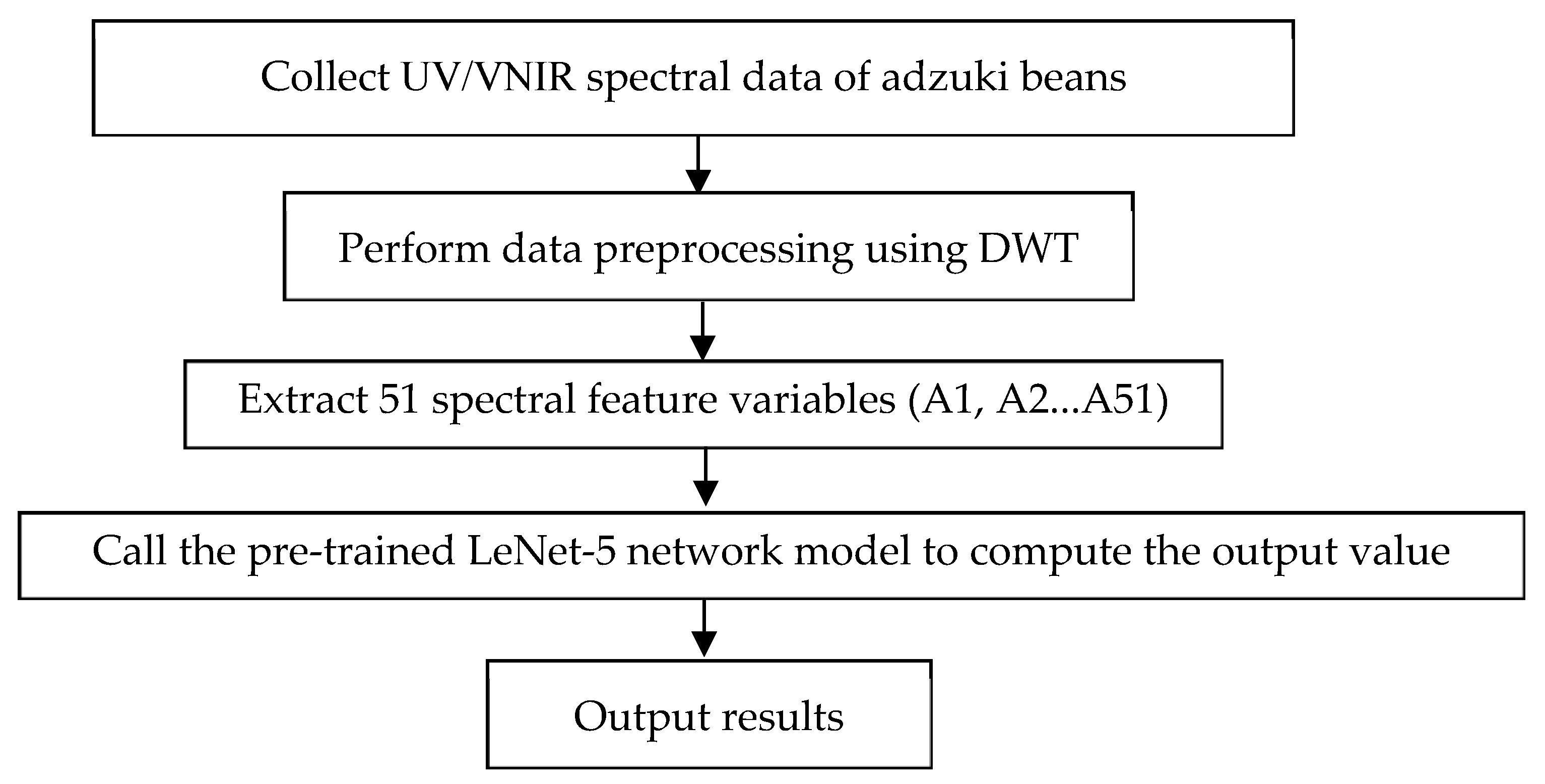
2.5. Construction of Diagnostic Model for the Adzuki Bean Rust Disease
2.5.1. LeNet-5 Network Architecture
2.5.2. Optimizer
- First, compute the gradient at the current time step, set the initial time step as , and then proceed with iterative training over time steps. During each iteration, the system automatically adjusts the model parameters based on the computed gradient values.
- Compute the exponentially weighted moving average of the gradient and initialize it to =0. The coefficient is the exponential decay rate that regulates the weight distribution. Typically, its value is set close to 1; is set to 0.9.
- Compute the exponentially weighted moving average of the squared gradients, initializing it to = 0. Here, is an exponential decay rate that regulates the influence of prior squared gradients. In this research, is set to 0.99.
- Given that = 0, this initialization may cause biased towards 0 during the early stages of training. To mitigate the influence of this bias on the initial phase, bias correction must be applied to the gradient mean .
- Similar to , bias correction must also be applied to .
- Update the parameters by setting the learning rate to = 0.001 and = 10−8.
2.5.3. Model Evaluation
3. Result
3.1. Analysis of Preprocessing Results
3.2. Analysis of Feature Extraction Results
3.3. Analysis of the Results Output from the LeNet-5 Model
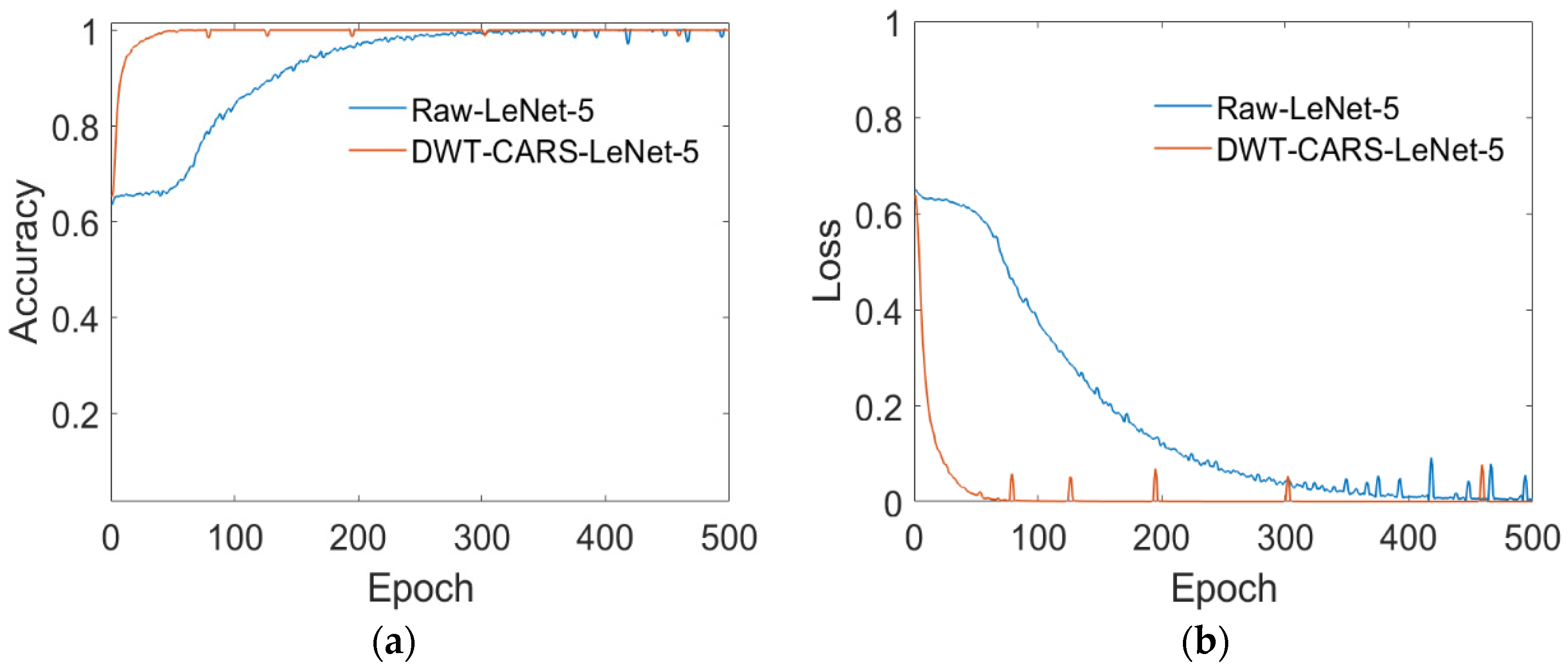
3.3.1. Model Training
- Hardware: NVIDIA GeForce GTX 1050 Ti GPU (4 GB VRAM).
- Software: Windows 10 (64-bit), Anaconda3, CUDA 10.2, Python 3.7, TensorFlow 2.3.0.
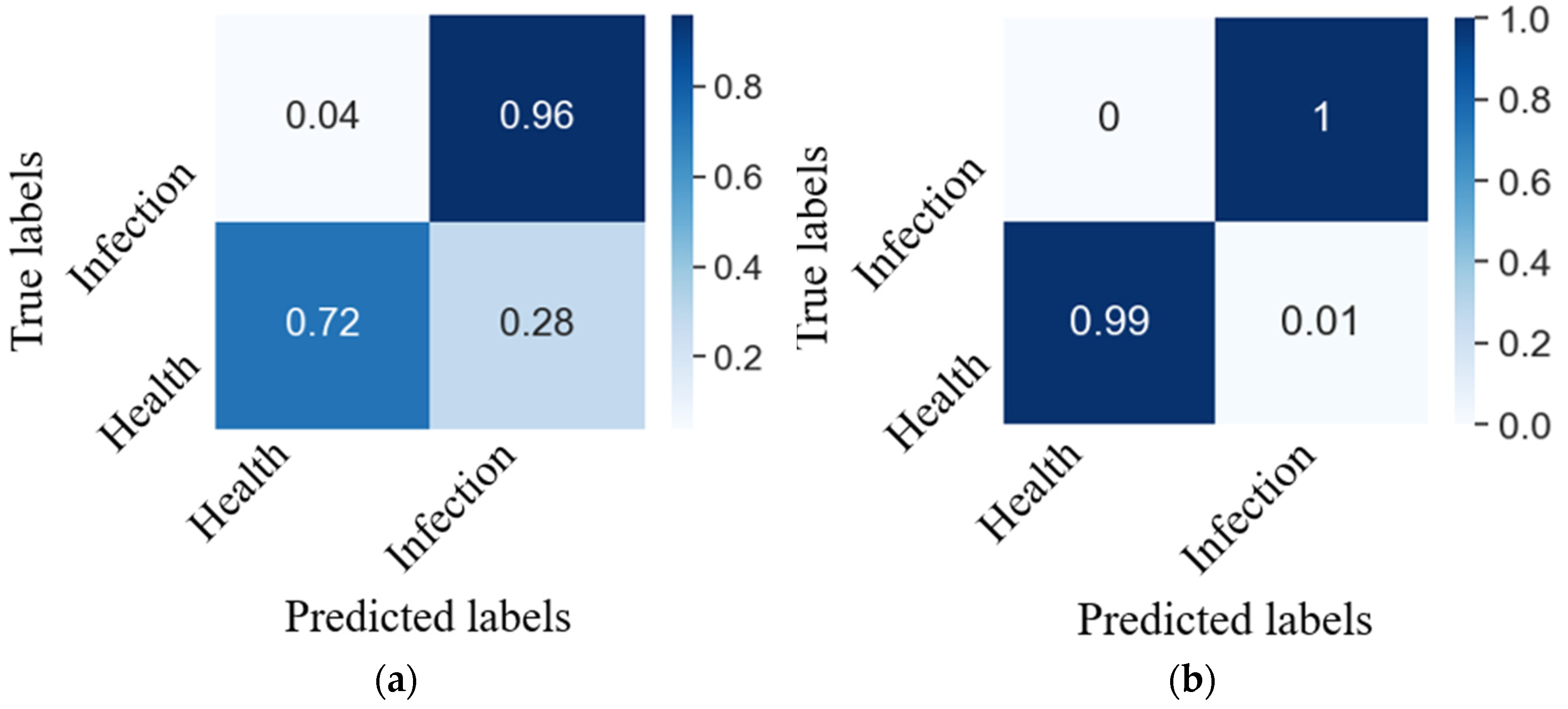
3.3.2. Model Testing
4. Discussion
4.1. Model Performance Analysis
4.2. Research Limitations
4.3. Future Work Outlook
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, L.; Zhang, J.; Zhang, G.; Liu, G.; Ke, X.; Zuo, Y. Construction and application of molecular detectionsystem for adzuki bean rust. Agric. Res. Arid Areas 2023, 41, 238–244. [Google Scholar]
- Liu, S.; Ding, X.; Li, Y.; Yin, L.; Ke, X.; Zuo, Y. Genome-wide identification of the NAC family genes of adzuki bean and their roles in rust resistance through jasmonic acid signaling. BMC Genom. 2025, 26, 283. [Google Scholar] [CrossRef]
- Velez, M.H.; Lopezrosa, J.; Freytag, G.F. Determination of yield loss caused by rust (Uromyces phaseoli (Reben) Wint.) in common bean (Phaseolus vulgaris L.) in Puerto Rico. Hum Genet. 1989, 80, 224–234. [Google Scholar] [CrossRef]
- Ke, X.; Wang, J.; Xu, X.; Guo, Y.; Zuo, Y.; Yin, L. Histological and molecular responses of Vigna angularis to Uromyces vignae infection. BMC Plant Biol. 2022, 22, 489. [Google Scholar] [CrossRef]
- Yang, C.; Ma, X.; Guan, H.; Li, L.; Fan, B. A rapid recognition method of auricularia auricula varieties based on near-infrared spectral characteristics. Infrared Phys. Technol. 2022, 125, 104239. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I. Visible and near-infrared reflectance techniques for diagnosing plant physiological status. Trends Plant Sci. 1998, 3, 151–156. [Google Scholar] [CrossRef]
- Ashurov, A.Y.; Al-Gaashani, M.S.A.M.; Samee, N.A.; Alkanhel, R.; Atteia, G.; Abdallah, H.A. Enhancing plant disease detection through deep learning: A Depthwise CNN with squeeze and excitation integration and residual skip connections. Front. Plant Sci. 2024, 15, 1505857. [Google Scholar] [CrossRef]
- Ji, X.; Xue, J.; Shi, J.; Wang, W.; Zhang, X.; Wang, Z.; Xu, N. Noninvasive Raman spectroscopy for the detection of rice bacterial leaf blight and bacterial leaf streak. Talanta 2025, 282, 126962. [Google Scholar] [CrossRef]
- Deng, J.; Zhang, X.; Yang, Z.; Zhou, C.; Wang, R.; Zhang, K.; Lv, X.; Yang, L.; Wang, Z.; Li, P. Pixel-level regression for UAV hyperspectral images: Deep learning-based quantitative inverse of wheat stripe rust disease index. Comput. Electron. Agric. 2023, 215, 108434. [Google Scholar] [CrossRef]
- Zhang, K.; Deng, J.; Zhou, C.; Liu, J.; Lv, X.; Wang, Y.; Sun, E.; Liu, Y.; Ma, Z.; Shang, J. Using UAV hyperspectral imagery and deep learning for Object-Based quantitative inversion of Zanthoxylum rust disease index. Int. J. Appl. Earth Obs. Geoinf. 2024, 135, 104262. [Google Scholar] [CrossRef]
- Yu, X.; Liu, S.; Wang, C.; Jiao, B.; Huang, C.; Liu, B.; Liu, C.; Yin, L.; Wan, F.; Qian, W. Detection of fungal disease in citrus fruit based on hyperspectral imaging. Inf. Process. Agric. 2025, in press. [Google Scholar] [CrossRef]
- Zheng, X.; Dong, Y.; Yang, Q.; Yu, M.; Zhao, Z.; Li, P.; Zheng, Y. Non-destructive Authentication of Dried Tangerine Peel Powder Based on Near-Infrared Spectroscopy Technology. China Fruits Veg. 2022, 42, 36–41. [Google Scholar]
- Zhang, F.; Liu, J.; Lin, J.; Wang, Z. Detection of Oil Yield from Oil Shale Based on Near-Infrared Spectroscopy Combined with Wavelet Transform and Least Squares Support Vector Machines. Infrared Phys. Technol. 2019, 97, 224–228. [Google Scholar] [CrossRef]
- Wang, F.; Chen, L.; Duan, D.; Cao, Q.; Zhao, Y.; Lan, W. Hyperspectral Monitoring of Total Nitrogen Content in Fresh Tea Leaves Based on Wavelet Analysis. Spectrosc. Spectr. Anal. 2022, 42, 3235–3242. [Google Scholar]
- Kumar, A.; Tomar, H.; Mehla, V.K.; Komaragiri, R.; Kumar, M. Stationary wavelet transform based ECG signal denoising method. ISA Trans. 2021, 114, 251–262. [Google Scholar] [CrossRef]
- Gao, J.; Wang, B.; Wang, Z.; Wang, Y.; Kong, F. A wavelet transform-based image segmentation method. Opt.-Int. J. Light Electron Opt. 2019, 208, 164123. [Google Scholar] [CrossRef]
- Zheng, R.; Wang, T.; Cao, J.; Vidal, P.P.; Wang, D. Multi-modal physiological signals based fear of heights analysis in virtual reality scenes. Biomed. Signal Process. Control 2025, 70, 102988. [Google Scholar] [CrossRef]
- Wu, G.; He, Y. Application Research of Wavelet Threshold Denoising Model in Infrared Spectral Signal Processing. Spectrosc. Spectr. Anal. 2009, 29, 3246–3249. [Google Scholar]
- Xu, T.; Jin, Z.; Guo, Z.; Yang, L.; Bai, J.; Feng, S.; Yu, F. Cooperative Inversion Method of Nitrogen and Phosphorus Content in Rice Leaves Based on CARS-RUN-ELM Algorithm. Trans. Chin. Soc. Agric. Eng. 2022, 38, 148–155. [Google Scholar]
- Yang, C.; Ma, X.; Guan, H.; Fan, B. Rapid detection method of Pleurotus eryngii mycelium based on near infrared spectral characteristics. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 271, 120919. [Google Scholar] [CrossRef]
- Sony, S.; Dunphy, K.; Sadhu, A.; Capretz, M. A systematic review of convolutional neural network-based structural condition assessment techniques. Eng. Struct. 2021, 226, 111347. [Google Scholar] [CrossRef]
- Yang, J.; Ma, X.; Guan, H.; Yang, C.; Zhang, Y.; Li, G.; Li, Z. A recognition method of corn varieties based on spectral technology and deep learning model. Infrared Phys. Technol. 2023, 128, 104533. [Google Scholar] [CrossRef]
- Zhai, N.; Yun, L.; Ye, Z.; Wang, Y.; Li, Y. Research on Prediction Method of Tobacco Mold in Storage Based on One-Dimensional Convolutional Neural Network. Comput. Eng. Sci. 2021, 43, 1833–1837. [Google Scholar]
- Li, G.; Yao, Q.; Fan, C.; Zhou, C.; Wu, G.; Zhou, Z.; Fang, X. An explainable one-dimensional convolutional neural networks based fault diagnosis method for building heating, ventilation and air conditioning systems. Build. Environ. 2021, 203, 108057. [Google Scholar] [CrossRef]
- Geetha, B.T.; Kumar, P.S.; Bama, B.S.; Neelakandan, S.; Dutta, C.; Babu, D.V. Green energy aware and cluster based communication for future load prediction in IoT. Sustain. Energy Technol. Assess. 2022, 52, 102244. [Google Scholar] [CrossRef]
- Dai, Z.; Li, D.; Zhou, Z.; Zhou, S.; Liu, W.; Liu, J.; Wang, X.; Ren, X. A strategy for high performance of energy storage and transparency in KNN-based ferroelectric ceramics. Chem. Eng. J. 2022, 427, 131959. [Google Scholar] [CrossRef]
- Deng, Y.; Zhou, X.; Shen, J.; Xiao, G.; Liao, B.Q. New methods based on back propagation (BP) and radial basis function (RBF) artificial neural networks (ANNs) for predicting the occurrence of haloketones in tap water. Sci. Total Environ. 2021, 772, 145534. [Google Scholar] [CrossRef]
- Blanco, V.; Japón, A.; Puerto, J. A Mathematical Programming Approach to SVM-Based Classification with Label Noise. Comput. Ind. Eng. 2022, 172, 108611. [Google Scholar] [CrossRef]
- Han, D.; Song, X.; Zhang, D. Occurrence and Integrated Control Techniques of Major Diseases and Pests of Adzuki Beans in Heilongjiang Province. Mod. Agric. 2018, 5, 2–5. [Google Scholar]
- Shen, X. Control Methods for Common Rust and Root Rot Diseases of Adzuki Beans in Heilongjiang Province. Heilongjiang Agric. Sci. 2017, 7, 132–133. [Google Scholar]
- Zhao, L.; Liu, C.; Xiao, Z. Occurrence and Control of Common Diseases and Pests of Adzuki Beans in Qinggang County. Mod. Agric. Sci. Technol. 2017, 6, 138+142. [Google Scholar]
- Fassio, A.S.; Restaino, E.A.; Cozzolino, D. Determination of oil content in whole corn (Zea mays L.) seeds by means of near infrared reflectance spectroscopy. Comput. Electron. Agric. 2015, 110, 171–175. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, W.; Li, J.; Liu, S.; Fan, S. Assessment of protein content and insect infestation of maize seeds based on on-line near-infrared spectroscopy and machine learning. Comput. Electron. Agric. 2023, 211, 107969. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl. -Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Chen, W.; Shi, C.; Ma, C. Crop Disease Recognition Method Based on Multi-modal Data Fusion. Comput. Appl. 2025, 45, 840–848. [Google Scholar]
- Hassanin, M.; Anwar, S.; Radwan, I.; Khan, F.S.; Mian, A. Visual attention methods in deep learning: An in-depth survey. Inf. Fusion 2024, 108, 102417. [Google Scholar] [CrossRef]
- Rinnan, Å.; Van Den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly accurate machine fault diagnosis using deep transfer learning. IEEE Trans. Ind. Inform. 2018, 15, 2446–2455. [Google Scholar] [CrossRef]






| No. | Wavenumbers (nm) | No. | Wavenumbers (nm) | No. | Wavenumbers (nm) | No. | Wavenumbers (nm) | No. | Wavenumbers (nm) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 430 | 2 | 441 | 3 | 445 | 4 | 449 | 5 | 450 |
| 6 | 453 | 7 | 465 | 8 | 466 | 9 | 467 | 10 | 475 |
| 11 | 493 | 12 | 494 | 13 | 518 | 14 | 529 | 15 | 530 |
| 16 | 531 | 17 | 534 | 18 | 536 | 19 | 545 | 20 | 548 |
| 21 | 549 | 22 | 551 | 23 | 552 | 24 | 566 | 25 | 567 |
| 26 | 568 | 27 | 570 | 28 | 571 | 29 | 573 | 30 | 577 |
| 31 | 578 | 32 | 579 | 33 | 583 | 34 | 592 | 35 | 593 |
| 36 | 594 | 37 | 611 | 38 | 612 | 39 | 616 | 40 | 622 |
| 41 | 623 | 42 | 677 | 43 | 684 | 44 | 696 | 45 | 703 |
| 46 | 722 | 47 | 742 | 48 | 761 | 49 | 777 | 50 | 809 |
| 51 | 812 |
| Plant Condition | Training Set | Test Set | Encoded Labels |
|---|---|---|---|
| Health | 1800 | 900 | [1, 0] |
| Infection | 3000 | 1500 | [0, 1] |
| Model | Training Set | Testing Set | ||
|---|---|---|---|---|
| Accuracy | Training Duration/s | Accuracy | Simulation Duration/s | |
| BP | 92.00% | 0.20 | 90.30% | 0.15 |
| KNN | 95.30% | 0.25 | 78.00% | 0.09 |
| SVM | 85.00% | 0.36 | 75.70% | 0.11 |
| LeNet5 | 100.00% | 0.35 | 99.65% | 0.10 |
| TCN | 98.60% | 0.75 | 85.00% | 0.09 |
| MobileNet | 100.00% | 0.67 | 55.92% | 0.09 |
| 1D-ResNet | 99.96% | 1.54 | 51.38% | 0.23 |
| InceptionTime | 99.69% | 0.79 | 54.42% | 0.09 |
| PLS | 90.10% | 0.14 | 89.70% | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Yang, J.; Guan, H. A Recognition Method for Adzuki Bean Rust Disease Based on Spectral Processing and Deep Learning Model. Agriculture 2025, 15, 1246. https://doi.org/10.3390/agriculture15121246
Li L, Yang J, Guan H. A Recognition Method for Adzuki Bean Rust Disease Based on Spectral Processing and Deep Learning Model. Agriculture. 2025; 15(12):1246. https://doi.org/10.3390/agriculture15121246
Chicago/Turabian StyleLi, Longwei, Jiao Yang, and Haiou Guan. 2025. "A Recognition Method for Adzuki Bean Rust Disease Based on Spectral Processing and Deep Learning Model" Agriculture 15, no. 12: 1246. https://doi.org/10.3390/agriculture15121246
APA StyleLi, L., Yang, J., & Guan, H. (2025). A Recognition Method for Adzuki Bean Rust Disease Based on Spectral Processing and Deep Learning Model. Agriculture, 15(12), 1246. https://doi.org/10.3390/agriculture15121246





