An Innovative Inversion Method of Potato Canopy Chlorophyll Content Based on the AFFS Algorithm and the CDE-EHO-GBM Model
Abstract
1. Introduction
2. Materials and Methods
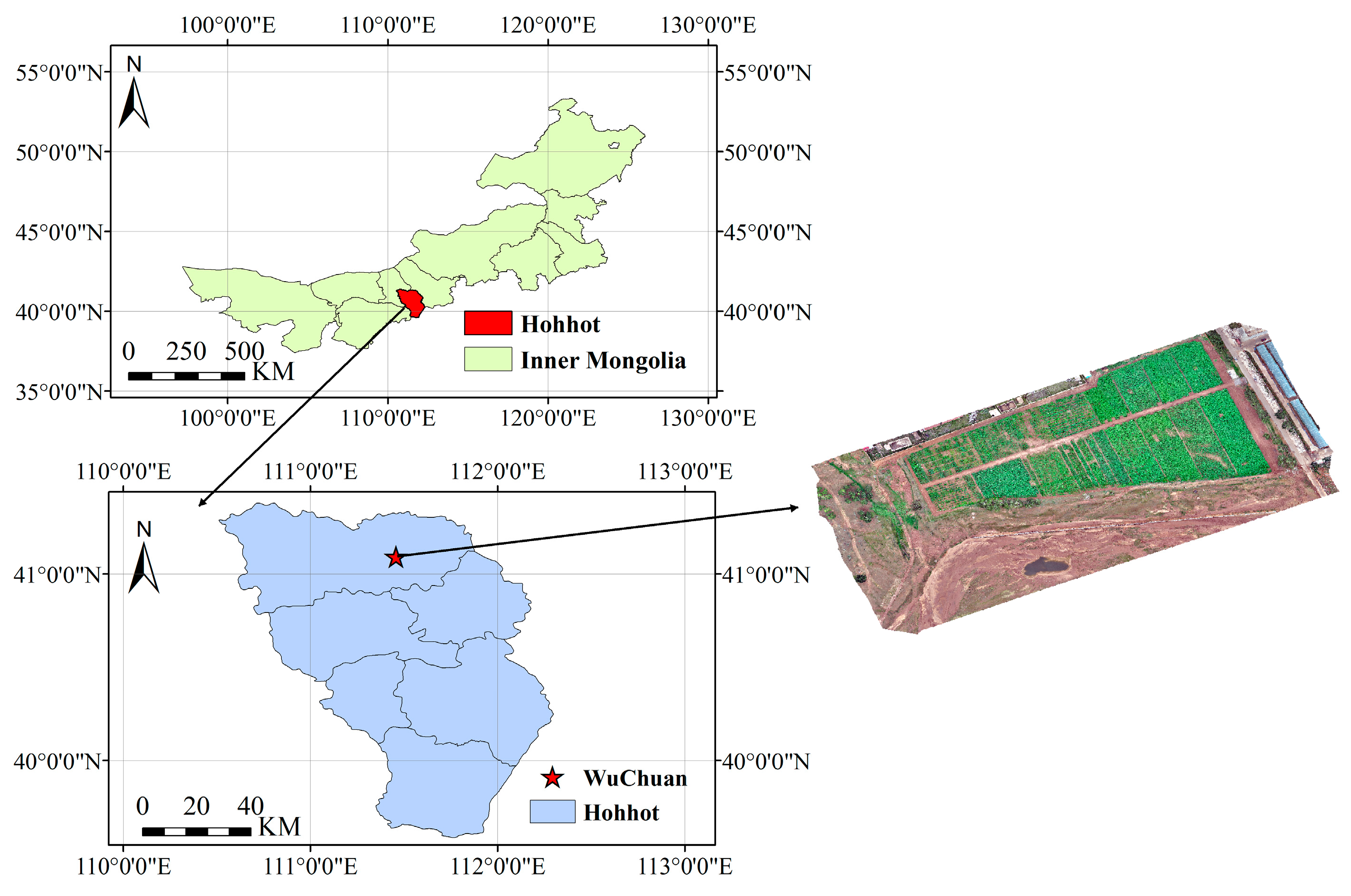
2.1. Study Area
2.2. Data Set
2.2.1. Measured Canopy SPAD Value Data
2.2.2. Remote Sensing Imagery Data from UAV
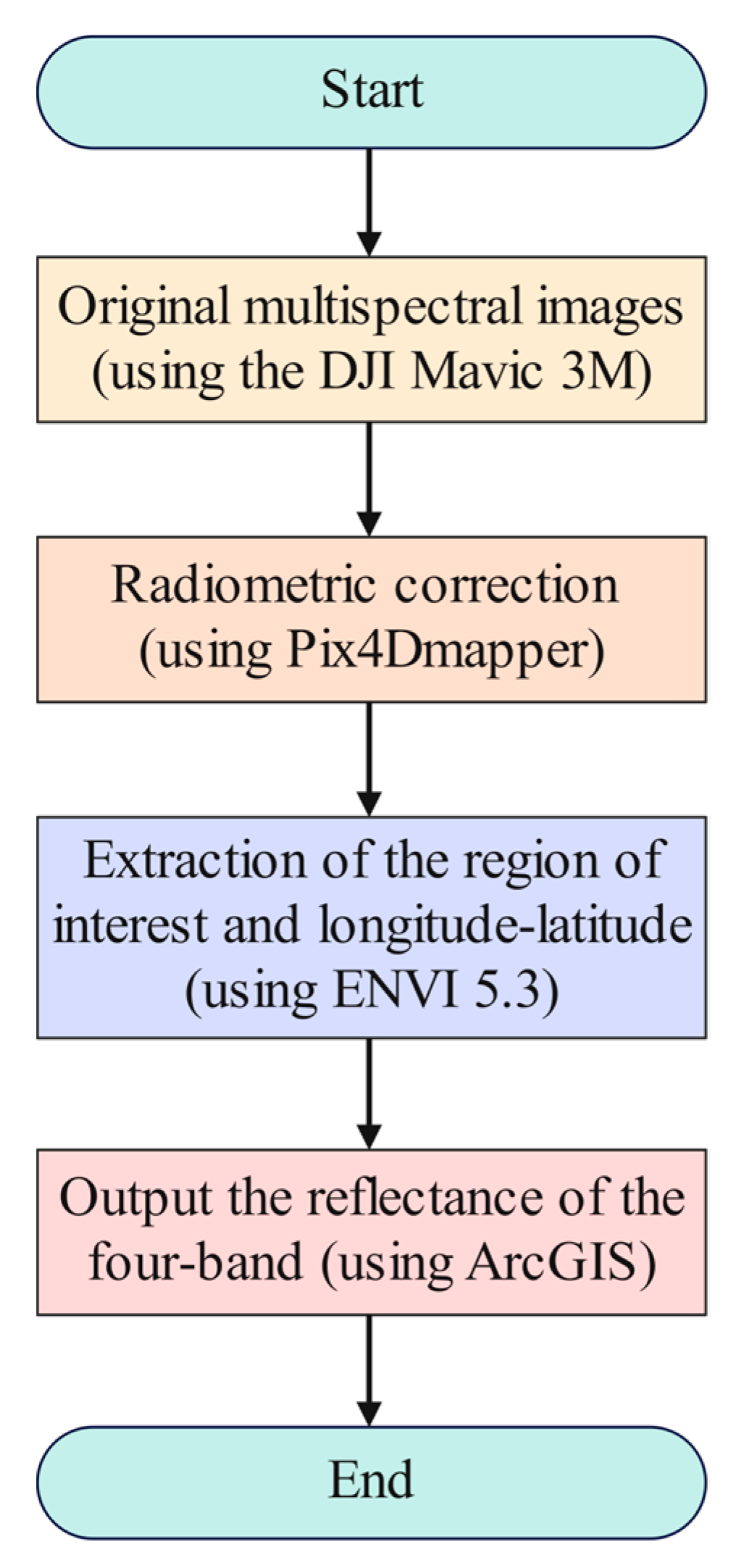
2.2.3. Preprocessing of Remote Sensing Data
2.3. Construct Feature Variables
2.4. Feature Selection Methods
2.4.1. Competitive Adaptive Reweighted Sampling Algorithm
2.4.2. Fast Forward Selection Algorithm
2.4.3. Adaptive Fast Forward Selection Algorithm
- Setting up. Assume that is the initial set of VIs, and that is the whole number of VIs. In this investigation, = 20. Set the feature subset to initialize , meaning that no features are chosen at the beginning.
- Preliminary assessment of features using FFS. Gradually add features from the existing VIs, and after each unselected VI has been added, assess how it affects the model’s efficiency. Determine the amount of change with the addition of feature , and the equation is displayed in Equation (4).
- 3.
- Adaptive weight calculation. In this study, an adaptive mechanism is introduced to dynamically calculate the weights of VIs according to their model performance. A regression model is created using the short-term VI subset , and the regression coefficient of each VI is obtained. Then, calculate the weight of VI at the kth iteration. As shown in Equation (5):of these, the quantity of features in the short-term VI subset is denoted by . The weight of VI is proportional to the ratio of its regression coefficient’s absolute value to the total of all features’ regression coefficients’ absolute values, according to this formula. The weight of the regression coefficient increases with its absolute value, indicating that it contributes more to the model.
- 4.
- Selection of weighted features. To thoroughly assess each unselected VI, add the performance change in each VI from Step 2 and the weight of each VI from Step 3. Add the feature to the existing VI subset if it yields the most weighted performance increase. For every unselected VI , determine the weighted performance change using the formula in Equation (6):
2.5. ML Models
2.5.1. Gradient Boosting Machine
- Considering the relationship between the VIs and the SPAD values, the selected loss function is the squared loss function, and Equation (7) provides its formula:here represents the VI feature vector, and represents the measured SPAD value.
- Start with a simple model . As indicated by Equation (8), is used in this study as the mean value of the SPAD values.among them, reflects the number of canopy SPAD values that were measured, and is the ith SPAD value’s actual value.
- Determine the loss function’s negative gradient with respect to model for every sample in the mth iteration. The equation is shown in Equation (9):
- Train new learners continually using the negative gradient as the target value and the VIs chosen by the aforementioned algorithm as input features. Equation (10) displays the formula for the final model that was produced.
2.5.2. Random Forest
2.5.3. Partial Least Squares Regression Model
2.6. Optimization Algorithm
2.6.1. Elephant Herd Optimization Algorithm
2.6.2. Firefly Optimization Algorithm
2.6.3. Dragonfly Optimization Algorithm
2.6.4. Grid Search Algorithm
2.6.5. DE Improves the Convergence Speed of EHO
- In this research, by introducing differential information, we disrupt the originally relatively stable family structure and the leader selection process of the EHO algorithm. This disruption successfully promotes population variety. Apart from the Euclidean distance, differential information is added when determining the distance between people for family partition. The equation is displayed in Equation (18):here is a regulatory parameter that regulates how much differential information is included in the distance computation. Equation (19) displays the formula for the thorough assessment value V of the leader selection:in this case, is the population’s size, is the weight coefficient. The smaller the comprehensive evaluation value is, the more likely it is to become the leader.
- In this study, the individual update stage of the EHO algorithm introduces the mutation operation of the DE method. This enables individuals to conduct searches in a broader space, thus improving the algorithm’s capacity for worldwide search. Equation (20) displays the updated individual position update formula:in this case, and represent the locations of two distinct people who were chosen at random from the population at the tth iteration. The Differential Evolution algorithm’s scaling factor, , typically has a value between 0 and 2.
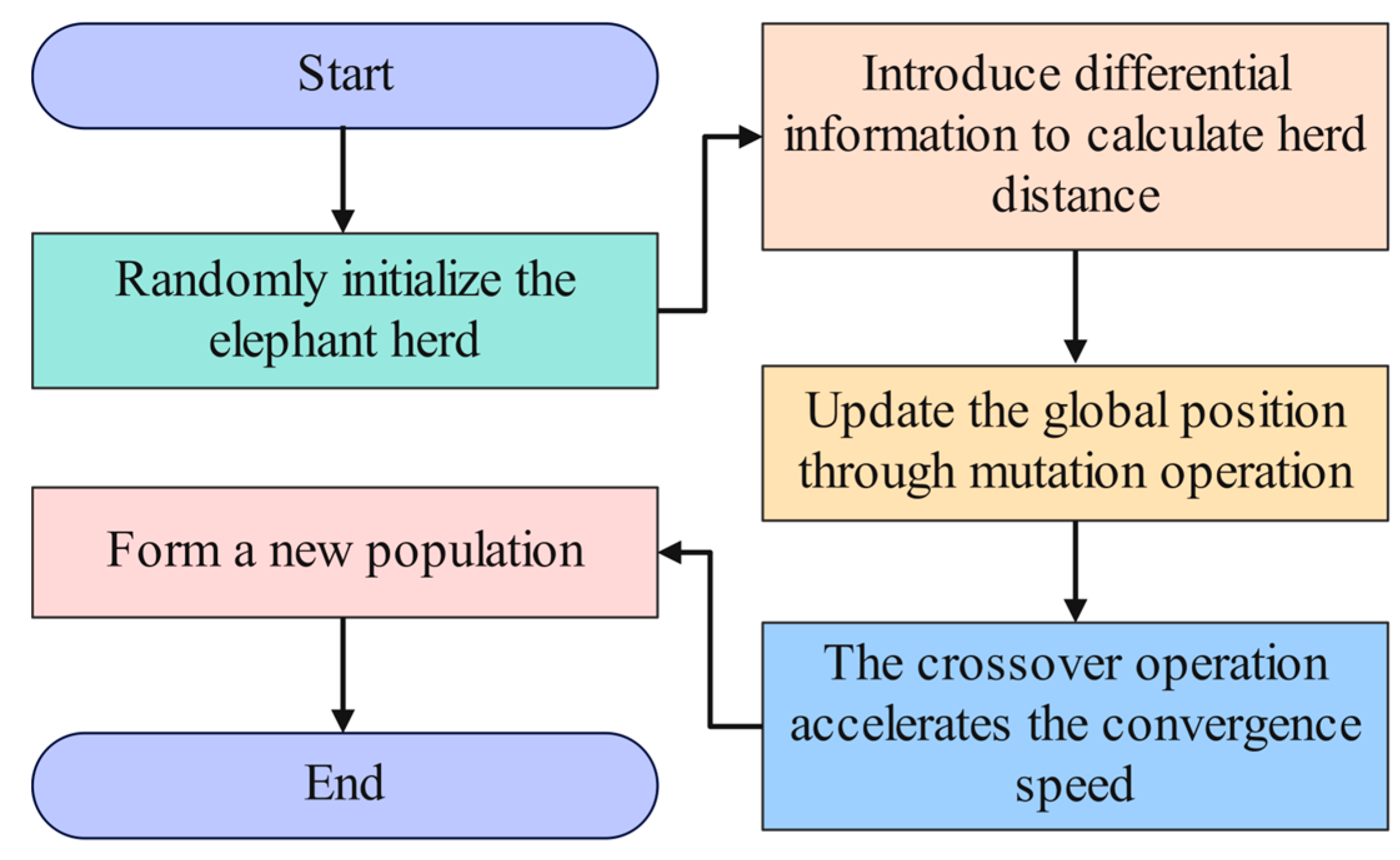
- Crossover operation of DE. For the individuals in EHO, the crossover operation is carried out with a certain crossover probability CR (usually between 0 and 1). Let is the trial individual, and the improved crossover operation formula is shown in Equation (21):in this case, is a randomly assigned number that ranges from 0 to 1. is a randomly chosen dimension between 1 to D, where D is the problem’s dimension. is the individual velocity attained following the above-described enhancement in the global search capability. Figure 5 introduces the flowchart of DE optimizing EHO.
2.6.6. CM Optimizes the Position Update of EHO
- During local search, the EHO algorithm is able to stay out of local optima. This is accomplished by utilizing the Cauchy distribution’s heavy-tailed characteristic. Equation (22) displays the Cauchy distribution’s density function for probability:the current individual position is typically used as the location parameter in local search, while the scale parameter is selected according to the algorithm’s requirements and the problem’s nature.
- Through the integration of the Cauchy mutation, individuals are empowered to perform a more elaborate search in the neighborhood of their current locations. Equation (23) displays the updated formula:in this case, the parameter regulates the degree of Cauchy mutation. In this investigation, represents a random number with a Cauchy distribution, a scale parameter of 1, and a location parameter of 0.
- Conduct local and global searches in a balanced manner. It is feasible to flexibly balance local and global search by dynamically modifying the settings of Cauchy mutation. Equation (24) illustrates the function of the Cauchy mutation intensity.among them, is the initial Cauchy mutation intensity, represents the quantity of iterations underway, symbolizes the most iterations possible, and is the parameter used to adjust the rate of change. The EHO flowchart optimized using CM is shown in Figure 6. EHO’s update approach and local search capability have greatly improved.
2.6.7. SPAD Value Inversion Model Based on CDE-EHO-GBM
- (1)
- Input the measured canopy SPAD values and the remote sensing image data from the UAV.
- (2)
- Feature selection. Raw vegetation indices were selected using CARS, FFS, and AFFS algorithms, and the screened key variables were input into the inversion models.
- (3)
- Create an inversion model for SPAD values depending on the GBM model.
- (4)
- Initialize the parameters. The number of iterations and the size of the elephant population were both determined to be 100, and the parameter ranges for this study are shown in Table 3.
- (5)
- Define the fitness function. The fitness function used in this model is the Mean Squared Error (MSE). The higher the fitness, the lower the fitness function value. As Equation (25) illustrates:here symbolizes the value that was really measured, and symbolizes the model’s anticipated value.
- (6)
- Determine the distance. Incorporate the differential information and calculate the distances between individual members of the elephant herd (according to Equation (18)).
- (7)
- Update the global position. Use crossover and mutation procedures to quicken the elephant herd’s rate of convergence (according to Equations (20) and (21)).
- (8)
- Conduct local optimization. Dynamically adjust the parameters of Cauchy mutation to shorten the search step size and examine the space of local optimal solutions (according to Equations (23) and (24)).
- (9)
- Update the best elephant herd’s location and fitness. Determine if the ceasing requirement is fulfilled. Continue to Step (10) if the requirement is met; if not, continue to Step (6).
- (10)
- Provide the precise position of the top herd of elephants (i.e., the optimal parameters of the CDE-EHO-GBM model).
- (11)
- Use the ideal parameters derived from the CDE-EHO technique to train the GBM model’s SPAD value inversion model and output the prediction SPAD results. Comparison of each model with measured SPAD data combined with calculation of evaluation metrics.
2.7. Model Evaluation Metrics
3. Results and Analysis
3.1. Characteristic Statistics for Potato Canopy SPAD Values and Model Parameter Settings
3.2. The Selection Results of VIs
3.3. Analysis of Model Performance Based on VIs
3.3.1. Analysis of Selection Algorithms and Model Performance During the Seedling Stage
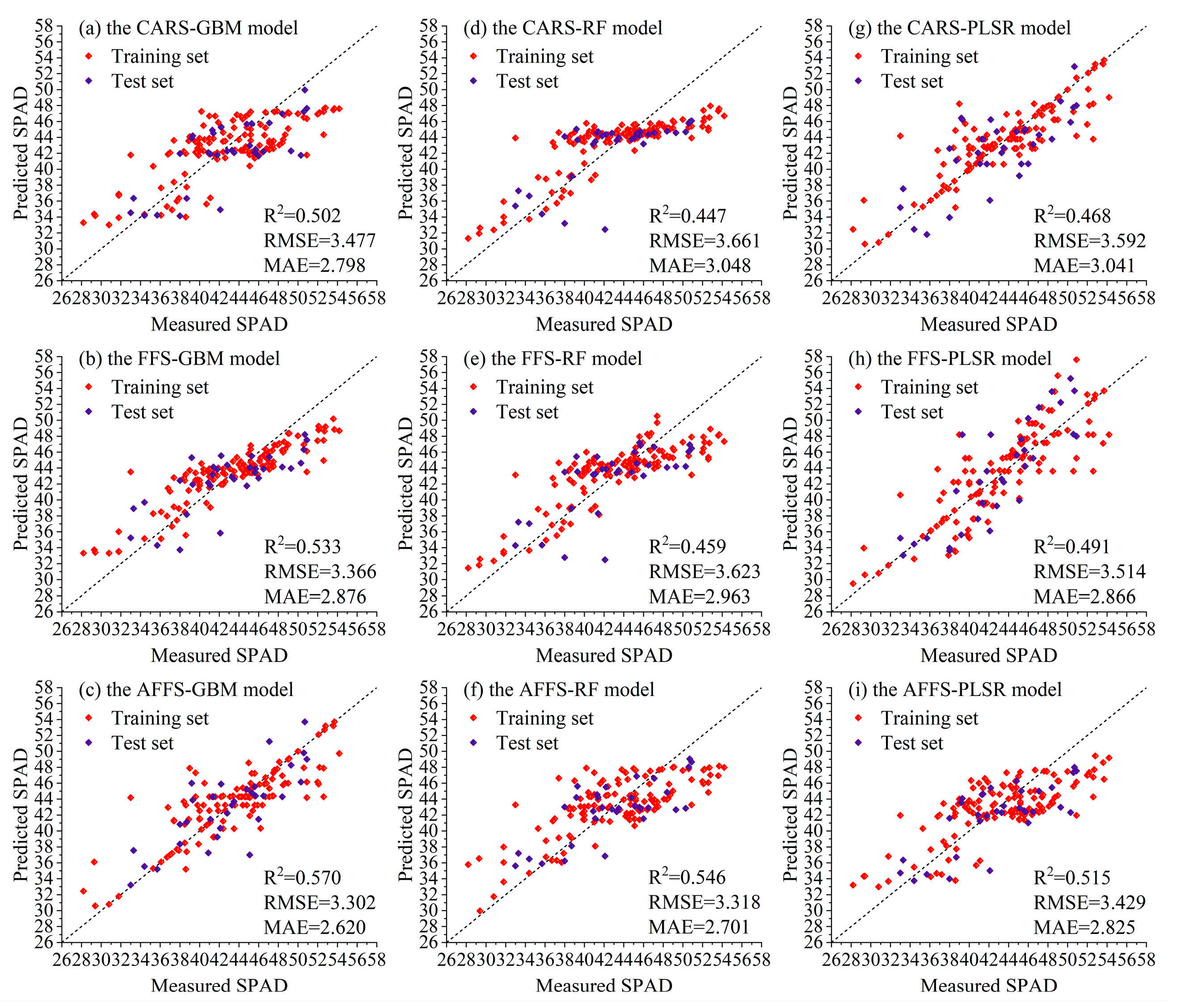
3.3.2. Analysis of Selection Algorithms and Model Performance During the Tuber Expansion Stage
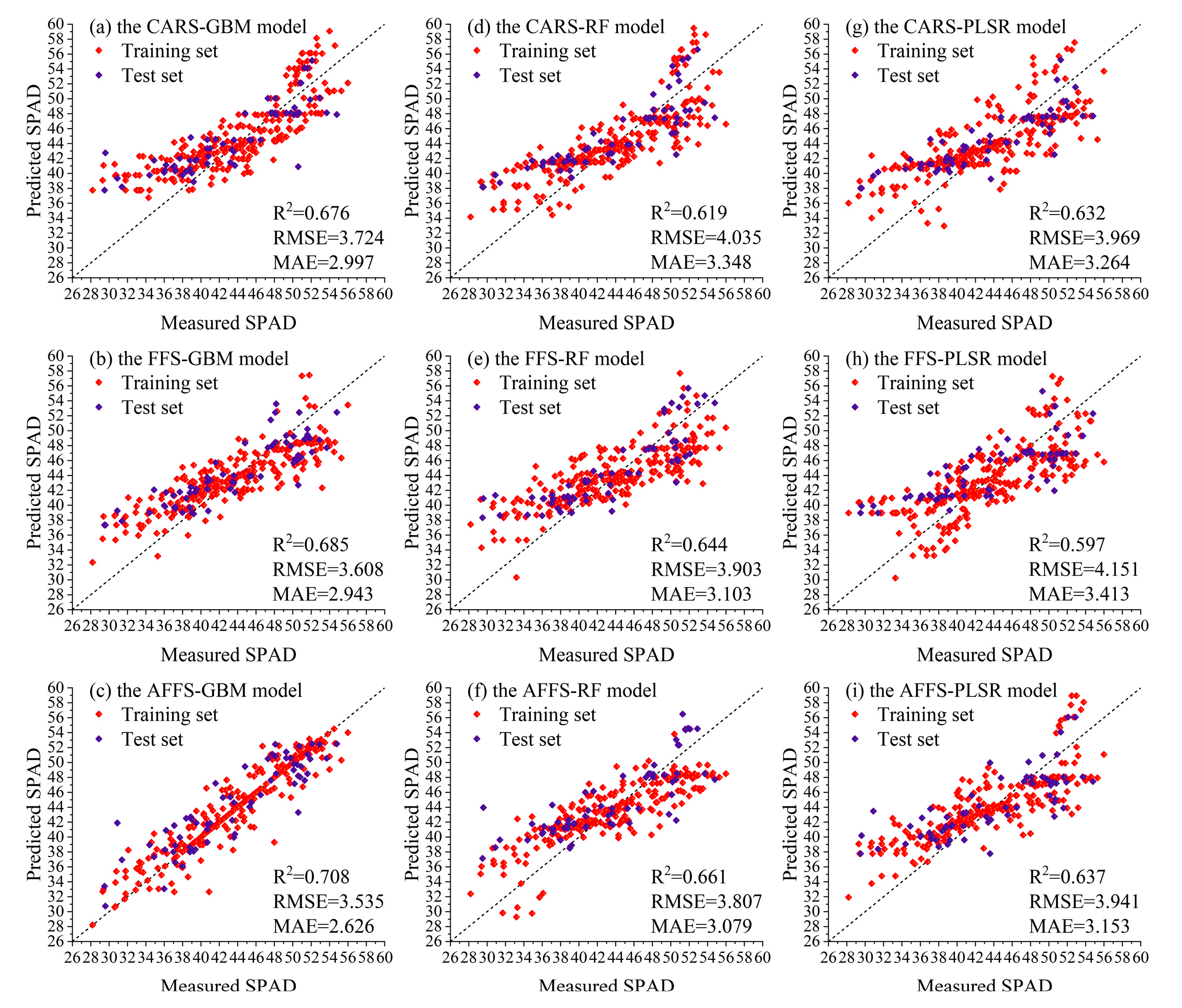
3.3.3. Analysis of Selection Algorithms and Model Performance During the Cross-Growth Stage
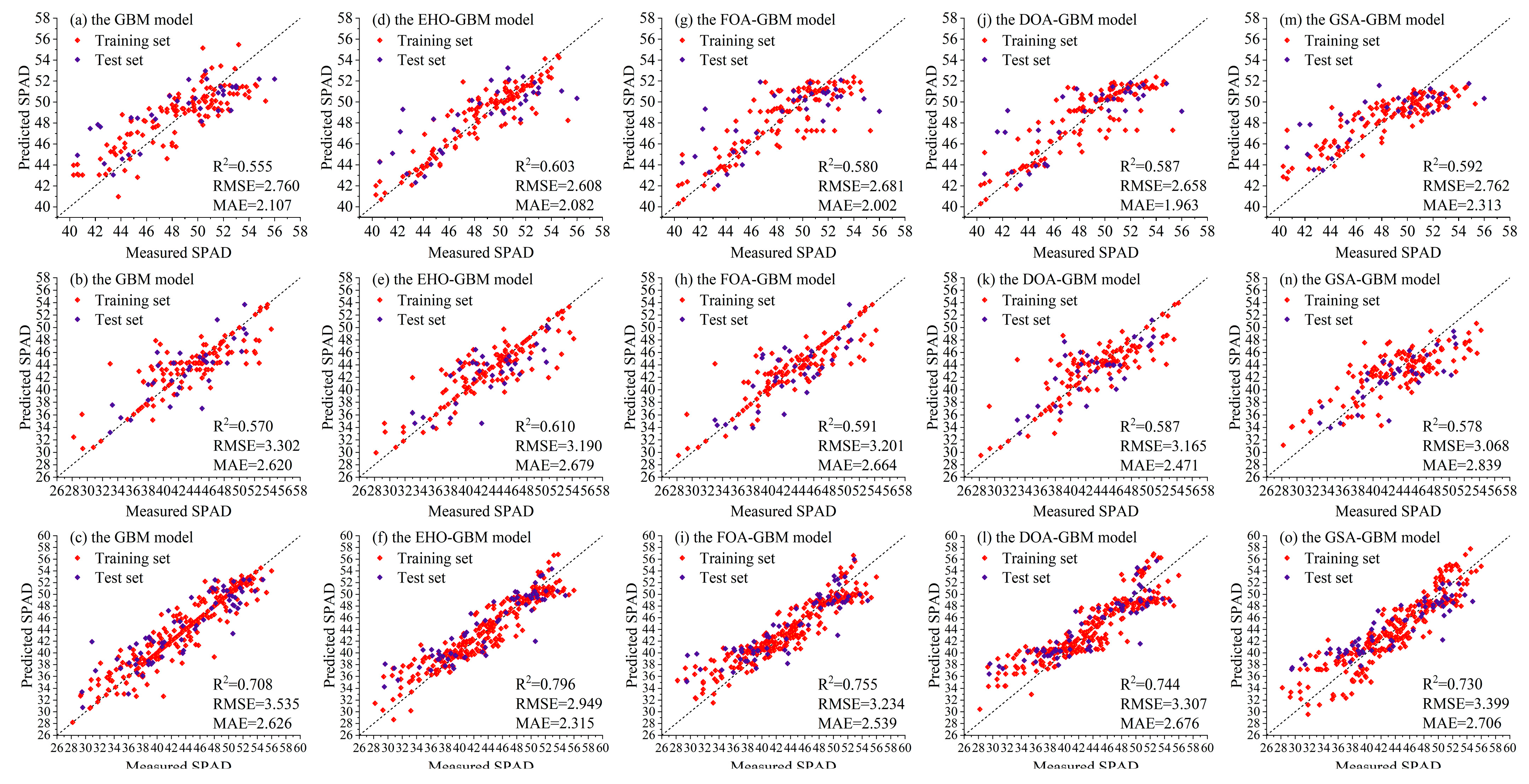
3.4. Intelligent Algorithms for Optimizing the GBM Model
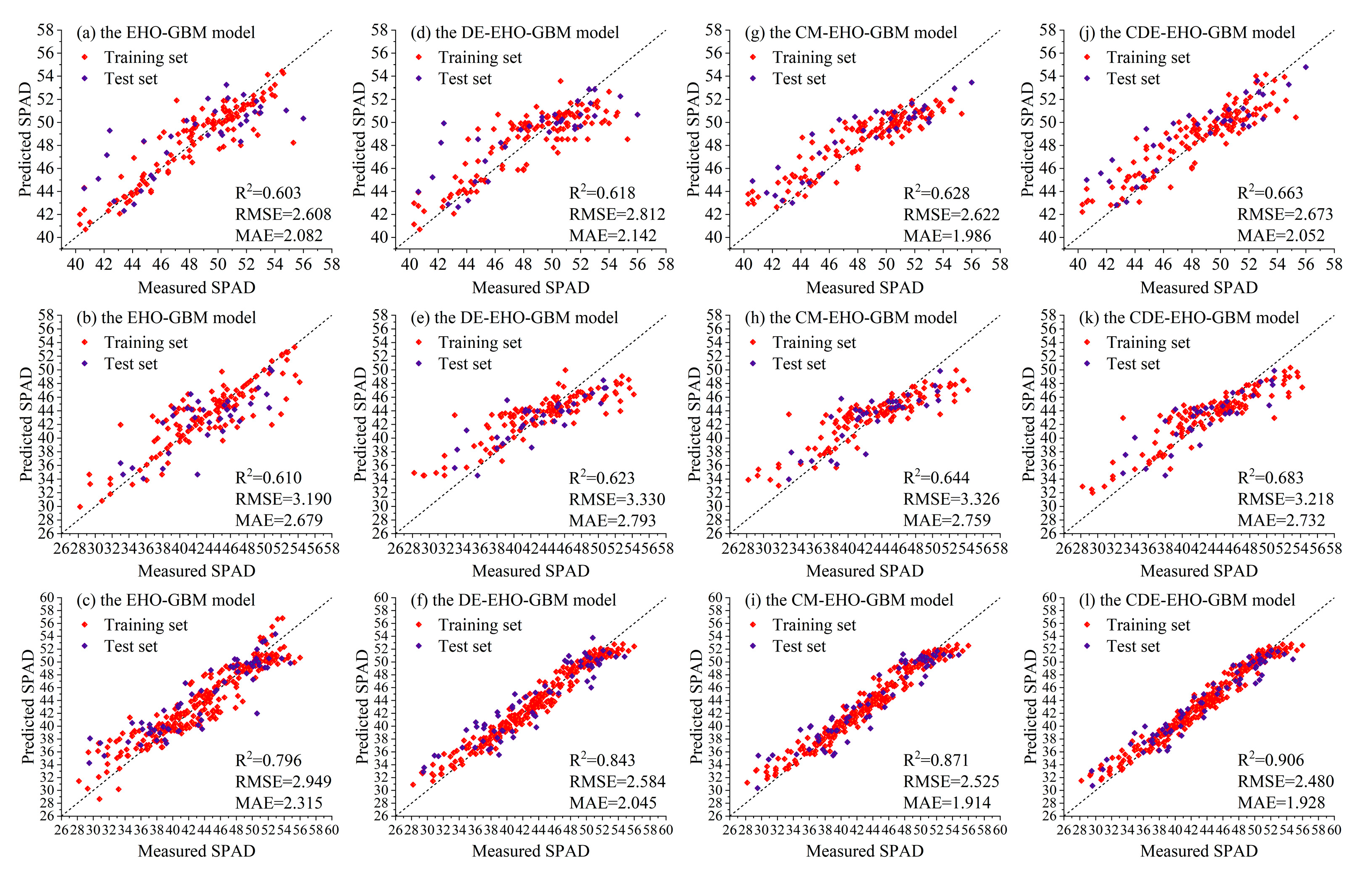
3.5. The CDE-EHO-GBM Model Based on the Improved Algorithms
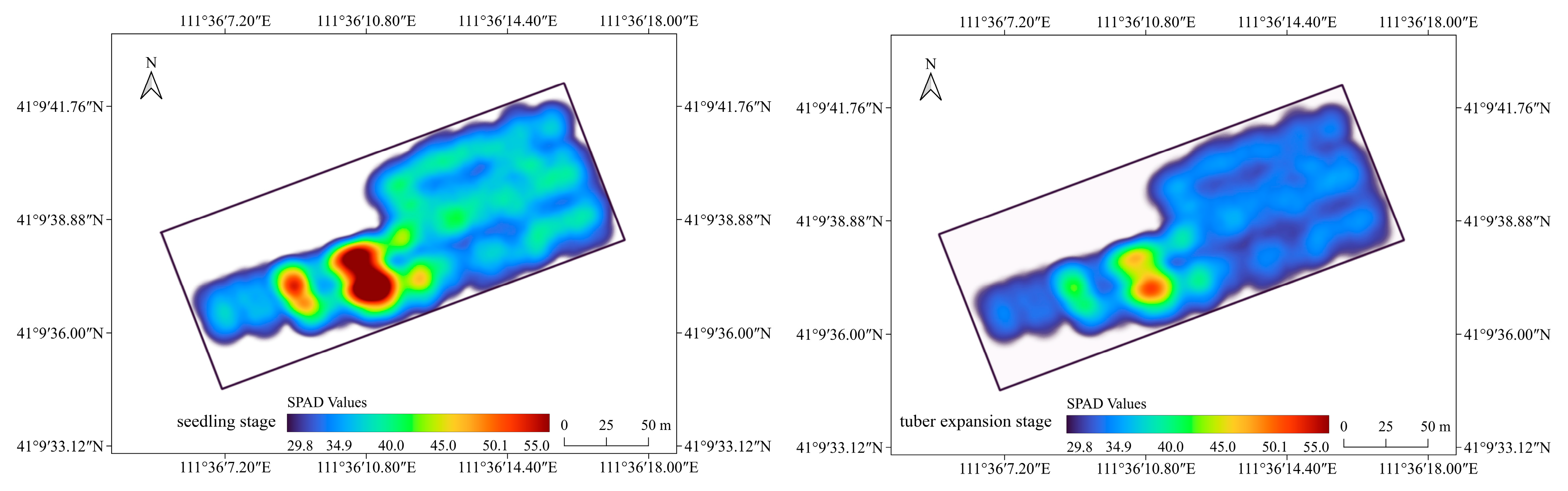
3.6. Temporal and Spatial Distribution of Chlorophyll Content in Potato Canopy
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.-J.; Liu, H.; Zeng, F.-K.; Yang, Y.-C.; Xu, D.; Zhao, Y.-C.; Liu, X.-F.; Kaur, L.; Liu, G.; Singh, J. Potato Processing Industry in China: Current Scenario, Future Trends and Global Impact. Potato Res. 2023, 66, 543–562. [Google Scholar] [CrossRef]
- Ma, Y.; Qiu, C.; Zhang, J.; Pan, D.; Zheng, C.; Sun, H.; Feng, H.; Song, X. Potato Leaf Chlorophyll Content Estimation through Radiative Transfer Modeling and Active Learning. Agronomy 2023, 13, 3071. [Google Scholar] [CrossRef]
- Shi, H.; Lu, X.; Sun, T.; Liu, X.; Huang, X.; Tang, Z.; Li, Z.; Xiang, Y.; Zhang, F.; Zhen, J. Monitoring of Chlorophyll Content of Potato in Northern Shaanxi Based on Different Spectral Parameters. Plants 2024, 13, 1314. [Google Scholar] [CrossRef]
- Mandal, B.K.; Ling, Y.-C. Analysis of Chlorophylls/Chlorophyllins in Food Products Using HPLC and HPLC-MS Methods. Molecules 2023, 28, 4012. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Othman, N.Q.H.; Li, Y.; Alsharif, M.H.; Khan, M.A. Unmanned aerial vehicles (UAVs): Practical aspects, applications, open challenges, security issues, and future trends. Intell. Serv. Robot. 2023, 16, 109–137. [Google Scholar] [CrossRef]
- Yang, H.; Hu, Y.; Zheng, Z.; Qiao, Y.; Hou, B.; Chen, J. A New Approach for Nitrogen Status Monitoring in Potato Plants by Combining RGB Images and SPAD Measurements. Remote Sens. 2022, 14, 4814. [Google Scholar] [CrossRef]
- Ma, W.; Han, W.; Zhang, H.; Cui, X.; Zhai, X.; Zhang, L.; Shao, G.; Niu, Y.; Huang, S. UAV multispectral remote sensing for the estimation of SPAD values at various growth stages of maize under different irrigation levels. Comput. Electron. Agric. 2024, 227, 109566. [Google Scholar] [CrossRef]
- Yang, H.; Hu, Y.; Zheng, Z.; Qiao, Y.; Zhang, K.; Guo, T.; Chen, J. Estimation of Potato Chlorophyll Content from UAV Multispectral Images with Stacking Ensemble Algorithm. Agronomy 2022, 12, 2318. [Google Scholar] [CrossRef]
- Awad, M.M. An innovative intelligent system based on remote sensing and mathematical models for improving crop yield estimation. Inf. Process. Agric. 2019, 6, 316–325. [Google Scholar] [CrossRef]
- Tian, B.; Yu, H.; Zhang, S.; Wang, X.; Yang, L.; Li, J.; Cui, W.; Wang, Z.; Lu, L.; Lan, Y.; et al. Inversion of Cotton Soil and Plant Analytical Development Based on Unmanned Aerial Vehicle Multispectral Imagery and Mixed Pixel Decomposition. Agriculture 2024, 14, 1452. [Google Scholar] [CrossRef]
- Elarab, M.; Ticlavilca, A.M.; Torres-Rua, A.F.; Maslova, I.; McKee, M. Estimating chlorophyll with thermal and broadband multispectral high resolution imagery from an unmanned aerial system using relevance vector machines for precision agriculture. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 32–42. [Google Scholar] [CrossRef]
- Singhal, G.; Bansod, B.; Mathew, L.; Goswami, J.; Choudhury, B.U.; Raju, P.L.N. Chlorophyll estimation using multi-spectral unmanned aerial system based on machine learning techniques. Remote Sens. Appl. Soc. Environ. 2019, 15, 100235. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, Y.; Zhao, Z.; Xie, M.; Hou, D. Estimation of Relative Chlorophyll Content in Spring Wheat Based on Multi-Temporal UAV Remote Sensing. Agronomy 2023, 13, 211. [Google Scholar] [CrossRef]
- Sarvakar, K.; Thakkar, M. Different Vegetation Indices Measurement Using Computer Vision. In Applications of Computer Vision and Drone Technology in Agriculture 4.0; Chouhan, S.S., Singh, U.P., Jain, S., Eds.; Springer Nature: Singapore, 2024; pp. 133–163. [Google Scholar]
- Xu, C.; Ding, Y.; Zheng, X.; Wang, Y.; Zhang, R.; Zhang, H.; Dai, Z.; Xie, Q. A Comprehensive Comparison of Machine Learning and Feature Selection Methods for Maize Biomass Estimation Using Sentinel-1 SAR, Sentinel-2 Vegetation Indices, and Biophysical Variables. Remote Sens. 2022, 14, 4083. [Google Scholar] [CrossRef]
- Guo, X.; Wang, R.; Chen, J.M.; Cheng, Z.; Zeng, H.; Miao, G.; Huang, Z.; Guo, Z.; Cao, J.; Niu, J. Synergetic inversion of leaf area index and leaf chlorophyll content using multi-spectral remote sensing data. Geo-Spat. Inf. Sci. 2025, 28, 22–35. [Google Scholar] [CrossRef]
- Houborg, R.; Soegaard, H.; Boegh, E. Combining vegetation index and model inversion methods for the extraction of key vegetation biophysical parameters using Terra and Aqua MODIS reflectance data. Remote Sens. Environ. 2007, 106, 39–58. [Google Scholar] [CrossRef]
- Carmona, F.; Rivas, R.E.; Fonnegra, D. Vegetation Index to estimate chlorophyll content from multispectral remote sensing data. Eur. J. Remote Sens. 2015, 48, 319–326. [Google Scholar] [CrossRef]
- Elbasi, E.; Zaki, C.; Topcu, A.E.; Abdelbaki, W.; Zreikat, A.I.; Cina, E.; Shdefat, A.; Saker, L. Crop Prediction Model Using Machine Learning Algorithms. Appl. Sci. 2023, 13, 9288. [Google Scholar] [CrossRef]
- Mishra, H.; Mishra, D. Artificial Intelligence and Machine Learning in Agriculture: Transforming Farming Systems. In Research Trends in Agriculture Science; Bhumi Publishing: Kolhapur, India, 2023; pp. 1–16. [Google Scholar]
- Kumari, S.; Venkatesh, V.G.; Tan, F.T.C.; Bharathi, S.V.; Ramasubramanian, M.; Shi, Y. Application of machine learning and artificial intelligence on agriculture supply chain: A comprehensive review and future research directions. Ann. Oper. Res. 2025, 348, 1573–1617. [Google Scholar] [CrossRef]
- Wang, T.; Gao, M.; Cao, C.; You, J.; Zhang, X.; Shen, L. Winter wheat chlorophyll content retrieval based on machine learning using in situ hyperspectral data. Comput. Electron. Agric. 2022, 193, 106728. [Google Scholar] [CrossRef]
- Shah, S.H.; Angel, Y.; Houborg, R.; Ali, S.; McCabe, M.F. A Random Forest Machine Learning Approach for the Retrieval of Leaf Chlorophyll Content in Wheat. Remote Sens. 2019, 11, 920. [Google Scholar] [CrossRef]
- Pan, F.; Li, W.; Lan, Y.; Liu, X.; Miao, J.; Xiao, X.; Xu, H.; Lu, L.; Zhao, J. SPAD inversion of summer maize combined with multi-source remote sensing data. Int. J. Precis. Agric. Aviat. 2018, 1, 45–52. [Google Scholar] [CrossRef]
- Zhao, X.; Qi, J.; Jiang, J.; Liu, S.; Xu, H.; Lin, S.; Yu, Z.; Li, L.; Huang, H. Fine-scale retrieval of leaf chlorophyll content using a semi-empirically accelerated 3D radiative transfer model. Int. J. Appl. Earth Obs. Geoinf. 2024, 135, 104285. [Google Scholar] [CrossRef]
- Li, W.; Pan, K.; Liu, W.; Xiao, W.; Ni, S.; Shi, P.; Chen, X.; Li, T. Monitoring Maize Canopy Chlorophyll Content throughout the Growth Stages Based on UAV MS and RGB Feature Fusion. Agriculture 2024, 14, 1265. [Google Scholar] [CrossRef]
- Elsayed, S.; El-Hendawy, S.; Elsherbiny, O.; Okasha, A.; El-Metwalli, A.; Elwakeel, A.; Memon, D.-M.S.; Ibrahim, M.; Ibrahim, H. Estimating Chlorophyll Content, Production, and Quality of Sugar Beet under Various Nitrogen Levels Using Machine Learning Models and Novel Spectral Indices. Agronomy 2023, 13, 104285. [Google Scholar] [CrossRef]
- Aliferis, C.; Simon, G. Overfitting, Underfitting and General Model Overconfidence and Under-Performance Pitfalls and Best Practices in Machine Learning and AI. In Artificial Intelligence and Machine Learning in Health Care and Medical Sciences: Best Practices and Pitfalls; Simon, G.J., Aliferis, C., Eds.; Springer International Publishing: Cham, Germany, 2024; pp. 477–524. [Google Scholar]
- Wang, J.; Lin, D.; Zhang, Y.; Huang, S. An adaptively balanced grey wolf optimization algorithm for feature selection on high-dimensional classification. Eng. Appl. Artif. Intell. 2022, 114, 105088. [Google Scholar] [CrossRef]
- Alizamir, M.; Heddam, S.; Kim, S.; Mehr, A.D. On the implementation of a novel data-intelligence model based on extreme learning machine optimized by bat algorithm for estimating daily chlorophyll-a concentration: Case studies of river and lake in USA. J. Clean. Prod. 2021, 285, 124868. [Google Scholar] [CrossRef]
- Lu, J.; Qiu, H.; Zhang, Q.; Lan, Y.; Wang, P.; Wu, Y.; Mo, J.; Chen, W.; Niu, H.; Wu, Z. Inversion of chlorophyll content under the stress of leaf mite for jujube based on model PSO-ELM method. Front. Plant Sci. 2022, 13, 1009630. [Google Scholar] [CrossRef]
- Wu, C.; Fu, X.; Li, H.; Hu, H.; Li, X.; Zhang, L. A Method Based on Improved Ant Colony Algorithm Feature Selection Combined With GA-SVR Model for Predicting Chlorophyll-a Concentration in Ulansuhai Lake. IEEE Access 2023, 11, 93180–93192. [Google Scholar] [CrossRef]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Guo, J.; Bai, Q.; Guo, W.; Bu, Z.; Zhang, W. Soil moisture content estimation in winter wheat planting area for multi-source sensing data using CNNR. Comput. Electron. Agric. 2022, 193, 106670. [Google Scholar] [CrossRef]
- Liu, M.; Liu, X.; Li, M.; Fang, M.; Chi, W. Neural-network model for estimating leaf chlorophyll concentration in rice under stress from heavy metals using four spectral indices. Biosyst. Eng. 2010, 106, 223–233. [Google Scholar] [CrossRef]
- Goel, N.S.; Qin, W. Influences of canopy architecture on relationships between various vegetation indices and LAI and Fpar: A computer simulation. Remote Sens. Rev. 1994, 10, 309–347. [Google Scholar] [CrossRef]
- Qiu, B.; Huang, Y.; Chen, C.; Tang, Z.; Zou, F. Mapping spatiotemporal dynamics of maize in China from 2005 to 2017 through designing leaf moisture based indicator from Normalized Multi-band Drought Index. Comput. Electron. Agric. 2018, 153, 82–93. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Raper, T.B.; Varco, J.J. Canopy-scale wavelength and vegetative index sensitivities to cotton growth parameters and nitrogen status. Precis. Agric. 2015, 16, 62–76. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Sankaran, S.; Zhou, J.; Khot, L.R.; Trapp, J.J.; Mndolwa, E.; Miklas, P.N. High-throughput field phenotyping in dry bean using small unmanned aerial vehicle based multispectral imagery. Comput. Electron. Agric. 2018, 151, 84–92. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Ihuoma, S.O.; Madramootoo, C.A. Sensitivity of spectral vegetation indices for monitoring water stress in tomato plants. Comput. Electron. Agric. 2019, 163, 104860. [Google Scholar] [CrossRef]
- Wang, Q.; Li, P.; Pu, Z.; Chen, X. Calibration and validation of salt-resistant hyperspectral indices for estimating soil moisture in arid land. J. Hydrol. 2011, 408, 276–285. [Google Scholar] [CrossRef]
- Boiarskii, B. Comparison of NDVI and NDRE Indices to Detect Differences in Vegetation and Chlorophyll Content. J. Mech. Contin. Math. Sci. 2019, 4, 20–29. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Breon, F.-M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Bagheri, N. Application of aerial remote sensing technology for detection of fire blight infected pear trees. Comput. Electron. Agric. 2020, 168, 105147. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Maimaitiyiming, M.; Hartling, S.; Peterson, K.T.; Maw, M.J.W.; Shakoor, N.; Mockler, T.; Fritschi, F.B. Vegetation Index Weighted Canopy Volume Model (CVMVI) for soybean biomass estimation from Unmanned Aerial System-based RGB imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 27–41. [Google Scholar] [CrossRef]
- Chang, J.; Shoshany, M. Red-edge ratio Normalized Vegetation Index for remote estimation of green biomass. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1337–1339. [Google Scholar]
- Li, H.; Liang, Y.; Xu, Q.; Cao, D. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration. Anal. Chim. Acta 2009, 648, 77–84. [Google Scholar] [CrossRef]
- Stoklosa, J.; Gibb, H.; Warton, D.I. Fast Forward Selection for Generalized Estimating Equations with a Large Number of Predictor Variables. Biometrics 2014, 70, 110–120. [Google Scholar] [CrossRef]
- Friedman, J. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J., III. The Collinearity Problem in Linear Regression. The Partial Least Squares (PLS) Approach to Generalized Inverses. SIAM J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Coelho, L.d.S. Elephant Herding Optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI), Bali, Indonesia, 7–9 December 2015; pp. 1–5. [Google Scholar]
- Yang, X.-S. Firefly Algorithms for Multimodal Optimization. In Proceedings of the Stochastic Algorithms: Foundations and Applications, Sapporo, Japan, 26–28 October 2009; pp. 169–178. [Google Scholar]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Wen, S.H.; Hsiao, C.K. A grid-search algorithm for optimal allocation of sample size in two-stage association studies. J. Hum. Genet. 2007, 52, 650–658. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Wu, Q.; Law, R. Cauchy mutation based on objective variable of Gaussian particle swarm optimization for parameters selection of SVM. Expert Syst. Appl. 2011, 38, 6405–6411. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, H.; Li, Q.; Fu, X.; Li, H. Estimating Canopy Chlorophyll Content of Potato Using Machine Learning and Remote Sensing. Agriculture 2025, 15, 375. [Google Scholar] [CrossRef]
- Chen, J.-J.; Zhen, S.; Sun, Y. Estimating Leaf Chlorophyll Content of Buffaloberry Using Normalized Difference Vegetation Index Sensors. HortTechnology Hortte 2021, 31, 297–303. [Google Scholar] [CrossRef]
- Xu, S.; Xu, X.; Blacker, C.; Gaulton, R.; Zhu, Q.; Yang, M.; Yang, G.; Zhang, J.; Yang, Y.; Yang, M.; et al. Estimation of Leaf Nitrogen Content in Rice Using Vegetation Indices and Feature Variable Optimization with Information Fusion of Multiple-Sensor Images from UAV. Remote Sens. 2023, 15, 854. [Google Scholar] [CrossRef]
- Zheng, K.; Li, Q.; Wang, J.; Geng, J.; Cao, P.; Sui, T.; Wang, X.; Du, Y. Stability competitive adaptive reweighted sampling (SCARS) and its applications to multivariate calibration of NIR spectra. Chemom. Intell. Lab. Syst. 2012, 112, 48–54. [Google Scholar] [CrossRef]
- Drias, H.; Drias, Y.; Houacine, N.A.; Bendimerad, L.S.; Zouache, D.; Khennak, I. Quantum OPTICS and deep self-learning on swarm intelligence algorithms for COVID-19 emergency transportation. Soft Comput. 2023, 27, 13181–13200. [Google Scholar] [CrossRef]
- Gao, S.; Yu, Y.; Wang, Y.; Wang, J.; Cheng, J.; Zhou, M. Chaotic Local Search-Based Differential Evolution Algorithms for Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3954–3967. [Google Scholar] [CrossRef]
- Lan, K.T.; Lan, C.H. Notes on the Distinction of Gaussian and Cauchy Mutations. In Proceedings of the 2008 Eighth International Conference on Intelligent Systems Design and Applications, Kaohsuing, Taiwan, 26–28 November 2008; pp. 272–277. [Google Scholar]





| Parameters | Specific Value |
|---|---|
| Flight velocity | 5 m/s |
| Flight altitude | 30 m |
| Lateral overlap rate | 70% |
| Longitudinal overlap rate | 80% |
| Wavelength range of green light | 560 nm ± 16 nm |
| Wavelength range of red light | 650 nm ± 16 nm |
| Wavelength range of red edge band | 730 nm ± 16 nm |
| Wavelength range of near-infrared band | 860 nm ± 26 nm |
| Vegetation Index | Name | Formula | References |
|---|---|---|---|
| GRVI | Green–Red Vegetation Index | GRVI = (G-R)/(G + R) | [33] |
| MCARI | Modified Chlorophyll Absorption Ratio Index | MCARI = (RE − R) − (0.2 × (RE − G)) × (RE/R) | [34] |
| DVI | Difference Vegetation Index | DVI = NIR − R | [35] |
| MTVI | Modified Tri-angular Vegetation Index | MTVI = 1.5 × (1.2 × (RE − G) − 2.1 × (R − G)) | [36] |
| WDRVI | Wide Dynamic Range Vegetation Index | WDRVI = (0.12 × NIR − R)/(0.12 × NIR + R) | [37] |
| EVI2 | Two-band Enhanced Vegetation Index | EVI2 = 2.5 × (NIR − R)/(NIR + 2.4 × R + 1) | [38] |
| RECI | Red Edge Chlorophyll Index | RECI = (NIR/RE) − 1 | [39] |
| GCI | Green Chlorophyll Index | GCI = (NIR/G) − 1 | [40] |
| NDVI | Normalized Difference Vegetation Index | NDVI = (NIR − R)/(NIR + R) | [41] |
| GNDVI | Green Normalized Difference Vegetation Index | GNDVI = (NIR − G)/(NIR + G) | [42] |
| RVI | Ratio Vegetation Index | RVI = NIR/R | [43] |
| NDGI | Normalized Difference Green Index | NDGI = (RE − G)/(RE +G) | [34] |
| MSRI | Modified Simple Ratio Index | MSR = (NIR/R − 1)/(NIR/R + 1) | [44] |
| OSAVI | Optimized Soil-Adjusted Vegetation Index | OSAVI = (NIR − R)/(NIR + R + 0.16) | [45] |
| SRI | Simple Ratio Index | SR = NIR/RE | [46] |
| NDRE | Normalized Difference Red Edge Index | NDRE = (NIR − RE)/(NIR + RE) | [47] |
| NLI | Nonlinear Vegetation Index | NLI = (NIR × NIR − R)/(NIR × NIR + R) | [48] |
| TVI | Triangular Vegetation Index | TVI = 0.5 × (120 × (NIR − RE) − 200 × (R − RE)) | [49] |
| GRRI | Green–Red Edge Ratio Index | GRRI = G/RE | [50] |
| RNVI | Red-Edge Normalized Vegetation Index | RNVI = (RE − R)/(RE + R) | [51] |
| Models | Parameters | Meaning | Range of Parameters |
|---|---|---|---|
| GBM | n_estimators | Number of iterations | 50–300 |
| learning_rate | Learning rate | 0.01–0.5 | |
| max_depth | Maximum depth | 3–10 | |
| min_samples_split | The minimum number of samples at internal nodes | 2–10 | |
| min_samples_leaf | The minimum number of samples in leaf nodes | 2–5 | |
| subsample | The sample proportion of weak learners | 0.5–1 | |
| random_state | Random generator seed | 30 | |
| RF | n_estimators | Number of iterations | 50–300 |
| max_depth | Maximum depth | 3–10 | |
| min_samples_split | The minimum number of samples at internal nodes | 2–10 | |
| PLSR | n_components | The number of latent variables | 2–8 |
| max_iter | Maximum number of iterations | 50–300 | |
| tol | Iteration convergence threshold | 0.00001–0.001 | |
| scale | Boolean parameter | True |
| Fertility | Samples | Min | Max | Mean | Extreme Difference | Standard Deviation | Coefficient of Variation |
|---|---|---|---|---|---|---|---|
| Seedling stage | 162 | 40.30 | 56.00 | 48.47 | 15.70 | 3.70 | 7.63% |
| Tuber expansion stage | 162 | 28.20 | 54.20 | 43.20 | 26.00 | 5.40 | 12.50% |
| Cross-growth stage | 324 | 28.20 | 56.00 | 45.84 | 27.80 | 5.33 | 11.63% |
| Feature Extraction | Seedling Stage | Tuber Expansion Stage | Cross-Growth Stage | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CARS | FFS | AFFS | CARS | FFS | AFFS | CARS | FFS | AFFS | |||||||||||||||||||
| GBM | RF | PLSR | GBM | RF | PLSR | GBM | RF | PLSR | GBM | RF | PLSR | GBM | RF | PLSR | GBM | RF | PLSR | GBM | RF | PLSR | GBM | RF | PLSR | GBM | RF | PLSR | |
| GRVI | √ | √ | √ | ||||||||||||||||||||||||
| MCARI | √ | √ | √ | √ | √ | √ | |||||||||||||||||||||
| DVI | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||||||||||
| MTVI | √ | √ | √ | √ | |||||||||||||||||||||||
| WDRVI | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||||||||||
| EVI2 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||||||||||||
| RECI | √ | √ | √ | √ | √ | ||||||||||||||||||||||
| GCI | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||||||||
| NDVI | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||||||||
| GNDVI | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||||||||||||
| RVI | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||||||||||
| NDGI | √ | √ | √ | √ | √ | ||||||||||||||||||||||
| MSRI | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||||||||||
| OSAVI | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||||||||||
| SRI | √ | √ | √ | √ | |||||||||||||||||||||||
| NDRE | √ | √ | √ | ||||||||||||||||||||||||
| NLI | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||||||||||
| TVI | √ | √ | √ | √ | √ | √ | |||||||||||||||||||||
| GRRI | √ | √ | √ | √ | √ | √ | |||||||||||||||||||||
| RNVI | √ | √ | √ | √ | |||||||||||||||||||||||
| Models | Feature Extraction | Train Data | Test Data | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
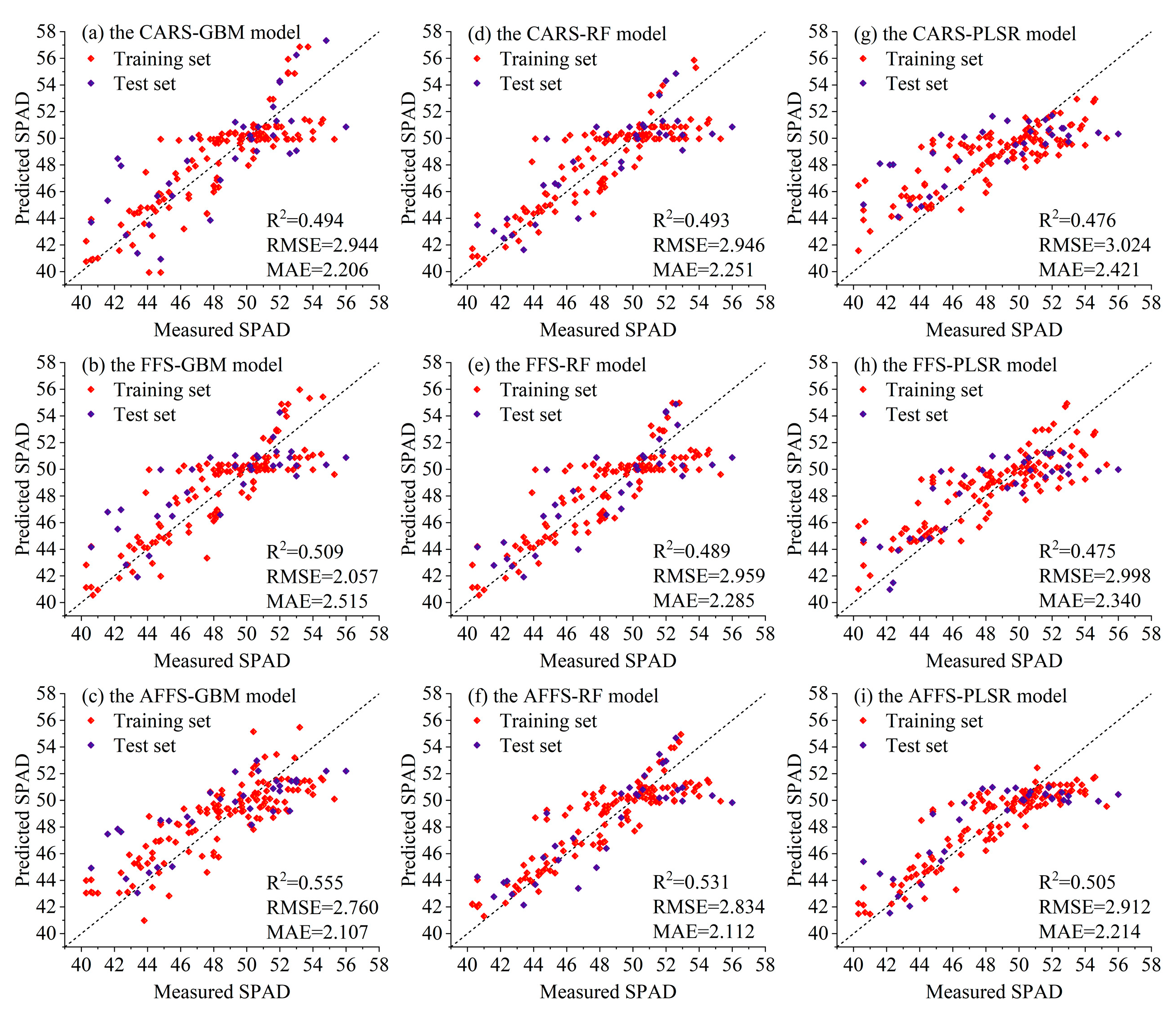
| GBM | CARS | 0.713 | 1.914 | 1.488 | 0.494 | 2.944 | 2.206 |
| FFS | 0.708 | 1.928 | 1.479 | 0.509 | 2.057 | 2.515 | |
| AFFS | 0.754 | 1.770 | 1.396 | 0.555 | 2.760 | 2.107 | |
| RF | CARS | 0.710 | 1.921 | 1.478 | 0.493 | 2.946 | 2.251 |
| FFS | 0.709 | 1.827 | 1.387 | 0.489 | 2.959 | 2.285 | |
| AFFS | 0.770 | 1.713 | 1.316 | 0.531 | 2.834 | 2.112 | |
| PLSR | CARS | 0.625 | 2.187 | 1.653 | 0.476 | 3.024 | 2.421 |
| FFS | 0.683 | 2.010 | 1.566 | 0.475 | 2.998 | 2.340 | |
| AFFS | 0.770 | 1.712 | 1.322 | 0.505 | 2.912 | 2.214 | |
| Models | Feature Extraction | Train Data | Test Data | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| GBM | CARS | 0.545 | 3.713 | 3.197 | 0.502 | 3.477 | 2.798 |
| FFS | 0.745 | 2.780 | 2.211 | 0.533 | 3.366 | 2.876 | |
| AFFS | 0.715 | 2.937 | 2.009 | 0.570 | 3.302 | 2.620 | |
| RF | CARS | 0.607 | 3.451 | 2.748 | 0.447 | 3.661 | 3.048 |
| FFS | 0.657 | 3.223 | 2.565 | 0.459 | 3.623 | 2.963 | |
| AFFS | 0.514 | 3.838 | 3.232 | 0.546 | 3.318 | 2.701 | |
| PLSR | CARS | 0.753 | 2.737 | 1.768 | 0.468 | 3.592 | 3.041 |
| FFS | 0.652 | 3.246 | 2.394 | 0.491 | 3.514 | 2.866 | |
| AFFS | 0.556 | 3.669 | 3.156 | 0.515 | 3.429 | 2.825 | |
| Models | Feature Extraction | Train Data | Test Data | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| GBM | CARS | 0.718 | 3.299 | 2.589 | 0.676 | 3.724 | 2.997 |
| FFS | 0.766 | 3.002 | 2.310 | 0.685 | 3.608 | 2.943 | |
| AFFS | 0.851 | 2.394 | 1.462 | 0.708 | 3.535 | 2.626 | |
| RF | CARS | 0.669 | 3.570 | 2.834 | 0.619 | 4.035 | 3.348 |
| FFS | 0.681 | 3.507 | 2.752 | 0.644 | 3.903 | 3.103 | |
| AFFS | 0.777 | 2.929 | 2.338 | 0.661 | 3.807 | 3.079 | |
| PLSR | CARS | 0.680 | 3.511 | 2.772 | 0.632 | 3.969 | 3.264 |
| FFS | 0.609 | 3.886 | 3.058 | 0.597 | 4.151 | 3.413 | |
| AFFS | 0.733 | 3.207 | 2.509 | 0.637 | 3.941 | 3.153 | |
| Growth Stage | Optimization Algorithm | Train Data | Test Data | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| Seedling stage | GBM | 0.754 | 1.770 | 1.396 | 0.555 | 2.760 | 2.107 |
| EHO-GBM | 0.829 | 1.475 | 1.014 | 0.603 | 2.608 | 2.082 | |
| FOA-GBM | 0.722 | 1.881 | 1.365 | 0.580 | 2.681 | 2.002 | |
| DOA-GBM | 0.700 | 1.954 | 1.522 | 0.587 | 2.658 | 1.963 | |
| GSA-GBM | 0.690 | 1.986 | 1.605 | 0.592 | 2.762 | 2.313 | |
| Tuber expansion stage | GBM | 0.715 | 2.937 | 2.009 | 0.570 | 3.302 | 2.620 |
| EHO-GBM | 0.757 | 2.712 | 1.776 | 0.610 | 3.190 | 2.679 | |
| FOA-GBM | 0.777 | 2.929 | 2.338 | 0.591 | 3.201 | 2.664 | |
| DOA-GBM | 0.710 | 2.965 | 2.055 | 0.587 | 3.165 | 2.471 | |
| GSA-GBM | 0.663 | 3.616 | 2.116 | 0.578 | 3.068 | 2.839 | |
| Cross-growth stage | GBM | 0.851 | 2.394 | 1.462 | 0.708 | 3.535 | 2.626 |
| EHO-GBM | 0.866 | 2.273 | 1.715 | 0.796 | 2.949 | 2.315 | |
| FOA-GBM | 0.841 | 2.477 | 1.919 | 0.755 | 3.234 | 2.539 | |
| DOA-GBM | 0.772 | 2.966 | 2.329 | 0.744 | 3.307 | 2.676 | |
| GSA-GBM | 0.756 | 3.158 | 2.386 | 0.730 | 3.399 | 2.706 | |
| Growth Stage | Optimization Algorithm | Train Data | Test Data | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| Seedling stage | EHO-GBM | 0.829 | 1.475 | 1.014 | 0.603 | 2.608 | 2.082 |
| DE-EHO-GBM | 0.789 | 1.325 | 1.217 | 0.618 | 2.812 | 2.142 | |
| CM-EHO-GBM | 0.772 | 1.705 | 1.361 | 0.628 | 2.622 | 1.986 | |
| CDE-EHO-GBM | 0.777 | 1.686 | 1.350 | 0.663 | 2.673 | 2.052 | |
| Tuber expansion stage | EHO-GBM | 0.757 | 2.712 | 1.776 | 0.610 | 3.190 | 2.679 |
| DE-EHO-GBM | 0.654 | 3.240 | 2.550 | 0.623 | 3.330 | 2.793 | |
| CM-EHO-GBM | 0.707 | 2.982 | 2.316 | 0.644 | 3.326 | 2.759 | |
| CDE-EHO-GBM | 0.771 | 2.634 | 1.953 | 0.683 | 3.218 | 2.732 | |
| Cross-growth stage | EHO-GBM | 0.866 | 2.273 | 1.715 | 0.796 | 2.949 | 2.315 |
| DE-EHO-GBM | 0.959 | 1.243 | 0.936 | 0.843 | 2.584 | 2.045 | |
| CM-EHO-GBM | 0.954 | 1.189 | 0.928 | 0.871 | 2.525 | 1.914 | |
| CDE-EHO-GBM | 0.964 | 1.170 | 0.889 | 0.906 | 2.480 | 1.928 | |
| Models | Parameters | Seedling Stage AFFS-GBM | Tuber Expansion Stage AFFS-GBM | Cross-Growth Stage AFFS-GBM | Cross- Growth Stage EHO-GBM | Cross- Growth Stage CDE-EHO-GBM |
|---|---|---|---|---|---|---|
| GBM | n_estimators | 133 | 97 | 253 | 145 | 175 |
| learning_rate | 0.50 | 0.32 | 0.15 | 0.22 | 0.35 | |
| max_depth | 7 | 6 | 8 | 6 | 9 | |
| min_samples_split | 5 | 7 | 4 | 5 | 3 | |
| min_samples_leaf | 2 | 4 | 4 | 5 | 3 | |
| subsample | 0.52 | 0.61 | 0.82 | 0.65 | 0.74 | |
| random_state | 30 | 30 | 30 | 30 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Li, Q.; Li, H.; Zhou, H.; Zhang, J.; Fu, X. An Innovative Inversion Method of Potato Canopy Chlorophyll Content Based on the AFFS Algorithm and the CDE-EHO-GBM Model. Agriculture 2025, 15, 1181. https://doi.org/10.3390/agriculture15111181
Yang X, Li Q, Li H, Zhou H, Zhang J, Fu X. An Innovative Inversion Method of Potato Canopy Chlorophyll Content Based on the AFFS Algorithm and the CDE-EHO-GBM Model. Agriculture. 2025; 15(11):1181. https://doi.org/10.3390/agriculture15111181
Chicago/Turabian StyleYang, Xiaofei, Qiao Li, Honghui Li, Hao Zhou, Jinyan Zhang, and Xueliang Fu. 2025. "An Innovative Inversion Method of Potato Canopy Chlorophyll Content Based on the AFFS Algorithm and the CDE-EHO-GBM Model" Agriculture 15, no. 11: 1181. https://doi.org/10.3390/agriculture15111181
APA StyleYang, X., Li, Q., Li, H., Zhou, H., Zhang, J., & Fu, X. (2025). An Innovative Inversion Method of Potato Canopy Chlorophyll Content Based on the AFFS Algorithm and the CDE-EHO-GBM Model. Agriculture, 15(11), 1181. https://doi.org/10.3390/agriculture15111181







