Enhancing Agricultural Futures Return Prediction: Insights from Rolling VMD, Economic Factors, and Mixed Ensembles
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description
2.1.1. Agricultural Futures Return Data
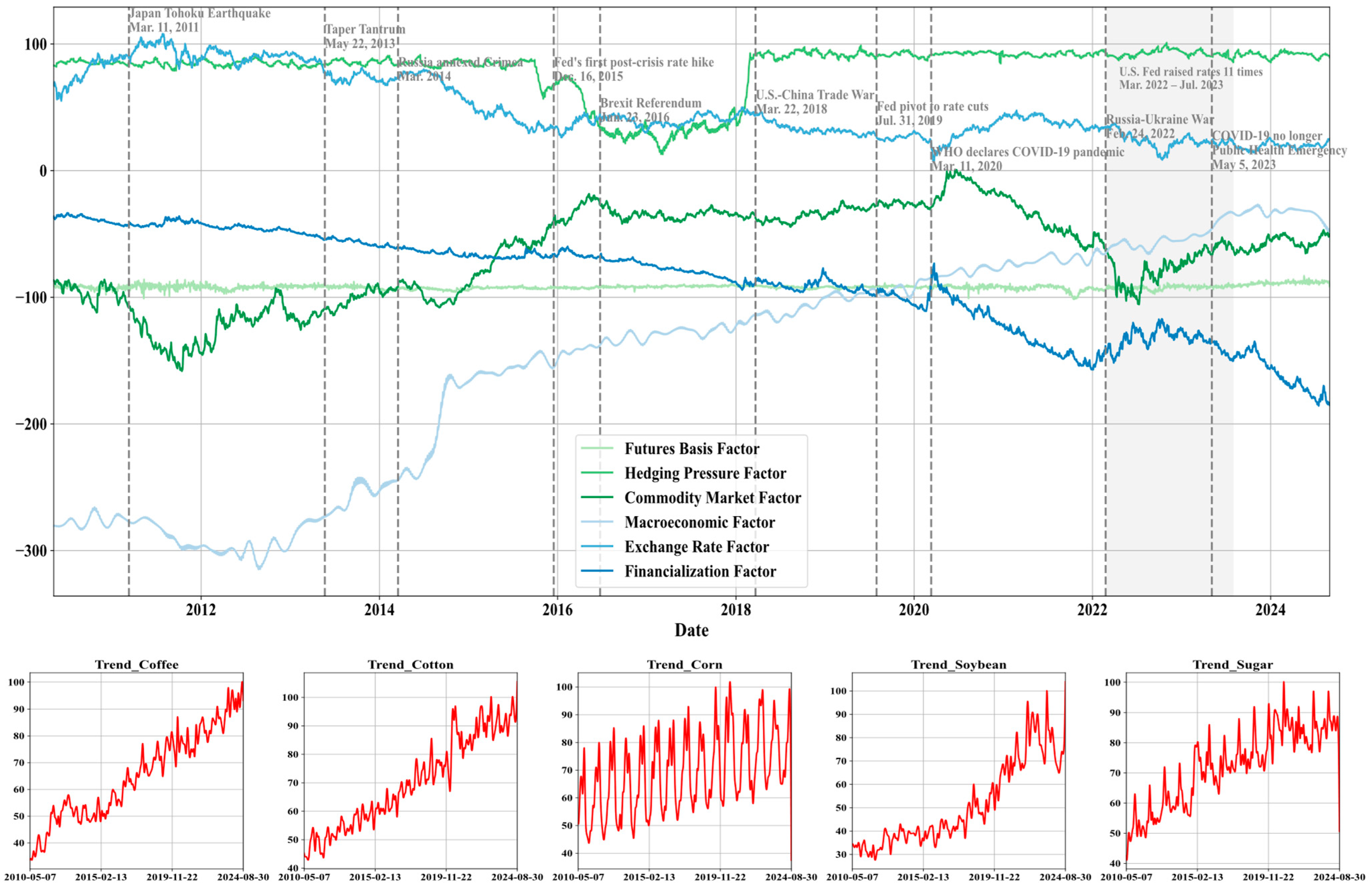
2.1.2. Construction of Seven Influencing Factors
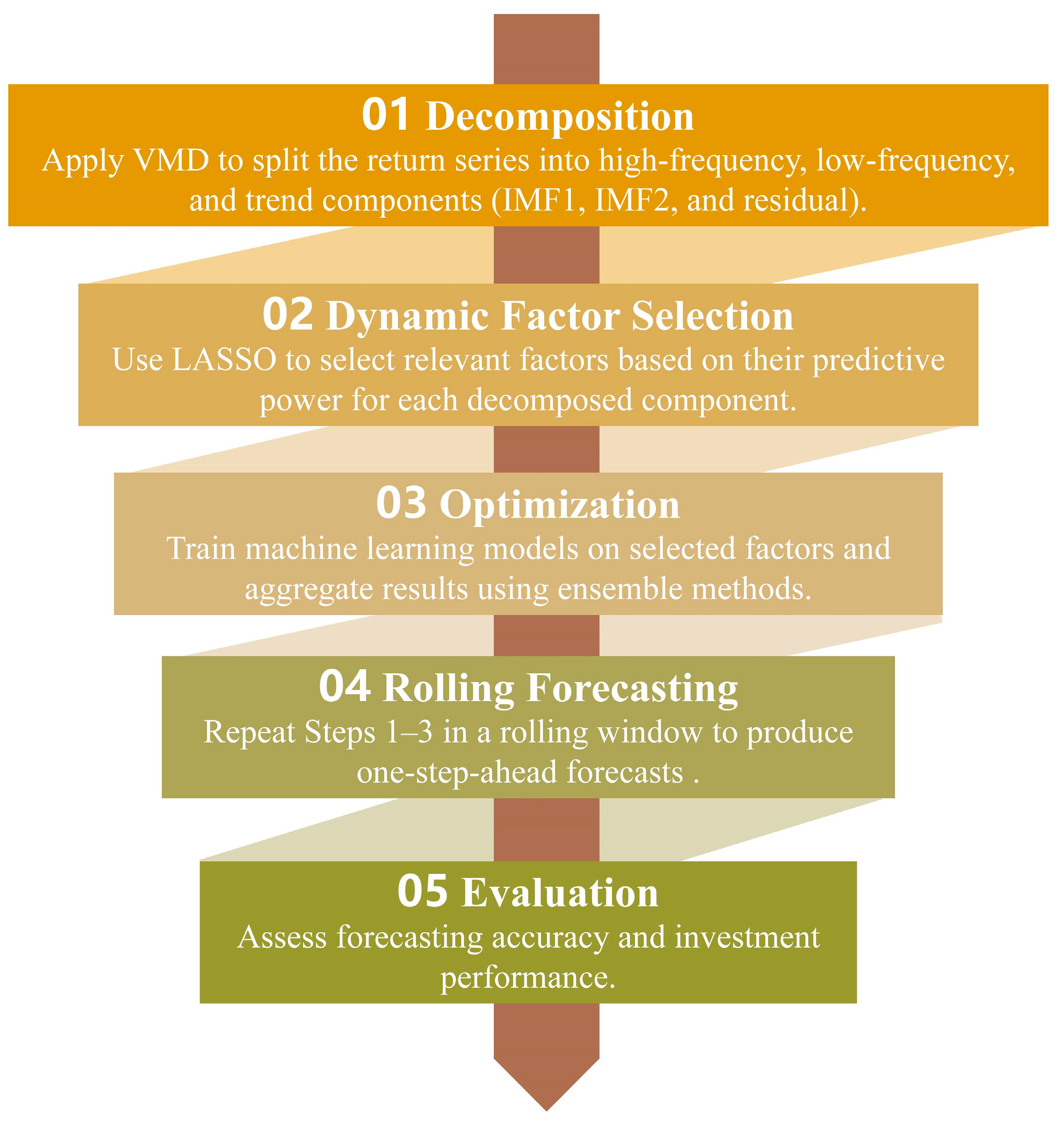
2.2. Methodology
2.2.1. Variational Mode Decomposition
2.2.2. Least Absolute Shrinkage and Selection Operator (LASSO)
2.2.3. Mixed Ensemble Method
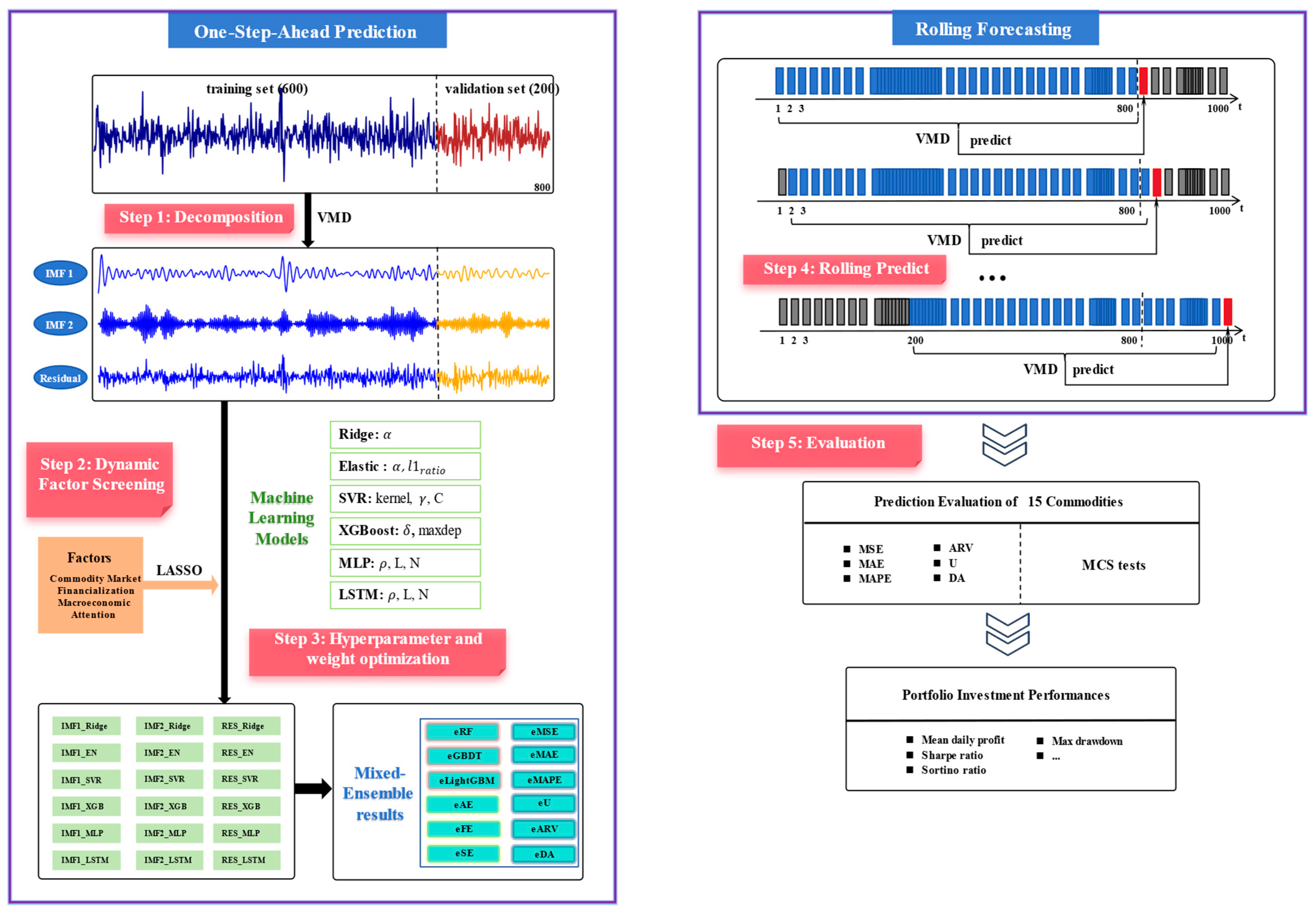
2.2.4. “Rolling VMD-LASSO-Mixed Ensemble” System for Commodity Returns Forecasting
3. Results
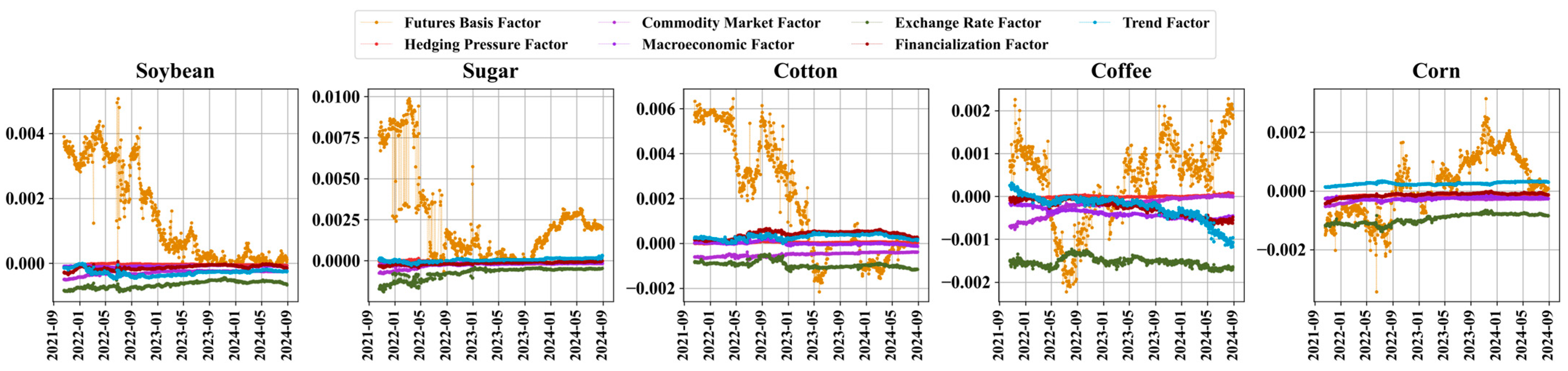
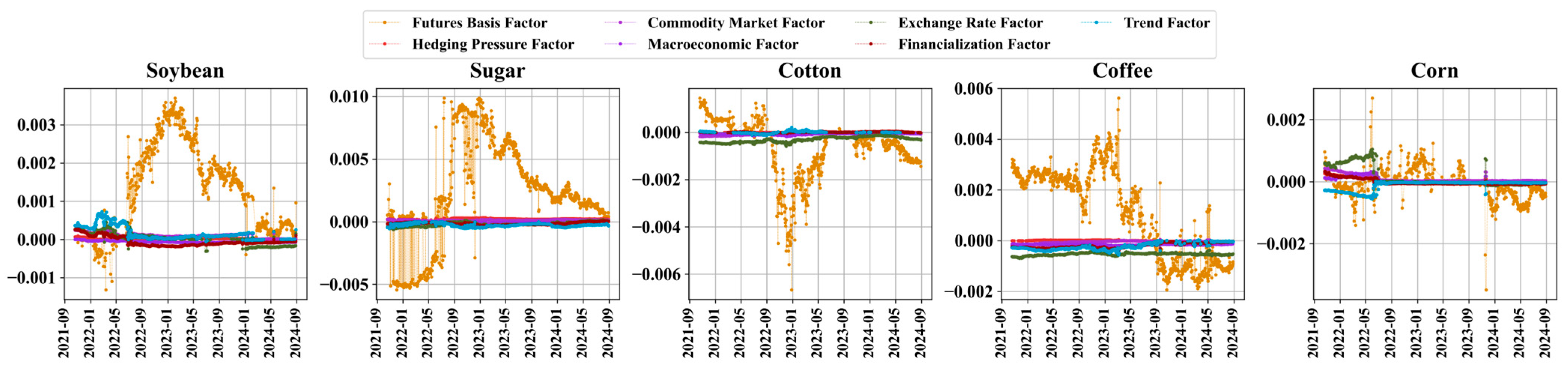
3.1. Result of LASSO Dynamic Factors Screening
3.2. Results of Hyperparameter Tuning
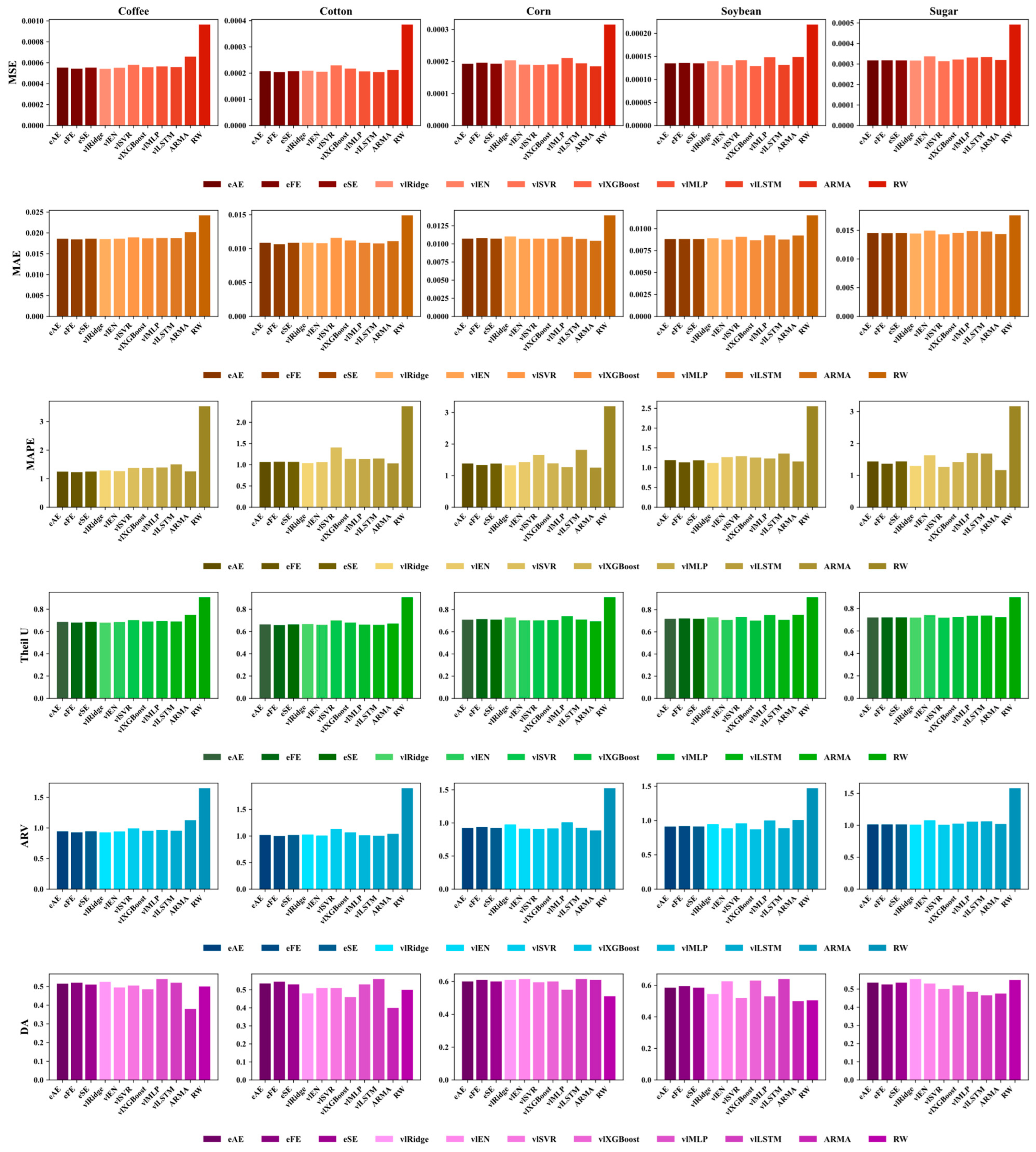
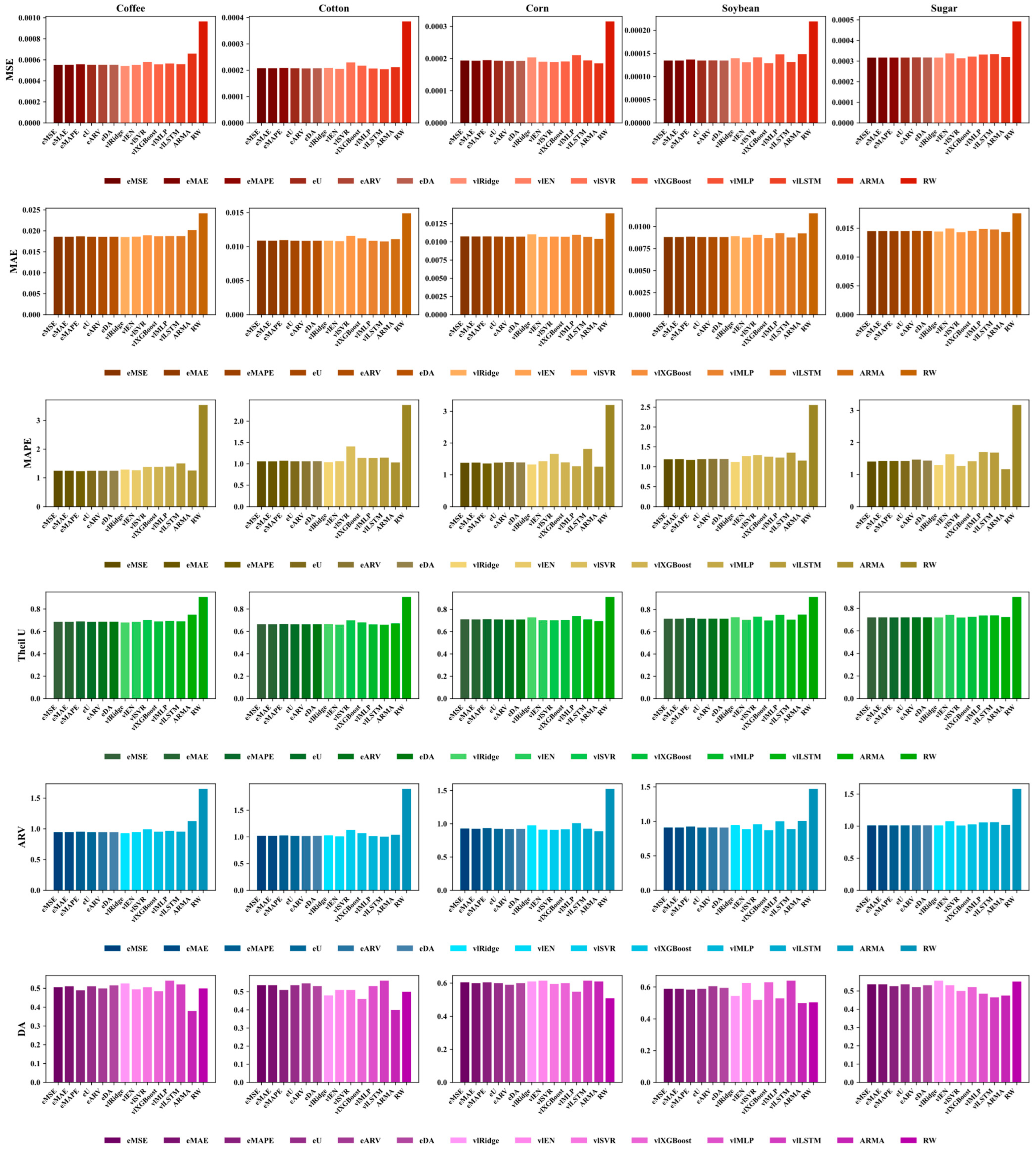
3.3. Prediction Results
3.3.1. Comparative Analysis of the “Rolling VMD” Forecasting System and Traditional Systems
3.3.2. Comparative Analysis of the “Rolling VMD-LASSO” Forecasting System and “Rolling VMD” Systems
3.3.3. Comparative Analysis of the “Rolling VMD-LASSO-Mixed Ensemble” Forecasting System and “Rolling VMD-LASSO” Systems
Prediction Results of the Ensemble Model Based on Error Metrics and Entropy Values
Prediction Results of the Decision Tree-Based Ensemble Model
4. Discussion
4.1. Advantages of This Study Compared to Previous Research
4.2. Discussion on the Investment Value Based on Prediction Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AE | Approximate Entropy |
| ARIMA | Autoregressive Integrated Moving Average |
| ARMA | Autoregressive Moving Average |
| ARV | Average Relative Variance |
| BPNN | Back Propagation Neural Network |
| CBOE | Chicago Board Options Exchange |
| CBOT | Chicago Board of Trade |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| COMEX | Commodity Exchange |
| CPI | Consumer Price Index |
| DA | Directional Accuracy |
| EEMD | Ensemble Empirical Mode Decomposition |
| EMD | Empirical Mode Decomposition |
| EN | Elastic Net |
| EPU | Economic policy uncertainty |
| EU ETS | EU Emissions Trading System |
| FE | Fuzzy Entropy |
| FIA | Futures Industry Association |
| FIGARCH | Fractional Integrated Generalized Autoregressive Conditional Heteroscedasticity |
| FSV | Fractional Stochastic Volatility |
| GARCH | Generalized Autoregressive Conditional Heteroskedasticity |
| GBDT | Gradient Boosting Decision Tree |
| GBM | Gradient Boosting Machine |
| GRU | Gated Recurrent Unit |
| HAR | Heterogeneous Autoregressive Model |
| HOLT | Holt Exponential Smoothing |
| IMF | Intrinsic Mode Function |
| KNN | K-Nearest Neighbors |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LightGBM | Light Gradient Boosting Machine |
| LME | London Metal Exchange |
| LSTM | Long Short-Term Memory neural network |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MCS | Model Confidence Set |
| MCX | Multi-commodity |
| COMDEX | Exchange Commodity Index |
| MLP | Multilayer Perceptron |
| MSE | Mean Square Error |
| MSPE | Mean Squared Prediction Error |
| MSVR | Multi-output Support Vector Regression |
| NMSE | Normalized Mean Squared Error |
| NYMEX | New York Mercantile Exchange |
| OTC | Over the Counter |
| QLIKE | Quasi-Likelihood Error |
| R² | Coefficient of Determination |
| RF | Random Forest |
| Ridge | Ridge Regression |
| RMSE | Root Mean Squared Error |
| RNN | Recurrent Neural Network |
| RW | Random Walk |
| SE | Sample Entropy |
| SSA | Singular Spectrum Analysis |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| U | the U of Theil statistic |
| VECM | Vector Error Correction Model |
| VIX | Volatility Index |
| VMD | Variational Mode Decomposition |
| WTI | West Texas Intermediate |
| XGBoost | Extreme Gradient Boosting |
Appendix A
Appendix A.1. Dynamic Factors Model
Appendix A.2. Related Machine Learning Models
Appendix A.3. Error Metrics of Prediction Results
| Factor | Mean | Median | Std | Kurtosis | Skewness | Range | Min | Max |
|---|---|---|---|---|---|---|---|---|
| Futures basis factor | −91.9436 | −91.9108 | 1.7426 | 3.5947 | −0.3233 | 18.1792 | −101.3845 | −83.2053 |
| Hedging pressure factor | 80.8176 | 87.2311 | 19.4257 | 2.6197 | −2.0012 | 88.0638 | 12.9354 | 100.9992 |
| Commodity market factor | −65.8379 | −58.4748 | 36.3452 | −0.8837 | −0.4316 | 158.8770 | −158.2512 | 0.6258 |
| Macroeconomic factor | −150.1331 | −126.5533 | 89.9496 | −1.2150 | −0.4856 | 287.9777 | −314.7341 | −26.7565 |
| Exchange rate factor | 48.7258 | 39.4481 | 25.6298 | −0.9473 | 0.6601 | 100.5115 | 7.4775 | 107.9890 |
| Financialization factor | −88.2492 | −79.6629 | 38.6009 | −0.7622 | −0.5674 | 152.1325 | −185.6267 | −33.4942 |
| Trend_Coffee | 65.2879 | 65.0328 | 16.4088 | −1.0222 | 0.0860 | 66.5245 | 33.5933 | 100.1178 |
| Trend_Cotton | 70.2375 | 68.9863 | 15.7619 | −1.2082 | 0.1593 | 62.5461 | 42.8412 | 105.3873 |
| Trend_Corn | 69.4271 | 68.4156 | 13.6862 | −0.8334 | 0.1969 | 64.2815 | 37.5324 | 101.8139 |
| Trend_Soybean | 51.3910 | 43.9766 | 17.9223 | −0.6405 | 0.7581 | 76.2414 | 27.5739 | 103.8153 |
| Trend_Sugar | 72.2897 | 73.7471 | 12.6377 | −0.8995 | −0.2932 | 59.0406 | 41.1065 | 100.1471 |
| Algorithm | Parameter | Value | Algorithm | Parameter | Value |
|---|---|---|---|---|---|
| Ridge | alpha | (0.1, 0.01, 0.001, 0.005) | EN | alpha | (0.1, 0.01, 0.001) |
| SVR | kernel | (‘linear’, ’rbf’) | (0.3, 0.5, 0.7) | ||
| epsilon | () | XGBoost | learning_rate | (0.1, 0.2, 0.3) | |
| C | (1 × 10−1, 1, 10, 100, 1000) | max_depth | (2, 3, 4, 5, 6, 7, 8) | ||
| LSTM | learning rate | (0.1, 0.01, 0.001) | MLP | learning_rate | (0.1, 0.01, 0.001) |
| L | (1, 2) | L | (5, 10, 20, 50, 100) | ||
| N | (64, 128) | N | (200, 300, 400) |



References
- Henrique, B.M.; Sobreiro, V.A.; Kimura, H. Literature Review: Machine Learning Techniques Applied to Financial Market Prediction. Expert Syst. Appl. 2019, 124, 226–251. [Google Scholar] [CrossRef]
- Lübbers, J.; Posch, P.N. Commodities’ Common Factor: An Empirical Assessment of the Markets’ Drivers. J. Commod. Mark. 2016, 4, 28–40. [Google Scholar] [CrossRef]
- Li, J.; Chavas, J.P.; Etienne, X.L.; Li, C. Commodity Price Bubbles and Macroeconomics: Evidence from the Chinese Agricultural Markets. Agric. Econ. 2017, 48, 755–768. [Google Scholar] [CrossRef]
- Han, M.; Dam, L.; Pohl, W. What Drives Commodity Price Variation? Rev. Financ. 2024, 29, 315–347. [Google Scholar] [CrossRef]
- Kacperska, E.M.; Łukasiewicz, K.; Skrzypczyk, M.; Stefańczyk, J. Price Volatility in the European Wheat and Corn Market in the Black Sea Agreement Context. Agricultrue 2025, 15, 91. [Google Scholar] [CrossRef]
- Ren, Y.; Tan, A.; Zhu, H.; Zhao, W. Does Economic Policy Uncertainty Drive Nonlinear Risk Spillover in the Commodity Futures Market? Int. Rev. Financ. Anal. 2022, 81, 102084. [Google Scholar] [CrossRef]
- Cheng, D.; Liao, Y.; Pan, Z. The Geopolitical Risk Premium in the Commodity Futures Market. J. Futures Mark. 2023, 43, 1069–1090. [Google Scholar] [CrossRef]
- Pan, Z.; Bai, Z.; Xing, X.; Wang, Z. US Inflation and Global Commodity Prices: Asymmetric Interdependence. Res. Int. Bus. Financ. 2024, 69, 102245. [Google Scholar] [CrossRef]
- Kocaarslan, B.; Soytas, U. How Do the Reserve Currency and Uncertainties in Major Markets Affect the Uncertainty of Oil Prices over Time? Int. J. Financ. Econ. 2024, 30, 2016–2041. [Google Scholar] [CrossRef]
- Ma, Y.R.; Ji, Q.; Wu, F.; Pan, J. Financialization, Idiosyncratic Information and Commodity Co-Movements. Energy Econ. 2021, 94, 105083. [Google Scholar] [CrossRef]
- Dai, X.; Chen, Y.; Zhang, C.; He, Y.; Li, J. Technological Revolution in the Field: Green Development of Chinese Agriculture Driven by Digital Information Technology (DIT). Agriculture 2023, 13, 199. [Google Scholar] [CrossRef]
- Fry-McKibbin, R.; McKinnon, K. The Evolution of Commodity Market Financialization: Implications for Portfolio Diversification. J. Commod. Mark. 2023, 32, 100360. [Google Scholar] [CrossRef]
- Gong, X.; Li, M.; Guan, K.; Sun, C. Climate Change Attention and Carbon Futures Return Prediction. J. Futures Mark. 2023, 43, 1261–1288. [Google Scholar] [CrossRef]
- Apergis, N.; Chatziantoniou, I.; Gabauer, D. Dynamic Connectedness between COVID-19 News Sentiment, Capital and Commodity Markets. Appl. Econ. 2023, 55, 2740–2754. [Google Scholar] [CrossRef]
- Vo, D.H.; Tran, M.P.B. Volatility Spillovers between Energy and Agriculture Markets during the Ongoing Food & Energy Crisis: Does Uncertainty from the Russo-Ukrainian Conflict Matter? Technol. Forecast. Soc. Change 2024, 208, 123723. [Google Scholar] [CrossRef]
- Szafraniec-Siluta, E.; Strzelecka, A.; Ardan, R.; Zawadzka, D. Determinants of Financial Security of European Union Farms—A Factor Analysis Model Approach. Agriculture 2024, 14, 119. [Google Scholar] [CrossRef]
- Degiannakis, S.; Filis, G. Forecasting Oil Price Realized Volatility Using Information Channels from Other Asset Classes. J. Int. Money Financ. 2017, 76, 28–49. [Google Scholar] [CrossRef]
- Bollerslev, T.; Hood, B.; Huss, J.; Pedersen, L.H. Risk Everywhere: Modeling and Managing Volatility. Rev. Financ. Stud. 2018, 31, 2729–2773. [Google Scholar] [CrossRef]
- Rad, H.; Low, R.K.Y.; Miffre, J.; Faff, R. The Strategic Allocation to Style-Integrated Portfolios of Commodity Futures. J. Commodity Mark. 2022, 28, 100259. [Google Scholar] [CrossRef]
- Lean, H.H.; Nguyen, D.K.; Sensoy, A.; Uddin, G.S. On the Role of Commodity Futures in Portfolio Diversification. Int. Trans. Oper. Res. 2023, 30, 2374–2394. [Google Scholar] [CrossRef]
- Zhang, D.; Dai, X.; Xue, J. Incorporating Weather Information into Commodity Portfolio Optimization. Financ. Res. Lett. 2024, 66, 105672. [Google Scholar] [CrossRef]
- Ma, F.; Liao, Y.; Zhang, Y.; Cao, Y. Harnessing Jump Component for Crude Oil Volatility Forecasting in the Presence of Extreme Shocks. J. Empir. Financ. 2019, 52, 40–55. [Google Scholar] [CrossRef]
- Wei, Y.; Liu, J.; Lai, X.; Hu, Y. Which Determinant Is the Most Informative in Forecasting Crude Oil Market Volatility: Fundamental, Speculation, or Uncertainty? Energy Econ. 2017, 68, 141–150. [Google Scholar] [CrossRef]
- Sun, S.; Sun, Y.; Wang, S.; Wei, Y. Interval Decomposition Ensemble Approach for Crude Oil Price Forecasting. Energy Econ. 2018, 76, 274–287. [Google Scholar] [CrossRef]
- Nadirgil, O. Carbon Price Prediction Using Multiple Hybrid Machine Learning Models Optimized by Genetic Algorithm. J. Environ. Manag. 2023, 342, 118061. [Google Scholar] [CrossRef] [PubMed]
- Xiong, T.; Li, C.; Bao, Y.; Hu, Z.; Zhang, L. A Combination Method for Interval Forecasting of Agricultural Commodity Futures Prices. Knowl.-Based Syst. 2025, 77, 92–102. [Google Scholar] [CrossRef]
- Das, S.P.; Padhy, S. A Novel Hybrid Model Using Teaching–Learning-Based Optimization and a Support Vector Machine for Commodity Futures Index Forecasting. Int. J. Mach. Learn. Cybern. 2018, 9, 97–111. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, F.; Wang, Y. Forecasting Crude Oil Prices with a Large Set of Predictors: Can LASSO Select Powerful Predictors? J. Empir. Finance 2019, 54, 97–117. [Google Scholar] [CrossRef]
- Ribeiro, M.H.D.M.; dos Santos Coelho, L. Ensemble Approach Based on Bagging, Boosting and Stacking for Short-Term Prediction in Agribusiness Time Series. Appl. Soft Comput. 2020, 86, 105837. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Huang, K.; Gui, W. Non-Ferrous Metals Price Forecasting Based on Variational Mode Decomposition and LSTM Network. Knowl. Based Syst. 2020, 188, 105006. [Google Scholar] [CrossRef]
- Alfeus, M.; Nikitopoulos, C.S. Forecasting Volatility in Commodity Markets with Long-Memory Models. J. Commod. Mark. 2022, 28, 100248. [Google Scholar] [CrossRef]
- Plakandaras, V.; Ji, Q. Intrinsic Decompositions in Gold Forecasting. J. Commod. Mark. 2022, 28, 100245. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Li, X.; Zhou, H. Artificial Bee Colony-Based Combination Approach to Forecasting Agricultural Commodity Prices. Int. J. Forecast. 2022, 38, 21–34. [Google Scholar] [CrossRef]
- Zheng, L.; Sun, Y.; Wang, S. A Novel Interval-Based Hybrid Framework for Crude Oil Price Forecasting and Trading. Energy Econ. 2024, 130, 107266. [Google Scholar] [CrossRef]
- Zhao, Z.; Sun, S.; Sun, J.; Wang, S. A Novel Hybrid Model with Two-Layer Multivariate Decomposition for Crude Oil Price Forecasting. Energy 2024, 288, 129740. [Google Scholar] [CrossRef]
- Yang, W.; Wang, J.; Niu, T.; Du, P. A Novel System for Multi-Step Electricity Price Forecasting for Electricity Market Management. Appl. Soft Comput. 2020, 88, 106029. [Google Scholar] [CrossRef]
- Cai, Y.; Tang, Z.; Chen, Y. Can Real-Time Investor Sentiment Help Predict the High-Frequency Stock Returns? Evidence from a Mixed-Frequency-Rolling Decomposition Forecasting Method. N. Am. J. Econ. Financ. 2024, 72, 102147. [Google Scholar] [CrossRef]
- Xu, K.; Niu, H. Denoising or Distortion: Does Decomposition-Reconstruction Modeling Paradigm Provide a Reliable Prediction for Crude Oil Price Time Series? Energy Econ. 2023, 128, 107129. [Google Scholar] [CrossRef]
- Xu, K.; Wang, W. Limited Information Limits Accuracy: Whether Ensemble Empirical Mode Decomposition Improves Crude Oil Spot Price Prediction? Int. Rev. Financ. Anal. 2023, 87, 102625. [Google Scholar] [CrossRef]
- Hasan, M.; Abedin, M.Z.; Hajek, P.; Coussement, K.; Sultan, N.; Lucey, B. A Blending Ensemble Learning Model for Crude Oil Price Forecasting. Ann. Oper. Res. 2024. Online First. [Google Scholar] [CrossRef]
- Bouteska, A.; Abedin, M.Z.; Hajek, P.; Yuan, K. Cryptocurrency Price Forecasting–A Comparative Analysis of Ensemble Learning and Deep Learning Methods. Int. Rev. Financ. Anal. 2024, 92, 103055. [Google Scholar] [CrossRef]
- Yuan, J.; Li, J.; Hao, J. A Dynamic Clustering Ensemble Learning Approach for Crude Oil Price Forecasting. Eng. Appl. Artif. Intell. 2023, 123, 106408. [Google Scholar] [CrossRef]
- Weng, F.; Zhu, M.; Buckle, M.; Hajek, P.; Abedin, M.Z. Class Imbalance Bayesian Model Averaging for Consumer Loan Default Prediction: The Role of Soft Credit Information. Res. Int. Bus. Financ. 2024, 74, 102722. [Google Scholar] [CrossRef]
- Guidolin, M.; Pedio, M. Forecasting Commodity Futures Returns with Stepwise Regressions: Do Commodity-Specific Factors Help? Ann. Oper. Res. 2021, 299, 1317–1356. [Google Scholar] [CrossRef]
- Anesti, N.; Galvão, A.B.; Miranda-Agrippino, S. Uncertain Kingdom: Nowcasting Gross Domestic Product and Its Revisions. J. Appl. Econom. 2022, 37, 42–62. [Google Scholar] [CrossRef]
- Ballarin, G.; Dellaportas, P.; Grigoryeva, L.; Hirt, M.; van Huellen, S.; Ortega, J.-P. Reservoir Computing for Macroeconomic Forecasting with Mixed-Frequency Data. Int. J. Forecast. 2024, 40, 1206–1237. [Google Scholar] [CrossRef]
- Tadjouddine, E.M. Calibration Based on Entropy Minimization for a Class of Asset Pricing Models. Appl. Soft Comput. 2016, 42, 431–438. [Google Scholar] [CrossRef]
- Greenhill, S.; Rana, S.; Gupta, S.; Vellanki, P.; Venkatesh, S. Bayesian Optimization for Adaptive Experimental Design: A Review. IEEE Access 2020, 8, 13937–13948. [Google Scholar] [CrossRef]
- Aunsri, N.; Taveeapiradeecharoen, P. A Time-Varying Bayesian Compressed Vector Autoregression for Macroeconomic Forecasting. IEEE Access 2020, 8, 192777–192786. [Google Scholar] [CrossRef]
- Zhang, D.; Sun, Y.; Duan, H.; Hong, Y.; Wang, S. Speculation or Currency? Multi-Scale Analysis of Cryptocurrencies—The Case of Bitcoin. Int. Rev. Financ. Anal. 2023, 88, 102700. [Google Scholar] [CrossRef]
- Yang, K.; Sun, Y.; Hong, Y.; Wang, S. Forecasting Interval Carbon Price through a Multi-Scale Interval-Valued Decomposition Ensemble Approach. Energy Econ. 2024, 139, 107952. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, X. Forecasting USD/RMB Exchange Rate Using the ICEEMDAN-CNN-LSTM Model. J. Forecast. 2025, 44, 200–215. [Google Scholar] [CrossRef]
- Pandit, P.; Sagar, A.; Ghose, B.; Paul, M.; Kisi, O.; Vishwakarma, D.K.; Mansour, L.; Yadav, K.K. Hybrid Modeling Approaches for Agricultural Commodity Prices Using CEEMDAN and Time Delay Neural Networks. Sci. Rep. 2024, 14, 26639. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Hu, X.; Hou, S.; Guo, Y. A Novel BiGRU-Attention Model for Predicting Corn Market Prices Based on Multi-Feature Fusion and Grey Wolf Optimization. Agriculture 2025, 15, 469. [Google Scholar] [CrossRef]




| Reference | Research Object | Decomposition Technique | Forecasting Models | Performance Metric |
|---|---|---|---|---|
| Xiong et al. (2025) [26] | Daily interval-valued cotton prices from the Zhengzhou Commodity Exchange and corn prices from the Dalian Commodity Exchange | - | VECM, MSVR | U, MAPE |
| Das and Padhy (2018) [27] | Daily MCX COMDEX index from the Multi-commodity Exchange of India Limited | - | SVM | RMSE, NMSE, MAE, DA |
| Sun et al. (2018) [24] | Daily interval-valued WTI and Brent crude oil price | EMD | MLP | U, ARV |
| Zhang et al. (2019) [28] | Monthly oil price data of WTI obtained from the U.S. Energy Information Administration | - | LASSO, EN | MSPE, DA |
| Ribeiro and Coelho (2020) [29] | Monthly soybean and wheat prices received by the producers in the state of Parana, Brazil. | - | GBM, SVR, LASSO, KNN, MLP, RF, XGBoost | MAE, MSE, MAPE, RMSE |
| Liu et al. (2020) [30] | Zinc, copper, and aluminum prices obtained from the website of the LME | VMD | LSTM | MAE, MAPE, RMSE, DA |
| Mesias and Christina (2022) [31] | 5-min intraday prices for the front-month commodity futures contracts in 22 commodities from Refinitiv DataScope Select | FIGARCH, FSV, HAR | RMSE, QLIKE | |
| Vasilios and Qiang (2022) [32] | Monthly excess gold returns measured in U.S. dollars per ounce from the London OTC market | EEMD | LASSO, SVR | , RMSE |
| Wang et al. (2022) [33] | Daily data from the CBOT corn and soybean closing prices | SSA, EMD, VMD | ARIMA, SVR, RNN, GRU, LSTM | RMSE, MAE, MAPE, DA |
| Nadirgil (2023) [25] | Daily carbon emission allowance futures prices from EU ETS | CEEMDAN, VMD | RNN, LSTM, MLP, BPNN, GRU | RMSE, MAE, MAPE |
| Zheng et al. (2024) [34] | Daily interval-valued data of WTI crude oil futures prices. | VMD | ARIMA, GARCH, HOLT, MLP, LSTM | U, ARV, MSE, MAE, MAPE |
| Commodity | Mean | Median | Std | Kurtosis | Skewness | Range | Min | Max |
|---|---|---|---|---|---|---|---|---|
| Coffee | 0.0202 | −0.0142 | 1.7893 | 3.5581 | 0.2765 | 22.5054 | −8.9792 | 13.5262 |
| Cotton | −0.0084 | 0.0061 | 1.6155 | 33.7260 | −2.2415 | 33.7551 | −26.0119 | 7.7432 |
| Corn | −0.0043 | 0.0000 | 1.5437 | 28.9286 | −0.9319 | 40.5209 | −20.8165 | 19.7044 |
| Soybean | 0.0005 | 0.0129 | 1.1774 | 22.2166 | −1.5801 | 21.9170 | −15.5512 | 6.3658 |
| Sugar | 0.0166 | −0.0125 | 1.6629 | 5.3001 | 0.2012 | 25.4977 | −11.6448 | 13.8529 |
| Type | Indicator | Frequency | Source |
|---|---|---|---|
| Futures basis factor | Spot price minus futures price | Daily | Wind |
| Hedging pressure factor | (Short hedge position—Long hedge position)/Total hedge position | Daily | Wind |
| Commodity market factor | Bloomberg Commodity | Daily | Investing database |
| Dow Jones Commodity | Daily | Investing database | |
| MCX ICOMDEX Composite | Daily | Investing database | |
| S&P GSCI Commodity | Daily | Investing database | |
| TR_CC CRB Excess Return | Daily | Investing database | |
| Macroeconomic factor | U.S. PPI | Monthly | Wind |
| U.S. CPI | Monthly | Wind | |
| U.S. GDP | Quarterly | Wind | |
| U.S. M2 | Monthly | Wind | |
| U.S. Unemployment Rate | Monthly | Wind | |
| Global Economic Policy Uncertainty Index | Monthly | Wind | |
| Exchange rate factor | EUR to USD Exchange Rate | Daily | Wind |
| USD to JPY Exchange Rate | Daily | Wind | |
| GBP to USD Exchange Rate | Daily | Wind | |
| USD to CHF Exchange Rate | Daily | Wind | |
| USD to CAD Exchange Rate | Daily | Wind | |
| AUD to USD Exchange Rate | Daily | Wind | |
| NZD to USD Exchange Rate | Daily | Wind | |
| USD to HKD Exchange Rate | Daily | Wind | |
| USD to SGD Exchange Rate | Daily | Wind | |
| Financialization factor | NASDAQ Composite Index | Daily | Wind |
| Standard and Poor’s 500 Index | Daily | Wind | |
| Dow Jones Industrial Average | Daily | Wind | |
| Federal Funds Rate | Daily | Wind | |
| U.S. 3 Month Treasury Yield | Daily | Wind | |
| U.S. 6 Month Treasury Yield | Daily | Wind | |
| U.S. 1 Year Treasury Yield | Daily | Wind | |
| U.S. 5 Year Treasury Yield | Daily | Wind | |
| U.S. 10 Year Treasury Yield | Daily | Wind | |
| Attention factor | Google Trends | Weekly | https://trends.google.com (accessed on 20 February 2025) |
| Panel A: TR | Panel B: TMAX | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Commodity | Coffee | Cotton | Corn | Soybean | Sugar | Coffee | Cotton | Corn | Soybean | Sugar |
| Ridge | 0.914(5) | 0.000 (10) | 0.006 (11) | 0.000 (8) | 0.937 (4) | 0.947 (5) | 0.215 (10) | 0.040 (11) | 0.004 (8) | 0.899 (4) |
| EN | 0.110 (11) | 0.041 (5) | 0.005 (12) | 0.000 (7) | 0.101 (11) | 0.332 (11) | 0.215 (5) | 0.019 (12) | 0.004 (7) | 0.381 (11) |
| SVR | 0.002 (12) | 0.000 (11) | 0.019 (7) | 0.000 (12) | 0.050 (12) | 0.242 (12) | 0.215 (11) | 0.971 (7) | 0.000 (12) | 0.381 (12) |
| XGBoost | 0.545 (9) | 0.041 (6) | 0.007 (10) | 0.000 (10) | 0.937 (3) | 0.676 (9) | 0.215 (6) | 0.104 (10) | 0.002 (10) | 0.899 (3) |
| MLP | 0.545 (8) | 0.000 (12) | 0.019 (8) | 0.000 (11) | 0.329 (7) | 0.900 (8) | 0.183 (12) | 0.568 (8) | 0.000 (11) | 0.418 (7) |
| LSTM | 0.858 (6) | 0.007 (9) | 0.026 (5) | 0.001 (6) | 0.269 (8) | 0.900 (6) | 0.215 (9) | 0.999 (5) | 0.190 (6) | 0.381 (8) |
| vRidge | 1.000 (1) | 0.041 (7) | 0.015 (9) | 0.000 (9) | 1.000 (1) | 1.000 (1) | 0.215 (7) | 0.568 (9) | 0.002 (9) | 1.000 (1) |
| vEN | 0.950 (3) | 1.000 (1) | 0.874 (2) | 0.875 (2) | 0.329 (6) | 0.949 (3) | 1.000 (1) | 0.999 (2) | 0.887 (2) | 0.424 (6) |
| vSVR | 0.950 (4) | 0.041 (4) | 0.874 (3) | 0.003 (5) | 0.937 (5) | 0.949 (4) | 0.215 (4) | 0.999 (3) | 0.412 (5) | 0.885 (5) |
| vXGBoost | 0.706 (7) | 0.067 (3) | 1.000 (1) | 0.254 (4) | 0.143 (9) | 0.900 (7) | 0.894 (3) | 1.000 (1) | 0.412 (4) | 0.381 (9) |
| vMLP | 0.950 (2) | 0.013 (8) | 0.085 (4) | 0.721 (3) | 0.937 (2) | 0.949 (2) | 0.215 (8) | 0.999 (4) | 0.609 (3) | 0.899 (2) |
| vLSTM | 0.404 (10) | 0.460 (2) | 0.026 (6) | 1.000 (1) | 0.142 (10) | 0.676 (10) | 0.894 (2) | 0.999 (6) | 1.000 (1) | 0.381 (10) |
| Panel A: TR | Panel B: TMAX | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Commodity | Coffee | Cotton | Corn | Soybean | Sugar | Coffee | Cotton | Corn | Soybean | Sugar |
| vRidge | 0.953 (3) | 0.022 (12) | 0.867 (5) | 0.004 (11) | 1.000 (1) | 0.863 (3) | 0.030 (12) | 0.933 (5) | 0.133 (11) | 1.000 (1) |
| vEN | 0.001 (12) | 0.380 (6) | 0.149 (7) | 0.020 (6) | 0.364 (7) | 0.045 (12) | 0.871 (6) | 0.933 (7) | 0.305 (6) | 0.491 (7) |
| vSVR | 0.001 (11) | 0.154 (7) | 0.000 (12) | 0.006 (9) | 0.115 (11) | 0.087 (11) | 0.871 (7) | 0.006 (12) | 0.179 (9) | 0.225 (11) |
| vXGBoost | 0.073 (9) | 0.754 (5) | 0.005 (10) | 0.006 (10) | 0.177 (10) | 0.767 (9) | 0.871 (5) | 0.014 (10) | 0.133 (10) | 0.225 (10) |
| vMLP | 0.892 (5) | 0.154 (8) | 0.867 (6) | 0.056 (5) | 0.711 (2) | 0.824 (5) | 0.162 (8) | 0.933 (6) | 0.305 (5) | 0.854 (2) |
| vLSTM | 0.019 (10) | 0.026 (11) | 0.867 (4) | 0.150 (3) | 0.184 (9) | 0.229 (10) | 0.090 (11) | 0.933 (4) | 0.464 (3) | 0.321 (9) |
| vlRidge | 0.953 (2) | 0.029 (10) | 0.061 (8) | 0.000 (12) | 0.711 (3) | 0.863 (2) | 0.162 (10) | 0.873 (8) | 0.133 (12) | 0.854 (3) |
| vlEN | 0.709 (7) | 0.908 (2) | 0.915 (2) | 0.150 (4) | 0.711 (6) | 0.824 (7) | 0.871 (2) | 0.933 (2) | 0.464 (4) | 0.840 (6) |
| vlSVR | 0.850 (6) | 1.000 (1) | 0.001 (11) | 0.020 (7) | 0.711 (5) | 0.824 (6) | 1.000 (1) | 0.008 (11) | 0.247 (7) | 0.840 (5) |
| vlXGBoost | 0.953 (4) | 0.908 (3) | 0.036 (9) | 0.150 (2) | 0.711 (4) | 0.863 (4) | 0.871 (3) | 0.176 (9) | 0.464 (2) | 0.840 (4) |
| vlMLP | 1.000 (1) | 0.111 (9) | 0.915 (3) | 0.017 (8) | 0.018 (12) | 1.000 (1) | 0.162 (9) | 0.933 (3) | 0.179 (8) | 0.086 (12) |
| vlLSTM | 0.617 (8) | 0.816 (4) | 1.000 (1) | 1.000 (1) | 0.194 (8) | 0.767 (8) | 0.871 (4) | 1.000 (1) | 1.000 (1) | 0.321 (8) |
| Panel A: TR | Panel B: TMAX | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Commodity | Coffee | Cotton | Corn | Soybean | Sugar | Coffee | Cotton | Corn | Soybean | Sugar |
| RW | 0.333 (10) | 0.000 (11) | 0.000 (11) | 0.000 (10) | 0.001 (10) | 0.556 (10) | 0.000 (11) | 0.000 (11) | 0.000 (10) | 0.001 (10) |
| ARMA | 0.000 (11) | 0.001 (10) | 0.000 (10) | 0.000 (11) | 0.000 (11) | 0.000 (11) | 0.009 (10) | 0.002 (10) | 0.000 (11) | 0.000 (11) |
| vlRidge | 0.706 (8) | 0.499 (5) | 0.000 (9) | 0.008 (7) | 0.909 (5) | 0.602 (8) | 0.566 (5) | 0.003 (9) | 0.009 (7) | 0.931 (5) |
| vlElastic | 0.883 (5) | 0.499 (6) | 0.979 (2) | 0.028 (5) | 0.909 (3) | 0.824 (5) | 0.524 (6) | 0.932 (2) | 0.014 (5) | 0.931 (3) |
| vlSVR | 1.000 (1) | 0.268 (8) | 0.979 (5) | 0.000 (8) | 0.779 (8) | 1.000 (1) | 0.524 (8) | 0.932 (5) | 0.003 (8) | 0.898 (8) |
| vlXGBoost | 0.635 (9) | 0.477 (7) | 1.000 (1) | 1.000 (1) | 0.059 (9) | 0.602 (9) | 0.524 (7) | 1.000 (1) | 1.000 (1) | 0.117 (9) |
| vlMLP | 0.868 (6) | 1.000 (1) | 0.071 (7) | 0.000 (9) | 0.909 (2) | 0.824 (6) | 1.000 (1) | 0.618 (7) | 0.002 (9) | 0.931 (2) |
| vlLSTM | 0.809 (7) | 0.019 (9) | 0.047 (8) | 0.008 (6) | 0.909 (6) | 0.679 (7) | 0.016 (9) | 0.310 (8) | 0.012 (6) | 0.898 (6) |
| eRF | 0.883 (3) | 0.871 (3) | 0.979 (3) | 0.098 (4) | 0.806 (7) | 0.850 (3) | 0.728 (3) | 0.932 (3) | 0.195 (4) | 0.898 (7) |
| eGBDT | 0.883 (4) | 0.871 (2) | 0.291 (6) | 0.583 (2) | 1.000 (1) | 0.850 (4) | 0.728 (2) | 0.618 (6) | 0.383 (2) | 1.000 (1) |
| eLightGBM | 0.941 (2) | 0.563 (4) | 0.979 (4) | 0.583 (3) | 0.909 (4) | 0.953 (2) | 0.670 (4) | 0.932 (4) | 0.380 (3) | 0.931 (4) |
| Model | Mean Daily Return (%) | Max. Drawdown (%) | Sharpe Ratio | Sortino Ratio |
|---|---|---|---|---|
| Ridge | −0.0508 | 13.1118 | −0.0602 | −0.0968 |
| vRidge | −0.0111 | 13.7374 | −0.0170 | −0.0272 |
| EN | −0.0553 | 13.4739 | −0.0649 | −0.1038 |
| vEN | 0.1175 | 5.7121 | 0.1727 | 0.3340 |
| SVR | −0.0921 | 19.9064 | −0.1041 | −0.1606 |
| vSVR | 0.1391 | 11.9576 | 0.2067 | 0.3778 |
| XGBoost | −0.0738 | 16.0165 | −0.0852 | −0.1450 |
| vXGBoost | 0.0066 | 13.0250 | 0.0027 | 0.0043 |
| MLP | −0.0352 | 10.9535 | −0.0450 | −0.0740 |
| vMLP | 0.0830 | 6.5121 | 0.1079 | 0.1784 |
| LSTM | −0.0008 | 7.9468 | −0.0056 | −0.0086 |
| vLSTM | 0.0612 | 9.0330 | 0.0770 | 0.1285 |
| Model | Mean Daily Return (%) | Max. Drawdown (%) | Sharpe Ratio | Sortino Ratio |
|---|---|---|---|---|
| vRidge | −0.0111 | 13.7374 | −0.0170 | −0.0272 |
| vlRidge | 0.1523 | 8.4274 | 0.2299 | 0.4138 |
| vEN | 0.1175 | 5.7121 | 0.1727 | 0.3340 |
| vlEN | 0.2060 | 3.8778 | 0.3463 | 0.7001 |
| vSVR | 0.1391 | 11.9576 | 0.2067 | 0.3778 |
| vlSVR | 0.1601 | 7.9393 | 0.2440 | 0.4283 |
| vXGBoost | 0.0066 | 13.0250 | 0.0027 | 0.0043 |
| vlXGBoost | 0.1340 | 5.1704 | 0.1983 | 0.3678 |
| vMLP | 0.0830 | 6.5121 | 0.1079 | 0.1784 |
| vlMLP | 0.1150 | 6.3632 | 0.1648 | 0.2790 |
| vLSTM | 0.0612 | 9.0330 | 0.0770 | 0.1285 |
| vlLSTM | 0.1192 | 6.7310 | 0.1601 | 0.2960 |
| Model | Mean Daily Return (%) | Max. Drawdown (%) | Sharpe Ratio | Sortino Ratio |
|---|---|---|---|---|
| vlRidge | 0.1523 | 8.4274 | 0.2299 | 0.4138 |
| vlEN | 0.2060 | 3.8778 | 0.3463 | 0.7001 |
| vlSVR | 0.1601 | 7.9393 | 0.2440 | 0.4283 |
| vlXGBoost | 0.1340 | 5.1704 | 0.1983 | 0.3678 |
| vlMLP | 0.1150 | 6.3632 | 0.1648 | 0.2790 |
| vlLSTM | 0.1192 | 6.7310 | 0.1601 | 0.2960 |
| eRF | 0.2174 | 4.3528 | 0.3696 | 0.6809 |
| eGBDT | 0.2152 | 4.8625 | 0.3629 | 0.6716 |
| eLightGBM | 0.2119 | 3.7032 | 0.3603 | 0.6759 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; Zhuang, X.; Yi, C.; Liu, D.; Tang, Z. Enhancing Agricultural Futures Return Prediction: Insights from Rolling VMD, Economic Factors, and Mixed Ensembles. Agriculture 2025, 15, 1127. https://doi.org/10.3390/agriculture15111127
Ye Y, Zhuang X, Yi C, Liu D, Tang Z. Enhancing Agricultural Futures Return Prediction: Insights from Rolling VMD, Economic Factors, and Mixed Ensembles. Agriculture. 2025; 15(11):1127. https://doi.org/10.3390/agriculture15111127
Chicago/Turabian StyleYe, Yiling, Xiaowen Zhuang, Cai Yi, Dinggao Liu, and Zhenpeng Tang. 2025. "Enhancing Agricultural Futures Return Prediction: Insights from Rolling VMD, Economic Factors, and Mixed Ensembles" Agriculture 15, no. 11: 1127. https://doi.org/10.3390/agriculture15111127
APA StyleYe, Y., Zhuang, X., Yi, C., Liu, D., & Tang, Z. (2025). Enhancing Agricultural Futures Return Prediction: Insights from Rolling VMD, Economic Factors, and Mixed Ensembles. Agriculture, 15(11), 1127. https://doi.org/10.3390/agriculture15111127






