The YOLOv8 architecture consists of three main components: the Backbone, Neck, and Detection Head. The Backbone is responsible for extracting fundamental features from the input image. The Neck then integrates and refines these multi-scale features through the Feature Pyramid Network (FPN), enhancing the model’s capability to extract information across different spatial resolutions.
Considering the limited computational resources in agricultural environments, the YOLOv8n (Nano) version, designed specifically for lightweight applications, is the basis for this study. This paper develops the YOLOv8-EGC-Fusion (YEF) model based on the YOLOv8n framework. The model architecture is illustrated in
Figure 4. Key modifications include the integration of Efficient Group Convolution (EGC) into the Backbone, improving the extraction of multi-scale features and decreasing the model’s parameter count. Additionally, a GCAA-Fusion module is designed to improve the capture of low-level features by optimizing the existing feature pyramid structure. The detailed design and performance optimization of the YEF model are further discussed in this paper.
2.2.1. C2f-EGC Module
- (1)
Efficient Group Convolution
In the initial YOLOv8 architecture, the convolutional module used in the feature extraction phase applies different convolutional kernels to capture useful features from the input data. This module primarily comprises convolutional layers created by conv2d, activation functions, and batch normalization layers [
25]. The computational complexity of the convolutional module determines the data processing speed, and the parameter count
Pconv is calculated as follows:
where
Cin represents the number of input channels.
Cout represents the number of output channels.
Kh ×
Kw represents the height and width of the convolutional kernel.
Each output channel in the convolutional module performs convolution operations over all input channels. In the convolutional modules of the YOLOv8 model, the channel dimensions are 128, 256, 512, and 1024, meaning that both computational cost and parameter count grow as the input and output channels increase. This leads to a greater demand for computational resources and longer processing times [
26]. Additionally, the convolutional kernel size in standard convolutions is fixed, which limits robustness against unknown geometric transformations, thus affecting the model’s generalization capability [
27].
This paper proposes the EGC module to address this issue. This module utilizes grouped convolutions with kernels of varying sizes to decrease the parameter count while also enhancing the capacity to capture multi-scale spatial features and enhancing generalization capability. The structure of the module is shown in
Figure 5. Let the input and output of the EGC module be denoted as
and
, where
C is the number of channels, and
H and
W represent the height and width of the feature map. The input feature map
Fin is split along the channel dimension into two paths:
and
. After splitting, the dimensions of the feature maps are as follows:
where “:” is used to indicate slicing operations across dimensions.
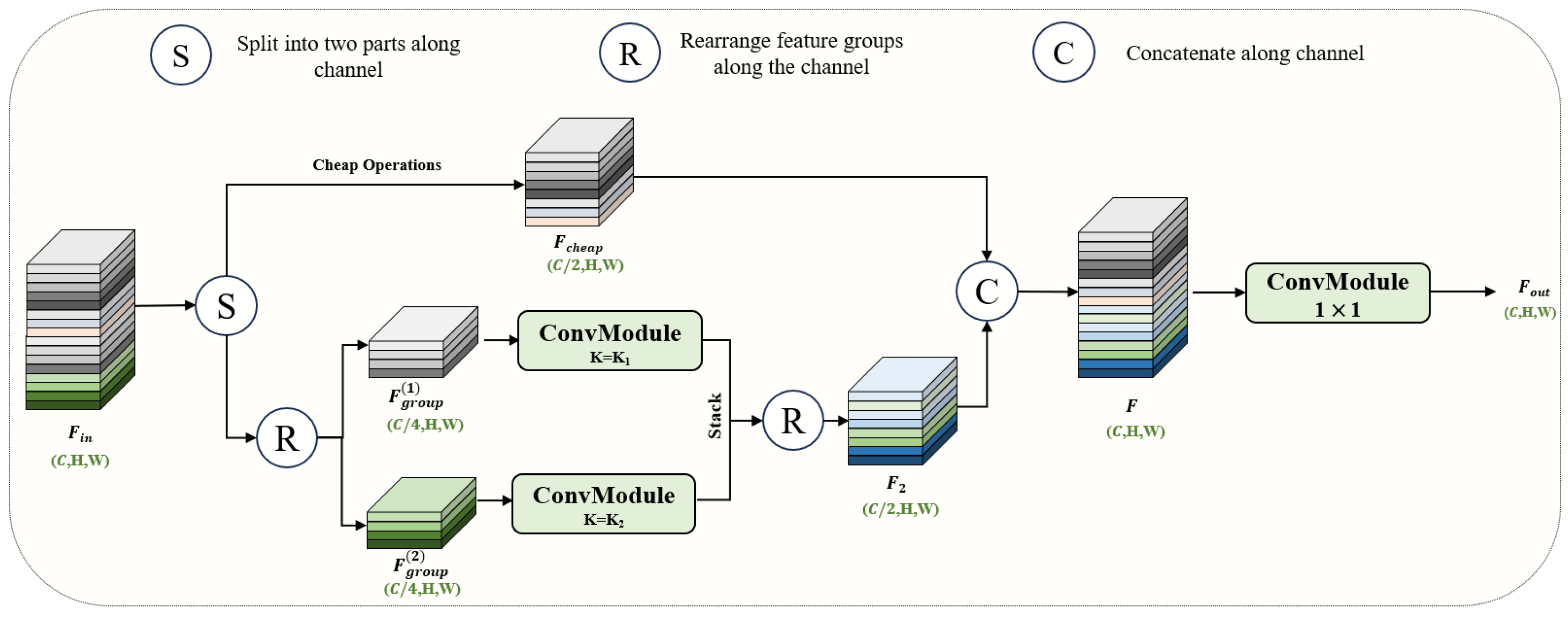
In the EGC, one path (
Fcheap) performs a simple operation to retain the original features, reducing redundancy in the feature mapping, as shown in
Figure 6. The other path (
Fgroup) undergoes group convolution, where
Fgroup is split into two groups:
. These are used as input for the group convolution, which, after processing and feature fusion, generates
. Finally, a pointwise convolution is applied to merge the feature channels from both paths, resulting in the fused output as:
By applying the EGC module for convolutional operations, the number of input and output channels is reduced to one-quarter of the original size, which subsequently decreases the parameter count accordingly. Equation (4) illustrates how the parameter count might be written as follows:
where
Cmin_in,
Cmin_out represent the number of channels after the split operation.
G denotes the number of groups.
Ki and
Kj allude to the grouped convolution kernels’ width and height, respectively.
The receptive field for recognizing image features is directly impacted by the convolution kernel’s size. A well-chosen convolution kernel can improve both the model’s performance and accuracy.
Table 1 demonstrates the parameter and computation costs for different kernel sizes. By combining 1 × 1 and 3 × 3 kernels, it is possible to maintain model performance while improving efficiency. Therefore, this study adopts the [1, 3] kernel combination to optimize model performance.
- (2)
C2f-EGC Module
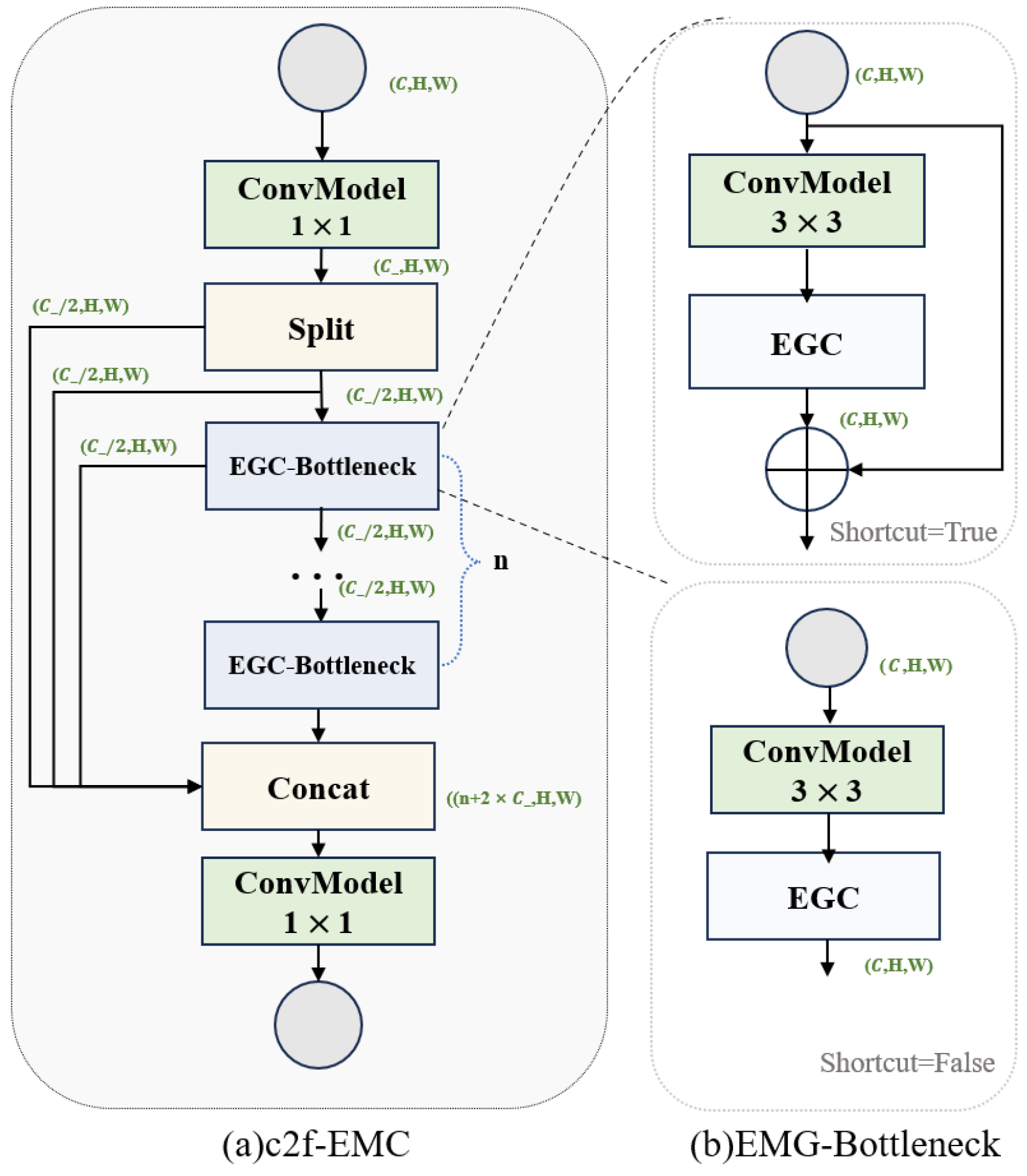
In the YOLOv8 model, the C2f module primarily extracts higher-level feature representations [
28]. Its core comprises convolution layers, activation functions, and Bottleneck modules [
29]. This study replaces the second standard convolution module in the Bottleneck with the EGC module, forming the EGC-Bottleneck module (as shown in
Figure 7b) to promote the exchange of multi-scale information within the model and capture local contextual information. By stacking multiple EGC-Bottleneck modules, a new network structure, C2f-EGC, is constructed (as shown in
Figure 7a).
In convolution layers with high channel numbers (128 and above), the C2f-EGC model replaces the original C2f module in this study. For layers with lower channel numbers (less than 128), the impact of grouped convolution is minimal, so the original C2f module is retained.
Table 2 compares the parameter counts between the C2f and C2f-EGC modules for high-channel layers. The results show that the C2f-EGC module reduces parameter count by more than 20% without compromising feature extraction capability.
2.2.2. Group Context Anchor Attention
In object detection, local information can be impacted by local blurring or noise, leading to decreased model performance. In vegetable and weed recognition, vegetables are typically planted in an organized manner, while weeds are randomly distributed [
30,
31]. This paper introduces the Group Context Anchor Attention (GCAA) mechanism, consisting primarily of pooling layers, EGC modules, depth-wise separable convolutions, and activation functions. The GCAA is intended to enhance the spatial feature representation for both weeds and vegetables by increasing the model’s ability to capture long-range contextual information.
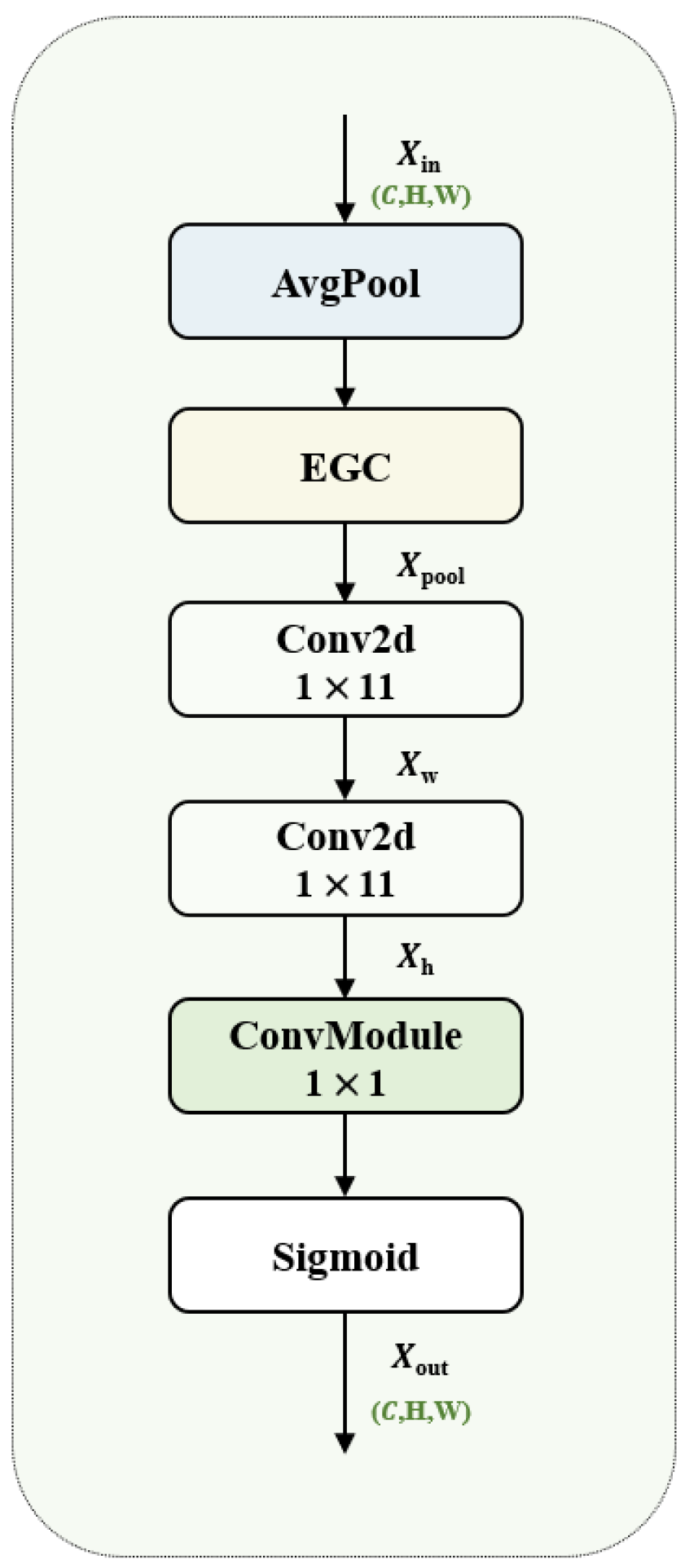
Figure 8 illustrates the GCAA model’s structure. First, an average pooling operation is applied to local regions, which averages out the local features, extracts global features, and reduces the dimensionality of the feature map. The local region’s features are then obtained using the EGC convolution procedure. The operation formula is as follows:
where
EGCi×i represents the convolution operation of the EGC module with
, indicating a convolution kernel size of [1, 3].
represents the average pooling operation.
represents the input value.
Then, depth-wise separable convolution is applied to capture long-range dependencies in both horizontal and vertical directions. Large convolution kernels of size 1 × 11 and 11 × 1 are used to perform convolutions along the vertical and horizontal axes. The operation is formulated as:
where
and
represent the output values after the 1 × 11 and 11 × 1 convolutions.
Conv represents the standard convolution operation.
Finally, a pointwise convolution is used to integrate and compress the features extracted from the separable convolution (
Xh) along the channel dimension. The sigmoid activation function is applied to perform a nonlinear transformation, generating the output feature
Xout as shown in Equation (8). For the feature fusion that follows, it is crucial to make sure that the output feature values fall between 0 and 1.
where
denotes the sigmoid function.
2.2.3. GCAA-Based Feature-Level Fusions Model
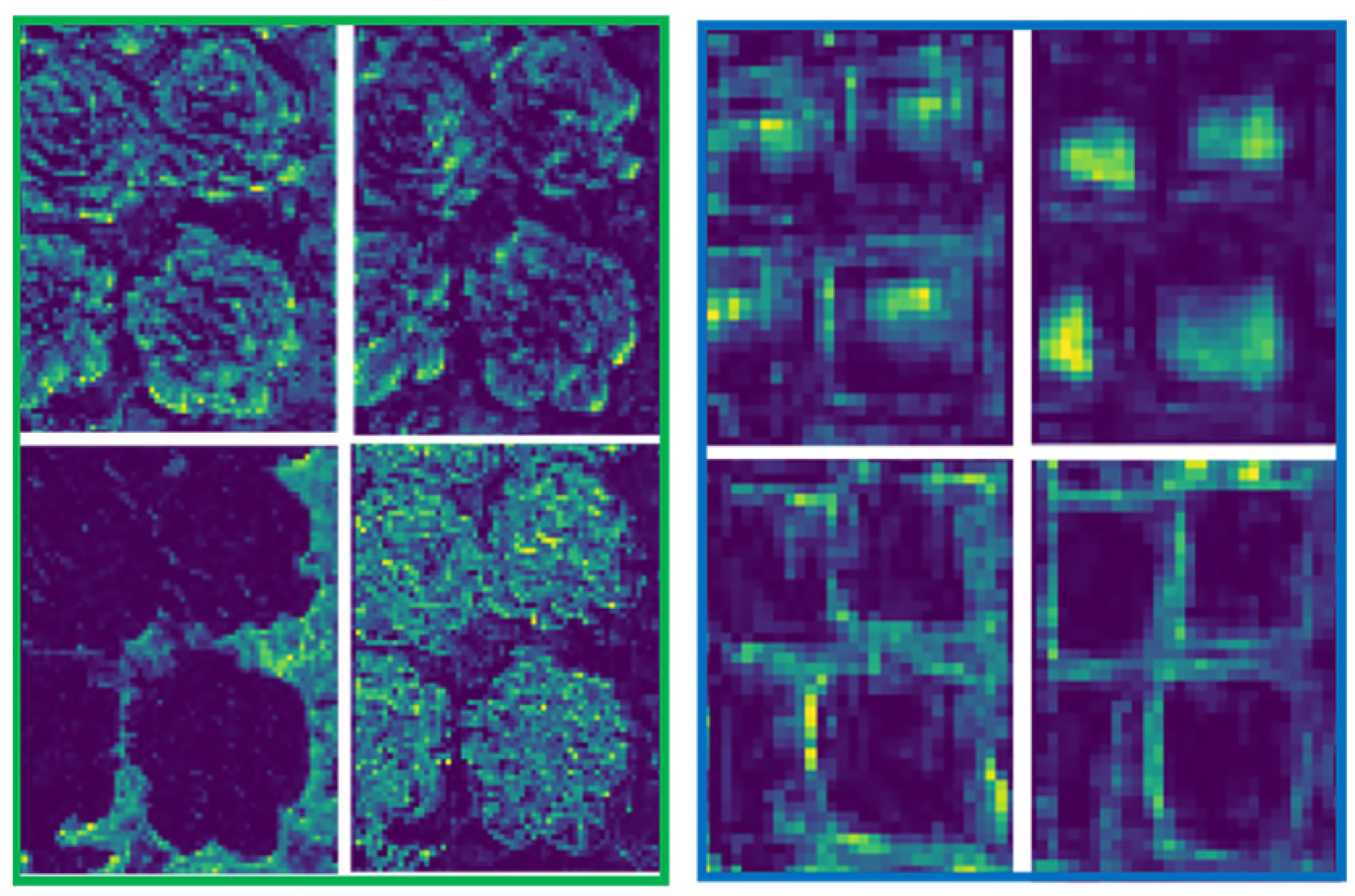
Shallow feature maps contain rich low-level information, such as edges and textures, which can effectively distinguish subtle differences between vegetables and weeds. However, during the object detection process, consecutive convolution and pooling operations reduce the resolution of deep feature maps, resulting in the loss of shallow information. Deep networks primarily extract abstract features such as object categories, negatively impacting the recognition of small objects and targets with similar shapes, as illustrated in
Figure 9 [
32,
33].
We assessed the Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) for images of various resolutions, as stated in Equations (9) and (10), aiming to examine better how image resolution affects feature extraction and object detection accuracy [
34].
where
MAX is the maximum pixel value of the image, and
MSE is the Mean Squared Error between two images. A higher PSNR value indicates better image quality.
where
and
are the means of images
x and
y,
and
are their variances,
is the covariance,
and
are constants to stabilize the division. Higher scores on the SSIM scale, which goes from 0 to 1, indicate more remarkable similarity.
The results are summarized in
Table 3. As the image resolution decreases, PSNR and SSIM values decline, indicating a loss of information and structural similarity. Lower-resolution images lose finer details, which potentially degrades deep networks’ ability to distinguish objects.
Feature enhancement is key to solving the problem of feature disappearance. In previous object detection algorithms, attention mechanisms are often used to highlight key features, which is effective but still faces the challenge of balancing and preserving low-level details and capturing high-level contextual information.
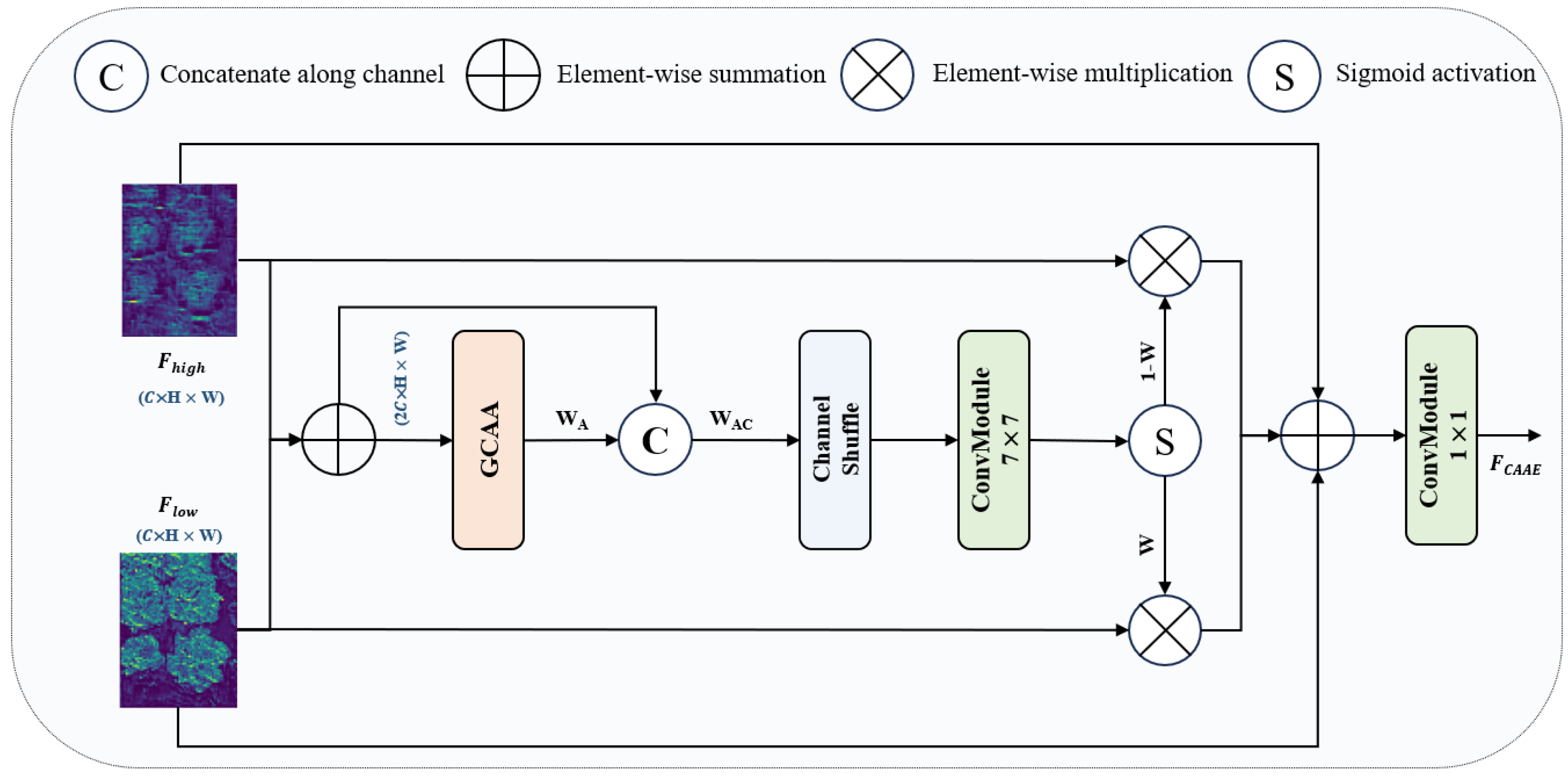
To address this issue, this paper introduces a feature fusion module based on GCAA (GCAA-Fusion). The module adaptively merges shallow and deep feature maps, enhancing both feature preservation and gradient backpropagation. As shown in
Figure 10, the low-level feature map
is combined with the high-level feature map
through simple addition. The combined features are then passed through the
GCAA attention module to generate an initial attention map
, integrating long-range contextual information with detailed features, as expressed in Equation (11).
where
represents the element-wise summation.
To obtain a more precise saliency feature map, the initial attention feature map
is first concatenated with the original feature map after the addition operation to form
. Then, channel shuffle operations are applied to rearrange the channels of
alternately. Finally, a 7 × 7 convolution operation followed by an activation function is applied to produce the feature weights
. The computation process is shown in Equations (12) and (13).
where
CS(·) refers to the channel shuffle operation.
depicts the convolution operation using a kernel size of 7 × 7.
The precise feature maps generated through weighted summation are then integrated, with skip connections introduced to enhance the input features. This helps mitigate the vanishing gradient problem and simplifies the training process. Given that shallow and deep features complement each other, the generated weight
W is applied to one module, while the fusion weight for the other module is represented as 1 −
W [
33]. Based on this, the fused features are mapped using a 1 × 1 convolution layer to obtain the final feature output, as indicated in Equation (14).
where
represents the elementwise multiplication.
2.2.4. Adaptive Feature Fusion (AFF)
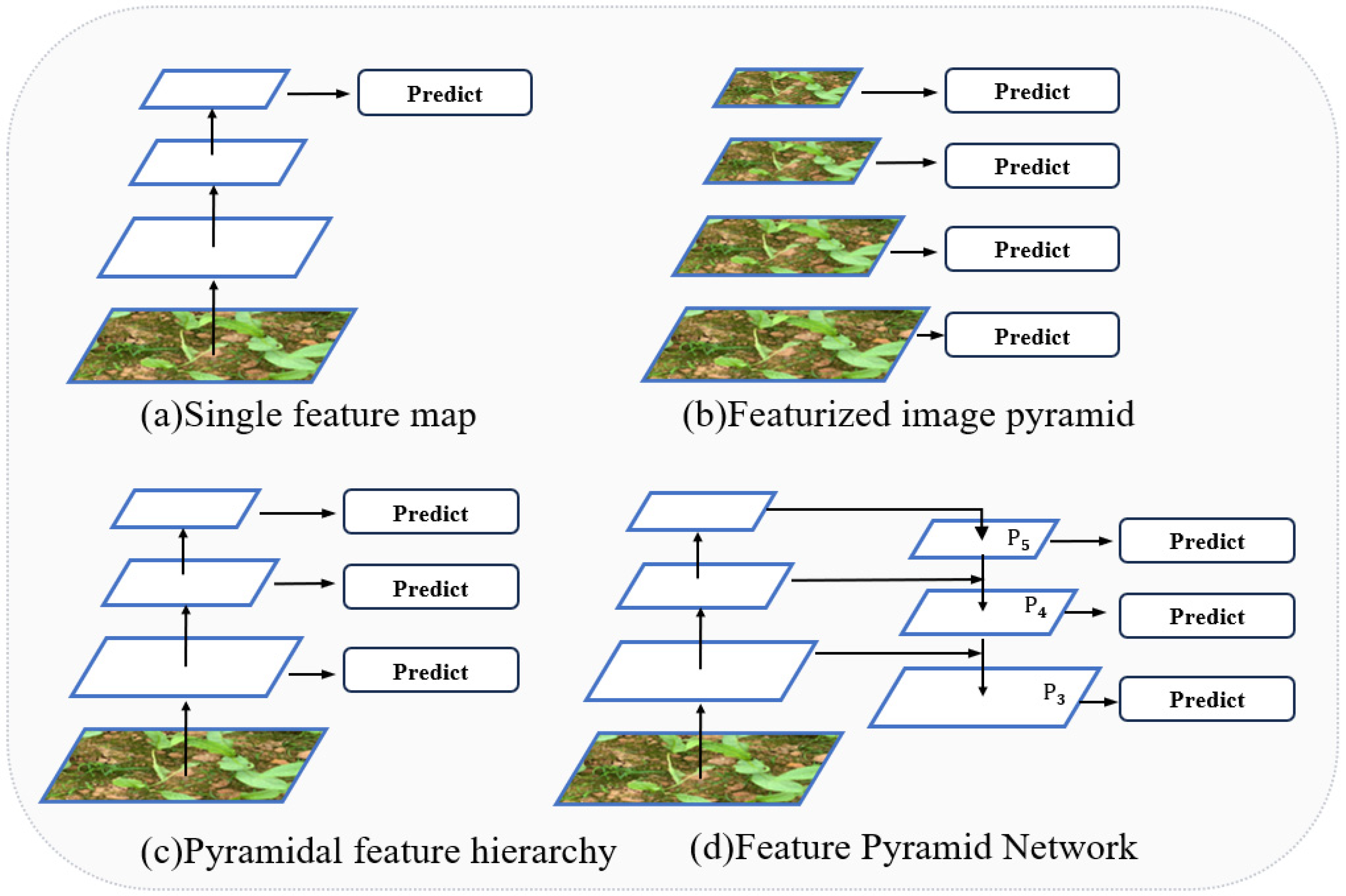
The Feature Pyramid is crucial in object detection for capturing multi-scale features.
Figure 11 outlines different pyramid structures. In
Figure 11a, a single feature map is used for prediction, limiting the ability to exploit multi-scale information.
Figure 11b presents an image pyramid approach where feature maps are generated at each scale, but this incurs a high computational cost [
35].
Figure 11c enhances detection performance by utilizing multi-layer feature extraction [
36], though it may lack precision in capturing fine details.
Figure 11d focuses on resolving the multi-scale challenge in object detection while reducing computational complexity, although efficiency could still be optimized [
37]. Improving feature extraction methods can substantially enhance the network’s detection accuracy. YOLOv8 employs the Path Aggregation Feature Pyramid Network (PAFPN) to facilitate information fusion across different layers, but deeper network layers can lead to feature loss.
This paper introduces an AFF structure built upon the PaFPN architecture to address the issue. As shown in
Figure 4 and
Figure 12, The orange dashed lines correspond to the 9th, 6th, and 4th layers, and the output layers N5, N4, and N3 correspond to the 15th, 18th, and 21st layers, respectively. Three GCAA-Fusion modules are incorporated before each Detection Head, with their inputs sourced from the 4th and 15th layers, the 6th and 18th layers, and the 9th and 21st layers. The AFF structure adaptively merges low-level and high-level features along the channel dimension, increasing the model’s ability to preserve features and raising object detection’s precision and effectiveness. This results in greater robustness and adaptability across various tasks.