A Standardized Treatment Model for Head Loss of Farmland Filters Based on Interaction Factors
Abstract
1. Introduction
2. Materials and Methods
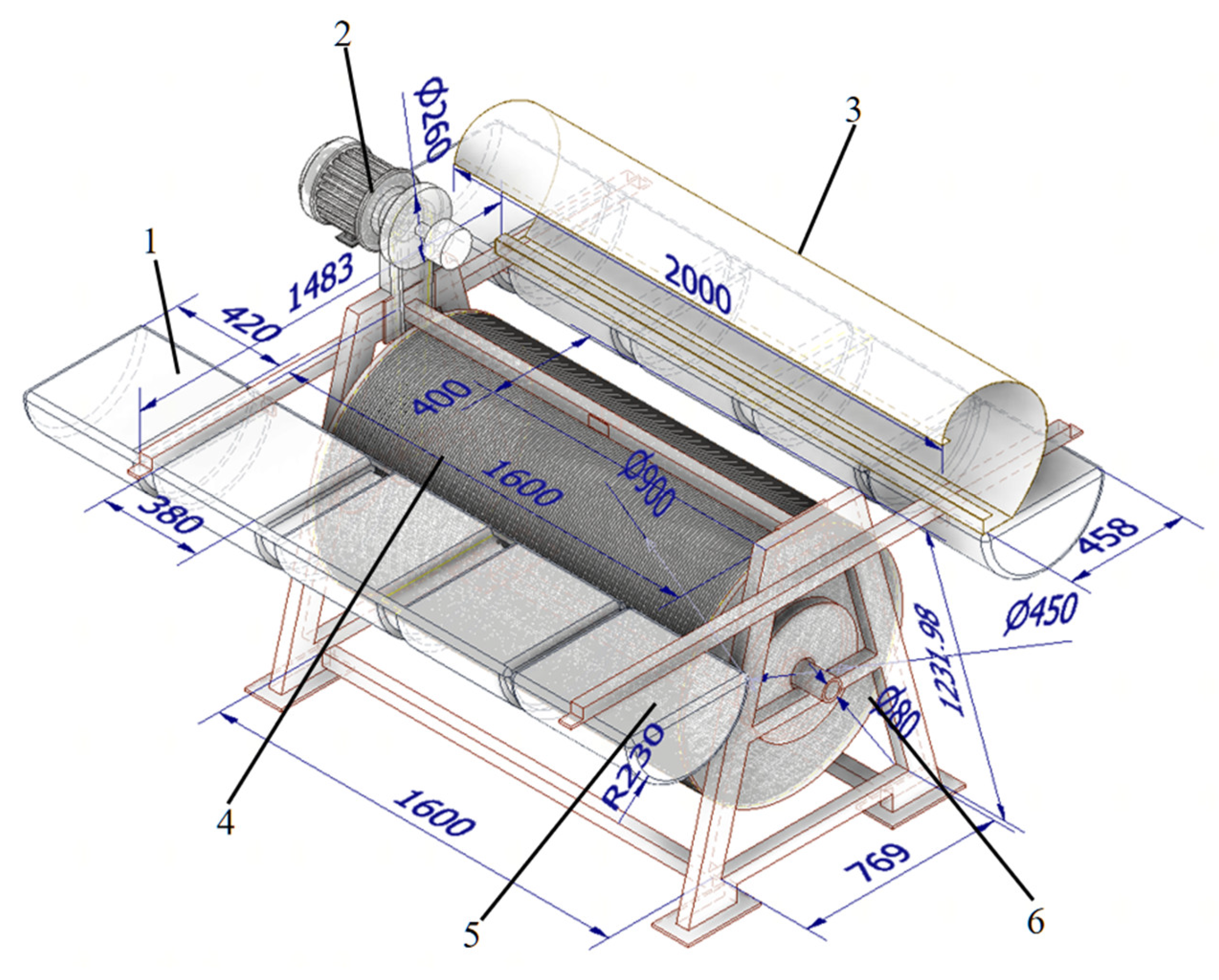
2.1. Structure of Pressure-Free Net Filter
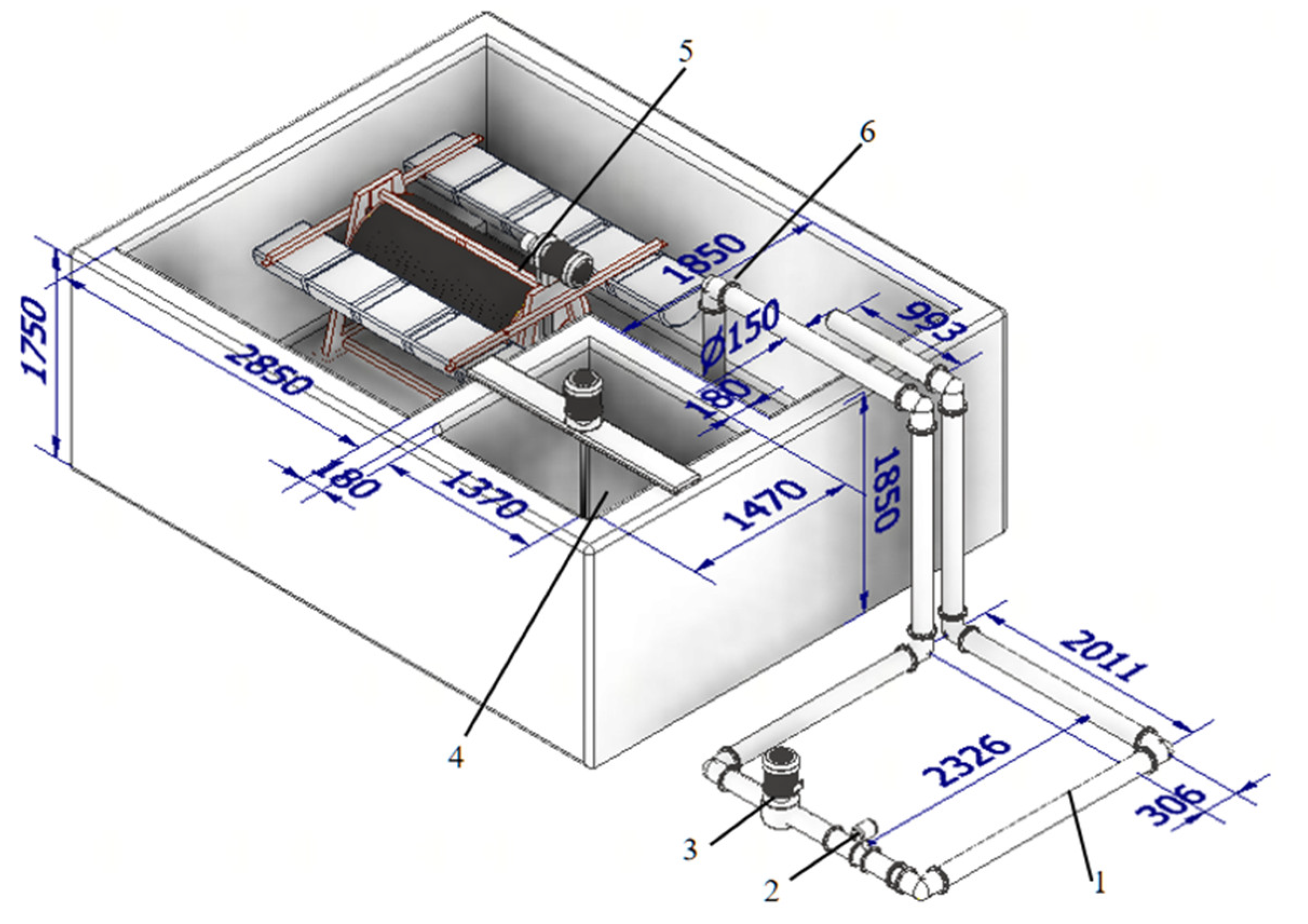
2.2. Test System
2.2.1. Test Device Structure
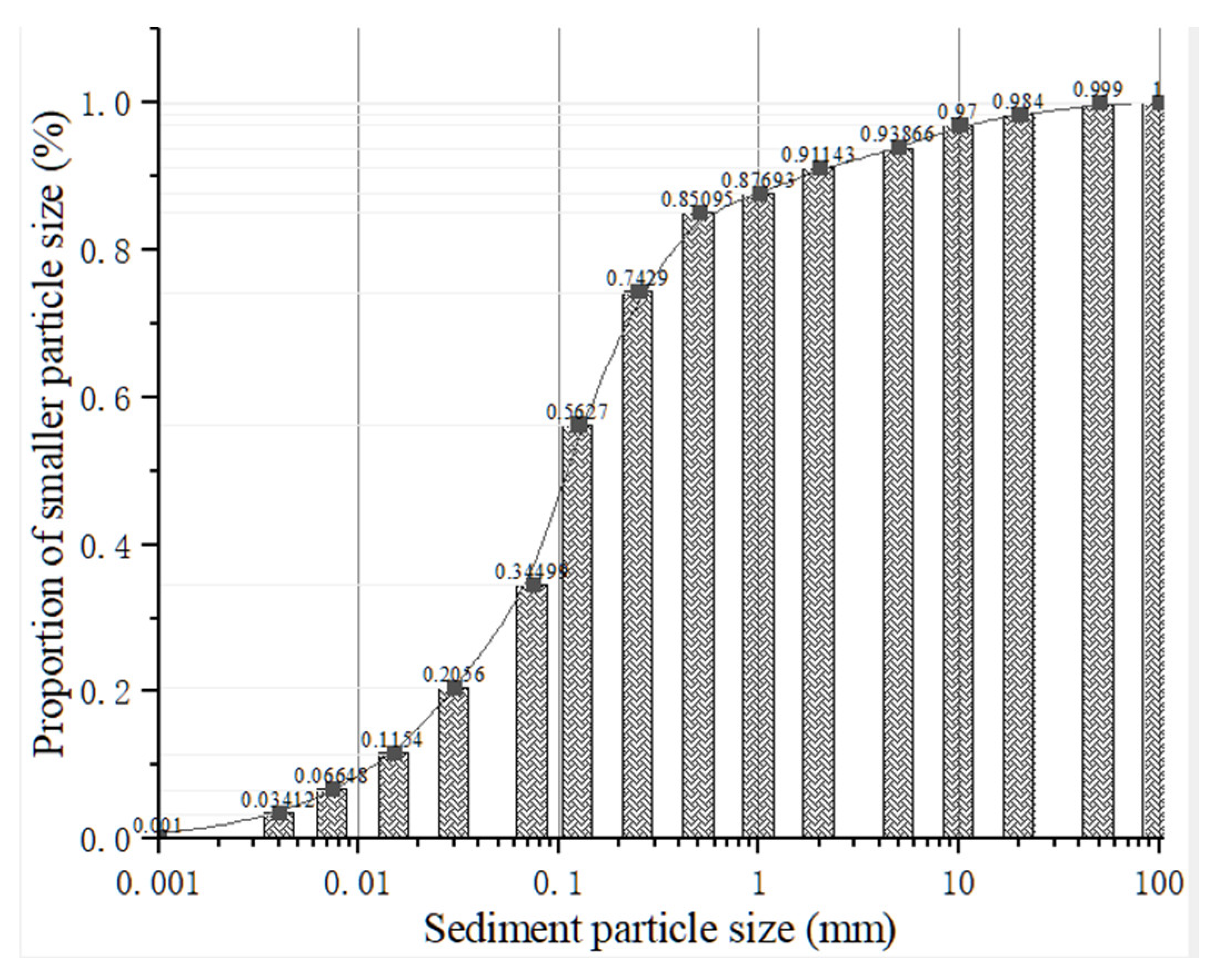
2.2.2. Test Flow and Materials
2.3. Analysis Methods
- (1)
- Establishment of the response surface function:
- (2)
- Construction matrix
- (3)
- Determine structural coefficients
- (4)
- Combining Equations (1)–(9) yields the following:
2.4. Standardized Processing
3. Results and Discussion
3.1. Head Loss Model Calculation and Variance Analysis
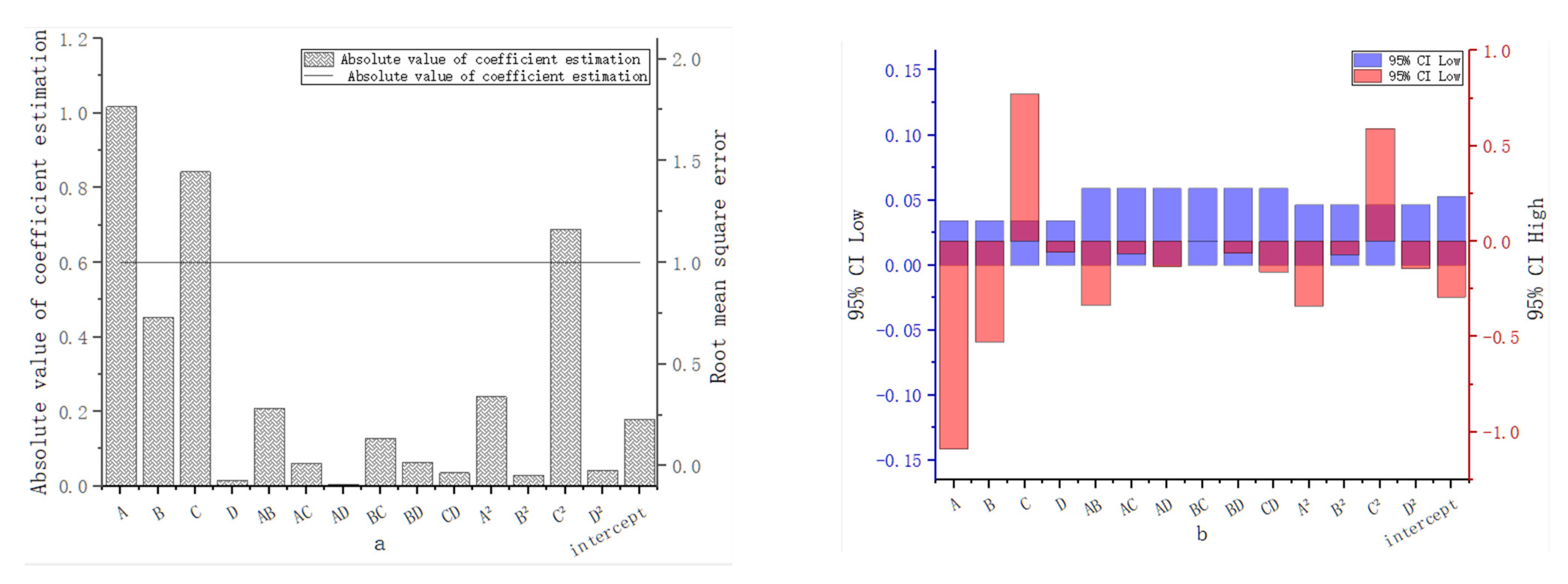
3.2. Factor Contribution to Head Loss
3.3. Response Surface Analysis
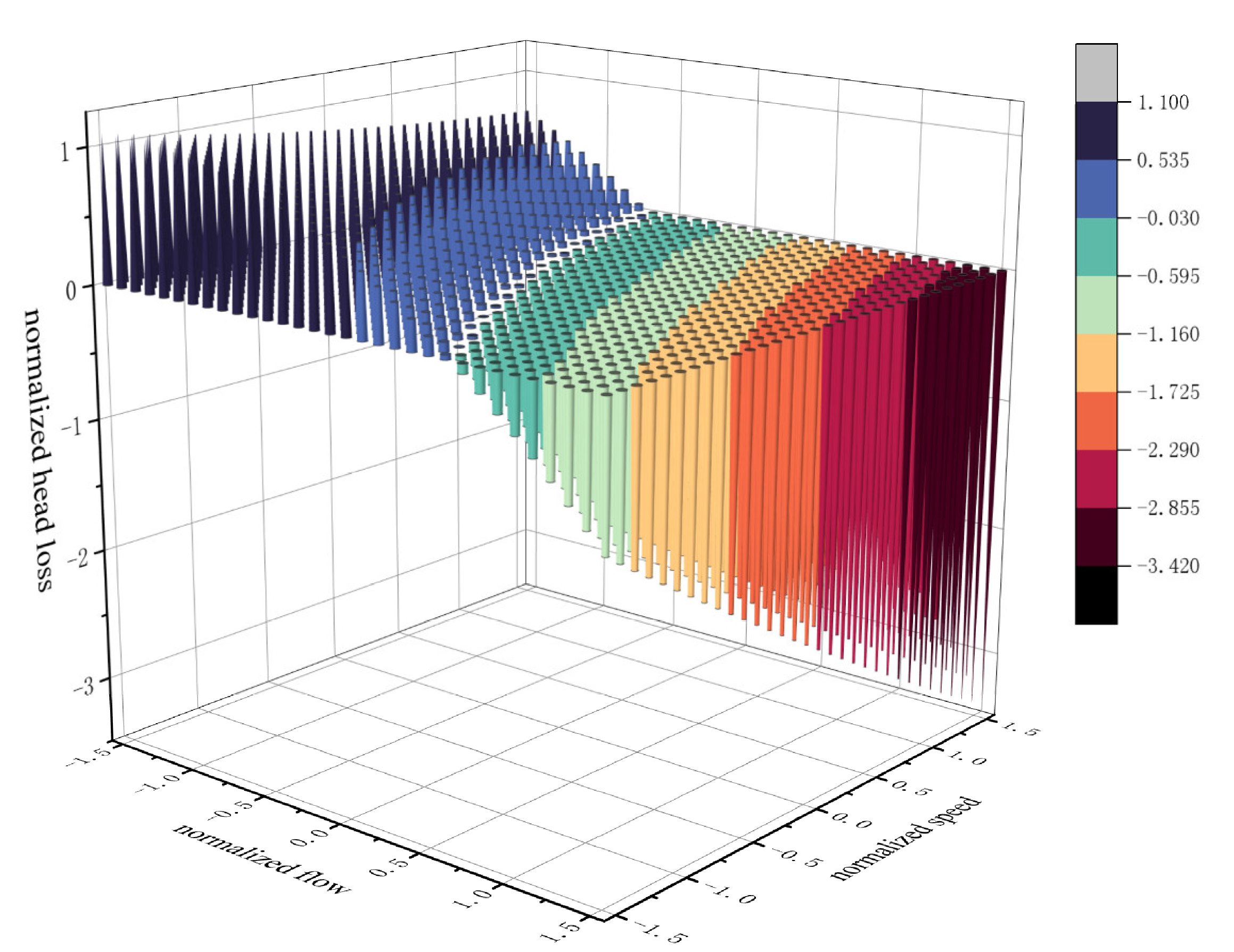
3.3.1. Interaction Term of Filter Flow Rate and Filter Cartridge Speed
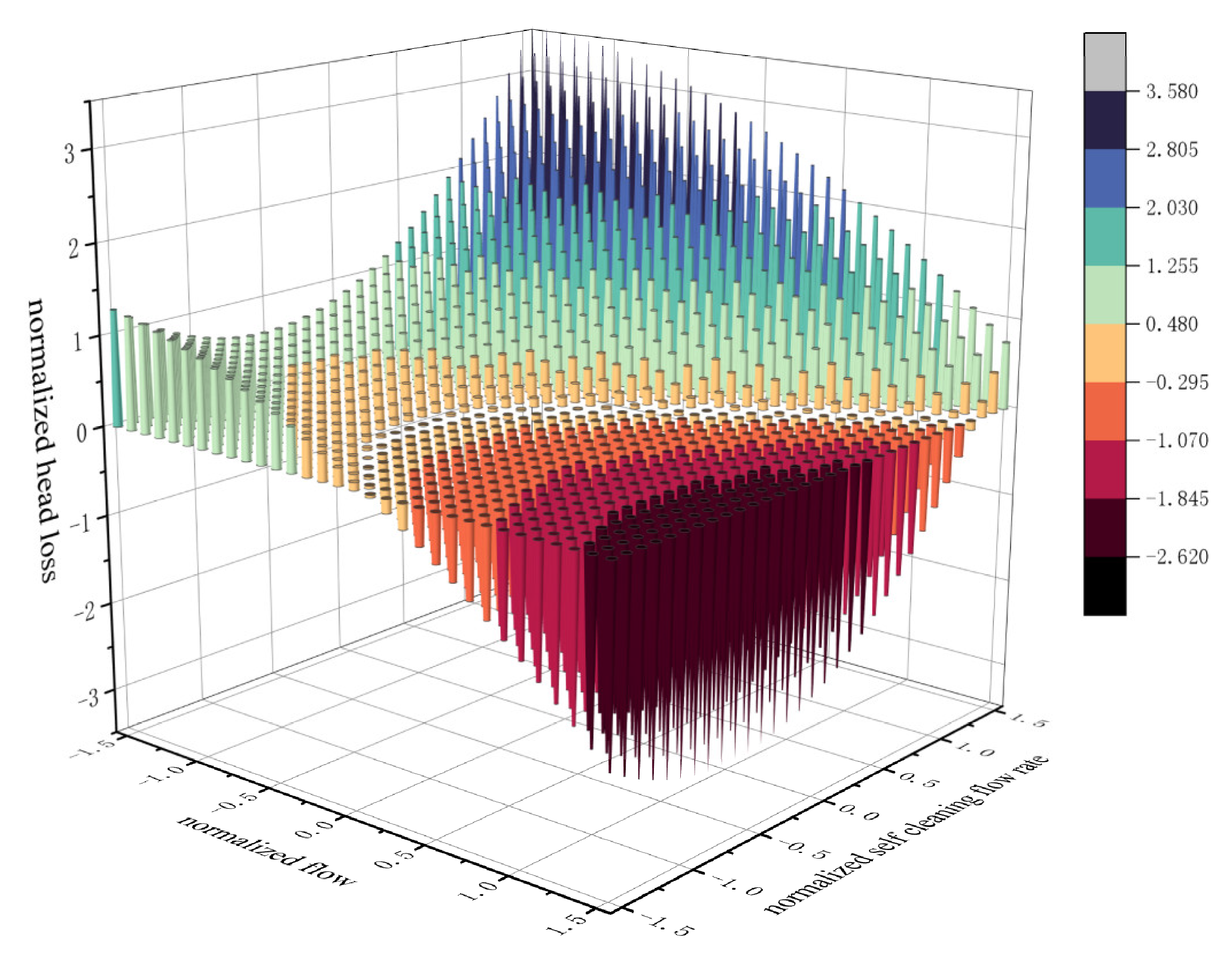
3.3.2. Filter Flow and Self-Cleaning Flow Interaction
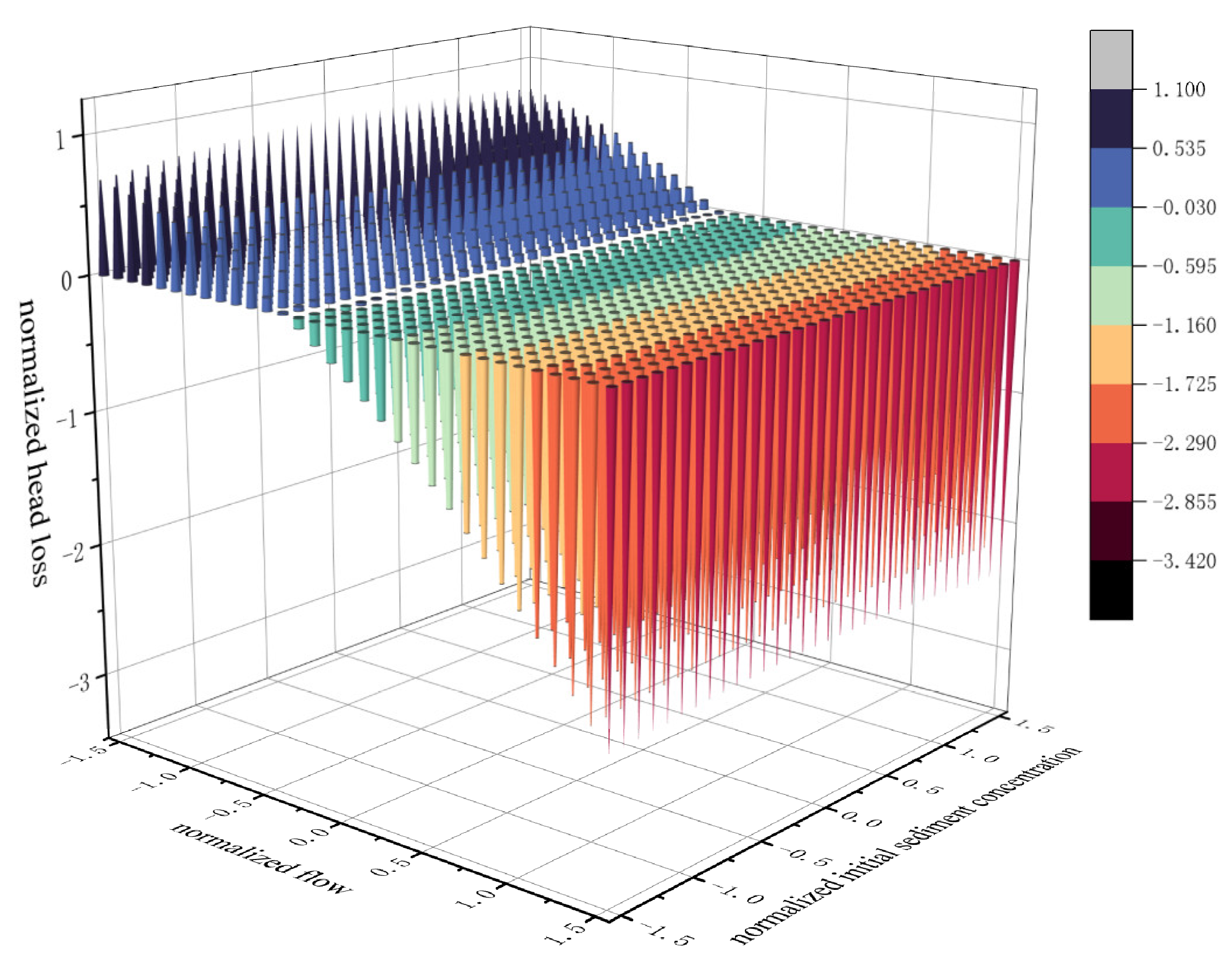
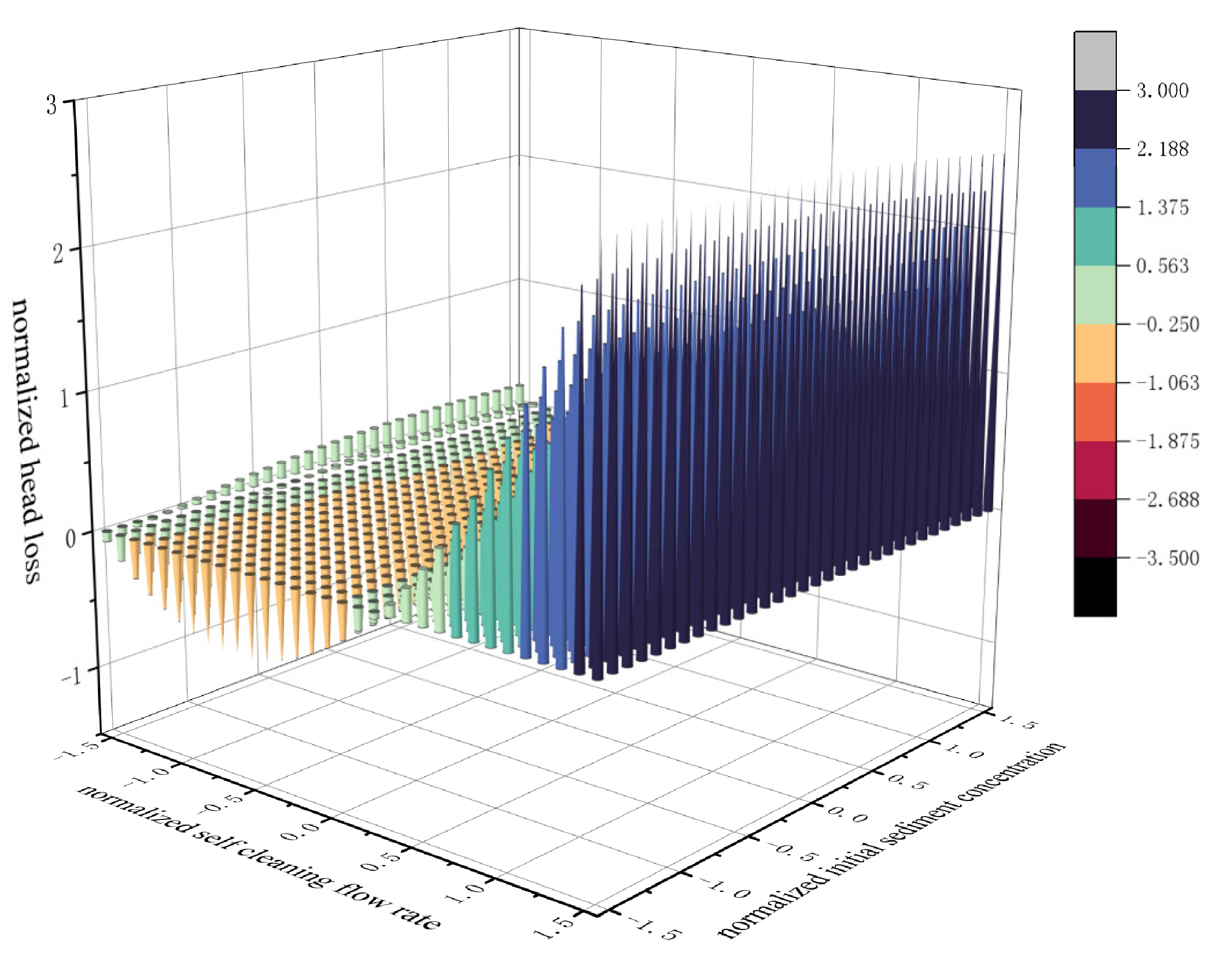
3.3.3. Filter Flow and Initial Sediment Concentration Interaction
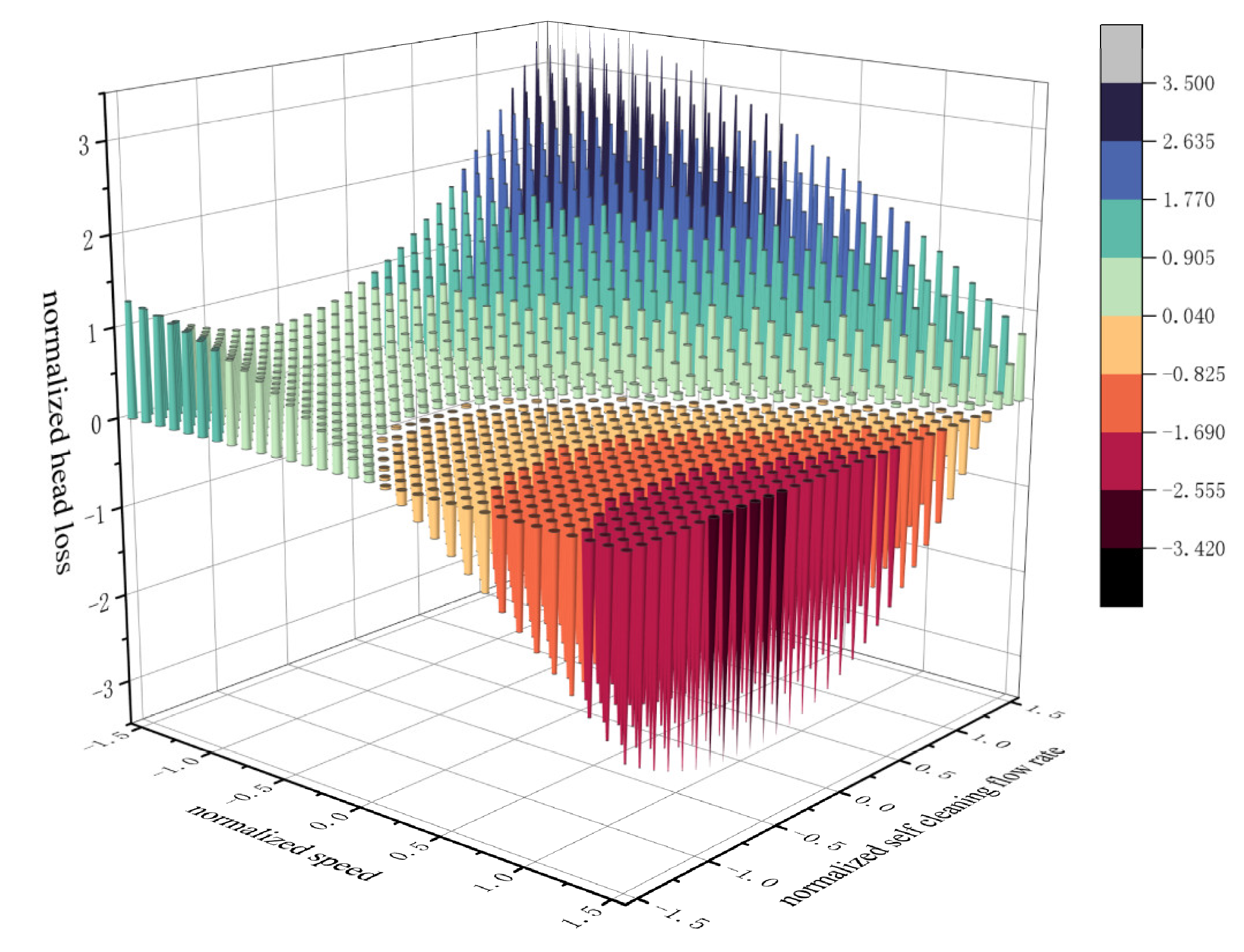
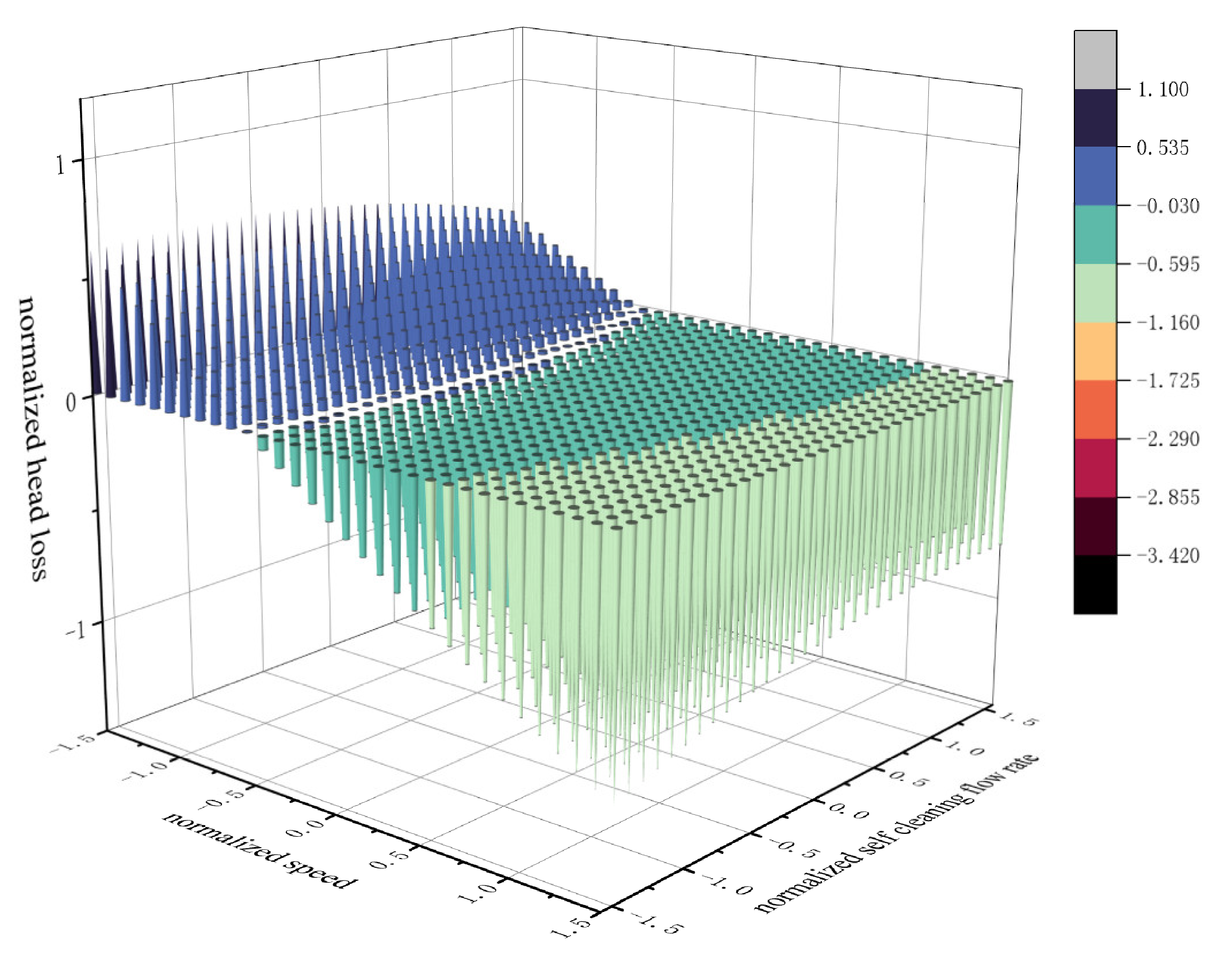
3.3.4. Interaction Term of Cartridge Speed and Self-Cleaning Flow Rate
3.3.5. Interaction Term between Filter Cartridge Speed and Initial Sediment Concentration, and Interaction Term between Self-Cleaning Flow Rate and Initial Sediment Concentration
3.4. Interaction Correction
4. Discussion
5. Conclusions
- Integrating four key test factors, including irrigation flow, filter cartridge speed, self-cleaning flow, and initial sand content, we developed a head loss model for pressureless mesh filters used in farmland irrigation. After refining the response surface, the model showed a significant improvement with a coefficient of determination of 98.61%.
- The total irrigation flow had a 17.20% higher contribution than the self-cleaning flow rate, while the initial sand content had the smallest contribution at 0.0166. Additionally, the self-cleaning flow rate had a 46.18% higher contribution than the filter cartridge speed, and the filter cartridge speed had a 96.34% higher contribution than the initial sand content.
- The interaction term between irrigation flow and filter cartridge speed had a contribution 218.25% higher than the interaction term between irrigation flow and initial sand content. The self-cleaning flow rate’s self-interaction had the highest contribution, while the filter cartridge speed’s self-interaction had the smallest contribution.
- By optimizing the response surface and the model, the optimal parameters were determined to be an irrigation flow rate of 121.687 m3·h−1, a filter cartridge speed of 1.331 r·min−1, a self-cleaning flow rate of 19.980 m3·h−1, and an initial sand content of 0.261 g·L−1, resulting in a minimum head loss of 21.671 kPa.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Niu, W.; Wu, P.; Li, J.; Shao, H. One of frontiers in agricultural and environmental biotechnology for the arid regions: Micro-pressure drip irrigation technology theory and practices. Afr. J. Biotechnol. 2010, 9, 2891–2897. [Google Scholar]
- Yildiz, H.; Kadayifci, A. Design and Operation Analysis of Drip Irrigation Systems Used in the Irrigation of Cherry Orchards in Isparta-Uluborlu Region, Turkey. Appl. Ecol. Environ. Res. 2018, 16, 3131–3143. [Google Scholar] [CrossRef]
- Tian, C.; Lv, Z.; Song, Y.; Zhang, H. Increasing the cotton yield and improving the ecology in cotton fields by utilizing the properties of natural resources in Xinjiang, China. In Ecosystems Dynamics, Ecosystem-Society Interactions, and Remote Sensing Applications for Semi-Arid and Arid Land; SPIE: Bellingham, WA, USA, 2003; Volume 4890, pp. 809–819. [Google Scholar] [CrossRef]
- Yu, L.M.; Li, J.L.; Li, N.; Wang, J.Y.; Wang, D.R. Wear Behavior and Vortex Characteristics of Y-Type Screen Filters with Various Inclination Angles and Inlet Flow Velocities: Numerical and Experimental Study. J. Irrig. Drain. Eng. 2023, 149, 04023014. [Google Scholar] [CrossRef]
- Sanderson, S.L.; Roberts, E.; Lineburg, J.; Brooks, H. Fish mouths as engineering structures for vortical cross-step filtration. Nat. Commun. 2016, 7, 11092. [Google Scholar] [CrossRef] [PubMed]
- Bayer-Raich, M.; Jordana, S.; Jaime, O.M.; Lynch, T.D.; McGillicuddy, K.B.; Guimera, J.; Jaime, M.J. Numerical Modeling of Head Losses in Different Types of Well Screens. Ground Water 2022, 60, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Houben, G.J.; Wachenhausen, J.; Morel, C.R.G. Effects of ageing on the hydraulics of water wells and the influence of non-Darcy flow. Hydrogeol. J. 2018, 26, 1285–1294. [Google Scholar] [CrossRef]
- Tao, H.; Shen, P.; Li, Q.; Jiang, Y.; Yang, W.; Wei, J. Research on head loss of pre-pump micro-pressure filter under clean water conditions. Water Supply 2022, 22, 3271–3282. [Google Scholar] [CrossRef]
- Demir, V.; Yürdem, H.; Yazgi, A.; Degirmencioglu, A. Determination of the head losses in metal body disc filters used in drip irrigation systems. Turk. J. Agric. For. 2009, 33, 219–229. [Google Scholar] [CrossRef]
- Cano, N.D.; Camargo, A.P.; Ait-Mouheb, N.; Muniz, G.L.; Guarnizo, J.A.Y.; Pereira, D.J.S.; Frizzone, J.A. Optimisation of the filter housing dimensions of an automatic flushing strainer-type filter. Biosyst. Eng. 2022, 219, 25–37. [Google Scholar] [CrossRef]
- Arbat, G.; Pujol, T.; Puig-Bargués, J.; Duran-Ros, M.; Barragán, J.; Montoro, L.; de Cartagena, F.R. Using Computational Fluid Dynamics to Predict Head Losses in the Auxiliary Elements of a Microirrigation Sand Filter. Trans. Asabe 2011, 54, 1367–1376. [Google Scholar] [CrossRef]
- Liu, F.; Liu, Y.A. Uplink scheduling for LTE-advanced system. In Proceedings of the 2010 IEEE International Conference on Communication Systems, Singapore, 17–19 November 2010; pp. 316–320. [Google Scholar]
- Samuel, M.P.; Senthilvel, S.; Tamilmani, D.; Mathew, A.C. Performance evaluation and modelling studies of gravel–coir fibre–sand multimedia stormwater filter. Environ. Technol. 2012, 33, 2057–2069. [Google Scholar] [CrossRef] [PubMed]
- Boyer, D.G. Assessment of a sinkhole filter for removing agricultural contaminants. J. Soil Water Conserv. 2008, 63, 47–52. [Google Scholar] [CrossRef]
- Carrión-Coronel, E.; Ortiz, P.; Nanía, L. Physical Experimentation and 2D-CFD Parametric Study of Flow through Transverse Bottom Racks. Water 2022, 14, 955. [Google Scholar] [CrossRef]
- Blocken, B.; Gualtieri, C. Ten iterative steps for model development and evaluation applied to Computational Fluid Dynamics for Environmental Fluid Mechanics. Environ. Model. Softw. 2012, 33, 1–22. [Google Scholar] [CrossRef]
- Shehzad, M.A.; Bashir, A.; Ul Amin, M.N.; Khosa, S.K.; Aslam, M.; Ahmad, Z. Reservoir Inflow Prediction by Employing Response Surface-Based Models Conjunction with Wavelet and Bootstrap Techniques. Math. Probl. Eng. 2021, 2021, 4086918. [Google Scholar] [CrossRef]
- Hassan, M.M.; Yun, J.S.; Rahman, M.M.; Choo, Y.W.; Han, J.T.; Kim, D. Centrifugal Test Replicated Numerical Model Updating for 3D Strutted Deep Excavation with the Response-Surface Method. Appl. Sci. 2022, 12, 665. [Google Scholar] [CrossRef]
- Kluz, R.; Habrat, W.; Bucior, M.; Krupa, K.; Sep, J. Multi-criteria optimization of the turning parameters of Ti-6Al-4V titanium alloy using the Response Surface Methodology. Eksploat. Niezawodn.-Maint. Reliab. 2022, 24, 668–676. [Google Scholar] [CrossRef]
- Zalewski, M.J.; Maminski, M.L.; Parzuchowski, P.G. Synthesis of Polyhydroxyurethanes-Experimental Verification of the Box-Behnken Optimization Model. Polymers 2022, 14, 4510. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Janardhan, G.; Sharma, V.K.; Kumar, V.; Joshi, R.S. Comparative prediction of surface roughness for MAFM finished aluminium/silicon carbide/aluminium trioxide/rare earth oxides (Al/SiC/Al2O3)/REOs) composites using a Levenberg–Marquardt Algorithm and a Box–Behnken Design. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 236, 790–804. [Google Scholar] [CrossRef]
- Toprak, D.; Demir, Ö.; Uçar, D. Extracellular azo dye oxidation: Reduction of azo dye in batch reactors with biogenic sulfide. Phosphorus Sulfur Silicon Relat. Elem. 2022, 197, 927–933. [Google Scholar] [CrossRef]
- Eltas, O.; Topal, M. Using Multivariate Analysis of Covariance in Genetic Parameter Estimation. Fresenius Environ. Bull. 2022, 31, 2015–2024. [Google Scholar]
- Jamshidi, L.; Declercq, L.; Fernandez-Castilla, B.; Ferron, J.M.; Moeyaert, M.; Beretvas, S.N.; Van den Noortgate, W. Multilevel meta-analysis of multiple regression coefficients from single-case experimental studies. Behav. Res. Methods 2020, 52, 2008–2019. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Xu, X.Z. Least Favorable Direction Test for Multivariate Analysis of Variance in High Dimension. Stat. Sin. 2021, 31, 723–747. [Google Scholar] [CrossRef]
- Kostousova, E.K. External Polyhedral Estimates of Reachable Sets of Discrete-Time Systems with Integral Bounds on Additive Terms. Math. Control. Relat. Fields 2021, 11, 625–641. [Google Scholar] [CrossRef]
- Zong, Q.L.; Zheng, T.G. Numerical Simulation on Flow Field of Screen Filter for Drip Irrigation in Field. In Proceedings of the International Conference on Civil, Architectural and Hydraulic Engineering (ICCAHE 2012), Zhangjiajie, China, 10–12 August 2012. [Google Scholar]
- Chi, Y.; Yang, P.; Ma, Z.; Wang, H.; Liu, Y.; Jiang, B.; Hu, Z. The Study on Internal Flow Characteristics of Disc Filter under Different Working Condition. Appl. Sci. 2021, 11, 7715. [Google Scholar] [CrossRef]
- Milstein, A.; Feldlite, M. Relationships between clogging in irrigation systems and plankton community structure and distribution in wastewater reservoirs. Agric. Water Manag. 2014, 140, 79–86. [Google Scholar] [CrossRef]
- Zhang, W.; Cai, J.; Zhai, G.; Song, L.; Lv, M. Experimental Study on the Filtration Characteristics and Sediment Distribution Influencing Factors of Sand Media Filters. Water 2023, 15, 4303. [Google Scholar] [CrossRef]
- Yamamoto, T.; Fujiyama, H.; Miyamoto, K.; Hatanaka, J.; Wen, G.; Asae, A. Optimizing water cleaning system for microirrigation in the Tokaku Irrigation Project of Japan. In Proceedings of the 4th National Irrigation Symposium, Phoenix, AZ, USA, 14–16 November 2000. [Google Scholar]
- Coelho, R.D.; De Almeida, A.N.; Costa, J.D.O.; De Sousa Pereira, D.J. Mobile drip irrigation (MDI): Clogging of high flow emitters caused by dragging of driplines on the ground and by solid particles in the irrigation water. Agric. Water Manag. 2022, 263, 107454. [Google Scholar] [CrossRef]
- Graciano-Uribe, J.; Pujol, T.; Puig-Bargues, J.; Duran-Ros, M.; Arbat, G.; Ramirez de Cartagena, F. Assessment of Different Pressure Drop-Flow Rate Equations in a Pressurized Porous Media Filter for Irrigation Systems. Water 2021, 13, 2179. [Google Scholar] [CrossRef]
- Jiao, Y.; Feng, J.; Liu, Y.; Yang, L.; Han, M. Sustainable operation mode of a sand filter in a drip irrigation system using Yellow River water in an arid area. Water Supply 2020, 20, 3636–3645. [Google Scholar] [CrossRef]
- De Deus, F.P.; Mesquita, M.; Testezlaf, R.; De Almeida, R.C.; de Oliveira, H.F.E. Methodology for hydraulic characterisation of the sand filter backwashing processes used in micro irrigation. MethodsX 2020, 7, 100962. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Cai, J.; Zhai, G.; Feng, J.; Fan, Y.; Han, J.; Hao, P.; Ma, N.; Miao, F. Comparative Study and Evaluation of Sediment Deposition and Migration Characteristics of New Sustainable Filter Media in Micro-Irrigation Sand Filters. Sustainability 2024, 16, 3256. [Google Scholar] [CrossRef]
| Administrative Levels | Flow (m3·h−1) | Speed of Self-Cleaning Device (r·min−1) | Flow of Self-Cleaning Device (m3·h−1) | Initial Sediment Concentration (g·L−1) |
|---|---|---|---|---|
| −1 | 120 | 1 | 1 | 0.2 |
| 0 | 140 | 2.5 | 10.5 | 0.5 |
| 1 | 160 | 4 | 20 | 0.8 |
| Std | Run | Factor 1 Flow | Factor 2 Speed | Factor 3 Self-Cleaning Flow Rate | Factor 4 Initial Sediment Concentration | Response: Head Loss |
|---|---|---|---|---|---|---|
| 23 | 1 | 0.000 | −1.528 | 0.000 | 1.528 | 0.169 |
| 16 | 2 | 0.000 | 1.528 | 1.528 | 0.000 | 0.982 |
| 3 | 3 | −1.528 | 1.528 | 0.000 | 0.000 | 0.456 |
| 17 | 4 | −1.528 | 0.000 | −1.528 | 0.000 | 0.500 |
| 10 | 5 | 1.528 | 0.000 | 0.000 | −1.528 | −1.446 |
| 27 | 6 | 0.000 | 0.000 | 0.000 | 0.000 | −0.285 |
| 11 | 7 | −1.528 | 0.000 | 0.000 | 1.528 | 0.500 |
| 18 | 8 | 1.528 | 0.000 | −1.528 | 0.000 | −1.811 |
| 9 | 9 | −1.528 | 0.000 | 0.000 | −1.528 | 0.445 |
| 13 | 10 | 0.000 | −1.528 | −1.528 | 0.000 | 0.323 |
| 1 | 11 | −1.528 | −1.528 | 0.000 | 0.000 | 0.860 |
| 19 | 12 | −1.528 | 0.000 | 1.528 | 0.000 | 2.160 |
| 14 | 13 | 0.000 | 1.528 | −1.528 | 0.000 | −0.871 |
| 8 | 14 | 0.000 | 0.000 | 1.528 | 1.528 | 1.374 |
| 20 | 15 | 1.528 | 0.000 | 1.528 | 0.000 | 0.097 |
| 25 | 16 | 0.000 | 0.000 | 0.000 | 0.000 | −0.285 |
| 7 | 17 | 0.000 | 0.000 | −1.528 | 1.528 | −0.241 |
| 4 | 18 | 1.528 | 1.528 | 0.000 | 0.000 | −1.966 |
| 15 | 19 | 0.000 | −1.528 | 1.528 | 0.000 | 1.662 |
| 22 | 20 | 0.000 | 1.528 | 0.000 | −1.528 | −0.750 |
| 5 | 21 | 0.000 | 0.000 | −1.528 | −1.528 | −0.418 |
| 2 | 22 | 1.528 | −1.528 | 0.000 | 0.000 | −0.727 |
| 21 | 23 | 0.000 | −1.528 | 0.000 | −1.528 | 0.346 |
| 6 | 24 | 0.000 | 0.000 | 1.528 | −1.528 | 1.341 |
| 24 | 25 | 0.000 | 1.528 | 0.000 | 1.528 | −0.672 |
| 26 | 26 | 0.000 | 0.000 | 0.000 | 0.000 | −0.285 |
| 29 | 27 | 0.000 | 0.000 | 0.000 | 0.000 | −0.019 |
| 12 | 28 | 1.528 | 0.000 | 0.000 | 1.528 | −1.413 |
| 28 | 29 | 0.000 | 0.000 | 0.000 | 0.000 | −0.025 |
| Divisor | The Squared Deviation | Number of Independent Coordinates | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 27.8 | 14 | 1.99 | 142.86 | <0.0001 |
| Flow | 12.38 | 1 | 12.38 | 890.68 | <0.0001 |
| Speed | 2.48 | 1 | 2.48 | 178.26 | <0.0001 |
| Self-cleaning flow rate | 8.56 | 1 | 8.56 | 615.39 | <0.0001 |
| Initial sediment concentration | 0.0033 | 1 | 0.0033 | 0.2376 | 0.6337 |
| Flow × speed | 0.1743 | 1 | 0.1743 | 12.54 | 0.0033 |
| Flow × self-cleaning flow | 0.0154 | 1 | 0.0154 | 1.11 | 0.3108 |
| Flow × initial sediment concentration | 0.0001 | 1 | 0.0001 | 0.0088 | 0.9270 |
| Speed × self-cleaning flow | 0.066 | 1 | 0.066 | 4.76 | 0.0467 |
| Speed × initial sediment concentration | 0.0163 | 1 | 0.0163 | 1.16 | 0.2989 |
| Self-cleaning flow × initial sediment concentration | 0.0052 | 1 | 0.0052 | 0.3718 | 0.5518 |
| Flow 2 | 0.3759 | 1 | 0.3759 | 27.06 | 0.0001 |
| Speed 2 | 0.0054 | 1 | 0.0054 | 0.3872 | 0.5438 |
| Self-cleaning flow 2 | 3.09 | 1 | 3.09 | 221.86 | <0.0001 |
| Initial sediment concentration 2 | 0.0121 | 1 | 0.0121 | 0.8665 | 0.3677 |
| Residual | 0.1947 | 14 | 0.0139 | ||
| Lack of fit | 0.1117 | 10 | 0.0112 | 0.5399 | 0.8044 |
| Pure error | 0.083 | 4 | 0.0208 | ||
| Cor total | 28 | 28 |
| Factor Name | Model Coefficients |
|---|---|
| Constant term | −0.1798 |
| Flow | −1.0156 |
| Speed | −0.4545 |
| Self-cleaning flow rate | +0.8445 |
| Flow × speed | −0.2088 |
| Speed × self-cleaning flow rate | +0.1285 |
| Flow 2 | −0.2407 |
| Self-cleaning flow rate 2 | +0.6896 |
| Coefficient of determination, R2 | 0.9861 |
| Layer | Coefficient Estimate | Root Mean Square Error | 95% CI Low | 95% CI High |
|---|---|---|---|---|
| Intercept | −0.1798 | 1 | 0.0527 | −0.2929 |
| A-A flow | −1.02 | 1 | 0.034 | −1.09 |
| B-B speed | −0.4545 | 1 | 0.034 | −0.5275 |
| C-C self-cleaning flow rate | 0.8445 | 1 | 0.034 | 0.7715 |
| D-D initial sediment concentration | 0.0166 | 1 | 0.034 | −0.0564 |
| AB flow × speed | −0.2087 | 1 | 0.059 | −0.3352 |
| AC flow × self-cleaning flow | 0.062 | 1 | 0.059 | −0.0645 |
| AD flow × initial sediment concentration | −0.0055 | 1 | 0.059 | −0.132 |
| BC speed × self-cleaning flow | 0.1285 | 1 | 0.059 | 0.002 |
| BD speed × initial sediment concentration | 0.0638 | 1 | 0.059 | −0.0627 |
| CD self-cleaning flow × initial sediment concentration | −0.036 | 1 | 0.059 | −0.1625 |
| A flow 2 | −0.2407 | 1 | 0.0463 | −0.34 |
| B speed 2 | 0.0289 | 1 | 0.0463 | −0.0704 |
| C self-cleaning flow 2 | 0.6896 | 1 | 0.0463 | 0.5903 |
| D initial sediment concentration 2 | −0.0432 | 1 | 0.0463 | −0.1425 |
| Head Loss | A | B | C | AB | BC | A2 | C2 |
|---|---|---|---|---|---|---|---|
| −20.28 | −1.83667 | −0.82167 | 1.526667 | −0.3775 | 0.2325 | −0.43542 | 1.247083 |
| significance level | <0.0001 | <0.0001 | < 0.0001 | 0.0033 | 0.0467 | 0.0001 | <0.0001 |
| R2 | 0.9930 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Lei, C.; Li, J.; Long, Y.; Lu, C. A Standardized Treatment Model for Head Loss of Farmland Filters Based on Interaction Factors. Agriculture 2024, 14, 788. https://doi.org/10.3390/agriculture14050788
Liu Z, Lei C, Li J, Long Y, Lu C. A Standardized Treatment Model for Head Loss of Farmland Filters Based on Interaction Factors. Agriculture. 2024; 14(5):788. https://doi.org/10.3390/agriculture14050788
Chicago/Turabian StyleLiu, Zhenji, Chenyu Lei, Jie Li, Yangjuan Long, and Chen Lu. 2024. "A Standardized Treatment Model for Head Loss of Farmland Filters Based on Interaction Factors" Agriculture 14, no. 5: 788. https://doi.org/10.3390/agriculture14050788
APA StyleLiu, Z., Lei, C., Li, J., Long, Y., & Lu, C. (2024). A Standardized Treatment Model for Head Loss of Farmland Filters Based on Interaction Factors. Agriculture, 14(5), 788. https://doi.org/10.3390/agriculture14050788





